Abstract
Several researchers have recommended that level-specific fit indices should be applied to detect the lack of model fit at any level in multilevel structural equation models. Although we concur with their view, we note that these studies did not sufficiently consider the impact of intraclass correlation (ICC) on the performance of level-specific fit indices. Our study proposed to fill this gap in the methodological literature. A Monte Carlo study was conducted to investigate the performance of (a) level-specific fit indices derived by a partially saturated model method (e.g., and ) and (b) and in terms of their performance in multilevel structural equation models across varying ICCs. The design factors included intraclass correlation (ICC: ICC1 = 0.091 to ICC6 = 0.500), numbers of groups in between-level models (NG: 50, 100, 200, and 1,000), group size (GS: 30, 50, and 100), and type of misspecification (no misspecification, between-level misspecification, and within-level misspecification). Our simulation findings raise a concern regarding the performance of between-level-specific partial saturated fit indices in low ICC conditions: the performances of both and were more influenced by ICC compared with and SRMRB. However, when traditional cutoff values (RMSEA≤ 0.06; CFI, TLI≥ 0.95; SRMR≤ 0.08) were applied, and were still able to detect misspecified between-level models even when ICC was as low as 0.091 (ICC1). On the other hand, both and were not recommended under low ICC conditions.
Keywords: intraclass correlation, level-specific fit index, model evaluation, multilevel structural equation modeling
Introduction
Multilevel structural equation modeling (MSEM) has recently gained more attention from researchers because of its flexibility for modeling relationships between observed and latent variables with multilevel data (e.g., students nested within schools; patients nested within clinics). A general model specification approach to MSEM is between-and-within specification (Bollen, Bauer, Christ, & Edwards, 2010), which can be traced back to the work of Goldstein and McDonald (see, Goldstein & McDonald, 1988; McDonald & Goldstein, 1989). By applying this model specification method, the observed score covariance matrix for individual-level variables is decomposed into between-level and within-level variance-covariance matrices, which are then simultaneously described by hypothesized between-level and within-level models formulated based on theory or previous studies, respectively (Bollen et al., 2010; Hox, 2010; B. O. Muthén & Asparouhov, 2009; Rowe, 2003). Although MSEM specification can be implemented in several major SEM statistical packages such as EQS, Lisrel, and Mplus, there are still unresolved issues related to model evaluation which need more attention (Ryu, 2014).
Previous studies show that traditional single-level tests of exact fit (i.e., chi-square [χ2] test statistics) and fit indices (e.g., root mean square error of approximation [RMSEA], comparative fit index [CFI], and Tucker–Lewis Index [TLI]) fail to detect misspecifications in the between-level model (Hsu, Kwok, Acosta, & Lin, 2015; Ryu & West, 2009). Hence, some researchers advocate for greater use of level-specific χ2 and fit indices, in particular for detecting misspecifications at between level (Ryu, 2011; Ryu & West, 2009; Schermelleh-Engel, Kerwer, & Klein, 2014). While we concur with these researchers’ recommendations, we also note that these previous simulation studies did not sufficiently consider the impact of intraclass correlation (ICC; also referred to as observed variable ICC or latent factor ICC; we describe the two types of ICC in Appendix A). For example, Ryu (2011) and Ryu and West (2009) used an identical two-level two-factor measurement model as a population model to generate simulation data with the latent factor ICC fixed to 0.50, which is not realistic, especially in educational settings with relatively lower ICC in cross-sectional multilevel studies (Hox, 2010). In another example, Schermelleh-Engel et al. (2014) used a population model comprising nonlinear latent interaction effects to generate simulation data without manipulating ICC. These aforementioned studies tend to overlook the impact of ICC on the effectiveness of level-specific fit indices (especially for between-level model). Hsu et al.’s (2015) study is the only one which considers the impact of a wider range of ICC. However, they only considered the impact of ICC on “traditional” (single-level) fit indices including RMSEA, CFI, and TLI in MSEM and their simulation results showed a negligible effect of ICC on the effectiveness of traditional fit indices. The reason of this finding is due to the focus of the single-level fit indices and the performances of these fit indices can be overpowered by the within-level model misspecification. Hsu et al. did not extend their investigation to the assessment of the potential impact of ICC on the performance of level-specific fit indices.
The association between lower ICC and greater biased parameter estimates in the between-level model (Hox & Maas, 2001; Lai & Kwok, 2015; Lüdtke et al., 2008; Preacher, Zhang, & Zyphur, 2011) as well as the association between lower ICC and lower convergence rates (Kim, Kwok, & Yoon, 2012; Lüdtke et al., 2008) are well documented in the literature. Given these findings, we believe that ICC might be crucial to the performance of between-level–specific fit indices. This argument can be justified by recalling the features of χ2 in structural equation modeling. The overall model χ2 value reflects the discrepancy between the observed and model-implied variance–covariance matrices. Theoretically, given data with larger relations (or covariances) among observed variables, a misspecified model tends to have poorer model fit (e.g., larger χ2 value). The reason is that stronger relations among observed variables lead to larger values in the observed variance–covariance matrix, which allows greater possible discrepancies between itself and the model-implied variance–covariance matrix to be estimated (Bowen & Guo, 2011; Kenny, 2015; Kline, 2011). Similarly, data with a higher level of ICC imply larger relations in between-level variables including observed variables and latent components of lower-level variables, compared with data with a lower level of ICC. Therefore, fitting a misspecified between-level model using data with higher ICC should result in a larger between-level–specific χ2 value (see Appendix B for more information). Because between-level–specific RMSEA, CFI, and TLI are a function of between-level–specific χ2, theoretically, we anticipate that the performance of these fit indices will be influenced by ICC as well (i.e., better performance with high ICC while worse performance with low ICC).
As stated above, previous studies investigating the performance of level-specific χ2 and level-specific fit indices (Ryu, 2011; Ryu & West, 2009; Schermelleh-Engel et al., 2014) did not sufficiently consider the impact of ICC. Our study extended this line of research specifically by furthering Hsu et al.’s (2015) study with the focus on how the effectiveness of “level-specific” fit indices is affected by varying ICC values. We aim to provide better understanding of the utilization of level-specific fit indices in MSEM given data with different levels of ICC, which has not yet been thoroughly investigated in previous level-specific fit index studies.
To bridge this literature gap, we conducted a Monte Carlo study to evaluate the effectiveness of level-specific fit indices derived from the partially saturated model method (PS-level–specific fit indices; Ryu & West, 2009) with the consideration of a more comprehensive range of ICCs in MSEM. Additionally, we also attempted to extend the understanding of model evaluation in MSEM by examining the performance of alternative level-specific fit indices obtained from Mplus, namely standardized root mean square residual for within-level model (SRMRW) and for between-level model (SRMRB), which have not yet been compared with other PS-level–specific fit indices under various ICCs in the previous literatures.
Our study addressed the following research questions:
Can the PS-level-specific fit indices (, , , ,, and ) consistently detect the lack of model fit at different data levels under various ICCs?
What is the performance of both and compared with other PS-level-specific fit indices under various ICCs?
Literature Review
Multilevel Structural Equation Model
Using similar notations as B. O. Muthén (1994) and Pornprasertmanit, Lee, and Preacher (2014), we outline a two-level confirmatory factor analysis (CFA) model with continuous indicators, which has also been the population model for data generation in this study. Let denote p-dimensional response vector for student i in school In MSEM, is decomposed into means, within-, and between-level components as shown in Equation (1):
where is a p-dimensional vector of grand means, is a p×m within-level factor loading matrix, where m indicates the number of within-level factors, is a m-dimensional vector of within-level factor scores for student i in school , is a p×h between-level factor loading matrix, where h indicates the number of between-level factors, is a h-dimensional vector of between-level factor scores for school , is a p-dimensional vector of within-level unique factors, and is a p-dimensional vector of between-level unique factors. Based on Equation (1), the covariance structure of can be decomposed into two orthogonal and additive components (Hox, 2010):
where is the total covariance matrix, is the within-level covariance matrix representing within-school, student-level variation, and is the between-level covariance matrix representing across-school variation (B. O. Muthén, 1994). Finally, the within- and between-level covariance structures of a two-level CFA model can be written as
where and are the factor covariance matrices for the within- and between-level components, respectively, and and are covariance matrices of unique factors for the within- and between-level components, respectively.
In the current study, we used a multilevel full information maximum likelihood (ML) estimator, which is commonly adopted by substantial studies for analyzing multilevel data (Kaplan, 2009; Liang & Bentler, 2004; Ryu & West, 2009). Assuming (a) multivariate normality for each of the within- and between-level component and (b) perfectly balanced case in which each group had equal individuals, the fitting function to obtain ML solution is expressed as
The fitting function involved between-level fitting function, , and within-level fitting function, , where is defined in terms of the vector of the estimated parameters that correspond to a specified model. In , is the between-level sample size (number of group); is the scaled between sample covariance matrix; is the implied scaled between covariance matrix; is the within-level total sample size. is the within-level sample covariance matrix, and is the implied within-level covariance matrix.
This full information ML estimator is implemented in Mplus (L. K. Muthén & Muthén, 1998-2015) by using the command “ESTIMATOR=MLR” in the current study. MLR and ML share the same fitting function and produce the same parameter estimates (Hox, Maas, & Brinkhuis, 2010), but MLR produces robust χ2 test statistic instead of traditional asymptotic χ2 test statistic. All the fit indices in the present simulation study were derived by using the robust χ2 value in the corresponding fit indices formulas as shown in Appendix B.
Level-Specific Fit indices
Two alternative methods can be applied for obtaining level-specific χ2 test statistics or fit indices: Yuan and Bentler’s (2007) segregating approach (YB method), and the PS model method. Note that only the PS method was considered in the current study because Ryu and West (2009) have demonstrated that the PS method outperforms the YB method in terms of convergence rates and Type I error rates. Furthermore, the performance of YB-level–specific fit indices has been evaluated in Schweig’s (2014) study.
In the PS method, a saturated model at a particular data level can be obtained by correlating all the observed variables and allowing all the covariances (or correlations) to be freely estimated. A saturated model can be treated as a just-identified model with zero degrees of freedom and the χ2 test statistic equals zero. Therefore, a saturated within-level or between-level model contributes nothing to the fitting function (Hox, 2010). This feature allows us to compute different fit indices at each level. For example, if one intends to evaluate the hypothesized between-level model, a saturated within-level model should be specified so that any misfit can be attributed to the possible misspecification at the between level. In other words, the fitting function only reveals between-level model misfit (i.e., ), which then can be used to compute χ2 for a between-level model (). In the same manner, χ2 for a within-level model () can be obtained by specifying the hypothesized within-level model and a saturated between-level model.
Few simulation studies have evaluated the promising sensitivity of PS-level–specific fit indices (Ryu, 2011; Schermelleh-Engel et al., 2014). Consequently, some researchers have recommended using PS-level–specific fit indices to evaluate the plausible misspecifications present in the specific level (Pornprasertmanit et al., 2014; Ryu, 2014). Nevertheless, it should be noted that previous simulations did not sufficiently consider the impact of ICC. The present study aims to fill this gap in the literature by investigating performance of PS-level–specific fit indices across a variety of ICC levels. The equations of the PS-level–specific fit indices as well as SRMRW and SRMRB are presented in Appendix B.
The Role of ICC in the Performance of Traditional and Level-Specific Fit Indices
The impact of ICC on the performance of “traditional” (single-level) fit indices, including RMSEA, CFI, and TLI in MSEM has been investigated in Hsu et al.’s (2015) study, where ICC was manipulated by varying the variation at the between level and fixing variation at the within level (three conditions: 0.16, 0.33, and 0.50). Hsu et al. (2015) found ICC had no substantial impact on the effectiveness of traditional fit indices. The major reason that Hsu et al. (2015) did not find ICC as an important factor is that the traditional single-level fit indices were the main focus and the performance of these traditional fit indices was in general overpowered by the within-level model misspecification.
On the other hand, the actual performance of the “level-specific” fit indices and the potential impact of ICC on the sensitivity of these level-specific fit indices have never been thoroughly studied. As we argued above, the between-level–specific χ2 is affected by the magnitude of the relations among the variables in the model (Bowen & Guo, 2011; Kenny, 2015). When a between-level model is misspecified, data with stronger relations among the variables at between-level (i.e., higher ICC condition) allow for possibly “greater” discrepancies between the model-implied and observed variance–covariance matrices (Kline, 2011). Hence, with an identical type of misspecification and sample size in the between-level model, would likely increase (i.e., more likely to reflect the misspecification) when ICC increased. The change in would lead to a change in the performance of between-level–specific fit indices. On the other hand, all the within-level–specific fit indices (e.g., , , and ) would generally not be influenced by the ICC given that the variation at the within level was held constant across the ICC conditions.
Regarding the performance of SRMR in MSEM, we hypothesized SRMRB would also be influenced by ICC. Note that SRMR is solely derived from the deviation between the observed variance–covariance matrix and the model-implied variance–covariance matrix. Given an identical type of misspecification and sample size in the between-level model, we suspected that the deviation between these two matrices would decrease when ICC decreased, which would lead to a less sensitive SRMRB. Alternatively, SRMRW was expected to be independent of ICC given our manipulation of the ICC conditions (with fixed variances and covariances at the within level).
Method
Following the protocol developed by Ryu and West (2009), we conducted a Monte Carlo study to evaluate the performance of level-specific fit indices produced by the PS method (, , , , , and ) for detecting misspecification in two-level models with varying levels of ICC. In addition, the effectiveness of SRMRW and SRMRB was also examined and compared with that of level-specific fit indices.
Data Generation
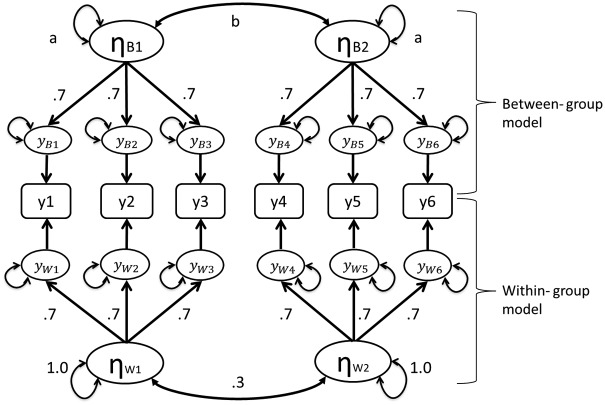
In the current study, the population model (see Figure 1) for simulation data generation was based on the population model presented in Ryu and West’s (2009) study. The population model was a two-level measurement model with two factors (ηW1 and ηW2) at the within level and two factors (ηB1 and ηB2) at the between level. In the within-level model, three continuous observed indicators were loaded on ηW1, while the other three indicators were loaded on ηW2. Parameters in the within-level model for generating data were as follows: factor loadings = 0.70, residual variances = 0.51, factor variances = 1.00, and factor covariance = 0.30. Factors and residual variances were uncorrelated with each other. Note that the covariance and correlation of two within-level factors were identical (.30) because variances of within-level factors were fixed at 1.00.
Figure 1.
The population model (true model; ModelC) for generating simulation data sets. In the within-level model, factor loadings = 0.7, residual variances = 0.51, factor variances = 1.0, and correlation between factors = 0.3. The between-level model shared the same factor structure and parameter settings as the within-level model, except that the factor variance a was set to 1.00 and varied from 0.10 to 0.50 and factor covariances b were equal to 0.30 given the intention to retain the magnitude of between-level factor correlation to be the same (0.3) across different ICC conditions.
The between-level model had an identical factorial structure with the within-level model. Between-level parameters for data generating are presented as follows: factor loadings = 0.70, residual variances = 0.51. Factors and residuals were uncorrelated with each other. To create different ICC conditions, variance of between-level factors (“a” shown in Figure 1) was set to 1.00 and varied within the range of 0.10 to 0.50 (six conditions). More detail regarding the manipulation of ICC is presented in the following subsection.
The present study applied the Monte Carlo procedure in Mplus 7.0 (L. K. Muthén & Muthén, 1998-2015). Data sets were generated from a standard multivariate normal distribution using a randomly chosen seed. The MLR was applied to obtain the model solutions. The simulation design factors are defined next.
Simulation Design Factors
Four design factors were considered in this study. These comprised (a) intraclass correlation, (b) number of groups, (c) group size, and (d) misspecification type. The details of these design factors are described below.
Intraclass Correlation (ICC)
We took the potential impact of ICC into account when designing the current simulation study (see Table 1). Note that the population model in the present simulation study had exactly the same model structure applied to both between-level and within-level models. Therefore, following the common practice in previous simulation studies, we constrained the variance of the within-level latent factors to 1.00 while varied the variance of the between-level factors to create different ICC conditions (i.e., latent factor ICC; Bollen et al., 2010; B. O. Muthén, 1991), which has also been considered in prior MSEM simulation studies (e.g., Hox & Maas, 2001; Kim et al., 2012; Wu & Kwok, 2012). In our simulation, the variances a of the between-level factors (see Figure 1) were 0.10, 0.20, 0.30, 0.40, 0.50, and 1.00, which resulted in six different ICC levels: 0.091 (ICC1), 0.167 (ICC2), 0.231 (ICC3), 0.286 (ICC4), 0.333 (ICC5), and 0.500 (ICC6). These latent factor ICCs could be converted to observed variable ICCs (see Appendix A). Ryu and West’s simulation study only considered the ICC6 condition, which limited the generalization of their research findings. The influence of ICC discussed in the current study referred to latent factor ICC rather than observed variable ICC.
Table 1.
Parameters for Data Generating in Between-Level Population.
| ICC condition | Factor variance | Latent factor ICC | Factor covariance |
|---|---|---|---|
| ICC1 | 0.1 | 0.091 | 0.03 |
| ICC2 | 0.2 | 0.167 | 0.06 |
| ICC3 | 0.3 | 0.231 | 0.09 |
| ICC4 | 0.4 | 0.286 | 0.12 |
| ICC5 | 0.5 | 0.333 | 0.15 |
| ICC6 | 1.0 | 0.500 | 0.30 |
Note. ICC = intraclass correlation. We manipulated the between-level factor variance to create different levels of latent factor ICC (ICC1-ICC6). In order to confine the factor correlation to 0.30 across different ICC models, the factor covariance was adjusted in corresponding to the magnitude of factor variance.
Number of Groups (NG)
Hox and Maas (2001) concluded that a large NG (i.e., larger than 100 groups/clusters) would be needed for an acceptable estimate of a between-level model with low ICC conditions. Moreover, based on traditional single-level SEM literature, a recommended minimum sample size for obtaining unbiased and consistent estimates is 200 when using the ML estimation method (Boomsma, 1987; Loehlin, 2004). Ryu and West (2009) considered NG = 50, 100, 200, and 1,000 in their simulation study: however, more serious and common nonconvergence problems occurred with NG = 50, which was consistent with Hox and Maas’s findings. Considering that NG = 1,000 might be unrealistic for practical studies, we adopted three NG conditions (i.e., 100, 200, and 500 groups) to evaluate whether NG affected the performance of level-specific fit indices when detecting model misspecification.
Group Size (GS)
Ryu and West (2009) considered GS = 30, 50, and 100 in their simulation study. Hox and Maas’ (2001) study adopted three levels of GS (i.e., 10, 20, and 50) and discovered that GS was not an influential design factor for the accuracy of the parameter estimates and standard errors in MSEM. Considering the complexity of simulation design, our simulation study adopted three GS levels (30, 50, and 100).
Misspecification Type (MT)
Three model misspecification conditions were considered by Ryu and West (2009): correct (non-misspecified) model (ModelC), misspecification in between-level model only (ModelB), and misspecification in within-level model only (ModelW). ModelC was the same as the population model (see Figure 1). ModelB as shown in the top of Figure 2 indicated that the between-level model was misspecified as a single-factor model, while the within-level model was correctly specified as a two-factor model. ModelW as shown in the bottom of Figure 2 indicated that the within-level model was misspecified as a single-factor model, while the between-level model was correctly specified as a two-factor model.
Figure 2.
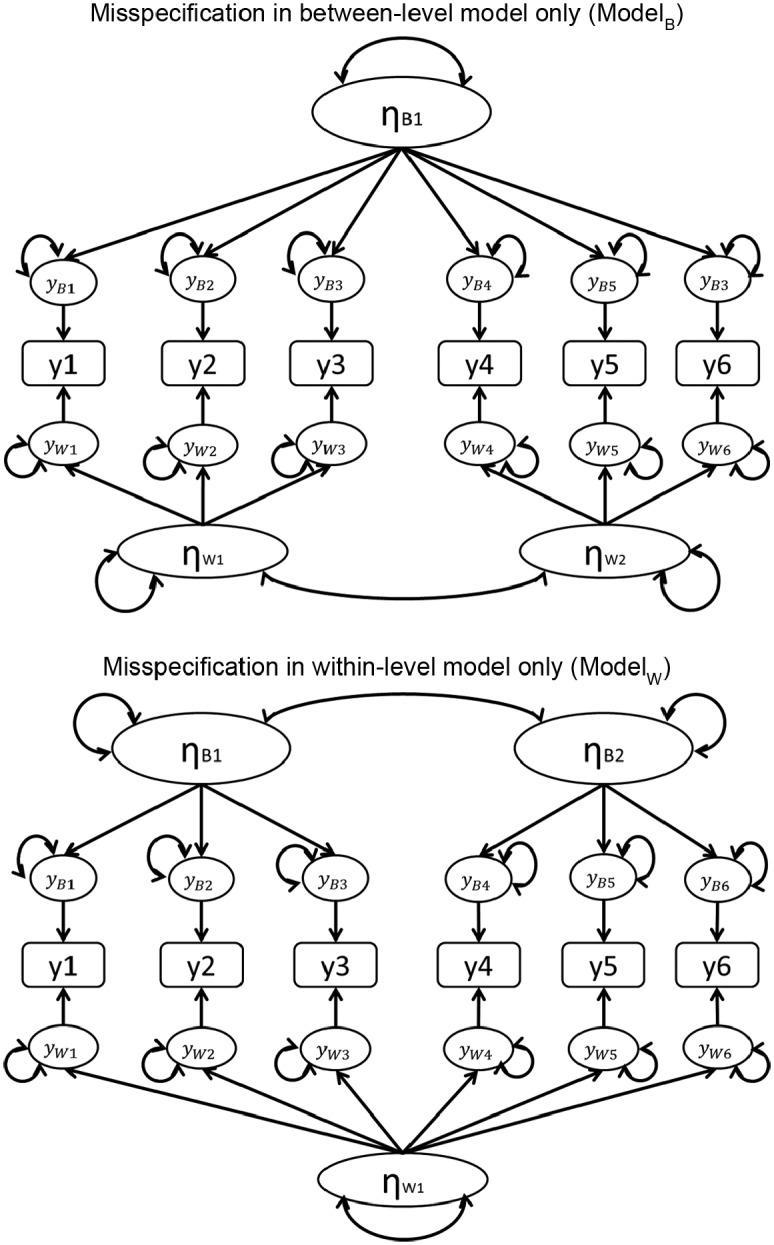
An illustration of mispecified two-level model (ModelW and ModelB).
Other Considerations
As previously mentioned, we manipulated the variances of between-level factors to create different levels of latent factor ICC (ICC1-ICC6). Yet the manipulation of between-level variances would also alter the correlations of between-level factors. Given our intention to retain the magnitude of between-level factor correlation to be the same (0.3) across different ICC conditions, we adjusted the between-level factor covariance (see “b” shown in Figure 1) based on the formula: 0.30 . For example, in the ICC1 condition, the adjusted between-factor covariance in the population model can be obtained by 0.30 , which was 0.03. Table 1 explicitly presents the values of between-level factor variance for manipulating: (a) ICC, (b) the corresponding latent factor ICC, and (c) the adjusted factor covariances under different ICC conditions.
Analysis
The four design factors included in this study were intraclass correlation (ICC: ICC1 to ICC6), number of group in between levels (NG: 100, 200, and 500), group sizes (GS: 30, 50, and 100), and misspecification type (MT: ModelC, ModelB, and ModelW). Factors were integrated into 162 conditions (6 ICC × 3 NG × 3 GS × 3 MT). For each condition, replications with convergence problems were excluded until at least 1,000 replications were generated. The parameter estimates, convergence information, and corresponding fit indices were saved for subsequent analyses. Means and standard deviations of each fit index were reported. If needed, factorial ANOVAs were conducted to determine the impact of the design factors on the effectiveness of the targeted fit indices. The total sum of squares (SOS) of each fit index showed the variability of the corresponding fit index across all replications under specific simulation conditions while eta-square (η2) indicated the proportion of the variance accounted for by a particular design factor or the interaction effect terms. Notably, η2 was obtained by dividing the Type III SOS of a particular predictor or the interaction effect by the corrected total SOS.
Results
Convergence Rates
Table 2 shows the results of convergence rates for each simulation scenario except for ICC5 and ICC6 with convergence rates equal to 100%. Generally speaking, convergence rates were positively associated with ICC. Convergence rates were close to 95% or higher when ICC was as large as 0.286 (ICC4). In ICC1, ICC2, and ICC3 conditions, sample size in the between-level model (number of groups, NG) was a more influential factor on convergence rates, compared with sample size in the within-level model (group size, GS). Note 1,000 replications without convergence problems were included for the analyses.
Table 2.
Results of Convergence Rates.
|
NG = 100; GS = 30 |
NG = 100; GS = 50 |
NG = 100; GS = 100 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | ICC1 | ICC2 | ICC3 | ICC4 | ICC1 | ICC2 | ICC3 | ICC4 | ICC1 | ICC2 | ICC3 | ICC4 |
| BC/WC | 50.63 | 77.63 | 75.83 | 97.58 | 51.87 | 76.77 | 92.13 | 97.67 | 57.73 | 79.70 | 93.63 | 98.50 |
| BC/WS | 50.53 | 77.57 | 92.57 | 97.50 | 52.30 | 77.80 | 93.80 | 98.25 | 60.87 | 81.93 | 93.80 | 98.25 |
| BS/WC | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| BM/WC | 60.60 | 79.13 | 89.50 | 92.67 | 60.53 | 79.90 | 89.20 | 94.42 | 60.97 | 81.63 | 90.87 | 95.25 |
| BM/WS | 59.80 | 79.43 | 89.30 | 93.08 | 60.67 | 79.90 | 89.20 | 94.17 | 60.50 | 81.33 | 90.80 | 95.25 |
| BC/WM | 52.63 | 80.07 | 93.47 | 97.33 | 53.13 | 78.80 | 92.37 | 97.58 | 55.83 | 78.40 | 92.13 | 97.75 |
| BS/WM | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
|
NG = 200; GS = 30 |
NG = 200; GS = 50 |
NG = 200; GS = 100 |
||||||||||
| Model | ICC1 | ICC2 | ICC3 | ICC4 | ICC1 | ICC2 | ICC3 | ICC4 | ICC1 | ICC2 | ICC3 | ICC4 |
| BC/WC | 60.53 | 92.13 | 99.33 | 99.92 | 61.33 | 93.63 | 99.27 | 100.00 | 67.07 | 92.70 | 99.50 | 100.00 |
| BC/WS | 60.53 | 92.30 | 99.37 | 99.92 | 60.77 | 93.60 | 99.33 | 100.00 | 67.90 | 92.90 | 99.53 | 100.00 |
| BS/WC | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| BM/WC | 70.00 | 89.30 | 95.23 | 98.17 | 71.80 | 91.87 | 96.83 | 98.50 | 72.17 | 91.63 | 96.87 | 98.42 |
| BM/WS | 70.00 | 89.37 | 95.23 | 98.17 | 72.20 | 91.97 | 96.87 | 98.42 | 72.30 | 91.47 | 96.80 | 98.58 |
| BC/WM | 64.77 | 93.40 | 99.90 | 99.75 | 63.73 | 93.50 | 99.13 | 99.83 | 63.17 | 88.83 | 97.47 | 99.25 |
| BS/WM | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
|
NG = 500; GS = 30 |
NG = 500; GS = 50 |
NG =500; GS =100 |
||||||||||
| Model | ICC1 | ICC2 | ICC3 | ICC4 | ICC1 | ICC2 | ICC3 | ICC4 | ICC1 | ICC2 | ICC3 | ICC4 |
| BC/WC | 83.60 | 99.80 | 99.97 | 100.00 | 86.10 | 99.87 | 100.00 | 100.00 | 86.97 | 99.77 | 100.00 | 100.00 |
| BC/WS | 84.00 | 99.83 | 99.97 | 100.00 | 86.33 | 99.87 | 100.00 | 100.00 | 84.77 | 99.27 | 100.00 | 100.00 |
| BS/WC | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| BM/WC | 85.03 | 97.83 | 99.50 | 99.83 | 87.37 | 98.23 | 99.67 | 99.92 | 86.87 | 98.60 | 99.87 | 99.92 |
| BM/WS | 85.07 | 97.80 | 99.50 | 99.92 | 87.20 | 98.20 | 99.70 | 99.92 | 86.80 | 98.53 | 99.87 | 99.92 |
| BC/WM | 86.07 | 99.80 | 99.90 | 100.00 | 87.20 | 98.93 | 99.87 | 99.83 | 80.47 | 93.23 | 97.97 | 99.50 |
| BS/WM | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
Note. ICC = intraclass correlation. All values in percentage. Convergence rates were computed based on total replication = 1,000. NG is group number; GS is group size. B and W denote between-level and within-level models, respectively. Subscripts C, S, and M denote correctly specified, saturated, and misspecified models, correspondingly.
Means of 2 Test Statistic and Model Fit Indices
Correct Model (Modelc)
Table 3 shows: (a) traditional χ2 test statistics, CFI, TLI, and RMSEA for the entire model; (b) χ2 test statistics and fit indices derived by the PS method; and (c) SRMR for between-level and within-level models obtained from Mplus. The pattern of the results was consistent through all sample size combinations in terms of the performance of χ2 test statistics and model fit indices. Therefore, we present the means of χ2 test statistics and model fit indices under the condition NG = 500 and GS = 100 across six levels of ICC conditions.
Table 3.
Means of Chi-Square Test Statistics and Model Fit Indices for the ModelC, ModelB, and ModelW (NG = 500, GS = 100).
| ICC1 = 0.091 | ICC2 = 0.167 | ICC3 = 0.231 | ICC4 = 0.286 | ICC5 = 0.333 | ICC6 = 0.500 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | B | W | T | B | W | T | B | W | T | B | W | T | B | W | T | B | W | |
| ModelC | ||||||||||||||||||
| CHI | 17.062 (7.893) |
9.000 (6.773) |
7.910 (3.860) |
15.990 (6.101) |
8.440 (5.078) |
7.976 (3.951) |
16.174 (5.941) |
8.225 (4.208) |
8.034 (3.982) |
15.733 (5.777) |
8.160 (4.192) |
7.744 (3.951) |
15.762 (5.620) |
8.168 (4.212) |
7.723 (4.017) |
15.947 (5.697) |
8.124 (4.100) |
7.765 (3.945) |
| Rejection rate (%) | 7.5 | 10.2 | 3.8 | 5.6 | 8.3 | 4.1 | 5.6 | 6.3 | 4.2 | 4.9 | 5.7 | 3.9 | 4.7 | 5.4 | 4.2 | 5.2 | 5.4 | 3.9 |
| RMSEA | 0.001 (0.002) |
0.014 (0.019) |
0.001 (0.002) |
0.001 (0.001) |
0.013 (0.018) |
0.001 (0.002) |
0.001 (0.001) |
0.013 (0.017) |
0.001 (0.002) |
0.001 (0.001) |
0.012 (0.017) |
0.001 (0.002) |
0.001 (0.001) |
0.012 (0.016) |
0.001 (0.002) |
0.001 (0.001) |
0.012 (0.016) |
0.001 (0.002) |
| CFI | 1.000 (0.000) |
0.919 (0.146) |
1.000 (0.000) |
1.000 (0.000) |
0.973 (0.059) |
1.000 (0.000) |
1.000 (0.000) |
0.988 (0.022) |
1.000 (0.000) |
1.000 (0.000) |
0.992 (0.014) |
1.000 (0.000) |
1.000 (0.000) |
0.994 (0.010) |
1.000 (0.000) |
1.000 (0.000) |
0.998 (0.004) |
1.000 (0.000) |
| TLI | 1.000 (0.000) |
0.851 (0.250) |
1.000 (0.000) |
1.000 (0.000) |
0.950 (0.101) |
1.000 (0.000) |
1.000 (0.000) |
0.977 (0.041) |
1.000 (0.000) |
1.000 (0.000) |
0.985 (0.027) |
1.000 (0.000) |
1.000 (0.000) |
0.989 (0.019) |
1.000 (0.000) |
1.000 (0.000) |
0.995 (0.008) |
1.000 (0.000) |
| SRMRB | 0.025 (0.006) |
— | — | 0.025 (0.007) |
— | — | 0.024 (0.006) |
— | — | 0.023 (0.006) |
— | — | 0.023 (0.006) |
— | — | 0.020 (0.006) |
— | — |
| SRMRW | 0.002 (0.000) |
— | — | 0.002 (0.000) |
— | — | 0.002 (0.001) |
— | — | 0.002 (0.001) |
— | — | 0.002 (0.001) |
— | — | 0.002 (0.001) |
— | — |
| ModelB | ||||||||||||||||||
| CHI | 24.489 (13.413) |
20.464 (49.147) |
— | 43.203 (22.957) |
39.518 (47.645) |
— | 74.986 (72.725) |
73.511 (56.685) |
— | 104.106 (65.547) |
117.221 (99.365) |
— | 140.121 (68.653) |
157.037 (101.565) |
— | 305.937 (49.380) |
331.263 (71.399) |
— |
| Rejection rate | 27.80 | 41.1 | — | 85.00 | 94.8 | — | 99.60 | 100 | — | 100 | 100 | — | 100 | 100 | — | 100 | 100 | — |
| RMSEA | 0.002 (0.002) |
0.031 (0.022) |
— | 0.005 (0.002) |
0.072 (0.021) |
— | 0.008 (0.002) |
0.108 (0.022) |
— | 0.010 (0.002) |
0.140 (0.024) |
— | 0.012 (0.002) |
0.168 (0.024) |
— | 0.018 (0.001) |
0.265 (0.021) |
— |
| CFI | 1.000 (0.000) |
0.754 (0.204) |
— | 1.000 (0.001) |
0.661 (0.156) |
— | 0.999 (0.000) |
0.616 (0.132) |
— | 0.999 (0.001) |
0.580 (0.123) |
— | 0.998 (0.001) |
0.560 (0.112) |
— | 0.996 (0.001) |
0.532 (0.064) |
— |
| TLI | 1.000 (0.001) |
0.592 (0.329) |
— | 0.999 (0.001) |
0.441 (0.248) |
— | 0.999 (0.002) |
0.367 (0.207) |
— | 0.998 (0.002) |
0.310 (0.186) |
— | 0.997 (0.002) |
0.275 (0.168) |
— | 0.993 (0.001) |
0.222 (0.101) |
— |
| SRMRB | 0.034 (0.008) |
— | — | 0.051 (0.010) |
— | — | 0.068 (0.010) |
— | — | 0.083 (0.011) |
— | — | 0.097 (0.011) |
— | — | 0.150 (0.013) |
— | — |
| SRMRW | 0.002 (0.001) |
— | — | 0.002 (0.001) |
— | — | 0.002 (0.001) |
— | — | 0.002 (0.001) |
— | — | 0.002 (0.001) |
— | — | 0.002 (0.001) |
— | — |
| ModelW | ||||||||||||||||||
| CHI | 31650 (947) | — | 35354 (1714) | 31495 (832) | — | 35428 (1741) | 31356 (808) | — | 35424 (1694) | 31228 (831) | — | 35373 (1704) | 31172 (835) | — | 35391 (1713) | 31096 (818) | — | 35363 (1677) |
| Rejection rate (%) | 100 | — | 100 | 100 | — | 100 | 100 | — | 100 | 100 | — | 100 | 100 | — | 100 | 100 | — | 100 |
| RMSEA | 0.193 (0.003) |
— | 0.282 (0.007) |
0.192 (0.003) |
— | 0.282 (0.007) |
0.192 (0.002) |
— | 0.282 (0.007) |
0.192 (0.003) |
— | 0.282 (0.007) |
0.191 (0.003) |
— | 0.282 (0.007) |
0.191 (0.003) |
— | 0.282 (0.007) |
| CFI | 0.536 (0.014) |
— | 0.481 (0.023) |
0.540 (0.011) |
— | 0.482 (0.023) |
0.543 (0.011) |
— | 0.482 (0.023) |
0.545 (0.011) |
— | 0.482 (0.023) |
0.546 (0.010) |
— | 0.482 (0.023) |
0.550 (0.010) |
— | 0.482 (0.023) |
| TLI | 0.182 (0.025) |
— | 0.135 (0.038) |
0.188 (0.020) |
— | 0.136 (0.039) |
0.193 (0.019) |
— | 0.136 (0.039) |
0.196 (0.019) |
— | 0.136 (0.038) |
0.199 (0.018) |
— | 0.136 (0.039) |
0.205 (0.018) |
— | 0.136 (0.038) |
| SRMRB | 0.023 (0.006) |
— | — | 0.024 (0.006) |
— | — | 0.024 (0.006) |
— | 0.023 (0.006) |
— | — | 0.023 (0.006) |
— | — | 0.020 (0.006) |
— | — | |
| SRMRW | 0.153 (0.001) |
— | — | 0.153 (0.001) |
— | — | 0.153 (0.001) |
0.153 (0.001) |
— | — | 0.153 (0.001) |
— | — | 0.153 (0.001) |
— | — | ||
Note. CHI = mean of model chi-square test statistics value; CFI = comparative fit index; TLI = Tucker–Lewis Index; RMSEA = root mean square error of approximation; SRMR = standardized root mean square residual. For between-level model (B) and for within-level model (W), a partially saturated model method was applied to compute χ2 test statistics value, CFI, TLI, and RMSEA separately. SRMR for between- and within-level models was obtained from Mplus. We do not present the decimals of CHI under ModelW condition to facilitate presenting all information in one table.
In the Modelc condition, the mean of test statistic approximated the degrees of freedom across different ICC conditions (df = 16 for the entire model [T]; df = 8 for the between-level model [B] and within-level model [W], respectively). For each ICC condition, it should be noted that the value of was approximately equal to the sum of , and . For example, when ICC = 0.500 (ICC6), the value of was 15.947, which was nearly the sum of (8.124), and (7.765). The rejection rate (i.e., Type I error rate) of was close to 5.0% (ranged from 4.7% to 5.6%) across ICC2 to ICC6 conditions, but was slightly inflated (7.5%) in ICC1. Additionally, Type I error rates of were satisfied (ranged from 3.9% to 4.2%) across various ICC conditions, while Type I error rates of exceeded 6.0% across ICC1 to ICC3 conditions.
Considering different ICC conditions, the mean CFI and TLI values for the entire model were approximately 1.000 with trivial SDs, while the mean RMSEA values for the entire model were close to 0.001 with trivial SDs. These three global fit indices correctly indicated good overall model fit. Moreover, the within-level specific fit indices, CFIPS_W, TLIPS_W, and RMSEAPS_W, also correctly indicated good within-level model fit across all ICC conditions
Regarding the between-level specific fit indices, we found the mean RMSEAPS_B varied slightly (range from 0.012 to 0.014) across ICC conditions. However, mean CFIPS_B, and TLIPS_B varied associated with the level of ICC. The mean of CFIPS_B was 0.998 in ICC6 and 0.919 in ICC1 and the change rate was 7.92% [= (0.998 − 0.919)/0.998)]. Alternatively, the mean of TLIPS_B was 0.995 in ICC6 and 0.851 in ICC1 and the change rate was 14.47% [= (0.995 − 0.0.851)/0.995)]. Both CFIPS_B, and TLIPS_B were less promising for correctly identifying good between-level model fit especially when ICC was 0.091 (ICC1). Finally, the means of SRMRB (ranged from 0.020 to 0.025) and SRMRW (0.002) were capable of indicating good between-level and within-level model fit, respectively.
Misspecified Between-Level Model (ModelB)
Table 3 presents the values of traditional and between-level-specific across various ICC scenarios under ModelB condition. Note the values of and decreased (i.e., less likely to detect the misspecified between-level model) when ICC became smaller. The statistical power of was more than 99% in ICC3 through ICC6 and dropped down to 85.00% and 27.80% in ICC2 and ICC1, respectively. On the other hand, the statistical power of was 100% in ICC 3-ICC6, shrank a little to 94.8% in ICC2, and became very low (41.1%) in ICC1. The means of traditional and were close to 1.000 and the means of traditional ranged from 0.002 to 0.018 across various ICC scenarios, which incorrectly indicated goodness-of-fit for the between-level model.
In terms of the performance of between-level-specific fit indices, we found (ranged from 0.031 to 0.265), (ranged from 0.532 to 0.754), and (ranged from 0.222 to 0.592) did vary associated with the level of ICC. Similarly, mean also changed in different ICC conditions. We present the means of , , and as well as across various ICC conditions in Figure 3 for comparison. Generally speaking, these level-specific fit indices were less promising for detecting misspecified between-level models as ICC decreased. Among these fit indices, changed most dramatically, followed by . The value of was 0.222 in ICC6 and 0.592 in ICC1 and the change rate was -166.67% [= (0.222 − 0.592)/0.222)]. was 0.265 in ICC6 and 0.031 in ICC1 and the change rate was 88.30% [= (0.265 − 0.031)/0.265)]. The change rates between ICC6 and ICC1 for (77.33%) and (−41.73%) were relatively small among targeted fit indices.
Figure 3.
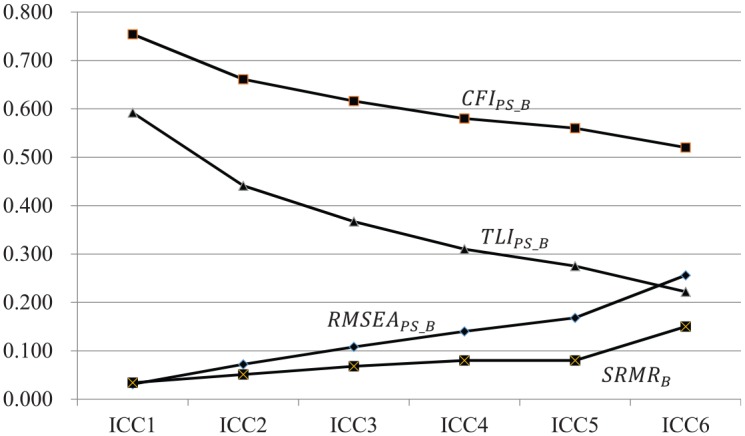
The mean , , and in different ICC conditions under Misspecified between-level model (ModelB) condition.
Since ICC was found to be an influential factor on the performance of between-level-specific fit indices, we further conducted factorial ANOVAs to compare the impact of the ICC with other design factors, number of groups (NG) and group size (GS). We first found that design factors had similar impacts on and . For , the eta-squares () of ICC, NG, GS, and all interaction terms were 17.48%, 3.74%, 0.01%, and 0.46%, respectively. For , the of ICC and NG was 17.96% and 3.92%, respectively and other were less than 0.30%. Furthermore, we found ICC accounted for around 80.00% of total SOS of (= 80.65%) and (= 80.29%), whereas other factors and interaction terms jointly accounted for less than 2.00% for both fit indices. The results indicated ICC was a most influential factor for all between-level-specific fit indices.
Misspecified Within-Level Model (ModelW)
The empirical power (rejection rate) of and were equal to 100% across different ICC conditions. The means of (range 0.536 to 0.550) and (0.481 to 0.482) varied slightly across various ICC conditions. Results suggested and correctly indicated poor model fit and ICC had trivial impact on them. These findings can also be applied to (and ) and (and ). In short, the traditional fit indices performed similarly as level-specific fit indices in terms of the sensitivities to misspecified within-level models. Moreover, the means of was 0.153 with small SDs across all ICC scenarios, which correctly indicated poor model fit.
Summary
This study investigated the performance of (a) PS-level-specific fit indices (, , , , , and ) and (b) and in terms of their performance in MSEM across varying ICCs. The design factors for the Monte Carlo study were type of misspecification (no misspecification, between-level misspecification, and within-level misspecification), numbers of groups in between-level models (NG: 50, 100, 200, and 1000), group size (GS: 30, 50, and 100), and intra-class correlation (ICC: ICC1 = 0.091 to ICC6 = 0.500). Under the ModelC scenario (correct model), simulation results showed that all within-level–specific fit indices (, , and ) were barely influenced by ICC. Therefore, we concluded within-level–specific fit indices were promising for correctly indicating good model fit regardless of ICC level. Considering the performance of between-level-specific fit indices, we found and were only slightly affected by ICC and capable of correctly indicating good model fit across various ICC conditions. Conversely, the impact of ICC on and was relatively larger. Both indices tended to be less promising for indicating good model fit when ICC decreased. Based on the traditional cutoff values (CFI, TLI≥ 0.95; Hu & Bentler, 1999), and are not recommended if ICC is small as 0.091.
Furthermore, under the ModelB scenario (misspecification in between-level model only), the means of between-level-specific fit indices, such as , , , and , varied with the level of ICC. As shown in Figure 3, we found that those fit indices were less promising in correctly indicating poor model fit of the between-level model as ICC decreased (i.e., from ICC6 to ICC1). Among these between-level-specific fit indices, had the greatest change associated with ICC, followed by , , and . Based on the traditional cutoff values (RMSEA≤ 0.06; CFI, TLI≥ 0.95; SRMR≤ 0.08; Hu & Bentler, 1999), and are still recommended even though they were dramatically influenced by ICC. However, and should be interpreted carefully if ICC is as low as 0.091 (ICC1 for ) and 0.231 (ICC 3 for ), respectively.
Finally, under the ModelW scenario (misspecification in within-level model only), we found the performance of within-level-specific fit indices, such as , , , and , was barely influenced by ICC. All these level-specific fit indices are recommended for detecting misspecified within-level models in MSEM.
Discussion
Based on our simulation results, this article raises concerns about the performance of between-level–specific fit indices especially under low ICC conditions. Figure 3 presents the means of between-level–specific fit indices related to ICC. The results indicated that between-level-specific fit indices became less promising for detecting misspecifications in between-level models when ICC decreased. Apparently, and were more sensitive to ICC compared to and , which showed a relatively large rate of change from ICC6 to ICC1. Yet, if traditional cutoff values (RMSEA≤ 0.06; CFI, TLI≥ 0.95; SRMR≤ 0.08; Hu & Bentler, 1998) are applied, practitioners would still consider both and being capable of detecting the misspecified between-level models even when ICC is as low as 0.091 (ICC1). On the other hand, and are not favored if ICC is too low. More specifically, would not be recommended if ICC is as low as 0.091 (ICC1); would not be recommended if ICC is as low as 0.231 (ICC3). In particular, practitioners should not overlook the plausible misleading interpretation of if traditional cutoff values were applied in educational studies, where ICCs are typically low (such as 0.220; Hedges & Hedberg, 2007).
The pattern of change in mean and across difference levels of ICC are expected. Both and are incremental fit indices (see their formulas in Appendix B) used for evaluating the between-level model fit by comparing the between-level hypothesized model with the between-level independence (or baseline) model. The more discrepancy between values of the between-level hypothesized model () and the independence model (), the larger and are (i.e., between-level model fit is reasonable). As previously discussed, values, including and , are influenced by ICC—stronger relations among the variables at between-level (i.e., higher ICC condition) allow for possibly “greater” discrepancies between the model-implied and observed variance–covariance matrices (Kline, 2011). In our simulation scenarios where the between-level model was misspecified, we found the value of mean decreased when ICC got smaller. For instance, with NG = 500 and NS = 100, mean was 331.263 under ICC6 and diminished to 20.464 under ICC1 (see Table 3). In the same manner, we found mean also decreased when the ICC became smaller (695.164 under ICC6 and 39.573 under ICC1). Lower ICC not only leads to smaller values of and , but also results in smaller discrepancies between and . Therefore, researchers should be aware that and are less likely to detect misspecified between-level models when ICC is low.
Unlike and , is not comparing with a baseline model but a function of the overall model chi-square value () while taking the model complexity into account (i.e., including the model degrees of freedom in the formula, see Appendix B for more information). As previously mentioned, in the simulation scenarios where the between-level model was misspecified, the mean decreased when ICC got smaller. Hence, it is easy to see a similar pattern of change in the mean given the change in the mean : from 0.265 under ICC6 to 0.031 under ICC1 with NG = 500 and NS = 100. Thus, shows less promise for detecting misspecification at the between-level when ICC is low. Similarly, was less effective on detecting misspecified between-level models when ICC was as low as 0.231 (ICC3). These results supported our hypothesis that given identical type of misspecification and sample size, the deviation between the model-implied and observed variance–covariance matrices would become smaller under the low ICC conditions.
The utilization of between-level–specific fit indices was discussed as follows. Previous simulation studies (e.g., Hsu et al., 2015; Hu & Bentler, 1998) have suggested that SRMR is more sensitive to misspecification in factor covariance (i.e., incorrectly constrain factor covariance as 0), while CFI, TLI, and RMSEA are more sensitive to misspecification in factor pattern (i.e., incorrectly constrain factor pattern to 0). Therefore, being unable to detect the misspecified factor covariance in MSEM in low ICC conditions continues to be a concern. Future studies are needed to investigate whether and are capable of detecting different types of misspecification in the between-level model. Moreover, considering the influence of ICC on the within-level-specific fit indices, we found that , , and were barely affected by the level of ICC. Therefore, we agree with Ryu and West (2009) in thinking that within-level–specific fit indices can only be used to assess the goodness of fit of within-level models. For practitioners, evaluation of within-level models in MSEM is not problematic because previous studies have shown that both within-level–specific and traditional fit indices reveal goodness of fit for within-level models regardless of ICC levels (Hsu et al., 2015). Our findings suggest that practitioners can rely on either within-level–specific or traditional fit indices to detect misspecifications in within-level models even when ICC is as low as 0.091.
Consistent with Kim et al. (2012) and Lüdtke et al. (2008), we found that ICC played an important role in the convergence problem occurring in our simulation and should be discussed. One may consider that the low convergence rate could be the result of the actual magnitude of the between-level and within-level variances (e.g., B = 0.1 and W = 1.0 which might seem to be small) we have manipulated in our simulation study rather than ICCs. We have done a further investigation on this issue and found that, regardless of the actual magnitude of the between-level and within-level variances, the convergence pattern was basically the same when ICC was the same across different combinations of W and B. Hence, we concluded that, rather than the magnitude of the between-level and within-level variances, ICC is the key to the convergence rate and performance of the level-specific fit indices. Based on convergence rates shown in Table 2, satisfied convergence rate (close to or higher than 95%) was achieved under high ICC conditions (i.e., ICC4 [0.286], ICC5 [0.333], and ICC6 [0.500]). On the other hand, when the latent factor ICC was low (i.e., ICC1, ICC2, and ICC3 conditions), using larger sample size in the between-level model (NG) seemed to compensate for the convergence problem. More specifically, NG = 200 is needed under ICC2 and ICC3 conditions, while for ICC1 condition, even NG = 500 seems insufficient. These findings were in line with Hox and Maas’s (2001) study findings where larger NG was related to admissible parameter estimates when ICC was low.
Limitations and Future Research Direction
This study has limitations that should be addressed. First, we adopted a multilevel CFA model as shown in Figure 1 for data generation. Therefore, findings should only be generalized to studies that apply multilevel CFA models. Further studies are needed to determine whether the current findings can also be replicated using different models (e.g., structural models). Second, we considered a limited number of design factors in the current study. Additional scenarios created by using different design factors such as unequal factor loadings, unbalanced designs (unequal group condition), and the number of observed indicators per latent factor are needed in future studies. Additionally, the ICC manipulated in the current simulation study is the latent factor ICC, which can be reasonably computed when the exact same model structure is applied to both between-level and within-level models. The aforesaid simulation findings and discussion provided insights into how latent factor ICC influenced the effectiveness of between-level-specific fit indices. Note that identical model structure can be a reasonable assumption in the simulation but may not be always true in real data. Thus, the generalizability of the findings based on this manipulation approach should be more conservative. Future research may also consider manipulating ICC for each observed variable (e.g., Pornprasertmanit et al., 2014) to validate our findings.
Concluding Remarks
In a recent review article written by Ryu (2014), she readdressed the importance of using level-specific fit indices to detect the lack of model fit in MSEM. However, based on our simulation results, we do not fully concur with her recommendation especially in terms of the performance of between-level–specific fit indices (e.g., , , , and ) under low ICC conditions. More specifically, the performance of and are more likely influenced by ICC compared with and . Nevertheless, when traditional cutoff values (RMSEA≤ 0.06; CFI, TLI≥ 0.95; SRMR≤ 0.08; Hu & Bentler, 1998) are applied, both and can still detect the misspecified between-level models even under low ICC conditions (i.e., ICC1 = 0.091). On the other hand, both and are not recommended especially under low ICC conditions (i.e., ICC1 to ICC3). Based on our simulation results, we recommend that substantive researchers should carefully evaluate and interpret the between-level specific fit indices under low ICC condition. Meanwhile, we also call for more attention to the question of how to appropriately evaluate between-level model with low ICC in MSEM.
Appendix A
Intraclass Correlation
Two types of ICC can be computed: latent factor ICC and observed variable ICC. Latent factor ICC is of more interest in multilevel CFA models (Heck & Thomas, 2009; B. O. Muthén, 1994) and has been considered in many prior MSEM simulation studies (e.g., Hox & Maas, 2001; Kim et al., 2012; Wu & Kwok, 2012). ICC for a latent factor in a multilevel CFA model is the proportion of the latent factor variance at the between-level (B) to the sum of the latent factor variances at both between- (B) and within-level (W):
Note that latent factor ICC can only be computed when the exact same model structure is applied to both between-level and within-level models (i.e., identical model structure assumption). As shown in previous simulation studies, manipulation of latent factor ICC is straightforward: fixing factor variance at within level as constant and varying factor variance at between level.
On the other hand, observed variable ICC can be understood as the proportion of an observed variable’s variance that is attributed to the between-group differences (Raudenbush & Bryk, 2002; Snijders & Bosker, 2012). Under a multilevel CFA modeling framework, the value of an observed variable ICC can be calculated as the proportion of between-level variance (b) to the sum of between-level variance and within-level variance (w) of that observed variable:
where b = (between-level factor loading)2× between-level factor variance + between-level residual variance and w = (within-level factor loading)2× within-level factor variance + within-level residual variance.
Given the between-level factor variance values manipulated in our simulation, the ICC values of the observed variables can be also calculated. For instance, under the ICC1 condition, the variance of the between-level factors (see Figure 1) was constrained to 0.10, resulting in a latent factor ICC equal to 0.091. The corresponding ICC for indicators y1 through y6 in ICC1 condition is 0.359 (B = 0.559; W = 1.000). The magnitudes of observed variable ICC under ICC2 to ICC6 conditions are 0.378, 0.397, 0.414, 0.430, and 0.500, respectively.
Appendix B
The Equations of the Partially Saturated Model Fit Indices1
Chi-Square Statistic
We first consider applying the PS method to obtain the :
where is the fitting function value for the saturated within-level model; is the fitting function value when both within-level and between-level levels are saturated (the fully saturated model). The degrees of freedom of (denoted by ) are equal to the difference between the number of parameters in the partially saturated model and the fully saturated model:
where and represent number of parameters in the saturated within-level model and fully saturated model, respectively.
The and its corresponding degree of freedom can be obtained through the Equations (B3) and (B4), respectively:
Root Mean Square Error of Approximation
Given and its corresponding df, the RMSEA for the between-level model (RMSEAPS_B) can be derived by the equation:
In Equation (B5), is between-level sample size (number of groups). To eliminate the random error component of , the noncentral parameter is subtracted from the (Rigdon, 1996). Thus, is an unbiased estimator of . The denominator in Equation (B5) functions as a penalty for large sample size, which will cause inflated effects on estimating . The in the denominator transfers into a measure of lack of fit per df. The is is set to zero providing is smaller than . The RMSEAPS_W can be obtained by the Equation (B6), where denotes the within-level total sample size:
Comparative Fit Index
CFI is an incremental fit index used to evaluate the goodness of fit by comparing the hypothesized model to the independence model (Bentler, 1990). According to Ryu and West (2009), the CFI for the between-level model can be defined as:
where and can be obtained by Equations (B1) and (B2), respectively. represents the test statistics with an independence (or null) between-level model and a saturated within-level model:
Note that an independence model can be obtained by correlating all the observed variables and constraining all the correlation coefficients to zero. The corresponding is defined as:
In sum, the is a criterion for testing exactly the goodness fit comparing the hypothesized model with the independence model at the between level, while the within-level model is saturated. Likewise, the can be computed by Equation (B10).
, shown in Equation (B11), represents the test statistics with a saturated between-level model and an independence within-level model. The corresponding can be computed by Equation (B12).
Tucker–Lewis Index
The TLI is a nonnormed fit index which penalizes for adding parameters in the model (Tucker & Lewis, 1973). The TLIPS_B can be used to evaluate the between-level model by comparing the hypothesized between-level model and the independence between-level model under the condition that the within-level model is saturated. On the other hand, the TLIPS_W can be used to evaluate the within-level model by comparing the hypothesized within-level model and the independence within-level model under the condition that the between-level model is saturated. The equations for and are presented in the following (Equations B13 and B14).
Standardized Root Mean Square Residual
SRMR can be computed for the within-level () and the between-level models (), respectively. Note SRMR is not a function of χ2 test statistics and can be derived from the deviation between the sample variance–covariance matrix and the reproduced variance–covariance matrix. Regular statistical packages like Mplus can now report and for model evaluation. More specifically, reflects the normed average distance between the sample variance matrix of p observed variables and model-implied variance matrix at the between level. The can represent as follows:
Likewise, reflects the normed average distance between the sample variance matrix and model-implied variance matrix at the within level. The can be represented as follows:
In the current study, all the χ2 values in the fit indices equations are robust χ2 values from MLR (maximum likelihood robust).
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
References
- Bentler P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107, 238-246. [DOI] [PubMed] [Google Scholar]
- Bollen K. A., Bauer D. J., Christ S. L., Edwards M. C. (2010). Overview of structural equation models and recent extensions. In Kolenikov S., Steinley D., Thombs L. (Eds.), Statistics in the social sciences: Current methodological developments (pp. 37-79). Hoboken, NJ: Wiley. [Google Scholar]
- Boomsma A. (1987). The robustness of maximum likelihood estimation in structural equation models. In Cuttance P., Ecob R. (Eds.), Structural modeling by example (pp. 160-188). New York, NY: University of Cambridge. [Google Scholar]
- Bowen N., Guo S. (2011). Structural equation modeling. New York, NY: Oxford University Press. [Google Scholar]
- Goldstein H. I., McDonald R. P. (1988). A general model for the analysis of multilevel data. Psychometrika, 53, 455-467. [Google Scholar]
- Heck R. H., Thomas S. L. (2009). An introduction to multilevel modeling techniques (2nd ed.). New York, NY: Routledge. [Google Scholar]
- Hedges L. V., Hedberg E. C. (2007). Intraclass correlation values for planning group-randomized trials in education. Educational Evaluation and Policy Analysis, 29, 60-87. [Google Scholar]
- Hox J. J. (2010). Multilevel analysis techniques and applications (2nd ed.). New York, NY: Routledge. [Google Scholar]
- Hox J. J., Maas C. J. M. (2001). The accuracy of multilevel structural equation modeling with pseudobalanced groups and small samples. Structural Equation Modeling, 8, 157-174. [Google Scholar]
- Hox J. J., Maas C. J. M., Brinkhuis M. J. S. (2010). The effect of estimation method and sample size in multilevel structural equation modeling. Statistica Neerlandica, 64, 157-170. doi: 10.1111/j.1467-9574.2009.00445.x [DOI] [Google Scholar]
- Hsu H.-Y., Kwok O., Acosta S., Lin J.-H. (2015). Detecting misspecified multilevel SEMs using common fit indices: A Monte Carlo study. Multivariate Behavioral Research, 50, 197-215. [DOI] [PubMed] [Google Scholar]
- Hu L., Bentler P. M. (1998). Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods, 3, 424-453. [Google Scholar]
- Kaplan D. (2009). Structural equation modeling: Foundations and extensions (2nd ed.). Thousand Oaks, CA: Sage. [Google Scholar]
- Kenny D. A. (2015, November 24). Measuring model fit. Retrieved from http://davidakenny.net/cm/fit.htm
- Kim E. S., Kwok O., Yoon M. (2012). Testing factorial invariance in multilevel data: A Monte Carlo study. Structural Equation Modeling, 19, 250-267. doi: 10.1080/10705511.2012.659623 [DOI] [Google Scholar]
- Kline R. B. (2011). Principles and practice of structural equation modeling (3rd ed.). New York, NY: Guilford Press. [Google Scholar]
- Lai M. H. C., Kwok O. (2015). Examining the rule of thumb of not using multilevel modeling: The “design effect smaller than two” rule. Journal of Experimental Education, 83, 423-438. [Google Scholar]
- Liang J., Bentler P. M. (2004). An EM algorithm for fitting two-level structural equation models. Psychometrika, 69, 101-122. [Google Scholar]
- Loehlin J. C. (2004). Latent variable models: An introduction to factor, path, and structural equation analysis (4th ed.). Mahwah, NJ: Lawrence Erlbaum. [Google Scholar]
- Lüdtke O., Marsh H. W., Robitzsch A., Trautwein U., Asparouhov T., Muthén B. O. (2008). The multilevel latent covariate model: A new, more reliable approach to group-level effects in contextual studies. Psychological Methods, 13, 203-229. [DOI] [PubMed] [Google Scholar]
- McDonald R. P., Goldstein H. (1989). Balanced versus unbalanced designs for linear structural relations in two-level data. British Journal Mathematical and Statistical Psychology, 42, 215-232. [Google Scholar]
- Muthén B. O. (1991). Multilevel factor analysis of class and student achievement components. Journal of Educational Measurement, 28, 338-354. [Google Scholar]
- Muthén B. O. (1994). Multilevel covariance structure analysis. Sociological Methods & Research, 22, 376-398. [Google Scholar]
- Muthén B. O., Asparouhov T. (2009). Beyond multilevel regression modeling: Multilevel analysis in a general latent variable framework. In Hox J., Roberts J. K. (Eds.), Handbook of advanced multilevel analysis (pp. 15-40). New York, NY: Routledge. [Google Scholar]
- Muthén L. K., Muthén B. O. (1998-2015). Mplus user’s guild (7th ed.). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Pornprasertmanit S., Lee J., Preacher K. J. (2014). Ignoring clustering in confirmatory factor analysis: Some consequences for model fit and standardized. Multivariate Behavioral Research, 49, 518-543. doi: 10.1080/00273171.2014.933762 [DOI] [PubMed] [Google Scholar]
- Preacher K. J., Zhang Z., Zyphur M. J. (2011). Alternative methods for assessing mediation in multilevel data: The advantages of multilevel SEM. Structural Equation Modeling, 18, 161-182. doi: 10.1080/10705511.2011.557329 [DOI] [Google Scholar]
- Raudenbush S. W., Bryk A. S. (2002). Hierarchical linear models: Applications and data analysis methods (2nd ed.). Thousand Oaks, CA: Sage. [Google Scholar]
- Rigdon E. E. (1996). CFI versus RMSEA: A comparison of two fit indexes for structural equation modeling. Structural Equation Modeling, 3, 369-379. [Google Scholar]
- Rowe K. J. (2003). Estimating interdependent effects among multilevel composite variables in psychosocial research: An example of the application of multilevel structural equation modeling. In Reise S. P., Duan N. (Eds.), Multilevel modeling methodological advances, issues, and applications (pp. 255-284). Mahwah, NJ: Lawrence Erlbaum. [Google Scholar]
- Ryu E. (2011). Effects of skewness and kurtosis on normal-theory based maximum likelihood test statistic in multilevel structural equation modeling. Behavior Research Methods, 43, 1066-1074. doi: 10.3758/s13428-011-0115-7 [DOI] [PubMed] [Google Scholar]
- Ryu E. (2014). Model fit evaluation in multilevel structural equation models. Frontiers in Psychology, 5, 1-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryu E., West S. G. (2009). Level-specific evaluation of model fit in multilevel structural equation modeling. Structural Equation Modeling, 16, 583-601. doi:10.1080/107055109 03203466 [Google Scholar]
- Schermelleh-Engel K., Kerwer M., Klein A. G. (2014). Evaluation of model fit in nonlinear multilevel structural equation modeling. Frontiers in Psychology, 5, 1-11. doi: 10.3389/fpsyg.2014.00181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweig J. (2014). Multilevel factor analysis by model segregation: New applications for robust test statistics. Journal of Educational and Behavioral Statistics, 39, 394-422. doi: 10.3102/1076998614544784 [DOI] [Google Scholar]
- Snijders T. A. B., Bosker R. J. (2012). Multilevel analysis: An introduction to basic and advanced multilevel modeling (2nd ed.). Thousand Oaks, CA: Sage. [Google Scholar]
- Tucker J. S., Lewis C. (1973). The reliability coefficient for maximum likelihood factor analysis. Psychometrika, 38, 1-10. [Google Scholar]
- Wu J.-Y., Kwok O. (2012). Using SEM to analyze complex survey data: A comparison between design-based single-level and model-based multilevel approaches. Structural Equation Modeling, 19, 16-35. [Google Scholar]
- Yuan K. H., Bentler P. M. (2007). Multilevel covariance structure analysis by fitting multiple single-level models. Sociological Methodology, 37, 53-82. [DOI] [PMC free article] [PubMed] [Google Scholar]