It Might Not Make a Big DIF

Abstract

Differential test functioning, or DTF, occurs when one or more items in a test demonstrate differential item functioning (DIF) and the aggregate of these effects are witnessed at the test level. In many applications, DTF can be more important than DIF when the overall effects of DIF at the test level can be quantified. However, optimal statistical methodology for detecting and understanding DTF has not been developed. This article proposes improved DTF statistics that properly account for sampling variability in item parameter estimates while avoiding the necessity of predicting provisional latent trait estimates to create two-step approximations. The properties of the DTF statistics were examined with two Monte Carlo simulation studies using dichotomous and polytomous IRT models. The simulation results revealed that the improved DTF statistics obtained optimal and consistent statistical properties, such as obtaining consistent Type I error rates. Next, an empirical analysis demonstrated the application of the proposed methodology. Applied settings where the DTF statistics can be beneficial are suggested and future DTF research areas are proposed.

Generally speaking, differential item functioning, or DIF, refers to any situation in which an item within a test or questionnaire measures an intended construct differently for one subgroup of a population than it does for another. Consequently, the presence of DIF implies that test validity is compromised for a given subgroup. DIF is often assessed using item response theory (IRT), which is a collection of models and methods for analyzing the relative performance of individual items within a given test and, importantly, for scoring the test (Thissen & Steinberg, 2009). In IRT, a set of item parameters is used to establish an item response function, or trace line, which characterizes the regression of the item response on the hypothetical construct, or latent variable, being measured. In this context, Lord (1980) explained that “if … an item has a different item response function for one group than for another, it is clear that the item is biased” (p. 212). This article is concerned with using IRT to measure how this item bias accumulates to produce biased test scores, or differential test functioning (DTF). If true differences on the latent variable are held constant across two or more groups, but the function relating expected test scores to the latent variable differs across groups, then the test displays DTF.

There is an enormous literature on methods for the detection of DIF, but comparatively little research has been dedicated to the consequences of DIF for subsequent test scoring, which, in turn, has ramifications for subsequent analyses and applications using tests that display DIF across known groups. If a set of items in a test has DIF effects which consistently favor (e.g., are easier for) one group over another, then the overall DTF may be substantial. But if a test has many items and only a few of them have DIF, or the DIF effects are weak (see, e.g., DeMars, 2011), then the impact of this DIF on the overall test scores may be negligible. In other situations, it might be that there are large DIF effects in one direction for some items, but these effects are canceled out by DIF in the opposite direction for other items. Therefore, detection of DIF for a subset of items in a test does not necessarily imply that the overall test itself is biased. For example, Flora, Curran, Hussong, and Edwards (2008) presented a DIF analysis in which 7 of 13 items in a test of childhood internalizing behavior contained DIF across age groups, yet subsequent analyses using test scores that incorporated the DIF effects obtained essentially the same results as parallel analyses based on test scores that ignored DIF. Thus, on discovering DIF, it can be useful for researchers to investigate whether, and to what extent, the DIF manifests itself at the level of the overall test scores to produce DTF. If the DTF appears negligible, then there may be no need to drop items with DIF (and thereby reduce reliability and content validity).

A set of methods proposed by Raju, van der Linden, and Fleer (1995) represents the most prominent framework on testing for DTF. As we explain later, these methods have several limitations, the most important of which is that they do not adequately account for sampling variability of the item parameter estimates in the different groups. This issue is important in DTF statistics because the degree to which the parameters are accurately estimated ultimately affects the item and test scoring functions. To overcome these limitations, this study introduces two DTF statistics to measure discordant test scoring properties between two or more groups of interest. The proposed statistics are designed to be omnibus tests of DTF, the first of which measures the amount of overall scoring bias between groups, while the second statistic measures the average difference between the groups across a given range of latent trait values. Both omnibus statistics have standardized counterparts which are useful for comparing results across tests with different lengths. A subsequent statistic derived as a special case of the scoring bias statistic will also be described, and pertains to specific latent trait levels rather than over a predetermined range of the latent trait. This statistic is used to build accurate confidence intervals as a post hoc diagnostic tool after one or both of the omnibus statistics discover the presence of DTF.

A statistical imputation approach to obtaining standard errors and confidence intervals for various test-level functions for the proposed DTF statistics is evaluated using two Monte Carlo simulation studies. These simulations were designed to determine Type I error rates and information about overall group differences using the omnibus statistics. Finally, an empirical data set is analyzed using the proposed statistics to demonstrate how researchers may apply these DTF methods to their test data.

Item Response Theory

IRT consists of a set of models that probabilistically map observed categorical item response data onto unobserved latent variable, where the latent variable (typically denoted by θ values) represents a hypothetical construct that the set of items purport to measure. An IRT model is selected for each item to determine the item response function, or trace line, given θ. One such model often used in educational measurement for modeling dichotomously scored items (e.g., multiple-choice items scored correct [1] or incorrect [0]) is the unidimensional three-parameter logistic model (Birnbaum, 1968), or 3PLM. With this model, the probability of positive item endorsement can be expressed as

$$P(y=1|\theta ,a,d,g)=g+(1-g)\frac{\exp (a\theta +d)}{1+\exp (a\theta +d)},$$

where y is the observed item response, θ represents the participant’s value on the latent variable, g is a lower bound parameter indicating the probability of answering the question correctly when θ = −∞ (often referred to as the “guessing parameter”), a is the slope or discrimination parameter, and d is the intercept. When g is fixed at zero, this model reduces to the well-known two-parameter logistic model (2PLM).

Next, the graded response model, or GRM, is a model for K-polytomous item responses ordered from lowest to highest. This model is often used for rating-scale items (e.g., Likert-type items) or for ability-testing scenarios when items can be scored using a partial-credit scoring rubric. The GRM can be understood as an ordered sequence of successive 2PLMs, where the probability of a response in a given category k is determined by the difference between the adjacent cumulative probability functions

$$P(y=k|\theta ,d_k,d_{k+1})=P(k|\theta ,a,d_k)-P(k-1|\theta ,a,d_{k+1}).$$

For the first category, where k = 0, the probability term on the left of Equation 2 is understood to be the constant 1, and for the last category, where k = K − 1, the second probability term on the right of Equation 2 is understood to be 0. In the unidimensional GRM there are K parameters to be estimated: one slope parameter (a) and K − 1 ordered intercepts (d_k).

Additional IRT item functions are available that can be useful for quantifying different item properties. The expected “score” for a respondent is a function that models what an individual’s expected observed item response value would be when given a person’s θ value and the item parameters. This item score function provides one simple way to express how individuals respond to the items, and is expressed as

$$S_j(\theta ,\mathbf{\psi })=\sum _{k=0}^{K-1}k·P(y=k|\theta ,{\mathbf{\psi }}_j),$$

where ψ _j is the vector of parameters relevant to the jth item. The expected score function collapses the expected probability of each category into a single value representing the average score at a particular θ value. In the special case when K = 2, the item score function is equivalent to the trace line giving the probability of positively endorsing the item.

Differential Item Functioning

Many different statistical approaches to detecting DIF in tests have been developed and extensively researched (Millsap, 2011). DIF refers to how items measure individuals in different groups unequally, which creates measurement bias in favor of one group over another at particular values along the latent variable distribution. In general, DIF for a given item can be depicted by simultaneously plotting each group’s item-level trace line (e.g., Equations 1 and 2) or scoring function (Equation 3). For the remainder of this exposition, we focus on the likelihood-ratio approach to DIF because it is very flexible and allows for the computation of accurate parameter covariance matrices when the IRT model is equated across groups (see Kolen & Brennan, 2004, for descriptions of additional DIF approaches).

In the simplest case, there are only two groups under investigation for DIF: a reference group and a focal group. The reference group is a baseline group against which all comparisons are to be made, while the focal group is drawn from the population in which DIF is suspected. The choice of the reference and focal groups is arbitrary for the likelihood-ratio approach (which is not the case for several other DIF methods). DIF is then tested through nested-model comparisons based on the likelihood-ratio or information statistics (such as Akaike information criterion and Bayesian information criterion), where various item parameters are constrained to be equal across groups in one model (the constrained model) and free to differ in another (the unconstrained model). Before likelihood-ratio tests can be carried out effectively for testing each item for DIF, it is important to equate the tests so that the group-level differences in their θ distributions, such as the latent means and variances, do not cause unwarranted DIF in the item parameter estimates (Kolen & Brennan, 2004). With the likelihood-ratio method, this equating is accomplished by selecting a subset of anchor items whose parameters are assumed to be equal across the groups (i.e., assumed free of DIF) during the multiple-group model estimation. After applying constraints for all anchor item parameters, the multiple-group model is then sufficiently identified across groups such that the mean and variance of θ for the focal group(s) can be freely estimated, thereby adjusting the metric for the item-level parameters during estimation. For more detailed information regarding the general application of likelihood-ratio testing of DIF, see Millsap (2011).

Differential Test Functioning

Following the detection of DIF, researchers are often faced with a difficult decision of what to do about items displaying consistent measurement bias across groups. The most popular approach is to discard items if the detected DIF is too large; this approach appears justified for applications such as computerized adaptive testing designs where items are selected based on the assumption that the items are unbiased (Wainer, 1990). Alternatively, however, one can inspect how the items containing DIF combine across the whole test to determine whether there is an overall bias at the test level. The inspiration for this approach is that when multiple items have known DIF, but the DIF is not in one particular direction across groups (e.g., items do not consistently score the focal group higher), then the effect of the bias may, on average, “cancel out” over the entire item set, thereby removing the local bias generated from any given item with DIF. For instance, in a test with dichotomous items, if two items exhibit DIF in the intercept parameters such that the focal group has a lower intercept on one item but a higher intercept on a different item, then the composite bias when measuring θ may turn out to be negligible. When differences between the groups are detectable or meaningfully large at the test level, then we can conclude that DTF has occurred.

It is also possible, however, to obtain nontrivial DTF in applications where little to no DIF effects have been detected. Meaningful DTF can occur in testing situations where DIF analyses suggest that no individual item appears to demonstrate a large amount of DIF. Specifically, substantial DTF can occur when the freely estimated parameters systematically favor one group over another. The aggregate of these small and individually insignificant item differences can become quite substantial at the test level, and in turn bias the overall test in favor of one population over another. Therefore, studying DTF in isolation and in conjunction with DIF analyses can be a meaningful and informative endeavor for test evaluators.

One straightforward approach to investigating DTF is to compare the expected test score functions for each group. The test score function, when properly equated across groups, gives an indication of whether there are differential effects between the reference and focal group(s). The test score function has the simple relationship to the expected item score function in Equation 3 in that it is simply the aggregate of each item score function,

$$T(\theta ,{\mathbf{\psi }}_G)=\sum _{j=1}^n{S}_j(\theta ,{\mathbf{\psi }}_G),$$

where ψ _G is the collection of all item-level parameters relevant to the Gth group. When exploring DTF, each group has a unique test score function, and if the groups’ scales have been properly linked then the test score functions can be compared graphically. The joint test score plot is useful as a visualization of potential DTF between groups.

Although visual inspection of the joint test score functions can be suggestive of the type of bias that may exist between groups the apparent differences should be interpreted carefully. In empirical applications where population parameters are estimated from sample data, the obtained estimates will contain some amount of sampling error.¹ As well, due to the additive nature in Equation 4, the standard errors for the test score function will not be uniform about its expected values and instead can be more variable at different values of θ. Properly accounting for sampling variability at the test level is the topic of the next section, but first we must consider which statistics should be investigated at the test level before we study their sampling variability.

Statistics for Differential Test Functioning

When analytically describing the discrepancies between the reference and focal group(s), it is beneficial to express the differences between the T(θ, ψ _G) functions numerically using summary statistics. Two important pieces of information should be captured about the difference between the test functions, both of which have the common goal of quantifying the degree of DTF between the reference and focal group(s). The first is whether there is a systematic test scoring bias, indicating that one or more groups are consistently scored higher across a specified range of θ, and the second is whether the test curves have a large degree of overall separation on average, suggesting that there may be nonignorable DTF at particular θ levels. An omnibus measure of the former criterion is presented below as the signed DTF measure, while an omnibus measure of the latter is given below as the unsigned DTF measure.

The signed DTF measure is

$$\mathrm{sDTF}=\int [T(\theta ,{\mathbf{\psi }}_R)-T(\theta ,{\mathbf{\psi }}_F)]g\left(\theta \right)d\theta ,$$

where g(θ) is a weighting function with the property that $\int g\left(\theta \right)d\theta =1.$ In practice, Equation 5 is numerically evaluated using Q discrete quadrature nodes

$$\mathrm{sDTF}\cong \sum _{q=1}^Q[T(X_q,{\mathbf{\psi }}_R)-T(X_q,{\mathbf{\psi }}_F)]g\left(X_q\right),$$

where X_q is a quadrature node and g(X_q) is the associated weight. The sample estimate of Equation 5, $s\widehat{\mathrm{DT}}F,$ is obtained by replacing ψ _R and ψ _F with ${\hat{\mathbf{\psi }}}_R$ and ${\hat{\mathbf{\psi }}}_F,$ respectively. To obtain the unweighted area between the response curves, all values of g(θ) are fixed to a single constant value. Equation 5 expresses the average amount of test scoring bias between the response curves and can range from −TS to TS, where TS represents the highest possible test score. Negative values of sDTF indicate that the reference group scores lower than the focal group on average, while positive values indicate that the focal group scores higher. Note that while this function is easily generalized to represent multiple focal groups at once, it is conceptually clearer to focus only on one focal group at a time.

Next, the unsigned DTF measure is

$$\mathrm{uDTF}=\int |T(\theta ,{\mathbf{\psi }}_R)-T(\theta ,{\mathbf{\psi }}_F)|g\left(\theta \right)d\theta ,$$

where g(θ) has the same properties as in Equation 5. Analogous to Equation 5, Equation 7 is also evaluated using Q quadrature nodes

$$\mathrm{uDTF}\cong \sum _{q=1}^Q|T(X_q,{\mathbf{\psi }}_R)-T(X_q,{\mathbf{\psi }}_F)|g\left(X_q\right).$$

The sample estimate of Equation 7, $u\widehat{\mathrm{DT}}F,$ is obtained by replacing ψ _R and ψ _F with ${\hat{\mathbf{\psi }}}_R$ and ${\hat{\mathbf{\psi }}}_F,$ respectively. The uDTF measure captures the average area between the two test curves, indicating absolute deviations in item properties that have been aggregated over the whole test. uDTF ranges from 0 to TS because the area between the curves is zero when the test scoring functions have exactly the same functional form. This nonnegative lower bound limit is problematic when researchers are interested in testing whether uDTF = 0 in the population, and therefore obtaining a suitable test statistic for this hypothesis is difficult (see Meeker & Escobar, 1995, for further discussion). Additionally, if the metric of uDTF is difficult to interpret directly then a suitable standardized effect size metric may be preferred, such as

$$uDTF\%=\frac{uDTF}{TS}·100,$$

which represents the percent scoring difference for the overall test. Using Equation 9, an appropriate cutoff value can be chosen which constitutes problematic DTF based on the absolute functional separation of the test scores.

When exploring omnibus DTF with the sDTF and uDTF statistics, there are four extreme outcomes that can be observed; these are listed in Table 1. The qualitative descriptors “large” and “small” are used in the table rather than specific numerical values because the importance of specific magnitudes of these statistics will contain different theoretical thresholds which depend on the empirical application. When large values for an omnibus DTF statistic are observed, a selection of θ values should be further investigated to determine where DTF occurs across this range of θ. This follow-up analysis can be accomplished re-evaluating the sDTF and uDTF statistics across a smaller θ integration range, or by evaluating the sDTF statistic at particular θ values over different locations along θ; the latter approach is referred to as sDTF _θ for the remainder of this article.

Table 1.

Possible Outcomes for sDTF and uDTF Combinations.

	Small sDTF	Large sDTF
Small uDTF	Little to no DTF present across the entire range of θ.	This is not possible to observe because the sDTF ≤uDTF property will always hold. When the curves do not cross, sDTF ≡ uDTF.
Large uDTF	Test curves intersect at one or more locations to create a balanced overall scoring. However, there is non-ignorable bias at particular θ levels.	Overall DTF present in total scores, systematic bias and noticeable overall curve differences. Potentially, there are larger levels of bias at different θ locations.

Equations 5 and 7 are relatively similar to the test-level DTF statistic and the item-level NCDIF statistic proposed by Raju et al. (1995), but have some fundamentally different properties. Raju et al. (1995) defined their compensatory DTF estimate as

$$\widehat{\mathrm{DTF}}={(\frac{1}{N_F}\sum _{i=1}^{N_F}(T({\hat{\theta }}_i,{\hat{\mathbf{\psi }}}_F)-T({\hat{\theta }}_i,{\hat{\mathbf{\psi }}}_R)))}^2,$$

where ${\hat{\theta }}_i$ is the latent trait estimate for the ith individual given the item parameter estimates from the focal group. Their noncompensatory DIF estimate was defined as

$$N\widehat{\mathrm{CD}}{\mathrm{IF}}_j=\frac{1}{N_F}\sum _{i=1}^{N_F}{|P_j({\hat{\theta }}_i,{\hat{\mathbf{\psi }}}_F)-P_j({\hat{\theta }}_i,{\hat{\mathbf{\psi }}}_R)|}^2,$$

where ${\hat{\theta }}_i$ has the same relationship as in the $\widehat{\mathrm{DTF}}$ statistic and N_F is the number of individuals in the focal group. Raju et al. (1995) note that there are two distinct sources of error in their statistics, “(1) estimation error resulting from the use of person and item parameter estimates, and (2) sampling error resulting from using a sample from a population of examinees” (p. 357).

In addition to these two sources of variation, several other less desirable factors will influence the sample estimates of the $\widehat{\mathrm{DTF}}$ and $N\widehat{\mathrm{CD}}{\mathrm{IF}}_j$ statistics, including the selection of a prediction method used to obtain $\hat{\theta }$ values (e.g., maximum-likelihood [ML] estimates, maximum or expected a posteriori estimates, weighted-likelihood estimates, etc.), test-dependent factors such as the number of items (longer tests will generally provide better predictions of $\hat{\theta }$), the use of $\hat{\mathbf{\psi }}$ as a stand-in estimates of ψ when computing $\hat{\mathbf{\theta }}$ estimates, the selection of which group is the focal group, the type of linking method used to equate the group parameters, and so on. Furthermore, although Raju et al. (1995) were able to derive approximate χ² and t distributional tests for these statistics the authors demonstrated that their approximations were overly sensitive to detecting DTF, and recommend that ad hoc cutoff values be used instead. Unfortunately, the ad hoc cutoff values selected were specific only to the properties investigated in the authors’ simulation study and do not appear to generalize to sample specific conditions (Oshima, Raju, & Nanda, 2006).

Our $s\widehat{\mathrm{DT}}F$ and $u\widehat{\mathrm{DT}}F$ statistics have subtle but important differences compared with the sample-based statistics proposed by Raju et al. (1995). First, sDTF and uDTF remain in the metric of the expected test scores (i.e., they are not squared) and therefore have a more natural interpretation. For instance, if sDTF = 1, a researcher can conclude that the reference group total scores will, on average, be one point higher than the focal group scores over the specified integration range; the exact value of the difference at a particular θ location, however, can be directly determined by evaluating sDTF _θ statistic. Second, sDTF and uDTF do not require any particular selection of which group is the focal or reference group; this decision is arbitrary. This property is important because the choice of the focal group in Raju et al.’s approach dictates how the density of the integration weights are determined when predicting stand-in $\hat{\theta }$ estimates. Third, compared to NCDIF, the uDTF statistic represents the unsigned difference for the entire test rather than on the basis of specific items, and therefore quantifies scoring differences in the test directly. Fourth, Raju et al.’s $\widehat{\mathrm{DTF}}$ and $N\widehat{\mathrm{CD}}{\mathrm{IF}}_j$ do not account for differences in the latent trait distributions directly, and therefore require group “linking” methods to rescale the parameter estimates so that the focal and reference item-parameter estimates are agnostic to the latent distributions (see Kolen & Brennan, 2004, for further details).

Lastly, and most importantly, the $s\widehat{\mathrm{DTF}}$ and $u\widehat{\mathrm{DTF}}$ statistics do not require plausible estimates for θ. This is especially important because the particular observed response patterns do not confound these statistics. Fundamentally, DTF is a property of the test rather than a relationship among individuals who take the test. Hence, DTF is a characteristic that exists independent of the particular $\hat{\theta }$ estimates and response patterns sampled from the populations; this fundamental property is analogous to how DIF is conceptualized, in that evidence of DIF can be obtained by testing the item-parameter estimates without any reference to the distribution of θ.² This essential property of DTF is not respected by Raju et al.’s (1995) family of statistics because supporting evidence in favor of (or against) DTF can only be concluded within the sample of individuals from which Raju et al.’s DTF statistics were computed. This limitation can be understood by constructing a simple example. Consider a test that demonstrates substantial scoring bias for individuals in the lower tail of the latent trait distribution, and two independent multiple-group samples which have taken this test. In the first sample, very few individuals with lower latent trait scores are sampled in one or more groups, while in the second sample there are many more individuals with lower trait scores in both groups. After computing Raju et al.’s DTF statistic on both multiple-group samples, only the second sample would provide evidence of DTF; clearly, these statistics result in inconsistent conclusions about the inherent DTF property in the measurement instrument. Both multiple-group samples should have reached the conclusion that estimates for the lower ability individuals are biased for one group. However, using sample-driven information about individuals alone does not provide evidence for this conclusion. Our sDTF and uDTF measures, on the other hand, do not have such a limitation because they pertain to all potential abilities in the population, and therefore capture evidence of DTF for trait levels which have not yet been observed.

Although the $s\widehat{\mathrm{DT}}F$ and $u\widehat{\mathrm{DT}}F$ estimates are theoretically not biased by varying sample sizes or test lengths, and also are not confounded by the use of plausible $\hat{\theta }$ estimates, up to this point these statistics have only been presented as fixed point estimates of the population values that converge as N tends to infinity. Therefore, in the next section we explore an effective statistical mechanism to account for sampling error in the proposed DTF statistics.

Approximating Sampling Variability in DTF Statistics

When using ML estimation methodology to obtain sample estimates for population parameters, the theoretical sampling variability is often quantified as the inverse of the observed-data information matrix (i.e., the Hessian matrix; Efron & Hinkley, 1978)

$$\Sigma \left(\widehat{\psi }\right)=I{\left(\widehat{\psi }\right)}^{-1},$$

where $\hat{\mathbf{\psi }}$ is a vector of the parameter estimates at the stationary ML location. $\mathbf{\Sigma }(\hat{\mathbf{\psi }})$ expresses the amount of parameter estimate variability (and covariation) due to random sampling, and under standard regularity conditions has a multivariate normal distribution

$$\widehat{\psi }\sim \varphi \left(\psi ,\Sigma \left(\widehat{\psi }\right)\right).$$

The $\mathbf{\Sigma }\left(\widehat{\mathbf{\psi }}\right)$ matrix has several other common uses, such as testing linear hypotheses regarding one or more parameters using the Wald approximation approach (Wald, 1943), generating point-wise standard error estimates, and determining whether the solution has reached a stable local optimum following convergence.

Another interesting and useful application for $\mathbf{\Sigma }\left(\widehat{\mathbf{\psi }}\right)$ demonstrated by Thissen and Wainer (1990), is to use the parameter covariance matrix to obtain nonlinear confidence intervals for functions in data space. Thissen and Wainer (1990) primarily used this method as a visual inspection tool to represent the variability in item trace lines for didactic purposes. However, this idea generalizes to the test scoring functions as well as for point estimates that depend on the variability in the estimated parameters. To obtain appropriate sampling variability of the test scoring functions, we follow the reasoning proposed by Thissen and Wainer (1990): stochastically impute plausible values of the population estimates using Equation 11, and evaluate $s\widehat{\mathrm{DTF}}$ and $u\widehat{\mathrm{DTF}}$ given the imputed values. The imputation algorithm works as follows:

1. Impute a vector of plausible parameter values, ψ*, from the sample-obtained estimates and their estimated variation using the multivariate normal relationship $\varphi (\hat{\mathbf{\psi }},\mathbf{\Sigma }(\hat{\mathbf{\psi }})).$

2. Evaluate the test scoring functions $T(\theta ,{\mathbf{\psi }}_R^{*})$ and $T(\theta ,{\mathbf{\psi }}_F^{*})$ across the range of −6 ≤ θ ≤ 6 (or some other predefined range) using t equally spaced quadrature nodes.

3. Compute the values for sDTF* and uDTF* from Equations 5 and 7 using $T(\theta ,{\mathbf{\psi }}_R^{*})$ and $T(\theta ,{\mathbf{\psi }}_F^{*})$ instead of the $\hat{\mathbf{\psi }}$ estimates. Store these values for later use.

4. Repeat Steps 1 to 3 M times until a suitable set of imputations has been collected.

After collecting M sets of sDTF* and uDTF* values from the imputed data sets, one can use the collected values to build empirical confidence intervals for any desired α level and obtain suitable standard error estimates by computing the standard deviation of the collected values. For generating item- and test-level graphics that account for parameter variability using the outlined imputation approach, refer to the recent work of Yang, Hansen, and Cai (2012).

There are several features that make this parameter imputation approach appealing. First, because the variability in the test score function is a direct consequence of the estimated item parameter variability, then as N→∞ the precision of the test score function improves and converges to the population function with zero variation in expectation. Second, because the nonlinearity of the test score function is handled in parameter space, the confidence interval coverage remains optimal, even in the presence of ceiling and floor effects in the test. Third, because of how the parameter matrix is computed, differences in sample sizes between the reference and focal groups will be directly accounted for. Therefore, unequal sample sizes will not cause systematic bias when computing the variability of $s\widehat{\mathrm{DTF}}$ and $u\widehat{\mathrm{DTF}}$. Finally, statistics based on the variability in T(θ, ψ _G) can be estimated to any degree of accuracy, and confidence intervals for measures which are not easily approximated through normal approximation theory (such as the uDTF) can easily be obtained. This capability also allows a formal test of the null hypothesis that a given sDTF equals zero ($H_0:\int (T(\theta ,{\mathbf{\psi }}_F)-T(\theta ,{\mathbf{\psi }}_R))g\left(\theta \right)=0$), the finite-sample properties of which we evaluate below.

In addition to determining the imputed standard errors and confidence intervals for $s\widehat{\mathrm{DT}}F$ and $u\widehat{\mathrm{DT}}F,$ one may also approximate the confidence interval for $s\widehat{\mathrm{DT}}{F}_{\theta }$ at any fixed value of θ. This method is demonstrated in the “Empirical Application” section below, and further augments the usefulness of sDTF _θ as a post hoc diagnostic tool. When unacceptable sDTF or uDTF values are detected, the applied practitioner will likely be interested in where along θ the group differences occur, while also being mindful of sampling uncertainties in the model. Investigating the range of θ where the selected confidence intervals are nonoverlapping provides one indication of where the systematic bias is located.³

Observed Information Matrix in IRT Models

Statistical models that directly optimize the observed-data log-likelihood will often be able to estimate $\hat{\mathbf{\psi }}$ and $\mathbf{\Sigma }(\hat{\mathbf{\psi }})$ following ML estimation by using analytic or numerical methods with little effort. However, calculating the ML parameter estimates in IRT is often difficult in practice for tests with moderate to large numbers of items, and psychometricians have instead recommended the use of partitioned marginal ML estimation procedures such as the Expectation-Maximization (EM) algorithm for routine use (Bock & Aitkin, 1981). An unfortunate consequence when using the EM algorithm is that the observed-data information matrix is not readily available following model convergence and must be estimated by other means.

Several approaches to estimating the observed-data information matrix have been proposed in the IRT literature. These include the supplemented EM (Cai, 2008), the exact approach outlined by Louis (1982), the cross-product and sandwich estimators (Yuan, Cheng, & Patton, 2013), which are variants of Louis’ method, and several others based on stochastic approximations (e.g., Cai, 2010). Most of these methods focus on approximating the observed-data information matrix rather than the parameter covariance matrix directly, but because of the relationship in Equation 10, inverting the information matrix will result in the appropriate covariance form. In the following simulation studies, only the cross-product method is used to compute the observed information matrix because it is computationally the easiest to obtain for larger tests compared with the other methods mentioned (Paek & Cai, 2014).

Simulation Studies

In this section, two comprehensive simulation studies using the 3PLM and GRM were constructed to examine the properties of the proposed multiple imputation approach to estimate variability of the sDTF and uDTF measures. The simulations were designed to represent a situation in which a small set of anchor items contained no DIF, while the remaining items, the studied items, contained parameters that were free to vary across groups. Not all the studied items contained DIF, but the approach was set up to remain agnostic to potential DIF; if in applied settings additional items are known to contain no DIF, then these may also be included as anchors. Type I error rates for the omnibus test of DTF using the $s\widehat{\mathrm{DT}}F$ statistic and suitable cutoff values for the uDTF_% were collected; these are summarized below.⁴

The test characteristics that were expected to affect the detection of DTF included sample size, test length, number of items with DIF, directionality of DIF relative to group membership (unidirectional vs. bidirectional), size of the DIF effects, and the type of DIF combinations present (i.e., DIF in the item intercepts, slopes, or both). Unidirectional DIF occurs when the effects of the DIF items are in the same direction. For instance, if the test has two items with DIF only in the intercept parameters, then unidirectional DIF occurs when both intercepts are higher in one group compared with the other. Bidirectional DIF, on the other hand, indicates that one group has larger parameters for some items and lower parameters for the others; this combination in turn causes a more balanced effect on the expected total score, and in some cases the effect of the DIF items on the test scoring functions cancel out to create negligible DTF.

Each of the test characteristics mentioned above were evaluated in the following simulation studies (one study for 3PLM, one for GRM). Within each study, there were three sample sizes (500, 1,000, and 3,000) evenly split between a focal and reference group, two DIF directionality conditions (unidirectional and bidirectional), two DIF effect sizes (0.5 and 1.0), three combinations of the type of DIF present (intercepts, slopes, and both), three test sizes (30, 40, and 50 items for the 3PLM design; 20, 25, and 30 items for the GRM design), and three conditions for the number of DIF items (4, 8, and 12 for the 3PLM design; 4, 6, and 8 for the GRM design). Both designs formed a total of 324 DTF cell combinations. In addition, nine extra conditions were constructed where no DIF was present, and therefore no DTF was present either. These conditions were created to determine whether the Type I error rates for the test that sDTF = 0) remain optimal under controlled conditions given various sample sizes and test length combinations, including an extra N=5000 to observe very large sample size behavior. Finally, the empirical p-values for sDTF were compared to the nominal α values 0.1, 0.05, and 0.01, while the upper 95th percentile for uDTF _% were compared to the cutoff percentage values 2, 2.5, 3.0, 3.5, and 4.

We expected to observe a few trends across the simulation design. Primarily, we expected that for the conditions with no DIF items, the sDTF estimates will obtain nominal Type I error rates even as sample and test sizes increase, and in conditions where DTF is present in the population, we expected an increase in power as the sample size increased. However, we predicted the increase in power would be different depending on the conditions because sDTF and uDTF capture different aspects of DTF. Furthermore, larger test sizes should produce more powerful and accurate DTF test statistics because the precision of θ is better quantified during estimation, thereby helping minimize the sampling variability caused by the parameter estimates. At the same time, larger test sizes should also be less affected by DIF because there are more non-DIF items present; thus, smaller DTF values should occur as the test size increases. Finally, in the bidirectional designs which contain DIF in the intercept parameters only we expected the DTF statistics to approach zero due to the matched DIF balancing which causes a cancellation effect at the test level.

The multiple-group IRT models were fitted by marginal ML with the EM algorithm using the mirt package (Chalmers, 2012) Version 1.4 in R (R Core Team, 2013). The mirt package was also used to generate the test data given the experimental conditions under investigation. Specifically, the simdata() function was used to generate the datasets and multipleGroup() was used to compute anchored multiple-group IRT models along with the parameter information matrix. Model convergence in the EM algorithm was set to .0001, and if models failed to reach this criterion the simulated data were discarded and redrawn. For the DTF statistics, the integration range for θ was set to [−6, 6] with 1,000 integration nodes, and the plausible population parameters were obtained from 1,000 independent imputations.

3PLM Study

The first study investigated the properties of the proposed DTF statistics for simulated data consistent with the 3PLM. The slope parameters were drawn from a log-normal distribution, a∼log N(0.2, 0.2), while the intercepts (d) were drawn from a standard normal distribution, d∼ N(0.1). The lower-bound parameters (g) were all set to 0.2 to reflect the theoretical chance of randomly guessing a correct answer given a five-option multiple choice design for each item. However, to deter the possibility of obtaining local minima during parameter optimization with the EM algorithm, the g values were all fixed to the population values of 0.2. This strategy is common in 3PLM items and is often the default choice in IRT software such as TESTFACT 4 (Wood et al., 2003). The latent distribution was set to a standardized normal distribution in the reference group and θ_F∼ N(0.25, 1.5) in the focal group. Finally, five anchor items containing no DIF were chosen in each cell of the design whereby the a and d parameters were constrained to be equal across groups.

Simulation results for the null DTF conditions, in which no DIF items were generated in the population, are displayed in Table 2. To demonstrate the properties of the DTF statistics in large sample sizes an N = 5,000 condition was also tested. From this table we observe that the empirical p values for the sDTF statistic were not systematically affected by test length. However, larger sample sizes generally lead to more liberal Type I error rates for the $\widehat{\mathrm{sDTF}}$ statistic. The uDTF_% confidence interval range behaved as expected in that as N increased, the value at the 95th percentile, as well as the uDTF _% value itself, approached the population value of 0, indicating that the group-based test curves were virtually indistinguishable in the population.

Table 2.

DTF Conditions for the 3PLM When No Items Contained DIF, Representing the Type I Error Rates (sDTF) and Cutoff Values at the 95% Percentile (uDTF).

N	Test length	sDTF			uDTF% (α = .95)
		p < .10	p < .05	p < .01	>2	>2.5	>	>3.5	>4
500	30	.137	.069	.017	.998	.829	.475	.273	.123
	40	.096	.044	.014	.996	.834	.495	.244	.121
	50	.090	.045	.010	1.000	.887	.538	.272	.124
1,000	30	.153	.094	.026	.356	.121	.034	.005	.001
	40	.175	.112	.032	.302	.095	.027	.003	.001
	50	.161	.106	.033	.292	.096	.025	.002	.001
3,000	30	.198	.140	.038	.003	.000	.000	.000	.000
	40	.186	.129	.044	.004	.000	.000	.000	.000
	50	.221	.152	.057	.002	.001	.000	.000	.000
5,000	30	.206	.116	.036	.000	.000	.000	.000	.000
	40	.208	.141	.050	.000	.000	.000	.000	.000
	50	.201	.122	.047	.000	.000	.000	.000	.000

The tables available in the online Appendix contain the results of the DTF conditions, separated by sample size and DIF direction. Additionally, the online Appendix contains Type I error rates when fitting 2PLMs instead of 3PLMs with a fixed lower-bound component. The main design effects behaved as expected, and contained various interactions between the design elements. For both DTF statistics, unidirectional DIF resulted in much larger rejection rates compared with the bidirectional DIF design, larger sample sizes increased the rejection rates, longer tests resulted in lower rejection rates, larger numbers of DIF items increased the rate of detecting DTF, and larger DIF sizes also resulted in detecting DTF more often. Rejection rates were highest when there was DIF in both the a and d parameters. However, when the a parameters alone contained DIF, the likelihood of detecting a significant sDTF was five times less than when the d parameters alone contained DIF. Therefore, sDTF was generally more sensitive to detecting aggregate DIF effects in intercept parameters compared with the slope parameters.

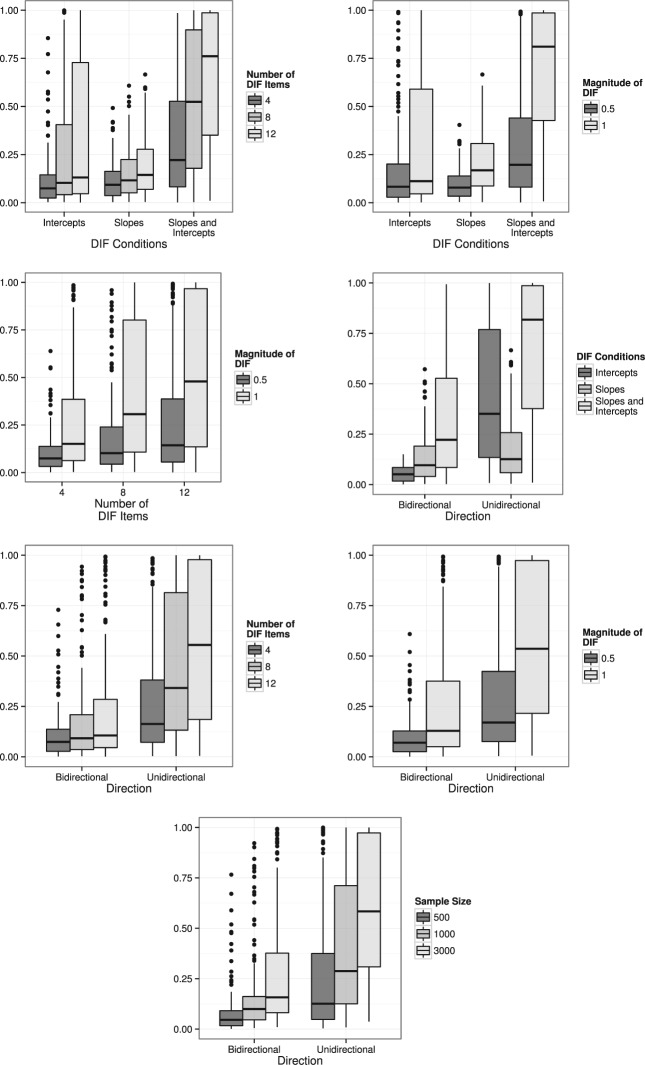
With respect to the sDTF statistic, we only describe the strongest interaction effects, and these are displayed in Figure 1. The direction of the DIF effect was dependent on the sample size condition such that larger sample sizes resulted in higher rejection rates in the unidirectional case than the bidirectional case. This result is not surprising because larger sample sizes increase power and unidirectional DIF generally causes larger DTF effects than bidirectional DIF. There was also an interaction between DIF direction and the number of DIF items, as well as the size of the DIF effects, where again the unidirectional DIF demonstrated higher rejection rates compared with the bidirectional design as the number of DIF items and DIF sizes increased. DIF direction interacted with the type of parameters demonstrating DIF; however, this effect was slightly more complex. In the bidirectional case, DTF was detected most often when both the a and d parameters contained DIF, followed by only as, and finally the ds in isolation. In contrast, DTF was detected in the unidirectional case more often when the ds contained DIF compared with the as, though when both a and d contained DIF the rejection rates were still the largest. Essentially, when there are DIF effects in the intercept parameters they are more likely to cancel out if the intercepts are opposite in direction. The number of DIF items also interacted with both DIF size and parameter type, such that DTF was better detected when more a and d parameters produced DIF, and DTF was better detected when more items contained larger DIF, sizes. Finally, the DIF effect interacted with parameter type in that larger DIF sizes combined with DIF in both the slope and intercept parameters increased the detection of DTF.

Figure 1.

sDTF empirical p value interaction plots at α = .05 for 3PLM simulation.

Regarding uDTF _% the main effects detected with sDTF were also present, although some were in the opposite direction due to the bounded nature of the statistic and confidence interval cutoff approach. The unidirectional condition contained higher uDTF _% values than the bidirectional, increasing the number of DIF items and DIF size also tended to increase detection rates for the statistic, and longer tests negatively affected the detection of DTF. The uDTF _% results differed from the sDTF with respect to sample size such that larger sample sizes tended to result in smaller uDTF_% (α = .95) values, and with respect to parameter type, where differences in the a parameters were largely responsible for larger values in uDTF _%. Not only was the detection rate substantially more variable in the DIF condition that manipulated only the a parameters, but the average marginal detection rate was much higher compared with the isolated d parameters. Therefore, as expected, the uDTF was better at detecting aggregate slope parameter effects compared with the intercept parameters.

For uDTF_%, there was an interaction between the DIF direction and sample size conditions such that larger sample sizes resulted not only in smaller uDTF_% (α = .95) values but were higher and much more variable for the unidirectional condition compared with the bidirectional condition. Unidirectional DIF also improved the detection of DTF when the d parameter caused DIF, but was even more effective at detecting DTF when the a parameters contained DIF (the combination of a and d added little to the detection rates). Increasing the DIF effect size and number of DIF items simultaneously also improved detection rates. These interaction results are presented visually in Figure 2.

Figure 2.

uDTF_% interaction plots with cutoff value of uDTF_% (α = .95) for 3PLM simulation.

Another important property was observed in the cells of the design where only the d parameters contained bidirectional DIF. For these conditions, regardless of test length, DIF size and number of DIF items, the Type I error rates in sDTF were close to the nominal level and uDTF_% approached the lower asymptote of 0. This finding is important, and indeed expected, because equal and opposite DIF intercept effects should produce negligible scoring bias in the overall test scores. Had the simulation designs been implemented with fixed slope coefficients (such as those in standard Rasch IRT models), then this effect would be prevalent and likely more stable. In this situation, the respective groups are scored with the same degree of accuracy regardless of the DIF effects and can offer justification for using similar scoring schemes in fixed length tests across groups (so long as the DIF parameter estimates are included).

GRM Study

The second study investigated the properties of the proposed DTF statistics applied to the GRM, where each item was constructed to contain five ordered response options. The slope parameters were again drawn from a log-normal distribution, a∼ log N(0.2, 0.2) while the ordered intercept parameters were constructed by adding standard normal deviation value, s^*∼ N(0, 1) to each value in the vector [1.5, 0.5, −0.5, −1.5]. Intercept parameters were constructed in this manner to limit sparse data tables. If data were drawn such that the number of categories for the item did not equal five, then the population parameters were redrawn. The latent distribution hyper-parameters were set to the standard normal distribution in the reference group and θ_F∼ N(0.5, 0.75) in the focal group. Finally, five anchor items containing no DIF were chosen in each cell of the design, whereby the a and d_k parameters were constrained to be equal across groups.

Simulation results for the null DTF conditions in which no DIF items were generated in the population are displayed in Table 3. To demonstrate the properties of the DTF statistics in large sample sizes, an N = 5,000 condition was also tested. The empirical p-values for sDTF did not appear to be highly influenced by sample size or test length; however, they were consistently conservative in the N = 500 condition. Overall, the DTF statistics for the GRM demonstrated nominal to slightly liberal Type I error rates, and generally provided smaller uDTF _% values than the previous 3PLM simulation

Table 3.

DTF Conditions for the GRM When No Items Contained DIF, Representing the Type I Error Rates (sDTF) and Cutoff Values at the 95% Percentile (uDTF).

N	Test length	sDTF			uDTF% (α = .95)
		p < .10	p < .05	p < .01	>2	>2.5	>3	>3.5	>4
500	20	.059	.029	.000	.662	.226	.078	.026	.007
	25	.038	.016	.000	.833	.366	.118	.032	.007
	30	.019	.008	.001	.938	.509	.197	.067	.017
1,000	20	.113	.061	.011	.059	.010	.001	.000	.000
	25	.095	.047	.009	.060	.008	.000	.000	.000
	30	.115	.047	.007	.060	.006	.002	.000	.000
3,000	20	.135	.084	.025	.000	.000	.000	.000	.000
	25	.116	.061	.019	.000	.000	.000	.000	.000
	30	.120	.066	.012	.000	.000	.000	.000	.000
5,000	20	.146	.074	.021	.000	.000	.000	.000	.000
	25	.125	.062	.019	.000	.000	.000	.000	.000
	30	.138	.092	.025	.000	.000	.000	.000	.000

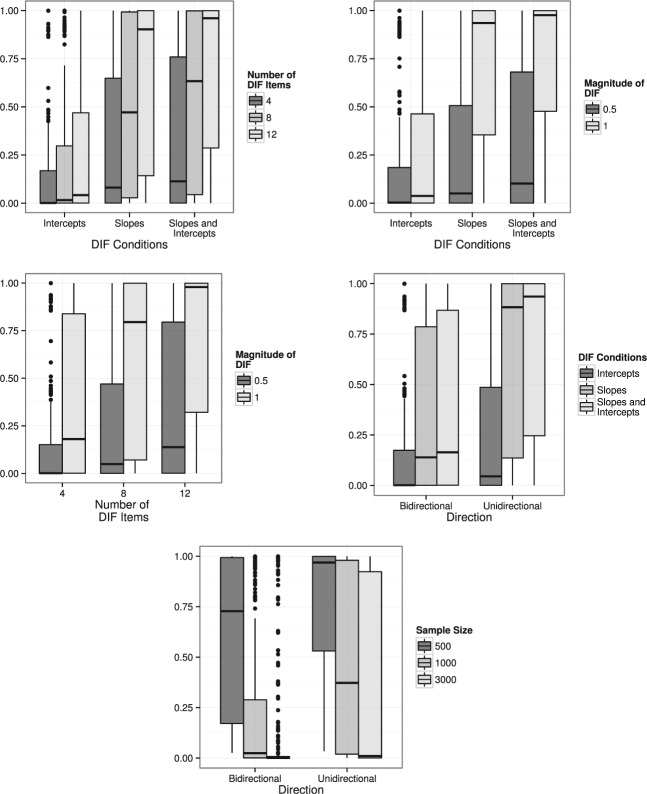
The tables available in the online Appendix contain the results of the simulation by sample size and DIF direction. The main design effects again behaved as expected, along with various interactions. For both DTF statistics, unidirectional DIF resulted in much larger rejection rates compared with the bidirectional DIF design, larger sample sizes increased the rejection rates, longer tests resulted in lower rejection rates, larger numbers of DIF items increased the rate of detecting DTF, and larger DIF sizes also resulted in detecting DTF more often. When there was DIF in both the a and d_k parameters, rejection rates were the highest; however, when the a parameters alone contained DIF, the variability of detecting a significant sDTF was five times less than when the d_k parameters contained DIF. Again, the $\widehat{\mathrm{sDTF}}$ statistic was generally more sensitive to differences in intercept parameters compared with the slope parameters.

The interactions effects were also very similar to the 3PLM study above. Given the similarity between the simulation designs, overall sDTF and uDTF estimates appeared to capture population-level DTF effects regardless of the IRT model selected. By and large, the sDTF statistic was more effective at capturing differences in unidirectional DIF in the intercept parameters, while the uDTF was more effective at capturing DTF when the DIF was in the slopes. Furthermore, detecting DTF improved for both statistics when both slopes and intercepts contained DIF, indicating that the complexity of DIF also contributes to the detection of DTF.

Empirical Application

To illustrate our utility of the DTF methods, we analyzed data from a study by Marjanovic, Greenglass, Fiksenbaum, and Bell (2013). A data set containing responses from the General Self-Efficacy Scale (GSE; Schwarzer & Jerusalem, 1995) was assessed for DIF and DTF across samples from Canada (n = 277) and Germany (n = 219). Both samples primarily consisted of students who were female and unmarried. The GSE was originally developed in German and translated into 31 languages, including English. The GSE includes ten rating-scale items with four ordinal options that assess the degree to which participants generally view their own actions as responsible for successful outcomes.

Before demonstrating the DTF effects, DIF analyses were performed between the two countries for each of the GSE’s items using the multiple-group GRM. All DIF analyses were conducted using the mirt package (Chalmers, 2012) with marginal ML estimation. To establish a set of potential anchor items, we used a multigroup GRM with no across-group equality constraints as a reference model. Next, likelihood-ratio tests were used to compare the reference model to models that added across-group equality constraints to the a and d_k parameters one item at a time. To account for the large number of likelihood ratio tests, we used the multiplicity control method of Benjamini and Hochberg (1995). Based on the DIF analysis, we determined that the third, sixth, seventh, and eighth items were invariant across the two countries. Therefore, these items were used as anchor items in the final multigroup IRT model so that the latent mean and variance parameters in the German group could be estimated. A likelihood-ratio test comparing our final model to a multigroup IRT model with no across-group equality constraints was not statistically significant, ${\chi }^2\left(14\right)=19.12,$p = .160. Using the Canadian group as the reference group (with latent mean fixed to 0 and variance fixed to 1), the German group had latent mean and variance estimates of −0.115 and 0.953, respectively. Table 4 presents the item parameter estimates for Canada and Germany with standard errors computed with the cross-product method. Overall, the final model fitted the data well according to the M2* family of statistics (Maydeu-Olivares & Joe, 2006), M2*(44) = 71.79, comparative fit index = .953, root mean square error of approximation = .035, with standardized root mean-squared residual values of .047 and .067 for the Canada and German groups, respectively.

Table 4.

Parameter Estimates With Standard Errors for Canada and German Samples for Final Anchored Model.

Group	Item	a	d 1	d 2	d 3
Canada	1	2.08 (0.27)	6.00 (0.83)	3.47 (0.42)	−1.58 (0.23)
	2	1.87 (0.23)	4.80 (0.52)	1.66 (0.21)	−2.77 (0.31)
	3	1.75 (0.17)	5.18 (0.49)	2.06 (0.18)	−2.14 (0.20)
	4	3.64 (0.47)	7.55 (1.05)	2.69 (0.40)	−3.17 (0.42)
	5	3.25 (0.40)	7.55 (1.35)	2.21 (0.32)	−3.17 (0.39)
	6	2.38 (0.25)	7.02 (0.72)	3.88 (0.32)	−1.23 (0.19)
	7	2.61 (0.22)	5.18 (0.42)	1.82 (0.20)	−2.59 (0.27)
	8	2.82 (0.27)	6.31 (0.54)	2.71 (0.28)	−2.89 (0.28)
	9	3.02 (0.43)	8.05 (1.14)	3.56 (0.43)	−2.35 (0.37)
	10	3.26 (0.38)	7.59 (0.88)	3.30 (0.39)	−2.89 (0.39)
Germany	1	1.55 (0.24)	5.55 (0.78)	4.72 (0.59)	−0.05 (0.19)
	2	2.08 (0.31)	5.96 (0.96)	3.67 (0.40)	−0.60 (0.23)
	3	—	—	—	—
	4	2.38 (0.30)	4.82 (0.50)	1.49 (0.26)	−3.41 (0.39)
	5	2.88 (0.46)	6.33 (0.74)	3.43 (0.55)	−2.00 (0.31)
	6	—	—	—	—
	7	—	—	—	—
	8	—	—	—	—
	9	1.79 (0.28)	4.88 (0.54)	2.61 (0.32)	−1.20 (0.23)
	10	1.69 (0.26)	4.89 (0.68)	3.28 (0.36)	−0.57 (0.21)

Note. Standard errors were estimated using the cross-product approximation. “—” lines indicate parameters that were constrained to be equal across groups.

These results demonstrate that DIF is present in 6 of the 10 items, however, the main purpose of these analyses is to examine differences between the groups at the test level. On the left of Figure 3, the expected total score functions and their imputed confidence intervals are displayed for the German and Canadian groups. As can be seen, there is a substantial amount overlap in the confidence regions for the two countries’ expected total scores at most levels of θ. The signed and unsigned DTF analyses help quantify the difference though, and provide information about whether there is biased scoring over and above sampling error. Generating 1,000 imputations for the DTF statistics using the method described earlier resulted in a statistically significant $s\widehat{\mathrm{DT}}F$ statistic (p < .0001), but represented a small effect size. Specifically, $s\widehat{\mathrm{DT}}F=-0.629$ (95% CI: 0.969 to −0.351) and $u\widehat{\mathrm{DT}}F=0.663$ (95% CI: 0.363 to 1.001), which overall represent a bias in the total scores of approximately 0.629 raw score points (or 1.57%) in favor of the German population. To follow up, we examined the $s\widehat{\mathrm{DT}}{F}_{\theta }$ across a large number of points to determine where these difference occurred. The right of Figure 3 demonstrates the amount of $s\widehat{\mathrm{DT}}{F}_{\theta }$ with the 95% confidence region. The figure demonstrates that at average to lower levels of θ, Canadians tend to score lower on the GSE.

Figure 3.

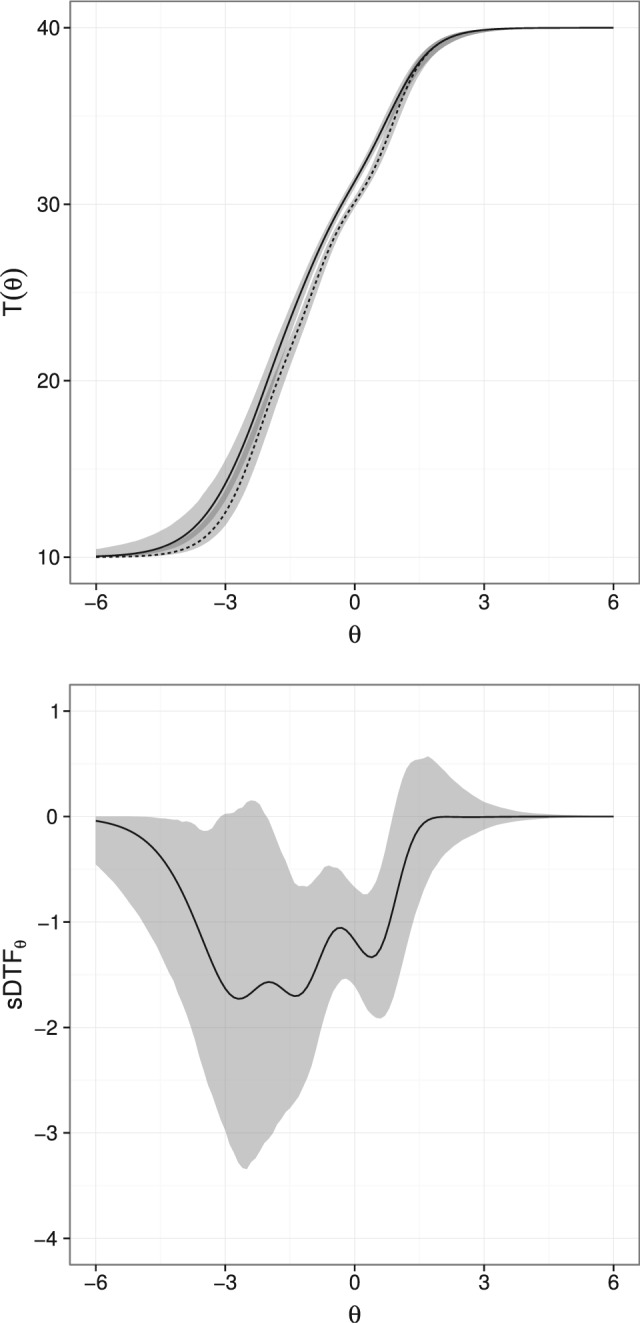
Empirical test-scoring functions with imputed 95% confidence intervals (left) for the German (solid) and Canadian (dashed) groups, and $s\widehat{\mathrm{DTF}}$ statistic evaluated at different locations along θ (right) with 95% confidence intervals.

This analysis highlights that if researchers were to naïvely use the unweighted total scores to compare the relative group responses, while ignoring the ordinal item content and differential weights due to group membership, they would come to the conclusion that the two populations had essentially equal mean test scores (t[478.11] = −1.314, p = .189). Therefore, researchers may wrongfully conclude the test functions equivalently in both populations. However, IRT analyses discovered that the German population had a lower latent mean compared with the Canadian population and the German population was scored more favorably on the test (i.e., received positively biased test scores), although this bias was small. These two events jointly contribute to the observed equivalence in the total scores, but have different theoretical interpretations and therefore different consequences for future empirical work.

Discussion

This article examined how different DTF properties could be captured using two proposed measures: sDTF and uDTF. The sDTF measures was designed to capture the average test-scoring bias across a prespecified range of latent trait scores, while uDTF measures was designed to quantify the average overall discrepancy between the test scoring functions across known populations. While we recommend that DTF always be examined graphically (e.g., Figure 3), these DTF measures provide valuable formal assessments of DTF which account for the sampling variability of the item parameter estimates. That is, these DTF measures quantify the accumulation of individual DIF effects across a whole test; ultimately, observing DIF in individual items may or may not cause substantially biased test scores.

In the simulation studies of the 3PLM and GRM, when no DIF existed in the population, the two statistics behaved appropriately, retaining nominal or slightly liberal Type I errors rates depending on the IRT model used, and provided evidence of equal test scoring functions as the sample sizes increased uDTF. The tables in online Appendices demonstrated the power to detect DTF using the sDTF and uDTF statistics given known population conditions. Overall, the sDTF statistic was more effective at detecting differential scoring when there was systematic DIF due to the intercept parameters, whereas the uDTF statistic more optimally detected differences due to differential variation in the slope parameters. However, when bidirectional DIF existed only in the intercept parameters the DTF statistics resembled a scenario in which there was no DIF present in any item due to the cancellation of the individual DIF effects.

Overall, the proposed DTF statistics demonstrated desirable properties that have not been available in previous DTF methods. Importantly, because the item parameter estimate variability was properly accounted for, the effect of increasing sample size did not adversely affect the Type I errors in situations with no DIF or where DIF effects were expected to largely cancel out. Although various test designs were assessed in these simulations, several areas for future research remain. Namely, the power to detect DTF may improve considerably by including additional information about parameter invariance, where only the items with known DIF contribute to the differences in the test-level functions. Doing so could dramatically reduce the number of parameters to estimate in the IRT model, further improve Type I error rates, and consequently reduce the overall sampling variability. In turn, this would reduce variability at the test level, thereby increasing the overall power of the DTF statistics. This approach was not used in this article so that the generality of the DTF statistics could be demonstrated in more suboptimal conditions where DIF was suspected in the majority of the test. Additionally, the DTF statistics may be further explored for fitting models other than the 3PLM and GRM, for multidimensional tests which demonstrate DIF, and for alternative test-level functions to detect other important systematic differences (for instance, using the test standard error functions to locate differences in measurement precision between groups). However, multidimensional DTF introduces a different challenge for the proposed DTF statistics due to the high-dimensional test-score surfaces that must be integrated across, and therefore Monte Carlo integration techniques may be required to maintain sufficient accuracy.

Follow-up analyses after DTF is detected can also be captured through the proposed methodology by selecting isolated integration values and evaluating the test-level differences at the respective θ locations. This method of post hoc analysis was demonstrated in the empirical analysis section of this article by utilizing sDTF _θ. However, the proposed DTF statistics have the added benefit that, in addition to evaluating single points along θ between test response curves, specific regions of θ may also be evaluated and subject to the same statistical testing methodology. For example, if a particular θ region is important in a decision-theory based test, where obtaining accurate and unbiased population measurements between, say, θ = 1.5 to θ = 2.0, may be important, then researchers could specify the integration grid to range within 15 ≤ θ ≤ 2.0. Interpreting the results for sDTF and uDTF using this integration range will test the DTF hypotheses specifically within the defined range while ignoring test effects outside this location. This type of analysis has important implications for tests that are designed specifically for diagnosing or detecting psychopathologies, or ‘giftendess’ in ability tests, given specific latent-variable cut-offs as well as other empirical situations where decisions above and below specific latent cut-score ranges are of little interest.

Assessing DTF is an important extension of DIF for understanding tests and the effect of scoring bias, but unfortunately it has received relatively little attention in applied measurement literature. We believe one prevalent reason for their limited usage has been due to the undesirable properties of the previously proposed DTF statistics, but also because researchers have not considered the overall importance of DTF in their testing applications. This article demonstrated more optimal approaches to investigating DTF statistics, and amended several of the undesirable DTF statistical issues present in previous DTF work. The methodology described herein offers a powerful, flexible, and promising method for examining multiple types of DTF in applied data analyses. With the help of these improved DTF statistics, and future work that extends on this methodology, we believe that practitioners will have more confidence in answering whether their DIF items really do make an overall “DIF-erence” when scoring their tests.