Partially Compensatory Multidimensional Item Response Theory Models

Abstract

Partially compensatory models may capture the cognitive skills needed to answer test items more realistically than compensatory models, but estimating the model parameters may be a challenge. Data were simulated to follow two different partially compensatory models, a model with an interaction term and a product model. The model parameters were then estimated for both models and for the compensatory model. Either the model used to simulate the data or the compensatory model generally had the best fit, as indexed by information criteria. Interfactor correlations were estimated well by both the correct model and the compensatory model. The predicted response probabilities were most accurate from the model used to simulate the data. Regarding item parameters, root mean square errors seemed reasonable for the interaction model but were quite large for some items for the product model. Thetas were recovered similarly by all models, regardless of the model used to simulate the data.

Responding to test items correctly may require multiple skills, and thus multidimensional models are needed for these responses. The most commonly used multidimensional item response theory (MIRT) models are compensatory. An increase in any ability will increase the probability of correct response. In contrast, partially compensatory MIRT models do not allow high levels of one ability to compensate fully for low levels of another ability required for correctly responding to the item. The purpose of this research is to assess the recovery of two partially compensatory models and to explore whether data generated to follow one partially compensatory model can be fit as well by another partially compensatory model or by a compensatory model. These models are described next, followed by a brief review of applications of partially compensatory models and studies of parameter recovery.

In its most general form, the compensatory MIRT model is

$$P_i(\mathbf{\theta })=c_i+(1-c_i)\frac{e^{({\mathbf{a}\prime }_i\mathbf{\theta }-d_i)}}{1+e^{({\mathbf{a}\prime }_i\mathbf{\theta }-d_i)}},$$

where P_i(θ) is the probability of correct response on item i given the θ vector of abilities for an examinee (examinee subscript omitted from the model) and the item parameters, c_i is the lower asymptote, a _i is a vector of discrimination parameters, and d_i is the item difficulty. Equation 1 is often labelled the 3-parameter-logistic (3PL) MIRT model; clearly, it has more than three item parameters, but it is an extension of the 3PL unidimensional model.

For short-answer items, or for multiple-choice items with very good distractors such that low-ability examinees are unlikely to guess the correct answer, the 2PL-MIRT model can be formed by fixing c to zero, thus removing it from the model. For the 1PL-MIRT model, the as within each dimension are set equal. Or equivalently, for the multidimensional Rasch model, the as are set to 1, removing them from the model, and the variance of the θs is a free parameter—the more discriminating the items on dimension ℓ, the greater the variance of θ_ℓ.

Partially compensatory or noncompensatory MIRT models are less frequently used than compensatory models. The terms partially compensatory and noncompensatory are used interchangeably in the literature and do not necessarily apply to different models. Some have argued that partially compensatory is more accurate, so that term will be applied throughout the remainder of this article. The product model and the interaction model are partially compensatory models.

Partially compensatory models may take the form of a product of probabilities, such that the probability of correct response is limited by the examinee’s lowest ability. Sympson’s (1977) model, with some changes in notation for consistency with Equation 1, is

$$P_i(\mathbf{\theta })=c_i+(1-c_i)\underset{\ell =1}{\overset{L}{\Pi }}\frac{e^{(a_{\mathrm{i}\ell }{\theta }_{\ell }-d_{\mathrm{i}\ell })}}{1+e^{(a_{\mathrm{i}\ell }{\theta }_{\ell }-d_{\mathrm{i}\ell })}},$$

where P_i(θ) is the probability of correct response on item i given the examinee’s θ vector of abilities and the item parameters, θ_ℓ is the element of that vector corresponding to ability ℓ, c_i is the lower asymptote, a_{i ℓ} is the item’s discrimination for ability ℓ, and d_{i ℓ} is the item’s difficulty for ability l. Sympson proposed the model in an exploratory context, with each item loading on all abilities, but it can also be used in a confirmatory manner. The model can be constrained to 1PL and 2PL forms. Maris (1995) labelled the 1PL variant the conjunctive Rasch model.

Embretson (initially writing under the name of Whitely, 1980) described several partially compensatory models; her independent components model is similar to Sympson’s (1977) model but with no discrimination parameter. As in unidimensional Rasch models, the discrimination is displaced onto the ability variance and thus is the same for all items measuring that trait. Unlike Rasch models, this model allowed for a guessing parameter if the model were used with multiple-choice items. Embretson (1984) later added an upper asymptote and used the label multicomponent latent trait model. She originally conceptualized the model in terms of separate scores for each ability the item measured. She later modified the estimation to enable the use of the model when there is a single score for each item (Embretson & Yang, 2006).

An alternative to Sympson’s (1977) and Embretson’s (1984) product models is an additive model with interaction terms. An additive model might present fewer estimation difficulties than a product model. An additive interaction model for two θs is

$$P_i(\mathbf{\theta })=c_i+(1-c_i)\frac{e^{(a_{1i}{\theta }_1+a_{2i}{\theta }_2+a_{3i}{\theta }_1{\theta }_2-d_i)}}{1+e^{(a_{1i}{\theta }_1+a_{2i}{\theta }_2+a_{3i}{\theta }_1{\theta }_2-d_i)}}.$$

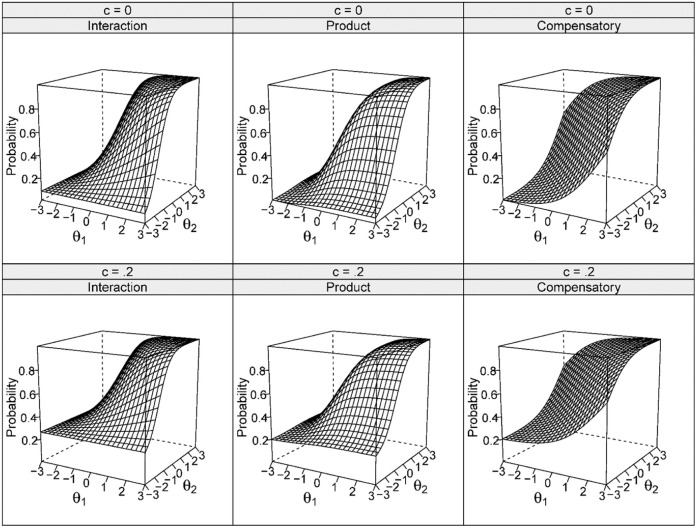
Examples of an interaction model with a positive interaction coefficient, a product model, and a compensatory model are shown in Figure 1. The item measures both θs equally, so a ₁ = a ₂, and in the product model d ₁ = d ₂. In the compensatory model, P(θ) approaches c when both θs are low and approaches 1 when both θs are high, with increases in P(θ) as either θ increases. In the interaction model, P(θ) is low whenever either θ is low, but does not quite approach c. The product model looks fairly similar to the interaction model, except that P(θ) approaches c as both θs decrease simultaneously.

Figure 1.

Three models for a middle difficulty item that measures two θs equally.

Conceptually, a large positive interaction means the item is largely noncompensatory; it takes both θs to solve the item. A small positive interaction indicates increases in either θ will increase the probability of correct response but increases in both together provide an added boost. One potential problem is that “if the interaction coefficient (a ₃) becomes too large, then the response surface may actually increase as θ values decrease” (Chalmers & Flora, 2014, p. 345). Buchholz (2014) described this as “double-winged” (p. 8). For a two-dimensional interaction model, the lowest (or highest) point of the function occurs at (−a ₂/a ₃, −a ₁/a ₃). If a ₃ is positive, predicted probabilities will increase as θ values decrease below this point. If a ₃ is negative, predicted probabilities will decrease as θ values increase above this point.

Applications of the Models

Buchholz (2014) fit 2PL compensatory, product, and interaction models to data from a reading test with two hypothesized dimensions. The interaction model fit better than the others but yielded the complication of increasing probabilities with decreasing θ within the range where there were nonnegligible proportions of examinees.

Bolt and Lall (2003) estimated a 2PL compensatory model and a 1PL product model for an English placement test intended to measure two skills. The estimates of the standard errors were lower for the compensatory model, and the log-likelihoods were higher in cross-validation samples.

Rizopoulos and Moustaki (2008) used a 2PL interaction model with data from a survey on communication related to workplace changes. They did not compare the model to other MIRT models. The results were conceptually interpretable.

Simpson (2005) applied a 1PL exploratory GMIRT model to matrix completion items theorized to measure correspondence finding and executive control. The GMIRT model is a hybrid of a compensatory and a product partially compensatory model. If the compensation parameter μ = 0, the model simplifies to the compensatory model, and if μ = 1 it simplifies to the product model. μ can take any value between 0 and 1 to combine the models. In the matrix completion data, most items had estimated µs between 0 and 0.2, and more difficult items had higher estimated μs, suggesting that the skills were less compensatory for harder items. Simpson also fit a 1PL compensatory model (equivalent to a GMIRT model with μ fixed to 0) and a 1PL product model (equivalent to a GMIRT model with μ fixed to 1) to the data. The estimated item difficulties were highly correlated across models. Predicted response probabilities were also similar in the regions where most examinees were.

Model Recovery

In this section, the term exploratory will be used to indicate that all items were free to load on all θs, and the term confirmatory will be used for models in which some items were specified to measure a subset of the θs. This distinction is relevant because of the rotational indeterminacy in exploratory models, which may make estimation more difficult.

Spray, Davey, Reckase, Ackerman, and Carlson (1990) found that the exploratory compensatory and product models fit partially compensatory data almost equally well; using the ideal observer index they were nearly indistinguishable. However, the parameters for the product model data generation were selected by generating compensatory data and finding the product model parameters which best fit the data, then using these product model parameters to generate the data. Other parameters for partially compensatory models might generate data that did not fit the compensatory model as well.

Bolt and Lall (2003) studied recovery of a 1PL product model with two dimensions using Monte Carlo Markov chains. They used an exploratory mode; all items measured both θs. The correct model provided better cross-validated fit than the compensatory model did. However, root mean square errors (RMSEs) of the b-parameters were large, much larger than typically seen with compensatory models, especially when the correlation between the θs was 0.6, the highest correlation they studied, although this would be quite low for cognitive θs. The covariance between the θs was recovered better as the number of examinees and items increased.

Simpson (2005) simulated data for a two-dimensional 1PL GMIRT model, a combination of the compensatory and product models, with all items loading on both factors. She found generally poor recovery of the item and person parameters, except for the compensation parameter that indicates the proportional weights of the compensatory and product models. Increasing the sample size or the correlation between the θs made little difference in the accuracy of parameter recovery. The GMIRT item difficulties were recovered much better if the model was specified with a single item difficulty, as is conventional for the compensatory model, instead of separate difficulties for each dimension, as is conventional for the product model.

Babcock (2011) explored a confirmatory 2PL product model with two dimensions. Unidimensional items were included to help anchor the axes. RMSE and bias in the item parameter estimates decreased as the number of unidimensional items increased, sample size increased, or correlation between the θs decreased. Babcock concluded that item parameter recovery was acceptable only with at least six unidimensional items on each dimension and a sample size of at least 4,000. Recovery of θ and of the correlation between the θs was less dependent on sample size. In contrast to the RMSEs for the item parameters, the RMSEs for the θ estimates decreased as the correlation between the θs increased, likely because information about one θ could be used in estimating the other θ.

Chalmers and Flora (2014) studied recovery of Sympson’s product model using an MH-RM algorithm in a confirmatory mode. Correlations among the dimensions were estimated well, especially for the 2PL data. θ recovery was also reasonably accurate. However, RMSE between the estimated and true item parameters tended to be quite large, much larger than the RMSEs for the unidimensional items included to anchor the rotation. RMSE was larger for 3PL data than for 2PL data, and larger for three dimensions than for two. For the 3PL data, as were considerably positively biased, ds, parameterized as item easiness, were negatively biased, and cs were somewhat positively biased; items appeared to be more discriminating and more difficult. For the two-dimensional, 2PL data, decreases in the correlation between abilities, increases in sample size or increases in number of simple structure items decreased the RMSE.

There has been even less work on recovery of parameters for the interaction model. Rizopoulos and Moustaki (2008) simulated data for a 2PL interaction model with two uncorrelated dimensions. All items measured both dimensions, so the analysis was exploratory. Bias was fairly small. RMSEs of item parameters decreased as sample size or test length increased. They did not examine the accuracy of recovery of θ, although they discussed procedures for estimating θ. Rizopoulos and Moustaki’s simulated data may not correspond well to cognitive tests; the main-effect a-parameter for one of the θs was negative, and the θs were uncorrelated. They suggested estimation might be more difficult for the interaction model if the θs were correlated.

Chalmers and Flora (2014) also examined how well the interaction model fit 2PL data generated using Sympson’s product model. Convergence was much faster, but the log-likelihood was lower. For the θ estimates, RMSE was only slightly larger.

In summary, there has been little research on parameter recovery with the linear interaction model. The only simulation studies to estimate this model were the following: (1) Chalmers and Flora (2014), who examined only a 2PL two-dimensional model, and only with data generated from a product model and (2) Rizopoulos and Moustaki (2008) who examined only an exploratory 2PL two-dimensional model with uncorrelated dimensions. Research is needed on the 3PL model, models with more dimensions, and data generated to fit the interaction model in addition to data generated to fit a product model. The interaction model may have the same difficulties as the product model with estimating the 3PL model or more than two dimensions, but it may prove easier to estimate under these conditions. Additionally, Chalmers and Flora appear to be the only published study of recovery of the 3PL product model or product models with more than two factors, so it is worthwhile to examine this model further.

The purpose of the current study is to assess the accuracy of parameter recovery for the interaction and product partially compensatory models, using data generated to fit 2PL and 3PL versions of both models with two or four dimensions, with varying numbers of unidimensional items and varying correlations among the θs. Accuracy will be judged by the bias and SE for the estimated correlations among θs, the RMSE between the true and estimated item response surfaces, bias and RMSE between the true and estimated item parameters, and correlations, bias, and RMSE between the θ true values and estimates. The information criteria from alternate models will also be compared.

Method

Each θ was measured by 25 items. As the number of θs changes, the total number of items and the number of items measuring each θ are necessarily confounded. Because in compensatory models the number of items measuring each θ seems to have the biggest influence, especially on θ recovery, this factor was kept constant such that the total number of items changed as the number of θs changed. For the 2-θ condition, there were 5 unidimensional items for each θ and 20 multidimensional items, for a total of 30 items. For the first 10 multidimensional items, both θs were conceptualized as equally weighted, a prototypical conjunctive relationship. In the product model, this was operationalized as equal item difficulties for both θs. In the interactive model, this was operationalized as equal a-parameters for both θs. For the next 10 multidimensional items, in the product model the item difficulty for θ₂ was kept constant, while the difficulty for θ₁ varied so that it was sometimes lower and sometimes higher than the difficulty for θ₂. This represents a conjunctive context in which a small amount of one skill is needed. In the interactive model, the main-effect a-parameters varied, sometimes higher for θ₁ and sometimes higher for θ₂, so that the item tapped one θ or the other more strongly.

For the 4-θ condition, there were 5 unidimensional items for each θ and 35 multidimensional items, for a total of 55 items. The first 30 multidimensional items measured one pair of θs, with each possible pair of θs mapped to 5 items. Each θ in the pair had the same difficulty (product model) and same a-parameter. The final 5 multidimensional items measured all 4 θs. Items that measure four distinct skills may not be very realistic, but were intended to challenge the algorithms.

Item difficulties were selected to keep observed proportion-correct between approximately 0.25 and 0.85 for the 2PL models. The difficulties and the theoretical proportion-corrects are shown in Tables 1 and 2 (4-θ condition available on request) for a multivariate standard normal population with no correlation among the θs. Aside from relatively equal proportion-correct, there was no effort to make the interaction item response functions (IRFs) similar to the product model IRFs to avoid privileging one model.

Table 1.

Unidimensional Item Parameters.

Item numbers: 2-θ	Item numbers: 4-θ	d	P, c = 0	P, c = 0.2
1, 6	1, 6, 11, 16	−2.250	0.84	0.87
2, 7	2, 7, 12, 17	−1.125	0.69	0.75
3, 8	3, 8, 13, 18	−0.750	0.63	0.70
4, 9	4, 9, 14, 19	0.000	0.50	0.60
5, 10	5, 10, 15, 20	1.125	0.31	0.45

Note. For items 1 to 5, a ₁ = 1.5 (0.88 on the normal metric); for Items 6 to 10, a ₂ = 1.5; for items 11 to 15, a ₃ = 1.5; for items 16 to 20, a ₄ = 1.5. All other as = 0. P is the theoretical proportion correct integrating over a standard multivariate normal distribution with 0 correlations among the θs.

Table 2.

Multidimensional Item Parameters: 2-θ Conditions.

Item	Interaction model					Product model
	d	a 1	a 2	P, c = 0	P, c = 0.2	d 1	d 2	P, c = 0	P, c = 0.2
11	−2.3	0.9	0.90	0.86	0.89	−3.375	−3.375	0.86	0.89
12	−1.9	0.9	0.90	0.81	0.85	−3.000	−3.000	0.82	0.85
13	−1.5	0.9	0.90	0.76	0.81	−2.625	−2.625	0.76	0.81
14	−1.1	0.9	0.90	0.69	0.75	−2.250	−2.250	0.70	0.76
15	−0.7	0.9	0.90	0.62	0.70	−1.875	−1.875	0.63	0.71
16	−0.3	0.9	0.90	0.55	0.64	−1.500	−1.500	0.56	0.65
17	0.1	0.9	0.90	0.47	0.58	−1.125	−1.125	0.48	0.58
18	0.5	0.9	0.90	0.40	0.52	−0.750	−0.750	0.40	0.52
19	0.9	0.9	0.90	0.33	0.46	−0.375	−0.375	0.32	0.46
20	1.3	0.9	0.90	0.26	0.41	0.000	0.000	0.25	0.40
21	−2.3	1.2	0.50	0.86	0.89	−4.500	−2.250	0.81	0.85
22	−1.9	1.1	0.65	0.81	0.85	−3.900	−2.250	0.80	0.84
23	−1.5	1.0	0.80	0.76	0.81	−3.300	−2.250	0.77	0.82
24	−1.1	1.0	0.80	0.69	0.75	−2.700	−2.250	0.74	0.79
25	−0.7	1.2	0.50	0.62	0.70	−2.100	−2.250	0.69	0.75
26	−0.3	1.2	0.50	0.55	0.64	−1.500	−2.250	0.63	0.70
27	0.1	1.0	0.80	0.47	0.58	−0.900	−2.250	0.55	0.64
28	0.5	1.0	0.80	0.40	0.52	−0.300	−2.250	0.46	0.57
29	0.9	1.1	0.65	0.33	0.46	0.300	−2.250	0.37	0.50
30	1.3	1.2	0.50	0.27	0.41	0.900	−2.250	0.29	0.43

Note. For the interaction model, a ₃ = 0.3 for items 11 to 30. For the product model, all as = 1.5. P is the theoretical proportion correct integrating over a standard multivariate normal distribution with 0 correlations among the θs.

For the unidimensional and product items, the a-parameters were 1.5 (0.88 on the normal metric) for low-to-moderate discrimination. The main effect a-parameters for the interaction items were 0.9 (0.53 on the normal scale). The last 10 items in the 2-θ condition were an exception: The main effect a-parameters varied, with $\sqrt{a_1^2+a_2^2}=1.3.$ The interaction a-parameters were 0.3, so the point at which probabilities began increasing for decreasing θ would occur at −3, −3 (except for the last 10 items in the 2-θ condition), a region where there were few examinees. Items 51 to 55 were exceptions; all six interaction a-parameters within each item equaled 0.1.

θs followed a standard multivariate normal distribution with correlations among the factors of 0, 0.7, or 0.9. A correlation of zero might occur between a cognitive θ and a θ that represented a personality factor. The zero correlation also served as a baseline for the other correlations. A correlation of 0.7 is the low end of what one might see for different content areas, and a correlation of 0.9 is the higher end of what one might see for different content areas or the lower end for what one might see for different subscales within a content area, such as algebra, geometry, probability, and number sense within mathematics. The lower asymptote was either 0 or 0.2 for all items.

In summary, the conditions were the following: Two generating models by two levels of number of θs by three correlations by two lower asymptotes. The data was generated for 100 replications.

For both the interaction and product model data, item parameters were estimated using each of the partially compensatory models as well as the compensatory model. The model was correctly specified as either 2PL or 3PL; the lower asymptote was not estimated when it was 0 in the data. Version 1.5 of the package mirt (Chalmers, 2012) in R 3.1.1 was used for estimation. The EM algorithm was selected, with 21 quadrature points per θ in the 2-θ condition and 15 quadrature points per θ in the 4-θ condition. The stopping criteria was set at a largest change of <0.001. Preliminary runs suggested that the interaction model needed only a few more iterations to converge at 0.0001, but the product model needed far more iterations, if it converged at all, for a criterion of 0.0001. Priors for the item parameters were selected to be relatively diffuse to avoid a large impact on the estimates, yet informative enough to prevent unreasonable values. They were also chosen not to perfectly match the true item parameters. Priors were N(1.7, 0.8²) for the main effect as, N(0, 1) for the interaction as, N(0, 3²) for the interaction and compensatory ds and the ds for the unidimensional items, N(1, 2²) for the multidimensional item ds in the product model, and N(−1.73, 0.4²) for the logit cs (corresponding to mean c = 0.15). Based on the estimated item parameters, expected-a-posteriori (EAP) qs were estimated.

Results

Model Fit

Model fit was assessed using information criteria: Akaike information criterion (AIC), Bayesian information criterion (BIC), and sample-size-adjusted Bayesian information criterion (SA-BIC). These indices include a penalty for the number of parameters estimated, but the penalty is greatest for the BIC. The indices are defined as follows:

$$\mathrm{AIC}=-2\mathrm{LL}+2\mathrm{p},$$

$$\mathrm{BIC}=-2\mathrm{LL}+\mathrm{p}\left(\ln \left(\mathrm{N}\right)\right),$$

and

$$\mathrm{SA}-\mathrm{BIC}=-2\mathrm{LL}+\mathrm{p}\left(\ln ((\mathrm{N}+2)/24)\right),$$

where LL is the log-likelihood, p is the number of parameters estimated, and N is the sample size. Smaller indices indicate better fit, but there is no statistical significance test. In the 2-θ condition, both partially compensatory models have the same number of estimated parameters, 20 more than the compensatory model because each multidimensional item has an additional interaction term in the interaction model or an additional item difficulty in the product model. In the 4-θ condition, compared to the compensatory model the last five items each have an additional six parameters in the interaction model but an additional three parameters in the product model. Thus, the interaction model has 15 more parameters than the product model, and 60 more than the compensatory model.

To summarize fit, the estimation model with the smallest value for an index was labelled the selected model for that index, with the results tabulated in Table 3. All three indices tended to select the correct model when the data were generated by the interaction model and c = 0. This was also true for the product model when r = 0, for both levels of c. In other conditions, the AIC tended to choose the correct model (except for the product data with c = 0.2 and r = .7 or .9), but the BIC and SSA-BIC tended to choose the more parsimonious compensatory model.

Table 3.

Number of Replications in Which Each Estimation Model Was Selected by AIC, BIC, SSA-BIC.

			c = 0 Estimation model			c = 0.2 Estimation model
	r	Generating model	Interaction	Product	Compensatory	Interaction	Product	Compensatory
2-θ		Interaction
	0		100/100/100	0/0/0	0/0/0	100/0/28	0/0/0	0/100/72
	.7		100/100/100	0/0/0	0/0/0	96/0/0	0/0/0	4/100/100
	.9		100/100/100	0/0/0	0/0/0	95/0/0	0/0/0	5/100/100
		Product
	0		0/0/0	100/100/100	0/0/0	0/0/0	100/80/100	0/20/0
	.7		0/0/0	99/0/6	1/100/94	0/0/0	9/0/0	91/100/100
	.9		1/0/0	79/0/0	20/100/100	1/0/0	1/0/0	98/100/100
4-θ
		Interaction
	0		100/100/100	0/0/0	0/0/0	100/0/61	0/0/0	0/100/39
	.7		100/99/100	0/0/0	0/1/0	93/0/0	0/0/0	7/100/100
	.9		100/100/100	0/0/0	0/0/0	75/0/0	0/0/0	25/100/100
		Product
	0		0/0/0	100/100/100	0/0/0	0/0/0	100/100/100	0/0/0
	.7		0/0/0	100/0/48	0/100/52	0/0/0	57/0/0	43/100/100
	.9		0/0/0	100/0/0	0/100/100	0/0/0	0/0/0	100/100/100

Note. AIC = Akaike information criterion; BIC = Bayesian information criterion; SSA-BIC = sample-size-adjusted Bayesian information criterion. First value in each cell corresponds to AIC, followed by BIC and SSA-BIC.

Correlations Among θs

Recovery of the correlations was measured by bias and SE and reported in Table 4. These were the direct estimates of the correlations, not the correlations between the estimated $\hat{\theta }\mathrm{s}.$ Generally, the correlations were estimated reasonably well when either the correct model or the compensatory model was used for estimation, with the exception of the .9 correlation with c = 0.2. In this condition, the correlation was consistently underestimated by all models, especially when there were only 2 θs. In all other conditions, using the product model on interaction data led to overestimates of the correlation. In a few conditions, using the interaction model on product data yielded underestimates of the correlation.

Table 4.

Bias and Standard Error of Estimated Correlation.

			c = 0 Estimation model			c = 0.2 Estimation model
	r	Generating model	Interaction	Product	Compensatory	Interaction	Product	Compensatory
2-θ		Interaction
	0		−0.01 (0.02)	0.06 (0.02)	0.00 (0.02)	0.00 (0.02)	0.07 (0.02)	0.01 (0.03)
	.7		−0.01 (0.02)	0.02 (0.02)	0.01 (0.02)	−0.01 (0.02)	0.00 (0.02)	−0.01 (0.02)
	.9		−0.03 (0.01)	0.02 (0.01)	0.00 (0.01)	−0.05 (0.01)	−0.05 (0.02)	−0.05 (0.01)
		Product
	0		−0.08 (0.02)	0.00 (0.02)	−0.01 (0.02)	−0.07 (0.03)	0.00 (0.03)	0.00 (0.03)
	.7		−0.01 (0.01)	0.00 (0.02)	0.00 (0.02)	−0.01 (0.02)	−0.01 (0.02)	−0.01 (0.02)
	.9		−0.04 (0.01)	−0.03 (0.01)	−0.01 (0.01)	−0.05 (0.01)	−0.05 (0.01)	−0.05 (0.01)
4-θ
	0	Interaction	0.00 (0.02)	0.04 (0.02)	0.00 (0.02)	0.00 (0.02)	0.04 (0.02)	0.00 (0.02)
	.7		0.01 (0.01)	0.03 (0.01)	0.00 (0.01)	0.00 (0.02)	0.02 (0.02)	0.00 (0.02)
	.9		−0.01 (0.01)	0.03 (0.02)	−0.01 (0.01)	−0.02 (0.01)	−0.02 (0.01)	−0.02 (0.01)
		Product
	0		−0.02 (0.02)	0.00 (0.02)	0.00 (0.02)	−0.02 (0.02)	0.00 (0.02)	0.00 (0.02)
	.7		0.01 (0.01)	0.01 (0.01)	0.00 (0.01)	0.00 (0.02)	0.00 (0.02)	0.00 (0.02)
	.9		0.00 (0.01)	0.00 (0.01)	−0.01 (0.01)	−0.02 (0.01)	−0.02 (0.01)	−0.02 (0.01)

Note. The value outside the parentheses is the estimated bias, and the value in parentheses is the standard deviation across replications.

Item Response Functions

Overall recovery of the item response function (IRF) was assessed by RMSE, defined as

$$\sum _{{\theta }_1}\sum _{{\theta }_2}\sum _{r}g({\theta }_1,{\theta }_2){[\hat{P}({\theta }_1,{\theta }_2)-P({\theta }_1,{\theta }_2)]}^2/R,$$

where g(θ₁, θ₂) is the density from a bivariate normal distribution, $\hat{P}$ is the estimated probability based on the estimated item parameters, which may be from a different model than the true parameters, P is the probability based on the true parameters, and R is the number of replications. The equation can be generalized for more dimensions. The integration was approximated at 625 points in the 2-θ conditions or 390,625 points in the 4-θ conditions, 25 for each dimension.

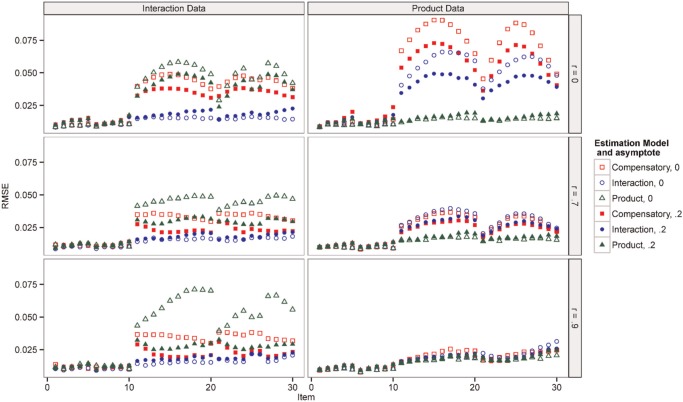
Table 5 shows the mean RMSE. Across items, the RMSE was lowest for the correct model. The compensatory RMSE was lower than the product RMSE for the interaction data, but the interaction RMSE was as low or lower than the compensatory RMSE for the product data. However, these means masks differences among items. Figure 2 shows the RMSE for each item in the 2-θ condition. Items 1 to 10 were unidimensional items. All three models are identical for these items, so in isolation, these items should be recovered well by any of the models, but the presence of the multidimensional items might have impacted the recovery of the IRF for the unidimensional items. However, this does not seem to have occurred, except to a small degree for the most difficult items when r = 0.

Table 5.

RMSE of Item Response Function, Averaged Across Items.

			c = 0 Estimation model			c = 0.2 Estimation model
	r	Generating model	Interaction	Product	Compensatory	Interaction	Product	Compensatory
2-θ
		Interaction
	0		0.014	0.041	0.037	0.017	0.035	0.030
	.7		0.014	0.038	0.028	0.016	0.025	0.020
	.9		0.015	0.048	0.029	0.017	0.024	0.020
		Product
	0		0.047	0.013	0.062	0.036	0.015	0.051
	.7		0.027	0.014	0.026	0.024	0.016	0.022
	.9		0.018	0.015	0.019	0.018	0.017	0.017
4-θ
	0	Interaction	0.014	0.045	0.034	0.017	0.038	0.028
	.7		0.015	0.039	0.029	0.019	0.027	0.020
	.9		0.013	0.050	0.030	0.018	0.023	0.020
		Product
	0		0.041	0.014	0.061	0.032	0.016	0.049
	.7		0.028	0.015	0.026	0.025	0.016	0.022
	.9		0.018	0.016	0.017	0.019	0.016	0.016

Note. RMSE = root mean square error.

Figure 2.

Root mean square error of item response function, 2-θ conditions.

For the remainder of the items, the IRF was better recovered by the correct model (plotted as circles for the interaction model and triangles for the product model), although the differences were quite small for the product model data when r = .9. When one of the wrong models was used (product or compensatory for the interaction data, or interaction or compensatory for the product data), the 3PL version (filled shapes) of the wrong model tended to fit better than the 2PL version (open shapes). Recall that the data and estimation model were not crossed; 2PL data were fit only by 2PL models and 3PL data were fit by 3PL models, so one might expect the 2PL data to be easier to recover. However, the extra parameter in the 3PL models apparently gave greater flexibility to fitting the IRF when the wrong model form was used. Item difficulty also impacted the recovery of the IRF. Each set of 5 or 10 items increased in difficulty. When the correct model was applied to the data, the RMSE increased slightly as item difficulty increased for the 3PL data and stayed constant for the 2PL data. When the wrong model was applied, for r = 0 (and r = .7 for the product data), the middle difficulty items had the largest RMSEs. For the other three conditions when the wrong model was applied, the trend depended on an interaction between estimation model, data model, and r.

Finally, Items 51 to 55 in the 4-θ conditions (not shown) loaded on all four θs instead of pairs of θ. For the interaction data, the RMSE tended to be larger for these items for all three estimation models. For the product data, there was no clear trend, depending on the combination of estimation model and r.

Individual Item Parameters

When the generated model was the same as the estimation model, recovery of individual item parameters was also studied. The IRF might be recovered well even when the item parameters were poorly estimated because errors in one parameter could compensate for errors in another parameter. The values are averaged across items in Tables 6 and 7. For both models, note that d in Equations 1 to 3 was the item difficulty, not the item easiness, so negative bias indicates the item was estimated to be easier than the true value. Although this is opposite the conventional direction used in the compensatory model, it is consistent with the typical direction of the item difficulty in the product model.

Table 6.

Interaction Model: Bias and RMSE of Item Parameter Estimates, Averaged Across Items.

		c = 0						c = 0.2
		Parameter						Parameter
		Main effect a		Interaction a		d		Main effect a		Interaction a		d		c
r		Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE
2-θ	0	0.010	0.056	0.008	0.066	−0.002	0.049	0.000	0.110	0.000	0.109	−0.061	0.153	−0.026	0.040
	.7	0.025	0.091	0.019	0.075	−0.020	0.057	0.000	0.148	0.023	0.146	−0.082	0.150	−0.033	0.042
	.9	0.024	0.147	0.011	0.071	−0.026	0.060	0.006	0.220	0.032	0.134	−0.090	0.150	−0.034	0.043
4-θ
	0	0.012	0.058	0.003	0.058	−0.003	0.052	0.003	0.114	−0.002	0.094	−0.052	0.166	−0.027	0.040
	.7	0.026	0.092	0.012	0.105	−0.016	0.057	0.016	0.161	0.001	0.227	−0.085	0.169	−0.031	0.042
	.9	0.032	0.116	0.020	0.103	−0.021	0.071	0.014	0.219	0.014	0.279	−0.100	0.163	−0.033	0.042

Note. RMSE = root mean square error.

Table 7.

Product Model: Bias and RMSE of Item Parameter Estimates, Averaged Across Items.

		c = 0				c = 0.2
		Parameter				Parameter
		a		d		a		d		c
	r	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE
2-θ	0	0.011	0.134	0.001	0.187	−0.009	0.197	−0.046	0.254	−0.024	0.037
	.7	0.018	0.200	0.004	0.282	0.007	0.234	−0.029	0.320	−0.020	0.035
	.9	0.026	0.243	0.008	0.409	0.021	0.245	−0.023	0.470	−0.020	0.034
4-θ
	0	0.029	0.154	−0.019	0.243	0.015	0.218	−0.072	0.316	−0.024	0.037
	.7	0.048	0.201	−0.019	0.295	0.042	0.246	−0.063	0.350	−0.020	0.036
	.9	0.057	0.242	−0.043	0.396	0.047	0.261	−0.092	0.448	−0.020	0.035

Note. RMSE = root mean square error.

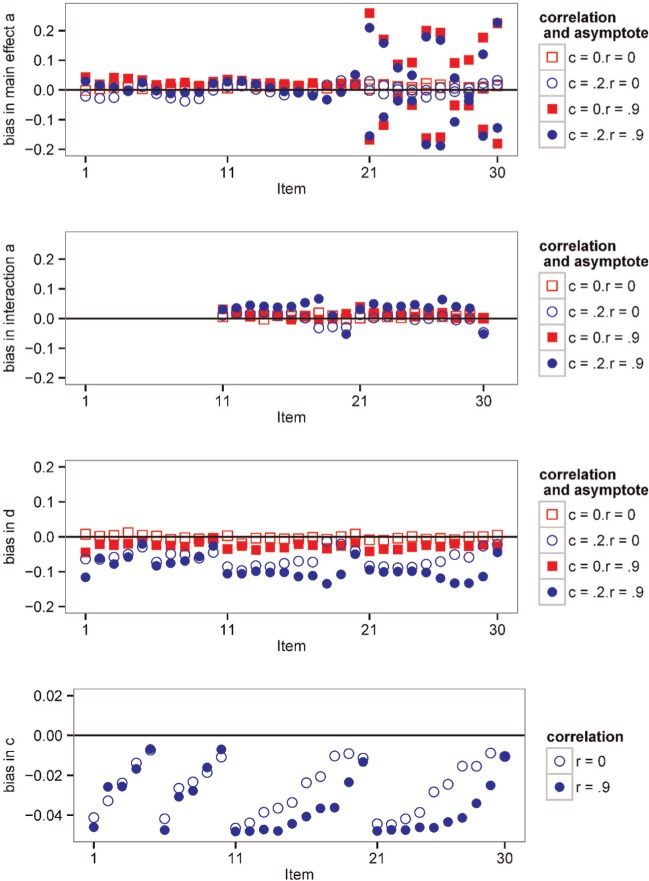
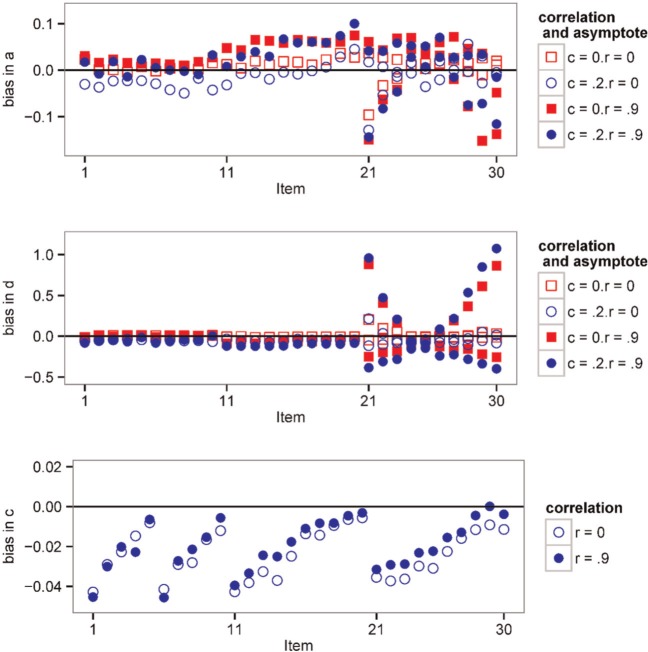
Figures 3 and 4 show the bias in each parameter for the 2-θ conditions. Whenever two or more parameters had the same true value within an item, their bias was averaged. The interaction and product models should not be directly compared because the parameters have different meanings, except for the c-parameter.

Figure 3.

Parameter recovery, 2-θ interaction model.

Figure 4.

Parameter recovery, 2-θ product model.

Interaction Model

Averaged across items, bias in the a-parameters was small but the RMSEs were about twice as large for the 3PL data compared with the 2PL data. The d-parameters had both more negative bias and larger RMSEs for the 3PL data. Looking at individual items, bias in the a-parameters for the main effects was generally quite small for the unidimensional items and for the items with equal as (Items 1-20). When r = .9, the easiest item in each set had positive bias, followed by less positive, or sometimes negative, bias for more difficult items. For the 2-θ conditions, when r = 0, bias remained small for Items 21 to 30, but when r = .9, a ₁ was negatively biased and a ₂ was positively biased. Items 21 to 30 had larger a ₁ but smaller a ₂, so this pattern indicates that when there was a high correlation between the θs the as were estimated to be of similar magnitude. This same pattern was seen for Items 51 to 55 in the 4-θ conditions (not shown), which measured all 4 θs but to differing degrees. Bias in the a-parameters for the interaction effects was small for all items and conditions, except that in the 4-θ, c = 0, r = .9 condition the easiest item in each set showed the most positive bias.

Averaged across items (Table 6), bias in the d-parameters was nearly zero for r = 0, c = 0, and slightly negative for higher correlations with c = 0. Bias was more negative for c = 0.2. Considering individual items, bias in the d-parameters was near 0 for all items when r = 0, c = 0, except for the easiest items in the 4-θ condition, in which bias was slightly negative. Bias was slightly negative for c = 0, r = .9, and more negative when c = .2, perhaps because of the bias in c. The c-parameters tended to have a small negative bias, with the bias more negative for the easier items and for r = 0.9. The easier items were pulled more toward the prior (mean = .15) because there was less information for estimating c for the easier items. Negative bias in the c-parameter should make items look slightly easier and slightly less discriminating. This was evident for the ds, and to a lesser extent in the main effect as, where the small positive bias for c = 0 decreased to nearly zero for c = 0.2.

Product Model

Bias in the a-parameters was slightly positive on average (Table 7), increasing as r increased. The RMSE, however, was large, indicating there was a great deal of variance across replications. Looking at the individual items, bias was generally quite small for the unidimensional items (Items 1-10). For the items that measured both θs equally (Items 11-20), the bias was somewhat positive, especially for r = .9. In the 2-θ conditions when d ₁ was lower than d ₂ (Items 21-23), a ₁ was negatively biased and a ₂ was positively biased, but when d ₁ was considerably higher than d ₂ (Items 27-30), a ₁ was positively biased and a ₂ was negatively biased. In other words, the item was estimated to discriminate slightly better than it really did for the harder skill. However, this pattern did not seem to hold for Items 52 to 55 in the 4-θ conditions; the bias of the as within each item varied less systematically.

Averaged across items, bias in the d-parameters was near 0 for the 2-θ 2PL data and negative for the other conditions. As with the a-parameters, the RMSEs were large. Focusing on individual items, the d-parameters was near 0 for the unidimensional items and for the items that measured both θs equally (Items 11-20). Bias remained near zero for the other items when r = 0, but when r = .9 the bias depended on the relative size of the d. When d ₁ was lower than d ₂ (Items 21-23), d ₁ was positively biased and d ₂ was negatively biased, but when d ₁ was higher than d ₂ (Items 27-30), d ₁ was negatively biased and d ₂ was positively biased. In other words, the easy skill appeared to be harder than it was, and the difficult skill appeared to be somewhat easier than it was.

Similar to the interaction model, the c-parameters tended to have a small negative bias, with the bias more negative for the easier items. This in turn led to slightly more negative bias in the d-parameter for the easiest items.

θ Estimation

Finally, accuracy in θ estimation was indexed by the correlation between true θ and $\hat{\theta }$ (the square root of reliability), and conditional bias and standard error in the 2-θ conditions. The correlations, shown in Tables 8 and 9, were based on the multivariate-normal data simulated to estimate the item parameters. For the 4-θ conditions, results were averaged across the θs because each θ was measured by identical parameters, unlike the 2-θ conditions where some of the interaction items measured θ₁ more than θ₂ and some of the product model items had different difficulties for θ₁ and θ₂. The standard error (standard deviation across replications) is not shown because it was quite small, with a maximum of 0.005. The correlation based on the correct estimation model was always as high or higher than the correlation from the wrong models, but differences were small. Correlations were reduced when c = 0.2 because there is less information when the data includes some degree of correct guessing.

Table 8.

Correlation Between True and Estimated θ, 2-θ Conditions.

		c = 0						c = 0.2
		Estimation model						Estimation model
		Interaction		Product		Compensatory		Interaction		Product		Compensatory
r	Generating model	θ1	θ2	θ1	θ2	θ1	θ2	θ1	θ2	θ1	θ2	θ1	θ2
	Interaction
0		0.88	0.85	0.87	0.84	0.87	0.84	0.83	0.79	0.83	0.79	0.83	0.79
.7		0.91	0.89	0.91	0.89	0.91	0.89	0.88	0.86	0.88	0.86	0.88	0.86
.9		0.93	0.93	0.93	0.92	0.93	0.92	0.91	0.90	0.91	0.90	0.91	0.90
	Product
0		0.87	0.85	0.88	0.86	0.86	0.84	0.82	0.80	0.82	0.81	0.81	0.79
.7		0.91	0.89	0.91	0.90	0.91	0.89	0.88	0.87	0.88	0.87	0.88	0.87
.9		0.93	0.93	0.93	0.93	0.93	0.92	0.91	0.90	0.91	0.90	0.91	0.90

Note. Bold values indicate the correct model.

Table 9.

Correlation Between True and Estimated θ, 4-θ Conditions.

		c = 0			c = 0.2
		Estimation model			Estimation model
r	Generating model	Interaction	Product	Compensatory	Interaction	Product	Compensatory
	Interaction
0		0.88	0.87	0.87	0.83	0.82	0.82
.7		0.91	0.90	0.91	0.88	0.88	0.88
.9		0.94	0.92	0.93	0.92	0.92	0.92
	Product
0		0.86	0.87	0.85	0.81	0.81	0.80
.7		0.90	0.91	0.91	0.88	0.88	0.88
.9		0.94	0.94	0.94	0.92	0.92	0.92

Note. Results were similar for all four dimensions and thus are averaged. Bold values indicate the correct model.

Even though the correlations between true and estimated θs were similar regardless of the estimation model, there might be systematic differences in the bias. For the conditional bias and standard error of θ (2-θ conditions only), a new set of 169 (13 for each θ) uniformly spaced θs were generated. These same θs were replicated, with new random responses, 100 times; each replication was scored based on a different set of item parameter estimates from the multivariate-normal data. The fixed θs were useful to get a precise estimate of the conditional bias and standard error at each point, but they would not be an appropriate sample for estimating the item parameters. Using the item parameter estimates from the multivariate normal samples allowed for a realistic degree of error in the item parameter estimates to contribute to error in the θ estimates.

To summarize the information across the θ distribution, the bias, error variance, and RMSE values were weighted by the density at each point and averaged, as shown in Table 10. Bias averaged nearly to zero across θs and thus was not included in the table. Overall, it made little difference whether the correct or an alternative model was used to estimate the θs. For a given condition and data generation model, the SE and RMSE were quite similar for all three estimation models.

Table 10.

Mean Conditional Standard Error and RMSE of θ, 2-θ Conditions.

			c = 0						c = 0.2
			Estimation model						Estimation model
			Interaction		Product		Compensatory		Interaction		Product		Compensatory
	r	Generating model	θ1	θ2	θ1	θ2	θ1	θ2	θ1	θ2	θ1	θ2	θ1	θ2
SE
		Interaction
	0		0.40	0.43	0.40	0.43	0.40	0.43	0.43	0.45	0.43	0.45	0.43	0.46
	.7		0.32	0.32	0.31	0.32	0.31	0.32	0.36	0.36	0.36	0.36	0.36	0.36
	.9		0.29	0.30	0.29	0.30	0.29	0.29	0.34	0.34	0.34	0.34	0.34	0.34
		Product
	0		0.41	0.42	0.40	0.41	0.41	0.42	0.45	0.45	0.44	0.44	0.44	0.44
	.7		0.33	0.34	0.33	0.34	0.33	0.34	0.37	0.37	0.37	0.37	0.37	0.37
	.9		0.30	0.29	0.30	0.29	0.30	0.29	0.33	0.33	0.34	0.33	0.34	0.33
RMSE
		Interaction
	0		0.48	0.53	0.49	0.54	0.49	0.54	0.55	0.60	0.56	0.61	0.56	0.61
	.7		0.41	0.44	0.42	0.45	0.42	0.44	0.48	0.51	0.48	0.51	0.48	0.51
	.9		0.36	0.38	0.37	0.39	0.37	0.39	0.42	0.44	0.42	0.44	0.42	0.44
		Product
	0		0.50	0.53	0.48	0.51	0.51	0.54	0.57	0.60	0.56	0.59	0.59	0.61
	.7		0.42	0.45	0.42	0.45	0.42	0.45	0.48	0.50	0.48	0.50	0.48	0.50
	.9		0.36	0.37	0.36	0.37	0.36	0.37	0.42	0.41	0.42	0.41	0.42	0.41

Note. SE = standard error; RMSE = root mean square error.

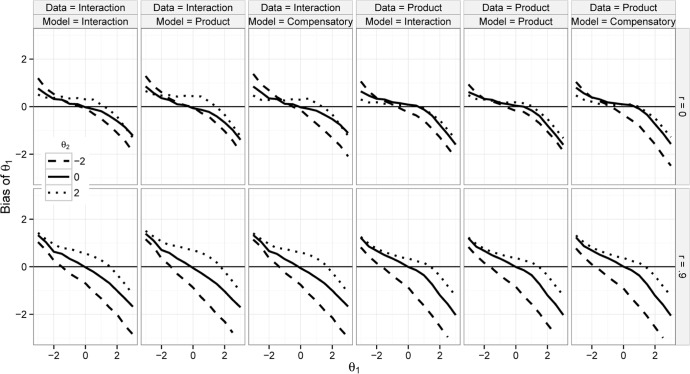
The difference between the SE and RMSE reflects the fact that the conditional bias was nonnegligible for some levels of θ even though the average bias was nearly zero. Because multidimensional plots can be hard to compare, Figure 5 shows the bias in θ₁ as a function of θ₁ at three fixed values of θ₂, cross-sections of the 3-D plot projected into the plane. To save space, only r = .9 and r = 0 are shown. Patterns were similar across c-parameters so only c = 0 is shown. When r = .9, the cross-sections of the prior were ellipsoidal and estimates of θ₁ were pulled toward the estimate of θ₂ as well as toward the mean of θ₁. Thus for more extreme θ₁, the bias was smallest in absolute value when θ₁ and θ₂ had the same sign. When r = 0, the prior for θ₁ was independent of θ₂; thus the relationship between θ₁ and θ₂ was not because of the prior. Rather, it was because of the effect that θ₂ has on the function relating θ₁ to the probability of correct response in partially compensatory models. Reckase (2007) noted that in the product model this conditional function reaches an upper asymptote of P(θ₂). When θ₂ is low, the slope of the conditional function is almost flat; little information is provided about the value of θ₁. The influence of the prior is inversely proportional to the information, so estimates of θ₁ are pulled into the mean more when θ₂ is low. Wang and Nydick (2015) also described this concept in terms of information.

Figure 5.

Conditional bias of θ₁, 2-θ conditions.

Note. The bias is plotted as a function of θ₁ at three fixed values of θ₂.

Discussion and Implications

In terms of information criteria, when the θs were highly correlated, the 2PL compensatory model fit the 2PL product data better than the correct model did. Looking back at Figure 1, the hardest areas for the compensatory model to fit partially compensatory data seem to be the areas where one θ is high and the other is low. These areas have very few examinees when the θs are highly correlated, and thus have little impact on the parameter estimation. These are the same areas where the discrepancy between the 2PL compensatory and the 2PL interaction model is greatest also, but the compensatory model did not generally fit better in that comparison. Perhaps this is because the interaction model is only slightly harder to fit than the compensatory model, but the product model is much more complicated. Model complexity often refers simply to the number of parameters, but in this context the product model may present additional estimation difficulties because of the model form. However, for the 3PL data, the compensatory model tended to fit both the interactive and the product model data better than the correct models when the θs were moderately or highly correlated. The flattening of the response surface because of the c-parameter may have made the partially compensatory function easier to fit with the compensatory model. Or possibly the extra parameter gave the compensatory model additional flexibility. The information criteria might lead to selecting the compensatory model, but it likely would not lead to selecting the wrong partially compensatory model. This is consistent with Chalmers and Flora’s (2014) finding that the LL was lower when product model data were fit to the product model rather than the interaction model. Bolt and Lall (2003) also found that the product model slightly but consistently fit 1PL product model data better than the compensatory model.

The compensatory model estimated the correlations among the θs as well as the correct model did. When the correlation was zero, the product model tended to overestimate the correlation in interaction data and the interaction model tended to underestimate the correlation in product model data. With higher correlations, the match of the model to the data made little difference. Researchers primarily interested in the correlations might prefer to use the simpler compensatory model, but the results would not vary too much if the wrong partially compensatory model were applied.

The RMSE of the response function was lower when the correct model was fit to the data. Thus, researchers who want to model the response probabilities accurately would benefit from using the correct model. This may be difficult with real data, where the RMSE of course is unknown and the information criteria may suggest the compensatory model is a better fit. Fortunately, the compensatory model is most likely to be erroneously selected when the correlations among the θs are high, which is also the context in which the compensatory model has RMSE closest to the correct model. The response surface is still misestimated, but the density is low in the most problematic regions so the response probabilities are estimated well for most examinees.

Although the response function as a whole had reasonable RMSE when the correct model was used, the RMSE for the item parameters seemed quite large for the product model, consistent with the results of Bolt and Lall (2003) and Chalmers and Flora (2014). For both models, individual item parameters had little bias for most items. However, in the interaction model the items that had different a-parameters for each θ tended to have biased a-parameters when the correlation between the θs was high. Similarly, in the product model the items that had different d-parameters for each θ tended to have bias in both the a-parameters and the d-parameters when the correlation between the θs was high. The bias was particularly large for some of the d-parameters; Chalmers and Flora (2014) also found large bias in d for 3PL data, but in the current study the bias was almost as severe for some 2PL items and the direction of the bias depended on the size of the d relative to other ds in the same item. The bias for c was small both in the current study and in Chalmers and Flora’s work but in opposite directions. The negative bias in the current study was likely because of the influence of the prior on the easiest items. Overall, highly correlated θs, as are generally seen for cognitive constructs, seem to present a particular challenge for estimating individual item parameters, even if the response function as a whole and the θs are estimated accurately. Babcock (2011), Bolt and Lall (2003), and Chalmers and Flora (2014) each found correlated θs increased the bias and/or RMSE in item parameters for the product model.

Corroborating Babcock’s findings, RMSE of the θ estimates decreased, and correlations with the true parameters increased, as r increased, in contrast to the opposite pattern for item parameter or response function RMSE. More correlated θs can share information, increasing accuracy. θ estimates appear to have approximately the same correlation with the true value and RMSE regardless of the model applied. Chalmers and Flora (2014) reported similar findings regarding the θ estimates from the interaction model applied to product model data. Researchers interested only in the θ estimates would get reasonable results from the simpler compensatory model.

Limitations and Further Study

As with all simulations, the number and types of conditions were limited. To give a good chance of accurate estimation, five unidimensional items were included for each θ to help anchor the solution. Further research should explore fewer unidimensional items or purely exploratory models in which all items are free to potentially load on all θs.

Many of the multidimensional items measured both θs equally. Recovery of the individual item parameters, although not recovery of the item response function, was worse for items which measured one θ more than the other, operationalized in the interaction model as different a-parameters and in the product model as different d-parameters. Including more of these types of items might be more interesting and more realistic. Additionally, different as, as well as different ds, could be simulated within some product model items, as Chalmers and Flora (2014) did. Furthermore, parameterizing the product model to have a single difficulty might yield more accurate parameter estimates when the difficulties vary by dimension, as Simpson (2005) found with the GMIRT model, although separate difficulties are appealing for cognitive interpretation.

In brief, the results of this study suggest that both of the partially compensatory models can be estimated with reasonable accuracy, with the exception of the product model item parameters. However, if one is primarily interested in either the correlations or the θ estimates, the compensatory model appears to work almost as well.