An Effect Size Measure for Raju’s Differential Functioning for Items and Tests

Abstract

This study established an effect size measure for differential functioning for items and tests’ noncompensatory differential item functioning (NCDIF). The Mantel–Haenszel parameter served as the benchmark for developing NCDIF’s effect size measure for reporting moderate and large differential item functioning in test items. The effect size of NCDIF is influenced by the model, the discrimination parameter, and the difficulty parameter. Therefore, tables of NCDIF’s effect size were presented at given levels of a, b, and c parameters. In addition, a general effect size recommendation for moderate and large NCDIF is also established.

Differential item functioning (DIF), often conceptualized in the context of item response theory (IRT), is a term used to describe test items that may favor one group over another after being matched on ability. It is important to determine whether an item is functioning significantly different for one group over another regardless as to why. Hypothesis testing is used to determine statistical significant DIF items (Monahan, McHorney, Stump, & Perkins, 2007). When hypothesis testing is conducted and a test item is flagged as significant, this test item functions differently for the examinees being measured. Typically, when test items are categorized as DIF, test publishers may remove these test items from the test bank. Constructing standardized tests is an arduous and costly process (Ramsey, 1993). A cost as described by Zieky (1993) is the fact that “the decisions associated with DIF are likely to be scrutinized in the adversarial arenas of legislation and litigation” (p. 337). Given the laborious nature of test construction and its cost, flagging a test item based only on hypothesis testing is not sufficient evidence to remove the test item. An effect size (ES) measure can be used in conjunction with a significant finding, to determine if DIF is large enough to warrant removal of the test item (Cohen, 1988; Hidalgo & Lopez, 2004; Kirk, 1996; Monahan et al., 2007).

Why use an ES if an item exhibits statistically significant DIF? DIF statistical techniques require large sample sizes. It is well known that the larger the sample size, the higher the probability of yielding a statistical significant finding. Moreover, an insignificant finding with a small sample may have a meaningful ES. Statistical significance does not guarantee practical significance; therefore, an ES helps quantify an insignificant finding with small samples and a statistical significant finding with large samples. A significance test answers only one important research question. In discussing significance testing, Hays (1981) states, “Virtually any study can be made to show statistically significant results if one uses enough subjects” (p. 293). There are two other important questions that must be answered beyond significance testing. If the observance is real, than how large is it? Next, is the size large enough to be useful (Kirk, 2001)? The importance of utilizing an ES with a statistical significance finding has been demonstrated in the DIF literature (DeMars, 2009; Meade, 2010; Jodoin & Gierl, 2001).

The differential functioning for items and tests (DFIT) framework as of today consists of a comprehensive set of methods for assessing DIF. Dichotomous and polytomous test items can be investigated. Unidimensional and multidimensional models can be the bases for investigating DIF. Individual test items as well as the entire test can be analyzed for differential item/test functioning. Uniform and nonuniform DIF can be detected equally effectively. Additional capabilities are also possible as stated by Oshima and Morris (2008): “It has been extended to a variety of applications such as differential bundle functioning (DBF) and conditional DIF” (p. 44). In addition, DFIT is the only parametric technique capable of handling multidimensional models. The major drawback today as related to DFIT is that it only lacks an ES measure.

Today, Mantel–Haenszel (MH) is arguably one of the most widely used approaches to studying DIF in operational settings (Clauser & Mazor, 1998). Consequently, other researchers have used the ES guidelines developed for MH by Educational Testing Service (ETS) as a benchmark in proposing the ES measures for other DIF indices.

SIBTEST’s ES guidelines were initially defined by Nandakumar (1993). These guidelines are not comparable with the ETS’s MH categories of negligible, moderate, and large DIF. Given the extensive research, popularity, and familiarity with the ETS’s categories of DIF, Roussos and Stout (1996) devised a method by which values of SIBTEST’s measure of DIF ${\hat{\mathrm{\beta }}}_{\mathrm{UNI}}$ could be interpreted using the ETS’s categories. ETS’s MH measure of DIF ${\hat{\mathrm{\Delta }}}_{\mathrm{MH}}$ and ${\hat{\mathrm{\beta }}}_{\mathrm{UNI}}$ are different metrics not on the same scale; therefore, as stated by Roussos and Stout, “no strict mathematical relationship exists between the two estimators that allows $\hat{\mathrm{\Delta }}$ cutoff values to be converted to equivalent $\hat{\mathrm{\beta }}$ values” (p. 219). But research has shown that these two estimators are highly correlated (Dorans & Holland, 1993). Thus, Shealy and Stout (1993) and Roussos and Stout (1996) defined an approximate linear relationship as ${\widehat{\beta }}_{UNI}=K\ast \widehat{\mathrm{\Delta }}.$ The constant K is defined as a constant with an approximate value of −15 for 1PL and 2PL data based on research by Shealy and Stout (1993). K is defined as a constant with an approximate value of −17 for 3PL data based on research by Roussos and Stout (1996).

In the literature related to the logistic regression DIF procedure, many different metrics have been reported to assess ES. These methods do not utilize instinctive metrics that can be derived from logistic regression, more specifically the odds ratio (Monahan et al., 2007), which is similar to MH’s odds ratio. Using Holland and Thayer’s (1988) conversion formula, logistic regression’s measure of DIF ${\hat{\mathrm{\Delta }}}_{\mathrm{LR}}$ can be defined similar to MH’s measure of DIF ${\hat{\mathrm{\Delta }}}_{\mathrm{MH}}$ (see Equation 1).

$${\widehat{\mathrm{\Delta }}}_{LR}=-2.35\ln ({\widehat{\alpha }}_{LR}),$$

where ${\hat{\alpha }}_{\mathrm{LR}}$ represents the reference to focal group odds ratio for answering a test item correctly. ${\hat{\mathrm{\Delta }}}_{\mathrm{LR}}$ can be summarized similarly to MH’s categories of negligible, moderate, and large DIF. Table 1 provides a summary of the most utilized nonparametric DIF statistics today with its ES.

Table 1.

Summary of DIF Procedures and Effect Sizes

DIF procedure	Effect size	Range	No DIF	Negligible DIF (A)	Moderate DIF (B)	Large DIF (C)
Mantel-Haenszel (1985)	ΔMH	−∞ to +∞; Midpoint 0	0	<1	≥1 < 1.5	≥1.5
Standardization (1986)	STDP-DIF	−1 to +1; Midpoint 0	0	−.05 to +.05	−.10 to −.05	> −.10 or > +.10
Logistic regression (1990)	${{\hat{\mathrm{\Delta }}}_{\mathrm{LR}}}_{\mathrm{LR}}$	−∞ to +∞; Midpoint 0	0	<1	≥ 1 < 1.5	≥1.5
SIBTEST (1PL/2PL) (1993)	${\hat{\beta }}_{\mathrm{UNI}}$	−∞ to +∞; Midpoint 0	0	<.067	≥.067 < .10	≥.10
SIBTEST (3PL) (1996)	${\hat{\beta }}_{\mathrm{UNI}}$	−∞ to +∞; Midpoint 0	0	<.059	≥.059 < .088	≥.088

Note. DIF = differential item functioning.

Importance

The purpose of this study is to establish an ES measure for DFIT noncompensatory differential item functioning (NCDIF). More specifically, to establish the NCDIF values that correspond to ES categories related to ETS’s MH categories at given levels of a, b, and c parameters. As did Monahan et al. (2007) and Shealy and Stout (1993), MH parameter served as the benchmark for developing NCDIF’s ES measure, for reporting moderate and large DIF in test items. The preliminary investigation indicated that a one-size-fits-all approach may not be advisable. The ES of NCDIF is influenced by the model, the discrimination parameter, and the difficulty parameter. This finding supports similar findings from DeMars’s (2011) results of investigating the comparison of ESs for DIF measures. While presenting tabled values of ES to align MH and DFIT, another purpose of this study is to offer a general ES recommendation for moderate and large NCDIF, which can be added to Table 1.

Mantel–Haenszel

MH as a practical technique to determine if a test item is functioning differently for two groups of examinees was first proposed by Holland (1985). Holland and Thayer (1988) provided the landmark study that explains in great detail the use of MH as a DIF technique. The value (i.e., MH’s ES) of α indicates how much more likely (i.e., multiplicative) the odds for the reference group is for answering the test item correctly over the focal group. In Equation 2, when Δ_MH is zero, the odds ratio α is one, indicating that the reference and focal groups odds are the same for getting a test item correct. A negative value for Δ_MH would indicate a test item favoring the reference group and positive values favoring the focal group (Holland & Thayer, 1988).

$${\mathrm{\Delta }}_{MH}=-2.35\ln ({\widehat{\alpha }}_{MH}).$$

The ETS’s DIF classification rules based on ES measured by Δ_MH is categorized as A, B, or C. “A” represents negligible DIF, “B” represents moderate DIF, and “C” represents large DIF (Dorans & Holland, 1993; Hidalgo & Lopez, 2004; Zwick & Ercikan, 1989). Equations 3, 4, and 5 define these classifications based on Δ_MH (see also Table 1).

$$\mathrm{A}\left(\mathrm{Negligible\; DIF}\right)=|{\mathrm{\Delta }}_{\mathrm{MH}}|<1,$$

$$\mathrm{B}\left(\mathrm{Moderate\; DIF}\right)=1\le |{\mathrm{\Delta }}_{MH}|<1.5,$$

$$\mathrm{C}\left(\mathrm{Large\; DIF}\right)=|{\mathrm{\Delta }}_{\mathrm{MH}}|\ge 1.5.$$

Roussos, Schnipke, and Pashley (1999) developed a generalized formula that calculates the true MH parameter given the a, b, and c parameters in the IRT model (see Equations 6 and 7). The specific details for Equations 6 and 7 can be found in Roussos et al.

$$\mathrm{\alpha }=\frac{{\int }_{-\infty }^{\infty }{P}_F\left(\mathrm{\theta }\right)Q_R\left(\mathrm{\theta }\right)\frac{{ℱ}_R\left(\mathrm{\theta }\right){ℱ}_F\left(\mathrm{\theta }\right)}{{\mathrm{\gamma }}_F{ℱ}_F\left(\mathrm{\theta }\right)+{\mathrm{\gamma }}_R{ℱ}_R\left(\mathrm{\theta }\right)}\mathrm{\alpha }\left(\mathrm{\theta }\right)d\mathrm{\theta }}{{\int }_{-\infty }^{\infty }{P}_F\left(\mathrm{\theta }\right)Q_R\left(\mathrm{\theta }\right)\frac{{ℱ}_R\left(\mathrm{\theta }\right){ℱ}_F\left(\mathrm{\theta }\right)}{{\mathrm{\gamma }}_F{ℱ}_F\left(\mathrm{\theta }\right)+{\mathrm{\gamma }}_R{ℱ}_R\left(\mathrm{\theta }\right)}d\mathrm{\theta }},$$

where

$$\mathrm{\alpha }(\mathrm{\theta })=\frac{P_R(\mathrm{\theta })Q_F(\mathrm{\theta })}{P_F(\mathrm{\theta })Q_R(\mathrm{\theta })}.$$

Differential Functioning for Items and Tests (DFIT)

DFIT as a statistical method primarily was developed to overcome limitations associated with Raju’s (1988) DIF area measure technique. The DFIT framework as of today consists of a comprehensive set of methods for assessing DIF. Dichotomous DFIT was the first significant development within the DFIT framework (Raju, van der Linden, & Fleer, 1995). The development consisted of NCDIF, compensatory DIF, and differential test functioning. Oshima and Morris (2008) provide this specific definition of NCDIF in stating, “. . . is defined as the average squared distance between the ICFs for the focal and reference groups” (p. 46). NCDIF measures the difference in probability of selecting a correct response to a test item between examinees from two different groups of interest (e.g., members from different ethnicity groups). In other words, is there a difference in probability for members of different groups endorsing a test item while having the same latent ability? The difference in probability is taken over the entire latent ability continuum for the focal group, denoted by Ef in Equation 9. NCDIF functions similarly to other item-level DIF statistics, in that all items are assumed to be DIF free with the exception of the item being investigated. In calculating NCDIF, squaring the difference between the item characteristic functions allows for both uniform and nonuniform DIF to be detected (see Equations 8 and 9).

$$d_i({\mathrm{\theta }}_s)=P_{\mathrm{iF}}({\mathrm{\theta }}_s)-P_{\mathrm{iR}}({\mathrm{\theta }}_s),$$

$${\mathrm{NCDIF}}_i=E_F[\mathrm{di}{({\mathrm{\theta }}_s)}^2],$$

where $P_{\mathrm{iF}}(\mathrm{\theta }s)$ and $P_{\mathrm{iR}}(\mathrm{\theta }s)$ are the probabilities of answering item i correctly by subject s with the ability level of $\mathrm{\theta }$ for the focal group and the reference group, respectively.

DFIT as a DIF technique is a promising new statistic in the area of DIF analysis (Osterlind & Everson, 2009). The statistic provides breadth and depth in many important areas lacking in other DIF statistics. The NCDIF statistical test is based on the item parameter replication algorithm. Essentially, using the focal group’s item parameters for a test item, a large number of pairs (e.g., 1,000) of these parameters are reproduced. NCDIF for each of these pairs is calculated. These replicated pairs represent the “No DIF” condition, and hence, any extreme differences observed would be considered beyond chance. The 1,000 pairs form the null distribution, and cutoffs are determined at the 90%, 95%, 99%, and 99.9% percentile rank scores. The NCDIF values at any of these levels will be used to determine statistical significance at .10, .05, .01, and .001, respectively. For a detailed description of the item parameter replication procedure, see Oshima, Raju, and Nanda (2006). DFIT provides a significance test of DIF, but currently lacks a very important measure, an ES.

Method

A two-stage methodological approach was used to determine the ES values for DFIT’s NCDIF. The first stage was to calculate and align the true parameters for both MH and NCDIF related to moderate and large DIF. The second stage was a Monte Carlo simulation study to validate the proposed NCDIF ES guidelines for moderate and large DIF.

To establish NCDIF values that correspond to ES categories defined by ETS’s MH at given levels of a parameters, b parameters, and c parameters (see Table 3), 187 conditions were defined. The a parameter had eight levels: 0.25, 0.50, 0.75, 1.00, 1.25, 1.50, 1.75, and 2.00. The b parameter had 11 levels: −3.0, −2.0, −1.5, −1.0, −0.5, 0, 0.5, 1.0, 1.5, 2.0, and 3.0. The c parameter was constant: 0.20. Thus, the numbers of conditions for 1PL, 2PL, and 3PL are 11 (difficulty level only), 88 (difficulty and discrimination), and 88 (difficulty and discrimination), respectively. The ability distributions for the reference and focal groups were N(0, 1) and N(0, 1), respectively. The calculated parameters for NCDIF and MH were based on the 1PL, 2PL, and 3PL models. The item score type for this study was dichotomous, with an equal population size for the reference and focal groups being 1,000. Finally, the choice of 0.20 for the pseudo-guessing parameter was associated with typical multiple choice exams having five choices.

Table 3.

NCDIF Recommended Effect Size—Moderate DIF: Category B (1PL/2PL).

Model →	1PL	2PL	2PL	2PL	2PL	2PL	2PL	2PL	2PL
Discrimination →	N/A	0.25	0.50	0.75	1.00	1.25	1.50	1.75	2.00
Difficulty ↓
−3	<0.001	0.006	0.002	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
−2	0.001	0.009	0.004	0.002	0.001	<0.001	<0.001	<0.001	<0.001
−1.5	0.001	0.009	0.006	0.003	0.002	0.001	0.001	0.001	<0.001
−1	0.002	0.010	0.007	0.005	0.003	0.002	0.002	0.001	0.001
−0.5	0.003	0.010	0.008	0.006	0.005	0.003	0.003	0.002	0.002
0	0.003	0.010	0.008	0.006	0.005	0.004	0.003	0.002	0.002
0.5	0.002	0.009	0.007	0.006	0.004	0.003	0.002	0.002	0.002
1	0.002	0.009	0.006	0.004	0.003	0.002	0.001	0.001	0.001
1.5	0.001	0.008	0.004	0.002	0.001	0.001	0.001	<0.001	<0.001
2	0.001	0.006	0.003	0.001	0.001	<0.001	<0.001	<0.001	<0.001
3	0.000	0.004	0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001

Note. NCDIF = noncompensatory differential item functioning; DIF = differential item functioning.

Stage 1: Calculating MH and NCDIF Parameters

In calculating the MH parameter values for each condition, Equations 6 and 7 were used. More specifically, software developed by Roussos et al. (1999) incorporating these formulas was utilized to calculate the true MH parameter. The software required input for the ability distributions, the population size for the focal and reference group, and values for the a parameter, b parameter, and c parameter. Depending on the test item parameters provided, this would dictate the model of 1PL, 2PL, or 3PL. NCDIF parameter values for each condition were calculated using Equations 8 and 9.

Stage 1: Determining NCDIF ES

Within each condition, DIF was embedded by manipulating the focal group’s b parameter, which was modeled in the software developed by Roussos et al. (1999). This approach allowed DIF to be measured by the difference in b parameters for the focal and reference groups (i.e., b_f−b_r). If the magnitude of DIF increases, one would expect for the ES measure to also increase. The amount of DIF varied depending on the condition. The amount of DIF varied in increments of .0125, .025, .05, or .10. The definition of moderate DIF as defined by the MH parameter is 1. A large DIF is defined as 1.5. The closest MH parameter value equal to 1 was used for moderate DIF. The closest MH parameter value equal to 1.5 was used for large DIF. The increments were chosen with the goal to be within .006 of the MH values of 1 and 1.5. For each condition, the correspondence of MH where Category A becomes Category B for moderate DIF, Category B becomes Category C for large DIF to NCDIF was recorded, to establish MH-based ES at the given level of the item parameters. In addition, given the adequate number of increments for each condition, the correlation index for MH and NCDIF was calculated. Finally, a general NCDIF ES value for moderate and large was proposed.

Table 2 is an illustration of how NCDIF was aligned with MH’s parameter value for ES Categories B and C. As can be seen, a b difference of .25 was required to reach moderate DIF, and a b difference of .37 was necessary for large DIF. For this condition, to calculate moderate DIF for NCDIF, the reference group’s b parameter used in Equation 8 would be −3 and the focal group’s b parameter would be −2.75. To calculate large DIF for NCDIF for this illustrative condition, the reference group’s b parameter used in Equation 8 would be −3 and the focal group’s b parameter would be −2.63. The MH’s parameter values and NCDIF’s parameter values for all other conditions were calculated similarly to determine moderate and large DIF.

Table 2.

Determining NCDIF Effect Size for Categories B and C.

Focal group’s b parameter (bf)	Reference group’s b parameter (br)	bf−br	True MH	MH (DIF) category	True NCDIF
−3.00	−3.00	.000	0.000	A	.0000000
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
−2.755	−3.00	−.245	−0.979	A	.0000708
−2.750	−3.00	−.250	−0.999	B	.000250951
−2.700	−3.00	−.300	−1.199	B	.000375360
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
−2.655	−3.00	−.345	−1.398	B	.0004561
−2.630	−3.00	−.370	−1.498	C	.000602042
−2.600	−3.00	−.400	−1.598	C	.000719743

Note. NCDIF = noncompensatory differential item functioning; MH = Mantel–Haenszel; DIF = differential item functioning. The items is bold represent the true parameter values, where Category A becomes Category B for moderate DIF, Category B becomes Category C for large DIF to NCDIF was established.

Stage 2: Generalizability for the Calculated ESs

To establish generalizability for the calculated ESs in practice, an extensive Monte Carlo simulation was conducted. A 61-item test was simulated where Item 61 represented the various degrees of a DIF item. The simulation was designed to reflect the exact conditions used to calculate the true parameters for MH and NCDIF. The IRTGEN software algorithm (Whittaker, Fitzpatrick, Williams, & Dodd, 2003) was used to generate the item responses. IRTGEN generates item responses and known trait scores for the 1PL, 2PL, and 3PL models, which were necessary for this simulation. Ducan’s (2006) estimated item parameters from a 60-item American College Testing administration were used for this simulation. In simulating Item 61, the reference group and focus groups’b parameters determined based on the MH and NCDIF parameter calculations in Stage 1 were used for this stage of the study. The a parameter and c parameters related to Item 61 were the same for both the focal and reference groups within each condition as was the case in Stage 1. There were 187 conditions as described earlier at different levels of a parameter and b parameter for the reference group (see Table 3). Fixed and equal sample size pairs of (1,000, 1,000) for the reference and focal groups were used. In this simulation, the sample size was not a factor being considered; therefore, the sample size was fixed throughout the simulation. The choice of using a sample size of 1,000 was based on sample sizes in actual testing scenarios ranging from 250 to 3,000 (Shealy & Stout, 1993), as well as on the recommendation by Oshima and Morris (2008) stating that DFIT should be used with equal sample sizes of 1,000 or more.

Stage 2: Estimating NCDIF

For each of the conditions for this study, the 1-0 data sets were simulated using SAS. The 1-0 data were then calibrated using BILOG-MG3 (Zimowski, Muraki, Mislevy, & Bock, 2003). NCDIF’s item parameter estimates were then put on a common scale using the ST program developed by Hanson & Zeng (1995), which incorporates the test characteristic curve method (Stocking & Lord, 1983). NCDIF was then estimated using the software DIFCUT developed by Nanda, Oshima, & Gagne (2006). It is recommended in practice to conduct a two-stage linking for DFIT, in which the second linking coefficients are obtained after removing large DIF after the first stage. In this simulation, it was assumed that this purification process was perfect by using only Items 1 to 60 for linking. Finally, for each of the 187 conditions, the number of replications for estimating NCDIF was 100. The estimated NCDIF values are therefore based on the average of 100 replicates.

Stage 2: Assessing Stability

To determine the veracity of the true NCDIF parameter values used to establish the ES values, item parameter recovery was investigated comparing the true NCDIF value and estimated NCDIF values over 100 replications within each condition. This study focused on the item recovery of Item 61 only. Systematic errors in an estimation can be interpreted by calibration bias. Bias for this study is defined as follows:

$$\mathrm{Bias}=\mathrm{EstimatedNCDIF}-\mathrm{TrueNCDIF}.$$

Recall that there were 187 conditions investigated in this study. In addition to assessing bias, the simulation was modified to simulate an actual test administration, to demonstrate the utility and necessity of the ES measures being proposed for DFIT’s NCDIF. Nanda et al.’s (2006) DIFCUT program was modified to include the proposed ES measure for the DIF test items related to NCDIF. To demonstrate the utility of the proposed ESs, selected conditions from the 187 investigated items were simulated with “no DIF,”“negligible DIF,”“moderate DIF,” and “large DIF.” Each of the selected conditions with the various DIF amounts was simulated with 100 replicates.

Results

Stage 1

The ES recommendation is based on the fact that a clear relationship exists between the MH parameter and the NCDIF parameter. The conditions investigated revealed through scatterplots a curvilinear relationship between MH and NCDIF. NCDIF by definition is the average squared distance between the focal and reference group’s ICCs. Applying a nonlinear transformation to NCDIF by taking the square root of each data point produced an acceptable linear relationship. Given the almost linear relationship between the two parameters, the relationship between MH and NCDIF can be now expressed as

$$\mathrm{NCDIF}={({\mathrm{\Delta }}_{\mathrm{MH}}/K)}^2.$$

Each of the other conditions had similar results after applying the transformation. For each condition, the correlation between the MH parameter and NCDIF was .87 or higher, with the majority being .99 after the transformation. In general, the 3PL conditions had the lower correlation indexes. In this study, the a parameter was held constant between the focal and reference groups, hence, essentially, modeling a special case of the 1PL model. Past research has shown the MH statistic to be reliable for 1PL and 2PL data.

The recommended ESs for DFIT’s NCDIF are presented in Tables 3, 4, 5, and 6. For example, for an item with medium difficulty and medium discrimination (b = 0 and a = 1, respectively), the moderate ES for NCDIF is .005 (see Table 3), while the large ES is .011 (see Table 5) for the 1PL/2PL model. Those values change to .007 (see Table 4) and .016 (see Table 6) for the 3PL model. The ES values vary substantially in each table. For example, moderate ES ranges from <.001 to .010 for the 1PL/2PL model (see Table 3). The variation is slightly larger for the 3PL model, ranging from <.001 to .011 (see Table 4). These tables suggest that a one-size-fits-all approach to develop a relationship between MH and DFIT is not advisable. In other words, a single constant K in Equation 10 cannot relate MH and DFIT.

Table 4.

NCDIF Recommended Effect Size—Moderate DIF: Category B (3PL).

Model →	3PL	3PL	3PL	3PL	3PL	3PL	3PL	3PL
Discrimination →	0.25	0.50	0.75	1.00	1.25	1.50	1.75	2.00
Difficulty ↓
−3	0.005	0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
−2	0.007	0.003	0.001	0.001	<0.001	<0.001	<0.001	<0.001
−1.5	0.008	0.005	0.003	0.002	0.001	0.001	<0.001	<0.001
−1	0.009	0.006	0.004	0.003	0.002	0.002	0.001	0.001
−0.5	0.010	0.008	0.006	0.005	0.004	0.003	0.003	0.003
0	0.011	0.009	0.008	0.007	0.006	0.005	0.005	0.004
0.5	0.011	0.010	0.009	0.008	0.007	0.007	0.006	0.006
1	0.011	0.009	0.008	0.008	0.007	0.007	0.006	0.006
1.5	0.010	0.009	0.008	0.007	0.007	0.007	*	*
2	0.010	0.008	0.007	*	*	*	*	*
3	0.009	*	*	*	*	*	*	*

Note. NCDIF = noncompensatory differential item functioning; DIF = differential item functioning.

^*MH never reached moderate DIF (Category B). Therefore, no corresponding NCDIF value is reported.

Table 5.

NCDIF Recommended Effect Size—Large DIF: Category C (1PL/2PL).

Model →	1PL	2PL	2PL	2PL	2PL	2PL	2PL	2PL	2PL
Discrimination →	N/A	0.25	0.50	0.75	1.00	1.25	1.50	1.75	2.00
Difficulty ↓
−3	0.001	0.016	0.004	0.001	<0.001	<0.001	<0.001	<0.001	<0.001
−2	0.002	0.020	0.010	0.004	0.002	0.001	0.001	<0.001	<0.001
−1.5	0.003	0.022	0.014	0.008	0.004	0.003	0.002	0.001	0.001
−1	0.005	0.023	0.017	0.011	0.008	0.005	0.004	0.003	0.002
−0.5	0.006	0.023	0.019	0.014	0.010	0.008	0.006	0.005	0.004
0	0.006	0.022	0.018	0.014	0.011	0.008	0.007	0.005	0.004
0.5	0.005	0.020	0.016	0.012	0.009	0.007	0.005	0.004	0.004
1	0.004	0.018	0.012	0.008	0.005	0.004	0.003	0.002	0.002
1.5	0.003	0.016	0.008	0.005	0.003	0.002	0.001	0.001	0.001
2	0.002	0.013	0.005	0.002	0.001	0.001	<0.001	<0.001	<0.001
3	<0.001	0.008	0.002	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001

Note. NCDIF = noncompensatory differential item functioning; DIF = differential item functioning.

Table 6.

NCDIF Recommended Effect Size—Large DIF: Category C (3PL).

Model →	3PL	3PL	3PL	3PL	3PL	3PL	3PL	3PL
Discrimination →	0.25	0.50	0.75	1.00	1.25	1.50	1.75	2.00
Difficulty ↓
−3	0.012	0.003	0.001	<0.001	<0.001	<0.001	<0.001	<0.001
−2	0.017	0.008	0.003	0.002	0.001	<0.001	<0.001	<0.001
−1.5	0.019	0.012	0.006	0.004	0.002	0.002	0.001	0.001
−1	0.021	0.015	0.011	0.008	0.006	0.004	0.003	0.003
−0.5	0.023	0.019	0.015	0.012	0.010	0.008	0.007	0.006
0	0.024	0.021	0.018	0.016	0.014	0.012	0.011	0.010
0.5	0.024	0.022	0.020	0.017	0.016	0.015	0.015	0.014
1	0.024	0.021	0.019	0.017	0.016	0.016	0.015	0.015
1.5	0.023	0.019	0.017	*	*	*	*	*
2	0.021	0.017	*	*	*	*	*	*
3	0.019	*	*	*	*	*	*	*

Note. NCDIF = noncompensatory differential item functioning; DIF = differential item functioning.

^*MH never reached large DIF (Category C). Therefore, no corresponding NCDIF value is reported.

As noted in Tables 4 and 6, there were quite a few problem conditions (indicated by the asterisk) related to the MH’s inability to detect DIF when DIF was lucidly apparent. These conditions are associated with the 3PL model. In using the b difference for the focal and reference groups (i.e., b_f−b_r) in defining large amounts of DIF, Swaminathan and Rogers (1990) used .64 as the baseline for purporting large DIF (Category C). Furthermore, they defined large DIF (Category C) as having an area measure of .80 or more. For all of the conditions with the asterisk in Tables 4 and 6, the b difference was at or above 1.0, and the area measure was greater than .80, clearly large DIF. There were 14 conditions (see Table 4) in which MH did not reach moderate DIF and 18 conditions (see Table 6) in which MH did not reach large DIF. Given MH’s inability to detect DIF in those conditions, there is no corresponding MH-NCDIF ES. To remedy the missing MH-NCDIF ESs for the conditions with the asterisk, one possible practical solution is to use the NCDIF value immediately above the asterisk within the same discrimination column.

Figures 1 and 2 depict the effects of b parameter and a parameter on MH-based ES for NCDIF (moderate). A similar trend was observed for the large ES. The effects are clear; items with medium difficulty tend to have a higher MH-based ES for NCDIF. Items with lower discrimination tend to have a higher MH-based ES for NCDIF. In addition, related to the 3PL model (Figure 2), as the item becomes more difficult in comparison with the 2PL model, a higher MH-based ES for NCDIF is observed. This suggests that more DIF is required to observe moderate DIF.

Figure 1.

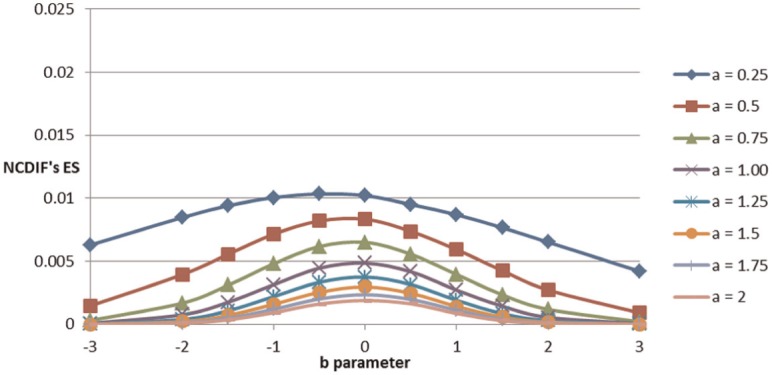
2PL conditions: Effects of b parameter and a parameter on NCDIF’s moderate ES.

Figure 2.

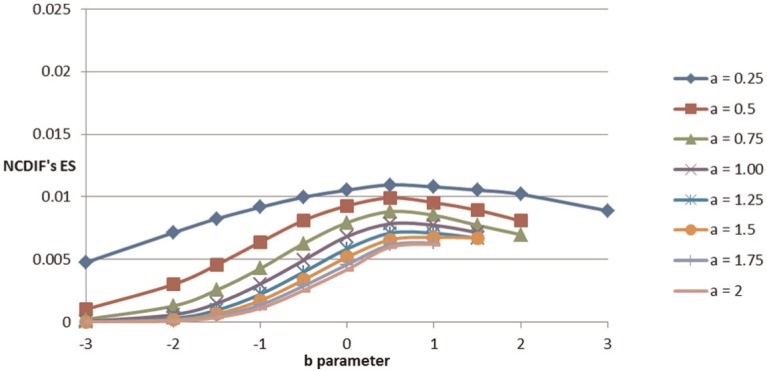
3PL conditions: Effects of b parameter and a parameter on NCDIF’s moderate ES.

Stage 2

In assessing bias for the item recovery investigation, the average difference between NCDIF estimated and true parameters for Item 61 was .0014 for items with moderate DIF and .0029 for large DIF. Recall, moderate means the lower bound for MH Category B, and large means the lower bound for MH Category C, which is 1 and 1.5, respectively. Overall, estimated NCDIF is slightly higher than true NCDIF (Meade, 2010). The correlation between true and estimated NCDIF is high, .90 for moderate DIF and .89 for large DIF. Figure 3 is a summary of bias for estimated NCDIF at various levels of difficulty and discrimination for the cutoff of moderate DIF. For large DIF (not reported in the figure), similar patterns were observed, except bias values were slightly more (about .001 more on the average). The following observations can be stated: (a) the difference is fairly small for 2PL across each of the levels of difficulty and discrimination; (b) the difference is larger for 1PL than 2PL. In addition, the difference was the largest at the medium difficulty range; and (c) for 3PL, problems occur at high discrimination and difficulty levels. This behavior was observed in Stage 1 with the true parameter calculations and has already been discussed. Marginal means were calculated to observe the effect of model, item difficulty, and item discrimination (see Table 7). The 11 levels of item difficulty were grouped into three categories, where the b parameters for “easy,”“medium,” and “hard” were “−3, −2, and −1.5”; “−1, −0.5, 0, 0.5, and 1”; and “1.5, 2, and 3,” respectively. Similarly, the a parameters were grouped into three categories: “low,”“medium,” and “high” for “0.25 and 0.50”; “0.75, 1.00, and 1.25”; and “1.50, 1.75, and 2.00,” respectively. As related to Table 7, for the effect of model, 2PL has the lowest bias between estimated NCDIF and true NCDIF; for the effect of difficulty, for 1PL, medium difficulty equals more difference between estimated and parameter values for NCDIF; and for discrimination, not much effect was observed. In summary, the recommended NCDIF values for ES (Tables 3-6), which were based on the true NCDIF values, may be slightly underestimating the cutoff for moderate and large DIF when facing the estimated item parameters in practice.

Figure 3.

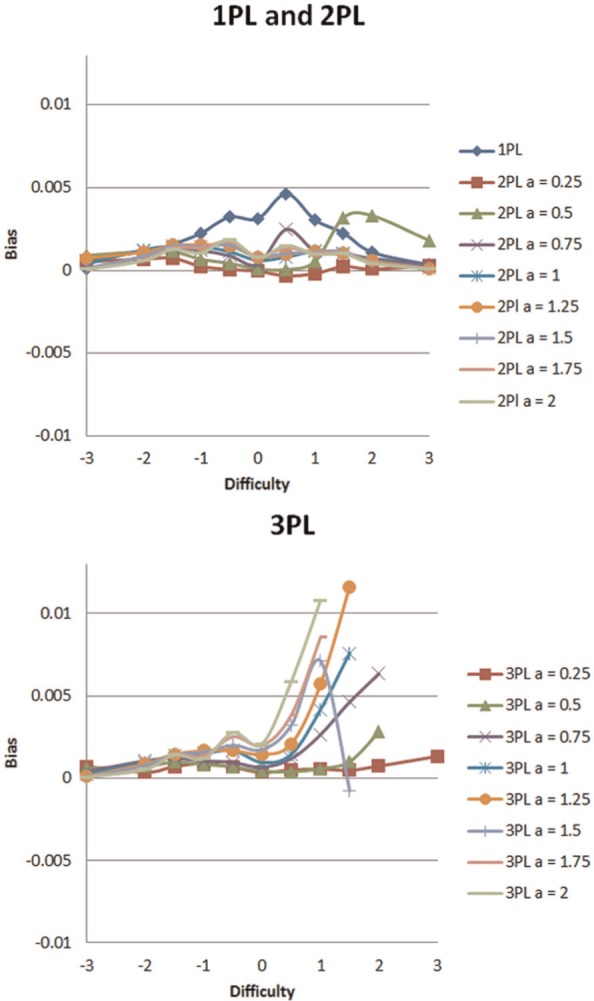
Bias of estimated NCDIF, at various levels of difficulty and discrimination at the cutoff for moderate DIF.

Table 7.

Average Bias for the Three Factors for Moderate DIF.

(a) Effect of model
Model
1PL	0.0020
2PL	0.0009
3PL	0.0020
(b) Effect of item difficulty
	1PL	2PL	3PL
Easy	0.0008	0.0009	0.0008
Medium	0.0033	0.0009	0.0023
Hard	0.0017	0.0008	0.0036
(c) Effect of item discrimination
	2PL	3PL
Low	0.0007	0.0008
Medium	0.0010	0.0024
High	0.0009	0.0025

Stage 2: Utility of the Proposed Effect Size for NCDIF

As stated by DeMars (2009), in referencing a study by Jodoin and Gierl (2001) related to the importance of ES, “Taking effect size into account greatly decreases the false hit rate” (p. 157). This is also demonstrated with the proposed ES for NCDIF in this study. Table 8 shows that false positives can be reduced by using both the significance test and the proposed ES. By nature of the significance test, where α = .05, 5 out of 100 replications are expected to show significance—that is, Type I error. In Table 8, the Type I error rate was inflated for 2PL but not for the 1PL and 3PL models. Despite the inflated Type I error for the 2PL model, the false positives rate was controlled if both significance test and ES were used. More important, Table 9 shows that the combination method of significance and ES is also useful where there is DIF. Negligible DIF should not be flagged in practice, although technically it should be detected by a significance test. The numbers of flagged items for negligible DIF were reduced from 16 to 2 for 1PL, from 25 to 3 for 2PL, and from 15 to 3 for 3PL. For moderate DIF, ES is essential, as it shows a variety of sizes: A, B, and C. The occurrence of A and B are expected as the size of DIF embedded for moderate is the lower bound of Category B. The occurrence of C for the 2PL moderate case supports the earlier finding, that NCDIF estimates tend to be slightly inflated in comparison with true NCDIF. Finally, for large DIF, the combination method is not required. The agreement of significance at α = .05 and ES of C was almost perfect (see Table 9).

Table 8.

NCDIF Values for Item 61 (With no DIF) Over 100 Replications From Selected Conditions (1PL: b = 0, 2PL: b = 0 and a = 1.25, and 3PL b = 0, a = 1.25, and c = 0.20).

1PL				2PL			3PL
Rep	NCDIF	Sig	ES	NCDIF	Sig	ES	NCDIF	Sig	ES
1	0.0040	***	B	0.0038	***	B	0.0025	**	A
2	0.0022	*	A	0.0034	***	B	0.0019	**	A
3	0.0021	*	A	0.0029	***	A	0.0019	**	A
4	0.0021	*	A	0.0028	***	A	0.0018	**	A
5	0.0016	*	A	0.0025	**	A	0.0017	**	A
6	0.0016	*	A	0.0019	**	A	0.0015	ns	A
7	0.0014	ns	A	0.0016	**	A	0.0014	ns	A
8	0.0014	ns	A	0.0015	**	A	0.0013	ns	A
9	0.0013	ns	A	0.0014	**	A	0.0013	ns	A
10	0.0013	ns	A	0.0013	**	A	0.0012	ns	A
11	0.0012	ns	A	0.0012	**	A	0.0011	ns	A
12	0.0011	ns	A	0.0010	ns	A	0.0010	ns	A
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
100	<0.0001	ns	A	<0.0001	ns	A	<0.0001	ns	A

Note. NCDIF = noncompensatory differential item functioning; DIF = differential item functioning; ES = effect size. 100 replications are ordered by the magnitude of NCDIF (largest to smallest).

^***Indicates significance at .001. **Indicates significance at .01. *Indicates significance at .05.

Table 9.

The Number of NCDIF Values Detected as DIF for Item 61 (With Three Levels of DIF) Over 100 Replications From Selected Conditions (1PL: b = 0, 2PL: b = 0 and a = 1.25, and 3PL b = 0, a = 1.25, and c = 0.20).

	1PL			2PL			3PL
	Negligible	Moderate	Large	Negligible	Moderate	Large	Negligible	Moderate	Large
# ES = A	98	12	0	97	36	0	97	28	0
# ES = B	2	40	0	3	50	2	3	42	0
# ES = C	0	48	100	0	14	98	0	30	100
# Significance at .05	16	98	100	25	98	100	15	92	100
# Significance at .05 + ES (B or C)	2	88	100	3	64	100	3	72	100

Note. NCDIF = noncompensatory differential item functioning; DIF = differential item functioning; ES = effect size. For 1PL, embedded DIF for negligible, moderate, and large was .05, .25, and .50, respectively. For 2PL, embedded DIF was .05, .20, and .35, respectively. For 3PL, embedded DIF was .05, .25, and .50, respectively.

Last, with an attempt to come up with a general ES for moderate and large for NCDIF, all the NCDIF values for the tables for moderate DIF and large DIF were averaged, respectively.

As discussed earlier, MH-based ES exhibited some problem conditions especially with extreme regions of difficulty. To exclude those conditions (i.e., outliers), the trimmed mean (Staudte & Sheather, 1990) using a criterion of 20% deletion of the smallest and largest NCDIF values was utilized in calculating the means. The resulting NCDIF’s general ES for moderate was .003. For large ES, it was .008.

Discussion

In determining a comparable ES for DFIT’s NCDIF, the MH-DIF measure, which is widely used today, served as the benchmark for this study. It is important to understand the results already presented related to the behavior of the MH-DIF measure. There is a plethora of empirical research on the MH-DIF measure in observing its behavior (Allen & Donoghue, 1996; Clauser, Mazor, & Hambleton, 1994; Donoghue, Holland, & Thayer, 1993; Holland & Thayer, 1988; Roussos et al., 1999; Roussos & Stout, 1996). The MH measure of DIF overestimates the amount of DIF for easy and hard test items related to the 1PL Rasch and 2PL models. There were 37 conditions where the MH parameter corresponded to moderate DIF (Category B) or large DIF (Category C) size, where the corresponding NCDIF value was less than .001 (see Tables 4 and 5). Those small values can be attributed to the very nature of MH mentioned above coupled with the way in which NCDIF is calculated. Unlike the area measure, NCDIF takes the number of examinees into account. Recall, the ability (θ) parameters for this study were randomly drawn from the normal distribution N(0, 1) for the focal group. The number of examinees in the extreme regions are limited, hence, the very small NCDIF values.

Specifically related to the 3PL model, MH underestimates the amount of DIF for 16% to 20% of the conditions; see the conditions with the asterisk in Tables 4 and 6. In other words, in those conditions, no item is flagged as DIF by using MH. In general, the underestimation and overestimation is more pronounced for all conditions in comparison with the 2PL model. Overall, in comparison with the 2PL model, the MH-DIF measure underestimates the amount of DIF. This behavior was identified in another study by Donoghue et al. (1993), in which the behavior is contributed to the fact of using a fixed c parameter for the reference and focal groups. This study utilized a fixed c parameter. The noise associated with random guessing may be contributing to the difficulty in measuring DIF between the focal and reference groups (Donoghue et al., 1993; Lord, 1980). Zwick, Thayer, and Wingersky (1994) provide the following as a possible explanation: “The more difficult the item, the closer the probability of correct response is to guessing value, and the more difficult the groups are to differentiate” (p. 135). Allen and Donoghue (1996) further purport that a b parameter of 0, 1, or 2 corresponds, respectively, with a z score of 0.875, 2.125, and 3.375. Given these z scores, the area to the right, hence, the number of examinees in this region, is limited. Allen and Donoghue further assert that given difficult test items, “It is not surprising that MH has little power to detect DIF” (p. 248). In sum, MH may not be reliable for specific 3PL conditions (DeMars, 2011).

Hence, it is clearly the limitation of this study that our proposed ES for NCDIF is tied to the ES for MH. However, it is a practical solution as the ES for MH is already widely used in practice. What constitutes “moderate” and “large” amounts of DIF, apart from the definition of ESs by MH, needs further investigation.

In summary, we propose a tables-based approach to define MH-based ES for DFIT (Tables 3 to 6). These tables were incorporated into the existing DFIT computer programs, which clearly demonstrated the utility of the proposed ESs. In addition, this study offers a general recommendation of the sizes of “moderate” and “large” ES for NCDIF (.003 and .008, respectively). The general recommendation should help DFIT users interpret the metric of NCDIF. For example, when one obtains NCDIF of .008, it is a “large” value in general. However, how large it is depends on the item parameters and the IRT model. For example, if the item is highly discriminating as well as very easy, the .008 value is very large, as MH-based ES for NCDIF is expected to be low under those conditions. On the other hand, if the item has low discrimination and medium difficulty, then the .008 value is not that large and may be even in the range of “moderate,” as MH-based ES for NCDIF under those conditions are expected to be high. It is analogous to saying that, given the average height for women is 5’4”, 5’7” is “tall” for a woman in general but not so for a professional female basketball player. Therefore, those general values for “moderate” (.003) and “large” (.008) should be used as a general rule of thumb only. We recommend the use of Tables 3 to 6 for the specific MH-based ES for NCDIF.