Abstract
Existing tests of interrater agreements have high statistical power; however, they lack specificity. If the ratings of the two raters do not show agreement but are not random, the current tests, some of which are based on Cohen’s kappa, will often reject the null hypothesis, leading to the wrong conclusion that agreement is present. A new test of interrater agreement, applicable to nominal or ordinal categories, is presented. The test statistic can be expressed as a ratio (labeled QA, ranging from 0 to infinity) or as a proportion (labeled PA, ranging from 0 to 1). This test weighs information supporting agreement with information supporting disagreement. This new test’s effectiveness (power and specificity) is compared with five other tests of interrater agreement in a series of Monte Carlo simulations. The new test, although slightly less powerful than the other tests reviewed, is the only one sensitive to agreement only. We also introduce confidence intervals on the proportion of agreement.
Keywords: interrater, agreement test, kappa
Introduction
Quantifying interrater agreement is useful in contexts where two raters must judge into what categories a series of observations shall be classified. If agreement between raters is perfect, all judgments will be identical, whereas if both raters use completely different criteria, agreement will occur only by chance. Agreement is often assessed using Cohen’s kappa (Cohen, 1960), for which a value greater than 0.40 is commonly considered a moderate agreement (Landis & Koch, 1977). Recently, Kraemer, Periyakoil, and Noda (2002) explained that a Cohen’s kappa for more than two categories is equal to a weighted average of individual kappas. The individual kappa indicates the agreement of the two raters with respect to category j only. Hence, if one category shows a very strong agreement but the others do not, the mean kappa may nevertheless be high.
As an example, consider the following situation in which two psychiatrists examine N = 100 patients suffering from depression in order to appraise the category of depression (this example is inspired from von Eye, Schauerhuber, & Mair, 2006). The psychiatrists used k = 3 categories of severity. Raters’ categorizations are summarized in Table 1 using a judgment matrix in which cell contains the number of observations that were classified as instances of the ith category by the first rater and of the jth category by the second one. Perfect agreement would result in the main diagonal summing to N, and off-diagonal cells containing zero observations.
Table 1.
Example Data of Ratings Performed by Two Raters (Psychiatrist 1 and Psychiatrist 2) Appraising the Severity of Depression of 100 Patients (N = 100) Using Three Categories of Depression (k = 3).
| Psychiatrist 2 | |||||
|---|---|---|---|---|---|
| Category of depression | |||||
| 1 | 2 | 3 | Row sums | ||
| Psychiatrist 1 | 1 | 81 | 1 | 1 | 83 |
| Category of depression | 2 | 1 | 3 | 5 | 9 |
| 3 | 1 | 5 | 2 | 8 | |
| Column sums | 83 | 9 | 8 | N = 100 | |
As seen, both raters share the belief that most patients belong to the first category of severity. This high prevalence does not explain the large number of concordant judgments in that category, as chance would only predict approximately 70 agreement ratings for the first category. Hence, there is good agreement regarding Category 1. On the other hand, the two psychiatrists rarely agree on Categories 2 and 3. For example, Psychiatrist 2 found a total of 8 cases belonging to the third category of severity; of those, only 2 cases are also put in the third category by Psychiatrist 1, a figure below what chance would predict. Instead, the results seem to indicate that what looks like a Level 2 depression to Rater 1 is a Level 3 depression to Rater 2 and vice versa. This suggests disagreement between the two raters on these two categories.
Overall, 86% of the cases are judged identically by the two raters (the cases found in the main diagonal). Should we conclude that, overall, the two raters are in good agreement? Cohen’s kappa suggests a moderate but significant agreement ( z = 3.43, p < .001), despite the fact that agreement is missing for two out of three categories.
Similarly, consider the results of Table 2. In this example, 127 cases were classified by two raters in one of 5 categories. Again, agreement is not clear. The raters seem to agree well regarding Categories 2 and 5. They also agree very well on Category 1 (nearly half of the ratings in this category are agreements). However, they agree little regarding Categories 3 and 4. Inspection of the data in Table 2, outside the diagonal, shows that the two raters have opposite interpretations regarding Categories 3 and 4: cases that are instances of Category 3 for Rater 1 are instances of Category 4 for the other. The two raters are not responding randomly, but they are not agreeing. Hence, whereas the rate of agreement is moderately good (32.3%), it does not mean that the two raters agree a little on all categories. The results instead suggest that the raters agree well on a few categories. Overall agreement is missing. Yet Cohen’s kappa is weak but still significantly different from zero ( z = 3.30, p < .001).
Table 2.
An Example Where Agreement for Three Categories Accompanies Disagreement for Two Categories.
| Rater 2 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | Row sums | ||
| Rater 1 | 1 | 8 | 2 | 1 | 2 | 4 | 17 |
| 2 | 4 | 11 | 5 | 5 | 2 | 27 | |
| 3 | 2 | 1 | 5 | 12 | 7 | 27 | |
| 4 | 1 | 4 | 15 | 7 | 3 | 30 | |
| 5 | 4 | 6 | 2 | 4 | 10 | 26 | |
| Column sums | 19 | 24 | 28 | 30 | 26 | N = 127 | |
Note. Contrary to Table 1, there is no significant difference in prevalence between the categories.
These two examples show the need for a statistic of agreement that can distinguish situations with much agreement for a few categories from situations with some agreement for most categories.
The purpose of this article is to present two new measures of interrater agreement, which we call Q A and PA. The first is more convenient as it uses the Fisher F tables for critical values, whereas the second is possibly more intuitive, as it is a proportion between 0 and 1. In the next section, we describe these measures, which can be used on nominal or ordinal classifications. Next, we examine the reliability of these measures along with their confidence intervals. Finally, we assess the statistical power but, more important, the specificity of this approach, that is, the ability of a test based on Q A (or PA) to make the difference between mixtures of agreeing and disagreeing category ratings from solely agreeing ratings. The approach developed is akin to analysis of variance, as it partitions variances found in each cell (not just those in the main diagonal) as supporting agreement or supporting disagreement.
In the remainder of this article, the judgments are structured in the form of a square k×k table of observed frequencies. Observed frequencies in cell {i, j} will be noted oi,j. As per the test on contingency table, we note ei,j the expected frequency in cell {i, j}, estimated from the marginal frequencies with where is the total of the ith column and is the total on the jth row.
Pearson’s chi-square test of independence has been used on occasion to ascertain the significance of the agreement. However, this test only examines the null hypothesis () of by-chance co-occurrences in any cell. It can be seen as an omnibus test in the sense that any type of nonrandom structure can lead to the rejection of the null hypothesis. Therefore, as already noted by Cohen (1960), a significant χ2 statistic calculated from a judgment matrix indicates the presence of any type of category coupling between the two raters, whether they be in agreement (in the main diagonal) or disagreeing (anywhere else in the matrix).
The reader can find a brief description of five alternative tests of interrater agreements in Appendix A. These tests will be compared to the present approach in the subsequent section.
Measures of the Global Structure of the Judgment Matrix
The new approach is a nonparametric one based on the same assumptions as Cohen’s kappa (Brennan & Prediger, 1981). As will be seen, it is sensitive because it uses information outside the main diagonal as well as in the main diagonal. The crucial observation is that high agreement rates in the diagonal cells necessarily imply a shortage of cases outside the diagonal, and conversely. Hence, the whole matrix, not just the diagonal, is informative as to whether there is agreement or not.
The present approach partitions the matrix based on whether the observed cell frequencies deviates from chance (judged by whether the observed count is different from its expected value) and whether such ratings are supportive of agreement or not.
More formally, under (no agreement), the observed frequencies oi,j in the k2 cells of the judgment matrix should fluctuate near their expected values ei,j. Hence, about half of the cells should have a frequency count above their respective ei,j, and the other half, below.1 As in the test, the difference between observed and expected frequencies is standardized with which under and for reasonably large counts is normally distributed.
The first statistic, Q A, is a ratio of cells favorable to agreement against cells unfavorable to agreement, the former being those that (i) on the main diagonal have counts higher than expected and (ii) off the main diagonal have counts smaller than expected, whereas the latter are those that (iii) on the main diagonal have counts smaller than expected and (iv) off the main diagonal have counts larger than expected. Hence, Q A is computed as
where the terms in the sums (the components) will be added depending on the sign of the difference between the observed frequency and the expected frequency using
QA values range from 0 to +∞, and under its central value is about 1. On average under, the numerator should contain entries from half of the matrix and is therefore on average a sum of squared z scores. Its distribution is thus close to the distribution with degrees of freedom (df). The same is true for the denominator. As a first approximation, the distribution of QA is therefore a Fisher F ratio distribution with both df equal to Hence, critical values for QA can be read from the right tail of the Fisher F ratio distribution.
The second statistic, PA, is the proportion of variance supporting agreement onto total variance. It can be obtained from the z scores or from QA with
The statistic PA is akin to the eta squared (η2) statistic and ranges from 0 to 1. When the ratings are random, its central value is ½, that is, 50% of the variance in the ratings suggest agreement and the other 50% of the variance suggest disagreement. Hence, a value of ½ supports neither interpretations and indicates random ratings. As found in the literature (e.g., Forbes, Evans, Hastings, & Peacock, 2010), a ratio of the form where X follows a Fisher F ratio distribution has a standard beta distribution with parameters a and b dependent on the df of the F ratio distribution, here
PA and QA are totally interchangeable. To detect whether the ratings deviate from random, one option is to use QA. The null hypothesis is : QA = 1, and the decision rule is to reject if the observed QA exceeds a critical value read on an F table with degrees of freedom. If PA is used, the null hypothesis is : PA = ½ and the decision rule is to reject if the observed PA exceeds a critical value read from a Beta distribution with parameters a and b equal to Note that, in principle, these tests could be left tailed, testing for significant disagreement between the raters, but results to be shown will indicate that they should not be used for that purpose. In between significant agreement and significant disagreement, there is a zone in which the ratings are inconclusive either way, as is the case for random ratings.
Under the null hypothesis, approximately half of the cells, should contribute to the numerator of these statistics and the other half to the denominator. If PA is larger than ½ (QA larger than 1), it suggests that more than one half of the cells contribute to the numerator and less than one half to the denominator. Hence, the distribution of PA for an observed result different from ½ has Beta distribution with degrees of freedom changed to and From this observation, confidence intervals can be obtained with
where denotes the quantile function of the Beta distribution with its parameters. The following section will verify this assertion.
Appendix B shows how QA and PA can be computed with the SPSS statistical package. It also shows how to get the p value of the test and confidence intervals for PA for any level Table 3 give some indications on how to interpret PA.
Table 3.
Interpretation of the Statistics PA.
| P A | Agreement is . . . |
|---|---|
| 0.40 . . . 0.60 | weak or absent |
| 0.60 . . . 0.70 | fair |
| 0.70 . . . 0.80 | moderate |
| 0.80 . . . 0.90 | strong |
| >0.90 | outstanding |
An Illustration With Computation of Formulas
We illustrate the computation of the QA statistic with an example involving two raters having to examine and codify 200 observations into a system of k = 5 categories, labelled 1 to 5. The judgment matrix and the marginal sums and are shown in Table 4, top part; the second part of Table 4 presents the expected theoretical frequencies finally, the standardized differences are shown in the third part of Table 4.
Table 4.
Cross-Classification Data From Two Simulated Raters, Indicating (Top) the Number of Ratings oi,j in Each i, j Cell, (Middle) Its Corresponding Theoretical Value , and (Bottom) the Standardized Differences (N = 200).
| Observed frequencies oi,j | |||||||
|---|---|---|---|---|---|---|---|
| Rater 2 | |||||||
| 1 | 2 | 3 | 4 | 5 | Row sums oi,* | ||
| Rater 1 | 1 | 7 | 5 | 2 | 1 | 3 | 18 |
| 2 | 5 | 13 | 10 | 7 | 8 | 43 | |
| 3 | 11 | 4 | 15 | 6 | 9 | 45 | |
| 4 | 8 | 11 | 7 | 9 | 6 | 41 | |
| 5 | 11 | 5 | 15 | 6 | 16 | 53 | |
| Column sums | o*j | 42 | 38 | 49 | 29 | 42 | N = 200 |
| Expected frequencies ei,j | |||||||
| Rater 2 | Row sums | ||||||
| 1 | 2 | 3 | 4 | 5 | ei,* | ||
| Rater 1 | 1 | 3.78 | 3.42 | 4.41 | 2.61 | 3.78 | 18 |
| 2 | 9.03 | 8.17 | 10.53 | 6.24 | 9.03 | 43 | |
| 3 | 9.45 | 8.55 | 11.02 | 6.53 | 9.45 | 45 | |
| 4 | 8.61 | 7.79 | 10.05 | 5.95 | 8.61 | 41 | |
| 5 | 11.13 | 10.07 | 12.98 | 7.68 | 11.13 | 53 | |
| Column sums e*,j | 42 | 38 | 49 | 29 | 42 | N = 200 | |
| Standardized differences zi,j | |||||||
| Rater 2 | |||||||
| 1 | 2 | 3 | 4 | 5 | |||
| Rater 1 | 1 | +1.656 | +0.854 | −1.148 | −0.997 | −0.401 | |
| 2 | −1.341 | +1.690 | −0.165 | +0.306 | −0.343 | ||
| 3 | +0.504 | −1.556 | +1.197 | −0.206 | −0.146 | ||
| 4 | −0.208 | +1.150 | −0.961 | +1.253 | −0.889 | ||
| 5 | −0.039 | −1.598 | +0.559 | −0.608 | +1.460 | ||
In this example, the component (i), includes all 5 diagonal cells, every cell being positive, and is . Its counterpart, (iii), is therefore zero. For the off-diagonal cells, the sum of negative-signed components (ii) is and the sum of positive-signed components (iv) is = Q A is therefore
This value, compared to a F critical value at α = .05, F(8, 8) = 3.438, suggests that the raters are in agreement, Q A(8, 8) = 8.23, p < .05.
Note that the sum of all the components of Q A, , equals the usual chi-square test, 25.03. With its degrees of freedom, the critical value being 26.30, we would infer that the data pattern observed in Table 4 does not exhibit any structure and may be ascribed to a pure chance mechanism, = 26.30, p > .05. The chi-square test does not detect agreement in Table 4 because, not being specifically suited for agreement detection, it lacks power and specificity (as our Monte Carlo experiments will confirm).
The second statistic, PA, is obtained with , well above the reference value of ½, suggesting a strong agreement. To get confidence intervals, computer software must be used as critical values for the Beta distribution are not given in statistics textbooks. We obtain a 95% confidence interval of [0.62, 0.99], not including ½.
For this example, five statistical tests (the four from Appendix A and QA) make the same decision, rejecting the null hypothesis even at the 0.01 level. However, the same does not happen for the previous examples of Tables 1 and 2 where Q A alone concludes that agreement is absent. Table 5 summarizes the results for the examples of Tables 1, 2, and 4.
Table 5.
| Table 1 |
Table 2 |
Table 4 |
||||
|---|---|---|---|---|---|---|
| Test result | p | Test result | p | Test result | p | |
| r | 0.860 | 0.323 | 0.300 | |||
| k | 0.528 | 0.148 | 0.125 | |||
| Tests on kappa | ||||||
| z k1 | 3.43 | <.01 | 3.30 | <.01 | 3.54 | <.001 |
| z k2 = z k3 | 6.86 | <.01 | 3.31 | <.01 | 3.58 | <.001 |
| Tests on the diagonal elements | ||||||
| z Σ1 * | 9.12 | <.001 | 3.10 | <.02 | 3.16 | <.001 |
| z Σ2 | 3.23 | <.002 | 3.42 | <.01 | 3.25 | <.001 |
| Tests on the structure of the matrix | ||||||
| χ2 | 8.20 | n.s. | 57.6 | <0.001 | 25.0 | n.s. |
| Q A | 0.62 | n.s. | 2.50 | n.s. | 8.23 | <.01 |
| Exact p value | .616 | .108 | .004 | |||
| P A | 0.38 | 0.714 | 0.892 | |||
| 95% CI of PA | [.01, .94] | [0.38, 0.95] | [0.62, 0.99] | |||
Note. *Denotes the test assuming the indifference principle. n.s. = nonsignificant at the .05 level.
Reliability of the Statistics and Their Distributions
To examine the merit of the present approach, we explored the statistic PA using Monte Carlo simulations (the same results were obtained exploring QA). In particular, we examined if the scores’ distributions correspond to their theoretical counterparts. To do so, we generated agreement matrices with various amount of true agreement and checked whether the theoretical 95% confidence intervals contained the results of 95% of the simulations (using the same methodology as in Harding, Tremblay, & Cousineau, 2014). We also checked 99% and 99.9% confidence intervals but the results were comparable and so we do not report the findings.
We manipulated the sample sizes (N, from 50 to 500 by increment of 50), the number of categories k (from 4 to 25), and the true probability of an agreement, ρA. Details are given in Appendix C.
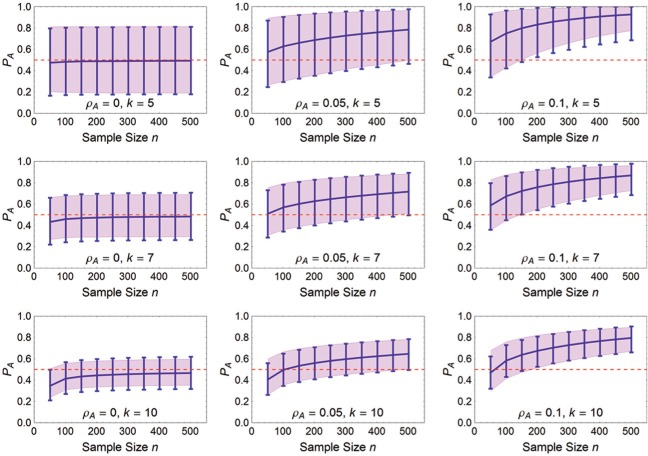
A subset of the results is shown in Figure 1. The first thing to note is that the theoretical confidence intervals (shown using error bars) match very closely the limits in which 95% of the simulated PA rest (shown using gray areas). The theoretical error bars are the least accurate for small number of categories and strong effect size where they overestimate the spread of the results.
Figure 1.
Mean PA (thick line), 95% confidence intervals (error bars), and spread where 95% of the simulated PA fell (gray area) as a function of sample size N, when ρA is varied from 0 to 0.10 (columns) and k is varied from 5 to 10 (rows). We see that PA is biased downward in the first column: with no effect, mean PA should be equal to zero for all N and all k.
Less visible but more critical, the average PA (as well as the average QA, not shown) is biased downward, underestimating the strength of the agreement. This bias is visible in the left panels where there is no agreement (ρA = 0), more so for large numbers of categories (e.g., k > 8) and for small sample sizes. We could not find a simple way to undo the bias, which would be suitable to all k. Because of the downward bias, these measures are biased toward detecting disagreement and against detecting agreement. This is why these measures should not be used for detecting disagreement (performing a left tail test of QA or PA). The bias results in a conservative test (i.e., less powerful than it could be). However, as we will see next, this has little impact on its specificity.
Sensitivity and Specificity of the Test
In order to evaluate the relative merits of the present test of agreement, we ran three more series of Monte Carlo experiments, comparing our ratio test to four other tests of agreement. In the first series, we explored statistical power by manipulating the true rate of agreement ρA from 0 to 1. In all the simulations, we manipulated the number of categories k (from 5 to 25), the total sample sizes N (from 50 to 500), and the significance levels (α, .05 and .01). The statistical tests to be compared (described in Appendix A) are the following:
Cohen’s simple z test
a z test using Fleiss, Cohen, and Everitt’s (1969) more accurate variance approximation
a sum-of-z test not assuming the indifference principle
QA, the ratio of agreement test (equivalent to PA)
the standard χ2 omnibus test of independence
We included the test even though it is not a test of agreement to provide a reference. We do not report results for (described in Appendix A) as its results are undistinguishable from nor do we report results from (for reasons explained in Appendix C).
Apart from being powerful, a good test should also be mostly, if not exclusively, sensitive to agreeing judgments, and not to any other type of consistent categorizations. For example, if observations classified as instances of category 2 by the first rater are systematically put in Category 3 by the second rater (as seen in Table 1), this is a consistent pairing, but not an agreement, and the tests should not reject based on situations of this type. The two raters, at least for these two categories, are consistent, but they nevertheless disagree. Specificity is that property of a statistical test in virtue of which it is most sensitive to data configurations relevant to its intended rejection condition but keeps relatively insensitive to other configurations. A test having high specificity should not reject at a rate higher than the significance level α when the hypothesized condition of rejection is not present.
The purpose of the last two series of Monte Carlo experiments is to evaluate the specificity of the tests. As before, we manipulated the parameters ρC, k, and N. However, in the present context, the parameter ρC represents the rate of consistent categorizations between raters. This rate is large when raters have consistent decision rules even if these rules are not in agreement. Overall, with large ρC, cases will be more frequent in cells not necessarily on the main diagonal.
In these two series of simulations, there is no overall agreement, but possibly accidental agreements for one or a few categories. Hence, the probability of rejecting should be small, otherwise the test is making too many Type I errors. Ideally, the probability of Type I errors should be equal to the significance level (5% in the subsequent figures) and fairly constant across rates of consistent categorizations.
To control precisely for the presence of accidental agreements, the two series present two conditions. In the Random with possible coincident pairings condition, Category “x” from Rater 1 is coupled to some Category “y” of Rater 2, where y may be any category among 1 to k, including by chance the same as Category x (an agreement for this category). In the Random excluding coincident pairings condition, there cannot be a single agreeing pair in the main diagonal.
A detailed description of the simulations’ parameters and algorithms is given in Appendix C.
Results
Because of the very large number of conditions explored, we only report illustrative results, shown in Figures 2 to 4, all using a significance level of .05; these results are typical of what was found in the other conditions and with a significance level of .01. Figure 2 presents the results for one set of parameter (k = 5 and N = 125), one panel per condition. In Figure 3, everything is the same as in Figure 2, except that the sample size is doubled (N =250); in Figure 4, everything is the same as in Figure 2, except that the number of categories is doubled (k = 10).
Figure 2.
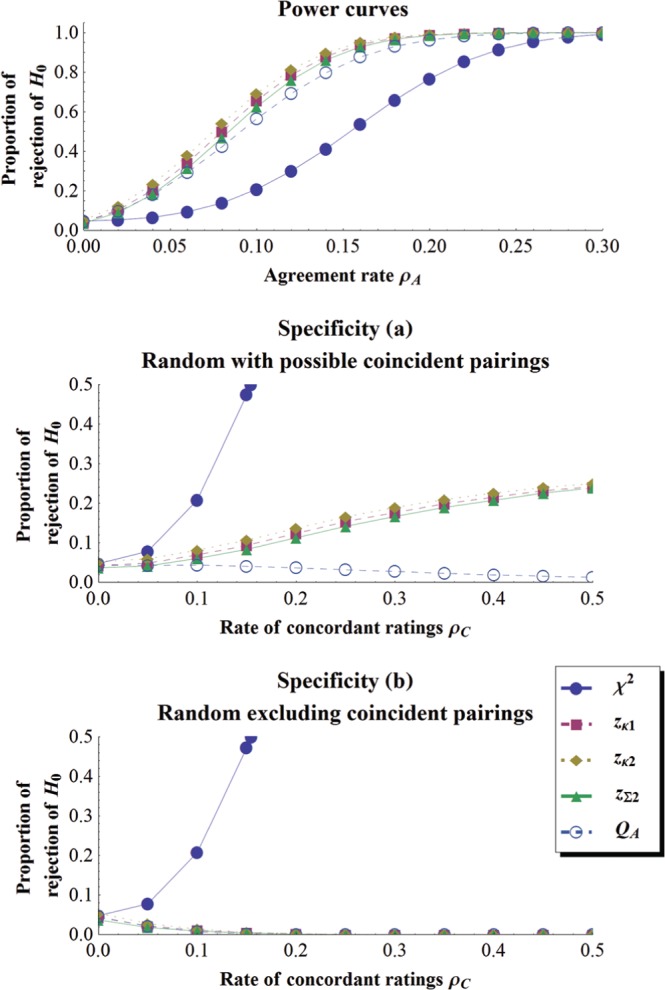
(Top panel) Power curve for 5 tests of interrater agreement as a function of the true agreement rate (ρA) when k = 5 and N = 125; (Middle and bottom panels) specificity for the same tests in the same condition as a function of the rate of consistent categorizations (ρC).
Figure 4.
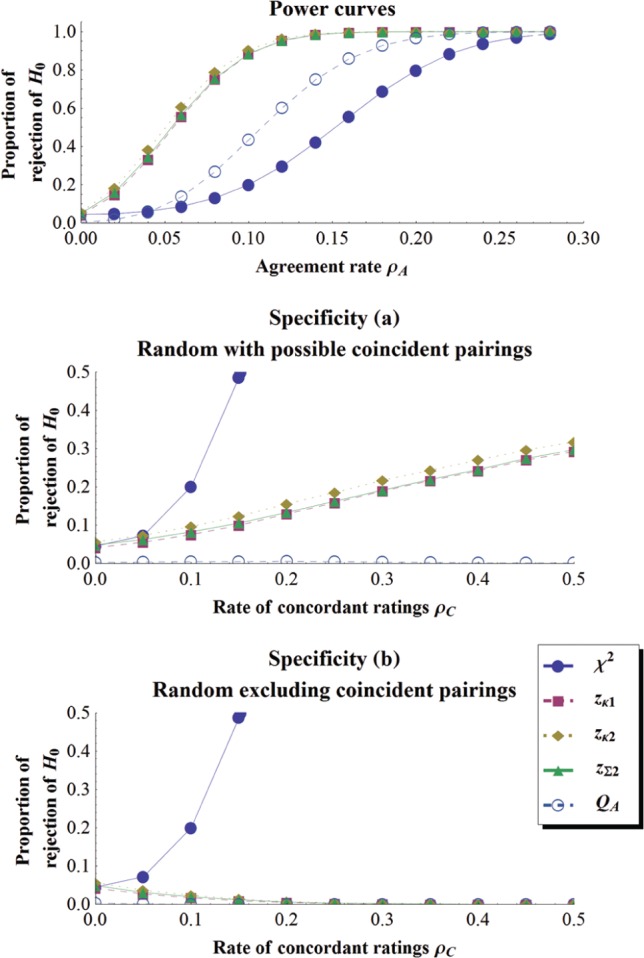
Power curve and specificity curves when k = 10 and N = 125 in the same format as Figure 2.
Figure 3.
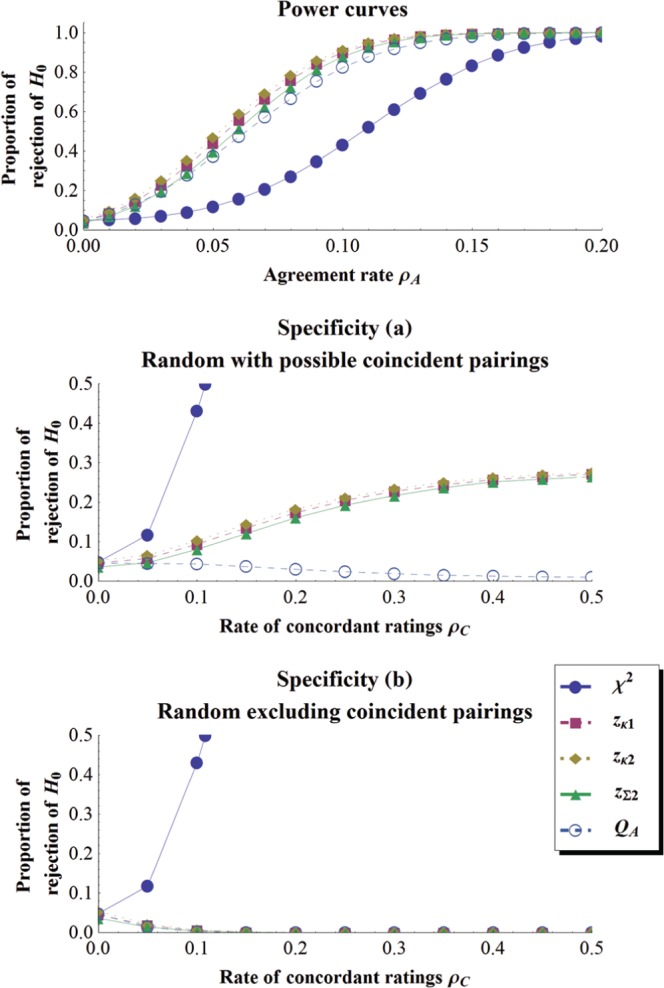
Power curve and specificity curves when k = 5 and N = 250 in the same format as Figure 2.
As seen, the results follow three patterns.
Chi-Square Test
As expected, all our results disqualify the test as a test of agreement. First, this test is the least powerful. In Figure 2, top panel, for example, the four other tests reach a power of 50% at ρA≈ 0.07 to 0.09, while chi-square needs to wait until ρA≈ 0.15 to attain it. Second, the test is the least specific, rejecting even when there is not a single coincident pairing (Random excluding coincident pairings condition).
Cohen’s (), Fleiss’ (), and the Sum-of-z () Tests
For the next three tests, Cohen’s simple formula (), Fleiss et al.’s (), and behave roughly in the same manner, be it for the power (top panels of Figures 2 to 4) or the specificity results (middle and lower panels of Figures 2 to 4). It is interesting to note that Fleiss et al.’s intricate formula for the variance of , despite its good performances, does not seem worth the effort as compared to Cohen’s much simpler one. The three tests display the best performance on power, surpassing the new QA test, more so when the number of categories is large. However, they are also markedly worse than the QA test regarding specificity (sometimes by as much as 40%). Hence, when the raters make disagreeing judgments in a consistent manner, those tests will spuriously signal agreement, an unwanted behavior. Indeed, under the condition of Random with possible coincident pairings (middle panels of Figures 2, 3, and 4), (like its variant ) and react positively to ρC, the rate of consistent categorizations, eating away its specificity. Only in conditions where not a single coincident pair is allowed (bottom panels of Figures 2, 3, and 4) do the three tests perform almost identically to the QA test.
QA Test
As can be seen in the top panels of Figures 2 and 3, power curves of the QA test follow well the power curves of the , , and tests more so if the number of categories is smaller. In the worst case presented (k = 10, top panel of Figure 4), a power of 50% is attained by QA at ρ≈ 0.046, and by Cohen’s test at ρ≈ 0.026. This loss of power continues to increase as k increases. On the other hand, the specificity curves present a remarkable stability for QA: the significance rate in all cases starts at the alpha value (e.g., .05) or below and declines steadily as the rate of consistent categorizations increases.
The QA test considers all circumstances in which the raters may agree and disagree. Hence, it rejects the null hypothesis only if the evidence gathered from the agreeing cells outweighs the evidence from the disagreeing cells. Consistent pairings outside the main diagonal is thus for QA a strong cue against agreement.
In sum, the new test QA was found to be just a little less powerful than the other tests when k is small (k < 8). However, these tests proved to be far less specific. One possibility is that on a small percentage of the simulations, random pairings might have occurred, triggering these tests to significance but not QA. Hence, it is not clear whether the new test is truly less powerful or is simply more selective.
General Discussion
We examined the performance of five tests for determining whether two observers, each one classifying N observations into a set of k categories, agree or not above chance level. Monte Carlo simulations were used to compare the five tests with respect to their sensitivity to true agreement—a quality that translates into statistical power—and their specificity, that is, their insensitivity to anything but true agreement. As could be expected (see for instance Cohen, 1960), the standard statistic on contingency tables, although not insensitive to true agreement, ranks well behind the other tests for power as well as for specificity. The κ-to-z tests (Cohen’s , Fleiss et al.’s ) and perform best on power, but they are impaired by their poor specificity, a problem that does not affect the ratio-based QA test.
The statistics described here provide a nice set of tools to quantify agreement and assess its significance. Confidence intervals are also defined, allowing for easy comparisons between studies. The only limitation of the present statistics is that they are all biased downward (and the bias is important for k≥ 10 and small N). Future work should try to find the correction to this limitation. In the meanwhile, the present statistics should not be used to detect significant disagreement.
Our results show that a significant test on kappa can indicate that agreement is strongly present in a few categories or weakly present in all categories (or a continuum between these extremes). On the other hand, a significant QA test only indicates that agreement is present in all the categories. The simulations showed that the QA test is the only test that is sensitive to agreement within all categories, not just a few, as seen by comparing the markedly different results in the Random excluding coincident pairings with the Random with possible coincident pairings simulations.
What does distinguish the κ-to-z and sum-of-z statistics, on the one hand, and QA, on the other, and wherefrom does the latter earn its high specificity? The uniqueness of QA comes from the fact that the whole matrix of agreement is used. Kappa-based and sum-of-z tests only exploit the main diagonal. Hence, they implicitly assume that information outside it is uninformative, which is obviously false, as we discussed with the first two examples.
Acknowledgments
We would like to thank Bradley Harding for his comments on an earlier version of this article.
Appendix A
Existing Tests of Interrater Agreement
In what follows, we note the rate of agreement (r) as the proportion of observed frequencies in the diagonal cells, and E(r) the expected rate of agreement that would arise by pure chance, where again are computed as in the test of independence using the row sums and the column sums
Two Tests Based on Cohen’s Kappa
Cohen (1960) proposed a descriptive measure for interrater agreement, the kappa coefficient (). This coefficient indicates the relative rate of above-chance agreement between raters. It is therefore an alternative to r. This coefficient, defined as
should be near zero under the null hypothesis of only chance agreement.
Cohen (1960, Equation 9) also presented an approximation for the variance of under the null hypothesis,
from which a -to-z transformation
can be used for testing the null hypothesis that κ = 0. If we ignore the ±½ continuity correction, this test is equivalent to a binomial test of proportion comparing the proportion r against its hypothesized counterpart E(r).2
Everitt (1968) derived the exact (but somewhat involved) formula for the variance of , whereas Fleiss et al. (1969, Equation 14) derived this more reliable approximation:
in which and are the row and column observed proportions found in the judgment matrix. Using this second approximation, a z test of the null hypothesis that population equals zero can be proposed using the observed κ,
This is the version of the kappa test implemented in SPSS using the CROSSTABS command.
Finally, if one is willing to compute the exact variance of observed found by Everitt (1968), the exact test of the null hypothesis can be derived (let us call it ). However, the gain in precision relative to is immaterial.
Two Tests on the Diagonal Elements
The above tests are based on a binomial distribution. They are then converted to a z score using the normal approximation to the binomial. We now examine two more tests that are built using a sum-of-z approach (sometimes called a pooled test). It is based on the idea that the sum of a number k of independent z scores is also a z score with mean zero and variance k. The sum-of-z test of agreement was first proposed by von Eye et al. (2006). It relies on the assumption that each entry in the main diagonal should contain only random agreements unaffected by the prevalence of the categories (the indifference principle). The test (referred to as Stouffer’s test in von Eye et al., 2006; see Stouffer, Suchman, DeVinney, Star, & Williams, 1949) is given by
in which This test simplifies to the following:
A generalization inspired by the above test is one in which the indifference principle is not assumed; the observed count in each cell of the diagonal is compared to its corresponding probable value under The formula is therefore
where Contrary to this formula cannot be further simplified.
Table A.1 summarizes all the tests reviewed in this appendix.
Table A.1.
Seven Test Formulas for Assessing Agreement From a Judgment Matrix.
| Name and formula | Null hypothesis | Reference |
|---|---|---|
| k-to-z tests | ||
| H 0: κ = 0 | Cohen (1960) | |
| H 0: κ = 0 | Fleiss et al. (1969) | |
| Sum-of-z tests | ||
| von Eye et al. (2006) a | ||
| This article | ||
| Tests on the structure of the judgment matrix | ||
| Pearson (1932) | ||
| This article | ||
| This article | ||
Note. k is the number of categories and N is the number of observations classified.
This test, based on the indifference principle, is not included in the simulations reported.
Appendix B
Computing Agreement With SPSS
Researchers can compute Cohen’s kappa and the test using SPSS. However, there are no computer packages that can compute the sum-of-z tests or the QA test. If the Essentials for Python extension to SPSS is installed (available free from the SPSS website), the following BEGIN PROGRAM END PROGRAM block will compute QA. The data editor must contain only the ratings and there must be as many lines as there are columns (i.e., the ratings must be in the form of an agreement matrix). To enter the commands, open a new “syntax” window and execute the following:
BEGIN PROGRAM python.
import spss
# Agreement test for SPSS
# D. Cousineau & L. Laurencelle, 2015. A ratio
# test of inter-rater agreement with high specificity
# get the observed frequencies o_{ij} from SPSS
dataCursor = spss.Cursor()
o = dataCursor.fetchall()
k = len(o[0])
dataCursor.close()
# get the marginal counts
totalrow = [sum(x) for x in o ]
totalcol = [sum(x) for x in zip(*o) ]
N = sum(totalrow)
# compute the expected frequencies e_{ij}
e = [[i*j/N for i in totalcol] for j in totalrow]
# compute the four terms of the test
z_ii_plus = sum(
pow((o[i][i]-e[i][i]),2.0)/e[i][i]
for i in range(k) if o[i][i] > e[i][i]
)
z_ii_minus= sum(
pow((o[i][i]-e[i][i]),2.0)/e[i][i]
for i in range(k) if o[i][i] < e[i][i]
)
z_ij_plus = sum(
pow((o[i][j]-e[i][j]),2.0)/e[i][j]
for i in range(k) for j in range(k) if (o[i][j] > e[i][j]) & (i!=j)
)
z_ij_minus= sum(
pow((o[i][j]-e[i][j]),2.0)/e[i][j]
for i in range(k) for j in range(k) if (o[i][j] < e[i][j]) & (i!=j)
)
# compute Q_A and P_A
Qa = (z_ii_plus + z_ij_minus) / ( z_ii_minus + z_ij_plus )
Pa = Qa / (1 + Qa)
# That’s it! Just show the results.
spss.StartProcedure("Agreement test")
spss.TextBlock("Result","Q_A = "+str(Qa))
spss.TextBlock("Result","P_A = "+str(Pa))
spss.EndProcedure()
END PROGRAM.
To compute significance of QA and confidence interval on PA, you may then run the following lines (there must be at least one line of data in the data editor), adjusting the first four lines to your results:
COMPUTE k = 3. /* number of categories */
COMPUTE n = 100. /* number of observations */
COMPUTE alpha = 0.05. /* for 95% confidence interval */
COMPUTE Qa = 0.6235. /* obtained from above script */
COMPUTE pvalue = 1 - cdf.F(Qa, 0.5*(k-1)**2, (1-0.5)*(k-1)**2).
FORMAT pvalue (f8.6).
COMPUTE Pa = Qa/(1 + Qa).
COMPUTE PaCIlo = idf.beta( alpha/2, Pa*(k-1)**2/2, (1-Pa)*(k-1)**2/2).
COMPUTE PaCIhi = idf.beta(1-alpha/2, Pa*(k-1)**2/2, (1-Pa)*(k-1)**2/2).
EXECUTE.
The results will appear in the data editor in new columns.
Appendix C
Simulation Procedures
The following describes the different parameters and procedures of our simulation experiments for assessing confidence intervals, the statistical power, and the specificity of the various test procedures. First, the true agreement rate between the two simulated raters was varied from no agreement between the raters () to perfect agreement () by increment of 1/200. Second, we varied the number of categories (k) from 5 to 25. Finally, the total number of observations was manipulated from small (N = 50) to large (N = 500).
The following algorithm was used to generate one judgment matrix:
Note that for such a scheme of data generation, the expected observed rate of agreement is given by (i.e., larger than ρA) because there may be an agreement by chance when selecting the categorization of Rater 2 randomly.
A Monte Carlo simulation went as follows. First, generate one square k×k matrix (using the algorithm above). Second, compute all test statistics, each compared with its appropriate critical value. This process is repeated 200,000 times for each combination. The significance level α (.05 or .01) is also varied. The proportion of rejections is then computed.
To examine specificity, the parameter ρC was used, this time with a different meaning, that is, as a “concordance rate” describing the rate of concordant but not necessarily agreeing judgments. This rate might apply to cells outside the main diagonal.
Two types of configurations were explored, each with its own set of Monte Carlo simulations: Random with possible coincident pairings and random excluding coincident pairings. In both scenarios, for each category x the first rater is choosing, the category y(x) is chosen by the second rater when they are classifying the observations in a concordant fashion. The two scenarios differ in whether they allow y(x) to be equal to x, that is, to be true agreement. In the Random with possible coincident pairings scenario, occasional agreeing pairings are possible by chance. For the Random excluding coincident pairings condition, occasional agreeing pairs were excluded to insure that there was not a single agreeing pairing. The following algorithm was used:
As previously, the algorithm was iterated 200,000 times, keeping track of the rejection rate of the six tests, for each combination of k, and N for each of the two scenarios described above. The significance level α (.05 or .01) was also varied.
In unreported simulations, we also manipulated the prevalence of the categories using a “slope” parameter Δ. For all k categories were equally frequent in the population (i.e., satisfying the indifference principle). For some categories are slightly more frequent than others (similar to the data of Table 4). For there is an important discrepancy between category frequencies. The data in Table 1 display extreme differences in category frequencies that would roughly correspond to Formally, is the ratio of the largest to the smallest category prevalence probability, The probabilities for the intermediate categories were varied linearly with the constraint that
By varying Δ, only one new result was apparent: The test, based on the indifference principle (the hypothesis of an equal, random, distribution of observations across categories), fares correctly on power as long as the observations are indeed evenly distributed across the categories (Δ = 1, in which case it superimposes on Cohen’s results). However, its power curve rises well above the alpha-level and unto unjustified heights, in conditions with uneven prevalence of categories (15% of Type I error rate for Δ = 3 and up to 50% for Δ =10). As a consequence, the does not respect the prescribed alpha level when there is no agreement (i.e., for ρA = 0) and displays spurious power when ρA is greater than zero and the prevalence of the categories are not uniform.
To be precise, half of the cells should have a count above the expected median but the median of a binomial distribution is complex to evaluate (Kaas & Buhrman, 1980) and close to the mean as soon as the expected value exceeds five.
Let the number of observed agreement be and the estimated probability of concordance be E(r). The distribution of x is approximately binomial, that is, and its normal approximation, is algebraically equivalent to Equation A.3.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
References
- Brennan R. L., Prediger D. J. (1981). Coefficient kappa: Some uses, misuses, and alternatives. Educational and Psychological Measurement, 41, 687-699. doi: 10.1177/001316448104100307 [DOI] [Google Scholar]
- Cohen J. (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20, 37-46. doi: 10.1177/001316446002000104 [DOI] [Google Scholar]
- Everitt B. S. (1968). Moments of the statistics Kappa and weighted Kappa. British Journal of Mathematical and Statistical Psychology, 21, 97-103. doi: 10.1111/j.2044-8317.1968.tb00400.x [DOI] [Google Scholar]
- Fleiss J. L., Cohen J., Everitt B. S. (1969). Large sample standard errors of kappa and weighted kappa. Psychological Bulletin, 72, 323-327. doi: 10.1037/h0028106 [DOI] [Google Scholar]
- Forbes C., Evans M., Hastings N., Peacock B. (2010). Statistical distributions. New York, NY: Wiley. [Google Scholar]
- Harding B., Tremblay C., Cousineau D. (2014). Standard errors: A review and evaluation of standard error estimators using Monte Carlo simulations. Quantitative Methods for Psychology, 10, 107-123. [Google Scholar]
- Kaas R., Buhrman J. M. (1980). Mean, median and mode in binomial distributions. Statistica Neerlandica, 34, 13-18. doi: 10.1111/j.1467-9574.1980.tb00681.x [DOI] [Google Scholar]
- Kraemer H. C., Periyakoil V. S., Noda A. (2002). Kappa coefficients in medical research. Statistics in Medicine, 21, 2109-2129. doi: [DOI] [PubMed] [Google Scholar]
- Landis J. R., Koch G. G. (1977). The measurement of observer agreement for categorical data. Biometrics, 33, 159-174. doi: 10.2307/2529310 [DOI] [PubMed] [Google Scholar]
- Stouffer S. A., Suchman E. A., De Vinney L. C., Star S. A., Williams R. M., Jr. (1949). The American soldier: Vol. I. Adjustment during army life. Princeton, NJ: Princeton University Press. [Google Scholar]
- von Eye A., Schauerhuber M., Mair P. (2006). Significance tests for the measure of raw agreement. Retrieved from http://interstat.statjournals.net