An Approach to Scoring and Equating Tests With Binary Items

Abstract

This article describes an approach to test scoring, referred to as delta scoring (D-scoring), for tests with dichotomously scored items. The D-scoring uses information from item response theory (IRT) calibration to facilitate computations and interpretations in the context of large-scale assessments. The D-score is computed from the examinee’s response vector, which is weighted by the expected difficulties (not “easiness”) of the test items. The expected difficulty of each item is obtained as an analytic function of its IRT parameters. The D-scores are independent of the sample of test-takers as they are based on expected item difficulties. It is shown that the D-scale performs a good bit better than the IRT logit scale by criteria of scale intervalness. To equate D-scales, it is sufficient to rescale the item parameters, thus avoiding tedious and error-prone procedures of mapping test characteristic curves under the method of IRT true score equating, which is often used in the practice of large-scale testing. The proposed D-scaling proved promising under its current piloting with large-scale assessments and the hope is that it can efficiently complement IRT procedures in the practice of large-scale testing in the field of education and psychology.

There are ongoing efforts in the theory and practice of measurement on comparing and bridging concepts and procedures from the classical test theory (CTT) and item response theory (IRT) (e.g., Bechger, Maris, Verstralen, & Beguin, 2003; DeMars, 2008; Dimitrov, 2003; Fan, 1998; Hambleton & Jones, 1993; Kohli, Koran, & Henn, 2015; Lin, 2008; MacDonald & Paunonen, 2002; Oswald, Shaw, & Farmer, 2015; Raykov & Marcoulides, 2016). Numerous CTT–IRT studies focus on the practical usefulness of combining CTT and IRT procedures of test scoring and item analysis to achieve simplicity in computations and interpretations, taking into account the specific context and purpose of measurement. The literature on CTT–IRT suggests that the trait-level estimation of individuals using the CTT often highly correlates with its more complex IRT counterpart (e.g., Embretson & Reise, 2000; Fan, 1998; Thorndike, 1982).

Without providing an extensive review of CTT-IRT integrations, we refer to a brief example in personality assessments with the use of the Navy Computer Adaptive Personality Scales (NCAPS; Houston, Borman, Farmer, & Bearden, 2006). Under the NCAPS, the examinee must choose between two stems that reflect different levels of a given trait, where stem levels were estimated by averaging subject matter expert ratings. In a study on NCAPS scoring, Oswald, Shaw, and Farmer (2015) compared an IRT-based scoring to much simpler alternative scoring methods. For example, under an alternative dichotomous scoring method, a test taker is given 1 point for endorsing the higher level stem in a pair and 0 points for the lower level stem; then the points across the number of attempted items are averaged. The score under this method is the proportion of the time a test taker endorsed the stem in the item that had the higher subject matter expert level. The authors concluded that

IRT-driven test scoring is certainly no worse than simpler methods but may not always be decisively better . . . when computerized tests are unavailable, then it is possible that simple CTT-driven approaches to item selection and item scoring may do no worse, which is heartening as a matter of convenience. (Oswald, Shaw, & Farmer, 2015, p. 152)

In line with psychometric efforts of using IRT information on test data to simplify test scoring and interpretations, this paper provides an approach to test scoring and equating which can be suitable for large-scale assessments using tests with dichotomously scored items; (as this is the main goal of the study, it should be kept in mind for better understanding of the purpose of methods and procedures presented in this paper). In the context of such assessments, item and person parameters are usually estimated with the use of IRT. Also, multiple forms of a given test are often equated to a base form of the test using, say, IRT true score equating under the nonequivalent groups with anchor test (NEAT) design (e.g., Angoff, 1971; Dorans, Moses, & Eignor, 2010; von Davier, Holland, & Thayer, 2004; Kolen & Brennan, 2014). Under this approach, the first step in the equating a new test form, A, to the scale of an old (base) form, B, is to rescale the item parameters of Form A onto the ability scale of Form B through linear transformations by using item characteristic curve methods (Haebara, 1980; Stocking & Lord, 1983) or the mean/mean and mean/sigma methods (Loyd & Hoover, 1980; Marco, 1977). The second step is to map the test characteristic curve (TCC) of Form A onto the TCC of Form B (e.g., Hambleton, Swaminathan, & Rogers, 1991; Kolen & Brennan, 2014; Lord, 1980). The outcome is that true scores on Form A are mapped on the true-score scale of Form B thus equating them. In practice, the equated true scores are usually treated as equated raw scores on the test; (e.g., see Kolen & Brennan, 2014, p. 197).

The IRT-based approach to test scoring and equating has advantages over CTT-based methods (e.g., van der Linden, 2013), but its practical implementation relates to conceptual and technical issues that deserve attention. For example, under the IRT true score equating described here above, the test performance of a person is reported and interpreted on the base of his or her raw score (the IRT score, θ, plays an intermediate role in the equating process). With this, the ability information encoded in the person’s response vector is “lost” because different response vectors generate the same raw score. Furthermore, the procedures for equating multiple test forms are very complex and run into technical problems with the mapping of multiple TCCs. A particular source of complexity and estimation error in mapping TCCs is the Newton–Raphson method which involves tedious iterations and the choice of poor initial values leads to erroneous solutions (e.g., see Kolen & Brennan, 2014, p. 194).

In an attempt to deal with these issues, the present article provides an approach to scoring and equating of tests with binary items which uses their IRT calibration to obtain test scores that depend on the person’s response vector, but not on the sample of examinees who took the test. Under the proposed approach, referred to here as delta-scoring (or D-scoring), the D-score of a person is derived from the person’s response vector weighted by the expected difficulty (delta, hence the name “delta-scoring”) of the items for the population of test takers. The equating of D-scores from multiple test forms on the D-scale of a base form, under the NEAT design, is greatly simplified as it avoids mapping of multiple TTCs (thus, the complexity and errors associated with the use of Newton–Raphson iterations are totally eliminated).

The procedures of D-scoring and equating, presented next, are currently under pilot applications with large-scale assessments at the National Center for Assessment (NCA) in Saudi Arabia. The motivation behind this effort came from the NCA call for developing an automated system of computerized scoring and equating. The currently existing system at the NCA provides the item scores (1/0) of the examinees, but all additional procedures of scoring and equating are conducted outside the system with the use of computer programs for IRT calibration under the three-parameter logistic (3PL) model and IRT true score equating of multiple test forms under the NEAT design. The integration of such procedures into an automated system for scoring and equating, including item bank feeding, runs into technical difficulties that relate to complex, tedious, and error-prone procedures of mapping multiple TTCs and other computations in a sequential test scoring and equating. Another task in the context of NCA testing is that, given the IRT item parameters of a test assembled from an item bank, the test score of an examinee should be known directly from his or her response vector; that is, the test score should reflect not only how many items, but which specific items, were answered correctly by that examinee. The effort is to address these issues with using the proposed D-scoring, which is described next and illustrated with real data from large-scale assessments at the NCA (of course, applications of the proposed is method are not limited to the context of NCA testing).

Theoretical Framework and Method

The idea behind the method of D-scoring and equating of tests with binary items is that (a) the D-score is based on the person’s response vector weighted by the expected difficulties of the items for the target population of test-takers, (b) the expected difficulties of the items are obtained as an analytic function of their IRT parameters, and (c) to equate the D-scores of two test forms, it is sufficient to rescale the item parameters of the new form to the scale of the base form. Thus, given the IRT estimates of item parameters (e.g., from an item bank), one can obtain the D-score for any response vector (pattern of 1/0 item scores) in two steps: (a) the expected item difficulties are obtained as a function of their IRT parameters, using an analytic formula and (b) the D-score is the sum of the 1/0 scores in the person’s response vector weighted by the expected difficulties of the items in that response vector. As the expected item difficulties are sample independent, the person’s D-score, which is based on the expected item difficulties, is also independent of the sample of test takers. Furthermore, the equating of D-scores under the IRT-based NEAT design eliminates the complex and error-prone procedure of mapping TTCs. Details on the D-scoring and equating method are provided next.

Expected Item Score

For the purposes of D-scoring, the expected item score, ${\pi }_i$, is obtained as a function of its parameters (a_i and b_i) under the two-parameter logistic (2PL) model in IRT (Dimitrov, 2003):

$${\pi }_i=\frac{1-\mathrm{erf}\left(X_i\right)}{2}$$

where $X_i=a_i{b}_i/\sqrt{2(1+a_i^2)}$, $\mathrm{erf}$ is the known mathematics function called error function, a_i is item discrimination, and b_i is item difficulty. With a relatively simple approximation provided by Hastings (1955, p. 185), the error function (for X > 0) can be evaluated with an absolute error smaller than 0.0005 as

$$\mathrm{erf}\left(X\right)=1-{(1+m_{1}X+m_2{X}^2+m_3{X}^3+m_4{X}^4)}^{-4},$$

where m₁ = 0.278393, m₂ = 0.230389, m₃ = 0.000972, and m₄ = 0.078108. When X < 0, one can use that $\mathrm{erf}(-X)=-\mathrm{erf}\left(X\right)$. The $\mathrm{erf}\left(X\right)$ is directly executable in computer programs for mathematics (e.g., MATLAB; MathWorks, Inc., 2015).

In case of IRT calibration under the 1PL, Equation (1) is used with a_i = 1, whereas under the 3PL, the expected item score is given by $c_i+(1-c_i){\pi }_i$, where c_i is the pseudo-guessing parameter in the 3PL model and ${\pi }_i$ is obtained under the 2PL via Equation (1) (Dimitrov, 2003, equation 22). Equation (1) is derived under the assumption that the latent trait, θ, measured by the test is normally distributed. In fact, the estimates of ${\pi }_i$ remain stable under moderate deviations from normality.

D-Scoring

As can be noticed, ${\pi }_i$ shows what proportion of the targeted population is expected to answer correctly item i. The ${\pi }_i$ is the CTT definition of expected item difficulty but, in fact, it represents the expected “easiness” of the item. Therefore, the difference ${\delta }_i=1-{\pi }_i$ is used here to represent the actual expected item difficulty for the population of test-takers. The D-score of person s (participant or examinee) is defined as the sum of ${\delta }_i$ values for the test items that the person answered correctly. That is, for a test of n binary items,

$$D_s=\sum _{i=1}^n{X_{\mathrm{si}}\delta }_i,$$

where $X_{\mathrm{si}}$ is the score of person s on item i ($X_{\mathrm{si}}$ = 1 for correct response; otherwise $X_{\mathrm{si}}$ = 0). Thus, the D-score is based on the person’s response vector and the expected item difficulties, ${\delta }_i$. The highest possible D-score on a test, $D_{\max }$, is the sum of expected difficulties for all items (i.e., $D_{\max }$ occurs when all items are answered correctly). Thus,

$$D_{\max }=\sum _{i=1}^n{\delta }_i=\sum _{i=1}^n(1-{\pi }_i)=n-\sum _{i=1}^n{\pi }_i.$$

The D-scale can be treated as a continuous numeric scale, with the scores on a test of n items ranging from 0 to $D_{\max }$. A score of 0 corresponds to zero correct responses and $D_{\max }$ corresponds to n correct responses. Theoretically, 0≤$D_{\max }$≤n (see Equation 4), but the two extreme values cannot occur in the practice of testing, so we have: 0 < $D_{\max }$ < n. Indeed, it is not realistic to expect that (a) $D_{\max }$ = n, which will occur if ${\delta }_1$ = ${\delta }_2$= ⋯ = ${\delta }_n$ = 1; that is, all items are answered incorrectly by the entire population of test takers and (b) $D_{\max }$ = 0, which will occur if ${\delta }_1$ = ${\delta }_2$= ⋯ = ${\delta }_n$ = 0; that is, all items are answered correctly at population level.

Consider a test of five binary items with expected item difficulties δ₁, δ₂, δ₃, δ₄, and δ₅. For a person with the response vector 1 1 0 0 1, we have D = ${\delta }_1+{\delta }_2+0+0+{\delta }_5$. If another person has the same total score on the test (X = 3), but different response vector, say, 0 1 0 1 1, then D = $0+{\delta }_2+0+{\delta }_4+{\delta }_5$. In this case, $D_{\max }$ = ${\delta }_1+{\delta }_2+{\delta }_3+{\delta }_4+{\delta }_5$; (0 < $D_{\max }$ < 5).

Standard Error of D-Scores

The derivation of the standard error of $D_s$ scores, SE($D_s)$, is provided in Appendix A.

The resulting formula is

$$\mathrm{SE}\left(D_s\right)=\sqrt{\sum _{i=1}^n{\delta }_i^2{P}_i\left({\theta }_s\right)[1-P_i\left({\theta }_s\right)]},$$

where $P_i\left({\theta }_s\right)$ is the probability of correct response on item i by person s, with ability ${\theta }_s$, which is obtained under the IRT (1PL, 2PL, or 3PL) model. As shown with the real-data illustration in the next section, the highest $\mathrm{SE}\left(D_s\right)$ values are in the middle of D-scale and decrease toward the (lowest and highest) ends of the scale.¹ This is just the opposite to the case of IRT ability scores, ${\theta }_s$, where the conditional standard errors, $\mathrm{SE}\left({\theta }_s\right)$, tend to increase toward the lowest and highest directions of the IRT logit scale (e.g., Embretson & Reise, 2000).

Item Reliability Under D-Scoring

Let X_i denotes the observed score on item i and ${\rho }_{\mathrm{ii}}\left(X\right)$ the reliability of X_i. Likewise, let D_i is the D score on item i and ${\rho }_{\mathrm{ii}}(D$) the reliability of D_i. As shown in Appendix B, the item reliability is the same under X-scoring (1/0) and D-scoring; that is,

$${\rho }_{\mathrm{ii}}(D)={\rho }_{\mathrm{ii}}\left(X\right).$$

This finding can be useful, say, in the selection of items that maximize the internal consistency reliability as the respective procedure uses the item reliability (e.g., Allen & Yen, 1979, p. 126).

Equating of D-Scales

The equating of D-scores on a new test form A onto the scale of an old (base) form B can be performed in two steps. First, the IRT item parameters of form A are rescaled onto the scale of form B through linear transformations by using methods such as the item characteristic curve methods (Haebara, 1980; Stocking & Lord, 1983), mean/mean method, and mean/sigma method (Loyd & Hoover, 1980; Marco, 1977). Second, by representing the IRT item parameters of two test forms on a common scale, the D-scores on these two forms, obtained through the use of Equations (1) to (3), are also on a common scale because they are direct functions of the IRT item parameters. The D-score equating approach can be particularly efficient when multiple new test forms (say, A₁, A₂, . . ., A_m) need to be equated to a base form, B. Specifically, after rescaling the IRT item parameters of the new forms onto the ability scale of form B through a sequence of scale transformations over a “chain” of test forms A₁→ A₂→⋯→ A_m→ B, the item parameters of all test forms are on a common scale, so the D-scores obtained as a function of these item parameters for each test form (via Equations 1-3) are also on a common scale. For details and formulas for such a chain rescaling, the reader may refer to Li, Jiang, and von Davier (2012).

Intervalness of the D-Scale

A key question about the delta scale (D-scale) is whether it is an interval scale and how D-scores compare with IRT ability scores (θs, “thetas”) in this regard. It is known that an interval scale exists when the axioms of additive conjoint measurement (ACM) hold within a given dataset (Luce & Tukey, 1964; see also, Karabatsos, 2001). Referring to a scale, the term intervalness is used in the literature to indicate the degree to which the scale data are consistent with the axioms of ACM (e.g., Domingue, 2014). From this perspective, the task here is to compare the D-scale and θ-scale on intervalness. As D-scores and their standard errors, SE(D), are obtained in the framework of IRT, where the θ-scale is supposed to be (close to) interval, the intervalness of the D-scale is compared to that of the θ-scale using a method proposed by Domingue (2014). As shown with the real-data example in the next section, the D-scale behaves better than the θ-scale on criteria of intervalness, with the difference in this regard decreasing with the increase of the number of test items.

Scaling of D-Scores

For practical reports and interpretations of test scores at the NCA, the D-scores are transformed, at the current piloting stage, into scale scores that range from 0 to 100, to be in line with the widely adopted scaling from 0 to 100 with educational assessments in Saudi Arabia. Specifically, D-scores are transformed into scale scores, S_D, using a linear transformation that results in a proportional “stretch” the D-scale from 0 to 100, namely: $S_D=100D/D_{\max }$. Under this scaling, D = 0 is assigned to 0 and D = D_max is assigned to 100; (D_max, the maximum possible D-score on the test, is the sum of the expected item difficulties of all test items). Along with the simplicity in computation and interpretation, the linear scaling of D-scores maintains their intervalness. Of course, other approaches to scaling D-scores can be used depending on the context and purpose of the assessment of interest.

Illustration With Real Data

As noted at the beginning, automated procedures of D-scoring and equating are under pilot applications with large-scale assessments at the NCA in Saudi Arabia. Most of these assessments are based on (a) aptitude and achievement tests administered to high school graduates, as a part of their application to Saudi universities and (b) multiple tests for teacher certification in Saudi Arabia. All tests are standardized and consist of dichotomously scored multiple-choice items, with an ongoing development of test forms and their equating using the IRT true score equating under the NEAT design. Because of the high complexity and efforts of scoring and equating in this context, the use of automated procedures of D-scoring and equating is deemed as very efficient, especially with the availability of an item bank which contain IRT item parameters (under the 3PL model). This allows for direct computations of expected item difficulties, δ_i, D-scores for response vectors of examinees, and (relatively fast and simple) D-score equating of multiple new test forms to the scale of a target test form. The procedures of D-scoring and equating are under piloting with real data on multiple forms for different tests at the NCA. A software, developed for this purpose, is named System for Automated Scoring and Equating (SATSE; Atanasov & Dimitrov, 2015).²

Because of space consideration, provided here are only some results and clarifications related to D-scoring and equating with real data from two tests at the NCA (a) the General Aptitude Test–Verbal Part (GAT-V), which is administered to high school graduates and (b) The General Teacher Test (GTT), which is used for certification of teacher candidates in Saudi Arabia. First, two test forms of GAT-V are used to illustrate D-scoring and equating. Second, comparison of D scores and IRT ability scores, θ, in terms of their intervalness, is provided with the use of data from GAT-V and GTT. Although GAT-V and GTT data were found to be unidimensional in previous studies on their validity and psychometric features testing for dimensionality and estimation of reliability were performed with the data used here. Specifically, the unidimensionality of the sample data on the two GAT-V forms and the GTT was supported by a tenable data fit of a one-factor model tested in the framework confirmatory factor analysis (CFA) with the use of the computer program Mplus (Muthén & Muthén, 2010). The results are summarized in Table 1.

Table 1.

Testing for Unidimensionality of Data From Two GAT-V Test Forms (Base and New) and GTT.

							90% CI for RMSEA
Test data	χ2	df	CFI	TLI	WRMRa	RMSEA	LL	UL
GAT-V(B)b	1233.224	170	.966	.962	2.155	.025	.024	.026
GAT-V(N)c	830.437	170	.982	.980	1.740	.020	.019	.021
GTT	33191.931	3002	.906	.903	2.614	.017	.016	.018

Note. GAT-V = General Aptitude Test–Verbal; GTT = General Teacher Test; CFI = comparative fit index, TLI = Tucker–Lewis index, WRMR = weighted root mean square residual, RMSEA = root mean square error of approximation; CI = confidence interval; LL = lower limit; UL = upper limit. A tenable data fit is in place with CFI > .90, TLI > .90, WRMR is close to 1, and RMSEA < .05.

^aIn Mplus, WRMR is used with categorical variables, which is the case with the study data (with continuous variables, standardized root mean square residual [SRMR] is used).

^bGAT-V base form.

^cGAT-V new form.

The reliability of the sample data was estimated under the latent variable modeling (LVM) approach using Mplus (e.g., Raykov, 2007; Raykov, Dimitrov, & Asparouhov, 2010). The resulting reliability estimates, provided in Table 2 with their 95% confidence intervals, range from .848 to .883, which is adequate for the purpose of this illustration. The Cronbach’s coefficient alpha for internal consistency reliability is also provided in Table 2. As can be seen, the alphas are smaller than their LVM-based counterparts. A plausible explanation is that the Cronbach’s alpha requires essentially tau-equivalent measures (i.e., all observed measures have equal loadings to the latent factor that they represent; e.g., Raykov & Marcoulides, 2016). However, this assumption is difficult to meet with congeneric binary measures, whereas it is not required with the LVM approach to reliability estimation.

Table 2.

Estimates of Score Reliability for Two Test Forms of GAT-V and GTT Under Two Approaches to Estimation (α and LVM).

		LVM-based estimation
Test data	Cronbach’s α	${\hat{\rho }}_{\mathrm{XX}}$	95% CI for ${\hat{\rho }}_{\mathrm{XX}}$
GAT-V(B)a	.731	.848	[.843; .853]
GAT-V(N)b	.776	.883	[.879; .887]
GTT	.783	.879	[.877; .881]

Note. GAT-V = General Aptitude Test–Verbal; GTT = General Teacher Test; LVM = latent variable modeling; CI = confidence interval. Cronbach’s α assumes that the measures are essentially tau-equivalent, whereas the LVM approach does not require this assumption.

^aGAT-V base form.

^bGAT-V new form.

Computation of D-Scores

The computation of D-scores is illustrated with data from a base test form of GAT-V, which has 20 dichotomously scored multiple-choice items that measure the examinees’ ability in reading comprehension and sentence completion. The data consist of the binary scores (1/0) of 9,937 high school graduates on the 20 items of this GAT-V test form. The distribution of total test scores (number correct responses) was close to normal, ranging from 1 to 18 (M = 8.43, SD = 2.96). The IRT estimates of the item parameters under the 3PL model are provided in Table 3 (a = discrimination, b = difficulty, and c = pseudo-guessing) (e.g., see Hambleton, Swaminathan, & Rogers, 1991). The IRT calibration was performed under maximum likelihood estimation with EM algorithm using the computer program Xcalibre 4.2 (Guyer & Thompson, 2013). The expected item difficulty, δ_i, is also given in Table 3; (i = 1, 2, . . ., 20). Recall that δ_i is the proportion of the target population of examinees who provided an incorrect response on the item; that is, δ_i shows how difficult is the item for the entire target population (δ_i = 1 –π_i, where π_i, the expected “easiness” of the item, is computed as a function of the item parameters via Equation 1).

Table 3.

Item Parameters and D-Scores for 3 Examinees on 20 Test Items of GAT-V Base Form, B.

	Item parameters (3PL)				X-scores			D-scores
Item	ai	bi	ci	δi	X i1	Xi 2	Xi 3	Di 1	Di 2	Di 3
1	0.792	−0.278	0.347	.282	1	0	1	.282	0	.282
2	0.636	−0.029	0.232	.380	1	1	1	.380	.380	.380
3	0.727	0.153	0.289	.381	1	0	1	.381	0	.381
4	0.954	0.014	0.239	.383	0	1	1	0	.383	.383
5	0.612	2.634	0.264	.674	1	0	1	.674	0	.674
6	1.040	−1.052	0.216	.176	1	0	1	0	0	.176
7	0.908	−1.429	0.223	.131	0	0	1	0	0	.131
8	1.017	0.600	0.215	.523	0	1	1	0	.523	.523
9	0.932	−1.453	0.224	.125	0	1	1	0	.125	.125
10	0.778	−1.236	0.216	.176	0	0	1	0	0	.176
11	0.471	1.008	0.256	.496	0	1	1	0	.496	.496
12	1.047	−0.403	0.212	.304	0	0	1	0	0	.304
13	1.372	0.392	0.163	.523	0	0	1	0	0	.523
14	0.988	0.547	0.179	.534	0	0	1	0	0	.534
15	1.100	−0.592	0.200	.264	0	0	1	0	0	.264
16	1.019	−1.059	0.196	.181	0	0	1	0	0	.181
17	0.879	−0.814	0.234	.226	0	0	1	0	0	.226
18	0.674	−0.024	0.187	.402	0	0	1	0	0	.402
19	1.761	3.463	0.116	.883	0	0	1	0	0	.883
20	1.008	−0.499	0.211	.285	0	0	1	0	0	.285
Total	7.327	5	5	20	1.717	1.907	7.327

Note. GAT-V = General Aptitude Test–Verbal; 3PL = three-parameter logistic. δ_i = expected item difficulty (the population proportion of incorrect item responses). Column D_is is the product of columns X_is and δ_i; that is, D_is = δ_iX_is; (i = 1, . . ., 20; s = 1, 2, 3). The D-score of person s is the sum of the entries in column D_is; that is, D_s = D_1s+⋯+D_20s. The maximum possible D-score (for all item responses correct) is D_max = δ₁+⋯+δ₂₀ = 7.327. Given in boldface are the numbers of seven items in the base form, B, which are used as common items with the new test form, A (see Table 4).

In Table 3, the columns labeled X_i1, X_i2, and X_i3 contain the response vectors of three examinees, with the first two having the same total test score (X₁ = X₂ = 5), but different response vectors, whereas the third person has all items correct (X₃ = 20). The response vectors X_i1, X_i2, and X_i3 are multiplied by the item difficulty vector, δ_i, and the resulting products are stored in the columns labeled D_i1, D_i2, and D_i3, respectively. Then, by the virtue of Equation (3), the sum of the entries in column D_is renders the D_s score of person s (s = 1, 2, 3), namely D₁ = 1.717, D₂ = 1.907, and D₃ = 7.327. Note that the score of the third person equals the maximum possible D score on the test, which is the sum of all δ_i values (D_max = 7.327), because that person has answered correctly all 20 items. On the other hand, although the first two persons have the same total score (X₁ = X₂ = 5), they have different D-scores because of having different response vectors; that is, they have answered items with different difficulties for the target population. The D-scores of the other examinees in the sample (N = 9,937) are obtained in the same way. The distribution of D-scores was close to normal, ranging from 0 to 7.327 (M = 3.802; SD = 1.272). The correlation of the D-scores with the total test score (X = number correct responses) was very high (0.962). However, the X-scores can take only 21 different values (from 0 to 20), whereas the D scores can take values generated from thousands different response vectors on 20 binary items.

The conditional standard error for each D_s score, SE(D_s), was computed via Equation (5); (the true scores, $P_i\left({\theta }_s\right)$, participating in Equation 5, were estimated with Xcalibre 4.2). The SE(D_s) values were relatively small, ranging from 0.072 to 0.815; (M = 0.767, SD = 0.069). As shown in Figure 1, the standard errors tend to decrease toward the extremes of the D-scale, particularly to the right; that is, the highest precision is with D-scores of high-ability examinees.¹

Figure 1.

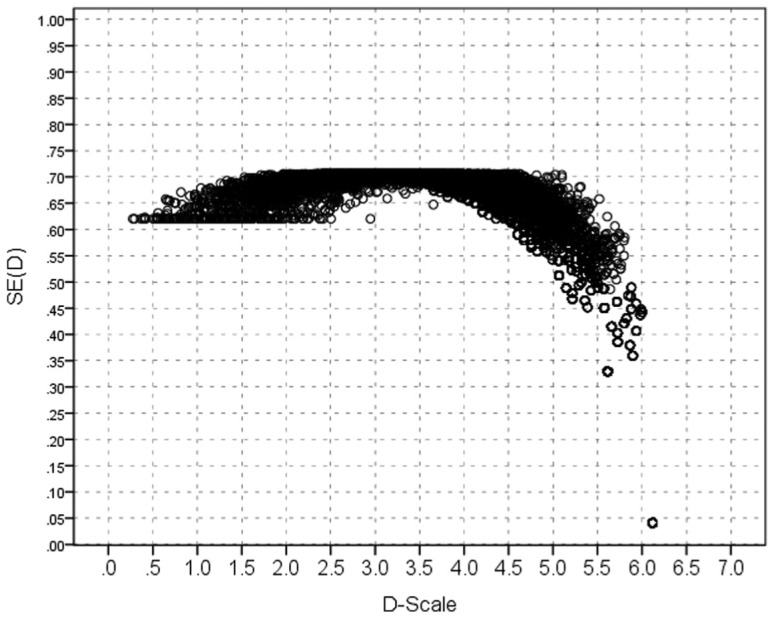
Standard errors of D-scores on GAT-V (form B) data. GAT-V = General Aptitude Test–Verbal.

It is also worth noting that the D scores provide higher differentiation of examinees with low or high abilities compared with IRT ability scores reported with the use of computer programs for IRT calibration. For example, although the theoretical values of IRT ability vary from −∞ to +∞, they are always reported in a practically reasonable interval, say, from −7 to 7 on the logit scale. Thus, the examinees assigned to an extreme category (say, −7 or 7) in IRT calibrations are much better differentiated on the D-scale. For example, under the IRT scoring, via Xcalibre 4.2, with the data on GAT-V form B (N = 9,937) (Figure 2), it was found that 204 examinees were assigned to the lowest score category (θ = −7) on the logit scale, whereas 172 of them were assigned different scores on the D-scale, ranging from 0 to 3.713 (M = 1.468, SD = 0.654).

Figure 2.

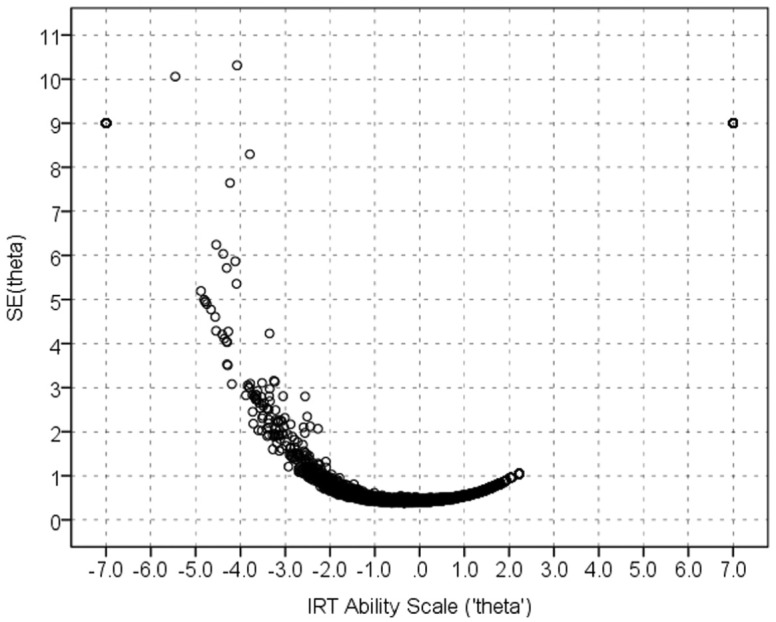
Standard errors of item response theory ability scores (thetas) on GAT-V (form B) data. GAT-V = General Aptitude Test–Verbal.

Equating of D-Scales

In this example, the D scores on a new test form of GAT-V (Form A) are equated to the D-scale of the base form of GAT-V (Form B) described in the previous section. The data on test form A consist of binary scores of 9,781 high school graduates on 20 items, seven of which are common items with the items of form B (as described earlier, test form B was administered to 9,937 high school graduates). The samples of examinees who took forms A and B, respectively, are treated as “nonequivalent groups” coming from two different populations of test takers on Forms A and B. The items of Forms A and B are calibrated under the 3PL model in IRT using Xcalibre 4.2. Items 1, 2, 3, 4, 11, 12, and 13 in Form B are common (anchor) items that correspond to Items 1, 2, 3, 4, 18, 19, and 20, respectively, in Form A. The correlation between the scores on the set of common items and the total test score is .883 and .887 for Forms A and B, respectively. The reliability estimates for the scores on the two test forms are also very similar, .883 and .848 for Forms A and B, respectively (see Table 2). These results are in support of the appropriateness of equating test Forms A and B (e.g., Kolen & Brennan, 2014).

The D-scale equating is performed in three major steps. First, the item parameters of the new Form A (a, b, c) are transformed onto the scale of the base Form B, thus obtaining rescaled item parameters A (a*, b*, c*). Second, the expected difficulties for the items of Form A are also “rescaled” by computing them as a function of the rescaled item parameters (a*, b*, c*), as described earlier. Thus, if ${\delta }_i$ is the expected difficulty of item i for the population of test takers on Form A, its rescaled value, ${\delta }_i^{*}$, is the expected difficulty of that item for the population of test takers on Form B. Third, if D_s is the score of person s with a given response vector on Form A, its equated value on the scale of Form B, denoted here $D_s^{*}$, is obtained by weighting that response vector with the rescaled expected item difficulties, ${\delta }_i^{*}$ (i = 1, 2, . . ., 20), as shown in the previous section. As a result, the D_s scores on Form A are equated to $D_s^{*}$ scores on the scale of base Form B (s = 1, . . ., N_A, with N_A = 9,781 in this example). The item parameter estimates of form A and the corresponding expected item difficulties, before and after rescaling, are given in Table 4.

Table 4.

Estimates of Item Parameters and Expected Item Difficulties for Test Form A, Before and After Their Rescaling Onto the Scale of Base Form B.

Item	Form A: Before rescaling				Form A: After rescaling
	a	b	c	δ	a*	b*	c*	δ*
1	0.859	−0.112	0.374	0.295	0.792	−0.278	0.347	0.282
2	0.658	0.089	0.240	0.395	0.636	−0.029	0.232	0.380
3	0.741	0.276	0.299	0.396	0.727	0.153	0.289	0.381
4	1.024	0.124	0.247	0.403	0.954	0.014	0.239	0.383
5	0.985	−1.012	0.222	0.186	0.954	−1.102	0.221	0.174
6	0.871	−1.415	0.218	0.138	0.847	−1.514	0.217	0.129
7	0.982	0.687	0.204	0.545	0.929	0.644	0.202	0.535
8	0.927	−1.409	0.221	0.132	0.897	−1.511	0.220	0.122
9	0.731	−1.220	0.216	0.185	0.710	−1.316	0.215	0.175
10	0.545	−1.115	0.243	0.224	0.528	−1.215	0.241	0.216
11	0.932	−0.751	0.205	0.242	0.904	−0.835	0.204	0.229
12	0.899	−1.474	0.262	0.120	0.869	−1.581	0.260	0.111
13	0.621	−0.828	0.233	0.254	0.601	−0.916	0.232	0.244
14	1.062	−0.702	0.186	0.248	1.030	−0.783	0.185	0.234
15	1.075	−0.493	0.230	0.276	1.042	−0.571	0.228	0.263
16	1.164	−0.690	0.199	0.240	1.129	−0.770	0.199	0.226
17	0.785	0.292	0.190	0.463	0.753	0.235	0.188	0.451
18	0.476	1.050	0.247	0.508	0.471	1.008	0.256	0.496
19	0.802	−0.369	0.215	0.321	1.047	−0.403	0.212	0.304
20	1.182	0.548	0.170	0.550	1.372	0.392	0.163	0.523

Note. Given in boldface are the numbers of seven items used as common items with the base test form B; (Items 1, 2, 3, 4, 18, 19, and 20 in form A are used as Items 1, 2, 3, 4, 11, 12, and 13, respectively, in the base test form B; see Table 3).

The examination of Table 4 shows that the rescaled values of expected item difficulties, ${\delta }_i^{*}$, are slightly smaller than the prior-to-equating values, ${\delta }_i$, across all items. This indicates that the items of Form A have become slightly less difficult after rescaling their parameters onto the scale of Form B; that is, Form B is slightly less difficulty than Form A at the population level. It follows then that the D_s scores on Form A will equate to slightly lower $D_s^{*}$ scores mapped onto the ability scale of form B. This was supported with the results for the D_s and $D_s^{*}$ scores obtained for the sample of examinees (N_A = 9,781), with a perfect correlation between them (r = 1) and the values of their difference (D_s−$D_s^{*}$) being all positive, ranging from 0.011 to 0.263. Also, the maximum possible score on form A is D_max = 6.120, prior to equating, and $D_{\max }^{*}$ = 5.857, after equating (one can check this by summing the values of ${\delta }_i$ and ${\delta }_i^{*}$, respectively, in Table 4).

For illustration, consider the response vector 1100110101000000000 of a person with 6 correct responses on the 20 items of Form A. The D_s score of that person on Form A, prior to its equating, is obtained by using Equation (3) with the given response vector and the expected item difficulties ${\delta }_i$ (in Table 4); that is, D_s = ${\delta }_1$+${\delta }_2$+${\delta }_5$+${\delta }_6$+${\delta }_8$+${\delta }_{10}$ = 1.370; (zeros excluded). Likewise, the equated value of D_s is obtained as $D_s^{*}$ = ${\delta }_1^{*}$+${\delta }_2^{*}$+${\delta }_5^{*}$+${\delta }_6^{*}$+${\delta }_8^{*}$+${\delta }_{10}^{*}$ = 1.303. For a person with 20 correct responses on Form A, D_s = 6.120 (= D_max) and its equated score on the scale of Form B is $D_s^{*}$ = 5.857 (= $D_{\max }^{*}$).

D-Scale Intervalness

A key question about the delta scale (D-scale) is whether it is an interval scale and how D-scores compare with IRT ability scores (thetas) in terms of intervalness. This question was addressed with a previous study at the NCA by comparing the D-scale with the IRT theta scale from the perspective of additive conjoint measurement using an approach referred to as ConjointChecks (Domingue, 2014). The details in methodology and findings, provided with a technical report on that study (Domingue & Dimitrov, 2015), are not presented here for space consideration, but some main points and results are replicated and illustrated with data in this example. Specifically, used are the data with the base form of GAT-V, described in the previous section, and data on the GTT. The GTT data consist of the binary scores (1/0) of 45,749 teacher candidates on 79 multiple-choice items.

In the case of item response data, the ACM axioms are concerned with orderings amongst the probabilities for individuals at different abilities responding to items with different difficulties. The ConjointChecks approach (Domingue, 2014) implements an algorithm for checking the axioms of ACM. The question is whether the observed proportion of correct item responses for a given set of respondents assumed to be at some common ability is consistent with the posterior distribution of the probabilities for correct responses generated by the algorithm. If not, the ConjointChecks algorithm is said to have detected a “violation.” The violation percentages (Vp) are checked in 3 × 3 submatrices of the full data matrix. These matrices are either formed via a random selection of items and groups of individuals or via the collection of adjacent items and groups of individuals.

The ConjointChecks approach is readily applied to discrete ability estimates, but in case of continuous data, such as D-scores and IRT thetas, a discretization of the continuous number line is achieved by a division of the line referred to as “banding.” Some bandings are more “stringent” than others in the sense that they are more likely to place a person in the wrong band given the error associated with the person’s score (here, D or theta). One can expect that a more stringent banding would produce fewer axiom violations (for details, see Domingue, 2014). In this example, the violation percentages (Vp) produced by common bandings of the D and theta scores are examined across levels of stringencies.³

Violation percentages based on the natural banding of the sum scores were computed for a set of 5,000 respondents. For the continuous abilities, the mean score (either theta or D) for individuals at a given sum score was considered. The banding was then defined by the midpoints between all consecutive means. The Vp were examined from two types of checks. The first check looks at all adjacent 3-matrices from the full data matrix while the second one considers 5,000 randomly chosen 3-matrices. Along with the unweighted Vp, weighted Vp were also considered, where violations at a given portion of the scale are weighted based on the number of individuals at that part of the scale. The results are summarized in Table 5. The sum scores generate the smallest percentages of violations (for all Vp), but this can be expected given that this banding is based on the sum scores. The D scores look very similar to the sum scores, especially on the weighted metrics. The theta scores produce more violations, notably more so for the randomly chosen 5,000 3-matrices. Also, the weighted metric performs better than its unweighted counterpart in terms of smaller percentage of violations.

Table 5.

Violation Percentages (Vp) for Natural Banding of Sum Scores.

	Vp-Adj		Vp-5k
Scale	Uw	W	Uw	W	Stringencya
NCR	0.37	0.34	0.09	0.05	—
Theta	0.41	0.37	0.14	0.07	10857
D-scale	0.38	0.34	0.10	0.05	7735

Note. Vp-Adj = all adjacent 3-matrices from the full data matrix; Vp-5k = 5,000 randomly chosen 3-matrices; Uw = unweighted; W = weighted; NCR = sum score (number correct responses).

^aLarger values indicate more stringent bandings (Domingue, 2014).

As there is no obvious banding available for the continuous theta and D scores, the effect of banding stringency on Vp was investigated for a number of potential bandings. Bandings are characterized by the number of cutpoints and the starting point of the first band in the banding; (the cutpoints are evenly spaced). The number between 10 and 190 were varied with increments of 20. For the GTT with 79 items, there are 80 bands in the sum score banding which is roughly the middle of the range used here. The first cutpoint were either at the 0.005, 0.01, or 0.015 quantile of the score distribution and then intervals were evenly spaced across the scale of the abilities, with the last cutpoint being at either the 0.985, 0.99, or 0.995 quantile, respectively. Unlike the case where the sum score banding was used as the basis for bandings for theta and D, now the banding is defined within the scale so that the Vp, based on a choice of banding, are optimal for each scale.

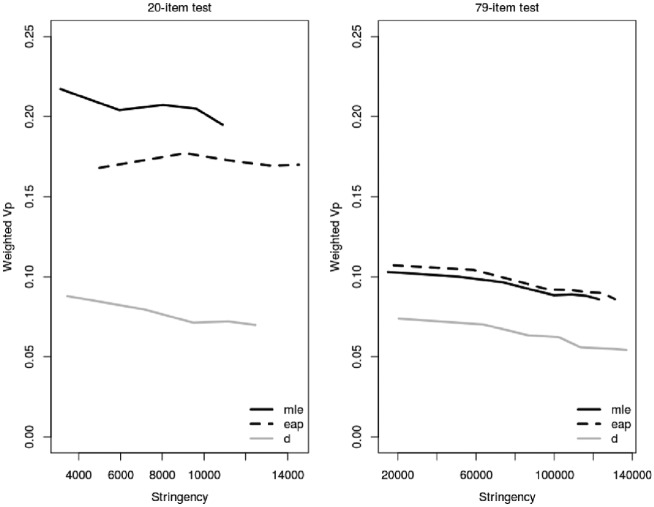
The results for the 20-item GAT-V and 79-item GTT are depicted in Figure 3. Used are only weighted Vp because they perform better (smaller percentage of violations) compared with unweighted Vp (see Table 5). The theta scores were obtained with IRT calibration under the 3PL using (a) maximum likelihood estimation (MLE) and (b) expected a priori (EAP) estimation (as a side note, the correlation between the D scores and IRT theta scores were 0.928 for the 79-item GTT data and 0.896 for the 20-item GAT-V data). As can be seen in Figure 3, the percentage of violation decreases with the increase of stringency in the banding, which supports the intuitively expected tradeoff between Vp and stringency (see Domingue, 2014). The D-scores consistently produce lower Vp compared with the IRT ability scores (thetas), regardless of the approach to theta estimation (MLE or EAP), with the difference tending to decrease with the increase of the test length. Thus, the D-scores produce fewer violations of the ordering axioms of ACM than do the IRT theta scores. In other words, the D-scale performs a good bit better than the IRT theta scale in terms of intervalness from the perspective of ACM, under the ConjointChecks approach to checking the ACM axioms (Domingue, 2014).

Figure 3.

Comparison of weighted Vp and stringency for GAT-V (20 items) and GTT (79 items).

Note. GAT-V = General Aptitude Test–Verbal; GTT = General Teacher Test; Vp = violation percentages; mle = maximum likelihood estimation (MLE); eap = expected a priori (EAP) estimation; d = D-scoring.

Conclusion

Under the delta-scoring (D-scoring), the score of an examinee on a test of n binary items is the sum of expected difficulties (${\delta }_i$) of the correctly answered items in the response vector of that examinee (Equations 1-3). Some of the advantages of this approach are that (a) D-scores are easy to compute and interpret; (b) D-scores are based on expected values and, therefore, do not depend on the sample of test takers; and (c) different item response vectors, including those that produce the same raw (NCR) score, result in different D-scores thus better differentiating examinees compared to NCR scores. The D-scoring is particularly useful in test equating. This is because it is sufficient to rescale the item parameters of a new test form onto the scale of a target (base) form, without mapping their test characteristic curves thus avoiding tedious computations and estimation errors associated with the use of Newton–Raphson iterations in such mapping (e.g., Kolen & Brennan, 2014, p. 177). The efficiency of equating test scores under D-scoring is even more pronounced when multiple new test forms (say, A₁, A₂, . . ., A_m) need to be equated to a base form, B. Specifically, after transforming the IRT item parameters of the new forms onto the ability scale of form B through a sequence of scale transformations over the “chain” of test forms A₁→ A₂→⋯→ A_m→ B (Li, Jiang, & von Davier, 2012), the item parameters of all test forms are on a common scale and thus the $D$-scores, which are obtained as a function of these item parameters for each test form (via Equations 1-3), are also on a common scale.

The results related to psychometric features of the D-scale, reported with the illustrative example, were replicated with numerous sets of real data from large-scale assessments at the NCA (not provided here for space consideration). In summary (a) the D-scores highly correlate (in the neighborhood of .90) with the IRT ability scores, θ; (b) the precision of the D-scores is higher for low- and high-ability examinees, which is just the opposite of IRT case, where the precision of θ estimates decreases for low- and high-ability examinees; (c) the D-scale performs a good bit better than the IRT theta scale in terms of intervalness, by criteria of the additive conjoint measurement, with the difference tending to decrease with the increase of the test length; and (d) the D-scores differentiate better between examinees who, under IRT estimation, are assigned to the extreme categories (say, −7 and 7) of a practically reasonable interval on the logit scale. These properties of the D-scale are particularly useful in testing that aims at differentiating among low test performers (e.g., to identify students “at risk”) or high test performers, say, in the context of medical education testing, admission of students to universities, teacher certification, and so forth.

As noted earlier, the development of D-scoring was motivated by a call at the NCA in Saudi Arabia for the development of procedures for automated test scoring and equating that are methodologically sound and technically feasible. An important aspect of this call was the request to use IRT item bank information for (a) test assembling; (b) direct scoring of tests based on the item parameters available in the bank, and response vectors of examinees; (c) sequential equating of multiple test forms; and (d) feeding the item bank with new trial items. The call was addressed with the development and piloting of D-scoring and equating at the NCA, with the procedures being implemented into a computerized system for automated test scoring and equating (SATSE; Atanasov & Dimitrov, 2015). Along with IRT estimates of the item parameters under the 3PL model, the item bank at the NCA is now upgraded to include the expected item difficulty, δ_i, as a direct function of these item parameters. As the item parameters in the item bank are on the same scale, the δ_i values are also on a common scale; that is, δ_i for an item shows how difficult is that item (as a “hurdle”) for the population of test takers on the scale of a designated base form of the test. When trial items are used with a new form of a test, their IRT parameters and expected difficulty, δ_i, for the population of test takers for the new test form are rescaled to the common scale for the target population of test takers for the base test form.

In conclusion, the proposed method of D-scoring and equating proved promising under its current piloting with large-scale assessments in Saudi Arabia and the hope is that this method can efficiently complement IRT procedures in the practice of large-scale testing in the field of education and psychology.

Appendix A

Derivation of the Formula for Standard Errors of D-Scores

As given with Equation (3), the D-score of person s is obtained as follows:

$$D_s=\sum _{i=1}^n{X}_{\mathrm{si}}{\delta }_i,$$

where $X_{\mathrm{si}}$ is the score of person s on item i ($X_{\mathrm{si}}$ = 1 for correct response; otherwise $X_{\mathrm{si}}$ = 0).

As the expected value of $X_{\mathrm{si}}$ is the probability of correct response on item i by person s with ability ${\theta }_s$, that is, $E\left(X_{\mathrm{si}}\right)$ = $P_i\left({\theta }_s\right)$, the expected value of the score $D_s$ is

$$E\left(D_s\right)=E\left(\sum _{i=1}^n{X}_{\mathrm{si}}{\delta }_i\right)=\sum _{i=1}^n{\delta }_{i}E\left(X_{\mathrm{si}}\right)=\sum _{i=1}^n{\delta }_i{P}_i\left({\theta }_s\right).$$

The error associated with $D_s$, denoted $\epsilon \left(D_s\right)$, is the difference between $D_s$ and its expected value. Thus, taking into account Equations (A1) and (A2), we obtain

$$\epsilon \left(D_s\right)=D_s-E\left(D_s\right)=\sum _{i=1}^n{X}_{\mathrm{si}}{\delta }_i-\sum _{i=1}^n{\delta }_i{P}_i\left({\theta }_s\right)=\sum _{i=1}^n{\delta }_i(X_{\mathrm{si}}-P_i\left({\theta }_s\right))$$

In Equations (A3), the difference $X_{\mathrm{si}}-P_i\left({\theta }_s\right)$ is the random error associated with the observed score $X_{\mathrm{si}}$; that is $e_{\mathrm{si}}$ = $X_{\mathrm{si}}-P_i\left({\theta }_s\right)$. Thus,

$$\epsilon \left(D_s\right)=\sum _{i=1}^n{\delta }_i{e}_{\mathrm{si}}.$$

The variance of $\epsilon \left({\mathrm{D}}_s\right)$ is then

$$\mathrm{VAR}\left(\epsilon \left(D_s\right)\right)=\mathrm{VAR}\left(\sum _{i=1}^n{\delta }_i{e}_{\mathrm{si}}\right)=\sum _{i=1}^n\mathrm{VAR}\left({\delta }_i{e}_{\mathrm{si}}\right)+2\sum {\delta }_i{\delta }_k\mathrm{COV}(e_{\mathrm{si}},e_{\mathrm{sk}}),$$

where $\mathrm{COV}(e_{\mathrm{si}},e_{\mathrm{sk}})$ is the covariance between the random errors $e_{\mathrm{si}}$ and $e_{\mathrm{sk}}$ of two different items, i and k, for the same person s. Under the IRT assumption of local independence, this covariance equals zero; that is, $\mathrm{COV}(e_{\mathrm{si}},e_{\mathrm{sk}})$ = 0. With this, we obtain from Equation (A5) that

$$\mathrm{VAR}\left(\epsilon \left(D_s\right)\right)=\sum _{i=1}^n\mathrm{VAR}\left({\delta }_i{e}_{\mathrm{si}}\right)=\sum _{i=1}^n{\delta }_i^2\mathrm{VAR}\left(e_{\mathrm{si}}\right),$$

On the other hand, it is known that the variance of the random error associated with a binary score, $X_{\mathrm{si}}$, equals the product $P_i\left({\theta }_s\right)[1-P_i\left({\theta }_s\right)]$, where $P_i\left({\theta }_s\right)$ is the probability for $X_{\mathrm{si}}$ = 1. With this, we obtain from Equation (A6) that

$$\mathrm{VAR}\left(\epsilon \left(D_s\right)\right)=\sum _{i=1}^n{\delta }_i^2{P}_i\left({\theta }_s\right)[1-P_i\left({\theta }_s\right)].$$

Thus, as given with Equation (5) in the main text, the standard error of score $D_s$ is

$$\mathrm{SE}\left(D_s\right)=\sqrt{\sum _{i=1}^n{\delta }_i^2{P}_i\left({\theta }_s\right)[1-P_i\left({\theta }_s\right)]}.$$

Appendix B

Identity of Item Reliability With the D-Scale and the Binary X-Scale

Let X_i stand for the binary score (1/0) on item i in a test. A fundamental assumption in CTT is that for this (and other) score we have: X_i = $T_{X_i}$+$E_{X_i}$, where $T_{X_i}$ and $E_{X_i}$ are the true score and error parts, respectively, for X_i. Under the CTT assumption of no correlation between true scores and errors, we have VAR(X_i) = VAR($T_{X_i}$) + VAR($E_{X_i}$). Then, if ${\rho }_{\mathrm{ii}}\left(X\right)$ is the reliability of X_i, by the CTT definition of reliability we have:

$${\rho }_{\mathrm{ii}}\left(X\right)=\mathrm{VAR}\left(T_{\mathrm{Xi}}\right)/\mathrm{VAR}\left(X_i\right)=\mathrm{VAR}\left(T_{\mathrm{Xi}}\right)/(\mathrm{VAR}\left(T_{\mathrm{Xi}}\right)+\mathrm{VAR}\left(E_{\mathrm{Xi}}\right)).$$

Likewise, if D_i is the D score on item i, the corresponding equations are: D_i = $T_{D_i}$+$E_{D_i}$; VAR(D_i) = VAR($T_{D_i}$) + VAR($E_{D_i}$); and item reliability on the D-scale:

$${\rho }_{\mathrm{ii}}\left(D\right)=\mathrm{VAR}\left(T_{\mathrm{Di}}\right)/\mathrm{VAR}\left(D_i\right)=\mathrm{VAR}\left(T_{\mathrm{Di}}\right)/(\mathrm{VAR}\left(T_{\mathrm{Di}}\right)+\mathrm{VAR}\left(E_{\mathrm{Di}}\right)).$$

On the other hand, $D_i$ = ${\delta }_i{X}_i$ = ${\delta }_i(T_{X_i}+E_{X_i})$ = ${\delta }_i{T}_{X_i}+{\delta }_i{E}_{X_i}$, where ${\delta }_i$ is the expected item difficulty. Thus, $T_{D_i}$= ${\delta }_i{T}_{X_i}$ and $E_{D_i}$= ${\delta }_i{E}_{X_i}$, from where we obtain VAR($T_{D_i}$) = ${\delta }_i^2$ VAR($T_{X_i}$) and VAR($E_{D_i})$ = ${\delta }_i^2$VAR($E_{X_i}$), respectively. Based on these results, we obtain from Equations (B1) and (B2) that

$${\rho }_{\mathrm{ii}}\left(D\right)={\delta }_i^2\mathrm{VAR}\left(T_{\mathrm{Xi}}\right)/({\delta }_i^2\mathrm{VAR}\left(T_{\mathrm{Xi}}\right)+{\delta }_i^2\mathrm{VAR}\left(E_{\mathrm{Xi}}\right))=\mathrm{VAR}\left(T_{\mathrm{Xi}}\right)/(\mathrm{VAR}\left(T_{\mathrm{Xi}}\right)+\mathrm{VAR}\left(E_{\mathrm{Xi}}\right))={\rho }_{\mathrm{ii}}\left(X\right).$$

Thus, as provided with Equation (6) in the main text, the item reliability is the same at the binary X-scale and the D-scale; that is

$${\rho }_{\mathrm{ii}}\left(D\right)={\rho }_{\mathrm{ii}}\left(X\right).$$