A New Monte Carlo Method for Estimating Marginal Likelihoods

Abstract

Evaluating the marginal likelihood in Bayesian analysis is essential for model selection. Estimators based on a single Markov chain Monte Carlo sample from the posterior distribution include the harmonic mean estimator and the inflated density ratio estimator. We propose a new class of Monte Carlo estimators based on this single Markov chain Monte Carlo sample. This class can be thought of as a generalization of the harmonic mean and inflated density ratio estimators using a partition weighted kernel (likelihood times prior). We show that our estimator is consistent and has better theoretical properties than the harmonic mean and inflated density ratio estimators. In addition, we provide guidelines on choosing optimal weights. Simulation studies were conducted to examine the empirical performance of the proposed estimator. We further demonstrate the desirable features of the proposed estimator with two real data sets: one is from a prostate cancer study using an ordinal probit regression model with latent variables; the other is for the power prior construction from two Eastern Cooperative Oncology Group phase III clinical trials using the cure rate survival model with similar objectives.

1 Introduction

The Bayes factor quantifying evidence of one model over a competing model is commonly used for model comparison or variable selection in Bayesian inference. The Bayes factor is a ratio of two marginal likelihoods, where the marginal likelihood is essentially the average fit of the model to the data. However, the integration for the marginal likelihood is often analytically intractable due to the complex kernel (product of likelihood and prior) structure. To deal with this computational problem, several Monte Carlo methods have been developed. They include the importance sampling (IS) of Geweke (1989), the harmonic mean (HM) of Newton and Raftery (1994) and its generalization (GHM) by Gelfand and Dey (1994), the serial approaches of Chib (1995) and Chib and Jeliazkov (2001), the inflated density ratio method (IDR) of Petris and Tardella (2003) and Petris and Tardella (2007), the thermodynamic integration (TI) of Lartillot and Philippe (2006) and Friel and Pettitt (2008), the constrained GHM estimator with the highest posterior density (HPD) region of Robert and Wraith (2009) and Marin and Robert (2010), and the steppingstone sampling of Xie et al. (2011) and Fan et al. (2011). Under some mild conditions, they are all shown to be asymptotically convergent to the marginal likelihood by the ergodic theorem. They vary in using Monte Carlo samples or kernels in the Monte Carlo integration.

We assume only a single Markov chain Monte Carlo (MCMC) sample from the posterior distribution, which may be readily available from standard Bayesian software, and the known kernel function for computing the marginal likelihood. The HM and IDR estimators are the only existing methods that need only these two minimal assumptions. The main difference between the HM and the IDR estimators lies in the different weights assigned to the inverse of the kernel function. The former uses the prior function as a weight, while the latter uses the difference between a perturbed density and its kernel function. Although the HM estimator has been used in practice because of its simplicity, it can be unstable when the prior has heavier tails than the likelihood function and it is known to overestimate the marginal likelihood (Lartillot and Philippe, 2006; Xie et al., 2011).

While the IDR estimator has better control over the tails of the kernel than the HM estimator, it requires reparameterization, posterior mode calculation, and a careful selection of radius. Under the aforementioned two minimal assumptions, we extend the HM and IDR methods to develop a new Monte Carlo method, namely, the partition weighted kernel (PWK) estimator. The PWK estimator is constructed by first partitioning the working parameter space, where the kernel is bounded away from zero, and then estimating the marginal likelihood by a weighted average of the kernel values evaluated at the MCMC sample, where weights are assigned locally using a representative kernel value in each subset. We show the PWK estimator is consistent and has finite variance. When the partition is refined enough to make the kernel values in the same region similar, we can construct the best (minimum variance) PWK estimator. Our simulation studies empirically show that the proposed PWK estimator outperforms both the HM and IDR estimators with respect to root mean square error.

The rest of the article is organized as follows. Section 2 is a review of the HM, GHM and IDR methods that motivate the PWK estimator. In Section 3, we develop the PWK estimator and its theoretical properties. Additionally, in the class of the general PWK estimator, we find the best (minimum variance) PWK estimator and provide a spherical shell approach to realize it. In Section 4, an extended general PWK estimator defined on the full support of the kernel function is investigated. Besides the theoretical properties, we show that the HM and IDR estimators are special cases in this family. In Section 5, we conduct simulation studies of a bivariate normal case with the normal-inverse-Wishart prior and a mixture of two bivariate normal distributions to compare the performance and computing time of the HM, IDR and PWK estimators. In Section 6, we compare the results and performance of the PWK estimator to the methods by Chib (1995) and Chen (2005) for an ordinal probit regression model. Moreover, we apply the PWK estimator to the determination of the optimal power prior using two Eastern Cooperative Oncology Group (ECOG) clinical trial data sets. Finally, we conclude with a discussion in Section 7. The proofs of all theorems are given in the Supplementary Web Materials (Wang et al., 2017a).

2 Preliminary

We review several Monte Carlo methods that only require a known kernel function and an MCMC sample from the posterior distribution to compute the marginal likelihood. Suppose θ is a p-dimensional vector of parameters and D denotes the data. Then, the kernel function for the joint posterior density π(θ|D) is q(θ) = L(θ|D)π(θ), where L(θ|D) is the likelihood function and π(θ) is a proper prior density. Assume Θ ⊂ R^p is the support of q(θ). The unknown marginal likelihood c is defined to be ∫Θq(θ)dθ. The integration is often analytically intractable due to complicated kernel structure.

To estimate the normalizing constant c, Newton and Raftery (1994) suggest the following equation to motivate the HM method,

$$\frac{1}{c}={\int }_{\mathbf{\Theta }}\frac{\pi (\mathit{\theta })}{q(\mathit{\theta })}\frac{q(\mathit{\theta })}{c}d\mathit{\theta }.$$ (1)

Let {θ_t, t = 1, …, T } be an MCMC sample from the posterior distribution π(θ|D) = q(θ)/c. The HM estimator is then given by

$${\widehat{c}}_{HM}=\frac{1}{\frac{1}{T}{\sum }_{t=1}^T\frac{1}{L({\mathit{\theta }}_t\mid D)}},$$ (2)

where the prior π(θ_t) can be viewed as the weight assigned to 1/q(θ_t). Although it has the features of simplicity and asymptotic convergence to the marginal likelihood, the finite variance is not guaranteed. Xie et al. (2011) also point out that the HM estimator tends to overestimate the marginal likelihood.

Gelfand and Dey (1994) suggest the GHM estimator where π(θ) in (1) is replaced by a lighter-tailed density function f(θ) compared to q(θ):

$${\widehat{c}}_{\mathit{GHM}}=\frac{1}{\frac{1}{T}{\sum }_{t=1}^T\frac{f({\mathit{\theta }}_t)}{q({\mathit{\theta }}_t)}}.$$ (3)

By proposing a light-tailed density, the ratio f(θ_t)/q(θ_t) can be controlled. Consequently, the estimator has finite variance. However, in high dimensional problems, finding a suitable density f(θ) may be a challenge.

Petris and Tardella (2003) propose the IDR estimator. They use the difference between a perturbed distribution q_r(θ), which is inflated in the center of the kernel, and the posterior kernel q(θ) as the weight. The perturbed density q_r(θ) is defined as

$$q_r(\mathit{\theta })=\{\begin{array}{ll}q(\mathbf{0})\hfill & \text{if}\Vert \mathit{\theta }\Vert \le r,\hfill \\ q(w(\mathit{\theta }))\hfill & \text{if}\Vert \mathit{\theta }\Vert >r,\hfill \end{array}$$ (4)

where r is the chosen radius and w(θ) = θ (1 − r^p/||θ||^p)^1/p. It follows,

$${\int }_{\mathbf{\Theta }}{q}_r(\mathit{\theta })d\mathit{\theta }={\int }_{\Vert \mathit{\theta }\Vert \le r}{q}_r(\mathit{\theta })d\mathit{\theta }+{\int }_{\Vert \mathit{\theta }\Vert >r}{q}_r(\mathit{\theta })d\mathit{\theta }=q(\mathbf{0})b_r+c,$$ (5)

where b_r = Volume of the ball {θ: ||θ|| ≤ r} = π^p/2r^p/Γ(p/2 + 1). This leads to the following equation,

$$\frac{q(\mathbf{0})b_r+c}{c}={\int }_{\mathbf{\Theta }}\frac{q_r(\mathit{\theta })}{q(\mathit{\theta })}\frac{q(\mathit{\theta })}{c}d\mathit{\theta },$$ (6)

and the IDR estimator is given by

$${\widehat{c}}_{\mathit{IDR}}=\frac{q(\mathbf{0})b_r}{\frac{1}{T}{\sum }_{t=1}^T\frac{q_r({\mathit{\theta }}_t)}{q({\mathit{\theta }}_t)}-1}.$$ (7)

Under some mild conditions, the estimator is shown to have finite variance by Petris and Tardella (2007). However, the method requires a careful selection of radius and unbounded support of q(θ). Any bounded parameter must be reparameterized to the full real line. Also, in order to have a more efficient estimator, mode finding is essential and standardization of an MCMC sample with respect to the mode and the sample covariance matrix is required.

3 A New Monte Carlo Estimator

We first modify (1) and (6) by imposing a working parameter space Ω ⊂ Θ, where Ω = {θ: q(θ) is bounded away from zero} to avoid regions with extremely low kernel values. Then we assume there is a function h(θ) such that ∫_Ω h(θ)dθ = Δ can be evaluated. Consequently, we have the identity:

$$\frac{\mathrm{\Delta }}{c}={\int }_{\mathrm{\Omega }}\frac{h(\mathit{\theta })}{q(\mathit{\theta })}\frac{q(\mathit{\theta })}{c}d\mathit{\theta }.$$ (8)

We next partition the working parameter space into K subsets, where the ratio of h(θ) over q(θ) has similar values within each subset, to reduce the variance of the Monte Carlo estimator. The general form of the PWK estimator with unspecified local weights is essentially a weighted average for the harmonic mean estimator for q(θ) with the same weights assigned locally to an MCMC sample in a subset.

The working parameter space is essentially the constrained support considered by Robert and Wraith (2009) and Marin and Robert (2010). However, we do not require h(θ) to be a density function as in GHM or constrained GHM. Consequently, we allow a larger class of estimators to be considered.

3.1 General Monte Carlo Estimator

Suppose {A₁, …, A_K} forms a partition of the working parameter space Ω, where for an integer K >0, w₁, …, w_K are the weights assigned to these K regions, respectively.

Let the weight function be the step function:

$$h(\mathit{\theta })=\sum _{k=1}^K{w}_{k}1\{\mathit{\theta }\in A_k\}.$$ (9)

So we can evaluate Δ:

$$\mathrm{\Delta }={\int }_{\mathrm{\Omega }}h(\mathit{\theta })d\mathit{\theta }=\sum _{k=1}^K{w}_{k}V(A_k),$$

where V (A_k) is the volume of the k^th subset in the partition, that is, V (A_k) = ∫_Ω 1{θ ∈ A_k}dθ.

Using the step function h(.) in (9), the PWK estimator for d ≡ 1/c is given by

$$\widehat{d}=\frac{\frac{1}{T}{\sum }_{t=1}^T{\sum }_{k=1}^K\frac{w_k}{q({\mathit{\theta }}_t)}1\{{\mathit{\theta }}_t\in A_k\}}{{\sum }_{k=1}^K{w}_{k}V(A_k)}.$$ (10)

In order to establish consistency and finite variance of the PWK estimator, we introduce two assumptions.

Assumption 1

The volume of each region V (A_k) < ∞ for k = 1, 2, …, K.

Assumption 2

q(θ) is positive and continuous on Ā_k, where Ā_k is the closure of A_k for k = 1, …, K.

Theorem 1

Under Assumptions 1 to 2 and certain ergodic (e.g., time-reversible, invariant, and irreducible) conditions, d̂ in (10) is a consistent estimator of d. In addition, Var(d̂) < ∞.

Note that we consider the estimator for d rather than c because we can obtain an unbiased estimator with finite variance for d = 1/c.

Remark 1

Another property of d̂ in (10) is that when a certain full conditional density is available, the computation can be lessened. This is often the case in the generalized linear model with latent variables or random effects, and in any Gibbs sampler or its hybrid. To be specific, let (ϑ₁,ϑ₂) be 2 blocks of parameters, ϑ₁ = (θ₁, …, θ_q)′ and ϑ₂ = (θ_q+1, …, θ_p)′. Assume that a full conditional density, π(ϑ₁|D,ϑ₂), is available. Then, the p-dimensional estimation problem can be reduced to p − q dimensions:

$$\begin{gathered} 1={\int }_{R^p}\frac{q(\mathit{\theta })}{c}d\mathit{\theta } \\ ={\int }_{R^{p-q}}{\int }_{R^q}\frac{q({\mathit{\vartheta }}_2)\pi ({\mathit{\vartheta }}_1\mid D,{\mathit{\vartheta }}_2)}{c}d{\mathit{\vartheta }}_{1}d{\mathit{\vartheta }}_2 \\ ={\int }_{R^{p-q}}\frac{q({\mathit{\vartheta }}_2)}{c}{\int }_{R^q}\pi ({\mathit{\vartheta }}_1\mid D,{\mathit{\vartheta }}_2)d{\mathit{\vartheta }}_{1}d{\mathit{\vartheta }}_2 \\ ={\int }_{R^{p-q}}\frac{q({\mathit{\vartheta }}_2)}{c}d{\mathit{\vartheta }}_2, \end{gathered}$$

where q(ϑ₂) = ∫_R^q q(θ)dϑ₁, which has a closed form expression. Therefore, instead of investigating the kernel q(θ), we can work on the kernel q(ϑ₂). In this case, (10) becomes

$$\widehat{d}=\frac{\frac{1}{T}{\sum }_{t=1}^T{\sum }_{k=1}^K\frac{w_k}{q({\mathit{\vartheta }}_{2_t})}1\{{\mathit{\vartheta }}_{2_t}\in B_k\}}{{\sum }_{k=1}^K{w}_{k}V(B_k)},$$

where {B₁, …, B_K} is a partition of the working parameter space Ω₂,Ω₂ ⊂ Θ₂, which is the support of q(ϑ₂), and V (B₁), …, V (B_K) are the corresponding volumes.

3.2 The Optimal Monte Carlo Estimation

Our next step is to find the optimal weight w_k in the class of PWK estimators (10), motivated by Chen and Shao (2002).

Assume {θ_t, t = 1, …, T } is an MCMC sample from the posterior distribution π(θ|D). Let $w_k^{\ast }=w_k/[{\sum }_{k=1}^K{w}_{k}V(A_k)]$ and α_k = E[(1/q²(θ))1{θ ∈ A_k}]. Write ${\widehat{d}}_t={\sum }_{k=1}^K\frac{w_k^{\ast }}{q({\mathit{\theta }}_t)}1\{{\mathit{\theta }}_t\in A_k\}$ such that $\widehat{d}=\frac{1}{T}{\sum }_{t=1}^T{\widehat{d}}_t$. Then, we have $\text{Var}({\widehat{d}}_t)={\sum }_{k=1}^K{w}_k^{\ast 2}{\alpha }_k-1/c^2$.

Theorem 2

Letting $w_{k,\mathit{opt}}^{\ast }=V(A_k)/\{{\alpha }_k[{\sum }_{k=1}^K{V}^2(A_k)/{\alpha }_k]\}$ for k = 1, …, K, we have ${\mathit{Var}}_{w_{k,\mathit{opt}}^{\ast }}({\widehat{d}}_t)=1/[{\sum }_{k=1}^K{V}^2(A_k)/{\alpha }_k]-1/c^2$, and ${\mathit{Var}}_{w_{k,\mathit{opt}}^{\ast }}({\widehat{d}}_t)\le {\mathit{Var}}_{w_k^{\ast }}({\widehat{d}}_t)$ for any weight function $w_k^{\ast }(.)$ defined on each A_k.

Remark 2

In practice, it is quite difficult to estimate the second moment α_k. A very large sample size is required in order to obtain an accurate estimate of α_k. However, the results shown in Theorem 2 shed light on the choices of A₁, …, A_K and w_k. First, it is only required that w_k be proportional to V (A_k)/α_k. Second, if q(θ) is roughly constant over A_k, then ${\alpha }_k\approx V(A_k)/[q({\mathit{\theta }}_k^{\ast })c]$, where ${\mathit{\theta }}_k^{\ast }\in A_k$. Thus, in this case, we can simply choose $w_k=q({\mathit{\theta }}_k^{\ast })$ and d̂ in (10) reduces to

$$\widehat{d}=\frac{\frac{1}{T}{\sum }_{t=1}^T{\sum }_{k=1}^K\frac{q({\mathit{\theta }}_k^{\ast })}{q({\mathit{\theta }}_t)}1\{{\mathit{\theta }}_t\in A_k\}}{{\sum }_{k=1}^{K}q({\mathit{\theta }}_k^{\ast })V(A_k)}.$$ (11)

Remark 3

Following on Remark 1, when a full conditional density π(ϑ₁|D,ϑ₂) is available, the estimator d̂ in (11) reduces further to

$$\widehat{d}=\frac{\frac{1}{T}{\sum }_{t=1}^T{\sum }_{k=1}^K\frac{q({\mathit{\vartheta }}_{2_k}^{\ast })}{q({\mathit{\vartheta }}_{2_t})}1\{{\mathit{\vartheta }}_{2_t}\in B_k\}}{{\sum }_{k=1}^{K}q({\mathit{\vartheta }}_{2_k}^{\ast })V(B_k)}.$$

Remark 4

In practice, the marginal likelihood is often reported in log scale. Considering the dependence within the MCMC sample, we use the Overlapping Batch Statistics (OBS) of Schmeiser et al. (1990) to estimate the Monte Carlo (MC) standard error of −log(d̂). Let η̂_b denote an estimate of the reciprocal of the marginal likelihood in log scale using the b^th batch, {θ_t, t = b, b + 1, …, b + B − 1}, of the MCMC sample for b = 1, 2, …, T − B + 1, where B < T is the batch size. Then, the OBS estimated MC standard error of η̂ = −log(d̂) is given by

$$\sqrt{\widehat{\text{Var}(\widehat{\eta })}}={\left\{\left[\frac{B}{T-B}\right]\frac{{\sum }_{b=1}^{T-B+1}{({\widehat{\eta }}_b-\overline{\eta })}^2}{T-B+1}\right\}}^{\frac{1}{2}},$$ (12)

where $\overline{\eta }={\sum }_{b=1}^{T-B+1}{\widehat{\eta }}_b/(T-B+1)$ and a batch size B is suggested to be 10 ≤ T/B ≤ 20 in Schmeiser et al. (1990).

3.3 Construction of the Partition with Subsets A1,A2, …, AK

In order to make q(θ) roughly constant over A_k for each k, which is a sufficient condition for the PWK estimator in (11) to be optimal, we provide the following rings approach for achieving it:

• Step 1: Assume Θ is R^p; if not, then a transformation ϕ = G₁(θ) is needed so that the parameter space of ϕ is R^p.

• Step 2: Use the MCMC sample to compute the mean ϕ̄ and the covariance matrix Σ̂ of ϕ and then standardize ϕ by ψ = G₂(ϕ) = Σ̂^−1/2(ϕ − ϕ̄).

• Step 3: Construct a working parameter space for ψ by choosing a reasonable radius r such that ||ψ|| < r for most of the standardized MCMC sample.

• Step 4: Partition the working parameter space into a sequence of K spherical shells such that A_k = {ψ: r(k − 1)/K ≤ ||ψ|| < rk/K}, with k = 1, …, K.

• Step 5: Select a ${\mathit{\psi }}_k^{\ast }$ in A_k as a representative point, for example a ${\mathit{\psi }}_k^{\ast }$ such that $\Vert {\mathit{\psi }}_k^{\ast }\Vert =r[k/K-1/(2K)]$.

• Sept 6: Compute the new kernel value $\stackrel{\sim }{q}({\mathit{\psi }}_k^{\ast })=q(G_1^{-1}(G_2^{-1}({\mathit{\psi }}_k^{\ast }))){\mid J\mid }_{\mathit{\psi }={\mathit{\psi }}_k^{\ast }}$, where J = |∂θ/∂ϕ||∂ϕ/∂ψ|. Also compute the new kernel value q̃(ψ_t), t = 1, …, T, for the standardized MCMC sample.

• Step 7: Estimate d = 1/c by

  $$\widehat{d}=\frac{\frac{1}{T}{\sum }_{t=1}^T{\sum }_{k=1}^K\frac{\stackrel{\sim }{q}({\mathit{\psi }}_k^{\ast })}{\stackrel{\sim }{q}({\mathit{\psi }}_t)}1\{{\mathit{\psi }}_t\in A_k\}}{{\sum }_{k=1}^K\stackrel{\sim }{q}({\mathit{\psi }}_k^{\ast })V(A_k)},$$ (13)

  where V (A_k) = {(rk/K)^p − [r(k − 1)/K]^p}π^p/2/Γ(p/2 + 1).

Remark 5

When K is sufficiently large, q̃(ψ_t) in (13) will be roughly constant over A_k and the PWK estimate will be close to optimal. In addition, each kernel value q̃(ψ_t) is simply the original kernel value q(θ_t) multiplied by the absolute value of the Jacobian function.

4 Extension of the General PWK Estimator

In this section, we generalize the PWK estimator from the working parameter space to the full support space and from the locally constant weight function to a general weight function of θ. We call this class extended PWK (ePWK) estimators.

Suppose {A₁, …, A_K^*} is a partition of Θ, and w_k(θ) is a weight function defined on A_k. We need the following assumption to define this ePWK class:

Assumption 3

The weight function w_k is integrable, that is, ∫ |w_k(θ)|dθ < ∞ for k = 1, …, K^*.

Under Assumption 3, the extended form of the general PWK in (10) is given by

$${\widehat{d}}^{\ast }=\frac{\frac{1}{T}{\sum }_{t=1}^T{\sum }_{k=1}^{K^{\ast }}\frac{w_k({\mathit{\theta }}_t)}{q({\mathit{\theta }}_t)}1\{{\mathit{\theta }}_t\in A_k\}}{{\sum }_{k=1}^{K^{\ast }}{\int }_{A_k}{w}_k(\mathit{\theta })d\mathit{\theta }}.$$ (14)

Theorem 3

Under Assumption 3 and q(θ) > 0, then the ePWK estimator d̂^* in (14) is a consistent estimator of d. In addition, if ∫_Ak [w_k(θ)²/q(θ)]dθ < ∞ for k = 1, …, K^*, then Var(d̂^*) < ∞.

Remark 6

It is easy to see that d̂ in (10) is a special case of d̂^* in (14). When K^* = K + 1 and each fixed weight w_k is assigned to an MCMC sample in each region A_k except w_K^* = 0, d̂^* reduces to d̂.

Remark 7

The HM estimator is another special case of d̂^* in (14). When using the prior π(θ_i) as weights, the inverse of d̂^* is the HM estimator.

$$\begin{gathered} {\widehat{d}}^{\ast }{\mid }_{w_k(\mathit{\theta })=\pi (\mathit{\theta })}=\frac{\frac{1}{T}{\sum }_{t=1}^T{\sum }_{k=1}^{K^{\ast }}\frac{\pi ({\mathit{\theta }}_t)}{q({\mathit{\theta }}_t)}1\{{\mathit{\theta }}_t\in A_k\}}{{\sum }_{k=1}^{K^{\ast }}{\int }_{A_k}\pi (\mathit{\theta })d\mathit{\theta }} \\ =\frac{\frac{1}{T}{\sum }_{t=1}^T\frac{\pi ({\mathit{\theta }}_t)}{q({\mathit{\theta }}_t)}{\sum }_{k=1}^{K^{\ast }}1\{{\mathit{\theta }}_t\in A_k\}}{{\int }_{\mathbf{\Theta }}\pi (\mathit{\theta })d\mathit{\theta }} \\ =\frac{1}{T}\sum _{t=1}^T\frac{1}{L({\mathit{\theta }}_t\mid D)}. \end{gathered}$$

Remark 8

In addition, d̂^* in (14) includes the IDR estimator as a special case. Let K^* = 2, A₁ = {θ: ||θ|| ≤ r}, w₁(θ) = q(0) − q(θ), A₂ = {θ: ||θ|| > r}, and w₂(θ) = q_r(θ) − q(θ). We can show that ∫_A1 w₁(θ)dθ = q(0)b_r − ∫_A1 q(θ)dθ and ∫_A2 w₂(θ)dθ = c − ∫_A2 q(θ)dθ, implying ${\sum }_{k=1}^2{\int }_{A_k}{w}_k(\mathit{\theta })d\mathit{\theta }=q(\mathbf{0})b_r$. Thus, the inverse of d̂^* reduces to the IDR estimator. Note w₁(θ_t) and w₂(θ_t) in IDR are allowed to be negative.

Remark 9

When the posterior kernel q(.) after the transformation is roughly symmetric, the constant weight w_k assigned to partition set A_k constructed using the rings approach discussed in Section 3.3 often leads to an efficient PWK estimator in (10) as empirically demonstrated in Section 5.1 and Section 6. However, when the posterior kernel q(.) is very skewed or multimodal, the constant weight w_k would result in an inefficient PWK estimator. For such a complex case, we can apply the ePWK estimator in (14). The functional weight w_k(θ) can be constructed as follows. We first divide the k^th ring A_k into m_k subsets A_k1, …, A_kmk based on m_k slices such that $A_k={\cup }_{\ell =1}^{m_k}{A}_{k\ell }$ and A_k1, …, A_kmk are disjoint, and then assign $w_k(\mathit{\theta })=q({\mathit{\theta }}_{k\ell }^{\ast })$ for θ ∈ A_kℓ, where ${\mathit{\theta }}_{k\ell }^{\ast }$ is a representative point in A_kℓ, for ℓ = 1, …, m_k. In Section 5.2, we apply this version of the ePWK estimator to an example involving a bimodal distribution to examine its empirical performance.

5 Simulation Studies

5.1 A Bivariate Normal Example

We apply the PWK estimator for computing the normalizing constant of the posterior of the parameters of a bivariate normal distribution with the normal-inverse-Wishart prior. We consider both location and scale parameters to be unknown. Including the scale parameters makes computation challenging. Let y = (y₁, y₂, …, y_n)′ be n observations from a bivariate normal distribution,

$${\mathit{y}}_i\mid \mathit{\mu },\mathrm{\sum }\stackrel{i.i.d.}{\sim }N(\mathit{\mu },\mathrm{\sum }),i=1,\dots ,n,$$

where μ ∈ R² and Σ are unknown parameters. The likelihood function is

$$L(\mathit{\mu },\mathrm{\sum }\mid \mathit{y})={(2\pi )}^{-n}{\mid \mathrm{\sum }\mid }^{-n/2}exp\left\{-\frac{1}{2}\sum _{i=1}^n{({\mathit{y}}_i-\mathit{\mu })}^{\prime }{\mathrm{\sum }}^{-1}({\mathit{y}}_i-\mathit{\mu })\right\}.$$

The prior for μ and Σ is specified as follows:

$$\mathit{\mu }\mid \mathrm{\sum }~N({\mathit{\mu }}_0,\mathrm{\sum }/{\kappa }_0)\text{and}\mathrm{\sum }~I{W}_{{\nu }_0}({\mathrm{\Lambda }}_0^{-1}),$$

with hyperparameters μ₀, κ₀, ν₀, and Λ₀. Then, the joint posterior kernel is given by

$$\begin{gathered} q(\mathit{\mu },\mathrm{\sum })=L(\mathit{\mu },\mathrm{\sum }\mid \mathit{y})\pi (\mathit{\mu }\mid \mathrm{\sum })\pi (\mathrm{\sum }) \\ ={(2\pi )}^{-n}{\mid \mathrm{\sum }\mid }^{-(n+{\nu }_0+2)/2-1}\frac{1}{\gamma }exp\left\{-\frac{1}{2}\sum _{i=1}^n{({\mathit{y}}_i-\mathit{\mu })}^{\prime }{\mathrm{\sum }}^{-1}({\mathit{y}}_i-\mathit{\mu })\right\}\times exp\left\{-\frac{{\kappa }_0}{2}{(\mathit{\mu }-{\mathit{\mu }}_0)}^{\prime }{\mathrm{\sum }}^{-1}(\mathit{\mu }-{\mathit{\mu }}_0)\right\}exp\left\{-\frac{1}{2}\text{trace}({\mathrm{\Lambda }}_0{\mathrm{\sum }}^{-1})\right\}, \end{gathered}$$

with $\gamma =2^{{\nu }_0+1}\pi {\mathrm{\Gamma }}_2({\nu }_0/2){\mid {\mathrm{\Lambda }}_0\mid }^{-{\nu }_0/2}{\kappa }_0^{-1}$, where Γ₂(ν₀/2) = π^1/2Γ(ν₀/2)Γ(ν₀/2 − 1/2). Under this setting, the analytical form of the normalizing constant is available as follows:

$$c=\frac{1}{{\pi }^n}\frac{{\mathrm{\Gamma }}_2({\nu }_n/2)}{{\mathrm{\Gamma }}_2({\nu }_0/2)}\frac{{\mid {\mathrm{\Lambda }}_0\mid }^{{\nu }_0/2}}{{\mid {\mathrm{\Lambda }}_n\mid }^{{\nu }_n/2}}\left(\frac{{\kappa }_0}{{\kappa }_n}\right),$$ (15)

where ${\mathrm{\Lambda }}_n={\mathrm{\Lambda }}_0+{\sum }_{i=1}^n({\mathit{y}}_i-\overline{\mathit{y}}){({\mathit{y}}_i-\overline{\mathit{y}})}^{\prime }+\frac{{\kappa }_{0}n}{{\kappa }_0+n}({\mathit{\mu }}_0-\overline{\mathit{y}}){({\mathit{\mu }}_0-\overline{\mathit{y}})}^{\prime }$, κ_n = κ₀ + n, and ν_n = ν₀ + n. We set the hyperparameters μ₀ = (0, 0)′, k₀ = 0.01, ν₀ = 3, and ${\mathrm{\Lambda }}_0=\left(\begin{array}{cc}1& 0.7\\ 0.7& 1\end{array}\right)$. We generated a random sample y with n = 200 from a bivariate normal distribution with μ = (0, 0) and $\mathrm{\sum }=\left(\begin{array}{cc}1& 0.7\\ 0.7& 1\end{array}\right)$. The corresponding sample mean ȳ was (−0.029, 0.040)′, and the sample variance–covariance matrix S was $\left(\begin{array}{cc}201.987& 143.330\\ 143.330& 192.365\end{array}\right)$. Using (15), the marginal likelihood in log scale is −507.278. In this example, in order to apply the spherical shell approach in Section 3.3, a transformation of Σ was needed. Here, we used the log transformation for each variance parameter and the Fisher z-transformation for the correlation coefficient parameter to have unbounded support for each of them. Then, we standardized each transformed MCMC sample from its transformed sample mean and standard deviation. In the new parameter space, we constructed the working parameter space and its partition by choosing r = 1.5, 2, or 2.5 and K = 10, 20, or 100. After selecting a representative point in each spherical shell, we estimated d = 1/c using (13). We compare our method to the HM and IDR methods based on 1,000 independent MCMC samples with T = 1, 000 or T = 10, 000 in Table 1. Let d̂_ℓ be the estimate of d based on the ℓ^th MCMC sample for ℓ = 1, 2, …, 1, 000. Then, the simulation estimate (Mean), the MC standard error (MCSE), and the root mean square error (RMSE) of the estimates in log scale are defined as $\widehat{logc}=\frac{1}{1000}{\sum }_{\ell =1}^{1000}(-log{\widehat{d}}_{\ell }),{\{\frac{1}{1000-1}{\sum }_{\ell =1}^{1000}{(-log{\widehat{d}}_{\ell }-\widehat{logc})}^2\}}^{1/2}$, and ${\{\frac{1}{1000}{\sum }_{\ell =1}^{1000}{(-log{\widehat{d}}_{\ell }-logc)}^2\}}^{1/2}$, respectively.

Table 1.

Simulation results for the bivariate normal case.

log c = −507.2776
			T=1,000			T=10,000			Time (sec.)
	K	r	Mean	MCSE	RMSE	Mean	MCSE	RMSE
HM			−494.671	0.908	12.639	−495.142	0.762	12.159	0.644
IDR		1.5	−509.064	0.302	1.811	−509.123	0.145	1.851	1.638
		2.0	−509.095	0.537	1.895	−509.284	0.387	2.043	1.634
		2.5	−508.926	0.710	1.795	−509.216	0.629	2.038	1.621
PWK	10	1.5	−507.260	0.064	0.067	−507.264	0.020	0.025	0.329
		2.0	−507.262	0.053	0.055	−507.264	0.016	0.021	0.596
		2.5	−507.259	0.057	0.060	−507.264	0.019	0.023	0.784
	20	1.5	−507.260	0.064	0.066	−507.264	0.020	0.024	0.327
		2.0	−507.262	0.052	0.054	−507.264	0.016	0.021	0.596
		2.5	−507.259	0.055	0.058	−507.264	0.018	0.023	0.792
	100	1.5	−507.260	0.064	0.066	−507.264	0.020	0.024	0.426
		2.0	−507.261	0.052	0.054	−507.264	0.016	0.021	0.660
		2.5	−507.260	0.055	0.058	−507.264	0.018	0.022	0.877

Table 1 shows the results, where the average computing time (in seconds) per MCMC sample on an Intel i7 processor machine with 12 GB of RAM memory using a Windows 8.1 operating system is given in the last column. From Table 1, we see that (i) PWK has the best performance with much smaller MCSE and RMSE than HM and IDR under both T = 1, 000 and T = 10, 000; (ii) when T increases, the MCSE and the RMSE of the PWK estimator become smaller under all choices of r and K; (iii) the performance of the HM estimator slightly improves but the IDR estimator does not when T increases; and (iv) the computing time of the PWK estimator is comparable to that of the HM estimator while the IDR estimator requires the most computing time. It is interesting to mention that the MCSE and the RMSE of the PWK estimator are very similar for all choices of r and K under each T, implying the robustness of the PWK estimator with respect to the specification of the working parameter space and the number of partition subsets.

In this example, we also examine the performance of ePWK by adding a subset A_K+1 = Θ ∩ Ω^c = {θ: ||θ|| > r} such that K^* = K + 1 and ${\cup }_{k=1}^{K^{\ast }}{A}_k=\mathbf{\Theta }$. We further specify $w_{K+1}(\mathit{\theta })=q({\mathit{\theta }}_{K+1}^{\ast })g(\mathit{\theta })$ for θ ∈ A_K+1, where ${\mathit{\theta }}_{K+1}^{\ast }$ is a point on the boundary of A_K+1 and

$$g(\mathit{\theta })=\frac{1}{{(2\pi )}^{2.5}}exp\left\{-\frac{{\mathit{\theta }}^{\prime }\mathit{\theta }}{2}\right\}/\left[1-P({\chi }_{(5)}^2\le r^2)\right].$$

Under this specification, we have ${\int }_{A_{K+1}}{w}_{K+1}(\mathit{\theta })d\mathit{\theta }=q({\mathit{\theta }}_{K+1}^{\ast })$. Holding the other subsets A₁, …, A_K and their corresponding weights the same as for PWK, the resulting values of MCSE and RMSE by ePWK are 0.06332 and 0.06579 when T = 1, 000, K = 100, and r = 1.5; 0.05167 and 0.05420 when r = 2.0; and 0.05500 and 0.05772 when r = 2.5. Compared to the results of PWK (0.06375 and 0.06621 when r = 1.5; 0.05168 and 0.05420 when r = 2.0; and 0.05499 and 0.05772 when r = 2.5), ePWK performs very similarly to PWK, which is expected since the posterior kernel has light tails and very low values on A_K+1.

To evaluate the effect of a vague prior on the precision of the PWK estimator, we extend our simulation study by considering different values of hyperparameters κ₀ and ν₀. Note that the value of log c in Table 1 is computed under κ₀ = 0.01 and ν₀ = 3, which corresponds to a relatively vague prior for (μ, Σ). Table 2 shows the simulation results of the PWK estimators with r = 2 and K = 100 for (κ₀, ν₀) = (0.0001, 3), (1, 3), and (1, 10) in addition to (0.01, 3). From Table 2, we see that the MCSE values under these different values of (κ₀, ν₀) are almost the same while the RMSE values are comparable except the last one with (κ₀, ν₀) = (1, 10), in which the RMSE values are slightly larger.

Table 2.

Simulation results of PWK estimators for different hyperparameters κ₀ and ν₀.

			T=1,000			T=10,000
κ0	ν0	log c	Mean	MCSE	RMSE	Mean	MCSE	RMSE
0.0001	3	−511.883	−511.866	0.052	0.054	−511.869	0.016	0.021
0.01	3	−507.278	−507.261	0.052	0.054	−507.264	0.016	0.021
1	3	−502.682	−502.665	0.052	0.054	−502.669	0.016	0.021
1	10	−512.773	−512.721	0.053	0.074	−512.725	0.016	0.050

5.2 A Mixture of Two Bivariate Normal Distributions Example

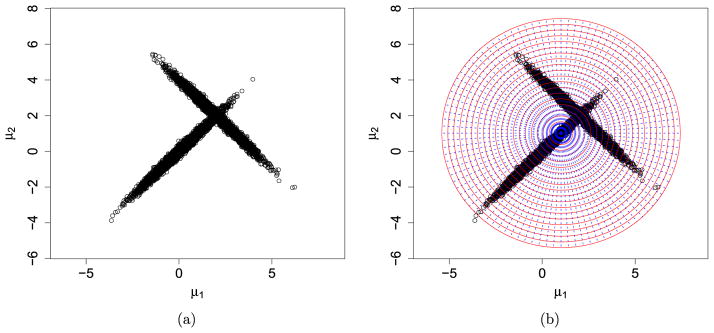
To evaluate the performance of ePWK, we consider the two-dimensional normal mixture in Chen et al. (2006)

$$\pi (\mathit{\mu })=\sum _{j=1}^2\frac{1}{2}\left[\frac{1}{2\pi }{\mid {\mathrm{\sum }}_j\mid }^{-1/2}exp\left\{-\frac{1}{2}{(\mathit{\mu }-{\mathit{\mu }}_{0j})}^{\prime }{\mathrm{\sum }}_j^{-1}(\mathit{\mu }-{\mathit{\mu }}_{0j})\right\}\right],$$ (16)

where μ = (μ₁, μ₂)′, μ₀₁ = (0, 0)′, μ₀₂ = (2, 2)′ and ${\mathrm{\sum }}_j=\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_1{\sigma }_2{\rho }_j\\ {\sigma }_1{\sigma }_2{\rho }_j& {\sigma }_2^2\end{array}\right)$ with σ₁ = σ₂ = 1, ρ₁ = 0.99, and ρ₂ = −0.99. Figure 1(a) is a scatter plot of a random sample with T = 10, 000 generated from (16). Based on the random sample, we apply ePWK to estimate the normalizing constant in (16), which is known to be 1. Due to the high but opposite correlations (i.e., ρ₁ = 0.99 and ρ₂ = −0.99), π(μ) cannot be homogeneous over a partition ring formed by the spherical shell approach in Section 3.3. To circumvent this difficulty, following Remark 9, we additionally slice the existing partition rings by dividing them equally along the angle from 0 to 360 degrees as shown by the dashed lines in Figure 1(b), where the center of the circle is the sample posterior mean (denoted as μ̂). Now, the heterogeneity of π(μ) over each partition subset is effectively eliminated by this additional slicing step. We note that this version of ePWK is the same as PWK except for additional slicing over the partition rings.

Figure 1.

Forming the working parameter space and its partition for a mixture normal distribution with means (0,0) and (2,2).

Table 3 shows the results of HM, IDR, and ePWK estimators based on 1,000 independent random samples with T = 1, 000 or T = 10, 000 from (16). For ePWK, we consider different values of K (the number of rings) with the same m_k = m (the number of slices) for k = 1, …, K and r (75%, 90%, or 95% × max_1≤t≤T ||μ_t − μ̂||). We use the same values of r for both IDR and ePWK. From Table 3, we see that (i) the RMSE values of the ePWK are considerably smaller than those of HM and IDR; (ii) the performance of ePWK improves when the sample size (T) or the number of rings (K) increases; and (iii) ePWK takes slightly longer computing time than HM and IDR.

Table 3.

Simulation results for the mixture normal with means equal to (0,0) and (2,2).

log c = 0
				T = 1,000			T = 10,000			Time (sec.)
	K	m	r	Mean	MCSE	RMSE	Mean	MCSE	RMSE
HM				−2.868	0.685	2.948	−3.069	0.519	3.113	1.647
IDR			5.065	1.879	0.639	1.985	1.706	0.448	1.764	1.680
			6.078	2.149	0.650	2.245	1.935	0.485	1.995	1.839
			6.415	2.243	0.659	2.337	2.015	0.485	2.073	1.717
ePWK	20	100	5.065	0.001	0.020	0.020	0.000	0.006	0.006	2.167
			6.078	0.000	0.025	0.025	0.000	0.008	0.008	2.375
			6.415	0.000	0.025	0.025	−0.001	0.008	0.008	2.187
	100	100	5.065	0.000	0.011	0.011	0.000	0.003	0.003	2.933
			6.078	0.000	0.011	0.011	0.000	0.004	0.004	3.037
			6.415	0.000	0.011	0.011	0.000	0.004	0.004	2.929

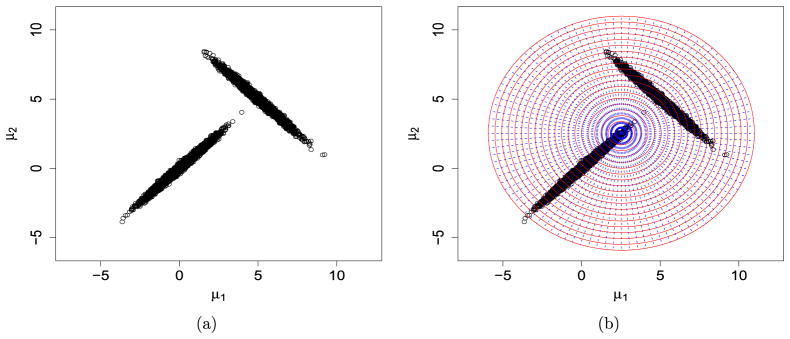
Next, we consider a more challenging case, where μ₀₂ is replaced by (5, 5)′ so that the two modes are much further away from each other. Figure 2(a) is a scatter plot of a random sample with T = 10, 000 and Figure 2(b) shows the partition subsets of the chosen working parameter space.

Figure 2.

Forming the working parameter space and its partition for a mixture normal distribution with means (0,0) and (5,5).

Table 4 summarizes the simulation results with the same simulation setting as before. We see that ePWK outperforms both HM and IDR under this more challenging case. As expected, the RMSE values in Table 4 are larger than those in Table 3 for all three methods. However, the RMSE values of the ePWK estimator are still quite small when K and T are reasonably large.

Table 4.

Simulation results for the mixture normal with means equal to (0,0) and (5,5).

log c = 0
				T = 1,000			T = 10,000			Time (sec.)
	K	m	r	Mean	MCSE	RMSE	Mean	MCSE	RMSE
HM				−2.915	0.681	2.993	−3.107	0.500	3.147	1.728
IDR			6.675	2.340	1.586	2.825	2.791	1.695	3.263	1.763
			8.011	1.658	1.780	2.429	2.409	1.350	2.760	1.730
			8.456	1.568	1.985	2.524	2.216	1.430	2.636	1.822
ePWK	20	100	6.675	−0.001	0.035	0.035	0.000	0.011	0.011	2.277
			8.011	0.003	0.060	0.060	0.000	0.019	0.019	2.253
			8.456	0.000	0.060	0.060	0.000	0.018	0.018	2.374
	100	100	6.675	0.000	0.018	0.018	0.000	0.006	0.006	3.022
			8.011	0.000	0.018	0.018	0.000	0.006	0.006	2.933
			8.456	0.000	0.019	0.019	0.000	0.006	0.006	3.114

6 Application of the PWK to Real Data Examples

6.1 The Ordinal Probit Regression Model

In the first example, we apply the PWK method to computing the marginal likelihood under the ordinal probit regression model. Let y = (y₁, y₂, …, y_n)′ denote the vector of observed ordinal responses, each is coded as one value from 0, 1, …, J −1, X denote the n × p covariate matrix with the i^th row equal to the covariate of the i^th subject $x_i^{\prime }$, and u = (u₁, u₂, …, u_n)′ denote the vector of latent random variables. We consider the following hierarchical model as in Albert and Chib (1993) such that

$$y_i=j,\text{if}{\gamma }_j\le u_i<{\gamma }_{j+1}$$

and

$$u_i={\mathit{x}}_i^{\prime }\mathit{\beta }+{\epsilon }_i,$$

where j = 0, 1, …, J − 1, β is a p-dimensional vector of regression coefficients, and ${\epsilon }_i\stackrel{i.i.d.}{\sim }N(0,{\sigma }^2)$. Based on the reparameterization of Nandram and Chen (1996), the cutpoints for dividing the latent variable u_i can be specified as −∞ = γ₀ < γ₁ = 0 ≤ γ₂ ≤ ⋯ ≤ γ_J−1 = 1 < γ_J = ∞. Under this setting, the likelihood function is given in Chen (2005)

$$L(\mathit{\theta }\mid D)=\prod _{i=1}^n\left[\mathrm{\Phi }\left(\frac{{\gamma }_{y_{i+1}}-{\mathit{x}}_i^{\prime }\mathit{\beta }}{\sigma }\right)-\mathrm{\Phi }\left(\frac{{\gamma }_{y_i}-{\mathit{x}}_i^{\prime }\mathit{\beta }}{\sigma }\right)\right],$$

where θ = (β′, σ, γ₂, …, γ_J−2)′ if J ≥ 4, otherwise, θ = (β′, σ)′, and Φ(.) is the cumulative standard normal distribution function. Then, we specify normal, inverse gamma, and uniform priors for the parameters β, σ², and γ, respectively.

To examine the performance of the PWK estimator under this model, we consider the prostate cancer data of n = 713 patients as in Chen (2005). In this data set, Pathological Extracapsular Extension (PECE, y) is a clinical ordinal response variable, and Prostate Specific Antigen (PSA, x₁), Clinical Gleason Score (GLEAS, x₂), and Clinical Stage (CSTAGE, x₃) are three covariates. PECE takes values of 0, 1, or 2, where 0 means that there is no cancer cell present in or near the capsule, 1 denotes that the cancer cells extend into but not through the capsule, and 2 indicates that cancer cells extend through the capsule. PSA and GLEAS are continuous variables while CSTAGE is a binary outcome, which was assigned to 1 if the 1992 American Joint Commission on cancer clinical stage T-category was 1, and assigned to 2 if the T-category was 2 or higher.

In this application, J = 3 so that all four cutpoints can be assigned to fixed values: −∞ = γ₀ < γ₁ = 0 < γ₂ = 1 < γ₃ = ∞. Then, the prior distribution is specified as

$$\pi (\mathit{\theta })=\pi (\mathit{\beta }\mid {\sigma }^2)\pi ({\sigma }^2),$$

where β|σ² ~ N(0, 10σ²I₄) and σ² ~ IG(a₀ = 1, b₀ = 0.1). The density function of an inverse gamma distribution IG(a₀, b₀) is proportional to (σ²)^−(a₀+1) exp(−b₀/σ²).

The marginal likelihood is not analytically available. Nevertheless, the estimates of this are obtained in Table 1 of Chen (2005) using the method proposed by Chen (called Chen’s method) and the method proposed by Chib (1995) (called Chib’s method). Chen’s method needs only a single MCMC sample from the joint posterior distribution π(β, σ²|D). However, Chib’s method with two blocks requires an additional MCMC sample from the conditional posterior distribution π(σ²|β^*,D), where β^* is the posterior mean of β. We compare PWK to these two methods under the same MCMC sample sizes T = 2, 500, or 5, 000 as in Chen (2005), except that Chib’s method doubles them.

For the PWK, we apply a log transformation for σ². Then, after the standardization of the transformed MCMC sample, we consider K = 10, 20, and 100 and $r=0.75\sqrt{{\chi }_{5,0.95}^2},\sqrt{{\chi }_{5,0.95}^2}$, and $1.25\sqrt{{\chi }_{5,0.95}^2}$ to investigate robustness of the PWK estimates with respect to these choices. We note that $\sqrt{{\chi }_{5,0.95}^2}$ is the square-root of the 95^th percentile of the Chi-square distribution with p = dim(θ) = 5 degrees of freedom, which is derived by computing the norm of p independent standard normal distributions as in Yu et al. (2015). Table 5 shows the PWK estimates and the corresponding estimated MCSE (eMCSE) under the MCMC samples with T = 2,500 and 5,000, where eMCSE is computed using (12) with T/B = 10. We note that we use the same MCMC sample sizes as in Chen (2005). The results show the PWK estimators are relatively robust to the choice of the radius r and the number K of partition subsets.

Table 5.

The PWK estimates of the marginal likelihood for the prostate cancer data.

$r=0.75\sqrt{{\chi }_{5,0.95}^2}$
	PWK (K=10)		PWK (K=20)		PWK (K=100)
T	−log d̂	eMCSE	−log d̂	eMCSE	−log d̂	eMCSE
2, 500	−758.73	0.026	−758.73	0.025	−758.73	0.025
5, 000	−758.70	0.021	−758.70	0.020	−758.70	0.020

$r=\sqrt{{\chi }_{5,0.95}^2}=3.327$
	PWK (K=10)		PWK (K=20)		PWK (K=100)
T	−log d̂	eMCSE	−log d̂	eMCSE	−log d̂	eMCSE
2, 500	−758.70	0.020	−758.70	0.019	−758.70	0.020
5, 000	−758.70	0.016	−758.70	0.016	−758.70	0.016

$r=1.25\sqrt{{\chi }_{5,0.95}^2}$
	PWK (K=10)		PWK (K=20)		PWK (K=100)
T	−log d̂	eMCSE	−log d̂	eMCSE	−log d̂	eMCSE
2, 500	−758.69	0.020	−758.69	0.019	−758.69	0.017
5, 000	−758.70	0.018	−758.70	0.015	−758.69	0.014

From Table 1 of Chen (2005), the estimates of log c and eMCSE’s are −758.71 and 0.038 based on Chen’s method and −758.67 and 0.037 based on Chib’s method for T = 2, 500; and −758.71 and 0.024 based on Chen’s method and −758.70 and 0.023 based on Chib’s method for T = 5, 000. We see from Table 5 that the PWK estimates of log c are similar to those under both Chen’s and Chib’s methods but with smaller eMCSE’s under the MCMC samples with T = 2,500 and 5,000, respectively. For instance, the PWK estimates of log c and the corresponding eMCSE’s are −758.70 and 0.020 for T = 2, 500 and −758.70 and 0.016 for T = 5, 000 when $r=\sqrt{{\chi }_{5,0.95}^2}$ and K = 100. Thus, the PWK yields a slightly more precise estimate of log c than the other two methods.

6.2 Analysis of ECOG Data

In this subsection, we apply the PWK estimator to the problem of determining the power prior based on historical data for the current analysis. Assume we have conducted two clinical trials for the same objective. A natural way to combine these two trials is to consider the power prior setting, which allows us to borrow information from the historical data to construct the prior for the current analysis. Assume we have an initial prior for the unknown parameters that is determined before observing the historical data. To quantify the heterogeneity between the current data and the historical data, the power prior weights the historical likelihood function by the power a₀, where 0 ≤ a₀ ≤ 1, to indicate the extent to which the historical likelihood is incorporated into the initial prior. Our objective is to find the optimal a₀ which maximizes the marginal likelihood for the current data. Ibrahim et al. (2015) point out the difficulty of finding this solution except for normal linear regression models. Therefore, they resort to using the deviance information criterion (DIC) and the logarithm of pseudo-marginal likelihood (LPML) criterion for constructing the parameter a₀ of the power prior in Ibrahim et al. (2012, 2015). To evaluate DIC, we need to plug the MCMC sample into the sum of the log likelihood over all data points; to evaluate LPML, we need to take the sum of the log transformation of each CPO, where the i^th CPO is the harmonic mean of the i^th likelihood evaluated at the MCMC sample from the posterior distribution based on the full sample. Both methods yield much less computational burden than the marginal likelihood method. We will show how the PWK estimator can circumvent the computational burden in evaluating the marginal likelihood.

The effectiveness of Interferon Alpha-2b (IFN) in immunotherapy for melanoma patients has been evaluated by two observation-controlled clinical trials: Eastern Cooperative Oncology Group (ECOG) phase III, E1684, followed by E1690. The first trial E1684 was conducted with 286 patients randomly assigned to either IFN or Observation. The IFN arm demonstrated a significantly better survival curve, but with substantial side effects due to high dose regimen. To confirm the results of the E1684 and the benefit of IFN at a lower dosage, a later trial E1690 was conducted with three arms: high dose IFN, low dose IFN, and Observation. We use the data in E1684 as the historical data and a subset (high dose arm and Observation) of the E1690 trial as our current data. There are 427 patients in this subset.

For n = 427 patients in the current trial (E1690), we follow the model in Chen et al. (1999). Let y_i denote the relapse-free survival time for the i^th patient, ν_i denote the censoring status, which is equal to 1 if y_i is a failure time and to 0 if it is right censored, x_i = (1, trt_i)′ denote the vector of covariates, where trt_i = 1 if the i^th patient received IFN and trt_i = 0 if the i^th patient was assigned to Observation. Then, the likelihood function is given by

$$L(\mathit{\beta },\mathit{\lambda }\mid D)=\prod _{i=1}^n{\left\{exp({\mathit{x}}_i^{\prime }\mathit{\beta })f(y_i\mid \mathit{\lambda })\right\}}^{{\nu }_i}exp\{-exp({\mathit{x}}_i^{\prime }\mathit{\beta })F(y_i\mid \mathit{\lambda })\},$$ (17)

where D = (n, y, ν, X) is the observed current data, β = (β₀, β₁)′, and F(y|λ) is the cumulative distribution function and f(y|λ) is the corresponding density function. In (17), we use the same piecewise exponential model for F(y|λ) as Ibrahim et al. (2012), which is given by

$$F(y\mid \mathit{\lambda })=1-exp\left\{-{\lambda }_j(y-s_j-1)-\sum _{g=1}^{j-1}{\lambda }_g(s_g-s_{g-1})\right\},$$

where s_j−1 ≤ y < s_j, s₀ = 0 < s₁ < s₂ < … < s₅ = ∞, and λ = (λ₁, …, λ₅)′.

For n₀ = 286 patients in the historical trial (E1684), we attempt to extract some of its information to set up the prior distribution for the current analysis. Similarly, we let y_0i denote the survival time for the i^th patient, ν_0i denote the censoring status, and x_0i = (1, trt_0i)′ denote the vector of covariates. So D₀ = (n₀, y₀, ν₀, X₀) is the observed historical data. Assume π₀(β, λ) is an initial prior. Here, we specify an initial proper prior N(0, 100I₂) for β and Exp(λ₀ = 1/100) (λ₀: rate parameter) for each λ_j, j = 1, …, 5, to come close to the flat prior in Ibrahim et al. (2012). To update the initial prior with the historical data, the power prior is intuitively set as the initial prior π₀ multiplied by the historical likelihood function with power a₀ as follows:

$$\pi (\mathit{\beta },\mathit{\lambda }\mid D_0,a_0)\propto {\left[\prod _{i=1}^{n_0}{\left\{exp({\mathit{x}}_{0i}^{\prime }\mathit{\beta })f(y_{0i}\mid \mathit{\lambda })\right\}}^{{\nu }_{0i}}exp\{-exp({\mathit{x}}_{0i}^{\prime }\mathit{\beta })F(y_{0i}\mid \mathit{\lambda })\}\right]}^{a_0}{\pi }_0(\mathit{\beta },\mathit{\lambda }),$$ (18)

where π(β, λ|D₀, a₀) is called the power prior and 0 ≤ a₀ ≤ 1. In this setting, we can see when a₀ = 0, the power prior is exactly equal to the initial prior, which integrates to be 1, and when a₀ ≠ 0, the power prior is equal to the right-hand side kernel function in (18) divided by c₀ = ∫ L(β, λ|D₀)^a₀π₀(β, λ)dβdλ. Combining the likelihood function in (17) and the power prior in (18), the posterior distribution of β and λ given (D, D₀, a₀) will be

$$\pi (\mathit{\beta },\mathit{\lambda }\mid D,D_0,a_0)\propto L(\mathit{\beta },\mathit{\lambda }\mid D)\pi (\mathit{\beta },\mathit{\lambda }\mid D_0,a_0).$$ (19)

In this framework, we compare the marginal likelihoods of L(β, λ|D)π(β, λ|D₀, a₀) for 0 ≤ a₀ ≤ 1. The one with the highest marginal likelihood is our final model, and its corresponding a₀ determines the power prior.

However, as we point out earlier, except for a₀ = 0, π(β, λ|D₀, a₀) is known up to a normalizing constant c₀. Hence, a two-step evaluation is needed to obtain the marginal likelihood:

$$\begin{gathered} c=\int L(\mathit{\beta },\mathit{\lambda }\mid D)\pi (\mathit{\beta },\mathit{\lambda }\mid D_0,a_0)d\mathit{\beta }d\mathit{\lambda } \\ =\frac{\int L(\mathit{\beta },\mathit{\lambda }\mid D)L{(\mathit{\beta },\mathit{\lambda }\mid D_0)}^{a_0}{\pi }_0(\mathit{\beta },\mathit{\lambda })d\mathit{\beta }d\mathit{\lambda }}{\int L{(\mathit{\beta },\mathit{\lambda }\mid D_0)}^{a_0}{\pi }_0(\mathit{\beta },\mathit{\lambda })d\mathit{\beta }d\mathit{\lambda }} \\ =\frac{c_1}{c_0}=\frac{d_0}{d_1}. \end{gathered}$$

We apply the PWK to estimate the numerator, L(β, λ|D)L(β, λ|D₀)^a₀π₀(β, λ), and the denominator, L(β, λ|D₀)^a₀π₀(β, λ), respectively.

For each choice of a₀ with an increment of 0.1 from 0 to 1, an MCMC sample size is fixed at 10,000. The log transformation of each λ_j is needed. After the standardization of the transformed MCMC sample, we choose the maximum radius $r=\sqrt{{\chi }_{7,0.95}^2}$ due to p = 7, and the number of spherical shells K = 100. By (13) and (12), we can obtain the marginal likelihood estimate and its eMCSE for each chosen a₀. We summarize the results in Table 6. Table 6 also includes the PWK estimates under $r=0.75\sqrt{{\chi }_{5,0.95}^2},1.25\sqrt{{\chi }_{5,0.95}^2}$ and K = 10, 20 to investigate the robustness of the PWK method.

Table 6.

PWK estimates for marginal likelihood with different power priors under different choices of r and K.

$r=0.75\sqrt{{\chi }_{7,0.95}^2}$
	K=10		K=20		K=100
a0	ln(d̂0/d̂1)	eMCSE	ln(d̂0/d̂1)	eMCSE	ln(d̂0/d̂1)	eMCSE
0.0	−552.717	0.028	−552.713	0.026	−552.709	0.028
0.1	−523.619	0.055	−523.614	0.051	−523.621	0.053
0.2	−522.091	0.044	−522.078	0.044	−522.073	0.044
0.3	−521.408	0.043	−521.420	0.043	−521.419	0.043
0.4	−521.336	0.046	−521.332	0.047	−521.338	0.045
0.5	−521.201	0.057	−521.229	0.060	−521.229	0.060
0.6	−521.189	0.037	−521.202	0.034	−521.187	0.033
0.7	−521.356	0.050	−521.363	0.044	−521.353	0.044
0.8	−521.553	0.054	−521.558	0.056	−521.576	0.058
0.9	−521.592	0.061	−521.618	0.051	−521.612	0.050
1.0	−521.702	0.052	−521.724	0.055	−521.732	0.050

$r=\sqrt{{\chi }_{7,0.95}^2}=3.751$
	K=10		K=20		K=100
a0	ln(d̂0/d̂1)	eMCSE	ln(d̂d0/d̂1)	eMCSE	ln(d̂0/d̂1)	eMCSE
0.0	−552.732	0.022	−552.707	0.025	−552.708	0.027
0.1	−523.633	0.059	−523.646	0.049	−523.624	0.054
0.2	−522.098	0.052	−522.093	0.050	−522.077	0.045
0.3	−521.433	0.039	−521.432	0.040	−521.417	0.043
0.4	−521.309	0.046	−521.321	0.048	−521.339	0.043
0.5	−521.179	0.062	−521.187	0.059	−521.230	0.059
0.6	−521.186	0.039	−521.174	0.037	−521.187	0.033
0.7	−521.365	0.034	−521.361	0.042	−521.349	0.044
0.8	−521.535	0.055	−521.568	0.056	−521.573	0.056
0.9	−521.627	0.047	−521.613	0.055	−521.613	0.050
1.0	−521.746	0.059	−521.739	0.049	−521.732	0.050

$r=1.25\sqrt{{\chi }_{7,0.95}^2}$
	K=10		K=20		K=100
a0	ln(d̂0/d̂1)	eMCSE	ln(d̂0/d̂1)	eMCSE	ln(d̂0/d̂1)	eMCSE
0.0	−552.740	0.039	−552.719	0.033	−552.708	0.027
0.1	−523.551	0.057	−523.622	0.052	−523.622	0.053
0.2	−522.105	0.045	−522.077	0.044	−522.071	0.045
0.3	−521.427	0.048	−521.422	0.045	−521.421	0.042
0.4	−521.311	0.048	−521.317	0.046	−521.335	0.044
0.5	−521.239	0.052	−521.232	0.057	−521.227	0.059
0.6	−521.186	0.037	−521.171	0.033	−521.184	0.032
0.7	−521.381	0.047	−521.376	0.045	−521.350	0.043
0.8	−521.569	0.067	−521.578	0.063	−521.578	0.057
0.9	−521.597	0.052	−521.621	0.054	−521.609	0.049
1.0	−521.705	0.060	−521.740	0.046	−521.730	0.051

Note the marginal likelihood function c can be shown to be continuous in a₀. Therefore, from Table 6, we see that the best choice of a₀ is between 0.5 and 0.6 under the marginal likelihood criterion. This result is quite comparable to the result of a₀ = 0.4 in Ibrahim et al. (2012) obtained by DIC and LPML criteria, where a suitable marginal likelihood computation was not accessible. We also observe that the results are quite robust to the different values of r and K, and all point out that the best choice of a₀ is between 0.5 and 0.6.

7 Discussion

The marginal likelihood is often analytically intractable due to a complicated kernel structure. Nevertheless, an MCMC sample from the posterior distribution is readily available from Bayesian computing software. Additionally, the likelihood values evaluated at the MCMC sample are output in a file. Consequently, we can produce kernel values easily using the output and the prior function. In this paper, we propose a new algorithm, PWK, for estimating the marginal likelihood based on this single MCMC sample and its corresponding kernel values. Unlike some existing algorithms requiring knowledge of the structure of the kernel, we only need to know the kernel values evaluated at the MCMC sample. Therefore, our algorithm can be applied to Bayesian model selection, assessing the sensitivity of conclusions to the prior distribution, and Bayes hypothesis tests. We implement our methodology using the R programming language (R Core Team, 2015). The R codes along with README files are available as Online Supplementary Materials (Wang et al., 2017b).

We extend PWK to handle the parameter space with the full support (ePWK) and we show that HM and IDR are special cases of ePWK. We conduct a simulation study from a bivariate normal distribution with 5 parameters in a Bayesian conjugate prior inference problem to compare our estimator to HM and IDR; our results show that PWK has the smallest empirical MCSE and RMSE. The computation time for our method is only slightly longer than that for the HM which indicates our spherical shell partition approach is very efficient. We conduct another simulation study for a mixture of two bivariate normal distributions to illustrate the ePWK estimator, which is obtained by additionally slicing the partition rings in the partition step of the PWK method. We show that the ePWK method reduces the MCSE and RMSE by a great deal when compared to the HM and IDR methods at the cost of slightly more computation time.

In example analyses of real data, we first consider an ordinal probit regression model, and compare our method to that in Chib (1995) and Chen (2005) with the same MCMC sample size for Chen’s method (Chib’s method requires twice this sample size). We find the three methods produce comparable estimates for the marginal likelihood and the PWK method produces the smallest eMCSE. In the second example, we consider a cure rate survival model with the piecewise constant baseline hazard function and a power prior construction based on two clinical trial data sets. We obtain the optimal power prior using the marginal likelihood criterion as opposed to the DIC and LPML methods considered by Ibrahim et al. (2012). We obtain similar results, except that the PWK approach indicates more borrowing of the historical data.

In unimodal problems, we suggest using the square root of the 95^th percentile in a Chi-square distribution with p degrees of freedom as a guide to choosing a value for the radius r for constructing the working parameter space of the standardized MCMC sample. This is because, after standardizing the MCMC sample, the marginal distribution of each parameter is approximately standard normal. Although the results are quite robust to the choices of r as shown in simulation and case studies, using the Chi-square distribution for guidance ensures that we make use of most of the MCMC sample and avoid the region with posterior density close to 0. For multimodal problems, we suggest using 95% × max_1≤t≤T ||μ_t − μ̂|| as a guide value for constructing the working parameter space of the transformed MCMC sample. Since this approach may result in many partition subsets with extremely small posterior density in the working parameter space, we can use the spherical rings approach as demonstrated in Section 5.2 to obtain the homogeneity of the MCMC sample in each subset. This new partition approach can also be extended to a p-dimensional problem (p > 2) by introducing another p − 2 angular coordinates as in Lehnen and Wesenberg (2003) and slicing them as in Section 5.2.