Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2018 May 9;4(5):559–566. doi: 10.1021/acscentsci.7b00586

Automatic Differentiation in Quantum Chemistry with Applications to Fully Variational Hartree–Fock

Teresa Tamayo-Mendoza †, Christoph Kreisbeck †,*, Roland Lindh ‡, Alán Aspuru-Guzik †,§,*
PMCID: PMC5968443  PMID: 29806002

Abstract

graphic file with name oc-2017-00586m_0004.jpg

Automatic differentiation (AD) is a powerful tool that allows calculating derivatives of implemented algorithms with respect to all of their parameters up to machine precision, without the need to explicitly add any additional functions. Thus, AD has great potential in quantum chemistry, where gradients are omnipresent but also difficult to obtain, and researchers typically spend a considerable amount of time finding suitable analytical forms when implementing derivatives. Here, we demonstrate that AD can be used to compute gradients with respect to any parameter throughout a complete quantum chemistry method. We present DiffiQult, a Hartree–Fock implementation, entirely differentiated with the use of AD tools. DiffiQult is a software package written in plain Python with minimal deviation from standard code which illustrates the capability of AD to save human effort and time in implementations of exact gradients in quantum chemistry. We leverage the obtained gradients to optimize the parameters of one-particle basis sets in the context of the floating Gaussian framework.

Short abstract

DiffiQult is a Hartree−Fock plain Python implementation that computes exact gradients with respect to any input parameter using automatic differentiation, without any explicit analytical gradient.

1. Introduction

Automatic differentiation (AD) is a conceptually well-established tool to calculate numerical gradients up to machine precision,1,2 by iteratively applying the chain rule and successively walking through the computational graph of numerically implemented functions. Therefore, AD facilitates the computation of exact derivatives of coded algorithms with respect to all its variables without having to implement any other expression explicitly. AD circumvents challenges arising in traditional approaches. For example, the evaluation of analytical expressions tends to be inefficient, and numerical gradients can be unstable due to truncations or round-off errors. Enabled by a variety of libraries,3−11 AD has been successfully implemented to various applications.12−14 For example, AD has been used for quantum control in open-quantum systems to find an optimal time-dependent field to obtain a specific state.15,16 Furthermore, new libraries developed in the context of deep learning9,17−19 make AD techniques even more accessible to a broader community. For instance, Leung et. al used a parallelized machine learning tool, TensorFlow, to obtain the optimal parameters to minimize several kinds of cost-functions to tune the evolution of quantum states.20

In this manuscript, we highlight the relevance of AD for quantum chemistry and demonstrate that AD provides a novel general path forward to reduce the human time spent on the implementation gradients for electronic structure methods. Gradients play a fundamental role in optimization procedures as well as for the computation of molecular response properties such as dipole moments polarizabilities, magnetizabilities, or force constants.21 Although analytical expressions are available for some derivatives in many cases,22−25 researchers typically spend a considerable amount of time finding suitable analytical forms when implementing new quantum chemistry methods.18 Depending on the complexity of the electronic structure method, this can result in a significant time delay between the development of the method and the implementation of its gradients. The implementation of geometrical gradients for MC-SCF21,26 has been published more than 10 years after the method itself.27 Moreover, some analytical gradients can be too complicated to be handled manually. For example, the complex analytical derivatives of the FIC-CASPT228,29 method, published more than two decades ago, has been only recently accessible through advances in automatic code generation.30,31

AD techniques could play an important role in quantum chemistry by marginalizing the complexity of implementing gradients, as it allows computing the gradients without coding them explicitly. The advantages of AD techniques have been used before in electronic structure methods.32−36 In these previous works, the implementations were tailored to the differentiation of the specific application. These typically require considerable changes to existing code or the explicit implementation of some analytical gradients, Taylor coefficients, or adjoints. For instance, in the context of density functional theory, a combined approach using analytical expression together with AD has been successfully applied to compute higher order derivatives of the exchange-correlation term.32 Further, Sorella et al.36 explicitly derived the appropriate sequence of computation of adjoints and their expressions for the kinetic and potential energy terms. Here, we apply AD in a broader context and demonstrate that AD tools are an efficient way to get arbitrary gradients for a complete quantum chemistry method with respect to any input parameter. To this end, we implement a fully autodifferentiable Hartree–Fock (HF) method which we distribute in our DiffiQult software package37 written in plain Python language. We have selected HF since it is not only used in many electronic correlation methods as an initial step but contains complex mathematical operations and functions, such as calculating derivatives of eigenvectors or special functions. The latter is also relevant for more sophisticated quantum chemistry methods38 and impose nontrivial requirements for suitable AD libraries as they need to lay out the complete computational graph rather than calling black-box routines, for example, implemented in LAPACK.39 We illustrate the capabilities of DiffiQult within the framework of a fully variational HF method, where we use a gradient-based optimization of the SCF-energy to optimize the parameters of the basis set within the Floating Gaussian framework.40,41 Our implementation sets the basis for extending the DiffiQult software package to include post-HF methods such as FCI and MP2, and to leverage higher order derivatives to obtain anharmonic corrections for rotational–vibrational spectroscopy.

This paper is organized as follows: In section 2, we provide a small review of the algebra behind automatic differentiation. In the section 3 we introduce the fully variational Hartree–Fock method. In section 4, we discuss in detail the key components of the canonical HF algorithm and explain how they were implemented in DiffiQult by considering an appropriate selection and usage of an AD library. In Section 5 we demonstrate the capabilities of our algorithm by optimizing the one-electron basis functions of small molecules. Finally, in section 6, we conclude with an outlook of future directions of DiffiQult, and a perspective of the role of AD in simplifying and accelerating the implementation of gradients of new quantum chemistry methods.

2. Automatic Differentiation

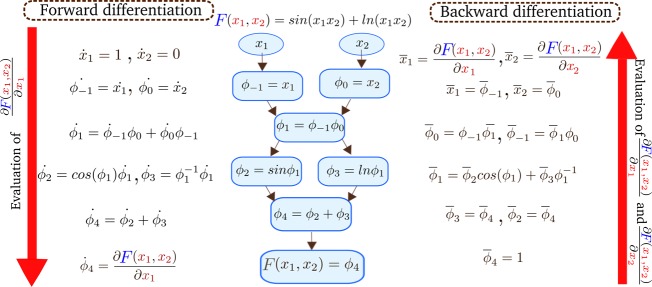
The idea behind automatic differentiation is that every algorithm, independent of its complexity, consists of a series of simple arithmetic operations that have known analytical forms, such as sums, multiplications, sines, cosines, or exponents. The sequence of these elementary operations is represented by a computational graph; see for example Figure 1. In this form, it is possible to compute the gradients of the outputs of a function with respect to its inputs by applying the chain rule and evaluating the analytical derivatives of all of these elementary operations in a given order. This implies that AD libraries can differentiate the entire algorithm not only mathematical expressions, written in an explicit form, but also all the control functions such as recursions, loops, conditional statements, etc. Therefore, AD computes the exact derivatives of any code with machine precision.1 In practice, there are two main forms to compute derivatives using the chain rule with AD tools: forward and backward mode. We illustrate both modes in Figure 1.

Figure 1.

Figure 1

Open in a new tab

The center depicts the computational graph of a simple function F(x1, x2) and its elementary operations. On the left and right, we illustrate the differentiation steps of forward and backward mode, respectively. In forward mode, the evaluation of the function at a given set of parameter and the derivative with respect to x1 is evaluated by computing the intermediate variables ϕi and their derivatives following the order of the computational graph using the chain rule. The direction of the evaluation is indicated by the left arrow. In backward mode, the function is evaluated first at a given value, and later the adjoints of all the intermediate variables are computed by iterating backward through the computational graph, indicated by the right arrow. Notice, in this mode, the partial derivatives of the function with respect to the two independent variables are computed together, whereas in forward mode each partial derivative of the function has to be evaluated separately. In this example, to compute the entire gradient, the number of operations in backward mode is smaller than in forward mode.

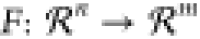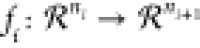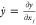Forward mode is conceptually the easiest way to compute gradients. Let us consider the function Inline graphic defined by a sequence of k functions, Inline graphic in the following way y = F(x) = (fk°fk–1°...f1°f0)(x). 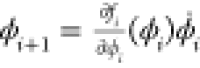In forward mode, the partial derivative of a function with respect to a given parameter xj, Inline graphic, is computed by evaluating simultaneously the intermediate variables ϕi+1 = fi(ϕi) and the derivatives Inline graphic, at a given x = a. 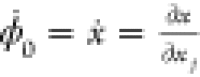Note that ϕ0 = x and Inline graphic. Once we defined the values of the independent variables, the algorithm proceeds to calculate ϕ1 and ϕ̇1, and will continue to compute the partial derivatives of the next elementary operations following the computational graph by sequentially applying the chain rule. For instance, the differentiation of a function F with a single dependent variable goes from right side to left side of the equation,

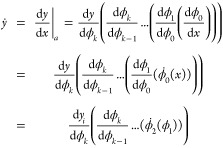2. 1

An example of forward differentiation of a more complex function with two variables is illustrated on the left side in Figure 1. We display the steps to compute the partial derivatives of the intermediate variables with respect to a single parameter. Since the forward mode relies on the generation of the derivatives of the elementary operations with respect to each individual input parameter, it is particularly suited for functions with few independent variables.

The second form is backward mode, which relies on the computation of the “adjoints” 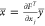Inline graphic by computing the adjoints of the intermediate variables, 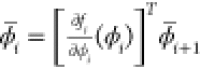Inline graphic. In contrast to forward mode, in backward mode the adjoints are computed following the opposite direction through the computational graph by iterating computing each adjoint of all the intermediate variables. The algorithm first evaluates the function F(x) at a given set of parameters x = a, and later proceeds to calculate the adjoints of the last intermediate variable to the first one iterating backward through the computational graph. 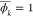By definition, ϕk = y, therefore Inline graphic. If F(x) only depends on a single parameter, this procedure is the equivalent of evaluating the chain rule from left to right,

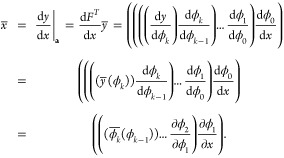2. 2

The last step of backward mode, after calculating all the intermediate adjoints, results in the partial derivatives of the function with respect to all parameters. An example with a more complex composition of function with two variables is illustrated on the right side of Figure 1, where we get the entire gradient of F(x1, x2) with a single backward propagation evaluation. Note that intermediate adjoints can be used at a later stage to obtain the partial derivatives with respect to both variables resulting in a reduction of operations compared to the forward differentiation. This characteristic generally makes the backward mode more efficient for a small number of dependent variables. For more details about the general differences over both modes and its implementation, the reader might refer to ref (2).

In practical applications, the choice of either differentiation mode depends on the specific form of the computational graph as well as on performance considerations taking into account the available computational resources. For example, backward mode requires either storing the complete sequence of operations of the algorithm to compute the function or recalculating the intermediate variables. On the other hand, this constraint might be compensated by the capability of the backward mode to efficiently evaluate derivatives of many parameters with fewer operations than the forward mode. In our particular case, this analysis is done by reviewing the relevant mathematical operations of a canonical HF algorithm for an efficient implementation of gradients with AD techniques.

3. Fully Variational Hartree–Fock

Our goal is to implement gradients with AD techniques for a quantum chemistry method without writing any explicit gradient. In this manuscript, as an illustrative, yet useful example, we apply AD to obtain HF energy gradients to optimize parameters of Gaussian basis functions. This algorithm will enable a more compact wave function representation while maintaining a comparable level of accuracy in energy achieved by using larger basis sets. Thus, this method will provide tailored molecular one-electron basis functions with greater flexibility compared to atomic-centered Gaussian expansions.

In the HF method, the wave function is constructed as a linear combination of one-electron basis functions, where we minimize the energy by finding the appropriate expansion coefficients. The selection of these basis functions is critical to accurately reproduce the behavior of a system.42 The most popular form of these basis functions is the atomic-centered contracted Gaussian functions because the computation of one- and two-electron integrals have well-established forms for their implementations.24,43−45 Each of these functions is defined by the set of following parameters: (i) the exponents {α} defining the Gaussian width, (ii) the contraction coefficients {c} defining the linear expansion of the Gaussian representation of the atomic orbital (AO), (iii) the coordinates A defining the center of the Gaussians, and (iv) the angular momentum a defining the order of the polynomial factor defined by the coordinate system (e.g., Cartesian or spherical harmonics).46

These one-electron basis functions are generally obtained by energy optimizations of single atoms with a certain level of theory and are intended to mimic AO.47 However, when AOs are used as a basis for molecules they require some degree of flexibility to describe more complex behaviors such as polarization effects. Therefore, one usually selects a relatively large number of basis functions with AOs of different exponents and sufficiently high angular momentum.42 The drawback of using a larger basis set is the increase in numerical complexity, imposing limitations on actual calculations.

To get a fully optimized wave function, we can minimize not only the expansion coefficients, but all types of variational parameters of the Gaussian AOs mentioned above, such as nuclear coordinates, Gaussian centers, contraction coefficients, and exponents. A fully variational approach may be useful to reduce the number of basis functions and to obtain a more compact representation of the wave function. This could either improve the calculation of molecular properties40,42,48 or yield a better reference state for certain higher levels of theory.49 A prominent example of a variational approach is the so-called Floating Gaussians41,50−52 in which the centers of the AOs are optimized. Some authors have partially optimized parameters such as the Gaussian widths for the valence shell40 or included extra orbitals around the region of the chemical bond.53,54 Furthermore, wave function parameters have been optimized within a higher level of theory,55,56 such as CASSCF and MP2,57 or HF over ab initio molecular dynamics.58,59 These methods have implemented gradient or Hessian-based optimization with analytical nuclear derivatives.

In this paper, we present a fully variational approach,56 where we optimize the molecular orbitals with a quasi-Newton method. Here, the gradients are calculated using solely a plain Python implementation of a HF and an AD library. By taking advantage of the AD techniques, we can compute numerically exact gradients with respect to any parameter without the need for implementing analytical gradients explicitly. This provides the flexibility to either simultaneously optimize the Gaussian exponents and positions, or to optimize them sequentially.

4. Implementation

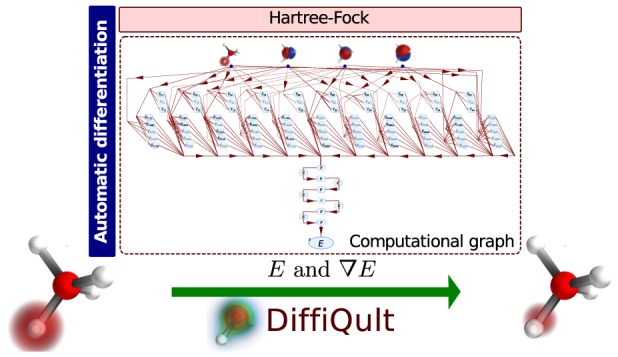
In the following section, we describe DiffiQult, a fully variational HF algorithm that calculates gradients employing AD. In particular, we discuss options and constraints that need to be considered when applying AD in a quantum chemistry method. DiffiQult contains two main parts, (i) a restricted HF implementation that provides HF energies as well as its derivatives with respect to any input parameter and (ii) a gradient-based optimization of wave function parameters. The scheme of our fully variational Hartree–Fock implementation is shown in Figure 2.

Figure 2.

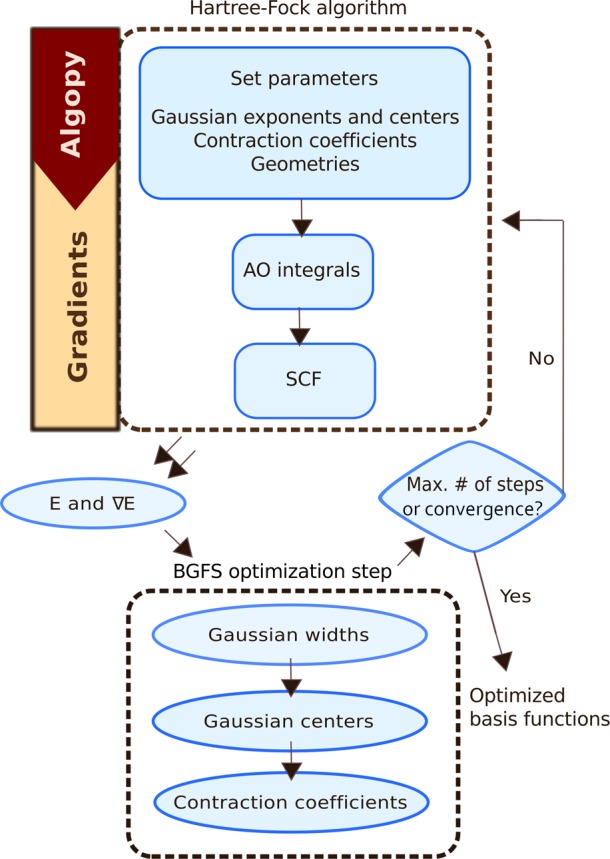
Figure 2

Open in a new tab

Diagram of the fully variational algorithm implemented in the DiffiQult package.

The philosophy behind using AD is centered around the idea of saving human effort in the implementation of gradients. Ideally, we would like to choose a suitable AD library capable of getting gradients from AD just by adding minimal changes to standard Python or C++ code. In this way, we would be able to significantly reduce the amount of time required for the implementation of gradients for new electronic structure methods. Moreover, we could link the AD library to existing electronic structure software packages for which analytical or numerical gradients might be inefficient. However, to what extent the aforementioned goals can be reached depends on the capabilities of the available AD libraries.3,4,60−63 Each of the libraries differs in some aspects, but all of them have in common that they are restricted in some way, and it remains to be analyzed which ones match the requirements for a quantum chemistry algorithm best. For example, we would need to differentiate some operations that are typically computed by library routines, e.g., LAPACK39 functions. To avoid explicit implementation of those methods, an appropriate library preferably supports linear algebra operations as well as calls to special functions such as the incomplete gamma function. Similarly, the AD modes, e.g., forward or backward mode, as discussed in section 2 exhibit different properties, and one might be more suitable for a particular implementation than the other. A majority of the requirements are shared among various electronic structure algorithms, including HF. Therefore, the gradients computed solely with AD techniques of a HF implementation in DiffiQult serves as a proof-of-concept that helps us to develop an understanding of the capabilities of AD in quantum chemistry.

In the following analysis, we review how the library and AD mode selection impact the implementation of DiffiQult. We should notice that certain operations that are simple in standard implementations can raise challenges depending on the selected AD library. For example, some control flow statements that depend on intermediate variables might impose some constraints in backward mode, if the library builds the computational graph before the evaluation of the function. In HF, control statements are for example implemented to determine the required number of SCF steps for convergence. Depending on the input parameter, e.g., the molecular geometry, fewer or more iterations are needed to reach convergence, and thus the computational graph consists of fewer or more operations. This has severe implications on the backward mode since for this mode the computational graph needs to be fixed before function evaluation. We might circumvent some of these issues by hard-coding the number of steps of the SCF, but this simple example demonstrates that the implementation of gradients with AD tools requires different considerations when compared to developing traditional software packages.

Another relevant aspect for the implementation of DiffiQult is the matrix operations. From the algorithmic point of view, we should leverage vectorized operations whenever possible.64 Vectorized operations are taken as elementary operations in most of the AD libraries, and the computation of their derivatives is typically stated in a simple vectorized form which avoids unnecessary storage and evaluations of intermediate variables. However, in HF, as essentially in all wave function based quantum chemistry methods, one and two electron integrals are typically defined by an element-wise array assignment (e.g., A[i,j] = k). This nonvectorized assignment represents a major challenge for backward mode regarding the amount of memory needed to store the computational graph as well as intermediate variables and derivatives.

The most critical component for our HF implementation in DiffiQult is matrix diagonalization. In some AD libraries such as autograd,65 this matrix operation is considered as an elementary operation, which can be implicitly differentiated to obtain its adjoints and derivatives, respectively for each mode. In backward mode, the analytical expression for the adjoint of the eigenvectors is in principle available. However, the adjoints of the eigenvectors corresponding to repeated eigenvalues are not differentiable;3,64 see Supporting Information. Therefore, we cannot use backward differentiation for matrix diagonalization of systems with degenerate molecular orbitals. Since we aim to compute general molecular systems, we exclude the backward mode for our implementation of DiffiQult. This leaves the forward mode as a possible option to circumvent the challenges of repeated eigenvalues. For the forward mode, the analytical expressions of the derivatives of eigenvectors are known, even for the degenerate case.66 This method relies on computing the nth-order derivative of the eigenvalues such that its diagonals are distinct and on computing the n + 1th-order derivative of the original matrix that needs to be diagonalized; see Supporting Information. Therefore, we would need an implementation that would depend on a case-by-case analysis. Alternatively, Walter et al.67 proposed a general algorithm to compute the diagonalization, based on univariate Taylor polynomials (Supporting Information),1,63 implemented in Algopy.63 This approach is mathematically equivalent to forward differentiation and considers the repeated eigenvalue problem. For further details, we refer the reader to the Supporting Information.

Even though we may consider reverse mode as a more efficient way for our implementation given the large number of input parameters and the small number of output variables, after this analysis, we conclude that an HF implementation is required to be based on the forward mode. Regarding the AD library, we have chosen Algopy,63 since it supports both AD modes, provides matrix diagonalization for repeated eigenvalues, and requires only minimal modifications to calculate gradients of functions implemented in plain Python.

Finally, once we have implemented an autodifferentiable HF algorithm in Algopy, we use a gradient-based optimization to optimize Gaussian centers, widths, and contraction coefficients either together or separately. We use the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm68 implemented in the scipy module. As recommended in ref (56), we take the natural logarithm to optimize the Gaussian exponents. No unexpected or unusually high safety hazards were encountered during the course of this study.

5. Results

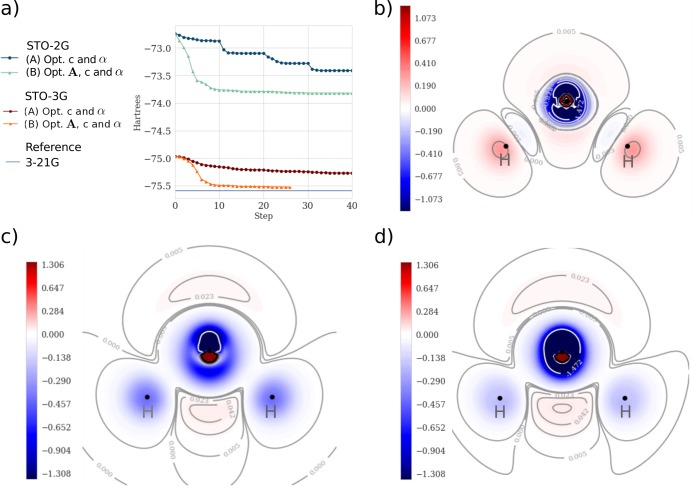
We tested our implementation by optimizing the STO-2G as well as the STO-3G minimal basis sets for the small molecules H2O, HF, NH3, CH4, and CH2O. Since we can obtain the gradients with respect to any input parameter, DiffiQult has the freedom to select different optimization procedures. Here, we illustrate two schemes: (A) optimizing the Gaussian exponents and contraction coefficients, sequentially, and (B) optimizing the contraction coefficients and exponents, followed by an optimization of the Gaussian centers. For the example of H2O, the improvement of the energies for each optimization step is illustrated in Figure 3. We find that the most efficient way to optimize the HF energy is by employing scheme (B) since it already converges after 10 basis set optimization steps. For a general assessment of which method works better than the other, we need to consider the trade-off between reaching fast convergence and computation time. For example, scheme (B) requires more time to perform a single optimization step since it requires computing more gradients for a larger number of parameters due to the line-search procedure within the BFGS algorithm. All optimizations were done until finding an infinite norm of the gradient of 10–5 or a total of 10 steps, respectively. Table 1 displays HF energies for optimized and nonoptimized basis sets for selected small molecules. The optimization scheme (B) results in an improvement of up to 0.18 hartree per electron.

Figure 3.

Figure 3

Open in a new tab

One-electron basis function optimizations of H2O. (a) Optimization steps of STO-3G and STO-2G with different optimization schemes. (A) Optimizing exponents and coefficients 10 steps each twice, and (B) optimizing exponents and coefficients together, followed by optimizing positions. (b) Contour of the difference in electronic density between the STO-3G basis and the optimized one-electron basis functions under scheme (B). (c) Contours of the difference in electronic density between the conventional STO-3G basis set and the reference 3-21G basis set. (d) Contour of the difference in electronic density between the optimized (scheme (B)) STO-3G basis set and the reference 3-21G basis set. An increase of density on the optimization is displayed in blue and a decrease is in red.

Table 1. Hartree–Fock Energies in Hartrees Test Molecules of the Nonoptimized and Optimized (Scheme (B)) basis sets STO-2G and STO-3Ga.

  basis
  STO-2G
 STO-3G
  
molecule none Opt. coef, α and A none Opt. coef, α and A reference: 3-21G
HF –95.60 –97.03 –98.57 –99.38 –99.46
H2O –72.74 –73.82 –74.96 –75.52 –75.59
NH3 –53.82 –54.65 –55.45 –55.83 –55.87
CH4 –38.59 –39.32 –39.72 –39.96 –39.98
CH3F –133.09 –134.96 –137.17 –137.43 –138.28
CH2O –109.02 –110.54 –112.35 –112.72 –113.22
Open in a new tab
a

As a reference, we show results for the larger 3-21G basis set.

The minimal basis sets we optimized lacked in flexibility to correctly represent polarization and dispersion in the core molecular orbitals. For instance, hydrogen contains only a single atom centered s-type orbital that is insufficient to display changes in the density induced by the surrounding charges. By optimizing the parameters of the atomic orbital of each hydrogen, we can partially take into account polarization effects. As is depicted in Figure 3b, the optimization of the basis STO-3G of H2O shifts the electronic density from the regions around the hydrogen atoms toward the bond regions. In the case of the oxygen, as it is shown in Figure 3c,d, the number of basis function is not sufficient to represent both the bond and the density around the oxygen itself, even after the optimization. Therefore, corrections to the core atomic orbitals of oxygen would need to include a greater number and higher angular momentum one-electron functions.

Finally, we discuss a common convergence problem of the HF method that can affect our fully variational HF implementation. It appears in our examples mainly in the line-search, when the optimizer by chance tests the parameter for which the SCF is difficult to get converged. In principle, this problem can be circumvented by suitable convergence strategies in the HF algorithm.

6. Conclusion and Perspective

AD offers a promising alternative solution for computing accurate derivatives of electronic structure methods. In this manuscript, we implemented DiffiQult, which serves as a proof-of-concept that helps us to develop an understanding of the capabilities of AD in quantum chemistry. Specifically, we presented and discussed the use of AD in the context of a fully variational HF method, which contains most of the mathematical components of other electronic structure methods. By using the Algopy AD library, we calculated gradients of any parameter with just minimal adjustments in the source code of the canonical HF energy, without any explicit implementation of a single derivative. With these gradients at hand, we are able to fully minimize the energy with respect to any parameter of the Gaussian one-particle basis. As a result, we capture, to some extent, polarization effects with a reduced number of atomic orbitals. Since the essential functions of many quantum chemistry methods are similar to the ones present in HF, we plan to extend DiffiQult to post-HF methods in future work.

DiffiQult can be seen as a general tool to obtain molecular tailored basis functions, that can be used as a starting point for other variational methods, e.g., FCI. An emerging application could be in the field of quantum computing for quantum chemistry,69 where the size of one-electron basis function is constrained by the number of qubits available in state-of-the-art hardware.70−74 Thus, experimental demonstrations of quantum algorithms for chemistry have been limited to conventional minimal basis sets.74,75 Here, the fully variational setting of DiffiQult could offer the advantage to optimize initial parameters of atomic orbitals, which could increase the accuracy of variational quantum chemistry simulations,69 while keeping the number of basis functions small.

Finally, the analysis of the advantages of AD technologies in the implementation of DiffiQult demonstrates that AD has a huge potential in future implementations. The AD tools could extend quantum chemistry methods in many ways. For example, in general, it is possible to mix different differentiation modes and approaches. We could use the forward mode to compute gradients of element-wise matrix definitions (or in general for complex computational graphs) and use the backward mode for vectorized functions. Furthermore, AD could be combined with symbolic algebra and automated code generation76−78 to build a general tool-chain to create software packages capable of computing a function and computing gradients with an AD library.

Acknowledgments

This project was supported by the NSF Award Number 1464862. R.L. acknowledges support by the Swedish Research Council (Grant 2016-03398). T.T-M. thanks CONACyT for scholarship No. 433469. T.T-M. appreciates the rich discussions with Jhonathan Romero Fontalvo and Benjamin Sanchez Langeling.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.7b00586.

  • Derivatives and adjoints of eigenvectors (S1). Description of a method used to compute the derivatives of repeated eigenvalues in forward mode, Univariate Taylor Arithmetic (S2) (PDF)

The authors declare no competing financial interest.

Supplementary Material

oc7b00586_si_001.pdf (162.9KB, pdf)

References

  1. Griewank A.; Walther A.. Evaluating Derivatives, Principles and Techniques of Algorithmic Differentiation, 2nd ed.; SIAM: Philadelphia, 2008. [Google Scholar]
  2. Bischof C. H.; Bücker M.. Computing derivatives of computer programs. In Modern Methods and Algorithms of Quantum Chemistry; Grotendorst J., Ed.; NIC, Series, 2000; Vol. 3 ; pp 315–327. [Google Scholar]
  3. Walther A.; Griewank A.. Getting started with ADOL-C. In Combinatorial Scientific Computing; Naumann U., Schenk O., Eds.; Chapman-Hall CRC Computational Science, 2012; Chapter 7, pp 181–202. [Google Scholar]
  4. Bischof C.; Khademi P.; Mauer A.; Carle A. Adifor 2.0: automatic differentiation of Fortran 77 programs. IEEE Comput. Sci. Eng. 1996, 3, 18–32. 10.1109/99.537089. [DOI] [Google Scholar]
  5. Bischof C. H.; Roh L.; MauerOats A. ADIC – An Extensible Automatic Differentiation Tool for ANSI-C. Software-Practice and Experience 1997, 27, 1427–1456. . [DOI] [Google Scholar]
  6. Bischof C.; Khademi P.; Mauer A.; Carle A. Adifor 2.0: automatic differentiation of Fortran 77 programs. IEEE Comput. Sci. Eng. 1996, 3, 18–32. 10.1109/99.537089. [DOI] [Google Scholar]
  7. Hascoët L.; Pascual V. The Tapenade Automatic Differentiation tool: Principles, Model, and Specification. ACM Transactions on Mathematical Software 2013, 39, 1–43. 10.1145/2450153.2450158. [DOI] [Google Scholar]
  8. Walther A.; Griewank A.. Getting started with ADOL-C. In Combinatorial Scientific Computing; Naumann U., Schenk O., Eds.; Chapman-Hall CRC Computational Science, 2012; Chapter 7, pp 181–202. [Google Scholar]
  9. Maclaurin D.; Duvenaud D.; Adams R. P.. Gradient-based Hyperparameter Optimization Through Reversible Learning. In Proceedings of the 32nd International Conference on International Conference on Machine Learning - Vol. 37; ICML’15; JMLR.org, 2015; pp 2113–2122. [Google Scholar]
  10. Revels J.; Lubin M.; Papamarkou T. JuliaDiff, https://github.com/JuliaDiff, 2017.
  11. Revels J.; Lubin M.; Papamarkou T.. Forward-Mode Automatic Differentiation in Julia. arXiv:1607.07892, 2016.
  12. Cohen A.; Shoham M. Application of hyper-dual numbers to rigid bodies equations of motion. Mech. Mach. Theory 2017, 111, 76–84. 10.1016/j.mechmachtheory.2017.01.013. [DOI] [Google Scholar]
  13. Henrard M. Calibration in Finance: Very Fast Greeks Through Algorithmic Differentiation and Implicit Function. Procedia Comput. Sci. 2013, 18, 1145–1154. 10.1016/j.procs.2013.05.280. [DOI] [Google Scholar]
  14. Niemeyer K. E.; Curtis N. J.; Sung C.-J. pyJac: Analytical Jacobian generator for chemical kinetics. Comput. Phys. Commun. 2017, 215, 188–203. 10.1016/j.cpc.2017.02.004. [DOI] [Google Scholar]
  15. Jirari H. Optimal control approach to dynamical suppression of decoherence of a qubit. Europhys. Lett. 2009, 87, 40003. 10.1209/0295-5075/87/40003. [DOI] [Google Scholar]
  16. Jirari H.; Wu N. Optimal state transfer of a single dissipative two-level system. Eur. Phys. J. B 2016, 89, 100. 10.1140/epjb/e2016-60523-y. [DOI] [Google Scholar]
  17. Schmidhuber J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
  18. Baydin A. G.; Pearlmutter B. A.; Radul A. A.; Siskind J. M.. Automatic differentiation in machine learning: a survey. Preprint arXiv:1502.05767, 2015.
  19. Bengio Y.Practical Recommendations for Gradient-Based Training of Deep Architectures. In Neural Networks: Tricks of the Trade: Second ed.; Montavon G., Orr G. B., Müller K.-R., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2012; pp 437–478. [Google Scholar]
  20. Leung N.; Abdelhafez M.; Koch J.; Schuster D. Speedup for quantum optimal control from automatic differentiation based on graphics processing units. Phys. Rev. A: At., Mol., Opt. Phys. 2017, 95, 042318. 10.1103/PhysRevA.95.042318. [DOI] [Google Scholar]
  21. Gauss J.Molecular properties. In Modern Methods and Algorithms of Quantum Chemistry; Grotendorst J., Ed.; NIC, Series, 2000; Vol. 3; pp 541–592. [Google Scholar]
  22. Almlöf J.; Taylor P. R. Molecular properties from perturbation theory: A Unified treatment of energy derivatives. Int. J. Quantum Chem. 1985, 27, 743–768. 10.1002/qua.560270610. [DOI] [Google Scholar]
  23. Helgaker T., Jørgensen P.. Analytical Calculation of Geometrical Derivatives in Molecular Electronic Structure Theory. In Adv. Quantum Chem.; Löwdin P.-O., Ed.; Academic Press, 1988; Vol. 19; pp 183–245. [Google Scholar]
  24. Obara S.; Saika A. Efficient recursive computation of molecular integrals over Cartesian Gaussian functions. J. Chem. Phys. 1986, 84, 3963–3974. 10.1063/1.450106. [DOI] [Google Scholar]
  25. Yamaguchi Y.; Schaefer H. F.. Analytic Derivative Methods in Molecular Electronic Structure Theory: A New Dimension to Quantum Chemistry and its Applications to Spectroscopy. In Handbook of High-Resolution; John Wiley & Sons, Ltd, 2011. [Google Scholar]
  26. Kato S.; Morokuma K. Energy gradient in a multi-configurational SCF formalism and its application to geometry optimization of trimethylene diradicals. Chem. Phys. Lett. 1979, 65, 19–25. 10.1016/0009-2614(79)80117-7. [DOI] [Google Scholar]
  27. Veillard A.; Clementi E. Complete multi-configuration self-consistent field theory. Theor. Chim. Acta 1967, 7, 133–143. 10.1007/BF01151915. [DOI] [Google Scholar]
  28. Andersson K.; Malmqvist P.-A.; Roos B. O.; Sadlej A. J.; Wolinski K. Second-order perturbation theory with a CASSCF reference function. J. Phys. Chem. 1990, 94, 5483–5488. 10.1021/j100377a012. [DOI] [Google Scholar]
  29. Andersson K.; Malmqvist P.-A.; Roos B. O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218–1226. 10.1063/1.462209. [DOI] [Google Scholar]
  30. MacLeod M. K.; Shiozaki T. Communication: Automatic code generation enables nuclear gradient computations for fully internally contracted multireference theory. J. Chem. Phys. 2015, 142, 051103. 10.1063/1.4907717. [DOI] [PubMed] [Google Scholar]
  31. Vlaisavljevich B.; Shiozaki T. Nuclear Energy Gradients for Internally Contracted Complete Active Space Second-Order Perturbation Theory: Multistate Extensions. J. Chem. Theory Comput. 2016, 12, 3781–3787. 10.1021/acs.jctc.6b00572. [DOI] [PubMed] [Google Scholar]
  32. Ekström U.; Visscher L.; Bast R.; Thorvaldsen A. J.; Ruud K. Arbitrary-Order Density Functional Response Theory from Automatic Differentiation. J. Chem. Theory Comput. 2010, 6, 1971–1980. 10.1021/ct100117s. [DOI] [PubMed] [Google Scholar]
  33. Bast R.; Ekström U.; Gao B.; Helgaker T.; Ruud K.; Thorvaldsen A. J. The ab initio calculation of molecular electric, magnetic and geometric properties. Phys. Chem. Chem. Phys. 2011, 13, 2627–2651. 10.1039/C0CP01647K. [DOI] [PubMed] [Google Scholar]
  34. Steiger R.; Bischof C. H.; Lang B.; Thiel W. Using automatic differentiation to compute derivatives for a quantum-chemical computer program. Future Gener. Comput. Syst. 2005, 21, 1324–1332. 10.1016/j.future.2004.11.011. [DOI] [Google Scholar]
  35. Barborini M.; Sorella S.; Guidoni L. Structural Optimization by Quantum Monte Carlo: Investigating the Low-Lying Excited States of Ethylene. J. Chem. Theory Comput. 2012, 8, 1260–1269. 10.1021/ct200724q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sorella S.; Capriotti L. Algorithmic differentiation and the calculation of forces by quantum Monte Carlo. J. Chem. Phys. 2010, 133, 234111. 10.1063/1.3516208. [DOI] [PubMed] [Google Scholar]
  37. Tamayo-Mendoza T.; Kreisbeck C.; Aspuru-Guzik A. DiffiQult, https://aspuru-guzik-group.github.io/DiffiQult, 2017.
  38. Jørgensen P.; Simons J.. Second Quantization-Based Methods in Quantum Chemistry, 1st ed.; Academic Press, 1981. [Google Scholar]
  39. Angerson E.; Bai Z.; Dongarra J.; Greenbaum A.; McKenney A.; Croz J. D.; Hammarling S.; Demmel J.; Bischof C.; Sorensen D.. LAPACK: A portable linear algebra library for high-performance computers. Proceedings SUPERCOMPUTING ’90. 1990; pp 2–11.
  40. Helgaker T.; Almlöf J. Molecular wave functions and properties calculated using floating Gaussian orbitals. J. Chem. Phys. 1988, 89, 4889–4902. 10.1063/1.455659. [DOI] [Google Scholar]
  41. Frost A. A. Floating Spherical Gaussian Orbital Model of Molecular Structure. I. Computational Procedure. LiH as an Example. J. Chem. Phys. 1967, 47, 3707–3713. 10.1063/1.1701524. [DOI] [Google Scholar]
  42. Helgaker T.; Jørgensen P.; Olsen J.. Molecular Electronc-Structure Theory, 1st ed.; John Wiley & Sons, 2000. [Google Scholar]
  43. Gill P. M. W.; Head-Gordon M.; Pople J. A. Efficient computation of two-electron - repulsion integrals and their nth-order derivatives using contracted Gaussian basis sets. J. Phys. Chem. 1990, 94, 5564–5572. 10.1021/j100377a031. [DOI] [Google Scholar]
  44. Reine S.; Helgaker T.; Lindh R. Multi-electron integrals. WIREs Comput. Mol. Sci. 2012, 2, 290–303. 10.1002/wcms.78. [DOI] [Google Scholar]
  45. Valeev E. F.Libint: A library for the evaluation of molecular integrals of many-body operators over Gaussian functions. http://libint.valeyev.net/, 2017; version 2.3.1.
  46. Schlegel H. B.; Frisch M. J. Transformation between Cartesian and pure spherical harmonic Gaussians. Int. J. Quantum Chem. 1995, 54, 83–87. 10.1002/qua.560540202. [DOI] [Google Scholar]
  47. Jensen F. Atomic orbital basis sets. WIREs Comput. Mol. Sci. 2013, 3, 273–295. 10.1002/wcms.1123. [DOI] [Google Scholar]
  48. Szabo A.; Ostlund N. S.. Modern Quantum Chemistry, 1st ed.; Dover Publication, 1996. [Google Scholar]
  49. Almlöf J.; Helgaker T.; Taylor P. R. Gaussian basis sets for high-quality ab initio calculations. J. Phys. Chem. 1988, 92, 3029–3033. 10.1021/j100322a003. [DOI] [Google Scholar]
  50. Huber H. Geometry optimization in AB initio calculations. Floating orbital geometry optimization applying the hellmann-feyman force. Chem. Phys. Lett. 1979, 62, 95–99. 10.1016/0009-2614(79)80420-0. [DOI] [Google Scholar]
  51. Huber H. Geometry optimization in ab initio SCF calculations. J. Mol. Struct.: THEOCHEM 1981, 76, 277–284. 10.1016/0166-1280(81)85004-X. [DOI] [Google Scholar]
  52. Hurley A. C. The computation of floating functions and their use in force constant calculations. J. Comput. Chem. 1988, 9, 75–79. 10.1002/jcc.540090110. [DOI] [Google Scholar]
  53. Neisius D.; Verhaegen G. Bond functions for ab initio calculations on polyatomic molecules. Molecules containing C, N, O and H. Chem. Phys. Lett. 1981, 78, 147–152. 10.1016/0009-2614(81)85573-X. [DOI] [Google Scholar]
  54. Neisius D.; Verhaegen G. Bond functions for AB initio calculations. MCSCF results for CH, NH, OH and FH. Chem. Phys. Lett. 1982, 89, 228–233. 10.1016/0009-2614(82)80047-X. [DOI] [Google Scholar]
  55. Tachikawa M.; Osamura Y. Simultaneous optimization of exponents, centers of Gaussian-type basis functions, and geometry with full-configuration interaction wave function: Application to the ground and excited states of hydrogen molecule. J. Chem. Phys. 2000, 113, 4942–4950. 10.1063/1.1288382. [DOI] [Google Scholar]
  56. Tachikawa M.; Taneda K.; Mori K. Simultaneous optimization of GTF exponents and their centers with fully variational treatment of Hartree-Fock molecular orbital calculation. Int. J. Quantum Chem. 1999, 75, 497–510. . [DOI] [Google Scholar]
  57. Shimizu N.; Ishimoto T.; Tachikawa M. Analytical optimization of orbital exponents in Gaussian-type functions for molecular systems based on MCSCF and MP2 levels of fully variational molecular orbital method. Theor. Chem. Acc. 2011, 130, 679–685. 10.1007/s00214-011-1052-3. [DOI] [Google Scholar]
  58. Perlt E.; Brussel M.; Kirchner B. Floating orbital molecular dynamics simulations. Phys. Chem. Chem. Phys. 2014, 16, 6997–7005. 10.1039/c3cp54797c. [DOI] [PubMed] [Google Scholar]
  59. Perlt E.; Apostolidou C.; Eggers M.; Kirchner B. Unrestricted Floating Orbitals for the Investigation of Open Shell Systems. Int. J. Chem. 2015, 8, 194. 10.5539/ijc.v8n1p194. [DOI] [Google Scholar]
  60. Theano Development Team, Theano: A Python framework for fast computation of mathematical expressions. Preprint arXiv: 1605.02688 2016.
  61. Abadi M.et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems; tensorflow.org, 2015.
  62. Hascoët L.; Pascual V. The Tapenade Automatic Differentiation tool: Principles, Model, and Specification. ACM Trans. Math. Software 2013, 39, 20. 10.1145/2450153.2450158. [DOI] [Google Scholar]
  63. Walter S. F.; Lehmann L. Algorithmic differentiation in Python with AlgoPy. J. of Comp. Sci. 2013, 4, 334–344. 10.1016/j.jocs.2011.10.007. [DOI] [Google Scholar]
  64. Giles M. B.Collected Matrix Derivative Results for Forward and Reverse Mode Algorithmic Differentiation. In Advances in Automatic Differentiation; Bischof C. H., Bücker H. M., Hovland P., Naumann U., Utke J., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2008; pp 35–44. [Google Scholar]
  65. Maclaurin D.; Duvenaud D.; Adams R. P.. Autograd: Effortless Gradients in Numpy. In ICML 2015 AutoML Workshop, 2015.
  66. Nelson R. B. Simplified calculation of eigenvector derivatives. AIAA J. 1976, 14, 1201–1205. 10.2514/3.7211. [DOI] [Google Scholar]
  67. Walter S. F.; Lehmann L.; Lamour R. On evaluating higher-order derivatives of the QR decomposition of tall matrices with full column rank in forward and reverse mode algorithmic differentiation. Optim. Method. Softw. 2012, 27, 391–403. 10.1080/10556788.2011.610454. [DOI] [Google Scholar]
  68. Nocedal J.; Wright S. J.. Numerical Optimization, 2nd ed.; Springer: New York, 2006; pp 497–528. [Google Scholar]
  69. Peruzzo A.; McClean J. R.; Shadbolt P.; Yung M.; Zhou X.-Q.; Love P.; Aspuru-Guzik A.; O'Brien J. L. A Variational Eigenvalue Solver on a Photonic Quantum Processor. Nat. Commun. 2014, 5, 4215. 10.1038/ncomms5213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Barends R.; et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014, 508, 500. 10.1038/nature13171. [DOI] [PubMed] [Google Scholar]
  71. Barends R.; et al. Digital quantum simulation of fermionic models with a superconducting circuit. Nat. Commun. 2015, 6, 7654. 10.1038/ncomms8654. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Ristè D.; Poletto S.; Huang M.-Z.; Bruno A.; Vesterinen V.; Saira O.-P.; DiCarlo L. Detecting bit-flip errors in a logical qubit using stabilizer measurements. Nat. Commun. 2015, 6, 6983. 10.1038/ncomms7983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Córcoles A. D.; Magesan E.; Srinivasan S. J.; Cross A. W.; Steffen M.; Gambetta J. M.; Chow J. M. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 2015, 6, 6979. 10.1038/ncomms7979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. O’Malley P. J. J.; et al. Scalable Quantum Simulation of Molecular Energies. Phys. Rev. X 2016, 6, 031007. [Google Scholar]
  75. Kandala A.; Mezzacapo A.; Temme K.; Takita M.; Brink M.; Chow J. M.; Gambetta J. M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. 10.1038/nature23879. [DOI] [PubMed] [Google Scholar]
  76. Hirata S.; Fan P. D.; Auer A. A.; Nooijen M.; Piecuch P. Combined coupled-cluster and many-body perturbation theories. J. Chem. Phys. 2004, 121, 12197–12207. 10.1063/1.1814932. [DOI] [PubMed] [Google Scholar]
  77. Janssen C. L.; Schaefer H. F. III The automated solution of second quantization equations with application equations with applications to the coupled cluster approach. Theor. Chim. Acta 1991, 79, 1–42. 10.1007/BF01113327. [DOI] [Google Scholar]
  78. Hirata S. Tensor Contraction Engine: Abstraction and Automated Parallel Implementation of Configuration-Interaction, Coupled-Cluster, and Many-Body Perturbation Theories. J. Phys. Chem. A 2003, 107, 9887–9897. 10.1021/jp034596z. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc7b00586_si_001.pdf (162.9KB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES