Abstract
A hybrid neuroprosthesis that combines human muscle power, elicited through functional electrical stimulation (FES), with a powered orthosis may be advantageous over a sole FES or a powered exoskeleton-based rehabilitation system. The hybrid system can conceivably overcome torque reduction due to FES-induced muscle fatigue by complementarily using torque from the powered exoskeleton. The second advantage of the hybrid system is that the use of human muscle power can supplement the powered exoskeleton’s power (motor torque) requirements; thus, potentially reducing the size and weight of a walking restoration system. To realize these advantages, however, it is unknown how to concurrently optimize desired control performance and allocation of control inputs between FES and electric motor. In this paper, a model predictive control-based dynamic control allocation (DCA) is used to allocate control between FES and the electric motor that simultaneously maintain a desired knee angle. The experimental results, depicting the performance of the DCA method while the muscle fatigues, are presented for an able-bodied participant and a participant with spinal cord injury. The experimental results showed that the motor torque recruited by the hybrid system was less than that recruited by the motor-only system, the algorithm can be easily used to allocate more control input to the electric motor as the muscle fatigues, and the muscle fatigue induced by the hybrid system was found to be less than the fatigue induced by sole FES. These results validate the aforementioned advantages of the hybrid system; thus implying the hybrid technology’s potential use in walking rehabilitation.
I. Introduction
Each year in the United States 17,000 people experience a spinal cord injury (SCI), and 41.3% of these injuries result in paraplegia [1]. The loss of lower limb motor function greatly inhibits the ability of a person with SCI to perform activities of daily living. Potentially, the lower limb function can be enhanced by using functional electrical stimulation (FES), which is an artificial stimulation of motor units to produce functional movements. By coordinated stimulation of the paralyzed lower limb muscles, the walking motion can be restored [2]–[5]. FES can be applied either using transcutaneous (surface) electrodes [3] or through percutaneous intramuscular electrodes or implanted electrodes [4], [6]. The intramuscular and implanted electrodes provide more selective recruitment of muscles [4], [7], while the transcutaneous electrodes are applied directly to the skin surface and can be adjusted and removed with ease when desired. However, stimulation through the surface electrodes causes non-selective and repeated muscle stimulation, which leads to the rapid onset of muscle fatigue [8]. FES-induced muscle fatigue decreases a muscle’s ability to produce or sustain a force, which can greatly inhibit the effectiveness of FES-based gait restoration devices and thus limit their duration of use.
To alleviate the effects of FES-induced muscle fatigue, FES-based devices can be combined with passive orthoses [9]–[11] to lower the overall stimulation duty cycle of FES. These hybrid devices lock the knee joints, which means that FES is not required to stimulate the quadriceps muscle to elicit standing. Another class of hybrid walking devices that combine FES with a powered exoskeleton gait have also been proposed [12]–[16]. These devices use the powered exoskeleton to dynamically compensate for the FES-induced muscle fatigue. Compared to sole FES-based walking systems, powered exoskeletons such as the Indego [17], ReWalk [18], Mina [19], and EKSO [20], [21] are capable of greater walking durations but may have higher power consumption to operate high torque motors. Bulky high torque motors and larger batteries increase weight and hence reduce wearability. The hybrid system can overcome these limitations by reducing power consumption and actuator size in the powered exoskeleton by combining it with FES.
A control method for the hybrid device has to simultaneously coordinate FES and the electric motor while maintaining desired control performance and compensating for the muscle fatigue. In [22], an open-loop control of stimulation was used to provide the active torque and controlled brakes were used like a dynamic stopper to restrict a single joint to a desired joint angle. In [23], this method was extended to a full orthosis with FES and controlled brakes at both the hip and knee joints of each leg. Similar to [22], the controlled brakes of the orthosis were used to eliminate the requirement for stimulation during standing and in between steps. The disadvantage of this method is that the antagonistic muscles are stimulated at the maximum stimulation to generate a raw joint torque, which is fine tuned through the controlled brakes. This may result in over stimulation of the muscles leading to the rapid onset of muscle fatigue. Later, in [24], a hybrid neuroprosthesis with 16 intramuscular stimulation channels combined with a locking orthosis was tested on participants with SCI. A pre-programmed open-loop stimulation was used, which may result in over stimulation and thus reduce the duration that such a device may be used.
In [25], a combination of FES and active actuators (electric motors) were used to control knee extension using an adaptive gain-based controller to allocate the control effort. The electric motors were controlled using a PD controller, while the stimulation was controlled by a proportional gain whose adaptation was dependent on the current sent to the electric motor. In [12] a cooperative knee joint controller was used in a hybrid knee-ankle-foot exoskeleton. The approach was tested on able-bodied subjects. A variable stiffness controller computed knee electric motor stiffness based on the measured interaction torque between the user and the exoskeleton. A PID controller controlled the stimulation to the quadriceps muscle and an iterative learning controller for stimulating the knee flexors was used. In [12], a fatigue estimator that measures torque-time integral was to detect the onset of fatigue and modify the stimulation parameters. In [13], another cooperative control approach was used to coordinate hip motors with the stimulation of the hamstrings and knee motors with the stimulation of quadriceps muscle. The approach was tested on three subjects with SCI. The motors were controlled using a high-bandwidth position feedback and the FES control was modified by the difference between the estimated muscle torque and the reference torque profile. Also the controller would turn-off the stimulation if in five consecutive trials FES is unable to generate over one third of the previous torque output.
In both [12] and [13] the controllers take into account the muscle fatigue for allocating control between FES and electric motors; however, their allocation is not computed as a result of an optimization and did not use a muscle fatigue model, and therefore may be sub-optimal. For example, traditional high-bandwidth feedback control methods used in these works do not provide an explicit way to optimally allocate control inputs in systems with redundant actuation, such as hybrid neuroprostheses. Therefore, the key control issue is how to optimally allocate control between the FES and the electric motor, simultaneously, while maintaining a desired control performance.
In our previous research, a dynamic optimization method was used to optimize a hybrid walking system (FES + passive orthosis) [11]. However, the method computes FES control inputs offline. Motivated to develop an optimization method for a real-time implementation, in [26], a linear model predictive control (MPC) method was proposed to dynamically allocate control in a hybrid knee joint control system composed of FES and an electric motor. However, a linearized musculoskeletal model was used for the linear MPC method, which may lose control performance outside the region of linearization. Therefore a nonlinear model predictive controller (NMPC) for an FES only case was developed in [27] to elicit knee extension in able-bodied participants.
The objective of this paper is to validate the NMPC-based dynamic control allocation (DCA) that is used to optimally allocate control between FES and an electric motor to elicit desired knee movement, and to show that the hybrid neuroprosthesis induces less muscle fatigue than neuroprostheses that strictly use FES. The DCA method solves a finite time optimal control problem [28], [29] such that the minimum control necessary is used to produce the movement. The key contribution of the paper is that a gradient projection algorithm [27], [30], [31], was used to facilitate real-time implementation of the DCA method while including the nonlinear musculoskeletal model, muscle fatigue dynamics, and constraints on the control inputs. The DCA algorithm was demonstrated through experiments on a lower leg extension machine that combines the stimulation of the quadriceps muscle with an electric motor. The DCA experimental results were obtained from an able-bodied participant and a participant with SCI.
II. Dynamic Model of the Hybrid Neuroprosthesis System
The dynamics of the hybrid leg extension neuroprosthesis system, illustrated in Fig. 1, can be modeled as
| (1) |
where are the angular position, velocity, and acceleration of the shank (lower leg and foot), respectively. The moment of inertia of the shank is and the gravitational term, , is given as G(θ) = mglcsin(θ + θeq), where the variables are the mass of the shank, gravitational acceleration, and length from the knee joint to the center of mass of the shank, respectively. The torque is the torque of the motor, is the joint torque due to passive dynamics (passive effects of muscles, tendons, and ligaments are all lumped into this function), and is the knee extension torque due to stimulation of the quadriceps muscle. Due to the fast response time of electric motors, in comparison to electrically stimulated muscles, the actuation dynamics of the motor were neglected. The passive and FES-induced muscle dynamics will be modeled based on the models in [32]. This model was selected over other models (such as those presented in [33], [34] and references there in) because it is a continuous model that sufficiently describes the dynamics without unnecessary complexities. Such a model is ideal for MPC because it is differentiable and its simplicity reduces the computation time when solving the optimal control problem. The passive joint torque can be expressed as a function of the anatomical knee joint angle, , as [32]
| (2) |
where and are subject specific parameters. The knee extension torque due to stimulation can be expressed as a function of the anatomical knee joint as [32]
| (3) |
where are subject specific parameters. It should be noted that the torque-velocity dependence in (3) is modified from the piece-wise continuous function used in [32] to a single function to simplify the optimal control problem. If the piece-wise force-velocity function were used, multiple gradients would need to be calculated to account for each piece-wise case, and the optimization algorithm would need to perform state-dependent switching between the gradients to compute the solution. One limitation of this simplification is that the torque-velocity function is now no longer bounded, unlike the piece-wise model in [32]. The muscle activation state, ake ∈ [0, 1], in (3) can be modeled as [35]
| (4) |
where is the muscle activation time constant. The normalized stimulation amplitude, uke ∈ [0, 1] in (4), can be determined from the stimulation current amplitude, , as
| (5) |
where are the threshold and saturation limits of the muscle, respectively. The threshold current amplitude, It, is defined as the minimum stimulation amplitude required to produce the first significant muscle contraction. The saturation current amplitude, Is, is defined as the minimum current amplitude that produces that maximum muscle contraction force.
Figure 1.
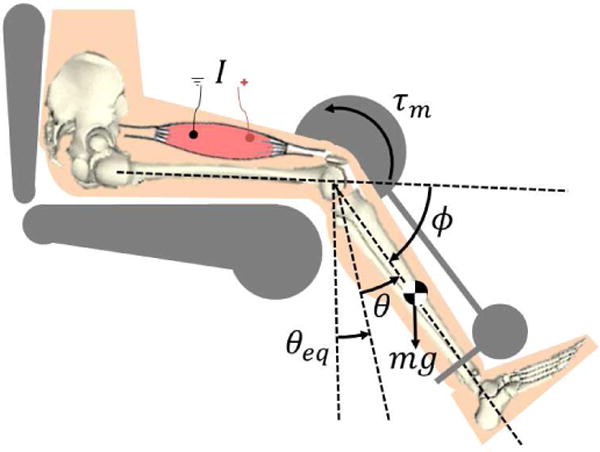
The hybrid leg extension neuroprosthesis uses a motor at the knee joint, τm, and electrical stimulation of the quadriceps muscles, I, to move the shank. The position of the shank relative to equilibrium is θ, and ϕ is the anatomical knee angle.
The muscle fatigue, μ ∈ [μmin, 1] in (3), has dynamics that are dependent on the muscle activation and can be represented as [36]
| (6) |
where μmin ∈ (0, 1) is the minimum fatigue level that the muscle can be, is the fatigue time constant, and is the recovery time constant. This fatigue model was chosen over the models presented in [33], [34] because of its simplicity (a first order differential equation) and is driven by the muscle activation, which is modulated via stimulation pulse width or amplitude, unlike fatigue models in [33], [34] that use frequency modulation as the input.
Using equations (1), (4), and (6) the dynamics of the hybrid neuroprosthesis system can be expressed in a state-space form as
| (7) |
where are the states of the system and u = [u1, u2]T = [τm, uke]T are the inputs. Note that although τm is applied to the system (1) directly, uke cannot be. It is mapped to normalized muscle activation ake via (4), and then ake is mapped to τke via (3). τke is the input that evolve the dynamics in (1). These relation are all embedded in the (7). Please note that the above state-space form in (7) is continuously differentiable. This is an important and necessary property for implementing the gradient projection algorithm, which is described in the next section.
III. Gradient Projection Dynamic Control Allocation
The control objectives are to regulate the knee angle to a desired position while allocating the control effort to the electric motor and FES and constraining the input region. These control objectives can be posed as an NMPC scheme based on the following optimal control problem
| (8) |
The objective of the optimal control problem is to solve for the optimal control input that minimizes the cost function in its prediction horizon.
In the cost function where are the desired and the nominal states. denotes the actual system state at time tk ∈ [t0, TN], where [t0, TN] denotes the period of the entire control process. The initial states of the nominal system is set to be xk for the prediction horizon τ ∈ [t0, T], for convenience we also denote as the nominal states with initial value, xk. , where is the desired input trajectory, and is the nominal input trajectory starts at tk, note that is the input constraint. After the optimal control input is solved, is applied to the actual system at tk, where is the actual input trajectory to the system and ε is an infinitesimal time constant that makes tk+1 = tk + ε.
In (8), V(∆x(T)) and are defined as
where and are positive-definite and symmetric weight matrices that may be tuned to achieve the desired performance. Although the presence of the nonlinear dynamics in the constraints means that the optimal control problem may have many local minimum, the positive-definite cost function ensures that the optimization will converge to a bounded solution that is a local minimum.
Pontryagin’s Minimum Principle states that solves the optimal control problem in (8) for the finite time horizon τ ∈ [t0, T) if it minimizes the Hamiltonian [37]. Given the definition of the optimal control problem in (8) the Hamiltonian is defined as
where is the costate vector. After analytically solving for the gradient of the Hamiltonian a gradient-based iterative solver can be used to solve for that minimizes the Hamiltonian and subsequently solves the optimal control problem in (8).
To solve the optimal control problem a gradient projection algorithm [31], [38], [39], is used. The detailed computation steps of the gradient projection algorithm can be found in [38], and summarized as in Table I for each time instant k.
Table I.
The NMPC-based DCA that uses gradient projection algorithm.
| 1 | Initialization: j = 0 |
| (a) | Set the convergence tolerance εj. |
| (b) | Choose initial control trajectory , where τ ∊ [t0, T]. |
| (c) | Integrate the system dynamics forward in time to solve for given and , where τ ∊ [t0, T]. |
| 2 | Gradient Step: |
| (d) | Integrate backward in time to solve for the costates λ(j) (τ) where is the terminal condition. |
| (e) | Compute the search direction, , from the Hamiltonian |
| (f) | Compute the step size,
|
| (g) | Compute the new control trajectory
, |
| (h) | Integrate the system dynamics forward in time (h1) solve for
given
, (h2) evaluate the cost function · |
| (i) | Check Quit Conditions(i1) quit if
, (i2) quit if j has exceeded the max iteration limit, Nt, (i3) otherwise set j = j + 1 and reiterate gradient step from (a). |
In this MPC-based DCA algorithm, a terminal cost function, V(∆x(T)) = ∆x(T)T P∆x(T), is used as a control Lyapunov function to ensure stability. The control Lyapunov condition is approximately satisfied by solving the algebraic Riccati equation [30], [38]
for the gain matrix P, where the matrices and are the linearized state-space dynamics of the nonlinear system, which are defined as
A terminal constraint could also have been used [40] to stabilize the system, but it can make the optimal control problem difficult and more time consuming to solve.
IV. Experiments
One person without SCI (labeled as S1; 30 year old, male, height 1.78m, weight 63.5kg) and one person with SCI (labeled as S2; 41 year old, male, height 1.70m, weight 70kg, with T10 AIS A paraplegia since 1994), participated in the study. Prior to any experiments, participant consent and approval from the Institutional Review Board of the University of Pittsburgh was obtained. S1 was instructed to remain relaxed during the procedures so that they would not influence the measurements with volitional muscle contractions. The experiments were performed using the modified leg extension machine shown in Fig. 2. The modified leg extension machine has an encoder (Hengxiang, CN) with 1024 pulses per revolution resolution to measure the joint angle, and a load cell (Omega, USA) to measure the joint torque. Also, the leg extension machine can be pinned in place and used for isometric contraction tests. A RehaStim 8-channel stimulator (Hasomed Inc., DE) was used to generate the biphasic pulse train to stimulate the muscles via surface electrodes, and a Harmonic Drive LPA-17-100-SP electric motor (Harmonic Drive, US) was used to generate torque. The Harmonic drive motor has a 100:1 gear ratio, a peak torque of 54Nm, and a maximum speed of 30rpm. Two sets of experiments were performed: 1) parameter estimation experiments and 2) DCA experiments.
Figure 2.
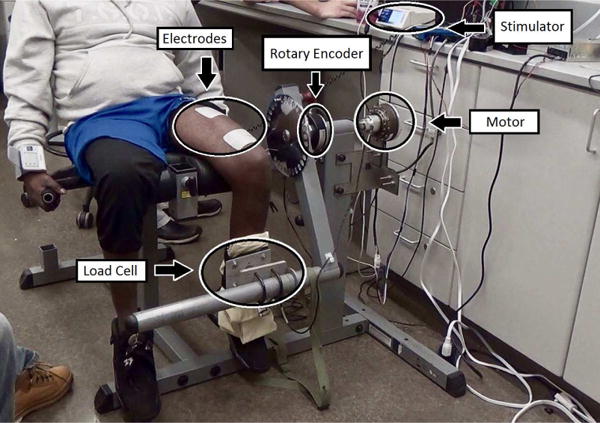
The modified hybrid neuroprosthesis system that combines FES quadriceps muscle with an electric motor.
A. Parameter Estimation
To implement the NMPC-based DCA method, the parameters of the dynamics in (7) must be estimated. The parameter estimation methods used in this paper were was also used in our previous work [27], and is based on the methods in [41]–[43]. The procedure for estimating the fatigue dynamics of the quadriceps muscles were based on methods in [36]. For all parameter estimation procedures, a biphasic 35Hz pulse train with a pulse width of 400μs was used as the wave form parameters of the pulse train. Six tests were performed in the modified leg extension machine to identify the musculoskeletal parameters. During the first five tests it was assumed that the duration of stimulation was short enough and sufficient time to rest were provided, so that muscle fatigue was assumed not to occur (this can be verified from the resulting, estimated muscle fatigue time constants), i.e. μ = 1 during these tests. Detailed descriptions of the parameter estimation procedures can be found in our previous work [27] as well as in the supplemental material.
The results of the parameter estimation for the both legs of the S1 participant (able-bodied) and both legs of S2 participant (with SCI) are shown in the Table II. The parameters in Table II are subject specific, and are specific to the stimulation pulse width and frequency used during the parameter estimation. During control validation experiments these stimulation parameters were kept constant and only the stimulation amplitude was input to the system. Small differences that can be seen between the right and left leg of each participant can possibly be attributed to asymmetry in the muscle structure between the participants right and left legs, and variations in positioning of the electrodes between each leg.
Table II.
Musculoskeletal parameters estimated for the right and left legs of each participant.
| Parameters of S1 | ||
|---|---|---|
| Parameter | Right Leg | Left Leg |
| It [mA] | 18.10 | 21.21 |
| Is [mA] | 60.00 | 60.00 |
| m [kg] | 4.69 | 4.68 |
| lc [m] | 0.37 | 0.37 |
| J [kg m2] | 0.19 | 0.18 |
| θeq [rads] | 1.20 | 1.18 |
| d1 [Nm] | 2.66×10−14 | 2.40×10−14 |
| d2 [Nm] | 1.68 | 3.50 |
| d3 [Nm] | 1.64 | 1.48×10−9 |
| d4 | 1.59 | 3.47 |
| d5 [Nm] | 0.76 | 4.37 |
| d6 | −39.09 | −39.97 |
| ϕ0 [rads] | 5.29×10−8 | 1.88×10−8 |
| c0 [Nm] | 78.78 | 80.36 |
| c1 [Nm] | 55.76 | 67.12 |
| c2 [Nm] | −49.02 | −56.25 |
| c3 | 1.44 | 1.04 |
| Ta [sec] | 0.26 | 0.25 |
| μmin | 2.61×10−9 | 3.15×10−9 |
| Tf [sec] | 29.17 | 30.14 |
| Tr [sec] | 48.09 | 41.50 |
| RMS [deg.] | 8.10 | 6.06 |
| Parameters of S2 | ||
|---|---|---|
| Parameter | Right Leg | Left Leg |
| It [mA] | 20.00 | 20.00 |
| Is [mA] | 70.00 | 70.00 |
| m [kg] | 2.10 | 2.59 |
| lc [m] | 0.18 | 0.16 |
| J [kg m2] | 0.18 | 0.24 |
| θeq [rads] | 1.30 | 1.24 |
| d1 [Nm] | 13.53 | 11.01 |
| d2 [Nm] | 1.95 | 2.01 |
| d3 [Nm] | 2.29×10−7 | 8.22×10−9 |
| d4 | 11.71 | 15.40 |
| d5 [Nm] | 2.59×10−6 | 0.99 |
| d6 | −6.40×10−5 | −21.27 |
| ϕ0 [rads] | 1.03 | 0.85 |
| c0 [Nm] | 51.08 | 30.37 |
| c1 [Nm] | −21.86 | 9.58 |
| c2 [Nm] | −17.49 | −17.49 |
| c3 | 1.69 | 0.90 |
| Ta [sec] | 0.41 | 0.50 |
| μmin | 6.54×10−2 | 2.55×10−10 |
| Tf [sec] | 9.34 | 24.89 |
| Tr [sec] | 68.19 | 71.46 |
| RMS [deg.] | 6.18 | 2.95 |
B. Dynamic Control Allocation Results
Experiments were run on both legs of S1 and both legs of S2, in which the knees were regulated to a desired angular position. The codes for the NMPC algorithm were compiled by C programming language, and they were embedded in Simulink® in the form of S-function. The discrete time step was set to be 0.01s, and the NMPC time horizon was chosen to be 0.5s. The desired angular position was set to be 40°. The desired inputs, which are supposed to be able to regulate the knee at the desired angular position, were computed based on the nominal model. The following experiments to evaluate the DCA-based control of a hybrid neuroprosthesis were performed within a few days of the parameter estimation procedures to ensure that the parameters used in the model-based controller were valid.
Four scenarios were designed to evaluate the regulation performance. (1) Motor-only: In this case only motor was used; (2) Motor and FES with constant ratio of desired inputs (fixed allocation): In this case motor and FES would cooperate with each other to regulate the knee. The DCA method balances the control performance and input while allocating the input efforts between motor and FES. Each input (motor and FES) would share 50% of the working load, i.e., the ratio of FES to motor is 1:1, and this ratio was kept constant through the experiment. (3) Motor and FES with varying ratio of desired inputs (varying allocation): This scenario is similar to (2), except that the desired input ratio was adapted as per the estimated fatigue. With the propagation of the muscle fatigue, desired motor input would share more work than FES, so that the muscle would have a chance to recover from the fatigue. This ratio updates automatically every 5 seconds based on , where μ ∈ [0, 1] is fatigue state defined in (6). (4) FES-only: In this scenario only FES was applied to the human leg. As the quadriceps muscle would get fatigued rapidly in this scenario, and no motor can share the load, this experiment was only run for 60 seconds for S1 and 30 seconds for S2, while other scenarios were run for 120 seconds for both participants. These cases were tested on different days to avoid creating bias in the results.
Fig. 3 demonstrates the regulation performance on the right leg of S1 and the left leg of S2. Table III summarizes the performance of the experiments for the right and left legs of both participants. Since the results for the right and left leg of each participant were qualitatively very similar only the results of the left leg of S1 and right leg of S2 will be plotted for brevity. Fig. 4 and Fig. 5 shows the control inputs and fatigue estimates during the four scenarios, respectively.
Figure 3.
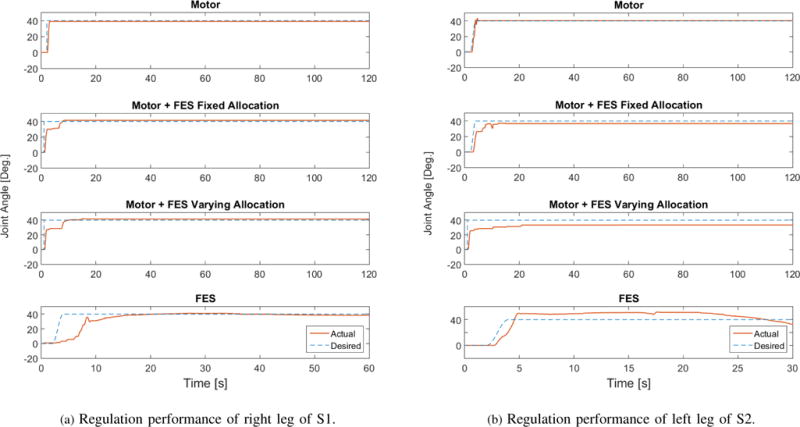
This figure shows the regulation performance of the two participants.
Table III.
Fits of parameter estimation for the both legs of each participant.
| Subject ID | S1R | S1L | S2R | S2L | Mean [deg.] |
|---|---|---|---|---|---|
| Scenario (1) RMS [deg.] | 2.69 | 2.45 | 3.29 | 1.20 | 2.40 |
| Scenario (2) RMS [deg.] | 3.60 | 7.43 | 5.09 | 4.68 | 5.20 |
| Scenario (3) RMS [deg.] | 3.99 | 9.00 | 6.67 | 7.90 | 6.88 |
| Scenario (4) RMS [deg.] | 9.23 | 8.32 | 9.87 | 9.30 | 9.18 |
| Mean [deg.] | 4.88 | 6.80 | 6.23 | 5.77 |
Figure 4.
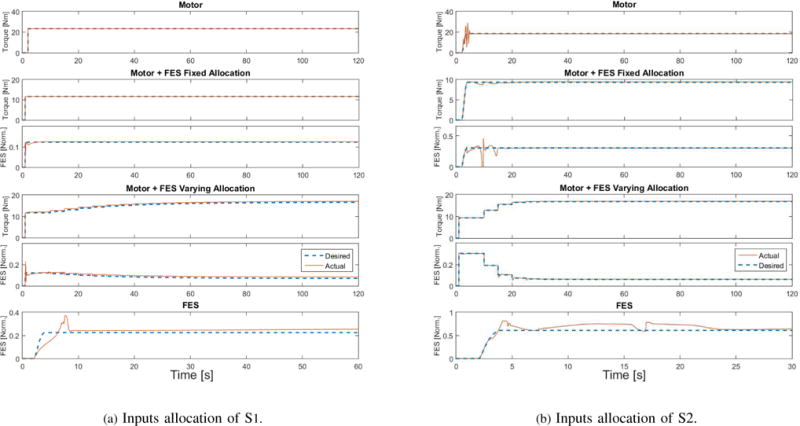
This figure shows the inputs applied to the right leg of S1 and left leg of S2. [Norm.] stands for normalized (no units). The dashed lines stand for desired control inputs, which were computed based on the musculoskeletal parameters as described in Section 4.2.
Figure 5.
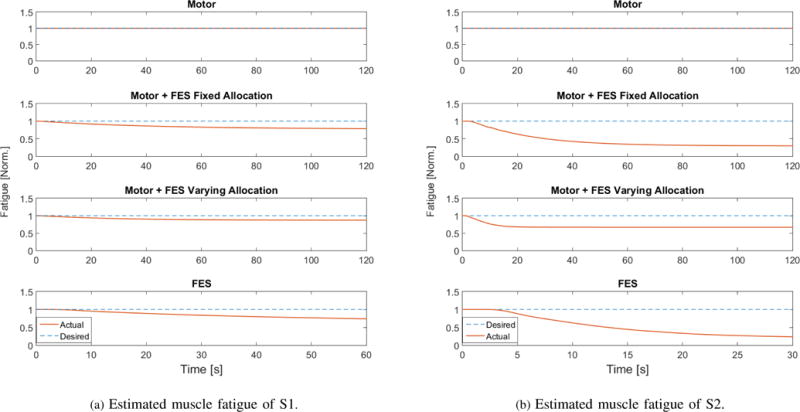
This figure shows the estimated muscle fatigue of the right leg of S1 and left leg of S2.
Because the fatigue, shown in Fig. 5, is only a model estimate, a post-experiment fatigue test was performed aiming to experimentally quantify the muscle fatigue effects. In this test, frequency and pulse width were kept the same as in the regulation test, except that the FES amplitude was set to be at the saturation level, which would recruit the maximum isometric torque. The tests were perfomed after 3 scenarios (Scenarios 1, 3, and 4). The decrease in the torque, which is shown in Fig. 6, indicates the residual torque levels after the regulation of each control scenario. A torque time integral (T-T) was used as a metric to measure the residual torque levels. The integrated joint torque also averages out any abnormal torque peaks. The initial torque levels at the start of the post-experiment fatigue test and at every 5 second intervals were also measured. The T-T and torque values for each scenario and the participants are listed in Table IV.
Figure 6.
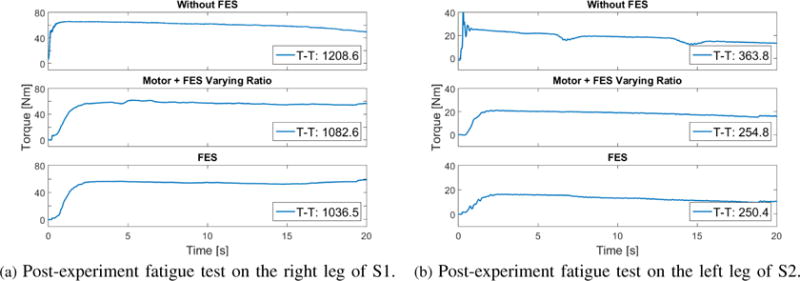
This figure shows the post-experiment fatigue test results after the 3 scenarios.
Table IV.
This table shows the T-T, measured peak torque, and measured torque every 5s for both participants in all the 3 scenarios.
| Scenario | No FES | Motor+FES | FES | |||
|---|---|---|---|---|---|---|
| S1R | S2L | S1R | S2L | S1R | S2L | |
| T-T [Nms] | 1208.6 | 363.8 | 1082.6 | 254.8 | 1036.5 | 250.4 |
| Peak [Nm] | 64.90 | 39.68 | 61.90 | 21.11 | 56.42 | 16.29 |
| 5s [Nm] | 64.85 | 21.88 | 60.92 | 19.99 | 56.08 | 15.82 |
| 10s [Nm] | 62.03 | 18.91 | 57.23 | 18.81 | 54.93 | 13.28 |
| 15s [Nm] | 58.62 | 12.72 | 54.56 | 17.16 | 52.63 | 11.16 |
| 20s [Nm] | 49.60 | 13.12 | 56.66 | 15.74 | 58.88 | 10.42 |
V. Discussion
The NMPC-based DCA control method was shown to regulate the knee extension. Unlike, the traditional high-bandwidth feedback control methods used in [12], [13], [25] for hybrid exoskeletons, control between the FES and the electric motor was simultaneously and optimally allocated. Importantly in Scenario 3, the DCA technique was shown to divert control from the FES to the electric motors as the muscles begin to fatigue, while maintaining the desired knee angle. Moreover, the motor torque recruited by the hybrid system was shown to be less than the motor-only system. This is consistent with the results obtained in [13], [25] that also show a decrease in the power consumption in the ‘with FES’ case compared to the ‘without FES’ case. We also found that the control performance was more accurate with the assistance of the electric motor than in the FES only case. For instance, the RMS of Scenario (2) was reduced by 43.3% compared to Scenario (4) (see Table. III).
Also to provide a qualitative measurement of muscle fatigue after the each scenario, post-experiment fatigue tests were conducted on the participants. As shown in Figs. 5 and 6 and Table IV, the fatigue-effects by the hybrid system were inferred to be lesser than the FES-only case and the least amount of fatigue was measured in the motor-only case. The torque values during the post-experiment (Scenario 4) fatigue test that was performed on the subject S1R remain pretty much plateaued except an increase at the end. It could be due to a sensor or voluntary disturbance during the force measurement. Overall, however, as seen in Table IV, the T-T and measured peak torque values are consistent with the aforementioned assertion, and the torque is also showing a decreasing trend. Note that although the FES-only cases (60 secs.) were run shorter than the other cases (120 secs.), the quadriceps muscles still seem to be more fatigued. According to the estimated fatigue shown in Fig. 5, the muscles of the S2 (participant with SCI) seem to be more fatigued than those of S1. Also, from Fig. 6 it seems that the torque (peak) value could be strongly affecting the T-T value than the plateau during the post fatigue experiment. This suggests it would have been interesting to measure the torque values before and after the controller experiments. Measuring drops in the torque values after the controller experiments could also be used as a metric to measure fatigue effects in addition to or instead of T-T values.
Limitations
In Fig. 3b, the joint angle error for the participant S2 is more in the ‘varying allocation’ case than in the ‘fixed allocation’ case. A decrease in performance in one of the experiments could be attributed to errors and limitations of the approach. One of the sources of error and limitations of this control method is that it is model dependent. In other words inaccuracies in the parameter estimation (e.g., variations resulting from positioning of electrodes, day-to-day parameter changes, etc.) will likely result in poor performance of the controller. Also, since the musculoskeletal system can change significantly over time, to be able to use this control method in a hybrid neuroprosthesis the parameter estimation must be performed regularly to ensure that the performance does not degrade. Another limitation of the controller presented in this paper is that it is only capable of regulation control. Regulation control is sufficient for sit-to-stand/stand-to-sit transfers, standing, and in between steps; however, further adaptions to the control method are required before it may be used for trajectory tracking control, which would be used for dynamic motions such as walking or stair climbing. To overcome these issues, an MPC approach for pure tracking task as well as a robust MPC approach to handle model uncertainties is needed for future work.
VI. Conclusion
In this paper a model based control allocation was developed for a hybrid neuroprosthesis device, which incorporates an electric motor to share the work load with FES. The advantage of this set-up is that it can alleviate effects of FES-induced muscle fatigue; thus the fatigue effects do not affect the overall performance of a neuroprosthesis. The control effort allocation was determined by an NMPC-based DCA method that used a gradient projection-based optimization algorithm. The experimental results on the knee joints of participants with and without SCI verified the performance of the proposed control method for the hybrid neuroprosthesis device. Motor torque requirements and fatigue estimation through different cases also validate the aforementioned advantages of the hybrid system. The results implied the potential of the hybrid technology for walking rehabilitation.
Supplementary Material
Acknowledgments
This work was funded by the NIH R03HD086529-01 and also in part by the NSF award numbers: 1462876 and 1511139.
Biographies

Nicholas Kirsch received a B.S. in mathematics with a physics minor from St. Vincent College in 2008. At the University of Pittsburgh he received a B.S. and M.S. in mechanical engineering, and then his Ph.D. in mechanical engineering for his research in restorative gait control under the advisement of Dr. Sharma. Nick is currently the senior robotics engineer at I am Robotics, USA.

Xuefeng Bao received a B.S. in physics from Xi’an Jiaotong University. He is currently pursuing a Ph.D. in mechanical engineering under the advisement of Dr. Nition Sharma.

Naji Alibeji received his Ph.D. from the Department of Mechanical Engineering and Material Science at the University of Pittsburgh in 2017 for his research in human motor control inspired control systems for a walking hybrid neuroprosthesis. As a graduate student, Naji received the 2014 best student paper award in robotics at the ASME DSC conference and was the recipient of the Swanson School of Engineering 2016 award for excellence as a ME research assistant. Naji is currently a Postdoctoral fellow at Case Western Reserve University where he is conducting research at the Advanced Platform Technologies center in control design for balanced standing/gait.

Brad E. Dicianno, MD is a physiatrist and bioengineer. He is an Associate Professor in the Department of Physical Medicine and Rehabilitation at the University of Pittsburgh School of Medicine and VA Pittsburgh Healthcare System. He serves as the Medical Director and COO of the Human Engineering Research Laboratories, Director of the Adult Spina Bifida Clinic, and Medical Director of the Center for Assistive Technology. His research interests focus on developing and studying interventions targeted to improving health and wellness in individuals with complex disabilities (wheelchairs, adaptive sports, telemedicine, virtual reality, and preventative care programs).

Nitin Sharma received his B.E. in Industrial Engineering in 2004 from Thapar University, India. He received his M.S. degree and Ph.D. degree in Mechanical Engineering from the Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, in 2008 and 2010, respectively. He was an Alberta Innovates-Health Solutions postdoctoral Fellow in the Department of Physiology at the University of Alberta, Edmonton, Canada. Since 2012, he is an Assistant Professor in the Department of Mechanical Engineering and Materials Science at the University of Pittsburgh. His research interests are modeling, optimization, and control of functional electrical stimulation-elicited walking. His current research in hybrid exoskeletons is funded by two NSF awards and one NIH R03 Award.
Footnotes
Digital Object Identifier: 10.1109/TNSRE.2017.2756023
Contributor Information
Nicholas A. Kirsch, Department of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA,USA 15261.
Xuefeng Bao, Department of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA,USA 15261.
Naji A. Alibeji, Department of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA, USA 15261
Brad E. Dicianno, Department of Physical Medicine and Rehabilitation Science, University of Pittsburgh, Pittsburgh, PA.
Nitin Sharma, Department of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA,USA 15261.
References
- 1.The National Spinal Cord Injury Statistical Center. Spinal cord injury (SCI) facts and figures at a glance. J Spinal Cord Med. 2015 [Google Scholar]
- 2.Kobetic R, Triolo R, Marsolais E. Muscle selection and walking performance of multichannel FES systems for ambulation in paraplegia. IEEE Trans Rehabil Eng. 1997;5(1):23–9. doi: 10.1109/86.559346. [DOI] [PubMed] [Google Scholar]
- 3.Bajd T, Kralj A, Turk R, Benko H, Šega J. The use of a four-channel electrical stimulator as an ambulatory aid for paraplegic patients. Phys Ther. 1983;63(7):1116–1120. doi: 10.1093/ptj/63.7.1116. [DOI] [PubMed] [Google Scholar]
- 4.Marsolais E, Kobetic R. Functional electrical stimulation for walking in paraplegia. J Bone Jt Surg. 1987;69(5):728–733. [PubMed] [Google Scholar]
- 5.Granat M, Ferguson A, Andrews B, Delargy M. The role of functional electrical stimulation in the rehabilitation of patients with incomplete spinal cord injury - observed benefits during gait studies. Spinal Cord. 1993;31(4):207–215. doi: 10.1038/sc.1993.39. [DOI] [PubMed] [Google Scholar]
- 6.Kobetic R, Triolo R, Uhlir JP, Bieri C, Wibowo M, Polando G, Marsolais EB, Davis JA, Ferguson KA, Sharma M. Implanted Functional Electrical Stimulation System for Mobility in Paraplegia: A Follow-Up Case Report. Rehabil Eng. 1999;7(4):390–398. doi: 10.1109/86.808942. [DOI] [PubMed] [Google Scholar]
- 7.Hardin E, Kobetic R, Murray L, Corado-Ahmed M, Pinault G, Sakai J, Bailey S, Ho C, Triolo R. Walking after incomplete spinal cord injury using an implanted FES system: a case report. J Rehabil Res Dev. 2007;44(3):333–346. doi: 10.1682/jrrd.2007.03.0333. [DOI] [PubMed] [Google Scholar]
- 8.Bickel C, Gregory C, Dean J. Motor unit recruitment during neuromuscular electrical stimulation: a critical appraisal. Eur J Appl Physiol. 2011;111(10):2399–2407. doi: 10.1007/s00421-011-2128-4. [DOI] [PubMed] [Google Scholar]
- 9.To C, Kobetic R, Schnellenberger J, Audu M, Triolo R. Design of a variable constraint hip mechanism for a hybrid neuroprosthesis to restore gait after spinal cord injury. IEEE/ASME Trans Mechatronics. 2008;13(2):197–205. [Google Scholar]
- 10.Isakov E, Douglas R, Berns P. Ambulation using the reciprocating gait orthosis and functional electrical stimulation. Spinal Cord. 1992;30(4):239–245. doi: 10.1038/sc.1992.62. [DOI] [PubMed] [Google Scholar]
- 11.Sharma N, Mushahwar V, Stein R. Dynamic Optimization of FES and Orthosis-based Walking using Simple Models. :1–29. doi: 10.1109/TNSRE.2013.2280520. [DOI] [PubMed] [Google Scholar]
- 12.Del-Ama A, Gil-Agudo A, Pons J, Moreno J. Hybrid FES-robot cooperative control of ambulatory gait rehabilitation exoskeleton. J Neuroeng Rehabil. 2014;11(1):1–15. doi: 10.1186/1743-0003-11-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ha K, Murray S, Goldfarb M. An approach for the cooperative control of fes with a powered exoskeleton during level walking for persons with paraplegia. IEEE Trans Neural Syst Rehabil Eng. 2015 doi: 10.1109/TNSRE.2015.2421052. [DOI] [PubMed] [Google Scholar]
- 14.Kirsch N, Alibeji N, Fisher L, Gregory C, Sharma N. A semi-active hybrid neuroprosthesis for restoring lower limb function in paraplegics. IEEE EMBC. 2014 doi: 10.1109/EMBC.2014.6944144. [DOI] [PubMed] [Google Scholar]
- 15.Quintero H, Farris R, Durfee W, Goldfarb M. Feasibility of a hybrid-FES system for gait restoration in paraplegics. IEEE EMBS. 2010:483–486. doi: 10.1109/IEMBS.2010.5627088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kirsch N, Alibeji N, Redfern M, Sharma N. Converging Clinical and Engineering Research on Neurorehabilitation II. Springer; 2017. Dynamic optimization of a hybrid gait neuroprosthesis to improve efficiency and walking duration: A simulation study; pp. 687–691. [Google Scholar]
- 17.Farris R, Quintero H, Goldfarb M. Preliminary evaluation of a powered lower limb orthosis to aid walking in paraplegic individuals. IEEE Trans Neural Syst Rehabil Eng. 2011;19(6):652–659. doi: 10.1109/TNSRE.2011.2163083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Esquenazi A, Talaty M, Packel A, Saulino M. The ReWalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury. Am J Phys Med Rehabil. 2012;91(11):911–921. doi: 10.1097/PHM.0b013e318269d9a3. [DOI] [PubMed] [Google Scholar]
- 19.Neuhaus P, Noorden J, Craig T, Torres T, Kirschbaum J, Pratt J. Design and evaluation of Mina: a robotic orthosis for paraplegics. IEEE Int Conf Rehabil Robot. 2011:1–8. doi: 10.1109/ICORR.2011.5975468. [DOI] [PubMed] [Google Scholar]
- 20.Strausser K, Kazerooni H. The development and testing of a human machine interface for a mobile medical exoskeleton. IEEE/RSJ Int Conf Intell Robot Syst. 2011:4911–4916. [Google Scholar]
- 21.Strickland E. Good-bye, wheelchair. IEEE Spectr. 2012;49(1):30–32. [Google Scholar]
- 22.Durfee W, Hausdorff J. Regulating knee joint position by combining electrical stimulation with a controllable friction brake. Annals of biomedical engineering. 1990;18(6):575–596. doi: 10.1007/BF02368449. [DOI] [PubMed] [Google Scholar]
- 23.Goldfarb M, Korkowski K, Harrold B, Durfee W. Preliminary evaluation of a controlled-brake orthosis for FES-aided gait. IEEE Trans Neural Syst Rehabil Eng. 2003;11(3):241–248. doi: 10.1109/TNSRE.2003.816873. [DOI] [PubMed] [Google Scholar]
- 24.Kobetic R, To C, Schnellenberger J, Audu M, Bulea T, Gaudio R, Pinault G, Tashman S, Triolo R. Development of hybrid orthosis for standing, walking, and stair climbing after spinal cord injury. J Rehabil Res Dev. 2009;46(3):447–462. [PubMed] [Google Scholar]
- 25.Quintero H, Farris R, Ha K, Goldfarb M. Preliminary assessment of the efficacy of supplementing knee extension capability in a lower limb exoskeleton with FES. IEEE EMBC. 2012:3360–3363. doi: 10.1109/EMBC.2012.6346685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kirsch N, Alibeji N, Sharma N. ASME Dyn Syst Control Conf. San Antonio, TX: 2014. Model predictive control-based dynamic control allocation in a hybrid neuroprosthesis. [Google Scholar]
- 27.Kirsch N, Alibeji N, Sharma N. Nonlinear model predictive control of functional electrical stimulation. Control Eng Pract. Accepted. [Google Scholar]
- 28.Mayne D, Rawlings J, Rao C, Scokaert P. Constrained model predictive control: stability and optimality. Automatica. 2000;36(6):789–814. [Google Scholar]
- 29.Camacho E, Alba C. Model predictive control. Springer; 2013. [Google Scholar]
- 30.Graichen K, Kugi A. Stability and incremental improvement of suboptimal MPC without terminal constraints. IEEE Trans Automat Contr. 2010;55(11):2576–2580. [Google Scholar]
- 31.Käpernick B, Graichen K. The gradient based nonlinear model predictive control software GRAMPC. IEEE Eur Control Conf. 2014:1170–1175. [Google Scholar]
- 32.Popović D, Stein R, Namik Oguztoreli M, Lebiedowska M, Jonic S, Joni S. Optimal control of walking with functional electrical stimulation: a computer simulation study. IEEE Trans Rehabil Eng. 1999;7(1):69–79. doi: 10.1109/86.750554. [DOI] [PubMed] [Google Scholar]
- 33.Ding J, Wexler A, Binder-Macleod S. A predictive fatigue model. I. Predicting the effect of stimulation frequency and pattern on fatigue. IEEE Trans Rehabil Eng. 2002;10(1):48–58. doi: 10.1109/TNSRE.2002.1021586. [DOI] [PubMed] [Google Scholar]
- 34.Ding J, Wexler A, Binder-Macleod S. A predictive fatigue model. II. Predicting the effect of resting times on fatigue. IEEE Trans Neural Syst Rehabil Eng. 2002;10(1):59–67. doi: 10.1109/TNSRE.2002.1021587. [DOI] [PubMed] [Google Scholar]
- 35.Veltink P, Chizeck H, Crago P, El-Bialy A. Nonlinear joint angle control for artificially stimulated muscle. IEEE Trans Biomed Eng. 1992;39(4):368–380. doi: 10.1109/10.126609. [DOI] [PubMed] [Google Scholar]
- 36.Riener R, Quintern J, Schmidt G. Biomechanical model of the human knee evaluated by neuromuscular stimulation. J Biomech. 1996;29(9):1157–1167. doi: 10.1016/0021-9290(96)00012-7. [DOI] [PubMed] [Google Scholar]
- 37.Ross I. A primer on Pontryagin’s Principle in optimal control. Collegiate Publishers; 2009. [Google Scholar]
- 38.Graichen K, Käpernick B. A real-time gradient method for nonlinear model predictive control. INTECH Open Access Publisher; 2012. [Google Scholar]
- 39.Luenberger D, Ye Y. Linear and nonlinear programming. Springer Science & Business Media; 2008. [Google Scholar]
- 40.Chen H, Allgöwer F. A quasi-infinite horizon nonlinear model predictive control scheme with guaranteed stability. Automatica. 1998;34(10) [Google Scholar]
- 41.Stein R, Zehr E, Lebiedowska M, Popovic D, Scheiner A, Chizeck H. Estimating mechanical parameters of leg segments in individuals with and without physical disabilities. IEEE Trans Rehabil Eng. 1996;4(3):201–211. doi: 10.1109/86.536776. [DOI] [PubMed] [Google Scholar]
- 42.Scheiner A, Stein R, Ferencz D, Chizeck H. Improved models for the lower leg in paraplegics. Proc 15th Annu Int Conf IEEE Eng Med Biol Soc. 1993:1151–1152. [Google Scholar]
- 43.Tomović R, Popović D, Stein R, Tomović R, Popović D. Nonanalytical methods for motor control. World Scientific; 1995. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


