Abstract
Background
Several mapping or cross-walking algorithms for deriving utilities from the European Organisation for Research and Treatment of Cancer Quality of Life Questionnaire for Cancer (EORTC QLQ-C30) scores have been published in recent years. However, the large majority used ordinary least squares (OLS) regression, which proved to be not very accurate because of the specifics of the quality-of-life measures.
Objective
Our objective was to compare regression methods that have been used to map EuroQol 5 Dimensions 3 Levels (EQ-5D-3L) utility values from the general EORTC QLQ-C30 using OLS as a benchmark while fixing the number of explanatory variables and to explore an alternative three-part model.
Methods
We conducted a regression analysis of predicted EQ-5D-3L utilities generated using data from an observational study in ambulatory patients with non-small-cell lung cancer in a Toronto hospital. Six alternative regression methods were compared with a simple OLS regression as benchmark. The six alternative regression models were Tobit, censored least absolute deviation, normal mixture, beta, zero–one inflated beta and a mix of piecewise OLS and logistic regression.
Results
The best predictive fit was obtained by a mix of OLS regression(s) for utilities lower than 1 with a cut-off point of 0.50 and a separate binary logistic regression for utilities equal to one. Zero–one inflated beta regression was also promising. However, OLS regression proved to be the most accurate for the mean. The prediction of utilities equal to one was poor in all regression approaches.
Conclusions
Three-part regression methods that separately target low, medium and high (<0.50, 0.51–0.99 or 1) utilities seem to have better prediction power than OLS with EQ-5D-3L data, although OLS also seems quite robust. Exploration of three-part approaches compared with single (OLS) regression should be further tested in other similar datasets or using individual pooled data from various clinical or observational studies. The use of alternative goodness-of-fit measures for mapping studies and their influence on the choice of the best performing methods should also be investigated.
Electronic supplementary material
The online version of this article (doi:10.1007/s41669-017-0049-9) contains supplementary material, which is available to authorized users.
Key Points For Decision Makers
| Mapping EuroQol-5 Dimensions (EQ-5D) utilities from cancer-specific non-preference measures have used ordinary least squares regression and, more recently, a variety of more complex statistical regression methods. |
| We have shown that these should be rejected in favour of three-part models that are more able to take into account the tri-modal distribution of the 3-level (EQ-5D-3L) measures. |
| Further research should be undertaken to validate our results in other cancer data and with the more recent 5-level (EQ-5D-5L) questionnaire. |
Introduction
Study Rationale
Economic evaluation of medical technology often emphasizes that outcomes be expressed in terms of quality-adjusted life-years (QALYs). In cancer, the main accepted primary long-term endpoints are overall survival and disease- or progression-free survival; however, the aggressiveness of the treatments means health-related quality of life (HRQOL) is often also measured using various disease-specific questionnaires such as the European Organisation for Research and Treatment of Cancer Quality-of-Life Questionnaire for Cancer (EORTC QLQ-C30) or the Functional Assessment of Cancer Therapy-General (FACT-G) and their variants.
As clinical trials or other clinical studies do not often collect preference-based measures, statistical mapping would provide a statistical model or formula that allows the estimation of utilities and the subsequent calculation of QALYs in clinical studies that do not use any preference-based HRQOL instrument, provided it has a good predictive accuracy.
We previously showed that current ordinary least squares (OLS)-based mapping algorithms showed poor external validity [1, 2].
Study Objective
While most previous studies used OLS regression, more complex methods such as beta-binomial (BB), normal mixture (NMIX) and beta-regression have recently been proposed in the mapping literature.
The aims of the current exploratory study were to compare these existing regression methods that have been used to map EuroQol 5 Dimensions 3 Levels (EQ-5D-3L) utility values from the general EORTC QLQ-C30 using OLS as benchmark while fixing the number of explanatory variables and to propose a possible simple three-part method in practice.
Reporting and article structure followed the recent Mapping onto Preference-based measures reporting Standards (MAPS) recommendations [3].
Methods
Patient Population and Setting
Estimation Sample
Jang et al. [4] collected QLQ-C30 and EQ-5D-3L data from a sample (N = 172) of ambulatory patients with mainly stage III/IV non-small cell lung cancer (NSCLC) who were relapse free post-resection with or without undergoing chemotherapy or combined radio-chemotherapy in a single major Canadian centre in Toronto on a single visit in 2009.
The mean age of the patients was 66 years, 46.5% were male, and the mean EQ-5D utility score was 0.76 ± 0.20 (valued by the D2 US valuation tariff of Shaw et al. [5]).
The mean QLQ-C30 scores were equal to ‘physical function’ (PF) 3.25; ‘role function’ (RF) 67.44; ‘emotional function’ (EF) 75.19; ‘cognitive function’ (CF) 79.84; ‘social function’ (SF) 73.16; and overall quality of life (QOL) 65.89. Most symptom scores were relatively low (<0.30), except for fatigue 40.83; dyspnoea 31.20 and insomnia 34.88, reflecting the expected symptoms profile of this population (for further details, see Jang et al. [4]). We re-analysed these data using instead the original UK EQ-5D-3L valuation tariff [6].
Jang et al. [4] performed a simple OLS regression with all the QLQ-C30 scores (called the full model) and a second one limited to a number of significant variables from the full regression (called the reduced model).
External Validation Sample
Given the exploratory nature of this study and the small number of observations, no external validation sample was used.
Instruments Description
Source and Target Measures
The EORTC QLQ-C30 version 3 is a cancer-specific patient-administered questionnaire of 30 questions (items) scored from 1 (very poor) to 7 (excellent) and incorporates five functional multi-item dimensions (PF, RF, CF, EF and SF); three symptom domains (fatigue, pain and nausea/vomiting); and a Global Health Status/QOL score (two items). A further six single items, mainly tracking symptoms, are also included (dyspnoea, insomnia, appetite loss, constipation, diarrhoea and financial difficulties).
The QLQ-C30 functional domain scores and item (i.e. symptom) scores can be standardized from the raw item scores to have a 0–100 range through a linear transformation. The combined HSQOL score was constructed as the average of the ‘health status’ (HS) and overall QOL scores.
For functional scores, a high score means a high level of functioning, whereas a high symptom score means a high level of symptom severity. The functional and symptom scores were constructed following the EORTC published scoring manual [7], resulting in a total of 15 distinct variables (five functions, eight symptoms, one overall QOL, one financial impact).
The EQ-5D-3L provides a simple descriptive QOL profile or vector of five items (mobility, self-care, usual activities, pain/discomfort and anxiety/depression) with three levels. Each individual EQ-5D-3L profile can be translated into utilities by applying country-specific general population-elicited ‘tariffs’ to generate a single utility index [5].
The EQ-5D-3L utilities were constructed using the original UK tariff instead of the original US tariff used by Jang et al. [4] to enhance comparisons, as this is the most widely used tariff in published mapping studies to date, and applied to the observed EQ-5D-3L health dimensions.
Statistical Analysis
Exploratory Analysis
However, the overlap of EQ-5D-3L items with those of the QLQ-C30 scores is only partial. To explore the overlap, we performed a non-parametric Spearman rank correlation analysis at a function/item level between the two.
Missing Data
All records were used; there were no missing data in the available dataset.
Modelling Approaches
Mapping methods can be divided into regression-based and non-regression methods (for an early literature review, see Mortimer and Segal [8]). Regression-based methods can be further subdivided into direct one-step models that estimate the target utility value or two-step models that estimate first the response level for each item of the multiple attribute utility (MAU) target measure and then apply a tariff formula to the estimated responses.
We then regressed all QLQ-C30 functional scores on the observed EQ-5D-3L utilities and reran the OLS regression with the restricted model-retained variables to get our benchmark OLS algorithm. As the goodness-of-fit (GOF) measures of the OLS regression between the full and reduced model were very close, we chose to use the reduced model for further analysis because including additional variables would not provide new information.
Six different regression methods were used to predict EQ-5D-3L utilities from the QLQ-C30 functional scores using OLS as benchmark. The other approaches were Tobit, censored least absolute deviation (CLAD), beta regression (BB), zero-one inflated beta regression (ZOIB), Gaussian Mixture (NMIX) with two or three components, and a three-part piecewise linear (PWL), comprising two separate OLS and one logistic regression to cover the most common as well as some more recent published mapping regression models for the QLQ-C30.
We did not investigate a response-level model, as this was outside the scope of this article [9, 10]. All calculations were conducted in STATA® version 14.
Estimation of Predicted Utilities
For ease of comparison between the different regression methods, the predictive variables were fixed in all regressions to include only the physical, emotional and pain QLQ-C30 scores as these corresponded to the original reduced model from Jang et al. [4] (except for role functioning, see Table 1); based on the results of a preliminary OLS regression involving all the QLQ-C30 functional and symptom scores and comparing its results with a reduced model by means of a likelihood ratio (LR) test.
Table 1.
Original non-small-cell lung cancer ordinary least squares results (Jang et al. [4]) with USA tariff compared with UK tariff regression
| Variables | Jang et al. [4] USA full modela |
UK tariff full model | Jang et al. [4] USA reduced modela |
UK tariff reduced model |
|---|---|---|---|---|
| Intercept | 0.3381 | 0.1873 (p = 0.177) | 0.4029 | 0.1963*** (p = 0.016) |
| Physical functioning (PF) | 0.0035*** | 0.0051*** (p = 0.000) | 0.0039*** | 0.0058*** (p = 0.000) |
| Role functioning (RF) | 0.0007 | 0.0011 (p = 0.158) | 0.0008*** | |
| Emotional functioning (EF) | 0.0011*** | 0.0016* (p = 0.064) | 0.0015*** | 0.0019*** (p = 0.005) |
| Cognitive functioning (CF) | 0.0007 | 0.0005 (p = 0.575) | ||
| Social functioning (SF) | −0.0007 | −0.0013 (p = 0.100) | −0.0007 | |
| Global health status/QOL (HSQOL) | 0.0009 | 0.0009 (p = 0.448) | ||
| Fatigue (FA) | 0.0003 | 0.0003 (p = 0.784) | ||
| Nausea and vomiting (NV) | −0.0002 | −0.0005 (p = 0.693) | ||
| Pain (PA)*** | −0.0021** | −0.0032*** (p = 0.000) | −0.0021** | −0.0034*** (p < 0.0001) |
| Dyspnoea (DY) | −0.0001 | −0.0002 (p = 0.735) | ||
| Insomnia (SL) | −0.0001 | −0.0002 (p = 0.712) | ||
| Appetite loss (AP) | −0.0001 | −0.0003 (p = 0.656) | ||
| Constipation (CO) | 0.0005 | 0.0006 (p = 0.267) | ||
| Diarrhoea (DI) | 0.0004 | 0.0006 (p = 0.380) | ||
| Financial difficulties (FI) | −0.0001 | −0.0001 (p = 0.494) |
* p < 0.10, ** p < 0.05, *** p < 0.01
a p values not published
The emphasis is therefore placed on the comparison between the different regression methods and not on providing a mapping algorithm as such (which would involve using all QLQ-C30 scores with a variable number of variables ultimately possibly being retained in each regression and exploring various functional forms of the regression equations).
Measures of Model Performance
First, the predicted utilities were plotted and visually compared with the observed utilities in a series of plots.
Second, the mean, standard deviation, median and upper and lower quintiles of the mapped utilities were compared with the original observed utilities. This allowed us to judge the bias and precision of the estimates.
Finally, a series of GOF statistics were calculated and summarized. These were mean absolute error (MAE), root mean squared error (RMSE) (or sigma for Tobit regression), the number of absolute errors >0.05 as an indication of minimal clinical important difference (MCID) and the number of estimated observations greater than one and lower than zero.
Validation Methods
Given the exploratory nature of this study and the small number of available observations, no in-sample cross-validation or external validation sample was performed. Generally, in-sample validation is of limited use as it preserves the internal structure of the data, which is not the case with independent external samples. It is our intent to explore this aspect in further research using a set of different external NSCLC patient samples.
Results
Exploratory Analysis
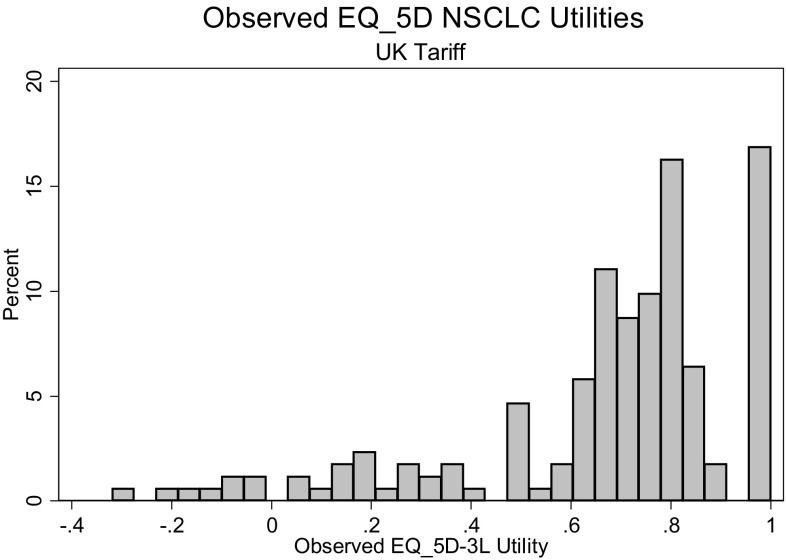
Typical of EQ-5D-3L utilities, we observed a large ceiling effect, a gap around 0.90 and a left skew with some negative observations and a clustering of values in the 0.60–0.85 range [mean 0.667; median 0.743; standard deviation (SD) 0.285; skewness −1.365; kurtosis 4.564] (Table 2).
Table 2.
Pearson correlations between QLQ-C30 scores and EQ-5D-3L for significant variables in the full model by Jang et al. [4] (all p < 0.001)
| QLQ-C30/EQ-5D-3L | Mobility | Self-care | Usual activity | Pain/discomfort | Depression/anxiety |
|---|---|---|---|---|---|
| Physical function (PF) | −0.603 | −0.595 | −0.609 | −0.427 | −0.268 |
| Role function (RF) | −0.415 | −0.391 | −0.683 | −0.412 | −0.213 |
| Emotional function (EF) | −0.162 | −0.286 | −0.374 | −0.350 | −0.590 |
| Social function (SF) | −0.277 | −0.305 | −0.516 | −0.391 | −0.232 |
| Fatigue (FA) | +0.469 | +0.380 | +0.555 | +0.501 | +0.256 |
| Pain (PA) | +0.275 | +0.348 | +0.366 | +0.699 | +0.256 |
| Dyspnoea (DY) | +0.372 | +0.301 | +0.453 | +0.278 | +0.167 |
The tri-modal aspect of the distribution is apparent with a long lower tail, a clustering at medium values and a high upper ceiling effect (Fig. 1).
Fig. 1.
Observed EQ-5D-3L utility values
Mapping still requires checking for some concordance between the dimensions of both questionnaires [11].
As one would expect, the pain items were highly correlated in both scales.
Fatigue symptoms were associated at more or less the same degree with mobility, usual activities and pain/discomfort, whereas dyspnoea was only associated with usual activity performance but not strongly with mobility (rho 0.35).
PF impairment was relatively highly associated with performing usual activities and somewhat lesser with mobility and self-care, as was RF except for self-care.
EF was clearly associated with depression/anxiety in the EQ-5D-3L.
Clearly, fatigue and diminished PF (which are themselves correlated, rho 0.68) have the broadest impact on the EQ-5D-3L dimensions, and there is strong one-to-one relationship between the items for pain and depression.
Dyspnoea is probably specific to this lung cancer patient population and was only moderately correlated with usual activity performance.
Some of the above QLQ-C30 items were also moderately to highly cross-correlated (ρ > 0.50–0.70), with some others such as PF with EF, fatigue and dyspnoea, RF with SF and fatigue, SF with fatigue, and finally fatigue with pain.
These inter-item correlations in the QLQ-C30 mean that some multicollinearity might be present when performing regressions using all the QLQ-C30 scores.
Individual Model Coefficients
Benchmark Ordinary Least Squares Regression on Non-Small-Cell Lung Cancer
We only retained the explanatory variables with p values <0.10 from the overall linear regression including all QLQ-C30 scores. The number of retained variables set using UK tariff values is more restricted than the original restricted formula published by Jang et al. [4] using a USA valuation tariff, i.e. respectively, PF-EF-PA versus PF-RF-EF-PA, with RF becoming non-significant. However, remarkably, the overall explained variance of the reduced model was similar (adjusted R 2 0.58), with barely a change in the adjusted R 2 compared with the full model and a similar RMSE of 0.187 and equal to that obtained by Jang et al. [4] (adjusted R 2 0.57 and 0.58 for the full and reduced linear models, respectively). The GOF statistics of the full and reduced UK tariff benchmark OLS model are presented in Table 3.
Table 3.
Goodness of fit measures for the full and reduced ordinary least squares regression non-small-cell lung cancer model (UK tariff)
| Adj-R 2 | Log-likelihood | AIC | BIC | RMSE | |
|---|---|---|---|---|---|
| Full model | 0.58 | 48.5 | −89.0 | −76.4 | 0.1847 |
| Reduced model | 0.57 | 52.77 | −73.6 | −23.2 | 0.1869 |
AIC Akaike information criterion, BIC Bayes information criterion, RMSE root mean square error
As the adjusted R 2 and RMSE were very close, we performed a classical LR test (χ 2 = 8.55, p = 0.74), which indicated the reduced model was not different from the full one; therefore, we decided to use the reduced model as our benchmark [12].
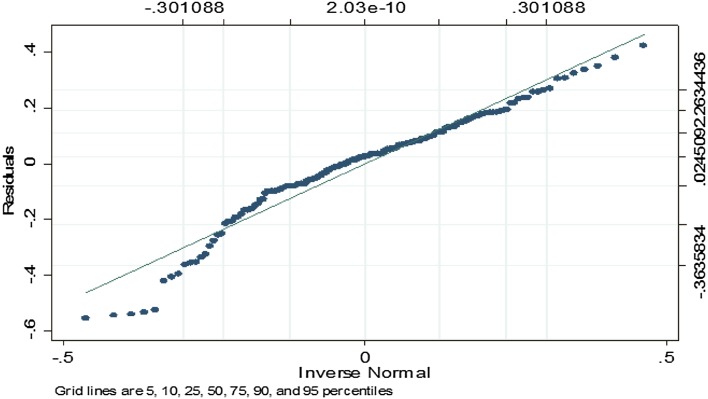
We also plotted the residuals to assess departure from normality (Fig. 2).
Fig. 2.
Normal quantile plot of residuals in benchmark non-small-cell lung cancer reduced ordinary least squares model
Clearly at the lower end of the quantile plot, residuals deviate from the normal quantile line but are otherwise rather well behaved.
We also formally tested for the presence of heteroscedasticity of the residuals and their normality by applying the Breusch–Pagan test and the Shapiro–Wilks test on the OLS residuals (Table 4).
Table 4.
Benchmark ordinary least squares model tests for heteroscedasticity and normality of residuals
| Breusch–Pagan test | Shapiro–Wilks test | Prob > z | |||||
|---|---|---|---|---|---|---|---|
| Variable χ 2 | χ 2 | p value | W | V | z | ||
| df | p | ||||||
| Physical functioning | 18.98 | 0.0000a | – | – | – | ||
| Emotional functioning | 12.58 | 0.0012a | – | – | – | ||
| Pain | 14.65 | 0.0004a | – | – | – | ||
| Simultaneous | 25.51 | 0.0000 | 0.95326 | 6.117 | 4.135 | 0.00002 | |
aBonferroni corrected
The assumption of homoscedasticity and normality of the residuals are rejected, with mainly a large non-normal residuals tail, which in theory leads to biased OLS estimators.
One can also see clearly that the estimated OLS utilities overestimate the ‘true’ observed utilities below 0.50 and underestimate utilities equal to one with the ‘best’ fitting occurring in the interval 0.50–0.85. Notice also the gap around 0.90 inherent to the UK Tariff valuation.
In the following sections, we present the results of alternative regression methods using the same reduced model. This allows us to estimate a ‘pure method’ effect compared with OLS without introducing additional explanatory variables.
Tobit Regression
We find very comparable results as in OLS and a somewhat improved fit for utilities equal to one. [see Appendix 4 and Fig. S1 in the Electronic Supplementary Material (ESM)].
CLAD regression
Visually, CLAD regression with a lower limit set at −0.319 does not seem to improve the fit much compared with OLS, with the fit perhaps even slightly worse for lower utilities (see Appendix 4 and Fig. S2 in the ESM).
Normal Mixture Regression
We first fitted an uncensored NMIX model with two and three components to the data. Compared with the two-component model, barely any difference can be distinguished between the two-component and three-component mixture models (see Appendix 4 and Figs. S3, S4 and S5 in the ESM). However, the fit for utilities = 1 was still poor in both models and did not improve in the three-component model.
Beta Regression
We also fitted a simple beta regression as proposed by Hunger et al. [13] using a maximum likelihood procedure (Betafit procedure in Stata).
We first transformed the utility range to constrain the data in the range ]0,1[ by applying the formula Uscale_UKbeta = (Uscale_UK × (172 − 1) + 0.5)/172 [14].
This generated a more constrained range of utilities with mean 0.675 (±0.283) very similar to the original data but with a maximum of 0.997 instead of 1. However, there were still eight observations with negative values, which were discarded from the regression.
No significant improvement in GOF seems to appear except for a slightly better fit for lower utilities (see Appendix 4 and Fig. S5 in the ESM).
Beta-Binomial Regression
Recently, some authors used a BB regression similar in some respects to the zero–one inflated beta (ZOIB) model for mapping purposes [15, 16].
We performed a similar regression using the ZOIB procedure in Stata [17] by putting all negative utility values equal to zero and considering only a one-inflated model.
This is obviously one of the drawbacks of all beta-regression approaches, as they are constrained to a [0, 1] interval. However, it did seem to improve somewhat the fit for low utility values compared with a simple beta-regression approach (see Appendix 4 and Fig. S6 in the ESM).
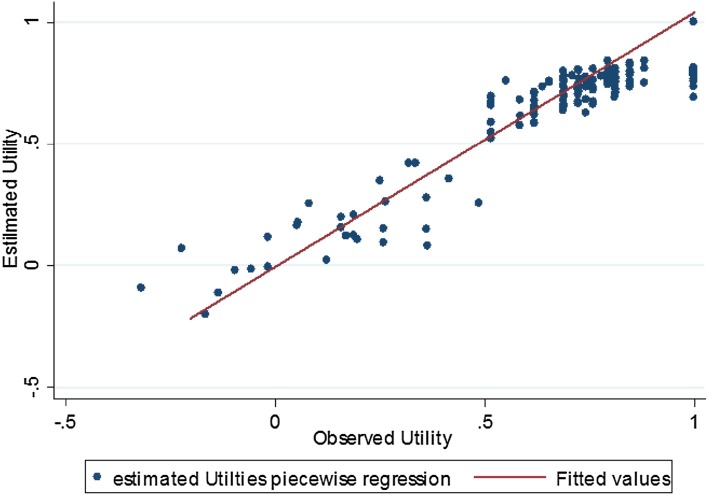
Piecewise Linear Regression
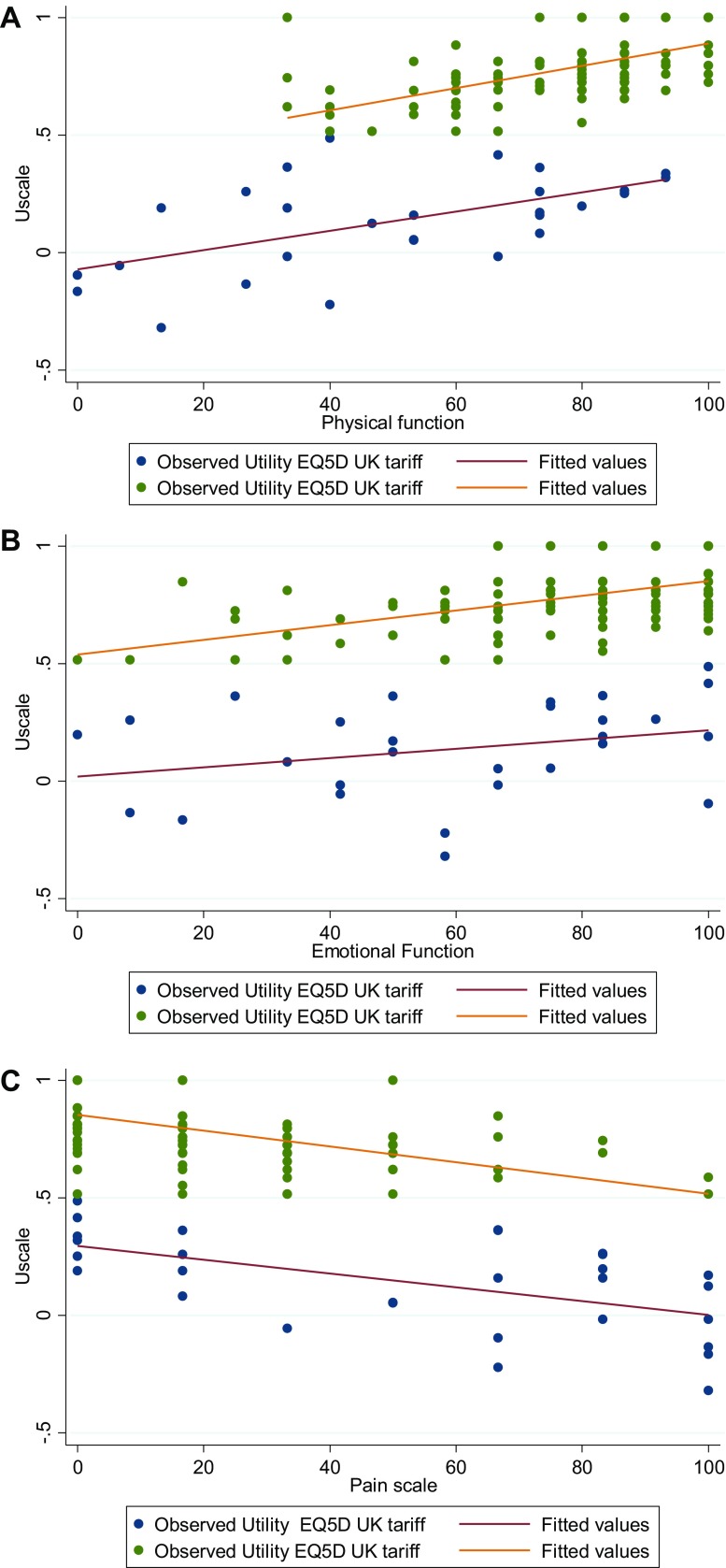
To construct a piecewise linear regression, we split the sample at 0.50 (following the OLS results in Fig. 3) to separate low utilities and higher utilities as demonstrated by Versteegh et al. [18]. Likewise, we separated utilities equal to one from the rest.
Fig. 3.
Predicted versus observed utilities in non-small-cell lung cancer ordinary least squares benchmark model. Diagonal line indicates the perfect fit
We therefore had three separate subgroups to estimate, with utilities ranging from −0.319 to 0.50, from 0.51 to 0.99 and equal to one.
We first used a logistic regression to predict which observations would be equal to one by setting all other observations equal to zero to obtain a binary dataset. We then regressed all QLQ-C30 functional scales on the binary utility outcome (0–1) to obtain a predictive fit (see the tables in the appendix in the ESM).
The two other subgroups were then estimated separately by OLS using only the three retained significant scores from the reduced benchmark OLS regression, as we expected a difference in the coefficients between the low and high utility subgroups.
As can be seen, the slopes of the regression lines were nearly identical between the low and high utility groups for all three scores (Fig. 4).
Fig. 4.
Low-high utilities separate regressions: a QLQ-C30 physical function (PFscore); b QLQ-C30 emotional function (EFscore); c QLQ-C30 pain score (PAscore)
We then joined the predictions of all three sub-models and compared the results with the original utility values (Fig. 5).
Fig. 5.
Predicted versus observed utilities in non-small-cell lung cancer: piecewise linear model. Diagonal line indicates the perfect fit
The piecewise OLS regression on utility values below one gave quite a good fit, with a nearly identical slope for the low and high regression lines in all cases. However, the logistic regression failed to adequately predict a number of observations with utility equal to one.
Even with the whole set of QLQ-C30 functional and symptom scores as predictors, the sensitivity was only equal to 0.52 with no more of 14 of the 29 observations correctly predicted, although specificity was high (0.95) (see Appendix 1 in the ESM). This is because a number of observations with observed utilities equal to one presented with some relatively low function scores and therefore these observations were not adequately predicted. Nevertheless, for other utility values than one, this approach seemed to give quite a good overall fit compared with OLS.
Summary of Goodness-of-Fit Measures Across Regression Methods
When looking at the regression coefficients per regression method (Table 5), we observed a relative closeness of the OLS, Tobit and CLAD coefficients but a much more pronounced difference between the simple and ZOIB approaches, whereas the two NMIX components are clearly different, as are the high and low parts of the piecewise regression. However, the odds ratios in the logistic regression are barely different from one, indicating a poor predictive value of the function scores for patients with utility equal to one.
Table 5.
Regression coefficients per regression method
| Dep variable | OLS | Tobit | CLAD | NMIX component 1 | NMIX component 2 | Simple beta | ZOIB | Piecewise linear logit | Piecewise linear OLS – low | Piecewise linear OLS – high |
|---|---|---|---|---|---|---|---|---|---|---|
| PFscore | 0.0058 | 0.0064 | 0.0059 | 0.0068 | 0.0031 | 0.0232 | 0.0156 | 0.6083 | −0.0053 | +0.0022 |
| EFscore | 0.0018 | 0.0021 | 0.0014 | 0.0034 | 0.0010 | 0.0104 | 0.0056 | 0.0350 | −0.0010 | +0.0010 |
| PAscore | −0.0033 | −0.0037 | −0.0033 | −0.0041 | −0.0016 | −0.0149 | −0.0092 | −0.0619 | +0.0033 | −0.0010 |
| Constant | 0.196 | 0.159 | 0.251 | −0.0594 | 0.493 | −1.1748 | −0.7221 | −8.882 | +0.5528 | 0.5085 |
As our emphasis is on the choice between regression methods and their likeness with a fixed set of explanatory variables and not to provide a usable mapping algorithm as such for the QLQ-C30, we chose not to present the confidence intervals in this table. All coefficients in all regressions were significant at the p = 0.05 level with narrow confidence intervals
CLAD censored least absolute deviation, EFscore emotional function, NMIX normal mixture, OLS ordinary least squares, PAscore pain, PFscore physical function, ZOIB zero–one inflated beta
Model Performance
The three-part model scored better on most validation statistics in Table 6, except for the mean utility estimation. The lower mean of the piecewise regression is partly due to the choice of the replacement estimated utility for the 18 observations with a mismatch between the binary utility estimation by the logistic regression and the observed utility (observed 1, estimated 0). In those cases, we substituted the predicted utility by its estimated value from the high utilities (range 0. 51–0.90) OLS regression. However, this underestimates the true utility value (mean 0.784, range 0.689–0.813). Using the predictive values from the overall benchmark OLS regression instead increased the estimate (mean 0.829, range 0.577–0.917) somewhat but not sufficiently, as both underestimated the utilities at the higher end above 0.90 (see Appendix 2 in the ESM).
Table 6.
Summary validation statistics of predicted utilities (YHAT)
| Methods | Observed | OLS | Tobit | CLAD | Simple beta | ZOIB | NMIX 2 components | Piecewise linear with logit component |
|---|---|---|---|---|---|---|---|---|
| Mean | 0.676 | 0.676 | 0.700 | 0.707 | 0.694 | 0.667 | 0.688 | 0.654–0.663a |
| Range | 1.319 | 1.075 | 1.194 | 0.872 | 0.823 | 0.934 | 0.917 | 1.203 |
| SD | 0.28 | 0.22 | 0.24 | 0.17 | 0.191 | 0.204 | 0.185 | 0.26 |
| Median | 0.74 | 0.73 | 0.76 | 0.75 | 0.755 | 0.698 | 0.72 | 0.74 |
| Minimum | −0.319 | 0.110 | −0.174 | 0.073 | 0.076 | 0.001 | 0.017 | −0.203 |
| Maximum | 1 | 0.965 | 1.021 | 0.946 | 0.898 | 0.935 | 0.934 | 1 |
| SEM | 0.017 | 0.016 | 0.018 | 0.013 | 0.015 | 0.016 | 0.014 | 0.019 |
| Lower 95% CI of mean | 0.643 | 0.645 | 0.674 | 0.681 | 0.664 | 0.637 | 0.660 | 0.617 |
| Upper 95% CI of mean | 0.709 | 0.708 | 0.746 | 0.733 | 0.722 | 0.697 | 0.714 | 0.691 |
| Skewness | −1.38 | −0.98 | −0.98 | −0.94 | −1.18 | −1.16 | −0.98 | −1.53 |
The SEM allows us to calculate the 95% confidence interval of the mapped means (CI = mean ± 1.96 SEM) in a hypothetical population
In bold, the best fitting method according to the criterion in question
CI confidence interval, CLAD censored least absolute deviation, OLS ordinary least squares, SD standard deviation, SEM standard error of the mean, ZOIB zero–one inflated beta
aDepending on the mismatch imputation method used
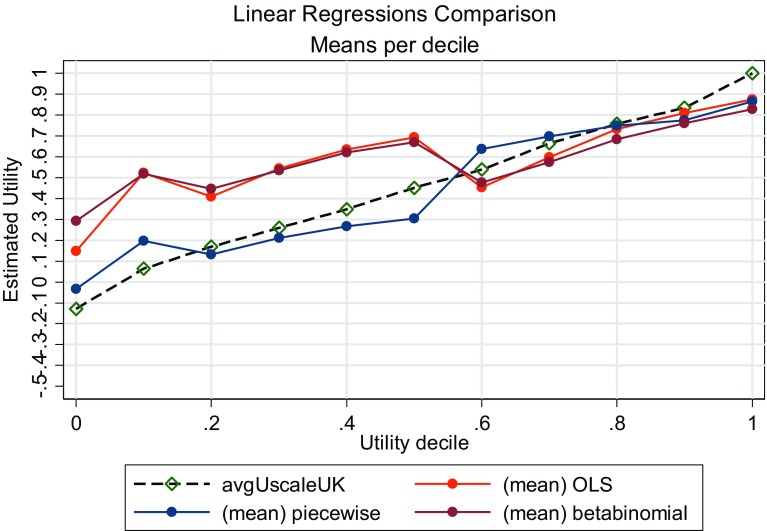
When focusing on the predicted mean utility, OLS proved the most accurate because its underestimation of high utilities was compensated by its overestimation of low utilities. Whether this is by happenstance or is a constant feature in QLQ-C30 mapping to the EQ-5D-3L is unclear (Fig. 6; Table 7).
Fig. 6.
Mean predicted utility per observed utility decile
Table 7.
Non-small-cell lung cancer regression goodness-of-fit data
| Methods | Observed | OLS | Tobit | CLAD | Simple beta | ZOIB01 | NMIX model 2 components | Three-part piecewise linearb |
|---|---|---|---|---|---|---|---|---|
| RMSE | – | 0.184 | 0.208a | 0.197 | 0.174 | 0.183 | 0.186 | 0.104 |
| MAE | – | 0.135 | 0.135 | 0.144 | 0.135 | 0.136 | 0.152 | 0.073 |
| BIC | −23 | +31 | NA | −187 | +68 | −115 | +123 −22 −281 |
|
| # Obs Abs error >0.05 | – | N = 130 | N = 125 | N = 124 | N = 122. | N = 131 | N = 148 | N = 87 |
| # Obs > 1 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| # Obs < 0 (negative utilities) | 8 | 1 | 12 | 0 | 0 | 0 | 0 | 6 |
abs absolute, BIC Bayesian information criterion, CLAD censored least absolute deviation, MAE mean absolute error, NA not applicable, NMIX normal mixture, obs observed, OLS ordinary least squares, RMSE root mean square error, ZOIB zero–one inflated beta
aSigma
blogistic, OLS < 0.50, OLS ≥ 0.50
GOF measures are all in favour of the three-part model, except for the Bayesian information criterion (BIC), which favours a simple beta regression. Although, when rerunning it per utility class of poor and good health patients, the BIC results were very similar (−20 and −285, respectively) to those of the piecewise model.
Discussion
Our results show that none of the alternative methods fared better than OLS except a three-part linear piecewise OLS/logit when based on the usual observation-based GOF measures.
The best predictive fit was obtained by a mix of OLS regression(s) for utilities lower than one with a cut-off point of 0.50 and a separate binary logistic regression for utilities equal to one, but single OLS had the best predicted mean utility. However, the prediction of utilities equal to one was poor in all regression approaches and should be further explored and improved in future mapping studies (see appendix 4 figures S1 to S7 in the ESM).
Comparison with Recent Studies
Khan and Morris [15] used a BB approach and compared it to linear, quadratic, Tobit, CLAD and quantile regression in data from two NSCLC trials (TOPICAL and SOCCAR) and obtained an MAE of, respectively, 0.10 and 0.13 and an RMSE of 0.09 and 0.11. The predicted mean compared with the observed mean utility were 0.608 versus 0.61 and 0.749 versus 0.75, with the BB regression yielding the best accuracy.
Nonetheless, when testing each developed model on the other trial data, performance was degraded, especially for the SOCCAR algorithm, resulting in an RMSE of 0.132 (TOPICAL → SOCCAR) and 0.159 (SOCCAR → TOPICAL) with the 95% confidence interval of the estimated mean only containing the true mean in 60% of the cases. They also showed that the worse the health state, the more the regressions, whatever the method, overstated the EQ-5D-3L utilities.
Wailoo et al. [19] used a bespoke mixture model with four components to map the Bath Ankylosing Spondylitis Disease Activity Index (BASDAI) to EQ-5D-3L utilities and compared it with a linear model and an indirect method based on a generalized ordered probit model. They showed that the best fit was obtained by their mixture model. However, MAE and RMSE were rather elevated: 0.158 and 0.210. To our knowledge, their method has not yet been applied to cancer data.
Skaltsa et al. [20] used a separate logistic model in a three-part approach to estimate EQ-5D-3L utilities from the FACT-P questionnaire in patients with prostate cancer (mean utility 0.688 ± 0.0282) and compared it with a single linear generalized estimating equation (GEE) regression and with a three-part model consisting of a logistic regression and two separate GEE regressions with a breakpoint fixed at 76 points of the total FACT score. The latter showed the best performance, with an RMSE of 0.162 and an MAE of 0.117 and a high R 2 of 0.718, with the predictive fit decreasing for utility values below 0.50.
Their results are largely in agreement with ours, highlighting the different nature of the data-generating process in patients in poor, good and perfect health.
Study Limitations
Our study compared alternative regression methods for mapping purposes in the cancer field. Nevertheless, it suffers from several limitations.
First, the UK EQ-5D-3L tariff was used in in all of the datasets to enhance comparability. It is possible that using the original tariffs from other countries would lead to some changes in the results, although comparisons of EQ-5D-3L tariffs, at least within European countries, show them to be quite close [21]. This effect would be expected to be more pronounced for non-European EQ-5D-3L tariffs [22, 23].
Second, some previous published studies used earlier versions of the QLQ-C30. Although the differences between the different versions of the QLQ-C30 are relatively small and relate only to two or three of the function scales, this may also possibly influence the external validity of the mapping algorithm. Regardless, QLQ-C30 version 3 is currently the most widely used.
Third, our sample is relatively small and does not include repeated measurements, which could introduce more variability and a possible time trend.
Fourth, we did not try to compare direct regression to indirect response mapping methods for mapping purposes, nor did we try to test our results on another independent data sample as this was outside the scope of the current study [24].
Scope of Applications
Although a linear piecewise three-part model approach looks promising and is relatively easy to use, more comparative research is needed with similar data both in lung cancer and in other cancer types to assess the stability and replicability of our results regarding the use of three-part models for the purposes of mapping QLQ-C30 scores to EQ-5D-3L utilities [24].
Conclusions
As yet, no preferred mapping method is advocated in the literature, so our primary goal was to compare whether some published or recommended single regression methods for mapping QLQ-C30 to the EQ-5D-3L would yield reasonably accurate predictive results in a selected dataset and whether we could improve on this using a three-part approach.
Our results indicate that the best approach is a piecewise mix of two separate OLS and one binary logistic regression, while—surprisingly—OLS still had the best predicted overall mean utility.
We conclude, nevertheless, that direct mapping regression methods based on a single distribution should be used with great care, especially for low and very high utilities, as these methods generally do not adequately represent the specifics of the tri-modal distribution of EQ-5D-3L preference values.
Therefore, EQ-5D-3L mapping methods based on three components or three-part models should be preferred [25, 26] and further investigated with emphasis on the upper ceiling problem.
Whether our results can also be extended to other cancer QOL scales such as the widely used FACT questionnaire or to generic utilities measures other than the EQ-5D-3L and in other cancer types remains to be assessed. Whether our findings also apply to the more recently developed five-level scale (EQ-5D-5L) is unknown.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
The author thanks Dr. Leighl from the Department of Medicine, Division of Medical Oncology, Princess Margaret Hospital, University of Toronto, and Dr. Mittmann from the Health Outcomes and PharmacoEconomic (HOPE) Research Centre, Sunnybrook Research Institute, University of Toronto, for their help in gaining access the NSCLC data.
Data Availability Statement
The data that support the findings of this study are available from Dr Leighl from the Department of Medicine, Division of Medical Oncology Princess Margaret Hospital, University of Toronto, Toronto, Canada, but restrictions apply to the availability of these data, as they were used under license for the current study and so are not publicly available.
Compliance with Ethical Standards
Funding
No funding was received for this study.
Conflict of interest
The author is not aware of any existing conflicts of interest.
Footnotes
Electronic supplementary material
The online version of this article (doi:10.1007/s41669-017-0049-9) contains supplementary material, which is available to authorized users.
References
- 1.Crott R, Versteegh M, Uyl-de-Groot C. An assessment of the external validity of mapping QLQ-C30 to EQ-5D preferences. Qual Life Res. 2013;22(5):1045–1054. doi: 10.1007/s11136-012-0220-9. [DOI] [PubMed] [Google Scholar]
- 2.Crott R. Mapping algorithms from QLQ-C30 to EQ-5D utilities: no firm ground to stand on yet. Expert Rev Pharmacoecon Outcomes Res. 2014;14(4):569–576. doi: 10.1586/14737167.2014.908711. [DOI] [PubMed] [Google Scholar]
- 3.Petrou Stavros, Rivero-Arias Oliver, Dakin Helen, Longworth Louise, Oppe Mark, Froud Robert, Gray Alastair. The MAPS reporting statement for studies mapping onto generic preference-based outcome measures: explanation and elaboration. Pharmacoeconomics. 2015;33(10):993–1011. doi: 10.1007/s40273-015-0312-9. [DOI] [PubMed] [Google Scholar]
- 4.Jang R, Isogai P, Mittmann N, et al. Derivation of utility values from European organization for research and treatment of cancer quality of life-core 30 questionnaire values in lung cancer. J Thorac Oncol. 2010;5(12):1953–1957. doi: 10.1097/JTO.0b013e3181f77a6a. [DOI] [PubMed] [Google Scholar]
- 5.Shaw JW, Johnson JA, Coons SJ. US valuation of the EQ-5D health states: development and testing of the D1 valuation model. Med Care. 2005;43(3):203–220. doi: 10.1097/00005650-200503000-00003. [DOI] [PubMed] [Google Scholar]
- 6.Dolan P. Modeling valuations for EuroQol health states. Med Care. 1997;35(11):1095–1108. doi: 10.1097/00005650-199711000-00002. [DOI] [PubMed] [Google Scholar]
- 7.EORTC QLQC30 Scoring Manual, EORTC, Brussels, Belgium http://groups.eortc.be/qol/manuals. Accessed 3 Aug 2017.
- 8.Mortimer D, Segal L. Comparing the Incomparable? A systematic review of competing techniques for converting descriptive measures of health status into QALY-weights. Med Decis Mak. 2008;28(1):66–89. doi: 10.1177/0272989X07309642. [DOI] [PubMed] [Google Scholar]
- 9.McKenzie L, Van der Pol M. Mapping the EORTC QLQ-C30 onto the EQ-5D instrument: the potential to estimate QALYs without generic preference data. Value Health. 2009;12:167–171. doi: 10.1111/j.1524-4733.2008.00405.x. [DOI] [PubMed] [Google Scholar]
- 10.Versteegh MM, Leunis MA, Luime JJ, et al. Mapping QLQ-C30, HAQ, and MSIS-29 on EQ-5D. Med Decis Mak. 2012;32(4):554–568. doi: 10.1177/0272989X11427761. [DOI] [PubMed] [Google Scholar]
- 11.Round J, Hawton A. Statistical alchemy: conceptual validity and mapping to generate health state utility values. Pharmacoecon Open. 2017 doi: 10.1007/s41669-017-0027-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Institute for Digital Research and Education. FAQ: How are the likelihood ratio, WALD, and Lagrange multiplier (score) tests different and/or similar. https://stats.idre.ucla.edu/other/mult-pkg/faq/general/faqhow-are-the-likelihood-ratio-wald-and-lagrange-multiplier-score-tests-different-andor-similar/. Accessed 17 July 2017.
- 13.Hunger M, Baumert J, Holle R. Analysis of SF-6D index data: is beta regression appropriate? Value Health. 2011;14(5):759–767. doi: 10.1016/j.jval.2010.12.009. [DOI] [PubMed] [Google Scholar]
- 14.Smithson M, Verkuilen J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol Methods. 2006;11(1):54–71. doi: 10.1037/1082-989X.11.1.54. [DOI] [PubMed] [Google Scholar]
- 15.Khan I, Morris S. A non-linear beta-binomial regression model for mapping EORTC QLQ- C30 to the EQ-5D-3L in lung cancer patients: a comparison with existing approaches. Health Qual Life Outcomes. 2014;12:163. doi: 10.1186/s12955-014-0163-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Arostegui I, Núñez-Antón V, Quintana J. Analysis of the short form-36 (SF-36): the beta-binomial distribution approach. Stat Med. 2006;26(6):1318–1342. doi: 10.1002/sim.2612. [DOI] [PubMed] [Google Scholar]
- 17.Buis M, Maarten L. ZOIB: Stata module to fit a zero-one inflated beta distribution by maximum likelihood. Statistical Software Components (2012). https://ideas.repec.org/c/boc/bocode/s457156.html. Accessed 30 July 2017.
- 18.Versteegh MM, Rowen D, Brazier JE, Stolk EA. Mapping onto Eq-5 D for patients in poor health. Health Qual Life Outcomes. 2010;8(1):1. doi: 10.1186/1477-7525-8-141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wailoo A, Hernández M, Philips C, Brophy S, Siebert S. modeling health state utility values in ankylosing spondylitis: comparisons of direct and indirect methods. Value Health. 2015;18(4):425–431. doi: 10.1016/j.jval.2015.02.016. [DOI] [PubMed] [Google Scholar]
- 20.Skaltsa K, Longworth L, Ivanescu C, et al. Mapping the FACT-P to the preference-based EQ-5D questionnaire in metastatic castration-resistant prostate cancer. Value Health. 2014;17(2):238–244. doi: 10.1016/j.jval.2013.12.005. [DOI] [PubMed] [Google Scholar]
- 21.Greiner W, Weijnen T, Nieuwenhuizen M, et al. A single European currency for EQ-5D health states. Results from a six country study. Eur J Health Econ. 2003;4(3):222–231. doi: 10.1007/s10198-003-0182-5. [DOI] [PubMed] [Google Scholar]
- 22.Karlsson JA, Nilsson JÅ, Neovius M, Kristensen LE, Gülfe A, Saxne T, Geborek P. National EQ-5D tariffs and quality-adjusted life-year estimation: comparison of UK, US and Danish utilities in south Swedish rheumatoid arthritis patients. Ann Rheum Dis. 2011;70(12):2163–2166. doi: 10.1136/ard.2011.153437. [DOI] [PubMed] [Google Scholar]
- 23.Lien K, Tam VC, Ko YJ, Mittmann N, Cheung MC, Chan KKW. Impact of country-specific EQ-5D-3L tariffs on the economic value of systemic therapies used in the treatment of metastatic pancreatic cancer. Curr Oncol. 2015;22(6):e443–e452. doi: 10.3747/co.22.2592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hernández Alava M, Wailoo A, Wolfe F, Michaud K. A comparison of direct and indirect methods for the estimation of health utilities from clinical outcomes. Med Decis Mak. 2014;34(7):919–930. doi: 10.1177/0272989X13500720. [DOI] [PubMed] [Google Scholar]
- 25.Kent S, Gray A, Schlackow I, Jenkinson C, McIntosh E. Mapping from the Parkinson’s disease questionnaire PDQ-39 to the generic EuroQol EQ-5D-3L: the value of mixture models. Med Decis Mak. 2015;35(7):902–911. doi: 10.1177/0272989X15584921. [DOI] [PubMed] [Google Scholar]
- 26.Verkuilen J, Smithson M. Mixed and mixture regression models for continuous bounded responses using the beta distribution. J Educ Behav Stat. 2012;37(1):82–113. doi: 10.3102/1076998610396895. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from Dr Leighl from the Department of Medicine, Division of Medical Oncology Princess Margaret Hospital, University of Toronto, Toronto, Canada, but restrictions apply to the availability of these data, as they were used under license for the current study and so are not publicly available.