Understanding Causal Distributional and Subgroup Effects With the Instrumental Propensity Score

Abstract

To address issues with measured and unmeasured confounding in observational studies, we developed a unified approach to using an instrumental variable in more flexible ways to evaluate treatment effects. The approach is based on an instrumental propensity score conditional on baseline variables, which can then be incorporated in matching, regression, subclassification, or weighting along with various parametric, semiparametric, or nonparametric methods for the assessment of treatment effects. Therefore, the application of the instrumental propensity score allows different methods for outcome effect evaluations in addition to standard 2-stage least square models while controlling for unmeasured confounders. Several properties of the instrumental propensity score are discussed. The approach is then illustrated using subclassification along with a semiparametric density ratio model and empirical likelihood. This method allows us to evaluate distributional and subgroup treatment effects in addition to the overall average treatment effect. Simulation studies showed that the method works well. We applied our method to a study of the effects of attending a Catholic school versus a public school and found that attending a Catholic school had significant beneficial effects on subsequent wages among a subgroup of subjects.

When randomized controlled studies are not feasible, observational studies offer an alternative way to evaluate the effectiveness of a treatment compared with control, controlling for measured confounders with matching, subclassification, and regression, possibly through propensity scores (1–3) or unmeasured confounders with instrumental variable (IV) methods when a valid IV can be found (4–9). Informally, a valid IV is a variable that: 1) affects the choice of treatment; 2) is independent of the unmeasured confounders; and 3) does not affect the outcome directly other than through its effect on the treatment.

When a linear model for the (continuous) outcome holds, the standard IV method based on 2-stage least squares (2SLS) provides consistent estimates of treatment effects conditioning on measured confounders (10, 11). Imbens and Angrist (12) and Angrist et al. (4) showed that the 2SLS estimand is the average treatment effect for a subgroup of subjects who adopt the treatment suggested by the instrument, called complier average causal effect (CACE). However, a linear model may not be appropriate for other skewed outcomes, and some existing IV methods that adjust for measured confounders for such outcomes may provide asymptotically biased estimates in some settings (13, 14). Heckman and Vytlacil (15, 16) showed identification and bounds of various treatment parameters with their relationship within a latent index model for general outcomes, and Carneiro et al. (17) considered additive structural models for continuous outcomes. Yau and Little (18), Barnard et al. (19), and Frangakis et al. (20) developed methods with an ordinal instrument and missing data. Tan (7) used an instrumental propensity score (IPS) in a weighting method to extend the IV estimator of Angrist et al. (4) for CACE with covariates. Recently, Baiocchi et al. (9) used optimal nonbipartite matching to construct pairs such that the IV is effectively random within each pair and then developed methods of permutation inference for effect ratios.

While most methods focus on average treatment effects over a population, knowing the treatment effect on the entire distribution of outcomes and on other functions of the outcome distributions, along with its heterogeneous effects across subgroups, can provide additional insights into how the treatment works, help with policy decisions, and enable clinicians and patients to select a treatment strategy based on their own situations. Abadie (5) estimated the cumulative distribution functions (CDFs) of the complier potential outcomes under treatment and control with the standard IV approach. However, the standard IV estimates of the potential CDFs may not be nondecreasing functions (5) and might be less efficient because they do not make full use of the mixture structure implied by the latent compliance class model (21, 22). Cheng et al. (22) provided empirical likelihood estimates for the potential CDFs of compliers in randomized trials with the randomization as an IV. All of those methods on distributional treatment effects do not adjust for measured confounders. In the present work, we evaluated the distributional treatment effects, other functions of outcome distributions, and heterogeneous treatment effects across subgroups in observational studies when the IV requires conditioning on measured confounders to be valid.

Our approach was based on an IPS. The IPS not only retains key advantages of the usual propensity score (1), such as reducing the dimensionality of the measured confounders, but it also deals with unmeasured confounders by the use of an IV. The IPS method parallels the blinding of a randomized trial; that is, the analysis for the IPS model can be worked on before looking at the outcome data. Diagnostics and adjustments can be done until the IPS model is adequate, all without looking at the outcome data. In other regression-based methods, such as 2SLS, one has often looked at the outcome data and estimated causal effects in the process of choosing covariate adjustment models, and it can be difficult to be completely objective in comparing different covariate adjustment models. Rubin (23) and Kang et al. (24) offer discussion of the value of blinding in observational studies. Also note that a complex outcome model with many covariates may make the estimation of treatment effects complicated, and many nonparametric and semiparametric causal methods for treatment effects do not incorporate covariates easily, especially when the dimension of covariates increases. The IPS provides a unified approach that adjusts for covariates for a valid IV for general types of outcomes. After the IPS model is adequate in terms of balancing the distributions of baseline covariates by the IV, different statistical methods (parametric, semiparametric, or nonparametric methods) can be used to estimate the treatment effects. We discuss the properties of the IPS and then show the method for distributional and subgroup treatment effects for general types of outcomes when conditioning on measured confounders is required for a valid IV.

Our work is motivated by studies on the effect of attending a Catholic school versus a public school on achievement. Coleman et al. (25) linked the higher achievement in Catholic schools to Catholic schools’ placing higher academic demands and imposing stricter discipline on their students than did public schools, after adjusting measured confounders. However, the finding was questioned with unmeasured confounders such as prior cognitive achievement (26). Catholic religion has then been considered as an IV in subsequent observational studies (27–29). In this work, we used Catholic religion as an IV conditioning on measured covariates to evaluate the distributional and subgroup effects of attending a Catholic school versus a public school on students’ subsequent wages, using data from the Wisconsin Longitudinal Study (WLS) (30). Previously, among others, Kim (29) and Bitler et al. (31, 32) defined a subgroup based on a single baseline covariate, and then used ordinary regression to assess the subgroup effects. However, such subgroup effects could be biased (29). Instead, our approach used an IV analysis for the distributional and subgroup effects, where the subgroups would be constructed based on several baseline covariates such that within a subgroup the IV is effectively random.

THE FRAMEWORK

We adopted the Neyman-Rubin potential outcome framework (33, 34) and considered a binary IV and treatment. However, the results can be extended to a general IV and treatment. We let X_i, Z_i, $D_i^z$, $Y_i^{z,d}$ be baseline covariates, IV, potential treatment received under z, and potential outcome under IV z and treatment d, respectively, for subject i, where z = 1 (encouragement to take treatment) or 0 (no encouragement) for a binary IV and d = 1 (treatment) or 0 (control) for a binary treatment. We make the regular IV assumptions (4): 1) Stable unit treatment value assumption: One subject’s outcome or treatment received is not related to other subjects’ IV assignment; 2) Independence of IV (conditional on covariates): The IV is independent of confounders after conditioning on measured covariates; 3) Exclusion restriction (ER): The IV affects subjects’ outcomes only through its effect on the treatment subjects received; 4) IV predicts the treatment received; 5) Monotonicity assumption: No subject would always take the treatment opposite of the treatment IV suggests. Note that under the ER assumption, $Y_i^d\equiv Y_i^{z,d}$, and the monotonicity assumption may not be needed if assuming no heterogeneity of treatment effects among the compliance classes (35) or if using a Bayesian approach and assuming that causal parameters among the compliance classes follow some prior distributions (21, 36). We let D_i and Y_i be the observed treatment received and outcome, respectively, and have $D_i=Z_i{D}_i^1+\mathrm{(1}-Z_i)D_i^0$ and $Y_i=D_i{Y}_i^1+\mathrm{(1}-D_i)Y_i^0$ under assumptions 1–5; that is, we observe only one version of the potential treatment received and outcome in a real study.

IPS AND ITS PROPERTIES

For general types of outcomes, we constructed a score for the IV based on measured covariates, called IPS, such that the IV is effectively random conditional on this score; then we do not need to control for confounders further. Previously, Tan (7) used an IPS in a weighting method to estimate CACE with covariates. We discuss the properties of the IPS in this section. Similar to the propensity score (function) (1, 37), we have:

Definition —

For a binary IV Z, the IPS is P(Z = 1|X = x) ≡ s(x) based on the measured covariates X.

The IPS reduces the dimensionality of the measured confounders and also deals with unmeasured confounders with the use of an IV. For general multilevel or continuous IVs, we can use the instrumental propensity function $p_{\phi }(Z|X)$ characterized by parameter $\phi$. For example, for a normally distributed IV conditional on X, the instrumental propensity function is the normal density function, $\phi =(\beta ,{\sigma }^2)$ and mean $\mu (X)=X^T\beta$ (37).

Result 1 —

The IPS is a balancing score:

$$X\perp Z|s(X).$$

Result 1 follows from $P(Z|X,s(X))=P(Z|X)=s(X)$ and $P(Z|s(X))={\int }_{x}P(Z|X,s(X))P(x|s(X))dx=s(X)$ and implies that, conditional on s(X), the IV Z is effectively random. That is, the conditional distribution of baseline covariates given s(X) is the same for subjects with Z = 1 and Z = 0.

Result 2 —

Suppose that an IV is strongly ignorable given X: $(Y^{z,d},D^z)\perp Z|X$ and $\mathrm{0\; <}p(Z\mathrm{=\; 1|}x\mathrm{)\; <\; 1}$; then it is strongly ignorable given s(X):

$$(Y^{z,d},D^z)\perp Z|s(X)\mathrm{and}\mathrm{0<}p(Z=\mathrm{1|}s(X\mathrm{))<1}.$$

Please see Web Appendix 1 (available at https://academic.oup.com/aje) for the proof. Result 2 implies that the adjustment for s(X) is sufficient to replace the adjustment for X for the ignorability of the IV.

Result 3 —

If the average effect of the IV on treatment is not zero conditional on X, then its effect on treatment is not zero conditional on s(X). Suppose that $E(D^z-D^{z\prime }|X)\ne 0$, for all X; then it is also true conditional on s(X):

$$E(D^z-D^{z\prime }|s(X))\ne \mathrm{0,}\mathrm{for}\mathrm{all}s(X\mathrm{)}.$$

Result 3 follows from $P(D^z-D^{z\prime }|s(X))={\int }_{x}P(D^z-D^{z\prime }|x)P(x|s(X))dx$ and implies that the IV affects the treatment conditional on s(X) if it affects the treatment conditional on X.

Result 4 —

Suppose that the ER assumption holds for an IV conditional on X:$P(Y^{z,d}|X)=P(Y^{z\prime ,d}|X)$; then it also holds conditional on s(X):

$$P(Y^{z,d}|s(X))=P(Y^{z\prime ,d}|s(X\mathrm{))}.$$

Result 4 follows from $P(Y^{z,d}|s(X))={\int }_{x}P(Y^{z,d},x|s(X))dx={\int }_{x}P(Y^{z,d}|x,s(X))P(x|s(X))dx={\int }_{x}P(Y^{z\prime ,d}|x,s(X))P(x|s(X))dx={\int }_{x}P(Y^{z\prime ,d},x|s(X))dx=P(Y^{z\prime ,d}|s(X)).$Note that Result 4 is a weaker ER than in Angrist et al. (4) for assuming only that the outcome distribution (rather than the outcomes themselves) is the same for fixed d. Robins (36) and Imbens and Rubin (38) suggested that inclusion of covariates may only have some subtle effect on the plausibility of the ER under the stochastic version; this result implies only that when the ER holds given covariates, the adjustment for s(X) is sufficient to replace the adjustment for X.

Result 5 —

Suppose that the monotonicity assumption holds for an IV Z conditional on X:$P(D^z\ge D^{z\prime }|X\mathrm{)}=1$, for $z\ge z\prime$; then it is also true conditional on s(X):

$$P(D^z\ge D^{z\prime }|s(X\mathrm{))=1,}\mathrm{for}z\ge z\prime .$$

Result 5 follows from $P(D^z\ge D^{z\prime }|s(X))={\int }_{x}P(D^z\ge D^{z\prime }|x,s(X))P(x|s(X))dx\mathrm{=1}$ and implies that the adjustment for s(X) is sufficient to replace the adjustment for X for the monotonicity assumption. As discussed above, one may make assumptions other than monotonicity for estimating a causal effect in a study, for which the IPS can still be used to address the confounding issue when an IV requires conditioning on covariates to be valid.

A UNIFIED APPROACH BASED ON THE IPS

In real observational studies, investigators often include numerous baseline covariates in models to control for confounding and have a valid IV. However, complicated models with many covariates may fail for causal effect inferences, and in many nonparametric and semiparametric methods it is not easy to incorporate covariates (5, 22, 39). The use of IPS allows complex models for the IV before looking at outcome data but simplifies the models for causal effect inferences, and the IPS can be incorporated into not only standard 2SLS models but also other recently developed IV methods for controlling for covariates.

• Step 1. We estimate the IPS $P(Z|X=x)$ through a model

  $$s(x,\mathbf{\eta })=P(Z|X=x)=g({\eta }^T\mathbf{m}(X)),$$ (1)

• where g is a link function, m is a vector of functions and η is a vector of parameters. For a binary IV, a natural choice of the link function in equation (1) is $logi{t}^{-1}$. Attention should be paid to identifying as many covariates as possible and checking for model misspecification (37, 40).

• Step 2. The estimated IPS $\hat{s}(x,\stackrel{\mathbf{ˆ}}{\mathbf{\eta }})$ can then be incorporated into different methods. For example, $\hat{s}(x,\stackrel{\mathbf{ˆ}}{\mathbf{\eta }})$ can be easily included in 2SLS models for continuous outcomes. For other types of outcomes, $\hat{s}(x,\stackrel{\mathbf{ˆ}}{\mathbf{\eta }})$ can be used in matching, subclassification, weighting, or regression along with various statistical methods.

Subclassification has been commonly used in propensity score approaches for measured confounding (1, 37). We used IPS-based subclassification to illustrate the use of IPS for treatment effects while dealing with measured and unmeasured confounding. We estimated the IPS $\hat{s}(x,\stackrel{\mathbf{ˆ}}{\mathbf{\eta }})$ by equation (1) for each subject, and checked the overlap of IV groups on their estimated IPS distributions. Lack of overlap of IV groups in estimated IPS relies on extrapolation and may lead to misleading results. We then classified subjects with similar values of $\hat{s}(x,\stackrel{\mathbf{ˆ}}{\mathbf{\eta }})$ into a stratum such that within each stratum the IV was effectively random. Strata can be constructed in different ways, for example: 1) Fixed-range strata based on the fixed cutoff values of $\hat{s}(x_i,\stackrel{\mathbf{ˆ}}{\mathbf{\eta }})$, (e.g., (0, 0.2], (0.2, 0.4], (0.4, 0.6], (0.6, 0.8], (0.8, 1) for 5 strata); or 2) Prespecified-size strata: The cut-off values of $\hat{s}(x,\stackrel{\mathbf{ˆ}}{\mathbf{\eta }})$ vary such that each stratum has specified size and similar scores. Equal-sized strata is a special case. When the IPS is approximately uniformly distributed between 0 and 1 in a study, it is easy to construct fixed-range strata. Otherwise prespecified-size strata can be constructed to avoid a stratum with few subjects while subclassifying subjects with similar IPS.

In subclassification, treatment effects within each stratum can be evaluated with an appropriate method. These stratum-specific causal effects provide information on treatment effects for subgroups of subjects who have similar IV distribution conditional on baseline covariates, and they therefore allow us to understand potentially heterogeneous treatment effects across subgroups defined by baseline covariates. The overall causal effects for the population can then be estimated across the IPS strata as a weighted average of stratum-specific effects with appropriate weight (e.g., weight proportional to the relative number of compliers in the subclass for estimating the population CACE).

Subjects in an IPS-stratum k have similar baseline characteristics, so we do not have to worry about confounding in the stratum k. In the IPS-stratum k, we define latent compliance classes $C_i^k$ based on their potential treatment behavior under each value of a binary IV: $C_i^k=\text{never-taker}\mathrm{if}{(D_i^0,D_i^1)}^k\mathrm{=\; (0,0)}$—these are subjects who would never take the treatment regardless of the IV value; complier if ${(D_i^0,D_i^1)}^k\mathrm{=\; (0,1)}$—subjects who would just follow the suggestion by the IV; always-taker if ${(D_i^0,D_i^1)}^k\mathrm{=\; (1,1)}$—subjects who would always take the treatment regardless of the IV level; and defier if ${(D_i^0,D_i^1)}^k=\mathrm{(1,0)}$—subjects who would always take the opposite of the IV-suggested treatment (4). The set of defiers is empty under monotonicity. Note that the latent compliance classes cannot be fully observed in a real study. Some observed groups in a real study are a mixture of 2 latent compliance classes (Table 1).

Table 1.

Relationship Between Observed Groups and Latent Compliance Classes in Instrumental Propensity Score Stratum k in a Simulation Study

Instrumental Variable Level	Treatment Received	Latent Compliance Class
1	1	Complier	Always-taker
1	0	Never-taker	Defiera
0	0	Never-taker	Complier
0	1	Always-taker	Defiera

^a The set of defiers is empty under the monotonicity assumption.

We allow the proportions of compliers, always-takers, and never-takers ${\varphi }_c^k,{\varphi }_a^k,{\varphi }_n^k$ be different across IPS strata. The treatment effect on compliers is of interest to understand how the treatment itself works. $CAC{E}^k=E(Y^{1^k}-Y^{0^k}|C_i^k=c)$ in stratum k is the average causal effect of receiving the treatment for a subgroup of people who would follow the suggestion by the IV in stratum k defined by baseline characteristics and can be estimated with different methods including standard IV, nonparametric, and semiparametric approaches (4, 22, 39, 41). If investigators are interested in the overall CACE in the population, the overall CACE across strata can be computed as a weighted average of stratum-specific $CAC{E}^k$, $k\mathrm{=1,...,}K$.

We estimated the distributional treatment effect and its general functions in addition to the CACE. Under assumptions 1–5 and according to Table 1, within each stratum we have

$$\begin{array}{c}{f}_{11}^k(y)={\lambda }^k{h}_{c^1}^k(y)+\mathrm{(1}-{\lambda }^k)h_a^k(y),f_{10}^k(y)=h_n^k(y),\\ f_{00}^k(y)={\tau }^k{h}_{c^0}^k(y)+\mathrm{(1}-{\tau }^k)h_n^k(y),f_{01}^k(y)=h_a^k(y),\end{array}$$ (2)

where $f_{zd}^k$ is observed outcome density under z and d, $h_{c^0}^k$, $h_{c^1}^k$, $h_n^k$, $h_a^k$ are potential outcome densities in stratum k for compliers under control and treatment, never-takers, and always-takers, respectively, and ${\lambda }^k=\frac{{\varphi }_c^k}{{\varphi }_c^k+{\varphi }_a^k}=\frac{1-{\varphi }_a^k-{\varphi }_n^k}{1-{\varphi }_n^k},{\tau }^k=\frac{{\varphi }_c^k}{{\varphi }_c^k+{\varphi }_n^k}=\frac{1-{\varphi }_a^k-{\varphi }_n^k}{1-{\varphi }_a^k}.$ Note that under the ER assumption, potential outcome densities for always-takers and never-takers are the same under treatment and control, so only one potential outcome density is defined for them $(h_n^k,h_a^k)$. Considering a semiparametric density ratio model (22, 42) in stratum k (k = 1, . . ., K), we have:

$$\frac{h_j^k(y)}{h_{c^0}^k(y)}=\exp ({\alpha }_j^k+{\beta }_j^{k}y),j=n,c^1,a,k\mathrm{=\; 1,}\dots ,K,$$ (3)

where the potential outcome densities are modeled nonparametrically except for being related by a parametric “exponential tilt.” The idea is similar to Cox’s proportional hazards models, although the computation is more complex. The density ratio model (equation (3)) includes many well-known parametric families (e.g., normal or Poisson) but also provides a good fit to data that do not belong to any parametric families (43–46). The empirical likelihood (47–49) will be used to make inferences about the potential outcome densities in IPS-stratum k. Note that the treatment effect can be different across strata, and when ${\mathrm{\alpha }}_{c^1}^k$ and ${\mathrm{\beta }}_{c^1}^k$ are zero, there is no treatment effect for the compliers in stratum k.

By maximizing the log empirical likelihood (see the Web Appendix) we obtain estimates on distributions, where $n^k$ is the number of subjects in the stratum k, and ${\hat{H}}_{c^0}^k(y)$ and ${\hat{H}}_{c^1}^k(y)$ are CDFs of compliers under control and treatment in stratum k respectively.

$$\begin{array}{c}{\hat{h}}_{c^0}^k(y_i)=\frac{1}{n^k}\frac{1}{1+\sum _j{\hat{\xi }}_j^k\{\exp ({\hat{\alpha }}_j^k+{\hat{\beta }}_j^k{y}_i)-\mathrm{1\}}},\hfill \\ {\hat{H}}_{c^0}^k(y)=\sum _i^{n^k}{\hat{h}}_{c^0}^k(y_i)I(y_i\le y),\hfill \\ {\hat{h}}_{c^1}^k(y_i)={\hat{h}}_{c^0}^k(y_i)\exp ({\hat{\mathrm{\alpha }}}_{c^1}^k+{\hat{\mathrm{\beta }}}_{c^1}^k{y}_i),\hfill \\ {\hat{H}}_{c^1}^k(y)=\sum _i^{n^k}{\hat{h}}_{c^0}^k(y_i)\exp ({\hat{\mathrm{\alpha }}}_{c^1}^k+{\hat{\mathrm{\beta }}}_{c^1}^k{y}_i)I(y_i\le y\mathrm{)}.\end{array}$$ (4)

We can then compute causal effects as different functions of the distributions, for example,

$$\begin{array}{c}{\widehat{CACE}}^k=\sum _{i\mathrm{=1}}^{n^k}{y}_i{\hat{h}}_{c^0}^k(y_i)\left\{\exp ({\hat{\mathrm{\alpha }}}_{c^1}^k+{\hat{\mathrm{\beta }}}_{c^1}^k{y}_i)-1\right\};\hfill \\ {\widehat{CQCE}}^k(\iota )=({\hat{H}}_{c^1}^k{)}^{-1}(\iota )-{({\hat{H}}_{c^0}^k)}^{-1}(\iota );\hfill \end{array}$$

where $CQC{E}^k(\iota )$ is the quantile treatment effect at quantile ι in stratum k. Note that although the $CAC{E}^k$ and $CQC{E}^k$ are a linear difference in compliers’ potential outcome distributions under treatment and control, we can use other functions of the compliers’ potential outcome distributions estimated by equation (4) for other causal effects of interest. The overall treatment effects for compliers can then be computed as a weighted average of stratum-specific effects with weight proportional to the number of compliers in stratum k: $\mathrm{(1}-{\varphi }_a^k-{\varphi }_n^k)\times n^k$, where $n^k$ is the number of subjects in stratum k.

SIMULATION STUDY

The baseline covariates were drawn independently from the following distributions: $\mathrm{Normal}\mathrm{(0,1)}$, $\mathrm{Bernoulli}\mathrm{(0.5)}$, $\mathrm{Gamma}\mathrm{(2,1)}$. Z_i was generated from: $P(Z_i\mathrm{=1}|X_i)=logi{t}^{-1}(-1.2+X_{1i}+0.5X_{2i}+0.5X_{3i}).$The latent compliance class C_i was generated using probabilities varying with covariates-based IPS strata (e.g., the proportion of compliers ranged between 50% and 90%, and future studies will develop methods for weak IVs). The observed treatment D_i was generated with the Z_i and C_i, based on the structure shown in Table 1.

We simulated the potential outcome distributions based on the baseline covariates and latent compliance classes, and we considered normal, log normal, exponential, and Poisson outcome distributions. We simulated 2 settings: with and without a treatment effect. Web Table 1 shows the true values of parameters of potential outcome distributions generating the data. The true values of causal effects were then calculated based on the true values of parameters of potential outcome distributions. Please see the detailed simulation information in the Web Materials. Note that in a real study, we did not observe the latent compliance classes and the corresponding potential outcomes but used only the observed treatment and outcomes for analyses. IV methods allow us to obtain consistent estimates on causal effects of compliers of our interest when there is a valid IV.

For each setting, we performed 10,000 and 1,000 Monte Carlo replications for Table 2 and Web Table 2 respectively. On each replication, 5 fixed-range or 4 equal-sized IPS strata were constructed for 1,000 subjects. One set of results for simulations with 5 fixed-range and 4 equal-sized strata for selected distributions is presented; however, the result pattern is similar under different settings.

Table 2.

Ordinary Least Square and Standard Instrumental Variable Estimates for Compliers Average Causal Effect Without Covariates, With Covariates, and With Instrumental Propensity Scores, Using Simulated Data

Distribution	CACE	$\widehat{\mathit{CACE}}\mathbf{(}\mathbf{S}\mathbf{E}\mathbf{)}$
		OLS (With X)	SIV (Ignoring X)	SIV (With X)	SIV (IPS-Based)
Normal
Overall	2.808	2.338 (0.114)	4.295 (0.180)	2.905 (0.178)	2.866 (0.202)
k = 1	1				1.127 (0.390)
k = 2	2				2.063 (0.252)
k = 3	3				3.035 (0.300)
k = 4	4				4.022 (0.471)
k = 5	5				5.011 (1.299)
Log normal
Overall	53.7	160.1 (27.3)	263.7 (53.7)	45.9 (48.9)	61.4 (75.1)
k = 1	2.8				4.1 (6.3)
k = 2	10.5				12.9 (11.1)
k = 3	31.5				36.6 (33.1)
k = 4	88.4				100.2 (128.3)
k = 5	243.0				176.2 (1,091.6)
Poisson
Overall	2.808	2.335 (0.159)	4.295 (0.230)	2.902 (0.239)	2.862 (0.261)
k = 1	1				1.129 (0.504)
k = 2	2				2.065 (0.346)
k = 3	3				3.028 (0.403)
k = 4	4				4.022 (0.616)
k = 5	5				4.973 (1.723)

Abbreviations: CACE, true complier average causal effect; $\widehat{\mathit{CACE}}$, estimated complier average causal effect; IPS, instrumental propensity score; k, instrumental propensity score stratum; OLS, ordinary least square; SE, standard error; SIV, standard instrumental variable with 2-stage least square.

Table 2 shows that the ordinary least square estimate adjusting for covariates is biased, and the standard IV-estimated CACE without covariates is also biased when the IV requires conditioning on covariates to be valid. Standard IV estimates with 2SLS conditional on covariates or based on IPS are close to true values for normal and Poisson outcomes, where IPS-based standard IV estimates with uncertainty in estimated IPS have a slightly larger standard error than 2SLS standard IV estimates conditional on covariates, and the IPS-based standard IV also provides stratum-specific estimates. However, even standard IV estimates conditional on covariates or based on IPS could be biased for log normal data when the distribution is skewed, indicating that when a linear model is not appropriate for the outcome data, a method not based on a linear model should be considered. For example, above we considered the use of IPS to deal with confounding and then incorporated the IPS into the semiparametric method to address the possible bias due to the use of a linear model for skewed data.

Web Table 2 shows that the bias and root mean squared errors of our semiparametric estimates on parameters of interest are small under all settings. The semiparametric empirical likelihood ratio statistic R was used to test $H_0:h_{c^0}^k(y)=h_{c^1}^k(y)$ or equivalently $H_0:{\mathrm{\alpha }}_{c^1}^k={\mathrm{\beta }}_{c^1}^k\mathrm{=0}$, and it had a null distribution of ${\chi }_1^2$ (22). The empirical rejection rates showed that the test rejects the null hypothesis around the nominal level (0.05) under the null and has good power (>0.80) under the alternative hypothesis.

Estimates of overall and stratum-specific CACE and complier quantile causal effect (CQCE) with the semiparametric and standard IV methods are included in Web Tables 3 and 4 respectively, showing that the semiparametric estimates were more efficient than the standard IV estimates.

APPLICATION TO THE EFFECT OF CATHOLIC VERSUS PUBLIC SCHOOLS

In the WLS, students who graduated from Wisconsin high schools in 1957 were randomly selected and followed in 1964, 1975, 1992, 2003, and 2011 to learn about their labor-market experience (30). Table 3 shows that students who attended Catholic schools had higher intelligence-quotient scores, and their parents had higher income and educational levels compared with students who attended public schools, indicating possible selection bias. Kim (29) used Catholic religion as an IV to assess the average effect of attending a Catholic school on subsequent wages in the WLS. Evans and Schwab (27) and Neal (28) used Catholic religion as an IV for the same question with other data sets.

Table 3.

Descriptive Statistics for Participants in Public and Catholic Schools, Simulation Study Using Data From the Wisconsin Longitudinal Study, 1957–2011

Characteristics	Public School (n = 3,261)		Catholic School (n = 420)
	Mean (SD)	%	Mean (SD)	%
Wages in 1974, $	15,274 (7,900)		18,108 (9,643)
Intelligence-quotient score	100.56 (15.16)		106.10 (14.53)
Family income in 1957, $	9,309 (5,656)		11,004 (7,737)
Father’s education, years	10.31 (2.99)		11.06 (3.08)
Mother’s education, years	10.63 (2.77)		11.17 (2.77)
Living with both parents		90.28		91.90
Catholic religion of the family		32.66		99.29
No. of siblings	3.23 (2.58)		3.11 (2.40)
Years of schooling	13.69 (2.77)		14.71 (2.60)

Abbreviation: SD, standard deviation.

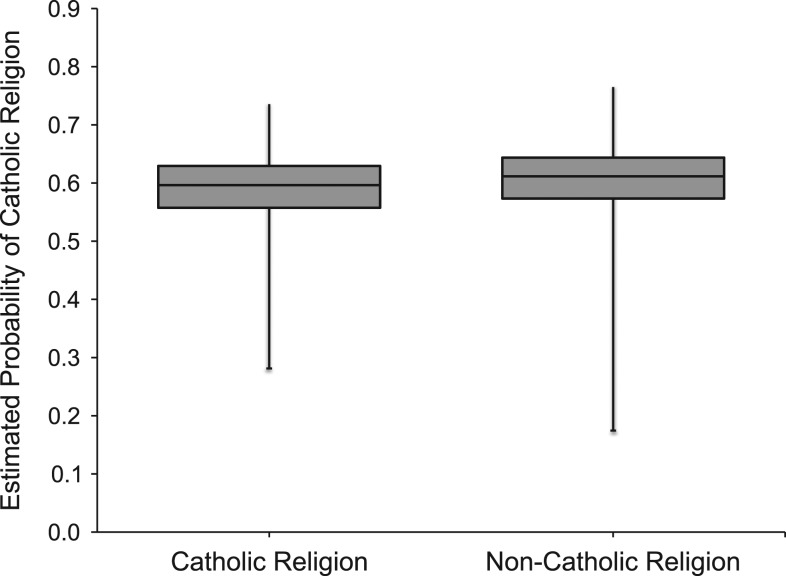
We also used the family’s Catholic religion in high school as an IV. We first estimated the 3,681 students’ IPS conditional on observed baseline variables (intelligence-quotient score, parents’ education, family income, number of siblings, living with both parents, etc.) but not on posttreatment covariates (e.g., years of schooling). Figure 1 shows box plots of the estimated IPS of the family’s Catholic religion in high school, which ranged between 0.17 and 0.76. Except for one non-Catholic student with lower estimated probabilities of Catholic religion than any Catholic student, almost every Catholic student had a comparable non-Catholic student with a similar estimated probability of Catholic religion. Because of the nonuniformly distributed IPS scores between 0 and 1, we constructed 4 equal-sized strata to avoid a stratum with few subjects. Table 4 shows that potential baseline confounders were balanced between non-Catholic and Catholic students, indicating that Catholic religion was highly likely independent of confounders within each stratum. Among the 420 students who went to Catholic schools, more than 99% of them had Catholic religion in high school. The first-stage F statistic of 138.68 in 2SLS indicated that the family’s Catholic religion in high school should work well as an IV in this study. Within each stratum, the Catholic and non-Catholic students had similar intelligence (intelligence-quotient score), education (years of schooling), and socioeconomic factors, so it seems reasonable to assume that the family’s Catholic religion in high school did not have a significant direct effect on their subsequent wages through other pathways not captured in Catholic schooling, because the education at a Catholic school versus a public school encompassed all aspects of education in high school given the comparable characteristics, total schooling years, and families’ socioeconomic factors. The 0.14% of non-Catholic students going to Catholic schools represented a mixture of always-takers and defiers, so it seems reasonable to assume monotonicity for this data.

Figure 1.

Box plots of the estimated instrumental propensity score of the participating family’s Catholic religion, from a simulation study using data from the Wisconsin Longitudinal Study, 1957–2011.

Table 4.

Selected Characteristics According to Presence of Catholic Religion, Stratified by the Instrumental Propensity Score Stratum, Simulation Study Using Data From the Wisconsin Longitudinal Study, 1957–2011

Characteristic and Stratum	Non-Catholic	Catholic
No. of subjects
1	636	284
2	560	360
3	520	400
4	483	438
Intelligence-quotient score
1	95.85	95.66
2	102.20	100.20
3	103.60	102.90
4	103.70	104.80
Family income in 1957, $
1	9,389	8,803
2	9,953	9,319
3	9,182	9,772
4	9,443	9,895
Father’s education, years
1	11.43	11.05
2	10.75	10.50
3	10.15	10.38
4	9.14	9.53
Mother’s education, years
1	12.78	12.65
2	11.23	11.07
3	9.87	9.97
4	8.83	9.09

We then modeled the log of students’ wages in 1974 with our method. Table 5 shows estimated overall average treatment effect for all students from an ordinary least square model and for compliers from 2SLS, controlling for baseline covariates as well as estimated subgroup effects and quantile effects from our semiparametric method with IPS. By semiparametric method, overall, the compliers, who would change their school choice because of their religion in high school, had a $116 higher average wage $(\exp \mathrm{(0.147)}\times \mathrm{\$100})$ 17 years after graduation from high school if they went to a Catholic school rather than going to a public school. In particular, the subgroup of compliers in stratum 3, who had relatively higher intelligence-quotient scores and whose mothers had relatively lower education level, had significantly different wage distribution (P = 0.0007) and had about a $135 higher average wage $(\exp \mathrm{(0.301)}\times \mathrm{\$100})$ if they went to a Catholic school rather than to a public school. The quantile effects show that the beneficial effect of attending a Catholic school in stratum 3 appeared stronger in those students with relatively higher income in this population.

Table 5.

Effect of Attending a Catholic School on Log of Students’ Wages per $100 in 1974 (Semiparametric Method with Instrumental Propensity Score), Simulation Study Using Data From the Wisconsin Longitudinal Study, 1957–2011

Effecta	Methods	Overall	Stratum 1	Stratum 2	Stratum 3	Stratum 4
		Estimate (95% CI)	Estimate (95% CI)	Estimate (95% CI)	Estimate (95% CI)	Estimate (95% CI)
CACE	OLS	0.101 (0.052, 0.150)
	2SLS	0.151 (0.034, 0.268)
	SEM	0.147 (0.052, 0.257)	0.172 (−0.115, 0.370)	0.028 (−0.171, 0.357)	0.301 (0.038, 0.490)	0.066 (−0.065, 0.401)
CQCE	SEM
0.10	SEM	0.105 (0.010, 0.223)	0.105 (−0.087, 0.347)	0 (−0.140, 0.355)	0.221 (0.018, 0.730)	0.054 (−0.105, 0.580)
0.25	SEM	0.083 (0, 0.167)	0.140 (−0.074, 0.254)	0.024 (−0.113, 0.250)	0.185 (0.008, 0.300)	0.025 (−0.051, 0.262)
0.50	SEM	0.102 (0, 0.134)	0.098 (−0.095, 0.222)	0.033 (−0.154, 0.208)	0.170 (0.012, 0.263)	0.007 (−0.030, 0.223)
0.75	SEM	0.105 (0, 0.201)	0.130 (−0.095, 0.288)	0.049 (−0.174, 0.272)	0.241 (0.029, 0.336)	0.040 (−0.042, 0.288)
0.90	SEM	0.197 (0, 0.310)	0.288 (−0.192, 0.464)	0.035 (−0.293, 0.460)	0.405 (0.041, 0.547)	0.087 (−0.049, 0.511)

Abbreviations: 2SLS, 2-stage least squares; CACE, complier average causal effect; CI, confidence interval; CQCE, complier quantile causal effect; OLS, ordinary least squares; SEM, semiparametric method.

^a Comparison on the treatment distributional effect between compliers under treatment and control: P = 0.5456 (stratum 1); P = 1.0000 (stratum 2); P = 0.0007 (stratum 3); P = 0.4647 (stratum 4).

Goodness of fit of the density ratio model (equation (3)) to the WLS data was evaluated by comparing the estimated model-based CDF with the empirical CDF (22, 50), showing no evidence of lack of fit of the model in this study overall.

SUMMARY

We developed a unified approach to using an IV based on IPS to evaluate treatment effects for general types of outcomes when the IV requires conditioning on covariates to be valid, and we tested it in a simulation study. The approach allows the use of different methods for outcome effect evaluations in addition to standard 2SLS models. In a simulation, the subclassification approach with a density ratio model provided information on distributional and subgroup treatment effects in addition to average effects in the overall population.

Abbreviations

2SLS

2-stage least squares

CACE

complier average causal effect

CDF

cumulative distribution function

ER

exclusion restriction

IPS

instrumental propensity score

IV

instrumental variable

WLS

Wisconsin Longitudinal Study