Quantifying precision in cardiac diffusion tensor imaging with second-order motion-compensated convex optimized diffusion encoding

Abstract

Purpose

To quantify the precision of in vivo cardiac DTI (cDTI) acquired with a spin echo, first- and second-order motion-compensated (M₁M₂), convex optimized diffusion encoding (CODE) sequence.

Methods

Free-breathing CODE-M₁M₂ cDTI were acquired in healthy volunteers (N = 10) at midsystole and diastole with 10 repeated acquisitions per phase. 95% confidence intervals of uncertainty in reconstructed diffusion tensor eigenvectors (E⃗₁, E⃗₂, E⃗₃), mean diffusivity (MD), fractional anisotropy (FA), and tensor Mode were measured using a bootstrapping approach. Trends in observed tensor metric uncertainty were evaluated as a function of scan duration, image SNR, cardiac phase, and bulk motion artifacts.

Results

For midsystolic scans including 5 signal averages (scan time: ~5min), the median myocardial 95% confidence intervals of uncertainties were: E⃗₁: 15.5 ± 1.2°, E⃗₂: 31.2 ± 3.5°, E⃗₃: 21.8 ± 3.1°, MD: 0.38 ± 0.02 × 10⁻³mm²/s, FA: 0.20 ± 0.01, and Mode: 1.10 ± 0.08. Uncertainty in all parameters increased for diastolic scans: E⃗₁: 31.9 ± 7.1°, E⃗₂: 59.6 ± 6.8°, E⃗₃: 40.5 ± 6.4°, MD: 0.52 ± 0.09 × 10⁻³ mm²/s, FA: 0.23 ± 0.01, and Mode: 1.57 ± 0.11. Diastolic cDTI also reported higher MD (MD_DIA = 1.91 ± 0.34 × 10⁻³ mm²/s vs. MD_SYS = 1.58 ± 0.09 × 10⁻³ mm²/s, P = 8 × 10⁻³) and lower FA values (FA_DIA = 0.32 ± 0.06 vs. FA_SYS = 0.37 ± 0.03, P = 0.03).

Conclusion

cDTI precision improved with increasing nondiffusion-weighted (b = 0) image SNR, but gains were minimal for SNR ≥ 25 (~10 averages). cDTI precision was also sensitive to intershot bulk motion artifacts, which led to better precision for midsystolic imaging.

1 | INTRODUCTION

Cardiac DTI (cDTI) is an emerging contrast-free technique for quantifying microstructure in healthy^1,2 and diseased myocardium.^3–5 cDTI provides quantitative maps of local cardiomyocyte orientation, the organization of myolaminar sheetlets, and microstructural anisotropy by probing the diffusion of water molecules contained in myocardial tissue. Increases in the mean diffusivity (MD) have been linked to the presence of fibrosis in myocardial infarction as well as changes in extracellular volume in hypertrophic cardiomyopathy. ^6,7 Changes in myocardial sheetlet dynamics have also been demonstrated in hypertrophic and dilated cardiomyopathies using cDTI.^3–5

As with any quantitative measure, several sources of error lead to uncertainty for in vivo cDTI measurements. These include, but are not limited to, noise, image distortions, and physiological variability. Noise can have a large impact on cDTI-derived parameters due to the low SNR of the acquired diffusion-weighted images that stems from the diffusion-induced signal decay and the general reliance on single-shot EPI (SS-EPI) readouts. Image distortions can also be substantial in cDTI due to eddy currents and sharp magnetic susceptibility gradients at the heart–lung interface that are exacerbated by the SS-EPI readout.⁸ Physiological variability is also significant in cDTI due to the presence of bulk cardiac and respiratory motion as well as pulsatile blood flow. This variability can lead to both corrupted individual measurements (i.e., intrashot motion effects) and mismatches between measurements (i.e., intershot variability between encoding directions or repetitions).

The propagation of these errors from the acquired image data through diffusion tensor reconstruction and on to derived tensor metrics is a complex problem that is not easily modeled. As a result, a nonparametric bootstrapped approach has been proposed for quantifying uncertainty in diffusion tensor orientation⁹ and shape^10,11 in neurological DTI. This approach provides insight into the uncertainty underlying neurological DTI experiments,^12,13 but these results do not directly apply to in vivo cDTI for several reasons. Namely, cardiomyocytes are approximately 10 times thicker in diameter than neuronal fibers,^14,15 which leads to diffusion tensors with substantially lower fractional anisotropy (FA) and consequently larger uncertainties in measures of fiber orientation. ⁹ Cardiac motion also necessitates the use of highly specialized pulse sequences, which employ either motion-compensated diffusion encoding gradients^16–19 or a STEAM with diffusion encoding spread across multiple heart beats.^20,21 Furthermore, even when using motion-compensated diffusion encoding schemes, slight variations in heart rate and breathing patterns throughout an acquisition contribute a degree of uncertainty to the measured tensor metrics. The impact of bulk physiological motion also depends on the pulse sequence timing within the cardiac cycle^17,19,22; thus, uncertainty is expected to depend on the cardiac phase selected for triggering, although this has not yet been characterized.

Currently, the many sources of variability and moderate SNR present in cDTI acquisitions result in the standard practice of acquiring multiple repetitions of the protocol and averaging the repeated data to increase SNR and thereby improve measurement precision. This, of course, increases the already long cDTI scan times that arise from the need for multiple diffusion encoding directions and both cardiac and respiratory triggering (or multiple repeated breath holds). Therefore, it is useful to quantify the precision of cDTI-derived tensor metrics made within clinically viable scan durations.

The first objective of this study was to use bootstrapped uncertainty measurements to characterize the precision of in vivo spin echo EPI (SE-EPI) cDTI measurements made using first- and second-order motion-compensated (M₁M₂) convex optimized diffusion encoding (CODE)¹⁹ at 2 points in the cardiac cycle (midsystole and diastole). The second objective was to quantify the precision of diffusion tensor orientation (i.e., tensor eigenvectors) and shape (i.e., tensor invariants) for cDTI acquisitions with scan times between 1 and 5min per slice to identify practical guidelines for efficiently measuring high-quality microstructural information.

2 | THEORY

Diffusion tensor uncertainty can be measured for a cDTI acquisition using bootstrapped resampling to generate a distribution of tensors that reflects the uncertainty inherent in the measurement. This was previously described for calculating uncertainty in the tensor primary eigenvector, which was referred to as the “cone of uncertainty.”⁹ This technique is briefly described herein and extended to quantify other aspects of diffusion tensor uncertainty, including the secondary and tertiary eigenvectors as well as several tensor invariants.

This bootstrapping technique requires the cDTI acquisition to be repeated twice to generate 2 independent but matched datasets. From these, a composite dataset can be generated by randomly selecting 1 image for each diffusion encoding direction from the 2 sets. This composite dataset, which includes 1 randomly chosen image for all diffusion encoding directions, can then be used to reconstruct a diffusion tensor at each voxel with a least squares linear regression. This process can then be repeated a large number of times (N_{bootstrap samples}) to generate a distribution of diffusion tensors at each voxel, which is much more efficient than actually acquiring N_boot repetitions. Eigensystem decomposition can then be performed on each diffusion tensor to determine their eigenvectors (E₁, E₂, and E₃) and eigenvalues (λ₁, λ₂, λ₃). Tensor invariant quantities such as MD, FA, and tensor Mode²³ can also be extracted from each diffusion tensor.

The precision of each eigenvector, E_j, can then be measured by first calculating the dyadic mean, ψ_j of the N_boot E_j vectors, and then measuring the angle, θ_j between each vector E_j and ψ_j. E_j precision (dE_j) can then characterized by the 1-sided 95% confidence interval (95CI) of the resultant θ_j distribution. A 1-sided 95CI is used because by definition θ_j ≥ 0. Note that dE₁ as described here is exactly the cone of uncertainty as described by Jones.⁹

Analogous measures of tensor invariant precision can be determined by analyzing their distributions across the N_boot repetitions (as done for FA in Pajevic and Basser¹⁰). Unlike the θ_j distributions describing vector uncertainties, which by definition are bounded between 0° and 90°, the invariants form 2-sided distributions and can meaningfully exhibit negative deviations from the median value. As such, their uncertainty should be represented by a 2-sided 95CI, which need not be symmetric about the median. The width of this 95CI (i.e., the upper bound minus the lower bound) can then be used to represent the underlying uncertainty (dMD, dFA, dMode).

3 | METHODS

3.1 | cDTI acquisition

cDTI were acquired in healthy volunteers (N = 10) on a 3.0T scanner (Siemens Prisma, Siemens HealthCare, Erlangen, Germany) after obtaining informed consent under an institutional review board-approved study using a SE-EPI DWI pulse sequence with convex optimized diffusion encoding with first- and second-order moment compensation (CODE-M₁M₂) to impart bulk motion compensation and reduce the TE, thereby increasing SNR.¹⁹ The acquisition included a single midventricular slice, 1 b value (b = 350 s/mm²) along 12 diffusion encoding directions plus 1 nondiffusion-weighted image (b = 0), and 2.0 × 2.0 × 5.0mm spatial resolution with inner volume excitation to reduce the FOV in the phase encode direction²⁴ (FOV = 200 × 160 mm, GRAPPA factor 2,²⁵ full-Fourier, water-only excitation, 90° flip angle, TE = 65 ms). There was a small b-value increase (<1 s/mm²) due to the imaging gradients and to use of a previously described concomitant field correction,¹⁹ but only the nominal b value was used for reconstruction. For each scan, 3 dummy scans were performed prior to acquiring images in order to reach a steady state. Local second-order B₀ shimming was performed in a focused shim box containing only the left ventricular (LV) myocardium to minimize susceptibility artifacts in the posterior wall. Imaging was timed to an end-expiratory respiratory phase using a liver-dome navigator trigger, which resulted in a TR of 1 respiratory cycle (average TR = 4.2 ± 1.4 s). Separate acquisitions were performed with ECG trigger delays timed to: 1) midsystole (fixed trigger delay = 100 ms); and 2) late diastole (subject-specific trigger delay determined by identifying diastasis from a balanced steady-state free precession cine image, which resulted in trigger delays of 705 ± 63 ms across all subjects). Ten signal repetitions were acquired in a single free-breathing scan at each cardiac phase to facilitate boot-strapped uncertainty measurement for datasets containing up to 5 averages (scan time: ~10 min per cardiac phase). Prior to reconstruction, all images were coregistered using a rigid transformation to correct for differences in cardiac position between scans.

3.2 | Image quality evaluation

Whereas SNR generally increases with additional signal averages ( $\text{SNR}\propto \sqrt{N_{\mathit{avg}}}$), it can vary substantially in space and between subjects due to differences in subject geometry and coil positioning. It is thus useful to quantify voxel-wise image SNR to more completely observe the relationship between SNR and cDTI uncertainty. Because 10 repetitions of each image were acquired, it was possible to map SNR for each reference DWI (b = 0) acquisition. In order to estimate SNR from images that included several averaged repetitions, a bootstrapped approach similar to that described above was used. For example, for N_avg = 5 averages, 5 b = 0 images were randomly chosen (with replacement) from the acquired set of 10 and magnitude averaged together (complex averaging was not performed because image intensities were sufficiently above the noise floor with respect to the moderate b value used²⁶. This process was repeated to generate a set of 300 images that each included 5 averages. SNR was then calculated at each voxel by dividing the mean signal value across the 300 images by their SD (no SNR differences were observed when the image sample size was increased beyond 300). SNR maps were generated in this manner for N_avg = 1–10.

Because all pulse sequence parameters and setup conditions were held constant between acquisitions at midsystole and diastole, we can assume that any differences observed between the acquisitions arise predominantly from physiological variability. Furthermore, if cardiac bulk motion effects are present in the images, it is expected that they will vary subtly from beat to beat²⁷ and lead to voxel-wise signal fluctuation between repetitions. To quantify this effect, the coefficient of variation (CoV) (i.e., the SD normalized by the mean) of the voxel-wise signal intensity across all 10 repetitions of each direction (CoV_DTI) was measured for both cardiac phases.

3.3 | cDTI precision measurement

Subsets of the set of 10 cDTI repetitions were first randomly selected and averaged together to reflect acquisitions with scan times ranging from approximately 1 to 5 min (N_avg = 1 to N_avg = 5). A second subset was then randomly generated for each case to facilitate bootstrapping. The uncertainty in tensor eigenvectors (dE₁, dE₂, dE₃) and invariants (dMD, dFA, dMode) was then measured from the 2 subsets as described above. These calculations used N_boot = 1000 boot-strapped samples, which was determined to be sufficient to generate stable statistical measures of uncertainty (i.e., increasing N_boot did not alter the measured tensor uncertainties) and is in line with previous studies.²

Histograms of the uncertainty in each tensor quantity were generated for all LV voxels within each subject for N_avg = 1 to N_avg = 5 at both midsystole and diastole. Median and maximum likelihood values were then extracted from each histogram. Global LV histograms of each quantity’s uncertainty were also generated from data pooled across all subjects at each cardiac phase.

Uncertainty was then characterized as a function of b = 0 image SNR on a voxel-wise basis. This was done by first binning all voxels by SNR (bin size: 2) and then generating histograms of uncertainty across all voxels contained in each SNR bin. The median uncertainty was then measured within each bin, and the 95CI of the median was measured using bootstrapping. Significant differences between midsystole and diastolic median uncertainties were identified by nonoverlapping 95CIs.

In order to examine the impact of variation in bulk motion-induced signal attenuation on precision, the same process was then carried out to measure the median uncertainty of each parameter as a function of CoV_DTI (bin size: 2%). The impact of tensor size and shape on precision was also evaluated by measuring the median uncertainties as functions of MD and FA (as reconstructed with 5 averages, MD bin size: 8 × 10⁻⁵mm²/s, FA bin size: 0.02).

3.4 | Tensor evolution with varying signal averages

The dependence of eigenvector and tensor invariant parameters was also evaluated as a function of N_avg. To do so, diffusion tensors were reconstructed from cDTI image subsets, including the full range of acquired signal averages (N_avg = 1–10; note that all 10 averages could be used for this analysis, which did not require bootstrapped resampling). Maps of E⃗₁, E⃗₂, E⃗₃, MD, FA, and tensor Mode were then generated for each subset.

Helix angle (HA) maps were also generated by measuring the elevation angle of the projection of E⃗₁ relative to the local circumferential tangent vector, C⃗.¹ C⃗ was defined by a b-spline vector fit to the endocardial and epicardial surfaces, as defined by 10 manually defined seed points on each endocardial and epicardial surface.¹ The average HA slope across the wall, HA_pitch, was calculated using a linear regression between HA and percent wall depth for each subject. Percent wall depth values were calculated at each LV voxel by linearly interpolating between the endo- and epicardial splines (where percent wall depth = 0% at the epicardial surface and 100% at the endocardial surface). Myocardial sheet angles (SA), SA2 and SA3 were then defined by the angles between the circumferential-long axis plane and E⃗₂ and E⃗₃, respectively.¹ Median myocardial HA, |SA2|, and |SA3|were then calculated for each subject for N_avg = 1–10. The median (m) SD (σ) of myocardial MD, FA, and Mode were also calculated for each subject for N_avg = 1–10 using the region between the endo- and epicardial splines described above to form the LV mask. Statistical differences between each median and SD across all subjects as a function of N_avg were identified using 1-way analysis of variation. If analysis of variation yielded significant differences, medians and SDs from N_avg = 1 were compared with N_avg ≥ 2 using paired t tests at a P = 0.05 significance level.

3.5 | Cardiac phase dependence of tensor parameters

Median myocardial HA, HA_pitch, |SA2|, |SA3|, MD, FA, and tensor Mode were also compared between midsystole and diastole with N_avg = 10 using paired t tests.

4 | RESULTS

4.1 | Image quality evaluation

cDTIs from all imaging experiments were included in analysis (no data was discarded). The average heart beat duration (R-R interval) was 1006 ± 101 ms, and the ECG trigger delays (TD) used for systolic (_SYS) and diastolic imaging (DIA) were TD_SYS = 100 ± 0 ms, which corresponded with 35.4% ± 2.6% of peak systolic contraction and TD_DIA = 705 ± 63 ms. The average scan time was 9.1 ± 3.1 min per cardiac phase (54.7 ± 18.5 s per cDTI average).

The mean nondiffusion-weighted (b = 0) image SNR in the LV increased from 8.0 ± 1.9 with N_avg = 1 to 22.3 ± 6.1 with N_avg = 10. No significant differences in SNR were observed between midsystolic and diastolic b = 0 images (8.2 ± 1.1 vs. 7.9 ± 2.6, P = NS). However, median myocardial CoV_DTI was significantly lower in midsystole than in diastole (16.7% ± 2.2% vs. 25.8% ± 9.1%, P = 0.006), which indicates higher signal variability during diastole.

4.2 | cDTI precision measurement

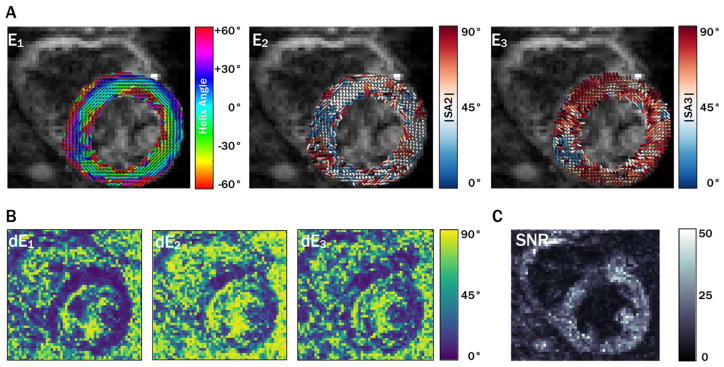
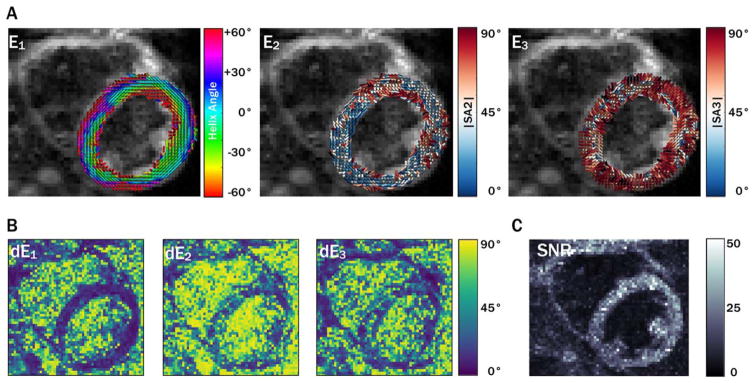
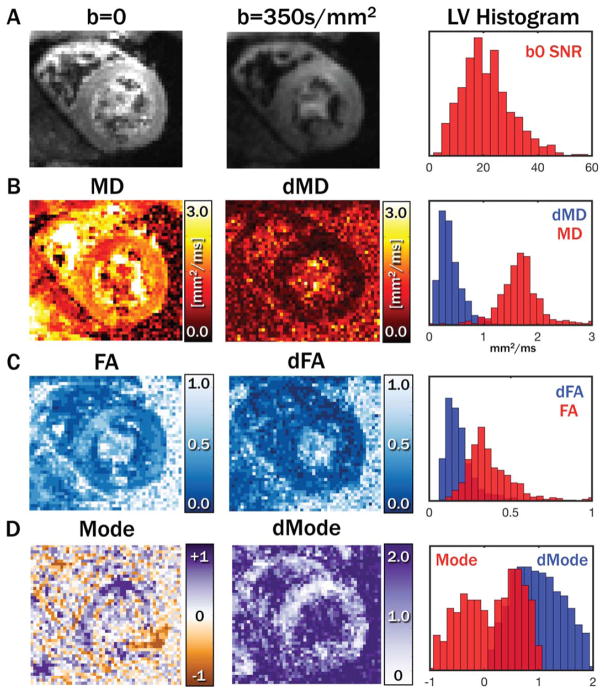
Primary, secondary, and tertiary eigenvector (E⃗₁, E⃗₂, and E⃗₃) maps, along with eigenvector uncertainty maps (dE₁, dE₂, and dE₃) and myocardial uncertainty histograms, are shown for a midsystolic acquisition with 5 averages from a single subject in Figure 1. Diastolic maps for the same subject are shown in Figure 2. Qualitatively, regions with increased uncertainty corresponded with regions with less coherent eigenvectors, and uncertainty was generally higher in the diastolic phase. cDTI images, along with reconstructed maps of MD, FA, and tensor Mode, as well as maps of each parameter’s uncertainty and histograms of myocardial uncertainty, are shown for the same subject (also with 5 averages) in the midsystolic cardiac phase in Figure 3. Analogous maps are shown for a different subject in the diastolic phase in Supporting Information Figure S1.

FIGURE 1.

Maps of eigenvector orientations (A) for 1 subject with 5 averages from a midsystolic cardiac phase with corresponding eigenvector orientation 95CI uncertainty maps (B) and b = 0 image SNR maps (C). Qualitatively, regions with increased uncertainty correspond with regions of eigenvector incoherence. Overall, uncertainty in E₂ was greater than uncertainty in E₁ and E₃, a trend that was observed in all subjects.

95CI, 95% confidence interval; E, eigenvector.

FIGURE 2.

Maps of eigenvector orientations (A) for the same subject shown in Figure 1 with 5 averages from a diastolic cardiac phase with corresponding eigenvector orientation 95CI uncertainty maps (B) and b = 0 image SNR maps (C). Overall, greater uncertainty was observed in diastole than in systole.

FIGURE 3.

Example systolic images with b = 0 and 350 s/mm² with 5 averages and a histogram of LV b = 0 SNR(A). Maps of tensor MD(B), FA (C), and Mode (D), with corresponding uncertainties and LV histograms. dMD was in general low compared with myocardial MD values, whereas dFA was somewhat closer to myocardial FA. Mode was not well separated from dMode.

FA, fractional anisotropy; LV, left ventricular; MD, mean diffusivity.

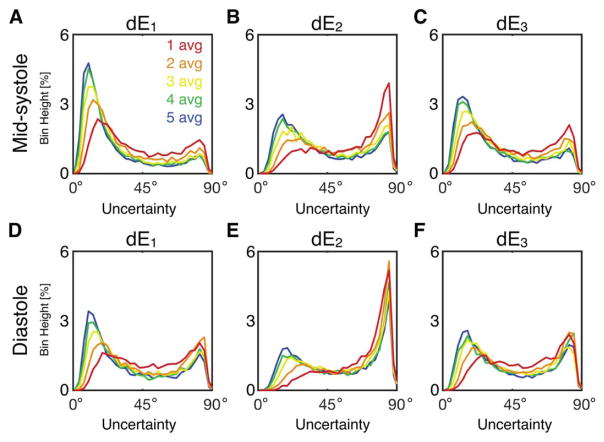
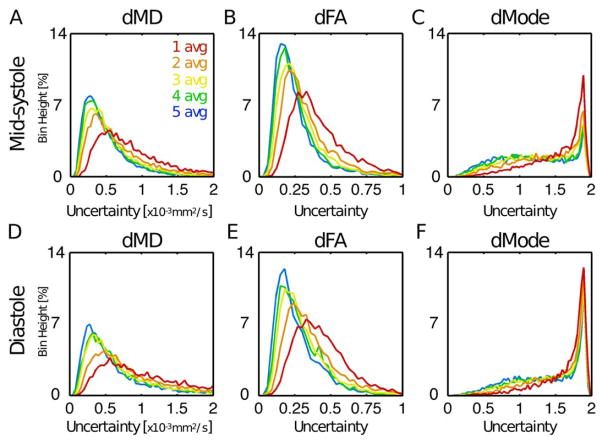
Histograms of tensor eigenvector uncertainty are shown in Figure 4 for midsystolic and diastolic cDTI, with N_avg = 1–5 pooled across all subjects at systole (Figures 4A–4C) and diastole (Figures 4D–4F). Uncertainty decreased with increasing signal averages; however, differences were minimal for N_avg ≥ 4 in systole (small differences between N_avg = 4 and 5 were observed in diastole). Uncertainty was generally larger for cDTI tensor metrics acquired in diastole than in midsystole. Analogous histograms of tensor invariant uncertainty (MD, FA, and Mode) are shown in Figure 5. Invariant uncertainty also decreased with increasing N_avg, however, with minimal differences for N_avg ≥ 4 in systole (small differences were again observed between N_avg = 4 and 5 in diastole). Differences in tensor invariant uncertainty histograms between midsystolic and diastolic cDTI were minimal.

FIGURE 4.

Histograms of uncertainty in tensor eigenvectors pooled from all LV voxels from all subjects at midsystole (A, B, C) and diastole (D, E, F) from acquisitions with N_avg = 1–5. Uncertainty decreased with additional signal averages, but differences were minimal for N_avg ≥ 4. Uncertainty was generally larger for diastolic cDTI.

FIGURE 5.

Histograms of uncertainty in tensor invariants pooled from all LV voxels from all subjects at midsystole (A, B, C) and diastole (D, E, F) from acquisitions with N_avg = 1–5. Differences between midsystolic and diastolic cDTI were minimal.

The median and maximum likelihood values from the uncertainty histograms generated for each subject are shown for N_avg = 5 in Table 1. Median and maximum likelihood uncertainties were lower in midsystole than in diastole for all parameters.

TABLE 1.

Maximum likelihood and median 95% confidence intervals for N_avg = 5 acquired at 2 cardiac phases (population mean ± SD)

		dE1 (degree)	dE2 (degree)	dE3 (degree)	dMD (x10−3mm2/s)	dFA (unitless)	dMode (unitless)
Midsystole	Maximum likelihood	9.7 ± 1.0	15.7 ± 1.0	12.1 ± 1.5	0.25 ± 0.02	0.13 ± 0.01	1.62 ± 0.47
	Median	15.5 ± 1.2	31.2 ± 3.5	21.8 ± 3.1	0.38 ± 0.02	0.20 ± 0.01	1.10 ± 0.08
Diastole	Maximum likelihood	17.8 ± 21.6	84.1 ± 1.5	42.7 ± 33.2	0.28 ± 0.07	0.16 ± 0.003	1.88 ± 0.02
	Median	31.9 ± 7.1	59.6 ± 6.8	40.5 ± 6.4	0.52 ± 0.09	0.23 ± 0.01	1.57 ± 0.11

95CI, 95% confidence interval.

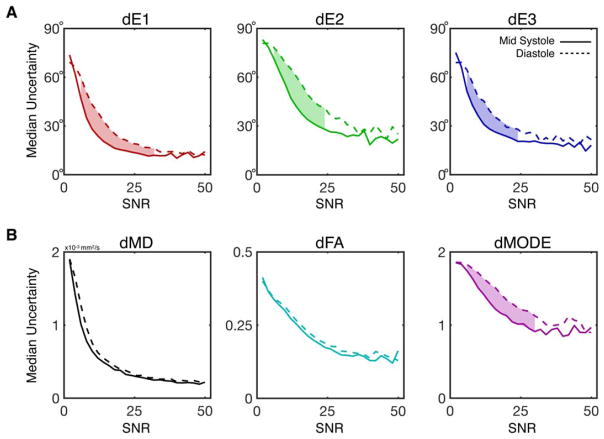
Median eigenvector and invariant uncertainties are plotted as functions of b = 0 image SNR in Figure 6. Uncertainty in all measured tensor metrics dropped consistently with increasing SNR. Uncertainty dropped faster with respect to SNR for midsystolic data, particularly in dE₁, dE₂, dE₃, and dMode, for which significant differences were observed between phases for intermediate SNRs as highlighted in Figure 6. Whereas the maximum observed SNR across all subjects and voxels was 95, histograms were only generated for SNR ≤ 50 due to a lack of sufficient data for meaningful statistics— as seen in the histograms of b = 0 SNR pooled across all subjects and cardiac phases, which are plotted for N_avg = 1–5 in Supporting Information Figure S2.

FIGURE 6.

Plots of median uncertainty in tensor eigenvalues (A) and invariants (B) as a function of b = 0 image SNR at midsystole (solid lines) and diastole (dotted lines). Median uncertainties and 95CI of the medians (not shown) were calculated from uncertainty distributions across all voxels and subjects with a particular b = 0 SNR (binned in SNR increments of 2) across images with N_avg = 1–5. Significant differences between midsystole and diastole were identified by nonoverlapping 95CI and are indicated by shaded regions between the plots. dE₁, dE₂, dE₃, and dMode were significantly lower at midsystole for moderate SNRs. Although differences in dMD or dFA were observed between phases, these differences did not reach statistical significance for any SNR bin.avg, average.

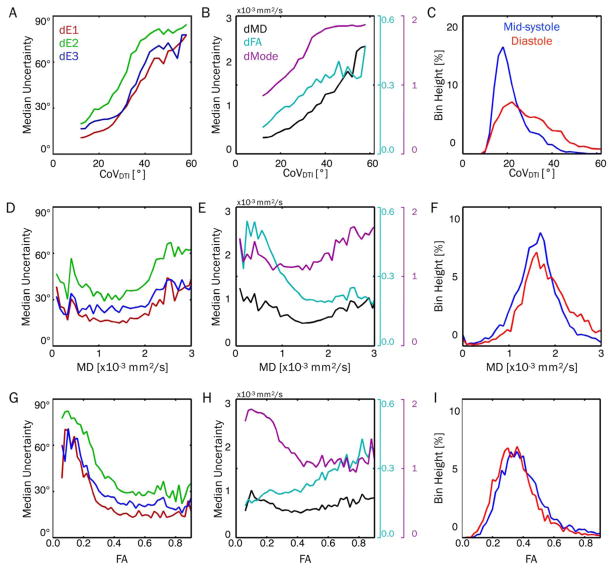
Median uncertainty values were plotted as functions of CoV_DTI, MD, and FA in Figure 7. There were clear increases in uncertainty for all parameters with increasing CoV_DTI (Figures 7A, 7B). Figure 7C shows global histograms of CoV_DTI, which demonstrates the increased CoV_DTI in the diastolic phase. Uncertainty in all parameters decreased with increasing MD up to approximately 1.5 × 10⁻³mm²/s and then increased at larger MDs for all parameters other than FA, which leveled off (Figures 7D, 7E). With increasing FA, uncertainty in all 3 tensor eigenvectors, MD, and Mode generally decreased, whereas FA uncertainty increased (Figures 7G, 7H). Histograms of myocardial MD and FA did not vary substantially between cardiac phases, although a larger population of MD values >2.5 × 10⁻³mm²/s were observed in diastole (Figures 7F, 7I).

FIGURE 7.

Plots of median uncertainty in tensor eigenvalues (left column) and invariants (center column) as functions of CoV_DTI (top row), MD (middle row), and FA (bottom row), with N_avg = 5 and pooled across all subjects and cardiac phases. Histograms of CoV_DTI, MD, and FA are also shown (right column) for midsystole and diastole. Median values were calculated from uncertainty distributions across all voxels and subjects with a particular CoV_DTI, MD, or FA. Uncertainty in all parameters increased with increasing CoV_DTI, indicating a strong sensitivity to bulk-motion– induced signal variations. This likely explains the increased uncertainty observed in diastolic cDTI, which had significantly higher CoV_DTI. Uncertainty in all parameters decreased with increasing MD up to approximately 1.5 × 10⁻³ mm²/s and then increased (aside from FA, which leveled off). With increasing FA, uncertainty in all 3 tensor eigenvectors, MD, and Mode generally decreased, whereas FA uncertainty increased. CoV, coefficient of variation; cDTI, cardiac DTI.

4.3 | Tensor evolution with varying signal averages

Measures of HA, HA_pitch, |SA2|, or |SA3| as a function of signal averages at either midsystole or diastole were not significantly different. Median myocardial values are tabulated for each parameter in Table 2.

TABLE 2.

Median and maximum likelihood eigenvector orientation metrics for two cardiac phases (population mean ± SD)

		Navg = 1		Navg = 5		Navg = 10
		Median	ML	Median	ML	Median	ML
Midsystole	HA	3.8 ± 3.5°	11.0 ± 22.1°	1.9 ± 3.8°	5.5 ± 8.6°	1.6 ± 3.1°	8.8 ± 22.3°
	HApitch	−1.2 ± 0.2°/%	NA	−1.2 ± 0.2°/%	NA	−1.2 ± 0.2°/%	NA
	|SA2|	40.9 ± 5.7°	24.6 ± 30.6°	38.2 ± 5.5°	22.7 ± 20.1°	36.6 ± 6.0°	23.7 ± v26.8°
	|SA3|	61.7 ± 4.3°	79.4 ± 12.6°	65.2 ± 5.5°	82.4 ± 9.4°	66.5 ± 4.8°	81.7 ± 10.2°
Diastole	HA	4.2 ± 4.5°	32.5 ± 38.2°	1.9 ± 3.4°	18.9 ± v35.6°	1.1 ± 4.1°	11.0 ± v27.9°
	HApitch	−1.3 ± 0.2°/%	NA	−1.3 ± 0.3°/%	NA	−1.2 ± 0.1°/%	NA
	|SA2|	41.2 ± 7.5°	36.0 ± 39.0°	37.8 ± 9.9°	23.0 ± 36.3°	35.0 ± 10.7°	13.9 ± 30.0°
	|SA3|	64.7 ± 7.1°	88.5 ± 3.2°	67.8 ± 7.7°	86.9 ± 8.0°	68.9 ± 8.1°	87.4 ± 6.0°

HA, helix angle; ML, maximum likelihood. NA, not applicable.

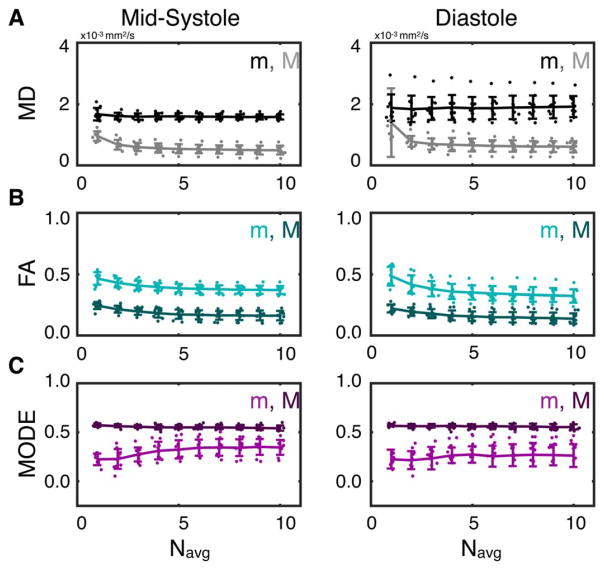
Median (m) and SD (σ) of MD, FA, and Mode across the LV myocardium are plotted for all subjects as functions of N_avg in Figure 8. No significant changes in m_MD were observed between any number of averages at either midsystole or diastole. Compared with N_avg = 1, σ_MD decreased significantly with N_avg ≥ 2 in midsystole (σ_MD,1avg = 0.95 ± 0.2 × 10⁻³ mm²/s vs. σ_MD,2avg = 0.67 ± 0.2 × 10⁻³ mm²/s, P = 8 × 10⁻⁴) and with N_avg ≥ 6 in diastole (σ_MD,1avg = 1.39 ± 1.1 × 10⁻³ mm²/s vs. σ_MD,6avg = 0.63 ± 0.2 × 10⁻³ mm²/s, P = 0.05).

FIGURE 8.

LV medians (m) and SDs (σ) of MD (A), FA (B), and Mode (C) from midsystolic (left) and diastolic (right) cDTI with N_avg = 1–10. Lines and error bars represent the population means and SDs across all subjects, and dots represent individual subject values. LVSDs decreased with increasing N_avg for all parameters but with diminishing changes with N_avg ≥ 4. Median FA values decreased with increasing N_avg, whereas median Mode values increased. Median MD values did not change with increasing N_avg.

Compared with N_avg = 1, m_FA decreased significantly with N_avg ≥ 3 at both midsystole (m_FA,1avg = 0.46 ± 0.05 vs. m_FA,3avg = 0.41 ± 0.04, P = 0.01) and diastole (m_FA,1avg = 0.48 ± 0.08 vs. m_FA,3avg = 0.38 ± 0.06, P = 4 × 10⁻³). Compared with N_avg = 1, σ_FA decreased significantly with N_avg ≥ 2 in midsystole (σ_FA,1avg = 0.24 ± 0.03 vs. σ_FA,2avg = 0.21 ± 0.03, P = 0.03) and with N_avg ≥ 3 in diastole (σ_FA,1avg = 0.22 ± 0.03 vs. σ_FA,3avg = 0.18 ± 0.04, P = 0.01).

A significant increase in m_Mode was observed in midsystole with N_avg ≥ 4 compared with N_avg = 1 (m_Mode,1avg = 0.22 ± 0.6 vs. m_Mode,4avg = 0.31 ± 0.9, P = 0.02). Compared with N_avg = 1, σ_Mode decreased significantly with N_avg ≥ 3 in midsystole (σ_Mode,1avg = 0.57 ± 0.02 vs. σ_Mode,1avg = 0.56 ± 0.01, P = 0.03). No corresponding significant differences were observed in diastole.

4.4 | Cardiac phase dependence of tensor parameters

With N_avg = 10, median myocardial MD was significantly lower in midsystole than in diastole (MD_SYS = 1.58 ± 0.09 × 10⁻³ mm²/s vs. MD_DIA = 1.91 ± 0.34 × 0⁻³mm²/s, P = 8 × 10⁻³), whereas FA was significantly higher in midsystole (FA_SYS = 0.37 ± 0.03 vs. FA_DIA = 0.32 ± 0.06, P = 0.03). No significant differences were observed between cardiac phases for any of the other parameters examined.

5 | DISCUSSION

The observed increase in bulk motion artifacts (higher CoV-_DTI) in diastolic cDTI compared with midsystolic cDTI is consistent with previous reports of the second-order motion-compensated diffusion encoding scheme.¹⁹ M₁M₂ nulled diffusion encoding relies on an assumption that cardiac motion can be well described by a second-order polynomial (i.e., only velocity and acceleration terms). Physiologic deviations from this assumption lead to bulk motion artifacts that appear as localized myocardial signal loss. If these artifacts are not reproducible from beat to beat, this leads to intershot signal fluctuations across cDTI images and consequently to elevated CoV_DTI measurements. The lower CoV_DTI values observed during systole thus indicate that systolic motion is more reproducible from beat to beat than diastolic motion. It is important to note, however, that CoV_DTI is not sensitive to systematic bias caused by higher order motion that is consistent from beat to beat. This means that the low CoV_DTI observed in systole does not necessarily imply complete motion compensation. However, the low level of intersubject variability in median midsystolic myocardial MD (Figure 8A) suggests that systolic motion is well characterized by second-order motion and thus is largely compensated by the CODE M₁M₂ nulled gradient waveform.

Diastolic motion, although smaller in magnitude than contractile motion, accords with a larger CoV_DTI than systolic motion. This indicates that diastolic motion does not meet the intrashot second-order assumption as closely (i.e., it is not fully compensated by the M₁M₂ nulling) and is more dependent on intershot (beat to beat) variations and changes in heart rate. These effects combine to cause deviations in the cDTI signal during an acquisition that result in elevated CoV_DTI. This is also reflected in an increase in intersubject variability in median myocardial MD in the diastolic phase (Figure 8B).

The strong positive correlation between CoV_DTI and median uncertainty (Figures 7A, 7B) indicates that bulk motion artifacts are a major driver of diffusion tensor uncertainty and explains the greater degree of uncertainty observed in diastolic cDTI.

The negative correlation between eigenvector uncertainty and MD for MD up to approximately 1.5 × 10⁻³ mm²/s (Figures 7D, 7E) indicates that sufficient diffusion weighting should be achieved to minimize uncertainty, echoing previous reports.^13,23,28 On the other hand, the increasing uncertainty with increasing MD beyond 1.5 × 10⁻³ mm²/s is likely caused by bulk motion effects. The negative correlation between eigenvector uncertainty and FA (Figures 7G, 7H) indicates that the achievable precision will likely vary in patients with conditions that reduce microscopic anisotropy such as diffuse fibrosis.²⁹

The uncertainty in diastolic diffusion tensor metrics could have been reduced by employing specialized image postprocessing algorithms to remove bulk-motion image artifacts such as constrained reconstruction³⁰ or maximum intensity projection.^27,31 These correction strategies would likely reduce the effects of physiological variability but limit the SNR gains from acquiring repeated acquisitions by omitting some of the acquired data. It is worth noting that this effect can be mitigated through postprocessing denoising techniques such as principal component analysis,³¹ which will have an unknown impact on tensor accuracy, precision, and optimal scan efficiency. It is also possible that a TR correction to account for heart rate variability, which was not implemented in this work, could reduce uncertainty.

Uncertainty varied substantially between tensor parameters and the 95CIs were the smallest for E⃗₁, MD, and FA; and they were the largest for E⃗₂, E⃗₃, and Mode. This indicates that SNR and scan time requirements vary depending on the parameters of interest in a given study. To contextualize these uncertainties, it is useful to consider examples of expected physiological variability. For example, the global HA_pitch value of 1.2% ± 0.2°/% observed in this work (which is in line with other in vivo studies^5,32 indicates an inherent range of myofiber orientations present in each imaging voxel. Assuming an LV wall thickness of 10mm and 2.0mm in-plane spatial resolution, each voxel will occupy approximately 20% of wall depth. Consequently, each voxel should contain a range of myofiber orientations, which vary by as much as 20° to 25°, thus placing a reasonable upper bound on the expected precision of E⃗₁. For a 5-min acquisition (5 averages, SNR~18), the maximum likelihood and median E⃗₁ precision were both well within this bound for midsystolic cDTI: dE₁ = 9.7 ± 1.0° and dE₁ = 15.4 ± 1.2°, respectively (Table 1).

In comparison to our observed eigenvector uncertainties, an ex vivo study of cDTI in rat hearts reported mean dE₁, dE₂, and dE₃ values of 3.7° ± 0.2°, 10.9° ± 0.4°, and 10.6° ± 0.5°, respectively.² However, this study was performed at high field (9.4T), employed gradients capable of amplitudes >10 × of standard clinical hardware (1T/m), and did not contend with physiological motion. Furthermore, the 0.1mm spatial resolution protocol resulted in substantially lower range of intravoxel myofiber orientations and thus less physiological variability within each voxel.

Our observed midsystolic uncertainties are consistent with Stoeck et al., who reported comparable E₁ uncertainties and lower E₂ uncertainties from 2 repeated measurements, with a similar M₁M₂ compensated SE-cDTI method in in vivo swine but with longer scans (14 signal averages).³³

Another example of expected physiological diffusion tensor variability is the 0.9 × 10⁻³ mm²/s MD increase observed in myocardial infarcts compared with healthy tissue observed by Nguyen et al.¹⁶ For the purpose of identifying infarcts, MD precision should thus be sufficiently small to detect this difference. The median MD uncertainty was within this difference for even just 1 average in midsystole (median dMD = 0.73 ± 0.04 × 10⁻³ mm²/s). However, the uncertainty histogram for 1 average (Figure 5) shows that nearly 40% of voxels exhibited MD uncertainties ≥ 0.9 × 10⁻³ mm²/s, a number that reduced to 11% with 5 averages (median dMD = 0.38 ± 0.02 × 10⁻³ mm²/s).

Our results indicate that little benefit in precision is achieved by increasing SNR beyond approximately 25 (Figure 6), which in this study corresponded to an approximately 10 min acquisition (i.e., 10 averages). Note that this study was conducted on a 3.0T clinical system with high-performance gradient hardware (Maximum gradient amplitude (G_max) = 76 mT/m), which reduces the minimum TE (65 ms) for the cDTI protocol compared with more commonly available gradient hardware sets (G_max = 40 mT/m and TE_Min = 85 ms). The baseline SNR on these systems will consequently be lower than those reported here—and will thus require longer scans to achieve the same degree of uncertainty. Further scan time increases will also be required for imaging at 1.5T or for nonoptimized M₁M₂-compensated diffusion encoding schemes with longer TEs.

Conversely, no significant changes in median myocardial tensor parameters or their SDs were achieved by increasing scan time beyond approximately 4 min, which corresponded with b = 0 image SNR = 16.0 ± 3.8 (i.e., 4 averages) (Figure 8). With low SNR (N_avg<4), we observed an upward bias in FA and a downward bias in Mode, which are both consistent with published reports based on numerical simulations.²³ Notably, no significant differences in median MD were observed between any number of signal averages. This indicates that MD measurement accuracy is very robust to variability and does not require long scan times. Whereas all reconstructions were performed using linear least squares, it has been shown that this can introduce bias in the presence of noise, and that this bias can be mitigated by using nonlinear least squares.³⁴ It is thus possible that nonlinear fitting could reduce the scan time requirements for accurate reconstruction.

The only significant differences observed between cardiac phases were an increase in MD and a decrease FA in diastole relative to midsystole. It is likely that the increase in MD in diastole stems from both the increased sensitivity to bulk motion in this phase¹⁹ and the increased variability of diastolic motion from beat to beat. The FA decrease may be due to an increase in myocardial blood volume in diastole, which contributes an isotropic diffusive compartment. This comes in contrast to the increase in FA in diastole observed with STEAM cDTI.³⁵ However, this increase was observed in comparison to peak systolic measurements as opposed to the midsystolic phase examined in this work.

The steepening of the secondary sheet angle in diastole compared with peak systole previously observed was not observed in this study. This may arise, in part, because the midsystolic phase imaged (TD_SYS = 100 ms corresponded with 35% of peak systole) does not correspond with a fully contracted myocardium, which limits the observable differences in sheetlet mobility. Furthermore, the relatively large E⃗₂ uncertainties indicate that the CODE-M₁M₂ method may not be as sensitive to sheetlet mobility, possibly because of the short diffusion times of the CODE-M₁M₂ sequence. This may also lead to sorting errors that can flip the order of eigenvectors, which could explain the secondary peaks in E⃗_1, E⃗₂, and E⃗₃ uncertainty observed at 90°.

This study only examines the precision in SE-EPI cDTI. Substantial differences may be observed in STEAM cDTI, which generally reports higher FA (FA_STEAM~0.5–0.6^35,36 vs. FA_SE~0.3–0.4 reported here and elsewhere³⁶ values than spin echo data, possibly due to the longer diffusion “mixing times” that allow diffusing molecules to probe larger length scales during diffusion encoding. The higher effective FA will likely reduce the inherent uncertainty in E¹. This may also reduce uncertainty in tensor Mode measurements, which can distinguish planar and linear diffusion anisotropy and have shown sensitivity to microstructural changes in pacing-induced heart failure³⁷ but were relatively imprecise in this study. However, STEAM cDTI has half the baseline SNR of SE-EPI cDTI and also double the scan time due to the need for 2 heartbeats per diffusion encode, which results in lower SNR efficiency.³⁶ Currently, however, it is unclear how the tradeoffs between FA and SNR efficiency affect the relative tensor uncertainty for the STEAM approach.

The number of unique diffusion encoding gradient orientations sampled in a DTI acquisition also impacts measurement precision.¹² Although studies in neurological and skeletal muscle tissue provide guidance in this regard (the 12-direction sampling scheme was used based on such guidance^12,38, it remains an open question whether additional signal averages or diffusion encoding directions more efficiently improve the precision of in vivo cDTI. Furthermore, it is unclear how to best employ EPI acceleration techniques such as parallel imaging and partial Fourier, which have complex relationships with image SNR in that they reduce SNR efficiency but often permit shorter TEs. Partial Fourier also has the added effect of increasing bulk motion sensitivity.³⁹ The b value of 350 s/mm² used in this study is lower than the optimal values proposed by Jones¹³ based on noise propagation (~700 s/mm² for the cardiac diffusivities observed in this study) or by Scott et al.²⁸ for STEAM cDTI (750 s/mm²). The b value of 350 s/mm² was chosen for this spin echo cDTI protocol to empirically balance bulk motion sensitivity, diffusion-weighted contrast, and SNR. However, the optimal b value and its effect on optimal scan efficiency for spin echo cDTI precision have yet to be determined and should be the focus of future study.

Although it would be interesting to observe the progression of tensor precision with N_avg>5, the bootstrapped technique used in this work requires a repeated acquisition and thus can only quantify uncertainties for datasets containing half of the acquired 10 averages. Model-based techniques such as the wild bootstrap,⁴⁰ however, can quantify precision without a repeated acquisition but require assumptions of the underlying uncertainties. It is unclear whether these approaches can be successfully applied to in vivo cDTI, and they have not been examined in this work.

6 | CONCLUSION

Acceptable levels of precision in E⃗₁, MD, and FA were achieved in a 5-min (per slice) free-breathing scan when using the CODE-M₁M₂ SE-EPI cDTI approach in vivo. Precision improved with increasing b = 0 image SNR, but gains were minimal for SNR ≥ 25, which corresponded with a ~10-min scan with this protocol. Lower uncertainty was observed in midsystolic compared to diastolic acquisitions, indicating that bulk cardiac motion effects are more consistently compensated by the M₁M₂ approach during midsystole.

Supplementary Material

Supplemental

Figure S1. Example diastolic images with b=0 and 350s/mm² with 5 averages and a histogram of LV b=0 SNR (A). Maps of tensor MD (B), FA (C), and Mode (D) with corresponding uncertainties and LV histograms. Uncertainty was generally higher in diastolic than in mid-systolic cDTI.

Figure S2. Histograms of b=0 image SNR within the LV with N_avg=1–5 for all subjects and phases. Median (±95CI) SNR increased from 7.4 ± 0.3 with N_avg = 1 to 16.7 ± 0.7 with N_avg = 5.