A Docked State Conformational Dynamics Model to Explain the Ionic Strength Dependence of FMN –Heme Electron Transfer in Nitric Oxide Synthase

Abstract

The FMN–heme interdomain electron transfer (IET) in nitric oxide synthase (NOS) is a key stage of the electron transport chain, which supplies the catalytic heme site(s) with the NADPH-derived electrons. While there is a recognition that this IET depends on both the electron tunneling and the conformational dynamics, the detailed mechanism remains unclear. In this work, the IET kinetics were measured by laser flash photolysis for a bidomain oxygenase/FMN (oxyFMN) construct of human inducible NOS (iNOS) over the ionic strength range from 0.1 to 0.5 M. The forward (heme → FMN, k_ETf) and backward (FMN → heme, k_ETb) intrinsic IET rate constants were determined from the analysis of the observed IET rates using the additional information regarding the conformational dynamics obtained from the FMN fluorescence lifetime measurements and theoretical estimates. Both k_ETf and k_ETb exhibit a bell-shaped dependence on the ionic strength, I, with the maximum rates corresponding to I ~ 0.2 M. This dependence was explained using a new model, which considers the effect of formation of pairs between the protein charged residues and solution ions on the docked state dynamics. The trial simulations of the intrinsic IET rate dependences using this model show that the data can be reproduced using reasonable energetic, structural, and chemical parameters. The suggested model can explain both the monophasic and biphasic ionic strength dependences and can be used to rationalize the interprotein/interdomain electron transfer rates for other types of protein systems where the docked state is sufficiently long-lived.

Graphical Abstract

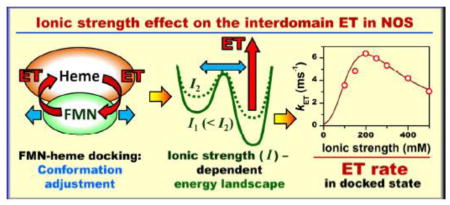
Laser flash photolysis results indicate that the ionic strength dependent solvent – protein ion pairs on the surfaces of the docked FMN and heme domains of nitric oxide synthase modify the energy landscape for structural optimization of the docking complex and affect the interdomain electron transfer rate.

Introduction

Nitric oxide synthases (NOSs) are indispensable enzymes in mammals because of the key roles of nitric oxide (NO) in signaling processes. NO is a reactive and generally short-lived free radical, and the NO signaling must therefore be tightly controlled through regulation of NOS activation. A dysregulated production of NO by NOS has been implicated in the pathology of several diseases that currently lack effective treatments, including stroke [1]. Despite significant progress in understanding of NOS enzymology, there is still much unknown about the details of the mechanisms of tight regulation of the NO production by NOS [2–4]. The large size and flexibility of NOS pose tremendous challenges to structural and mechanistic studies, and ultimately, to advancing our understanding of NOS control mechanism.

NOS is a homodimeric flavo-hemoprotein that catalyzes the 5-electron oxidation of L-arginine (L-Arg) to NO using NADPH and O₂ as co-substrates [5]. Each monomeric subunit has two domains joined by a calmodulin (CaM) binding linker: a C-terminal reductase domain consisting of discrete NADPH/FAD and FMN binding (sub)domains and an N-terminal heme-containing oxygenase domain, which is also referred to as heme domain.

There are three mammalian NOS isoforms: endothelial NOS (eNOS), neuronal NOS (nNOS), and inducible NOS (iNOS). In iNOS, the CaM-binding linker binds CaM at a basal level of Ca²⁺, while in nNOS and eNOS the CaM binding requires an increase in intracellular [Ca²⁺]. The CaM binding activates the NO synthesis by unlocking the FMN domain from the rest of the reductase domain and enabling conformational changes, which bring the FMN and heme domains together into a docking position required for the interdomain electron transfer (IET) event, where the NADPH-derived electron is transferred from FMN to the heme center. In addition to releasing the FMN domain from the docked FAD/FMN state, CaM facilitates the FMN-heme domain docking by imposing restrictions on the FMN domain rotational mobility and by docking itself alongside the FMN domain onto the heme domain [6, 7].

The structural rearrangements of NOS are described by the tethered shuttle model originally proposed by Salerno and Ghosh [8] (see Figure S1 of Supporting Information (SI)). The recent cryo-electron microscopy studies of the three NOS isoforms [6, 7, 9, 10] have confirmed the shuttling motion of the FMN domain and detected the docking of CaM and FMN domain onto the heme domain. The CaM and FMN domain docked states were also detected by pulsed electron paramagnetic resonance (EPR) [11, 12]. In addition, the pulsed EPR[11] and the FMN fluorescence lifetime [13, 14] measurements have determined the population of the docked state in NOS proteins.

The FMN-heme domain docking complex (the output state) is stabilized by electrostatic interactions between localized surface charges near the FMN and heme redox centers [6, 15] and by hydrophobic interactions [16]. Several docking models were proposed based on the domain interacting interface [11, 12, 15, 17–20], but the atomic-level structure of the FMN-heme domain docking complex has so far eluded the experimental determination. There is growing evidence that the docking complex is not static, but undergoes short-range structural adjustments (conformational sampling), which bring the docked domains to an IET-competent alignment [6, 18, 21].

The information about the domain dynamics in the docked state can be gleaned from comparison of the intrinsic docked state IET rate with the expected electron tunneling rate that can be predicted based on the output state models. Such an information can be obtained by laser flash photolysis (LFP) [3], which we have used in this work to investigate the kinetics of the FMN–heme IET in human iNOS bidomain oxygenase/FMN (oxyFMN) construct. This construct only consists of the oxygenase and FMN domains connected by the CaM-binding linker [22]. It represents a minimal electron transfer (ET) complex designed to favor the interactions between the FMN and heme domains [22]. Biochemical, kinetic, and spectroscopic results have shown that the CaM-bound oxyFMN construct is a valid model of the NOS output state for NO production [22–25]. Using iNOS oxyFMN simplifies the experiments because CaM is tightly bound. For similar experiments with other NOS isoforms, one has to use the oxyFMN construct with added CaM and sufficient concentration of Ca²⁺ to ensure the CaM binding [25].

Using the oxyFMN construct rather than the full-length enzyme allows one to more readily disentangle various processes contributing to the bulk FMN – heme IET and to obtain information specifically pertaining to the FMN/heme domain docking complex. For example, utilization of a similar bi-domain construct of P450 BM3 yielded useful results in understanding the full-length enzyme mechanism [26, 27]. To gain insight into the role of electrostatic interactions in the conformational dynamics of the undocked and docked states, the measurements were performed as a function of ionic strength. The bell-shaped ionic strength dependence of the IET rate obtained in our measurements is rationalized by considering the effect of ion pair formation on the short-range conformational dynamics of the FMN-heme domain docking complex.

Materials and Methods

Expression and purification of human iNOS oxyFMN and iNOSoxy proteins

The oxyFMN construct was obtained as previously described [28]. CaM binds tightly to iNOS and is retained in the purified iNOS oxyFMN protein. NOSoxy construct, in which only the heme-containing oxygenase domain is present, was prepared as reported earlier [29].

Laser flash photolysis

The IET kinetic measurements were conducted on an Edinburgh LP920 LFP spectrometer equipped with a Q-switched Continuum Surelite I-10 Nd:YAG laser and a Continuum Surelite optical parametric oscillator. The CO photolysis experiments were performed as described elsewhere.[24, 25, 29] Briefly, the LFP sample contained ~ 20 μM dRF and 5 mM fresh semicarbazide in a pH 7.6 buffer (40 mM bis-Tris propane, 2 mM L-Arg, 20 μM H₄B, 1 mM Ca²⁺ and 10 % glycerol). The ionic strength of the buffer was adjusted as needed by addition of NaCl. A sample without protein in a 1 cm cuvette sealed with a rubber septum was deaerated by bubbling with mixed CO/Ar (v/v 1:3) gas for 1h. The gas was blown over the sample surface to remove traces of O₂ added upon introduction of iNOS protein aliquots to the sample. The pre-degassed sample was illuminated for 2 – 4 minutes with white light to obtain a partially reduced form of [Fe(II) CO][FMNH^•]. The sample was then excited with a 446 nm laser flash to trigger the FMN heme IET, which was followed by the loss of absorbance of FMNH^• at 580 nm [28]. The rate of CO rebinding to the heme center(s) in oxyFMN construct was measured at 446 and/or 580 nm. The experiments were repeated two times for each ionic strength. The transient absorbance changes were averaged and analyzed using OriginPro 9.0 (OriginLab).

Fluorescence lifetime measurements

The FMN fluorescence decays were measured on a Mini-tau spectrometer (Edinburgh, U.K.) using time-correlated single-photon counting technique. The sample was excited at 450 nm with a picosecond pulsed diode laser (EPL-450, Edinburgh, U.K.) triggered at 5 MHz repetition rate. The emission was detected at 530 nm with a polarizer oriented at 54.7° with respect to the linearly polarized excitation light. This magic-angle polarization condition was used to avoid the effects of rotational diffusion on the intensity decays. The detected fluorescence intensity decays were analyzed using a biexponential model. The measurements were performed at least twice for each ionic strength.

Results and Discussions

Theoretical and experimental background

The detailed implementation and analysis of the LFP experiment for studying the IET in NOS was described in our previous work [30]. Briefly, a laser pulse at λ = 446 nm causes a dissociation of the CO molecule from the ferrous heme center in the IET-ready state (R-state) of NOS (see Figure 1). The heme center becomes IET-active (A-state) and capable of donating an electron to FMN semiquinone, FMNH^•. This ET converts the system to the final state (F-state). The backwards ET from FMN hydroquinone (FMN_hq) to the ferric heme center is also possible because the redox potentials of Fe(III)/Fe(II) and FMNH^•/FMN_hq are similar [22]. The intrinsic IET processes occur in the docked heme – FMN state and are described by the rate constants k_ETf for the forward IET from the ferrous heme to FMNH^• (from A- to F-state) and k_ETb for the backward IET from FMN_hq to the ferric heme center (from F- to A-state).

Figure 1.

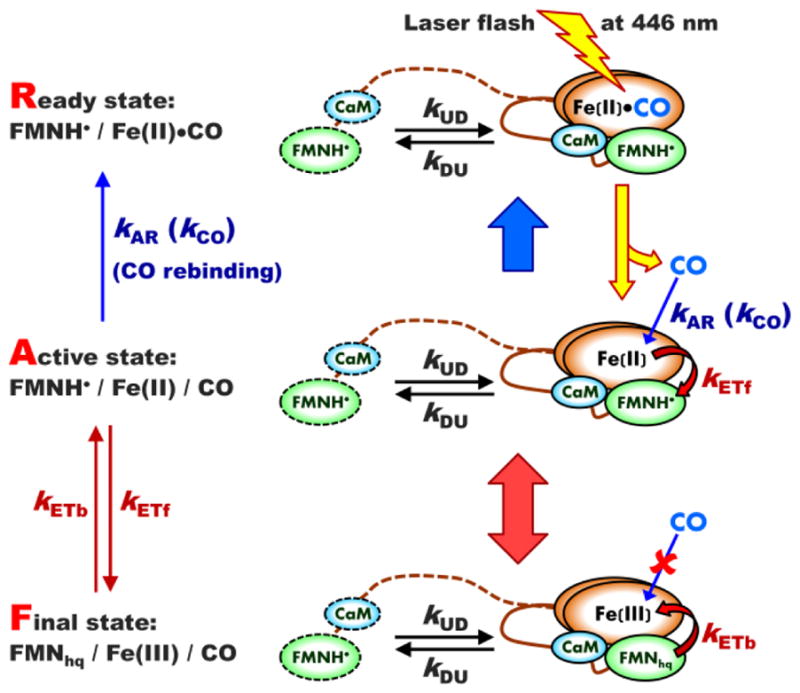
The scheme of an LFP experiment showing all relevant kinetic rate constants and using iNOS oxyFMN construct as an example. The ready (R) state, [FMNH^•][Fe(II)–CO], is prepared from the initial [FMN][Fe(III)] state by a continuous illumination of CO-containing NOS solution with white light for 2 – 4 minutes. The sample in the R-state is then illuminated by a laser flash at 446 nm, which results in dissociation of CO ligand from the ferrous heme center(s). The resulting [FMNH^•][Fe(II)] state is an active (A) state in terms of the forward heme → FMN IET. Such an IET converts the enzyme to the final (F) [FMN_hq][Fe(III)] state, from which the backward FMN → heme IET converting the system back to the A-state is possible. The solution CO molecules can rebind to the ferrous heme center(s) in the A-state, which gradually returns the system back to the R-state. The CaM-binding tether and the outlines of the FMN domain and CaM corresponding to the undocked state are shown by dashed lines, while those corresponding to the docked state are shown by solid lines.

The dissociated CO molecules slowly rebind to the ferrous heme in the A-state, gradually converting the system back to the R-state. The intrinsic CO rebinding rate (the conversion from A- to R-state) is described by the rate constant k_AR.

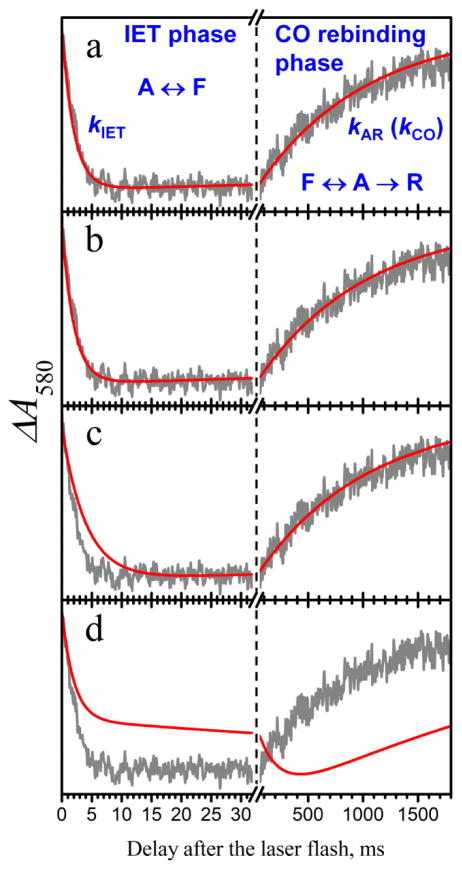
A typical LFP trace (see, e.g., the gray experimental trace in Figure 2) contains two regions where the absorbance changes happen on dramatically different time scales: the rapid decay at short times (milliseconds) after the laser flash and the slow increase that becomes dominant at a long time scale (seconds). Theoretically, the rapid decay represents a sum of two components. The minor (in terms of the amplitude) component corresponds to the IET from the docked FMN/heme state existing at the time of laser pulse and decays with the rate constant k = k_ET + k_UD + k_DU, where k_ET = k_ETf + k_ETb, and k_UD and k_DU are the docking and undocking rate constants, respectively (“UD” stands for “undocked → docked” and “DU” stands for “docked → undocked”). The major component stems from the IET in the whole pool of the NOS molecules and accounts both for intrinsic IET processes and the conformational dynamics responsible for formation and dissociation of the FMN – heme docked state. In a practical experiment, only the major rapid IET component is observed, while the minor one apparently is too fast and small (in terms of amplitude) to be detected. The observed rate constant corresponding to the major IET component is denoted byk _IET and is given by [30]:

$$k_{\text{IET}}=\frac{k_{\text{ET}}{k}_{\text{UD}}}{k_{\text{ET}}+k_{\text{UD}}+k_{\text{DU}}}$$ (1)

Figure 2.

Examples of LFP experimental and simulated traces. Gray trace in all panels, experimental LFP trace at I = 200 mM. Red traces are simulated for the following parameters: panel a, (k_UD, k_ET) = (100, 3.16) ms⁻¹; panel b, (k_UD, k_ET) = (0.505,100) ms⁻¹; panel c, (k_UD, k_ET) = (0.25, 100) ms⁻¹; panel d, (k_UD, k_ET) = (0.001,0.5) ms⁻¹. The following simulation parameters were similar for all panels: P_d = 0.16, k_ETf/k_ETb = 3.1, k_AR = 4.25 s⁻¹. The k_DU values derived from the abovementioned k_UD and P_d are 525 ms⁻¹, 2.65 ms⁻¹, 1.32 ms⁻¹, and 5.25 s⁻¹ for panels a, b, c, and d, respectively. The annotations in panel a show the assignment of the distinct phases of the LFP trace to the IET and CO rebinding processes and to the transitions between the R, A, and F-states shown in Figure 1. Note that in panel d the IET stage actually partly extends to the right-hand side of the Figure.

The long time scale (seconds) region of the LFP trace (observed as an increase in absorbance) corresponds to the gradual depopulation of the IET-active state due to the rebinding of the CO ligand to the ferrous heme center and is described by the rate constant k_CO. For an isolated oxygenase domain (NOSoxy construct) containing only the heme domain, k_CO equals to the intrinsic CO-rebinding rate constant, k_AR. For the bidomain oxyFMN construct, however, k_CO is smaller than k_AR because the A-state is also coupled to the F-state by the IET reactions (Figure 1). From k_CO (measured for the oxyFMN construct) and k_AR (measured for the NOSoxy construct) one can estimate the ratio of intrinsic ET rate constants, k_ETb and k_ET [30]:

$$\frac{k_{\text{ETb}}}{k_{\text{ET}}}\approx \frac{k_{\text{CO}}}{k_{\text{AR}}}$$ (2)

The rate constants k_IET determined from the LFP traces and the ratios k_ETf/k_ETb estimated from k_CO and k_AR are listed in Table 1, while the measured values of k_CO and k_AR are given in Table S1 of Supporting Information (SI).

Table 1.

k_IET and k_ETf/k_ETb values determined by LFP and P_d values determined by FMN fluorescence lifetime measurements.

Ionic Strength (mM)	kIET (s−1)	kETf/kETb	Pd
100	438.0 ± 2.8	2.41 ± 0.18	0.219 ± 0.012
150	475.3 ± 2.1	2.88 ± 0.19	0.187 ± 0.010
200	505.0 ± 1.4	3.09 ± 0.17	0.160 ± 0.009
250	460.0 ± 7.1	2.85 ± 0.23	0.143 ± 0.009
300	409.0 ± 9.9	2.61 ± 0.11	0.130 ± 0.010
400	321.0 ± 11.3	2.37 ± 0.15	0.110 ± 0.011
500	231.0 ± 5.7	2.08 ± 0.21	0.099 ± 0.010

Equation 1 shows that k_IET is determined by both the intrinsic IET and conformational rate constants. Therefore, various combinations of these parameters can result in the same observed IET rate. In particular, assuming k_ET ≫ (k_UD, k_DU) results in k_IET ≈ k_UD. This determines the smallest possible value of k_UD, which does not contradict to the measured k_IET. In the opposite extreme of k_ET ≪ (k_UD, k_DU), the observed IET constant equals to k_IET ≈ k_ET·P_d, where P_d = k_UD/(k_UD + k_DU) is the equilibrium population of the docked state.

As an example, Figure 2 compares the experimental LFP kinetics (gray traces) obtained at the ionic strength I = 200 mM with the results of numerical calculations for several combinations of intrinsic IET and conformational rate constants. The intrinsic CO rebinding constant, k_AR = 4.25 s⁻¹ (see the SI) was determined from the measurements on the iNOSoxy construct, the ratio k_ETf/k_ETb ~ 3.1 was estimated from k_CO and k_AR using Eq. 2, and the docked state population, P_d ≈ 0.16 was determined in FMN fluorescence lifetime measurements (see Table 1). Panels a and b in this Figure correspond to k_ET ≪ (k_UD, k_DU) and k_ET ≫ (k_UD, k_DU), respectively. A two-fold decrease of the conformational constants from those used in panel b results in significant disagreement at the short-time (IET) part of the LFP trace, while the long-time (CO rebinding) part of the trace is not sensitive to such relatively minor variations (panel c). Further decrease in the conformational rates, however, results in a significant disagreement for the long-time part of the trace. As an example, panel d corresponds to k_UD = 1 s⁻¹, on par with the correlation time attributed (tentatively) to the formation of the FMN-heme docked state in the single molecule FRET (smFRET) measurements [31]. Our numerical calculations thus show that such an assignment of the long (~1 s) correlation times in the smFRET measurements would be in a dramatic disagreement with the LFP kinetics. It is of note, however, that the smFRET work was done on an eNOS holoprotein, which may very likely possess different conformational rates from the iNOS oxyFMN protein studied here.

The above considerations and simulations show that, without information about the conformational rate constants, including the knowledge of P_d, any k_ET value within the range from k_IET to infinity can be in agreement with the measured k_IET. Unfortunately, the NOS conformational rate constants are not known from any direct experiments. Therefore, to narrow down the range of possible k_ET values, we will rely on additional experiments and theoretical estimates that can give us more information about the conformational rate constants and docking equilibrium.

FMN fluorescence lifetime measurements

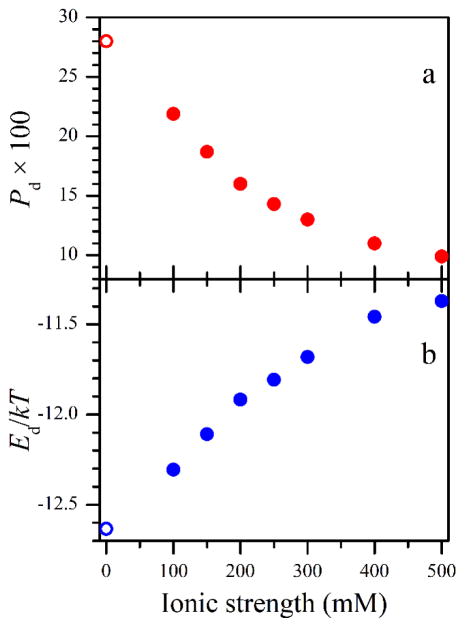
The FMN fluorescence lifetime measurements have been used in the literature to determine the population of the FMN – heme domain docked state, P_d, in various NOS isoforms and constructs [13, 14]. In this work, similar measurements have been performed for the human iNOS oxyFMN construct as a function of ionic strength. A representative experimental FMN fluorescence trace (deconvoluted from the instrument response function, see SI) is shown in Figure 3 along with the simulated exponential functions corresponding to the FMN fluorescence in the docked and undocked states. The fluorescence traces were with good accuracy biexponential, with the major slow exponent (dashed red trace in Figure 3) corresponding to the undocked state and the minor fast exponent (solid blue trace in Figure 3) corresponding to the docked state [14]. The characteristic decay time of the slow exponent was about 4 ns, although it decreased monotonically with the ionic strength from 4.3 ± 0.2 ns at I = 100 mM to 3.6 ± 0.2 ns at I = 500 mM. The fast exponent decay time was 0.8 ± 0.1 ns and did not depend on I. The obtained decay times are in a good agreement with the results of fluorescence lifetime measurements on iNOS oxyFMN sample in the literature [14]. The relative amplitude of the minor (fast) exponent directly corresponds to the population of the docked state. The P_d values obtained in our measurements are presented in Table 1 and in Figure 4a.

Figure 3.

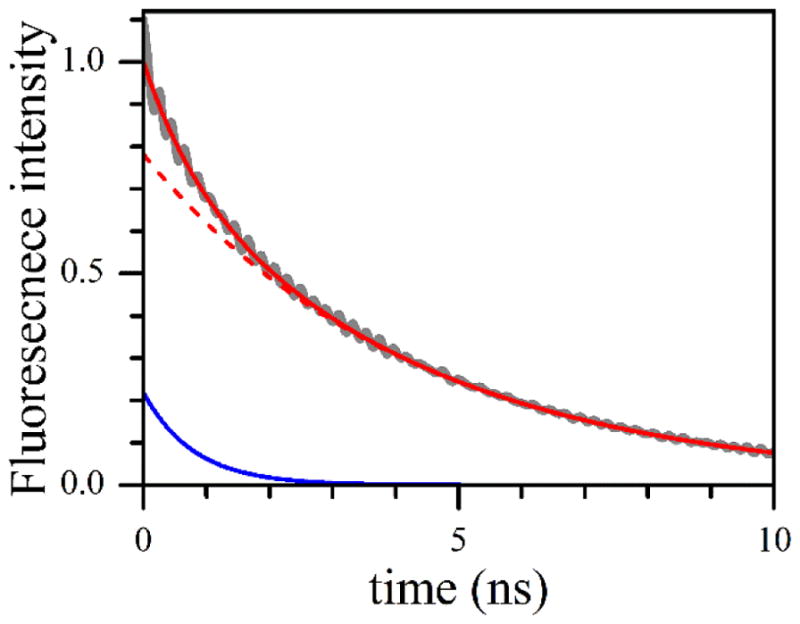
Gray trace, the experimental transient FMN fluorescence trace obtained by the deconvolution of the raw experimental trace and the instrument response function (see the SI for details). The experimental trace corresponds to I = 100 mM. Solid red line, the least squares fit using two exponential functions. The constituent exponents are shown by the red dashed line (amplitude = 0.78; decay time = 4.3 ns) and solid blue line (amplitude = 0.22; decay time = 0.8 ns). The small-amplitude 6 GHz oscillation in the experimental trace is the result of data processing (see the SI).

Figure 4.

Panel a, the docked state populations found from the FMN fluorescence lifetime measurements. Panel b, docked state stabilization energies (relative to kT at room temperature) estimated using Eq. 3 from the P_d values shown in panel a. The P_d value at I = 0 mM shown by the open circle in panel a was reported in ref. 13, and the corresponding E_d value (open circle in panel b) was estimated in this work.

From these data, one can see that, as the ionic strength increases, the docked state population monotonically decreases. This dependence is caused by the screening of the charged protein residues on the domains in general and at the domain docking interface in particular. In our measurements, the largest P_d value of about 0.22 was observed for the smallest ionic strength of 100 mM (see Table 1). An observation of P_d ≈ 0.28 made without added NaCl (I ~ 0 mM) in an earlier work[14] is in agreement with the trend observed in our measurements.

The obtained P_d values can be used to estimate the stabilization energy of the docked state, E_d. For this, one can write the Boltzmann equilibrium as:

$$P_{\mathrm{d}}=\frac{V_{\mathrm{d}}{\mathrm{\Omega }}_{\mathrm{d}}{\psi }_{\mathrm{d}}exp(-E_{\mathrm{d}}/kT)}{V_{\mathrm{u}}{\mathrm{\Omega }}_{\mathrm{u}}{\psi }_{\mathrm{u}}+V_{\mathrm{d}}{\mathrm{\Omega }}_{\mathrm{d}}{\psi }_{\mathrm{d}}exp(-E_{\mathrm{d}}/kT)}$$ (3)

where V_d and V_u are the characteristic volumes available for the FMN domain in the docked and undocked states, respectively (the heme domain center is taken as the coordinate origin). Similarly, Ω_d and Ω_u are the corresponding ranges of angular orientations of the FMN domain docking region with respect to the coordinate system with the origin at the FMN domain center (this orientation can be described by the polar and azimuthal angles, θ and ϕ, respectively). Finally, ψ_d and ψ_u are the ranges of angular orientations of the FMN domain docking region corresponding to the rotation of the FMN domain around the normal passing through the center of the docking area. This angle is responsible for the proper positioning of CaM once the FMN domain is docked onto the heme domain.

These parameters can be estimated from the characteristic dimensions of the domains and the tether shown in Figure 5 (see the SI for details): V_u ~ 5·10⁶ ų (estimated using the characteristic length of the FMN – heme domain tether of 110 Å and taking into account the position restrictions imposed by the size of the heme domain), V_d ~ 10³ ų (as obtained from the diameter of the docking area of about 15 Å [18, 19] and the maximum possible distance between the FMN and heme domain surfaces in the docked state of about 5 Å), Ω_u ~ 4π (corresponds to all orientations being possible), Ω_d ~ 1 (corresponds to the diameter of the docking area of about 15 Å), ψ_u ~ 2π (all orientations possible), and ψ_d ~ 0.5 (corresponds to a ~15 Å segment at a ~30 Å radius). Thus, for P_d ≈ 0.22 obtained at I = 100 mM, one can estimate E_d ~ −12.3kT, while for P_d ≈ 0.1 obtained at I = 500 mM, the absolute value of stabilization energy is about 0.9kT smaller: E_d~ −11.4kT. The obtained dependence E_d(I) is shown in Figure 4b.

Figure 5.

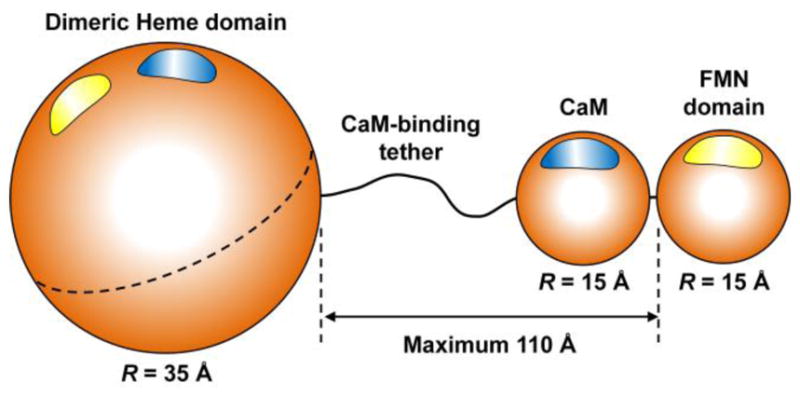
The structural model of NOS oxyFMN construct used in this work for estimating the diffusion-controlled domain docking rate constant, k_UD, and stabilization energy of the FMN-heme domain docking complex, E_d. The NOS domains and bound CaM are represented by spheres, whose characteristic diameters are indicated in the Figure. The maximum edge-to-edge distance between the heme and FMN domains determined by the tether length is also indicated. See the SI for details regarding the sizes of the domains and CaM and the tether length. The blue and yellow spots on the surfaces of the modules represent docking regions (hot spots). The heme domain is taken as dimeric (as indicated by the dashed equatorial line), but FMN and CaM correspond to one monomeric subunit only (they dock to the part of the heme domain corresponding to the other subunit).

One must note that the parameters V_u, Ω_u, and ψ_u used for these calculations are probably overestimated because the positional and orientational restrictions imposed by the tether are not considered. Therefore, the obtained absolute values of E_d can be considered as an upper bound to the actual values. However, since E_d is a logarithmic function of (Ω_uV_uψ_u)/(Ω_dV_dψ_d), this estimate is very tolerant to even large variations of model parameters. For example, even assuming Ω_uV_uψ_u to be an order of magnitude smaller than the value used for our calculations above will only reduce the estimated |E_d| by 2.3kT.

The docked state stabilization energy is obviously contributed to by both the Coulomb interaction between the charged residues located at the docking interface and the hydrophobic interaction. Unfortunately, the FMN fluorescence lifetime experimental data do not allow one to disentangle these contributions.

The experimental P_d (i.e., k_UD/(k_UD+k_DU)) values can be used to calculate the dependence of k_UD/k_DU on the ionic strength. Such a calculation shows that within the range of I from 0 to 500 mM, k_UD/k_DU decreases by nearly four-fold. Qualitatively, the screening of the charged residues at the domain surfaces by the solution ions should affect both, k_UD and k_DU. In the next section, we will show, however, that the effect on k_UD, at least for I ≥100 mM, is negligible, and the changes in P_d can be solely attributed to the changes ink _DU.

Estimating k_UD from domain diffusion considerations

As discussed above, the intrinsic IET rate constant estimated from the observed bulk IET rate heavily depends on the magnitudes of the conformational rate constants: without any information on k_UD and k_DU, one can only state that k_ET ≥ k_IET/P_d. The FMN fluorescence lifetime measurements have provided us with the P_d values, but this is still not sufficient for a meaningful interpretation of the LFP results in terms of k_ET. Therefore, to narrow down the range of possible k_ET estimates, we will now make an order-of-magnitude estimate of the docking rate constant, k_UD, by considering the diffusion of the FMN domain relative to the heme domain. In doing so, we will use a model, which treats the motion of the tethered FMN domain as a free diffusion of a particle representing the FMN domain in a spherical volume. The center of this spherical volume is occupied by the particle representing the heme domain. Based on the characteristic structural parameters of NOS (see Figure 5), the quantitative parameters of our model are as follows: the radius of the sphere, R_s ~ 160 Å; the radius of the central particle representing the heme domain, R_c ~ 50 Å (a sum of characteristic radii of the heme and FMN domains); the particle modeling FMN in this model represents a dimensionless point. The relative diffusion coefficient of the FMN particle, D, is a sum of the estimated diffusion coefficients of the heme domain and the block consisting of FMN domain and CaM, which we will consider as a single unit. Based on the molecular masses of (CaM + FMN domain) and heme domain (36 and 50 kDa, respectively), one can estimate D ~ 10⁻⁶ cm²/s = 10¹⁰ Ų/s [32].

The docking complex formation rate in such a model is:

$$k_{\text{UD}}=k_{\mathrm{c}}(I)F$$ (4)

where k_c(I) is the rate of collisions, which is controlled by diffusion in the presence of electrostatic interaction between the domains, and F is a steric factor describing the average probability of correct relative orientations of the domains that can lead to the formation of the docked state. The rate of collisions can be expressed as a product:

$$k_{\mathrm{c}}(I)=k_{\mathrm{c}0}\mathit{\Phi }(I)$$ (5)

where k_c0 is the rate of collisions in the absence of the electrostatic interactions and Φ(I) is the factor accounting for the electrostatic interaction. Using the spherical model described above, k_c0 can be estimated as [33]:

$$k_{\mathrm{c}0}\approx \frac{3D{R}_{\mathrm{c}}}{R_{\mathrm{s}}^3}$$ (6)

Using the model parameters (R_c, R_s, and D) described above, one finds k_c0~ 3.7·10⁵ s⁻¹.

The electrostatic factor, Φ(I), is given by [34]:

$$\mathit{\Phi }(I)={\left[R_{\mathrm{c}}\underset{R_{\mathrm{c}}}{\overset{R_{\mathrm{s}}}{\int }}\frac{exp(E(I)/kT)}{r^2}dr\right]}^{-1}$$ (7)

where E(I) is the electrostatic interaction energy (modeling the protein domains by uniformly charged spheres):

$$E(I)=k_{\mathrm{e}}\frac{n_1{n}_2{e}^2}{\epsilon r}exp(-r/\lambda (I))$$ (8)

In this expression, k_e is the Coulomb’s constant, n₁ and n₂ are the total numbers of electron charges on the domains, e is the charge of the electron, ε is the dielectric constant, and λ(I) is the Debye length [35–37]:

$$\lambda (I)=\sqrt{\frac{\epsilon kT}{8\pi k_{\mathrm{e}}{e}^2{N}_{\mathrm{A}}I}}$$ (9)

where N_A is the Avogadro’s number and I is in mM (which is equal to mol/m³). For water at room temperature (ε ≈ 80, T ≈ 300 K), λ(I) ≈ (96 Å·mM^1/2) ·I^−1/2.

To estimate the effect of electrostatic interaction on the FMN domain diffusion, we have calculated the electrostatic factor, Φ(I), by using numerical integration of Eq. 7. Figure 6 shows representative results of these calculations in the form of difference between the rates with and without the electrostatic interaction relative to the rate without the electrostatic interaction, i.e., (k_c(I)-k_c0)/k_c0. The red trace in the Figure corresponds to the interaction between the heme and FMN domains in iNOS, which contain total unbalanced charges of +10 and +4 on the solvent accessible surfaces of the domains; the unbalanced charge numbers can be calculated from the known amino acid sequences and the crystal structures of the human iNOS heme and FMN domains (pdb 1NSI and 3HR4, respectively). The docking interfaces, however, contain opposite charges, the electrostatic attraction between which dominates at short distances. Figure 6 shows that even for n₁n₂ as large as 100, the effect of ionic strength exceeding I = 100 mM on k_c is within 1.5% and can be neglected, i.e., one can safely use k_c(I) = k_c0~ 3.7·10⁵ s⁻¹.

Figure 6.

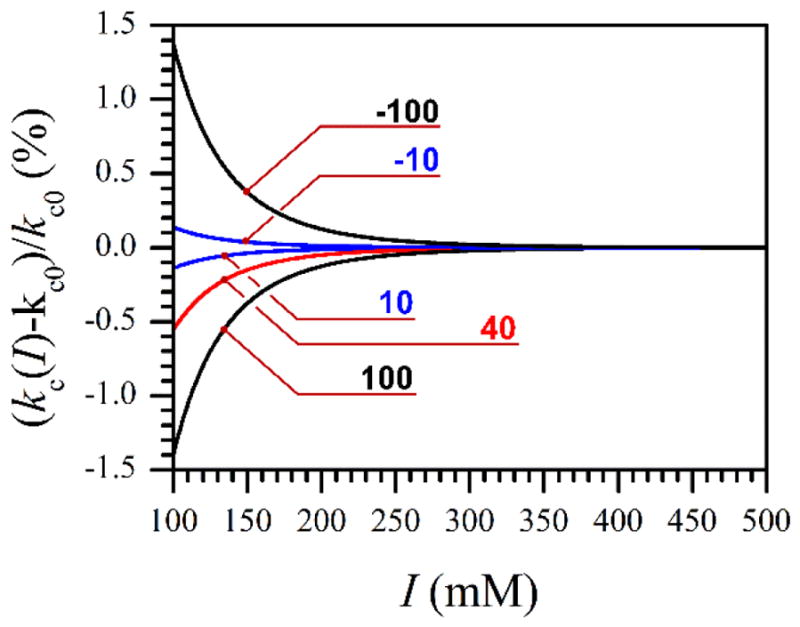
Effect of ionic strength on the protein/domain collision rate, numerically calculated using Eqs. 5 and 7–9 for several different protein charges, n₁ and n₂ (see Eq. 8). The numbers at the traces indicate the products n₁n₂, for which these traces were calculated.

Let us now consider the steric factor, F, in Eq. 4. This factor describes the probability for the domains in a collision encounter to have a proper relative orientation that will allow them to form the interdomain docking complex. For NOS, one has to specifically take into account that the productive docking of the FMN domain is facilitated by the simultaneous docking of CaM, which is bound to the FMN-heme domain tether. Therefore, F is a product of the steric factors corresponding to the FMN domain and CaM docking, F_FMN and F_CaM, respectively: F = F_FMN × F_CaM.

To describe this interaction anisotropy, a notion of a “hot spot” is introduced for each of the domains. In terms of hot spots, the formation of the docking complex in a given collision encounter is possible if the hot spots on the FMN and heme domains overlap. The angular size of the hot spots equals to the maximum angular mismatch, for which the formation of the docking complex is still possible. By using the characteristic angular sizes of the hot spots δ_FMN ~ 55° – 75° for FMN domain and δ_heme ~ 25° – 35° for heme domain (correspond to the approximate sizes of the docking areas of 15 – 20 Å) one can estimate:[38] F_FMN ~ sin²(δ_FMN/2)sin(δ_heme/2) ~ 0.05 – 0.1.

The second steric factor, F_CaM, is responsible for the proper orientation of the FMN-CaM block on the surface of the heme domain, assuming the FMN domain has already achieved the docking position. This factor can be estimated from the angular size of the CaM docking region as seen from center of the docking region of the FMN domain, δ_CaM ~ 28° – 38°, and therefore F_CaM ~ δ_CaM/360° ~ 0.08 – 0.1. Thus, the total steric factor is: F = F_FMN × F_CaM = ~ 4·10⁻³ – 10⁻². Substituting the estimated k_c (3.7·10⁵ s⁻¹) and F into Eq. 4 results in k_UD ~ (1.5 – 3.7) ·10³ s⁻¹.

Although in the above model the range of relative domain motion is limited, in other respects the presence of the tether between the heme and FMN domains is neglected. The numerical simulations of diffusion of a tethered ball [39] (with the ball size and tether length comparable to those of the domain size and tether length in iNOS) show that the presence of a tether can slow the domain diffusion down, but this effect is not dramatic and can result in decrease of D and the rate of collisions, k_c, by less than an order of magnitude. In addition, the tether can limit the range of accessible relative orientations of the domains, but this effect is only pronounced when the tether is close to full extension. It is conceivable that when the tether is wrapped around the heme domain, the orientational limitations can effectively result in some increase of the steric factor, F. However, its effect on k_UD is likely to be cancelled out by the decrease of k_c.

Ionic strength dependence of k_ET from the LFP measurement results

Armed with the P_d and k_UD values (estimated experimentally and theoretically, respectively), we can now analyze the LFP measurement results to estimate the intrinsic IET rate, k_ET, and its dependence on the ionic strength. For this, Eq. 1 can be rewritten as:

$$k_{\text{ET}}=\frac{k_{\text{IET}}}{P_{\mathrm{d}}(1-k_{\text{IET}}/k_{\text{UD}})}$$ (10)

As shown above, k_UD practically does not depend on the ionic strength within the studied range of I between 100 and 500 mM. The minimum possible k_UD corresponds to k_ET → ∞ and equals to k_IET (see Eq. 1). The minimum k_UD value valid for all values of I is then simply equal to the largest k_IET = 505 s⁻¹ obtained at I = 200 mM (see Table 1). Given the estimates in the previous section, the actual k_UD is expected to be on the order of 10³ s⁻¹.

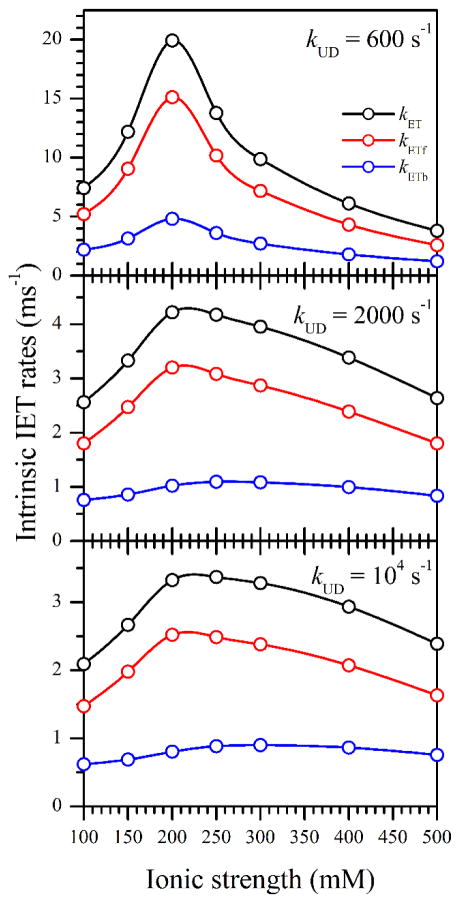
To establish the general features of k_ET(I), we have performed the calculations using Eq. 10 for several k_UD values between 600 s⁻¹ (to keep the denominator reasonably far from zero) and 10⁴ s⁻¹ (which results in k_ET within 5% from the asymptotic values corresponding to k_UD → ∞). The results of the calculations are shown in Figure 7. In addition to k_ET(I), Figure 7 shows the ionic strength dependences of the forward and backward intrinsic IET rates, k_ETf and k_ETb, respectively, which were calculated from k_ET and the k_ETf/k_ETb ratios (Table 1). One can see that regardless of our assumptions about k_UD, the dependences k_ETf(I) and k_ETb(I) are bell-shaped (biphasic), with the maximum at I = 200 – 250 mM.

Figure 7.

Ionic strength dependences of the intrinsic IET rates obtained from the bulk IET rates, k_IET, presented in Table 1. The k_ET values were calculated using Eq. 10 and the P_d values taken from Table 1. The docking rate constants, k_UD, used in these calculations are shown in the panels. The separate forward (k_ETf) and backward (k_ETb) intrinsic IET rates were calculated using the k_ETf/k_ETb ratios given in Table 1.

Explaining k_ET(I) based on conformational sampling model

In this section, we will discuss the intrinsic IET rate, which reflects the events (including the ET per se) happening in the FMN-heme docked state. The docking complex formed in a collision encounter of the FMN and heme domains may initially have a structure (i.e., the domain alignment) not optimal for an efficient IET. The ensuing sequence of short-range rearrangements often referred to as the conformational sampling, however, may optimize the docking structure and allow the IET to take place during the lifetime of the docking complex. We will consider below a functional model of the docking complex, which links the intrinsic IET rate, k_ET = k_ETf + k_ETb, to the conformational sampling and electron tunneling rates and eventually explains the dependence of k_ET on the ionic strength.

Our docking complex model is schematically shown in Figure 8. The docking hot spot area is divided into two regions: the non-tunneling region, from where the ET is negligible or not possible, and the tunneling region, from which the ET occurs with the tunneling rate constant k_t. The electrostatic potential energies within these regions are assumed to be constant and equal to E_nt and E_t + E_nt, respectively. These regions are separated by the potential energy barrier of height E_b (absolute energy E_b + E_nt). Since only the relative energies are important for the kinetics, it is convenient to assume E_nt = 0.

Figure 8.

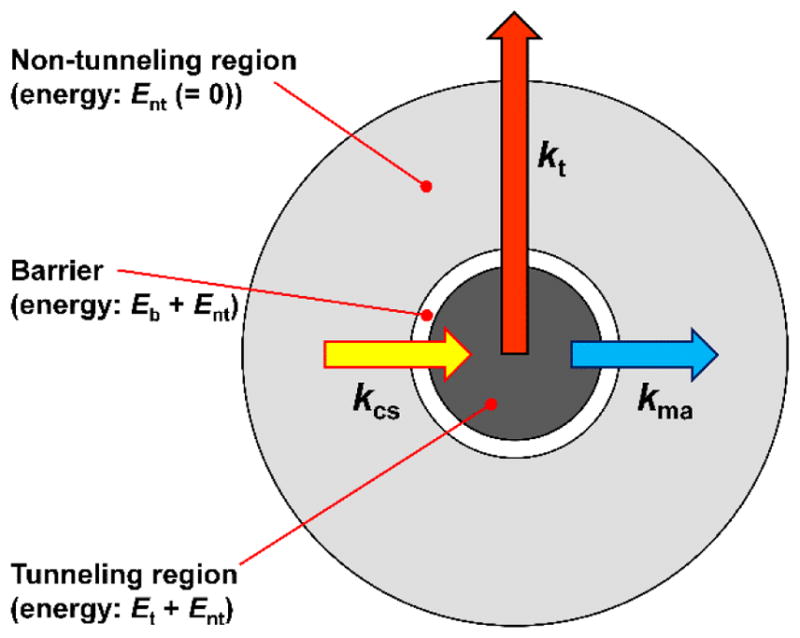
The docked state model used for describing the dependence of the intrinsic IET rate constant, k_ET, on the electron tunneling rate constant, k_t, and the diffusion-controlled conformation sampling and domain misalignment rate constants (k_cs and k_ma, respectively).

From the non-tunneling region, the docking complex can make a transition to the tunneling region with the conformational sampling rate constant k_cs (yellow arrow in Figure 8). From the tunneling region, the docking complex can either transition back to the non-tunneling one with the misalignment rate constant k_ma (blue arrow in Figure 8) or undergo an IET with the tunneling rate constant, k_t (red arrow in Figure 8). In addition, depending on the rates of these internal processes, one might need to consider the docking complex formation and dissociation rates, k_UD and k_DU, respectively. In such a model, the ionic strength dependence of the overall intrinsic ET rate, k_ET, is mostly caused by the variations in E_t and E_b resulting from screening of the interacting electric charges at the domain docking interface by the solution ions. We will formulate a mathematical model for this dependence below. First, however, we need to make an order of magnitude estimate of the pertinent rate constants k_cs, k_ma, and k_t.

The conformational sampling rate constant k_cs in our model is obviously:

$$k_{\text{cs}}=k_{\text{cs}0}exp(-E_{\mathrm{b}}/kT)$$ (11)

where we consider E_b ≥ 0. The preexponent, k_cs0, is given by the expression similar to Eq. 4, with the collision rate, k_c, determined by the relative size and position of the tunneling area and the diffusion coefficient describing the relative lateral diffusion of the docked domains. For a circular tunneling area of radius r in the center of the hot spot of radius R [40]:

$$k_c\approx \frac{2D}{R^{2}ln(R/r)}$$ (12)

To account for the surface interactions between the docked domains, the diffusion coefficient will be taken one order of magnitude [41] smaller than that used in estimating k_UD: D ~ 10⁹ Ų/s. Then, under reasonable assumptions that r is significantly smaller than R (R ~ 7 – 10 Å), but greater than 1 Å, one can estimate k_c~ 10⁷ s⁻¹.

To estimate the steric factor, F (see Eq. 4), we have to take into account that the rotational mobility of the docked FMN domain is strongly limited by CaM, which docks to the heme domain alongside the FMN domain [6, 11, 18] and in this way facilitates the proper FMN domain docking and orientation [7]. Based on these considerations, the steric factor should be reasonably large, and we can safely assume F ~ 1. The resulting conformational sampling rate is then estimated as k_cs0 ~ 10⁷ s⁻¹, based on the expression similar to Eq. 4.

The misalignment rate constant, k_ma, can be found by considering the Boltzmann equilibrium between the non-tunneling and tunneling states:

$$k_{\text{ma}}\approx k_{\text{cs}}\left(\frac{V_{\text{nt}}}{V_{\mathrm{t}}}\right)·exp(E_{\mathrm{t}}/kT)=k_{\text{cs}0}\left(\frac{V_{\text{nt}}}{V_{\mathrm{t}}}\right)·exp(-(E_{\mathrm{b}}-E_{\mathrm{t}})/kT)$$ (13)

In this expression, V_nt and V_t are the characteristic volumes of the non-tunneling and tunneling states, respectively. Since we are considering the conformational sampling as surface diffusion, these volumes actually represent areas of the parts of the docking interface surface corresponding to the non-tunneling and tunneling situations. The characteristic radius of the tunneling area is between 1 Å and ~ 10 Å, one can therefore expect V_nt/V_t to be between 1 and 100. The energy difference E_b –E_t in Eq. 13 represents an energy barrier for the domain misalignment process.

The rate constant of the electron tunneling between the FMN and heme domains, k_t, can be estimated using the “Dutton’s ruler” [42]:

$${log}_{10}{k}_{\mathrm{t}}=15-0.6R_{\mathrm{t}}-3.1{(\mathrm{\Delta }G+\lambda )}^2/\lambda$$ (14)

where R_t is the distance between the ET cofactors and ΔG and λ are the Gibbs free energy and reorganization energy, respectively. Using the edge-to edge heme – FMN distance R_t ≈ 11.2 – 13.1 Å arising from the docking models [12, 19] and supported by pulsed electron paramagnetic resonance (EPR) measurements [12], ΔG ≈ −0.03 eV, and λ ≈ 1.4 eV [43], the tunneling IET rate constant can be estimated as k_t ~ 10⁴ – 10⁵ s⁻¹.

Note that the above estimates of k_cs, k_ma, and k_t are order of magnitude only. Therefore, we did not make any distinction between such constants corresponding to the forward and backward ET. The possible differences between the parameters corresponding to the forward and backward ET should be insignificant, though, because the ratios k_ETf/k_ETb found from the analysis of the LFP data are on the order of 1 (see Table 1).

Since k_cs ≫ (k_UD, k_DU) and k_t ≥ (k_UD, k_DU), the conformational and ET steps in the docked state can, to a good accuracy, be considered in isolation from the large-scale docking/undocking rearrangements. The intrinsic ET in the docked state can therefore be described by the set of kinetic equations similar to those used for deriving Eq. 1 [30], and after the appropriate change in notation, the same equation can be used to describe the intrinsic IET rate constant in the docked state, k_ET:

$$k_{\text{ET}}=\frac{k_{\mathrm{t}}{k}_{\text{cs}}}{k_{\mathrm{t}}+k_{\text{cs}}+k_{\text{ma}}}$$ (15)

We will now introduce a model that enables us to qualitatively explain the dependence of k_ET on the ionic strength. The continuum electrostatic models discussed in the literature [35, 44–46] were mostly aimed at accounting for the electrostatic interactions in the diffusion controlled rate of protein collision encounters and are not directly applicable to the conformational sampling in a docking complex, where the distances between the charged amino acid residues responsible for stabilizing the docked state are relatively small (just a few Å) and ion pairing effects are significant; see the relevant discussion in [47].

Unlike the previous models based on the Debye-Hückel theory, which consider the charge screening by the “cloud” of solution ions, our model considers the change of the electrostatic interaction energy by ion pair formation. Since the details of the charge distribution over the protein domain surfaces are generally either unknown or not easily accounted for, we will simply treat the electrostatic interaction energy as arising from two effective charges, Q₁ and Q₂, located at the effective distance R from each other:

$$E\approx k_{\mathrm{e}}\frac{Q_1{Q}_2}{\epsilon R}$$ (16)

Each of the electric charges is contributed to by one or more charged amino acid residues.

The kinetic and balance equations for the ion pair formation between the charged protein amino acid residues (A) and the solvent ions (B) can be written as follows:

$$\begin{gathered} [\stackrel{.}{\mathrm{A}}]=-k_{\text{on}}[\mathrm{A}][\mathrm{B}]+k_{\text{off}}[\text{AB}] \\ [\mathrm{A}]+[\text{AB}]={[\mathrm{A}]}_{\mathrm{o}} \\ [\mathrm{B}]+[\text{AB}]={[\mathrm{B}]}_{\mathrm{o}} \end{gathered}$$ (17)

The equilibrium concentration of A is readily found as (see the SI for details):

$$[\mathrm{A}]\approx \frac{{[\mathrm{A}]}_{\mathrm{o}}}{1+{[\mathrm{B}]}_{\mathrm{o}}/({[\mathrm{A}]}_{\mathrm{o}}+k_{\mathrm{d}})}$$ (18)

where k_d = k_off/k_on is the equilibrium ion pair dissociation constant. Finally, given that [A] is proportional to the unscreened electric charge on each of the protein domains and [B]_o is equal to the ionic strength (for a monovalent electrolyte), one can write:

$$E\approx E_{\mathrm{o}}/{(1+\sigma I)}^n$$ (19)

where σ = 1/([A]_o + k_d); n = 1 if only Q₁ or Q₂ is screened, and n = 2 if both charges are screened (intermediate situations are possible, but will not be considered now). Combining Eqs. 13, 15, and 19, one obtains:

$$k_{\text{ET}}\approx \frac{k_{\mathrm{t}}}{1+(k_{\mathrm{t}}/k_{\text{cs}0})exp(E_{\mathrm{b}}/[kT{(1+\sigma I)}^n])+(V_{\text{nt}}/V_{\mathrm{t}})exp(E_{\mathrm{t}}/[kT{(1+\sigma I)}^n])}$$ (20)

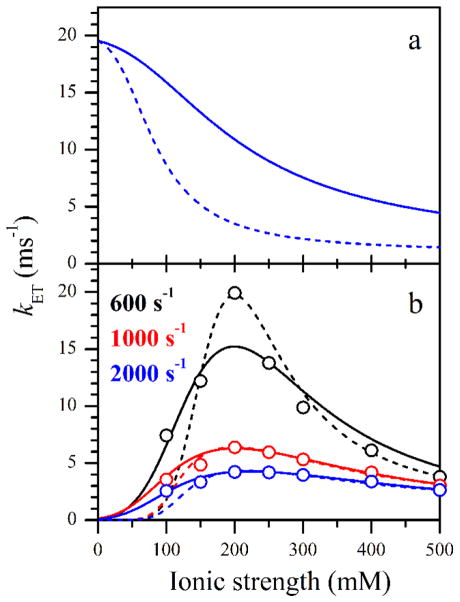
In the above derivation, we did not distinguish between the contact and solvent-separated (solvent-shared) ion pairs and simply assumed that the ion pair formation eliminates (or reduces) the monopole interaction and does not create higher order electrostatic interactions (dipole, quadrupole, etc.). Also, no charge screening by unpaired solvent ions was considered. This is somewhat justifiable because the Debye length in this situation should be generally comparable with the effective distance between the charges, but certainly does not add to the quantitative aspect of the model. In qualitative terms, however, this model allows to explain both the monotonically decaying (monophasic) and bell-shaped (biphasic) dependences of the IET rate constants. The former one is observed when the transition from the non-tunneling to the tunneling area is essentially barrierless (E_b ~ 0, see Figure 9a), while for E_b > 0 a bell-shaped or increasing (to an asymptote) dependence will be observed (Figure 9b).

Figure 9.

Ionic strength dependences of k_ET calculated using Eq. 20. Panel a, monotonic (monophasic) dependences obtained for E_b = 0. Panel b, bell-shaped (biphasic) dependences approximately fitting those obtained in the LFP experiments (open circles). The calculation parameters are given in Table 2. The color-coded legend in panel b shows the k_UD values used to obtain the experimental k_ET values presented in this panel. The colors of the lines and circles in panel b correspond to those in the legend.

Although the presented model is rather simplistic and can mostly be used for a qualitative explanation of the observed dependence of k_ET on I, it is tempting to see if one can simulate the k_ET(I) dependences obtained in our LFP experiments (Figure 7) using sensible model parameters. In such simulations, to decrease the number of variables, we have assumed E_b = −E_t. The screening factor, σ, was taken to be approximately equal to 1/k_d for ion pair formation between Cl⁻ in solution and positively charged amino acid residues (k_d ~ 150 mM[48]): σ = 6 M⁻¹ (since the NOS concentration was only about 15 μM, the concentration of the charged residues, [A]_o, in the denominator of Eq. 18 was neglected). The examples of simulations for n = 1 and 2 are shown in Figure 9b by solid and dashed traces, respectively, and the simulation parameters are given in Table 2.

Table 2.

Docked state model parameters used for simulations shown in Figure 9. The E/kT values correspond to room temperature.

Fig. 9 panel / trace	kt (s−1)	kcs0 (s−1)	Eb/kT	Et/kT	Vnt/Vt	σ (M−1)	n
a / blue solid	2·104	4·106	0	−7	20	6	1
a / blue dashed	2·104	4·106	0	−7	20	6	2
b / black solid	2.6·104	2.08·107	12.4	−12.4	100	6	1
b / black dashed	3.5·104	7·106	21	−21	30	6	2
b / red solid	9.1·103	4.55·106	10.4	−10.4	25	6	1
b / red dashed	7.3·103	6.57·106	20.1	−20.1	4.6	6	2
b / blue solid	5.75·103	2.88·106	10.4	−10.4	15	6	1
b / blue dashed	5·103	2.5·106	19.5	−19.5	3	6	2

From the data presented in Figure 9b, one can see that the simulations for both n = 1 and 2 can qualitatively reproduce the experimental k_ET(I) dependences. For the energies E_b and E_t, which allow one to fit the experimental data, the predicted k_ET values approach zero for I → 0 because the adjustment of the relative domain position then becomes very slow (k_cs ~ 0). Accounting for the docking/undocking process, formally necessary in this limit, will result in k_ET being determined by the probability of direct docking into the tunneling region of the docking hot spot: k_ET = (V_t/V_nt)k_UD. Since V_t/V_nt < (≪) 1 (see Table 2), it is clear that the calculations presented in Figure 9b will not be significantly affected by taking the docking/undocking process into account.

The energies E_b and E_t are in the ballpark of the Coulomb interactions expected for the docked state: e.g., the energy of interaction between two electron charges 6 Å apart is about (3 – 5)kT (at room temperature and assuming the dielectric constant at the protein surface of ε = 20 – 30 [49]. Thus, the E_b and E_t values for most simulations in Table 2 reasonably suggest an interaction between multiple electric charges.

The simulations show that the ionic strength dependences of k_ET obtained from the experimental k_IET(I) assuming k_UD < 600 s⁻¹ and k_UD > 2000 s⁻¹ will not be possible to reproduce using the k_t, k_cs0, and V_nt/V_t values reasonably close to those obtained by our theoretical estimates above. Indeed, already for k_UD = 2000 s⁻¹, the k_t and k_cs0 rate constants required to reproduce the experimental k_ET(I) become significantly smaller than the theoretically estimated values of 10⁴–10⁵ s⁻¹ and 10⁷ s⁻¹, respectively (see Table 2), and this disagreement will increase for larger assumed k_UD values. On the other hand, for k_UD < 600 s⁻¹, the maximum in the k_ET(I) dependence becomes excessively sharp, and such a dependence is not possible to reproduce. In fact, already the simulations for k_UD = 600 s⁻¹ presented in Figure 9b demonstrate significant differences between the experimental and simulated k_ET(I). These observations thus provide additional support to our theoretical estimate of k_UD as (1.5–3.7)·10³ s⁻¹ (see above).

We conclude that the ion pairing model, in spite of its simplicity, is capable of qualitatively (and possibly, even semiquantitatively) explaining the effect of ionic strength on the rate of interdomain/interprotein ET in the docking complexes. From the perspective of this model, the bell-shaped dependence of k_ET on the ionic strength indicates that the energy landscape in the docked state is rugged, with the regions of slow and fast electron tunneling being separated by significant electrostatic barriers, which depend on the ionic strength. To become more rigorous, the ion pairing model can be extended to explicitly account for the formation and dissociation of the docking complex, which may become important if the rate of short-range conformational rearrangements in the docked state, k_cs, is comparable to or slower than the large-scale conformational constants, k_UD and k_DU.

Finally, it is interesting to note that the results of this work show that the optimal FMN–heme IET takes place at a physiological ionic strength (200 mM), which indicates that NOS has evolved to operate efficiently under normal cellular conditions. Ionic strength has also been shown to influence other electron transfer steps in NOS. For example, flavin reduction in nNOS reductase construct in the absence of CaM is ionic strength dependent [50], indicating that electrostatic attraction plays a role in stabilizing the FAD–FMN domain interface. In that work, only three different ionic strength conditions were tested, and the reported effect was smaller than in our work.

Conclusion

In this work, we have used the LFP technique to study the dependence of the FMN–heme IET rate as a function of the ionic strength. The auxiliary information necessary to translate the observed IET rates into the intrinsic IET rates in the FMN-heme domain docked state was obtained using the FMN fluorescence lifetime measurements and order of magnitude theoretical estimates. The dependences of the observed and intrinsic IET rates on the ionic strength were biphasic (bell-shaped). The literature models explaining the bell-shaped IET rate dependences are based on continuum electrostatics models (Debye-Hückel theory) and are not applicable to the processes in the docked state, which determine the intrinsic IET rates. We have proposed a complementary model, where the ionic strength effect is accounted for at the local level, through the formation of ion pairs between the solvent ions and charged protein residues. This new model can explain both the monophasic and biphasic ionic strength dependences. The trial simulations of the intrinsic IET rate dependences using this model show that the data can be reproduced using reasonable energetic (E_b, E_t), structural (V_nt/V_t), and chemical (σ) parameters.

The docking state model formulated in this work, including the ion pairing aspect, can be used to rationalize the interprotein/interdomain ET rates for other types of protein systems where the docked state is sufficiently long-lived. This model can, in principle, be upgraded to various degrees of complexity to include the specific location, number, and type of charged residues, the electric dipole interactions, continuum charge screening, etc. This, however, would require a detailed knowledge of the structure of the docking complex, which will represent a significant obstacle for this direction of development. A much more plausible and necessary development would be to explicitly account for the docking complex formation and dissociation rates when describing the interconversions between tunneling and non-tunneling geometries of the docked state. Such work is currently in progress.

Finally, we wish to elaborate on three additional points. First, this study was performed on the iNOS oxyFMN construct, which provides the benefit of relative structural and functional simplicity and allows to readily interpret the LFP results in terms of conformational dynamics and electron tunneling between the FMN and heme centers. Extrapolation of the results obtained for iNOS oxyFMN to all isoforms of full-length NOS should be done with caution because the presence of the NADPH-FAD binding domain not only changes the structural characteristics of the system (size and mass), but also adds additional processes that have to be considered explicitly (interactions and electron transfer within the reductase domain; Ca²⁺-dependent CaM binding and release in nNOS and eNOS). We believe, however, that the appropriate modifications and extensions of the analysis to account for the greater complexity of the holo-NOS can be readily made.

Second, in this work, the ionic strength was controlled using NaCl, while in cells K⁺ is about an order of magnitude more abundant than Na⁺. However, both K⁺ and Na⁺ are much less efficient in forming ion pairs with charged protein residues than Cl⁻ [47, 51]. Therefore, the ionic strength dependences of the IET rate for both NaCl and KCl should be mostly determined by Cl⁻ and are expected to be similar. Indeed, the effect of K⁺ and Na⁺ on NOS activity is virtually identical in a wide range of ionic strength values [52].

The third comment refers to the fact that our measurements were performed in a dilute water solution, while cytosol is crowded by the presence of various proteins at relatively high concentrations. Qualitatively, two effects of the macromolecular crowding can be envisioned. First, the diffusion coefficients of NOS domains in the crowded solution will likely decrease, which, taken alone, would result in decreased k_UD and IET rate. On the other hand, the restrictions imposed by nearby proteins on the domain diffusion range (the effect of excluded volume) will likely work in opposite direction. It is difficult to predict which of these effects will prevail, and an experimental study of IET in crowded solutions is necessary. Such measurements will be conducted in the future.

Research Highlights.

• The FMN-heme electron transfer in inducible NO synthase was studied vs. ionic strength.

• The time scales of the various events contributing to the observed rate were estimated.

• The forward and backward intrinsic electron transfer rate constants were determined.

• Both intrinsic rates exhibit a bell-shaped dependence on the ionic strength.

• A docked state conformational dynamics model was builtto explain the dependence profile.

Abbreviations

NO

nitric oxide

NOS

nitric oxide synthase

iNOS

inducible NOS

nNOS

neuronal NOS

eNOS

endothelial NOS

CaM

calmodulin

oxyFMN

bi-domain NOS construct in which only the heme-containing oxygenase and FMN domains along with the CaM binding linker are present

NOSoxy

oxygenase domain construct of NOS

FMNH^•

FMN semiquinone

FMNH₂

FMN hydroquinone

LFP

laser flash photolysis

ET

electron transfer

IET

interdomain electron transfer

dRF

5-deazariboflavin

H₄B

(6R)-5,6,7,8-tetrahydrobiopterin