Nanophotonic particle simulation and inverse design using artificial neural networks

New deep learning techniques may hold the key to solving intractable photonics problems.

Abstract

We propose a method to use artificial neural networks to approximate light scattering by multilayer nanoparticles. We find that the network needs to be trained on only a small sampling of the data to approximate the simulation to high precision. Once the neural network is trained, it can simulate such optical processes orders of magnitude faster than conventional simulations. Furthermore, the trained neural network can be used to solve nanophotonic inverse design problems by using back propagation, where the gradient is analytical, not numerical.

INTRODUCTION

Inverse design problems are pervasive in physics (1–4). Quantum scattering theory (1), photonic devices (2), and thin film photovoltaic materials (3) are all problems that require inverse design. A typical inverse design problem requires optimization in high-dimensional space, which usually involves lengthy calculations. For example, in photonics, where the forward calculations are well understood with Maxwell’s equations, solving one instance of an inverse design problem can often be a substantial research project.

There are many different ways to solve inverse design problems, which can be classified into two main categories: the genetic algorithm (5, 6) (searching the space step by step) and adjoint method (7) (mathematically reversing the equations). For problems with many parameters, solving these with genetic algorithms takes a lot of computation power and time, and this time grows exponentially as the number of parameters increases. On the other hand, the adjoint method is far more efficient than the genetic algorithms; however, setting up the adjoint method often requires a deep knowledge in photonics and can be quite nontrivial, even with such knowledge.

Neural networks (NNs) have previously been used to approximate many physics simulations with high degrees of precision. Recently, Carleo et al. (8) used NNs to solve many-body quantum physics problems, and Faber et al. (9) used NNs to approximate density functional theory. Here, we propose a novel method to further simulate light interaction with nanoscale structures and solve inverse design problems using artificial NNs. In this method, an NN is first trained to approximate a simulation; thus, the NN is able to map the scattering function into a continuous, higher-order space where the derivative can be found analytically, based on our earlier work presented in the study of Peurifoy et al. (10). The “approximated” gradient of the figure of merit with respect to input parameters is then obtained analytically with standard back propagation (11). The parameters are then optimized efficiently with the gradient descent method. Finally, we compare our performance with the standard gradient-free optimization method and find that our method can be more effective and orders of magnitude faster than traditional methods.

While we focus here on a particular problem of light scattering from nanoparticles, the approach presented here can be fairly easily generalized to many other nanophotonic problems. This approach offers both the generality present in numerical optimization schemes (where only the forward calculation must be found) and the speed of an analytical solution (owing to the use of an analytical gradient). Conceptually, there are a number of reasons why the approach used here is useful for a myriad of branches of physics. After the NN is trained, there are three key uses discussed here.

Approximate

Once the NN is trained to approximate a complex physics simulation (such as density functional theory or finite-difference time-domain simulation), it can approximate the same computation in orders of magnitude less time.

Inverse design

Once trained, the NN can solve inverse design problems more quickly than its numerical counterpart because the gradient can be found analytically instead of numerically. Furthermore, the series of calculations for inverse design can be computed more quickly due to the faster backward calculation. Finally, the NN can search more easily for a global minimum possibly because the space might be smoothed in the approximation.

Optimization

Similarly to inverse design, the network can be asked to optimize for a desired property. This functionality can be implemented simply by changing the cost function used for the design and without retraining the NN.

RESULTS

NNs can learn and approximate Maxwell interactions

We evaluate this method by considering the problem of light scattering from a multilayer (denoting the nanoparticle layer by shell from here on) dielectric spherical nanoparticle (Fig. 1). Our goal is to use an NN to approximate this simulation. For definiteness, we choose a particle that has a lossless silica core (ϵ = 2.04) and then alternating lossless TiO₂ ($\mathrm{ϵ}=5.913+\frac{0.2441}{{\mathrm{\lambda }}^2-0.0803}$) and lossless silica shells. Specifically, we consider eight shells between 30- and 70-nm thicknesses per shell. Thus, the smallest particle we consider is 480 nm in diameter, and the largest is 1120 nm.

Fig. 1. The NN architecture has as its inputs the thickness of each shell of the nanoparticle, and as its output the scattering cross section at different wavelengths of the scattering spectrum.

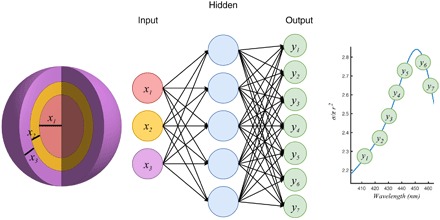
Our actual NN has four hidden layers.

This problem can be solved analytically or numerically with the Maxwell equations, although for multiple shells, the solution becomes involved. The analytical solution is well known (12). We used the simulation to generate 50,000 examples from these parameters with the Monte Carlo sampling.

Next, we trained the NN using these examples. We used a fully connected network, with four layers and 250 neurons per layer, giving us 239,500 parameters. The input was the thickness of each nanomaterial shell (the materials were fixed), and the output was the spectrum sampled at points between 400 and 800 nm. The training error is graphed in Fig. 2A, and a table of cross-validation responses for various particle configurations is presented in Table 1. For each nanoparticle configuration, a hyperparameter search (that is, changing learning rates and the number of neurons per layer) was performed to minimize the validation error. In our experience, changing the architecture of the model, such as the number of neurons, by a small amount did not affect the mean relative error (MRE) significantly. Additional details about the network architecture, training data, and loss computation are discussed in the Methods section, and all codes used to generate the simulations and results, as well as implement the model discussed here for a general problem, can be accessed at https://github.com/iguanaus/ScatterNet. Once the training was complete, the weights of the NN were fixed and saved into files, which can be easily loaded and used. Next, we began to experiment with applications and uses of this NN.

Fig. 2. NN results on spectrum approximation.

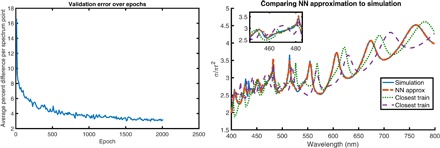
(A) Training loss for the eight-shell case. The loss has sharp declines occasionally, suggesting that the NN is finding a pattern about the data at each point. (B) Comparison of NN approximation to the real spectrum, with the closest training examples shown here. One training example is the most similar particle larger than desired, and the other is the most similar particle smaller than desired. These results were consistent across many different spectra.

Table 1. Network architecture and cross-validation results for various sizes of nanoparticles.

The common architecture throughout is a four-layer densely connected network. The errors are presented as the mean percent off per point on the spectrum (subtracting the output by desired and dividing by the magnitude). The validation set was used to select the best model; the test was never seen until final evaluation. The errors are close, suggesting that not much overfitting is occurring, although the effects become more pronounced for more shells.

Nanoparticle shells	Neurons per layer	MRE (train)	MRE (validation)	MRE (test)
8	250	1.4%	1.5%	1.5%
7	225	0.98%	1.0%	1.0%
6	225	0.97%	1.0%	1.0%
5	200	0.45%	0.46%	0.46%
4	125	0.60%	0.60%	0.60%
3	100	0.32%	0.33%	0.32%
2	100	0.29%	0.30%	0.29%

The first application was to test the forward computation of the network to see how well it approximates the spectra it was not trained on (for an example, see Fig. 2B). Impressively, the network matches the sharp peaks and high Q features with much accuracy, although the model was only trained with 50,000 examples, which is equivalent to sampling each shell thickness between 30 and 70 nm only four times.

To study whether the network learned anything about the system and can produce features it was not trained on, we also graphed the closest examples in the training set. The results show that the network is able to match quite well spectra even outside of the training set. Furthermore, the results from Fig. 2B visually demonstrate that the network is not simply interpolating, or averaging together the closest training spectra. This suggests that the NN is not simply fitting to the data, but instead discovering some underlying pattern and structure to the input and output data such that it can solve problems it had not encountered and, to some extent, generalize the physics of the system.

This method is similar to the well-known surrogate modeling (13), where it creates an approximation to solve the computationally expensive problem, instead of the exact solution. However, the result indicates that NNs can be very powerful in approximating linear optical phenomena (such as nanoparticle scattering phenomena shown here).

NNs solve nanophotonic inverse design

For an inverse design, we want to be able to draw any arbitrary spectrum and find the geometry that would most closely produce this spectrum. Results demonstrate that NNs are able to efficiently solve inverse design problems. With the weights fixed, we set the input as a trainable variable and used back propagation to train the inputs of the NN. In simple terms, we run the NN “backward.” To do this, we fix the output to the desired output and let the NN slowly iterate the inputs to provide the desired result. After a few iterations, the NN suggests a geometry to reproduce the spectrum.

We test this inverse design on the same problem as above—an eight-shell nanoparticle made of alternating shells of TiO₂ and silica. We choose an arbitrary spectrum and have the network learn what inputs would generate a similar spectrum. We can see an example optimization in Fig. 3. To ensure that we have a physically realizable spectra, the desired spectrum comes from a random valid nanoparticle configuration.

Fig. 3. Inverse design for an eight-shell nanoparticle.

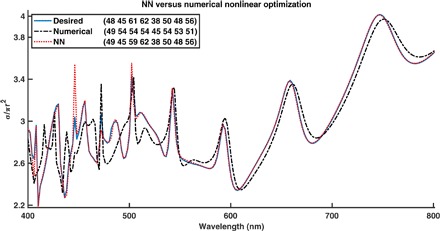
The legend gives the dimensions of the particle, and the blue is the desired spectrum. The NN is seen to solve the inverse design much more accurately.

We also compare our method to state-of-the-art numerical nonlinear optimization methods. We tested several techniques and found that interior-point methods (14) were most effective for this problem. We then compared these interior-point methods to our results from the NN, shown in Fig. 3. Visually, we can see that the NN is able to find a much closer minimum than the numerical nonlinear optimization method. This result is consistent across many different spectra, as well as for particles with different materials and numbers of shells.

We found that for a few parameters to design over (for three to five dielectric shells), the numerical solution presented a more accurate inverse design than the NN. However, as more parameters were added (regimes of 5 to 10 dielectric shells), the numerical solution quickly became stuck in local minima and was unable to solve the problem, while the NN still performed well and found quite accurate solutions to inverse design. Thus, for difficult inverse design problems involving many parameters, NNs can often solve inverse design easily. We believe that this might be because the optimization landscape might be smoothed in the approximation.

We further studied how the NN behaves in regions where ϵ has a strong dependence on ω, such as the case of J aggregates (15). This material produced complex and sharp spectra, and it is interesting to study how well the NN approximated these particles, particularly for particles that it had not trained on. Results demonstrate that the network was able to behave fine in these situations (see the Supplementary Materials for more details).

NNs can be used as an optimization tool for broadband and specific-wavelength scattering

For optimization, we want to be able to give the boundary conditions for a model (for instance, how many shells, how thick of a particle, and what materials it could be) and find the optimal particle to produce σ(λ) as close as possible to the desired [σ_desired(λ)]. Now that we can design an arbitrary spectrum using our tool with little effort, we can further use this as an optimization tool for more difficult problems. Here, we consider two: how to maximize scattering at a single wavelength while minimizing the rest, and how to maximize scattering across a broad spectrum while minimizing scattering outside of it.

To do this, we fix the weights of the NN and create a cost function that will produce the desired results. We simply compute the average of the σ(λ) inside of the range of interest and compute the average of the points outside the range and then maximize this ratio. This cost function J is given by

$$\mathit{J}=\frac{\overline{{\mathrm{\sigma }}_{\text{in}}}}{\overline{{\mathrm{\sigma }}_{\text{out}}}}$$ (1)

Ideally, this optimization would be performed using metals and other materials with plasmonic resonances (15) in the desired spectrum range. These materials are well suited for having sharp, narrow peaks and, as such, can generate spectra that are highly efficient at scattering at precisely a single wavelength. Our optimization here uses alternating layers of silver and silica, although we also found that using solely dielectric materials, we were able to force the NN to find a total geometry that still scatters at a single peak, despite the underlying materials being unable to. A figure showing the results of this for a narrow set of wavelengths close to 465 nm can be seen in Fig. 4A.

Fig. 4. Spectra produced by using our approach as an optimization tool.

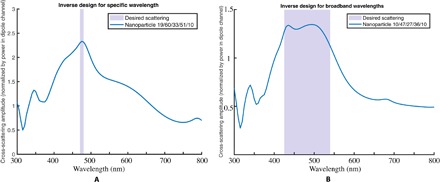
(A) Scattering at a narrow range close to a single wavelength. Here, we force the NN to find a total geometry that scatters around a single peak, using alternating layers of silver and silica. (B) Scattering across a broadband of wavelengths. The legend specifies the thickness of each shell in nanometers, alternating silica and silver shells. The network here was restricted to fewer layers of material (only five shells) but given a broader region of shell sizes than previously (from 10 to 70 nm).

Next, we consider the case of broadband scattering, where we want a flat spectrum across a wide array of wavelengths. For this case, we allow the optimization to consider metal layers as well (modeled by silver, with the inner core still silica). In this case, we choose the same J as above, maximizing the ratio of values inside to outside. After training the network for a short number of iterations, we achieve a geometry that will broadband scatter across the desired wavelengths. A figure of this can be seen in Fig. 4B.

Comparison of NNs with some conventional inverse design algorithms

As mentioned, we tested several techniques and found that interior-point methods (14) were most suited for nanoparticle inverse design. To compare this numerical nonlinear optimization method to our NN, we use the same cost function for both, namely, that of the mean square distance between points on the spectra. For definiteness, we code both the NN and simulation in Matlab. This allows for reasonably fair comparisons of speed and computation resources.

We train a different NN on each number of particle shells from 2 to 10. The networks’ size increased as we increased the number of shells, and the training can often require substantial time. However, once the networks were trained, the runtime of these was significantly less than the forward computation time of the simulation. We tested this by running 100 spectra and then finding the average time required for the computation. These were run on a 2.9-GHz Intel Core i5 processor, and all were parallelized onto two CPUs. A plot of these results is shown in Fig. 5. Once fitting with lines, it is evident that if the problem becomes complex, then the simulation would struggle to run more than a few shells, while the NN would be able to handle more. Thus, the NN approach has much to offer to physics and inverse design even in just speeding up and approximating simulations.

Fig. 5. Comparison of forward runtime versus complexity of the nanoparticle.

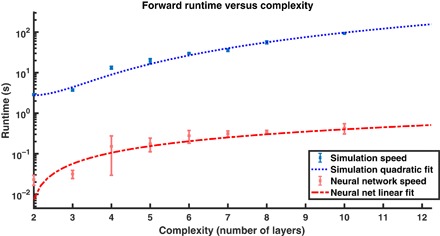
The simulation becomes infeasible to run many times for large particles, while the NN’s time increases much more slowly. Conceptually, this is logical as the NN is using pure matrix multiplication—and the matrices do not get much bigger—while the simulation must approximate higher and higher orders. The scale is log-log. The simulation was fit with a quadratic fit, while the NN was a linear fit. See the Supplementary Materials for more details and inverse design speed comparison.

Next, we looked at the optimization runtime versus the complexity of the problem, once again comparing our method against interior-point algorithms. To find the speed of this optimization, we chose a spectrum, set a threshold cost, and timed how long it took for the methods to find a spectrum that is below that cost or converged into a local minimum. On a number of spectra, we found that both methods were often sensitive to initialization points. To investigate these results rigorously, and not be influenced by the choice of initial conditions, we took 50 starting points for each spectrum and tested three spectra for each number of shells. Results demonstrate that inverse design using the NN was able to handle more complex problems than the numerical inverse design (see the Supplementary Materials for more details).

DISCUSSION

The results of this method suggest that it can be easily used and implemented, even for complex inverse design problems. The architecture used in the examples above—a fully connected layer—was chosen without much optimization and still performs quite well. Our preliminary testing with other architectures (convolutions, dropouts, and residual networks) appeared to have further promise as well.

Perhaps the two most surprising results were how few examples it takes for the network to approximate the simulation, as well as how complex the approximation can really be. For instance, in the eight-shell case, the NN only saw 50,000 examples over eight independent inputs. This means that, on average, it sampled only four times per shell thickness and yet could reproduce the entire range of 30- to 70-nm shell thickness continuously. The approximation was even able to handle quite sharp features in the spectrum that it otherwise had not seen.

Promising and effective results have been seen by applying this method to other nanophotonic inverse design problems. Recently, Liu et al. (16) demonstrated that by using a bidirectional NN (17), optimization and inverse design can be performed for one-dimensional shells of dielectric mediums. The approach was to first train the network to approximate the forward simulation and then do a second iteration of training (in the inverse direction) to further improve the accuracy of the results. By using a second iteration of training, Liu et al. (16) was able to overcome degeneracy problems wherein the same spectrum can be generated by particles of different geometrical arrangements. Overall, this and similar work are promising to the idea that experimenting with different architectures, and adding more training data, can allow these NNs to be useful for solving inverse design in many more scenarios.

Another interesting aspect of this method is to study the smoothness and robustness of these networks. The validation results show the network to be likely smooth—in particular that there is not much difference in the cross-validation errors. On the other hand, the optimization methods and results can be used to investigate the robustness of the networks. In particular, the optimization presented here was done by an ensemble optimization, wherein the network was initialized several times at different starting points, and each time allowed to converge to a single point. In a typical run, several different initialization points were found to converge to similar error amounts (with possibly different parameters), the lowest of which was chosen as global minimum for the inverse design problem. This finding is consistent with other findings in the field of machine learning, where almost all local minima have similar values to the global optimum of the NN (18). These experiments showed that the NN was not entirely accurate—still getting stuck in local minima on some trial—but preliminary testing suggested that this performs more robustly than the numerical counterpart, as depicted above.

One clear concern with the method is that we still have to generate the data for each network, and this takes up time for each inverse design problem. It is true that generating the data takes significant effort, but there are two reasons why this method is still very useful. First, hardware is cheap, and the generation of data can be done easily in parallel across machines. This is not true for inverse design. Inverse design must often be done in a serial approach as each step gets a little closer to the optimal, so the time cannot be reduced significantly by parallel computation. The second reason this method is highly valuable is while the forward propagation is linear in complexity, the optimization is often polynomial. Specifically, by looking at Fig. 5 and the inverse design runtimes (see the Supplementary Materials), we can see that the inverse design speed is growing much faster than the forward runtime. This is important because it means that for complex simulations, the numerical inverse design could take an infeasible amount of time (especially when one needs to solve many inverse design problems for the same physical system), while the NN inverse design may not take long; it will simply have many variables.

This method could be used in many other fields of computational physics; it would allow us to approximate physics simulations in fractions of the time. Furthermore, owing to the robustness of back propagation, this method allows us to solve many inverse design problems without having to manually calculate the inverse equations. Instead, we simply have to write a simulation for the forward calculation and then train the model on it to easily solve the inverse design.

METHODS

Analytically solving scattering via the transfer matrix method

We use the transfer matrix method, described in the study of Qiu et al. (19). We consider a multishell nanoparticle. Because of spherical symmetry, we decompose the field into two parts: transverse electric (TE) and transverse magnetic (TM). Both these potentials satisfy the Helmholtz equation, and each scalar potential can be decomposed into a discrete set of spherical modes

$${\mathrm{\phi }}_{\mathit{l}\mathit{m}}={\mathit{R}}_{\mathit{l}}(\mathit{r}){\mathit{P}}_{\mathit{l}}^{|\mathit{m}|}(\text{cos} \mathrm{\theta }){\mathit{e}}^{\mathit{i}\mathit{m}\mathrm{\Phi }}$$ (2)

For a specific wavelength, because the dielectric constant is constant within each shell, R_l(r) is a linear combination of the first and second kinds of spherical Bessel functions within the two respective shells

$${\mathit{R}}_{\mathit{l}}(\mathit{r}){|}_{\mathit{i}}={\mathit{A}}_{\mathit{i}}{\mathit{j}}_{\mathit{l}}({\mathit{k}}_{\mathit{i}}\mathit{r})+{\mathit{B}}_{\mathit{i}}{\mathit{y}}_{\mathit{l}}({\mathit{k}}_{\mathit{i}}\mathit{r})$$ (3)

We can solve for these coefficients with the transfer matrix of the interface. Thus, we can calculate the transfer matrix of the whole system by simply telescoping these solutions to individual interfaces

$$\left[\begin{array}{c}{\mathit{A}}_{\mathit{n}+1}\\ {\mathit{B}}_{\mathit{n}+1}\end{array}\right]={\mathit{M}}_{\mathit{n}+1,\mathit{n}}{\mathit{M}}_{\mathit{n},\mathit{n}-1}\dots {\mathit{M}}_{3,2}{\mathit{M}}_{2,1}\left[\begin{array}{c}{\mathit{A}}_1\\ {\mathit{B}}_1\end{array}\right]=\mathit{M}\left[\begin{array}{c}{\mathit{A}}_1\\ {\mathit{B}}_1\end{array}\right]$$ (4)

For the first shell, the contribution from the second kind of Bessel function must be zero because the second kind of Bessel function is singular at the origin. Thus, A₁ = 1 and B₁ = 0. The coefficients of the surrounding shell are given by the transfer matrix element A_{n + 1} = M₁₁ and B_{n + 1} = M₂₁. To find the coefficients of this surrounding medium, we write the radical function as a linear combination of spherical Hankel functions

$${\mathit{R}}_{\mathit{l}}(\mathit{r}){|}_{\mathit{n}+1}={\mathit{C}}_{\mathit{n}+1}{\mathit{h}}_{\mathit{l}}^1({\mathit{k}}_{\mathit{n}+1}\mathit{r})+{\mathit{D}}_{\mathit{n}+1}{\mathit{h}}_{\mathit{l}}^2({\mathit{k}}_{\mathit{n}+1}\mathit{r})$$ (5)

Here, ${\mathit{h}}_{\mathit{l}}^1({\mathit{k}}_{\mathit{n}+1}\mathit{r})$ and ${\mathit{h}}_{\mathit{l}}^2({\mathit{k}}_{\mathit{n}+1}\mathit{r})$ are the outgoing and incoming waves, respectively, using the convention that fields vary in time as e^−iωt. The reflection coefficients r_l are given by

$${\mathit{r}}_{\mathit{l}}=\frac{{\mathit{C}}_{\mathit{n}+1}}{{\mathit{D}}_{\mathit{n}+1}}=\frac{{\mathit{M}}_{11}-\mathit{i}{\mathit{M}}_{21}}{{\mathit{M}}_{11}+\mathit{i}{\mathit{M}}_{21}}$$ (6)

By solving for the reflection coefficients r_l, we can find the scattered power in each channel

$${\mathit{P}}_{\mathit{l},\mathit{m}=\pm 1}^{\text{sca}}=\frac{{\mathrm{\lambda }}^2}{16\mathrm{\pi }}(2\mathit{l}+1){\mathit{I}}_0{|1-{\mathit{r}}_{\mathit{l}}|}^2$$ (7)

Last, by summing overall channel contributions of the TE and TM polarization (both of the σ terms), we find the total scattering cross section

$${\mathrm{\sigma }}_{\text{sca}}={\displaystyle \sum _{\mathrm{\sigma }}}{\displaystyle \sum _{\mathit{l}=1}^{\infty }}\frac{{\mathrm{\lambda }}^2}{8\mathrm{\pi }}(2\mathit{l}+1){|1-{\mathit{r}}_{\mathrm{\sigma },\mathit{l}}|}^2$$ (8)

For practical reasons, the l summation did not go to ∞. Instead, before the training data were generated, the order of l was slowly increased until the spectrum had converged, and adding more orders would not change the result. For a typical calculation here, the order ranged from 4 l terms to 18 l terms.

Inverse design with NNs

The arrangement of the network was a fully connected dense feedforward network. This smallest network we used had four layers, with 100 neurons per layer, which gave the network around 50,300 parameters. The network size was increased as the number of layers increased, with the maximum size being four layers with 300 neurons each for the particle with 10 alternating shells. The input to this network was the normalized (subtracting the mean and dividing by the SD) thickness of each shell of the particle (with the materials fixed), and the output was an unnormalized spectrum sampled at 200 points between 400 and 800 nm. As a common practice, we found that normalizing the inputs helped training, but equivalent results were found with unnormalized inputs—just taking longer to converge. We intentionally did not normalize the output to not give any outside knowledge of what the range of outputs should be.

Between each layer was an activation function of a rectified linear unit (20). There was also one last matrix multiplication after the final layer of the network to map the output to the 200 dimensional desired output. This transformation had no nonlinearity. To initialize the weights, we used a simple normal distribution around 0 with an SD of 0.1 for all weights and biases.

We trained the network using a batch size of 100 and a root mean square prop optimizer (21). We split the data into three categories: train, validation, and test (80, 10, and 10, respectively). The train loss was used to generate the gradients, while we stopped training when the validation loss stopped improving. Several different architectures and models (for example, neuron counts) were tested, and the model with the lowest validation loss was chosen. The test loss was used as a final marker that was never trained to ensure cross-validation accuracy. Note that all figures in the paper are from the validation set, so the model was never trained on these particular examples, but we did optimize the model to ensure suitable performance. Most trials took around 1000 to 2000 epochs of 50,000 data points to train, using a learning rate of 0.0006 and decay of 0.99. These parameters were not heavily optimized, and more efficient schemes can certainly be found.

There were two cost functions used for training. One was used in actual training and back propagation, and the other was used for illustrative purposes in this paper. The first cost function that we used is the mean square error between each point on the spectrum and the 200 dimensional output of the NN. This cost function was consistent between the training and inverse design; for the training data set, each input had a unique and different output, but for the inverse design, we fixed what we wanted the output to be and modified the input.

The other cost function used for illustrative purposes, and presented in Table. 1, was the mean percent off per point on the spectrum. This meant that we found the error between the output of the NN and the desired spectrum, then normalized by the value of the desired spectrum, and found the mean over the whole spectrum. The idea of this function is to offer a more physically meaningful interpretation of how the network is performing—in giving how much each “average point on the spectrum is off by.” All codes can be found at https://github.com/iguanaus/ScatterNet.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/6/eaar4206/DC1

section S1. Details for the comparison of NNs with inverse design algorithms

section S2. J aggregates

fig. S1. Comparison of inverse design runtime versus complexity of the nanoparticle.

fig. S2. Comparison of NN approximation to the real spectrum for a particle made with a J-aggregate material.

fig. S3. Optimization of scattering at a particular wavelength using the J-aggregate material.