Abstract
Cyanobacteria are photosynthetic microorganisms whose metabolism can be modified through genetic engineering for production of a wide variety of molecules directly from CO2, light, and nutrients. Diverse molecules have been produced in small quantities by engineered cyanobacteria to demonstrate the feasibility of photosynthetic biorefineries. Consequently, there is interest in engineering these microorganisms to increase titer and productivity to meet industrial metrics. Unfortunately, differing experimental conditions and cultivation techniques confound comparisons of strains and metabolic engineering strategies. In this work, we discuss the factors governing photoautotrophic growth and demonstrate nutritionally replete conditions in which a model cyanobacterium can be grown to stationary phase with light as the sole limiting substrate. We introduce a mathematical framework for understanding the dynamics of growth and product secretion in light-limited cyanobacterial cultures. Using this framework, we demonstrate how cyanobacterial growth in differing experimental systems can be easily scaled by the volumetric photon delivery rate using the model organisms Synechococcus sp. strain PCC7002 and Synechococcus elongatus strain UTEX2973. We use this framework to predict scaled up growth and product secretion in 1 L photobioreactors of two strains of Synechococcus PCC7002 engineered for production of L-lactate or L-lysine. The analytical framework developed in this work serves as a guide for future metabolic engineering studies of cyanobacteria to allow better comparison of experiments performed in different experimental systems and to further investigate the dynamics of growth and product secretion.
Keywords: Photobioreactor, Cyanobacteria, Light-Limitation, Photosynthetic efficiency, Scale-Up
1. Introduction
Cyanobacteria are attractive platforms for developing microbial cell factories because biosynthetic pathways for producing high-value compounds can be directly linked to photosynthesis. Therefore, the use of engineered photoautotrophs bypasses the barriers associated with cultivation, harvest, and deconstruction of plant biomass that limit common biorefinery strategies (Yenkie et al., 2016). Among photoautotrophs, cyanobacteria are the easiest to manipulate genetically and are the fastest growing species in most environmental conditions. Given these advantages, cyanobacteria have been engineered to produce many commercially relevant compounds including organic acids, alcohols, and secondary metabolites (Angermayr et al., 2015; Oliver et al., 2016; Xue and He, 2015). Unlike heterotrophic conversions where yield (amount of product made per amount of substrate fed) is often the critical performance metric, cyanobacteria production strategies are evaluated by productivity (amount of product per time) and product titer (amount of product per volume). While many examples of chemical production using cyanobacterial biocatalysts have been demonstrated, few have attained product titers equivalent to those reached by heterotrophic bioconversions, most require weeks to maximize titer, and nearly all have been restricted to laboratory scale. These demonstrations have used a wide range of experimental conditions which confound comparative evaluations and scale-up projections (Schuurmans et al., 2017, 2015). Overcoming these challenges is the goal of many ongoing metabolic and biochemical engineering studies. As researchers develop novel strains and engineering strategies, it is critical to provide a common basis for comparison and kinetic framework for evaluating cyanobacterial strains.
The key difference between cultivating cyanobacteria and heterotrophic microbes is the lack of a universal, scalable bioreactor layout due to the need to provide light to cells (i.e. most fermenters have a consistent geometry that can be scaled from lab to industrial scale). To maximize light delivery, photobioreactors (PBRs) are designed to maximize the surface area per culture volume. Designs for large-scale industrial reactors include open raceway ponds and closed tubular/rectangular vessels with large aspect ratios (i.e. depth of reactor is much smaller than its length and/or height). These photobioreactors are spread in parallel over acres of land to maximize the capture of solar irradiance required to support the desired culture volume. In contrast, laboratory cyanobacterial cultivation systems are often built using equipment intended for cultivating heterotrophs that is augmented with exterior lighting. Common laboratory systems include tubes, flasks, bottles, flat plate PBRs, and instrumented bioreactors augmented with lighting shrouds. The different vessel geometries result in quite different photon delivery, which makes comparison of strain performance difficult. Furthermore, the difference in PBR designs between lab and industrial size provide a barrier to making accurate scale-up projections and technoeconomic assessments.
Unstructured kinetic models of heterotrophic cell growth inspired by the work of Monod, Pirt, and others (Monod, 1949; Pirt, 1965) have guided the design and analysis of many industrial biocatalysts (Youngquist et al., 2012). These models provide a framework to relate growth and product generation to the abundance of a limiting substrate (i.e. glucose) and thereby enable the simulation of cultivation schemes to predict bioprocess performance. Industrial cultivations of cyanobacteria will be provided excess nutrients (i. e. N-, P-, metals) and CO2 from low-cost waste streams and rely on solar irradiance for energy to minimize operating costs. For this reason, it is prudent to characterize engineered cyanobacteria with light as the limiting nutrient. Pirt provided an overview of the energetics of photosynthetic growth that provided the foundation for modeling light-limited growth of photosynthetic organisms (Pirt, 1986). Subsequent studies focused on models of light distribution inside of continuous growth experiments considering spatially varying irradiation (Evers, 1991; Perin et al., 2017), spatially averaged irradiation (Du et al., 2016; Grima et al., 1997), or measured total light absorbance (Schuurmans et al., 2015; Touloupakis et al., 2015). Each yielded useful information regarding light-limited growth parameters. However, continuous growth experiments are technically challenging and frequently performed with cell densities much lower than those desired for a large-scale process. Adapting the kinetic models for batch growth experiments will make this type of systematic analysis accessible to many researchers studying photosynthetic chemical production and inform process scale-up.
In this work, we first examine considerations for ensuring that light is the sole limiting substrate in laboratory cyanobacterial cultivation experiments by eliminating limitations from CO2 and soluble nutrient availability. We then examine the phases of cyanobacterial batch growth with light as the sole limiting substrate while developing a mathematical framework for growth and product secretion, which enables determination of photosynthetic efficiency (η) and growth associated productivity of secreted molecules (ρ) for batch growth experiments. Finally, we observe how η and ρ vary across different experimental systems for wild type and engineered strains of the model cyanobacteria Synechococcus sp. strain PCC7002 (PCC7002) and Synechococcus elongatus strain UTEX2973 (UTEX2973) to show that: (1) photosynthetic efficiency (η) is consistent across a variety of experimental conditions and can be used to compare studies performed in different experimental systems, (2) stationary phase can be achieved with light as the sole limiting substrate, and (3) the proposed framework can provide insight into metabolic engineering of cyanobacterial strains for secreted products.
2. Results
2.1. Light-Limitation in Cyanobacterial Growth Experiments
The mathematical framework discussed in this work assumes that light is the sole limiting substrate. This requires elimination of CO2-limitation (see Supplementary Note) and limitation by soluble nutrients. Depletion of soluble nutrients can cause a culture to enter stationary phase while light is still in excess. A stoichiometric analysis of two common cyanobacterial growth media (Table 1) reveals deficiencies in metabolizable nitrogen, phosphorous, sulfur, magnesium, and iron, even at cell densities below 1 g of dry cell weight per liter (g DW L−1), suggesting that cultures in these media are limited by soluble nutrients (Egli, 2015). CO2-replete cultures of PCC7002 grown in Media A enter stationary phase at a much lower cell density than cultures grown in Modified Media A (Figure 1, Table 1 – Modified Media A supplemented with excess iron, nitrate, and/or phosphate). The reported media composition required per 1 g DW L−1 of biomass was calculated using the stoichiometric composition of typical biomass as described by Egli (Egli, 2015). Concentrations of supplemented components were chosen such that the concentrations would not be limiting even in the extremes of biomass composition.
Table 1.
Elemental Composition of Cyanobacteria Media
| Element | Media A | BG11 | Required per 1 g DW L−1 of Biomassa | Modified Media A (MMA) |
|---|---|---|---|---|
| N | 12 | 19 | 9 | 122 |
| P | 0.4 | 0.2 | 1 | 31 |
| S | 20 | 0.3 | 0.3 | 20 |
| Mg | 20 | 0.3 | 0.2 | 20 |
| Fe | 0.03 | 0.06 | 0.1 | 1.1 |
All concentrations are in mM.
Calculated using stoichiometric composition of typical biomass as described in reference (Egli, 2015).
Figure 1.
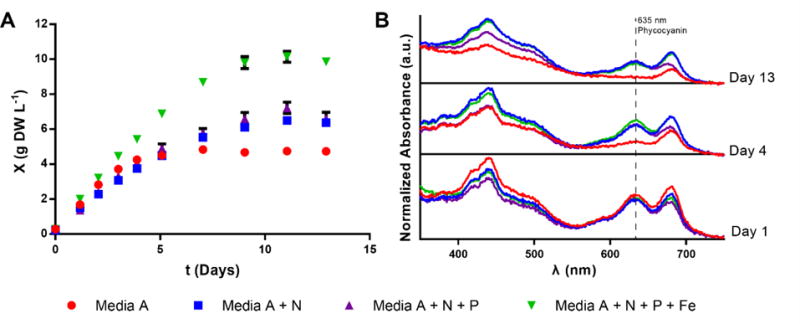
Nutrient supplementation allows growth to higher cell density with light as the sole limiting substrate. (A) Cell density (OD730 converted to g DW L−1 as described in methods) over time measured for cultures of PCC7002 grown in shake flasks in 1% CO2 and 37°C in Media A with no supplement (red), supplemented with 110 mM NaNO3 (blue), supplemented with 110 mM NaNO3 and 31 mM KH2PO4 in a fed batch scheme as described in the methods (purple), or supplemented with 110 mM NaNO3, 31 mM KH2PO4 in a fed batch scheme, and 1.1 mM FeCl3 (green). Error bars are standard error of 3 biological replicates for red, blue, and purple or 2 biological replicates for green. (B) Average absorbance scans normalized to OD730 of samples from the flasks described in (A) are shown over time to show loss of pigmentation in nutrient deplete media and pigment persistence in nutrient sufficient media. Absorbance profiles over time are offset on the y-axis for clarity (baselines in black).
Further insight can be found in examining the absorbance spectra of the cells grown in each case. Transcriptomics analysis has shown that when PCC7002 experiences limitation in iron, nitrogen, sulfur, or phosphate, the gene nblA is upregulated, initiating the degradation of phycobiliproteins (Ludwig and Bryant, 2012). When grown in the nutrient deficient Media A, cells exhibit this nutrient deprivation phenotype (phycobilisome degradation resulting in a decrease in absorbance around 635 nm (Jackson et al., 2015; Stevens et al., 1981)) as they transition into stationary phase. When excess soluble nutrients are supplemented, cells continue to grow to twice the final density and maintain phycobilisomes as they eventually transition into stationary phase. For the cultures supplemented with N, P, and Fe, the culture achieved a density of 10 g DW L−1 at stationary phase (Figure 1). As can be observed in Table 1, the N, P, and Fe concentration in Modified Media A exceed the amount required for 10 g L−1 biomass. As shown in later sections, light can be verified as the sole limiting substrate in a cultivation by increasing the volumetric photon delivery rate of a culture that has entered stationary phase. These observations suggest that while common historical media recipes are sufficient for growth at low cell densities (<1 g DW L−1), supplementation of N, P, and Fe are necessary to eliminate limitations on growth at higher cell densities. For subsequent experiments in this work, Media A or BG11 were used when biomass did not accumulate above 1 g DW L−1 and Modified Media A (MMA) was used for high cell density experiments.
2.2. Modeling the Phases of Growth in Light-Limited Cyanobacterial Cultures
In the seminal work The Growth of Bacterial Cultures, Jacques Monod outlined distinct phases of the growth of bacterial batch cultures (Monod, 1949). For heterotrophic bacteria, the most well studied phase of growth is the exponential phase, where the specific growth rate is constant, as this phase is where most biomass is produced. As the growth substrate is depleted far below the affinity of the rate limiting step in substrate utilization, a brief growth retardation phase begins and the specific growth rate quickly decreases to 0 at which point all substrate has been consumed and stationary phase begins. The previous section established batch growth conditions for phototrophic bacteria in which light is the only limiting substrate. The following sections consider the light distribution and consequent growth dynamics of cyanobacteria in differing phases of growth analogous to those for heterotrophic growth.
2.2.1. Exponential Growth Phase in the Limit of Low Cell Density
The typical Monod growth model for microorganisms describes the phases of growth resulting from changes in the specific growth rate as a function of limiting substrate concentration (Figure 2A–B) (Monod, 1949). Two differences exist in considering light as a substrate. First, a molecular substrate can be depleted, but light is provided continuously from the exterior of the culture vessel. Second, due to mixing, molecular substrate concentrations are considered constant in spatial dimensions whereas irradiance varies spatially due to absorbance by the cells, a phenomenon referred to as cell-shading (Figure 2D–F).
Figure 2.
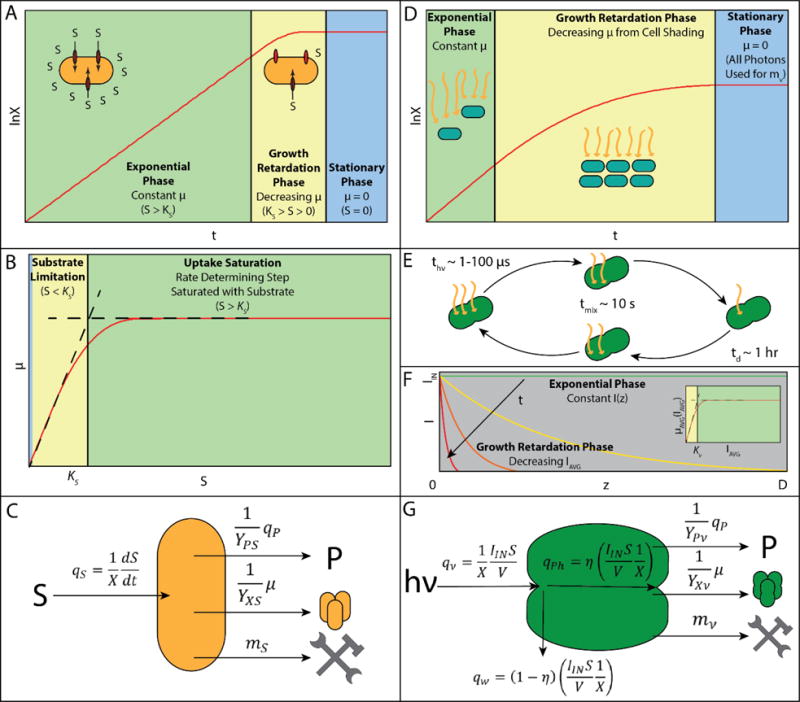
Comparison of phenomena driving different growth phases for molecular substrate limitation (A–C) or light-limitation (D–G). (A) Uptake saturation results in an exponential growth phase until substrate is depleted and the culture enters a short growth retardation phase. Once substrate is fully depleted, the culture enters stationary phase. (B) Monod kinetic model says that high substrate concentration results in uptake saturation leading to constant specific growth rate. As substrate is depleted to the region of Ks, substrate limitation begins resulting in rapidly decreasing specific growth rate. (C) Substrate balance says that substrate uptake rate (qS) is equal to the sum of substrate utilization for product synthesis (qPYPS−1), growth (μYXS−1), and maintenance (mS). (D) Light-Limited batch growth of cyanobacteria has a short exponential growth phase followed by a long growth retardation phase caused by cell-shading, eventually leading to stationary phase when all incident photons are used for maintenance and product synthesis. As cell density increases the biomass specific photon delivery rate decreases until all incident photons are required for cell maintenance, at which point the culture enters stationary phase. (E) The difference in order of magnitude between the characteristic times of mixing (tmix), light reactions (thν), and growth (td) suggest that specific growth rate can be accurately estimated by IAVG. (F) When cultures are at low cell density, the light intensity I(z) approximately constant across the thickness of the reactor (z). As cell density increases, I(z) is determined by Beer’s law and results in decreasing IAVG. (F-Inset) Using IAVG, one can write a Monod growth law for μAVG (Equation 4). (G) Photon balance says that the specific photon uptake rate (qν) multiplied by the photosynthetic efficiency (η) is equal to the sum of energy utilization for product synthesis (qPYPν−1), growth (μYXν−1), and maintenance (mν).
The growth phases of light-limited growth are determined by changes in the spatial irradiance distribution (I(z)) inside the culture vessel (Equation 3).
| (3) |
IIN is the irradiance of photons on the surface of the vessel, z is the path length, X is the biomass density, and α is the biomass specific absorbance of photons.
For very low X, light attenuation is minimal and I(z) is approximately constant resulting in an exponential growth phase where all cells grow with constant specific growth rate, μ. Experiments in this phase can be used to experimentally determine the Monod growth model (Monod, 1949; Pirt, 1986) for a given microorganism assuming IIN is sufficiently low to prevent photoinhibition (Bernstein et al., 2016). The exponential growth rates of low cell density cultures of PCC7002 under various irradiances were measured and fit to the Monod growth model (Equation 4), giving the maximum specific growth rate (μmax) and the saturation irradiance (Kν) (Figure 3).
| (4) |
For irradiances much higher than those used in this work, photoinhibition negatively influences the growth rate and Equation 4 overpredicts μ. For this reason, the specific growth rate specified by μmax in Figure 3 would not be achieved in practice as the required irradiance would be outside of the range in which this simple model is valid.
Figure 3.
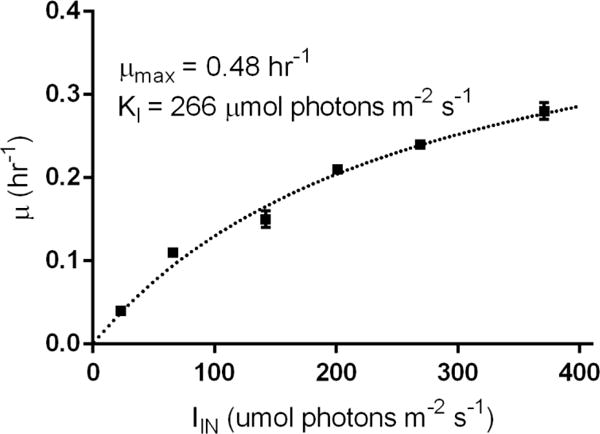
Monod growth model fit from exponential phase batch cultures of PCC7002. μ values are calculated from the exponential growth rate of cultures grown in the specified IIN with all cell density measurements made at OD730 less than 0.1 to limit the effect of cell shading on IAVG. Error bars represent the standard error of at least three biological replicates.
2.2.2. Growth Retardation Phase Driven by Light Attenuation
As cell density increases, light attenuation affects I(z). In most laboratory culture vessels, the mixing time occurs on the order of 10-100 s (Barbosa et al., 2003; Shuler and Kargi, 1992). Therefore, a cell will visit all spaces in a photobioreactor many times over the course of one cell cycle, which occurs on the order of hours. Time constants for excitation and relaxation of a photosynthetic unit through photochemical quenching are on the order of 100 μs and 1 μs, respectively (García-Camacho et al., 2012). Therefore, photosystems cycle through the light reactions many times at each location (Figure 2E). Taking these considerations into account, a simplifying assumption is made such that the cells experience a spatially average irradiance (IAVG). Thus, the average specific growth rate is determined by the specific growth rate for IAVG (Equation 5).
| (5) |
A differential expression for the growth of bacteria neglecting cellular maintenance and secreted products can be written based on the work of Monod and Pirt, and others (Equation 6) (Monod, 1949; Pirt, 1965).
| (6) |
A photon balance accounting for the distribution of energy produced from absorbed photons can be used to study the effects of cellular maintenance and secreted product synthesis on growth (Equation 7, developed by addition of a product synthesis term to a model based on the work of (Du et al., 2016; Evers, 1991; Pirt, 1986)).
| (7) |
Here, η is the photosynthetic efficiency, IIN is the irradiance at the surface of the vessel, S is the irradiated surface area of the vessel, V is the culture volume, qP is the biomass specific rate of synthesis of a secreted product, mν is the biomass specific photon utilization for maintenance, YXν is the theoretical maximum yield of biomass on photons, and YPν is the theoretical maximum yield of product on photons. In the growth retardation phase, cell density is sufficient for all photons entering the culture vessel to be absorbed by the biomass. Thus, the photons used for energy production can be determined by multiplying the volumetric photon delivery rate (IINSV−1) by the photosynthetic efficiency (η). The energy produced from these photons is then used for growth, secreted products, and cellular maintenance (Figure 2G). This is similar to the common representation of the substrate balance in heterotrophic microorganisms (Figure 2C). In this work, η, mν, YXν and YPν are considered constant in time.
The maximum theoretical yield on photons of either biomass (YXν) or a product (YPν) can be readily calculated using genome-scale metabolic models. These models are mathematical representations of metabolic networks and are genomic and biochemical knowledge bases of an organism’s metabolism (Lewis et al., 2012). In this work, YXν and YPν were calculated with the PCC7002 genome-scale metabolic model, iSyp708, and used to fit batch growth data and L-lactate and L-lysine production data (Vu et al., 2013). Additionally, the YPv for a variety of other compounds were determined and are reported in Table 2. These compounds are potential metabolic engineering targets and many of them have previously been produced in cyanobacteria.
Table 2.
Theoretical Yields in PCC7002 for Various Compounds
| Product Name | Theoretical Yield (nmol product per μmol photons) | Product Name | Theoretical Yield (nmol product per μmol photons) |
|---|---|---|---|
| Ethanol | 41.7 | Sucrose | 10.3 |
| Acetone | 29.4 | Isoprene (MEP Pathway) | 17.9 |
| Isopropanol | 27.4 | Isoprene (MVA Pathway) | 16.9 |
| 1-Butanol | 20.8 | Limonene (MEP Pathway) | 8.93 |
| Isobutyraldehyde | 22.7 | Limonene (MVA Pathway) | 8.48 |
| Isobutanol | 20.8 | Bisabolene (MEP Pathway) | 5.95 |
| 2-Methyl-1-Butanol | 16.7 | Bisabolene (MVA Pathway) | 5.65 |
| 1,2-Propanediol | 31.3 | Squalene (MEP Pathway) | 2.94 |
| 2,3-Butanediol | 22.7 | Squalene (MVA Pathway) | 2.81 |
| L-Lactate | 41.7 | Octanoic Acid | 11.4 |
| 3-Hydroxybutyrate | 27.2 | Octanol | 10.4 |
| Glycerol | 35.7 | Dodecanoic Acid | 7.35 |
| D-Mannitol | 19.2 | Dodecanol | 6.94 |
| L-Lysine (Nitrate media) | 11.4 | Hexadecanoic Acid | 5.44 |
| L-Lysine (Ammonia media) | 17.9 | Hexadecanol | 5.21 |
If Equation 7 is rearranged to solve for μAVG, it can be substituted into Equation 6 to generate Equation 8.
| (8) |
The photon balance described in Equation 8 includes a term for secreted products, allowing analysis of cyanobacteria engineered for production of secreted molecules. This analysis considers a growth associated product such that the specific productivity of P is proportional to the specific growth rate (Equation 9).
| (9) |
Here, ρ is the growth-associated productivity parameter (mol P (g DW)−1). This model should be applicable to most molecules of interest as chemical production is often tied to growth in cyanobacteria. However, a similar analysis could easily be performed for cases where this does not apply by defining a different productivity model.
Combining the productivity model with the photon balance and differential growth equation (Equation 8) produces Equation 10.
| (10) |
The corresponding product balance expression is given in Equation 11.
| (11) |
An analytical solution to Equations 10 and 11 yields expressions for cell density and product concentration as a function of time, given in Equations 12–15 (See Supplementary Note for derivation).
| (12) |
| (13) |
| (14) |
| (15) |
Here, XS is the stationary phase cell density predicted by model parameters and κ is a characteristic time constant for transition to stationary phase. Equation 12–16 provide a mathematical framework for characterizing the productivity of cyanobacteria cultures with the key parameters η, ρ, and mν.
2.2.3. Initial Rate Analysis for Determination of η and ρ
Initial rate analysis is useful for expediting experimentation as measuring an initial linear growth rate is less time consuming than measuring an entire batch growth into stationary phase.
Equation 16 gives the derivative of Equation 12 with respect to time.
| (16) |
Equation 17 defines the linear growth rate (LGR), by taking the limit as t goes to zero (beginning of growth retardation phase) for Equation 16 with the assumption that is small.
| (17) |
A similar analysis for P produces the definition of linear production rate (LPR) given in Equation 18.
| (18) |
This result allows η and ρ to be determined from the initial linear rates of growth (LGR) and product secretion (LPR).
The theoretical maximum productivity of P assuming all incident photons are converted to product is given in Equation 19.
| (19) |
Combining Equations 18 and 19 allows determination of the percentage of maximum productivity achieved for a given experiment (Equation 20), giving a sense of the potential for improvement possible through metabolic engineering.
| (20) |
2.3. Experimental Investigations Using Mathematical Framework
2.3.1. Photosynthetic Efficiency for Scaling
Table 3 gives values of η calculated using Equation 17 from the LGR of cultures of Wild Type PCC7002 and UTEX2973 grown across different vessel geometries, IIN, temperature, and salinity (assuming ρ=0 for wild type organisms). For PCC7002, η did not vary significantly from the average of 0.26 except in the presence of excessive salinity (72 g L−1 NaCl, approximately twice the salinity of sea water) where η was severely decreased to 0.11. For UTEX 2973 grown in the freshwater BG11 medium, η did not vary significantly from the average of 0.40, 50% higher than PCC7002 grown in Media A. However, when grown in BG11 supplemented with NaCl to the content of Media A (18 g L−1 NaCl), η for UTEX2973 dropped severely to 0.16. When BG11 was supplemented with twice the NaCl content of Media A to simulate the salinity of sea water (36 g L−1 NaCl), no growth of UTEX2973 was observed (η=0). These results suggest that while the photosynthetic efficiency of UTEX2973 grown in freshwater media is much higher than that of PCC7002, UTEX2973 is unable to maintain this efficiency in brackish or sea water media.
Table 3.
Photosynthetic Efficiency Under Various Experimental Conditions
| Vessel | Osmolarity (mM) | T (°C) | S/V (m−1) | IINa | (IINSV−1)b | LGRc | η |
|---|---|---|---|---|---|---|---|
| Synechococcus PCC7002 | |||||||
| Flask (25 mL)e | 720 | 37 | 201 | 180 | 130000 | 62±3 | 0.23±0.03 |
| Tube | 720 | 38 | 106 | 270 | 100000 | 51±6 | 0.25±0.04 |
| Flask (45 mL) e | 720 | 37 | 120 | 180 | 78000 | 41±3 | 0.26±0.03 |
| Tube | 720 | 38 | 106 | 200 | 77000 | 38±2 | 0.25±0.03 |
| Tube | 720 | 38 | 106 | 140 | 54000 | 28±2 | 0.26±0.03 |
| Tube | 720 | 38 | 106 | 66 | 25000 | 15±0.8 | 0.29±0.03 |
| Tube | 720 | 38 | 106 | 23 | 8600 | 4.5±0.2 | 0.26±0.03 |
| Lower Temperature | |||||||
| Tube | 720 | 30 | 106 | 270 | 100000 | 63±3 | 0.31±0.03 |
| Tube | 720 | 30 | 106 | 66 | 25000 | 12±0.8 | 0.24±0.03 |
| Higher Salinity | |||||||
| Bottle (MMA) | 1000 | 30 | 40 | 330g | 47000 | 17±0.9 | 0.18±0.01 |
| Bottle (MMA) | 1000 | 30 | 40 | 180g | 26000 | 10±0.2 | 0.20±0.01 |
| Tube (2× NaCl) | 1300 | 38 | 106 | 270 | 100000 | 46±3 | 0.22±0.03 |
| Tube (4× NaCl) | 2600 | 38 | 106 | 270 | 100000 | 22±3 | 0.11±0.02 |
| Synechococcus elongatus UTEX2973 | |||||||
| Flask (25 mL) e | 38 | 37 | 201 | 180 | 130000 | 95±4 | 0.36±0.04 |
| Tube | 38 | 38 | 106 | 220 | 84000 | 74±3 | 0.44±0.05 |
| Flask (50 mL) e | 38 | 37 | 110 | 180 | 72000 | 62±4 | 0.43±0.05 |
| Tube | 38 | 38 | 106 | 180 | 70000 | 58±3 | 0.41±0.05 |
| Tube | 38 | 38 | 106 | 150 | 56000 | 41±2 | 0.37±0.04 |
| Flask (100 mL) e | 38 | 37 | 64 | 180 | 42000 | 25±4 | 0.29±0.05 |
| Tube | 38 | 38 | 106 | 75 | 29000 | 23±1 | 0.40±0.04 |
| Higher Salinity | |||||||
| Flask (1× NaCl)e,f | 346 | 37 | 100 | 180 | 72000 | 23±0.9 | 0.16±0.02 |
| Flask (2× NaCl)e,f | 654 | 37 | 100 | 180 | 72000 | 0 | 0 |
| Vessel | Osmolarity (mM) | T (°C) | S/V (m−1) | IIN | Ref. | Yieldd | Inferred η |
| Synechococcus PCC7002 - High Light | |||||||
| Tube | 720 | 38 | NA | ~2000g | (Xiong et al., 2015) | NA | ~0.04h |
[μmol photons m−2 s−1 Standard error is 10% of measured value. Light provided by 4000K Cool White LED light unless otherwise specified.
[μmol photons L−1 hr−1]
[mg DW−1 L hr−1]
[g DW (mol photons)−1]
Flask experiments performed in 250 mL shake flasks with varying volume.
UTEX2973 experiments with BG11 supplemented with specified Media A equivalents of NaCl.
Halogen light.
Experiment from Xiong, et al. found an 80% decrease in linear growth rate when IIN was increased from 50 umol m−2 s−1 to 2000 umol m−2 s−1 (Xiong et al., 2015). This was used to estimate η under very high light intensity from the experiments performed in this work. Error values are standard error of the mean propagated from LGR and IIN measurements of at least three biological replicates. Bold text to emphasize variables of interest for each experiment. MMA is Modified Media A (Table 1).
To further illustrate the usefulness of IINSV−1 as a scaling factor for predicting cyanobacterial growth rate in different experimental systems, Figure 4 shows LGR plotted versus IINSV−1 for different vessel geometries (culture tubes, shake flasks, and 1 L culture bottles) for PCC7002 and UTEX2973. As also shown in Figure 4, η is an easily calculated and useful parameter for identifying changes in culture conditions that cause deviations in photosynthetic efficiency from standard conditions. This approach is useful in quantifying how variations in culture conditions in a scaled-up process that differ from standard experimental conditions can affect photosynthetic efficiency.
Figure 4.
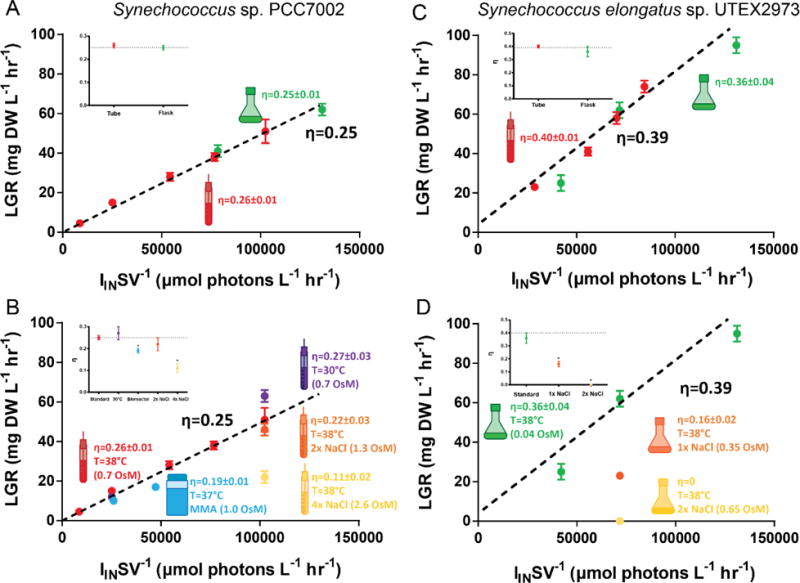
Calculating photon utilization efficiency (η) from linear growth rate and photon utilization rate allows simple determination of the effects of vessel geometry and important process parameters on growth. Plotting linear growth rate versus volumetric photon delivery rate gives a linear trend across different vessel geometries for both PCC7002 (A) and UTEX2973 (C). Decreasing temperature to 30°C has minimal effect on photon utilization efficiency in PCC7002 (B). PCC7002 is salt tolerant, but extreme increase in osmolarity to approximately 2× the osmolarity of seawater (2.6 OsM) by the addition of NaCl significantly decreases photon utilization efficiency. While UTEX2973 grown in BG11 has a higher photon utilization efficiency than PCC7002, UTEX2973 is not salt tolerant as evidenced by the major decrease in photon utilization efficiency upon growth in BG11 supplemented with NaCl to the concentration in Media A (D). Insets on each plot show η for each treatment compared to standard conditions for that organism. Error bars represent the standard error of at least three biological replicates (except for the lower IINSV−1 flask of PCC7002, n=2). Non-visible error bars are smaller than the data symbol. Data points with an asterisk differ significantly from standard conditions per a two-tailed Student’s t-test (p<0.05).
2.3.2. Transition to Stationary Phase in Batch Growth
Stationary phase is characterized by a net growth rate of zero. In Equation 8, this occurs when the biomass specific rate of photon utilization (qPh =ηIINSV−1X−1, Figure 2G) has decreased to the point where all photons are being used for maintenance. No further increase in cell density is observed after this point without perturbation in the volumetric photon delivery rate. In practice, the onset of stationary phase occurs abruptly and at cell densities much lower than predicted by the model in Equation 8. This is likely due to regulatory changes induced by low biomass-specific photon delivery rate.
While η can be calculated from the initial LGR, mν requires information about growth rate at cell densities approaching XS (Equation 15). To accomplish this, cultures of PCC7002 were grown in photobioreactors with Media A supplemented with NaNO3, FeCl3, and KH2PO4 until stationary phase under two different IIN (Figure 5). The average value of η for these cultures was 0.18±0.01 or 0.20±0.01 for 330 or 180 μmol photons m−2 s−1, respectively, as determined by initial rate analysis (LGR calculated from first 3 days of growth). Using these values of η in Equation 12 and fitting the resulting equation to growth data gave an average mν of 1100±60 or 420±20 μmol photons (g DW)−1 hr−1 for 330 or 180 μmol photons m−2 s−1, respectively. A sensitivity analysis looking at the goodness of fit of the model given in Equations 12–15 while varying the parameters shows that the fit is much less sensitive to changes in mν than to changes in η or ρ (See Supplementary Note Figure S3). This analysis suggests that the batch culture method for determination of mν is accurate only in order of magnitude and continuous cultures study is necessary for more accurate quantification of cellular maintenance. The mν values calculated here are on the same order of magnitude as the values of 900 μmol photons (g DW)−1 hr−1 for Synechocystis PCC 6803 (Touloupakis et al., 2015) and 1250 μmol photons (g DW)−1 hr−1 for Oscillatoria agardhii (Evers, 1991), both determined by continuous culture experiments.
Figure 5.
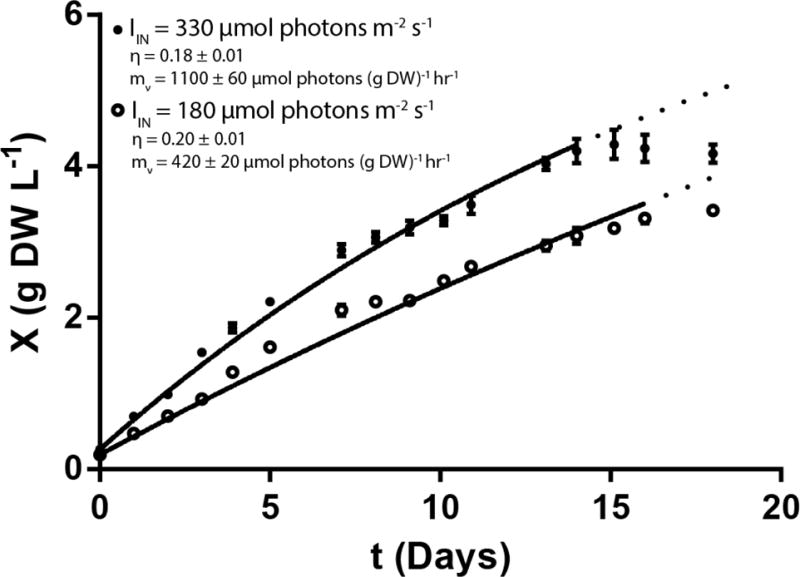
PCC7002 was grown to stationary phase under light limitation in photobioreactors at IIN of 330 (closed circles) or 180 (open circles) μmol photons m−2 s−1. Cell density was measured approximately every 24 hours and the growth retardation phase model was fit to the resulting data set for the first 14 days or 16 days for 330 and 180 μmol photons m−2 s−1 respectively. Growth deviated significantly from predictions (dotted line) after these periods, so subsequent data points were not included in the fit. The initial rate method was used to determine η and then mν was determined using the best fit of Equation 12. Error bars and parameter errors represent the standard error of three biological replicates.
2.3.3. Predicting Scale-Up for PCC7002 Strains Engineered for L-lactate Secretion
In previous work, the PCC7002 strain CC131 was engineered for secretion of L-lactate through heterologous expression of an L-lactate dehydrogenase mutated to co-utilize NADPH and NADH as reducing agents to convert pyruvate to L-lactate and through introduction of a CRISPRi system targeted to the metabolic regulator glnA (Gordon et al., 2016). In that work, CC131 cultures were grown in tubes in 1% CO2 with 250 μmol photons m−2 s−1 (IINSV−1 =95,400 μmol photons L−1 hr−1) with a resulting LGR of 35±1 mg DW L−1 hr−1 and a LPR of 92±1 μM L-lactate hr−1 (Note that in (Gordon et al., 2016), cell pellets were washed with Tris-buffered saline before determining dry weight rather than distilled water, as was done in this work. To correct for this, dry weight measurements were multiplied by 0.75, the ratio of the dry weight of a distilled water washed pellet to a Tris-buffered saline washed pellet). Using Equations 17 and 18, the photosynthetic efficiency (η) was calculated to be 0.18±0.02 and the growth associated productivity (ρ) was calculated to be 2.61±0.09 mmol L-lactate (g DW)−1. Using these values, we predicted the scaled-up LGR and LPR of CC131 in 1 L culture bottles (IINSV−1 =47,000 μmol photons L−1 hr−1) to be 17±2 mg DW L−1 hr−1 and 45±6 μM L-lactate hr−1, respectively (Table 4).
Table 4.
Scale-Up Predictions for Engineered L-lactate and L-lysine Producing Cyanobacteria
| CC131 L-lactate Production | ||||
|---|---|---|---|---|
| Tube | Bioreactor | Flask (Perturbation) | ||
| IINSV−1 (μmol photons L−1 hr−1) | 95400 | 47000 | 99000 | |
| Predicted | Measured | |||
| LGR (mg DW L−1 hr−1) | 35±1 | 16±2 | 14±0.3 | |
| LPR (μM L-lactate hr−1) | 92±1 | 45±6 | 21±0.9 | |
| Best Fit Parameters | ||||
| η | 0.18±0.02 | 0.16±0.01 | 0.17±0.01 | |
| ρ (mmol L-lactate (g DW)−1) | 2.6±0.09 | 1.5±0.07 | 4.4±0.03 | |
| mν (μmol photons (g DW)−1 hr−1) | 1070±110 | |||
| % Theoretical Productivity | 2% | 1% | 3% | |
| TK32 L-lysine Production | ||||
| Flask | Bioreactor | Flask (Perturbation) | ||
| IINSV−1 (μmol photons L−1 hr−1) | 59000 | 47000 | 99000 | |
| Predicted | Measured | |||
| LGR (mg DW L−1 hr−1) | 25±1 | 17±4 | 10±0.4 | |
| LPR (μM L-lysine hr−1) | 10±2 | 7±2 | 13±0.5 | |
| Best Fit Parameters | ||||
| η | 0.23±0.05 | 0.13±0.01 | 0.14±0.02 | |
| ρ (mmol L-lysine (g DW)−1) | 0.40±0.08 | 1.4±0.08 | 0.30±0.2 | |
| mν (μmol photons (g DW)−1 hr−1) | 1150±100 | |||
| % Theoretical Productivity | 2% | 3% | 0.9% | |
Experiments from reference (Gordon et al., 2016).
Experiments from reference (Korosh et al., 2017).
To test these predictions, cultures of CC131 were grown in 1 L bottle photobioreactors with Media A supplemented with NaNO3, FeCl3, and KH2PO4 until stationary phase and the cell density and L-lactate concentration were measured over time (Figure 6). The LGR and LPR were 14±0.3 mg DW L−1 hr−1 and 21±0.9 μM L-lactate hr−1, respectively (calculated from the first 3 days of growth and L-lactate production). While the LGR was close and within error of the predicted value, the LPR was substantially lower than expected. The average values of η and ρ for these cultures were 0.16±0.01 and 1.5±0.07 μmol L-lactate (mg DW)−1 determined by initial rate analysis. This substantial decrease in growth associated productivity (ρ) suggests that the ability of cells to convert pyruvate into L-lactate is reduced in the condition of lower qPh (ηIINSV−1X−1, Figure 2G) where cellular energy content is lower.
Figure 6.
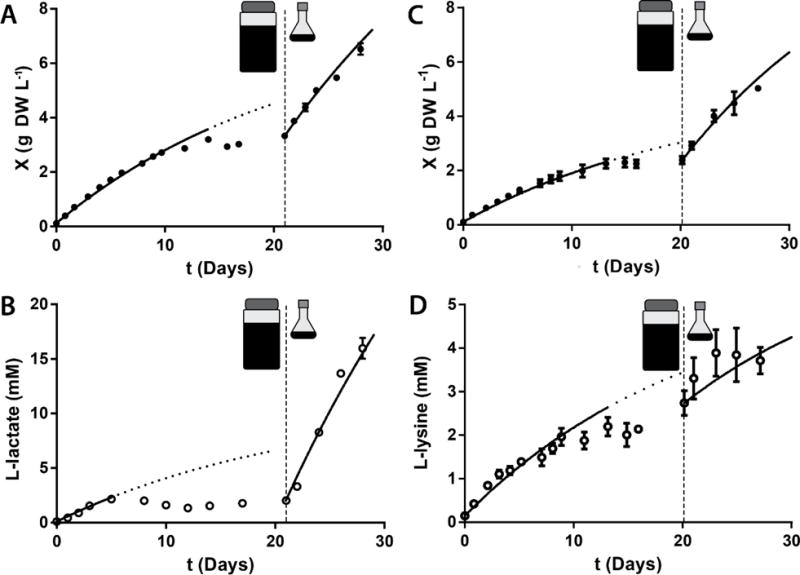
CC131 growth (A) and L-lactate production (B) and TK.032 growth (C) and L-lysine production (D) were measured in photobioreactors to stationary phase. Subsequently, light limitation was verified by transfer of culture to flasks in which IINSV−1 was significantly higher. Samples were obtained for cell density measurement approximately every 24 hours and L-lactate or L-lysine concentration was determined. The growth retardation phase model was fit to the first 14 days of growth and the first 5 days of L-lactate or L-lysine production after which values deviated significantly from predictions (dotted line). The initial rate method was used to determine η and ρ and then mν was determined using the best fit of Equations 17 and 18. After ~21 days (vertical dashed line), samples from each photobioreactor were transferred to shake flasks. η and ρ were determined for this new growth condition by a best fit of Equations 17 and 18 using the value of mν determined in the photobioreactors. Parameter values are given in Table 4. Error bars represent the standard error of at least two biological replicates. Non-visible error bars are smaller than the data symbol.
Using these values of η and ρ in Equations 12 and 13 and fitting the resulting equations to growth and L-lactate secretion data for 14 days of growth yielded an average mν of 1100±110 μmol photons (g DW)−1 hr−1, which is similar to that determined for Wild Type PCC7002 (Figure 5). It is interesting to note that the L-lactate production rate substantially deviated from the model fit after 5 days of growth (approximately 2 g DW L−1 and 2 mM L-lactate) and the growth rate substantially deviated from the model fit after 14 days of growth (approximately 3 g DW L−1), suggesting changes in metabolism with decreasing qPh. Data after 14 days were not included in the fit to determine mν as the model does not adequately describe this result.
When the cultures achieved stationary phase and maintained the same cell density for 7 days, the effect of a perturbation in the volumetric photon delivery rate was studied by transferring a 30 mL sample of each culture from the photobioreactor (IINSV−1 =47,000 μmol photons L−1 hr−1) to a shake flask (IINSV−1 =99,000 μmol photons L−1 hr−1) (Figure 6). An immediate restoration of growth and L-lactate production was observed and a model fit (Equations 13 and 14) using mν=1100 μmol photons (g DW)−1 hr 1 yielded values for the constants η=0.17±0.01 and ρ=4.4±0.03 mmol L-lactate (g DW)−1. This result suggests that the stationary phase observed in the photobioreactors before the perturbation was due to light limitation as hypothesized. The value of η determined after the perturbation was similar in value to that determined before the perturbation, but the value of ρ was more than two-fold higher after the perturbation. This suggests that the metabolism of CC131 converts fixed carbon to L-lactate more effectively in the condition of higher qPh in agreement with our previous observations. Notably, the L-lactate titer (15.9±1 mM) achieved in this cultivation was almost twice as high as the highest previously reported titer of photosynthetically produced L-lactate (Gordon et al., 2016).
At the time of perturbation, samples were taken from each reactor and the spent media was isolated by centrifugation and decanting. Fresh cultures of CC131 were unable to grow in 25 mL of this supernatant in shake flasks (IINSV−1=49,000 μmol photons L−1hr−1) even when supplemented with vitamin B12 or KH2PO4. This result in comparison to the robust growth of directly cultured samples discussed previously suggests that the cultures had either sequestered at least one essential nutrient (other than vitamin B12 and phosphate) into their biomass leaving the extracellular medium depleted. Alternatively, the culture accumulated some molecule that is toxic at low cell densities (high biomass specific photon delivery rate), but not high cell densities (low biomass specific photon delivery rate).
This analysis highlighted a potential relationship between qPh and the specific productivity of L-lactate. This phenomenon would be an interesting area of further investigation to increase L-lactate productivity. For example, transcriptomics and metabolomics methods could be used to investigate the shift in metabolism occurring between early and late batch cultivation when the deviation in L-lactate production was observed in Figure 6B. The resulting understanding could be used to devise an engineering approach to redirect metabolic flux to the desired product.
2.3.4. Predicting Scale-Up for PCC7002 Strains Engineered for L-lysine Secretion
In previous work, the PCC7002 strain TK.032 was engineered for secretion of L-lysine through heterologous expression of an E. coli amino acid transporter ybjE and an aspartate kinase insensitive to feedback regulation (Korosh et al., 2017). In that work, TK.032 cultures were grown in shake flasks in 1% CO2 with 180 μmol photons m−2 s−1 (IINSV−1 =59,000 μmol photons L−1 hr−1) and induced with 1 mM IPTG and 100 ng mL−1 atc with a resulting LGR of 25±1 mg DW L−1 hr−1 and LPR of 10±2 μM L-lysine hr−1. Using Equations 17 and 18, the photosynthetic efficiency (η) was calculated to be 0.23±0.05 and the growth associated productivity (ρ) was calculated to be 0.40±0.08 mmol L-lysine (g DW)−1. Using these values, we predicted the scaled-up LGR and LPR of TK.032 in 1 L culture bottles (IINSV−1 =47,000 μmol photons L−1 hr−1) to be 17±4 mg DW L−1 hr−1 and 7±2 μM L-lysine hr−1, respectively (Table 4).
To test these predictions, cultures of TK.032 were grown in 1 L bottle photobioreactors with Media A supplemented with NaNO3, FeCl3, and KH2PO4 until stationary phase and the cell density and L-lysine concentration were measured over time (Figure 5). The LGR and LPR were 10±0.4 mg DW L−1 hr−1 and 13±0.5 μM L-lysine hr−1, respectively (calculated from the first 3 days of growth and L-lactate production). The LGR was much lower than predicted, but the LPR exceeded the prediction. The average values of η and ρ for the photobioreactor cultures were 0.13±0.01 and 1.35±0.08 mmol L-lysine (g DW)−1, respectively. In this experiment, growth associated productivity (ρ) increased relative to the experiments in shake flasks, but photosynthetic efficiency (η) decreased by approximately 30%. This contrasts with the scale-up of CC131 where photosynthetic efficiency did not change, but a decrease in growth-associated productivity accounted for the difference between predicted and actual L-lactate productivity.
The decrease in η for TK.032 observed after moving to the photobioreactors was likely due to osmotic stress associated with nutrient supplementation. We suspect that TK.032 may be less robust to osmotic changes than other strains of PCC7002 due to high expression of the membrane protein ybjE. This hypothesis is supported by the observation that TK.032 required approximately 48 hours after reactor inoculation to enter growth retardation phase, approximately twice as long as observed for other strains of PCC7002, which could be a result of reduced ability to adapt to the higher osmolarity of Modified Media A.
Using η and ρ in Equations 12 and 13 and fitting the resulting equations to growth and L-lysine secretion data for 13 days of growth yielded an average mν of 1150±100 μmol photons (g DW)−1 hr−1, which is similar to that determined for Wild Type PCC7002 (Figure 5). It is interesting to note that the growth rate substantially deviated from the model fit after 13 days of growth (approximately 2 g DW L−1), suggesting changes in metabolism with very low IAVG. Data after 13 days were not included in the fit to determine mν as the model does not adequately describe this result.
The same perturbation in volumetric photon delivery rate described earlier for cultures of CC131 was performed on the TK.032 cultures (Figure 6). An immediate restoration of growth was observed, but L-lysine secretion was minimal. A model fit (Equations 13 and 14) using mν=1150 μmol photons (g DW)−1 hr−1 yielded values for the constants η=0.14±0.02 and ρ=0.30±0.2 mmol L-lysine (g DW)−1. The value of η determined after the perturbation was similar in value to that determined before the perturbation, but the value of ρ was lowered by more than one third after the perturbation. This suggests that some irreversible change in metabolism occurred during stationary phase that substantially decreased the L-lysine production potential.
This analysis highlighted two potential areas of interest for further investigation to improve L-lysine productivity. First, the potential sensitivity of TK.032 to high osmolarity could be investigated and engineering strategies developed to reduce this stress. Second, the reduction in specific productivity of L-lysine at very low qPh could be investigated using transcriptomics and metabolomics methods for an approach similar to that described earlier for the L-lactate example.
3. Discussion
For the purposes of engineering cyanobacteria for fuel and chemical production, it is preferable to study behavior under light-limitation as this is the desired limitation in an industrial process where CO2 and soluble nutrients can be provided in excess from waste sources (Yenkie et al., 2016). Failure to eliminate other limitations in laboratory cyanobacterial cultivation experiments can lead to confounding results. For example, overexpression of RuBisCO has been studied as a strategy for increased photosynthetic production of fatty acids (Ruffing, 2014), isobutyraldehyde (Atsumi et al., 2009), and sucrose (Ducat et al., 2012) by engineered cyanobacteria, suggesting carbon fixation could be rate-limiting. In subsequent studies, several genes in carbon-fixation were overexpressed in Synechocystis PCC6803, some of which caused large increases in O2-evolution but only minimal increases in growth rate (Liang and Lindblad, 2017, 2016). A key difference between these studies and the previously mentioned successful RuBisCO overexpression studies is that growth experiments were performed in ambient air rather than environments in which inorganic carbon was supplemented in the form of gas phases with elevated CO2 or addition of NaHCO3. Thus, eliminating CO2-limitation in these growth experiments could elucidate why observed increases in O2-evolution were not accompanied by increased CO2-fixation.
Similarly, glycogen accumulation in cyanobacteria has been studied for potential application as an alternative feedstocks for biofuels (Aikawa et al., 2015; Möllers et al., 2014; Song et al., 2016). However, all experiments have been performed in nutrient limiting media where nitrogen limitation triggers the accumulation of glycogen. In practice, nitrogen limitation would limit biomass titer as observed in this work, substantially increasing downstream processing costs (Yenkie et al., 2016). Increasing glycogen accumulation without nutrient limitation is an interesting engineering challenge that will have major implications on the feasibility of this biotechnological pursuit.
In evaluating candidate cyanobacterial species as hosts for photosynthetic chemical production, specific growth rate or doubling time are often reported as the defining growth parameters for which organism is “best” (Yu et al., 2015), often ignoring the transition to linear phase in this calculation (Schuurmans et al., 2017). The short duration of the exponential growth phase practically necessitates the use of a different parameter to compare strains. We propose that photosynthetic efficiency (η) calculated from the linear growth rate (LGR) is a better means of comparison between different cyanobacterial species. As observed in this work, the primary advantage of PCC7002 in the context of photosynthetic chemical production is not the often-lauded high exponential growth rate, but rather its ability to maintain a high photosynthetic efficiency across a wide range of osmolarities, temperatures, and irradiances. Conversely, UTEX2973 has a higher η under its preferred freshwater conditions, but this efficiency is quickly reduced upon the addition of salt. Using this type of analysis to understand the strengths and weaknesses of cyanobacterial strains will be crucial for choosing a host organism for a given engineering application.
Productivities of secreted molecules are often reported in units of mg L−1 OD−1 hr−1, a quantity that describes the biomass specific productivity of a molecule given that the biomass is irradiated with excess photons (Oliver and Atsumi, 2014). In addition to ignoring differences in OD to dry cell weight measurements from different laboratories, this method of reporting is not useful for predicting productivities in a scaled-up process where light is limiting and the biomass specific productivity varies over the course of a batch as shown in this and other work (Kopka et al., 2017). We propose that the standard method of reporting for cyanobacteria engineered for product secretion should include LGR (g DW L−1 hr−1) and LPR (mM Product hr−1) as well as the volumetric photon delivery rate (IINSV−1, μmol photons L−1 hr−1). Photosynthetic efficiency (η) and growth associated productivity (ρ) can be determined from these measurements allowing easy comparison across experimental systems for future research to build on previous results. While the simple model for qP used in this work does not capture all the dynamics of product secretion, it does provide some information about how productivity changes over the course of a batch and across different experimental systems. Future studies should consider how qP varies in time and under relevant process conditions, providing interesting insight into the dynamics of metabolism in engineered cyanobacteria.
Biomass titer and product titer at stationary phase are key factors affecting process economics (Yenkie et al., 2016). As demonstrated in this work, biomass titer is largely determined by specific maintenance, but substantial deviations from predicted biomass accumulation occur at high cell densities as observed in Figures 5 and 6. Physiological changes during the transition from growth retardation phase to stationary phase could elucidate the biological mechanisms limiting the achievable biomass titer. Transcriptional changes for light-dark transitions in cyanobacteria have been shown to be regulated by the stringent response (Hood et al., 2016), so it is possible that light-limited stationary phase is triggered due to buildup of (p)ppGpp as the biomass specific photon delivery rate decreases to a point of starvation.
4. Conclusions
This work identified conditions for batch growth of cyanobacteria under which light-limitation can be maintained through stationary phase. Mathematical descriptions of the phases of growth provided insight into key factors that limit the productivity and achievable titer of cyanobacterial cultures, including high irradiance, high salinity, and cellular maintenance. Experimental and data analysis methods outlined in this work provide a framework for quantification of bioenergetics of cyanobacteria engineered to secrete molecules in simple batch culture experiments. Utilization of this framework by researchers of metabolic engineering in cyanobacteria will improve comparisons of experiments performed under different conditions to improve understanding of key factors for photosynthetic chemical production.
5. Methods
5.1. Culturing Cyanobacteria
Wild Type PCC7002, TK.032, and CC131 were maintained on Media A adapted from Stevens et al (Stevens et al., 1973) (308 mM NaCl, 20 mM MgSO4, 0.08 mM Na2EDTA, 8 mM KCl, 3 mM CaCl2, 12 mM NaNO3, 0.37 mM KH2PO4, 8 mM Tris Base, 30 μM Ferric Ammonium Citrate, 554 μM H3BO3, 22 μM MnCl2, 2.3 μM ZnCl2, 208 nM MoO3, 12 nM CuSO4, 51 nM CoCl2, 3 nM cobalamin) with 1.5% (w/v) Bacto-Agar (Fisher). CC131 was acquired from Gordon, et al (Gordon et al., 2016) and was maintained with the addition of 100 μg mL−1 kanamycin and 30 μg mL−1 gentamicin. TK.032 was obtained from Korosh, et al (Korosh et al., 2017) and was maintained with the addition of 100 μg mL−1 kanamycin. Synechococcus elongatus UTEX 2973 was maintained on BG11 medium (Rippka, 1988) with 1.5% (w/v) Bacto-Agar (Fisher). Inoculum for experiments was prepared by transferring biomass from solid media to 250 mL shake flasks containing 50 mL of the appropriate medium with a sterile loop and incubating the resulting culture in a Kuhner Climo-Shaker ISF1-X outfitted with a white LED (1% (v/v) CO2, 37°C, 75 μmol photons m−2 s−1 from 4000 K White LED). Optical density at 730 nm was measured in a Genesys 20 spectrophotometer (Thermo Scientific) in 1 cm cuvettes. All samples were diluted into the linear range of OD730 between 0.01-0.30. For cultures in which excess nutrients were added, the dilutions used were sufficient to dissolve any precipitates such that they did not contribute significantly to light scattering. An OD730 to g DW L−1 conversion was determined to be 0.26±0.01 g DW L−1 OD730−1 for PCC7002 and 0.34±0.004 g DW L−1 OD730−1 for UTEX2973 by weighing cell pellets washed three times with MilliQ filtered water and then lyophilized (reported error is the standard error of the mean of at least three biological replicates).
5.2. Light Quality Calculations
Luminous flux was determined with a Traceable Dual-Range Light Meter (Fisher Scientific). Total PAR radiant intensity was calculated using a conversion factor for the light source used to calibrate the meter. A normalized radiant intensity spectrum for a given light source was measured with a GoDirect SpectroVis Plus Spectrophotometer (Vernier). The total radiant intensity was combined with this radiant flux spectrum to determine the radiant intensity distribution, which was converted to a photonic flux distribution using the photonic energy. IChla was determined to be the sum of all photonic flux between 380-480 nm and 660-700 nm. IPhyc was determined to be the sum of all photonic flux between 600-660 nm (Supplementary Data 1).
5.3. Photobioreactor Cultivation
The photobioreactors used in this work are described previously (Clark et al., 2017). Briefly, the reactor vessels were 1 L Corning glass wide mouth bottles with modified caps for instrumentation (SV−1=40 m−1). The gas phase was mixed to the specified PCO2 using two mass flow controllers, one for air and one for pure industrial grade CO2, before being delivered to the reactors at approximately 0.3 L min−1. Light was provided by cool white fluorescent bulbs with average IIN of 110 μmol photons m−2 s−1. The temperature was maintained at the specified value by a cooling fan (heat provided by the fluorescent bulbs).
The initial working volume for all photobioreactor experiments was 900 mL. For CO2 transfer optimization, photobioreactors were inoculated with Wild Type PCC7002 to an initial OD730 of 0.05 (three biological replicates per condition). Samples were taken approximately every 24 hours after adjusting the reactor volume with sterile MilliQ to make up for evaporation and OD730 was measured. The first sample taken (approximately 24 hours after inoculations) was determined to be time zero for determination of LGR by fitting a line to the cell density measurements for the first 72 hours.
5.4. Nutrient Supplementation in Shake Flasks
40 mL cultures of PCC7002 in Media A were prepared in 250 mL shake flasks inoculated to a final OD730 of 0.05. Media A + N cultures were supplemented with 110 mM NaNO3. Media A + N + P cultures were supplemented with 110 mM NaNO3 and 5.2 mM KH2PO4. Media A + N + P + Fe cultures were supplemented with 110 mM NaNO3, 5.2 mM KH2PO4, and 1.1 mM FeCl3 and then adjusted to a pH of 7 by addition of NaOH. Samples to which KH2PO4 was added were supplemented with additional aliquots of 5.2 mM KH2PO4. Addition of these excess nutrients did lead to the formation of significant precipitates. This precipitate did not affect the optical density measurements as the samples were diluted by at least a factor of 10 in Media A in cuvettes in order to be in the linear range of the spectrophotometer, allowing dissolution of precipitates. This was verified by diluting culture medium with precipitates but without cyanobacteria into blank Media A and verifying no change in the optical density. These flasks were place in the shaking incubator (1% (v/v) CO2, 37°C, 180 μmol photons m−2 s−1 from 4000 K White LED) and time zero for growth retardation was taken to be approximately 24 hours after inoculation (OD730~1). + P cultures were supplemented with additional aliquots of 5.2 mM KH2PO4 on days 0, 1, 2, 3, and 4 for a total addition of 31 mM KH2PO4. Approximately every 24 hours sterile MilliQ water was added to make up for evaporation and OD730 was measured. The samples that were diluted for OD730 measurement were then analyzed for their absorbance spectrum of light from 350-750 nm (1 nm band) in an Infinite M1000 plate reader (Tecan). The resulting spectrum was normalized by dividing by the average OD measurement in the range of 730-750 nm and inserting a baseline at this average value.
5.5. Exponential Growth Rate Measurements
Cultures were grown in glass tubes (2×15 cm) containing 20 mL of Media A inoculated to an initial OD730 of 0.01. Tubes were placed in a custom plexiglass water bath maintained at 38°C and illuminated from one side by a White (4000 K) LED Panel with the specified incident irradiance, IIN. OD730 measurements were made at time intervals less than the doubling time for a given condition and all measurements were made below OD730=0.1. Exponential growth rate was determined by the slope of a plot of ln(OD730) over time for each sample (Supplementary Data 2).
5.6. Linear Growth Rate Measurements
Cultures were treated as described in “Exponential Growth Rate Measurements”, but samples were taken in the range of OD730 0.5-5. The water bath temperature was adjusted for varying temperature samples. High osmolarity cultures were grown in Media A supplemented with NaCl to the specified osmolarity. Synechococcus Elongatus UTEX 2973 was cultured in BG11. LGR was determined by the slope of a plot of OD730 over time for each sample (Supplementary Data 2). Yields were calculated by the ratio of LGR to the volumetric photon delivery rate (IINSV−1).
5.7. Photobioreactor IIN Variation Experiments
Photobioreactors were inoculated with Wild Type PCC7002 to an OD730 of 0.05 with a working volume of 900mL of Media A. The temperature controller was set to maintain the reactors at 30°C. Reactors with IIN=180 μmol photons m−2 s−1 had 4 of the 8 fluorescent bulbs removed. Time zero for growth retardation was taken to be 24 hours after inoculation (OD730~1). Nutrients were added in aliquots containing 18.3mM NaNO3, 183μM FeCl3, and 5.2mM KH2PO4 on Days 0, 2, 4, 7, and 10 for reactors with IIN=330 μmol photons m−2 s−1 and on Days 0, 3, 5, and 10 for reactors with IIN=180 μmol photons m−2 s−1. Samples were taken approximately every 24 hours after adjusting the reactor volume with sterile MilliQ to make up for evaporation and the OD730 was measured (Supplementary Data 3).
5.8. Photobioreactor L-lactate and L-lysine Production Experiments
Photobioreactors were inoculated with CC131 or TK.032 to an OD730 of 0.05 with a working volume of 930mL of Media A supplemented with 110mM NaNO3, 1.1mM FeCl3, and 5.2mM KH2PO4. Reactors with CC131 were supplemented with 100 μg/mL kanamycin, 30 μg/mL gentamicin, and 1mM IPTG. Reactors with TK.032 were supplemented with 100 μg/mL kanamycin, 1mM IPTG, and 100 ng/mL anhydrous tetracycline. The temperature controller was set to maintain the reactors at 37°C. A gas phase containing 5% CO2 was introduced at a flow rate of 0.3 L min−1 and the system was given 1 hour to equilibrate, at which point the pH of each culture was adjusted to 7 by adding approximately 1.7mL of 5M NaOH. Time zero for growth retardation phase was taken to be 24 hours after inoculation for CC131 and 48 hours after inoculation for TK.032 (OD730~1). Samples were taken approximately every 24 hours after adjusting the reactor volume with sterile MilliQ to make up for evaporation and the pH and OD730 were measured. Samples were centrifuged and the supernatant was saved for L-lactate or L-lysine quantification (stored at −20°C until measurement). Additional KH2PO4 was added in 5.2mM aliquots on days 3, 6, and 8 for CC131 and days 2 and 6 for TK.032 (pH fluctuated between 6.7 and 7.2 as KH2PO4 was added and subsequently consumed).
Once stationary phase was achieved and maintained for 4 days (21 days after start of experiment), 30 mL samples were transferred from each reactor to 250 mL shake flasks and placed into the shaking incubator (1% (v/v) CO2, 37°C, 75 μmol photons m−2 s−1 from 4000 K White LED) where sampling was continued similarly to the photobioreactors for 7 days. Additional samples were taken from the reactors at the same time and centrifuged to remove biomass. The resulting supernatant was inoculated to an OD730 of 0.05 with fresh CC131 culture, but no growth was observed.
5.9. L-lactate Quantification
L-lactate concentrations were determined using a L-lactate assay kit (Sigma Aldrich) where an enzymatic reaction results in a colorimetric (450 nm) product. Measurements were made using the protocol contained in the kit. Briefly, standards containing 0, 2, 4, 6, 8, or 10 nmol of L-lactate in 100uL of reaction buffer with the provided enzyme mix and substrate were placed into wells of a 96-well plate. Samples to be quantified were diluted to be within the range of standards (≤2.5 μL of each sample) into reaction buffer with the provided enzyme mix and substrate and placed into wells of a 96-well plate. The same process was repeated for standards and samples excluding the enzyme mix to control for background florescence. The plates were incubated at ambient temperature in the dark for 30 minutes and the absorbance at 450nm was measured with an Infinite M1000 plate reader (Tecan). The absorbance of the control plates was subtracted from the reaction plates and a standard curve was determined from the standards by fitting a line to all samples. This standard curve was used to determine the L-lactate concentration of the samples.
5.10. L-lysine Quantification
L-lysine quantification was performed using HPLC (Shimadzu Co., Columbia, MD, USA) equipped with a quaternary pump, autosampler, vacuum degasser, photodiode array and fluorescence detector. HPLC separations were performed using a Xbridge C18 column (2.1 × 150 mM, 3.5 μm, Waters) as described previously (Korosh et al., 2017). The method employed a 20-minute linear gradient starting with 100% Buffer A: [925 ml of 100 mM Acetate (pH 6.95); 50 ml of HPLC Grade Methanol: 25 ml of HPLC Grade Tetrahydrofuran] to 100% Buffer B: [975 ml of HPLC Grade Methanol: 25 ml of HPLC Grade Tetrahydrofuran] before returning to the initial conditions for 10 mins. The flow rate was 0.400 mL/min, column temperature 40°C, and injection volume 10 μL. Amino acid samples and standards were quantified by comparison with peaks generated by monitoring the fluorescence (Ex 320 nm/Em 450 nm) of known amounts of standards in Media A+, after precolumn derivatization with 3 mg/ml o-phthalaldehyde with 3-mercaptopropionic acid in 0.4 M borate buffer.
5.11. Theoretical Yield Calculations
Theoretical maximum yields on photons of both biomass and the products in Table 2 were calculated using a genome-scale metabolic model of 7002, iSyp708. Within the model, the total photon uptake flux (i.e. r_EX_PHOTONPSII_E + r_EX_PHOTONPSI_E) was constrained to be less than or equal to 1 mmol photons (g DW)−1 hr−1. The uptake fluxes of carbon dioxide, nitrate, water, oxygen, phosphate, sulfate, magnesium, and protons were unconstrained. The bidirectional hydrogenase and pyruvate synthase reactions were disabled as those reactions are known to be inactive in the presence of oxygen. For simulations maximizing the yields of non-native compounds, the appropriate biosynthesis pathways were added to the model (Supplementary Data 4). Additionally, when simulating terpenes produced via the non-native mevalonate pathway, the native MEP pathway in the model was inactivated by disabling flux through the 2-C-methyl-D-erythritol-2,4-cyclodiphosphate dehydratase reaction. “Demand” reactions were added to the model to remove the products of interest from the cytosol. Given these constraints, flux balance analysis (FBA) was performed with the objective of maximizing the production of biomass or the specific product of interest (Orth et al., 2010). Yields were determined by dividing this maximum production flux by the photon uptake flux. For all yield calculations, it was verified that the total photon uptake flux was unique given the maximized objective. All simulations were performed in GAMS (GAMS Development Corporation, Washington, DC) using the CPLEX solver.
It should be noted that there is a small degree of uncertainty in these YPν values stemming from uncertainty in the exact H+/ATP ratio utilized by the ATP synthase in 7002 (the published iSyp708 model uses a ratio of 4). To examine the magnitude of this uncertainty on the yields reported in Table 2, the H+/ATP ratio in the metabolic model was varied from 3 to 5 and the percent change in each product yield across this range was calculated. The largest percent decrease in YPν from H+/ATP=3 to H+/ATP=5 was ~15% for acetone, with most compounds having a percent decrease well below 10%. As such, it seems that the uncertainties in the calculated YPν should have relatively little impact on the accuracy of the models developed in this work.
5.12. Model Fits
Model fits were determined using the Solver tool in Microsoft Office Excel 2016. For each data point the normalized square error was normalized by the theoretical yield on photons and summed using Equations 21 and 22.
| (21) |
| (22) |
SSRX and SSRP were each divided by the number of data points of the given type and the sum of these two values was used as the objective function. The fit was optimized using the Microsoft Excel Solver tool by setting the objective function to zero and changing the specified parameters.
Supplementary Material
Highlights for Clark et al.
A kinetic model is presented to standardize reports of cyanobacteria studies
Light-limited stationary phase is demonstrated for Syn. sp PCC7002
Model is used to predict scale-up of two cyanobacteria across varied reactors
Acknowledgments
This work was supported by the National Science Foundation (EFRI-1240268) and the US Department of Energy (DE-SC0008103). R.L.C. was supported by the NIH NHGRI Genomic Sciences Training Program (T32 HG002760). T.C.K. was supported by a Biotechnology Training Program Fellowship (NIGMS - 5 T32 GM08349).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Bibliography
- Aikawa S, Ho SH, Nakanishi A, Chang JS, Hasunuma T, Kondo A. Improving polyglucan production in cyanobacteria and microalgae via cultivation design and metabolic engineering. Biotechnol J. 2015;10:886–898. doi: 10.1002/biot.201400344. [DOI] [PubMed] [Google Scholar]
- Angermayr SA, Gorchs Rovira A, Hellingwerf KJ. Metabolic engineering of cyanobacteria for the synthesis of commodity products. Trends Biotechnol. 2015;33:352–361. doi: 10.1016/j.tibtech.2015.03.009. [DOI] [PubMed] [Google Scholar]
- Atsumi S, Higashide W, Liao JC. Direct photosynthetic recycling of carbon dioxide to isobutyraldehyde. Nat Biotechnol. 2009;27:1177–80. doi: 10.1038/nbt.1586. [DOI] [PubMed] [Google Scholar]
- Barbosa MJ, Janssen M, Ham N, Tramper J, Wijffels RH. Microalgae cultivation in air-lift reactors: Modeling biomass yield and growth rate as a function of mixing frequency. Biotechnol Bioeng. 2003;82:170–179. doi: 10.1002/bit.10563. [DOI] [PubMed] [Google Scholar]
- Bernstein HC, McClure RS, Hill EA, Markillie LM, Chrisler WB, Romine MF, McDermott JE, Posewitz MC, Bryant DA, Konopka AE, Fredrickson JK, Beliaev Unlocking the Constraints of Cyanobacterial Productivity: Acclimations Enabling Ultrafast Growth. MBio. 2016;7 doi: 10.1128/mBio.00949-16.Editor. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark RL, McGinley LL, Quevedo DF, Root TW, Pfleger BF. Construction and Operation of an Affordable Laboratory Photobioreactor System for Simultaneous Cultivation of up to 12 Independent 1 L Cyanobacterial Cultures. bioRxiv 2017 [Google Scholar]
- Du W, Jongbloets JA, Pineda Hernández H, Bruggeman FJ, Hellingwerf KJ, Branco dos Santos F. Photonfluxostat: A method for light-limited batch cultivation of cyanobacteria at different, yet constant, growth rates. Algal Res. 2016;20:118–125. doi: 10.1016/j.algal.2016.10.004. [DOI] [Google Scholar]
- Ducat DC, Avelar-Rivas JA, Way JC, Silver Pa. Rerouting carbon flux to enhance photosynthetic productivity. Appl Environ Microbiol. 2012;78:2660–8. doi: 10.1128/AEM.07901-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egli T. Microbial growth and physiology: a call for better craftsmanship. Front Microbiol. 2015;6:287. doi: 10.3389/fmicb.2015.00287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evers EG. A model for light-limited continuous cultures: growth, shading, and maintenance. Biotechnol Bioeng. 1991;38:254–259. doi: 10.1002/bit.260380307. [DOI] [PubMed] [Google Scholar]
- García-Camacho F, Sánchez-Mirón A, Molina-Grima E, Camacho-Rubio F, Merchuck JC. A mechanistic model of photosynthesis in microalgae including photoacclimation dynamics. J Theor Biol. 2012;304:1–15. doi: 10.1016/j.jtbi.2012.03.021. [DOI] [PubMed] [Google Scholar]
- Gordon GC, Korosh TC, Cameron JC, Markley AL, Begemann MB, Pfleger BF. CRISPR interference as a titratable, trans-acting regulatory tool for metabolic engineering in the cyanobacterium Synechococcus sp strain PCC 7002. Metab Eng. 2016;38:170–179. doi: 10.1016/j.ymben.2016.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grima EM, Camacho FG, Pérez JaS, Fernéndez FGA, Sevilla JMF. Evaluation of photosynthetic efficiency in microalgal cultures using averaged irradiance. Enzyme Microb Technol. 1997;21:375–381. doi: 10.1016/S0141-0229(97)00012-4. [DOI] [Google Scholar]
- Hood RD, Higgins SA, Flamholz A, Nichols RJ, Savage DF. The stringent response regulates adaptation to darkness in the cyanobacterium Synechococcus elongatus. Proc Natl Acad Sci U S A. 2016;113:E4867–E4876. doi: 10.1073/pnas.1524915113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson SA, Eaton-Rye JJ, Bryant DA, Posewitz MC, Davies FK. Dynamics of photosynthesis in a glycogen-deficient glgC mutant of Synechococcus sp strain PCC 7002. Appl Environ Microbiol. 2015;81:6210–6222. doi: 10.1128/AEM.01751-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopka J, Schmidt S, Dethloff F, Pade N, Berendt S, Schottkowski M, Martin N, Dühring U, Kuchmina E, Enke H, Kramer D, Wilde A, Hagemann M, Friedrich A. Systems analysis of ethanol production in the genetically engineered cyanobacterium Synechococcus sp PCC 7002. Biotechnol Biofuels. 2017;10:56. doi: 10.1186/s13068-017-0741-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korosh TC, Markley AL, Clark RL, Mcginley LL, McMahon KD, Pfleger BF. Engineering Photosynthetic Production of L-lysine. Metab Eng. 2017;44 doi: 10.1016/j.ymben.2017.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis NE, Nagarajan H, Palsson BO. Constraining the metabolic genotype–phenotype relationship using a phylogeny of in silico methods. Nat Rev Microbiol. 2012;10:291–305. doi: 10.1038/nrmicro2737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang F, Lindblad P. Synechocystis PCC 6803 overexpressing RuBisCO grow faster with increased photosynthesis. Metab Eng Commun. 2017;4:29–36. doi: 10.1016/j.meteno.2017.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang F, Lindblad P. Effects of overexpressing photosynthetic carbon flux control enzymes in the cyanobacterium Synechocystis PCC 6803. Metab Eng. 2016;38:56–64. doi: 10.1016/j.ymben.2016.06.005. [DOI] [PubMed] [Google Scholar]
- Ludwig M, Bryant DA. Acclimation of the global transcriptome of the cyanobacterium Synechococcus sp strain PCC 7002 to nutrient limitations and different nitrogen sources. Front Microbiol. 2012;3:145. doi: 10.3389/fmicb.2012.00145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Möllers KB, Cannella D, Jørgensen H, Frigaard NU. Cyanobacterial biomass as carbohydrate and nutrient feedstock for bioethanol production by yeast fermentation. Biotechnol Biofuels. 2014;7:64. doi: 10.1186/1754-6834-7-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monod J. The Growth of Bacterial Cultures. Annu Rev Microbiol. 1949 doi: 10.1146/annurev.mi.03.100149.002103. [DOI] [Google Scholar]
- Oliver JWK, Atsumi S. Metabolic design for cyanobacterial chemical synthesis. Photosynth Res. 2014 doi: 10.1007/s11120-014-9997-4. [DOI] [PubMed] [Google Scholar]
- Oliver NJ, Rabinovitch-Deere CA, Carroll AL, Nozzi NE, Case AE, Atsumi S. Cyanobacterial metabolic engineering for biofuel and chemical production. Curr Opin Chem Biol. 2016;35:43–50. doi: 10.1016/j.cbpa.2016.08.023. [DOI] [PubMed] [Google Scholar]
- Orth JD, Thiele I, Palsson BØ. What is flux balance analysis? Nat Biotechnol. 2010;28:245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perin G, Bernardi A, Bellan A, Bezzo F, Morosinotto T. A mathematical model to guide genetic engineering of photosynthetic metabolism. Metab Eng. 2017;44:337–347. doi: 10.1016/j.ymben.2017.11.002. [DOI] [PubMed] [Google Scholar]
- Pirt SJ. The thermodynamic efficiency (quantum demand) and dynamics of photosynthetic growth. New Phytol. 1986;102:3–37. doi: 10.1111/j.1469-8137.1986.tb00794.x. [DOI] [PubMed] [Google Scholar]
- Pirt SJ. The Maintenance Energy of Bacteria in Growing Cultures. Proc R Soc London Ser B, Biol Sci. 1965;163:224–231. doi: 10.1098/rspb.1965.0069. [DOI] [PubMed] [Google Scholar]
- Rippka R. Isolation and Purification of Cyanobacteria. Methods Enzymol. 1988;167:3–27. doi: 10.1016/0076-6879(88)67004-2. [DOI] [PubMed] [Google Scholar]
- Ruffing AM. Improved Free Fatty Acid Production in Cyanobacteria with Synechococcus sp PCC 7002 as Host. Front Bioeng Biotechnol. 2014;2:17. doi: 10.3389/fbioe.2014.00017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuurmans RM, Matthijs JCP, Hellingwerf KJ. Transition from exponential to linear photoautotrophic growth changes the physiology of Synechocystis sp PCC 6803. Photosynth Res. 2017;132:69–82. doi: 10.1007/s11120-016-0329-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuurmans RM, Van Alphen P, Schuurmans JM, Matthijs HCP, Hellingwerf KJ. Comparison of the photosynthetic yield of cyanobacteria and green algae: Different methods give different answers. PLoS One. 2015;10:1–17. doi: 10.1371/journal.pone.0139061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shuler ML, Kargi F. Bioprocess engineering: basic concepts. Prentice Hall; 1992. [Google Scholar]
- Song K, Tan X, Liang Y, Lu X. The potential of Synechococcus elongatus UTEX 2973 for sugar feedstock production. Appl Microbiol Biotechnol. 2016;100:7865. doi: 10.1007/s00253-016-7510-z. [DOI] [PubMed] [Google Scholar]
- Stevens SE, Balkwill DL, Paone DAM. The Effects of Nitrogen Limitation on the Ultrastructure of the Cyanobacterium Agmenellum quadruplicatum. Arch Microbiol. 1981;130:204–212. [Google Scholar]
- Stevens SE, Patterson COP, Myers J. The Production of Hydrogen Peroxide by Blue-Green Algae: A Survey. J Phycol. 1973;9:427–430. doi: 10.1111/j.1529-8817.1973.tb04116.x. [DOI] [Google Scholar]
- Touloupakis E, Cicchi B, Torzillo G. A bioenergetic assessment of photosynthetic growth of Synechocystis sp PCC 6803 in continuous cultures. Biotechnol Biofuels. 2015;8:133. doi: 10.1186/s13068-015-0319-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vu TT, Hill Ea, Kucek La, Konopka AE, Beliaev AS, Reed JL. Computational evaluation of Synechococcus sp PCC 7002 metabolism for chemical production. Biotechnol J. 2013;8:619–30. doi: 10.1002/biot.201200315. [DOI] [PubMed] [Google Scholar]
- Xiong Q, Feng J, Li S, Zhang G, Qiao Z, Chen Z. Integrated Transcriptomic and Proteomic Analysis of the Global Response of Synechococcus sp PCC 7002 to High Light Stress. Mol Cell Proteomics. 2015;14:1038–1053. doi: 10.1074/mcp.M114.046003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue Y, He Q. Cyanobacteria as cell factories to produce plant secondary metabolites. Front Bioeng Biotechnol. 2015;3:57. doi: 10.3389/fbioe.2015.00057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yenkie KM, Wu WZ, Clark RL, Pfleger BF, Root TW, Maravelias CT. A roadmap for the synthesis of separation networks for the recovery of bio-based chemicals: Matching biological and process feasibility. Biotechnol Adv. 2016;34:1362–1383. doi: 10.1016/j.biotechadv.2016.10.003. [DOI] [PubMed] [Google Scholar]
- Youngquist JT, Lennen RM, Ranatunga DR, Bothfeld WH, Marner WD, Pfleger BF. Kinetic modeling of free fatty acid production in Escherichia coli based on continuous cultivation of a plasmid free strain. Biotechnol Bioeng. 2012;109:1518–27. doi: 10.1002/bit.24420. [DOI] [PubMed] [Google Scholar]
- Yu J, Liberton M, Cliften PF, Head RD, Jacobs JM, Smith RD, Koppenaal DW, Brand JJ, Pakrasi HB. Synechococcus elongatus UTEX 2973, a fast growing cyanobacterial chassis for biosynthesis using light and CO2. 2015:5–7. doi: 10.1038/srep08132. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


