Abstract
Hydrodynamic properties are useful parameters for estimating the size and shape of proteins and nucleic acids in solution. The calculation of such properties from structural models informs on the solution properties of these molecules and complements corresponding structural studies. Here we report, to our knowledge, a new method to accurately predict the hydrodynamic properties of molecular structures. This method uses a convex hull model to estimate the hydrodynamic volume of the molecule and is orders of magnitude faster than common methods. It works well for both folded proteins and ensembles of conformationally heterogeneous proteins and for nucleic acids. Because of its simplicity and speed, the method should be useful for the modification of computer-generated, intrinsically disordered protein ensembles and ensembles of flexible, but folded, molecules in which rapid calculation of experimental parameters is needed. The convex hull method is implemented in a Python script called HullRad. The use of the method is facilitated by a web server and the code is freely available for batch applications.
Introduction
Hydrodynamic properties such as sedimentation and diffusion coefficients and their related hydrodynamic radii are useful parameters to estimate the size and shape of biological molecules in solution (1). Experimental methods such as analytical ultracentrifugation (2), small-angle x-ray scattering (3), dynamic light scattering (4), fluorescence polarization (5), size exclusion chromatography (6), and NMR (7) have all been used to measure these hydrodynamic properties experimentally. Hydrodynamic properties may also be predicted for three-dimensional structural models of proteins and nucleic acids. Comparisons of these predicted and experimentally determined hydrodynamic properties are useful to probe the solution properties of crystalline structures.
There are several methods available to predict the hydrodynamic properties of biological molecules from three-dimensional models: a boundary element method (BEST) that uses triangulation of the solvent accessible surface (8); bead-modeling methods (HYDROPRO, SOMO, AtoB), as reviewed in (9, 10); methods based on the construction of an ellipsoidal shell (ELLIPS, ELM) (11, 12); and a numerical path integration method (ZENO) (13). The major disadvantage of the above methods is slow speed. The HYDROPRO program that implements a bead modeling algorithm has been most often used to calculate hydrodynamic properties from protein structures (14). Several of these methods have been integrated into the UltraScan analytical ultracentrifugation analysis software suite (15).
The method described here for predicting hydrodynamic properties is orders of magnitude faster than other methods. The method has comparable accuracy with commonly used methods, it is suitable for both translational and rotational diffusion, it does not require runtime configuration files, it works for both folded and disordered proteins and for nucleic acids, and it accepts the largest known molecular structures without modification of input parameters. The new algorithm uses a convex hull to model the hydrodynamic volume of a molecular structure. The convex hull is a three-dimensional mathematical construct related to Voronoi diagrams. It is the smallest convex envelope that contains a set of points. It has been applied to areas such as cluster analysis, collision detection for robotic systems, and crystal growth, as well as many other mathematical problems (16). It also has been used previously to estimate the particle size and surface roughness of aggregates and nanomaterials (17, 18). The convex hull of a three-dimensional molecular model encapsulates both the overall volume of the molecule as well as its shape asymmetry and surface roughness; all characteristics that influence hydrodynamic diffusion.
The convex hull method is implemented in a simple Python script called HullRad. The program code is made freely available and the method may also be accessed through a web server.
Methods
Convex hull transport model
A convex hull is mathematically defined as the smallest convex envelope that contains a set of points. We implemented calculation of the convex hull to model the hydrodynamic behavior of a molecular structure in a Python script entitled HullRad. HullRad reads coordinates of a standard Protein Data Bank (PDB) file as input; makes a reduced atom model of the structure (detailed below); calls an open source C-code version of Qhull (19), which returns the convex hull volume and surface area from the atom center point set; expands the initial convex hull volume to account for hydration (discussed below); calculates a shape factor correction based on an ellipsoid of revolution; and finally calculates the following hydrodynamic parameters: R0, RT, RR, s, DT, DR, f/f0, and [η], all defined as follows.
R0 is the radius in Å of an equivalent sphere corresponding to the volume of the anhydrous molecule (Eq. 1),
| (1) |
where equals the anhydrous molecular volume in Å3 defined as
| (2) |
where M is the molar mass (g mol−1), NA is Avogadro's number, and is the partial specific volume (ml g−1). The anhydrous partial specific volumes of amino acids were taken from those reported by Cohn and Edsall (20) as corrected by Perkins (21); the volumes of nucleic acids are as reported in (22) and (23).
and (Å) are the translational and rotational hydrodynamic radii calculated from a sphere with the equivalent volume (VTH or VRH) as the expanded convex hull for a particular molecule (described below) and corrected by the translational or rotational shape factors FT and FR, respectively.
| (3) |
| (4) |
The hull volume expansion to account for hydration is different for translational diffusion and rotational diffusion as described below. The frictional ratio, f/f0, is defined as RT,calc/R0.
A translational diffusion shape factor, FT, is calculated as follows: the major axis (a) of a prolate ellipsoid of revolution is estimated from the maximum dimension of the initial convex hull of a molecule. The minor axis is calculated from Eq. 5, assuming the volume of a prolate ellipsoid is 4πab2/3.
| (5) |
where VH is the equivalent volume of the initial convex hull for a particular molecule. From the axial ratio, a/b, a translational shape factor based on Perrin’s equation (24) is obtained. A prolate ellipsoid of revolution is used to model the nonsphericity of all molecules. For molecules with axial ratios less than 5:1, the translational shape factors for prolate and oblate ellipsoids of revolution are similar within 2%. Rotational shape factors are more complicated because the effect of shape depends on the axis of revolution for an ellipsoid and the overall tumbling is characterized by a rotational diffusion tensor (25). In addition, rotational shape factors are significantly larger than translational shape factors (1). However, as described below and in the Supporting Material, we empirically derived a rotational shape factor FR = FT4 that accurately predicts the overall rotational hydrodynamic properties of elongated molecules up to an axial ratio of 2.62, the most nonspherical molecule in our data set.
The sedimentation coefficient, , (in units of seconds) is calculated at 20°C in water. HullRad predicts this value from using the Svedberg equation, Eq. 6:
| (6) |
where is the water density at 20°C (g mL−1), NA is Avogadro’s number, is water viscosity at 20°C (poise), the 108 term converts from Å to cm to convert the answer to the correct order of magnitude for the sedimentation coefficient, and other terms are as previously defined.
(cm2 s−1) and (s−1) are the translational and rotational diffusion coefficients calculated from their respective hydrodynamic radii as follows:
| (7) |
| (8) |
where is Boltzmann’s constant and other terms are as previously described. The temperature (T) employed in these calculations is 20°C because this is the standard used for hydrodynamic modeling.
The intrinsic viscosity, [η], is defined by Eq. 9.
| (9) |
By mathematical definition, the vertices of the convex hull are placed at the outermost surface atom centers. This has several implications for subsequent hydrodynamic calculations. First, an individual structure file contains a static, snapshot representation of the atomic coordinates. For proteins, the specific side chain conformations encoded by the PDB file will influence the corresponding convex hull for a particular protein. In contrast, side chain motion in solution would lead to an ensemble of side chain conformations and corresponding variations in the positions of the convex hull vertices. These alternate positions in turn lead to variations in the hull volumes. To average surface-exposed side chain conformations represented in a particular protein coordinate file, each side chain is represented by a single, unified pseudoatom located along the Cα – Cβ vector. This pseudoatom is displaced outward by a distance equal to the radius of a sphere corresponding to the respective side chain volume. To maintain the fold represented in the original PDB file, all backbone atoms, including those that are surface-exposed, are unchanged. It is this latter pseudoatom model from which the initial convex hull is created. Images of initial convex hulls shown in the figures were created by using PyMOL (26).
To improve computational speed, a reduced atom model of nucleic acids is made by using only the nitrogen and oxygen atoms of the molecule. The difference in the volumes of convex hulls made with the reduced atom nucleic acid models compared to models that also contained carbon and phosphorus atoms is small. This is because almost all vertices of the convex hull are determined by either phosphate oxygen atoms or base nitrogen atoms in nucleic acid structures. The volume difference for DNA duplexes was 0.5%, for transfer RNA it was 0.8%, and for 50 s ribosomal subunit it was 0.01%. Interestingly, the sign of the difference was dependent on the structure, and a variation of this magnitude is consistent with the averaging effect of pseudoatom side chains in proteins.
A second issue for hydrodynamic modeling is that proteins and nucleic acids are hydrated in solution. This aspect is not taken into account when calculating the initial convex hull above because the input structural model is anhydrous. To account for hydration, the initial convex hull volume is increased by expanding the planes of the hull outward. As with other commonly used hydrodynamic modeling algorithms, the extent of expansion was empirically determined by optimizing agreement of the calculated parameters with experimental hydrodynamic data. The resulting total expanded hull volume is assumed to be the hydrodynamic volume of the molecule. The hydrodynamic radii are calculated from a sphere of volume equal to that of the expanded convex hull corrected by a shape factor as described below. Because hydration is manifested differently in translational and rotational transport, separate hull expansions were empirically determined and optimized for RT and RR as described in Results and Discussion.
To take full advantage of experimental hydrodynamic data, we used jackknife resampling (27) of the translational protein data set to test for bias caused by specific proteins during optimization of the hull expansion for hydration. Following this procedure, each protein in the data set in turn was omitted during determination of the optimal hull expansion. The RT of the omitted protein was calculated by using the optimal hull expansion value determined by using all other proteins in the set. This calculated RT,calc was compared to experimental RT,exp to estimate the independent error.
Code execution
The HullRad method is available as a web server (http://www.hullrad.wordpress.com), and the Python script will be made freely available on-line upon publication. Qhull is freely available at http://www.qhull.org. The HullRad code is designed to be user-friendly from the command line and is suitable for batch calculation of multiple structures. Neither preparation of a configuration file nor manipulation of the molecular structure file is necessary. The same fitted parameters are used for all molecular sizes. A simple command with a PDB file name as input results in output of the format shown in Fig. 1 (PDB code: 5PTI shown for example).
Figure 1.
Sample output for execution of HullRad using the PDB file for bovine pancreatic trypsin inhibitor.
An option for code execution includes output of the reduced atom structure used in construction of the convex hull as a PDB file. The README file in the code distribution contains instructions for installation, execution, and convex hull image generation. HullRad has been tested on Windows, Mac, and UNIX platforms. Prior installation of Python 2.7 is required.
Transformation of experimental coefficients
For ease of comparison between experimental values obtained by using different methods, all experimental hydrodynamic data were converted to equivalent hydrodynamic radii. Sedimentation coefficients were converted to equivalent RT,exp (in Å) according to the Svedberg relationship in Eq. 10. These values were provided in the literature at the standard of 20°C and pure water.
| (10) |
where the 108 term converts the value from cm to Å and other terms are as previously defined.
Experimental translational diffusion coefficients, DT, were converted to equivalent RT,exp (in Å) according to Eq. 11.
| (11) |
Similarly, protein rotational correlation times were converted to equivalent RR,exp in Å by using the following relationship,
| (12) |
where is the overall rotational correlation time (seconds) assuming isotropic rotation, and the other terms are as previously defined. Correlation times obtained by NMR are typically reported for the conditions of data collection and were converted to 20°C by using the known dependence of water viscosity on temperature by multiplying the experimentally observed τ by the factor (28, 29).
As a measure of protein backbone expansion of intrinsically disordered proteins (IDPs) (see Fig. 7), we used the radius of gyration calculated by Eq. 13.
| (13) |
where N is the number of atoms, mi represents the mass of each atom, ri represents the Cartesian position of each atom and COM is the center of mass of the protein. This is an anhydrous, geometric RG of the protein atoms alone and is not the same as the radius of gyration determined by scattering experiments. The radius of gyration determined by x-ray scattering includes effects from waters of hydration (30) and requires a consideration of explicit solvent positions for accurate calculation (31). The convex hull method is an empirical method that does not consider explicit waters of hydration and therefore does not predict experimental RG.
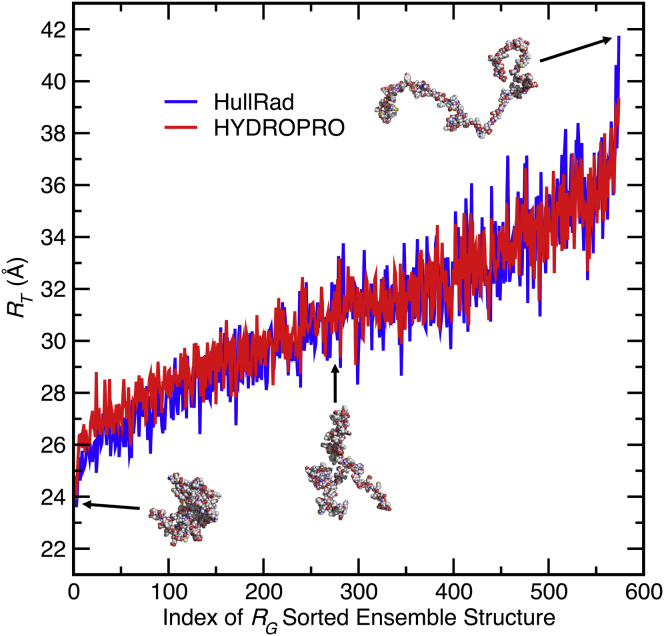
Figure 7.
Prediction of hydrodynamic properties for a disordered protein ensemble. Shown are the effective translational hydrodynamic radii of disordered protein structures calculated using HullRad (dark gray, blue online) or HYDROPRO (light gray, red online). The structures are sorted by compactness using the anhydrous RG calculated using Eq. 13. Three example structures representing different degrees of compactness are shown as atomic sphere models. The ensemble contains 575 generated structures of α-synuclein from the Protein Ensemble Database (accession number PED9AAC). To see this figure in color, go online.
Bead modeling calculations
Hydrodynamic parameters were independently calculated by using the program HYDROPRO Version 10 (14). For most structures, the atomic-level primary model was used with default values of 2.9 Å for the radius of the elements in the primary model and σ= 6. For the large complex of GroEL (M = 828,989) the atomic level calculation was unsuccessful, and we therefore used the residue-level primary model with a default radius of 4.8 Å. We used the default option to estimate σ by the program. Residue level calculations were also carried out for the benchmarking shown in Fig. 4. We used the default temperature and viscosity values of 20°C and 0.01 poise, respectively.
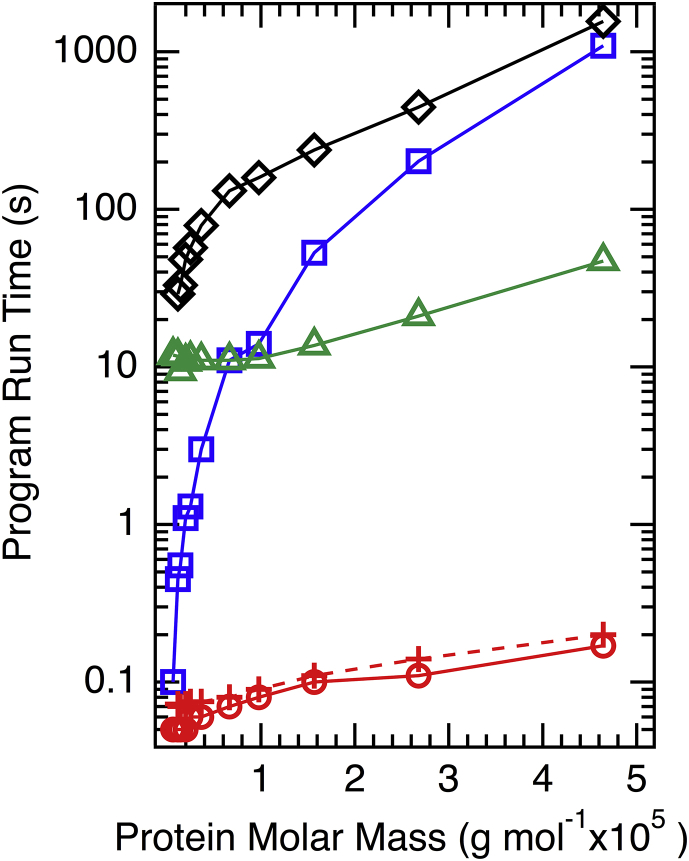
Figure 4.
HullRad execution is orders of magnitude faster than other common hydrodynamic prediction algorithms for most proteins. The red circles and crosses are data for HullRad measured on an Intel ×64 machine running Ubuntu Linux and a MacOS laptop computer, respectively; the blue squares and green triangles are HYDROPRO runtimes on Linux using the default atom and residue options, respectively; black diamonds are SOMO runtimes on a Macintosh laptop. The points for each series are connected by lines for clarity. To see this figure in color, go online.
Protein data sets
Folded protein structures from previous hydrodynamic property predictions (12, 32) were used as a starting point to assemble the sets of proteins employed. Additionally, larger proteins as well as proteins for which new experimental data were available were added to the set. When possible, updated experimental results were used. Some proteins were discarded if the confidence in experimental values was not high. Some structures used for translational property calculations had missing residues built in (Table 1), and these structures were generously provided by Olwyn Byron and Mattia Rocco. In the case of rotational diffusion, only proteins for which the rotational diffusion was determined by using NMR methods were considered. For DNA structures, four different lengths of duplexes (8–24 basepair), for which hydrodynamic properties have been published (33, 34, 35, 36) were used for code validation. RNA molecules in isolation are flexible (37, 38), so we used two different protein-RNA complexes—histidinyl-tRNA synthetase (39, 40) and bacterial 50s ribosomal subunit—to test the method on known structures containing RNA that are expected to be less flexible.
Table 1.
Translational Hydrodynamic Radii for Folded Proteins
| Protein (PDB ID) | M (Da) | Chains | RT,expa (Å) | RT,calc (Å) | % Signed Error | % Error (Jackknifed) | a/bb | Reference(s) |
|---|---|---|---|---|---|---|---|---|
| BPTI (5PTI) | 6518 | 1 | 14.5 | 14.3 | −1.61 | −3.41 | 1.66 | (65) |
| Cytochrome c (1HRC) | 11,703 | 1 | 17.3c | 17.2 | −0.39 | −0.56 | 1.16 | (66, 67, 68) |
| RNase A (8RAT) | 13,692 | 1 | 18.9 | 19.0 | +0.37 | +0.27 | 1.31 | (65) |
| Lysozyme (1AKI) | 14,315 | 1 | 18.6 | 18.5 | −0.54 | −0.75 | 1.51 | (65) |
| LegHb (1LH1) | 16,657 | 1 | 21.4 | 20.2 | −5.72 | −5.86 | 1.43 | (69) |
| Apo-Mb (1MGN) | 17,359 | 1 | 20.8 | 19.9 | −4.19 | −4.52 | 1.35 | (70) |
| Soy TI (1AVU)d | 19,984 | 1 | 22.6 | 21.9 | −3.21 | −3.43 | 1.10 | (71) |
| Trypsinogen (1TGN) | 22,620 | 1 | 22.1 | 22.1 | −0.11 | −0.25 | 1.15 | (72) |
| β-trypsin (1TPO) | 23,124 | 1 | 22.8 | 22.2 | −2.74 | −2.96 | 1.13 | (73) |
| α-chymotrypsin (4CHA)d | 25,041 | 1 | 22.7 | 22.9 | +0.80 | +0.72 | 1.15 | (71) |
| Chymotrypsinogen (2CGA)d | 25,670 | 1 | 22.6 | 23.3 | +2.91 | +2.91 | 1.08 | (74) |
| Carbonic anhydrase (2CAB)d | 28,757 | 1 | 24.1 | 23.9 | −0.71 | −0.84 | 1.36 | (75) |
| Superoxide dismutase (2SOD)d | 31,089 | 2 | 25.9 | 25.8 | −0.58 | −0.73 | 1.59 | (76) |
| Pepsin (4PEP)d | 34,516 | 1 | 24.6 | 26.2 | +6.26 | +6.38 | 1.37 | (77) |
| β-lactoglobulin (1BEB)d | 36,606 | 2 | 27.4 | 27.3 | −0.52 | −0.66 | 1.83 | (78) |
| TPI (8TIM) | 52,996 | 2 | 29.7 | 30.5 | +2.42 | +2.39 | 1.45 | (66) |
| Hb (CO) (1HCO) | 61,942 | 4 | 31.5 | 31.6 | +0.24 | +0.15 | 1.11 | (79) |
| HSA (1AO6) | 66,482 | 1 | 34.0 | 35.1 | +3.21 | +3.21 | 1.49 | (80) |
| Alkaline phosphatase (1ALK) | 94,082 | 2 | 37.6 | 36.5 | −2.94 | −3.10 | 1.67 | (81) |
| Citrate synthase (1CTS)d | 97,835 | 2 | 37.0 | 37.7 | +2.06 | +2.03 | 1.53 | (82) |
| Inorganic PPase (2AU9) | 1,17,361 | 6 | 37.6 | 39.4 | +4.72 | +4.77 | 1.23 | (81) |
| Trp. synth. (1KFK) | 1,38,595 | 4 | 44.4 | 45.8 | +3.11 | +3.11 | 2.20 | (83) |
| Human IgG (1HZH) | 1,433,37 | 4 | 55.1 | 54.9 | −0.37 | −0.44 | 2.07 | (84) |
| Apo-G3PD (2GD1)d | 1,43,743 | 4 | 42.9 | 43.3 | +1.00 | +0.95 | 1.16 | (85) |
| Apo-LDH (5LDH)d | 1,45,749 | 4 | 42.5 | 42.5 | −0.07 | −0.14 | 1.20 | (86) |
| Aldolase (1ADO)d | 1,56,776 | 4 | 47.6c | 47.7 | +0.12 | +0.03 | 1.30 | (87, 88, 89) |
| Holo calalase (4BLC)d | 2,30,321 | 4 | 52.3 | 52.4 | +0.17 | +0.11 | 1.47 | (90) |
| Xanthine oxidase (1FIQ) | 2,67,770 | 6 | 54.5 | 54.5 | −0.14 | −0.21 | 1.78 | (91) |
| β-galactosidase (4V40) | 4,64,490 | 4 | 68.5 | 67.1 | −2.02 | −2.10 | 1.63 | (92) |
| Apoferritin (3AJO) | 5,120,84 | 24 | 67.4 | 64.7 | −4.00 | −4.11 | 1.00 | (93) |
| Urease (3LA4) | 5,397,00 | 6 | 65.8c | 66.6 | +1.26 | +1.23 | 1.13 | (94, 95) |
| GroEL (2CGT) | 8,28,989 | 21 | 82.8 | 86.3 | +4.26 | +4.27 | 1.40 | (96) |
| YMV capsid (1AUY) | 3,456,960 | 60 | 151.2 | 152.4 | +0.28 | +0.28 | 1.06 | (97) |
| mean % signed error | +0.10 | −0.04 | ||||||
Hb, hemoglobin; HSA, human serum albumin; IgG, immunoglobulin G; TI, trypsin inhibitor; TPI, triose phosphate isomerase; Trp. Synth., tryptophan synthase; YMV, Yellow Mosaic Virus.
All experimental hydrodynamic coefficients as reported in the references were converted to RT for comparison.
Axial ratio of a prolate ellipsoid with volume equal to the initial convex hull volume.
Average value of those reported in cited publications.
PDB files for these structures provided by Mattia Rocco and Olwyn Byron. Missing residues were modeled as described in (32).
These procedures resulted in three final data sets of folded structures to validate the convex hull method: one data set for which translational hydrodynamic properties of proteins have been experimentally determined (Table 1), one data set for which rotational properties of proteins have been experimentally determined (Table 2), and one data set of DNA duplexes and RNA-protein complexes for which several types of experimental data are available (Table 3). In addition, the largest current protein model in the PDB (HIV-1 capsid, PDB code 3J3Q) was used to test for any size limitations.
Table 2.
Rotational Hydrodynamic Radii for Folded Proteins
| Protein (PDB ID) | M (Da) | RR,expa (Å) | RR,calc (Å) | % Signed Error | a/bb | Reference | |
|---|---|---|---|---|---|---|---|
| BPTI (5PTI) | 6518 | 15.3 | 15.9 | +3.73 | 1.66 | (65) | |
| Calbindin (1IG5) | 8502 | 17.0 | 16.6 | −2.29 | 1.10 | (98) | |
| Ubiquitin (1UBQ) | 8566 | 16.8 | 17.3 | +2.68 | 1.49 | (7) | |
| Cytochrome c (351C) | 8696 | 17.1 | 16.8 | −2.22 | 1.10 | (99) | |
| Plastocyanin (1PCS) | 10,322 | 18.0 | 17.6 | −2.06 | 1.19 | (100) | |
| Binase (1GOU) | 12,214 | 19.7 | 19.3 | −2.03 | 1.27 | (101) | |
| Ribonuclease A (1AQP) | 13,692 | 20.0 | 20.4 | +1.65 | 1.34 | (65) | |
| Azurin (1E5Y) | 13,948 | 19.7 | 19.7 | +0.25 | 1.31 | (102) | |
| Lysozyme (1AKI) | 14,315 | 19.2 | 20.1 | +5.06 | 1.51 | (65) | |
| Spo0F (2FSP) | 14,230 | 20.1 | 20.2 | +0.25 | 1.24 | (103) | |
| DHFR (1DYI) | 18,003 | 22.6 | 22.0 | −2.87 | 1.20 | (104) | |
| β-lactoglobulin (2AKQ) | 17,104 | 22.1 | 21.3 | −3.48 | 1.21 | (105) | |
| Apo-AK (4AKE) | 23,589 | 26.1 | 26.2 | +0.31 | 1.43 | (106) | |
| Holo-AK (1AKE) | 24,616 | 23.7 | 23.9 | +0.93 | 1.14 | (106) | |
| mean % signed error | −0.08 | ||||||
DHFR, dihydrofolate reductase.
Experimental hydrodynamic coefficients (τc, DR) as reported in the references were converted to RR for comparison.
Axial ratio of a prolate ellipsoid with volume equal to the initial convex hull volume.
Table 3.
Hydrodynamic Radii for Nucleic Acids and Complexes
| Molecule (PDB ID) | M (Da) | RT,expa (Å) | RT,calc (Å) | % Signed Error | RR,expa (Å) | RR,calc (Å) | a/bb | Reference(s) | |
|---|---|---|---|---|---|---|---|---|---|
| DNA duplex 8merc | 4850 | 14.1 | 13.8 | −1.9 | 14.5 | 14.8 | 1.13 | (33, 65) | |
| DNA duplex 12mer (5NT5) | 7331 | 16.6d | 16.4 | −1.2 | 18.3 | 18.0 | 1.61 | (33, 35, 36) | |
| DNA duplex 20mer (5F9I) | 12,288 | 19.7 | 20.5 | +4.1 | 25.0 | 24.7 | 2.62 | (33) | |
| DNA duplex 24mere | 14,758 | 22.5 | 22.6 | +0.4 | ND | ND | 2.92 | (34) | |
| tRNA-HisRS (4RDX) | 70,463 | 37.4 | 37.8 | +1.1 | ND | ND | 1.60 | (39) | |
| Bacteria ribosome 50S (5HKV) | 1,263,178f | 92.9 | 95.32 | +2.6 | ND | ND | 1.26 | (40) | |
| mean % signed error | +0.85 | ||||||||
ND, not determined.
Experimental hydrodynamic coefficients as reported in the references were converted to RT or RR for comparison.
Axial ratio of prolate ellipsoid with maximum dimension and volume equal to the respective convex hull.
The structure in PDB file 5NT5 was edited to be equivalent to an 8mer.
Average of values reported in cited references.
The structure in PDB file 5F9I was used to model a 24mer with the same pitch.
Molar mass of the structure in 5HKV. A reported actual molar mass of 1,364,954 g mol−1 (107) was used with a sedimentation coefficient of 50.0 and partial specific volume of 0.614 to calculate RT,exp.
For analysis of conformationally heterogeneous proteins, a disordered state ensemble of α-synuclein (accession number PED9AAC) was downloaded from the Protein Ensemble Database (41). This ensemble contains 575 structures and was generated as described in (42).
Benchmarking
Benchmarking was carried out to measure and compare the execution speeds for HullRad, HYDROPRO, and SOMO. HYDROPRO speed was measured on an Intel ×64 machine running Ubuntu Linux; SOMO speed in Ultrascan (15) version 3.3 Rev 2202 was measured on a MacIntosh 2.2 GHz Intel core i7 laptop running OS X 10.11.6; HullRad speed was measured on both platforms. The following PDB files were used for this comparison purpose: 5PTI, 1HRC, 1AKI, 1AVU, 4CHA, 1BEB, 1AO6, 1CTS, 1ADO, 1FIQ, and 4V40.
Results and Discussion
Convex hull method predicts translational hydrodynamic radius of folded proteins
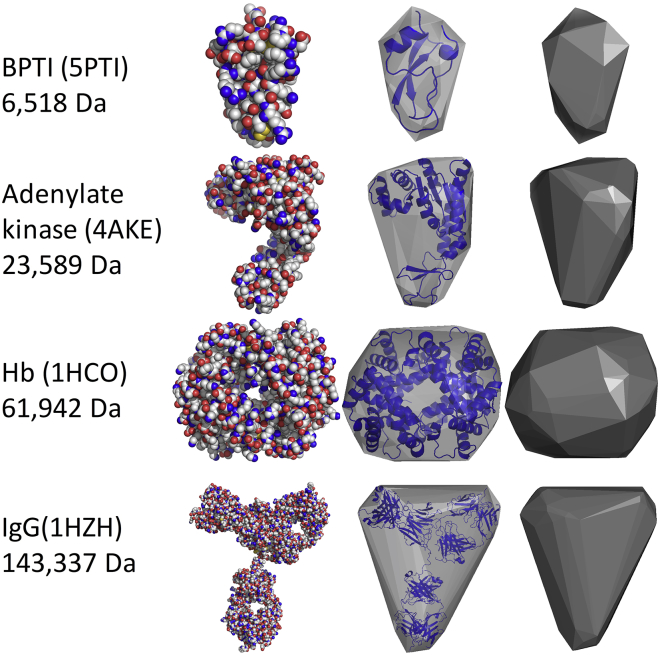
A convex hull model of molecular structures was implemented in a program entitled HullRad. HullRad predicts the translational hydrodynamic radius, RT, of folded proteins over a large range of protein sizes (6518–3,456,960 Da) and shapes. Fig. 2 shows representative images of initial convex hulls overlaid upon ribbon representations for select proteins spanning a range of molecular mass and shape. Fig. S2 shows a depiction of the unified side chain model together with the convex hull construct for the same proteins.
Figure 2.
Convex hull representations of protein volumes. Four proteins of different sizes and shapes are depicted showing the relationship of a convex hull model to atomic space filling and backbone ribbon models. The left vertical column gives the PDB ID and molecular mass for each protein. The second vertical column shows an atomic sphere representation; the third column shows backbone cartoon diagram representations for each protein (blue online) enclosed by its semitransparent initial convex hull (gray online); the right vertical panel shows the convex hull model as a solid. This figure was created in PyMOL. The transparent and solid convex hull planes are CGOs created within PyMOL by using the convex hull vertices. A PyMOL script to generate these CGOs is included with the HullRad code. CGO, compiled graphic object. To see this figure in color, go online.
Table 1 lists the experimental set used to validate folded protein translational hydrodynamic radii calculations. The set consists of data derived from 33 nonhomologous proteins and represents independent measurements of sedimentation or diffusion coefficients derived from three different experimental methods. As described in the Methods, the joint comparison of these data is easily conducted by using the equivalent RT,exp value for each observable.
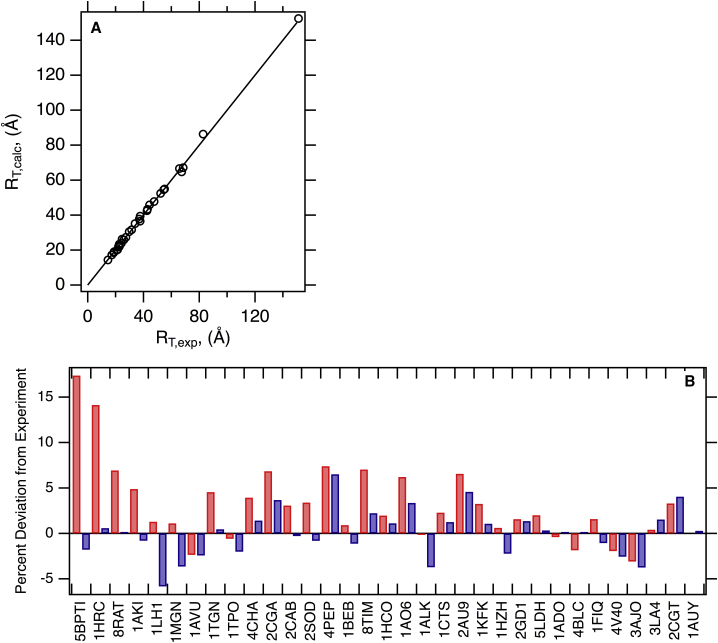
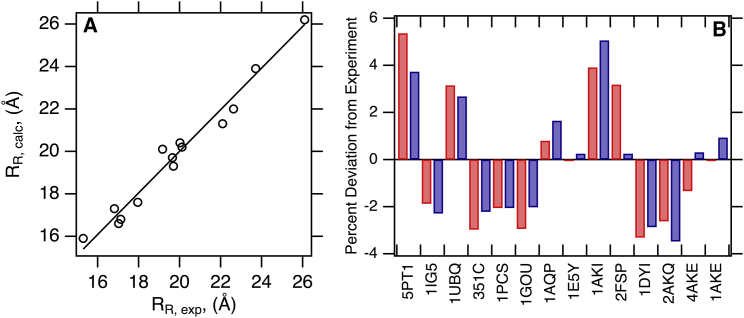
Fig. S3 A shows the optimized hydration shell thickness for translational diffusion as 2.8 Å. Incorporation of this expansion on the initial hull results in the final volumes used in the hydrodynamic calculations. Fig. 3 A shows the excellent agreement between experimental and calculated values for this set. Fig. 3 B and Table 1 show the deviations of the calculated values from the experimental numbers. The percent signed error (100×(RT,calc−RT,exp)/RT,exp) of HullRad as compared to experimental values ranges from −5.7 to +6.3 with a mean value of 0.1. The mean percent signed error for these independent jackknifed predictions is −0.04, with a range of −5.9 to +6.4. These minimum and maximum percent signed errors increased only slightly when the jackknife procedure was conducted, indicating that no one protein overly influences the fit. The original grouped errors and jackknifed independent errors are found to not be significantly different when using a t-test with a t-value of 0.19 and p-value of 0.43. Notably, all calculated values are well within the accuracy of experimentally determined hydrodynamic properties by analytical ultracentrifugation (43), one of the most accurate experimental methods available for determining hydrodynamic properties.
Figure 3.
The convex hull method accurately predicts experimental protein translational hydrodynamic radii. (A) HullRad predicted RT,calc for folded proteins are plotted versus experimental RT,exp values. The black line represents a slope of one and intercept of zero; the correlation coefficient for a linear regression of the data (data not shown) is 0.998. (B) Percent signed errors of calculated to experimental RT for folded proteins are plotted as bars. Dark gray (blue online) was calculated with HullRad; light gray (red online) was calculated with HYDROPRO. In this comparison, all HYDROPRO calculations used atomic-level beads except the structure 2CGT, for which residue level beads were used. Only HullRad was used to calculate hydrodynamic properties for the largest example, 12AUY. The individual proteins are labeled according to respective PDB IDs; common names, molecular masses, number of chains, and respective hydrodynamic radii are listed in Table 1. This figure was created in Igor. To see this figure in color, go online.
Fig. 3 B shows for comparison the percent signed deviations of calculated RT from HYDROPRO. This program, too, has excellent accuracy except for the smallest proteins in the set where the HullRad method is slightly better when default values are used in the HYDROPRO program. The source of the discrepancy for small proteins can be explained by the default value of 2.9 Å for the primary element radius in the HYDROPRO program, which is optimized for a set of proteins with larger sizes than included here; more accurate calculated values could be obtained with a protein-size-optimized primary element radius. Rocco and Byron have previously shown that the SOMO implementation in Ultrascan as well as the standalone program ZENO reproduce hydrodynamic parameters within similar (∼5%) deviation from the experiment (32).
HullRad execution is fast and easy
Given comparable accuracy to other hydrodynamic prediction programs, two main attractions of HullRad are its ease of use and its speed of execution. Calculations involve running a simple Python script with a PDB file as input as described in the Methods. A custom user script can easily be written to run HullRad on a list of PDB files, which means that HullRad has the capability to analyze ensembles of structures generated, for example, in a molecular dynamics trajectory or a Monte Carlo simulation that seeks to explore conformational properties of members of an ensemble. Thousands of structures could easily be parsed in a short time as described below in the section on IDPs. In addition, HullRad handles large files. Although there is no experimental data for comparison, we validated the ability of HullRad to calculate hydrodynamic parameters of very large macromolecular assemblies using the HIV-1 capsid model, which is currently the largest atomic structure available in the Research Collaboratory for Structural Bioinformatics with 2,440,801 atoms (M = 34,795,461; PDB identifier [ID] = 3J3Q). The calculated RT is 416 Å.
We further demonstrate the execution speed advantage of the HullRad algorithm by benchmarking its performance against both HYDROPRO and SOMO. Fig. 4 shows that HullRad output was generated on the millisecond time scale irrespective of protein size over the range tested (6518 to 464,490 Da). HullRad is orders of magnitude faster than either HYDROPRO or SOMO for all proteins, except HullRad is only twice as fast as HYDROPRO for the smallest test example (bovine pancreatic trypsin inhibitor [BPTI], M = 6518 Da). HullRad is also much faster than ZENO, for which calculation times have been reported to be on the order of minutes for a 100-residue protein (13).
Convex hull method predicts rotational hydrodynamic radii of folded proteins
Fig. 5 A shows that the convex hull method also accurately predicts isotropic rotational hydrodynamic radii for a data set of folded protein structures. The experimental and calculated values are listed in Table 2, in which the mean percent signed error of calculated to experimental values is −0.08 with a range of −3.5 to +5.1. The individual protein prediction errors of calculated rotational radii to experimental values from the convex hull and bead modeling algorithms are graphically compared in Fig. 5 B. Both programs are accurate within ∼5% error.
Figure 5.
The convex hull method accurately predicts experimental rotational hydrodynamic radii. (A) HullRad-predicted RR for the proteins listed in Table 2 are plotted versus experimental RR values (circles). The line represents a slope of one and intercept of zero; the correlation coefficient for a linear regression of the data (data not shown) is 0.993. (B) Percent signed errors of calculated to experimental RR for the list of proteins in Table 2 are plotted as bars. Dark gray (blue online) was calculated with the program HullRad; light gray (red online) was calculated with HYDROPRO. The individual proteins are labeled according to respective PDB IDs; common names, molecular masses, and respective hydrodynamic radii are listed in Table 2. To see this figure in color, go online.
Fig. S3 B shows the optimized hull expansion for calculation of rotational diffusion properties using a shape factor correction, FR = FT4. The optimal hydration thickness shown in Fig. S3 B (4.3 Å) is larger than that required to accurately predict translational diffusion (2.8 Å) in agreement with the theoretical difference between translational and rotational hydration effect described in the theory section of Supporting Materials and Methods.
Convex hull method predicts hydrodynamic radii of nucleic acids and protein-nucleic acid complexes
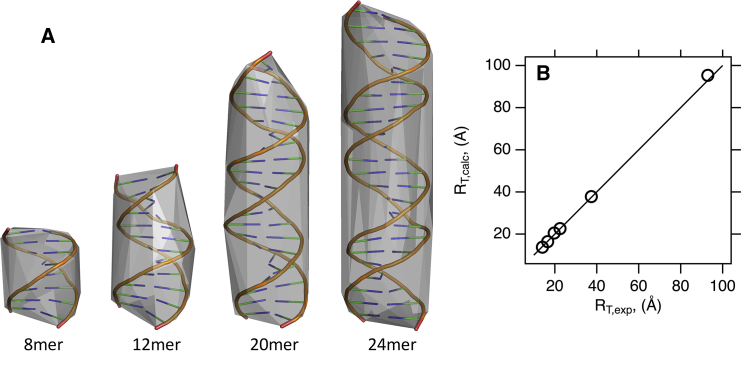
Fig. 6 A shows four DNA duplex structures with their respective initial convex hull representations. HullRad predicts both the RT and RR of these DNA molecules with excellent accuracy as shown in Fig. 6 B and Table 3. Note that accurate prediction of the translational hydrodynamic radii for DNA is achieved with the same convex hull hydration expansion used for proteins as expected (44). Furthermore, HullRad predicts the translational hydrodynamic radii of the protein-RNA complexes, histidinyl-tRNA synthetase, and bacterial 50s ribosomal subunit with excellent accuracy as shown in Table 3. HullRad calculates the hydrodynamic properties of the 50s ribosomal subunit structure with a molecular weight of 1.26 million in 0.57 s on a laptop computer running MacOS.
Figure 6.
The convex hull method accurately predicts experimental hydrodynamic radii for nucleic acids and protein-nucleic acid complexes. (A) Shown are convex hull representations of DNA duplexes used for validation of HullRad. Each image shows the PyMOL backbone cartoon representation enclosed by its semitransparent initial convex hull. The PDB IDs, respective molecular masses, hydrodynamic radii, and ellipsoidal axial ratios are listed in Table 3. (B) A comparison of HullRad calculated and experimental hydrodynamic radii for nucleic acids and protein-nucleic acid complexes listed in Table 3. The line represents a slope of one and intercept of zero; the correlation coefficient for a linear regression of the data (data not shown) equals 0.999. To see this figure in color, go online.
Convex hull method predicts translational hydrodynamic radii of IDPs
In addition to folded proteins with a defined three-dimensional structure, much of the proteome consists of polypeptides that do not form unique native structures (45). These proteins are referred to as IDPs. Proteins can have both stable, folded regions as well as intrinsically disordered regions. These intrinsically disordered regions are now recognized to be important for a number of functions: motif display sites, chaperones, scavengers, complex assembly, effector ligands, and entropic chains (45).
The sizes and shapes of IDPs are topics of intense interest (46, 47). These proteins exist as conformationally heterogeneous ensembles in solution, and there are many efforts to measure both the average degree of structure and their dynamics. Approaches include experimentally measuring specific residue contacts, residue dipolar couplings, and/or hydrodynamic properties. Small angle x-ray scattering, analytical ultracentrifugation, and NMR are techniques frequently employed for this purpose. However, these experiments report ensemble averaged observables and rely on models for interpretation (46). The structural disorder inherent in IDPs creates a challenge to the generation of such structural models. In particular, large numbers of individual structural models may need to be created to accurately construct a distribution of conformations. Even though molecular simulations are able to generate large numbers of atomic coordinate models, a rapid method to calculate the desired physical parameters from this ensemble of structures is required (47).
The HullRad algorithm has the speed, accuracy, and ease of use to be well suited for this task. We demonstrate this using a conformationally heterogeneous ensemble of α-synuclein. This protein is a 140-residue (MW 14,462), natively disordered protein and is present in the protofibrils found in Parkinson’s disease (48). The experimentally determined RT for α-synuclein in 100 mM NaCl is 32.0 Å (49), indicating a slightly more compact ensemble than a protein of the same size denatured in urea (33.0 Å), but more extended than a premolten globule state (26.4 Å) (50). Allison et al. (42) used paramagnetic relaxation enhancement NMR spectroscopy to obtain 595 intermolecular distances for the natively unfolded α-synuclein. These inter-residue distances were used as ensemble-averaged restraints in multiple replicate molecular dynamics simulations to generate a disordered state ensemble of 575 structures.
Fig. 7 shows a comparison of calculated effective RT values for this ensemble using both HullRad and HYDROPRO. The results were sorted by compactness by using anhydrous RG calculated from the protein atomic coordinates only. The calculated ensemble mean HYDROPRO hydrodynamic radius is ∼0.7% larger than the HullRad hydrodynamic radius (mean RT,calc = 31.13 vs. 30.90 Å, respectively). A larger individual difference is apparent for the more compact structures. This is expected from the differences between these programs for small proteins shown in Fig. 3 B. The individual RT,calc values from both methods are highly correlated (see Fig. S4). HullRad processes these files much more quickly: computer runtimes on a typical ×86 chip for analysis of the 575 structures of α-synuclein are 24 s for HullRad and 27 min for HYDROPRO.
The agreement shown in Fig. 7 and Fig. S4 indicate that the convex hull method works well even for the unusual, extended conformations found in such a disordered state ensemble. HullRad and HYDROPRO are similarly accurate for disordered structures.
The mean HullRad calculated RT,calc of 30.9 Å for the α-synuclein ensemble is smaller than the experimentally determined RT,exp of 32.0 Å. This difference suggests that modifying the simulation-generated α-synuclein ensemble to contain a higher proportion of extended structures would more closely mimic the experimental ensemble. Further exploration and culling of this ensemble will be easy to accomplish given the ease of use and execution speed inherent in HullRad.
Shape factors and ellipsoidal representations
Fig. 8 shows both the initial convex hull and ellipsoid of revolution models for the most elongated protein in our data sets (tryptophan synthetase) and the longest DNA duplex tested (24 basepair). The respective ellipsoids of revolution were constructed with the same maximum length and volume of the initial convex hull for calculation of a shape factor.
Figure 8.
Comparison of convex hull and ellipsoid of revolution models. (A) Tryptophan synthetase as atomic spheres (green online). (B) Shown is a DNA duplex with 24 base pairs as atomic spheres. Each molecular structure is overlaid with a semitransparent (gray online) initial convex hull (left) or prolate ellipsoid of revolution (right) of volumes and maximum lengths equal to that of the respective convex hull. To see this figure in color, go online.
The translational diffusion shape factor used by HullRad is based on the Perrin equation for a prolate ellipsoid (24). The Perrin-derived shape factors for prolate and oblate ellipsoids are different by only 5.5% up to axial ratios of 10:1 (1). This axial ratio represents far more nonsphericity than encountered for most biomolecules studied by diffusion measurements. The maximum axial ratio observed in the above ensemble of intrinsically disordered α-synuclein is 4.62. This fact, together with the significant increase in computing time necessary to calculate the best-fit general tri-axial ellipsoid of a molecule, led us to use the simple construction of a prolate ellipsoid described above to estimate the effect of elongation on translational diffusion. As shown in Tables 1 and 3, this approximation allowed accurate calculation of translational diffusion properties for all the molecules tested.
Calculation of the rotational shape factors for elongated molecules is more complicated than the corresponding translational factors because 1) rotations around different axes of the molecule can proceed at different rates, and rotation is best described by a rotational tensor (25); and 2) the rotational tensors are significantly different for prolate and oblate ellipsoidal shapes (51). HullRad is limited to the calculation only of isotropic tumbling. We found by empirical comparisons that a rotational shape factor correction, FR = FT4, allowed accurate prediction of isotropic rotational diffusion radii for the most elongated, rigid structures for which experimental data is available (Fig. S5 and Table S1). Although an anisotropic diffusion model is required for accurate analysis of NMR rotational relaxation of highly nonspherical molecules, an isotropic model is sufficient for many biological molecules given the precision of relaxation data (12). The HullRad code prints a warning to users when a molecule has an axial ratio larger than 2.62, which is the largest in the experimental data available for comparison in this study.
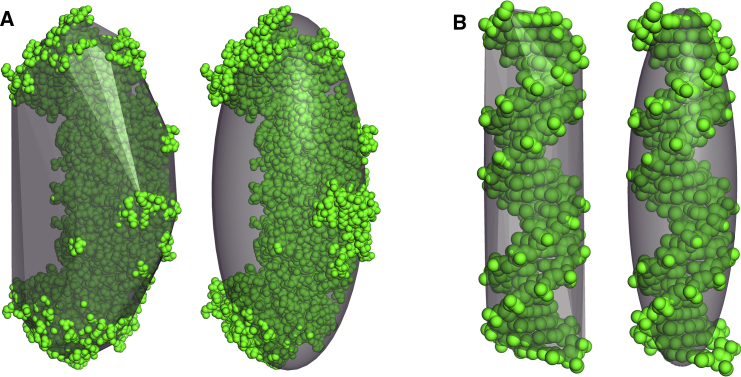
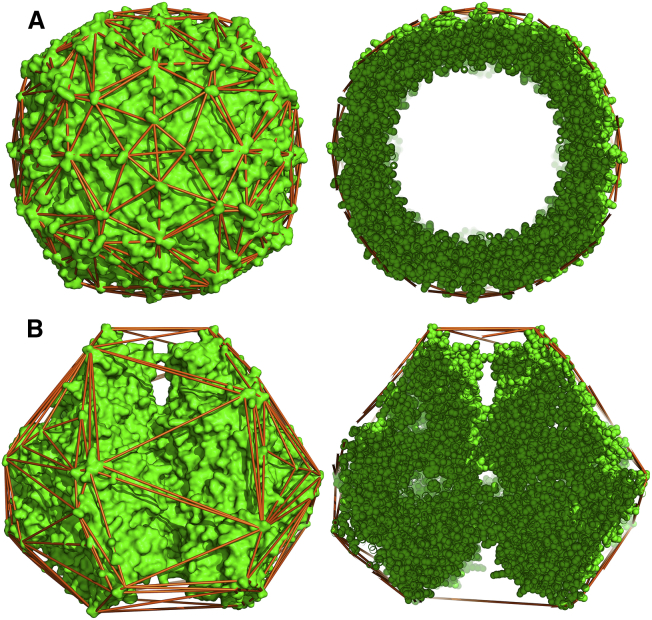
Internal cavity and external crevice water are hydrodynamically equivalent
The convex hull transport model also illustrates the hydrodynamic equivalence of internally buried cavity water and surface crevice water as shown in Fig. 9. Fig. 9 A (top row) shows apoferritin, which is a hollow protein sphere containing a large water-filled cavity as illustrated by the cross-sectional view in the right panel. The hydrodynamic RT,exp of apoferritin is 64.71 Å, and the anhydrous protein volume R0 is 51.83 Å. Because this molecule is nearly spherical, the difference in these two parameters is due to a combination of hydration and hydrodynamic water. Hydration water is inherently part of the diffusing molecule and is frequently modeled by a molecular surface expansion of 1.1–2.8 Å (8, 12). Here, hydrodynamic water is that water not considered true hydration water but rather water that is entrained by the indentations in the molecular surface or trapped in internal cavities. Clearly, the water trapped in the cavity of apoferritin is hydrodynamic water in the sense that it diffuses with the protein even if, dynamically, it is able to exchange with bulk water.
Figure 9.
The hydrodynamic hydration water in internal cavities and surface crevices is equivalent. (A) shows apoferritin (PDB ID: 3AJO); (B) shows urease (PDB ID: 3LA4). In the left vertical panel, molecular surface renderings (green online) with convex hull edges as sticks (orange online) are shown. In the right vertical panel, 30 Å slabs of the same structures are shown as atomic spheres instead of molecular surfaces. This figure was created in PyMOL. To see this figure in color, go online.
Fig. 9 B (bottom row) shows that the structural arrangements and hydration patterns of urease are distinct from apoferritin, yet the implication for hydrodynamic volume is the same. Urease is a comparably sized protein with a similar hydrodynamic radius (RT,exp = 66.58 Å) and anhydrous protein volume radius (R0 = 54.09 Å), yet it has no large internal cavity. In contrast, most of the urease hydrodynamic water is in medium-sized surface crevices encapsulated by the convex hull as shown in the right panel of Fig. 9 B. The observation that the convex hull model accurately predicts the translational diffusion of urease is evidence that the water distributed in surface crevices on this structure also affects the diffusional volume of the protein in a manner similar to the internal cavity water of apoferritin. We postulate that this protein-specific inclusion of different amounts of water in the convex hull transport model may contribute to its accuracy. A further discussion of hydration and hydrodynamic water is included in the Supporting Materials and Methods.
We note that the convex hull transport model recapitulates hydrodynamic properties based only on geometry of the protein. It does not take into account any of the chemical details of the surface atoms that are also known to determine the dynamics of hydration shell water (52). As with most other predictive methods, the convex hull method smooths and averages the effects of hydration volume. We recognize that methods to predict location-specific waters of hydration do exist (53, 54, 55, 56, 57), but these are too time consuming for the purpose of the rapid prediction discussed here.
Conclusions
The convex hull volume of a macromolecule accurately predicts the hydrodynamic volume of that molecule. A Python script called HullRad is provided, which calculates sedimentation coefficients, translational and rotational diffusion coefficients, and hydrodynamic radii for protein and nucleic acid molecules using a convex hull algorithm. The method is orders of magnitude faster than common methods and works for molecules with significant shape asymmetry and surface rugosity, including the extended structures of a disordered state ensemble. The same fitted parameters are used for molecules that extend over two orders of magnitude in size. Application of this method to the modification of computer-generated disordered state ensembles should provide a better agreement of the calculated and experimental ensembles of IDPs.
Author Contributions
P.J.F. designed and performed the research. P.J.F. and K.G.F. wrote the paper.
Acknowledgments
The authors thank Margaret Johnson, Ananya Majumdar, Walter F. Stafford III, James Wrabl, and the members of the K.G.F. lab for helpful discussions and Olwyn Byron and Mattia Rocco for providing their data set of protein structures.
Funded by the National Institutes of Health (grant No. R01GM079440) and National Science Foundation (grant No. MCB1412108 to K.G.F.).
Editor: David Eliezer.
Footnotes
Supporting Materials and Methods, five figures, and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30065-1.
Supporting Citations
References (58, 59, 60, 61, 62, 63, 64) appear in the Supporting Material.
Supporting Material
References
- 1.Cantor C.R., Schimmel P.R. W. H. Freeman; New York: 1980. Biophysical Chemistry: Part II: Techniques for the Study of Biological Structure and Function. pp. 561–565. [Google Scholar]
- 2.Cole J.L., Lary J.W., Laue T.M. Analytical ultracentrifugation: sedimentation velocity and sedimentation equilibrium. Methods Cell Biol. 2008;84:143–179. doi: 10.1016/S0091-679X(07)84006-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pilz I. Proteins. In: Glatter O., Kratky O., editors. Small Angle X-ray Scattering. Academic Press; New York: 1982. pp. 239–293. [Google Scholar]
- 4.Serdyuk I.N., Zaccai N.R., Zaccai J. Cambridge University Press; Cambridge, UK: 2007. Methods in Molecular Biophysics. pp. 481–504. [Google Scholar]
- 5.Badea M.G., Brand L. Time-resolved fluorescence measurements. Methods Enzymol. 1979;61:378–425. doi: 10.1016/0076-6879(79)61019-4. [DOI] [PubMed] [Google Scholar]
- 6.Himmel M.E., Squire P.G. Size exclusion parameters. In: Dubin P.L., editor. Aqueous Size Exclusion Chromatography. Elsevier; New York: 1988. pp. 3–22. [Google Scholar]
- 7.Tjandra N., Kuboniwa H., Bax A. Rotational dynamics of calcium-free calmodulin studied by 15N-NMR relaxation measurements. Eur. J. Biochem. 1995;230:1014–1024. doi: 10.1111/j.1432-1033.1995.tb20650.x. [DOI] [PubMed] [Google Scholar]
- 8.Aragon S. A precise boundary element method for macromolecular transport properties. J. Comput. Chem. 2004;25:1191–1205. doi: 10.1002/jcc.20045. [DOI] [PubMed] [Google Scholar]
- 9.García De La Torre J., Huertas M.L., Carrasco B. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 2000;78:719–730. doi: 10.1016/S0006-3495(00)76630-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rocco M., Byron O. Hydrodynamic modeling and its application in AUC. Methods Enzymol. 2015;562:81–108. doi: 10.1016/bs.mie.2015.04.010. [DOI] [PubMed] [Google Scholar]
- 11.Harding S.E., Rowe A.J. Modeling biological macromolecules in solution. II. The general tri-axial ellipsoid. Biopolymers. 1983;22:1813–1829. doi: 10.1002/bip.360220714. [DOI] [PubMed] [Google Scholar]
- 12.Ryabov Y.E., Geraghty C., Fushman D. An efficient computational method for predicting rotational diffusion tensors of globular proteins using an ellipsoid representation. J. Am. Chem. Soc. 2006;128:15432–15444. doi: 10.1021/ja062715t. [DOI] [PubMed] [Google Scholar]
- 13.Kang E.H., Mansfield M.L., Douglas J.F. Numerical path integration technique for the calculation of transport properties of proteins. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;69:031918. doi: 10.1103/PhysRevE.69.031918. [DOI] [PubMed] [Google Scholar]
- 14.Ortega A., Amorós D., García de la Torre J. Prediction of hydrodynamic and other solution properties of rigid proteins from atomic- and residue-level models. Biophys. J. 2011;101:892–898. doi: 10.1016/j.bpj.2011.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Demeler B. Hydrodynamic methods. In: Rashidi H., Buehler L., editors. Bioinformatics Basics: Applications in Biological Science and Medicine. CRC Press; Boca Raton, Florida: 2005. pp. 226–255. [Google Scholar]
- 16.Aurenhammer F. Voronoi diagrams - a survey of a fundamental geometric data structure. ACM Comput. Surv. 1991;23:345–405. [Google Scholar]
- 17.Babick F., Mielke J., Hodoroaba V.D. How reliably can a material be classified as a nanomaterial? Available particle-sizing techniques at work. J. Nanopart. Res. 2016;18:158. doi: 10.1007/s11051-016-3461-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Babick F. Springer International Publishing; Switzerland: 2016. Suspensions of Colloidal Particles and Aggregates. p. 171. [Google Scholar]
- 19.Barber C.B., Dobkin D.P., Hannu H. The Quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996;22:469–483. [Google Scholar]
- 20.Cohn E.J., Edsall J.T. Reinhold Publ. Corp.; New York: 1943. Proteins, Amino Acids and Peptides as Ions and Dipolar Ions. pp. 155–176. [Google Scholar]
- 21.Perkins S.J. Protein volumes and hydration effects. The calculations of partial specific volumes, neutron scattering matchpoints and 280-nm absorption coefficients for proteins and glycoproteins from amino acid sequences. Eur. J. Biochem. 1986;157:169–180. doi: 10.1111/j.1432-1033.1986.tb09653.x. [DOI] [PubMed] [Google Scholar]
- 22.Nadassy K., Tomás-Oliveira I., Wodak S.J. Standard atomic volumes in double-stranded DNA and packing in protein--DNA interfaces. Nucleic Acids Res. 2001;29:3362–3376. doi: 10.1093/nar/29.16.3362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Voss N.R., Gerstein M. Calculation of standard atomic volumes for RNA and comparison with proteins: RNA is packed more tightly. J. Mol. Biol. 2005;346:477–492. doi: 10.1016/j.jmb.2004.11.072. [DOI] [PubMed] [Google Scholar]
- 24.Perrin F. Mouvement Brownian d’un ellipsoide II. Rotation libre et dépolarisation des fluorescences. Translation et diffusion de molécules ellipsoïdales. J. Phys. Radium. 1936;7:1–11. [Google Scholar]
- 25.Favro L.D. Theory of the rotational brownian motion of a free rigid body. Phys. Rev. 1960;119:53–62. [Google Scholar]
- 26.Delano W.L. Schrödinger; LLC: 2015. The PyMOL Molecular Graphics System, version 1.8. [Google Scholar]
- 27.Efron B., Stein C. The jackknife estimate of variance. Ann. Stat. 1981;9:586–596. [Google Scholar]
- 28.Lavalette D., Tétreau C., Blouquit Y. Microscopic viscosity and rotational diffusion of proteins in a macromolecular environment. Biophys. J. 1999;76:2744–2751. doi: 10.1016/S0006-3495(99)77427-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.The International Association for the Properties of Water and Steam. 2008. Release on the IAPWS Formulation 2008 for the Viscosity of Ordinary Water Substance.
- 30.Perkins S.J. X-ray and neutron scattering analyses of hydration shells: a molecular interpretation based on sequence predictions and modelling fits. Biophys. Chem. 2001;93:129–139. doi: 10.1016/s0301-4622(01)00216-2. [DOI] [PubMed] [Google Scholar]
- 31.Knight C.J., Hub J.S. WAXSiS: a web server for the calculation of SAXS/WAXS curves based on explicit-solvent molecular dynamics. Nucleic Acids Res. 2015;43(W1):W225–W230. doi: 10.1093/nar/gkv309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rocco M., Byron O. Computing translational diffusion and sedimentation coefficients: an evaluation of experimental data and programs. Eur. Biophys. J. 2015;44:417–431. doi: 10.1007/s00249-015-1042-9. [DOI] [PubMed] [Google Scholar]
- 33.Eimer W., Pecora R. Rotational and translational diffusion of short rodlike molecules in solution: Oligonucleotides. J. Chem. Phys. 1991;94:2324–2329. [Google Scholar]
- 34.Lapham J., Rife J.P., Crothers D.M. Measurement of diffusion constants for nucleic acids by NMR. J. Biomol. NMR. 1997;10:255–262. doi: 10.1023/a:1018310702909. [DOI] [PubMed] [Google Scholar]
- 35.Birchall A.J., Lane A.N. Anisotropic rotation in nucleic acid fragments: significance for determination of structures from NMR data. Eur. Biophys. J. 1990;19:73–78. doi: 10.1007/BF00185089. [DOI] [PubMed] [Google Scholar]
- 36.Bonifacio G.F., Brown T., Lane A.N. Comparison of the electrophoretic and hydrodynamic properties of DNA and RNA oligonucleotide duplexes. Biophys. J. 1997;73:1532–1538. doi: 10.1016/S0006-3495(97)78185-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Porschke D., Antosiewicz J. Permanent dipole moment of tRNA’s and variation of their structure in solution. Biophys. J. 1990;58:403–411. doi: 10.1016/S0006-3495(90)82386-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Benítez A.A., Hernández Cifre J.G., de la Torre J.G. Prediction of solution properties and dynamics of RNAs by means of Brownian dynamics simulation of coarse-grained models: ribosomal 5S RNA and phenylalanine transfer RNA. BMC Biophys. 2015;8:11. doi: 10.1186/s13628-015-0025-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bovee M.L., Yan W., Francklyn C.S. tRNA discrimination at the binding step by a class II aminoacyl-tRNA synthetase. Biochemistry. 1999;38:13725–13735. doi: 10.1021/bi991182g. [DOI] [PubMed] [Google Scholar]
- 40.Hill W.E., Anderegg J.W., Van Holde K.E. Effects of solvent environment and mode of preparation on the physical properties of ribosomes fron Escherichia coli. J. Mol. Biol. 1970;53:107–121. doi: 10.1016/0022-2836(70)90048-3. [DOI] [PubMed] [Google Scholar]
- 41.Varadi M., Kosol S., Tompa P. pE-DB: a database of structural ensembles of intrinsically disordered and of unfolded proteins. Nucleic Acids Res. 2014;42:D326–335. doi: 10.1093/nar/gkt960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Allison J.R., Varnai P., Vendruscolo M. Determination of the free energy landscape of alpha-synuclein using spin label nuclear magnetic resonance measurements. J. Am. Chem. Soc. 2009;131:18314–18326. doi: 10.1021/ja904716h. [DOI] [PubMed] [Google Scholar]
- 43.Zhao H., Ghirlando R., Schuck P. A multilaboratory comparison of calibration accuracy and the performance of external references in analytical ultracentrifugation. PLoS One. 2015;10:e0126420. doi: 10.1371/journal.pone.0126420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Fernandes M.X., Ortega A., García de la Torre J. Calculation of hydrodynamic properties of small nucleic acids from their atomic structure. Nucleic Acids Res. 2002;30:1782–1788. doi: 10.1093/nar/30.8.1782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.van der Lee R., Buljan M., Babu M.M. Classification of intrinsically disordered regions and proteins. Chem. Rev. 2014;114:6589–6631. doi: 10.1021/cr400525m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Best R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017;42:147–154. doi: 10.1016/j.sbi.2017.01.006. [DOI] [PubMed] [Google Scholar]
- 47.Nygaard M., Kragelund B.B., Lindorff-Larsen K. An efficient method for estimating the hydrodynamic radius of disordered protein conformations. Biophys. J. 2017;113:550–557. doi: 10.1016/j.bpj.2017.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Stefanis L. α-Synuclein in Parkinson’s disease. Cold Spring Harb. Perspect. Med. 2012;2:a009399. doi: 10.1101/cshperspect.a009399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Binolfi A., Rasia R.M., Fernández C.O. Interaction of alpha-synuclein with divalent metal ions reveals key differences: a link between structure, binding specificity and fibrillation enhancement. J. Am. Chem. Soc. 2006;128:9893–9901. doi: 10.1021/ja0618649. [DOI] [PubMed] [Google Scholar]
- 50.Uversky V.N. What does it mean to be natively unfolded? Eur. J. Biochem. 2002;269:2–12. doi: 10.1046/j.0014-2956.2001.02649.x. [DOI] [PubMed] [Google Scholar]
- 51.Koenig S.H. Brownian-motion of an ellipsoid - A correction to perrins results. Biopolymers. 1975;14:2421–2423. [Google Scholar]
- 52.Qin Y., Wang L., Zhong D. Dynamics and mechanism of ultrafast water-protein interactions. Proc. Natl. Acad. Sci. USA. 2016;113:8424–8429. doi: 10.1073/pnas.1602916113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Venable R.M., Hatcher E., Pastor R.W. Comparing simulated and experimental translation and rotation constants: range of validity for viscosity scaling. J. Phys. Chem. B. 2010;114:12501–12507. doi: 10.1021/jp105549s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Makarov V.A., Andrews B.K., Pettitt B.M. Residence times of water molecules in the hydration sites of myoglobin. Biophys. J. 2000;79:2966–2974. doi: 10.1016/S0006-3495(00)76533-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Virtanen J.J., Makowski L., Freed K.F. Modeling the hydration layer around proteins: HyPred. Biophys. J. 2010;99:1611–1619. doi: 10.1016/j.bpj.2010.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Neumayr G., Rudas T., Steinhauser O. Global and local Voronoi analysis of solvation shells of proteins. J. Chem. Phys. 2010;133:084108. doi: 10.1063/1.3471383. [DOI] [PubMed] [Google Scholar]
- 57.Fogarty A.C., Laage D. Water dynamics in protein hydration shells: the molecular origins of the dynamical perturbation. J. Phys. Chem. B. 2014;118:7715–7729. doi: 10.1021/jp409805p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kuntz I.D., Jr., Kauzmann W. Hydration of proteins and polypeptides. Adv. Protein Chem. 1974;28:239–345. doi: 10.1016/s0065-3233(08)60232-6. [DOI] [PubMed] [Google Scholar]
- 59.Aragon S., Hahn D.K. Precise boundary element computation of protein transport properties: diffusion tensors, specific volume, and hydration. Biophys. J. 2006;91:1591–1603. doi: 10.1529/biophysj.105.078188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Denisov V.P., Halle B. Protein hydration dynamics in aqueous solution. Faraday Discuss. 1996;103:227–244. doi: 10.1039/fd9960300227. [DOI] [PubMed] [Google Scholar]
- 61.Halle B., Davidovic M. Biomolecular hydration: from water dynamics to hydrodynamics. Proc. Natl. Acad. Sci. USA. 2003;100:12135–12140. doi: 10.1073/pnas.2033320100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tanford C. Wiley; New York: 1961. Physical Chemistry of Macromolecules. p. 337. [Google Scholar]
- 63.Bird R.B., Stewart W.E., Lightfoot E.N. J. Wiley; New York: 2002. Transport Phenomena. [Google Scholar]
- 64.Edwardes D. Steady motion of a viscous liquid in which an ellipsoid is constrained to rotate about a principal axis. Quarterly Journal of Pure and Applied Mathematics. 1893;26:70–78. [Google Scholar]
- 65.Rai N., Nöllmann M., Rocco M. SOMO (SOlution MOdeler) differences between X-Ray- and NMR-derived bead models suggest a role for side chain flexibility in protein hydrodynamics. Structure. 2005;13:723–734. doi: 10.1016/j.str.2005.02.012. [DOI] [PubMed] [Google Scholar]
- 66.Wilkins D.K., Grimshaw S.B., Smith L.J. Hydrodynamic radii of native and denatured proteins measured by pulse field gradient NMR techniques. Biochemistry. 1999;38:16424–16431. doi: 10.1021/bi991765q. [DOI] [PubMed] [Google Scholar]
- 67.Walters R.R., Graham J.F., Anderson D.J. Protein diffusion coefficient measurements by laminar flow analysis: method and applications. Anal. Biochem. 1984;140:190–195. doi: 10.1016/0003-2697(84)90152-0. [DOI] [PubMed] [Google Scholar]
- 68.Clark S.M., Leaist D.G., Konermann L. Taylor dispersion monitored by electrospray mass spectrometry: a novel approach for studying diffusion in solution. Rapid Commun. Mass Spectrom. 2002;16:1454–1462. doi: 10.1002/rcm.732. [DOI] [PubMed] [Google Scholar]
- 69.Broughton W.J., Dilworth M.J., Godfrey C.A. Molecular properties of lupin and serradella leghaemoglobins. Biochem. J. 1972;127:309–314. doi: 10.1042/bj1270309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Gast K., Damaschun H., Damaschun G. Compactness of protein molten globules: temperature-induced structural changes of the apomyoglobin folding intermediate. Eur. Biophys. J. 1994;23:297–305. doi: 10.1007/BF00213579. [DOI] [PubMed] [Google Scholar]
- 71.Hanlon A.D., Larkin M.I., Reddick R.M. Free-solution, label-free protein-protein interactions characterized by dynamic light scattering. Biophys. J. 2010;98:297–304. doi: 10.1016/j.bpj.2009.09.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Tietze F. Molecular-kinetic properties of crystalline trypsinogen. J. Biol. Chem. 1953;204:1–11. [PubMed] [Google Scholar]
- 73.Cunningham L.W., Jr. Molecular-kinetic properties of crystalline diisopropyl phosphoryl trypsin. J. Biol. Chem. 1954;211:13–19. [PubMed] [Google Scholar]
- 74.Wilcox P.E., Kraut J., Neurath H. The molecular weight of alpha-chymotrypsinogen. Biochim. Biophys. Acta. 1957;24:72–78. doi: 10.1016/0006-3002(57)90147-6. [DOI] [PubMed] [Google Scholar]
- 75.Armstrong J.M., Myers D.V., Edsall J.T. Purification and properties of human erythrocyte carbonic anhydrases. J. Biol. Chem. 1966;241:5137–5149. [PubMed] [Google Scholar]
- 76.Wood E., Dalgleish D., Bannister W. Bovine erythrocyte cupro-zinc protein. 2. Physicochemical properties and circular dichroism. Eur. J. Biochem. 1971;18:187–193. doi: 10.1111/j.1432-1033.1971.tb01229.x. [DOI] [PubMed] [Google Scholar]
- 77.Edelhoch H. The denaturation of pepsin. I. macromolecular changes. J. Am. Chem. Soc. 1957;79:6100–6109. [Google Scholar]
- 78.Cecil R., Ogston A.G. The sedimentation constant, diffusion constant and molecular weight of lactoglobulin. Biochem. J. 1949;44:33–35. doi: 10.1042/bj0440033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Kawahara K., Kirshner A.G., Tanford C. DISSOCIATION OF HUMAN CO-hemoglobin by urea, guanidine hydrochloride, and other reagents. Biochemistry. 1965;4:1203–1213. doi: 10.1021/bi00883a001. [DOI] [PubMed] [Google Scholar]
- 80.Charlwood P.A. Sedimentation and diffusion of human albumins. I. Normal human albumins at a low concentration. Biochem. J. 1952;51:113–118. doi: 10.1042/bj0510113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Wong S.C., Hall D.C., Josse J. Constitutive inorganic pyrophosphatase of Escherichia coli. 3. Molecular weight and physical properties of the enzyme and its subunits. J. Biol. Chem. 1970;245:4335–4345. [PubMed] [Google Scholar]
- 82.Wu J.Y., Yang J.T. Physicochemical characterization of citrate synthase and its subunits. J. Biol. Chem. 1970;245:212–218. [PubMed] [Google Scholar]
- 83.Lane A.N., Kirschner K. The quaternary structure of tryptophan synthase from Escherichia coli. Fluorescence and hydrodynamic studies. Eur. J. Biochem. 1983;129:675–684. [PubMed] [Google Scholar]
- 84.Jøssang T., Feder J., Rosenqvist E. Photon correlation spectroscopy of human IgG. J. Protein Chem. 1988;7:165–171. doi: 10.1007/BF01025246. [DOI] [PubMed] [Google Scholar]
- 85.Jaenicke R., Gratzer W.B. Cooperative and non-cooperative conformational effects of the coenzyme on yeast glyceraldehyde-3-phosphate dehydrogenase. Eur. J. Biochem. 1969;10:158–164. doi: 10.1111/j.1432-1033.1969.tb00668.x. [DOI] [PubMed] [Google Scholar]
- 86.Jaenicke R., Gregori E., Laepple M. Conformational effects of coenzyme binding to porcine lactic dehydrogenase. Biophys. Struct. Mech. 1979;6:57–65. doi: 10.1007/BF00537595. [DOI] [PubMed] [Google Scholar]
- 87.Christen P., Goschke F., Schmid A. Uber die aldolase der Kaninchenleber molekulargewicht, dissoziation in untereinheiten. Helv. Chim. Acta. 1965;48:1050–1056. doi: 10.1002/hlca.19650480510. [DOI] [PubMed] [Google Scholar]
- 88.Kawahara K. Evaluation of diffusion coefficients of proteins from sedimentation boundary curves. Biochemistry. 1969;8:2551–2557. doi: 10.1021/bi00834a043. [DOI] [PubMed] [Google Scholar]
- 89.Taylor J.F., Green A.A., Cori G.T. Crystalline aldolase. J. Biol. Chem. 1948;173:591–604. [PubMed] [Google Scholar]
- 90.Samejima T. Splitting of catalase molecule by alkali treatment. J. Biochem. 1959;46:155–159. [Google Scholar]
- 91.Andrews P., Bray R.C., Shooter K.V. The chemistry of xanthine oxidase. 11. Ultracentrifuge and gel-filtration studies on the milk enzyme. Biochem. J. 1964;93:627–632. doi: 10.1042/bj0930627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Sund H., Weber K. Studies on the lactose-splitting enzyme. XIII. Quantity and configuration of beta-galactosidase from E. Coli. Biochem. Z. 1963;337:24–34. [PubMed] [Google Scholar]
- 93.May C.A., Grady J.K., Chasteen N.D. The sedimentation properties of ferritins. New insights and analysis of methods of nanoparticle preparation. Biochim. Biophys. Acta. 2010;1800:858–870. doi: 10.1016/j.bbagen.2010.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Sumner J.B., Gralen N., Eriksson-Quensel I.B. The molecular weight of urease. J. Biol. Chem. 1938;125:37–44. doi: 10.1126/science.87.2261.395. [DOI] [PubMed] [Google Scholar]
- 95.Follmer C., Pereira F.V., Carlini C.R. Jack bean urease (EC 3.5.1.5) aggregation monitored by dynamic and static light scattering. Biophys. Chem. 2004;111:79–87. doi: 10.1016/j.bpc.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 96.Behlke J., Ristau O., Schönfeld H.J. Nucleotide-dependent complex formation between the Escherichia coli chaperonins GroEL and GroES studied under equilibrium conditions. Biochemistry. 1997;36:5149–5156. doi: 10.1021/bi962755h. [DOI] [PubMed] [Google Scholar]
- 97.Harding S.E., Johnson P. Physicochemical studies on turnip-yellow-mosaic virus. Homogeneity, relative molecular masses, hydrodynamic radii and concentration-dependence of parameters in non-dissociating solvents. Biochem. J. 1985;231:549–555. doi: 10.1042/bj2310549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Kördel J., Skelton N.J., Chazin W.J. Backbone dynamics of calcium-loaded calbindin D9k studied by two-dimensional proton-detected 15N NMR spectroscopy. Biochemistry. 1992;31:4856–4866. doi: 10.1021/bi00135a017. [DOI] [PubMed] [Google Scholar]
- 99.Russell B.S., Zhong L., Bren K.L. Backbone dynamics and hydrogen exchange of Pseudomonas aeruginosa ferricytochrome c(551) J. Biol. Inorg. Chem. 2003;8:156–166. doi: 10.1007/s00775-002-0401-z. [DOI] [PubMed] [Google Scholar]
- 100.Bertini I., Bryant D.A., Zhao J. Backbone dynamics of plastocyanin in both oxidation states. Solution structure of the reduced form and comparison with the oxidized state. J. Biol. Chem. 2001;276:47217–47226. doi: 10.1074/jbc.M100304200. [DOI] [PubMed] [Google Scholar]
- 101.Pang Y., Buck M., Zuiderweg E.R. Backbone dynamics of the ribonuclease binase active site area using multinuclear ((15)N and (13)CO) NMR relaxation and computational molecular dynamics. Biochemistry. 2002;41:2655–2666. doi: 10.1021/bi011657f. [DOI] [PubMed] [Google Scholar]
- 102.Kalverda A.P., Ubbink M., Canters G.W. Backbone dynamics of azurin in solution: slow conformational change associated with deprotonation of histidine 35. Biochemistry. 1999;38:12690–12697. doi: 10.1021/bi990624l. [DOI] [PubMed] [Google Scholar]
- 103.Feher V.A., Zapf J.W., Cavanagh J. High-resolution NMR structure and backbone dynamics of the Bacillus subtilis response regulator, Spo0F: implications for phosphorylation and molecular recognition. Biochemistry. 1997;36:10015–10025. doi: 10.1021/bi970816l. [DOI] [PubMed] [Google Scholar]
- 104.Mauldin R.V., Sapienza P.J., Lee A.L. Structure and dynamics of the G121V dihydrofolate reductase mutant: lessons from a transition-state inhibitor complex. PLoS One. 2012;7:e33252. doi: 10.1371/journal.pone.0033252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Uhrínová S., Smith M.H., Barlow P.N. Structural changes accompanying pH-induced dissociation of the beta-lactoglobulin dimer. Biochemistry. 2000;39:3565–3574. doi: 10.1021/bi992629o. [DOI] [PubMed] [Google Scholar]
- 106.Shapiro Y.E., Meirovitch E. Evidence for domain motion in proteins affecting global diffusion properties: a nuclear magnetic resonance study. J. Phys. Chem. B. 2009;113:7003–7011. doi: 10.1021/jp9009806. [DOI] [PubMed] [Google Scholar]
- 107.Matzov D., Eyal Z., Yonath A. Structural insights of lincosamides targeting the ribosome of Staphylococcus aureus. Nucleic Acids Res. 2017;45:10284–10292. doi: 10.1093/nar/gkx658. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.