Abstract
For many years, curve-fitting software has been heavily utilized to fit simple models to various types of biophysical data. Although such software packages are easy to use for simple functions, they are often expensive and present substantial impediments to applying more complex models or for the analysis of large data sets. One field that is reliant on such data analysis is the thermodynamics and kinetics of protein folding. Over the past decade, increasingly sophisticated analytical models have been generated, but without simple tools to enable routine analysis. Consequently, users have needed to generate their own tools or otherwise find willing collaborators. Here we present PyFolding, a free, open-source, and extensible Python framework for graphing, analysis, and simulation of the biophysical properties of proteins. To demonstrate the utility of PyFolding, we have used it to analyze and model experimental protein folding and thermodynamic data. Examples include: 1) multiphase kinetic folding fitted to linked equations, 2) global fitting of multiple data sets, and 3) analysis of repeat protein thermodynamics with Ising model variants. Moreover, we demonstrate how PyFolding is easily extensible to novel functionality beyond applications in protein folding via the addition of new models. Example scripts to perform these and other operations are supplied with the software, and we encourage users to contribute notebooks and models to create a community resource. Finally, we show that PyFolding can be used in conjunction with Jupyter notebooks as an easy way to share methods and analysis for publication and among research teams.
Introduction
The past decade has seen a shift in the analysis of experimental protein folding and thermodynamic stability data from the fitting of individual data sets using simple models to increasingly complex models using global optimization over multiple large data sets [examples include (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21)]. This shift in focus has required moving from user-friendly, but expensive software packages to bespoke solutions developed in computing environments such as MATLAB and Mathematica or by using in-house solutions [examples include (3, 6, 12, 21, 22)]. However, as these methods of analysis have become more essential, simple curve-fitting software no longer provides sufficient flexibility to implement the models. Thus, there is an increasing need for substantially more computational expertise than previously required. In this respect, the protein folding field contrasts with other fields, for example x-ray crystallography, where free or inexpensive and user-friendly interfaces and analysis packages have been developed (23).
Here, we present PyFolding, a free, open-source, and extensible framework for graphing, analysis, and simulation. At present, it is customized for the analysis and modeling of protein folding kinetics and thermodynamic stability. To demonstrate these and other functions, we present a number of examples as Jupyter notebooks. The software, coupled with the supplied models/Jupyter (iPython) notebooks, can be used by researchers with less programming expertise to access more complex models/analyses and share their work with others. Moreover, PyFolding also enables researchers to automate the time-consuming process of combinatorial calculations, fitting data to multiple models or multiple models to specific data. This enables novice users to simply replace the filenames of the data sets with their own and execute the same calculations for their systems. For more advanced users, new models and functionality can be added with ease by utilizing the template models. The Jupyter notebooks provided also show how PyFolding provides an easy way to share analysis for publication and among research teams.
Materials and Methods
PyFolding was developed using Python 2.7 and additional libraries NumPy, SciPy, and Matplotlib. Analyses were performed on either an i5 Macbook Pro with 8 Gb RAM running macOS Sierra, a Dell Precision T3600 Workstation running Ubuntu 16.04LTS with 64 Gb RAM and an NVIDIA GTX1080 GPU, or a virtual PC running Windows 10 (64 bit) in VirtualBox on an i7 Macbook Air. Example data for the associated notebooks were taken from existing publications or extracted from original publications using engauge digitizer (https://github.com/markummitchell/engauge-digitizer). The PyFolding software, notebooks, and example data are distributed through github at https://github.com/quantumjot/PyFolding.
Results and Discussion
PyFolding is implemented in Python and is distributed as a lightweight, open-source library through github and can be downloaded with instructions for installation from the authors’ site (https://github.com/quantumjot/PyFolding). PyFolding has several dependencies, requiring Numpy, SciPy, and Matplotlib. These are now conveniently packaged in several Python frameworks, enabling easy installation of PyFolding even for those who have never used Python before (described in the “SETUP.md” file of PyFolding and as a series of instructional videos to demonstrate the installation and use of PyFolding; https://github.com/quantumjot/PyFolding/wiki). As part of PyFolding, we have provided many commonly used folding models as standard, such as two- and three-state equilibrium folding and various equivalent kinetic variations (Supporting Material, Jupyter notebooks 1–4 and 8). Functions and models themselves are open source and are thus available for inspection or modification by both reviewers and authors. Moreover, due to the open-source nature, users can introduce new functionality by adding new models into the library, building upon the template classes provided. We encourage users to contribute notebooks and models to create a community resource.
Fitting and evaluation of typical folding models within PyFolding
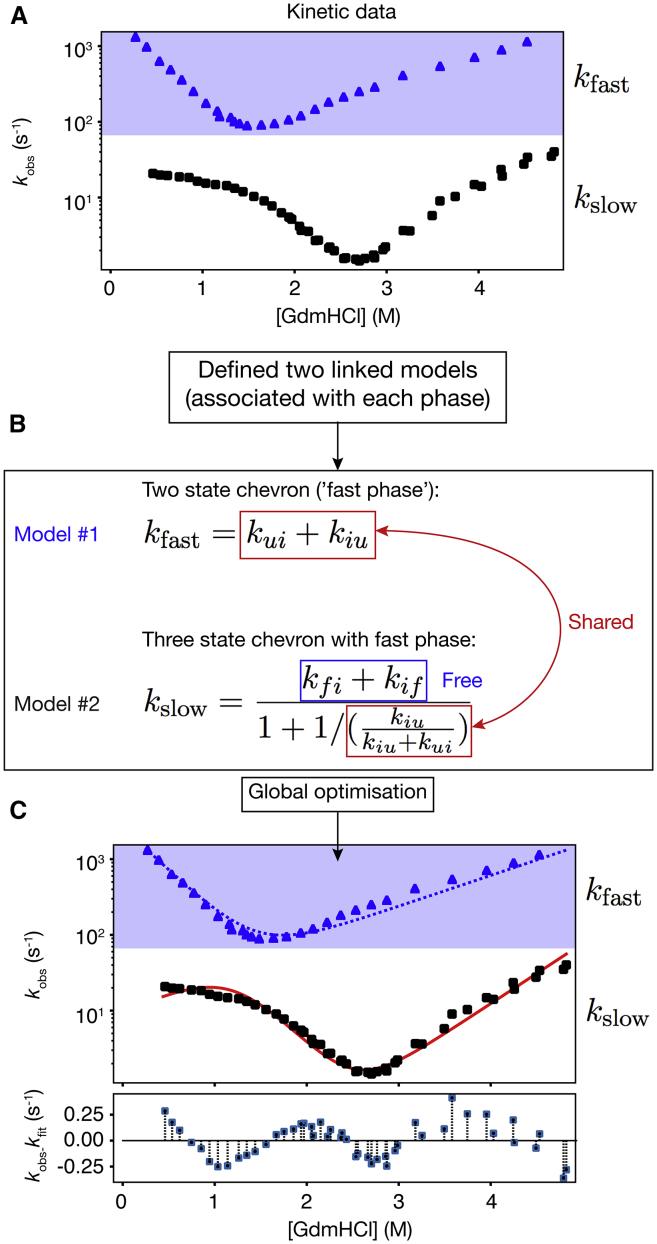
PyFolding uses a hierarchical representation of data internally. Proteins exist as objects that can have metadata as well as multiple sets of kinetic and thermodynamic data associated with them. Input data such as chevron plots or equilibrium denaturation curves can be supplied as comma separated value files (CSV). Once loaded, each data set is represented in PyFolding as an object, associating the data with numerous common calculations. Models are represented as functions that can be associated with the data objects you wish to fit. As such, data sets can have multiple models and vice versa enabling automated fitting and evaluation (Supporting Material, Jupyter notebooks 1–3). Parameter estimation for simple (non-Ising) models is performed using the Levenberg-Marquardt nonlinear least-mean-squares optimization algorithm to optimize the appropriate objective function [as implemented in SciPy (24)]. The output variables (with SE) and fit of the model to the data set (with R2 coefficient of determination and 95% confidence levels) can be viewed within PyFolding and/or the fit function and parameters written out as a CSV file for plotting in your software of choice (Supporting Material, Jupyter notebooks 1–3). Importantly, by representing proteins as objects, containing both kinetic and equilibrium data sets, PyFolding enables users to perform and automate higher-level calculations such as Φ-value analysis (25, 26), which can be tedious and time-consuming to perform otherwise (Supporting Material, Jupyter notebook 3). Moreover, users can define their own calculations so that more complex data analysis can be performed. For example, multiple kinetic phases of a chevron plot (fast and slow rate constants of folding) can be fitted to two linked equations describing the slow and fast phases of a three-state folding regime (Fig. 1; Supporting Material, Jupyter notebook 4). We believe that this type of fitting is extremely difficult to achieve with the commercial curve-fitting software commonly employed for analyzing these data, owing to the complexity of parameter sharing among different models and data sets.
Figure 1.
Work flow example of the fitting linked equations in PyFolding. (A) Unfolding and folding kinetics (chevron plots) showing the distinct fast and slow phases for the three-state folding thermophilic AR protein (tANK) identified in the archaeon Thermoplasma (2) are loaded into PyFolding as chevron objects. (B) Two linked models (functions) are associated with the chevron data. These describe the fast (model 1) and slow phases (model 2) of the chevrons. Certain rate constants and their associated m-values are shared between the two models. The other parameters are “free” and associated and fitted only in the slow-phase model. (C) Global optimization within PyFolding enables simultaneous fitting of the two models with shared parameters to the two respective phases. The resultant fits for the fast (blue dotted line) and slow phases (red solid line) are shown overlaid on the observed data. The residuals show the difference between the slow-phase observations and fit. These calculations can be found in Supporting Material, Jupyter notebook 4. GdmHCl, guanidinium chloride. To see this figure in color, go online.
More complex fitting, evaluation, and simulations using the Ising model
Ising models are statistical, thermodynamic, nearest-neighbor models that were initially developed for ferromagnetism (27, 28). Subsequently, they have been used with great success in both biological and nonbiological systems to describe order-disorder transitions (12). Within the field of protein folding and design, they have been used in a number of instances to model phenomena such as helix-to-coil transitions, β-hairpin formation, prediction of protein folding rates/thermodynamics, and with regards to the postulation of downhill folding (6, 12, 20, 29, 30, 31, 32, 33, 34). Most recently, two types of one-dimensional (1-D) variants have been used to probe the equilibrium and kinetic un/folding of repeat proteins (3, 12, 17, 21, 22, 35, 36). The most commonly used, and mathematically less complex, has been the 1-D homopolymer model (also called a homozipper). Here, each arrayed element of a protein is treated as an identical, equivalent, independently folding unit, with interactions between units via their interfaces. Analytical partition functions describing the statistical properties of this system can be written. By globally fitting this model to, for example, chemical denaturation curves for a series of proteins that differ only by their number of identical units, the intrinsic energy of a repeated unit and the interaction energy between the folded units can be delineated. However, this simplified model cannot describe the majority of naturally occurring proteins where subunits differ in their stabilities, and varying topologies and/or noncanonical interfaces exist. In these cases, a more sophisticated and mathematically more complex heteropolymer Ising model must be used. Here, the partition functions required to fit the data are dependent on the topology of interacting units and thus are unique for each analysis.
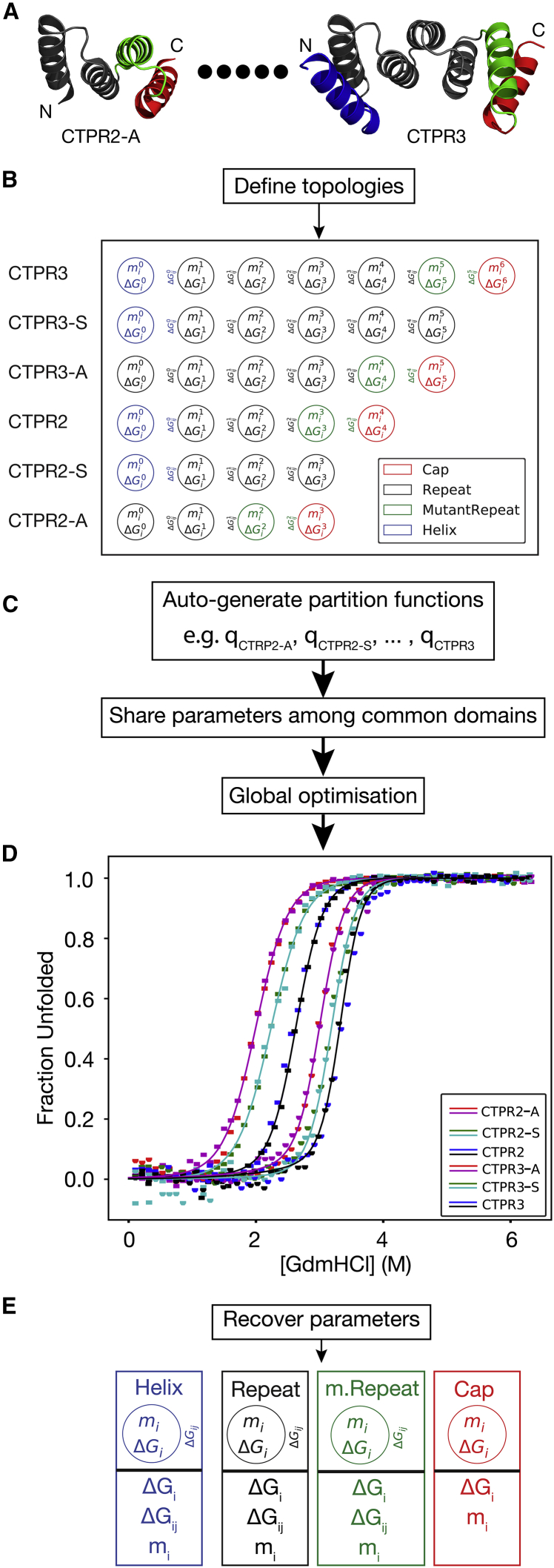
At present, there is no freely available software that can globally fit multiple folding data sets to a heteropolymer Ising model, and only a few that can adequately implement a homopolymer Ising model. Therefore, most research groups have had to develop bespoke solutions to enable analysis of their data (3, 21, 22, 35, 36). Significantly, in PyFolding we have implemented methods to enable users to easily fit data sets of proteins with different topologies to both the homozipper and heteropolymer Ising models. To achieve this goal, PyFolding presents a flexible framework for defining any nondegenerate 1-D protein topology using a series of primitive protein folding “domains/modules” (Fig. 2). Users define their proteins’ 1-D topology from these domains (Supporting Material, Jupyter notebooks 5–6). PyFolding will then automatically calculate the correct partition function for the defined topology, using the matrix formulation of the model [as previously described (12)], and globally fit the equations to the data as required (Supporting Material, Jupyter notebooks 5–6). The same framework also enables users to simulate the effect of changing the topology, a feature that is of great interest to those engaged in rational protein design (Supporting Material, Jupyter notebook 7).
Figure 2.
Work flow example of global optimization of a heteropolymer Ising model in PyFolding. (A) Guanidinium chloride (GdmHCl)-induced equilibrium denaturations of a series of single-helix deletion CTPRn proteins are loaded into PyFolding as EquilibriumDenaturation objects. In the figure, we schematically represent these as individual protein structures corresponding to the smallest in the series (CTPR2-A) up to (dots) the largest (CTPR3) (3). The figures were made with Pymol and individual helices are colored by the user-defined topology used by the Ising model: helix (blue), repeat (black), a mutant repeat (green), or a cap (red). (B) Using PyFolding’s built-in primitive protein folding “domains/modules,” one can define topologies for each protein in the series. Each primitive is a container for several thermodynamic parameters to describe the intrinsic and interfacial stability terms. (C) Using the topologies defined in (B), PyFolding will automatically generate the appropriate partition functions (q) for each protein in the series using a matrix formulation, and share parameters between other proteins in the series. (D) A final global fitting step finds the optimal set of parameters to describe the series. (E) The optimal parameters (and their estimated errors/confidence intervals) for each domain primitive are recovered and output for the user. These calculations can be found in Supporting Material, Jupyter notebook 6. To see this figure in color, go online.
To determine a globally optimal set of parameters that minimizes the difference between the experimental data sets and the simulated unfolding curves, PyFolding uses the stochastic differential evolution optimization algorithm (37) implemented in SciPy (24). In practice, experimental data sets may not adequately constrain parameters during optimization of the objective function, despite yielding an adequate curve fit to the data. It is therefore essential to carefully assess the output of the model to verify the validity of any topologies and the resultant parameters. A description of how PyFolding provides the error estimates and determines how constrained parameters are is given in the error analysis section below. As with the simpler models, PyFolding can be used to visualize the global minimum output variables (with SEs) and the fit of the model to the data set (with R2 coefficient of determination) (Supporting Material, Jupyter notebooks 5–6). The output can also be exported as a CSV file for plotting in your software of choice. In addition, PyFolding outputs a graphical representation of the topology used to fit the data and a graph of the denaturant dependence of each subunit used (Fig. 2). Thus, PyFolding enables nonexperts to create and analyze protein folding data sets with either a homopolymer or heteropolymer Ising model for any reasonable 1-D protein topology. Moreover, once the 1-D topology of your protein has been defined, PyFolding can also be used to simulate and thereby predict folding behavior of both the whole protein and the subunits that it is composed of (Supporting Material, Jupyter notebook 7). In principle, this type of approach could be extended to higher dimensional topologies, thus providing a framework to enable rational protein design.
Error analysis
We calculate various metrics to assess the quality of the output from PyFolding. All independent nonconstant variables are reported with a SE of each parameter, i:
| (1) |
where is the covariance matrix (where represents the variance of parameter i), are the y-values of the fit at the observed x-values, are the observed y-values of the data, and d represents the degrees of freedom (the number of data points minus the number of free variables). From these values, we can also calculate the confidence interval (nominally at 95%), where the confidence interval for parameter i is
| (2) |
where is the value of parameter i and is the t-distribution at 95% with d degrees of freedom. Finally, we report the coefficient of determination () as a statistical measure of the error between the data and the fitted model:
| (3) |
where represents the mean of the observed data.
In all models other than the heteropolymer Ising model, we utilize a gradient optimizer such as the Levenberg-Marquardt algorithm that yields a covariance matrix of the fitted parameters. However, since we must utilize a different optimization method (the differential evolution optimizer) for the global fitting of heteropolymer Ising models, we calculate the errors in a slightly different way. The optimizer does not yield a covariance matrix as default, so we calculate a numerical approximation based on the Jacobian matrix (here, a matrix of numerical approximations of all the partial differentials of all variables) as follows:
| (4) |
where is the Jacobian matrix, and is the mean squared error of the fit.
In PyFolding, we have provided estimates of the standard error and confidence intervals for each parameter (calculated as described above) using this numerical approximation of the covariance matrix. In general, estimating errors for the parameters or the uniqueness of the solution in heteropolymer models is a complex problem, owing to the method of optimization used. Interestingly, Aksel and Barrick (12) used Bootstrap analysis to evaluate parameter confidence intervals. However, many of the published studies either do not describe how error margins were determined or simply list the error between the data and curve fit. Here, when confronted with ill-posed data sets or poorly chosen topologies, which can produce an adequate curve fit to the data (as measured by ), PyFolding’s numerical error approximation becomes unstable, leading to large errors. Thus, in evaluating the determinant of the Jacobian as well as the estimated errors, it is possible to assess the quality of the model and the validity of the solution: large errors show that the model parameters are not properly constrained. In such cases, PyFolding raises the appropriate warnings to enable the user to quickly interpret the results and adjust the topologies and members of a data set appropriately.
Conclusions
Here we have shown that PyFolding, in conjunction with Jupyter notebooks, enables researchers with minimal programming expertise the ability to fit both typical and complex models to their thermodynamic and kinetic protein folding data. The software is free and can be used to both analyze and simulate data with models and analyses that expensive commercial user-friendly options cannot. In particular, we have incorporated the ability to fit and simulate equilibrium unfolding experiments with user defined protein topologies, using a matrix formulation of the 1-D heteropolymer Ising model. This aspect of PyFolding will be of particular interest to groups working on protein folds composed of repetitive motifs such as Ankyrin repeats and tetratricopeptide repeats, given that these proteins are increasingly being used as novel antibody therapeutics (38, 39, 40, 41) and biomaterials (42, 43, 44, 45, 46, 47). Further, as analysis can be performed in Jupyter notebooks, it enables novice researchers to easily use the software and for groups to share data and methods. We have provided a number of example notebooks and accompanying video tutorials as a resource accompanying this manuscript, enabling other users to recreate our data analysis and modify parameters. Finally, due to PyFolding’s extensible framework, it is straightforward to extend, thus enabling fitting and modeling of other systems or phenomena such as protein-protein and other protein-binding interactions. Such extensions can be rapidly and seamlessly deployed as a community resource, thus broadening the functionality of the software.
Author Contributions
A.R.L. wrote the software. A.R.L. and E.R.G.M. developed the models. A.R.L., E.R.G.M., L.S.I., and A.P.-R. tested the software and performed data analysis and simulations. A.R.L. and E.R.G.M. created the supplemental Jupyter Notebooks. E.R.G.M. created the online tutorials. E.R.G.M. and A.R.L. wrote the manuscript, and all authors edited and approved the manuscript.
Acknowledgments
We would like to thank Dr. Jonathan Phillips for insightful discussion, helpful comments and suggestions.
L.S.I. acknowledges the support of a Senior Fellowship from the UK Medical Research Foundation. A.P.-R. was supported by a Biotechnology and Biological Sciences Research Council Doctoral Training Programme scholarship and an Oliver Gatty Studentship. E.R.G.M. and L.S.I. laboratories acknowledge support from a Leverhulme Trust project grant.
Editor: Daniel Raleigh.
Footnotes
Supporting Materials and Methods are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)35041-5.
Contributor Information
Alan R. Lowe, Email: a.lowe@ucl.ac.uk.
Ewan R.G. Main, Email: e.main@qmul.ac.uk.
Supporting Material
References
- 1.Main E.R., Fulton K.F., Jackson S.E. Folding pathway of FKBP12 and characterisation of the transition state. J. Mol. Biol. 1999;291:429–444. doi: 10.1006/jmbi.1999.2941. [DOI] [PubMed] [Google Scholar]
- 2.Löw C., Weininger U., Balbach J. Structural insights into an equilibrium folding intermediate of an archaeal ankyrin repeat protein. Proc. Natl. Acad. Sci. USA. 2008;105:3779–3784. doi: 10.1073/pnas.0710657105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Millership C., Phillips J.J., Main E.R.G. Ising model reprogramming of a repeat protein’s equilibrium unfolding pathway. J. Mol. Biol. 2016;428:1804–1817. doi: 10.1016/j.jmb.2016.02.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jackson S.E., Fersht A.R. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry. 1991;30:10428–10435. doi: 10.1021/bi00107a010. [DOI] [PubMed] [Google Scholar]
- 5.Schätzle M., Kiefhaber T. Shape of the free energy barriers for protein folding probed by multiple perturbation analysis. J. Mol. Biol. 2006;357:655–664. doi: 10.1016/j.jmb.2005.12.081. [DOI] [PubMed] [Google Scholar]
- 6.Naganathan A.N., Muñoz V. Thermodynamics of downhill folding: multi-probe analysis of PDD, a protein that folds over a marginal free energy barrier. J. Phys. Chem. B. 2014;118:8982–8994. doi: 10.1021/jp504261g. [DOI] [PubMed] [Google Scholar]
- 7.Ferreiro D.U., Wolynes P.G. The capillarity picture and the kinetics of one-dimensional protein folding. Proc. Natl. Acad. Sci. USA. 2008;105:9853–9854. doi: 10.1073/pnas.0805287105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Barrick D., Ferreiro D.U., Komives E.A. Folding landscapes of ankyrin repeat proteins: experiments meet theory. Curr. Opin. Struct. Biol. 2008;18:27–34. doi: 10.1016/j.sbi.2007.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.DeVries I., Ferreiro D.U., Komives E.A. Folding kinetics of the cooperatively folded subdomain of the IκBα ankyrin repeat domain. J. Mol. Biol. 2011;408:163–176. doi: 10.1016/j.jmb.2011.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Maxwell K.L., Wildes D., Plaxco K.W. Protein folding: defining a “standard” set of experimental conditions and a preliminary kinetic data set of two-state proteins. Protein Sci. 2005;14:602–616. doi: 10.1110/ps.041205405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wensley B.G., Batey S., Clarke J. Experimental evidence for a frustrated energy landscape in a three-helix-bundle protein family. Nature. 2010;463:685–688. doi: 10.1038/nature08743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Aksel T., Barrick D. Analysis of repeat-protein folding using nearest-neighbor statistical mechanical models. Methods Enzymol. 2009;455:95–125. doi: 10.1016/S0076-6879(08)04204-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mallam A.L., Jackson S.E. A comparison of the folding of two knotted proteins: YbeA and YibK. J. Mol. Biol. 2007;366:650–665. doi: 10.1016/j.jmb.2006.11.014. [DOI] [PubMed] [Google Scholar]
- 14.Scott K.A., Randles L.G., Clarke J. The folding of spectrin domains II: phi-value analysis of R16. J. Mol. Biol. 2004;344:207–221. doi: 10.1016/j.jmb.2004.09.023. [DOI] [PubMed] [Google Scholar]
- 15.Hutton R.D., Wilkinson J., Itzhaki L.S. Mapping the topography of a protein energy landscape. J. Am. Chem. Soc. 2015;137:14610–14625. doi: 10.1021/jacs.5b07370. [DOI] [PubMed] [Google Scholar]
- 16.Tsytlonok M., Craig P.O., Itzhaki L.S. Complex energy landscape of a giant repeat protein. Structure. 2013;21:1954–1965. doi: 10.1016/j.str.2013.08.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Javadi Y., Main E.R. Exploring the folding energy landscape of a series of designed consensus tetratricopeptide repeat proteins. Proc. Natl. Acad. Sci. USA. 2009;106:17383–17388. doi: 10.1073/pnas.0907455106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lowe A.R., Itzhaki L.S. Biophysical characterisation of the small ankyrin repeat protein myotrophin. J. Mol. Biol. 2007;365:1245–1255. doi: 10.1016/j.jmb.2006.10.060. [DOI] [PubMed] [Google Scholar]
- 19.Xu M., Beresneva O., Roder H. Microsecond folding dynamics of apomyoglobin at acidic pH. J. Phys. Chem. B. 2012;116:7014–7025. doi: 10.1021/jp3012365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Garcia-Mira M.M., Sadqi M., Muñoz V. Experimental identification of downhill protein folding. Science. 2002;298:2191–2195. doi: 10.1126/science.1077809. [DOI] [PubMed] [Google Scholar]
- 21.Aksel T., Majumdar A., Barrick D. The contribution of entropy, enthalpy, and hydrophobic desolvation to cooperativity in repeat-protein folding. Structure. 2011;19:349–360. doi: 10.1016/j.str.2010.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kajander T., Cortajarena A.L., Regan L. A new folding paradigm for repeat proteins. J. Am. Chem. Soc. 2005;127:10188–10190. doi: 10.1021/ja0524494. [DOI] [PubMed] [Google Scholar]
- 23.Winn M.D., Ballard C.C., Wilson K.S. Overview of the CCP4 suite and current developments. Acta Crystallogr. D Biol. Crystallogr. 2011;67:235–242. doi: 10.1107/S0907444910045749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jones, E., T. Oliphant, …, P. Peterson. 2001. SciPy: Open source scientific tools for Python. http://www.scipy.org.
- 25.Serrano L., Matouschek A., Fersht A.R. The folding of an enzyme. III. Structure of the transition state for unfolding of barnase analysed by a protein engineering procedure. J. Mol. Biol. 1992;224:805–818. doi: 10.1016/0022-2836(92)90563-y. [DOI] [PubMed] [Google Scholar]
- 26.Fersht A.R., Matouschek A., Serrano L. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J. Mol. Biol. 1992;224:771–782. doi: 10.1016/0022-2836(92)90561-w. [DOI] [PubMed] [Google Scholar]
- 27.Brush S.G. History of the Lenz-Ising model. Rev. Mod. Phys. 1967;39:883–893. [Google Scholar]
- 28.Niss M. History of the Lenz-Ising model 1920–1950: from ferromagnetic to cooperative phenomena. Arch. Hist. Exact Sci. 2005;59:267–318. [Google Scholar]
- 29.Zimm B.H., Bragg J.K. Theory of the phase transition between helix and random coil in polypeptide chains. J. Chem. Phys. 1959;31:526–535. [Google Scholar]
- 30.Muñoz V., Thompson P.A., Eaton W.A. Folding dynamics and mechanism of beta-hairpin formation. Nature. 1997;390:196–199. doi: 10.1038/36626. [DOI] [PubMed] [Google Scholar]
- 31.Muñoz V., Eaton W.A. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. USA. 1999;96:11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kubelka J., Henry E.R., Eaton W.A. Chemical, physical, and theoretical kinetics of an ultrafast folding protein. Proc. Natl. Acad. Sci. USA. 2008;105:18655–18662. doi: 10.1073/pnas.0808600105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kubelka G.S., Kubelka J. Site-specific thermodynamic stability and unfolding of a de novo designed protein structural motif mapped by 13C isotopically edited IR spectroscopy. J. Am. Chem. Soc. 2014;136:6037–6048. doi: 10.1021/ja500918k. [DOI] [PubMed] [Google Scholar]
- 34.Lai J.K., Kubelka G.S., Kubelka J. Sequence, structure, and cooperativity in folding of elementary protein structural motifs. Proc. Natl. Acad. Sci. USA. 2015;112:9890–9895. doi: 10.1073/pnas.1506309112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wetzel S.K., Settanni G., Plückthun A. Folding and unfolding mechanism of highly stable full-consensus ankyrin repeat proteins. J. Mol. Biol. 2008;376:241–257. doi: 10.1016/j.jmb.2007.11.046. [DOI] [PubMed] [Google Scholar]
- 36.Aksel T., Barrick D. Direct observation of parallel folding pathways revealed using a symmetric repeat protein system. Biophys. J. 2014;107:220–232. doi: 10.1016/j.bpj.2014.04.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Storn R., Price K. Differential evolution - A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997;11:341–359. [Google Scholar]
- 38.Rasool M., Malik A., Kamal M.A. DARPins bioengineering and its theranostic approaches: emerging trends in protein engineering. Curr. Pharm. Des. 2017;23:1610–1615. doi: 10.2174/1381612822666161208121829. [DOI] [PubMed] [Google Scholar]
- 39.Jost C., Plückthun A. Engineered proteins with desired specificity: DARPins, other alternative scaffolds and bispecific IgGs. Curr. Opin. Struct. Biol. 2014;27:102–112. doi: 10.1016/j.sbi.2014.05.011. [DOI] [PubMed] [Google Scholar]
- 40.Ernst P., Plückthun A. Advances in the design and engineering of peptide-binding repeat proteins. Biol. Chem. 2017;398:23–29. doi: 10.1515/hsz-2016-0233. [DOI] [PubMed] [Google Scholar]
- 41.Cortajarena A.L., Yi F., Regan L. Designed TPR modules as novel anticancer agents. ACS Chem. Biol. 2008;3:161–166. doi: 10.1021/cb700260z. [DOI] [PubMed] [Google Scholar]
- 42.Sawyer N., Speltz E.B., Regan L. NextGen protein design. Biochem. Soc. Trans. 2013;41:1131–1136. doi: 10.1042/BST20130112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Main E.R., Phillips J.J., Millership C. Repeat protein engineering: creating functional nanostructures/biomaterials from modular building blocks. Biochem. Soc. Trans. 2013;41:1152–1158. doi: 10.1042/BST20130102. [DOI] [PubMed] [Google Scholar]
- 44.Grove T.Z., Regan L., Cortajarena A.L. Nanostructured functional films from engineered repeat proteins. J. R. Soc. Interface. 2013;10:20130051. doi: 10.1098/rsif.2013.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Phillips J.J., Millership C., Main E.R.G. Fibrous nanostructures from the self-assembly of designed repeat protein modules. Angew. Chem. Int. Engl. 2012;51:13132–13135. doi: 10.1002/anie.201203795. [DOI] [PubMed] [Google Scholar]
- 46.Grove T.Z., Regan L. New materials from proteins and peptides. Curr. Opin. Struct. Biol. 2012;22:451–456. doi: 10.1016/j.sbi.2012.06.004. [DOI] [PubMed] [Google Scholar]
- 47.Grove T.Z., Forster J., Regan L. A modular approach to the design of protein-based smart gels. Biopolymers. 2012;97:508–517. doi: 10.1002/bip.22033. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.