Abstract
Distortion product otoacoustic emissions are sounds that are emitted by the cochlea due to the nonlinearity of the outer hair cells. These emissions play an important role both in clinical settings and research laboratories. However, how distortion products propagate from their generation location to the middle ear remains unclear; whether distortion products propagate as a slow reverse traveling wave, or as a fast compression wave, through the cochlear fluid has been debated. In this article, we evaluate the contributions of the slow reverse wave and fast compression wave to the propagation of intracochlear distortion products using a physiologically based nonlinear model of the gerbil cochlea. This model includes a 3D two-duct model of the intracochlear fluid and a realistic model of outer hair cell biophysics. Simulations of the distortion products in the cochlear fluid pressure in response to a two-tone stimulus are compared with published in vivo experimental results. Whereas experiments have characterized distortion products at a limited number of locations, this model provides a complete description of the fluid pressure at all locations in the cochlear ducts. As in experiments, the spatial variations of the distortion products in the fluid pressure have some similarities with what is observed in response to a pure tone. Analysis of the fluid pressure demonstrates that although a fast wave component is generated, the slow wave component dominates the response. Decomposition of the model simulations into forward and reverse wave components shows that a slow forward propagating wave is generated due to the reflection of the slow reverse wave at the stapes. Wave interference between the reverse and forward components sometimes complicates the analysis of distortion products propagation using measurements at a few locations.
Introduction
The cochlea is a fluid-filled biological sensory system with high frequency selectivity, high sensitivity, and a wide dynamic range that spans several orders of magnitude (1). The nonlinear active feedback mechanism behind these characteristics originates from the outer hair cells (OHCs) and is commonly called the “cochlear amplifier” (2). Because of the active OHC feedback, the healthy cochlea can generate sounds, called “otoacoustic emissions” (3). Because otoacoustic emissions can be easily measured by placing a probe in the ear canal, they are commonly used both clinically and in research to study the functional status and biophysics of the ear (e.g., (4, 5, 6)). The focus of this article is on a specific type of otoacoustic emissions called “distortion product otoacoustic emissions” (DPOAEs); DPOAEs are generated by OHCs due to the nonlinear interaction of two stimulus tones (of frequencies f1 and f2, where f2 > f1) (7). Intracochlear measurements of the basilar membrane (BM) velocity (8, 9, 10) or fluid pressure (11) in response to a two-tone stimulus have confirmed that distortion products (DPs) are generated in the cochlea. It is generally agreed that DPOAEs are generated by the OHCs (8) due to the nonlinearity of the mechanoelectrical transduction (MET) channel (12). In any nonlinear system, DPs occur at linear combinations of the two stimulus tones; due to the specific form of cochlear nonlinearity, the low-side cubic DP of frequency, fDP = 2f1 – f2, tends to have the highest amplitude and is the most commonly studied DP (10).
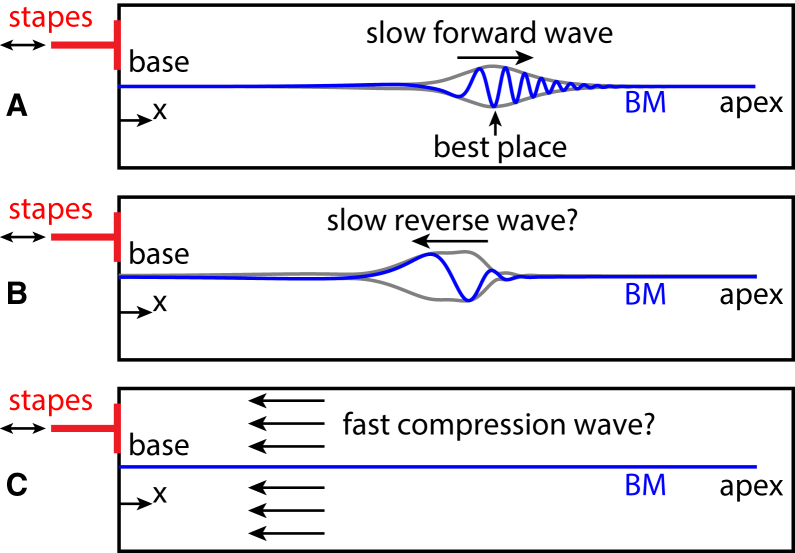
In response to an acoustic stimulus in the ear canal, a wave propagates on the BM in the forward direction, i.e., from the base toward the apex of the cochlea (in the +x direction; see Fig. 1 A). The magnitude of the wave peaks at a location that depends on the stimulus frequency, called the “best place”. Because the wave speed (from tens of m/s to a few m/s) is much smaller than the speed of sound in water, this wave is commonly called the “slow forward traveling wave”. Despite the common use of DPOAEs, questions still remain as to how DPs propagate in the reverse direction (−x direction) from their generation sites to the ear canal. Two main hypotheses, shown in Fig. 1, B and C, have been proposed for how DPs propagate: 1) as a slow reverse traveling wave along the BM (7, 13) or 2) as a fast compression wave through the cochlear fluid (14, 15). The fast compression wave is a longitudinal pressure wave that travels at the speed of sound in water (1500 m/s). A clear understanding of how DPs propagate within the cochlea is needed to improve the usefulness of DPOAE measurements in clinical and research settings.
Figure 1.
Schematics of wave propagation in the cochlea. (A) Here we show response to an acoustic stimulus. Given here are proposed hypotheses for DP propagation as (B) slow reverse wave and (C) fast compression wave. BM, basilar membrane. To see this figure in color, go online.
In the slow wave theory, once the reverse traveling wave reaches the stapes, part of the DP wave is transmitted through the middle ear and into the ear canal where it can be measured as a DPOAE; the other part is reflected at the stapes and propagates as a slow forward wave. Early models (e.g., (16)) have shown that DPs are expected to propagate back to the stapes as slow traveling waves. However, measurements of the BM velocity at the DP frequency have not provided any direct evidence for slow reverse propagation. Ren (14) measured the DP in the BM velocity at multiple positions and found that the phase is consistent with a forward propagating wave even though the locations were hypothesized to be basal to the DP generation site (such that a slow reverse traveling wave was expected to be observed). These results were interpreted as evidence that the DP propagates as a fast compression wave in the cochlear fluid; according to this theory, the fast compression wave would be reflected at the stapes, which would launch a slow forward traveling wave. Simultaneous measurements of the DP at the stapes and two longitudinal BM positions in a subsequent article (15), and of the phase of the stapes vibrations relative to the BM vibrations at the DP frequency (17), were interpreted as further supporting the theory of fast compression waves.
However, it has been argued that the BM measurements of Ren and co-workers (14, 15, 17) might be within the region in which DPs are generated, which might complicate the interpretation (18). Indeed, theoretical efforts using one-duct models that only allow slow wave components (19, 20, 21, 22, 23) have demonstrated that these measurements are not necessarily inconsistent with the reverse traveling wave theory. Analysis using 1D nonlinear cochlear models have shown that DP generation extends over a wide region that extends toward the base for low f2/f1 ratios and moderate to high stimulus levels (20, 22). Similarly, Sisto et al. (21) found that a region dominated by a forward traveling wave is expected whenever DP generation occurs over a wide region and/or the stapes has high reflectivity. Using a more realistic 2D one-duct cochlear model, Vetešník and Gummer (23) also explained the observation of forward traveling waves in (14, 15, 17) by the fact that the measurement locations might be located at or apical to the DP generation sites. In (19), DP propagation was studied using a nonlinear 3D cochlear model with the stimulus applied from within the cochlea instead of from the stapes; decomposition of the DP response into forward and reverse traveling waves showed that the response is dominated by a slow reverse traveling wave from around the f2 best place to the stapes. de Boer et al. (24) measured DPs with a frequency well below the characteristic frequency (CF) of the measurement location and observed that whereas a forward traveling wave is observed when f2 is near CF, a slow reverse traveling wave is observed when f2 is lower than CF.
It is more advantageous to investigate DP propagation by measuring the intracochlear pressure instead of the BM response because pressure measurements can detect both the compression and slow traveling wave modes (25). Many theoretical articles have investigated intracochlear fluid mechanics in response to a pure tone (26, 27, 28). In particular, it is well understood that the fluid pressure is truly 3D close to the peak of the traveling wave in the short-wave region (i.e., in the region where the wavelength of the slow wave is small compared to the height of the cochlear ducts), whereas it is ∼1D closer to the base, in the long wavelength region (i.e., in the region where the wavelength is large compared to the duct height) (29). Using novel pressure sensors (30), Olson characterized the in vivo response of the intracochlear fluid pressure to a pure tone (31, 32). More recently, Dong and Olson (11, 25) and Dong (33) measured the intracochlear pressure DP in response to a two-tone stimulus. When the CF of the measurement location is near the f2 and fDP best places, it was found that the DP pressure in the scala tympani (ST) is localized around the BM (11). In these measurements, the amplitude of the DP decreases at a similar rate as a pure tone of the same frequency with increasing distance from the BM; such a decay of the amplitude is at odds with the compression wave theory. Subsequent measurements in (25) provided strong evidence for the reverse traveling wave hypothesis, because the ear canal pressure is delayed relative to the intracochlear DP for f2 frequencies that are significantly lower than the CF of the measurement location. Recent measurements of the pressure at two basal intracochlear locations by Dong (33) confirmed that the DPs are generated near the f2 best place and have both forward and reverse traveling wave components.
Despite the critical role of the intracochlear fluid in the propagation of the DP from its generation site to the stapes, no model has investigated the DP intracochlear pressure. It is challenging to measure the fluid pressure at multiple longitudinal locations in vivo. Because of the presence of multiple waves (slow reverse wave, slow forward wave, and fast wave), measurements at one or two longitudinal location(s) are difficult to interpret. Furthermore, although the ST fluid pressure has been measured in active cochleae (32), measurements of the fluid pressure in the scala media have only been possible in passive cochleae (34). Hence, a model is needed to clarify how DPs vary spatially within the cochlear fluid pressure. The objective of this work is to analyze the generation of DPs and to quantify the relative contributions of slow reverse waves and fast compression waves to DP propagation. Because cochlear fluid mechanics is 3D and includes fast and slow modes, these physiological questions are addressed using a physiological two-duct 3D model of the cochlea. Furthermore, the active feedback mechanism is based on a realistic model of OHC biophysics that includes nonlinear MET channels and linearized somatic electromotility. Responses of the fluid pressure in response to a two-tone stimulus are compared to published in vivo measurements for model validation. Spatial variations of the total fluid pressure and of the different pressure modes are analyzed to gain a more complete understanding of how DPs propagate from their generation location out of the cochlea.
Methods
Cochlear model
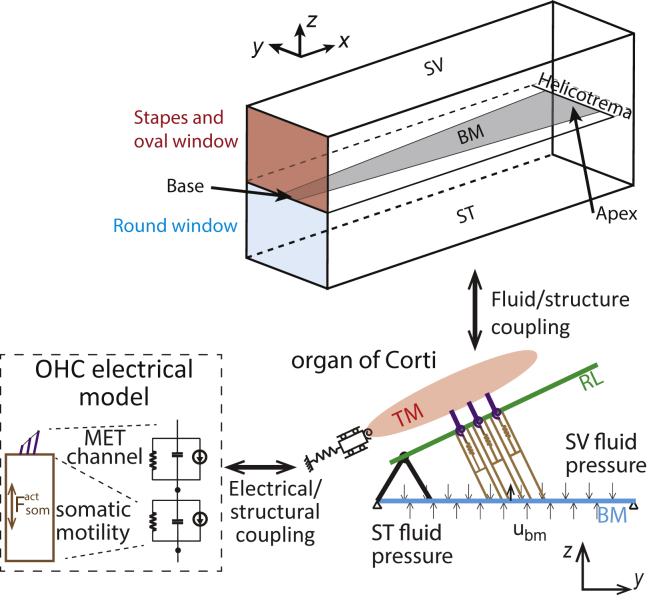
A model of the gerbil cochlea was developed because measurements of the intracochlear DP pressure have been performed in this species (e.g., (11, 25, 33)). This model is adapted from the physiologically based 3D model of the guinea pig presented in a series of articles (35, 36, 37). The model is based on the finite element method and includes mechanical, acoustic, and electrical physics to represent the cochlea (see Fig. 2 for a schematic and the Supporting Material for a brief description of the model equations). The model includes a realistic model of the organ of Corti geometry (see the Supporting Material) and micromechanics, with degrees of freedom for the tectorial membrane (TM) (both a bending and shear displacement, as described in (38)) and for the BM; the BM transverse displacement is assumed to be given by ubm(x,y,t) = Ubm(x,t)ψ(y), where ψ(y) is a half-sinusoid and Ubm(x,t) is the BM displacement at the center of the cross section. Longitudinal coupling is included for both the BM and TM, as described in (39).
Figure 2.
Schematic of the cochlear model fluid, structural, and electrical domains. TM, tectorial membrane; RL, reticular lamina; BM, basilar membrane; ST, scala tympani; SV, scala vestibuli; OHC, outer hair cell; MET, mechanoelectrical transduction. is the force applied by the OHCs on the RL and BM, and Ubm is the displacement of the BM. To see this figure in color, go online.
Fluid model. The geometry of the cochlear ducts is described by a straight box model with two ducts. Although a two-duct model is not needed to predict the BM response because the BM is only excited by the pressure difference across the cochlear partition, a two-duct model is required to obtain realistic simulations of the intracochlear fluid pressure. The cochlear fluid is assumed to be incompressible (which implies that the speed of the fast wave is infinite in the model). Furthermore, fluid viscosity is ignored; the effect of viscosity is lumped into the damping parameters of the structural model. The fluid at the oval window is coupled to the stapes via the linearized Euler equation, the round window is modeled as a pressure release, and all other bony walls of the cochlea are rigid. As introduced in (40), the pressure, PT(x,y,z,t), is decomposed into radial mode shapes so that a 2D mesh can give a 3D solution:
| (1) |
where x, y and z are the distance in the longitudinal (from the stapes), radial (from the center of the duct), and transverse directions (from the BM), respectively; t is the time; m is the mode number; PT(m) is the modal amplitude of the mth mode; ϕm(y) is the mth mode shape; and w is the width of the cochlear duct. Radial symmetry is assumed so that only the even modes are necessary. Unlike in previous works (e.g., (37, 38)) that only used the first three modes, the first 25 even modes (M = 48) are included in this work to give a more accurate calculation of the 3D pressure (see the Supporting Material for a convergence study). The fluid elements directly above (in the scala vestibuli, SV) and below (in the ST) the cochlear partition are coupled to the BM displacement. To determine the contributions of the slow traveling wave and fast compression wave, the pressure is decomposed into the sum of an antisymmetric part, Pas, and of a symmetric part, Ps (26):
| (2) |
| (3) |
Because the SV and ST dimensions are identical in the model and the fluid is only coupled to the BM, only the antisymmetric component interacts with the BM. Hence, the antisymmetric and symmetric components correspond to the slow traveling wave and fast compression wave, respectively (26, 34). Because the round window is modeled as a pressure release, the symmetric and antisymmetric components must be equal at x = 0.
OHC electrical model. The model uses the same electrical domain model as developed in (37). The MET current, IMET, is modeled with the Boltzmann function:
| (4) |
where θhb/rl is the angular deflection of the hair bundle, Ghbmax is the saturating hair bundle MET conductance, P0s is the resting open probability of the MET channel, ΔVhb0 is the resting value of the difference between the scala media potential and intracellular OHC potential, Lhb is the length of the hair bundles, and X0 and ΔX are constant displacements. Somatic electromotility is modeled by the following equations:
| (5) |
| (6) |
where iohc, Δϕohc, and fohc are the perturbations in the somatic current, transmembrane potential, and electromechanical force from their resting values, respectively; is the OHC compression; Gm and Cm are the basolateral conductance and capacitance, respectively; ε3 is the electromechanical coupling coefficient; and Kohc is the OHC stiffness.
Calibration of the cochlear model. To accurately model the response of the gerbil cochlea, it was necessary to adjust many of the parameters from the guinea pig model of (37). When possible, parameters, such as the anatomical geometry or the mass of the TM in bending and shear, were chosen based on available measurements (e.g., (41, 42)). Remaining parameters were either kept at the value previously used in (37) or adjusted manually so that the model response approximated available measurements for the response of the gerbil cochlea to a pure tone (43, 44, 45). A complete list of the model parameters can be found in the Supporting Material.
Boundary conditions at the stapes. To enable easy modification of the boundary conditions at the stapes, the stapes was modeled as a one-degree-of-freedom system instead of using a more realistic model of middle ear. The response of the coupled cochlea-stapes system is obtained by applying a force on the stapes. The amplitude of the force was converted to an ear canal pressure in dB SPL (sound pressure level, using 20 μPa as the reference pressure) by examining the amplitude of the pressure at the stapes in the SV in response to a pure tone; the ear canal pressure was assumed to be 30 dB lower than the SV pressure at the stapes, based on measurements from (32, 46).
Distortion product simulations. For this work, we consider the low-side cubic DP at the frequency fDP = 2f1 – f2, where f1 and f2 (in which f2 > f1) are the primary frequencies that comprise the two-tone stimulus. Only equilevel primaries are considered for all results shown in this article. As in our recent work (37), simulations of the nonlinear response are run in the time-domain using the state space approach described by Elliott et al. (47). To avoid any broadband excitation of the model at the stimulus onset, the onset of the two primaries had a raised cosine envelope with a rise time of 1 ms. The response at the primary and DP frequencies was obtained using MATLAB’s (The MathWorks, Natick, MA) built-in FFT function. In addition to the distortion source, DPOAEs are also known to have a reflection source component due to coherent reflection by inhomogeneities near the DP best place (48). To simplify the analysis, a smooth cochlear model is employed and only the distortion source component is investigated.
Decomposition of the slow wave into reverse and forward wave components
Following the approach from (19), the model response at the DP frequency is decomposed into approximate forward and reverse traveling wave components. The procedure involves taking the spatial Fourier transform of the antisymmetric pressure at the DP frequency, PasDP(x,y,z), into the wavenumber domain:
| (7) |
where k is the wavenumber and is the wavenumber spectrum of . The wavenumber spectrum is then separated into a forward wave component, , and a reverse wave component, by assuming that for k ≠ 0:
| (8) |
Once the two components are found in the wavenumber domain, the value of the forward and reverse wave components in the spatial domain, PasDP,f and PasDP,r, are given by the inverse Fourier transform of the two components in the wavenumber domain:
| (9) |
| (10) |
Equation 8 does not specify the values of the forward and reverse components at k = 0; these values were found by making sure that the ratio of PasDP,f to PasDP,r at x = 0 is equal to the stapes reflection coefficient, using the approach described in the Supporting Material.
Results
Pure tone response
The response of the model to a pure tone is first discussed. At a longitudinal position x and frequency ω, the gain of the BM velocity relative to the stapes velocity is defined as:
| (11) |
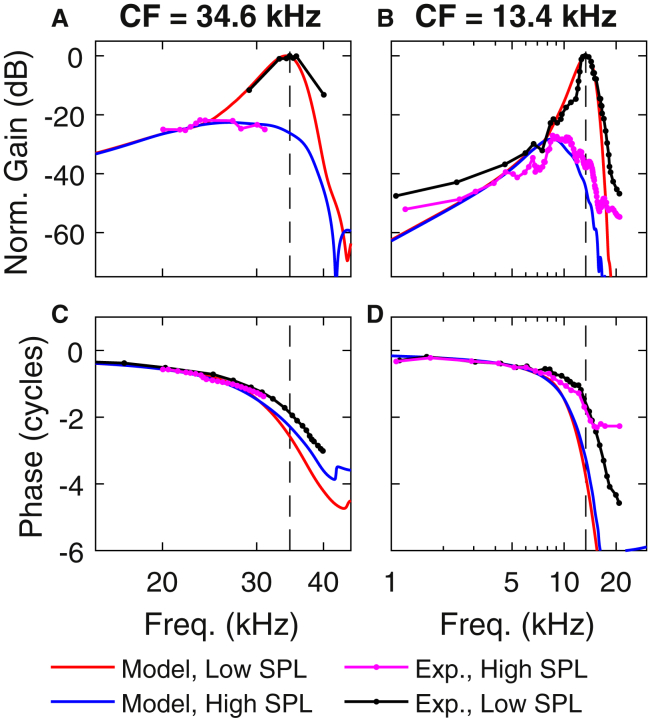
where vbm (given by iωUbm, in which Ubm is the displacement of the BM at the center of the BM) and vs are the velocities of the BM and stapes, respectively. In Fig. 3, A and B, the magnitude of the gain is normalized by the low SPL value of the gain at CF (to aid in comparison with experimental data) and is plotted as a function of frequency at two longitudinal locations (chosen to match the positions of measurements of the BM response in (43) and (44)) in Fig. 3. At both positions, the sharpness of tuning seen in the low SPL results is similar to what is seen in the experimental data; furthermore, the gain of the low SPL to high SPL model results (22.6 dB for CF = 34.6 kHz and 28.5 dB for CF = 13.4 kHz) is similar to what is seen in the experimental data. This is a result of an effort during the calibration process to match the experimental gain and tuning sharpness seen in these experiments. At the more basal position (CF = 34.6 kHz), the model high SPL results peak at 26 kHz and the experimental high SPL results peak at 24–25 kHz, whereas, at the more apical position (CF = 13.4 kHz) both model and experimental high SPL results peak at 8–9 kHz. In Fig. 3 C, the model phase decreases at almost the same rate as the experimental results. In Fig. 3 D, both the low and high SPL model phases decrease at a faster rate than the experimental data. Model and experimental results for the fluid pressure are compared in Fig. S4.
Figure 3.
Comparison of BM pure tone response for model and experimental data was taken from (43, 44). (A and B). Gain of the BM velocity relative to the stapes velocity. The model gain was normalized by the gain predicted by the model at low SPL at CF (55 dB in A and 60 dB in B); the experimental gain was normalized by the gain seen at CF in the low SPL experiments (53 dB in A and 49 dB in C). (C and D) Phase of the BM velocity relative to the stapes velocity. (A and C) Experimental data from (44) is given. (B and D) Experimental data from (43) is given. (A and C) Results for 30- and 90 dB SPL and 50- and 90 dB SPL stimuli, respectively. (B and D) Results for 30- and 100 dB SPL stimuli. The vertical black dashed lines denote CF. To see this figure in color, go online.
Two-tone response
Response on the basilar membrane
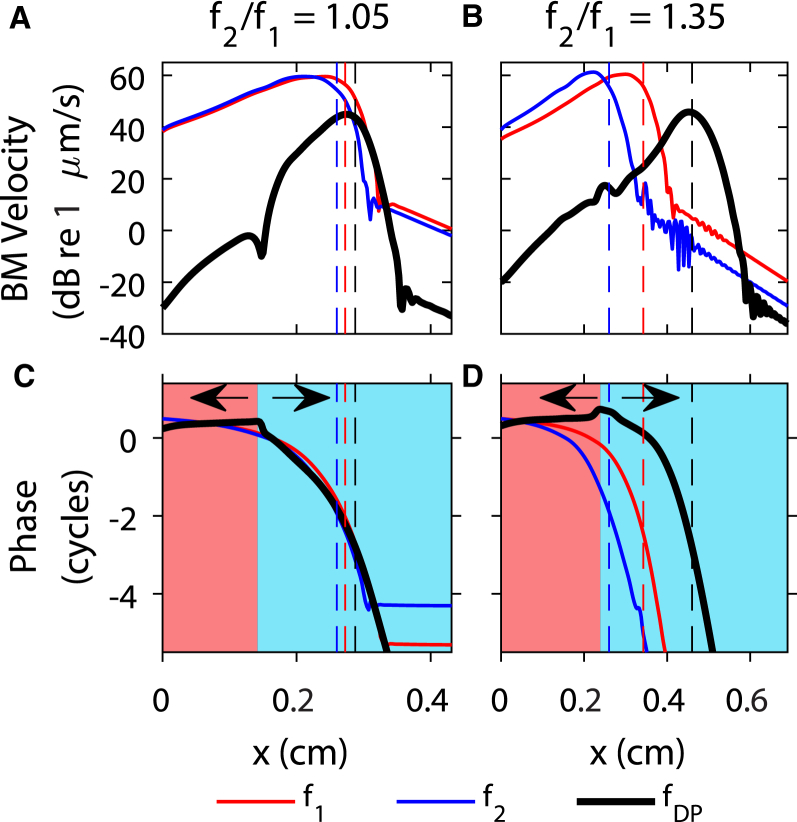
The spatial response of the BM to a two-tone stimulus is shown in Fig. 4 for two primary frequency ratios (f2/f1 = 1.05 in Fig. 4, A and C; f2/f1 = 1.35 in Fig. 4, B and D). As in most of the intracochlear DP pressure measurements (11, 33), the level of the primaries was chosen to be 80 dB SPL. For both primary ratios, the f1 and f2 responses have peaks of similar amplitude (Fig. 4, A and B) and the primaries peak at a location basal to their best places due to the relatively high stimulus level of the two primaries. The DP peaks slightly basal to its best place for f2/f1 = 1.05 and at its best place for f2/f1 = 1.35. Two different regions can be identified in the plot of the phase at the DP frequency (Fig. 4, C and D): in the basalmost red-shaded region, the slope of the phase is positive, such that DP propagation is dominated by a slow reverse traveling wave; in the blue-shaded region, the phase slope is negative, which indicates that DP propagation is dominated by a slow forward traveling wave. For f2/f1 = 1.05, this transition from reverse to forward wave propagation occurs basal to the f2 best place, whereas for f2/f1 = 1.35, this transition occurs approximately at the f2 best place.
Figure 4.
(A–D) BM velocity of the DP and primaries as a function of longitudinal position for primary frequency ratios, f2/f1, of 1.05 and 1.35, f2 = 24 kHz, and primary stimuli levels of 80 dB SPL. The vertical dashed lines from left to right indicate the f2, f1, and fDP best places, respectively. The red shading indicates when the phase has a positive slope and the cyan shading indicates when the phase has a negative slope. To see this figure in color, go online.
Spatial variations in intracochlear pressure
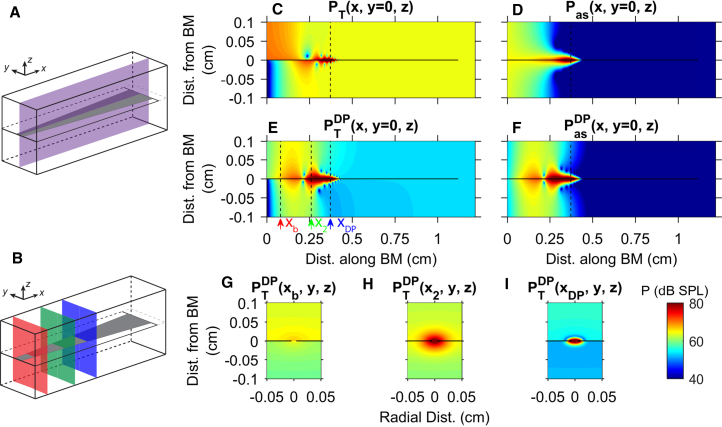
Because the cochlear fluid plays a critical role in the propagation of both slow and fast waves, the spatial variations of the pressure were analyzed (Fig. 5). In this work, unless stated otherwise, pressure magnitudes are presented in dB SPL with a reference pressure of 20 μPa. In Fig. 5, C–F, the pressure magnitude is plotted as a function of x and z for positions within the plane shown in Fig. 5 A. To help understand the DP response in response to a two-tone stimulus, the pure tone response is first presented in Fig. 5, C and D; the stimulus frequency was chosen to match the frequency of the DP (16 kHz) seen in the two-tone results. As described in the Methods, the total pressure was decomposed into its symmetric and antisymmetric components, which correspond to the fast and slow waves, respectively. The spatial variations of the fluid pressure in response to a pure tone are similar to what has been previously observed in 3D two-duct cochlear models (e.g., (27, 28, 49)). For brevity and because it is nearly uniform throughout both cochlear ducts, the symmetric pressure is not shown; the amplitude of the symmetric component corresponds to the total pressure amplitude in the most apical region near the helicotrema where the antisymmetric pressure has a low amplitude. The lobes seen in the total pressure close to the BM from x = 0.2 to 0.5 cm (Fig. 5 C) are due to wave interference between the antisymmetric (shown in Fig. 5 D) and symmetric components. Similar notches in the pressure have been observed experimentally (e.g., (11, 25)). At the base, in the long-wave region, the antisymmetric pressure is ∼1D, whereas it becomes more localized and 3D around the BM closer to the 16 kHz best place, in the short-wave region.
Figure 5.
(A and B) Box models are given with planes indicating where the pressure is shown in (C–F) and (G–I), respectively. Total and antisymmetric pressure component magnitudes for pure-tone (C and D) and two-tone stimuli are given (E and F). Cross sections of pressure magnitude at several positions are given (G–I). The pure-tone stimuli (C and D) was at 16 kHz and 40 dB SPL and the two-tone stimuli (E–I) has 2f1 – f2 = 16 kHz, primary frequency ratio f2/f1 = 1.20, and primary stimulus level of 80 dB SPL. The horizontal black line represents the cochlear partition. The vertical dashed line in (C), (D), and (F) denotes the 16 kHz best place. The arrows and vertical dashed lines on (E) from left to right denote the positions shown in (G–I), respectively. The three positions shown in (G–I) are an arbitrarily chosen basal position, xb = 0.08 cm; the f2 best place (x2 = 0.26 cm); and the DP best place (xDP = 0.37 cm), respectively. To see this figure in color, go online.
The fluid pressure at the DP frequency in response to a two-tone stimulus shares some similarities with the pure tone response. In addition to the pressure as a function of x and z (Fig. 5, E and F), the DP results include the pressure as function of y and z (Fig. 5, G–I) at three longitudinal locations identified by the three planes shown in Fig. 5 B. The DP antisymmetric pressure is 1D in the long wave region and 3D in the short wave region (Fig. 5 F). As with the pure tone, the DP symmetric pressure is nearly uniform throughout the cochlear ducts and the amplitude of the symmetric component corresponds to the total pressure in the apical regions. However, some notable differences between the pure tone and DP responses can be observed. The magnitude of the pure-tone symmetric pressure is much higher than the DP symmetric pressure, such that lobes of minimum pressure close to the BM are not observed in the total DP response in Fig. 5 E. Furthermore, a region of minimum magnitude is observed in both the total and antisymmetric DP pressure at ∼x = 0.20 cm; this minimum, not observed in the pure tone response, relates to the minimum or notch in the BM response in Fig. 4 and will be discussed further below. Model simulations for the spatial variations of the DP pressure are compared to experimental results in Fig. S6.
Effects of varying f2 on DP propagation at fixed location
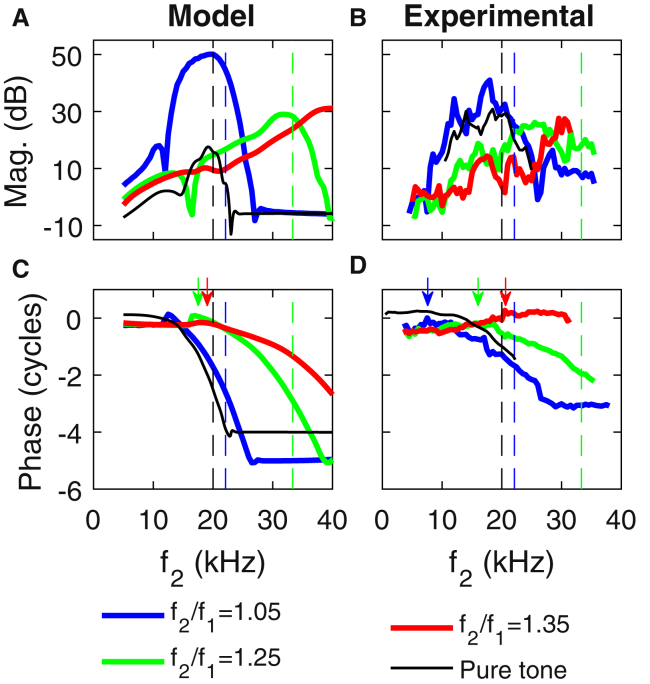
Although cochlear models easily provide the response for a given frequency at all positions, it is much easier to measure the response at a fixed position and sweep frequency in an experiment. In a scale-invariant cochlea, these two methods should be equivalent (24). In Fig. 6, the effects of varying f2 at a fixed position (20 kHz best place) for different f2/f1 ratios are shown. This scheme is commonly used in experiments (e.g., (15, 17, 24, 25, 33)) to investigate intracochlear DP response and propagation. The magnitude and phase of the ratio of the pressure in the ST close to the BM to the pressure in the SV close to the stapes is compared with recent measurements from Dong (33). Due to variability in the experimental results, only the pressure ratios are compared here.
Figure 6.
Shown here is the magnitude (A and B) and phase (C and D) of the ratio of the DP pressure in the ST, 10 μm from the BM, to the DP pressure in the SV next to the stapes (halfway between the BM and the top of the SV) as a function of f2. (A and C) Model results are given. (B and D) Measurements from (33) are shown. All results are at the 20-kHz best place. Model and experimental DPs had primary stimuli levels of 80 dB SPL. For reference, the response to a pure tone with a 40 dB SPL stimulus is also shown. The vertical dashed lines indicate f2 when fDP (or f for the pure tone) corresponds to the CF of 20 kHz. Vertical arrows mark the transition from reverse to forward waves. To see this figure in color, go online.
As in the measurements (Fig. 6 B), the peak of the DP response shifts to higher frequency as the frequency ratio is increased (Fig. 6 A); this is because the DP is approximately tuned to its own CF and the x axis is f2. Although the magnitude of the pressure ratio agrees well with experiments for f2/f1 = 1.25 and 1.35, it is ∼10 dB higher than in the experiments for f2/f1 = 1.05, and 13 dB lower than in the experiments for the pure tone results. Both in the model and the experiments, the DP response for f2/f1 = 1.05 has similar tuning as the pure tone response, whereas it has broader tuning at higher ratios. In contrast to the experimental results, the curves obtained with the model are smooth, possibly because the reflection from the DP best place due to cochlear roughness is not taken into account in the model. Similar to the lobes in Fig. 5 C, the pure tone shows notches in amplitude at ∼14 and 23 kHz that are due to interactions between the symmetric and antisymmetric pressure. For f2 > 30 kHz, the magnitudes of the f2/f1 = 1.05 DP and pure tone are almost constant, indicating that the total pressure is converging to the symmetric pressure.
The phase of the ST pressure at the 20 kHz best place relative to the SV phase at the stapes, shown in Fig. 6, C and D, is particularly important for determining how DPs propagate. Two frequency regions can be identified, both in the case of the model simulations (Fig. 5 C) and the experiments (Fig. 5 D). At low frequency, the slope of the phase tends to be shallow; it is positive (indicating a slow reverse traveling wave) for f2/f1 = 1.25 and 1.35, although both positive and negative slopes are observed for f2/f1 = 1.05 (indicating wave interference). At higher frequencies, a negative slope that progressively becomes steeper (indicating a forward traveling wave that slows down) is observed. For f2/f1 = 1.05 and 1.25, the region dominated by the forward wave starts at frequency f2 below the CF of the location; for f2/f1 = 1.35, this frequency region starts approximately when f2 = CF in the model simulations, although a forward traveling wave is not clearly observed for the frequencies that were measured in the experiment. As in the pure tone response, the phase predicted by the model has a steeper slope when fdp ≈ CF than in the experiment.
Forward and reverse wave components
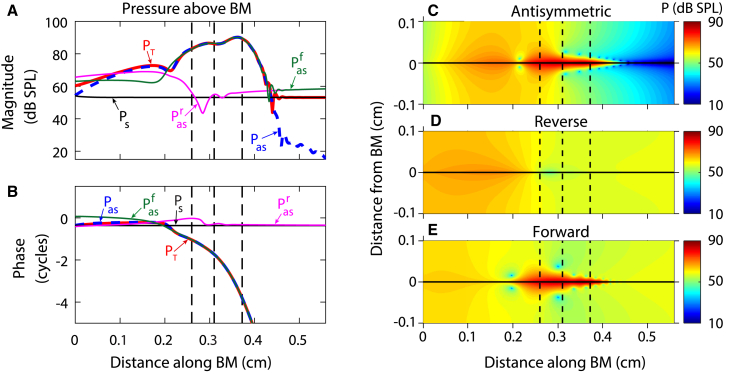
To further analyze DP propagation, the DP fluid pressure was first decomposed into its symmetric and antisymmetric components and then the antisymmetric pressure was decomposed into forward and reverse components. As required by the pressure release boundary condition at the round window, the symmetric pressure equals the antisymmetric pressure at x = 0 (Fig. 7 A); furthermore, the symmetric pressure is nearly constant. As expected, the phase lag of the forward waves increases as it propagates forward whereas the phase lag of the reverse wave increases as it propagates toward the stapes (Fig. 7 B). This confirms that the wave decomposition method is able to separate the total response into forward and reverse wave components. Next to the stapes (at x = 0), the reverse traveling wave is >10 dB higher than the symmetric pressure, implying that emissions are dominated by the slow reverse traveling wave. The decomposition is particularly useful in interpreting the magnitude and phase of the total response. For example, the reverse wave has a higher magnitude than the forward wave basal to x = 0.20 cm in Fig. 7 A; hence, the total response is dominated by the reverse wave at the base and the phase of the total response has a positive slope (Fig. 7 B). Near x = 0.20 cm, both forward and reverse waves have similar magnitudes but phases that differ by nearly half a cycle. This results in wave interference and a minimum in the total and antisymmetric pressure (Fig. 7, A and C). Apical to x = 0.20 cm, the magnitude of the reverse wave decreases and the magnitude of the forward wave matches the total response almost exactly (Fig. 7 A); no reverse traveling waves are expected to be generated near or apical to the DP best place and thus, the response should be dominated by the forward traveling wave. Because the response is dominated by a forward wave, the phase of the total response has a negative slope. Because the DP reverse traveling wave originates basal to the region of amplification, the reverse wave is similar to the pure tone response (if the phase is negated). Furthermore, the phase accumulation of the reverse wave from the generation site to the stapes is very limited because the wavelength of a slow wave (both in the case of a forward or reverse wave) is large at locations basal to the best place.
Figure 7.
Given here is decomposition of the DP pressure for equilevel primaries of 80 dB SPL with f2/f1 = 1.20 and f2 = 24 kHz. (A and B) Magnitude and phase of the total pressure, PT; symmetric pressure, Ps; antisymmetric pressure Pas; forward wave component of the antisymmetric pressure, Pasf; and reverse wave component of the antisymmetric pressure, Pasr are all taken directly above the BM in the SV. (C–E) Magnitude of the antisymmetric pressure (C), reverse wave component of antisymmetric pressure (D), and forward wave component of antisymmetric pressure (E) are shown. The vertical dashed lines indicate, from left to right, the f2, f1, and fDP best places. To see this figure in color, go online.
For the case shown in Fig. 7 B, the phase delay of the forward and reverse waves relative to the position of maximum phase (x = 0.16 cm) can be calculated as
| (12) |
where τϕ is the phase delay, and ϕDP is the phase of the antisymmetric pressure at fDP. The phase delay for the forward wave between x = 0.16 cm and the DP best place (x = 0.37 cm) is 0.22 ms, corresponding to an average phase velocity of ∼9 m/s. The phase delay for the reverse wave between x = 0.16 cm and x = 0 is 0.014 ms, corresponding to an average phase velocity of ∼112 m/s. Thus, the reverse wave propagates back to the base from the generation region ≈12 times faster than the forward wave propagates from the generation region to the DP best place.
Examining the spatial variations of the pressure in x and z (Fig. 7, C–E) yields similar findings to Fig. 7 A. Like the antisymmetric pressure, the forward wave pressure is localized around the BM near the primary and DP best places. The reverse wave appears less localized around the BM and the pressure is nearly 1D because the reverse wave has a maximum amplitude in the long wave region for the DP frequency. Furthermore, the zone of low pressure in the antisymmetric pressure close to the BM at x ≈ 0.22 cm is due to wave interference between the forward and reverse waves. Additional results for the effects of varying the stapes reflection coefficient, Rst, and the primary frequency ratio, f2/f1, on the forward and reverse waves are shown in Figs. S9 and 10 and in Movies S1 and S2. Observation of the reverse wave, in particular, makes it possible to visualize how the DP generated near the f2 best place progressively propagates toward the stapes.
Discussion
Strengths and limitations of this modeling approach
The propagation of DPs is examined in this article using a physiologically based model that is more realistic than in previous theoretical studies (19, 20, 21, 22, 23): our model includes a detailed representation of OHC biophysics, with nonlinear MET channels and linearized somatic electromotility; furthermore, the fluid model is based on a two-duct 3D model. Although 3D cochlear models have previously examined intracochlear fluid mechanics in response to a pure tone (26, 27, 28), intracochlear fluid mechanics is analyzed, to our knowledge, for the first time in response to two-tone stimuli in this work. Note, however, that the fluid is only coupled to the BM in this model. Direct coupling of the ST fluid to the TM, as in some recent models (50, 51, 52), might better represent intracochlear fluid mechanics; however, the coupling considered in this article is simpler to analyze, because decomposition of the pressure into symmetric and antisymmetric components makes it possible to identify the slow and fast waves. To get insight into how DPs propagate, the slow wave component of the fluid pressure was decomposed into forward and reverse waves using the method previously proposed for the decomposition of the BM velocity by de Boer et al. (19).
The model was calibrated such that the gain and sharpness of tuning in response to a pure tone are similar to in vivo measurements of the BM response to sound in the gerbil cochlea (43, 44). Because of the existence of extensive sets of experimental data, models have been previously developed by other researchers for the gerbil cochlea (28, 52). As in some previous studies (28), we found that matching the phase of the model pure tone response to measurements was more challenging than matching the magnitude. Due to the discrepancy between model and experiments in the phase of the pure tone response, the slope of the phase of the DP response when fdp ≈ CF is steeper than in the measurements; furthermore, the magnitude of the DP pressure decays at a faster rate as the location moves away from the BM than in experiments (see Fig. S6, A–C).
Another limitation of this research is that all results are based on a smooth cochlear model. Because of the absence of cochlear roughness, the model only includes the distortion source, i.e., DPOAEs are only generated due to nonlinear distortion in the region where the two primaries interact. However, it is well known that DPOAEs also include a reflection source component that is commonly hypothesized to be generated due to coherent reflection by putative inhomogeneities close to the peak of the DP response (48). The presence of another source of DPOAE would complicate the analysis because more reverse wave components might be expected. The reflection source, which plays a particularly significant role in the case of the 2f2 – f1 DP, will be analyzed in future work.
Analysis of the spatial variations of the DP fluid pressure
In a two-duct model, the response of the fluid pressure is the superposition of a symmetric, fast wave mode and of an antisymmetric, slow wave mode that propagates on the BM due to the fluid/structure interaction between the BM and the fluid. The presence of both modes is predicted both in the case of the pure tone response and of the DP response; furthermore, the main properties of the two modes are the same in the pure tone and DP responses. Because we use a rectangular geometry for the two ducts, the fast compression mode is nearly uniform throughout the cochlear ducts (29) (Figs. 5, 7, and S6). The properties of the slow wave mode depend on the local wavelength of the traveling wave. Close to the stapes, the wavelength is long, such that the pressure is 1D and varies only with longitudinal position with little phase accumulation. As the wave approaches its best place, the wavelength becomes shorter and the wave slows down, resulting in more phase accumulation. In this short wave region, the pressure becomes more 3D and localized around the BM. Both in model simulations and in experiments (11, 33), the fluid pressure in the ST decays exponentially as the measurement location is moved away from the BM when fdp ≈ CF. This is because the symmetric pressure (which is nearly uniform) has a much smaller amplitude than the antisymmetric pressure (Fig. 5). Furthermore, the DP pressure decays at a similar rate as a pure tone pressure of the same frequency (Fig. S6), as observed experimentally (11).
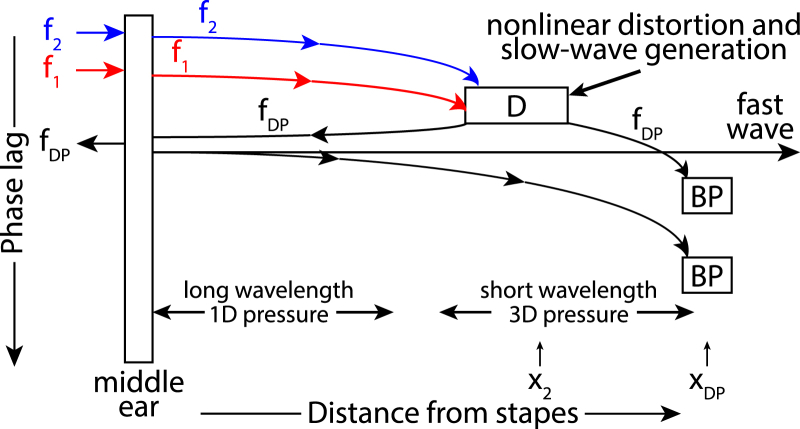
The propagation of DPs can be represented by the schematics of Fig. 8 (which is an extension of Fig. 12 from Shera and Guinan (13)). In response to a two-tone stimulus, the two primaries propagate along the BM. A DP is generated due to nonlinear distortion in the region where the response to both primaries has a sufficiently high amplitude. According to our results, this DP propagates as a slow reverse wave toward the stapes and as a slow forward wave toward the helicotrema. As the forward wave approaches the DP best place, the forward wave is amplified and slows down (such that the wavelength becomes shorter); because of the short wavelength, the pressure is highly 3D and localized to the BM. The reverse wave propagates back to the base with little phase accumulation (because the wavelength is very long basal to the DP generation site); furthermore, because of the long wavelength, the pressure is ∼1D. When this reverse wave reaches the stapes, part of this wave is transmitted by the middle ear (hence, a DPOAE is measured in the ear canal), whereas the other part is reflected by the stapes such that a slow forward traveling wave is generated. Simultaneously satisfying the boundary conditions at the stapes and round window requires the pressure to have a symmetric component, such that a DP fast wave is also generated. The DP fast mode is not directly generated by the OHCs because excitation of the fast wave by OHCs would require them to change volume. The fast wave instantly fills the cochlear ducts (because the fluid is assumed to be incompressible in the model), whereas the slow wave propagates forward with increasing phase accumulation as it approaches its best place.
Figure 8.
Schematics of DP propagation. The figure from (13) was redrawn and extended to include the fast wave, the long wavelength region, and the short wavelength wave region. Note that (D) is the distortion source; (BP) is the DP best place, xDP; and (x2) is the f2 best place. To see this figure in color, go online.
Due to the presence of slow reverse and forward waves, a zone of wave interference is observed in the DP response of the BM velocity and fluid pressure. As found in previous BM DP modeling work (19, 20, 21, 22, 23) and experiments (14, 15, 17, 33), by varying the stimulus parameters, the longitudinal position and the stapes reflectivity affects where and whether the forward or reverse wave dominates. Determining whether DPs propagate as a slow wave or a fast wave using only measurements at a couple of longitudinal locations is particularly challenging, due to the complicated influence of the stimulus parameters (such as the levels or frequency ratio of the primaries) and to the wave interference between the forward and reverse waves.
Conclusions
In this article, a two-duct 3D model with a realistic model of OHC biophysics was used to investigate how DPs vary spatially in the intracochlear fluid pressure. Some similarities with the pressure obtained in response to a pure tone are observed in the DP pressure. At positions at which the wavelength of the traveling wave is short, the DP pressure is 3D whereas it is ∼1D closer to the base where the wavelength is long. Simulations demonstrate the presence of a fast compression wave, and a slow traveling wave that could be decomposed into forward and reverse traveling waves to help clarify DP propagation. At the base (x = 0), the fast compression and slow traveling waves are equal in amplitude, but the reverse traveling wave is substantially larger than the fast compression wave. Thus, emissions are dominated by the slow traveling wave mode.
Author Contributions
J.M. planned the research. T.B. wrote computer codes and performed the numerical simulations. Both authors analyzed the results and wrote the manuscript.
Acknowledgments
This research is funded by National Science Foundation (NSF) grant No. CMMI-1536830 to J.M. and a National Defense Science & Engineering Graduate Fellowship to T.B.
Editor: Daniel Beard.
Footnotes
Supporting Materials and Methods, nine figures, four tables, and two movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)35084-1.
Supporting Citations
References (53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64) appear in the Supporting Material.
Supporting Material
All pressure components are normalized by the maximum total pressure value. Because most of the pressure amplitudes are much smaller than the maximum normalized pressure of 1, the color-bar limits were set to a smaller value (−0.05 to 0.05) to highlight the spatial variations of the pressure. The waveform shows the normalized total pressure at the stapes in the center of the SV.
All pressure components are normalized by the maximum total pressure value. Because most of the pressure amplitudes are much smaller than the maximum normalized pressure of 1, the color-bar limits of the pressure were set to a smaller value (−0.05 to 0.05) to highlight the spatial variations of the pressure. The waveform shows the normalized total pressure at the stapes in the center of the SV.
References
- 1.Robles L., Ruggero M.A. Mechanics of the mammalian cochlea. Physiol. Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ashmore J., Avan P., Canlon B. The remarkable cochlear amplifier. Hear. Res. 2010;266:1–17. doi: 10.1016/j.heares.2010.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kemp D.T. Stimulated acoustic emissions from within the human auditory system. J. Acoust. Soc. Am. 1978;64:1386–1391. doi: 10.1121/1.382104. [DOI] [PubMed] [Google Scholar]
- 4.Lonsbury-Martin B.L., Martin G.K. The clinical utility of distortion-product otoacoustic emissions. Ear Hear. 1990;11:144–154. doi: 10.1097/00003446-199004000-00009. [DOI] [PubMed] [Google Scholar]
- 5.Shera C.A., Guinan J.J., Jr., Oxenham A.J. Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements. Proc. Natl. Acad. Sci. USA. 2002;99:3318–3323. doi: 10.1073/pnas.032675099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kemp D.T. Otoacoustic emissions, their origin in cochlear function, and use. Br. Med. Bull. 2002;63:223–241. doi: 10.1093/bmb/63.1.223. [DOI] [PubMed] [Google Scholar]
- 7.Kemp D.T. Otoacoustic emissions, travelling waves and cochlear mechanisms. Hear. Res. 1986;22:95–104. doi: 10.1016/0378-5955(86)90087-0. [DOI] [PubMed] [Google Scholar]
- 8.Robles L., Ruggero M.A., Rich N.C. Two-tone distortion in the basilar membrane of the cochlea. Nature. 1991;349:413–414. doi: 10.1038/349413a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Robles L., Ruggero M.A., Rich N.C. Two-tone distortion on the basilar membrane of the chinchilla cochlea. J. Neurophysiol. 1997;77:2385–2399. doi: 10.1152/jn.1997.77.5.2385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cooper N.P., Rhode W.S. Mechanical responses to two-tone distortion products in the apical and basal turns of the mammalian cochlea. J. Neurophysiol. 1997;78:261–270. doi: 10.1152/jn.1997.78.1.261. [DOI] [PubMed] [Google Scholar]
- 11.Dong W., Olson E.S. Two-tone distortion in intracochlear pressure. J. Acoust. Soc. Am. 2005;117:2999–3015. doi: 10.1121/1.1880812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fettiplace R., Hackney C.M. The sensory and motor roles of auditory hair cells. Nat. Rev. Neurosci. 2006;7:19–29. doi: 10.1038/nrn1828. [DOI] [PubMed] [Google Scholar]
- 13.Shera C.A., Guinan J.J., Jr. Evoked otoacoustic emissions arise by two fundamentally different mechanisms: a taxonomy for mammalian OAEs. J. Acoust. Soc. Am. 1999;105:782–798. doi: 10.1121/1.426948. [DOI] [PubMed] [Google Scholar]
- 14.Ren T. Reverse propagation of sound in the gerbil cochlea. Nat. Neurosci. 2004;7:333–334. doi: 10.1038/nn1216. [DOI] [PubMed] [Google Scholar]
- 15.He W., Fridberger A., Ren T. Reverse wave propagation in the cochlea. Proc. Natl. Acad. Sci. USA. 2008;105:2729–2733. doi: 10.1073/pnas.0708103105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.de Boer E., Kaernbach C., Schillen T. Forward and reverse waves in the one-dimensional model of the cochlea. Hear. Res. 1986;23:1–7. doi: 10.1016/0378-5955(86)90171-1. [DOI] [PubMed] [Google Scholar]
- 17.He W., Fridberger A., Ren T. Fast reverse propagation of sound in the living cochlea. Biophys. J. 2010;98:2497–2505. doi: 10.1016/j.bpj.2010.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shera C.A., Tubis A., Talmadge C.L. Auditory Mechanisms: Processes and Models. World Scientific; Singapore: 2006. Four counter-arguments for slow-wave OAEs; pp. 449–457. [Google Scholar]
- 19.de Boer E., Nuttall A.L., Shera C.A. Wave propagation patterns in a “classical” three-dimensional model of the cochlea. J. Acoust. Soc. Am. 2007;121:352–362. doi: 10.1121/1.2385068. [DOI] [PubMed] [Google Scholar]
- 20.Zhang X., Mountain D.C. Distortion product emissions: where do they come from? In: Cooper N.P., Kemp D.T., editors. Concepts and Challenges in the Biophysics of Hearing: Proceedings of 10th International Workshop on the Mechanics of Hearing. World Scientific Publishing; Singapore: 2009. pp. 48–54. [Google Scholar]
- 21.Sisto R., Moleti A., Shera C.A. Distortion products and backward-traveling waves in nonlinear active models of the cochlea. J. Acoust. Soc. Am. 2011;129:3141–3152. doi: 10.1121/1.3569700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Young J.A., Elliott S.J., Lineton B. Investigating the wave-fixed and place-fixed origins of the 2f1−f2 distortion product otoacoustic emission within a micromechanical cochlear model. J. Acoust. Soc. Am. 2012;131:4699–4709. doi: 10.1121/1.4707447. [DOI] [PubMed] [Google Scholar]
- 23.Vetešník A., Gummer A.W. Transmission of cochlear distortion products as slow waves: a comparison of experimental and model data. J. Acoust. Soc. Am. 2012;131:3914–3934. doi: 10.1121/1.3699207. [DOI] [PubMed] [Google Scholar]
- 24.de Boer E., Zheng J., Nuttall A.L. Inverted direction of wave propagation (IDWP) in the cochlea. J. Acoust. Soc. Am. 2008;123:1513–1521. doi: 10.1121/1.2828064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dong W., Olson E.S. Supporting evidence for reverse cochlear traveling waves. J. Acoust. Soc. Am. 2008;123:222–240. doi: 10.1121/1.2816566. [DOI] [PubMed] [Google Scholar]
- 26.Peterson L.C., Bogert B.P. A dynamical theory of the cochlea. J. Acoust. Soc. Am. 1950;22:369–381. [Google Scholar]
- 27.Steele C.R., Taber L.A. Comparison of WKB calculations and experimental results for three-dimensional cochlear models. J. Acoust. Soc. Am. 1979;65:1007–1018. doi: 10.1121/1.382570. [DOI] [PubMed] [Google Scholar]
- 28.Yoon Y.J., Puria S., Steele C.R. Intracochlear pressure and derived quantities from a three-dimensional model. J. Acoust. Soc. Am. 2007;122:952–966. doi: 10.1121/1.2747162. [DOI] [PubMed] [Google Scholar]
- 29.de Boer E. The Cochlea. Springer; Berlin, Germany: 1996. Mechanics of the cochlea: modeling efforts; pp. 258–317. [Google Scholar]
- 30.Olson E.S. Observing middle and inner ear mechanics with novel intracochlear pressure sensors. J. Acoust. Soc. Am. 1998;103:3445–3463. doi: 10.1121/1.423083. [DOI] [PubMed] [Google Scholar]
- 31.Olson E.S. Direct measurement of intra-cochlear pressure waves. Nature. 1999;402:526–529. doi: 10.1038/990092. [DOI] [PubMed] [Google Scholar]
- 32.Olson E.S. Intracochlear pressure measurements related to cochlear tuning. J. Acoust. Soc. Am. 2001;110:349–367. doi: 10.1121/1.1369098. [DOI] [PubMed] [Google Scholar]
- 33.Dong W. Simultaneous intracochlear pressure measurements from two cochlear locations: propagation of distortion products in gerbil. J. Assoc. Res. Otolaryngol. 2017;18:209–225. doi: 10.1007/s10162-016-0602-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kale S.S., Olson E.S. Intracochlear scala media pressure measurement: implications for models of cochlear mechanics. Biophys. J. 2015;109:2678–2688. doi: 10.1016/j.bpj.2015.10.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Meaud J., Grosh K. Response to a pure tone in a nonlinear mechanical-electrical-acoustical model of the cochlea. Biophys. J. 2012;102:1237–1246. doi: 10.1016/j.bpj.2012.02.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Meaud J., Grosh K. Effect of the attachment of the tectorial membrane on cochlear micromechanics and two-tone suppression. Biophys. J. 2014;106:1398–1405. doi: 10.1016/j.bpj.2014.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Meaud J., Lemons C. Nonlinear response to a click in a time-domain model of the mammalian ear. J. Acoust. Soc. Am. 2015;138:193–207. doi: 10.1121/1.4921282. [DOI] [PubMed] [Google Scholar]
- 38.Ramamoorthy S., Deo N.V., Grosh K. A mechano-electro-acoustical model for the cochlea: response to acoustic stimuli. J. Acoust. Soc. Am. 2007;121:2758–2773. doi: 10.1121/1.2713725. [DOI] [PubMed] [Google Scholar]
- 39.Meaud J., Grosh K. The effect of tectorial membrane and basilar membrane longitudinal coupling in cochlear mechanics. J. Acoust. Soc. Am. 2010;127:1411–1421. doi: 10.1121/1.3290995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Parthasarathi A.A., Grosh K., Nuttall A.L. Three-dimensional numerical modeling for global cochlear dynamics. J. Acoust. Soc. Am. 2000;107:474–485. doi: 10.1121/1.428352. [DOI] [PubMed] [Google Scholar]
- 41.Edge R.M., Evans B.N., Dallos P. Morphology of the unfixed cochlea. Hear. Res. 1998;124:1–16. doi: 10.1016/s0378-5955(98)00090-2. [DOI] [PubMed] [Google Scholar]
- 42.Richter C.-P., Emadi G., Dallos P. Tectorial membrane stiffness gradients. Biophys. J. 2007;93:2265–2276. doi: 10.1529/biophysj.106.094474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ren T., Nuttall A.L. Basilar membrane vibration in the basal turn of the sensitive gerbil cochlea. Hear. Res. 2001;151:48–60. doi: 10.1016/s0378-5955(00)00211-2. [DOI] [PubMed] [Google Scholar]
- 44.Overstreet E.H., 3rd, Temchin A.N., Ruggero M.A. Basilar membrane vibrations near the round window of the gerbil cochlea. J. Assoc. Res. Otolaryngol. 2002;3:351–361. doi: 10.1007/s101620020023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dong W., Olson E.S. Detection of cochlear amplification and its activation. Biophys. J. 2013;105:1067–1078. doi: 10.1016/j.bpj.2013.06.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dong W., Olson E.S. Middle ear forward and reverse transmission in gerbil. J. Neurophysiol. 2006;95:2951–2961. doi: 10.1152/jn.01214.2005. [DOI] [PubMed] [Google Scholar]
- 47.Elliott S.J., Ku E.M., Lineton B. A state space model for cochlear mechanics. J. Acoust. Soc. Am. 2007;122:2759–2771. doi: 10.1121/1.2783125. [DOI] [PubMed] [Google Scholar]
- 48.Kalluri R., Shera C.A. Distortion-product source unmixing: a test of the two-mechanism model for DPOAE generation. J. Acoust. Soc. Am. 2001;109:622–637. doi: 10.1121/1.1334597. [DOI] [PubMed] [Google Scholar]
- 49.Wang Y., Steele C.R., Puria S. Cochlear outer-hair-cell power generation and viscous fluid loss. Sci. Rep. 2016;6:19475. doi: 10.1038/srep19475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lamb J.S., Chadwick R.S. Dual traveling waves in an inner ear model with two degrees of freedom. Phys. Rev. Lett. 2011;107:088101. doi: 10.1103/PhysRevLett.107.088101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cormack J., Liu Y., Gracewski S.M. Two-compartment passive frequency domain cochlea model allowing independent fluid coupling to the tectorial and basilar membranes. J. Acoust. Soc. Am. 2015;137:1117–1125. doi: 10.1121/1.4908214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Liu Y., Gracewski S.M., Nam J.H. Consequences of location-dependent organ of Corti micro-mechanics. PLoS One. 2015;10:e0133284. doi: 10.1371/journal.pone.0133284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fernández C. Dimensions of the cochlea (guinea pig) J. Acoust. Soc. Am. 1952;24:519–523. [Google Scholar]
- 54.Richter C.-P., Edge R., Dallos P. Development of the gerbil inner ear observed in the hemicochlea. J. Assoc. Res. Otolaryngol. 2000;1:195–210. doi: 10.1007/s101620010019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ghaffari R., Aranyosi A.J., Freeman D.M. Longitudinally propagating traveling waves of the mammalian tectorial membrane. Proc. Natl. Acad. Sci. USA. 2007;104:16510–16515. doi: 10.1073/pnas.0703665104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Puria S. Measurements of human middle ear forward and reverse acoustics: implications for otoacoustic emissions. J. Acoust. Soc. Am. 2003;113:2773–2789. doi: 10.1121/1.1564018. [DOI] [PubMed] [Google Scholar]
- 57.Shera C.A., Zweig G. Reflection of retrograde waves within the cochlea and at the stapes. J. Acoust. Soc. Am. 1991;89:1290–1305. doi: 10.1121/1.400654. [DOI] [PubMed] [Google Scholar]
- 58.de la Rochefoucauld O., Decraemer W.F., Olson E.S. Simultaneous measurements of ossicular velocity and intracochlear pressure leading to the cochlear input impedance in gerbil. J. Assoc. Res. Otolaryngol. 2008;9:161–177. doi: 10.1007/s10162-008-0115-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Overstreet E.H., 3rd, Ruggero M.A. Development of wide-band middle ear transmission in the Mongolian gerbil. J. Acoust. Soc. Am. 2002;111:261–270. doi: 10.1121/1.1420382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Johnson S.L., Beurg M., Fettiplace R. Prestin-driven cochlear amplification is not limited by the outer hair cell membrane time constant. Neuron. 2011;70:1143–1154. doi: 10.1016/j.neuron.2011.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Iwasa K.H., Adachi M. Force generation in the outer hair cell of the cochlea. Biophys. J. 1997;73:546–555. doi: 10.1016/S0006-3495(97)78092-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Dallos P., Evans B.N. High-frequency motility of outer hair cells and the cochlear amplifier. Science. 1995;267:2006–2009. doi: 10.1126/science.7701325. [DOI] [PubMed] [Google Scholar]
- 63.Strelioff D. A computer simulation of the generation and distribution of cochlear potentials. J. Acoust. Soc. Am. 1973;54:620–629. doi: 10.1121/1.1913642. [DOI] [PubMed] [Google Scholar]
- 64.Greenwood D.D. A cochlear frequency-position function for several species—29 years later. J. Acoust. Soc. Am. 1990;87:2592–2605. doi: 10.1121/1.399052. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
All pressure components are normalized by the maximum total pressure value. Because most of the pressure amplitudes are much smaller than the maximum normalized pressure of 1, the color-bar limits were set to a smaller value (−0.05 to 0.05) to highlight the spatial variations of the pressure. The waveform shows the normalized total pressure at the stapes in the center of the SV.
All pressure components are normalized by the maximum total pressure value. Because most of the pressure amplitudes are much smaller than the maximum normalized pressure of 1, the color-bar limits of the pressure were set to a smaller value (−0.05 to 0.05) to highlight the spatial variations of the pressure. The waveform shows the normalized total pressure at the stapes in the center of the SV.