Homeostatic cell growth is accomplished mechanically through membrane tension-inhibition of cell wall synthesis

Summary

Feedback mechanisms are required to coordinate balanced synthesis of subcellular components during cell growth. However, these coordination mechanisms are not apparent at steady state. Here, we elucidate the interdependence of cell growth, membrane tension, and cell-wall synthesis by observing their rapid re-coordination after osmotic shocks in Gram-positive bacteria. Single-cell experiments and mathematical modeling demonstrate that mechanical forces dually regulate cell growth: while turgor pressure produces mechanical stress within the cell wall that promotes its expansion through wall synthesis, membrane tension induces growth arrest by inhibiting wall synthesis. Tension-inhibition occurs concurrently with membrane depolarization, and depolarization arrested growth independently of shock, indicating that electrical signals implement the negative feedback characteristic of homeostasis. Thus, competing influences of membrane tension and cell-wall mechanical stress on growth allow cells to rapidly correct for mismatches between membrane and wall synthesis rates, ensuring balanced growth.

eTOC blurb

Rojas et al. discover an elegant feedback mechanism ensuring balanced membrane and cell-wall growth in the bacterium Bacillus subtilis through mechanically induced electrical depolarization that transiently halts wall synthesis.

Introduction

Bacterial cell growth is a complex process in which synthesis and uptake of all cytoplasmic and cell-surface components must be coordinated with increases in cell size. Many bacteria can double their volume rapidly, in as little as six minutes (Labbe and Huang, 1995), providing them a competitive advantage in nutrient-rich environments and highlighting the need for exquisite feedback between the biochemical syntheses of cellular components and the biophysical mechanisms of cell growth. While biosynthetic pathways have been well characterized, little is known about how they are coordinated with one another or with physical growth of the cell.

Cell volume and surface area in bacteria are defined by the size and shape of the cell envelope, including the membrane(s) and the cell wall. The envelope is inflated by turgor pressure, the intracellular hydrostatic pressure that results from the concentration differential across the membrane, which is balanced by mechanical stress in the cell wall. Therefore, the expansion of the cell wall is the ultimate process that determines the rate of cell growth. Some requirements for cell-wall expansion are known. Since the peptidoglycan cell wall is a single, covalently linked macromolecule, hydrolysis of this material is essential for cell wall expansion. Accordingly, many of the relevant hydrolases have been identified (Hashimoto et al., 2012; Singh et al., 2012). New peptidoglycan must also be synthesized as the area of the cell surface increases. Plant cells, which possess relatively thick walls (≥100 nm; (Albersheim et al., 2010)), additionally require turgor pressure to drive proportional mechanical expansion of their walls during cell growth, producing an increase in surface area (Green, 1968; Proseus et al., 2000). In contrast, we recently showed that turgor pressure is less important for cell-wall expansion in the Gram-negative bacterium Escherichia coli (Rojas et al., 2014), whose cell wall is thin (≈ 3 nm; (Gan et al., 2008)). Whether turgor pressure is important for wall expansion in Gram-positive bacteria is unknown, but these organisms possess a thicker cell wall (Misra et al., 2013) and are believed to maintain a higher turgor pressure (Whatmore and Reed, 1990) than Gram-negative bacteria (Cayley et al., 2000; Deng et al., 2011). These differences suggest the possibility wall thickness, turgor pressure, and the strategy for cell wall expansion (pressure-driven vs. non-pressure-driven) co-evolved across the tree of life.

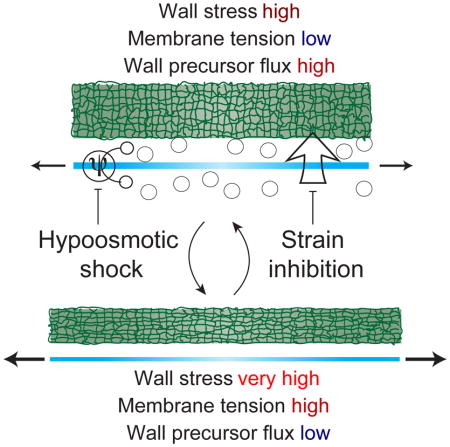
In the current study, we applied osmotic shock, which simultaneously perturbs turgor pressure and cell size, to Bacillus subtilis and other Gram-positive bacteria in order to probe the interdependence of peptidoglycan synthesis, turgor pressure, and cell growth. After rapid swelling in response to acute hypoosmotic shock, B. subtilis cells displayed a transient period of slow or arrested growth. Through a combination of experiments and mathematical modeling, we discovered that this growth inhibition results from negative feedback between cell volume enlargement and peptidoglycan synthesis, which is mediated by mechanical tension in the plasma membrane. We also found that growth is slowed by hyperosmotic shock, and that this reduction was larger than what would be expected from the effect of osmolarity alone, pointing to a role for turgor pressure as an important factor required for cell-wall expansion. These results elucidate an intriguing control system by which turgor-induced forces within the cell regulate cell growth in two complementary ways: membrane tension inhibits cell wall expansion by interfering with peptidoglycan synthesis, while mechanical stress within the cell wall promotes its irreversible expansion. This system dictates that growth can occur only when membrane tension and cell-wall stress are in optimal ranges, ensuring balanced syntheses of the membrane and cell wall.

Results

During growth in lysogeny broth (LB), B. subtilis JH642 (Brehm et al., 1973) cells form long (~5–50 μm) chains (Figures 1A and 1B). Under favorable, chemostatic conditions, cells elongate exponentially (Wang et al., 2010), and it is therefore useful to define the relative rate of elongation, ė = (dl/dt)/l, where l is the axial length of the chain. This empirical quantity is able to describe both reversible elongation of the cells (when the cytoplasm acquires water and the cell wall stretches elastically) and irreversible elongation (when water uptake is accompanied by synthesis, hydrolysis, and/or reorganization of the cell wall). While changes in turgor pressure result in reversible elongation, irreversible elongation occurs during steady-state growth. Note that in this study, we assume that steady-state growth reflects constant turgor pressure and balanced coordination between synthesis of the cell wall and membrane, and that if two steady states are quantitatively identical, these parameters are also the same between the two growth environments. For example, if ė is the same when the cell is growing at steady-state in LB or LB+500 mM sorbitol, we conclude that parameters reflecting cell envelope synthesis and turgor pressure are the same in both conditions.

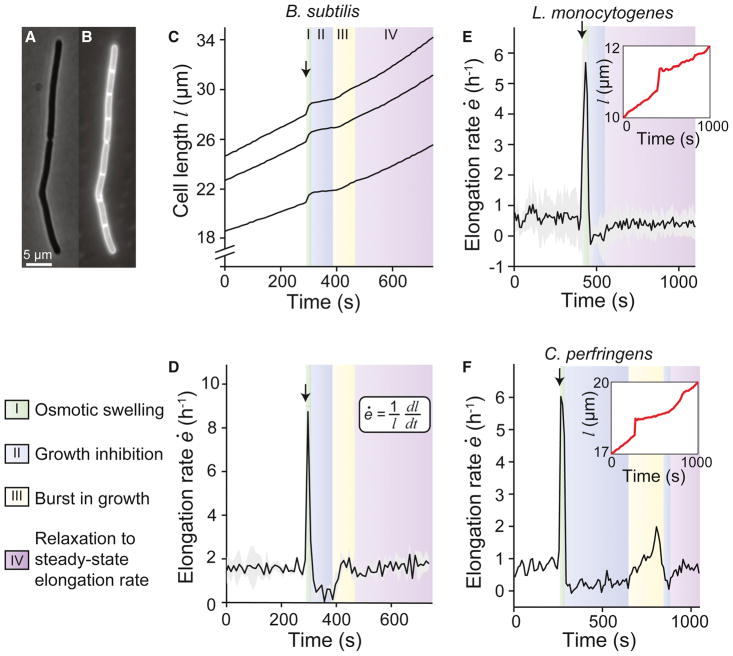
Figure 1. B. subtilis cells exhibit growth inhibition after hypoosmotic shock.

(A) Phase contrast micrograph of a chain of B. subtilis cells. (B) Fluorescence micrograph of the same chain showing the membrane stained with FM 4–64. (C) Length of three B. subtilis chains during an 800-mM hypoosmotic shock (from LB+1 M sorbitol to LB+0.2 M sorbitol; n = 3). Arrow indicates the time of shock. (D) Population-averaged elongation rate of B. subtilis chains during the same shock. Arrow indicates the time of shock. Shading indicates ±1 standard deviation (s.d.). (E) Population-averaged elongation rate of L. monocytogenes cells during an 800-mM hypoosmotic shock (from BHI+800 mM sorbitol to BHI; n = 107). (inset) Length of a representative cell during the shock. (F) Elongation rate of a C. perfringens cell-chain during a 1-M hypoosmotic shock (from RCM + 1 M sorbitol to RCM; n = 1). (inset) Length of the cell during the shock. See also Figure S1.

Hypoosmotic shock inhibits cell elongation

To probe the feedback mechanisms that control cell growth in B. subtilis, we subjected cells to hypoosmotic shock and examined subsequent cell elongation using time-lapse microscopy (Movie S1; STAR Methods). To perform hypoosmotic shocks, we used a microfluidic flow cell to culture cells to steady-state growth in high-osmolarity LB (by supplementing it with sorbitol) and then rapidly exchanged the medium with lower-osmolarity LB. There were four characteristic phases of the elongation rate following hypoosmotic shock. As expected, during the shock cells swelled due to the acute increase in turgor pressure, which corresponded to a sharp peak in elongation rate (Phase I; Figures 1C and 1D). Immediately after shock, cells exhibited a period of slow or arrested elongation (Phase II). Cells then exhibited a second, smaller, burst of elongation (Phase III) before relaxing to an elongation rate that approximately equaled the pre-shock rate (Phase IV). We tested the generality of this phenomenon by examining the response of other bacterial species to hypoosmotic shock. The Gram-positive, rod-shaped organisms Listeria monocytogenes and Clostridium perfringens both displayed swelling and subsequent growth inhibition (Figures 1E and 1F). Whereas L. monocytogenes did not undergo a second burst of elongation (Figure 1E), C. perfringens exhibited both a second burst of elongation and a second period of growth inhibition before relaxing to a steady elongation rate (Figure 1F). For Gram-negative E. coli, we did not observe growth inhibition in response to hypoosmotic shock (Figure S1).

Building a quantitative understanding of the cellular response to osmotic shock

To begin to distinguish between the many classes of mechanism that could underlie the four phases we observe, we examined the dependence of the B. subtilis response on hypoosmotic shock magnitude, starting from either LB+1 M or LB+1.5 M sorbitol. First, we quantified the extent of swelling during Phase I by calculating the mechanical strain acquired during this period, ε_l = (l_f − l_i)/l_i, where l_i and l_f are the lengths of cell chains at the beginning and end of swelling, respectively (Figure 2A). Mechanical strain was approximately proportional to shock magnitude (Figure 2B), demonstrating that cells behave analogously to linear springs during this phase of the response. The y-intercept of the linear fit to these data is non-zero because, at a shock magnitude of zero, cells still elongate during the ≈ 20 s in which medium is exchanged. The minimum elongation rate during the period of growth inhibition, ė_min (Figure 2A), approached zero as shock magnitude was increased (Figure 2C); that is, cells did not shrink substantially during Phase II of the response for any shock magnitude. Finally, the inhibition period, τ, defined as the time between the first and second peaks in elongation rate (Figure 2A), was approximately proportional to the shock magnitude, with a minimum value of ≈ 80 s for small shocks (Figure 2D). Together, these three scaling relationships constitute a strong constraint for any model of growth inhibition.

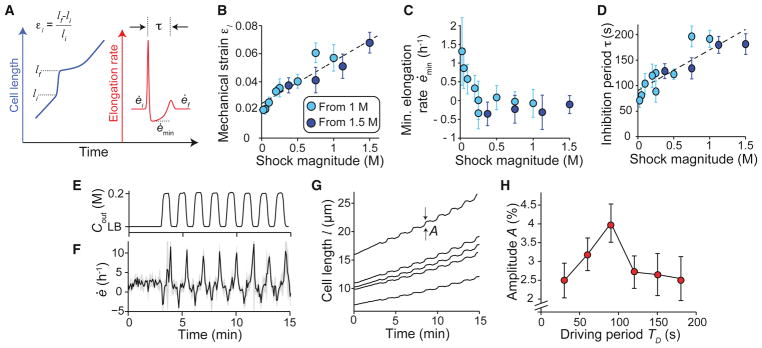
Figure 2. Mechanical strain and inhibition period scale with the magnitude of hypoosmotic shock.

(A) Schematic of key variables defining the response to hypoosmotic shock. (B) Mechanical strain induced by hypoosmotic shock scales linearly with shock magnitude. Two series of experiments from different initial sorbitol concentrations are overlaid. The dotted line is a linear best fit to the combined data set. Error bars indicate ± 1 s.d. (C) Minimum elongation rate during growth inhibition decreases to a plateau of approximately zero with increasing shock magnitude. Error bars indicate ± 1 s.d. Each data point is the average over 2–50 cell chains. (D) Inhibition period scales linearly with shock magnitude. The dotted line is a linear best fit of the combined data set. Error bars indicate ± 1 s.d. Each data point is the average over 2–50 cell chains. (E) Medium osmolarity during a 200-mM oscillatory osmotic shock with 90-s period. (F) Population-averaged elongation rate of B. subtilis cell-chains during oscillatory shock (n = 31). Shading indicates ± 1 s.d. (G) Length trajectories of five cell chains during oscillatory shock, where A is the amplitude of length oscillations. (H) Amplitude of length oscillations peaks at a ≈ 90-s driving period for 200-mM oscillatory osmotic shocks. Error bars indicate ± 1 s.d. Each data point is the average over 6–67 cell chains. See also Figure S2.

The response of elongation rate to hypoosmotic shock was qualitatively similar to a ringing response in physics (a damped oscillation of an output signal in response to a sudden change in an input signal) with a period of oscillation equal to the inhibition period, τ. Accordingly, we asked whether we could drive resonance of this system, a key feature of a ringing response. We subjected B. subtilis cell-chains to 200-mM oscillatory osmotic shocks (Figures 2E and 2F, Movie S2) and measured the amplitude of the resulting oscillations in length (Figure 2G) as a function of the driving period of the oscillations, T_d. Amplitude was maximized at T_d ≈ 90 s (Figure 2H), which is close to the inhibition period for this shock magnitude (Figure 2D). Taken together, these observations support the notion that the B. subtilis growth is driven by a regulatory network that exhibits damped oscillations in response to a hypoosmotic shock.

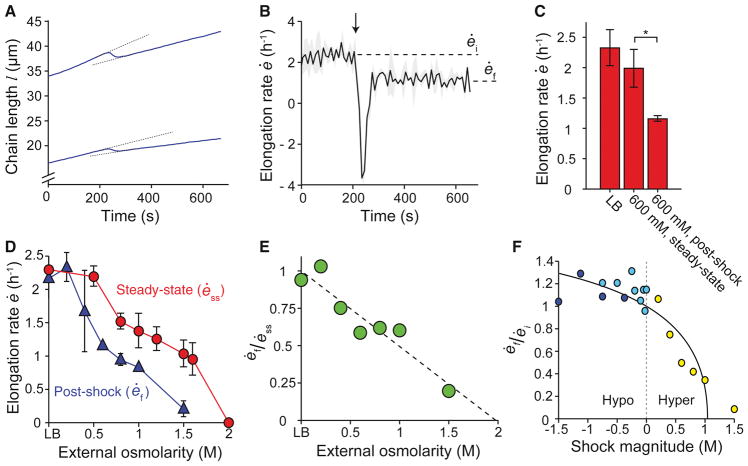
Having defined a basic framework for understanding the hypoosmotic shock response, we next examined the B. subtilis response to hyperosmotic shock (Movie S3). As expected, when subjected to hyperosmotic shock, B. subtilis cells acutely shrank (Figure 3A). After this shrinking, cells resumed elongation at a rate lower than the pre-shock rate (Figures 3B and 3C). As we previously observed with E. coli (Rojas et al., 2014), the steady-state elongation rate of B. subtilis cells decreased as medium osmolarity increased (Figure 3D). Therefore, the reduction in elongation rate we observed after hyperosmotic shock could result from a change in turgor pressure, from a pressure-independent effect of medium osmolarity, or from both. The elongation rate after hyperosmotic shock was less than the steady-state elongation rate in the more concentrated medium (Figures 3C and 3D), indicating that hyperosmotic shock reduced the elongation rate more than would be expected due to the effect of medium osmolarity alone. The degree to which post-shock elongation rate was reduced below steady-state elongation rate was approximately proportional to shock magnitude (Figure 3E). These observations are in sharp contrast to the behavior of E. coli cells, which elongate at a rate faster than their steady-state elongation rate immediately after hyperosmotic shock (Rojas et al., 2014). The effect that osmotic shock has on elongation rate can also be quantified by the ratio of post- to pre-shock elongation rate (Figures 2A and 3B): across a range of shock magnitudes, hyperosmotic shock caused a reduction in elongation rate in a shock-magnitude dependent manner and hypoosmotic shock caused, after transient growth-inhibition, a modest increase in elongation rate that was not strongly dependent on shock magnitude (Figure 3F). These data suggest that the B. subtilis elongation rate depends on turgor pressure in addition to medium osmolarity.

Figure 3. B. subtilis elongation rate is reduced by hyperosmotic shock.

(A,B) Response of cell length (A) and population-averaged elongation rate (B) of B. subtilis chains to hyperosmotic shock, from LB to LB + 600 mM sorbitol (n = 2). Arrows indicate the time of shock. Dotted lines in (A) illustrate that elongation rate after the shock (ė_f) is lower than the steady-state elongation rate before the shock (ė_i). Shading indicates ±1 s.d. (C) Comparison of the population-averaged steady-state elongation rate in LB (n = 6), the steady-state elongation rate in LB + 600 mM sorbitol (n = 4), and the elongation rate after a hyperosmotic shock from LB to LB + 600 mM sorbitol (n = 3). Error bars are 1 s.d. *: Student’s t-test, modified for small n, p < 0.05 (Methods). (D) Population-averaged elongation rate of B. subtilis cell chains at steady state and immediately after hyperosmotic shock from LB versus sorbitol concentration. (E) Ratio between the post-hyperosmotic shock elongation rate and steady-state elongation rate decreases linearly with increasing medium osmolarity. The dotted line is a linear best fit. (F) The ratio of post-shock to pre-shock elongation rate as a function of shock magnitude for hypoosmotic shocks from LB + 1 M sorbitol (dark blue circles), hypoosmotic shocks from LB + 1.5 M sorbitol (light blue circles), and hyperosmotic shocks from LB (yellow circles). The solid line is the prediction of the tension-inhibition model.

A tension-inhibition model predicts the experimental scaling relationships

To probe other factors besides turgor pressure that regulate cell expansion, we returned to our hypoosmotic shock response data (Figure 2B–2D). To understand the origins of hypoosmotic shock-induced growth inhibition and subsequent dynamics, we explored three possible mathematical models of Bacillus subtilis elongation that relied on distinct mechanisms of growth regulation (Figure 4A). These models were developed specifically because of their potential to yield damped oscillations and hence growth inhibition; they intentionally exhibit similar qualitative behaviors but differ in their quantitative response across a range of shock magnitudes.

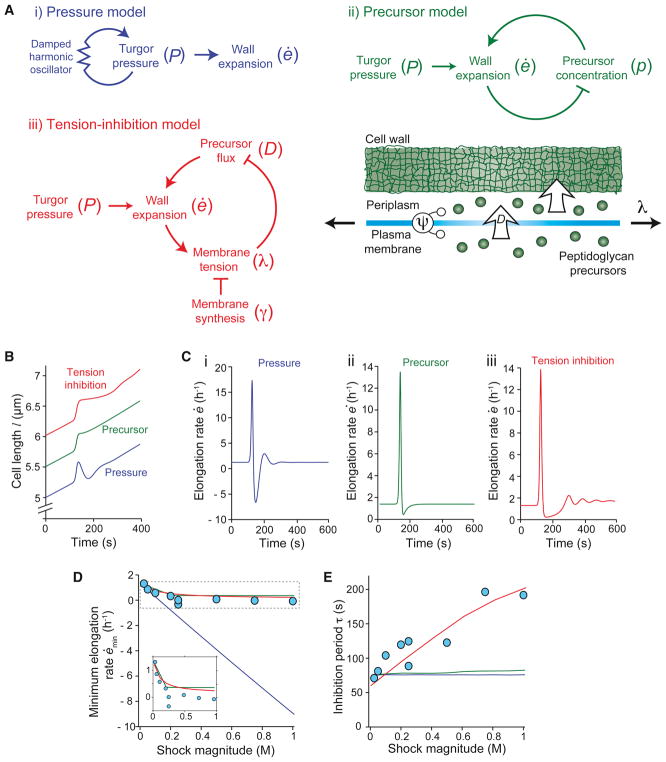
Figure 4. The tension-inhibition model predicts scaling relationships related to growth inhibition.

(A) Schematic of i) the pressure model; ii) the precursor model; and iii) the tension-inhibition model. See main text for definition of variables. (B) Simulated lengths of B. subtilis cells according to the pressure, precursor, and tension-inhibition models in response to a 750-mM hypoosmotic shock. (C) Elongation rate of B. subtilis cells corresponding to the simulated length trajectories in (B) displays an interval of growth inhibition after hypoosmotic shock for all three models. (D) Best fit of experimental measurements of minimum elongation rate versus shock magnitude by the three models shows that the pressure model is not consistent with experimental measurements. See Supplemental Information for fitting strategies. Inset: zoom-in on the dotted box. (E) Best fit of inhibition period versus shock magnitude by the three models shows that the pressure and precursor depletion models are not consistent with experimental measurements. See also Figure S4.

Each model that we investigated is derived and explained in detail in the Supplemental Information. First, in the pressure model, both the apparent growth inhibition and the secondary burst in elongation rate result from underlying oscillations in turgor pressure (Figure 4Ai). The negative feedback that is characteristic of oscillations is provided by the spring-like restoring force of the pressure model −α(P − P₀), where P − P₀ is the difference in turgor pressure P relative to its steady-state value P₀ (STAR Methods). Second, in the precursor model, growth inhibition is caused by depletion of peptidoglycan precursors, which occurs during a rapid burst of elongation in response to hypoosmotic shock (Figure 4Aii). Third, in the tension-inhibition model, growth inhibition occurs when high mechanical tension in the plasma membrane inhibits peptidoglycan synthesis (Figure 4Aiii). Because growth was inhibited within seconds upon hypoosmotic shock (Figure 1C), we did not include transcription-mediated feedback as a possible mechanism. This conjecture is further supported by the observation that B. subtilis cells lacking the sigma factor σ_w, which is responsible for the transcriptional response during osmotic stress (Cao et al., 2002), exhibited a growth-inhibition response similar to that of wild-type cells (Figure S2). For each model considered, we performed parameter-space searches to determine values that explain growth inhibition qualitatively and, more importantly, to fit the stringent scaling relationships between shock magnitude, mechanical strain, inhibition period, and minimum elongation rate (Figures 2B–D; see STAR Methods for fitting strategy and parameter-space search bounds). Because these models reflect different underlying biology, interrogating them allowed us to identify experiments that either demonstrate their unique experimental validity or render them invalid.

The pressure model asserts that the mechanisms of osmoregulation in B. subtilis yield damped oscillations of turgor pressure in response to hypoosmotic shock, and that growth inhibition appears to occur during a period when turgor pressure is being lowered, thereby offsetting elongation with osmotic shrinking (Figure 4Ai). To formulate this idea, we modeled the osmoregulatory system as a damped harmonic oscillator, P̈ = −α(P − P₀) − βṖ, where P₀ is the constant steady-state turgor pressure and α and β are constants (the model has three free parameters: α, β, and E, the Young’s modulus of the cell wall). While this model by design generates damped oscillations in elongation rate (Figures 4B and 4C) qualitatively similar to our experimental measurements, there are several lines of evidence against it stemming from the quantitative scaling relationships we have measured (Figures 2B–2D). First, the pressure model incorrectly predicts that, for moderate shocks, the cells should undergo a phase of shrinking after the initial swelling (Figures 4B and 4C), which we do not observe experimentally (Figures 1C and 2C). Similarly, independent of model parameters, it predicts a linear scaling between the minimum elongation rate and shock magnitude (Figure 4D), in contrast to our experimental data (Figure 2C). It also predicts that elongation-rate oscillations should result from both hypo- and hyperosmotic shocks of the same magnitude, but we did not observe oscillations in response to hyperosmotic shock (Figure 3A). Further, in this model, the inhibition period is independent of shock magnitude (regardless of model parameters), whereas the experimental scaling is approximately linear (Figure 4E). Most importantly, the pressure model predicts that a mutant strain of B. subtilis that lacks its full complement of stretch-activated ion channels (SMB80), which are thought to down-regulate turgor pressure upon hypoosmotic shock (Hoffmann et al., 2008), should exhibit reduced growth inhibition. We observed the opposite: cells without stretch-activated ion channels exhibited stronger growth inhibition upon hypoosmotic shock (Figure S3A and S3B).

The precursor model relies on the premise that the rapid expansion of the cell wall during hypoosmotic shock depletes the pool of peptidoglycan precursors (that is, that precursor synthesis not only causes wall expansion, but wall expansion also sequesters precursors), causing a subsequent period of reduced growth (Figures 4B and 4C); we assumed that these precursors are replenished at a constant rate by biosynthesis (this model has two free parameters, see STAR Methods). This model gives favorable scaling between the minimum elongation rate and shock magnitude because beyond a critical shock magnitude, the precursor pool is completely depleted by hypoosmotic shock, and hence the elongation rate approaches zero (Figure 4D). However, this model predicts that the inhibition period, which is determined by the time scale for precursor replenishment, should be independent of shock magnitude, contrary to our observations (Figure 4E). Since the precursor model does not yield a secondary elongation-rate peak (Figure 4C), we defined the inhibition period as the time it takes for the elongation rate to relax to 90% of its steady-state value. These scaling relationships are independent of model parameters. An alternative model, similar to the precursor model, for the observed growth inhibition is that it is induced by loss of key metabolites (e.g. precursors, amino acids, ATP, etc.) through stretch-activated ion channels (Berrier et al., 1992; Tsapis and Kepes, 1977). Not only would this mechanism yield scaling similar relationships similar to those of the precursor model but, as mentioned above, the absence of stretch-activated ion channels actually exacerbates growth inhibition (Figure S3A and S3B). Therefore, stretch-activated ion channels cannot be responsible for growth inhibition through metabolite loss.

Given that models focused on either turgor pressure (the pressure model) or biochemical depletion (the precursor model) alone cannot explain the full set of responses to hypoosmotic shock, we explored the possibility that feedback between cell envelope mechanics and precursor insertion into the cell wall determined these responses. In the tension-inhibition model (Figure 4A), we assumed that mechanical tension in the membrane inhibits transmembrane flux of peptidoglycan precursors:

$$J\propto \frac{p}{1+\frac{\lambda }{{\lambda }_t}}$$ (1)

where J is the flux, λ is the tension, λ_t is the scale determining how strongly tension inhibits flux, and p is the concentration of peptidoglycan precursors in the cytoplasm. We assumed that membrane is synthesized at a rate equal to the steady-state elongation rate of the cell and that, in the absence of perturbation, λ = 0. To account for the chemistry associated with cell wall assembly, we included a characteristic rate, k, at which peptidoglycan precursors are incorporated into the cell wall after they arrive in the periplasm. In this model, elongation is a direct result of incorporation, implying that hydrolysis of the cell wall is exactly balanced by insertion of new cell wall material (Misra et al., 2013). Finally, to account for the empirical observation that hyperosmotic shock reduces elongation rate (Figure 3), we prescribed that the cell-wall expansion rate scales linearly with cell wall stress, which scales linearly with turgor pressure. The tension-inhibition model has three free parameters: E, k, and λ_t.

Simulations of hypoosmotic shock using the tension-inhibition model yielded an elongation rate response that agreed qualitatively with our experimental observations (Figures 4B and 4C; compare to Figures 1C and 1D), and also predicted the two key experimental scaling relationships: an asymptotic relationship between minimum elongation rate and shock magnitude (Figure 4D) and an approximately linear scaling between the inhibition period and shock magnitude (Figure 4E). These relationships are independent of model parameters and straightforward to interpret in terms of the model. First, in response to hypoosmotic shock, peptidoglycan flux through the membrane is reduced according to Equation 1. For large shocks, the flux asymptotically approaches zero, and thus the elongation rate also approaches zero. Second, the time scale for reestablishment of precursor flux and elongation, which determines the inhibition period, is set by the rate of membrane synthesis, which acts to reduce membrane tension. The larger the shock, the longer this process takes, yielding positive scaling between inhibition period and shock magnitude. In effect, membrane synthesis must be allowed to catch up to the stretched size of the cell wall, ensuring balanced expansion of the membrane and wall.

Perturbations of membrane tension affect growth inhibition

Given that the tension-inhibition model explains the key observations associated with hypoosmotic shock-induced growth inhibition (Figure 4), we used this model to generate other experimentally testable predictions. According to the model, growth inhibition explicitly depends on elevated membrane tension, while the secondary burst in elongation rate depends on elevated flux of peptidoglycan precursors. Thus, we perturbed these factors and measured their effect on the elongation-rate response to hypoosmotic shock.

The model predicted that, if membrane tension were reduced prior to hypoosmotic shock, then growth inhibition would not occur. Accordingly, when we lowered membrane tension by performing a 1-M hyperosmotic shock just before a 500-mM hypoosmotic shock, no growth inhibition was detectable (Figure 5A). Similarly, the model predicted that, if the cells relieved turgor pressure after hypoosmotic shock, then the cells would shrink and resume elongation within a shorter time than they would in the absence of normal osmoregulation. Notably, we found that cells shrunk after hypoosmotic shock when in the presence of 500 mM potassium chloride (i.e. from LB+1 M sorbitol+500 mM potassium chloride to LB+500 mM potassium chloride; Figure 5B) and that this shrinkage corresponded to a drastically reduced inhibition period (Figure 5C). We do not yet understand why cells appear to perform osmotic down-regulation of turgor pressure (the presumed cause of shrinkage) in the presence of potassium chloride and not otherwise.

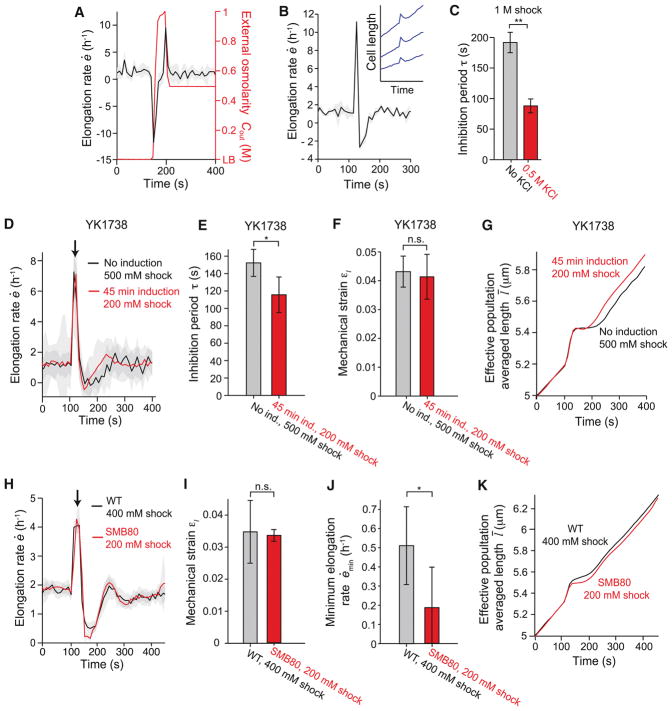
Figure 5. Cells producing membrane at an accelerated rate display attenuated growth inhibition.

(A) Population-averaged elongation rate of WT cells in response to a 1-M hyperosmotic shock followed by a 500-mM hypoosmotic shock does not display growth inhibition (n = 7). (B) In the presence of 500 mM KCl, population-averaged elongation rate in response to a 1-M hypoosmotic shock becomes negative, indicating cell shrinkage (n = 3). Inset: length of three cell chains during the same shock. (C) Inhibition period in response to a 1-M hypoosmotic shock decreases in the presence of 500 mM KCl (n = 21 and n = 3 for 0 and 0.5 M KCl, respectively). **: Student’s t-test, p < 10⁻⁵. (D) Population-averaged elongation rate of B. subtilis YK1738 with wild-type levels of AccDA (black line) and induction of AccDA overexpression (red line) during hypoosmotic shock (n = 21 and n = 164 cell chains for uninduced and induced, respectively). Shock magnitudes (500 mM and 200 mM, respectively, from LB + 1 M sorbitol) were chosen to yield approximately equal mechanical strains. Shading indicates ±1 s.d. (E) The population-averaged mechanical strain of B. subtilis YK1738 was similar between populations with wild-type levels of AccDA and with induction (“ind.”) of AccDA overexpression during the hypoosmotic shocks in (D). *: Student’s t-test, p < 0.005. (F) The population-averaged ihibition of B. subtilis YK1738 was similar between populations with wild-type levels of AccDA and with induction (“ind.”) of AccDA overexpression during the hypoosmotic shocks in (D). n.s.: Student’s t-test, not significant. (G) Effective population-averaged length of B. subtilis YK1738 with induction of AccDA overexpression (red line) illustrates the shorter inhibition period relative to wild-type levels of AccDA during hypoosmotic shock. (H) Population-averaged elongation rate of wild-type B. subtilis JH642 (black line) and B. subtilis SMB80 lacking stretch-activated ion channels (red line) during hypoosmotic shock from LB + 500 mM sorbitol (n = 19 and n = 20 chains for WT and SMB80, respectively). Shading indicates ±1 s.e.m. (I) The mechanical strain induced in wild-type cells by a 400-mM hypoosmotic shock was similar to that of SMB80 cells by a 200-mM shock. Error bars indicate ±1 s.d. n.s.: Student’s t-test, not significant. (J) The minimum elongation rate caused in wild-type cells by a 400-mM hypoosmotic shock was lower than that caused in SMB80 cells by a 200-mM shock. Error bars indicate ±1 s.d. *: Student’s t-test, p < 0.005. (K) Effective population-averaged length of WT and SMB80 illustrates the lower minimum elongation rate of SMB80 cells during hypoosmotic shock. See also Figure S3.

Although these observations are consistent with our tension-inhibition model, they could also be explained by the mechanical stress within the cell wall concurrently generated by turgor. To verify that membrane tension, and not mechanical stress within the cell wall, was responsible for growth inhibition, we altered membrane tension independently of cell wall stress during hypoosmotic shock. We made use of a strain of B. subtilis (YK1738) in which membrane can be synthesized at an accelerated rate by inducing overexpression of a key protein complex, AccDA, involved in fatty acid synthesis (Mercier et al., 2013). Upon induction, this strain accumulates excess membrane in its cytoplasm, until cells begin to lyse after ≈ 3 h (Mercier et al., 2013); accordingly, we utilized only short (45-min) induction periods that avoid impacting growth rate. Our model predicted that growth inhibition following hypoosmotic shock would be attenuated when the rate of membrane synthesis was increased. For reasons we do not understand, AccDA overexpression caused a large increase in cell swelling compared to cells with wild-type levels of AccDA for a given hypoosmotic shock magnitude (Figures S3C and S3D). Nonetheless, as predicted, inducing AccDA overexpression for 45 min reduced the period of growth inhibition (Figures 5D and 5E) for a given degree of cell swelling (Figure 5F). The effective population-averaged length (the length that a cell that elongated with the population-averaged elongation rate; (Rojas et al., 2014)) highlights the early exit from growth inhibition elicited by AccDA overexpression (Figure 5G). Similar results were obtained across a range of shock magnitudes (Figure S3E). These data support our model that membrane tension causes growth inhibition upon hypoosmotic shock.

Further, we reasoned that we could also modulate membrane tension by adjusting the abundance of membrane proteins. It is well understood that stretch-activated channels protect cells from hypoosmotic shock-induced death (Hoffmann et al., 2008; Levina et al., 1999). We confirmed that, in our microfluidic assay, 100% of mutant SMB80 cells, which possess none of the known stretch-activated channels (Hoffmann et al., 2008), lysed upon hypoosmotic shocks greater than 300 mM in magnitude (data not shown). It is commonly believed that the mechanism for this protection lies in the ability of these channels to release solutes from the cell when they are activated by membrane tension, thereby reducing turgor pressure. However, as stated before, we observed no shrinking of wild-type cells after hypoosmotic shock (Figure 2C), and for small, non-lytic shocks (≤ 200 mM), SMB80 cells swelled only marginally more than wild-type cells (Figures S3A and S3B). In addition, wild-type cells can tolerate membrane swelling (Figure 2B) to a degree that causes SMB80 cells to lyse. Taken together, these observations suggest that stretch-activated ion channels confer resistance to hypoosmotic shock in a manner that depends on more than just relief of turgor pressure. One proposed mechanism is that additional surface area from channel opening acts to relieve tension in the phospholipid bilayer (Boucher et al., 2009). Our tension-inhibition model then predicted that cells without stretch-activated channels would exhibit stronger growth inhibition than wild-type cells. Indeed, we found this to be the case when we exposed wild-type and SMB80 cells to shock magnitudes that produced a similar degree of swelling (ΔC_out = 400 and 200 mM, respectively; Figures 5H and 5I). Notably, whereas membrane overproduction attenuated growth-inhibition by reducing the period of inhibition during AccDA overexpression, expression of stretch-activated ion channels did so by increasing the minimum elongation rate (Figure 5J). Again, the effective population-averaged length clearly demonstrates the advantage for SMB80 cells when growth inhibition is attenuated (Figure 5K).

In addition, the tension-inhibition model predicted that the secondary peak in elongation rate (Phase III, Figure 2C) would depend on an accumulation of peptidoglycan precursors during the period of growth inhibition and, in turn, that we could abolish this peak by performing a hypoosmotic shock and simultaneously inhibiting the incorporation of precursors into the cell wall. When B. subtilis cells underwent a hypoosmotic shock from LB + 800 mM sorbitol to LB + 10 μg/mL vancomycin, a drug that prevents incorporation of peptidoglycan precursors, a secondary peak in elongation rate was not observed (Figure S4A).

Given these observations, we hypothesized that reducing the flux through the peptidoglycan synthesis pathway by inhibiting upstream reactions would also have an effect on the elongation rate response to hypoosmotic shock. Chloramphenicol inhibits protein synthesis, which slows cell growth (Figure S4B) and, implicitly, the rate of peptidoglycan synthesis. We found that chloramphenicol treatment abolished the secondary peak in elongation rate in a dose-dependent manner (Figure S4C). Our model accurately predicted this non-intuitive relationship between elongation rate, the rate of peptidoglycan synthesis, and secondary peak dynamics (Figure S4D). As further confirmation that this effect is largely due to changes in the rate of synthesis of peptidoglycan precursors, we also found that sub-inhibitory concentrations of fosfomycin, which inhibits the first committed reaction in this pathway, had an effect to similar to that of chloramphenicol (Figure S4E).

Finally, we tested whether the tension-inhibition model could explain the post-shock elongation rate for both hypo- and hyperosmotic shocks. In response to hypoosmotic shock, after the transient period of growth inhibition, B. subtilis cells ultimately relaxed to an elongation rate that was marginally higher than the pre-shock rate (Phase IV; Figures 1D and 3F), whereas hyperosmotic shock reduced the elongation rate (Figure 3). For hypoosmotic shock, the tension-inhibition model predicted that the ratio of the post- to pre-shock elongation rate should asymptotically approach the maximum elongation rate allowed by peptidoglycan precursor production (Figure 3F); for hyperosmotic shock, the model predicted that this ratio should decrease with increasing shock magnitude and reach zero when this magnitude equals the cytoplasmic osmolarity. These predictions agreed well with the experimental data throughout the entire range of shocks (Figure 3F). Taken together, these results constitute evidence that turgor pressure, membrane tension, and cytosolic peptidoglycan precursor concentration collectively regulate elongation rate in B. subtilis.

Dynamics of Mbl motion and membrane potential underlie those of elongation rate

To determine the molecular mechanisms responsible for tension-mediated growth inhibition, we next addressed a key premise of our model: that membrane tension inhibits cell elongation by interfering with peptidoglycan synthesis. To assay peptidoglycan synthesis, we measured the dynamics of Mbl, one of three actin homologues that orchestrate synthesis. In B. subtilis, Mbl forms membrane-bound puncta that move either diffusively or processively (Domínguez-Escobar et al., 2011; Garner et al., 2011). Blocking peptidoglycan synthesis arrests the motion of processive puncta, while blocking cell growth via other means does not (Garner et al., 2011). In E. coli, the speed of MreB (the single Mbl homolog in this species) is linearly correlated with elongation rate in media of varying osmolarity (Rojas et al., 2014). We tested whether this was also true in B. subtilis. To overcome the technical difficulty of distinguishing slow-moving, processive puncta from diffusive puncta, we defined the fractional Mbl speed, v_f = (n_proc/n_tot)v_Mbl, where n_proc is the number of processive puncta, n_tot is the total number of puncta, and v_Mbl is the speed of processive puncta. We found that both the steady-state speed (Figure S5A, Movie S4) and fractional speed (Figure 6A) of GFP-Mbl puncta were reduced as medium osmolarity was increased, with the fractional speed being a better predictor of elongation rate (Figures 6B and S5B). Furthermore, hyperosmotic shock reduced the fractional speed beyond its steady-state value, mirroring the effect that the shock has on elongation rate (Figure 6A). Therefore, the fractional speed of Mbl is a reliable proxy for cell growth rate and the rate of peptidoglycan synthesis.

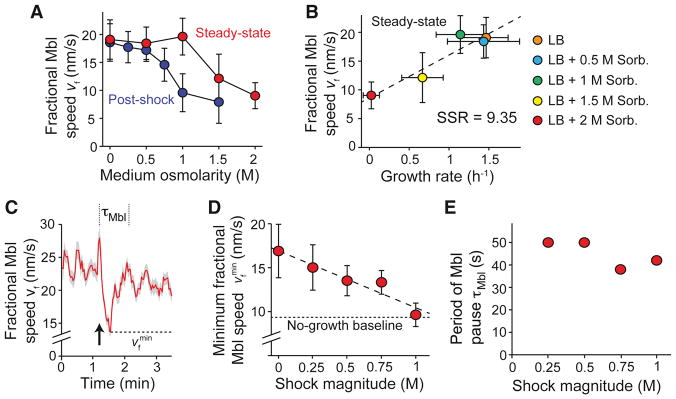
Figure 6. Hypoosmotic shock inhibits Mbl motion.

(A) Population-averaged fractional speed of Mbl puncta versus osmolarity during steady-state growth (red dots) and after hyperosmotic shock (blue dots; each point represents the average of 491–1742 puncta). Error bars indicate ±1 s.e.m. (B) Population-averaged fractional speed of Mbl puncta increased with increasing steady-state elongation rate when elongation rate was modulated with medium osmolarity. Error bars indicate ±1 s.e.m. SSR: Sum of squared residuals. (C) Population-averaged fractional speed of Mbl puncta transiently decreased during a 500-mM hypoosmotic shock (from LB + 1 M sorbitol to LB + 500 mM sorbitol; n = 1742 puncta). The arrow indicates the time of shock. Shading indicates ±1 s.e.m. The dotted lines indicate the period during which Mbl slows. The dashed line indicates the minimum fractional speed during hypoosmotic shock. (D) Minimum population-averaged speed of Mbl puncta during hypoosmotic shock decreased with increasing shock magnitude. The dotted line indicates the fractional Mbl speed in cells growing at a negligible rate in LB + 2 M sorbitol. Error bars indicate ±1 s.e.m. (E) The period during which Mbl slows during hypoosmotic shock was approximately constant across shock magnitudes. See also Figure S5.

To test whether hypoosmotic shock inhibits peptidoglycan synthesis, we measured the response of Mbl motion to a range of shock magnitudes. We found that hypoosmotic shock caused a sharp pause in Mbl motion (Figure 6C, Movie S5), reminiscent of hypoosmotic shock-induced growth inhibition (Figure 1D). The degree to which fractional Mbl speed decreased was linearly dependent on shock magnitude (Figure 6D), as would be expected in our tension-inhibition model. Furthermore, large (1 M) hypoosmotic shocks, which completely stop the cell from growing during growth inhibition (Figure 2C), caused the fractional speed of Mbl to drop to a value that was approximately equal to that of non-growing cells cultured in very high osmolarity medium (Figure 6A,D). The period of Mbl pausing was approximately independent of shock magnitude (≈ 40–50 s, Figure 6E).

Because Mbl localization depends on the transmembrane electric potential (Strahl et al., 2014), we hypothesized that changes in Mbl speed were elicited by hypoosmotic shock-induced membrane depolarization. To test this hypothesis, we loaded cells with the membrane-potential indicator 3,3′-diethyloxacarbocyanine (DiOC₂(3)), which is a fluorescent, membrane-permeable cation that partitions into the cytoplasm (Figure 7A) in a manner that depends on the degree of membrane polarization (Figure S6). Upon hypoosmotic shock, B. subtilis cells underwent partial depolarization for ≈ 30 s, followed by an extended period of hyperpolarization, before achieving electrical homeostasis (Figure 7B, Movie S6). Similar to the response of Mbl fractional speed, the degree of depolarization was proportional to the shock magnitude (Figure 7C), while the period of depolarization was independent of shock magnitude (Figure 7D). Together, these data support a model in which hypoosmotic shock inhibits peptidoglycan synthesis via membrane depolarization, thereby causing growth inhibition. In support of this model, brief depolarization of the membrane with a 30-s pulse of the proton ionophore 2,4-dinitrophenol caused depolarization of the cell (Figure 7E), an arrest in Mbl motion (Figure 7F, Movie S7), and growth inhibition (Figure 7G), similar to the effects of hypoosmotic shock. Therefore, our data demonstrate that B. subtilis cells control elongation via an integrated feedback system involving chemical, mechanical, and electrical factors.

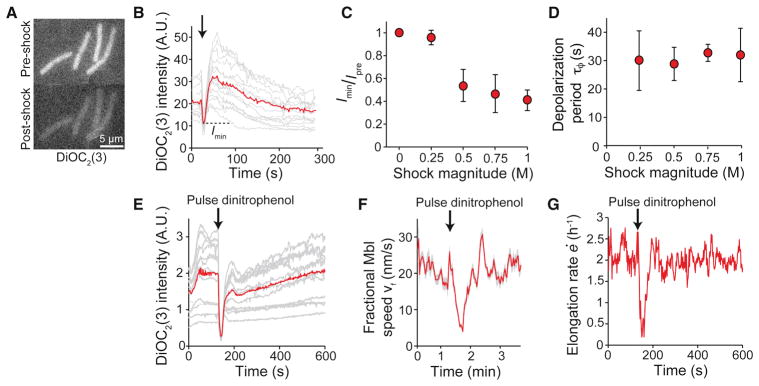
Figure 7. Hypoosmotic shock causes membrane depolarization.

(A) B. subtilis cells stained with DiOC₂(3) before and immediately after 1-M hypoosmotic shock. (B) Fluorescence intensity of DiOC₂(3)-stained cells decreased immediately during a 500-mM hypoosmotic shock (gray lines; n = 19). The arrow indicates the time of the shock. The red line indicates the population average. (C) Population-averaged ratio of minimum DiOC₂(3) intensity during hypoosmotic shock, I_min, and intensity before hypoosmotic shock, I_pre, decreased with increasing shock magnitude. Error bars indicate ±1 s.d. Each data point is averaged over 8–30 cells. (D) Population-averaged depolarization period was approximately constant across shock magnitudes. Error bars indicate ±1 s.d. Each point represents the average of 8–30 cells. (E) Fluorescence intensity of cells stained with DiOC₂(3) during a 15-s pulse of dinitrophenol (gray lines). Red line is population average (n = 32). (F) Population-averaged fractional Mbl speed decreases during a 30-s pulse of 200 ug/mL dinitrophenol (n = 1204 puncta), similar to hypoosmotic shock. Shading indicates ±1 s.e.m. (G) Population-averaged elongation rate for cells in (F) also decreased during the dinitrophenol pulse (n = 74 cell chains). See also Figure S6.

Discussion

In this study, we subjected B. subtilis and other Gram-positive bacteria to hypo- and hyperosmotic shock to probe the feedback mechanisms that govern their growth. By combining microfluidics and microscopy, we measured the elongation rate response of single cells at short time scales after osmotic shock, a strategy that is not feasible using bulk-culture assays. We found that cells exhibited a short period of inhibited growth in response to hypoosmotic shock (Figures 1C and 1D) and a sustained period of reduced elongation rate in response to hyperosmotic shock (Figure 3A). The immediate inhibition of growth suggested that it was not mediated by transcription but by biochemical and/or biophysical feedback. We proposed a model in which mechanical forces dually regulate cell growth: while mechanical stress within the cell wall promotes its expansion in a peptidoglycan synthesis-dependent manner, tension within the membrane inhibits peptidoglycan synthesis (Figure 4A). Since cell wall synthesis can only proceed when membrane tension is below a certain threshold, this interplay of forces within the cell envelope ensures that cell-wall synthesis is balanced with that of the membrane, on a more rapid time scale than homeostatic mechanisms that rely on gene regulation. While other models of growth inhibition yielded qualitatively similar elongation-rate responses to hypoosmotic shock, they do not quantitatively predict many experimental results, nor do they guarantee cell envelope homeostasis.

Membrane tension-based growth inhibition as a mechanism for ensuring balance between the syntheses of the membrane and the cell wall may be common among Gram-positive organisms (Figure 1), with broad physiological implications. Cell wall expansion could outpace membrane synthesis due to extrinsic factors (such as hypoosmotic shock) or due to intrinsic fluctuations in the production rate of peptidoglycan, both of which would increase mechanical tension in the membrane and retard wall expansion by inhibiting peptidoglycan synthesis. Importantly, membrane overproduction would negate the tension-inhibition mechanism for balanced synthesis of the membrane and cell wall and would thus be predicted to cause growth defects over long time scales; indeed, this has been observed for extended AccDA overexpression (Mercier et al., 2013). In the future, it will be interesting to test whether plants, which, like Gram-positive bacteria, have a relatively thick cell wall (Albersheim et al., 2010) and exhibit pressure-dependent growth (Green, 1968; Proseus et al., 2000), also exhibit tension inhibition.

Questions remain as to how tension inhibition is implemented biochemically within the cell. We observed that hypoosmotic shock induced membrane depolarization and a pause in Mbl motion (Figure 5), indicating that membrane potential is an important factor in the molecular mechanism for tension inhibition of cell-wall growth. This adds to an emerging body of knowledge regarding mechanisms by which bacteria harness electrical signals to perform critical processes, such as long-range communication within biofilms (Prindle et al., 2015). However, our finding that the duration over which Mbl speed and membrane potential were reduced by hypoosmotic shock did not scale linearly with shock magnitude (Figures 6E and 7D) suggests that membrane depolarization does not act alone. Instead, these observations imply that there are other critical steps in peptidoglycan synthesis, downstream of Mbl motion, that directly depend on membrane tension. For example, B. subtilis employs two flippases to translocate lipid II, a committed precursor of peptidoglycan, through the plasma membrane (Meeske et al., 2015); these transporters are potential candidates for molecular sensors of membrane tension and/or effectors of tension-induced growth inhibition.

We did not formulate osmoregulation explicitly into our tension-inhibition model, although B. subtilis does possess mechanisms for both up- and down-regulation of turgor pressure (Kempf and Bremer, 1998; Wahome and Setlow, 2008). There are several justifications for this simplification. First, while it is clear that stretch-activated ion channels are engaged during hypoosmotic shock, they apparently do so without greatly reducing turgor, since cells do not shrink after shock (Figure 2C) and the swelling induced by hypoosmotic shock in wild-type cells is not greatly different from that induced in mutants without stretch-activated ion channels (Figure 5A). Also, the mechanical strain induced by hypoosmotic shock is approximately proportional to shock magnitude (Figure 2B), as would be expected if no osmoregulation occurred. Finally, the reduction in elongation rate in response to hyperosmotic shock persists for tens of minutes, and the elongation rate is nearly constant over this period (Figure 3A). If turgor pressure were rapidly up-regulated during this time, then an acceleration in elongation rate due to osmotic swelling would be expected; we did not detect this signature in the elongation rate (Figure 3B) or in the length trajectories (Figure 3A). Taken together with the success of the tension-inhibition model in explaining the breadth of our experimental data, these observations suggest that osmoregulation is not an important determinant of the elongation-rate response of B. subtilis to osmotic shock.

It is unclear why stretch-activated ion channels do not appear to down-regulate turgor pressure after hypoosmotic shock, except when bacteria were exposed to potassium chloride during the shock (Figure 4G). This effect is potassium-specific, since we did not observe shrinking when the same concentration of sodium chloride was added to the medium (data not shown). While B. subtilis possesses no homolog of E. coli MscK, an ion channel that is gated by both membrane tension and extracellular potassium (Li et al., 2002), it may possess another channel with similar function that accounts for this phenomenon.

The hypothesis that turgor pressure drives cell-wall expansion in bacteria has been promoted for nearly a century (Koch et al., 1982; Walter, 1924), yet recent studies have arrived at conflicting models of this process. Based on a theoretical model, it was recently suggested that the layered architecture of the B. subtilis cell wall should lead to a pressure-dependent elongation rate (Misra et al., 2013). A complementary theory suggested that elongation rate and peptidoglycan synthesis should be directly proportional to mechanical stress in the cell wall (Amir and Nelson, 2012); this theory was validated by showing that the rate of cell-wall expansion in filamentous E. coli and B. subtilis cells can be altered by external bending forces (Amir et al., 2014). The present study provides additional evidence that B. subtilis cell elongation directly depends on turgor pressure, and as such, it underscores an important evolutionary constraint faced by bacteria. Cell growth, which requires hydrolysis and expansion of the cell wall, is a precarious process for bacteria due to the constant risk of turgor-induced cytolysis. Therefore, turgor pressure is, in some sense, a necessary evil for bacterial cells, which must concentrate the biochemicals required for life while coping with diverse and dynamic osmotic environments. Here, we have shown that B. subtilis not only surmounts this challenge, but exploits it to achieve growth homeostasis by elegantly integrating up- and down-regulation of cell elongation by turgor pressure.

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for reagents may be directed to, and will be fulfilled by, corresponding author KC Huang (kchuang@stanford.edu).

Experimental Model and Subject Details

Table S1 lists bacterial strains used in this study. Concentrated rich medium was made by adding sorbitol (Sigma-Aldrich, St. Louis, MO, USA) to lysogeny broth (LB Miller; Merck Millipore, Billerica, MA, USA) for B. subtilis and E. coli, brain heart infusion broth (Becton, Dickson, and Company, Franklin Lakes, New Jersey, USA) for L. monocytogenes, and reinforced clostridial medium for C. perfringens. Unsupplemented LB has an osmolality of 260 mmol/kg, as measured with a vapor pressure osmometer (Wescor Environmental, Logan, UT, USA). We used the osmometer to confirm that osmolality scales linearly with osmolarity across the range of concentrations used for this study (Rojas et al., 2014).

Models for hypoosmotic shock-induced growth inhibition

Pressure model

One potential scenario that would yield apparent growth inhibition and a secondary peak in elongation rate in response to hypoosmotic shock is if turgor pressure itself exhibited damped oscillations. In this case, the apparent oscillations in growth rate would simply be the superposition of a constant growth rate with elastic deformations due to oscillations in turgor. An osmotic shock can be described by the equation

$$C_{\text{out}}=C_1+\frac{C_2-C_1}{1+e^{-(t-t_s)/\mathrm{\Delta }t}},$$ (2)

where C_out is the osmolarity of the growth medium, C₁ is the pre-shock medium osmolarity, C₂ is the post-shock medium osmolarity, t_s is the time of the shock, and Δt determines the time required for medium exchange. We model the osmoregulatory response to osmotic shock as a damped harmonic oscillator

$${\ddot{C}}_{\text{in}}=-\alpha (C_{\text{in}}-C_{\text{out}}-C_0)-\beta {\stackrel{.}{C}}_{\text{in}},$$ (3)

where C_in is the osmolarity of the cytoplasm, C₀ is the steady-state differential in osmolarity between the inside and the outside of the cell, α is a constant that determines the magnitude of osmoregulation in response to perturbations in turgor pressure, and β is a damping constant. Turgor pressure obeys the Morse Equation, P = RT(C_in − C_out), where R is the gas constant and T is the temperature. Elongation rate is assumed to be given by

$$\stackrel{.}{e}={\stackrel{.}{e}}_0+\frac{\stackrel{.}{P}}{P-\frac{2\delta E}{r}},$$ (4)

where ė₀ is the steady-state elongation rate, δ is the thickness of the cell wall, E is Young’s modulus of the cell wall, and r is the radius of the cell. The second term in Eq. 3 accounts for reversible shrinking and swelling of the cell due to variation in turgor pressure, assuming linear elastic mechanics. Eq. 1–3 can be non-dimensionalized using the following definitions:

$$\begin{gathered} C_{\text{in}}^{\ast }=\frac{C_{\text{in}}}{C_0}{C}_{\text{out}}^{\ast }=\frac{C_{\text{out}}}{C_0}{t}^{\ast }=\frac{t}{\mathrm{\Delta }t} \\ {P}^{\ast }=\frac{P}{{\mathit{RTC}}_0}{\stackrel{.}{e}}^{\ast }=e\stackrel{.}{\mathrm{\Delta }}t{C}_2^{\ast }=\frac{C_2}{C_0} \\ {C}_1^{\ast }=\frac{C_1}{C_{\text{in}}}{\alpha }^{\ast }=\alpha \mathrm{\Delta }{t}^2{\beta }^{\ast }=\beta \mathrm{\Delta }t \\ {E}^{\ast }=\frac{2\delta }{{\mathit{rRTC}}_0}E{t}_{\mathrm{s}}^{\ast }=\frac{t_{\mathrm{s}}}{\mathrm{\Delta }t}. \end{gathered}$$ (5)

We constrain the variables as follows. First, we set the time scale Δt = 3.3 s such that the medium switching time equals the experimental value of ≈ 30 s. The initial elongation rate of the cell chains is also set by experimental data: ė₀ = 3.7 × 10⁻⁴ s⁻¹ for cells growing at steady state in LB + 1 M sorbitol (Figure 3D). The turgor pressure of B. subtilis is thought to be ≈ 10 atm (Whatmore and Reed, 1990), which corresponds to C₀ = 0.38 M at T = 310 K. The wall thickness is δ ≈ 30 nm (Misra et al., 2013). C₁ and C₂ are experimental parameters.

Other useful experimental quantities that we can calculate from the experimental data are the period of growth inhibition, τ; the amplitudes of the peaks in elongation rate, A_i; the minimum elongation rate during growth inhibition, ė_min; and the strain acquired during the shock, ε_l. To test the model, we fit these variables for small shock magnitudes and then determined whether the predicted scaling relationships (Figures 4D and 4E) agreed with the experimental scalings.

The logarithmic decrement, η, is a non-dimensional parameter that we can estimate from the experimental data,

$$\eta =ln\left(\frac{A_1}{A_2}\right),$$ (6)

where A₁and A₂ are the amplitudes of the first and second peaks in the elongation-rate oscillations, respectively. For small shocks, η ≈ 2 (Figure 1D) and τ ≈ 79 s (Figure 2D). Using these values, we calculated α^* and β^* using the following identities (Inman, 2014):

$$\zeta =\frac{{\beta }^{\ast }}{2\sqrt{{\alpha }^{\ast }}}=\frac{1}{\sqrt{1+2\pi /\eta }},$$ (7)

$$\omega =\frac{2\pi }{{\tau }^{\ast }}=\sqrt{{\alpha }^{\ast }(1-{\zeta }^2)},$$ (8)

where ζ is the damping ratio, ω is the natural frequency of oscillation (Inman, 2014), and τ^*=τ/Δt is the non-dimensional inhibition period. These equations yield α^* = 0.04 and β^* = 0.19.

This calculation leaves only one free parameter, E^*, which we estimated by fitting the experimental scaling between ε_l and ΔC, yielding E^* = 10; we searched the parameter space between 0 < E^* < 20. Because α and β are properties of the cell, they are not expected to depend on shock magnitude, and thus we can explore the scalings of τ, η, and ė_min with ΔC. From Eq. 7, the predicted inhibition period is an intrinsic property of the oscillator and does not depend on the shock magnitude (Figure 4E). On the other hand, ė_min is predicted to scale linearly with a negative slope (Figure 4D). Both predictions are inconsistent with our experimental data (Figures 2D and 2C, respectively).

Precursor model

For a model that relies on peptidoglycan precursor depletion to elicit hyposmotic-shock induced growth inhibition, the elongation rate, ė, must depend on the concentration of available peptidoglycan precursors, p, and these precursors must be depleted by osmotic swelling. One simple framework for implementing this scenario is to conceptualize the cell wall as two species: cross-linked material and free periplasmic precursors. We assume that the elongation rate can be expressed as

$$\stackrel{.}{e}=\alpha p+\frac{\stackrel{.}{P}}{P-\frac{2{\delta }_{\chi }E}{r}},$$ (9)

where α is a rate constant linking precursor insertion to growth, P is the turgor pressure, δ is the thickness of the cell wall, E is Young’s modulus of the cell wall, and r is the radius of the cell. The total thickness of the wall can be expressed as the sum of the thicknesses of the load-bearing, cross-linked portion of the wall and the portion composed of free precursors, δ = δ_χ + δ_p (these two portions need not be separated in space). In the simplest case, the thickness of the cross-linked portion of the wall, δ_χ, is constant, which results in the relation

$$p=\frac{\delta -{\delta }_{\chi }}{\delta }{p}_m,$$ (10)

where p_m is the total concentration of peptidoglycan subunits, cross-linked or free, in the wall. The dynamical equation describing the total thickness of the wall is assumed to be given by conservation of mass:

$$\stackrel{.}{\delta }=S-\stackrel{.}{e}\delta ,$$ (11)

where S is the rate of addition of free precursors to the wall. The osmolarity of the medium is given by Equation 1, and the turgor pressure is given by the Morse equation, P = RT(C_in − C_out), as before. The system of equations can be non-dimensionalized using the following definitions:

$$\begin{gathered} {\delta }^{\ast }=\frac{\delta }{{\delta }_{\chi }}{C}_{\text{out}}^{\ast }=\frac{C_{\text{out}}}{C_{\text{in}}}{t}^{\ast }=\frac{t}{\mathrm{\Delta }t} \\ {P}^{\ast }=\frac{P}{{\mathit{RTC}}_{\text{in}}}{\stackrel{.}{e}}^{\ast }=e\stackrel{.}{\mathrm{\Delta }}t{C}_2^{\ast }=\frac{C_2}{C_{\text{in}}} \\ {C}_1^{\ast }=\frac{C_1}{C_{\text{in}}}{\alpha }^{\ast }=\alpha p_m\mathrm{\Delta }t{S}^{\ast }=\frac{S\mathrm{\Delta }t}{{\delta }_{\chi }} \\ {E}^{\ast }=\frac{2{\delta }_{\chi }}{{\mathit{rRTC}}_{\text{in}}}E{t}_{\mathrm{s}}^{\ast }=\frac{t_{\mathrm{s}}}{\mathrm{\Delta }t}. \end{gathered}$$ (12)

We constrain the variables with experimental values, as for the Pressure Model. We set the time scale of Δt = 3.3 s such that the switching time of the medium equals the experimental value of ≈ 30 s. C₁ and C₂ are experimental parameters representing, for example, a series of hypoosmotic shocks where media was switched from LB + 1 M sorbitol to LB + a lower concentration of sorbitol.

Within this model, the steady-state elongation rate is

$${\stackrel{.}{e}}_0^{\ast }=\frac{S^{\ast }}{\frac{S^{\ast }}{\alpha }+1}.$$ (13)

By requiring that this quantity equal our experimental measurement, we reduce the number of free parameters by defining S^* in terms of α^*. Thus, there are only two free parameters in the model, α^* and E^*. We simulated hypoosmotic shock according to this model and performed a parameter-space search to determine how the elongation-rate response depends on α^* and E^* (0 < E^* < 20, 0.05 < α^* < 0.15). Although the precursor model predicts growth arrest in response to hypoosmotic shock, it does not predict a secondary peak in elongation rate (Figure 4C). Therefore, we defined the inhibition period within this model as the time for the system to reach ė_crit = 0.9(ė − ė_min) after hypoosmotic shock. Our parameter space search revealed that only α^*, and not E^*, affects the inhibition period; α^* = 0.13 yielded a good fit of the inhibition for small hypoosmotic shocks (<100 mM) (Figure 4E). E^* was then used to fit the experimental scaling between mechanical strain and shock magnitude (Figure 2B), which yielded E^* = 6. These parameters provide a good fit of the scaling between minimum elongation rate and shock magnitude (Figure 4D). However, because α^* is an intrinsic property of the cell, and not dependent on shock magnitude, the inhibition period is also independent of shock magnitude (Figure 4E).

Tension-inhibition model

The elongation rate according to the tension-inhibition model is formulated similarly to that of the precursor model:

$$\stackrel{.}{e}=\frac{V_{pg}}{\delta }J(t-{\tau }_d)+\frac{\stackrel{.}{P}}{P-\frac{2{\delta }_E}{r}}$$ (14)

where J is the flux of peptidoglycan precursors through the plasma membrane, V_pg is the volume that a precursor contributes to the cell wall, δ is the thickness of the cell wall, τ_δ = 1/k is a delay between the time precursors are translocated through the plasma membrane and the time they are incorporated into the cell wall, E is Young’s modulus of the cell wall, and r is the radius of the cell. To implement tension inhibition, we required that the peptidoglycan flux be dependent on both the cytoplasmic precursor concentration, p, and the membrane tension, λ:

$$J=k_2\frac{p}{1+\frac{\lambda }{{\lambda }_t}},$$ (15)

where k₂ is a rate constant and λ_t describes the degree to which membrane tension inhibits flux. To explain the observation that hyperosmotic shock reduces elongation rate (Figure 3E), we assumed that peptidoglycan flux depends linearly on the mechanical stress in the cell wall:

$$k_2=c\sigma =c\frac{Pr}{2\delta },$$ (16)

where c is a constant, P is the turgor pressure, and r is the radius of the cell.

The dynamics of the cytoplasmic concentration of peptidoglycan precursors are assumed to be described by

$$\stackrel{.}{p}=k_1-\frac{2J}{r}-p\stackrel{.}{e},$$ (17)

where k₁ is a constant that describes the rate at which peptidoglycan precursors are synthesized in the cytoplasm. Finally, the dynamics of membrane tension result from opposing processes: whereas growth tends to increase membrane tension, membrane synthesis decreases tension. We can formulate the dynamics of membrane tension by considering mechanical strain in the membrane, ε ∝ λ:

$$\stackrel{.}{\epsilon }=(1+\epsilon )(\stackrel{.}{e}-\gamma ),$$ (18)

where γ is the rate of membrane production, which must be equal to the steady-state fixed point of the elongation rate, ė₀, to ensure a stable value for membrane tension.

The osmolarity of the medium is given by Equation 1, and the turgor pressure is given by the Morse equation, P = RT(C_in − C_out), as before. The system of equations can be non-dimensionalized using the following definitions:

$$\begin{gathered} p^{\ast }=p{V}_{pg}{C}_{\text{out}}^{\ast }=\frac{C_{\text{out}}}{C_{\text{in}}}{t}^{\ast }=\frac{t}{\mathrm{\Delta }t} \\ {P}^{\ast }=\frac{P}{{\mathit{RTC}}_{\text{in}}}{\stackrel{.}{e}}^{\ast }=e\stackrel{.}{\mathrm{\Delta }}t{C}_2^{\ast }=\frac{C_2}{C_{\text{in}}} \\ {C}_1^{\ast }=\frac{C_1}{C_{\text{in}}}{k}_1^{\ast }=t_s{V}_{pg}{k}_1{k}_2^{\ast }=\frac{{\mathit{cRTC}}_{\text{in}}{t}_s}{\delta } \\ {E}^{\ast }=\frac{2{\delta }_{\chi }}{{\mathit{rRTC}}_{\text{in}}}E{t}_{\mathrm{s}}^{\ast }=\frac{t_{\mathrm{s}}}{\mathrm{\Delta }t}. \end{gathered}$$ (19)

The fixed-point of the system can be solved analytically, taking the steady-state value for membrane strain to be zero:

$$p_0^{\ast }=\frac{\delta }{r}\left(\sqrt{1+\frac{2r}{\delta }\frac{k_1^{\ast }}{k_2^{\ast }(1-C_{\text{out}}^{\ast })}}-1\right),$$ (20)

$$e_0^{\ast }=\frac{k_2^{\ast }(1-C_{\text{out}}^{\ast })}{2}\left(\sqrt{1+\frac{2r}{\delta }\frac{k_1^{\ast }}{k_2^{\ast }(1-C_{\text{out}}^{\ast })}}-1\right).$$ (21)

The number of free parameters can be reduced by requiring that the steady-state elongation rate is equal to the experimentally observed values, which defines $k_1^{\ast }$ in terms of $k_2^{\ast }$ according to Eq. 20. We used Eq. 20 to fit the data in Figure 3E, which shows the ratio of the elongation rates after and before osmotic shock. This calculation yielded $k_1^{\ast }=3.1\times {10}^{-3},k_2^{\ast }=6.3\times {10}^{-5}$, and P₀ = 26 atm. Note that steady-state turgor pressure is a fitting parameter within this model rather than a parameter derived from the literature. We set the time scale Δt = 3.3 s such that the medium switching time equals the experimental value of ≈ 30 s.

There are three remaining free parameters in the model: λ_t, E^*, and τ_d. A three-dimensional parameter space search was performed to fit the scaling relationships in Figures 2B, 2C, and 2D. This search was simplified by the fact that the scaling relationship between mechanical strain induced by hypoosmotic shock and shock magnitude (Figure 2B) is only sensitive to the value of Young’s modulus. We searched the following parameter space: 0 < λ_t < 0.01, 6< E^* < 10, and 0 < τ_d < 10 s. For values of τ_d < 5 s, the simulations of hypoosmotic shock did not yield secondary peaks in elongation rate. For values of τ_d > 5 s, the scalings between period of growth inhibition, minimum elongation rate, and shock magnitude were not greatly affected by τ_d, which mainly modulated the persistence of growth oscillations (data not shown). That is, in this region of parameter space, ε_c is the sole parameter that determines these scalings. Therefore, the multivariate problem was reduced to three independent best fits using three independent free parameters. We found that the parameter set E^* = 6.75, λ_t = 0.006, and τ_d = 6 s yielded an excellent fit of the functional scaling relationships between the key experimental variables: an asymptotic relationship between ė and ΔC_out (Figure 4D), and an approximately linear relationship between τ and ΔC_out (Figure 4E).

To simulate our experiment in which vancomycin was applied during hypoosmotic shock, we specified that the constant k₂ go to zero as the shock is performed:

$$k_2(t)=-\frac{\text{constant}}{1+exp((t-t_s)/\mathrm{\Delta }t)}.$$ (22)

To simulate hypoosmotic shocks in the presence of chloramphenicol, we constrained the steady-state elongation rate to be equal to the experimentally observed value for a given chloramphenicol concentration (Figure 5L). We also specified τ_d = 4 for these simulations because it gave the best initial fit of the elongation rate response for the untreated case.

Method Details

Microfluidic Application of Osmotic Shocks

Before osmotic shock experiments, overnight bacterial cultures in species-specific rich medium were diluted 100-fold into medium supplemented with a defined amount of sorbitol (0–2 M) and incubated at 37 °C until the cells were in mid-exponential phase. These cultures were diluted 100-fold into pre-warmed medium and loaded into a CellASIC B04A microfluidic flow cell (Hayward, CA, USA). To ensure that the cells were growing at steady state, the flow cell was incubated for an additional 30 min in the microscope environmental chamber (HaisonTech, Taipei, Taiwan), which was pre-heated to 37 °C before the cells were imaged. Before loading cells into the imaging chamber of the flow cell, the chamber was primed with growth medium using the ONIX microfluidic perfusion platform (CellASIC). While imaging, fresh medium was perfused through the flow cell. The cell-trapping mechanism used by the microfluidic chips had no detrimental effect on the elongation or morphology of cell chains, as compared with cells growing on agarose pads or liquid culture (data not shown).

During osmotic shock, the medium in the flow cell was exchanged using the ONIX system. To monitor medium osmolarity during osmotic shock, 0.5 μg/mL Alexa Fluor 647 carboxylic acid, succinimidyl ester dye (Life Technologies, Carlsbad, CA, USA) was included with the concentrated medium as a tracer dye. The intensity of the tracer dye was monitored using far-red (650 nm) excitation, and the osmolarity was calculated by calibrating the high and low osmolarities with the maximum and minimum fluorescence intensities, respectively.

For overexpression of AccDA in B. subtilis YK1738, 0.5% xylose was added to cultures 45 min before imaging, and xylose was also included with the medium in the loading reservoir and in all perfusion media. For hypoosmotic shocks in the presence of chloramphenicol or fosfomycin, the antibiotic was included at the specified concentration in the loading reservoir and in all perfusion media. Cells were thus exposed to the antibiotic for 30 min after they were loaded into the microfluidic plate before imaging.

Time-lapse imaging

For phase contrast microscopy, time-lapse images (10-s intervals) were acquired using a Nikon Eclipse inverted microscope (Nikon, Tokyo, Japan) and an Andor DU885 EMCCD camera (Andor Technology, South Windsor, CT, USA). Phase contrast images had signal-to-noise ratios of 21.3 ± 2.5 (data not shown). Cell tracking was performed using custom MATLAB (Mathworks, Natick, MA, USA) routines similar to those described previously (Rojas et al., 2014). To calculate the amplitude of the length oscillations that resulted from oscillatory hyperosmotic shock (Figures 2G and 2H), we first computationally determined the intervals of the oscillatory cycle when the medium was being exchanged. Then, for every cell chain, we calculated the mechanical strain induced by osmotic shock during each of these phases, ε_l = (l_f − l_i)/l_i, where l_i and l_f are the lengths of the chain at the beginning and the end of the interval, respectively. The amplitude, A, was calculated as the average of the absolute value of the strain, averaged over cell chains and intervals.

Total internal reflection fluorescence excitation of Mbl-sfGFP was performed with a 488-nm fiber-pigtailed laser (Coherent Inc., Santa Clara, CA, USA). Images were acquired every 2 s. Mbl puncta were tracked with u-track, an open-source spot tracker (Jaqaman et al., 2008). For calculation of the population-averaged speed of puncta, tracks shorter than 4 time points or longer than 10 time points were ignored. We fit the mean squared displacement of each track to a parabola, y = at², and classified the punctum as “processive” if R² > 0.95, where R is the correlation coefficient between the mean squared displacement and the best fit. The speed of each track was taken to be $\sqrt{a}$ (Lee et al., 2014). The speeds were then averaged over the ensemble at each time point to find v_Mbl, the average speed of Mbl as a function of time. We then calculated the fractional Mbl speed as v_f = (n_proc/n_tot)v_Mbl where n_proc is the number of processive tracks and n_tot is the total number of tracks (between four and ten time points).

Measurements of membrane potential

The microfluidic flow cell was first primed for 3 h with medium that included 3 μM DiOC₂(3) (Life Technologies). Cells were incubated in the flow cell in media containing 0.3 μM DiOC₂(3) for 30 min prior to imaging. We also included 0.3 μM DiOC₂(3) in the medium to which the cells were exposed during imaging. The period of depolarization was calculated as the interval between the first time point before depolarization began and the hyper-polarization peak.

When applying dinitrophenol (Sigma-Aldrich, St. Louis, MO, USA), 500 μg/mL was added to the media.

Experimental design

Each data point or curve in the figures typically represents the mean across many cells (number of cells indicated in the captions) for a single experiment. Experiments comparing response across a range of values of an input parameter such as shock magnitude were carried out on the same day as much as possible. No randomization, stratification, or blinding was carried out. Sample size was defined as the number of segmented cells (or chains of cells, as indicated) or the number of segmented Mbl puncta. No data was excluded from analysis.

Quantification and Statistical Analysis

Statistical t-test for comparing means with small sample sizes

For Figure 3C, the numbers of chains used to compute the power were low (n = 3 and n = 4). Hence, although the p-value was calculated by a conventional Student’s t-test to be <0.0006, we conservatively estimated that p<0.05; simulations showed that the false positive rate (p>0.05) given the null hypothesis that the samples have equal mean is <5% (de Winter, 2013).

Data and Software Availability

Custom code used to segment cells, define cell contours, segment fluorescence puncta, and quantify internal fluorescence will be provided upon request to the Lead Contact.

Supplementary Material

1. Supplemental Table 1: List of strains used in this study.

Related to STAR Methods.

2. Supplemental Movie 1: Time-lapse phase-contrast micrographs of B. subtilis cells undergoing a 750-mM hypoosmotic shock, from LB+1 M sorbitol to LB+250 mM sorbitol.

Related to Figure 1

3. Supplemental Movie 2: Time-lapse phase-contrast micrographs B. subtilis cells undergoing an 800-mM oscillatory osmotic shock (between LB and LB + 800 mM sorbitol) with 2-min period.

Related to Figure 2.

4. Supplemental Movie 3: Time-lapse phase-contrast micrographs B. subtilis cells undergoing an 800-mM hyperosmotic shock, from LB to LB+800 mM sorbitol.

Related to Figure 3.

5. Supplemental Movie 4: Time-lapse total internal reflection fluorescence micrographs of Mbl puncta within B. subtilis cells cultured in LB (left) and LB + 2 M sorbitol (right).

Related to Figure 6.

6. Supplemental Movie 5: Time-lapse total internal reflection fluorescence micrographs of Mbl puncta during a 1-M hypoosmotic shock.

Related to Figure 6.

7. Supplemental Movie 6: Time-lapse epifluorescence micrographs of B. subtilis cells stained with DiOC₂(3) during a 500-mM hypoosmotic shock.

Related to Figure 7.

8. Supplemental Movie 7: Time-lapse total internal reflection fluorescence micrographs of Mbl puncta during a 30-s pulse of dinitrophenol (DNP).

Related to Figure 7.

Highlights.

• Turgor pressure drives mechanical expansion of the cell wall in Bacillus subtilis

• Hypoosmotic shock transiently inhibits growth and slows cell-wall synthesis

• Membrane tension induces the growth arrest via electrical depolarization

• Growth homeostasis emerges from balance between membrane tension and wall stress