Multivariate Hypothesis Testing Methods for Evaluating Significant Individual Change

Abstract

The measurement of individual change has been an important topic in both education and psychology. For instance, teachers are interested in whether students have significantly improved (e.g., learned) from instruction, and counselors are interested in whether particular behaviors have been significantly changed after certain interventions. Although classical test methods have been unable to adequately resolve the problems in measuring change, recent approaches for measuring change have begun to use item response theory (IRT). However, all prior methods mainly focus on testing whether growth is significant at the group level. The present research targets a key research question: Is the “change” in latent trait estimates for each individual significant across occasions? Many researchers have addressed this research question assuming that the latent trait is unidimensional. This research generalizes their earlier work and proposes four hypothesis testing methods to evaluate individual change on multiple latent traits: a multivariate Z-test, a multivariate likelihood ratio test, a multivariate score test, and a Kullback–Leibler test. Simulation results show that these tests hold promise of detecting individual change with low Type I error and high power. A real-data example from an educational assessment illustrates the application of the proposed methods.

The measurement of individual change is important in many applications of psychology. In clinical, counseling, and medical settings, measures of individual change are used to evaluate improvement or deterioration of a wide variety of symptoms and behaviors. In education and training environments in industry, measures of individual change are used to inform and guide the outcomes of instruction. Different examinees can vary in their levels of the measured variables at the first measurement occasion and they can vary in both level and pattern of change over time, as well as ending at different levels on the measured traits.

There has been considerable effort focused on the statistical evaluation of measured change, as evidenced by a continuing stream of books on the topic (e.g., Hoffman, 2014; Molenaar & Newell, 2010). These efforts have focused almost exclusively on measuring change at the group level, using mixed-effects models or structural equation models (e.g., multilevel models, latent growth curve (LGC) or latent transition models, and growth mixture models; Bollen & Curran, 2006). Other methods are based in item response theory (IRT), including a generalized explanatory longitudinal item response model (Cho, Athay, & Preacher, 2013), an IRT LGC model (C. Wang, Kohli, & Henn, 2016), and a multidimensional Rasch model (W. C. Wang, Wilson, & Adams, 1997). Group change is often measured to determine whether a certain instruction approach is effective for a group of students in an education context, or whether a certain intervention is effective for a group of patients in clinical settings. These group-based approaches to measuring change have, however, little to offer with regard to measuring change for an individual to tailor instruction or intervention. For instance, a therapist might want to discuss the termination of treatment when a patient’s score on a depression scale is much lower compared with his or her previous depression score, showing significant improvement in terms of depression symptoms. This and similar applications call for methods for reliably evaluating the significance of individual change. Although some of the above-mentioned models allow an analysis of individual change, it is typically determined relative to the group in which the examinee is embedded, resulting in the possibility that a given degree of individual change can have different meaning and utility depending on the group with which the examinee happens to be measured. If a given individual happens to be an outlier relative to the group, his or her individual growth trajectory might not be recovered precisely. This research intends to provide a sound solution to the practical question:

• Research Question: Is the “change” in latent trait estimates for each individual significant across occasions?

The proposed solution is group independent,¹ and it allows the latent trait to be multidimensional.

Prior Literature

Given the need for providing change information in applied environments, a few efforts have been made to measure individual change, despite long-standing controversy surrounding the issue (e.g., Willett, 1997; Williams & Zimmerman, 1996). For example, simple difference scores based on sum scores have demonstrated a negative correlation with the initial status (Bereiter, 1963; Thorndike, 1963), low reliability (Hummel-Rossi & Weinberg, 1975; Lord, 1963; Willett, 1988), and regression toward the mean (e.g., Bereiter, 1963).

Because classical test theory methods appear to be unable to adequately measure individual change, in recent years IRT methods have been applied to this problem. For example, Fischer (1983) proposed a linear logistic model within the framework of the generalized Rasch model. However, his approach is appropriate only for measuring group change because the treatment and trend effects are assumed to be constant for all examinees across all occasions. Embretson (1991) proposed a multidimensional Rasch model for learning and change designed to measure individual change across k repeated measurements, which Mellenbergh and van den Brink (1998) generalized to a two-parameter model. Although this approach measures individual change, model complexity increases as more measurements are taken, that is, more parameters are estimated on later occasions, so that parameter estimation accuracy at later occasions would decrease.

Willett (1988, 1997) proposed intra-individual methods for observing change across multiple occasions. His approach requires multiple measurements on a single individual on a single variable. He then fits individual regressions across measurement occasions, both linear and nonlinear, and estimates slopes and intercepts. The intercepts provide information on an individual examinee’s beginning level on the trait while the slopes provide information on the rate of change and, when change is nonlinear, the pattern of change. His approach is intra-individual so that change is not group dependent. It is limited, however, because slopes and intercepts based on a small number of observations (e.g., six or seven measurements or even fewer) are highly unreliable and cannot easily be tested for statistical significance due to their large statistical sampling errors. These methods are also limited in that they are designed for unidimensional variables.

Most recently, Jabrayilov, Emons, and Sijtsma (2016) proposed an IRT-based method for determining the significance of individual change. Their method uses the difference between two IRT-based trait (θ) estimates, divided by the sum of the IRT-based standard errors to create a Z statistic. They then, in simulation, compared the performance of their test with the reliable change index (RCI) based on the same data. Their data showed that the RCI method performed better in terms of Type I error and power for polytomous scales with fewer than 20 items and that the IRT method was better for longer scales. However, their conclusions are limited by the single set of discriminations used in their simulations.

Purpose

The present research was designed to develop and evaluate methods that overcome the limitations of prior research on the measurement of intra-individual change. In particular, the methods (a) are based in IRT and take full advantage of the improvements that IRT provides in measuring at the individual level, (b) are entirely intra-individual, (c) provide for drawing conclusions about the psychometric significance of observed change, and (d) are multivariate, allowing multiple measurements on a single individual repeated over time.

Method

This research builds upon the work of Finkelman, Weiss, and Kim-Kang (2010); Lee (2015); Lee and Weiss (2015); and Phadke, Weiss, and Christ (2016) who developed and evaluated methods for identifying psychometrically significant change when a latent trait is unidimensional. When the latent trait of interest is multidimensional, using the existing unidimensional IRT-based hypothesis testing methods will have two adverse consequences: (a) model misfit, yielding inaccurate item and person parameter estimates (e.g., Hulin, Drasgow, & Parsons, 1983); and (b) higher standard errors of measurement for the latent trait, leading to lower power for detecting significant change (e.g., Kirisci, Hsu, & Yu, 2001). In contrast, using multidimensional IRT (MIRT) models is more appropriate because the individual’s latent traits can be more precisely recovered (e.g., Reckase, 2009; Svetina, Valdivia, Underhill, Dai, & Wang, 2017; C. Wang, 2014, 2015; C. Wang & Chang, 2011; C. Wang, Chang, & Boughton, 2011). This study extended the current hypothesis testing methods to a multidimensional scenario. It should be noted that all of the hypothesis testing methods proposed and evaluated in this study are strictly intra-individual. They are based entirely on a single examinee’s responses at two occasions to one or more sets of items for which MIRT item parameters have been previously estimated.

MIRT Model

This study used the compensatory MIRT model (Reckase, 2009; C. Wang & Nydick, 2015) which is the most widely applied MIRT model for measuring different types of latent traits. Let ${\mathbf{\theta }}_i=({\mathrm{\theta }}_i^1,....,{\mathrm{\theta }}_i^D{)}^T$ denote a D-by-1 latent trait vector for examinee i; then the item response function (IRF) for the multidimensional three-parameter logistic (M3PL) model is

$$P(Y_{\mathrm{ij}}=1|{\mathbf{\theta }}_i)=c_j+\frac{1-c_j}{1+\exp [-({\mathbf{a}}_j^T{\mathbf{\theta }}_i-b_j)]},$$

where $Y_{\mathrm{ij}}$ denotes the response of examinee i to item j with $Y_{\mathrm{ij}}=1$, indicating a correct response. ${\mathbf{a}}_j^T$ is a row vector of discrimination parameters for item j, $b_j$ relates to the location of the item on the latent trait continua, and $c_j$ is the lower asymptote parameter. When a test displays a simple structure (i.e., between-item multidimensionality), then only one element in ${\mathbf{a}}_j$ is nonzero. Equation 1 is used as the underlying MIRT model throughout this study. However, the hypothesis testing methods that are proposed can be used with any MIRT model.

Omnibus Hypothesis Testing for Multivariate Change

Four omnibus tests are introduced, and their performance is evaluated based on their Type I error and power. Type I error is defined as the proportion of simulees who have no change but are erroneously identified as having significant change, and power is defined as the proportion of simulees who have a specified level of change and are correctly identified as having changed. If an omnibus test is significant, then a post hoc comparison follows to identify the specific dimension(s) on which the change occurred.

Multivariate Z-test (MZ; Wald test)

For examinee i, the null hypothesis, ${\mathrm{H}}_0:{\mathbf{\theta }}_{i2}={\mathbf{\theta }}_{i1}$, is tested against the alternative hypothesis, ${\mathrm{H}}_a:{\mathbf{\theta }}_{i2}\ne {\mathbf{\theta }}_{i1}$. This is an overall test; hence, the change can occur in any direction or pattern (i.e., a two-tailed test) and involve one or more dimensions. When the instrument is precalibrated with item parameters known, which is the typical case for IRT-constructed instruments, then for each examinee, ${\mathbf{\theta }}_{i1}$ and ${\mathbf{\theta }}_{i2}$ can be estimated via maximum likelihood estimates (MLEs or ${\hat{\mathbf{\theta }}}^{\mathrm{mle}}$).

When the number of items approaches infinity, the covariance matrix of ${\hat{\mathbf{\theta }}}^{\mathrm{mle}}$ is equal to the inverse of the Fisher test information matrix evaluated at the true latent trait level, that is, $I^{-1}(\mathbf{\theta })$ (Segall, 1996; C. Wang, 2014; C. Wang & Chang, 2011). As a direct generalization of Finkelman et al.’s (2010) univariate Z-test, ${\hat{\mathbf{\theta }}}_{i1}^{\mathrm{mle}}$ and ${\hat{\mathbf{\theta }}}_{i2}^{\mathrm{mle}}$ can first be obtained for examinee i at two occasions separately, then a test statistic can be constructed as

$$Z_i={({\hat{\mathbf{\theta }}}_{i1}^{\mathrm{mle}}-{\hat{\mathbf{\theta }}}_{i2}^{\mathrm{mle}})}^{\mathrm{T}}{\sum }_{{\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}}^{-1}({\hat{\mathbf{\theta }}}_{i1}^{\mathrm{mle}}-{\hat{\mathbf{\theta }}}_{i2}^{\mathrm{mle}}),$$

where $\sum _{{\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}}=I_1^{-1}({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}})+I_2^{-1}({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}})$. ${\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}$ is the MLE of θ by combining the response vectors from both occasions, and it can also be viewed as the MLE under the null hypothesis. $I_1({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}})$ and $I_2({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}})$ are test information from Time 1 and Time 2 evaluated at ${\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}$. The Fisher test information has a closed-form expression (C. Wang & Chang, 2011). The test statistic in Equation 2 is compared with a chi-square distribution with degrees of freedom D (i.e., total number of dimensions) and depending on the significance level α, examinee i is considered as either having significant change or not.

Likelihood ratio (LR) test

This change detection method (Finkelman et al., 2010) is based on a LR test adapted from a method that is described by Agresti (1996) for categorical data. In the current context for testing individual change across occasions, the condition “parameters satisfy H₀” is ${\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}$. In the denominator, under the alternative hypothesis, the likelihood is maximized by computing the MLEs separately at each occasion. The LR statistic, therefore, is

$$\mathrm{LRT}=-2\log \left[\frac{L({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}};{\mathbf{Y}}_{1+2})}{L({\hat{\mathbf{\theta }}}_{i1}^{\mathrm{mle}};{\mathbf{Y}}_1)\times L({\hat{\mathbf{\theta }}}_{i2}^{\mathrm{mle}};{\mathbf{Y}}_2)}\right],$$

where ${\mathbf{Y}}_1$ and ${\mathbf{Y}}_2$ denote response vectors for examinee i from Time 1 and Time 2, respectively, and ${\mathbf{Y}}_{1+2}$ is the combined response vector from two occasions; $L({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}};{\mathbf{Y}}_{1+2})$, $L({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}};{\mathbf{Y}}_1)$, and $L({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}};{\mathbf{Y}}_2)$ denote likelihood functions. The statistic is compared with a chi-square distribution with D degrees of freedom to determine the significance of change.

Score test (ST)

The ST is another commonly used method for testing hypotheses about parameters in a likelihood framework (Rao, 1948). The hypothesis under investigation is typically expressed as one or more constraints on the values of parameters; thus, the ST includes a restricted maximum likelihood estimation problem solved by the Lagrangian method. The ST requires only estimation of the parameters subject to the constraints specified by the null hypothesis:

$$\mathrm{LMT}=\mathbf{S}\left({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}\right)\prime {\mathbf{I}}^{-1}\left({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}\right)\mathbf{S}\left({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}\right){\tilde{\chi }}_{\mathrm{df}=D}^2.$$

In Equation 4, $\mathbf{S}({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}})$ is a 2D-by-1 vector computed from the first derivative of the log likelihood—it is the slope of the tangent line at ${\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}$ along the log-likelihood function. The first D elements of $\mathbf{S}({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}})$ are computed from

$${\mathbf{S}}_{D\times 1}\left({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}\right)=\frac{\mathrm{d}\log L(\mathbf{\theta };{\mathbf{Y}}_1)}{\mathrm{d}\mathbf{\theta }}{|}_{\mathbf{\theta }={\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}},$$

where $L(\mathbf{\theta },{\mathbf{Y}}_1)$ denotes the likelihood obtained from the response vector at Time 1. When the M3PL model in Equation 1 is used,

$${\mathbf{S}}_{D\times 1}\left({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}\right)=\sum _{j=1}^n{a}_{j1}\frac{[y_{\mathrm{ij}1}-P\left({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}\right)][P\left({\hat{\mathit{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}\right)-c_{j1}]}{P\left({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}\right)(1-c_{j1})},$$

where $y\mathrm{ij}1$ denotes examinee i’s response on item j at Time 1. Note that $\mathbf{I}({\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}})$ in Equation 4 is a 2D-by-2D block-diagonal matrix in which the first D-by-D block is the Fisher information matrix evaluated at ${\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}$ with the item parameters from Time 1. The second D-by-D block is the Fisher information matrix computed at ${\hat{\mathbf{\theta }}}_{\mathrm{pooled}}^{\mathrm{mle}}$ with the item parameters from Time 2.

Kullback–Leibler (KL) divergence test

This new test does not rely upon any point estimate of $\mathbf{\theta }$, and thus it avoids any possible contamination introduced by errors in the MLEs. The KL divergence is widely used for measuring the distance between two distributions (Cover & Thomas, 1991; Lehmann & Casella, 1998). In the current context, the divergence between two posterior distributions,$\mathrm{\pi }({\mathbf{\theta }}_{i1}|{\mathbf{Y}}_1)$ and $\mathrm{\pi }({\mathbf{\theta }}_{i1}|{\mathbf{Y}}_1)$, is of interest. If no significant change occurs, the KL distance will be close to 0; otherwise, the KL distance will be large. From a Bayesian theorem, for examinee i, the posterior distribution of ${\mathbf{\theta }}_{i1}$, given the responses to the test at Time 1, is computed as

$$\pi ({\mathrm{\theta }}_{i1}|{\mathbf{Y}}_1)=\frac{L({\mathrm{\theta }}_{i1},{\mathbf{Y}}_1)f\left(\mathrm{\theta }\right)}{\int ...\int L({\mathrm{\theta }}_{i1},{\mathbf{Y}}_1)f\left(\mathrm{\theta }\right)\partial \mathrm{\theta }},$$

where $L({\mathrm{\theta }}_{i1},{\mathbf{Y}}_1)$ denotes the likelihood as in Equation 3, and $f(\mathrm{\theta })$ denotes the prior. A noninformative flat prior was used throughout the study. The denominator is a D-fold multiple integral. $\mathrm{\pi }({\mathrm{\theta }}_{i2}|{\mathbf{Y}}_2)$ is computed in a similar fashion. Then, the KL divergence between the two posterior distributions is calculated as

$$\mathrm{KLD}=E_{\mathrm{\pi }({\mathrm{\theta }}_{i1}|Y_1)}\left[\log \frac{\mathrm{\pi }({\mathbf{\theta }}_{i1}|{\mathbf{Y}}_1)}{\mathrm{\pi }({\mathbf{\theta }}_{i2}|{\mathbf{Y}}_2)}\right].$$

Equation 8 can be numerically approximated by

$$\sum _{i_1=1}^q...\sum _{i_D=1}^q{\pi }^{*}([{\theta }_{i_1},...{\theta }_{i_D}]|{\mathbf{Y}}_1)\left[\log \frac{{\pi }^{*}([{\theta }_{i_1},...{\theta }_{i_D}]|{\mathbf{Y}}_1)}{{\pi }^{*}([{\theta }_{i_1},...{\theta }_{i_D}]|{\mathbf{Y}}_2)}\right],$$

where there are q quadrature points along each dimension, and ${\pi }^{*}([{\theta }_{i_1},...{\theta }_{i_D}]|{\mathbf{Y}}_1)$ and ${\pi }^{*}([{\theta }_{i_1},...{\theta }_{i_D}]|{\mathbf{Y}}_2)$ are normalized probability mass functions satisfying $\sum _{i_1=1}^q...\sum _{i_D=1}^q{\pi }^{*}([{\theta }_{i_1},...{\theta }_{i_D}]|{\mathbf{Y}}_1)=1$ and $\sum _{i_1=1}^q...\sum _{i_D=1}^q{\pi }^{*}([{\theta }_{i_1},...{\theta }_{i_D}]|{\mathit{Y}}_2)=1$. Although Equation 9 contains multiple summations which will be computationally intensive if D is large, if the test displays a simple structure, such computation can be expressed in matrix form to substantially reduce the calculation burden (see the appendix).

Belov and Armstrong (2011) showed that, under certain reasonable assumptions common in psychometrics, the distribution of KL divergence follows, asymptotically, a scaled (noncentral) chi-square distribution. Although their argument is based on a unidimensional latent trait, the same arguments can be made in the multidimensional case. It can be shown that, if the posterior covariance matrix of ${\mathbf{\theta }}_{i1}$ and ${\mathbf{\theta }}_{i2}$ from the two occasions are close, then KL divergence follows a chi-square distribution with D degrees of freedom. Therefore, for each examinee, the observed KL divergence can be compared with the chi-square distribution to compute the p value under the null hypothesis. Different from the other three tests, the KL test forms the test statistic based on the equivalency of the two posterior distributions.

Post Hoc Comparisons

The four hypothesis tests can all be viewed as omnibus tests to determine whether the two latent trait profiles are the same across two occasions. When the omnibus null hypothesis is rejected, it is equally important to identify the specific dimensions on which the significant change occurs. This post hoc comparison can be done using a simple univariate Z-test, but either (a) controlling for family-wise error rates using a Bonferroni correction (e.g., Dunn, 1961), or (b) controlling for false discovery rate using a Benjamini–Hochberg (BH) procedure (Benjamini & Hochberg, 1995). Specifically, for examinee i who is identified as having a significant change by one of the four omnibus tests,

$$Z_i^d=\frac{{({\hat{\mathrm{\theta }}}_{i1}^d-{\hat{\mathrm{\theta }}}_{i2}^d)}^2}{{\left({\mathbf{\Sigma }}_{{\hat{\mathrm{\theta }}}_{\mathbf{pooled}}^{\mathbf{mle}}}\right)}_{\mathrm{dd}}}$$

can be computed where ${\mathbf{\Sigma }}_{{\hat{\mathrm{\theta }}}_{\mathbf{pooled}}^{\mathbf{mle}}}$ is defined in Equation 2 and $({\mathbf{\Sigma }}_{{\hat{\mathit{\theta }}}_{\mathbf{pooled}}^{\mathbf{mle}}}{\mathbf{)}}_{\mathbf{dd}}$ denotes the dth diagonal element in this matrix. Then with Bonferroni correction, $Z_i^d$, computed for each dimension, can be compared with a standard normal distribution with significance level of $\mathrm{\alpha }/D$ . With the BH correction, $Z_i^d$ is compared with a standard normal distribution to obtain a corresponding p value, denoted as, $P_i^d$. Then all D p values are ranked in order from smallest to largest, $(P_i^d{)}_1,\dots ,(P_i^d{)}_k,\dots ,(P_i^d{)}_D$, where the subscript “k” denotes the kth smallest p value from the list. Each individual p value is then compared with the BH critical value, $(k/D)q$, where q is the false discovery rate. Then, find the largest $(P_i^d{)}_k$ that satisfies $(P_i^d{)}_k\le (k/D)q$, then all of the p values smaller than k are considered significant. Usually q is larger than α (McDonald, 2014), and while α = .05, q was chosen to be 0.15 in this study. This decision was made for two reasons: (a) conceptually, q = 0.15 indicates an expected 15% false discoveries among all the significant results across three dimensions, each of which could be considered as having a 5% false discovery per dimension²; (2) the simulation results presented below showed that setting q = 0.15 maintained good power and kept the Type I error rate below or at 0.05 (with only a few exceptions). Of course, setting a lower q value will further bring down the Type I error rate but at the sacrifice of the power. Note that in this study, only the simple univariate Z-test was considered for post hoc comparisons. The possibilities of modifying LR and ST for such purpose are discussed below.

Simulation Studies

Study I: Evaluating the Performance of the Omnibus Tests

Method

Using simulated repeated measures of test data, the performance of the proposed four omnibus tests was examined in terms of Type I error and power. A simulee’s latent trait profile at Time 1 (${\mathbf{\theta }}_{i1}$) was simulated from a multivariate normal distribution with a mean vector of 0s and a covariance matrix with 1s along the diagonal and 0.5s off the diagonals. This level of correlation is seen in real testing, such as the ASVAB (Armed Services Vocational Aptitude Battery; Yao, Pommerich, & Segall, 2014). To evaluate the power of each method, simulees’ profiles at Time 2 were generated from an LGC model, that is, ${\mathbf{\theta }}_{i2}={\mathbf{\theta }}_{i1}+{\mathbf{\beta }}_i+\mathbf{\epsilon }$, where the residuals, ε, followed a multivariate normal distribution with a mean vector of 0s and a diagonal covariance matrix with 0.5 along the diagonals. In this study, the residual variance was kept fixed because estimating θ was not the primary objective, but rather evaluating the efficiency of the proposed methods when the level of average change varied. The value of .5 was chosen such that the intraclass correlation (ICC) was approximately .66, which is close to the ICC in some real longitudinal data (e.g., Kwok et al., 2009). The individual slope parameter ${\mathbf{\beta }}_i$ also followed a multivariate normal distribution with a diagonal covariance matrix with 0.1 along the diagonals. This value was selected to allow enough variability across different simulees so that some might have a higher level of change than others. The mean of ${\mathbf{\beta }}_i$ increased from a vector of 0.2 to a vector of 0.8 (with 0.2 increment) to induce different levels of change. Multivariate change was computed as the average Euclidean distance between ${\mathbf{\theta }}_{i1}$ and ${\mathbf{\theta }}_{i2}$ (denoted as $\Vert {\mathbf{\theta }}_{i1}-{\mathbf{\theta }}_{i2}\Vert$ = $\sqrt{\sum _{d=1}^D{({\mathrm{\theta }}_{i1}^d-{\mathrm{\theta }}_{i2}^d)}^2}$) divided by the number of dimensions, D,

$$\mathbf{\Delta }=\frac{1}{N}\sum _{i=1}^N{\mathbf{\Delta }}_i=\frac{1}{N}\sum _{i=1}^N(\frac{1}{D}\Vert {\mathbf{\theta }}_{i1}-{\mathbf{\theta }}_{i2}\Vert ),$$

where D = 3, and N is the sample size. Equation 11 roughly indexes the average change along each dimension. This method generated an average change (i.e., quantified by the magnitude of Δ) in the latent traits that was similar to the observed change in patients’ depression levels before and after intervention (see Table 3, Brouwer, Meijer, & Zevalkink, 2013, or Finkelman et al., 2010). Sample size was set at 10,000. To evaluate Type I error of each method, no change was imposed; hence, ${\mathbf{\theta }}_{i1}$ = ${\mathbf{\theta }}_{i2}$ for that sample of 10,000 simulees.

Table 3.

Power for Post Hoc Comparisons at Four Levels of Multivariate Change (Δ) for a 60-Item Test.

Test structure	Change size (Δ)	Dimension 1			Dimension 2			Dimension 3
		No	B	BH	No	B	BH	No	B	BH
Simple structure	0.125	0.041	0.030	0.050	0.044	0.031	0.051	0.039	0.031	0.048
	0.251	0.104	0.086	0.119	0.096	0.073	0.112	0.099	0.069	0.120
	0.376	0.222	0.177	0.258	0.241	0.193	0.284	0.248	0.189	0.303
	0.502	0.398	0.334	0.449	0.398	0.306	0.466	0.380	0.280	0.469
Complex structure	0.125	0.044	0.011	0.050	0.044	0.012	0.050	0.046	0.012	0.053
	0.251	0.109	0.040	0.127	0.109	0.039	0.127	0.128	0.047	0.148
	0.376	0.192	0.083	0.235	0.219	0.095	0.262	0.235	0.107	0.295
	0.502	0.325	0.171	0.386	0.316	0.161	0.391	0.333	0.183	0.424

Note.“No” denotes no correction, “B” denotes Bonferroni correction, and “BH” denotes Benjamini–Hochberg correction.

Both within- and between-item multidimensionality structures were considered. For a between-item multidimensional test (i.e., simple structure), the item discrimination parameters were simulated from a normal distribution with a mean of 0 and a standard deviation of 0.15 with a scaling factor of 1.7 (Finkelman et al., 2010), the difficulty parameters were simulated from a N(0, 1) distribution, and the guessing parameters were simulated from a U[0, 0.2] distribution (e.g., C. Wang & Chang, 2011). It was assumed that the test measured three correlated dimensions. Test length was 15, 30, 60, or 90 items. For the complex structure tests, the item parameters were obtained from 30 dichotomously scored items in Reckase (2009, p. 153, Table 6.1), which were cloned and a very small distrurbance was added to create 60- and 90-item tests. A random half of the items were used for the 15-item condition. The scaling factor of 1.7 was used, as well.

Results

Tables 1 and 2 present the power and Type I error for the four hypothesis testing methods at four levels of multivariate change (Δ) and four test lengths for both the simple and complex multidimensional structures, respectively. There are several sailent trends in Table 1. First, and unsurprisingly, increasing the number of items always increased the power of all methods, regardless of Δ. This is because increasing test length increases the test information and thereby decreases the measurement error. Second, as the level of change increased, detecting individual change became easier, resulting in higher power. As shown in Table 2, the majority of the values of Type I error for the LR and ST fell close to the nominal level of .05 with ST being slightly more conservative, whereas for MZ and KL, Type I errors were generally above the .05 level, especially for short tests. ST and LR were relatively conservative among the four hypothesis tests but they both generated acceptably high power combined with low Type I error rate with reasonable test length.

Table 1.

Mean Power for Four Hypothesis Testing Methods at Four Levels of Multivariate Change (Δ) and Four Test Lengths for Simple and Complex Structure Data.

Test length and method	Simple structure				Complex structure
	0.493	0.624	0.800	1.008	0.491	0.620	0.800	1.001
15 items
MZ	0.272	0.313	0.563	0.721	0.271	0.381	0.525	0.618
LR	0.171	0.246	0.329	0.444	0.183	0.270	0.405	0.521
ST	0.127	0.252	0.286	0.326	0.150	0.219	0.335	0.453
KL	0.130	0.193	0.335	0.517	0.229	0.318	0.470	0.577
30 items
MZ	0.378	0.479	0.691	0.754	0.469	0.585	0.717	0.796
LR	0.293	0.423	0.498	0.713	0.385	0.509	0.650	0.743
ST	0.275	0.390	0.416	0.684	0.355	0.481	0.621	0.716
KL	0.264	0.421	0.577	0.732	0.461	0.589	0.721	0.807
60 items
MZ	0.563	0.660	0.814	0.898	0.610	0.719	0.826	0.882
LR	0.518	0.630	0.784	0.892	0.561	0.692	0.803	0.870
ST	0.499	0.619	0.754	0.885	0.551	0.690	0.801	0.876
KL	0.541	0.640	0.807	0.885	0.615	0.740	0.840	0.902
90 items
MZ	0.660	0.784	0.884	0.953	0.706	0.789	0.872	0.913
LR	0.629	0.761	0.877	0.952	0.671	0.777	0.860	0.911
ST	0.616	0.746	0.872	0.953	0.675	0.787	0.870	0.925
KL	0.639	0.783	0.869	0.949	0.706	0.806	0.889	0.932

Note. MZ = multivariate Z-test; LR = likelihood ratio test; ST = score test; KL = Kullback–Leibler test.

Table 2.

Type I Error Rate for Four Hypothesis Testing Methods at Four Test Lengths for Simple and Complex Structure Data.

Method	Simple structure				Complex structure
	15	30	60	90	15	30	60	90
MZ	0.247	0.114	0.089	0.066	0.149	0.095	0.078	0.078
LR	0.051	0.057	0.058	0.054	0.045	0.043	0.046	0.049
ST	0.044	0.046	0.052	0.052	0.023	0.032	0.040	0.049
KL	0.050	0.070	0.064	0.053	0.083	0.072	0.068	0.068

Note. MZ = multivariate Z-test; LR = likelihood ratio test; ST = score test; KL = Kullback–Leibler test.

Study II: Evaluating the Performance of the Post Hoc Comparisons

The second study was designed to evaluate whether the dimension(s) on which the psychometrically significant change occurred could be correctly identified for simulees who were classified as having significant change at the profile level. For this purpose, simulees’ latent profiles were simulated so that it was known exactly on which dimension(s) the true change occurred. Ignoring the direction of change, there were six core types of change patterns that encompassed all possible patterns of interest.

Method

In total, 60,000 examinees were simulated, evenly distributed among the six change patterns with 10,000 having each pattern. The θ vector at Time 1 was simulated from a multivariate normal distribution in the same way as in Study 1; the θ vector at Time 2 was simulated by adding a vector of (δ,δ,δ) along with a random disturbance vector to the θ vector at Time 1. Four levels of δ were considered: 0.25, 0.5, 0.75, and 1. The three-dimensional random disturbance vector was simulated from a multivariate normal distribution with a mean vector of 0 and a diagonal covariance matrix with 0.001 (to create a small disturbance) along the diagonals. Test length was fixed at 60 items, and LR was used for testing the omnibus hypothesis. Both simple and complex multivariate structures were examined. Power was computed as the proportion of 10,000 simulees of each change type (or simulees having a change on a certain dimension) correctly identified as having changed, whereas Type I error was computed as the proportion of the simulees not having a change on a certain dimension who were identified as having significant change.

Results

Tables 3 and 4 summarize the power and Type I error for the post hoc comparisons at four different levels of multivariate change. Consistent with both Tables 1 and 2, there was increased power with increased individual change. Type I error rate was uniformly lower (with two exceptions) than the nominal level of .05, which resulted in low power. The Bonferroni correction tended to be too conservative, and with only three comparisons, even without correction, the pairwise Z-test still maintained Type I error below .05. For the BH correction, because the false discovery rate was set at .15, the Type I error was slightly above .05 in some cases but with substantially higher power. Table 5 shows the power of detecting each level of change for different change patterns. For simple structure tests, when the change occurred on all three dimensions (Change Types 1-3), the power was the highest. When there was no change on certain dimensions (Types 4-6), the power decreased. The amount of power appears to be related to the Euclidean distance between the two θ vectors, as shown in Table 6, and that might be the reason why Type 5 yielded the lowest power among the six types.

Table 4.

Type I Error for Post Hoc Comparisons for a 60-Item Test.

Test structure	Dimension 2			Dimension 3
	No	B	BH	No	B	BH
Simple structure	0.036	0.024	0.051	0.048	0.030	0.074
Complex structure	0.026	0.006	0.039	0.025	0.006	0.042

Note.“No” denotes no correction, “B” denotes Bonferroni correction, and “BH” denotes Benjamini–Hochberg correction. Dimension 1 is not included due to the manner in which θs were simulated: A specific level of change was always added on the first dimension.

Table 5.

Power of Detecting Six Types of Change at Four Levels of Change (δ = 0.25, 0.50, 0.75, and 1.0) for a 60-Item Test Using the LR Test.

Type of change	Simple structure				Complex structure
	0.25	0.50	0.75	1.0	0.25	0.50	0.75	1.0
1 (+++)	0.075	0.218	0.470	0.701	0.113	0.395	0.727	0.813
2 (++−)	0.095	0.202	0.446	0.679	0.083	0.222	0.516	0.698
3 (+−−)	0.063	0.192	0.436	0.653	0.099	0.221	0.486	0.697
4 (++ 0)	0.089	0.149	0.337	0.524	0.084	0.216	0.438	0.648
5 (+0 0)	0.075	0.118	0.183	0.258	0.062	0.106	0.194	0.330
6 (+−0)	0.087	0.169	0.315	0.508	0.075	0.163	0.322	0.473

Note.“+” indicates positive change on a dimension, “0” indicates no change, and “−” indicates negative change. LR = likelihood ratio test.

Table 6.

Mean Δ by Change Type at Four Levels of Change for Simple Stucture Multidimensionality.

Type of change	Level of change
	0.25	0.50	0.75	1.0
1 (+++)	0.144	0.289	0.433	0.577
2 (++−)	0.144	0.289	0.433	0.577
3 (+−−)	0.144	0.289	0.433	0.577
4 (++ 0)	0.118	0.236	0.354	0.471
5 (+0 0)	0.083	0.167	0.250	0.333
6 (+−0)	0.118	0.236	0.354	0.471

Note.“+” indicates positive change on a domension, “0” indicates no change, and “–” indicates negative change.

A Real-Data Example

A real-data analysis was conducted to illustrate the performance of the four omnibus hypothesis testing methods. This data set contained 1,024 students’ responses to a math test in Grades 3 and 4. In each administration, 52 items were administered that measured five dimensions (the values in parentheses are the number of items measuring each dimension for each of the 2 years, respectively): (a) number and operation (22, 21); (b) geometry and spatial sense (5, 7); (c) data analysis, statistics, and probability (6, 7); (d) measurement (13, 9); and (e) algebra, functions, and patterns (6, 8). The entire test exhibited a simple structure as each item loaded only on one dimension based on item content. The item M3PL parameters were obtained from the field test sample with 6,682 observations. When the five-dimensional M3PL model was fit to the original field test sample using flexMIRT (Cai, 2013) for each time point separately, the full-information global fit statistic of the fitted model, root mean square error approximation (RMSEA), was 0.06 and 0.07, respectively. Different from the typical upper threshold of .08 for RMSEA (Hu & Bentler, 1999) for covariance structure models, the cutoff for bivariate RMSEA and full-information RMSEA for categorical data are 0.05 and 0.03, respectively (Maydeu-Olivares & Joe, 2014). According to these criteria, it was concluded that the five-dimensional M3PL showed some level of misfit to the data. However, the item parameter estimates were plausible and their corresponding standard errors were reasonable; hence, the item parameters were used for the follow-up analysis.³ All students had mixed response patterns on all items belong to each domain, thereby ensuring the MLEs to be finite. The four omnibus tests were performed using each student’s scored item responses, and each student was classified as either having significant change or not by every test.

Table 7 shows that the agreement between LR and ST was the highest (.870), whereas the agreement between KL and the other three was relatively low. Moreover, KL was the most conservative among the four, with the fewest number of students identified as having significant change: The proportion of significant change was 56%, 60%, 66%, and 27% for MZ, LR, ST, and KL, respectively. This observation contradicts the simulation results that KL is more liberal and thus more powerful; one possible reason is that the real test contained fewer items per domain than used in the simulation study, and therefore MLEs would be outwardly biased. As a result, significance tests that rely on MLEs would tend to capitalize on the outward bias and identify more students as having significant change. Another reason is that the KL test relies on the assumption of multivariate normality of the posterior distribution of θ, which might be violated with short tests and low test information. Therefore, the chi-square distribution might not be a good approximation to the sampling distribution of KL divergence, causing the lower power.

Table 7.

Classification Agreement Between Pairs of Significance Tests.

Method	MZ	LR	ST
LR	0.734
ST	0.716	0.870
KL	0.685	0.642	0.594

Note. MZ = multivariate Z-test; LR = likelihood ratio test; ST = score test; KL = Kullback–Leibler test.

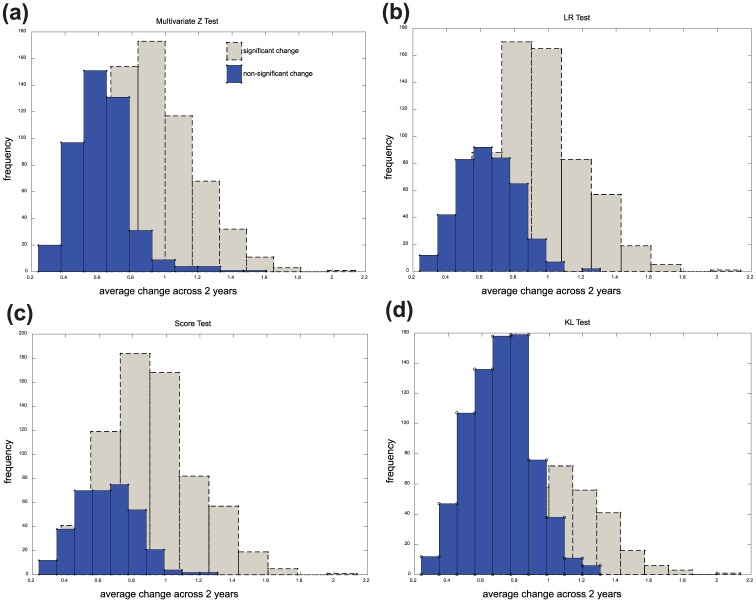
Figure 1 shows frequency histograms of students’ average change (defined by ${\Delta }_i$ in Equation 11) for each of the omnibus test methods. Unsurprisingly, for all four methods, students classified as having nonsignificant change tended to have lower average change than those who were classified as having significant change. KL was the most stringent test by classifying the majority of students as having no significant change, whereas ST was the most liberal test. The figures also show that a given degree of multivariate change was not a guarantee of significance or nonsignificance, except for the highest and lowest levels of change. For middle ranges of change, there were some students identified by all methods whose change was significant and others whose change was not.

Figure 1.

Histogram of average change (i.e., ${\Delta }_i$) for students with significant and nonsignificant change: (a) MZ, (b) LR, (c) ST, and (d) KL.

Note. MZ = multivariate Z-test; LR = likelihood ratio test; ST = score test; KL = Kullback–Leibler test.

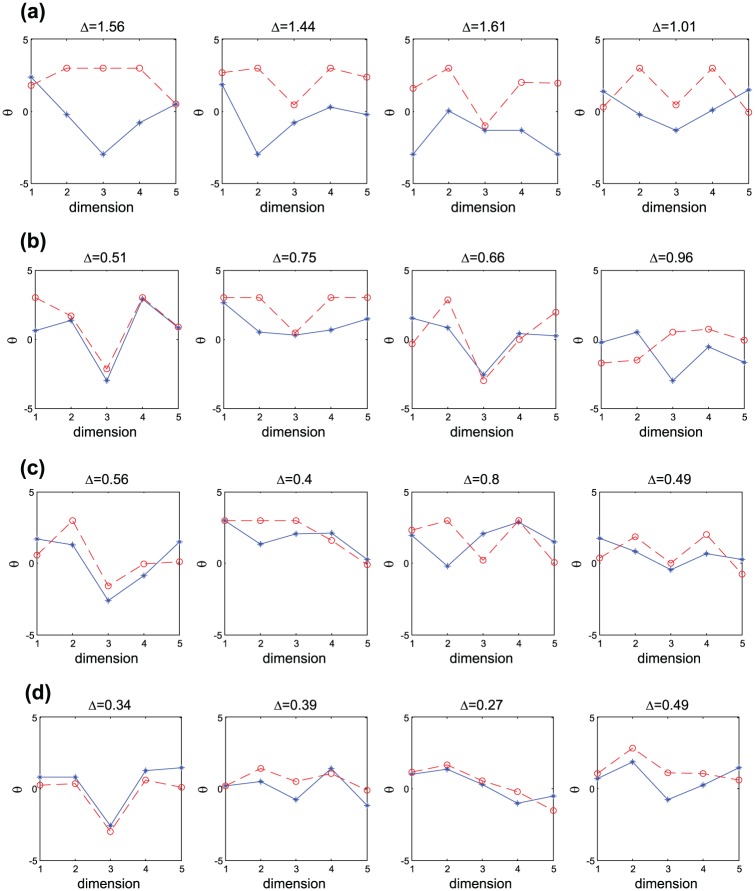
Figure 2 shows score profiles for selected students with varying levels of change for each of the 2 years. The general trend is clear that if a student is identified as having a significant change by more methods, then the actual estimated change of ${\Delta }_i$ is generally larger, even though the reverse pattern also exists. The figure also shows that for those students for whom change was reliably identified by the four methods (Figure 2a and 2b), both the pattern and level of change varied across students, as did their patterns of scores on both testing occasions.

Figure 2.

Cognitive profiles of individual students in Year 1 (—) and Year 2 (--) for different levels of change (i.e., ${\Delta }_i$): Profiles of (a) four students who had significant change identified by all four methods, (b) four students who had significant change identified by three of four methods, (c) four students who had significant change identified by either one or two methods, and (d) four students who were classified by all four methods as having no significant change.

Discussion and Conclusion

Individual Change Versus Group Change

A measure of individual change is useful when (a) it can differentiate change that is due only to random factors (e.g., error of measurement) from change that is meaningful, (b) it is able to measure change that occurs across two or more measurement occasions, (c) it is applicable to measurements of any kind of psychological and educational variable, and (d) it provides results that can be immediately available for use in an applied setting.

The methods for determining change developed and evaluated in this research have the potential to satisfy all of these criteria. Because they are based in IRT, they permit measurements that are entirely intra-individual. Once IRT item parameters are estimated on a previous sample, only those parameter estimates and a single examinee’s responses to a subset of items are necessary to estimate an examinee’s θ levels and corresponding standard errors of measurement, both of which are used in various ways by the change methods analyzed here.

The change methods studied are designed to permit a determination of whether a single examinee’s observed change is meaningful or “psychometrically significant.”“Significance” is based on psychometric theory, utilizing the characteristics of the likelihood function from a single person, and thus observed change is determined to be “psychometrically significant.”

Group-based methods for analyzing change, such as LGC modeling, can also produce estimates of individual change. The individual intercept and slope are obtained via a simple closed form, known as the empirical Bayes estimate. Moreover, when group information is taken into consideration, the correlations among multiple dimensions can be used, which echoes the statistical advantage of “borrowing strength” from correlated dimensions in MIRT. As a result, an individual’s latent traits can be more accurately estimated with smaller measurement errors (e.g., Reckase, 2009; C. Wang, 2015; C. Wang & Chang, 2011). However, as indicated above, the individual parameters are obtained relative to the group in which the individual is embedded; hence, an individual’s change trajectory might take different shapes depending on the group information. This is less ideal than the intra-individual change method advocated in this study. Moreover, the methods proposed here have two other advantages as compared with the popular alternatives, such as LGC modeling: (a) The present methods can be used with as few as two measurement occasions: regression slopes and intercepts based on two observations for a single individual will have very large standard errors and will be difficult to classify as “statistically significant” using statistical sampling theory; (b) when generalized beyond two occasions (Phadke & Weiss, 2017), these methods do not require the specification of a functional relationship describing change (e.g., linear, quadratic); instead, change is evaluated and the nature of the functional relationship can be determined afterward at the individual level.

The change methods studied were originally developed to detect significant change on a single variable across two measurement occasions (Finkelman et al., 2010). The present research extended the number of variables to three in the simulation studies and five in the real-data analysis. The methods, therefore, can be used with any number of measurements taken on an examinee on two occasions. Because the simple and complex structure tests used in the study utilized items from different distributions, a direct comparison between the two test structures was not possible, nor was it the intention of the study. Instead, the studies were designed to assess the performance of the methods under conditions commonly encountered in practice. Although simple structure emerges in many real tests (such as the ASVAB, or in the real-data example), as more measurements are taken on an examinee, the possibility arises that the factorial structure will become more complex. In either case, increasing test information (by, for instance, increasing the values of a parameters) will help improve the power of the tests.

Main Findings and Significance

Willett (1988, 1997) has argued that a proper analysis of change requires measurement on a single variable on more than two occasions. Although the present change methods have been studied only for the two-occasion case, their generalization to multiple occasions is straightforward. Work is underway to accomplish this generalization and to evaluate the performance of the change methods when an individual is measured on more than two occasions. Because the change methods have been developed within the context of IRT, they can be used with any type of measurements that can be fit with an IRT model, whether it is dichotomously or polytomously scored. The final generalization of the methods proposed here is to extend them to simultaneously analyze individual change on more than two measurements taken on more than two occasions.

As indicated, a change detection method is maximally useful when its results provide actionable data. Obviously, because of the IRT underpinnings of these methods, psychological practitioners will not be able to compute them in an applied setting. However, as electronic testing and IRT-based tests continue to replace paper-and-pencil testing in many testing programs, the computations necessary to determine significant change can easily be programmed into the output from major testing programs. Any testing program that delivers its instruments electronically could incorporate the change methods studied here to provide psychologists and educators, on retest of any examinee, with instant determinations of significant change on one or more measured variables.

Simulation studies using artificial data demonstrated the promise of all four change detection methods, among which both the ST and LR test provided good balance between high power and low Type I error rate. Because the power is slightly low when test length is short, one future direction is to use computerized adaptive testing (CAT), because CAT can provide more precise measurements with a given number of items, thus reducing the effects of measurement errors in the detection of change and thereby providing the potential for improved power. All methods for the measurement of change are based on the assumption that the latent construct of interest is invariant across measurement occasions. This assumption can be formally checked (see Liu et al., 2016, for details).

The real-data results demonstrated the complexity of multivariable change over two testing occasions. Figure 2 shows that, for a given level of multivariate change, psychometric significance is not guaranteed, particularly in the middle ranges of average change. This is due to (a) the differing levels of change that result in a given amount of average change and (b) the different precision associated with each examinee’s measured level of change on each variable. A similar observation was made by Phadke et al. (2016) based on unidimensional change data in reading and math. Figure 2 also demonstrates the complexity of multivariate change. In Figure 2a and 2b, different students have different levels and patterns of test scores at both Time 1 and Time 2, resulting in different levels and patterns of significant change across students.

Future Studies

As the first study to investigate the identification of significant multivariate individual change using IRT, the generality of the findings is, of course, limited. Further research is needed with more than three dimensions, more than two occasions, a wider range of multivariate structures (e.g., bifactor structures, other complex structures), different IRT models (e.g., Hong, Wang, Lim, & Douglas, 2015; W. C. Wang, Qiu, Chen, Ro, & Jin, 2017), and different post hoc tests that were not evaluated in the current study. Future research should also examine the application of these methods within the context of multivariate CAT and consider the performance of various omnibus tests coupled with different item selection rules in CAT (e.g., Finkelman et al., 2010).

To elaborate on the post hoc comparisons, take LR test as an example. If testing ${\mathrm{H}}_0:{\mathrm{\theta }}_{i1}^d={\mathrm{\theta }}_{i2}^d={\mathrm{\theta }}_i^d$ against ${\mathrm{H}}_a:{\mathrm{\theta }}_{i1}^d\ne {\mathrm{\theta }}_{i2}^d$, then under the null hypothesis, the likelihood is maximized with respect to ${\theta }_i^d$, ${\mathrm{\theta }}_{i1}^{-d}$, ${\mathrm{\theta }}_{i2}^{-d}$ jointly, where the superscript “–d” indicates all but the dth component of the latent trait. Under the alternative hypothesis, the likelihood is maximized at ${\hat{\mathbf{\theta }}}_{i1}^{\mathrm{mle}}$ and ${\hat{\mathbf{\theta }}}_{i2}^{\mathrm{mle}}$ as before. Then the LR statistic is compared with a chi-square distribution with one degree of freedom. The ST can also be modified in a similar fashion. That is, let ${\mathbf{\theta }}_{H_0}=({\mathrm{\theta }}_i^d,{\mathrm{\theta }}_{i1}^{-d}{\mathrm{\theta }}_{i2}^{-d})$ denote a 2D-by-1 vector after putting the elements in ${\mathrm{\theta }}_i^d$, ${\mathrm{\theta }}_{i1}^{-d}$, ${\mathrm{\theta }}_{i2}^{-d}$ in appropriate order, then the test statistic becomes $\mathrm{ST}=\mathit{S}({\mathbf{\theta }}_{H_0})\prime {\mathit{I}}^{-1}({\mathbf{\theta }}_{H_0})\mathit{S}({\mathbf{\theta }}_{H_0})~{\mathrm{\chi }}_{\mathrm{df}=1}^2$. The performance of the LR and Lagrange multiplier (LM) statistics for post hoc comparisons should be evaluated in future studies.

Appendix

Matrix Computation of Kullback–Leibler (KL) Divergence

Consider 61 points spanning from −3 to 3 with 0.1 increments along each ability dimension, and let ${\mathbf{\pi }}_1$ denote a 61-by-D matrix, with the (l, d)th element being $\underset{j=1}{\overset{n_d}{\Pi }}P{({\mathrm{\theta }}_i^d)}^{\mathrm{ij}}{(1-P({\mathrm{\theta }}_i^d))}^{1-\mathrm{ij}}$. ${\mathbf{\pi }}_2$ is computed similarly with item parameters and the response vector from the second occasion. Then the likelihood at every possible ability point (there are ${61}^D$ points in total) forms a ${61}^{D-1}$-by-61 matrix ${\mathbf{Ɵ}}_t$ computed recursively as ${\mathbf{Ɵ}}_t^d={\mathbf{Ɵ}}_t^{d-1}\otimes {\mathbf{\pi }}_t^d$, for t = 1 or 2, and D > 2, d = 2,. . ., D. ${\mathbf{\pi }}_t^d$ denotes the dth column of ${\mathbf{\pi }}_t$, ⊗ denotes Kronecker products, and ${\mathbf{Ɵ}}_t^2={\mathbf{\pi }}_t^1({\mathbf{\pi }}_t^2{)}^T$ when D = 2. After expressing the posterior likelihood as a matrix operation in matrix form, the computation of Equation 9 becomes much simpler. In all computations, only one loop with 61 iterations is needed, regardless of the size of D.