FUN-LDA: A Latent Dirichlet Allocation Model for Predicting Tissue-Specific Functional Effects of Noncoding Variation: Methods and Applications

Abstract

We describe a method based on a latent Dirichlet allocation model for predicting functional effects of noncoding genetic variants in a cell-type- and/or tissue-specific way (FUN-LDA). Using this unsupervised approach, we predict tissue-specific functional effects for every position in the human genome in 127 different tissues and cell types. We demonstrate the usefulness of our predictions by using several validation experiments. Using eQTL data from several sources, including the GTEx project, Geuvadis project, and TwinsUK cohort, we show that eQTLs in specific tissues tend to be most enriched among the predicted functional variants in relevant tissues in Roadmap. We further show how these integrated functional scores can be used for (1) deriving the most likely cell or tissue type causally implicated for a complex trait by using summary statistics from genome-wide association studies and (2) estimating a tissue-based correlation matrix of various complex traits. We found large enrichment of heritability in functional components of relevant tissues for various complex traits, and FUN-LDA yielded higher enrichment estimates than existing methods. Finally, using experimentally validated functional variants from the literature and variants possibly implicated in disease by previous studies, we rigorously compare FUN-LDA with state-of-the-art functional annotation methods and show that FUN-LDA has better prediction accuracy and higher resolution than these methods. In particular, our results suggest that tissue- and cell-type-specific functional prediction methods tend to have substantially better prediction accuracy than organism-level prediction methods. Scores for each position in the human genome and for each ENCODE and Roadmap tissue are available online (see Web Resources).

Introduction

Understanding the functional consequences of noncoding genetic variation is one of the most important problems in human genetics. Comparative genomics studies suggest that most of the mammalian conserved and recently adapted regions consist of noncoding elements.^{1, 2, 3} Furthermore, most of the loci identified in genome-wide association studies (GWASs) fall in noncoding regions and are likely to be involved in gene regulation in a cell-type- and tissue-specific manner.⁴ Noncoding variants are also known to play an important role in cancer. Somatic variants in noncoding regions can act as drivers of tumor progression, and germline noncoding variants can act as risk alleles.⁵ Thus, improved understanding of tissue-specific functional effects of noncoding variants will have implications for multiple diseases and traits.

Prediction of the functional effects of genetic variation is difficult for several reasons. To begin with, there is no single definition of function. As previously discussed,⁶ there are several possible definitions depending on whether one considers genetic, evolutionary conservation, or biochemical perspectives. These different approaches each have limitations and vary substantially with respect to the specific genomic regions that they predict to be functional. In particular, the genetic approach, which is based on experimental evaluation of the phenotypic consequence of a sequence alteration (e.g., through measurement of the impact of individual alleles on gene expression in a particular context, massively parallel reporter assays [MPRAs],⁷ and CRISPR/Cas-9 mediated in situ saturating mutagenesis⁸), is currently laborious, has modest throughput, and can miss elements that lead to phenotypic effects only in rare cells or specific contexts. The evolutionary approach relies on accurate multispecies alignment, which makes it challenging to identify certain functional elements, such as distal regulatory elements, known to evolve rapidly, although recently several approaches have been developed for primate- or even human-specific elements.⁹ An additional limitation of the evolutionary approach is that it is not sensitive to tissue or cell type. Finally, the biochemical approach adopted by projects such as ENCODE³ and Roadmap Epigenomics,¹⁰ although helpful in identifying potentially regulatory elements in specific contexts, does not provide definitive proof of function given that the observed biochemical signatures can occur stochastically and in general are not completely correlated with function. Besides the difficulty in precisely defining function, a challenge is that the use of functional genomics features from ENCODE and Roadmap Epigenomics (e.g., chromatin immunoprecipitation sequencing [ChIP-seq] and DNase I hypersensitive site [DHS] signals) are mostly useful for predicting the effects of variants in cis-regulatory elements, such as promoters, enhancers, silencers, and insulators. Other classes of functional variants, for example, those with effects on post-transcriptional regulation by alteration of RNA secondary structure or RNA-protein interactions, would be missed by these features.

Recently, several computational approaches have been proposed for the prediction of functional effects of genetic variation in noncoding regions of the genome on the basis of epigenetic and evolutionary conservation features.^{2, 11, 12, 13, 14, 15, 16} These predictions are at the organism level and are not specific to particular cell types or tissues. Here, we are interested in predicting functional effects of genetic variants in specific cell types and tissues. The ENCODE and Roadmap Epigenomics projects have profiled various epigenetic features, including histone modifications and chromatin accessibility, genome-wide in more than a hundred different cell types and tissues. Histone modifications are chemical modifications of the DNA-binding histone proteins and influence transcription as well as other DNA processes. Particular histone modifications have characteristic genomic distributions.¹⁷ For example, trimethylation of histone H3 lysine 4 (H3K4me3) is associated with promoter regions, monomethylation of histone H3 lysine 4 (H3K4me1) is associated with enhancer regions, and acetylation of histone H3 lysine 27 (H3K27ac) and of histone H3 lysine 9 (H3K9ac) are associated with increased activation of enhancer and promoter regions.¹⁰ Repressive marks include trimethylation of histone H3 lysine 27 (H3K27me3) and trimethylation of histone H3 lysine 9 (H3K9me3), both associated with inactive promoters of protein-coding genes; H3K27me3 is found in facultatively repressed genes by Polycomb-group factors, whereas H3K9me3 is found in heterochromatin regions corresponding to constitutively repressed genes.¹⁸ Dozens of chromatin marks have been assayed in large numbers of different cell types and tissues, and studying them individually is inefficient.

Several unsupervised approaches exist for the integration of these epigenetic features in specific cell types and tissues. Such integrative approaches reflect the belief that epigenetic features interact with one another to control gene expression. One class of methods attempts to segment the genome into non-overlapping segments, representing major patterns of chromatin marks, and labels these segments by using a small set of labels, such as active transcription start site, enhancer, strong transcription, weak transcription, quiescent, etc. This class includes methods such as ChromHMM^{10, 19, 20} and Segway,²¹ which are based on hidden Markov models (HMMs) and dynamic Bayesian networks (DBNs), respectively. ChromHMM is based on the complete pooling of data from multiple tissues and fitting a single model to this superdataset, whereas Segway is based on fitting separate models to data from each tissue (no pooling). Various extensions of these early segmentation approaches have been proposed. Several approaches have focused on better modeling the read count data by using Poisson-lognormal and negative multinomial distributions,^{22, 23} whereas others have focused on better modeling of the correlations among related cell types and tissues.^{24, 25, 26} Yet another approach attempts to improve the HMM parameter estimation procedure in ChromHMM by replacing the expectation-maximization algorithm with a spectral learning procedure.²⁷ Another class of methods focuses exclusively on predicting functional effects of variants rather than segmenting the genome as discussed above. A recent method in this class, GenoSkyline,²⁸ is based on fitting a two-component mixture model of multivariate Bernoulli distributions to epigenetic data for each tissue separately and then computing a posterior probability that each variant is in the functional class. Recently, several supervised approaches have been proposed as well, and these include deltaSVM²⁹ and cepip.³⁰ Although supervised approaches can be more efficient than the unsupervised ones when high-quality, unbiased labeled data are available for training, unsupervised approaches as proposed here can provide more robust, less biased functional predictions across a large number of tissues and cell types when such unbiased labeled data are scarce, as it is the case now.

We introduce here an integrated functional score that combines different epigenetic features in specific cell types and tissues. Our model is based on the latent Dirichlet allocation (LDA) model,³¹ a generative probabilistic model that is often used in the topic modeling literature and allows joint modeling of data from multiple cell types and tissues. In our context, the latent functional classes correspond to latent topics in the topic modeling setting, the various tissues correspond to different documents, and the tissue-specific variant scores correspond to words in a document. The proposed LDA model has several advantages. First, our method makes no distributional assumptions on the data, allowing us to avoid various data transformations employed by other approaches (such as binary peak calling or dichotomization) and facilitating the integration of annotation data on the original scale (e.g., quantitative, binary, etc.). Second, because the model is fit jointly to data from multiple cell types and tissues, cross-tissue comparisons are meaningful. Third, relative to existing methods, our method can improve the precision of locating functional variants. Fourth, even though we provide only functional scores in the tissues and cell types available in Roadmap, it is easy to perform functional prediction in additional cell types and tissues once the model has been fit to the original Roadmap data. Furthermore, although we regard FUN-LDA as primarily an approach for performing cell-type- and tissue-specific functional prediction, we additionally assign functional variants to “active promoter” or “active enhancer” elements.

In the Results section, we demonstrate the usefulness of our predictions through several validation experiments. In summary, we present the following results: (1) we provide cell-type- and tissue-specific functional predictions for every possible position in the hg19 human genome build (UCSC Genome Browser) for 127 cell types and tissues in Roadmap, (2) we provide a global view of the sharing of predicted functional variants across a large number of cell types and tissues and show that predicted functional variants that fall in enhancers are more likely to be tissue specific than those that fall in promoters, (3) we show that expression quantitative trait loci (eQTLs) identified in specific tissues from several sources (Genotype-Tissue Expression [GTEx] project, Geuvadis, and TwinsUK) tend to be most enriched among the predicted functional variants in a relevant Roadmap tissue, (4) we use these cell-type- and tissue-specific scores in conjunction with summary statistics from 21 GWASs to identify the most likely causal cell type or tissue implicated for a particular trait and estimate a tissue-based correlation matrix among these complex traits, and (5) we use experimentally validated functional variants in the literature and variants possibly implicated in disease by previous studies to rigorously compare FUN-LDA with state-of-the-art tissue- and cell-type-specific functional annotation methods, such as GenoSkyline,²⁸ ChromHMM,¹⁹ Segway,²¹ IDEAS,²⁶ deltaSVM²⁹ (when available), and cepip,³⁰ as well as organism-level functional prediction methods, such as CADD,¹¹ Eigen,¹³ DANN,¹⁴ DeepSea,¹⁵ and LINSIGHT.¹⁶

Material and Methods

LDA Model for Functional Annotation

We propose an application of the LDA model,³¹ a generative probabilistic model, in the setting of functional genomics annotations with the goal of computing posterior probabilities that variants belong to different functional classes.

Let us assume that we have a set of m genetic variants in the training set together with a set of k functional annotations. For each variant i, we have k tissue-specific functional scores: X_i = (X_i1, …, X_ik). Let X = (X₁, …, X_m) be the set of (continuous) functional scores for all the variants. These scores are epigenetic features (histone modifications and DNase) from ENCODE and Roadmap Epigenomics across a varied set of tissues and cell types. Let l be the number of tissues and m_j be the number of variants with tissue j annotations in the training set $\left(m={\sum }_{j=1}^l{m}_j\right)$. For each variant i ≤ m in the training set, we denote by t_i the corresponding tissue (i.e., the annotations corresponding to this variant are for tissue t_i). For each tissue, the variants’ scores are represented as a mixture over latent functional classes, where each functional class is characterized by a distribution over variant scores. In what follows, for ease of presentation, we assume only two latent functional classes, but the number of classes can be chosen to be greater than two (see Choosing the Number of Functional Classes in the LDA Model according to the Perplexity Measure for a discussion on the choice of the number of functional classes). We let C = (C₁, …, C_m) denote the set of indicator variables for all the variants, where C_i = 1 if variant i belongs to the first functional class and C_i = 0 otherwise. We are not able to observe C.

Let α = (α₀, α₁) be the hyperparameter vector with α₀ and α₁ > 0. We assume that the functional annotation data have been generated from the following generative model:

• (1)For each tissue j, choose (1 − π_j, π_j) ∼ Dir(α₀, α₁).
• (2)Given π_j, for each variant i with t_i = j, choose a class C_i ∼ Bern(π_j).
• (3)Given C₁, …, C_m, X₁, …, X_m are independently generated such that each X_i is generated from the appropriate multivariate distribution: F₁ if C_i = 1 and F₀ otherwise.

Here, π = (π₁, … π_l) and C are latent variables. We want to calculate the posterior probability that each variant i is in the first functional class,

$$w_i=P\left(C_i=1|\mathit{X},\mathit{\alpha }\right),$$

and the densities f₀ and f₁. Also, we want to estimate the hyperparameter α = (α₀, α₁) empirically by using X. For a given tissue, the conditional density of (π, C) given X and α is

$$p\left(\pi ,\mathit{C}|\mathit{X},\mathit{\alpha }\right)=\frac{p\left(\pi ,\mathit{C},\mathit{X}|\mathit{\alpha }\right)}{p\left(\mathit{X}|\alpha \right)}.$$

For the numerator, we have

$$p\left(\pi ,\mathit{C},\mathit{X}|\mathit{\alpha }\right)=p\left(\pi |\mathit{\alpha }\right)\prod _{i=1}^{m}p\left(C_i|\pi \right)p\left({\mathit{X}}_i|C_i\right).$$

This is easy to compute. However, the denominator is not. For the denominator, we have

$$p\left(\mathit{X}|\mathit{\alpha }\right)=\int p\left(\pi |\mathit{\alpha }\right)\left(\prod _{i=1}^m\sum _{C_i}p\left(C_i|\pi \right)p\left({\mathit{X}}_i|C_i\right)\right)d\pi .$$

There are 2^m terms in the summation, so this is difficult to compute for moderately large m. We propose instead to use a variational approach as previously described.³¹ In the variational inference approach, we first introduce a family of distributions {q(·,· | a, w)} over the latent variables (π, C) with its own variational parameters α = (α₀, α₁) and w (these are tissue-specific parameters).

Then

$$q\left(\pi ,\mathit{C}|\mathit{a},\mathit{w}\right)=q\left(\pi |\mathit{a}\right)\prod _{i=1}^{m}q\left(C_i|w_i\right),$$

where q(π | a) is the density of Dir(a), and q(C_i | w_i) is the probability mass function of Bern(w_i) for i = 1 … m.

Using Jensen’s inequality, we have

$$\log p\left(\mathit{X}|\mathit{\alpha }\right)=\text{log}\int \sum _{\mathit{C}}p\left(\mathit{\pi },\mathit{C},\mathit{X}|\mathit{\alpha }\right)d\mathit{\pi }=\text{log}\int \sum _{\mathit{C}}\frac{p\left(\mathit{\pi },\mathit{C},\mathit{X}|\alpha \right)}{q\left(\mathit{\pi },\mathit{C}|\mathit{a},\mathit{w}\right)}q\left(\mathit{\pi },\mathit{C}|\mathit{a},\mathit{w}\right)d\pi \ge \int \sum _{\mathit{C}}q\left(\mathit{\pi },\mathit{C}|\mathit{a},\mathit{w}\right)\log p\left(\mathit{\pi },\mathit{C},\mathit{X}|\mathit{\alpha }\right)d\mathit{\pi }-\int \sum _{\mathit{C}}q\left(\mathit{\pi },\mathit{C}|\mathit{a},\mathit{w}\right)\log q\left(\mathit{\pi },\mathit{C}|\mathit{a},\mathit{w}\right)d\pi =E_q\log p\left(\mathit{\pi },\mathit{C},\mathit{X}|\alpha \right)-E_q\log q\left(\mathit{\pi },\mathit{C}|\mathit{a},\mathit{w}\right)=L\left(\mathit{a},\mathit{w}|\mathit{\alpha }\right).$$

Note that L(a, w | α) is a lower bound on the log likelihood. So instead of maximizing the log likelihood directly, we maximize this lower bound with respect to the variational parameters a and w, as well as the hyperparameter α. It can be shown that log p(X | α) − L(a, w | α) is the Kullback-Leibler (KL) divergence between the true posterior p(π, C | α, X) and the variational posterior q(π, C | a, w) with respect to q(π, C | a, w). Therefore, by maximizing L(a, w | α) with respect to a and w, we minimize the KL divergence between the variational posterior probability and the true posterior probability. Then we can estimate P(C_i = 1 | α, X) by w_i for each variant i. Below, we describe the variational inference algorithm.

Variational Inference Algorithm

Assume the initial state (w₁, …, w_m, f₀, f₁, α). The algorithm proceeds as follows:

Step 1: Kernel Density Estimation

Fit a multivariate kernel density estimate for each annotation and component separately ($f_{0s}^{\text{new}}$ and $f_{1s}^{\text{new}}$ for each annotation s = 1, …, k) by weighting variants by component membership probability. Specifically, for any $\mathbf{x}=\left(x_1,\dots ,x_k\right)\in {\mathbb{R}}^k$ and s = 1, …, k, we let

$$f_{0s}^{\text{new}}\left(x_s\right)=\frac{{\sum }_{i=1}^m\left(1-w_i\right){\text{K}}_{h_s}\left(x_s-X_{is}\right)}{{\sum }_{i=1}^m\left(1-w_i\right)}$$

and

$$f_{1s}^{\text{new}}\left(x_s\right)=\frac{{\sum }_{i=1}^m{w}_i{\text{K}}_{h_s}\left(x_s-X_{is}\right)}{{\sum }_{i=1}^m{w}_i}.$$

The scaled kernel ${\text{K}}_{h_s}\left(a\right)=\left(1/h_s\right)K\left(a/h_s\right)$, where K(·) is taken to be the probability density function of a standard normal, and the bandwidth parameter h_s is chosen to be

$$h_s=0.9\min \left\{{\text{SD}}_s,{\text{IQR}}_s/1.34\right\}{m}^{-1/5}$$

according to a rule of thumb from Silverman,³² where SD_s and IQR_s are the standard deviation and interquartile range of annotation s, respectively. Then,

$$f_0^{\text{new}}\left(\mathit{x}\right)=\prod _{s=1}^k{f}_{0s}^{\text{new}}\left(x_s\right)\text{and}{f}_1^{\text{new}}\left(\mathit{x}\right)=\prod _{s=1}^k{f}_{1s}^{\text{new}}\left(\mathit{x}\right).$$

Step 2: Variational Step

For each tissue j, we obtain w_i for all variants i with t_i = j and $\left(a_0^j,a_1^j\right)$ by maximizing the lower bound on the marginal likelihood of X, i.e., L(a, w | α), with respect to a and w. Details are shown in the Supplemental Data.

This results in the following iterative algorithm:

$$\begin{array}{c}{w}_i=\frac{f_1\left({\mathbf{X}}_i\right)\text{exp}\left(\text{Ψ}\left(a_1^j\right)\right))}{f_1\left({\mathbf{X}}_i\right)\text{exp}\left(\text{Ψ}\left(a_1^j\right)\right)+f_0\left({\mathbf{X}}_i\right)\text{exp}\left(\text{Ψ}\left(a_0^j\right)\right)}\text{for}\text{variants}i\text{with}{t}_i=j,\\ a_0^j={\alpha }_0+\sum _{t_i=j}\left(1-w_i\right)\text{and}{a}_1^j={\alpha }_1+\sum _{t_i=j}{w}_i,\end{array}$$

where $\text{Ψ}\left(x\right)=d\log \text{Γ}\left(x\right)/dx$, and $\text{Γ}\left(x\right)$ is the gamma function.

Step 3: Newton-Raphson Algorithm for Estimating the Hyperparameters α

Obtain the empirical Bayes estimate of α = (α₀, α₁) by maximizing the bound L(a, w | α) with the Newton-Raphson algorithm, where a and w are from step 2. That is, we find optimal α by iterating

$${\mathit{\alpha }}_{n+1}\leftarrow {\mathit{\alpha }}_n-H^{-1}\left({\mathit{\alpha }}_n\right)\nabla L\left({\mathit{a}}^{\text{new}},{\mathit{w}}^{\text{new}}|{\mathit{\alpha }}_n\right),$$

where H(α) is the Hessian matrix evaluated at current α.

The gradient $\nabla L\left(\mathit{\alpha }\right)$ has this form:

$$\frac{\partial L\left(\mathit{\alpha }\right)}{\partial {\alpha }_r}=l\left(\text{Ψ}\left({\alpha }_0+{\alpha }_1\right)-\text{Ψ}\left({\alpha }_r\right)\right)+\sum _{j=1}^l\left(\text{Ψ}\left(a_r^j\right)-\text{Ψ}\left(a_0^j+a_1^j\right)\right)\text{for}r=0,1.$$

The Hessian matrix takes the following form:

$$H\left(\mathit{\alpha }\right)=\text{Diag}\left(l{\text{Ψ}}^{\text{'}}\left({\alpha }_0\right),l{\text{Ψ}}^{\text{'}}\left({\alpha }_1\right)\right)-l{\text{Ψ}}^{\text{'}}\left({\alpha }_0+{\alpha }_1\right){11}^{\text{'}}.$$

LDA Implementation

We have implemented the above algorithm in an R package, FUNLDA. In our implementation, we assume a symmetric Dirichlet prior, with α = 1, corresponding to a uniform distribution. For training purposes, we select 4,000 random positions in each of the 127 tissues. The positions are chosen among 9,254,335 single-nucleotide polymorphisms (SNPs) with a minor allele count greater than 5 in European samples from the 1000 Genomes Project. We have also looked at other ways to select variants in the training set (e.g., randomly from across the entire genome or with enrichment near genes), and the results were similar, suggesting that our predictions are robust to the choice of variants used in the training sets. The number of outer iterations in the variational inference algorithm is 250, and the number of inner iterations is 200.

We compute FUN-LDA by fitting the LDA model with nine classes to valley scores for the four activating histone modifications (H3K4me1, H3K4me3, H3K9ac, and H3K27ac) and quantitative DNase. For the histone modifications and DNase, we start with the negative log₁₀ of the Poisson p value of ChIP-seq or DNase counts relative to expected background counts, as output by ChromImpute.²⁰ The valley scores are computed as previously reported;³³ for every window of 25 bp, we calculate the maximum score for the two regions from −100 to −500 bp and from 100 to 500 bp. If the score at the 25 bp window is less than 90% of the minimum of those two maxima, we set the value in that window to that minimum. Otherwise, we set the value in that 25 bp window to 0. For each variant, we get a set of nine posterior probabilities that the variant is in a specific functional class. To get a functional score, we sum the posterior probabilities for the active functional classes, namely active promoters and active enhancers (Figure S1 and Table S1).

Prediction in a New Tissue

Once the LDA model has been fit to the epigenetic data for cell types and tissues available in Roadmap, making predictions for a new cell type or tissue is easy. Basically, one only needs to run the iterative algorithm in step 2 of the variational inference algorithm on the epigenetic data for the new tissue.

Choosing the Number of Functional Classes in the LDA Model according to the Perplexity Measure

Choosing the number of functional classes in the LDA model is not straightforward. Too few classes can be insufficient and can lower the accuracy of the resulting classifier. Too many classes can lead to an overly complex model and is subject to overfitting.

Heuristic methods exist on the basis of computing the perplexity of a model with a given number of clusters on held-out datasets. Perplexity is used in information theory to describe how well a statistical model fits the data. The lower the perplexity, the better the model and its generalization performance. In our case, if we let $L\left({\mathit{X}}_{t_i}\right)=\text{log}\left(p\left({\mathit{X}}_{t_i}|\mathit{\alpha }\right)\right)$ be the log-likelihood for a held-out set of variants for each tissue t_i, the perplexity is defined as

$$\text{perplexity}\left({\mathit{X}}_{\text{test}}\right)=\text{exp}\left\{-\frac{{\sum }_{i=1}^{l}L\left({\mathit{X}}_{t_i}\right)}{{\sum }_{i=1}^l{m}_i}\right\},$$

where l is the total number of tissues, and m_i is the number of variants for tissue t_i. Evaluating the perplexity measure directly is computationally intractable (the computation of the likelihood for each tissue involves a summation over $K^{m_i}$ terms, where K is the number of classes), and therefore we use the lower bound on the log-likelihood, i.e., L(a, w | α) (see Supplemental Data), to derive an upper bound on the perplexity. This upper bound on the perplexity is referred to as the variational Bayesian bound on the perplexity. In the large data limit, the bound on the log perplexity evaluated on the training data converges to the Bayesian information criterion (BIC) for the model.³⁴ If the training and testing datasets are assumed to come from the same distributions, then the variational Bayesian bound on the log perplexity converges to the BIC.

Alternative Functional Annotation Methods Used in Our Comparisons

We compare our approach with the following state-of-the-art functional annotation methods.

Tissue- and Cell-Type-Specific Functional Prediction Methods

Individual Histone Modifications and DNase Scores

Instead of integrating the various epigenetic marks, one can use the individual scores to predict functional variants. For the histone modifications and DNase, we use the negative log₁₀ of the Poisson p value of ChIP-seq or DNase counts relative to expected background counts, as output by ChromImpute.²⁰ In addition, for DNase, we also use narrow peaks and gapped peaks (defined as broad peaks that contain at least one strong narrow peak).

GenoSkyline: Multivariate Bernoulli Mixture Models

A simpler mixture model than the LDA described here is the two-component mixture model $\psi =\left(\pi ,f_0,f_1\right)$, where f₀ and f₁ are the probability densities for each of the components, and π is a mixing parameter. We can fit such a model to data from each tissue separately and calculate posterior probabilities that each variant is in the “functional” class given the observed scores X, i.e., $P_{\psi }\left(C_i=1|\mathbf{X}\right)$. For tractability, it is often assumed that the individual scores are conditionally independent given the functional class. Such a two-component multivariate Bernoulli mixture model using dichotomized data from peak-calling algorithms—an approach called GenoSkyline—has been proposed previously.²⁸

ChromHMM

ChromHMM¹⁹ is a method for chromatin-state discovery and characterization through the integration of multiple chromatin datasets. The underlying algorithm is a multivariate HMM that produces a segmentation of the genome; each segment is assigned a putative function on the basis of enrichment analyses of different biological states in these segments. The ChromHMM 25-state model²⁰ is based on 12 marks and, like ours, uses imputed data: H3K4me1, H3K4me2, H3K4me3, H3K9ac, H3K27ac, H4K20me1, H3K79me2, H3K36me3, H3K9me3, H3K27me3, H2A.Z, and DNase. ChromHMM is based on the complete pooling of data from multiple tissues and fitting a single model to this superdataset.

Segway

Like ChromHMM, Segway²¹ is a genome segmentation approach based on a DBN model. Segway is based on fitting separate models to data from each tissue. Segmentations for most of the cell types and tissues in Roadmap have been recently generated.³⁵

IDEAS

IDEAS²⁵ is an integrative and discriminative epigenome annotation algorithm that, like ChromHMM and Segway, segments the genome and assigns each segment a specific functional class. Unlike ChromHMM and Segway, IDEAS models the correlations both along the genome and across cell types. Segmentations for all 127 cell types and tissues in Roadmap have been produced with IDEAS.²⁶

deltaSVM

deltaSVM²⁹ is a new sequence-based computational method that predicts the effect of regulatory variation by using a classifier (gkm-SVM) that encodes cell-specific regulatory sequence vocabularies. The induced change in the gkm-SVM score, deltaSVM, quantifies the effect of variants.

cepip

By connecting large-scale epigenome profiles to eQTLs across human tissues and cell types, Li et al.³⁰ identified combinations of chromatin features that are predictive of a variant’s regulatory potential. They developed a joint likelihood framework to measure the probability that genetic variants are functional in a context-dependent manner.

Organism-Level Functional Prediction Methods

CADD

CADD¹¹ is based on a supervised approach (support vector machine) to training a discriminative model. That is, it begins with two sets of variants—one labeled deleterious and the other labeled benign—and fits a model that best separates the two sets. It selects benign variants by comparing the human genome to the inferred genome of the most recent shared human-chimpanzee ancestor. Alleles that are not found in the common ancestor and that are fixed in the human genome are assumed to be mostly benign. These are compared with de novo variants generated randomly according to models of mutation rates across the genome.

Eigen

Eigen¹³ is an unsupervised spectral approach for scoring variants and does not make use of labeled training data. Eigen uses a variety of functional annotations in both coding and noncoding regions and combines them into one single measure of functional importance. Eigen produces estimates of predictive accuracy for each functional annotation score and subsequently uses these estimates of accuracy to derive the aggregate functional score.

DANN

DANN¹⁴ uses the same feature set and training data as CADD to train a deep neural network (DNN). Unlike CADD, which trains a linear kernel support vector machine to differentiate between likely benign and likely deleterious variants and therefore cannot capture non-linear relationships among the features, DNNs can capture non-linear and interactive relationships among features.

LINSIGHT

LINSIGHT¹⁶ is a statistical method that combines a generalized linear model for functional genomic data with a probabilistic model of molecular evolution to predict the fitness consequences of mutations.

DeepSea

DeepSea¹⁵ is a deep-learning-based approach for predicting the chromatin effects of sequence alterations with single-nucleotide sensitivity.

PhyloP

PhyloP³⁶ quantifies evolutionary conservation at individual sites.

Generalized Jaccard Index of Overlap

We are interested in computing a similarity measure of predicted functional variants in two different tissues. Because the distribution of posterior probabilities in any one tissue is highly bimodal (where most of the mass is at 0 and a small proportion of variants have posterior probabilities close to 1; in other words, we are dealing with sparse binary data), a natural measure of similarity is the Jaccard measure of overlap, defined as follows. If X = (x₁, …, x_k) and Y = (y₁, …, y_k) are two vectors with x_i and y_i ≥ 0, respectively (e.g., vectors of posterior probabilities that variants are in the functional components for two different tissues), then the generalized Jaccard index of overlap is defined as

$$J\left(\mathbf{X},\mathbf{Y}\right)=\frac{{\sum }_i\text{min}\left(x_i,y_i\right)}{{\sum }_i\text{max}\left(x_i,y_i\right)}.$$

When X and Y are binary vectors, then the Jaccard index of overlap is simply the size of the intersection divided by the size of the union of the two sets. The closer it is to 1, the more overlap there is between the two sets. A Jaccard index of 0 means no overlap.

Promoter and Tissue-Specific Enhancer Regions

The promoter region of a protein-coding gene is defined as the union of the regions 2,500 bases upstream of any protein-coding transcripts for the gene, as defined by GENCODE version 24. For enhancer regions, we use the Roadmap Stringent enhancer list available at the Reg2Map website.

eQTL Enrichment

Let G₁, …, G₄₄ be the 44 GTEx tissues with at least 70 samples (Table S2) and R₁, …, R₁₂₇ be the 127 Roadmap tissues. For a given tissue in GTEx G_i, we are interested in identifying the Roadmap tissue R_j with a higher enrichment in eQTLs from G_i than other tissues in Roadmap.

Let

$$p_{G_i|R_j}=\frac{\text{no}\text{.}\text{of}\text{eQTLs}\text{in}\text{tissue}{G}_i\text{in}\text{functional }\text{component}{R}_j}{\text{no}\text{.}\text{of}\text{eQTLs}\text{in}\text{functional}\text{component}{R}_j}.$$

Note that the number of eQTLs in GTEx tissue G_i is a weighted count (an eQTL is weighted by the inverse of the number of GTEx tissues in which the variant is eQTL) such that ${\sum }_i{p}_{G_i|R_j}=1$. This way, eQTLs that are unique to tissue G_i are given higher weight than eQTLs that are shared across many tissues. For GTEx tissue G_i, to test whether there is an enrichment in the functional component of Roadmap tissue R_j, we compare $p_{G_i|R_j}$ with

$$p_{G_i|R_{-j}}=\frac{\text{no}\text{.}\text{of}\text{eQTLs}\text{in}\text{tissue}{G}_i\text{in}\text{functional}\text{components}\text{excluding}{R}_j}{\text{no}\text{.}\text{of}\text{eQTLs}\text{in}\text{functional}\text{components}\text{excluding}{R}_j}.$$

The null hypothesis is $H_{\text{0}}\text{:}{P}_{G_i|R_j}=P_{G_i|R_{-j}}$ versus $H_{\text{0}}\text{:}{P}_{G_i|R_j}>P_{G_i|R_{-j}}$. We apply a two-sample proportion test for each Roadmap tissue R_j and report the Roadmap tissue with minimum p value in Table 1. Also reported in Table 1 is the enrichment ratio $P_{G_i|R_j}/P_{G_i|R_{-j}}$.

Table 1.

Enrichment of eQTLs from Different Sources (GTEx, Geuvadis, and TwinsUK Cohort) among Functional Variants Predicted by FUN-LDA in Tissues and Cell Types in Roadmap Epigenomics

Tissue	Roadmap Epigenomics Name	−log10(p)	−log10(FDR.p)	Enrichment Ratio
GTEx
Whole blood	primary neutrophils from peripheral blood	189.72	185.92	1.38
Cells – transformed fibroblasts	muscle satellite cultured cells	62.69	59.59	1.22
Cells – EBV-transformed lymphocytes	GM12878 lymphoblastoid cells	37.74	35.23	1.48
Liver	liver	31.82	29.45	1.68
Muscle – skeletal	skeletal muscle male	19.42	17.26	1.13
Heart – left ventricle	fetal heart	15.83	13.74	1.22
Esophagus – mucosa	esophagus	12.78	10.74	1.15
Pancreas	pancreas	10.84	8.89	1.25
Colon – transverse	rectal mucosa donor 31	10.46	8.52	1.23
Artery – tibial	stomach smooth muscle	7.74	5.87	1.10
Esophagus muscularis	stomach smooth muscle	6.74	4.91	1.11
Thyroid	fetal intestine small	5.96	4.19	1.06
Skin – sun exposed (lower leg)	foreskin keratinocyte primary cells skin03	5.47	3.73	1.07
Spleen	primary B cells from peripheral blood	5.35	3.61	1.22
Artery – aorta	aorta	5.28	3.57	1.14
Brain – hippocampus	brain cingulate gyrus	5.10	3.42	1.38
Small intestine – terminal ileum	fetal intestine large	5.04	3.37	1.37
Heart – atrial appendage	fetal heart	4.90	3.25	1.15
Adipose – subcutaneous	adipose nuclei	4.74	3.11	1.07
Colon – sigmoid	colon smooth muscle	4.62	2.99	1.19
Brain – caudate (basal ganglia)	brain substantia nigra	4.17	2.60	1.18
Nerve – tibial	brain hippocampus middle	4.11	2.56	1.05
Adrenal gland	fetal adrenal gland	3.94	2.42	1.14
Skin – not sun exposed (suprapubic)	foreskin keratinocyte primary cells skin03	3.56	2.07	1.09
Brain – putamen (basal ganglia)	brain substantia nigra	3.36	1.90	1.23
Brain – cerebellum	primary T cells from cord blood	3.20	1.78	1.11
Brain – cerebellar hemisphere	brain angular gyrus	3.08	1.67	1.12
Stomach	stomach mucosa	3.02	1.63	1.13
Lung	primary hematopoietic stem cells G-CSF-mobilized male	2.42	1.13	1.05
Adipose – visceral (omentum)	primary T helper cells from peripheral blood	2.00	0.82	1.08
Brain – nucleus accumbens (basal ganglia)	H9 cells	1.80	0.67	1.17
Pituitary	ES-I3 cells	1.75	0.64	1.13
Brain – cortex	primary natural killer cells from peripheral blood	1.61	0.54	1.11
Esophagus – gastresophageal junction	primary B cells from peripheral blood	1.49	0.46	1.09
Artery – coronary	primary B cells from peripheral blood	1.35	0.38	1.10
Brain – hypothalamus	primary natural killer cells from peripheral blood	1.26	0.33	1.16
Brain – frontal cortex (BA9)	H1 cells	1.08	0.22	1.11
Brain – anterior cingulate cortex (BA24)	primary natural killer cells from peripheral blood	1.00	0.19	1.12
Geuvadis
Lymphoblastoid cell line	GM12878 lymphoblastoid cells	9.27	7.35	1.13
TwinsUK
Blood	primary neutrophils from peripheral blood	7.30	5.46	1.42
Fat	mesenchymal stem cell derived adipocyte cultured cells	6.26	4.45	1.21
Skin	foreskin keratinocyte primary cells skin02	3.99	2.45	1.18
Lymphoblastoid cell line	GM12878 lymphoblastoid cells	3.08	1.67	1.08

The top Roadmap tissue (with smallest enrichment p value) is given for each eQTL tissue, along with the p value from a two-sample proportion test, the FDR-adjusted p value (FDR.p), and the enrichment ratio (see Material and Methods). Tests that are significant at an FDR of 0.05 have −log₁₀(FDR.p) > 1.30.

The eQTLs that we used in these analyses are all significantly associated SNP-gene pairs for eGenes in each of these 44 GTEx tissues and were obtained by the permutation-threshold-based approach described by the GTEx Consortium³⁷ (see Web Resources for more details). For the follow-up study making use of eQTLs from Geuvadis and the TwinsUK cohort, we used the lead eQTLs, i.e., those most strongly associated with gene expression (publicly available for download from Brown et al.³⁸).

Stratified LD Score Regression Approach to Identifying the Tissue of Interest

The stratified linkage disequilibrium (LD)-score regression approach¹ uses two sets of SNPs, reference SNPs and regression SNPs. The regression SNPs are SNPs that are used in a regression of chi-square statistics from GWASs against the LD scores of those regression SNPs. The LD score of a regression SNP is a numeric score that captures the amount of genetic variation tagged by the SNP. Here, following Finucane et al.,³⁹ we use HapMap3 SNPs as regression SNPs because of their high imputation quality and use SNPs with a minor allele count greater than 5 in the 379 European samples from the 1000 Genomes Project as reference SNPs.² We first compute tissue-specific scores by using each of our methods for the 9,254,335 reference SNPs.

In the stratified LD-score regression approach, a linear model is used to model a quantitative phenotype y_i for an individual i:

$$y_i=\sum _{j\in G}{X}_{ij}{\beta }_j+{\mathrm{ϵ}}_i.$$

Here, G is some set of SNPs, X_ij is the standardized genotype of individual i at SNP j, β_j is the effect size of SNP j, and ${\mathit{ϵ}}_i$ is mean-zero noise. In this framework, β, the vector of all β_j, is modeled as a mean-zero random vector with independent entries, and the variance of β_j depends on the functional categories included in the model. We have a set of functional categories, C₁, …, C_C, and the variance of a SNP’s effect size will depend on which functional categories it belongs to:

$$\text{Var}\left({\beta }_j\right)=\sum _{c:j\in C_c}{\tau }_c.$$

Here, ${\tau }_c$ is the per-SNP contribution to heritability of SNPs in category C_C. Lindblad-Toh et al.¹ show that under this model, ${\tau }_c$ can be estimated through the following equation:

$$E\left[{\chi }_j^2\right]=N\sum _c{\tau }_{c}l\left(j,c\right)+1.$$

Here, ${\chi }_j^2$ is the chi-square statistic for SNP j from a GWAS, N is the sample size from that study, and l(j, c) is the LD score of SNP j with respect to category C_c, $l\left(j,c\right)={\sum }_{k\in C_c}{r}_{jk}^2$. This equation therefore allows for the estimation of ${\tau }_c$ via the regression of the chi-square statistics from a GWAS on the LD scores of the regression SNPs.

Here, we extend the stratified LD score by allowing SNPs to be assigned to a category C_c probabilistically, i.e., we assume a probability p_kc that SNP k belongs to category C_c and therefore that the variance of its effect size is affected by its membership in that category. This involves only minor changes to the above equations, namely, we have that

$$\text{Var}\left({\beta }_j\right)=\sum _{c:j\in C_c}{p}_{jc}{\tau }_c,$$

where p_jc is the probability that SNP j belongs to category C_c, and as above,

$$E\left[{\chi }_j^2\right]=N\sum _c{\tau }_{c}l\left(j,c\right)+1,$$

although now $l\left(j,c\right)={\sum }_{k\in C_c}{p}_{kc}{r}_{jk}^2$, where p_kc is the probability that SNP k belongs to category C_c. We can therefore still estimate ${\tau }_c$ via the regression of the chi-square statistics from a GWAS on the LD scores of the regression SNPs, but in calculating these LD scores, we weight the squared correlation of a SNP k with a regression SNP j by the probability that SNP k belongs to a particular category.

For each tissue and phenotype and each of our functional scores, we fit a separate LD-score regression model, including the LD score derived from the posterior probability that each regression SNP is in the functional component in that tissue, to estimate the per-SNP contribution of SNPs belonging to that component to heritability. To control for overlap of the tissue-specific functional score with other functional categories, we use the same 54 baseline categories used in Lindblad-Toh et al.,¹ which represent various non-tissue-specific annotations, including histone-modification measurements combined across tissues, measurements of open chromatin, and super enhancers.

Assessing Pairwise Correlations among 21 Complex Traits

Our aim here is to calculate a correlation matrix of 21 phenotypes on the basis of the Z scores from the LD-score regression procedure and a p value corresponding to each pair of phenotypes. From the LD-score regression approach, we obtain a matrix of Z scores corresponding to 127 (p = 127) tissues and 21 (q = 21) phenotypes. The main issue we need to account for when computing the correlations and the p values is that the tissues are correlated.

Let Z_ij be the Z score corresponding to the i^th tissue and j^th phenotype, and let Z_i = (Z_i1, …, Z_iq) and Z^j = (Z_1j, …, Z_pj) be the row and column vectors, respectively, of matrix Z. Given that the elements of Z are Z scores, we assume Z_i ∼ N(0, Σ_q) and Z^j ∼ N(0, Σ_p).

Estimation of the Correlation Matrix

We aim to estimate Σ_q, but the problem is that Z_i values are not independent. To solve the problem, we propose the following perturbation method.

Let B be the number of perturbation replicates. For the b^th replicate, we generate p independent random variables from N(0, 1), α_b1, …, α_bp. Let

$${\mathbf{X}}_{\mathbf{b}}=\frac{1}{\sqrt{p}}\sum _{1\le i\le p}{\alpha }_{bi}{\mathbf{Z}}_{\mathbf{i}}.$$

It can be shown that cov(X_b) = Σ_q and cov(X_b, X_b′) = 0 for any 1 ≤ b and b′ ≤ B, so we are able to use the uncorrelated perturbation samples X₁, …, X_B to approximate Σ_q and the corresponding correlation matrix P_q. We take B = 100,000.

p Values Corresponding to All Pairs of Phenotypes

For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of a certain function of Pearson’s correlation coefficient follows Student’s t distribution with degrees of freedom M − 2, where M is the number of uncorrelated random variables. Specifically, if the underlying variables have a bivariate normal distribution, the variable

$$t=\rho \sqrt{\frac{M-2}{1-{\rho }^2}}$$

follows a Student’s t distribution with degrees of freedom M − 2.

In our case, the number of uncorrelated random variables M depends on the correlation structure of the 127 tissues. M can be understood as the effective number of tissues. Similar to the calculation of the number of effective tests by Gao et al.,⁴⁰ we estimate M by applying an eigen decomposition to the Jaccard matrix. Suppose that λ₁ ≥ λ₂ ≥ … ≥ λ_p are the eigenvalues arranged in descending order. We estimate M by the smallest value such that $\left({\sum }_{i=1}^M{\lambda }_i/{\sum }_{i=1}^p{\lambda }_i\right)>C$. It should be noted that a smaller C will result in more conservative p values because the number of “effective tissues” is smaller, e.g., M = 124 when C = 99.5% and M = 96 when C = 95%. A threshold C that is too large or too small could cause M to be either overly liberal or overly conservative. The p values were calculated on the basis of C = 99.5%.

Availability of Code and Functional Scores

We have implemented the LDA algorithm into an R package, FUNLDA. The package and FUN-LDA scores for all genome-wide positions across all 127 tissues and cell types are available online (see Web Resources).

Results

Overview of the FUN-LDA Approach

We propose here an integrative functional score for predicting the functional effects of genetic variants at a tissue- and cell-type-specific level. The model is based on the LDA model, a generative probabilistic model commonly used in the topic modeling literature. The variant scores in each tissue are modeled as a mixture over latent functional classes. In the mixture distribution, we assume that the mixture components are shared across all tissues, whereas the mixture proportions for the different functional classes can vary from tissue to tissue (more details on the model and inference algorithm are given in the Material and Methods). Because our primary goal is to provide a functional score (as opposed to a functional element annotation), we focus on integrating four activating histone modifications (i.e., H3K4me1, H3K4me3, H3K9ac, and H3K27ac) and DNase. For the data on the four activating histone modifications, we compute “valley” scores (Material and Methods) on the basis of previous work showing that within regions of high histone acetylation, local minima (or valleys) are strongly associated with transcription factor binding sites.³³ We fit the LDA model with multiple functional classes to these data and compute for each position its posterior probability of belonging to a functional class in a specific tissue. We define the functional score at a position as the sum of posterior probabilities for the designated active functional classes (see next sub-section).

FUN-LDA Model with Nine Classes

Here, we use data on four activating histone modifications, namely H3K4me1, H3K4me3, H3K9ac, and H3K27ac, and DNase for 127 different cell types and tissues represented in the Roadmap datasets (see Tables S3 and S4). Not all of the histone marks were profiled for each of the 127 different cell types and tissues. However, using the relationships between different marks within and across tissues, previous studies have predicted signal tracks for each of these marks across all tissues.^{10, 20} We make use of these predicted signal tracks to compute integrated functional scores for every possible position in the human genome for 127 cell types and tissues. Specifically, using the perplexity-based criterion (see Material and Methods), visual inspection of the resulting classes, and prior knowledge of the relationship between histone modifications and chromatin states, we investigate models with varying numbers of classes and chose as our final model a model with nine classes (as shown in Figure S2, the perplexity measure begins to plateau with models with nine classes). We fit the LDA model with nine classes to the valley scores for the data on active histone modification and quantitative DNase and compute posterior probabilities at each position for the different functional classes in the different tissues and cell types. The active functional classes correspond to active promoters and active enhancers (Figure S1). As in genome segmentation approaches such as ChromHMM (25-state model), Segway, and IDEAS, we also make a similar partition (see Material and Methods and Table S1). For each position, both our method and ChromHMM use the sum of the posterior probabilities for the classes in the functional group to score the position. Segway and IDEAS provide only a functional-class assignment for each position for each cell type and tissue in Roadmap, and we use these assignments to identify the functional variants. The proportions of positions in the functional groups across different tissues and cell types for each method are shown in Figure S3. FUN-LDA, ChromHMM, and DNase-narrow (DNase narrow peaks) estimate that an average of 2% of the genome is functional in a cell type or tissue in Roadmap, and the remaining methods produce higher estimates for the size of the functional component.

Sharing Predicted Functional Variants across Tissues and Cell Types

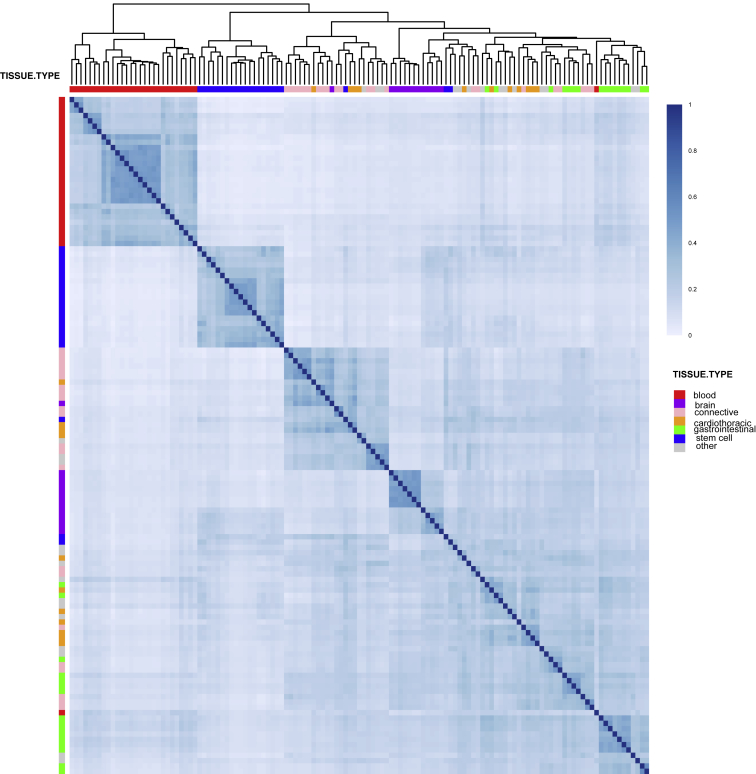
For each variant in the 1000 Genomes Project, we separately compute the probability that each Roadmap tissue is in the functional class. In Figure 1, we provide a global picture of the sharing of predicted functional variants across tissues in Roadmap by using the generalized Jaccard similarity index, a measure of overlap between predicted functional variants in two tissues (see Material and Methods). General tissue groupings are indicated in different colors. As expected, tissues that are functionally related tend to cluster together. There are roughly three major groups: blood cells (indicated in red), including various primary immune cell subtypes, stem cells (indicated in blue), and a third group corresponding to various solid organs (this grouping is also apparent in the multi-dimensional scaling visualization of the correlations between the functional scores in Figure S4; see also Kundaje et al.,¹⁰ Ernst and Kellis,¹⁹ and Figure S5 for related results using single histone marks and DNase).

Figure 1.

Jaccard Index of Overlap among Predicted Functional Variants in Different Cell Types and Tissues in Roadmap Epigenomics

Hierarchical clustering is used for clustering the different cell types and tissues.

Overall, the median Jaccard index across all pairs of tissues is 0.24. As a comparison, we also compute the Jaccard overlap indices by using predicted functional variants that fall in promoters and separately in enhancers (Material and Methods; see also Figures S6 and S7, which show the Jaccard indices for all pairs of tissues by using predicted functional variants that fall in promoters and enhancers, respectively). The median Jaccard index for variants falling in promoters is 0.33, and that for variants falling in enhancers is 0.16, concordant with existing literature showing that there tends to be more tissue specificity (less sharing) for predicted functional variants in enhancers than for those in promoters.⁴¹

Enrichment Analyses Using eQTLs from the GTEx, Geuvadis, and TwinsUK Data

eQTLs from the GTEx Project

The GTEx project is designed to establish a comprehensive data resource on genetic variation, gene expression, and other molecular phenotypes across multiple human tissues.³⁷ We focus here on the cis-eQTL results from the GTEx v.6 release, which comprises RNA sequencing data on 7,051 samples in 44 tissues, each with at least 70 samples (Table S2). For each GTEx tissue, we are interested in identifying the Roadmap tissue that has a more significant enrichment of eQTLs from that GTEx tissue than from other Roadmap tissues (see Material and Methods). We exclude from analysis the sex-specific GTEx tissues (ovary, vagina, uterus, testis, prostate, and breast), most of which have no relevant counterpart in Roadmap. In Table 1, we show the top Roadmap tissue for each remaining GTEx tissue, along with the p value and the enrichment ratio from the enrichment test. In most cases, eQTLs from a GTEx tissue show the most significant enrichment in the functional component of a relevant Roadmap tissue. For example, for liver tissue in GTEx, liver is the Roadmap tissue with the most significant enrichment; for pancreas tissue in GTEx, pancreas is the Roadmap tissue with the most significant enrichment; for skeletal muscle tissue in GTEx, skeletal muscle is the corresponding Roadmap tissue. However, there are also a few cases where the top tissue is not necessarily the most intuitive one, such as for lung and several brain tissues. Generally, the tissues with unexpected combinations tend to either have small sample sizes for eQTL discovery in GTEx (such as brain tissues) or inadequate representation in Roadmap (e.g., thyroid, pituitary gland, tibial artery, coronary artery, gastroesophageal junction of the esophagus, etc.). Controlling the false-discovery rate (FDR) at the 0.05 level, we find that most of the mismatches are not significant at this level (Table 1). We note that enrichment ratios tend to be small, especially for those tissues above the FDR threshold. This might be due to considerable tissue sharing of cis-eQTL effects reported in the GTEx study.⁴²

eQTLs from the Geuvadis and TwinsUK Data

We sought to perform similar analyses by using eQTLs identified in other studies, particularly those in lymphoblastoid cell lines (LCLs) from the Geuvadis project and four tissues (fat, LCLs, skin, and whole blood) in individuals from the TwinsUK cohort. We have focused here on the lead eQTLs, i.e., those variants most associated with gene expression levels.³⁸ As shown in Table 1, in each case, the most significantly enriched Roadmap tissue corresponds very well to the tissue of origin used in the eQTL discovery, providing an independent validation of the findings using the eQTLs from GTEx.

Prediction of Causal Tissues for 21 Complex Traits

As an application of our scores to the genetics of complex traits, we use the recently developed stratified LD-score regression framework³⁹ to identify the most relevant cell types and tissues for 21 complex traits for which moderate to large GWASs have been performed (Table 2).^{43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63} The stratified LD-score regression approach uses information from all SNPs and explicitly models LD to estimate the contribution to heritability of different functional classes of variants. We modify this method to weigh SNPs by their tissue-specific functional score (e.g., FUN-LDA), and in this way we assess the contribution to heritability of predicted functional SNPs in a particular Roadmap cell type or tissue (see Material and Methods for more details).

Table 2.

Top Cell Types and Tissues in Roadmap for 21 GWAS Traits according to FUN-LDA Posterior Probabilities

Trait	Roadmap Epigenomics Name	−log10(p)	nGWAS
Schizophrenia	fetal brain female	14.69	82,315
Height	mesenchymal-stem-cell-derived chondrocyte cultured cells	12.27	133,653
Rheumatoid arthritis	GM12878 lymphoblastoid cells	6.92	58,284
Crohn disease	primary B cells from cord blood	6.24	20,883
Age at menarche	H9-derived neuronal progenitor cultured cells	6.14	132,989
Educational attainment	fetal brain female	5.83	101,069
BMI	brain germinal matrix	4.79	123,865
HDL	liver	4.72	99,900
Coronary artery disease	liver	4.60	86,995
Ulcerative colitis	primary T helper 17 cells PMA-I stimulated	4.44	27,432
Type 2 diabetes	pancreatic islets	4.20	69,033
Epilepsy	brain anterior caudate	4.11	34,853
Triglycerides	liver	4.10	96,598
LDL	liver	4.08	95,454
Alopecia areata	primary T cells from cord blood	3.90	7,776
Alzheimer	primary hematopoietic stem cells G-CSF-mobilized male	3.78	54,162
IGAN	primary natural killer cells from peripheral blood	3.28	11,946
Bipolar disorder	fetal brain female	3.19	16,731
Ever smoked	brain inferior temporal lobe	2.67	74,035
Autism	primary monocytes from peripheral blood	2.40	10,263
Fasting glucose	pancreatic islets	1.44	58,074

The p value from the stratified LD-score regression and the GWAS sample size are reported for each trait.

In Table 2, we show the top Roadmap cell type or tissue (the one with the smallest p value from testing whether predicted functional variants in a tissue contribute significantly to SNP heritability) for each of the 21 complex traits from using FUN-LDA to predict functional variants in specific cell types and tissues. For most disorders, the top tissue has previously been implicated in their pathogenesis. For example, the top tissues for body mass index (BMI) are brain tissues, consistent with recent findings indicating that BMI-associated loci are enriched with expression in the brain and central nervous system.⁶⁴ Similarly, the brain represents the top tissue for most neuropsychiatric disorders, education levels, and smoking. Blood-derived and immune cells represent the top tissue for virtually all of the autoimmune conditions available for analysis. For example, GWAS findings for ulcerative colitis map specifically to the regulatory elements in T helper 17 cells, whereas LCLs represent the top cell type for rheumatoid arthritis. Another interesting finding involves primary hematopoietic stem cells for Alzheimer disease, consistent with emerging data on the involvement of bone-marrow-derived immune cells in the pathogenesis of neurodegeneration.⁶⁵ For the top cell type or tissue for each trait, we further estimate the contribution to heritability of variants in different functional classes (in Figure S1) and show that, overall, the variants in active promoters and active enhancers for the top tissue are the most enriched in heritability, whereas many of the non-functional classes show no enrichment or disenrichment.

Although in Table 2 we report only the top-ranked tissue for each trait, clearly other top-ranked tissues might be relevant as well. Indeed, as a result of high correlation among particular tissue and cell types in Roadmap (e.g., many different blood cell types, including various primary immune cell subtypes), it is difficult to distinguish among the top tissues. As shown in Figure S8, for autoimmune and inflammatory conditions (including Crohn disease, alopecia areata, rheumatoid arthritis, and immunoglobulin A [IgA] nephropathy), because of the large number of immune cells in Roadmap, several top cell types show similar patterns of enrichment. On the other hand, for traits such as low-density lipoprotein (LDL), high-density lipoprotein (HDL), and triglycerides, the top tissue (liver) is substantially more enriched than the next few tissues.

Results for other methods are shown in Tables S5–S7. Estimates of enrichment (defined as the proportion of SNP heritability in the category divided by the proportion of SNPs in that category) for the functional component in the top tissues in Tables S5–S7 are shown in Figure S9. On average across traits, the functional component for the top tissue as defined by FUN-LDA shows a higher enrichment than other methods. FUN-LDA is followed closely by DNase-narrow and ChromHMM. Methods such as DNase-gapped, GenoSkyline, Segway, and IDEAS show substantially lower enrichments. However, in terms of actual heritability explained, methods such as DNase-gapped, Segway, and IDEAS lead to more explained heritability than methods such as FUN-LDA (Figure S9). For example, for FUN-LDA, 2% of the SNPs (functional in the top tissue) explain an estimated 32% of SNP heritability, whereas for IDEAS, 7.1% SNPs explain an estimated 52% of heritability. Essentially, FUN-LDA tends to have higher specificity at the expense of lower sensitivity, whereas methods such as IDEAS and Segway tend to have higher sensitivity and lower specificity. In the next sub-section, we compare these different methods on the basis of the AUROC (area under a receiver operating characteristic curve), which rigorously accounts for sensitivity-specificity tradeoffs, for different test datasets.

In terms of the top tissues identified by each method, it is difficult to make an objective comparison given that the underlying tissues and cell types are not known for many complex traits. However, looking at the results in Tables S5–S7, one can point out several likely mismatches, such as “lung” identified for coronary artery disease by both GenoSkyline and DNase-narrow or “Dnd41 T cell leukemia cell line” and “fetal thymus” identified for epilepsy by DNase and DNase-narrow, respectively. Notably, for type 2 diabetes, FUN-LDA, Segway, and DNase-gapped are the only methods to point to pancreatic tissue, well-known to be relevant to type 2 diabetes.

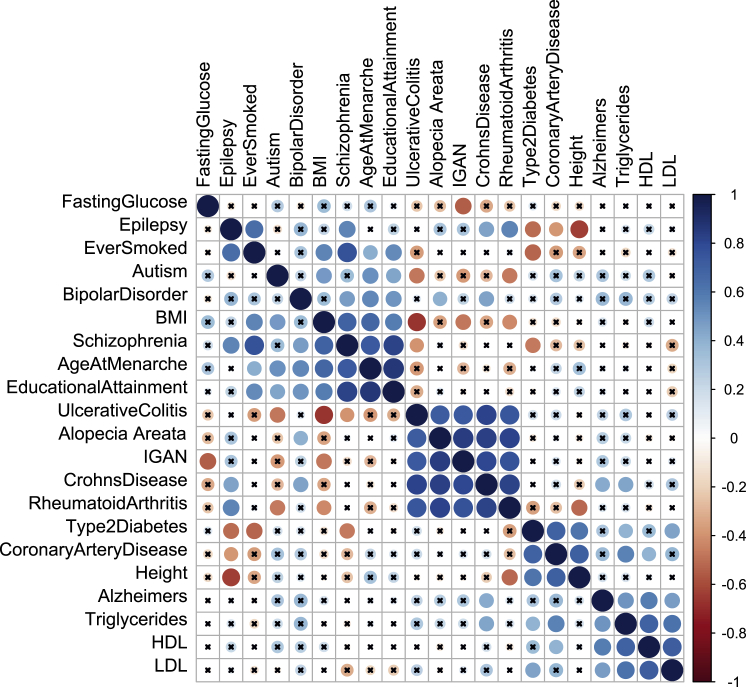
In Figure 2, we show the correlation matrix for the 21 traits on the basis of the Z scores from the LD-score regressions (see Material and Methods for more details on how these pairwise correlations were estimated). This correlation matrix reflects the extent to which traits share the same causal tissues rather than the genetic correlation.⁶⁶ Three large phenotypic clusters are clearly evident. The most tightly correlated cluster contains autoimmune and inflammatory conditions, including Crohn disease, alopecia areata, rheumatoid arthritis, and IgA nephropathy. As expected, these conditions share the highest functional scores in blood-derived immune cells. The second most strongly inter-correlated cluster is driven by scores in neuronal tissues and consists of BMI, age at menarche, educational attainment, schizophrenia, and smoking history, as well as somewhat weaker correlations with autism, epilepsy, and bipolar disorder. Lastly, there is a clear co-clustering of cardiometabolic traits that map to the tissues of liver, pancreas, and small intestine. Also, as shown, Alzheimer disease clusters with LDL, HDL, and triglycerides, concordant with recent reports on a link between cardiovascular disease and Alzheimer disease.⁶⁷

Figure 2.

Tissue Correlations for 21 Common Traits

Hierarchical clustering (average linkage method) is used for clustering diseases. The x symbol indicates that those correlations are not significant at the 0.0001 level.

Validations of Our Model’s Predictions and Comparisons with Existing Methods for Functional Annotation

To further assess the accuracy of our predictions and compare with existing approaches for functional prediction, we use variants that have been shown in the literature to have some evidence of a regulatory function. We focus on several main lists of variants with tissue- and/or cell-type-specific functional evidence: (1) eight variants that have been implicated in Mendelian and complex diseases and have additional experimental validation of their functional effects;^{68, 69, 70, 71, 72, 73, 74, 75} (2) confirmed regulatory variants from a multiplexed reporter assay in LCLs;⁷⁶ (3) regulatory motifs in 2,000 predicted human enhancers from a MPRA in two human cell lines: liver carcinoma (HepG2) and erythrocytic leukemia (K562);⁷⁷ (4) a collection of dsQTLs (DNase I sensitivity quantitative trait loci) in LCLs;⁷⁸ and (5) validated enhancers in 167 ultra-conserved sequence elements.⁷⁹ We also employed several non-tissue-specific datasets: (6) manually curated, experimentally validated regulatory SNPs;⁸⁰ (7) allelic-imbalanced SNPs in chromatin accessibility from a large number of DNase sequencing (DNase-seq) assays;⁸¹ (8) refined causal SNPs in noncoding regions from different sources (including the Human Gene Mutation Database [HGMD], ClinVar, and OregAnno) and variants from fine-mapping candidate causal SNPs for 39 immune and non-immune diseases in a recent fine-mapping study;⁸⁰ and (9) eQTLs from 11 uniformly processed fine-mapping studies.³⁸

Tissue- and Cell-Type-Specific Functional Predictions

Noncoding Variants Implicated in Mendelian and Complex Traits with Experimentally Predicted Regulatory Function

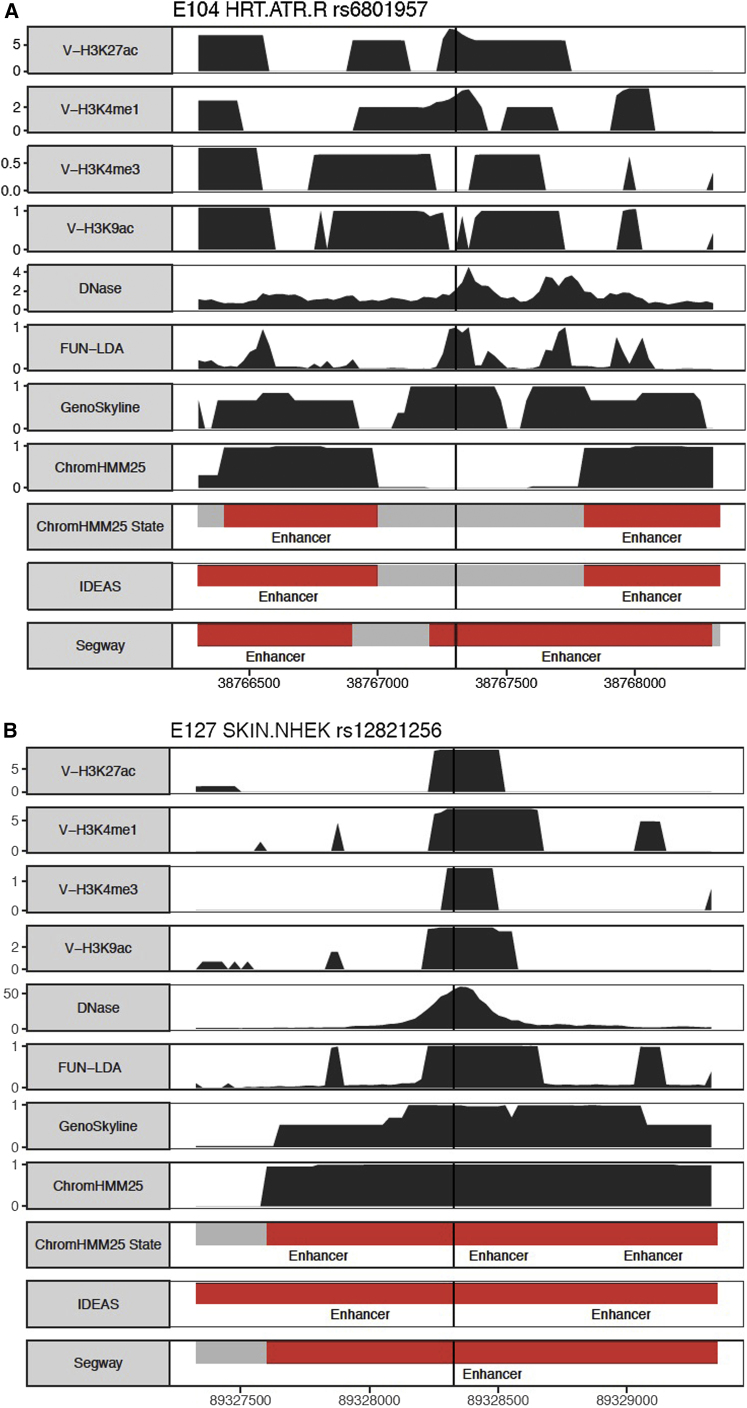
We selected the following eight SNPs that have been shown experimentally to have a regulatory function in particular tissues: rs6801957,⁶⁸ rs12821256,⁶⁹ rs12350739,⁷⁰ rs12740374,⁷¹ rs356168,⁷² rs2473307,⁷³ rs227727,⁷⁴ and rs144361550.⁷⁵ In Figure 3 and Figures S10–S15, we show the predictions in ∼2 kb windows centered at these SNPs from the different approaches: FUN-LDA, GenoSkyline, ChromHMM (25-state model), Segway, and IDEAS. For each of these SNPs, we selected the Roadmap tissue that we believe is closest to the tissue used in the original functional studies^{68, 69, 70, 71, 72, 73, 74, 75} (Table S8). We summarize below the results for two of the SNPs (rs6801957 and rs12821256) that showed more tissue specificity than the other SNPs in the set (i.e., were predicted to be functional in a small number of Roadmap tissues). For the remaining six SNPs, the results are summarized in the Supplemental Material and Methods and Figures S10–S15.

Figure 3.

Functional Predictions from Different Methods

Valley scores for four activating histone marks and DNase, posterior probabilities from FUN-LDA, GenoSkyline, and ChromHMM, and segmentations from ChromHMM, IDEAS, and Segway are shown in 2 kb windows centered around the lead SNPs. For clarity, we highlight in the segmentations only the type of states we consider functional (enhancer states in red and promoter states in blue) for the different segmentation approaches.

In their report, van den Boogaard et al.⁶⁸ showed that SNP rs6801957, found to be associated with electrocardiography measures in GWASs, is associated with lower SCN5A (MIM: 600163) expression in heart tissue in humans and mice. In Figure 3, we show the predictions for Roadmap tissue E104 (right atrium).

SNP rs12821256, associated with blond hair color in Iceland and the Netherlands, is located in an enhancer and influences expression of KITLG (MIM: 184745) in cultured human keratinocytes.⁶⁹ In Figure 3, we show the predictions for Roadmap tissue E127 (primary normal human epidermal keratinocytes).

For both SNPs, FUN-LDA assigns a posterior probability of 1 that they are functional in the corresponding tissues. Compared with that of existing integrative methods (last five rows in Figure 3), the region predicted to be functional by FUN-LDA tends to be substantially smaller, and therefore FUN-LDA has a better ability to predict the causal variant in a region of interest than commonly used approaches.

Confirmed Regulatory Variants (emVars) from a Multiplexed Reporter Assay

Tewhey et al.⁷⁶ applied a new version of the MPRA to identify variants with effects on gene expression. In particular, they applied it to 32,373 variants from 3,642 cis-eQTLs and control regions in LCLs and identified 842 variants showing differential expression between alleles, or emVars (expression-modulating variants). We used this set of 842 emVars as positive control variants. We paired each positive control with four variants tested by using the MPRA where neither allele showed expression different from that of the control and applying a threshold of 0.1 for the Bonferroni-corrected p value. After removing from the list of positive and negative control variants those variants that we could not map to a genomic location by using Ensembl (see Web Resources), we were left with 693 positive control variants and 2,772 negative control variants.

We computed the AUROC and AUPR (area under the precision-recall curve) values for several methods, including FUN-LDA, GenoSkyline, ChromHMM (250state model), Segway, IDEAS, and cepip (both cepip_cell and cepip_combined). For ChromHMM, we partitioned the 25 states into two groups, functional and non-functional; the functional group consisted of TssA (active transcription start site [TSS]), PromU (promoter upstream TSS), PromD1 (promoter downstream TSS 1), PromD2 (promoter downstream TSS 2), EnhA1 (active enhancer 1), EnhA2 (active enhancer 2), and EnhAF (active enhancer flank). For each variant, we used the sum of ChromHMM posterior probabilities for the classes in the functional group above to score the variant. For FUN-LDA, we similarly grouped the designated active promoter and active enhancer classes to form the functional class (see the Material and Methods and Table S1). Segway and IDEAS provided only a functional-class assignment for each position, and we used these assignments to identify the functional variants. Results are shown in Table 3. As shown, FUN-LDA had a higher AUROC (0.707) than the existing methods: ChromHMM (0.669), GenoSkyline (0.673), IDEAS (0.645), Segway (0.622), cepip_cell (0.653), and cepip_combined (0.642). Compared with DNase, FUN-LDA performed significantly better than the two binarized versions—DNase-narrow (0.666) and DNase-gapped (0.659), the two versions commonly used in practice—but it did not outperform the quantitative DNase (0.718). We report the results in terms of both AUROC and AUPR, which exhibited similar patterns.

Table 3.

Tissue- and Cell-Type-Specific Functional Predictions

Method	AUROC	AUPR
emVars in Tewhey et al.,76E116
FUN-LDA	0.707	0.468
GenoSkyline	0.673	0.394
ChromHMM	0.669	0.420
Segway	0.622	0.356
IDEAS	0.645	0.321
DNase	0.718	0.540
DNase-narrow	0.666	0.406
DNase-gapped	0.659	0.335
cepip_cell	0.653	0.321
cepip_combined	0.642	0.373
Regulatory Motifs in Kheradpour et al.,77E118 and HepG2
FUN-LDA	0.691	0.445
GenoSkyline	0.629	0.331
ChromHMM	0.606	0.344
Segway	0.618	0.334
IDEAS	0.546	0.290
DNase	0.719	0.506
DNase-narrow	0.561	0.312
DNase-gapped	0.550	0.291
cepip_cell	0.592	0.300
cepip_combined	0.641	0.364
Regulatory Motifs in Kheradpour et al.,77E123 and K562
FUN-LDA	0.645	0.287
GenoSkyline	0.620	0.256
ChromHMM	0.634	0.263
Segway	0.585	0.241
IDEAS	0.615	0.231
DNase	0.656	0.337
DNase-narrow	0.524	0.191
DNase-gapped	0.565	0.205
cepip_cell	0.606	0.217
cepip_combined	0.625	0.247
dsQTLs in Degner et al.,78E116
FUN-LDA	0.750	0.374
GenoSkyline	0.740	0.368
ChromHMM	0.639	0.303
Segway	0.580	0.277
IDEAS	0.677	0.330
DNase	0.823	0.474
DNase-narrow	0.665	0.345
DNase-gapped	0.662	0.313
cepip_cell	0.741	0.379
cepip_combined	0.760	0.398
deltaSVM	0.751	0.589
dsQTLs and eQTLs in Degner et al.,78E116
FUN-LDA	0.793	0.476
GenoSkyline	0.756	0.372
ChromHMM	0.721	0.403
Segway	0.648	0.340
IDEAS	0.700	0.334
DNase	0.832	0.529
DNase-narrow	0.713	0.376
DNase-gapped	0.701	0.327
cepip_cell	0.753	0.381
cepip_combined	0.769	0.473
deltaSVM	0.708	0.509

AUROC and AUPR values for discriminating between variants likely to be functional and control variants are shown. Results are shown for several datasets (three different cell lines) with experimental validation (MPRA) of potential regulatory variants and one dsQTL dataset (dsQTLs and eQTLs contains a subset of dsQTLs that are also eQTLs). Methods include FUN-LDA, GenoSkyline, ChromHMM (25-state model), Segway, IDEAS, DNase (quantitative, DNase-narrow, and DNase-gapped), cepip, and deltaSVM (note that deltaSVM predictions are available only for the dsQTL dataset).

Regulatory Motifs in 2,000 Predicted Human Enhancers from a MPRA

Kheradpour et al.⁷⁷ used a MPRA to measure the transcriptional levels produced by targeted motif disruptions in 2,104 candidate enhancers in two human cell lines, liver carcinoma (HepG2) and erythrocytic leukemia (K562) cell lines, providing one of the largest resources of experimentally validated enhancer manipulations in human cells. We used as positive control variants those variants where the p value comparing expression values for the sequence including the motif with expression values for the sequences including scrambled versions of the motif was less than 0.05. We used as negative control variants those variants where this p value was greater than 0.1. After removing those variants whose genomic coordinates we could not resolve, we were left with 525 positive and 1,451 negative control variants for HepG2 and 342 positive and 1,578 negative control variants for K562. For all methods, we calculated the scores for these motifs by averaging across all bases in the motifs. As shown in Table 3, FUN-LDA had better accuracy than GenoSkyline, ChromHMM, IDEAS, Segway, and cepip, and for HepG2, the improvement was substantial (e.g., AUROC = 0.691 for FUN-LDA, 0.606 for ChromHMM, 0.629 for GenoSkyline, 0.592 for cepip_cell, and 0.641 for cepip_combined).

We attempted to form the functional group in an objective manner on the basis of prior knowledge of which functional classes from the different segmentation approaches (ChromHMM, Segway, and IDEAS) should be considered active functional elements. We performed an additional analysis where we computed the AUROC for all combinations of states (individual AUROC ≥ 0.5) for each segmentation method and selected the state combination with the highest AUROC for the three datasets above. The results from these analyses are shown in Table S10. Even with this optimized state combination, the AUROCs for the various methods were mostly lower than for our (unbiasedly selected) state combination for FUN-LDA. Furthermore, the state combination with the maximum AUROC often contained states such as poised and bivalent promoters, which would not be considered functional a priori.

dsQTLs in LCLs

We also utilized a collection of dsQTLs in human LCLs, originally identified with the use of DNase I sequencing data from human LCLs.⁷⁸ Lee et al.²⁹ further processed this list of dsQTLs and generated 579 dsQTLs (with p value < 1 × 10⁻⁵) and randomly selected as controls a larger set of common SNPs (minor allele frequency > 5%) only from the top 5% of DHSs that had been used for identifying dsQTLs in the original study.⁷⁸ After removing variants with missing functional predictions, we were left with 560 dsQTLs in the positive control set. We paired each of these dsQTLs with four randomly selected controls (2,236 negative controls). In addition, Degner et al.⁷⁸ observed that a substantial fraction (16%) of dsQTLs are also associated with variation in the expression levels of nearby genes (i.e., these loci are also eQTLs). Therefore, we also separately considered 102 dsQTLs that are also eQTLs and paired them with 408 randomly selected (from the set above) negative controls. We present the results in Table 3. It should be noted that the vast majority of dsQTLs reside close to the target DHS, and hence methods such as DNase and deltaSVM are expected to perform well for these datasets. Despite this, FUN-LDA attained an AUROC similar to that of deltaSVM for the dsQTL dataset and a substantially higher value for the dsQTL and eQTL dataset (0.793 for FUN-LDA and 0.708 for deltaSVM). In terms of AUPR, FUN-LDA performance was third after DNase and deltaSVM.

In Figure S16, we use hierarchical clustering to show how the different tissue-specific methods are grouped together. Methods such as DNase and FUN-LDA are closest together in terms of AUROC and tend to perform best across the various tissue-specific datasets, whereas segmentation methods such as ChromHMM, Segway, and IDEAS are grouped together along with the binary DNase scores (DNase-gapped and DNase-narrow).

Ultra-conserved Sequence Elements

Pennacchio et al.⁷⁹ used extreme evolutionary sequence conservation as a filter to identify putative gene regulatory sequences. Using this approach, they identified 167 ultra-conserved sequence elements and then used a transgenic mouse enhancer assay that linked each of these candidate elements to a mouse promoter fused to a lacZ reporter gene. In total, 75 of 167 candidate sequences functioned reproducibly as tissue-specific enhancers of gene expression by the readout of lacZ expression at mouse embryonic day 11.5 (E11.5). Out of 75 positive fragments, 50 mapped to a single anatomical structure in the E11.5 embryonic tissue, whereas the remaining 25 enhancers directed expression to two or more anatomical structures. Here, we compare the functional scores for the variants falling into these 75 positive enhancers with scores of variants in the remaining 92 elements. In Table S11, we show the top Roadmap tissue for each method and the corresponding AUROC values. Notably, most methods, including FUN-LDA, selected embryonic tissue as the top tissue, consistent with the conducted experiment. Importantly, FUN-LDA outperformed all other methods except for GenoSkyline in predicting functional elements on the basis of these enhancer assays. Results based on AUPR values show similar patterns. It is important to bear in mind that the negative controls we used in this analysis (and more generally in our other analyses) could in fact be functional in different experimental environments, and the performance of the prediction methods we considered was affected by such misclassifications.

Widths of Predicted Functional Regions for Each Method

In Figure S17, we show the distribution of the widths of predicted functional regions that include validated functional variants from the three lists above for the tissue- and cell-type-specific methods. We determined the width of the functional region around a variant by finding the width of the window around the variant for which the value of the score (the probability) was greater than 0.5. Widths were truncated at 20,000 bp (so all widths greater than 20,000 bp were represented as 20,000 bp). Regions predicted by FUN-LDA were predicted to be substantially narrower than those predicted by the other methods (median width was 600 bp for FUN-LDA, 2,100 bp for ChromHMM, 1,800 bp for GenoSkyline, 1,100 bp for DNase-narrow, 4,400 bp for DNase-gapped, 4,100 bp for IDEAS, 1,300 bp for Segway, and 2,300 bp for cepip_cell); hence, compared with existing methods, FUN-LDA has the ability to more precisely localize the functional variants in a region of interest.

Comparison with Organism-Level Functional Prediction Methods on Tissue- and Cell-Type-Specific Datasets

Whereas above we focused on comparing FUN-LDA with other tissue- and cell-type-specific functional prediction methods on datasets with available tissue- and cell-type-specific predictions for variants, we also compared them on the same datasets with some of the more popular organism-level prediction methods, including phyloP,³⁶ CADD, DANN, Eigen, DeepSea, and LINSIGHT. The results are in Table S12. In most cases, FUN-LDA had a higher AUROC and AUPR than the organism-level methods, illustrating that prediction at the level of the tissue or cell type is more informative than it should be given that the underlying functional effects of variants are tissue or cell-type specific and can vary from tissue to tissue. Note, however, that for the dsQTLs, DeepSea performed better than FUN-LDA most likely because DeepSea was trained to predict DHSs, and the vast majority of dsQTLs reside close to the target DHSs. This is similar to what we observed with DNase as well, namely that DNase substantially outperformed other methods, including FUN-LDA, on those datasets.

Organism-Level Functional Predictions

In addition to considering tissue- and cell-type-specific functional predictions, we also considered applications to datasets where the functional evidence is not restricted to a particular tissue. In such cases, for the tissue and cell-type functional prediction methods discussed above, we defined the functional score for a variant as the maximum of the functional scores across the 127 tissues in ENCODE and Roadmap (this is the most severe functional score and is similar to common practice, e.g., when a variant matches multiple functional categories in the Ensembl Variant Effect Predictor). We were unable to include cepip and deltaSVM in these comparisons because these two methods’ scores are not yet available across all 127 tissues and cell types in Roadmap. We compared our proposed method with several popular organism-level functional prediction methods, including phyloP (primate), CADD, Eigen, DANN, DeepSea, and LINSIGHT.

Validated Regulatory SNPs

We used a set of 76 manually curated experimentally validated regulatory SNPs⁸⁰ and the same set of 156 frequency-matched background SNPs within 10 kb of the curated causal variants as in Li et al.⁸⁰ The results are shown in Table 4. FUN-LDA achieved an excellent AUROC of 0.878, substantially outperforming the organism-level functional prediction methods phyloP (0.575), CADD (0.718), Eigen (0.806), DANN (0.711), DeepSea (0.774), and LINSIGHT (0.818).

Table 4.

Organism-Level Functional Prediction

Method	AUROC	AUPR
Validated Regulatory SNPs
FUN-LDA-max	0.878	0.764
GenoSkyline-max	0.846	0.647
ChromHMM-max	0.865	0.796
Segway-max	0.711	0.461
IDEAS-max	0.694	0.451
DNase-max	0.885	0.818
DNase-narrow-max	0.828	0.707
DNase-gapped-max	0.807	0.590
Eigen	0.806	0.679
CADD	0.718	0.492
DANN	0.711	0.531
LINSIGHT	0.818	0.615
PhyloP	0.575	0.417
DeepSea	0.774	0.680
Allelic-Imbalanced SNPs in Chromatin Accessibility
FUN-LDA-max	0.935	0.899
GenoSkyline-max	0.906	0.849
ChromHMM-max	0.863	0.846
Segway-max	0.793	0.688
IDEAS-max	0.794	0.694
DNase-max	0.968	0.952
DNase-narrow-max	0.869	0.859
DNase-gapped-max	0.849	0.778
Eigen	0.753	0.732
CADD	0.692	0.638
DANN	0.619	0.557
LINSIGHT	0.880	0.815
PhyloP	0.581	0.584
DeepSea	0.865	0.839
Refined Causal SNPs
FUN-LDA-max	0.803	0.534
GenoSkyline-max	0.811	0.529
ChromHMM-max	0.748	0.504
Segway-max	0.714	0.332
IDEAS-max	0.720	0.342
DNase-max	0.807	0.510
DNase-narrow-max	0.680	0.411
DNase-gapped-max	0.756	0.418
Eigen	0.655	0.206
CADD	0.591	0.122
DANN	0.587	0.109
LINSIGHT	0.775	0.435
PhyloP	0.560	0.257
DeepSea	0.686	0.379
Fine-Mapped eQTLs
FUN-LDA-max	0.775	0.727
GenoSkyline-max	0.785	0.725
ChromHMM-max	0.680	0.671
Segway-max	0.687	0.603
IDEAS-max	0.686	0.605
DNase-max	0.778	0.721
DNase-narrow-max	0.615	0.611
DNase-gapped-max	0.707	0.655
Eigen	0.653	0.616
CADD	0.621	0.562
DANN	0.573	0.506
LINSIGHT	0.777	0.685
PhyloP	0.548	0.519
DeepSea	0.684	0.629

AUROC and AUPR values for discriminating between variants likely to be functional and control variants for are shown for four non-tissue specific datasets. Methods include FUN-LDA-max (maximum across 127 different tissues), GenoSkyline-max, ChromHMM-max (25-state model), Segway-max, IDEAS-max, and DNase-max (quantitative, DNase-narrow, and DNase-gapped). In addition, results for several organism-level functional prediction methods, including phyloP (primate), Eigen, CADD, DANN, DeepSea, and LINSIGHT, are reported.

Allelic-Imbalanced SNPs in Chromatin Accessibility

We also considered a dataset of allelic-imbalanced SNPs in chromatin accessibility (9,456 positive controls and 9,678 negative controls) identified by a large number of DNase-seq assays.⁸¹ The negative controls were frequency-matched background SNPs around the nearest TSS of randomly selected genes. After removing variants with missing functional predictions, we were left with 8,592 dsQTLs and 9,610 controls. It should be noted that the allelic-imbalanced SNPs were identified by DNase-seq assays, and hence DNase was expected to perform well for this dataset. As shown in Table 4, FUN-LDA performed very well with an AUROC of 0.935, higher than that of tissue-specific functional prediction methods GenoSkyline (0.906), ChromHMM (0.863), Segway (0.793), and IDEAS (0.794) and substantially better than that of organism-level functional prediction methods phyloP (0.581), CADD (0.692), Eigen (0.753), DANN (0.619), DeepSea (0.865), and LINSIGHT (0.880).

Refined Causal SNPs

We used a collection of 5,229 refined “causal” SNPs in noncoding regions from different sources, including the HGMD, ClinVar, and ORegAnno, and variants from fine-mapping candidate causal SNPs for 39 immune and non-immune diseases in a recent fine-mapping study.⁸⁰ The controls consisted of 20,916 randomly selected frequency-matched noncoding SNPs. FUN-LDA performed very well with an AUROC of 0.803, outperforming almost all the other functional prediction methods, especially the organism-level prediction methods (Table 4): phyloP (0.560), CADD (0.591), Eigen (0.655), DANN (0.587), DeepSea (0.686), and LINSIGHT (0.775).

Fine-Mapped eQTLs

Finally, we used a collection of eQTLs (31,118 positive controls and 36,540 negative controls) from the uniformly processed eQTL fine-mapping data in Brown et al.³⁸ The eQTLs were originally identified by multi-trait Bayesian linear regression models from 11 studies on 7 tissues and cell lines and then pre-processed by Li et al.⁸⁰ for the generation of a dataset of 31,118 most likely functional eQTLs (our positive controls) and 36,540 frequency-matched background SNPs around the nearest TSS of randomly selected genes (our negative controls). FUN-LDA performed very well with an AUROC of 0.775, which was the same as that of LINSIGHT but substantially better than that of phyloP (0.548), CADD (0.621), Eigen (0.653), DANN (0.573), and DeepSea (0.684). With AUROCs of 0.785 and 0.778, respectively, GenoSkyline and DNase performed slightly better than FUN-LDA for this dataset.

In Figure S18, we use hierarchical clustering to show how the different organism-level methods are grouped together. As with the tissue-specific datasets, methods such as DNase and FUN-LDA are closest together in terms of AUROC and tend to perform best across the various datasets, whereas segmentation methods such as ChromHMM, Segway, and IDEAS are grouped together along with the binary DNase scores (DNase-gapped and DNase-narrow).

Discussion

Here, we have introduced FUN-LDA, an unsupervised approach that uses histone modification and DNase data from the ENCODE and Roadmap Epigenomics projects for the functional prediction of genetic variation in specific cell types and tissues, and have provided comparisons with commonly used functional annotation methods both at the tissue- and cell-type-specific level and at the organism level. FUN-LDA is based on a mixture model that focuses on identifying the narrow genomic regions whose disruption is most likely to interfere with function in a particular cell type or tissue. Such context-specific functional prediction of genetic variation is essential for understanding the function of noncoding variation across cell types and tissues and for interpreting genetic variants uncovered in GWASs and sequencing studies. Although existing segmentation approaches can be used to derive a numeric functional score as well, we have shown that they tend to be less accurate at predicting functional effects and tend to predict wider functional regions than the proposed approach. Relative to other recently developed functional scores, such as GenoSkyline, FUN-LDA can have substantially better prediction accuracy, can use annotation data on the original scale (e.g., quantitative or binary), and furthermore makes it explicit which classes are considered functionally active, namely active promoters and active enhancers, providing an attractive tool for functional scoring of variants.

In terms of prediction accuracy, we have shown that, overall, FUN-LDA outperforms existing methods over a variety of test datasets, sometimes substantially. In particular, FUN-LDA has substantially better accuracy than popular organism-level functional scores, such as phyloP, CADD, Eigen, DANN, DeepSea, and LINSIGHT. We have also shown that quantitative DNase can have a higher predictive power than FUN-LDA and other tissue- and cell-type-specific functional prediction methods, although the difference between FUN-LDA and DNase is minor in most comparisons and is smaller than the difference between FUN-LDA and other integrative methods (except for the DNase-based datasets, such as dsQTLs and allelic-imbalanced SNPs in chromatin accessibility, where DNase has an inherent advantage). This observation is concordant with a recent study showing that within open chromatin regions, transcription factor binding is strongly correlated with the quantitative level of chromatin accessibility (as measured by DNase-seq).⁸² Therefore, the proposed FUN-LDA method, by being able to integrate annotation data with arbitrary distributions, has clear advantages over other mixture-based methods such as GenoSkyline and ChromHMM, which make use of binary peak calls. However, not being a probabilistic score is a significant deficiency of DNase (e.g., it is more difficult to implement and interpret enrichment analyses shown here for eQTLs and LD-score regression analyses), and in practice, in the vast majority of cases, researchers use binary DNase peak calls (DNase-narrow and DNase-gapped) rather than quantitative DNase scores; as we have shown, FUN-LDA significantly outperforms DNase peaks on the metrics we considered. One approach of interest would be to develop a probabilistic DNase score. Using FUN-LDA or other non-parametric mixture models with only DNase is not straightforward, given that in general, non-parametric mixture models are not identifiable with only one dimension, so one needs to either add additional annotations as we have done here or make parametric assumptions on the distribution of DNase (which is not straightforward). We leave this extension to future work.

These cell-type- and tissue-specific functional scores have numerous applications. We have shown here that eQTLs from several large studies, such as GTEx, Geuvadis, and the TwinUK cohort, are most enriched in the functional components from relevant Roadmap tissues. As previously shown,³⁹ and as illustrated here as well, they can be used for inferring the most relevant cell types and tissues for a trait of interest and can help focus the search for causal variants in complex traits by restricting the set of candidate variants to only those that are predicted to be functional in tissues relevant for the trait under consideration. Beyond the applications shown here, such functional predictions have numerous other applications. They can naturally be used in gene-discovery studies to potentially improve power in sequence-based association tests such as SKAT and burden^{83, 84} and in fine-mapping studies.^{85, 86} They can also be used in identifying regulatory regions that are depleted in functional variation in a specific tissue, similar to recent efforts to identify coding regions that are depleted in functional variation (e.g., missense, nonsense, and splice acceptor or donor variants).⁹ Other applications include improving power of trans-eQTL studies by using cell-type- and tissue-specific functional predictions as prior information. Similarly, studies on gene-gene and gene-environment interactions can benefit from an analysis focused on variants predicted to be functional in a cell type or tissue relevant to the trait under study.

Choosing the number of functional classes in the LDA model is not an easy task, partly because the number of functional classes is not well defined. Here, we focused on a model that includes nine functional classes and is based on combining an objective measure (such as the perplexity of the model), visual inspection of the resulting states, and biological knowledge. In our investigations, the results were not very sensitive to the number of classes, but models with fewer classes (i.e., 3–7) were not able to distinguish among different functional classes (such as enhancers and promoters). There is some subjectivity in any method that seeks to partition the genome into functional classes both in terms of the number of such classes and in terms of their interpretation. Further experiments that produce catalogs of specific types of elements with validated tissue-specific functions would aid in determining the number of states that a genomic annotation model should have and interpreting those states, leading to potential improvements in the accuracy of such functional predictors. Such tissue-specific experimental data would also allow the use of supervised methods that could lead to improved tissue-specific functional scores.

Unlike our method, most of the existing segmentation methods smooth the genomic signal spatially. Although they thereby use information from neighboring regions in making predictions for a particular variant, they can be less able to predict functionality of narrow regions with different histone-modification profiles from neighboring regions. Another difference between our method and those that use binary peak calls is that ours can incorporate the quantitative level of the functional annotations, which can be important; for example, in the case of DNase, it has been recently shown that the quantitative level of chromatin accessibility is strongly correlated with transcription factor binding.⁸² Furthermore, the use of the valley score allows our method to predict narrower functional regions than existing methods.

Overall, we propose a general framework for integrating various features in order to predict the functional effects of variants in noncoding regions of the genome. Although the epigenetic features we integrate are mostly helpful for predicting the effects of variants in cis-regulatory elements, such as promoters, enhancers, silencers, and insulators, the integration of additional features can lead to the discovery of other types of functional variants, such as those with effects on post-transcriptional regulation by alteration of RNA secondary structure or RNA-protein interactions. Similar to segmentation approaches (such as ChromHMM and Segway), our LDA framework could also be used for segmenting the genome into detailed functional classes.

We have computed FUN-LDA posterior probabilities for every position in the human genome for 127 tissue and cell types available in Roadmap. These scores are available on our website and can be imported into the UCSC Genome Browser. Note also that it is easy to make predictions in a new tissue once the model has been fit to the tissues in Roadmap. Furthermore, as with some other existing methods,¹⁹ it is possible to make predictions in a new tissue even if not all the epigenetic features we included are available, as long as one can impute the missing features by taking advantage of the correlations of epigenetic signals across both marks and samples as in ChromImpute.²⁰

Published: May 3, 2018

Web Resources

• 1000 Genomes, http://www.1000genomes.org/

• CADD, http://cadd.gs.washington.edu/

• cepip, http://jjwanglab.org/cepip/

• ChromHMM, http://compbio.mit.edu/ChromHMM/

• DANN, http://jjwanglab.org/PRVCS/index.html#Download

• deltaSVM, http://www.beerlab.org/deltasvm/

• Eigen, http://www.columbia.edu/∼ii2135/eigen.html

• ENCODE, https://www.encodeproject.org/

• Ensembl, http://grch37.ensembl.org/index.html

• FUNLDA: Genomic Latent Dirichlet Allocation, https://cran.r-project.org/web/packages/FUNLDA

• FUN-LDA, http://www.funlda.com/

• GenoSkyline, http://genocanyon.med.yale.edu/GenoSkyline

• GIANT consortium data files (BMI, height), http://www.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files

• GTEx Portal, http://www.gtexportal.org/home/

• GTEx analysis methods, https://www.gtexportal.org/home/documentationPage#staticTextAnalysisMethods

• IDEAS, http://bx.psu.edu/∼yuzhang/Roadmap_ideas/

• Reg2Map, https://personal.broadinstitute.org/meuleman/reg2map/HoneyBadger2-intersect_release/

• Roadmap Epigenomics, http://www.roadmapepigenomics.org/

• Segway, http://noble.gs.washington.edu/proj/encyclopedia/

• UCSC Genome Browser, https://genome.ucsc.edu/

• GWAS Summary Statistics:

• Age at Menarche, http://www.reprogen.org/Menarche_Nature2014_GWASMetaResults_17122014.zip

• Alopecia areata (link no longer available), http://www.broadinstitute.org/∼sripke/sharelinks/sRSxpynHPaYRJ1SnYXD17eo3qK8IE6daner_ALO4_1011b_mdsex/

• Alzheimer disease, http://web.pasteur-lille.fr/en/recherche/u744/igap/igap_download.php

• Autism, http://www.med.unc.edu/pgc/shared-methods/data-access-portal

• Bipolar disorder, http://www.med.unc.edu/pgc/files/resultfiles/pgc.bip.2012-04.zip

• Crohn disease, ftp://ftp.sanger.ac.uk/pub/consortia/ibdgenetics/cd-meta.txt.gz

• Coronary artery disease, ftp://ftp.sanger.ac.uk/pub/cardiogramplusc4d/cardiogram_gwas_results.zip

• Educational attainment, http://ssgac.org/documents/SSGAC_Rietveld2013.zip

• Epilepsy, http://www.epigad.org/gwas_ilae2014/ILAE_All_Epi_11.8.14.txt.gz

• Ever smoked, http://www.med.unc.edu/pgc/files/resultfiles/tag.evrsmk.tbl.gz

• Fasting glucose, ftp://ftp.sanger.ac.uk/pub/magic/MAGIC_Manning_et_al_FastingGlucose_MainEffect.txt.gz

• HDL, http://www.broadinstitute.org/mpg/pubs/lipids2010/HDL_ONE_Eur.tbl.sorted.gz

• IgA nephropathy, https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000431.v2.p1

• LDL, http://www.broadinstitute.org/mpg/pubs/lipids2010/LDL_ONE_Eur.tbl.sorted.gz

• Rheumatoid arthritis, http://plaza.umin.ac.jp/yokada/datasource/files/GWASMetaResults/RA_GWASmeta_European_v2.txt.gz

• Schizophrenia, http://www.med.unc.edu/pgc/files/resultfiles/scz2.snp.results.txt.gz

• Triglycerides, http://www.broadinstitute.org/mpg/pubs/lipids2010/TG_ONE_Eur.tbl.sorted.gz

• Type 2 diabetes, http://www.diagram-consortium.org/downloads.html

• Ulcerative colitis, ftp://ftp.sanger.ac.uk/pub/consortia/ibdgenetics/ucmeta-sumstats.txt.gz