Condition-Specific Modeling of Biophysical Parameters Advances Inference of Regulatory Networks

SUMMARY

Large-scale inference of eukaryotic transcription-regulatory networks remains challenging. One underlying reason is that existing algorithms typically ignore crucial regulatory mechanisms, such as RNA degradation and post-transcriptional processing. Here, we describe InfereCLaDR, which incorporates such elements and advances prediction in Saccharomyces cerevisiae. First, InfereCLaDR employs a high-quality Gold Standard dataset that we use separately as prior information and for model validation. Second, InfereCLaDR explicitly models transcription factor activity and RNA half-lives. Third, it introduces expression subspaces to derive condition-responsive regulatory networks for every gene. InfereCLaDR’s final network is validated by known data and trends and results in multiple insights. For example, it predicts long half-lives for transcripts of the nucleic acid metabolism genes and members of the cytosolic chaperonin complex as targets of the proteasome regulator Rpn4p. InfereCLaDR demonstrates that more biophysically realistic modeling of regulatory networks advances prediction accuracy both in eukaryotes and prokaryotes.

Graphical abstract

In Brief: This work demonstrates that extending the biophysical accuracy of the assumed model of transcriptional regulation improves large-scale regulatory network inference. As a proof of concept, Tchourine et al. show that incorporating RNA degradation into the model results in better network recovery while simultaneously predicting accurate RNA degradation rates.

INTRODUCTION

Inference of large-scale transcription regulatory networks is an active research area with many broad applications. Network inference typically assumes that changes in RNA expression levels inform of regulatory relationships between transcription factors (TFs) and their target genes. Ideally, orthogonal data on protein-protein and protein-DNA interactions, such as protein binding assays (Valouev et al., 2008; Mundade et al., 2014), DNA accessibility assays (Davie et al., 2015), and motif enrichment analysis (Setty and Leslie, 2015; Guo et al., 2012), com plement these expression data. Various machine learning approaches are then used to infer the network. The approaches have multiple levels of complexity, ranging from Boolean networks and network module approaches (Shmulevich et al., 2002; Lähdesmäki et al., 2003; Segal et al., 2003; Pe’er et al., 2001) to approaches that explicitly or implicitly model dynamics, TF interactions, and activity (Honkela et al., 2010; Äijö et al., 2013; Intosalmi et al., 2016; Studham et al., 2014).

Recent comprehensive, blind assessments of various network inference approaches concluded that inference in eukaryotes is systematically more challenging than in prokaryotes, with nearly random performance in yeast (Marbach et al., 2012). Other recent studies showed that results from incorporating prior interaction data also dramatically differ between prokaryotes and eu-karyotes, and performance in yeast remained poor (Greenfield et al., 2013; Wilkins et al., 2016; Siahpirani and Roy, 2016; Äijö and Bonneau, 2016). This discrepancy is likely due to increased complexity of eukaryotic transcriptional regulation, but most existing inference methods, such as those based on random forest (Huynh-Thu et al., 2010; Petralia et al., 2015), cannot directly incorporate new parameters.

The Inferelator is a method based on constrained regression (Bonneau et al., 2006; Greenfield et al., 2013; Arrieta-Ortiz et al., 2015). In contrast to other large-scale inference methods, it allows explicit modeling of biophysical processes via differential equations (see Inferelator Implementation in the Experimental Procedures). We and others have shown that inference of transcription- and translation-related parameters via ordinary differential equations produces robust genome-wide models in various organisms (Tchourine et al., 2014; Schwanhäusser et al., 2013; Peshkin et al., 2015). Importantly, the differential equations also allow for incorporation of additional regulatory parameters.

One such crucial regulatory component is RNA degradation. For yeast, experimental data highlight the large range in RNA half-lives and their extensive changes across different conditions and genetic backgrounds (Miller et al., 2011; Schwalb et al., 2012; Sun et al., 2012; Neymotin et al., 2014; Munchel et al., 2011). In addition, high correlation between degradation and transcription rates across mutant strains suggests extensive feedback between the two processes, controlled by factors such as XRN1 (Sun et al., 2013). Because expression regulation also depends on external conditions, networks are remodeled in a condition-specific manner (Lehtinen et al., 2013; Shivaswamy and Iyer, 2008) and can be captured in a low-dimensional space of expression clusters that correspond to different biological function that are highly utilized under those conditions (Hart et al., 2015).

These findings render the inclusion of RNA half-lives into condition-specific modeling of transcription regulation critical. Here we developed InfereCLaDR, an inference framework derived from the Inferelator, with the addition of expression sub-space clustering and explicit modeling of RNA degradation rates. InfereCLaDR infers the RNA degradation rate for every gene and condition cluster in the expression data by optimizing the cluster’s network inference accuracy and then combines the networks derived using optimized RNA half-lives. InfereCLaDR also uses a high-quality Gold Standard (GS) data-set we created. We showed that InfereCLaDR not only improved inference but also resulted in accurate condition-and gene-specific RNA half-life predictions. The final, combined network produced by InfereCLaDR has an area under the precision-recall curve (AUPR) of 0.33, which is far larger than other existing approaches in yeast, providing insights into various regulatory mechanisms. InferCLaDR is generalizable, as demonstrated by estimation of global RNA half-lives in other systems, such as Bacillus subtilis, and provides the first proof of concept that explicitly accounting for RNA degradation is necessary for accurate regulatory network inference from large and heterogeneous datasets.

RESULTS

Curation and Assembly of Comprehensive Datasets for High-Quality Network Inference

To develop InfereCLaDR, we leveraged the information available for baker’s yeast across a broad range of experimental conditions. We first assembled a list of 563 potential TFs from various sources, a Gold Standard of interactions, and an RNA expression dataset (see Data Acquisition and Normalization and Curation of the Gold Standard of Regulatory Interactions in the Experimental Procedures). The expression data originated from 119 labs and diverse experimental conditions but used the same transcriptomics platform throughout. With 5,716 genes and 2,577 samples (Figure 1C), it is one of the largest expression datasets used for network inference in yeast (Marbach et al., 2012; Danziger et al., 2014; Petralia et al., 2015; Siahpirani and Roy, 2016).

Figure 1. Network Inference Is Sensitive to RNA Half-Lives in Both Eukaryotes and Pro-karyotes in a Condition- and Gene-Specific Manner.

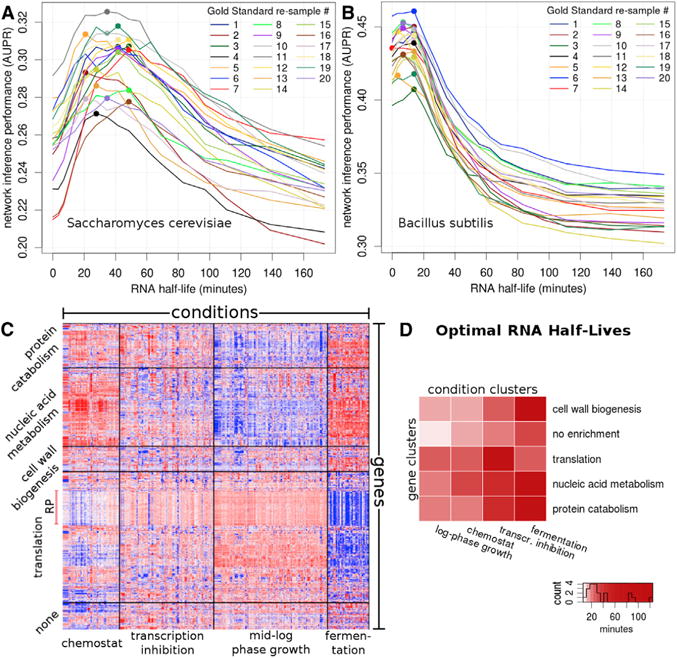
(A and B) AUPR is shown as a function of preset RNA half-life (A) in Saccharomyces cerevisiae and (B) in Bacillus subtilis. Each line denotes one of the 20 independent gold standard re-samples, and colored dots represent the maximum AUPR for a given re-sample.

(C) Over two thousand expression datasets group into 20 bi-clusters (unrelated to 20 Gold Standard re-samples) with gene- and condition-specific properties. Red and blue denote high and low expression levels, respectively. Gene cluster names correspond to the most highly enriched function category. Condition cluster names represent the most highly enriched terms in the meta-data. The heatmap shows the 997 genes from the Gold Standard. Note that the final network was derived from expression data of 5,716 genes mapped onto these clusters.

(D) Shades of red denote the optimal half-life, in minutes, for each of the 20 bi-clusters. The color scale is devised to discriminate half-lives < 50 min, which contain 16/20 of the predictions.

For the full plot of AUPR and AUROC trajectories for every bi-cluster, see Figures S4 and S5, respectively. See also Figures S1 and S6A–S6H.

We developed a new Gold Standard of regulatory interactions that combines multiple types of regulatory evidence from several databases (Table S1). It includes 1,403 signed interactions that distinguish between activation and repression, which is important for accurate calculation of TF activities (TFAs) (Arrieta-Ortiz et al., 2015). Although the Gold Standard represents only a fraction of all potential regulatory interactions in yeast, it is highly enriched in true positives: each interaction is confirmed by at least three orthogonal sources, one of which is direct (e.g., chromatin immunoprecipitation with DNA microarray [ChIP-chip]) and two are indirect (e.g., based on TF knockout expression changes). Further, Figures 3A and S3 show that a small, high-quality gold standard provides more self-consistent regulatory networks than larger and lower-quality reference sets, such as those commonly used (MacIsaac et al., 2006; Marbach et al., 2012; Ma et al., 2014; Petralia et al., 2015; Siahpirani and Roy, 2016).

Figure 3. InfereCLaDR Outperforms Previous Network Inference Approaches by Predicting New High-Confidence Condition-Specific Interactions.

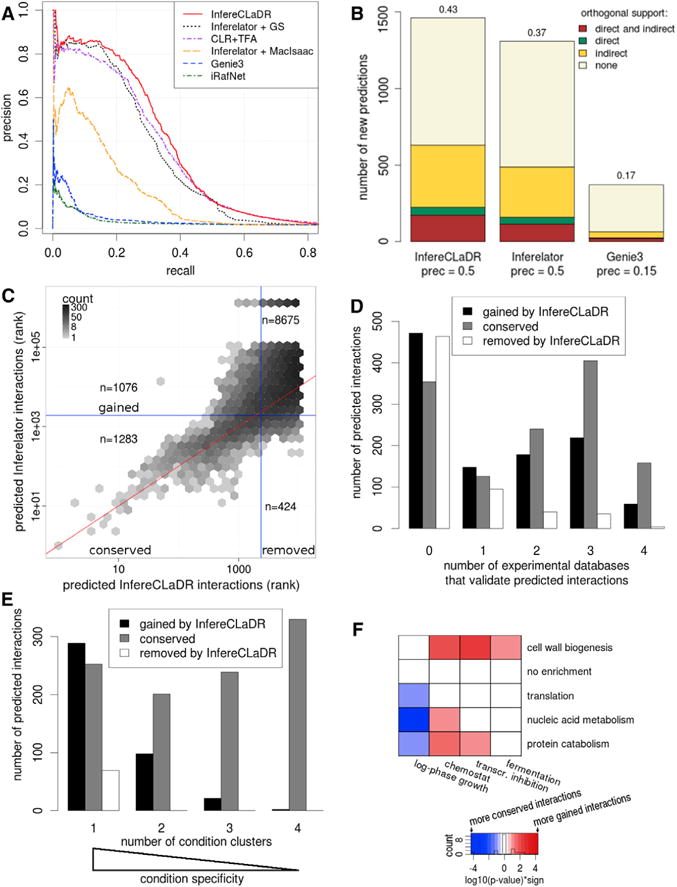
(A) The improvement in the precision-recall curve is a result of the use of a high-quality Gold Standard, bi-cluster specific network inference, and optimization of bi-cluster specific RNA half-lives. We compare InfereCLaDR (red line) with Inferelator without bi-clustering or half-life optimization (black dotted line), with the Inferelator using the MacIsaac gold standard of interactions (orange dashed line), and with context likelihood of relatedness (CLR), Genie3, and iRafNet (purple dash-dotted line, blue dashed line, and green dash-dotted line, respectively). Each curve is constructed using median precision and recall values across 20 re-samples. For improvement based on AUROC, see Figure S1F.

(B) The number of new predicted interactions (i.e., interactions not in the Gold Standard), obtained using the optimized bi-cluster-specific half-lives and the full Gold Standard for training, compares favorably with new predictions from the original Inferelator and from Genie3. The height of a section within each bar corresponds to the number of new interactions that were confirmed by the corresponding type of evidence in orthogonal data. Direct evidence refers to physical protein-DNA interactions, and indirect evidence refers to knockout and overexpression assays (Table S1). The number above each bar denotes the fraction of new interactions supported by at least one orthogonal source. Prec, precision.

(C) High-scoring regulatory interactions correlate between InfereCLaDR and Inferelator, but InfereCLaDR predicts many new interactions. The vertical and horizontal blue lines show the precision = 0.5 rank cutoff for InfereCLaDR and Inferelator, respectively (Supplemental Experimental Procedures). The lower the rank, the higher the confidence in the prediction. The red line maps the InfereCLaDR rank to the same rank in Inferelator. See also Figures S6I–S6K.

(D) Most (56%) regulatory interactions that were newly predicted by InfereCLaDR have orthogonal support to validate them. In comparison, Inferelator’s predictions that were removed in InfereCLaDR have little support, suggesting that they had been false positives. Black bars denote the bottom right quadrant in (C) (gained), gray bars denote the top left quadrant in (C) (lost), and white bars denote the interactions in the bottom left quadrant of (C) (conserved).

(E) InfereCLaDR’s gained interactions are often specific to experimental conditions. Each bar displays how many regulatory interactions were above the rank-based cutoff (Supplemental Experimental Procedures) for the given number of clusters. Interactions that only appear in one cluster are very condition-specific, whereas interactions that appear in all four clusters are more general and independent of experimental conditions. The graph shows only the high-confidence predictions that were above the cutoff for at least one cluster prior to rank-combining.

(F) InfereCLaDR’s gained predictions are often specific to non-standard conditions. Each interaction was assigned a bi-cluster based on the gene cluster of the target gene and a condition cluster in which this interaction had the best rank. Red cells represent bi-clusters with significantly more gained interactions, blue cells represent bi-clusters with significantly fewer gained interactions, and white cells represent no enrichment (Supplemental Experimental Procedures).

InfereCLaDR Accurately Estimates RNA Degradation Rates for Condition and Gene Clusters

To assess whether network prediction is, in general, sensitive to RNA degradation rates, we first tested the original Inferelator on the entire dataset for a range of preset half-lives. Indeed, prediction was sensitive to RNA half-lives and affected the AUPR. The AUPR was maximized for an RNA half-life of 20 to 50 min (Figure 1A; Figures S1A–S1D). Intriguingly, this range is highly consistent with experimental measurements (Miller et al., 2011; Neymotin et al., 2014; Munchel et al., 2011).

To demonstrate that network inference is sensitive to transcript stability across organisms, we also estimated the optimal half-life for B. subtilis (Figures 1B and S1B), predicting 6–13 min as the optimal half-life. Again, this range is similar to experimentally measured RNA half-lives of < 7 min for about 80% of the transcripts (Hambraeus et al., 2003). These results, derived entirely from changes in RNA expression, encouraged the inclusion of RNA half-life in network prediction.

Because the data used in our work span a variety of conditions, we extended RNA half-life optimization and network inference to 20 bi-clusters consisting of four condition and five gene clusters (Figures S1E and S1G; Expression Data Clustering in the Experimental Procedures). This simultaneous clustering of genes and conditions with the subsequent optimization of RNA half-lives comprises the core of the InfereCLaDR. To maximize the accuracy of RNA half-life predictions, we used the Split A approach (Figure S2), which makes use of connectivity information from the entire gold standard. In the Split A approach, we use the entire gold standard for training TFAs and half-life fitting but exclude the validation step. For most bi-clusters, the AUPR trajectory peaked inside a narrow range of half-lives (Figure S4), and the median half-lives for each bi-cluster are summarized in Figure 1D. For some bi-clusters, especially in the “fermentation” cluster, the AUPR trajectory did not peak at a specific half-life, indicating that accurate regulatory network modeling is not contingent on RNA degradation in these regimes. We excluded the RNA half-life predictions made in the fermentation cluster from the following analyses.

To validate the newly predicted RNA degradation rates, we compared them with measured RNA half-lives. Note that our approach predicted bi-cluster and not gene-specific RNA half-lives, therefore preventing direct gene-wise comparison with experimental measurements (see RNA Half-Life Estimation in the Experimental Procedures; Figure S1I). Therefore, we tested whether predicted RNA degradation rates for condition and gene clusters that are significantly different from the norm are similarly different for distributions of experimentally measured RNA half-lives across the genes in the corresponding clusters. Figure 2 shows that this is indeed the case; e.g., when comparing all genes under minimally perturbed conditions (Figures 2A and 2E) with all genes under “transcription inhibition” conditions (Figures 2D and 2H). The predicted increase in RNA stability under transcriptional inhibition conditions (Wilcoxon p < 1 × 10⁻¹⁰) is corroborated by the fact that experimental designs that used transcription inhibition to measure RNA decay rates vastly overestimated true RNA half-lives (Neymotin et al., 2014). In another example, ribosomal mRNAs are known to be more stable than other transcripts under normal conditions (Neymotin et al., 2014; Munchel et al., 2011). Indeed, the predicted half-life for the 115 ribosomal genes in the “translation” gene cluster was signifycantly higher than that of other genes (Figure 2C; Wilcoxon p < 4 × 10⁻³; see RNA Half-Life Estimation in the Experimental Procedures), confirming our approach.

Figure 2. InfereCLaDR Recapitulates Known Differences between RNA Half-Lives of Different Genes and Conditions and Identifies New Relationships.

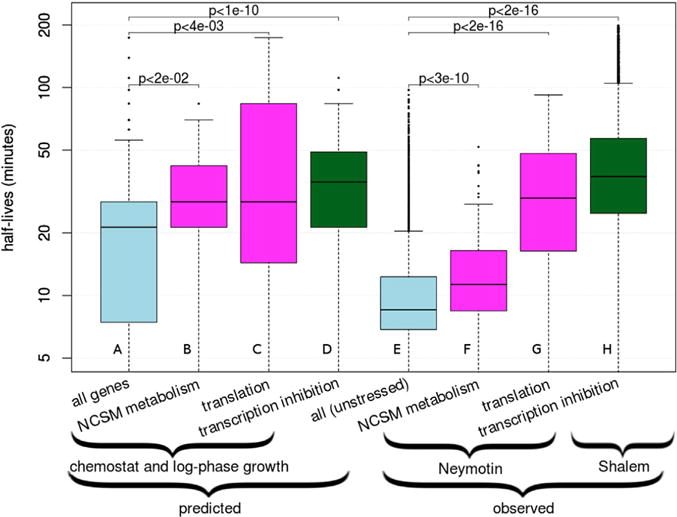
(A–H) The boxes show median RNA half-lives with the first and third quartiles. (A)–(D) show the distribution of predicted values across 20 Gold Standard re-samples, and (E)–(H) show values measured experimentally across genes. Predicted values are produced by InfereCLaDR; observed values are from experimental datasets. Magenta color denotes minimally perturbed conditions (i.e., chemostat and log phase growth) (predicted) and Neymotin et al. (2014) experimental data for subsets of genes; i.e., nucleobase-containing small-molecule metabolism (NCSM) and translation. We highlight the NCSM category because its high half-lives was the most prominent predicted pattern under minimally perturbed conditions. Light blue denotes all genes predicted or observed under unperturbed conditions. Green denotes half-lives of all genes predicted or observed under conditions of transcription inhibition (Shalem et al., 2008). See also Figure S4.

InfereCLaDR’s half-life optimization also revealed new trends across bi-clusters. Most prominently, “nucleic acid metabolism” genes under the “chemostat” and “log phase” conditions showed very high RNA half-lives (Figures 1D and 2B; Wilcoxon p < 0.02). Genes in this cluster function in nucleobase-containing small-molecule metabolism (NCSM), a category of genes that has not been noted for increased RNA half-lives in existing literature. We extracted the 207 NCSM genes from experimental RNA half-life measurements (Neymotin et al., 2014) and confirmed that, in line with the InferCLaDR predictions, the NCSM mRNAs were significantly more stable than all transcripts (Figure 2F; Wilcoxon p ≤ 5 × 10⁻¹⁰). The increase in RNA half-lives for both the translation and nucleic acid metabolism gene categories under normal conditions, as well as the global increase in RNA half-lives under the transcription inhibition conditions, was also confirmed when area under the receiver operating characteristic curve (AUROC) was used as an alternative measure for half-life fitting (Figure S1H), as well as by correlation analysis (Figure S1I; r_s = 0.7). These examples support our confidence in accurate predictions of RNA half-lives within the InfereCLaDR framework.

InfereCLaDR Improves Network Inference by Recovering Condition-Specific Interactions

Next we tested whether rank-combining the bi-cluster-specific networks improves prediction accuracy. To avoid circularity, we used non-overlapping, randomly chosen subsets of the gold standard to train the model, fit RNA half-lives for individual bi-clusters, and validate the predictions (Figure S2, Split B). We repeated the procedure for each of the 20 re-samples (the choice of 20 is unrelated to the number of bi-clusters, which is also 20), and compared InfereCLaDR with other methods (Figure 3A; Table 1). We calculated the AUPR on the respective validation subset of the gold standard, using the single value of half-life optimized on the corresponding fitting subset of the gold standard. RNA Half-Life Estimation in the Experimental Procedures details this method.

Table 1.

Expression Data Bi-clustering, RNA Half-Life Fitting, and a High-Quality Gold Standard Underlie InfereCLaDR’s Superior Performance

Method	Re-samples Outperforming Inferelator + GS	Re-samples Outperformed by InfereCLaDR	Median AUPR
InfereCLaDR (GS + clustering + RNA half-life)	19/20 –	–	0.328
Inferelator + GS + clustering	20/20	17/20	0.319
Inferelator + GS + RNA half-life	19/20	19/20	0.305
Inferelator + GS	–	19/20	0.290
Inferelator + MacIsaac	0/20	20/20	0.146
Genie3 + GS	0/20	20/20	0.042
iRafNet + GS	0/20	20/20	0.031

Each modification independently outperforms the original Inferelator using the Gold Standard (second column). “Inferelator + MacIsaac” shows the results of the Inferelator when the MacIsaac standard of interactions was used for training and Gold Standard for evaluation. Combining all modifications optimizes performance compared with using them separately (third column). Columns two and three show the number of times one method outperformed the other in a re-sample, as specified by the corresponding row and column, in terms of AUPR. The fourth column shows the median AUPR. See Sub-sampling the Gold Standard for RNA Half-Life Fitting and Error Estimation, RNA Half-Life Estimation, and Supplemental Experimental Procedures for further details. See also Table S2.

The two algorithmic modifications of the InfereCLaDR (bi-cluster-specific network inference and RNA half-life optimization) improve accuracy significantly over inference without these advances (p < 0.05; Figures 3A and S1F; Tables 1 and S2). In total, 115 of 120 pairwise comparisons resulted in larger AUPRs when these modifications were used together and separately (Table 1), showing that half-life estimation and bi-clustering result in significantly improved network inference and that combining the two significantly improves inference further. The final AUPR value of 0.33 represents an almost 8-fold increase compared with Genie3 (Table 1), the best-performing method in a recent competition (Marbach et al., 2012). Using AUROC yielded a similar outcome (Figure S1; Table S2). Sub-Sampling the Gold Standard for RNA Half-Life Fitting and Error Estimation in the Experimental Procedures and the Supplemental Experimental Procedures provide further details.

To maximize the size and accuracy of the final integrated network, we repeated the whole procedure with the Split A approach (Figure S2). At 50% precision, this final network contained a total of 2,924 interactions (Figure 4; Data S1), 1,462 of which were “new”; i.e., absent from the Gold Standard. Of these 1,462 interactions, 631 (43%) were validated by independent data that had been excluded from the modeling (Figure 3B). The high fraction of independently confirmed interactions suggests that the remaining 831 new interactions are also strongly enriched in true positives.

Figure 4. Condition-Specific Networks Reveal New Predictions and Regulatory Relationships beyond What a Global Network Can Show.

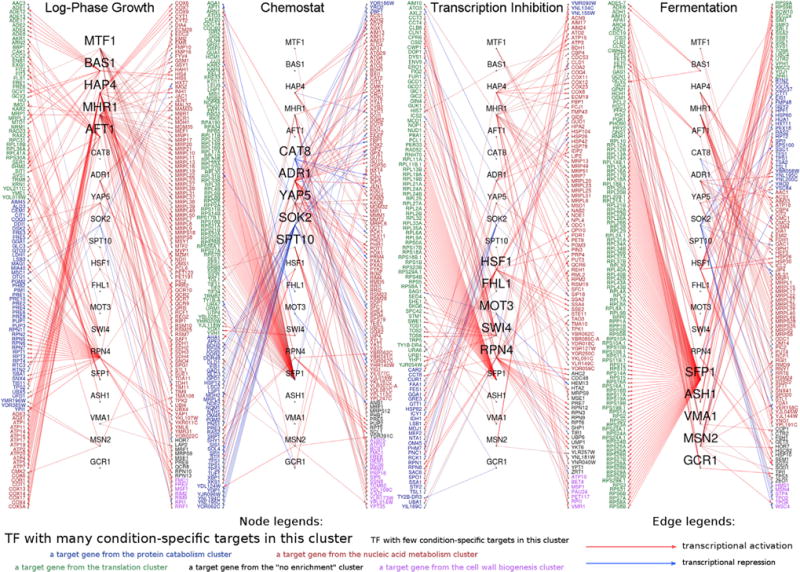
The figure displays the final high-confidence regulatory network split into four parts, based on the four experimental condition clusters, where each interaction was detected with the strongest confidence. Transcription factors are shown in black (center), and target genes are colored (periphery). Different colors indicate different gene clusters, as shown in the legend. The colors of the edges correspond to predicted transcriptionally activating (red) and repressive (blue) regulation, respectively. A stronger color denotes high confidence. A large font size denotes the five transcription factors that are most specific to each condition cluster. TFs that were not among the top 5 in terms of cluster specificity in any of the clusters are not shown.

Next we compared InfereCLaDR with original Inferelator predictions. We focused on three categories of interactions: those that were predicted by InfereCLaDR but not the Inferelator (“gained”), those that were predicted by both InfereCLaDR and the Inferelator (“conserved”), and those that were not predicted by InfereCLaDR but were by the Inferelator (“removed”) (Figure 3C). Conserved interactions correlated in rank; i.e., both approaches had similar confidence in accuracy of these predictions. InfereCLaDR predicted more interactions than Inferelator, both outside of the Gold Standard (Figures 3B and S6I–S6K) and in total; the number of gained interactions was much larger than that of removed ones (Figure 3C). Notably, this increase was not due to overfitting or error because orthogonal support for the gained interactions also increased in InfereCLaDR compared with the original approach (Figure 3D). These lines of evidence suggest that bi-clustering and RNA half-life fitting implemented in InfereCLaDR resulted in hundreds of new high-quality interactions and also removed many false positives.

One of InfereCLaDR’s major strengths lies in recovering condition-specific regulatory interactions. For example, most of the gained interactions passed the precision = 0.5 cutoff (Supplemental Experimental Procedures) in only one or two condition clusters; i.e., they were highly condition-specific. In contrast, most conserved interactions were above threshold in 3 or 4 condition clusters; i.e., they were more general (Figure 3E). We examined these gained interactions more closely to determine which bi-clusters accounted for new predictions (Figure 3F). Consistent with our expectations, gained interactions occurred frequently among NCSM metabolism genes in the chemostat cluster, which uses one of the longest RNA half-lives (Figures 1D, 2F, and S4). Similarly, gained interactions involved target genes from protein catabolism and cell wall biogenesis when predicted under perturbed conditions but not under normal conditions; e.g., during log phase growth (Figure 3F), confirming predicted transcript stabilization for these genes under perturbed conditions (Figures 1D and S4). In comparison, other gained interactions occurred in bi-clusters with short RNA half-lives; i.e., for protein catabolism genes and cell wall biogenesis genes in the chemostat cluster, confirming that InfereCLaDR also captured condition-specific network rewiring events that were independent of RNA half-life changes. In sum, InfereCLaDR not only outperformed Inferelator and other methods in terms of accuracy of newly gained interactions but did so by recovering interactions that only appear under specific conditions, under which RNA half-lives typically deviated from the norm.

New Predictions Are Corroborated by Literature

To illustrate the value of new interactions, we list the top new targets of highly and medium-connected TFs (Tables 2 and S3). Importantly, many of the predictions are validated by independent datasets (Tables 2 and S3) and function annotation. For example, Sfp1p is a known regulator of ribosomal protein genes (Marion et al., 2004; Cipollina et al., 2008; Reja et al., 2015), and all of its top predicted targets are ribosomal subunits and are supported independently (Table S3). Rpn4p is known to activate proteasome expression (Karpov et al., 2008a, 2008b), and, indeed, most of its predicted targets of activation are proteasomal genes, consistent with known biology.

Table 2.

InfereCLaDR Top-Ranking Predictions and Their Precision Values

A
RAP1		GCN4		SFP1		MSN2		SOK2		YAP1		HSF1		RPN4		ABF1		TEC1
SEC14	0.67	LYS1	0.85	RPS24A	0.98	YDR391C	0.71	YRO2	0.67	GAC1	0.48	OPI10	0.81	RPN12	0.93	YER010C	0.31	TRX2	0.26
YEL1	0.62	HOM2	0.84	RPL18B	0.92	CMK2	0.64	UIP4	0.67	TAH18	0.46	GGA1	0.66	RPT2	0.92	COA3	0.28	CRH1	0.25
PMT4	0.54	BAT1	0.82	RPS16A	0.92	YLR257W	0.43	YNL194C	0.61	ISF1	0.44	RTC3	0.64	PRE10	0.92	GET2	0.24	YOL019W	0.23
FEN1	0.52	HIS2	0.82	RPL8A	0.90	STF2	0.38	GAD1	0.60	YNR034W-A	0.25	YRO2	0.62	RPT5	0.92	BSD2	0.23	RAX2	0.20
ALG7	0.50	STR2	0.80	RPS18B	0.91	RCN2	0.32	JIP4	0.59	MBR1	0.22	APJ1	0.61	RPN7	0.88	YAH1	0.22	YOL014W	0.18
RBD2	0.44	SDT1	0.76	RPS18A	0.90	HAL5	0.25	MSC1	0.59	MRK1	0.20	LSB1	0.57	RPN1	0.85	TDA5	0.22	TGL2	0.16
RPL18B	0.43	RIB3	0.75	RPL40B	0.90	OXR1	0.24	TFS1	0.56	TCB2	0.18	YGR127W	0.53	RPN10	0.83	MIM1	0.22	YPS3	0.15
RPL16B	0.41	PSF2	0.75	RPL42B	0.88	PNC1	0.24	YNL195C	0.56	GAT2	0.18	YGR250C	0.51	PRE7	0.82	YDR541C	0.18	PHM8	0.14
YLR412C-A	0.40	POS5	0.74	RPS22A	0.88	DOA1	0.23	YJR096W	0.54	YLR460C	0.16	CUR1	0.51	YBR062C	0.81	MGR2	0.18	YBL111C	0.12
HXK2	0.40	SRY1	0.74	RPL9A	0.88	MRP8	0.22	OM45	0.49	ATR1	0.16	SAF1	0.45	PUP1	0.81	SLC1	0.17	RIB4	0.11
B
MGA2M		MOT3M		INO2M		MSN4M		FKH2M		FLO8M		RTG3M		STP1M		LEU3M		NRG1M
PLB2	0.83	FIG2	0.49	HNM1	0.84	YHR022C	0.47	AIM20	0.83	FLO9	0.33	IDH2	0.71	VHR2	0.33	OAC1	0.74	PDE2	0.60
TDA4	0.71	PRM1	0.48	SAH1	0.81	CRS5	0.37	HOF1	0.84	TIR4	0.24	PDH1	0.30	MET17	0.33	BAT1	0.72	PRM7	0.40
YLR413W	0.66	SAG1	0.46	FAS1	0.81	JLP1	0.22	ALK1	0.82	DED81	0.17	AAT2	0.27	MET3	0.32	FRS2	0.66	VTS1	0.28
ALE1	0.65	TIR1	0.46	SAM2	0.78	SNO4	0.20	CLB1	0.81	PAU7	0.15	CPR4	0.22	SUL1	0.30	ILV5	0.52	YLR407W	0.27
FAS1	0.50	PAU24	0.39	CHO1	0.75	FRE7	0.16	YMR030W-A	0.79	MSC7	0.15	ARP3	0.14	MET10	0.28	LEU1	0.49	GFD2	0.26
HEM13	0.46	AAC3	0.39	EPT1	0.67	PUG1	0.13	BUD4	0.78	PAU5	0.14	WTM1	0.14	MET5	0.27	SSB1	0.43	YGR079W	0.24
SUR2	0.36	TIR4	0.35	ADO1	0.63	YEL073C	0.13	CDC5	0.77	ERG24	0.14	IDP1	0.13	MEP2	0.27	MAE1	0.33	YNL095C	0.21
NEM1	0.35	EUG1	0.31	OPI3	0.63	PDC6	0.12	YMR001C-A	0.76	PAU24	0.14	URA8	0.12	PET8	0.21	PAB1	0.26	TRM5	0.20
PEX31	0.35	TIR2	0.27	EHT 1	0.59	GCY1	0.11	KIN3	0.75	NCP1	0.13	ADE3	0.10	GNP1	0.21	YPL260W	0.25	PHO90	0.19
FHN1	0.35	FIG1	0.26	YIP3	0.55	FMP48	0.11	HST3	0.67	YGL108C	0.13	SLP1	0.10	DAL80	0.18	ILV1	0.22	MCH5	0.16

(A) New targets (i.e., interactions not in the Gold Standard) of the ten transcription factors (top row) that are most connected in the Gold Standard. The table also lists the precision values of these interactions, with darker green denoting higher precision.

(B) New targets of ten TFs of medium connectivity. Precision values are calculated using the entire matrix of prediction confidence scores, containing 5,716 genes and 557 TFs. The list of true positives was defined by the Gold Standard. Bold targets correspond to interactions that were not found in any of the four orthogonal datasets listed in Table S1; i.e., these regulatory interactions are entirely new. See Table S3 and Data S1 for more details.

In contrast, InfereCLaDR also predicted that Rpn4p activates the expression of four previously unknown targets, CCT2, CCT3, CCT4, and CCT8, which are not part of the proteasome but subunits of the cytosolic chaperonin Cct ring complex and are required for actin and tubulin function (Chen et al., 1994; Vinh and Drubin, 1994). These four interactions were largely absent from the existing databases listed in Table S1, and InfereCLaDR detected them in a subset of regulatory regimes (Data S1). We found additional evidence that supports the validity of the prediction. Rpn4p is known to bind the proteasome-associated control element (PACE; 5′-GGTGGCAAA-3′; Mannhaupt et al., 1999) and also regulates proteasome assembly chaperones through binding to a smaller region, 5′-(A/G)GTGGC-3′, known as the PACE core region (Shirozu et al., 2015). Examining the promoter region of the CCT genes, all four contained the PACE core element (Supplemental Experimental Procedures). These interactions were specific to the transcription inhibition and fermentation clusters (Figure 4; Supplemental Notes), explaining why they were undetected in previous studies, which typically excluded the condition-specific regulatory regimes tested here.

Of the 100 new interactions in Table S3, 13 were absent from the orthogonal validation datasets discussed above. We examined some of these interactions further and found evidence supporting their validity. For example, Hsf1p is a key regulator of diverse stresses and monitors the cell’s translation status by interacting with the ribosome quality control (RQC) complex (Brandman et al., 2012). InfereCLaDR predicts that Hsf1p acti vates LSB1 and SAF1 in a condition-specific manner (Figure 4, transcription inhibition cluster). SAF1 has four other transcription regulators (Bur6p, Med6p, Spt10p, and Sua7p), which are all, similarly to Hsf1p, detected under various stresses, especially heat shock (Mendiratta et al., 2006; Venters et al., 2011), suggesting that Hsf1p could also be a member of the heat shock regulators of SAF1. In comparison, Lsb1p controls actin assembly and prion modulation in yeast (Ali et al., 2014) and has not been reported as a target of Hsf1p. Several recent studies have linked Hsf1p to actin assembly. Yeast deficient in the RQC-Hsf1 regulatory system has altered actin cytoskeletal structures (Yang et al., 2016), overexpressing HSF1 in worms increases actin cytoskeleton integrity and lifespan (Baird et al., 2014), and active Hsf1p affects the actin cytoskeleton in mammalian cells (Toma-Jonik et al., 2015). Therefore, it is tempting to hypothesize that LSB1 is the missing link by which Hsf1p affects actin skeleton assembly. The Supplemental Notes outline additional examples that validate InfereCLaDR’s new predictions, including condition-specific interactions and combinatorial regulation of gene categories, which we summarize in Figure 4. In sum, InfereCLaDR predicted hundreds of novel high-confidence interactions in yeast that are consistent with previously known roles of the regulators and suggest new regulatory relationships.

DISCUSSION

We present InfereCLaDR, a network inference framework with several conceptual advances over existing methods (Greenfield et al., 2013; Arrieta-Ortiz et al., 2015; Ciofani et al., 2012), demonstrating, for the first time, that biophysically relevant models that incorporate RNA degradation improve large-scale network prediction. InfereCLaDR includes a new, high-quality Gold Standard of regulatory interactions and infers separate networks across subsets of genes and conditions. We built the Gold Standard that accompanies this work from several benchmark datasets (Teixeira et al., 2006, 2014; Monteiro et al., 2008; Abdulrehman et al., 2011; Cherry et al., 2012; Costanzo et al., 2014; Kemmeren et al., 2014), and, importantly, accounted for the direction of the interaction (i.e., activation versus repression) and our confidence in the data source. We show that this approach, which improved the quality of a gold standard but not necessarily its size, vastly outperformed alternative approaches (Figure S3). In addition, InfereCLaDR showed that bi-clustering expression data, cluster-specific network inference, and optimization and use of cluster-specific RNA half-lives improved prediction accuracy and sensitivity even further (Figures 3 and S1).

Using these advances, InfereCLaDR resulted in a genome-wide regulatory network that is more accurate and comprehensive than previous approaches. At 50% precision, InfereCLaDR predicts >1400 new interactions in yeast (Figure 4), 43% of which are validated by independent datasets, and 57% are entirely new (Figure 3B). Approximately 80% of these interactions were activating and 20% were repressive. Compared with other approaches (e.g., Genie3), this was an 8-fold improvement. We validated new interactions using existing direct (i.e., TF-DNA contact) and indirect (i.e., knockout/overexpression) evidence. The success of rank-combining cluster-specific networks suggested that previous approaches often missed condition-specific regulatory interactions (Figures 3 and S2; Tables 1), especially for conditions with altered RNA half-lives (Figures 2D and 2H and 3F). The result was consistent with the findings that both RNA degradation and transcription regulation are specific to different gene sets and adjust to changing environmental conditions (Munchel et al., 2011; Miller et al., 2011; Lehtinen et al., 2013; Hart et al., 2015; Yang and Leskovec, 2014).

Most importantly, we showed that including RNA degradation in network prediction boosts inference of transcriptional regulatory networks. To the best of our knowledge, InfereCLaDR is the only approach capable of doing so on a genome-wide scale. InfereCLaDR does not make prior assumptions on RNA stability but learns optimal degradation rates directly from expression data. The resulting rates were similar to experimentally measured rates, validating our approach. In addition, optimized (predicted) half-lives accurately reflected expected trends across conditions and across organisms; e.g., for ribosomal genes (Figure 2). InfereCLaDR is also generalizable to other organisms. In B. subtilis, it accurately predicted that bacterial RNA transcripts are less stable than yeast transcripts (Figure 1), as confirmed by experiments (Neymotin et al., 2014; Sun et al., 2012; Pelechano and Pérez-Ortín, 2008; Hambraeus et al., 2003).

InfereCLaDR has several applications. First, it can predict RNA degradation rates for different gene clusters or conditions from expression data alone. Such predictions are valuable because it is still challenging to measure RNA degradation, and only a few datasets exist (Miller et al., 2011; Schwalb et al., 2012; Sun et al., 2012; Neymotin et al., 2014; Munchel et al., 2011). Second, InfereCLaDR can reveal new trends, such as the long half-lives of genes in nucleic acid metabolism (Figure 2). Third, InfereCLaDR can predict new regulatory interactions missed before. We showed that even the predicted interactions not seen in other studies are likely valid.

To the best of our knowledge, our approach is the first attempt at incorporating RNA degradation into large-scale automated network learning. Our work should therefore be viewed primarily as a proof of concept, demonstrating that expanding the biophysical complexity of the underlying model of regulation improves network prediction accuracy while also accurately estimating the dynamic parameters of transcriptional regulation. This step brings the field of machine learning-based network inference closer to the field of detailed mathematical modeling of biophysical processes. However, InfereCLaDR also has limitations that need to be addressed in future versions. One such limitation is the requirement of a large enough RNA expression dataset to distinguish between different modes of regulation under different conditions or cell types. A substantial portion of the data needs to stem from time series experiments, and the condition cluster label assignments require semi-manual inspection of the meta-data for heterogeneous expression datasets for better interpretability. Another limitation is the availability of a reliable gold standard of interactions. Both of these requirements are already met in well-studied model organisms, such as E. coli (Fang et al., 2017), C. elegans (Cheng et al., 2011), and some human cell lines (ENCODE Project Consortium, 2012). As more experimental data become available through technological advances such as assay for transposase-accessible sequencing (ATAC)-seq, Infer-eCLaDR in its current form will be applicable to other systems.

In addition, future research will determine the sensitivity of InfereCLaDR to the quality of the collection of prior known interactions and to the technique employed for bi-clustering the data, which are beyond the scope of the present study. Other extensions could expend the Inferelator framework to infer RNA degradation rates from a continuous distribution and using the same prior known interactions for both RNA degradation rate fitting and TFA estimation, which would address limitations regarding the size of the Gold Standard and the requirement to select a discrete set of potential RNA half-lives. Finally, future extensions could eliminate the need for gene-wise clustering by estimating the optimal RNA half-life separately for every gene through application of the same Bayesian model selection the Inferelator uses to select the best regulatory model for every gene.

In a broader context, InfereCLaDR advances inference methods through improved biophysical modeling of biological processes by approximating the rates of synthesis and degradation using mass action laws and experimental designs that include time series. This approach outperforms other methods that are agnostic of underlying mechanisms (and unaware of underlying temporal designs), such as Random Forest (Huynh-Thu et al., 2010; Petralia et al., 2015), conditional entropy (Karlebach and Shamir, 2012), partial correlation (Yuan et al., 2011), or probabilistic graphical models (Siahpirani and Roy, 2016). The results of this study encourage further incorporation and recovery of biophysical parameters, such as interaction terms between co-regulating TFs, separation of transcriptional activators and repressors, which has only been done on a small scale (Noman and Iba, 2005; Liu and Wang, 2008; Äijö and Bonneau, 2016; Intosalmi et al., 2016), and modeling protein modifications that affect TF activity. Given the growing body of literature on RNA-binding proteins (Hogan et al., 2008; Mittal et al., 2009; Janga and Mittal, 2011), our results also inspire potential approaches to model the RNA decay term explicitly as a sum of contributions from RNA degradation factors. Therefore, we argue that it is time to move inference of transcription regulatory networks toward more biophysically relevant models, and the work presented here provides an important step toward this goal.

EXPERIMENTAL PROCEDURES

Data Acquisition and Normalization

We acquired four regulatory interaction datasets (known priors) from the sources listed in Table S1, originating predominantly from ChIP-chip, chromatin immunoprecipitation sequencing (ChIP-seq), knockout, and overexpression assays (Teixeira et al., 2006, 2014; Monteiro et al., 2008; Abdulrehman et al., 2011; Cherry et al., 2012; Costanzo et al., 2014; Kemmeren et al., 2014). The list of 563 TFs includes all genes annotated as either “DNA-binding” or “Regulation of transcription, DNA-templated” in the Saccharomyces Genomes Database (SGD) (Cherry et al., 2012; Costanzo et al., 2014) and all regulators in the YEASTRACT database of regulatory interactions (Teixeira et al., 2006, 2014; Monteiro et al., 2008; Abdulrehman et al., 2011). We downloaded 179 RNA expression datasets from 119 different labs from the GEO (Edgar et al., 2002; Barrett et al., 2013) using the R Bioconductor package GEOquery (Huber et al., 2015; Davis and Meltzer, 2007). To obtain a high-quality, consistent data-set and to avoid platform-specific batch effects, we exclusively used the Yeast Affymetrix 2.0 platform (GPL2529) because it contained the largest number of unique samples in the GEO database. Raw CEL files for every GEO sample (GSM) measured on this platform were downloaded on March 23, 2015, along with their meta-data. We processed and normalized the raw CEL files using the R packages affy (Gautier et al., 2004) and gcrma (Wu et al., 2004), adjusting for background intensities, optical noise, and non-specific binding in a probe sequence-specific fashion. Methods correcting for batch/lab effect did not improve inference performance (data not shown). The meta-data were processed manually to identify time series experiments. The full meta-data, as downloaded from the GEO, are included in the Data S1. The final yeast RNA expression dataset used for the work described here included 2,577 samples, each containing the expression data for 5,716 genes.

For B. subtilis, all relevant data, including the gold standard of interactions, the list of TFs, expression data, and the meta-data, were taken from Arrieta-Ortiz et al. (2015). We used the BSB1 expression dataset employed in Arrieta-Ortiz et al. (2015), which was measured on the B. subtilis strain BSB1, a derivative of strain 168. This dataset can be found under GEO: GSE27219 (Nicolas et al., 2012).

Expression Data Clustering

We scaled the expression data so that every row (gene) had mean 0 and variance 1. The 2,577 expression samples were then clustered using the Euclidean distance metric. We then performed principal-component analysis on the entire RNA expression matrix and excluded all but the first 16 dimensions to remove the cumulative effect of noisy low-variance components and facilitate condition-wise clustering. We then performed k-means clustering with k = 4. This number was optimized as described in the Supplemental Experimental Procedures (Figure S1E). We performed all downstream analyses on the resulting clusters using the original (normalized but unscaled) expression data.

To annotate the four condition clusters, we parsed the meta-data from the GEO, employing the R packages tm (Feinerer and Hornik, 2015; Feinerer et al., 2008) and SnowballC (Bouchet-Valat, 2014). First, we used the binomial test to determine which words are enriched in a given condition cluster compared with the remaining clusters. To avoid words with a p value of 0 and to minimize lab-specific effects, we then excluded words that had zero counts in all but one cluster. This resulted in a list of words sorted by p value enrichment in each cluster. The p values were then corrected for multiple hypotheses testing using the Bonferroni correction. Word clouds were created from terms with p values smaller than 10 ²⁰ using the wordcloud package in R (Fellows, 2012). The final label assignments were determined via a detailed, manual inspection of enriched terms in the word clouds (Supplemental Notes). See the Supplemental Experimental Procedures for more details and Data S2 for the complete lists of terms.

In addition to condition-wise clustering, we also performed row (gene-wise) clustering. To do so, we first hierarchically clustered the 997 genes in the Gold Standard and then generalized these clusters to the 5,716 genes present in the entire expression dataset. This procedure resulted in five clusters, for which we performed gene ontology enrichment analysis as described in the Supplemental Experimental Procedures. See the Supplemental Experimental Procedures for more details.

The bi-clustering of genes and conditions was used to separate genes with heterogeneous functions and samples coming from heterogeneous conditions into several broad classes based on gene function and type of condition. The goal of this bi-clustering was to capture the known condition and gene specificity of RNA half-lives (Neymotin et al., 2014; Munchel et al., 2011) and condition-specific network remodeling (Lehtinen et al., 2013; Hart et al., 2015). Note that this is unrelated to the bi-clustering used in Bonneau et al. (2006) to identify co-regulated genes and conditions.

Curation of the Gold Standard of Regulatory Interactions

A key aspect of the work was the construction of a high-quality Gold Standard of regulatory interactions, which we used as prior interactions data for transcription regulatory network (TRN) training, for fitting RNA half-lives, and for validating the predicted interactions (GS-train, GS-fit, and GS-fit/GS-validate in Figure S2, respectively). The Gold Standard was derived by combining binding and expression information from three major sources (Table S1). We obtained the core data from the YEASTRACT repository (Teixeira et al., 2006, 2014; Monteiro et al., 2008; Abdulrehman et al., 2011), which is a curated repository of > 200,000 regulatory interactions in yeast with >1,300 bibliographic references. The repository contains two types of evidence for each potential regulatory interaction: direct and indirect. Direct evidence denotes an interaction coming from an assay that directly established a physical binding event, such as ChIP-seq or one-hybrid assay. Indirect evidence comes from differential expression analysis of a TF knockout or overexpression experiment. We first filtered these data to obtain a conservative list of 2,577 regulatory interactions that have at least one source of direct evidence and two sources of indirect evidence. At this stage, these interactions were unsigned; i.e., they did not include information about whether the regulatory interaction is positive or negative.

Because TFA estimation performs best when all prior known interactions are signed (Supplemental Experimental Procedures), we processed the list further to maximize the number of signed interactions. YEASTRACT provides information on the signs for some interactions; e.g., those derived from expression analysis of knockout mutants. To add signs from the YEASTRACT database, we used the following rule: a regulatory interaction was deemed “positive” when the target gene was downregulated upon TF knockout, and “negative” for the opposite case. Because some interactions were detected in multiple experiments with opposite sign annotations, we only considered the signs that were measured in assays conducted under normal conditions, labeled as “YPD medium; mid-log phase” in the YEASTRACT database. In case there was still a conflict, we employed the majority rule, and in the case of a tie, the interaction was discarded (set to 0). This procedure resulted in 1,155 signed interactions in total.

To expand this dataset, we obtained additional, curated regulatory interactions from the SGD (Cherry et al., 2012; Costanzo et al., 2014) and from a published dataset of 1,484 knockout experiments (Kemmeren et al., 2014). We used these interactions only to assign signs to interactions that were still unsigned in the list of 2,577 interactions with one direct and two indirect evidence types in YEASTRACT (see above). These additions expanded our list of signed interactions to 1,403.

These 1,403 interactions constitute the set of signed prior known interactions used throughout this paper, which we denote as the “Gold Standard.” The Supplemental Experimental Procedures, Figure S3, and Data S1 describe more details about the creation of Gold Standard and its performance compared with other collections of interactions.

Inferelator Implementation

We used and modified code for the Inferelator version 2015.03.03 (Bonneau et al., 2006; Greenfield et al., 2013; Arrieta-Ortiz et al., 2015). We describe the original Inferelator core model in this section, and more details can be found in the Supplemental Experimental Procedures. The Inferelator algorithm calculates the optimal model of regulation for each target gene independently of other genes. The model for each gene i is based on the assumption that the dynamics of transcription regulation are governed by the following relation:

$$\frac{d{X}_i}{dt}=-{\alpha }_i{X}_i+\sum _{j\in P_i}{\stackrel{\sim }{\beta }}_{i,j}{A}_i,$$ (Equation 1)

where X_i is the RNA expression level of gene i, P_i is the set of potential regulators of gene i, A_j is the activity of TF j, ${\stackrel{\sim }{\beta }}_{i,j}$ is the coefficient of regulatory interaction between TF j and gene i, and α_i is the RNA degradation rate of gene i.

To estimate the parameters ${\stackrel{\sim }{\beta }}_{i,j}$, we can approximate Equation 1 using finite differences and divide both sides by α_i:

$${\tau }_i\frac{X_i\left(t_{k+1}\right)-X_i\left(t_k\right)}{t_{k+1}-t_k}+X_i=\sum _{j\in P_i}{\beta }_{i,j}{A}_j\left(t_k\right),$$ (Equation 2)

where the time axis t has been broken up into discrete time points at which the data was collected, indexed by k. The left side of Equation 2 is the response variable, whereas the right side is the design variable. Note that ${\tau }_i={\alpha }_i^{-1}$ and is related to the RNA transcript half-life HL_i via HL_i = τ_ilog(2) and ${\beta }_{i,j}={\tau }_i{\stackrel{\sim }{\beta }}_{i,j}$. Also note that, throughout our analysis, no corrections for cell division times were made because it was impossible to determine them for each of the 2,577 experiments coming from 119 labs. Given that median RNA half-lives are much shorter than cell doubling times, we consider the omission tolerable. In the original Inferelator framework, the RNA half-life had been set to 14 min for all yeast genes and conditions (i.e., τ = 20).

Furthermore, note that Equation 1 holds true for both steady-state data and time series data, which can be used to perform regression simultaneously. For steady-state conditions, the first term on the left side of the equation is 0, and A_j(t_k) becomes A_j,_k, where k denotes the steady-state condition. In the data-sets employed in this paper, 963 of the 2,577 (37%) yeast data points and 160 of the 266 (60%) B. subtilis data points were derived from time series experiments; the remainder were derived from steady-state conditions.

The response variable is first used together with prior known interactions to calculate TFAs for every TF (Supplemental Experimental Procedures). TFA is derived from expression changes of the prior known targets of a TF and has been shown to improve TRN inference dramatically in prokaryotes (Arrieta-Ortiz et al., 2015).

The same prior known interactions are then used in a constrained regression step that selects the most likely model of regulation for every gene using a data-driven approach called Bayesian best subset regression (BBSR). To calculate TFA and BBSR, we used the entire gold standard or a subset of it as prior known interactions. Figure S2 and Sub-Sampling the Gold Standard for RNA Half-Life Fitting and Error Estimation in the Experimental Procedures outline the workflows employed in this paper, specifying how the gold standard was split, sub-sampled, and used for inference. The procedure does not use any training data for testing. The new framework, InfereCLaDR, is defined by bi-cluster-specific network inference using the Inferelator and explicit modeling and optimization of the RNA half-life descriptor τ for each gene and condition cluster.

The final output of the Inferelator and InfereCLaDR is a list of confidence scores for all possible regulatory interactions, determined by a “computational knockout assay.” Each Inferelator run was performed on 50 bootstraps of the RNA expression data, and the final confidence scores for all interactions were computed by rank-combining the confidence scores across bootstraps. For more detail, see the Supplemental Experimental Procedures.

Sub-sampling the Gold Standard for RNA Half-Life Fitting and Error Estimation

To use our gold standard for both parameter fitting and method evaluation without overfitting, we used two strategies for re-sampling the gold standard (Figure S2). For assessing the overall dependency of inference accuracy on RNA half-life (Figures 1A and 1B) and obtaining optimal gene- and condition-specific RNA half-lives (Figures 1D, 2, and S4), we used Split A. This method involved randomly selecting a pre-specified fraction of gold standard interactions to be in the training set (GS-train), with the rest of the interactions to be used for fitting half-lives (GS-fit). We set the fraction of data used in the “training” set to 0.5, although all results also hold for other values (Figures S6A–S6H). The procedure was repeated 20 times, and for each re-sample, RNA half-lives were fit as described in RNA Half-Life Estimation in the Experimental Procedures. Note that the choice of 20 re-samples is unrelated to the number of bi-clusters in the yeast expression dataset used here, which is also 20.

To assess whether fitting condition- and gene-specific RNA half-lives in this manner improves performance (Figures 3A; Table 1), we used Split B, where a third set of Gold Standard interactions (GS-valid) was held out and used only for estimating the accuracy of our algorithm’s predictions. We created GS-valid to avoid over-fitting, and this set was exclusively used to estimate the accuracy of the network computed using prior known interactions in GS-train and half-lives obtained using GS-fit. In other words, the evaluation set GS-valid was completely separate from the training sets. Each interaction was assigned one of the three categories randomly (GS-train, GS-fit, or GS-validate), with probabilities of 0.34, 0.33, and 0.33, respectively. This way of splitting the gold standard was also applied to the other methods (Genie3 and iRafNet), keeping the random assignments of interactions into GS-train, GS-fit, and GS-valid identical across the methods for each Gold Standard re-sample.

In both splitting approaches, the random separation of interactions into two or three categories was performed on the basis of regulatory interactions between TFs and target genes. It is also possible to perform the separation on the basis of target genes. However, in the yeast dataset, 695/993 (70%) of all genes in the yeast Gold Standard have only one interaction in the Gold Standard (i.e., they are only known to be regulated by one TF). This number also comprises 50% of all interactions in the Gold Standard. Hence, splitting the training, fitting, and validation networks based on target genes is essentially equivalent to splitting them based on interactions, and so the two approaches are basically equivalent.

We used two measures of network prediction accuracy to assess the quality of our predictions: AUPR and AUROC. The two measures were calculated in the standard way, as described in the Supplemental Experimental Procedures. All results are similar for both measures (Figures S1C–S1D, S1F, S5, and S6; Table S2). We focus here on AUPR because it is more sensitive for high-scoring interactions compared with AUROC, which distributes the weights more equally across the entire list of predictions. A model with maximal AUPR is desirable for small-scale, targeted validation experiments. Further, AUPR is superior to AUROC in a class-imbalanced (skewed) regime, in which the sizes of true positives and false positives differ substantially (Davis and Goadrich, 2006), which is the case for our data.

RNA Half-Life Estimation

The primary advance described here is the explicit modeling and incorporation of RNA degradation rates into large-scale network inference. To do so, we first developed a procedure to compare different models across parameter settings. As shown in Figure S2, Split A involves sub-sampling two equal sets of interactions from the gold standard: one for training TFA and BBSR (GS-train) and one for calculating AUPR (GS-fit). We pre-specified values of the RNA half-life parameter τ at 0, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 140, 160, 200, and 250 min, designed to span the range of expected half-lives in yeast (Neymotin et al., 2014; Munchel et al., 2011; Sun et al., 2013; Schwalb et al., 2012; Miller et al., 2011). Splitting the Gold Standard into a training and a fitting set is required because our RNA half-life estimations rely on optimization of network inference. Because our algorithm already uses some interactions for TFA and BBSR estimation (GS-train), a second leave-out set of interactions is necessary for unbiased evaluation of network inference accuracy (GS-fit) and, subsequently, for RNA half-life optimization.

InfereCLaDR uses the Inferelator while setting τ to a given value (as specified above) for every gene under every condition either in the given bi-cluster (Figures 1D and S4, S1H, and S5) or for the entire dataset (Figures 1A and 1B and S1C and S1D), using GS-train as the prior known interactions. Precision and recall curves were computed for each run corresponding to a re-sample and a value of τ, using GS-fit as the set of true interactions. We compared precision-recall curves across RNA half-lives by taking the element-wise median of the precision and recall vectors across Gold Standard re-samples for a given value of RNA half-life (Figures S1A and S1B). Conversely, to create a half-life-versus-AUPR curve for each re-sample, we compared AUPRs measured for different t’s, without changing GS-train and GS-fit between τ values or bi-clusters. These comparisons are represented by isochromatic curves in Figures 1A and 1B and S4. We chose an optimal τ for each re-sample by maximizing AUPR along the corresponding curve. We also compared performances between models with different RNA half-lives using AUROC instead of AUPR, yielding similar optimal half-lives (Figures S1C, S1D, and S5). For best RNA half-life inference results, we recommend that at least 30% of samples belong to time series of reasonable spacing (i.e., measured in minutes or hours but not days or weeks).

Finally, we considered the distribution of optimal RNA half-lives across the 20 re-samples for each condition and gene bi-cluster using the Split A procedure in Figure S2. These distributions are shown in Figure 2, and their medians are shown in Figure 1D (and in Figure S1F for AUROCs). The median values of AUPR constitute the RNA half-life predictions for each gene and condition bi-cluster. Comparisons of predicted and observed RNA half-lives in the minimally perturbed condition clusters were performed by comparing median predicted RNA half-lives across re-samples with the median experimentally measured RNA half-lives across genes. Predicted and observed median values for each gene cluster were averaged across the chemostat and log phase growth condition clusters (Figure S1I).

To predict RNA half-lives for translation genes only (Figures 2C and S4), we applied the same AUPR maximization procedure to each condition cluster, using only known cytoplasmic translation genes and their known regulators for AUPR calculations. To predict RNA half-lives for nucleotide metabolism genes, we used the entire gene cluster because it was strongly enriched in the respective genes. Data S3 contains the final RNA half-life predictions for each gene and condition cluster. For more detail, see the Supplemental Experimental Procedures.

To demonstrate the improvement in TRN inference gained in InfereCLaDR compared with the original framework, we first split the gold standard according to Split B into GS-fit, GS-train, and GS-validate. For a given re-sample, we predicted RNA half-lives by maximizing AUPR (as measured on GS-fit) on each bi-cluster, using GS-train for training TFA and BBSR. Using those half-life values and the same re-sample of the gold standard, the model was trained again, but now using a union of GS-train and GS-fit (GS-train+fit) for TFA and BBSR computation. We calculated the final precision-recall curve by adding confidence scores across condition clusters for each re-sample, estimating precision and recall only on the GS-valid set corresponding to that re-sample (because GS-valid was not used to produce the predicted network) and then taking the element-wise median of the precision and the recall vectors across the 20 re-samples (Figure 3A). Figure S1F was calculated the same way but with number of true positives and number of false positives instead of precision and recall in the last (validation) step. Note that the Split B approach (Table 1) underestimates the magnitude of the increase in inference accuracy because of half-life fitting compared with the actual increase in accuracy of our final predicted network, which is produced using the Split A approach (Supplemental Experimental Procedures).

Highlights.

• Explicitly accounting for RNA degradation improves regulatory network inference

• Network-based optimization of RNA half-lives predicts correct RNA stability values

• Resulting networks are specific to groups of similar genes and conditions

• Importance of accounting for RNA half-lives is shown for yeast and B. subtilis