Bayesian multivariate meta-analysis of multiple factors

Abstract

In medical sciences, a disease condition is typically associated with multiple risk and protective factors. Although many studies report results of multiple factors, nearly all meta-analyses separately synthesize the association between each factor and the disease condition of interest. The collected studies usually report different subsets of factors, and the results from separate analyses on multiple factors may not be comparable because each analysis may use different subpopulation. This may impact on selecting most important factors to design a multi-factor intervention program. This article proposes a new concept, multivariate meta-analysis of multiple factors (MVMA-MF), to synthesize all available factors simultaneously. By borrowing information across factors, MVMA-MF can improve statistical efficiency and reduce biases compared with separate analyses when factors were missing not at random. As within-study correlations between factors are commonly unavailable from published articles, we use a Bayesian hybrid model to perform MVMA-MF, which effectively accounts for both within- and between-study correlations. The performance of MVMA-MF and the conventional methods are compared using simulations and an application to a pterygium dataset consisting of 29 studies on 8 risk factors.

1. Introduction

As a disease condition is typically associated with many risk and protective factors in medical sciences, many randomized controlled trials and observational studies considered multiple factors.^1–4 Reliable summary of association between each factor and the disease condition is crucial for the design of a multi-factor intervention program. The growth of interest in evidence-based medicine has led to a dramatic increase in attention paid to systematic reviews and meta-analyses. In prevention studies, it has become increasingly popular to perform meta-analyses on multiple risk and protective factors to summarize existing evidence; however, currently, nearly all meta-analyses are performed on each factor separately.^5–7 Different studies usually focus on different subsets of all risk and protective factors, and may only selectively report some significant factors in peer-reviewed articles; some factors may be reported by only a few studies. Hence, if we organize the collected data in a matrix with rows and columns indexing studies and factors respectively, then the data matrix is expected to contain many missing entries; see the example in Table 1. The conventional meta-analysis separately estimates each factor’s association with the disease condition, so it cannot borrow information across the factors. Moreover, results from separate meta-analyses may not be directly comparable because they may be based on different subpopulations. This limits medical investigators to select most important factors for the design of a multi-factor intervention program.

Table 1.

The pterygium data containing 29 studies with 8 risk factors. The effect size is log odds ratio with within-study standard error in parentheses. The blank entries indicate that the risk factors are unavailable from the corresponding studies.

	Risk factor
Study	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
1	−0.08 (0.34)
2						1.54 (0.10)
3	0.28 (0.17)	0.53 (0.10)	0.53 (0.13)
4	0.45 (0.11)					0.41 (0.10)		0.97 (0.23)
5	0.30 (0.40)
6				0.12 (0.40)	0.48 (0.70)
7	1.40 (0.23)
8	0.39 (0.13)	0.05 (0.13)
9	0.55 (0.22)	−0.04 (0.26)
10	3.04 (1.03)
11	1.95 (0.40)	1.21 (0.42)		0.67 (0.36)	−1.34 (0.34)		0.12 (0.31)
12	1.10 (0.30)
13	2.03 (0.39)			−0.69 (0.21)	−1.14 (0.38)		−1.64 (0.21)	2.99 (0.74)
14	0.83 (0.09)	0.11 (0.09)	0.91 (0.09)		−0.58 (0.12)	1.14 (0.13)
15	0.41 (0.22)
16		−0.20 (0.24)				1.73 (0.18)
17	0.42 (0.15)	−0.11 (0.25)	0.38 (0.21)	0.22 (0.15)	−0.64 (0.15)		−0.52 (0.37)
18	0.63 (0.12)	0.03 (0.05)	1.24 (0.24)
19	0.89 (0.08)	−0.08 (0.07)		1.70 (0.08)	−0.17 (0.08)		−0.06 (0.14)
20	0.39 (0.22)	−0.13 (0.30)
21	0.90 (0.30)							0.85 (0.49)
22	−0.48 (0.25)	0.31 (0.25)	0.87 (0.20)
23								0.66 (0.26)
24				−0.46 (0.72)			−0.73 (0.52)
25	0.76 (0.34)	−0.48 (0.55)	1.05 (0.33)
26		0.03 (0.11)	0.19 (0.09)
27	1.16 (0.36)	0.53 (0.23)	0.83 (0.25)
28	0.12 (0.03)	0.14 (0.20)	1.43 (0.28)			1.43 (0.22)
29	0.41 (0.09)	−0.26 (0.10)	0.46 (0.09)

Risk factors: (1) occupation type; (2) smoking status; (3) education attainment; (4) use of hat; (5) use of spectacles; (6) area of residence; (7) use of sunglasses; and (8) latitude of residence.

Recently, Serghiou et al.⁸ introduced field-wide systematic review and meta-analysis to report and assess the entire field of putative factors for a disease condition. Based on this concept, researchers can learn the selective availability and different adjustments of factors and the patterns of modeling. Although multiple factors were collected, the authors pooled the results for each factor separately; this is not efficient to analyze the multivariate data from a field-wide systematic review.

This article proposes multivariate meta-analysis of multiple factors (MVMA-MF) to jointly synthesize all risk and protective factors in the field-wide systematic review. Compared with separate meta-analyses that use different subpopulations, the results produced by jointly modeling of multiple factors have better interpretation and generalizability because they are based on the whole population in the multivariate meta-analysis. Multivariate meta-analysis methods have gained much attention in the recent literature^9–12, and they improve effect estimates by borrowing information from the correlations between multiple endpoints.^13–15 The multivariate meta-analysis models have been applied to several areas, such as meta-analysis of diagnostic tests^16–18, meta-analysis of multiple outcomes^19,20, and network meta-analysis of mixed treatment comparisons.^21–26 Mixed treatment comparisons use both direct and indirect evidence of treatment contrasts to synthesize the comparisons between multiple treatments; its focus differs from MVMA-MF, because MVMA-MF is interested in estimating the effect of multiple factors, not the contrasts between them.

Multivariate random-effects model generally requires correlations within each collected study. In some situations, within-study correlations are known to be zero. For example, in meta-analysis of diagnostic tests, the study-specific sensitivity and specificity are uncorrelated within studies because they are calculated from the true negative and true positive patients respectively.¹⁰ However, in MVMA-MF, the factors can be correlated within each study because they may be measured on same patients. Such within-study correlations are unknown unless individual patient data are available. Ignoring within-study correlations in the standard multivariate random-effects model may have great impact on the estimated overall effect sizes.²⁷

To deal with unknown within-study correlations, this article considers an alternative Bayesian model for MVMA-MF. The conventional multivariate model partitions the overall variance-covariance matrix into two parts: the within-study level that is due to sampling error and the between-study level that is due to heterogeneity between the collected studies. Instead of partitioning the overall correlations into the two levels, the alternative model directly specifies one single overall correlation matrix; hence, it may be viewed as a hybrid approach. This model is the Bayesian version of the model introduced by Riley et al.²⁸ Currently, Riley’s model is implemented in a frequentist way, such as using the restricted maximum likelihood method.²⁹ However, the data of MVMA-MF are usually fairly sparse (Table 1), and our simulations in Section 5 show that the frequentist method generated poor 95% confidence intervals for sparse data; also, the algorithm for maximizing the (restricted) likelihood did not converge for many simulated data. Instead of using the frequentist method, we present a fully Bayesian method to perform MVMA-MF. Although Bayesian methods have been introduced to deal with multivariate meta-analyses by Lu and Ades³⁰ and Wei and Higgins³¹, the former paper considered mixed treatment comparisons which focused on treatment contrasts, and the latter assumed known within-study covariance matrices. Hence, both Bayesian methods may not be directly applied to MVMA-MF. The Bayesian version of Riley’s model will be detailed in Section 4. We will use simulations and reanalyze the real data in Serghiou et al.⁸ to demonstrate the benefit of the joint Bayesian model for MVMA-MF, and we will conclude this article with brief discussion.

2. The motivating pterygium data

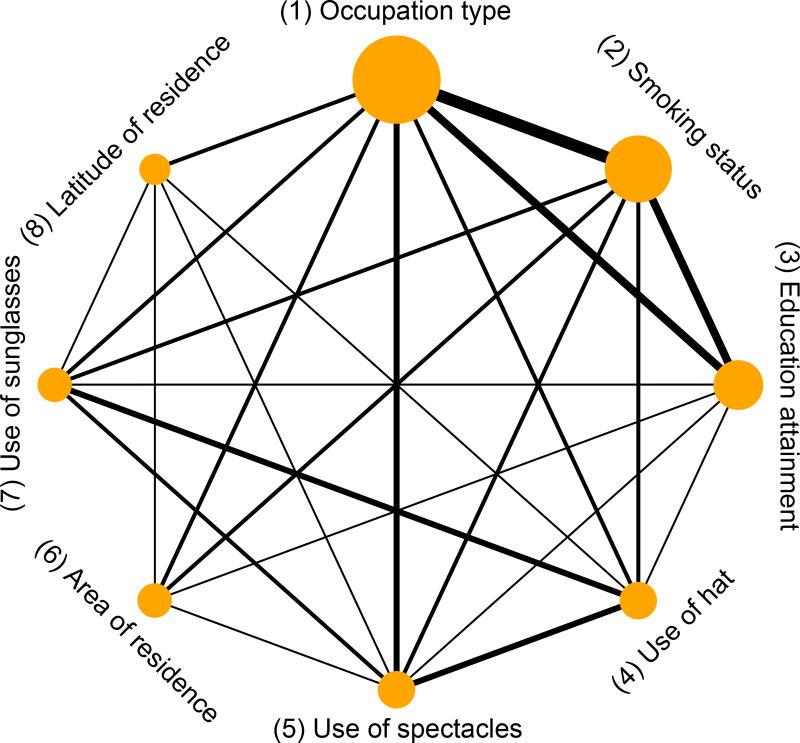
Pterygium is one of the most common eye conditions, and it may be related to many risk factors.³² Instead of reporting only one risk factor at a time, Serghiou et al.⁸ collected the odds ratios of all putative risk factors for pterygium. Specifically, they identified 60 eligible studies reporting on a total of 65 risk factors. Since most risk factors were only reported in less than 3 studies, we focus on the following 8 risk factors, each of which was reported in at least 4 studies: (1) occupation type (outdoor vs. indoor); (2) smoking status (yes vs. no); (3) education attainment (low vs. high); (4) use of hat (yes vs. no); (5) use of spectacles (yes vs. no); (6) area of residence (rural vs. urban); (7) use of sunglasses (yes vs. no); and (8) latitude of residence (low vs. high). These risk factors are sorted according to their frequencies reported in the collected studies (from high to low). Also, we cleaned the data by removing the log odds ratios that were obtained using multivariate regression model, because they were adjusted for different risk factors in different studies. Table 1 presents the cleaned data and Figure 1 shows the network plot of the 8 risk factors. The network indicates that most pairs of risk factors are simultaneously reported in some studies, but several pairs, such as area of residence and use of hat, are not. From Table 1, the risk factor latitude of residence was reported in only 4 studies, while 23 studies reported occupation type. Most studies reported different subsets of the 8 risk factors, and many entries in Table 1 are missing. The estimated overall effect sizes produced by univariate models may be poor because some risk factors have few samples. Also, many factors (e.g., area of residence and education attainment) are expected to be correlated, so a multivariate model may be more appropriate for this dataset than univariate models.

Figure 1.

Network plot of the pterygium data. The nodes represent the risk factors, and the edge between two nodes indicate that these nodes are simultaneously reported in common studies. The node size is proportional to the number of studies that report the corresponding risk factor, and the edge thickness is proportional to the number of studies that simultaneously report the corresponding two risk factors.

3. Conventional meta-analysis models

This section reviews some existing models for general multivariate meta-analysis. Suppose that n independent studies are collected; each study reports a p-dimensional vector of effect sizes, denoted as y_i = (y_i1, …, y_ip)^T, and denote its within-study variance-covariance matrix as S_i (i = 1, …, n). The conventional univariate meta-analysis pools the results for each j = 1, …, p separately; a fixed- or random-effects model is applied to the data ${\{(y_{\mathit{\text{ij}}},v_{\mathit{\text{ij}}})\}}_{i=1}^n$, where v_ij is the within-study variance, i.e., the jth diagonal element in S_i.^33,34 Since most studies are conducted by different research teams in different places using different methods, the studies are usually expected to be heterogeneous.³⁵ Also, the random-effects model may produce more conservative results than the fixed-effects model^36,37, so this article focuses on the random-effects setting that accounts for the heterogeneity between studies. We denote the univariate model as Model U, which ignores both within- and between-study correlations.

Multivariate meta-analysis recently gains much attention to simultaneously synthesize the p-dimensional effect sizes.^9–11 Given that the within-study variance-covariance matrices S_i are known, the commonly used random-effects model is specified as follows to analyze the multivariate data ${\{({\mathit{y}}_i,{\mathbf{S}}_i)\}}_{i=1}^n$:

$${\mathit{y}}_i~N({\mathit{\mu }}_i,{\mathbf{S}}_i);$$

$${\mathit{\mu }}_i~N(\mathit{\mu },\mathbf{T}),$$

where μ_i represents study i’s underlying true effect sizes, μ = (μ₁, …, μ_p)^T contains the overall effect sizes, and T = (τ_ij) is the p × p between-study variance-covariance matrix. We denote this multivariate model as Model M. Note that within-study variances are routinely reported in published articles, but within-study correlations are usually unavailable. Let D_i = diag(S_i) be the diagonal matrix consisting of the within-study variances. To analyze the data ${\{({\mathit{y}}_i,{\mathbf{D}}_i)\}}_{i=1}^n$ when the within-study correlations are unknown, a naïve multivariate method is to simply ignore these correlations by setting them to zero but still account for the between-study correlations; we denote this model as Model M₀. Nevertheless, ignoring within-study correlations could lead to poor estimated effect sizes, especially when the within-study correlations are comparable to or greater than the between-study correlations.²⁷ The following section introduces an alternative model that can incorporate both within- and between-study correlations for MVMA-MF.

4. Multivariate meta-analysis of multiple factors

4.1 Multivariate hybrid meta-analysis model

Model M may be deemed ideal to perform MVMA-MF: it uses the within-study correlations between multiple factors that are usually unknown, and it provides a benchmark for the performance of other potential models. Note that study i’s marginal variance-covariance matrix in Model M is M_i = S_i + T, and it can be written as M_i = (D_i + Δ)^1/2R_i(D_i + Δ)^1/2, where $\mathbf{\Delta }=\text{diag}({\tau }_1^2,\dots ,{\tau }_p^2)$ contains between-study variances (i.e., diagonal elements in T), and D_i is the diagonal matrix containing within-study variances (i.e., diagonal elements in S_i). The marginal correlation matrix of study i, R_i, is determined by both S_i and T, and thus it needs to be estimated if the within-study correlations are unknown. It may be inefficient to use the data from merely n studies to simultaneously estimate all R_i’s, which involve too many parameters.

Alternatively, extending the bivariate model in Riley et al.²⁸, we consider a multivariate model that does not require within-study correlations to perform MVMA-MF:

$${\mathit{y}}_i~N(\mathit{\mu },{({\mathbf{D}}_i+\mathbf{\Psi })}^{1/2}\mathbf{R}{({\mathbf{D}}_i+\mathbf{\Psi })}^{1/2}),$$

where $\mathbf{\Psi }=\text{diag}({\psi }_1^2,\dots ,{\psi }_p^2)$ is a diagonal matrix that consists of additional variances beyond sampling error due to between-study heterogeneity for the p effect sizes. In this model, all collected studies are assumed to share a common marginal correlation matrix R. This assumption effectively reduces the number of parameters to be estimated and accounts for both within- and between-study correlations. Like Model M, the alternative model partitions the marginal variances of y_i, D_i + Ψ, into the within- and between-study levels; however, it directly uses the matrix R to model the overall correlations, instead of partitioning the correlations into the previous two levels. Therefore, the alternative model may be deemed hybrid, and we denote it as Model H.

4.2 Missing data

So far, the models for complete data have been discussed. In MVMA-MF, each collected study often reports a small subset of the complete factors, and many factors are missing as in Table 1. It is straightforward to extend the four methods (i.e., Models U, M, M₀, and H) to deal with missing data under the assumption of missing at random. Model H for missing data will be detailed here. Suppose that ỹ_i = (ỹ_i1, …, ỹ_ip)^T contains the complete p factors in study i; however, we only observe t_i factors and their within-study variances (1 ≤ t_i ≤ p). Denote the effect sizes of the t_i factors as y_i = (y_i1, …, y_iti)^T, which is a t_i-dimensional sub-vector of ỹ_i, and let D_i be the t_i × t_i diagonal matrix containing the within-study variances. We write y_i = X_iỹ_i, where X_i = (e_i1, …, e_iti)^T is a t_i × p matrix indicating missingness.³¹ Specifically, for each j = 1, …, t_i, e_ij = (e_ij1, …, e_ijp)^T with e_ijk = 1 if the observed y_ij is the effect size of factor k and e_ijk = 0 otherwise. For example, for study 3 in the pterygium data (Table 1),

$${\mathbf{X}}_3=\left[\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$$

Recall that μ, Ψ, and R represent the overall mean effect sizes, the between-study variances, and the marginal correlation matrix for the complete p factors, respectively. Hence, for the observed t_i-dimensional vector y_i, its overall mean is X_i μ, its marginal variances form the diagonal matrix ${\mathbf{D}}_i+{\mathbf{X}}_i\mathbf{\Psi }{\mathbf{X}}_i^T$, and its marginal correlation matrix is ${\mathbf{X}}_i\mathbf{R}{\mathbf{X}}_i^T$. Consequently, the hybrid model for missing data can be specified as

$${\mathit{y}}_i~N({\mathbf{X}}_i\mathit{\mu },{\mathbf{\Phi }}_i),\text{ where }{\mathbf{\Phi }}_i={({\mathbf{D}}_i+{\mathbf{X}}_i\mathbf{\Psi }{\mathbf{X}}_i^T)}^{1/2}{\mathbf{X}}_i\mathbf{R}{\mathbf{X}}_i^T{({\mathbf{D}}_i+{\mathbf{X}}_i\mathbf{\Psi }{\mathbf{X}}_i^T)}^{1/2}.$$

Although the derivation here is based on the assumption of missing at random³⁸, the simulations in Section 5 will compare the performance of Model H with Models M, M₀, and U when some factors are missing under various mechanisms (including missing not at random).

4.3 Bayesian hybrid model

Currently the existing statistical software, such as the Stata command “mvmeta”, can only implement Model H in a frequentist way.^28,29 However, when the dimension of factors p is large compared with the number of collected studies, the estimated variance-covariance matrix using the frequentist method may be inconsistent³⁹, leading to poor interval estimates. Indeed, the simulations in Section 5 show that the frequentist method produced poor 95% confidence intervals when the data of MVMA-MF were sparse, and the algorithm for maximizing the (restricted) likelihood did not converge for many simulated data. Therefore, we use a fully Bayesian approach to estimating the overall multivariate effect size μ and its variance-covariance matrix that are of interest in Model H. Vague priors are assigned to both the mean and variance-covariance structures. The Supporting Information provides the details of implementing the Bayesian MVMA-MF and its R and JAGS code. The simulations in Section 5 indicate that the 95% CrIs obtained using the Bayesian method generally had higher coverage probabilities than those obtained using the frequentist method for sparse data, which are common in MVMA-MF.

5. Simulations

We conducted simulations under various settings to compare the performance of the hybrid model (Model H) with the ideal model that uses within-study correlations (Model M), the model that ignores within-study correlations but accounts for between-study correlations (Model M₀), and the univariate model that ignores both types of correlations (Model U). Bias and root mean squared error (RMSE) of point estimate and 95% CI/CrI coverage probability were used to evaluate the models’ performance. We set the number of studies in each simulated MVMA-MF dataset to 30 and considered 5 factors in total. The true overall effect sizes of the 5 factors were zero, i.e., μ = (0, 0, 0, 0, 0)^T. Also, the between-study standard deviation τ was 1 for each factor; the within-study standard deviation of each factor σ was set to 0.5, 1, or 2. These choices for σ represented different extents of heterogeneity between studies. Moreover, we considered the exchangeable correlation structure for both the between- and within-study correlation matrices, R_B = (r_Bij) and R_W = (r_Wij), which were determined by the correlation parameters ρ_B and ρ_W, respectively; that is, r_Bij = ρ_B and r_Wij = ρ_W for 1 ≤ i ≠ j ≤ 5. The between-study correlations ρ_B were 0.2, 0.5, or 0.8, and the within-study correlations ρ_W were drawn from U(0, 0.3), U(0.3, 0.6), or U(0.6, 0.9). For each setting, 1,000 MVMA-MF datasets were simulated using the ideal Model M with S_i = σ²R_W and T = τ²R_B. Three missingness scenarios were considered: (I) all 5 factors were observed in all studies, i.e., the data were complete; (II) the data of factors 1, 3, and 5 in 10 studies were missing completely at random; and (III) the smallest 10 effect sizes of factors 1, 3, and 5 were missing. The missingness that was not at random in scenario (III) may be viewed as the effect of reporting bias. We also considered a missingness scenario that was similar to (III) but contained more missing data: (III′) the smallest 25 effect sizes of factors 1, 3, and 5 were missing; in this case, the three factors were only available from 5 studies, so the simulated MVMA-MF data were much sparser than the previous scenarios. Both the REML and Bayesian methods were applied to implement the four models. For the Bayesian analyses, we used the priors specified in Section S1.2 of the Supporting Information. The Markov chain Monte Carlo (MCMC) algorithm was used for estimation with one chain, having a run of 10,000 updates after a 10,000-run burn-in period.

Table 2 presents the results when ρ_B was 0.5, and Tables S1 and S2 in the Supporting Information present those when ρ_B was 0.2 and 0.8, respectively. First, since the data of factors 2 and 4 were complete under all scenarios, their corresponding results produced by the four models were almost the same; all models led to nearly unbiased estimates and proper 95% CI/CrI coverage probabilities for these two factors. Second, the results of factors 1, 3, and 5 produced by the four models also differed little when the data were complete or missing completely at random. This is expected from the perspective of missing data analysis.³⁸ Third, if the missingness was not at random, the results produced by the four models were noticeably different. The univariate model led to the largest bias and RMSE and the lowest 95% CI/CrI coverage probability. Since Model M₀ still accounted for the between-study correlations, its performance was similar to Model H when ρ_W was small compared to ρ_B. However, Model H outperformed Model M₀ when ρ_W was larger than ρ_B, because the within-study level dominated the estimation of the overall effect sizes in this situation, but Model M₀ ignored correlations at this level. Finally, note that Model M was ideal as it used the within-study correlations that are usually unavailable in real world. Although Model H did not use the within-study correlations, the biases and RMSEs produced by Model H were fairly close to the ideal Model M under various settings. Also, the 95% CI/CrI coverage probability produced by Model H was generally higher than those produced by Models M₀ and U.

Table 2.

The simulation results produced by Models M, H, M₀, and U in various settings of within-study variances and correlations under different missingness scenarios. The results outside parentheses were obtained using the Bayesian method; those inside parentheses were obtained using the restricted maximum likelihood method.

	Factor 1			Factor 2			Factor 3			Factor 4			Factor 5
Model	Bias	RMSE	CP (%)	Bias	RMSE	CP (%)	Bias	RMSE	CP (%)	Bias	RMSE	CP (%)	Bias	RMSE	CP (%)
τ = 1, σ = 1, ρB = 0.5, ρW ~ U(0.6, 0.9):
No missing data (I)
M	0.00 (0.00)	0.26 (0.26)	94 (94)	0.00 (0.00)	0.26 (0.26)	92 (93)	0.00 (0.00)	0.25 (0.25)	94 (95)	0.01 (0.01)	0.26 (0.26)	93 (93)	0.01 (0.01)	0.25 (0.25)	94 (95)
H	0.00 (0.00)	0.26 (0.26)	95 (94)	0.00 (0.00)	0.26 (0.26)	95 (93)	0.00 (0.00)	0.25 (0.25)	96 (95)	0.01 (0.01)	0.26 (0.26)	95 (93)	0.01 (0.01)	0.25 (0.25)	96 (94)
M0	0.00 (0.00)	0.26 (0.26)	96 (95)	0.00 (0.00)	0.26 (0.26)	96 (94)	0.00 (0.00)	0.25 (0.25)	97 (96)	0.01 (0.01)	0.26 (0.26)	96 (95)	0.01 (0.01)	0.25 (0.25)	97 (96)
U	0.00 (0.00)	0.26 (0.26)	95 (94)	0.00 (0.00)	0.26 (0.26)	94 (94)	0.00 (0.00)	0.25 (0.25)	96 (95)	0.01 (0.01)	0.26 (0.26)	95 (94)	0.01 (0.01)	0.25 (0.25)	96 (95)
Factors 1, 3, and 5 in 10 studies were missing completely at random (II)
M	0.00 (0.00)	0.29 (0.30)	95 (93)	0.00 (0.00)	0.26 (0.26)	93 (94)	0.01 (0.00)	0.28 (0.30)	95 (93)	0.01 (0.01)	0.26 (0.26)	94 (93)	0.01 (0.01)	0.28 (0.29)	94 (93)
H	0.00 (0.00)	0.29 (0.31)	96 (92)	0.00 (0.00)	0.26 (0.26)	94 (93)	0.01 (0.00)	0.29 (0.30)	96 (92)	0.01 (0.01)	0.26 (0.26)	95 (93)	0.00 (0.01)	0.28 (0.30)	96 (92)
M0	0.00 (0.00)	0.29 (0.30)	97 (96)	0.00 (0.00)	0.26 (0.26)	95 (94)	0.01 (0.00)	0.28 (0.29)	98 (95)	0.01 (0.01)	0.26 (0.26)	96 (94)	0.01 (0.01)	0.28 (0.29)	97 (96)
U	0.00 (−0.01)	0.32 (0.32)	95 (94)	0.00 (0.00)	0.26 (0.26)	94 (94)	0.02 (−0.01)	0.31 (0.32)	96 (94)	0.01 (0.01)	0.26 (0.26)	95 (94)	0.01 (0.01)	0.31 (0.32)	95 (93)
Factors 1, 3, and 5 in 10 studies were missing not at random (III)
M	0.48 (0.46)	0.56 (0.54)	54 (51)	0.00 (0.00)	0.26 (0.26)	94 (94)	0.48 (0.46)	0.55 (0.54)	52 (48)	0.01 (0.01)	0.26 (0.26)	94 (94)	0.48 (0.47)	0.56 (0.55)	51 (47)
H	0.51 (0.49)	0.58 (0.57)	54 (43)	0.00 (0.00)	0.26 (0.26)	96 (94)	0.52 (0.48)	0.59 (0.56)	49 (41)	0.01 (0.01)	0.26 (0.26)	95 (94)	0.53 (0.50)	0.60 (0.57)	48 (41)
M0	0.58 (0.56)	0.64 (0.62)	53 (44)	0.00 (0.00)	0.26 (0.26)	95 (94)	0.61 (0.55)	0.67 (0.62)	46 (41)	0.01 (0.01)	0.26 (0.26)	95 (94)	0.62 (0.56)	0.67 (0.63)	46 (41)
U	0.75 (0.75)	0.80 (0.80)	19 (16)	0.00 (0.00)	0.26 (0.26)	94 (94)	0.75 (0.75)	0.80 (0.80)	18 (14)	0.01 (0.01)	0.26 (0.26)	94 (94)	0.75 (0.75)	0.80 (0.80)	17 (13)
τ = 1, σ = 1, ρB = 0.5, ρW ~ U(0, 0.3):
Factors 1, 3, and 5 in 10 studies were missing not at random (III)
M	0.69 (0.68)	0.74 (0.74)	26 (23)	0.01 (0.01)	0.26 (0.26)	95 (94)	0.70 (0.68)	0.75 (0.73)	23 (22)	0.02 (0.02)	0.26 (0.26)	94 (93)	0.70 (0.68)	0.75 (0.74)	25 (22)
H	0.68 (0.67)	0.74 (0.73)	30 (21)	0.01 (0.01)	0.26 (0.26)	96 (94)	0.69 (0.67)	0.74 (0.73)	27 (21)	0.02 (0.02)	0.26 (0.26)	95 (93)	0.69 (0.67)	0.74 (0.73)	30 (21)
M0	0.71 (0.69)	0.76 (0.75)	26 (22)	0.01 (0.01)	0.26 (0.26)	95 (94)	0.72 (0.70)	0.77 (0.75)	24 (21)	0.02 (0.02)	0.26 (0.26)	94 (93)	0.72 (0.70)	0.77 (0.75)	25 (22)
U	0.75 (0.75)	0.80 (0.80)	19 (16)	0.01 (0.01)	0.26 (0.26)	95 (94)	0.75 (0.75)	0.80 (0.80)	16 (12)	0.02 (0.02)	0.26 (0.26)	94 (93)	0.75 (0.75)	0.80 (0.80)	18 (14)
τ = 1, σ = 0.5, ρB = 0.5, ρW ~ U(0.6, 0.9):
Factors 1, 3, and 5 in 10 studies were missing not at random (III)
M	0.47 (0.44)	0.52 (0.50)	36 (31)	0.00 (0.00)	0.21 (0.21)	95 (93)	0.46 (0.43)	0.51 (0.49)	35 (30)	0.01 (0.01)	0.21 (0.21)	95 (93)	0.47 (0.45)	0.52 (0.50)	33 (28)
H	0.46 (0.45)	0.51 (0.50)	43 (30)	0.00 (0.00)	0.21 (0.21)	96 (93)	0.46 (0.44)	0.51 (0.49)	39 (29)	0.01 (0.01)	0.21 (0.21)	96 (93)	0.47 (0.45)	0.52 (0.50)	37 (26)
M0	0.45 (0.45)	0.51 (0.51)	39 (31)	0.00 (0.00)	0.21 (0.21)	95 (93)	0.46 (0.44)	0.51 (0.49)	37 (30)	0.01 (0.01)	0.21 (0.21)	95 (93)	0.47 (0.46)	0.52 (0.51)	35 (27)
U	0.60 (0.59)	0.64 (0.64)	15 (13)	0.00 (0.00)	0.21 (0.21)	95 (93)	0.59 (0.59)	0.63 (0.63)	14 (12)	0.01 (0.01)	0.21 (0.21)	94 (93)	0.60 (0.60)	0.64 (0.64)	14 (12)
τ = 1, σ = 2, ρB = 0.5, ρW ~ U(0.6, 0.9):
Factors 1, 3, and 5 in 10 studies were missing not at random (III)
M	0.57 (0.58)	0.73 (0.74)	74 (70)	0.01 (0.01)	0.41 (0.42)	96 (96)	0.59 (0.59)	0.74 (0.74)	73 (70)	0.02 (0.02)	0.41 (0.41)	95 (96)	0.59 (0.59)	0.74 (0.74)	73 (70)
H	0.63 (0.60)	0.78 (0.76)	74 (66)	0.01 (0.01)	0.42 (0.42)	97 (96)	0.65 (0.61)	0.80 (0.76)	72 (65)	0.02 (0.02)	0.41 (0.41)	97 (97)	0.67 (0.62)	0.81 (0.77)	71 (64)
M0	0.96 (0.90)	1.05 (1.00)	62 (56)	0.01 (0.01)	0.42 (0.42)	97 (96)	1.01 (0.90)	1.10 (1.00)	56 (55)	0.02 (0.02)	0.41 (0.41)	97 (97)	1.02 (0.91)	1.11 (1.01)	56 (54)
U	1.18 (1.18)	1.26 (1.26)	29 (25)	0.01 (0.01)	0.42 (0.42)	96 (94)	1.19 (1.19)	1.27 (1.27)	28 (24)	0.02 (0.02)	0.41 (0.41)	96 (94)	1.19 (1.19)	1.27 (1.27)	28 (24)
Factors 1, 3, and 5 in 25 studies were missing not at random (III′)
M	1.57 (1.60)	1.72 (1.76)	76 (32)	0.01 (−0.01)	0.42 (0.41)	95 (95)	1.58 (1.60)	1.73 (1.77)	75 (31)	0.02 (0.02)	0.41 (0.42)	96 (94)	1.60 (1.59)	1.74 (1.76)	75 (34)
H	2.36 (1.46)	2.75 (1.64)	65 (26)	0.01 (−0.02)	0.42 (0.43)	96 (93)	2.45 (1.47)	2.73 (1.67)	65 (27)	0.02 (0.01)	0.41 (0.43)	96 (93)	2.50 (1.48)	2.79 (1.66)	67 (28)
M0	3.05 (2.92)	3.11 (2.99)	73 (4)	0.01 (−0.01)	0.42 (0.41)	96 (96)	3.14 (2.95)	3.20 (3.02)	62 (3)	0.02 (0.02)	0.41 (0.42)	97 (96)	3.11 (2.93)	3.17 (3.00)	60 (3)
U	3.21 (3.19)	3.28 (3.26)	11 (1)	0.01 (−0.01)	0.42 (0.41)	95 (94)	3.23 (3.21)	3.30 (3.27)	9 (1)	0.02 (0.02)	0.41 (0.42)	96 (94)	3.21 (3.18)	3.28 (3.24)	9 (1)

RMSE: root mean square error; CP: 95% CI/CrI coverage probability.

In most situations, the biases and RMSEs of point estimates obtained using the REML method were close to those obtained using the Bayesian method. However, under the missingness scenarios (III) and (III′), the 95% CrI coverage probabilities for factors 1, 3, and 5 obtained using the Bayesian method were generally higher than those obtained using the REML method. As noted in Section 4.3, this may be due to that the estimated variance-covariance matrix was inconsistent when many observations were missing and the dimension was close to the sample size (only five observations for each of factors 1, 3, and 5). Also, under scenario (III′), the biases and RMSEs produced by Model H using the REML method were noticeably different from those using the Bayesian method for factors 1, 3, and 5; again, these differences may be caused by the sparsity of the simulated data. In addition, when Model H was used under scenario (III′), the optimization algorithm for the REML estimates did not converge for many simulated replicates. We ran around 2,500 iterations to obtain 1,000 datasets that produced converged REML estimates, and these 1,000 datasets were used to produce the results for scenario (III′). Hence, the Bayesian method is preferred to implement the multivariate hybrid model when the dimension of factors is high but the observations are limited.

Moreover, we conducted an additional simulation study driven by the pterygium data. The conclusions are similar to those presented here. For more details, see Section S2 in the Supporting Information.

6. Real data analysis

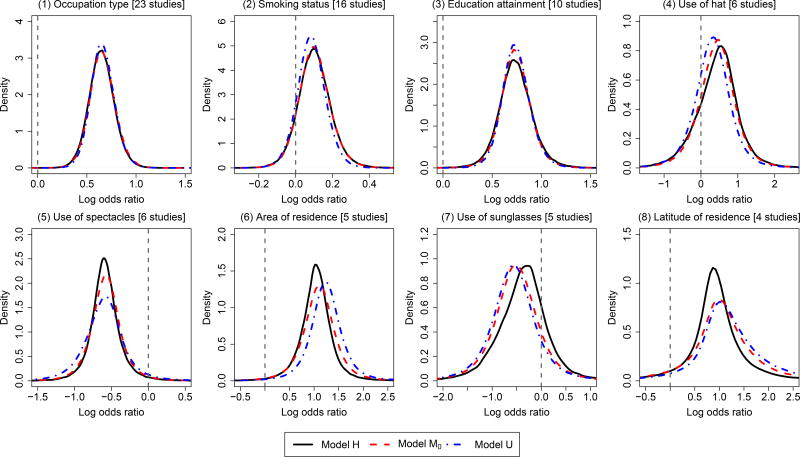
The pterygium dataset has been introduced in details as our motivating example. Since the within-study correlations were unknown, we used Models H, M₀, and U but not Model M to estimate the overall log odds ratios of the 8 risk factors. Due to the sparsity of the dataset, the models were implemented using Bayesian analyses. The estimates were based on three MCMC chains, each containing a run of 100,000 updates after a 100,000-run burn-in period. The convergence of the chains was checked using their trace plots. Table 3 presents the median overall log odds ratios with 95% CrIs. Figure 2 shows the posterior density plots of the 8 risk factors.

Table 3.

The estimated overall log odds ratios (95% CrI) of the 8 risk factors in the pterygium data obtained by Model H (accounting for both between- and within-study correlations), Model M₀ (only accounting for between-study correlations), and Model U (univariate model ignoring both between- and within-study correlations) using the Bayesian method.

Risk factor	No. of studies	Estimated overall log odds ratio
		Model H	Model M0	Model U
(1) Occupation type	23	0.65 (0.40, 0.92)	0.65 (0.41, 0.93)	0.66 (0.42, 0.91)
(2) Smoking status	16	0.10 (−0.07, 0.29)	0.10 (−0.07, 0.29)	0.08 (−0.07, 0.25)
(3) Education attainment	10	0.73 (0.40, 1.10)	0.74 (0.42, 1.07)	0.74 (0.46, 1.06)
(4) Use of hat	6	0.47 (−0.87, 1.62)	0.44 (−0.77, 1.55)	0.32 (−0.84, 1.41)
(5) Use of spectacles	6	−0.59 (−1.02, −0.09)	−0.58 (−1.06, −0.06)	−0.60 (−1.26, 0.05)
(6) Area of residence	5	1.04 (0.29, 1.78)	1.10 (0.22, 1.97)	1.24 (0.39, 2.11)
(7) Use of sunglasses	5	−0.36 (−1.53, 0.74)	−0.51 (−1.64, 0.62)	−0.57 (−1.76, 0.63)
(8) Latitude of residence	4	0.92 (−0.74, 2.72)	1.04 (−0.98, 3.10)	1.14 (−0.70, 3.37)

Figure 2.

Posterior density plots produced by Model H (accounting for both between- and within-study correlations), Model M₀ (only accounting for between-study correlations), and Model U (univariate model ignoring both between- and within-study correlations) for the overall log odds ratios of the 8 risk factors in the pterygium data.

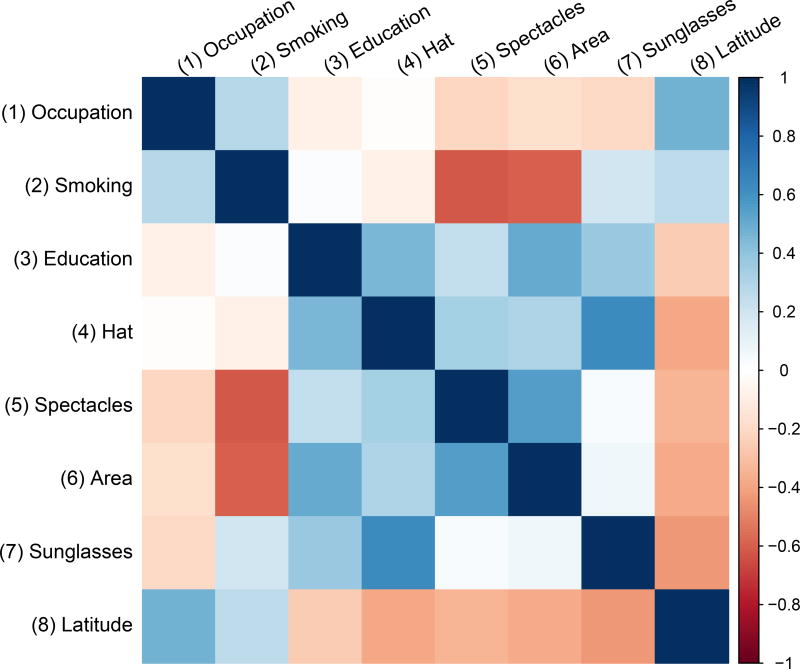
For risk factors that were reported in a relatively large number of studies (e.g., occupation type, smoking status, and education attainment), the three models yielded similar estimated overall log odds ratios; their density curves were also fairly similar. For risk factors that were only reported in a few studies (e.g., use of spectacles, area of residence, and latitude of residence), the peaks of the density curves produced by Model H were narrower and higher compared with those produced by Models M₀ and U, indicating that Model H produced narrower 95% CrIs. Also, for the risk factor use of sunglasses, the location of its density curve produced by Model H was noticeably different from those produced by the other two models. Figure 3 depicts the estimated overall correlations between the 8 risk factors produced by Model H. It shows that many factors were correlated and some correlations were fairly high. Hence, ignoring the within-study correlations could lead to fairly different estimated overall log odds ratios; the unknown within-study correlations need to be carefully considered in MVMA-MF.

Figure 3.

Plot of the estimated overall correlations between the 8 risk factors produced by Model H in the pterygium data. Darker color implies higher correlation.

The priors in the above real data analyses were specified in Section S1.2 of the Supporting Information; specifically, uniform priors U(0, 10) were assigned for the between-study standard deviations. We examined the results’ sensitivity to prior specification by changing U(0, 10) priors to U(0, 3), U(0, 100), and U(0, 1000). In addition, we altered the order of the 8 risk factors in the data analysis; this basically changed the priors assigned to the correlation matrices in Models H and M₀ (see Section S1 in the Supporting Information). Table S3 in the Supporting Information presents the results. In sum, changing priors had little impact on the risk factors occupation type, smoking status, and education attainment, which were reported in at least ten studies. When the priors for the between-study standard deviations varied from U(0, 3) to U(0, 100), the point estimates of the overall log odds ratios of all 8 risk factors remained nearly unchanged. The CrIs for risk factors use of sunglasses and latitude of residence noticeably became wider. Compared with other risk factors, since the data for these two factors were limited, the priors had larger influence on their posteriors. When the priors for the between-study standard deviations varied from U(0, 100) to U(0, 1000), most results did not change. Changing the priors for the correlation matrices in Models H and M₀ had some impact on the CrIs for the risk factors that were reported in no more than six studies. Nevertheless, the CrIs produced by Model H were still narrower than those produced by Models M₀ and U. For more details, see Section S3 in the Supporting Information.

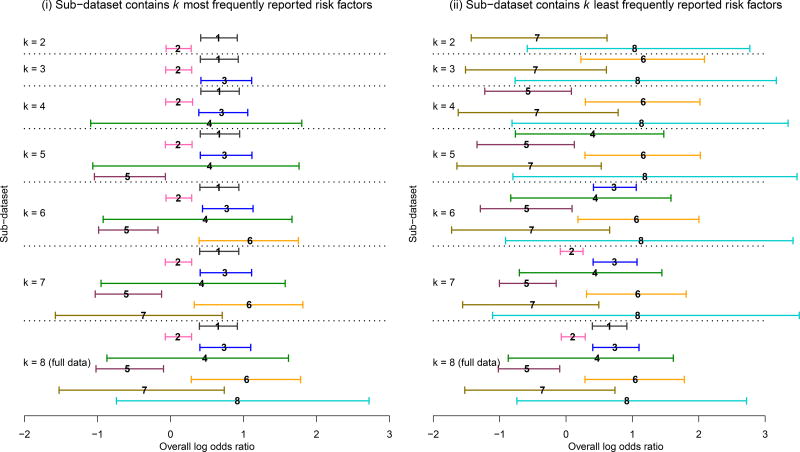
We also performed additional sensitivity analyses to investigate the impact of risk factor selection on the estimated overall log odds ratios. We considered two scenarios for the set of risk factors to be included in MVMA-MF: (i) sub-dataset consisted of the k most frequently reported risk factors; and (ii) sub-dataset consisted of the k least frequently reported risk factors (k = 2, …, 8). For example, when k = 2, the sub-dataset under scenario (i) contained the risk factors (1) occupation type and (2) smoking status; the sub-dataset under scenario (ii) contained the risk factors (7) use of sunglasses and (8) latitude of residence. Model H was implemented to analyze these sub-datasets.

Figure 4 shows the 95% CrIs of the overall log odds ratios under both scenarios; the labels of risk factors used in this figure can be found in Table 3’s first column. In scenario (i), starting from the two most frequently reported risk factors, infrequently reported risk factors were iteratively added to the MVMA-MF. Figure 4(i) shows that the estimated overall log odds ratios of risk factors 4 and 5 had some changes as new factors were added to the sub-datasets. The 95% CrIs of the three most frequently reported risk factors 1–3 changed little. This might be explained by two reasons. First, the correlations between these three factors were weak (Figure 3), so the addition of risk factor 3 had little impact on estimating the effect sizes of factors 1 and 2. Second, the later added factors 4–8 provided much fewer information (no more than six studies) compared with factors 1–3, which were reported in more than ten studies, so the correlations contributed little to the effect size estimation for factors 1–3.

Figure 4.

Bayesian estimates of overall log odds ratios produced by Model H based on subsets of the pterygium data. Each horizontal solid line represents 95% CrI of log odds ratio. The number placed at the median log odds ratio within each 95% CrI represents the corresponding risk factor’s label. The results of the sub-datasets that contain k = 2, …, 8 risk factors are accordingly listed from upper to lower, separated by the dotted lines.

Compared with scenario (i), Figure 4(ii) shows larger changes of estimated overall log odds ratios in scenario (ii). Under this scenario, starting from the two least frequently reported risk factors, more frequently reported factors were iteratively added to the MVMA-MF. The 95% CrIs of infrequently reported risk factors, such as 5 and 6, became narrower as more reported risk factors were included in the MVMA-MF. This illustrates the benefit of jointly modeling multiple factors: the inference on infrequently reported factors can be strengthened by borrowing information from frequently reported factors through the correlations between them.

7. Discussion

This article has introduced MVMA-MF with application to the pterygium data. In contrast to the tradition of meta-analyzing each single factor separately, this article encourages researchers to collect all possible factors and analyze them jointly to enhance the estimation of overall effect sizes. A Bayesian multivariate hybrid model has been introduced to implement MVMA-MF in which within-study correlations are usually unknown. The simulations have shown that, when many factors are missing not at random, Bayesian MVMA-MF can use the information across multiple factors to impute missing data and thus can produce better estimates than separate meta-analyses. Our results are consistent with those produced by Kirkham et al.¹⁴ using frequentist bivariate and univariate meta-analyses; that is, “borrowing of strength” from the correlations between factors can reduce bias under the setting of missing not at random. For example, consider two highly correlated factors with a correlation coefficient close to one, and the results for factor 1 are fully observed. Even if the results for factor 2 are missing not at random, the missing results can be largely recovered through the high correlation between the two factors, so the bias in the estimate of factor 2 may be greatly reduced.

The hybrid model effectively reduces model complexity by specifying a common marginal correlation matrix for all studies. This model could be a proper tradeoff between goodness-of-fit and model complexity in some situations; however, if the collected studies’ marginal correlation matrices differ a lot, the hybrid model may fit the data poorly. Future work is needed to generalize the hybrid model by allowing more degrees of freedom and select the best model using deviance information criterion.⁴⁰

An important issue of MVMA-MF is to incorporate the effect size of a certain factor that has been adjusted for other factors. For example, in the original pterygium data presented in Serghiou et al.⁸, many collected studies only reported log odds ratios that were obtained using multivariate regression after adjusting different factors (e.g., age and gender), while log odds ratios without any adjustments were unavailable from these studies. We did not include such data in Table 1 due to the inconsistent adjustments. How to incorporate such data with different adjustments is of great interest to enrich the MVMA-MF and enhance the robustness and precision of the results.^41,42 We leave this to future studies.

Another interesting but challenging problem is to identify the factors’ missingness mechanism and impute the missing factors more properly when the missingness is not at random. The factors could be missing completely at random, missing at random, or missing not at random.⁴³ If the missingness of a factor does not depend on any observed or unobserved data, then this factor is missing completely at random. It is also possible that this factor is missing because of some observed data in some earlier studies; this is the case of missing at random. Bayesian inference under these two missingness mechanisms is valid when restricted to the observed data.³⁸ However, the missingness not at random closely relates to publication and reporting bias, when some studies or factors were intended to be not published or reported due to their negative results.^44,45 Although our simulations showed that the proposed hybrid model performed better than Models M₀ and U when missingness was not at random, both its bias and 95% CrI coverage probability were expected to be further improved. Approaches to correcting publication or reporting bias have been introduced and widely used in univariate meta-analysis⁴⁶; similar methods are highly needed for multivariate meta-analysis.