Multi-resolution Simulation of Focused Ultrasound Propagation through Ovine Skull from a Single-element Transducer

Abstract

Transcranial focused ultrasound (tFUS) is emerging as a non-invasive brain stimulation modality. Complicated interactions between acoustic pressure waves and osseous tissue introduce many challenges in the accurate targeting of an acoustic focus through the cranium. Image-guidance accompanied by a numerical simulation is desired to predict the intracranial acoustic propagation through the skull; however, such simulations typically demand heavy computation, which warrants an expedited processing method to provide on-site feedback for the user in guiding the acoustic focus to a particular brain region. In this paper, we present a multi-resolution simulation method based on the finite-difference time-domain (FDTD) formulation to model the transcranial propagation of acoustic waves from a single-element transducer (250 kHz). The multi-resolution approach improved computational efficiency by providing the flexibility in adjusting the spatial resolution. The simulation was also accelerated by utilizing parallelized computation through the graphic processing unit (GPU). To evaluate the accuracy of the method, we measured the actual acoustic fields through ex vivo sheep skulls with different sonication incident angles. The measured acoustic fields were compared to the simulation results in terms of focal location, dimensions, and pressure levels. The computational efficiency of the presented method was also assessed by comparing simulation speeds at various combinations of resolution grid settings. The multi-resolution grids consisting of 0.5 and 1.0 mm resolutions gave acceptable accuracy (under 3 mm in terms of focal position and dimension, less than 5% difference in peak pressure ratio) with a speed compatible with semi real-time user feedback (within 30 s). The proposed multi-resolution approach may serve as a novel tool for simulation-based guidance for tFUS applications.

1. Introduction

Focused ultrasound (FUS) technique, in which acoustic pressure waves are delivered to a small and localized area in the body, has been widely used in the field of non-invasive therapeutic applications, such as thermal ablation (McDannold et al., 1998; Tung et al., 2006; McDannold et al., 2006; Liu et al., 2007; Coluccia et al., 2014) and extracorporeal shockwave therapies (Madersbacher and Marberger, 2003; Bailey et al., 2014). The accurate placement of the FUS focus to a targeted specific-region of tissue through bone poses significant challenges due to complicated interactions between acoustic waves and osseous tissue, such as absorption, refraction, and reflection (Konofagou et al., 2001; Hynynen et al., 2001; Pinton et al., 2012). Transcranial application of FUS to the brain is particularly vulnerable to problems such as high energy loss through the cranium, poor focusing, and formation of extra foci (Deffieux and Konofagou, 2010; Kyriakou et al., 2015; Jing et al., 2012; Robertson et al., 2017b).

The use of low fundamental frequency ultrasound (typically ≤ 1 MHz) (Clement et al., 2005), much lower than the 1–15 MHz range used for clinical ultrasound imagers, helps to alleviate concerns over significant wave attenuation and refraction of acoustic energy through the skull. The use of a phased-array FUS transducer configuration (consists of > 500 ultrasound elements surrounding the head) and their independent actuation, combined with phase correction schemes via a time-reversal technique (Jing et al., 2012; Chauvet et al., 2013), compensates for acoustic aberration caused by the skull (Aubry et al., 2003; Hynynen et al., 2004). This method, combined with magnetic resonance (MR) guidance, has been utilized for thermal ablation of brain tumors and functional neurosurgery in humans through the use of high intensity FUS (HIFU), typically using a few hundred to thousand watts (Martin et al., 2009; McDannold et al., 2010; Elias et al., 2013). The MR-guided transcranial FUS (tFUS) was also applied for temporary disruption of the blood brain barrier (BBB) using the concomitant vascular injection of microbubbles in animal models (Sheikov et al., 2004; Hynynen et al., 2006; Hynynen, 2008).

Single-element FUS transducer configurations, although lacking an aberration correction mechanism, have also been successfully implemented in transcranial applications by positioning the transducer over the scalp, being acoustically-coupled using water-containing bags, cones, or polymer hydrogels (Kim et al., 2014; Lee et al., 2015; Kim et al., 2012b; Younan et al., 2013). For example, FUS-mediated brain stimulation, utilizing the low-intensity pulsed ultrasound, has been demonstrated in small animals (Kim et al., 2014; Yoo et al., 2011; Kim et al., 2015; Kim et al., 2012b; Yoo et al., 2017), sheep (Lee et al., 2016c) and non-human primates (Deffieux et al., 2013; Wattiez et al., 2017), and in humans (Lee et al., 2016b; Legon et al., 2014; Lee et al., 2015; Lee et al., 2016a; Lee et al., 2017). Single-element FUS transducers have also been used to study the disruption of the BBB in several animal models (McDannold et al., 2008; Downs et al., 2015; McDannold et al., 2011).

A geometric derivation of the acoustic focal location and an acoustic intensity estimated from the simple application of attenuation factor in the acoustic path have been adopted (Kim et al., 2012a; Lee et al., 2016c; Lee et al., 2015). These techniques are typically administered at a low-intensity under the threshold that can cause temperature changes or pressure changes detectable by in vivo imaging techniques such as MR thermometry (Ishihara et al., 1995; Yoo et al., 2011) or acoustic radiation force imaging (ARFI) (Kaye et al., 2011; Kennedy, 2005). Therefore, a separate mode of image-guidance/planning for the sonication is needed to accurately place the small and invisible acoustic focus to a specific region-of-interest, which may differ anatomically and functionally depending on individuals. To augment this process, a numerical simulation that estimates the location and intensity of the acoustic focus is desired for the accurate and quantifiable administration of tFUS (White et al., 2006; Schwenke et al., 2015).

Various numerical studies have been conducted to develop simulation methods to characterize the acoustic propagation during tFUS (Mueller et al., 2017; Yin and Hynynen, 2005; Pulkkinen et al., 2014; Baron et al., 2009; Robertson et al., 2017a; Pinton et al., 2009). The finite element method (FEM) has been used to solve the wave equations to model the acoustic pressure propagation through the human cranium (Legon et al., 2014), but it requires a computationally demanding process such as finding an inverse system matrix (Bathe, 2006). The finite-difference time-domain (FDTD) method greatly improves computational efficiency by progressively solving the pressure and velocity of sound waves that are discretized in both time and space domains (Taflove and Hagness, 2005), and is available through commercial and non-commercial software (Treeby and Cox, 2010; Kaufman et al., 2008; Comsol, 2005). FDTD has been used to estimate the location and in situ pressure level of acoustic focus for BBB disruption (Deffieux and Konofagou, 2010), neuromodulation (Mueller et al., 2017; Robertson et al., 2017b), and sonothrombolysis (Baron et al., 2009).

FDTD-based simulations are typically performed based on setting the simulation grid in a fixed spatial resolution (at the highest resolution possible) across an entire simulation volume. In the present study, we were motivated to examine the utility of employing a multi-resolution approach in FDTD to achieve a semi real-time simulation (for enabling on-line/on-site feedback) necessary to track/estimate the orientation and location of the acoustic focus from a single-element FUS transducer. Non-uniform grid (Jiang and Arai, 1998) can be alternatively used for providing a degree of flexibility in setting multiple resolutions, but it requires the spatial matching between adjacent grids at the interfaces that have different resolutions (Krumpholz and Katehi, 1996; Zhi et al., 2013). Multi-resolution approaches are generally adopted to probe the spatially-restricted areas-of-interest and able to solve the wave propagation problem at the non-matching grid/node interfaces (Krumpholz and Katehi, 1996; Zhi et al., 2013). The approaches have been utilized in expediting the data processing/acquisition, for example, in an optical geo-survey (van Lier et al., 2009; Kurtz et al., 2014) or in functional neuroimaging (Yoo et al., 1999; Yoo et al., 2001). We hypothesized that a similar multi-resolution approach is applicable to simulate the wave propagation when a single-element FUS transducer having a fixed focal length (i.e., rough a priori information on the focal location is known) is used to sonicate a specific location of the brain. For example, a high spatial resolution grid is used to simulate wave propagation from the transducer to the focal areas (as a primary local region-of-interest) while sparse spatial sampling can be used to model the area outside without sacrificing the overall simulation quality.

To assess the accuracy and performance envelop (such as incident angle of sonication) of the proposed method, we conducted the FDTD-based acoustic simulation using different grid dimension settings (fixed- and multi-resolution approaches) to model FUS application through ex vivo sheep skull caps, and compared the results to the ones obtained from actual mapping of acoustic pressure using a hydrophone. We also performed the simulation using a closed sheep skull sample. The simulation was implemented in a graphic processing unit (GPU) environment with parallel processing capability to expedite the computation, and the resulting computational speed was compared to that from using a central processing unit (CPU).

2. Methods

2.1. Sheep skull preparation and CT data acquisition

All procedures for obtaining ex vivo sheep skulls were carried out in accordance with the ethical and safety rules set forth by a local Institutional Animal Care and Use Committee (IACUC). Five adult sheep (Dorset, all female, weight = 35.8 ± 6.1 kg) were euthanized, and a skull cap (having hexagonal shape over the brain, approximately 8 cm in anterior-posterior length and 6 cm in width right-left) was excised and fixated with 10% formalin for approximately one year. In two skulls (named ‘S1’ and ‘S2’ herein), effort was made to remove the periosteum and dura mater around the skull (by scraping the skull surface inside and out) using surgical scalpels and rongeurs (‘processed skull’ referred herein). The other three skulls (named ‘S3’, ‘S4’ and ‘S5’) had most of the soft tissue/skin remaining, preserving the overall tissue structures (i.e., ‘intact skull’). A ceramic screw was implanted at the posterior edge of each skull to place a plastic applicator containing four donut-shaped fiducial markers (Pinpoint, Beekley Corp., Bristol, CT), which were later used for co-registration between the actual and virtual spaces of the skull phantom. A holder was connected to the applicator to rotate the skull with respect to the incident FUS beam (figure 1). The skull samples were preserved in degassed water for at least 24 h inside a vacuum chamber (Best Value Vacs, Naperville, IL) prior to acoustic mapping.

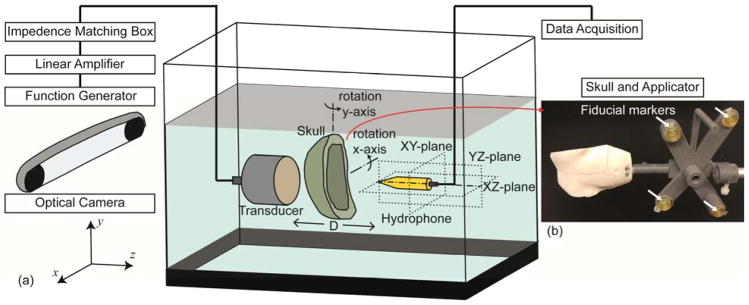
Figure 1.

(a) Schematic of the acoustic field measurement setup in the actual space (not drawn to scale). The transducer was actuated by an electrical signal generated and amplified by a function generator and a linear amplifier, respectively, with impedance matching. Hydrophone scanning was conducted in YZ-, XZ-, XY-planes, and the skull was rotated along each of the x and y axis (0°, ±10° and ±15°). (b) An example of a sheep skull with an applicator. The actual location and orientation of the skull was obtained by an optical tracking system and co-registered to the skull CT data using the coordinate information of the corresponding four fiducial markers indicated with white arrows.

To obtain the geometric information of the sheep skull phantoms (being attached to the applicator), a three-dimensional (3D) computed tomography (CT) scan (Aquilion ONE, Toshiba, Japan) was conducted with an isotropic voxel of 0.5 × 0.5 × 0.5 mm³, covering the field-of-view (FOV) of 150 × 125 × 125 mm³. Due to the high degrees of individual variability in cranial structures (Lee et al., 2015) and ultrasound propagation being sensitive to a specific skull geometry (Hynynen et al., 2001; Konofagou et al., 2001), a CT scan for each skull was necessary.

2.2. Characterization of acoustic field via hydrophone measurement

The schematics of the acoustic field measurement setup are illustrated in figure 1. The experiments were carried out in a water tank that contained degassed, distilled water. The pressure field was generated by a single-element FUS transducer (GPS200-400128, Ultran Group, Hoboken, NJ) whereby the acoustic waves generated by a piezoelectric disc are focused using a concave acoustic lens. The diameter/aperture (D_t) of the transducer was 37 mm and the focal length was 30 mm from the exit plane. The pulsed sinusoidal waves were generated using a function waveform generator (33500B, Keysight, Santa Rosa, CA) operating at a frequency of 250 kHz, tone burst duration (TBD) of 100 μs at a 3% duty cycle. The generated sinusoidal waves (input peak-to-peak amplitude of 100 mV) were amplified (a linear power amplifier, 240L, Electronics and Innovations, Rochester, NY) and transmitted to the FUS transducer via an impedance matching box (JT-800, Electronics and Innovations, Rochester, NY). A plastic applicator holding the transducer had two fiducial markers to register its location and orientation with respect to the virtual simulation space.

The measurements were conducted by a needle-type hydrophone (HNR500, Onda, Sunnyvale, CA) attached to a three-axis robotic stage (Bi-Slides, Velmex, Bloomfield, NY) that shared the mutual spatial coordinates of the transducer. The center lines of the transducer and hydrophone were aligned using the robotic stage, and each of the prepared skulls were placed between the transducer and hydrophone so that the wave front met the skull surface as perpendicular as possible. The distance between the skull and the transducer exit plane was 5.1 ± 0.2 mm (n = 5 skulls). The acoustic pressure field was measured in three planes that were longitudinal and perpendicular to the FUS transducer (see figure 1 for the illustration of the axis), i.e., YZ-plane (ΔY = 21 mm, ΔZ = 41 mm, Δm = 1 mm at D = 20 mm), XZ-plane (ΔX = 21 mm, ΔZ = 41 mm, Δm = 1 mm at D = 20 mm), XY-plane (ΔX = 21 mm, ΔY = 21 mm, Δm = 1 mm at D = 30 mm) where ΔX, ΔY, ΔZ are respectively the x, y, z-directional length of the scanning plane, Δm is the measuring interval, and D indicates the distance between the hydrophone tip and the exit plane of the transducer. At each coordinate, the value from averaged hydrophone readings was used in the acoustic mapping (n = 32 measurements). We also increased the TBD up to 10 ms to examine the presence of reverberations or interference that could occur at longer sonication durations (n = 2 skulls), and found that the use of a long TBD did not alter the measured pressure values. Therefore, we kept the TBD of 100 μs for all the measurements to expedite the mapping procedure. With nine varying incident angles of FUS beam (i.e., 0°, x±10°, x±15°, y±10°, y±15°) with respect to the normal skull surface at the geometric entry point, a total of 27 acoustic field maps were generated for each of the skull phantoms covering three planes.

2.3. Co-registration between the actual and simulation spaces

The co-registration between the actual measurement space and the virtual simulation space was performed through optical-based position-tracking whereby the detailed protocol can be found elsewhere (West and Maurer, 2004; Kim et al., 2012a; Lee et al., 2015). Briefly, the spatial coordinates of the four fiducial markers were obtained from the virtual simulation coordinate system (i.e., the acquired CT data), and registered to the actual space using an optical tracking system (Polaris Vicra and NDI Tool Track, Northern Digital Inc., Ontario, Canada) (figure 1). Subsequently, the coordinate transformation equation between the two coordinate systems was derived using a point-based rigid body registration method (Fitzpatrick et al., 1998; Moghari and Abolmaesumi, 2007; Pietrzyk et al., 1994). The location and orientation of the FUS transducer (represented as a center position and its normal vector) was found by collecting the spatial coordinates from two fiducial markers on the transducer applicator.

Through the above procedure, we co-registered nine sets of sonication angles (0°, x±10°, x±15°, y±10°, and y±15° from the normal vector to the skull surface) for respective skull phantoms (a total of 45 registrations were conducted; 9 angles × 5 skulls). The registration error, in terms of root-mean-square (RMS) distance, between the actual and registered coordinates of the four fiducial markers was less than 1 mm for each angle condition and skull phantom (0.41 ± 0.15 mm, across 45 registrations).

2.4. Simulation hardware

We implemented a FDTD formulation and the corresponding multi-resolution simulation approach through parallel computation utilizing a GPU device, with the aim of semi-real time feedback for the operators. The simulation was performed using a quad-core work station (Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz, 64 GB memory, Microsoft Windows 10 64bit) and GPU device (Nvidia’s single Pascal card, GeForce GTX 1080, 2560 cores, 8 GB GDDR5X memory @ 320 GB/s bandwidth). The computational implementation was written in CUDA (Nvidia, Santa Clara, CA) and C++ languages.

2.5. FDTD formulation

We used the second-order Westervelt-Lighthill equation (Westervelt, 1957; Lighthill, 1978; Jing et al., 2011) to mathematically define the mechanical pressure wave propagation through the media,

$${\nabla }^{2}p-\frac{1}{c^2}\frac{{\partial }^{2}p}{\partial t^2}+\frac{\delta }{c^4}\frac{{\partial }^{3}p}{\partial t^3}+\frac{\beta }{\rho c^4}\frac{{\partial }^2{p}^2}{\partial t^2}=0,$$ (1)

where p is the acoustic pressure, c is the ultrasound speed, t is the time, δ is the ultrasound diffusivity, and β is the nonlinearity coefficient (which governs wave attenuations through media). The equation is suitable for solving nonlinear phenomena such as sound wave propagation through materials with variable shear and bulk viscosity (e.g., skulls) (Solovchuk et al., 2013).

To replace nonlinear terms, which may decrease computational efficiency, we used the linearized version of Westervelt-Lighthill equation as a governing equation (Liebler et al., 2004; Kyriakou et al., 2015),

$${\nabla }^{2}p-\frac{1}{c^2}\frac{{\partial }^{2}p}{\partial t^2}-\frac{\stackrel{\sim }{a}}{c^2}\frac{\partial p}{\partial t}=0\text{with}\stackrel{\sim }{a}=2a\sqrt{\frac{a^2{c}^4}{4{\pi }^2{f}^2}+c^2},$$ (2)

in which a is the attenuation coefficient of the medium and f is the fundamental frequency of the ultrasound.

By employing the staggered FDTD algorithm (Taflove and Hagness, 2005; Pinton et al., 2009), the pressure and velocity field was discretized as,

$$\begin{gathered} {{}^{t+\mathrm{\Delta }t}P}_{i,j,k}={{}^{t}P}_{i,j,k}-C_{i,j,k}^p\left[({{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^x-{{}^{t+1/2\mathrm{\Delta }t}V}_{i-1,j,k}^x)+({{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^y-{{}^{t+1/2\mathrm{\Delta }t}V}_{i,j-1,k}^y)+({{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^z-{{}^{t+1/2\mathrm{\Delta }t}V}_{i,j-1,k}^z)\right]-A_{i,j,k}{{}^{t}P}_{i,j,k}, \\ {{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^x={{}^{t-1/2\mathrm{\Delta }t}V}_{i,j,k}^x-C_{i,j,k}^{vx}\left[{{}^{t}P}_{i+1,j,k}-{{}^{t}P}_{i,j,k}\right], \\ {{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^y={{}^{t-1/2\mathrm{\Delta }t}V}_{i,j,k}^y-C_{i,j,k}^{vy}\left[{{}^{t}P}_{i,j+1,k}-{{}^{t}P}_{i,j,k}\right], \\ {{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^z={{}^{t-1/2\mathrm{\Delta }t}V}_{i,j,k}^z-C_{i,j,k}^{vz}\left[{{}^{t}P}_{i,j,k+1}-{{}^{t}P}_{i,j,k}\right], \\ \text{with}{C}_{i,j,k}^p={\rho }_{i,j,k}{c}_{i,j,k}^2\frac{\mathrm{\Delta }t}{\mathrm{\Delta }s},A_{i,j,k}=2\mathrm{\Delta }t{a}_{i,j,k}\sqrt{\frac{a_{i,j,k}^2{c}_{i,j,k}^4}{4{\pi }^2{f}^2}+c_{i,j,k}^2} \\ \text{and}{C}_{i,j,k}^{vx}=\frac{2}{{\rho }_{i,j,k}+{\rho }_{i+1,j,k}}\frac{\mathrm{\Delta }t}{\mathrm{\Delta }s},C_{i,j,k}^{vy}=\frac{2}{{\rho }_{i,j,k}+{\rho }_{i,j+1,k}}\frac{\mathrm{\Delta }t}{\mathrm{\Delta }s},C_{i,j,k}^{vz}=\frac{2}{{\rho }_{i,j,k}+{\rho }_{i,j,k+1}}\frac{\mathrm{\Delta }t}{\mathrm{\Delta }s}, \end{gathered}$$ (3)

where ^tP_i,j,k is the nodal pressure value, and each of ${{}^{t}V}_{i,j,k}^x,{{}^{t}V}_{i,j,k}^y$ and ${{}^{t}V}_{i,j,k}^z$ denotes the nodal wave velocity values from x, y, z coordinates at time t. c_i,j,k, ρ_i,j,k, and a_i,j,k are ultrasound speed, density, and attenuation coefficient of the corresponding media in the discretized domain (i, j, and k are nodal indices), respectively. Δt is the time interval, and Δs is the discretized spatial interval.

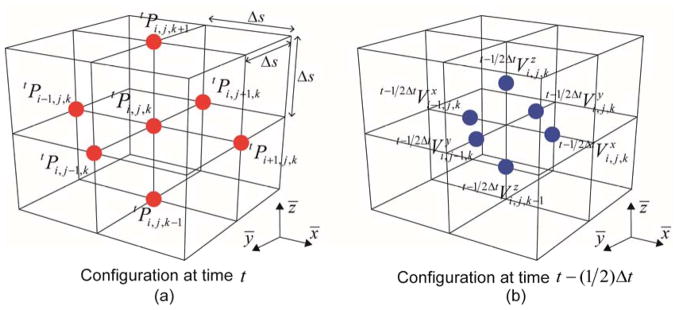
The graphical illustration of staggered grids for estimating the nodal pressure and velocity is shown in figure 2. The propagation of the ultrasound was obtained by iteratively evaluating equation (3) for each time step until reaching the desired simulation time.

Figure 2.

The graphical illustration of the staggered grids (solid lines) and the corresponding pressure and velocity nodes (dots). (a) The pressure grid and nodes at time t and (b) the velocity grid and node set-up at time t−(1/2)Δt.

In general, the algorithm that solves explicit dynamic processes, including FDTD, may become spurious and non-physically diverse due to numerical error (Namiki, 2000; Noh and Bathe, 2013). Hence, it is essential in FDTD analysis to satisfy the stability condition called Courant-Friedrichs-Lewy (CFL) criterion which is written as the following equation (4) in 3D cases:

$$\mathrm{\Delta }t\le \frac{\mathrm{\Delta }s}{\sqrt{3}c}.$$ (4)

2.6. Multi-resolution approach

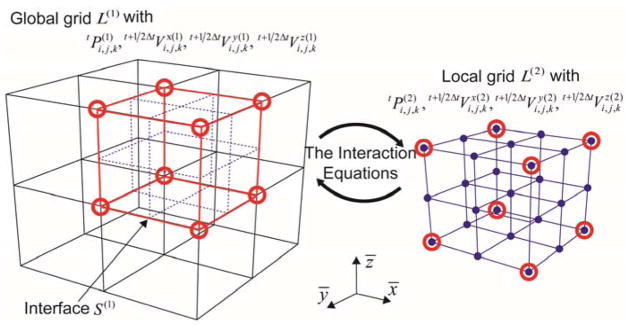
The framework of the multi-resolution analysis consists of interconnecting the nodal pressure and velocity values (obtained according to equation (3) at the respective time step) between different resolution configurations. To use the FDTD in the context of the multi-resolution approach, we adopted the use of sequence of nested grids, L⁽ⁱ⁾ (i is the index for the grid level) having different resolutions (see figure 3 for the example of 2-level, multi-resolution grids; i = 1 for the global grid and i = 2 for the local grid).

Figure 3.

Conceptual description of multi-resolution grids approach. The red circles (nodal points) and red lines (interface) represent the key interactions where equations (6) and (7) were used to interconnect the grids of differing resolutions.

The pressure and velocity at nodes in the respective grids were analyzed by equation (3), and these values were bridged between different resolution grids (i.e., local and global) using a set of two interaction equations (6) and (7). For convenience of algebraic manipulation, we defined the vector form of the nodal pressure and velocity values defined in the respective grids L⁽ⁱ⁾, as represented in equation (5).

$$\begin{gathered} {{}^t\mathbf{P}}^{(i)}={\left[\begin{array}{cccc}{{}^{t}P}_{1,1,1}^{(i)}& {{}^{t}P}_{2,1,1}^{(i)}& \cdots & {{}^{t}P}_{n_x,n_y,n_z}^{(i)}\end{array}\right]}^T, \\ {{}^{t+1/2\mathrm{\Delta }t}\mathbf{V}}^{x(i)}={\left[\begin{array}{cccc}{{}^{t+1/2\mathrm{\Delta }t}V}_{1,1,1}^{x(i)}& {{}^{t+1/2\mathrm{\Delta }t}V}_{2,1,1}^{x(i)}& \cdots & {{}^{t+1/2\mathrm{\Delta }t}V}_{n_x,n_y,n_z}^{x(i)}\end{array}\right]}^T, \\ {{}^{t+1/2\mathrm{\Delta }t}\mathbf{V}}^{y(i)}={\left[\begin{array}{cccc}{{}^{t+1/2\mathrm{\Delta }t}V}_{1,1,1}^{y(i)}& {{}^{t+1/2\mathrm{\Delta }t}V}_{2,1,1}^{y(i)}& \cdots & {{}^{t+1/2\mathrm{\Delta }t}V}_{n_x,n_y,n_z}^{y(i)}\end{array}\right]}^T, \\ {{}^{t+1/2\mathrm{\Delta }t}\mathbf{V}}^{z(i)}={\left[\begin{array}{cccc}{{}^{t+1/2\mathrm{\Delta }t}V}_{1,1,1}^{z(i)}& {{}^{t+1/2\mathrm{\Delta }t}V}_{2,1,1}^{z(i)}& \cdots & {{}^{t+1/2\mathrm{\Delta }t}V}_{n_x,n_y,n_z}^{z(i)}\end{array}\right]}^T. \end{gathered}$$ (5)

The following interaction equation (6) was used for updating pressure values from the high-resolution local nodes to the low-resolution global nodes.

$${{}^{t}P}_{i,j,k}^{(i)}=\sum _{l=1}^8\left[W_{i,j,k}^{(i+1),l}{\mathbf{B}}_{i,j,k}^{(i+1),l}\right]{{}^t\mathbf{P}}^{(i+1)}\text{in}{L}^{(i+1)},$$ (6)

in which $W_{i,j,k}^{(i+1),l}$ is the trilinear interpolation weight (Bathe, 2006) for evaluating the global nodal pressure values ( ${{}^{t}P}_{i,j,k}^{(i)}$) from the local nodal pressure values ( ${{}^{t}P}_{i,j,k}^{(i+1)}$), and ${\mathbf{B}}_{i,j,k}^{(i+1),l}$ is the Boolean vector for connecting the local nodes to the corresponding global nodes.

Likewise, nodal velocity values were updated using equation (7) by evaluating the interaction equation on the interface between the low-resolution global nodes and the high-resolution local nodes,

$$\begin{gathered} {{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{\mathrm{x}(i+1)}=\sum _{l=1}^4\left[{\overline{W}}_{i,j,k}^{(i),l}{\overline{\mathbf{B}}}_{i,j,k}^{(i),l}\right]{{}^{t+1/2\mathrm{\Delta }t}\mathbf{V}}^{\mathrm{x}(i)}\text{on}{S}^{(i)}, \\ {{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{y(i+1)}=\sum _{l=1}^4\left[{\overline{W}}_{i,j,k}^{(i),l}{\overline{\mathbf{B}}}_{i,j,k}^{(i),l}\right]{{}^{t+1/2\mathrm{\Delta }t}\mathbf{V}}^{y(i)}\text{on}{S}^{(i)}, \\ {{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{z(i+1)}=\sum _{l=1}^4\left[{\overline{W}}_{i,j,k}^{(i),l}{\overline{\mathbf{B}}}_{i,j,k}^{(i),l}\right]{{}^{t+1/2\mathrm{\Delta }t}\mathbf{V}}^{z(i)}\text{on}{S}^{(i)}, \end{gathered}$$ (7)

where ${\overline{W}}_{i,j,k}^{(i),l}$ is the bilinear interpolation weight (Bathe, 2006) for evaluating the local nodal velocity values ( ${{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{\mathrm{x}(i+1)},{{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{y(i+1)},{{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{z(i+1)}$) from the global nodal velocity values $({{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{\mathrm{x}(i)},{{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{y(i)},{{}^{t+1/2\mathrm{\Delta }t}V}_{i,j,k}^{z(i)}),{\overline{\mathbf{B}}}_{i,j,k}^{(i),l}$ is the Boolean vector for connecting the global nodes to the corresponding local nodes, and S⁽ⁱ⁾ is the interface between L⁽ⁱ⁾ and L⁽ⁱ⁺¹⁾. A conceptual description of the process is shown in figure 3.

2.7. Transducer modeling

Accurate representation of the acoustic source is an important part of tFUS simulation. The FUS transducer used in the present study consisted of a piezoelectric disc and an acoustic lens material (figure 4). Ultrasound waves generated from the piezoelectric disc yielded different phase and attenuation of the waves when exiting the source surface due to the curvature of the lens. To model the semi-spherical shape of the acoustic lens, we used a discrete source model (Martin et al., 2016) having a diameter (D_t) of 37 mm and a radius of curvature (κ) of 20 mm. At the determined source position, we substituted the pressure input values using the following equation (8):

$$P_{\mathit{source}}=\alpha A_{0}sin(2\pi ft-\mathrm{\Delta }\phi )\text{with}\mathrm{\Delta }\phi =\frac{2\pi d}{\lambda }\text{and}\alpha =e^{-a_{tr}df},$$ (8)

where α is attenuation ratio, A₀ is amplitude of ultrasound, Δφ is phase difference, f is operating frequency, t is time, λ is wavelength of the ultrasound, a_tr is an attenuation coefficient, and d is wave travel distance from the piezoelectric disc to the source surface geometry. Considering the specification of actual transducer lens material (Ultem 1000, SABIC Innovative Plastics, Burkville, AL), we used the parameters of f = 250 kHz, λ = 9.61 mm (derived from (Sheen et al., 1997)) and a_tr = 164 Np·m⁻¹·MHz⁻¹ from actual measurements on a same material (at 250 kHz) in equation (8).

Figure 4.

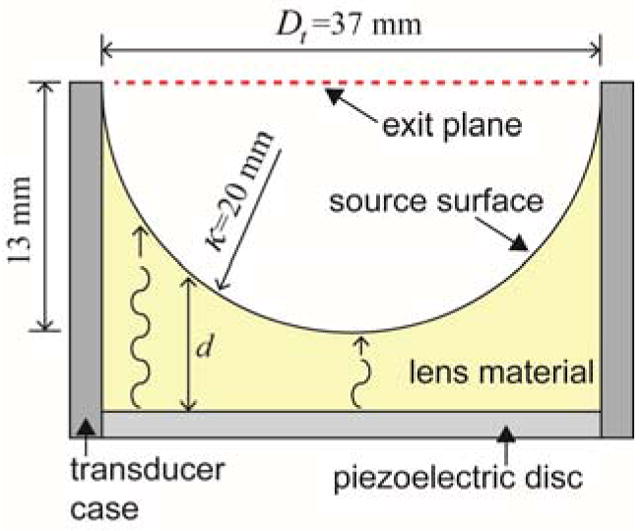
Dimensions and composition of FUS transducer used. The concave lens material focuses the ultrasound waves generated from the piezoelectric disc. κ is the radius of the concave lens (20 mm), and d is wave travel distance in the lens material. D_t indicates the diameter of the transducer opening at the exit plane.

2.8. Preparation of skull CT data and parameter assignment for simulation

The acquired CT images were resampled to isotropic voxels (1.0 × 1.0 × 1.0 mm³ and 2.0 × 2.0 × 2.0 mm³) using Lanczos filter algorithm (Burger and Burge, 2009) for constructing various resolution grids. Because the CT data was acquired at 0.5 mm isotropic voxel, the highest resolution for the simulation was set at 0.5 mm in an isotropic grid. To describe the porous and inhomogeneous characteristics of the skulls, we evaluated the normalized CT intensity map ϕ_i,j,k (0 ≤ ϕ_i,j,k ≤1) without any thresholding. Due to the presence of the large deviations in the simulation result (in terms of the acoustic pressure) from two ‘processed’ skulls (‘S1’ and ‘S2’; data not shown), intensity threshold (average 48% from the maximum) was applied to ‘S1’ and ‘S2’ for segmenting osseous structure from the CT volumetric data.

Acoustic parameters, material density (ρ _i,j,k), wave speed (c_i,j,k), and attenuation factors (a_i,j,k), were represented as following equation (9);

$$\begin{gathered} {\rho }_{i,j,k}={\rho }_{\mathit{water}}+({\rho }_{\mathit{skull}}-{\rho }_{\mathit{water}}){\varphi }_{i,j,k}, \\ {c}_{i,j,k}=c_{\mathit{water}}+({\mathrm{c}}_{\mathit{skull}}-{\mathrm{c}}_{\mathit{water}}){\varphi }_{i,j,k}, \\ {a}_{i,j,k}=a_{\mathit{water}}+(a_{\mathit{skull}}-a_{\mathit{water}}){\varphi }_{i,j,k}, \end{gathered}$$ (9)

in which ρ_skull is the density of the skull, ρ_water is the density of water, c_skull is the ultrasound speed in the skull, c_water is the ultrasound speed in water, a_skull is the attenuation coefficient of the skull, and a_water is the attenuation coefficient of water. We used the acoustic properties, ρ_skull = 2,200 kg/m³, ρ_water = 1,000 kg/m³, c_skull = 2,800 m/s, c_water = 1,500 m/s, a_skull = 20 Np·m⁻¹, and a_water = 0 Np·m⁻¹ (Goss et al., 1979; Fry and Barger, 1978; Kyriakou et al., 2015; Deffieux and Konofagou, 2010). The linear scaling of the wave speed and attenuation factor with respect to the bone density was applied according to the work by Evans and Tavakoli (1990).

2.9. Preparation of various resolution grids for simulation

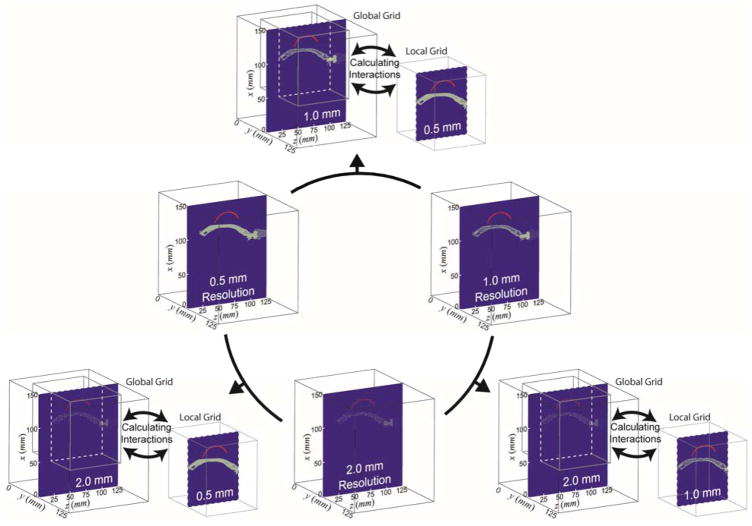
We constructed a total of six different virtual simulation spaces, each with a different combination of resolution grids. Three of them utilize the fixed grid resolutions and the other three are based on the multi-resolution approach. The detailed size of the resolution grid, the number of matrices, their node numbers, and the size of the physical field are all tabulated in table 1. The spatial resolutions of 0.5 mm, 1.0 mm, and 2.0 mm correspond to 1/12, 1/6, and 1/3 of the wavelength (λ) at frequency of 250 kHz in the water, respectively. The graphical depiction of the grid settings is illustrated in figure 5. Two levels of global and local grid settings were used for the multi-resolution simulation. The higher resolution was assigned to the local grid volume that includes (1) transducer, (2) skull, and (3) geometric focal point while the global grid was assigned to the volume that surrounds the local grid.

Table 1.

Detailed description of the virtual simulation space. The simulations on ‘0.5 mm grid’, ‘1.0 mm grid’ and ‘2.0 mm grid’ were performed using fixed resolution grids. ‘0.5&1.0 mm grids’, ‘0.5&2.0 mm grids’ and ‘1.0&2.0 mm grids’ denote the simulation conducted using multi-resolution grids. All represented in isotropic voxels.

Grid Settings		Resolution (mm)	Number of Matrices	Number of Nodes	Physical Field Size (mm3)	Discretized Time Interval (μs)	Number of Time Steps
Fixed-resolution
0.5 mm	Fixed	0.5	300 × 250 × 250	18,750,000	150 × 125 × 125	0.05	1,200
1.0 mm	Fixed	1.0	150 × 125 × 125	2,343,750	150 × 125 × 125	0.05	1,200
2.0 mm	Fixed	2.0	75 × 62 × 62	288,300	150 × 124 × 124	0.05	1,200
Multi-resolution
0.5&1.0 mm	Global	1.0	150 × 125 × 125	2,343,750	150 × 125 × 125	0.05	1,200
	Local	0.5	201 × 151 × 151	4,583,001
0.5&2.0 mm	Global	2.0	75 × 62 × 62	288,300	150 × 124 × 124	0.05	1,200
	Local	0.5	201 × 153 × 153	4,705,209
1.0&2.0 mm	Global	2.0	75 × 62 × 62	288,300	150 × 124 × 124	0.05	1,200
	Local	1.0	101 × 77 × 77	598,829

Figure 5.

Schematics of the grid settings for the implemented acoustic simulation. The fixed-resolution simulations were performed with various resolution settings of ‘0.5 mm grid’ (left, middle row), ‘1.0 mm grid’ (right, middle row), and ‘2.0 mm grid’ (middle, bottom row). The multi-resolution simulations were performed using the combination of two resolution settings (‘0.5&1.0 mm grids’, ‘0.5&2.0 mm grids’, and ‘1.0&2.0 mm grids’). The higher resolution setting was assigned to the local grid. On the blue-colored planes, red-colored profiles depict the acoustic source surface profile of the FUS transducer and the gray dots (conveying the information on resolutions) delineate the skull profile.

2.10. Measures for evaluating the simulation results

Following the CFL criterion in equation (4) (Δt ≤ 0.1 μs for 0.5 mm resolution, Δt ≤ 0.2 μs for 1.0 mm resolution, Δt ≤ 0.4 μs for 2.0 mm resolution), all simulations were conducted with a discretized time interval of Δt = 0.05 μs (sufficiently conforms to the criteria across all the resolution conditions) and 1,200 incremental steps, covering physical time of 60 μs (= 0.05 μs × 1,200 time steps). The use of a 60 μs time window was sufficient for observing the initial formation of the focus, which also shared the similarity to the actual field mapping (100 μs). From the simulation results, we evaluated acoustic pressure fields on YZ-, XZ-, XY-planes in the same location as the actual measurement.

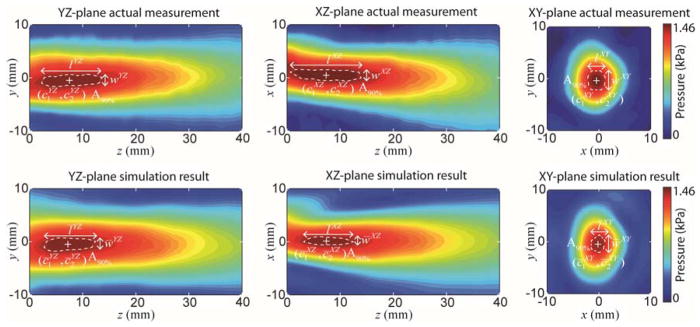
Three physical quantities—(1) the spatial location of the focus, (2) the dimension of the focus (length and width of the ellipsoidal focus), and (3) the pressure peak ratio at the focus, were separately measured from the respective simulation planes and were compared to the results obtained from the actual measurement. In more detail, the spatial location of the focus ( $c_1^{ij},c_2^{ij}$) was defined as the center of the focal area at 90%-maximum (denoted as A_90%) in which the index ij represents the respective planes (i.e., ij ∈ {YZ, XZ, XY}). A higher threshold, as opposed to the conventional full-width-at-half-maximum (FWHM) for the area definition, was applied to closely estimate the areas of neuromodulatory effects (Kim et al., 2013 and Kim et al., 2014). The dimension of the focus, measured in terms of length l^ij and width w^ij, was also evaluated on the A_90%. The pressure peak ratio R^ij was defined as the ratio of the peak pressure after the transcranial application to the peak pressure which was measured in the absence of skull. Since the actual pressure output from the transducer varies according to the electrical input/amplification/impedance matching, the derivation of the ratio R^ij was used, instead of absolute pressure values, in evaluating the performance of simulation. All the quantities obtained from simulation results are noted by upper bar on the corresponding symbols ( ${\overline{c}}_1^{ij},{\overline{c}}_2^{ij}$, l̄^ij, w̄^ij, and R̄^ij). The example from one skull sample (‘S3’) is shown in figure 6.

Figure 6.

An example of acoustic pressure distribution on the YZ-, XZ-, XY-plane (from left to right columns) from the actual measurement (top row) and the simulation results (bottom row) obtained from a skull phantom (‘S3’, at y+15° configuration). The resolution setting of ‘0.5 mm grid’ was used. ‘+’ denotes the center of the focus. The white dashed line indicates the region of A_90%.

The difference between the actual measurement and simulation results was represented by the following performance indices, in terms of location of focus (Δ_F), length (Δ_l), width (Δ_w), and peak ratio (Δ_PR) to quantify the accuracy of the simulation:

$$\begin{gathered} {\mathrm{\Delta }}_F=\sqrt{{\left(c_1^{ij}-{\overline{c}}_2^{ij}\right)}^2+{\left(c_2^{ij}-{\overline{c}}_2^{ij}\right)}^2}, \\ {\mathrm{\Delta }}_l=\left|l^{ij}-{\overline{l}}^{ij}\right|\text{and}{\mathrm{\Delta }}_w=\left|w^{ij}-{\overline{w}}^{ij}\right|, \\ {\mathrm{\Delta }}_{PR}=\frac{\left|R^{ij}-{\overline{R}}^{ij}\right|}{R^{ij}}\text{with}ij\in \{\text{YZ},\text{XZ},\text{XY}\}. \end{gathered}$$ (10)

2.11. Simulation setting for a closed skull sample

We further applied the multi-resolution simulation approach to model the soundwave propagation inside the closed cranial cavity. An ovine skull (Skulls Unlimited, Oklahoma City, OK) was purchased and underwent the same procedure (i.e., application of a plastic applicator containing fiducial markers and acquisition of CT) to obtain information on the skull geometry. The location of the FUS transducer was maneuvered to place the focus near the left side of the somatosensory area. For the numerical simulation, the discretized time interval (Δt = 0.05 μs; as same as ex vivo skull samples) was used, but the simulated physical time was doubled (2,400 incremental steps, therefore, 120 μs) to observe the effects of prolonged wave propagations within the skull. The simulation time of 120 μs allows for reasonable observation of the possible formation of standing wave whereby the incident wave front passes through the focal region approximately four times (inner diameter of the skull cavity was ~50 mm). To compensate for increased computational load accompanying the longer simulation time, the physical field size was adjusted to fit the size of the skull as close as possible (on the order of 100 × 150 × 125 mm³; reducing the number of nodes for the simulation; i.e., the processing time). The simulation accuracy is not affected by the chosen field size as long as the field contains the main areas-of-interest for wave propagation. The detailed specification of the simulation grids were tabulated in table 2.

Table 2.

Detailed description of the simulation space for the closed skull. The simulations on ‘0.5 mm grid’, ‘1.0 mm grid’ and ‘2.0 mm grid’ were performed using fixed resolution grids. ‘0.5&1.0 mm grids’, ‘0.5&2.0 mm grids’ and ‘1.0&2.0 mm grids’ denote the simulation conducted using multi-resolution grids. All represented in isotropic voxels.

Grid Settings		Resolution (mm)	Number of Matrices	Number of Nodes	Physical Field Size (mm3)	Discretized Time Interval (μs)	Number of Time Steps
Fixed-resolution
0.5 mm	Fixed	0.5	200 × 300 × 250	15,000,000	100 × 150 × 125	0.05	2,400
1.0 mm	Fixed	1.0	100 × 150 × 125	1,875,000	100 × 150 × 125	0.05	2,400
2.0 mm	Fixed	2.0	50 × 75 × 62	232,500	100 × 150 × 124	0.05	2,400
Multi-resolution
0.5&1.0 mm	Global	1.0	100 × 150 × 125	1,875,000	100 × 150 × 125	0.05	2,400
	Local	0.5	140 × 140 × 120	2,352,000
0.5&2.0 mm	Global	2.0	50 × 75 × 62	232,500	100 × 150 × 124	0.05	2,400
	Local	0.5	140 × 140 × 120	2,352,000
1.0&2.0 mm	Global	2.0	50 × 75 × 62	232,500	100 × 150 × 124	0.05	2,400
	Local	1.0	70 × 70 × 60	294,000

3. Results

3.1. Qualitative evaluation of the overall accuracy at highest grid resolution (‘0.5 mm grid’)

Prior to evaluating the efficacy of the multi-resolution approach, simulation results obtained from the highest spatial resolution setting (fixed ‘0.5 mm grid’) were evaluated with respect to those obtained from the actual measurements across four performance indices, i.e., differences in focal position (Δ_F), in focal dimension (length and width, Δ_l and Δ_w respectively), and in peak pressure ratio (Δ_PR). The results were further divided into two sub-groups, (1) data from the processed skulls (having the soft tissue removed, i.e., ‘S1’ and ‘S2’, named Case A in table 3), and (2) the same data sets obtained from the intact skulls (‘S3’, ‘S4’, and ‘S5’, Case B in table 3). The detailed individual data is given in the Supplemental Data (see tables A1–A3).

Table 3.

The comparisons for simulation performance among different conditions of the skull processing and incident sonication angles. Case A was performed using processed skulls for all angles (n = 2 sheep × 9 angles; 0°, x±10°, x±15°, y±10°, y±15°). Case B was conducted using intact skulls for all angles (n = 3 sheep × 9 angles; 0°, x±10°, x±15°, y±10°, y±15°). Case C was done using intact skulls with restricted angles (n = 3 sheep × 5 angles; 0°, x±10° and y±10°).

	Simulation Conditions
	Case A*	Case B	Case C
Measurement Plane	Focal Position ΔF (mm)
YZ	3.7 ± 2.1	1.6 ± 1.0	1.4 ± 0.9
XZ	4.4 ± 2.5	1.3 ± 0.7	1.2 ± 0.6
XY	2.7 ± 0.9	1.4 ± 0.6	1.4 ± 0.7
	Focal Dimension (mm)
	Length Δl
YZ	4.4 ± 2.7	2.3 ± 2.0	2.2 ± 1.7
XZ	5.5 ± 4.3	2.7 ± 1.8	2.2 ± 1.2
XY	0.8 ± 0.9	0.5 ± 0.5	0.5 ± 0.5
	Width Δw
YZ	1.0 ± 0.6	0.7 ± 0.5	0.7 ± 0.5
XZ	1.2 ± 1.6	0.8 ± 0.5	0.7 ± 0.5
XY	0.9 ± 0.8	0.6 ± 0.6	0.6 ± 0.5
	Peak Pressure ΔPR (%)
YZ	9.9 ± 5.2	5.9 ± 6.2	4.9 ± 4.3
XZ	10.1 ± 6.0	6.3 ± 6.5	4.1 ± 3.4
XY	8.3 ± 6.6	5.2 ± 6.4	3.1 ± 3.2

^*Note that segmentation and rescaling of CT image intensity was applied to Case A.

We found that the results acquired from the intact skull (Case B in table 3) yielded smaller differences in terms of focal position (Δ_F : 1.3–1.6 mm), compared to the measurements from the processed skulls (Case A, 2.7–4.4 mm). A similar trend was observed from the perspective of differences in focal dimension (Δ_l and Δ_w, table 3), and in peak pressure level (Δ_PR: 5.2–6.3% from the intact skulls compared to the 8.3–10.1% in processed skulls, table 3).

To examine the effects of incident angle in regards to the skull surface on simulation quality, we derived the performance indices from the three intact skull phantoms (‘S3’, ‘S4’, and ‘S5’) at a reduced range of sonication angles (0°, x±10° and y±10°: Case C in table 3). The effect of the narrowing incident sonication angle yielded smaller differences in focal position and dimensions (most of them become less than 1 mm). This restriction of the sonication angle yielded better approximation of the pressure (Δ_PR) compared to Case B (all angle condition), being closer to the actual measured value (less than 5% averaged differences).

3.2. Evaluation of the multi-resolution approach in estimating the focal location/dimension/pressure level

We compared the accuracy and computational cost in numerical simulations using different resolution grids including the use of multi-resolution grids. After determining the effects from the choice of skull samples and the range of incident sonication angles, simulations in this section were performed only on the intact skulls at the incident angles covering up to ±10°. The simulation performance was assessed using the same set of performance indices (Δ_F, Δ_l, Δ_w and Δ_PR) and the computational time. The detailed comparison data was given in the Supplemental Data (see tables A4–A15), while the summary of the results was tabulated in table 4.

Table 4.

The comparisons among various resolution grids used in simulation and its computational time.

Measurement Plane	Fixed-resolution grid			Multi-resolution grids
	0.5 mm	1.0 mm	2.0 mm	0.5&1.0 mm	0.5&2.0 mm	1.0&2.0 mm
	Focal Position ΔF (mm)
YZ	1.4 ± 0.9	2.4 ± 1.1	7.8 ± 0.7	1.5 ± 1.1	1.5 ± 1.0	2.3 ± 1.1
XZ	1.2 ± 0.6	1.7 ± 0.7	7.8 ± 1.7	1.3 ± 0.7	1.1 ± 0.6	1.7 ± 0.6
XY	1.4 ± 0.7	2.2 ± 1.0	8.9 ± 3.6	1.5 ± 0.6	1.4 ± 1.0	2.2 ± 1.0
	Focal Dimension (mm)
	Length Δl
YZ	2.2 ± 1.7	2.5 ± 1.9	14.6 ± 1.0	2.1 ± 1.9	2.3 ± 1.8	2.0 ± 1.7
XZ	2.2 ± 1.2	1.9 ± 0.9	14.5 ± 2.2	2.3 ± 1.2	2.7 ± 2.2	1.5 ± 1.4
XY	0.5 ± 0.5	0.8 ± 0.7	3.5 ± 4.5	0.3 ± 0.5	0.4 ± 0.6	0.9 ± 0.5
	Width Δw
YZ	0.7 ± 0.5	0.8 ± 0.6	1.7 ± 3.0	0.6 ± 0.6	0.7 ± 0.6	0.6 ± 0.6
XZ	0.7 ± 0.5	0.3 ± 0.5	1.3 ± 1.2	0.7 ± 0.5	0.7 ± 0.5	0.4 ± 0.5
XY	0.6 ± 0.5	0.3 ± 0.5	4.5 ± 5.5	0.7 ± 0.5	0.5 ± 0.5	0.3 ± 0.5
	Peak Pressure ΔPR (%)
YZ	4.9 ± 4.3	6.8 ± 5.4	24.4 ± 10.4	5.4 ± 4.3	5.3 ± 2.5	7.1 ± 5.8
XZ	4.1 ± 3.4	6.9 ± 5.3	20.7 ± 12.4	4.2 ± 3.3	4.8 ± 4.4	7.5 ± 6.1
XY	3.1 ± 3.2	3.2 ± 3.0	47.7 ± 18.2	3.2 ± 2.8	4.5 ± 2.9	3.5 ± 2.9
	Time (s)
	63	8	1	30	21	4

In terms of difference in focal position (Δ_F) compared to the actual measurement, the results obtained from the use of ‘0.5 mm grid’ showed the smallest difference (1.2–1.4 mm) among the simulation settings. The use of ‘1.0 mm grid’ increased the Δ_F slightly compared to the use of ‘0.5 mm grid’ (e.g., 1.7–2.4 mm); however, the use of ‘2.0 mm grid’ markedly increased the Δ_F to 7.8–8.9 mm. In multi-resolution approaches involving 0.5 mm grid setting in the local grid (i.e., ‘0.5&1.0 mm grids’ and ‘0.5&2.0 mm grids’), Δ_F was almost identical to the result from the use of ‘0.5 mm grid’ (i.e., less than 1.5 mm in difference). On the other hand, the use of ‘1.0&2.0 mm grids’, resulted in slightly higher Δ_F (e.g., 1.7–2.3 mm), resembling the results obtained from using ‘1.0 mm grid’.

Regarding the differences in focal dimension (represented in Δ_l and Δ_w), the use of ‘1.0 mm grid’ generated comparable results to those from the use of ‘0.5 mm grid’. The use of ‘2.0 mm grid’, however, yielded much greater differences, more than a six-fold increase in the focal size compared to the use of ‘0.5 mm grid’. All other multi-resolution settings, on the other hand, generated similar degrees of differences in focal dimension compared to those from using ‘0.5 mm grid’.

The difference in peak pressure ratio (Δ_PR), measured from the use of ‘1.0 mm grid’ (3.2–6.9%), was comparable to that of using ‘0.5 mm grid’ (3.1–4.9%). The use of ‘2.0 mm grid’ generated greater differences (on the order of 3–4 times, 20.7–47.7%) compared to the use of a smaller grid size. Multi-resolution simulation, performed using ‘0.5&1.0 mm grids’ or ‘0.5&2.0 mm grids’ settings, generated Δ_PR values similar to the values obtained at ‘0.5 mm grid’, showing less than 5% in Δ_PR. The use of ‘1.0&2.0 mm grids’ yielded slightly higher Δ_PR (3.5–7.5%; table 4) than the use of ‘1.0 mm grid’, but it was far smaller than the use of ‘2.0 mm grid’.

The computational time measured from using ‘0.5 mm grid’ was 63 s. It was even further decreased to 8 s in the use of ‘1.0 mm grid’ and 1 s in the use of ‘2.0 mm grid’ (table 4). In the multi-resolution simulations, 30 s and 21 s was measured for completing the stimulations using ‘0.5&1.0 mm grids’ and ‘0.5&2.0 mm grids’, respectively. We also performed an additional simulation with ‘0.5 mm grid’ by using only a single core CPU on the same computer hardware platform to evaluate efficacy of GPU multi-threading process, and the simulation took 1,421 s.

3.3. Evaluation of multi-resolution approach in a closed skull sample

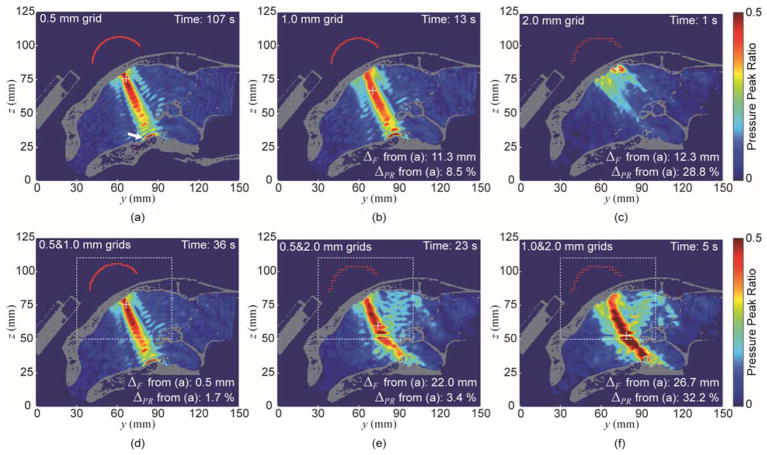
The simulation results (illustrated in figure 7 and table 5) were expressed in terms of pressure distribution, computational time, the differences in pressure peak ratio (Δ_PR), and focal position (Δ_F) with respect to the results obtained from the highest spatial resolution setting (i.e., fixed ‘0.5 mm grid’; figure 7(a)). From the analysis of the ‘0.5 mm grid’ setting, unlike the open skull example, signs of reverberations (a formation of multiple local maximum pressures along the acoustic pathway) were evident as well as the presence of high pressure level near the floor of the skull (marked by the arrow; figure 7(a)). The processing time was 107 s in this setting. The use of ‘1.0 mm grid’ setting captured many of these features but showed difference of 11.3 mm in terms of focal position (Δ_F) and 8.5% Δ_PR (figure 7(b)). In ‘2.0 mm grid’, although the simulation was quick (1 s), the pressure map became vastly different from the ones used in the higher resolution grid, with increased differences of Δ_F = 12.3 mm and Δ_PR = 28.8% (figure 8(c)). The multi-resolution approach of ‘0.5&1.0 mm grids’ setting showed a similar acoustic map to that of the ‘0.5 mm grid’ setting (figure 7(d)), and gave comparable accuracy (Δ_F = 0.5 mm and Δ_PR = 1.7%) to the ‘0.5 mm grid’ setting, but with reduced processing time (36 s). The use of ‘0.5&2.0 mm grids’ (figure 7(e)) and ‘1.0&2.0 mm grids’ (figure 7(f)), on the other hand, started to deviate from the above pressure distribution in both local and global grids, with marked increase in both Δ_F and Δ_PR.

Figure 7.

The simulation results of acoustic pressure distribution on the sagittal plane obtained from (a) ‘0.5 mm grid’, (b) ‘1.0 mm grid’, (c) ‘2.0 mm grid’, (d) ‘0.5&1.0 mm grid’, (e) ‘0.5&2.0 mm grid’, and (f) ‘1.0&2.0 mm grid’. ‘+’ denotes the location of the maximum pressure value. The pressure level inside the skull was pseudo-colored, being scaled with reference to the peak pressure value obtained in the absence of the skull, to represent the pressure peak ratio R^YZ. The white dashed line indicates the region of the local grid.

Table 5.

The comparisons among various resolution grids used in a closed-skull simulation and its computational time.

Fixed-resolution grid			Multi-resolution grids
0.5 mm	1.0 mm	2.0 mm	0.5&1.0 mm	0.5&2.0 mm	1.0&2.0 mm
Focal Position ΔF (mm)
Ref.*	11.3	12.3	0.5	22.0	26.7
Peak Pressure ΔPR (%)
Ref.*	8.5	28.8	1.7	3.4	32.2
Time (s)
107	13	1	36	23	5

^*Reference value for comparison

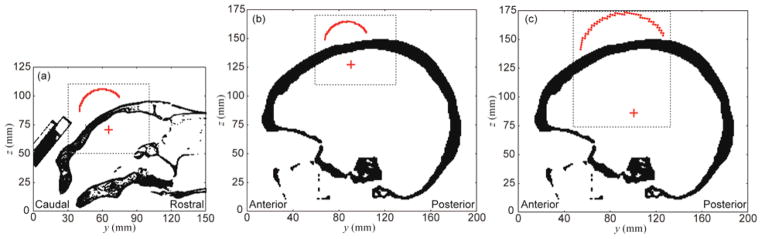
Figure 8.

Global (entire field-of-view) and local grid settings (dotted rectangular area) for the multi-resolution approach illustrated in sheep and human skull models (shown on the sagittal plane using the same spatial scale). The profile of the transducer surface is outlined in red while the estimated focal location is denoted as a red crosshair. A uniform spatial scale was used across all figures for their size comparisons. (a) The sheep skull model showing 100 × 150 × 125 global (at 1 mm resolution) and 140 × 140 × 120 local grids (at 0.5 mm resolution), (b) an example of human skull model for cortical area stimulation with 180 × 200 × 175 global (at 1 mm resolution) and 140 × 140 × 120 local grids (at 0.5 mm resolution), and (c) an example of human skull model for deep brain stimulation with 180 × 200 × 175 global (at 1 mm resolution) and 180 × 180 × 200 local grids (at 0.5 mm resolution).

4. Discussion

The neuromodulatory potentials of tFUS, with its non-invasiveness, spatial specificity, and penetrability into the deep brain regions, may provide unique therapeutic applications for addressing various neurological and psychiatric disorders. Due to the use of low-intensity ultrasound that is evasive to in vivo detection, computer-based, on-site simulation of transcranial acoustic propagation becomes a desired feature in guiding the acoustic focus to a specific brain region-of-interest. In this study, we presented a multi-resolution FDTD simulation approach to model the transcranial acoustic wave propagation generated by a single-element FUS transducer using an ovine skull model. Our multi-resolution approach using GPU-based parallel processing allowed for simulation within 30 s, while achieving simulation accuracy under 3 mm in focal position and dimension, and less than 5% difference in peak pressure ratio (when compared to the actual acoustic mapping). The implementation made a vast improvement over the use of a single-CPU environment which took a much longer time (1,421 s), and is capable of providing semi-real time feedback guidance for tFUS applications.

We prepared ex vivo ovine skulls in two different conditions, i.e., dividing them to ‘processed’ and ‘intact’ skulls, and evaluated their effects on the simulation quality. The simulations using intact, unprocessed skulls (Case B in table 3) generated more accurate estimations compared to the simulations using processed skulls (Case A in table 3) across the location/dimension of the focus and its pressure level. Our results suggest that the use of intact skulls is more appropriate to examine the transcranial transmission of ultrasound. This finding was puzzling, because we initially anticipated that removal of the soft tissue, by reducing tissue inhomogeneity, would yield a more accurate prediction from the simulation. Although we could not isolate the definite causes for the findings, we hypothesized that the mechanical means used for the removal of soft tissue (the periosteum or dura mater) might have introduced additional structural changes (e.g., dents/damages to the skull surface) that cannot be properly characterized by the numerical simulation. Further investigation is necessary, for example, to evaluate the effects from different methods for skull preparation.

Numerical modeling of the cranial structure was also an important factor in the tFUS simulation. The cranium has two main structural features, a dense solid (compact bone) and a porous network of cancellous bone/trabeculae (Fellah et al., 2004), each having different acoustic properties (i.e., density and wave speed). FDTD offers an efficient method for analyzing wave propagation in an orthogonal grid setting; however, complicated skull geometry or interfaces between the trabeculae and inner/outer compact bone, would require increased number of nodes/finer grids for their proper spatial description (Yu and Chen, 2009).

Since it is difficult to assign a single acoustic property to model the highly-inhomogeneous cancellous bone, we used variable acoustic properties based on the interpolation of a CT intensity map, as shown in equation (9). Due to the use of low frequency in the present work (i.e., 250 kHz), relatively long wavelength (on the order of 6 mm) is less likely to interact with the heterogeneous diploë (trabeculae) in the skull (Deffieux and Konofagou, 2010). On the other hand, a previous study by Aubry and colleagues (Aubry et al., 2003) suggested that the heterogeneous structure of the skull, such as diploë, can yield higher attenuation compared to the (more dense) compact bone. We note that accurate modeling of attenuation coefficient for the transcranial propagation of ultrasound has been challenging due to the presence of complicated acoustic interactions, such as mode conversion and backscattering (Marquet et al., 2009; Pinton et al., 2012). In addition, the spatial resolution of cranial CT data may insufficiently characterize the wave propagation through the complicated microstructure of the diploë (Marquet et al., 2009; Pinton et al., 2012). Further investigation is necessary to identify the unequivocal method for the proper assignment of CT-based cranial information to acoustic simulation parameters.

This interpolation method (in equation (9)) favored the use of high spatial resolution grid in modelling the skull structures (‘0.5 mm grid’ to results in good accuracy), but was computationally demanding. Biot’s theory (Fellah et al., 2004; Lee et al., 2007; Hosokawa, 2005) or the use of a grid (mesh) free method (Ala et al., 2006; Yu and Chen, 2009; Liu and Liu, 2003) can be adopted to represent acoustic properties in a porous medium having complicated geometry, and warrants future investigation. We also note that the present simulation did not account for the presence of gray and white matter structures of brain, and inclusion of realistic brain tissues and their material characteristics would be conducive to increasing the overall accuracy of the acoustic simulation.

Based on the analysis of the simulation performance at the grid resolution of 0.5 mm, we found that the use of a sonication angle of ±15° (away from the normal vector to the skull surface) generated more error in estimating the focal location and the pressure level from the actual measurement (in table 3). The simulation showed an acceptable level of accuracy within 10° incident angles (less than 2 mm difference of focal location and less than 5% difference of peak pressure ratio compared to the actual mapping results). We conjectured that tFUS administration with an incident angle greater than 10° started to introduce mode conversion that could not be properly described in the present simulation models (White et al., 2006; Marquet et al., 2009; Pinton et al., 2012). The highly-convoluted inner surface of the ovine skulls (having short-radius curvatures), in conjunction with insufficient CT image resolution to reflect this geometry, might have contributed to the findings. For the actual implementation of the current simulation settings in ovine model, therefore, the operator may need to keep the incident angle as perpendicular as possible to the skull surface (within 10°) for accuracy. Further investigation is necessary to probe source for the departure in simulation accuracy affected by the range of incident angles.

Accuracy and computational cost in different simulation resolution settings were also investigated (the results are shown in table 4). The use of ‘0.5 mm grid’ would not be applicable for semi real-time guidance due to its long computational time (63 s). The use of ‘2.0 mm grid’ expedited the simulation to mere 1 s, but with a sacrifice in the accuracy of modeling. The ‘1.0 mm grid’ setting, on the other hand, generated significantly higher performance while showing excellent computational speed (8 s). The results from the ‘0.5&1.0 mm grids’ setting improved the accuracy compared to the use of ‘1.0 mm grid’ alone, showing comparable accuracy to that of ‘0.5 mm grid’. The computation speed in this case was compatible for semi real-time user feedback (30 s). For these reasons, we concluded that the multi-resolution analysis approach allowed for a faster simulation with a minimal fidelity loss. We note that, although we used a combination of only two levels of resolution grids in the present work, more than two levels can be employed to cover a greater volume. The use of a time-variant adaptive discretization method (called as ‘re-meshing technique’) (Bouchard et al., 2000) can also be considered to flexibly allocate the localized grid settings to track the location of acoustic wave front while the simulation is running.

The simulation time period used in this study was 60 μs, which was enough to characterize the initial propagation to the focal point in space (our actual measurement was done covering a 100 μs time period). The use of longer sonication duration (TBD = 10 ms) did not affect the actual measurement, suggesting the choice of the period for the simulation was appropriate for our experimental setting in the open skull configuration. However, the use of short simulation time may not adequately characterize the acoustic profiles resulting from the steady-state wave propagations inside of the closed cranium (such as reverberations (Younan et al., 2013) or the formation of the standing wave in human and primate skulls (Deffieux and Konofagou, 2010)). Indeed, based on our simulation on a closed ovine skull using a longer simulation time, we observed presence of reverberations and standing wave formation near the floor of the skull (figure 7). In addition, we note that the use of ‘0.5&1.0 mm grids’ showed improved simulation speed while retaining the accuracy, compared to the other multi-resolution settings (i.e., ‘0.5&2.0 mm grids’ and ‘1.0&2.0 mm grids’). In conjunction with the findings from ex vivo skull simulations (open-skull configurations), our findings confirm the computational efficacy of the multi-resolution approach for later in vivo applications.

Performing a simulation using a closed skull is ideal; however, hydrophone measurements performed in a completely closed skull is a challenging task. Use of the higher acoustic intensity and non-invasive method such as ARFI (Kaye et al., 2011) can be gainfully used to validate the simulation accuracy. The expansion of the simulation volume, for example, to cover the typical adult human head will inevitably increase the computation time, even using the multi-resolution approach. Figure 8 illustrates the two-level, multi-resolution grid settings adapted to simulate tFUS application in a human skull (Visible Human Project CT datasets (Ackerman, 1998)) as well as a sheep skull (settings are shown in table 6). In the human skull, assuming the same type of transducer used in the sheep application (i.e., focal length 30 mm), the FUS focus is likely to be administered only to the cortical area. In this case, the number of nodes for the global grid is 6,300,000 (= 180 × 200 × 175, assigned as the field size) and 2,352,000 (= 140 × 140 × 120, i.e., dotted box in the figure 8(b)) for the local grid. If we were to use a larger transducer (e.g., 80 mm aperture) with greater focal length (90 mm) for deep brain stimulation in humans (as conducted in Deffieux and Konofagou, 2010), the global grid nodes would remain the same (i.e., 6,300,000), however, the local grid size must be expanded to include the larger transducer and greater focal length. Thus, it increases the number of local grid nodes to 6,480,000 (= 180 × 180 × 200, i.e., dotted box in the figure 8(c)). Factoring in the increased number of time steps (6,000 steps, which is ~2.5 times greater than the simulation in a sheep skull; table 6) to reflect the size of the skull cavity in humans, the computational time will increase ~5 times (150 s) for the case of the cortical stimulation and ~7.5 times (225 s) for the case of deep brain stimulation. These approximations leave a margin of improvement for reducing the computation time by optimizing the simulation parameters through multiple levels of resolution grids. Employing a GPU device with higher processing capability (in both speed and parallel threading) can also be helpful to further alleviate the concerns over the computational time. Application of the technique in humans and its detailed quantitative evaluation constitute subjects for further investigation.

Table 6.

Comparisons among multi-resolution modeling of tFUS through sheep and human skulls. The local grid was assigned to model the space encompassing both transducer and the focal area.

Model		Resolution (mm)	Number of Matrices	Number of Nodes	Total Number of Nodes	Physical Field Size (mm3)	Discretized Time Interval (μs)	Number of Time Steps	Estimated Computation Time (s)
Sheep Skull	Global	1.0	100 × 150 × 125	1,875,000	4,227,000	100 × 150 × 125	0.05	2,400	30
	Local	0.5	140 × 140 × 120	2,352,000
Human Skull (Cortical)	Global	1.0	180 × 200 × 175	6,300,000	8,652,000	180 × 200 × 175	0.05	6,000	150
	Local	0.5	140 × 140 × 120	2,352,000
Human Skull (Deep brain)	Global	1.0	180 × 200 × 175	6,300,000	12,780,000	180 × 200 × 175	0.05	6,000	225
	Local	0.5	180 × 180 × 200	6,480,000

The developed simulation method aims to provide the operator with information regarding the estimated position, shape, and pressure level of the focus with respect to the position of the FUS transducer. However, the manual maneuvering of the transducer in space is still subject to inadvertent human error. The adoption of the inverse analysis techniques (Rekanos, 2002; Abenius and Strand, 2006) can be used to automatically identify the optimal position/orientation of the transducer with respect to the head. The technique, when combined with a robotic transducer positioning system (Kim and Lee, 2016), will be conducive to delivering the desired pressure level of sonication to the region-of-interest with minimal human intervention.

5. Conclusion

A multi-resolution approach, designed for simulating transcranial acoustic propagation from a single-element transducer, was implemented and evaluated in an ovine skull model. The flexibility of assigning different combinations of resolution grids, combined with the use of a GPU-based parallel computation environment, allowed for achieving simulation accuracy while greatly improving the computation speed. The approach is capable of providing on-site feedback information to the operator regarding the location and pressure amplitude of the acoustic focus. The extension and evaluation of the method in a human setting are needed to promote safety and efficacy of tFUS-mediated brain stimulation for neuroscientific research and therapeutic applications.