Abstract
Single-cell RNA sequencing (scRNA-seq) has significantly deepened our insights into complex tissues, with the latest techniques capable of processing tens of thousands of cells simultaneously. Analyzing increasing numbers of cells, however, generates extremely large data sets, extending processing time and challenging computing resources. Current scRNA-seq analysis tools are not designed to interrogate large data sets and often lack sensitivity to identify marker genes. With bigSCale, we provide a scalable analytical framework to analyze millions of cells, which addresses the challenges associated with large data sets. To handle the noise and sparsity of scRNA-seq data, bigSCale uses large sample sizes to estimate an accurate numerical model of noise. The framework further includes modules for differential expression analysis, cell clustering, and marker identification. A directed convolution strategy allows processing of extremely large data sets, while preserving transcript information from individual cells. We evaluated the performance of bigSCale using both a biological model of aberrant gene expression in patient-derived neuronal progenitor cells and simulated data sets, which underlines the speed and accuracy in differential expression analysis. To test its applicability for large data sets, we applied bigSCale to assess 1.3 million cells from the mouse developing forebrain. Its directed down-sampling strategy accumulates information from single cells into index cell transcriptomes, thereby defining cellular clusters with improved resolution. Accordingly, index cell clusters identified rare populations, such as reelin (Reln)-positive Cajal-Retzius neurons, for which we report previously unrecognized heterogeneity associated with distinct differentiation stages, spatial organization, and cellular function. Together, bigSCale presents a solution to address future challenges of large single-cell data sets.
Single-cell RNA sequencing (scRNA-seq) is at the forefront of techniques to chart molecular properties of individual cells. Recent microfluidic-based methods are scalable to tens of thousands of cells, enabling an unbiased sampling and in-depth characterization without prior knowledge (Klein et al. 2015; Macosko et al. 2015; Zheng et al. 2017). Consequently, studies are less confined by the number of cells and aim to produce comprehensive cellular atlases of entire tissues, organs, and organisms (Regev et al. 2017). Increasing cell numbers, however, generate extremely large data sets, which extend processing time and challenge computing resources. Current scRNA-seq analysis tools are not designed to analyze data sets larger than thousands of cells and often lack sensitivity and specificity to identify marker genes for cell populations or experimental conditions.
To address the challenges of large scRNA-seq data sets, we developed bigSCale, an analytical framework for the sensitive detection of population markers and differentially expressed genes, being scalable to analyze millions of single cells. Unlike other methods that use simple or mixture probabilistic models with predefined distributions to handle the noise and sparsity of scRNA-seq data (Kharchenko et al. 2014; Finak et al. 2015; Satija et al. 2015; Korthauer et al. 2016), bigSCale does not assume an a priori defined distribution. Instead, bigSCale uses large sample sizes to estimate a highly accurate and comprehensive numerical model of noise. The framework further includes modules for differential expression (DE) analysis, cell clustering, and population marker identification. Moreover, a directed convolution strategy allows the processing of extremely large data sets, while preserving the transcript information from individual cells.
We evaluate the performance of bigSCale using a defined biological model for reduced or elevated gene expression levels by performing scRNA-seq of neuronal progenitors derived from induced pluripotent stem (iPS) cells of Williams-Beuren (WB) (Pober 2010) and 7q11.23 microduplication (Dup7) (Morris et al. 2015) syndrome patients. Simulated data sets of different size and sparsity were utilized to underline the accuracy and speed of bigSCale in DE analysis. To demonstrate its suitability for unsupervised clustering and population marker identification using its probabilistic model of cell-distances, we applied bigSCale to cluster cell types of the somatosensory cortex and hippocampus from adult mouse brains (Zeisel et al. 2015). Lastly, the bigSCale framework was applied to convolute and characterize 1.3 million cells derived from the developing mouse forebrain, detecting profound heterogeneity in rare neuronal subpopulations. We believe bigSCale presents an adequate solution for the processing and analysis of scRNA-seq data from millions of single cells. Its speed and sensitivity make it suitable to address future challenges of large single-cell data sets.
Results
The bigSCale framework
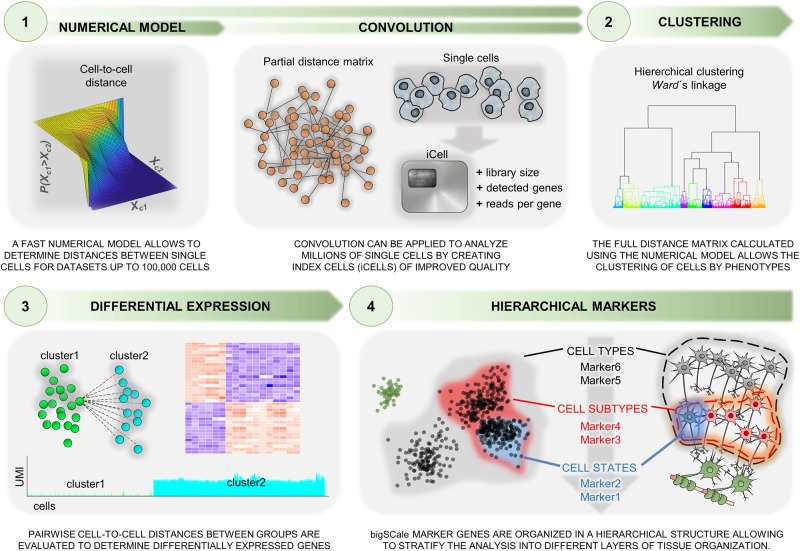
Data sets from scRNA-seq display sparse and noisy gene expression values, among other sources due to drop-out events, amplification biases, and variable sequencing depth. The bigSCale framework builds a probabilistic model to define phenotypic distance between pairs of cells that considers all sources of variability. Compared with other methods that assume negative binomial, gamma, or Poisson distributions in simple or mixture probabilistic models, bigSCale estimates a highly accurate and comprehensive numerical model of noise. The model allows to quantify distances between cells, which provide the basis for DE analysis and cell clustering (Fig. 1, Methods).
Figure 1.
Schematic representation of the bigSCale framework for analyzing millions of single-cell transcriptomes. The analytical framework includes a numerical model step to determine distances between single cells and modules for differential expression (DE) analysis, cell clustering, and population marker identification. An optional convolution strategy allows the processing of extremely large data sets (preserving the transcript information from individual cells).
To generate the model, cells featuring highly similar transcriptomes are grouped together. Next, the expression variation within groups is used as an estimator of noise. Unlike previous methods, bigSCale models differences in expression levels rather than expression levels themselves. Therefore, a P-value is assigned to each gene, representing the likelihood of a change of expression from one cell to another. Notably, variations in the preclustering step (change in correlation metric, linkage, precluster numbers) only marginally affect the final results (Supplemental Fig. S1). Prior to model computation, a module for batch effect removal can be applied.
For DE, bigSCale assigns a P-value to each gene, representing the likelihood of an expression change between two groups of cells. To this end, all pairwise cell comparisons between two groups are performed. Genes repeatedly differing in expression between cells cumulate higher scores, which are next adjusted and normalized into P-values.
Cellular clustering is achieved by computing all pairwise cell distances to generate a distance matrix and to assign cells into groups (via Ward's linkage). Specifically, the distance matrix is computed over a set of overdispersed genes, namely, genes presenting a high degree of variation across the data set. To improve the feature quality, skewed, isolated, and perfectly correlating genes are discarded. The latter are prone to generate artificial transcript clusters and consist of genes with a common 3′-end, being indistinguishable by digital counting scRNA-seq methods. Undesired confounding signatures, such as gender-related or cell cycle–related genes, can be identified and isolated to improve cluster information (Supplemental Fig. S2).
Following the identification of cell clusters, bigSCale conducts an iterative DE analysis between populations of cells for the sensitive detection of markers, defined by genes unevenly expressed across populations. Notably, most current tools lack the option to model multifaceted phenotype structures with overlying molecular signatures of cells. Conversely, bigSCale allows disclosure of multiple alternative phenotypes of a given cell by ordering markers in a hierarchical structure, in which increasing layers of phenotypic complexity (from cell types to subtypes or states) are represented by markers at increasing hierarchical levels.
While bigSCale's intrinsic speed allows the direct analysis of data sets up to a 100,000 cells, adjustments are needed to handle millions of cells. For these scenarios, the cell numbers are scaled down by pooling (convoluting) information from cells with analogous transcriptional profiles into index cell (iCell) profiles. Here, iCells are defined by adding transcript counts from pools of similar single cells, significantly increasing molecule and gene counts, and overall improving the expression profile quality. Accordingly, iCells allow discrimination of subpopulations with higher precision and sensitivity. Most importantly, iCells preserve the transcript information from individual cells and can be deconvoluted for targeted analysis of populations of interest.
Identification of differentially expressed genes
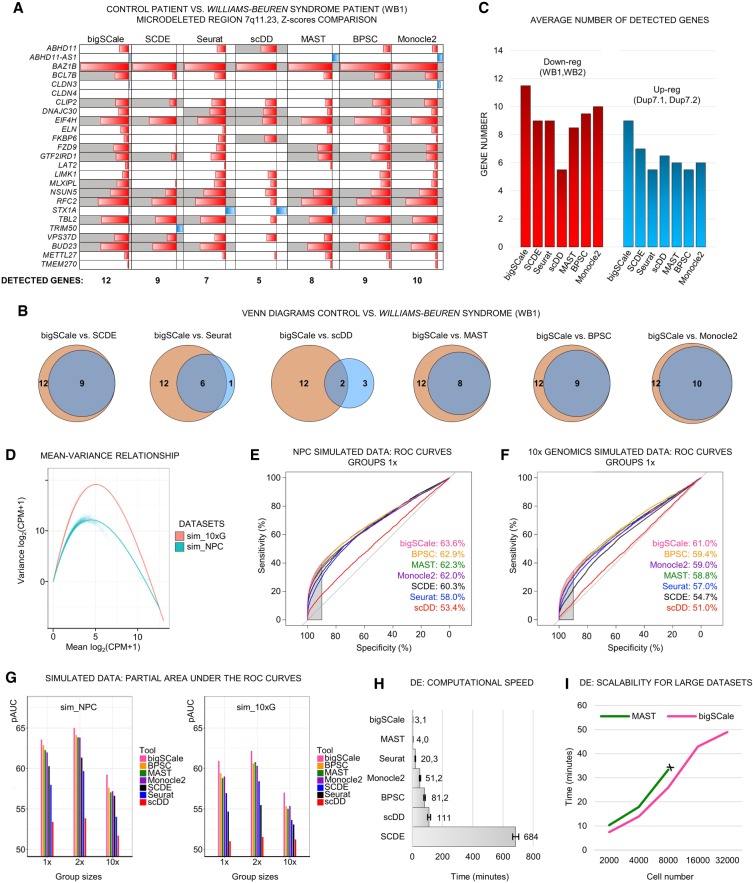
We evaluate the performance of bigSCale using a biological model for reduced and elevated gene expression levels. Specifically, we performed scRNA-seq of 1920 neuronal progenitor cells (NPCs) derived from iPS cells of two patients with WB and two with Dup7 syndrome. Both are multisystemic disorders caused by a heterozygous deletion or duplication, respectively, of 1.5–1.8 Mb at the chromosome band 7q11.23. This region is flanked by segmental duplications with high sequence identity that can mediate nonhomologous recombination with the consequent loss or gain of 26–30 contiguous genes, whose transcriptional levels vary in line with their allele dosage (Pober 2010; Morris et al. 2015). To benchmark bigSCale against other common single-cell DE tools, NPCs from four syndromic patients (WB1/2, n = 742; Dup7.1/2, n = 735) were compared to NPCs derived from a healthy donor (WT, n = 369 cells). The sensitivity of each algorithm was evaluated by counting the number of genes detected to be significantly down- or up-regulated in patients against the control. To achieve the same level of specificity among tools, the top 1500, 2000, and 2500 deregulated genes were used in each comparison.
For the WB1 sample harboring a deleted allele, bigSCale presented the highest sensitivity by detecting 12 down-regulated genes, followed by Monocle2 (Qiu et al. 2017), BPSC (Vu et al. 2016), SCDE (Kharchenko et al. 2014), MAST (Finak et al. 2015), Seurat (Satija et al. 2015), and scDD (Fig. 2A; Korthauer et al. 2016). Notably, bigSCale finds the same genes as the other best-performing tools, plus additional events (Fig. 2B). Consistently, bigSCale displayed the highest sensitivity also in the remaining three comparisons (Supplemental Fig. S3A–C), with an overall average of 11.5 detected down-regulated genes in WB patients and nine up-regulated genes in Dup7 patients (Fig. 2C). Moreover, bigSCale proved to be the most sensitive method at all tested specificity levels, with an average of 8.75 (top 2000) and 6.75 (top 1500) detected DE genes (Supplemental Fig. S3D). These results indicate that bigSCale outperforms other methods for single-cell DE analysis in sensitivity when using biological data.
Figure 2.
Benchmarking of sensitivity, specificity, and speed of bigSCale, SCDE, Seurat, MAST, scDD, BPSC, and Monocle2. (A) DE analysis in iPS cell–derived neuronal progenitor cells (NPCs) from healthy and Williams-Beuren (WB) syndrome donors (WT vs. WB1). For the genes located in the deleted region, the P-values of each tool are shown in Z-score scale. (Red) Down-regulated; (blue) up-regulated. Genes correctly detected as down-regulated are highlighted (gray). Total numbers of correctly assigned genes are indicated (below). (B) Venn diagrams for WT versus WB1 comparing the identity of correctly assigned genes. (Orange) bigSCale; (blue) others. (C) Average number of detected down-regulated (red) and up-regulated (blue) genes in the two WB and Dup7 patients, respectively, compared with a healthy donor. (D) Comparison of the mean-variance relationship in the two simulated data sets (sim_NPC and sim_10×). (E,F) Partial AUCs of ROC curves computed across the tools in the two simulated data sets (sim_NPC, E; sim_10×, F) with group sizes having proportions 1:1 (1×). The sensitivity at high level of specificity (>90%) is highlighted (gray area). (G) Barplots of partial AUC across tools for all tested proportions (1×, 2×, 10×) in DE analysis of simulated data sets (sim_NPC and sim_10×). (H) Average required time for computing DE in the NPC cell model (average 739 total cells per comparison, four comparisons, tools run on one CPU-core). (I) Scalability of bigSCale and MAST with large data sets. MAST could not be tested beyond 8000 cells due to excessive RAM requirements (>16 Gb).
To further test the performances in determining DE genes, we benchmarked bigSCale against the previous tools using simulated data sets. For data simulation, we used Splatter (Zappia et al. 2017), which allows to generate and control true-positive DE genes. Simulations have been performed estimating parameters from two data sets representing different characteristics of large-scale experiments, namely, our NPC data set (sim_NPC) and a droplet-based experiment consisting of approximately 2500 cells sequenced to low coverage (10x Genomics, sim_10×G; Methods). The two data sets widely differed in the number of detected genes per cell, sparsity, and heterogeneity (Fig. 2D; Supplemental Fig. S4A). In both simulations, we recreated distributions of gene expression levels and library properties highly similar to the original data sets and preserved the original number of cells and genes. Six cell types of different proportions were simulated in each data set, allowing for testing of DE between groups of proportions 1:1 (1×), 1:2 (2×), and 1:10 (10×). Each tool has been applied to the complete data set at the model-building step prior to test DE between groups of cells.
The ability to correctly classify true DE genes against non-DE genes was evaluated calculating the area under the curve (AUC) of a receiver operating characteristic (ROC) curve, ranking genes in their order of significance as determined by the tools. To test the capacity of controlling false-positive events, we focused on the partial AUC with high specificity being >90%. All tools performed better in the simulated NPC data set, and the order of tools was consistent across all group sizes (Fig. 2E,F; Supplemental Fig. S4B–E). bigSCale outperformed the other tools, reaching the highest levels of sensitivity and specificity in all tested conditions (Fig. 2G). The BPSC performance was the closest to bigSCale, with the gap being more evident in more distinct proportional contexts (10×) (Supplemental Fig. S4C,E). To evaluate the impact of varying settings, we evaluated different parametric tests (negative binomial and Poisson) implemented in the Seurat pipeline, in addition to the default setting (bimodal) (Supplemental Fig. S5). We found that bigSCale also outperformed negative binomial and Poisson in five out of six scenarios using different simulated data sets. The bigSCale framework further allows the integration of external tools for additional data normalization. As a prototypical example, we applied scran normalization (Lun et al. 2016) to simulated data and compared the pAUC with the bigSCale default method (library size normalization). We found no significant differences and a nearly perfect correlation of scran and library size coefficients (Supplemental Fig. S6).
In the view of increasing data sets sizes, we further evaluated bigSCale's speed in DE analysis. In the biological model (NPC), bigSCale proved to be the fastest tool (3.1 min) in performing DE, followed by MAST (4.0 min) (Fig. 2H). The slowest tool was SCDE (684 min), as reported in previous studies (Sengupta et al. 2016; Jaakkola et al. 2017). We next compared the scalability of bigSCale to MAST with respect to samples sizes. To this end, we created a simulated matrix of 40,000 genes and 32,000 cells and performed DE analyses between pairs of groups with sizes ranging from 2000–32,000 cells. bigSCale was faster for all conditions (Fig. 2I). Moreover, bigSCale could process data sets larger than 8000 cells, whereas MAST was limited by the RAM requirements, denoting a broader perspective of applicability for bigSCale.
Cellular clustering and population marker identification
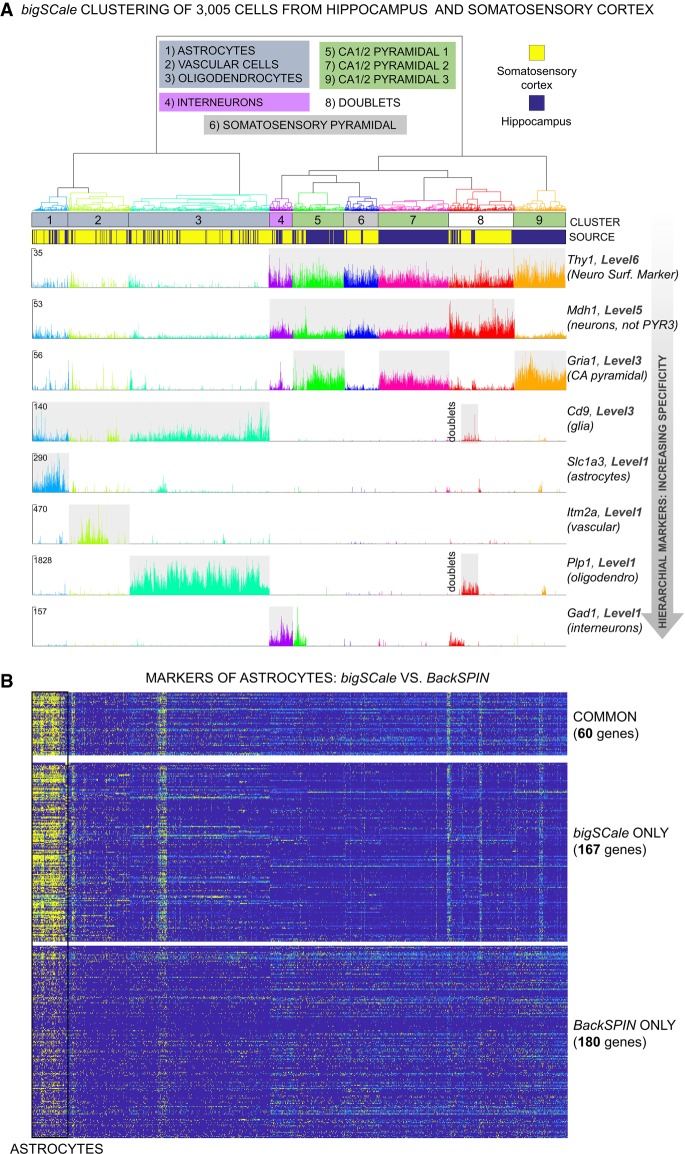
To evaluate the ability of bigSCale to identify cell types and subpopulations in complex tissues, we analyzed 3005 cells of the somatosensory cortex and hippocampus dissected from the adult mouse brains (Zeisel et al. 2015). Consistent with previous analyses (Zeisel et al. 2015; Fan et al. 2016), bigSCale was able to segregate all major brain cell types, namely, somatosensory pyramidal neurons, different types of CA1/2 pyramidal neurons, interneurons, astrocytes, oligodendrocytes, and vascular cells (Fig. 3A). We increased the number of differentially expressed genes across brain cell populations four-/fivefold compared with the original analysis using BackSPIN (Zeisel et al. 2015) and, moreover, defined markers of higher-order cell types (Fig. 3A). Specifically, bigSCale determined 9258 differentially expressed genes across populations, including 7167 previously unidentified genes (Supplemental Table S1). The expression patterns of the novel markers were highly specific to the respective populations of cells, as shown for astrocytes (Fig. 3B), oligodendrocytes, vascular cells, neurons, and interneurons (Supplemental Fig. S7A,B), pointing to a high accuracy of bigSCale. In line, external bulk RNA-seq signatures supported the novel markers to be highly specific for the respective populations (Lein et al. 2007; Zhang et al. 2014) (astrocytes, P < 4.9−62; oligodendrocytes, P = 9.9−18; interneurons, P = 9.8−19; neurons, P = 2.3−34; vascular, P = 1.0−67). Furthermore, the novel markers included established marker for brain subtypes, such as Atp1a2 (Gritz and Radcliffe 2013), Slc1a3 (Roales-Buján et al. 2012), Mt1 (Chung et al. 2008), and Aqp4 (Hubbard et al. 2015) for astrocytes or Stmn3 (Chauvin and Sobel 2015) and Snap25 (Antonucci et al. 2016) for neurons (Supplemental Fig. S8A–C).
Figure 3.
bigSCale analysis of scRNA-seq data from 3005 mouse cortical and hippocampal cells (Zeisel et al. 2015). (A) Dendrogram and expression plots reporting examples of hierarchical markers. Dendrogram was cut at 20% of its total depth to segregate nine different clusters of cells, which correspond to the main brain cell types. In the expression plots, UMI counts are shown at single-cell level for markers of different hierarchical marker levels (Methods). Marker genes for decreasing marker levels, representing distinct brain cell types are displayed. (B) Comparison of bigSCale and BackSPIN (Zeisel et al. 2015) in the detection of gene markers for astrocytes. bigSCale identified 167 additional markers with high specificity for astrocytes (high expression, yellow; low expression, blue). Vice versa, markers uniquely identified by BackSPIN display a weak specificity and achieved low scoring in bigSCale.
Differently to other methods, bigSCale marker genes are organized in a hierarchical structure, allowing stratification of the analysis into different layers of tissue organization. This enabled the assignment of markers to subpopulations but also higher-order cell types, such as glia cells or neurons (Supplemental Fig. S7B). In this regard, current experimental designs fail to reliably separate intact neurons from glia cells, as established markers (e.g., NeuN) are located in the nuclear membrane and are not suitable for isolating entire neurons. Our analysis identified 1656 marker genes silenced in glial cells and expressed in neuronal populations (Supplemental Table S1), such as the neuronal surface receptor CD90 (Thy1) (Fig. 3A), potentially suitable for isolating intact neurons from complex brain samples.
Convolution of large data sets into iCells
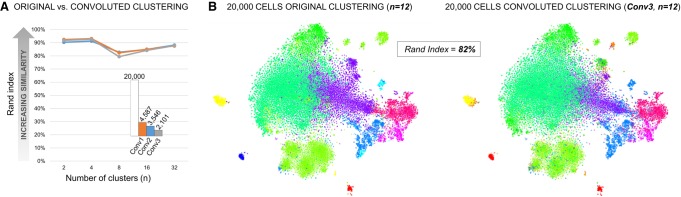
To analyze very large data sets of millions of cells, bigSCale convolutes the original cells into iCells with improved transcriptional profiles after the numerical model has been computed using the entire data set (Methods). To ensure that the convolution strategy does not deteriorate cellular phenotypes and related cell clustering, we evaluated its performance by analyzing 20,000 brain cells (randomly downsampled data set, 10x Genomics). Specifically, we tested the cluster assignment of all cell pairs within the data set before and after increasing degree of convolution (from 4587 to 2,101 iCells) and for different cluster numbers (n = 2–32). Similarities of classification were defined by the Rand index (RI), a metric suitable for comparative cluster assessment (Wang et al. 2017), where RI = 100% implies complete similarity of clusterings. We observed a highly similar cluster assignment between original and convoluted data sets with RI > 80% (Fig. 4A). The RI was also stable with increasing cluster numbers or degree of convolution, indicating a robust strategy to reduce cell numbers. In line, visualizing cells in two-dimensional plots (t-SNE) confirmed the high similarity of cluster assignment between original and iCells (Fig. 4B). Together, the results support the utility of bigSCale convolution to reduce data set sizes without the introduction of artifacts.
Figure 4.
Assessment of the cell convolution strategy in bigSCale. (A) Comparison of original and convoluted clustering with the Rand index (RI). Pairwise cell comparisons were performed for three increasing degrees of convolution (Conv1,2,3) into iCells (numbers indicated). Similarity of clustering (RI; y-axis) were evaluated at different resolution (n cluster numbers; x-axis). RI were >80% for all tested combinations, pointing to highly similar cluster assignment for original and iCells. (B) t-SNE plots comparing original and convoluted clustering. The example displays a comparison with RI = 82% and 12 clusters. The high degree of concordance between experiments is visible through the consistent cluster assignment of cell pairs.
Analysis of 1,306,127 cells of the developmental pallium
Among the most extensive data sets to date for scRNA-seq are 1,306,127 sequenced mouse brain cells from the developmental (E18) dorsal and medial pallium. The data were produced using droplet-based library preparation (Chromium v2) and are publicly available (10x Genomics). Despite being the sole developmental scRNA-seq data set of crucial regions such as cortex, hippocampus, and the subventricular zone, its large size yet prevented any detailed analysis. We reasoned that the bigSCale analytical framework would be suitable to analyze such large data set and performed an in-depth analysis of cell types and states, including rare and poorly described subpopulations. This analysis serves as proof-of-concept for bigSCale's suitability to process millions of cells from complex tissues in an unbiased manner.
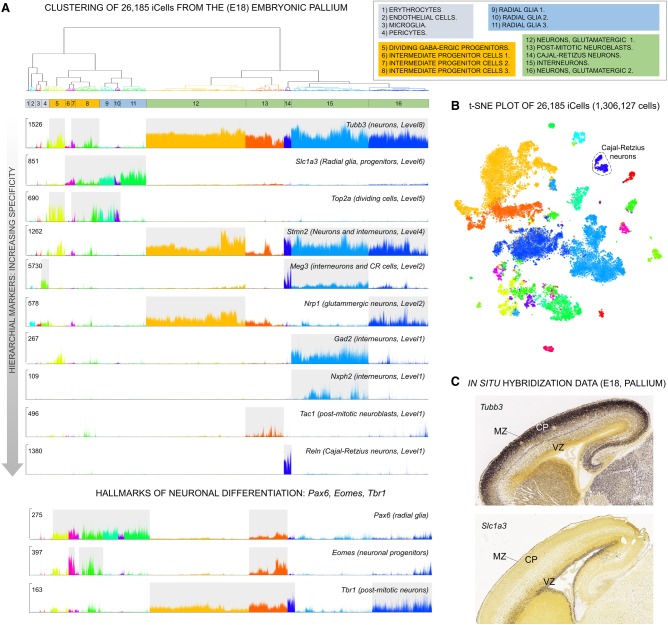
Initially, we applied our convolution strategy to reduce the data set size 50-fold from 1,306,127 cells to 26,185 iCells. As expected iCells were of improved quality with average library size increasing 50-fold (from 4890 to 238,500 UMIs) and detected genes per cell increasing fivefold (from 2009 to 9360). In line, average expression level increased from to 2.4 UMIs to 25.5 UMIs. The convolution retained 1,244,298 cells (95.27%), discarding 61,829 cells (4.73%). Clustering of the iCells revealed 16 major cell populations and captured 16,242 differentially expressed markers (Fig. 5A,B; Supplemental Table S2). We classified the 16 populations in four main cell types: nonneuronal (1–4), neuronal progenitors (5–8), radial glia (9–11), and post-mitotic neurons (12–16). We compared our cell types and markers with results from another developmental brain scRNA-seq data set (E12 to E18) (La Manno et al. 2016) and to transcriptional profiles of the adult human brain (Hawrylycz et al. 2012). Although stringent similarities could not be expected given the different brain areas (forebrain against midbrain) or developmental stage (E18 against adult brain), we found significant gene set enrichments pinpointing to the validity of our clusters (Supplemental Tables S3, S4).
Figure 5.
bigSCale analysis of 26,185 iCells (convoluted from 1,306,127 single cells) of the embryonic pallium (E18). (A) Dendrogram of 16 iCell clusters representing the major cell types (split by color) and subpopulations (cluster 1–16). Single-cell expression plots (UMI counts) present marker genes (decreasing levels of hierarchical markers) for the main subpopulations and specific markers for neuronal differentiation (lower panel). (B) t-SNE representation of the 16 populations of pallial cells identified by bigSCale clustering. (C) In situ hybridization data for Tubb3 and Slc1a3. Post-mitotic neurons (Tubb3 positive) locate to the outer neocortical layers, including cortical plate (CP) and marginal zone (MR), and radial glia and progenitors (Scl1a3 positive) are found in the ventricular and subventricular zone (VZ).
The hierarchical markers of bigSCale allowed to sharply disentangle cell types and subtypes, as well as stages of lineage commitment. Higher-order markers, such as Tubb3 and Slc1a3, mark the two main cell types: post-mitotic neurons of the intermediate/marginal zones (MZs) and radial glia and progenitors of the ventricular zone, respectively (Fig. 5A,C). Similarly, bigSCale captured the hallmarks of the main stages of the neuronal lineage (Englund et al. 2005), indicated by the expression of Pax6 (radial glia), Eomes (TBR2, committed progenitors), and Tbr1 (differentiated neurons) (Fig. 5A). On the other hand, the most significant markers shaping the heterogeneity of post-mitotic neurons are Stmn2 (silenced in neuroblasts), Meg3 (interneurons and Cajal-Retzius [CR] neurons), Nrp1 (glutamatergic neurons), Tac1 (neuroblasts), Reln (CR neurons), and Gad2 (gabaergic interneurons).
As expected, some radial glia (C9, C10) and progenitor populations (C5, C7, C8) represent dividing cells, indicated by Top2a expression and other cell cycle genes (Fig. 5A; Supplemental Table S2). bigSCale also identified a population of dividing GABAergic progenitors (C5) characterized, among other markers, by simultaneous expression of Gad2, Pax6, and Top2a. Subpatterns of expression within populations of cells further indicate the presence of subtypes of cells, as displayed by the uneven expression of the signaling molecule Nxph2 within Gad2-positive interneurons (Fig. 5A). Given the association of Nxph2 with an attention-deficit/hyperactivity disorder (Porfirio et al. 2012), Gad2/Nxph2-positive cells could represent a previously unknown developmental subtype of interneurons with roles in behavior and neurocognitive functions.
Deconvolution for high-resolution subpopulation analysis
While bigSCale enabled the convolution of 1.3 million cells to characterize the main cellular types of the developmental pallium with unprecedented detail, the information of single-cell transcriptional profiles was maintained. Consequently, population-specific deconvolution allows the in-depth analysis of populations of interest at the resolution of individual cells. We were especially interested in the population of Reln-positive cells, also known as Cajal-Retzius (CR) neurons, a transient type of neuron that regulates the laminar formation of the developing neocortex and whose malfunctioning causes major neurodevelopmental disorders like autism or schizophrenia (Fatemi 2005).
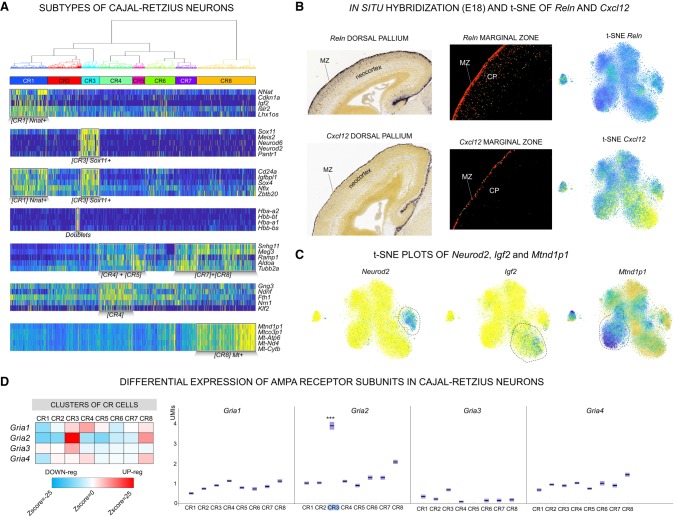
To date, a comprehensive phenotypic characterization of the CR cells and its potential subtypes remains elusive, mostly due to their transient nature and to the lack of unambiguous markers. To unravel the diversity of CR cells, we deconvoluted 480 Reln-positive iCells to 17,543 individual Reln-positive cells, an unprecedented resource to phenotype this cell type (Fig. 6A). Reln was expressed uniformly in all deconvoluted cells, confirming the specificity of the convolution strategy (Fig. 6B). Furthermore, Trp73 (also known as p73), a well-known marker of neocortical CR cells of later developmental stages (E18), was also uniformly expressed. Expression of Trp73 indicates that the CR cells were originated from the cortical hem, which is the major source of neocortical CR cells (Kirischuk et al. 2014). We determined CR cell–specific markers, in addition to Reln and Trp73, which included Cacna2d2, a calcium channel subunit, and Eya2, a transcriptional coactivator (Methods). Unsupervised clustering revealed eight major subpopulations of CR cells (Fig. 6A) and a total of 8174 differentially expressed markers genes (Supplemental Table S5). The clusters also included cell doublets, an inevitable artifact of microfluidic-based sample processing, recognizable by cells with simultaneous expression of Reln and erythrocytes genes (Fig. 6A).
Figure 6.
Subtypes of Cajal-Retzius (CR) cells disentangled by bigSCale. (A) Dendrogram and heatmap of the five top-scoring population markers (CR1–8; high expression, yellow; low expression, blue). (B) Comparison of Reln (top) and Cxcl12 (bottom) expression spatially resolved (in situ immunostaining [left] and fluorescence-staining [center]; source Allen Brain Atlas: Mouse Brain). Reln consistently marks all CR cells (t-SNE; right) located in the MZ and the CP. Cxcl12 is expressed in a CR subpopulation and in situ experiments indicate that Cxcl12-positive cells are exclusively located in the MZ. (C) t-SNE representation of Neurod2-positive, Igf2-positive, and Mt-nd1–positive subpopulations of CR cells. (D) DE of AMPA receptor subunits in CR cells. (Left) Heatmap (Z-scores) representing the relative expression level of each AMPA subunit in the CR subpopulations. (Red) Higher expression; (blue) lower expression. (Right) Expression of AMPA receptors displayed by UMI counts (y-axis). Significant DE is indicated; (***) Z-score > 10.
The eight subclusters pointed to a yet-undescribed heterogeneity of CR cells and to spatial and functional differences within the developmental pallium. We found Cxcl12, a chemokine secreted by the meninges and regulating the tangential migration of the CR cells (Kirischuk et al. 2014), to be also expressed by subtypes of CR cells (Fig. 6B). Notably, in situ hybridization data from E18 mice (Allen Brain Atlas: Mouse Brain) indicated that Cxcl12+/Reln+ CR cells are located within the MZ, whereas Cxcl12-/Reln+ are positioned outside the MZ, in the inner layers of the neocortex. This points to a self-regulated migration capacity of the CR neurons of the MZ.
The bigSCale analysis further unveiled potentially distinct differentiation stages of CR cells, marked by either Sox11/Neurod2 or Nnat/Igf2 (Fig. 6A,C). Likewise, we found a population of CR cells (CR8) expressing higher levels of mitochondrial genes, an indicator of apoptotic or disrupted cells (Fig. 6A,C). Considering that we did not find a similar cluster in the other pallial cell types, we excluded a technical artifact and suggest a cell subtype–specific phenotype. CR cells were previously shown to initiate cell death at post-natal stages (Kirischuk et al. 2014). Consequently, CR8 cells could represent an intriguing population of CR neurons committed to die already at the last stages of embryonic development (E18).
Lastly, neurotransmitter receptors are one of the most important features of CR cells. We specifically interrogated the expression of the 62 subunits of the nine major receptor types. We found a number of subunits to be differentially expressed, pointing to CR subtypes with different membrane properties (Supplemental Fig. S9). The most striking variation was found for the Gria2, a pivotal subunit of AMPA channels strongly influencing receptor properties, assembly, trafficking, and long-term synaptic plasticity (Fig. 6D).
Discussion
Current scRNA-seq analytic tools use simple or mixture probabilistic models that require predefined distributions to handle noise and sparsity. bigSCale bypasses this requirement by estimating a numerical model of noise. Furthermore, it determines the extent of the variation between cells without estimating actual gene expression value. These stratagems allowed us to build a highly optimized code, which can rapidly process large cell numbers while showing an improved sensitivity and specificity to detect differentially expressed genes, as shown for biological and simulated data sets.
Several tools for the analysis of scRNA-seq data sets have been proposed. Typically, scRNA-seq analysis starts with data normalization, accounting for technical sources of variation. Additionally, effects of confounding signatures can be removed to facilitate interpretation. Methods then proceed to cell clustering, gene markers extraction, DE analysis, pseudotime inference, and other high-level analyses. bigSCale presents a complete standalone package combining the aforementioned analysis steps. Of note, bigSCale can be used in combination with external normalization tools (Lun et al. 2016; Bacher et al. 2017), as we have shown for scran normalization applied to our simulated data sets (Supplemental Fig. S6).
We benchmarked the performance of bigSCale against tools that largely differ in their assumptions and models to estimate gene expression levels and DE genes. MAST uses a hurdle model with logistic regression, normal and gamma distributions, and χ2 test (Finak et al. 2015). Monocle2 uses generalized additive models (GAMs) with a Tobit model, normal distribution (for the error), and a χ2 test (Qiu et al. 2017). scDD estimates the gene expression via a Dirichlet process mixture (DPM) of normal distributions (Korthauer et al. 2016). Lastly, SCDE uses a mixture mode of negative binomial and Poisson, Seurat features different parametric tests (e.g., negative binomial), and BPSC uses a beta-Poisson model (Kharchenko et al. 2014; Satija et al. 2015; Vu et al. 2016). Despite the aforementioned differences, all tools make use of a priori defined distributions (normal, negative binomial, gamma, beta, Poisson, etc.) to model gene expression levels and DE. However, erroneous or suboptimal selection of the distribution function can strongly affect the final results. In addition, each model suffers from specific weaknesses. For example, it was recently pointed out that hurdle models (e.g., MAST) cause a decrease in numerical stability and design flexibility for the user (Qiu et al. 2017). In contrast, bigSCale offers a radical change of perspective by avoiding to model gene expression (instead modelling directly the change of expression) and using an empirical fitting that does not require any a priori defined distribution. The principal weakness of empirical fitting is the so-called overfitting (incorporating the noise into the model). However, according to the strong law of large numbers (Glivenko–Cantelli theorem), the empirical distribution function converges to the underlying distribution function with the increase of sampling size. As a consequence, the large sample numbers of scRNA-seq data sets allow building of an empirical model that does not suffer from overfitting (Supplemental Fig. S1).
With the advent of microfluidic-based scRNA-seq library preparation methods and the associated decrease in costs, experiments are now scalable to profile millions of cells simultaneously. The latest methods even provide single-cell transcriptomes without the physical separation of cells (through combinatorial indexing) (Cao et al. 2017), paving the way to affordable big-scale projects and the comprehensive charting of tissue and organism compositions. With bigSCale, we provide an analytical framework that addresses the computational challenges of future large data sets. While current tools are not applicable for experiments exceeding thousands of cells, DE analysis and clustering with bigSCale is practical for 100,000 cells. Beyond that, its convolution module allows the analysis of millions of cells as shown here for the developing pallium. Further, we foresee a potential application of the convolution strategy in other large data types, such as single-cell mass cytometry data, where iCells could improve resolution and decrease computation time (van Unen et al. 2016; Bendall et al. 2014).
With decreasing expenses for library preparation, sequencing costs become a limiting factor. Here we showed that despite being sequenced to low coverage (average 18,500 reads per cell), the analysis of more than a million cells is capable of identifying heterogeneity even in rare cell types. Indeed, the convolution into iCells and related improvements of expression profiles allowed us to draw a high-resolution atlas of the developing pallium, providing a rich resource of novel marker genes for subsequent studies. Further, the size of the data set enabled us to describe a yet-unprecedented heterogeneity in a rare, transient brain cell type (CR neurons, 1% of total cells), producing novel, founded hypotheses that can be used to enhance our mechanistic insights in brain development. Overall, these results illustrate the value of lowly sequenced large data sets. Nevertheless, for even sparser data sets, such as those obtained from the sequencing of nuclei (Habib et al. 2017), the performance of bigSCale still needs to be evaluated. Furthermore, the heuristic bigSCale uses for DE analysis leaves space for future improvements. The current heuristic works by adapting to groups of cells the numerical model built on pairwise comparisons. This increases computational time and also creates numerical instability that requires proper normalization steps (see Methods).
Together, we present an analytical framework for scRNA-seq analysis that provides a solution for challenges arising from future large-scale efforts to systematically and comprehensively chart cellular composition of complex organisms, including the human body (Regev et al. 2017).
Methods
Numerical probabilistic model
The probabilistic model is established as follows. First, cells are clustered in groups sharing similar expression profiles. We refer to this clustering as preclustering, as it is different from the final cell clustering achieved at the end of the pipeline. The purpose of the preclustering step is to group cells sharing highly similar transcriptomes, which are next treated as biological replicates to allow evaluation of the noise. Preclustering is achieved by (1) normalizing the reads/UMIs to library size (xij = cij/LS for i = 1,…,tot_genes, where xij is the normalized expression for gene i in cell j, c the nonnormalized expression and LS = Sum(cij) the library size); (2) transforming the normalized expression levels in log10(x+1); and (3) normalizing the log-transformed values to the same interval for each gene. This step is required; otherwise, only highly expressed genes would drive the clustering: (4) clustering the cells using Pearson-correlation and hierarchical clustering with Ward's linkage. bigSCale automatically attempts to find the deepest possible cut (on average 10%–15% of total tree height) in the tree to ensure that only highly similar cells are grouped together. At the same time, it avoids cuts that are too deep and would produce clusters that are too small for computing the numerical model (for details and pseudocode, see Supplemental Material).
To test the robustness of the numerical model and final clustering against variations of the preclustering heuristic, we evaluated the similarity of the final clustering calculated from different cutting depths and hence different numerical models (Supplemental Fig. S1). Forcing the cutting depth to 4% and 20% (unsupervised heuristic cut was 7%) resulted in large variations in the number of preclusters (nine and 1160, respectively). As the number of preclusters (20%, nine preclusters) must be higher than the number of final clusters (11), higher cutting depths (>20%) were not tested. Indeed, higher cutting would cause an overestimation of the noise, as biologically different cells would be treated as biological replicates. Similarly, testing values <4% would result in too low numbers of data points to calculate the numerical model. In fact, given the excessive fragmentation associated with cutting depth = 4% (1160 preclusters), the number of data points for the model was already reduced by greater than fivefold compared with the unsupervised cut (7%). Importantly, these large changes in the number of preclusters translate into marginal changes of the resulting numerical model and the final clustering (RI: 95%–97%) (Supplemental Fig. S1).
We further tested the cluster robustness against a change of the correlation metric. Namely, instead of Pearson correlation (suitable to quantify linear relationships between random variables), we applied Spearman correlation, which is less sensitive to outliers and can detect monotonic relationships between random variables. Again, this change translates into a neglectable variation of the final clustering (RI = 97.26%) (Supplemental Fig. S1), indicating high robustness of the preclustering and numeric model heuristic. Finally, we tested the effects of changes in the linkage metric by switching from Ward's linkage to complete linkage or weighted average distance (WPGMA). Single, average, and centroid linkage could not be tested because they produced an excessive chaining of the cells that prevented the assignment of clusters. In line with previous results, the change of the linkage, although associated with a massive increase in the number of preclusters (from 52 up to 1683 with complete linkage), causes only marginal changes in the final clustering (Supplemental Fig. S1). Overall, these results indicate the heuristic to be robust and capable of adapting to different data sets in a completely unsupervised way.
At this stage, we now treat the cells within each group as replicates, assuming their changes of expression to be solely due to noise and not to biological differences. Second, all within-group pairwise comparisons between cells are enumerated in order to determine how rare/common (i.e., assigning a P-value) each combination of expression values is. Specifically, if a precluster contains n cells, it produces C(n,2) = n*(n−1)/2 combinations of cells. Each of these combinations contain k couples of expression values (Xcell1, Xcell2), where k is equal to the total number of genes and Xcell1, Xcell2 is the expression of a gene in the two compared cells. Each couple of expression values of each combination is summed into a 3D histogram that represents a numerical approximation of a cumulative distribution function (Supplemental Fig. S10A,B). The assigned P-values are related to the difference in gene expressions across all cells. For instance, if a gene has zero UMIs in cell X and two UMIs in cell Y, its P-value would be larger than for a gene with zero UMIs in cell X and 20 UMIs in cell Y, as such differences are rare.
The fitting takes into account the library size, meaning that it accounts for the higher dispersion of values of low-sized libraries. Specifically, when two cells of one precluster are compared during the enumeration, they are normalized for the library size according to the formula xij = cij/Sum(cij)*((LS1+LS2)/2) for i = 1,..,tot_genes, where xij is the normalized expression for gene i in cell j = 1 or j = 2, c is the nonnormalized expression, and LS1,LS2 are the library sizes of cells j = 1 and j = 2.
Learning this numerical, probabilistic model from the data is possible because single-cell data sets contain hundreds to thousands of cells, which allows us to enumerate up to hundreds of billions of couples and, hence, to gain a high precision in the estimated P-values. Ultimately, the model allows to assign a P-value to each gene, indicating the probability of a difference in the expression when comparing two cells.
DE model and hierarchical markers
The purpose of DE analysis is to assign P-values to genes that indicate the likelihood of an expression change between two groups of cells. The core of bigSCale is the empirical, numerical model of expression change between one cell to another. While this is directly applicable to find a DE gene when comparing two cells, its use to identify DE between groups of cells needs special adjustments. In particular, each cell of one group is compared to each of the cells of the other group, resulting in a total of n1*n2 comparison, where n is the number of cells of each group. For each gene, the n1*n2 log10 transformed P-values (derived from the probabilistic model and signed to represent up- or down-regulation) are summed into a total raw score. Genes up(down)-regulated in one group compared with the other will cumulate high (positive or negative) total raw scores. Here, the raw score is an empirical measure indicative of the likelihood of an expression change between the two groups. In this aspect, bigSCale radically differs from the other tools benchmarked for the DE, which either perform parametric fitting followed by, for example, binomial or Poisson tests or use nonparametric tests that do not estimate a model of the noise.
The raw score is next adjusted (1) for the total number of comparison, using a curve smoothing spline (the rationale for this adjustment is to take into account that genes with sparser expression will produce smaller scores compared to genes expressed in high frequency) (Supplemental Fig. S10C) and (2) for the within-group variability, which is estimated by running a DE analysis between randomly reshuffled cells in a way that cells of the same group are compared. Specifically, two null-groups are created by taking an equal proportion of cells from the two original groups. For example, in the case of two groups of 100 cells each, the null-groups will each be formed by mixed 50+50 cells randomly extracted from original group one and two, respectively. For comparison involving fewer than 2000 total cells, five such permutations are performed. Each of the five permutations will determine an average expression value for any given gene, which is centered on its expected value with a very low standard deviation. For this reason, we found that five permutations are enough for group sizes involving fewer than 2000 total cells. For comparison involving more than 2000 total cells, the number of permutations is progressively scaled down with the increase of cell numbers. The reason is that large groups allow to fit the within-group variability already with one or few permutations.
Aside from being a standalone tool, the DE script is also iteratively applied between clusters at the end of the clustering pipeline to isolate markers genes, that is, genes expressed only in specific cell types (i.e., clusters). Upon completion of the clustering, a DE analysis is performed among all the pairs of clusters, resulting in (N2) comparisons, where N = number of clusters. Generally, the user can select the desired number of clusters, according to the desired detail of analysis. Nonetheless, bigSCale will calculate a hierarchical structure of the markers, which allows recognition of the main cell types even when setting a high N to inspect cell subtypes. In this way, the number of clusters N can be freely set to any level without the risk of losing phenotypic information.
As the last step, genes presenting significant changes of expression throughout the data set are selected and organized in a hierarchical structure. Genes that are up-regulated in one population compared with each of the other populations are classified as markers specific to that population (Level 1 markers). Level 1 makers capture the phenotypes being unique and peculiar to populations of cells. Each Level 1 marker has a score, which corresponds to the highest (less significant) log10 transformed P-value out of the N−1 comparison. In the next step, Level 2 markers are calculated. These markers are up-regulated in at most two populations of cells compared with each of the other populations. Essentially this means that Level 2 markers are genes expressed in two populations of cells among all populations. This computation iteratively continues up to Level N − 1 markers. For example, we assume four populations: radial glia, neuronal progenitors, dividing neuronal progenitors, and differentiated neurons. Level 1 markers would represent genes expressed only in one of the populations, such as radial glia–specific markers. Level 2 markers would be genes shared by two populations, such as the neuronal progenitors markers, which are expressed both in the neuronal progenitors and in the dividing neuronal progenitors. Lastly, Level 3 markers are shared by three populations, for example, neuronal markers, which are expressed in the dividing and nondividing progenitors and in the differentiated neurons.
Overview of the clustering
Once the probabilistic model has been fitted, it is possible to calculate distances between cells. First, overdispersed genes, namely, genes with high variation of expression throughout the data set, are determined by means of empirical noise model learned from the data (Supplemental Fig. S10D–F). To further improve the features section, extremely skewed genes (Supplemental Fig. S10G) and isolated genes (not correlated with any others) are discarded. Furthermore, perfectly correlating genes are discarded as they belong to families with shared 3′-exons (such as Pcdh or Uty), for which most scRNA-seq techniques (e.g., MARS-Seq [Jaitin et al. 2014; Paul et al. 2015] or chromium-based [Zheng et al. 2017] methods) cannot differentiate between transcripts. These families can otherwise generate artificial clusters, as it happens with other tools (Fan et al. 2016).
Second, distances for all pairs of cells are calculated, and the obtained distance matrix is used to cluster the cells (hierarchical clustering, Ward's linkage). The distance between two given cells is calculated as the sum of the log10 transformed P-values of overdispersed genes. Cells presenting many overdispersed DE genes will cumulate higher sums and eventually result very distant. Only genes with DE P-values <0.01 are retained in the sum to ensure that only significant changes determine the final distance.
Hierarchical clustering is a direct clustering type that provides a visual aid (dendrogram) to put the increasing complexity of cell types into context. More importantly, in the bigSCale workflow the hierarchical clusters work in synergy with the hierarchical markers of higher-order cell types, as shown, for example, in Figure 3. Without a hierarchical clustering, it would not be possible to clearly visualize the association between cell types and higher-order markers such as Thy1 or Gria1. The combined strength of hierarchical clustering and hierarchical markers further allows us to overcome the difficulties of determining cluster numbers, as higher-order phenotypes (the main cell types corresponding to the minimal, informative, cluster number) are always recollected and visible. Furthermore, unlike other kinds of clustering such as k-means, hierarchical clustering allows us to use directly the distances calculated by bigSCale's numerical model to cluster cells.
Prior to the calculation of the numerical model and distance matrix, batch correction can be applied to level out the batch-related variance in expression. Briefly, batch correction forces each gene to follow the same distribution in each batch, condition-wise (Supplemental Fig. S10H). In this way, the batch-effects are removed while preserving the original distributions of expression (Supplemental Fig. S10H,I). Similarly, confounding gene expression signatures, such as gender-related or cell cycle–related genes, can be isolated by bigSCale and removed (or reduced) to allow a clustering of informative differences (Supplemental Fig. S2).
Convolution of large data sets
To convolute large data set, bigSCale performs the following pipeline. (1) The numerical model of the data set is calculated. (2) For each cell, its distances against a number n of other random cells are calculated. The number of random cells n is normally set to thousands. The higher n, the longer the computational time, but the lower the distortion introduced by the convolution. The final output of this step is a m*n matrix, where m is the number of cells in the original data set and n is the number of random cells for which distances are calculated. (3) A pooling algorithm is applied to the m*n distance matrix to determine all groups of cells that will be summed into iCells. The rationale of the algorithm is that, for each cell, its closest neighbor among the n other random cells can be considered as an analogous phenotype. To increase the convolution factor, k closest neighbors, instead of one, can be chosen. The pipeline pools the cells in order of similarity, starting with the closest ones, up to a maximum distance determined by percentile values. Initially, the algorithm starts with a stringent percentile value (P = 5% of the total computed distances) and attempts pooling k closest neighbors for each cell. When there are no more cells with k closest neighbors within the maximum distance (P = 5%), k is relaxed to k − 1. This cycle continues until k = 1, to which point the maximum distance allowed is increased to P = 10%. These inner (k) and outer (p) cycle continue until P = 50%. Cells ending up with no neighbors are considered outliers and discarded. While it is easy to locate neighbors for cells belonging to abundant (frequent) types, for rare cell types it becomes harder. Essentially, the two k–p cycles maximize the probability to find neighbors for every cell, both common and rare ones.
The ratio n/k is proportional to the quality of the convolution. In fact, a high n/k ratio implies that the k-closest neighbors chosen for each cell are selected from a much larger population of n random cells, which increases the chances to find the “real” neighbors, especially for rare cell types. Convolution of very large data sets can be split in multiple rounds to further reduce artifacts by using better n/k ratios, as done in the case of the 1.3 million cells data set (1.3 Million Brain Cells from E18 Mice, 10x Genomics; https://support.10xgenomics.com/single-cell-gene-expression/datasets). Specifically, we convoluted the data set with a final factor k = 75 in three rounds. In fact, calculating n = 4000 for 1.3 million cells already requires approximately 12 h of CPU-time, nonetheless yielding in a bad n/k = 4000/75 = 53,3 ratio, if convolution was in one round. Therefore, we proceeded with three rounds of convolution. The convolution factors used for each round were (n1 = 4000, k1 = 3), (n2 = 5000, k2 = 5), and (n3 = 7000, k2 = 5), which all showed high, good n/k ratios (1333, 1000, and 1400, respectively). The first round reduced the size to 456,274 iCells, the second round to 110,583 iCells, and the third round to 26,185 iCells.
Data access
Raw data counts and the expression matrix for the NPC cell data set from this study have been submitted to the NCBI Gene Expression Omnibus (GEO; http://www.ncbi.nlm.nih.gov/geo/) under accession number GSE102934. bigSCale v1.0 is freely available at GitHub (https://github.com/iaconogi/bigSCale) and as Supplemental Software.
Supplementary Material
Acknowledgments
H.H. is a Miguel Servet (CP14/00229) researcher funded by the Spanish Institute of Health Carlos III (ISCIII). This work was further supported by the grants from Fundación Ramón Areces, the marathon “Todos Somos Raros, Todos Somos Únicos” (Proyecto 52). R.C. is recipient of a Marie Skłodowska-Curie Actions fellowship (656359, H2020). Core funding is from the ISCIII and the Generalitat de Catalunya.
Author contributions: H.H. and G.I. conceived the study. G.I. developed bigSCale and performed the statistical analysis. E.M. conceived and conducted the simulation analysis. A.G.-A. generated the MARS-Seq sequencing libraries. G.R.-E. performed primary data processing. R.C., I.C., and L.A.P.-J. contributed human NPC samples. M.G. and I.G. performed sequencing and provided computing infrastructure. H.H. and G.I. wrote the manuscript with support from E.M. All authors read and approved the final manuscript.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.230771.117.
Freely available online through the Genome Research Open Access option.
References
- Antonucci F, Corradini I, Fossati G, Tomasoni R, Menna E, Matteoli M. 2016. SNAP-25, a known presynaptic protein with emerging postsynaptic functions. Front Synaptic Neurosci 8: 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacher R, Chu L-F, Leng N, Gasch AP, Thomson JA, Stewart RM, Newton M, Kendziorski C. 2017. SCnorm: robust normalization of single-cell RNA-seq data. Nat Methods 14: 584–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendall SC, Davis KL, Amir ED, Tadmor MD, Simonds EF, Chen TJ, Shenfeld DK, Nolan GP, Pe'er D. 2014. Single-cell trajectory detection uncovers progression and regulatory coordination in human B cell development. Cell 157: 714–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao J, Packer JS, Ramani V, Cusanovich DA, Huynh C, Daza R, Qiu X, Lee C, Furlan SN, Steemers FJ, et al. 2017. Comprehensive single-cell transcriptional profiling of a multicellular organism. Science 357: 661–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chauvin S, Sobel A. 2015. Neuronal stathmins: a family of phosphoproteins cooperating for neuronal development, plasticity and regeneration. Prog Neurobiol 126: 1–18. [DOI] [PubMed] [Google Scholar]
- Chung RS, Penkowa M, Dittmann J, King CE, Bartlett C, Asmussen JW, Hidalgo J, Carrasco J, Leung YKJ, Walker AK, et al. 2008. Redefining the role of metallothionein within the injured brain: extracellular metallothioneins play an important role in the astrocyte-neuron response to injury. J Biol Chem 283: 15349–15358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Englund C, Fink A, Lau C, Pham D, Daza RAM, Bulfone A, Kowalczyk T, Hevner RF. 2005. Pax6, Tbr2, and Tbr1 are expressed sequentially by radial glia, intermediate progenitor cells, and postmitotic neurons in developing neocortex. J Neurosci 25: 247–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Salathia N, Liu R, Kaeser GE, Yung YC, Herman JL, Kaper F, Fan J-B, Zhang K, Chun J, et al. 2016. Characterizing transcriptional heterogeneity through pathway and gene set overdispersion analysis. Nat Methods 13: 241–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fatemi SH. 2005. Reelin glycoprotein in autism and schizophrenia. Int Rev Neurobiol 71: 179–187. [DOI] [PubMed] [Google Scholar]
- Finak G, McDavid A, Yajima M, Deng J, Gersuk V, Shalek AK, Slichter CK, Miller HW, McElrath MJ, Prlic M, et al. 2015. MAST: a flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol 16: 278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gritz SM, Radcliffe RA. 2013. Genetic effects of ATP1A2 in familial hemiplegic migraine type II and animal models. Hum Genomics 7: 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habib N, Avraham-Davidi I, Basu A, Burks T, Shekhar K, Hofree M, Choudhury SR, Aguet F, Gelfand E, Ardlie K, et al. 2017. Massively parallel single-nucleus RNA-seq with DroNc-seq. Nat Methods 14: 955–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawrylycz MJ, Lein ES, Guillozet-Bongaarts AL, Shen EH, Ng L, Miller JA, van de Lagemaat LN, Smith KA, Ebbert A, Riley ZL, et al. 2012. An anatomically comprehensive atlas of the adult human brain transcriptome. Nature 489: 391–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubbard JA, Hsu MS, Seldin MM, Binder DK. 2015. Expression of the astrocyte water channel aquaporin-4 in the mouse brain. ASN Neuro 7: 1759091415605486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaakkola MK, Seyednasrollah F, Mehmood A, Elo LL. 2017. Comparison of methods to detect differentially expressed genes between single-cell populations. Brief Bioinform 18: 735–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaitin DA, Kenigsberg E, Keren-Shaul H, Elefant N, Paul F, Zaretsky I, Mildner A, Cohen N, Jung S, Tanay A, et al. 2014. Massively parallel single-cell RNA-seq for marker-free decomposition of tissues into cell types. Science 343: 776–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kharchenko PV, Silberstein L, Scadden DT. 2014. Bayesian approach to single-cell differential expression analysis. Nat Methods 11: 740–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirischuk S, Luhmann HJ, Kilb W. 2014. Cajal–Retzius cells: update on structural and functional properties of these mystic neurons that bridged the 20th century. Neuroscience 275: 33–46. [DOI] [PubMed] [Google Scholar]
- Klein AM, Mazutis L, Akartuna I, Tallapragada N, Veres A, Li V, Peshkin L, Weitz DA, Kirschner MW. 2015. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 161: 1187–1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korthauer KD, Chu L-F, Newton MA, Li Y, Thomson J, Stewart R, Kendziorski C. 2016. A statistical approach for identifying differential distributions in single-cell RNA-seq experiments. Genome Biol 17: 222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 580.e19.La Manno G, Gyllborg D, Codeluppi S, Nishimura K, Salto C, Zeisel A, Borm LE, Stott SRW, Toledo EM, Villaescusa JC, et al. 2016. Molecular diversity of midbrain development in mouse, human, and stem cells. Cell 167: 566–. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lein ES, Hawrylycz MJ, Ao N, Ayres M, Bensinger A, Bernard A, Boe AF, Boguski MS, Brockway KS, Byrnes EJ, et al. 2007. Genome-wide atlas of gene expression in the adult mouse brain. Nature 445: 168–176. [DOI] [PubMed] [Google Scholar]
- Lun ATL, Bach K, Marioni JC. 2016. Pooling across cells to normalize single-cell RNA sequencing data with many zero counts. Genome Biol 17: 75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macosko EZ, Basu A, Satija R, Nemesh J, Shekhar K, Goldman M, Tirosh I, Bialas AR, Kamitaki N, Martersteck EM, et al. 2015. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell 161: 1202–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris CA, Mervis CB, Paciorkowski AP, Abdul-Rahman O, Dugan SL, Rope AF, Bader P, Hendon LG, Velleman SL, Klein-Tasman BP, et al. 2015. 7q11.23 duplication syndrome: physical characteristics and natural history. Am J Med Genet A 167A: 2916–2935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul F, Arkin Y, Giladi A, Jaitin DA, Kenigsberg E, Keren-Shaul H, Winter D, Lara-Astiaso D, Gury M, Weiner A, et al. 2015. Transcriptional heterogeneity and lineage commitment in myeloid progenitors. Cell 163: 1663–1677. [DOI] [PubMed] [Google Scholar]
- Pober BR. 2010. Williams–Beuren syndrome. N Engl J Med 362: 239–252. [DOI] [PubMed] [Google Scholar]
- Porfirio MC, Lo-Castro A, Giana G, Giovinazzo S, Purper Ouakil D, Galasso C, Curatolo P. 2012. Attention-deficit hyperactivity disorder and binge eating disorder in a patient with 2q21.1-q22.2 deletion. Psychiatr Genet 22: 202–205. [DOI] [PubMed] [Google Scholar]
- Qiu X, Hill A, Packer J, Lin D, Ma Y-A, Trapnell C. 2017. Single-cell mRNA quantification and differential analysis with Census. Nat Methods 14: 309–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regev A, Teichmann SA, Lander ES, Amit I, Benoist C, Birney E, Bodenmiller B, Campbell PJ, Carninci P, Clatworthy M, et al. 2017. Science forum: the human cell atlas. eLife 6: e27041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roales-Buján R, Páez P, Guerra M, Rodríguez S, Vío K, Ho-Plagaro A, García-Bonilla M, Rodríguez-Pérez L-M, Domínguez-Pinos M-D, Rodríguez E-M, et al. 2012. Astrocytes acquire morphological and functional characteristics of ependymal cells following disruption of ependyma in hydrocephalus. Acta Neuropathol (Berl) 124: 531–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satija R, Farrell JA, Gennert D, Schier AF, Regev A. 2015. Spatial reconstruction of single-cell gene expression data. Nat Biotechnol 33: 495–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengupta D, Rayan NA, Lim M, Lim B, Prabhakar S. 2016. Fast, scalable and accurate differential expression analysis for single cells. bioRxiv 10.1101/049734. [DOI]
- van Unen V, Li N, Molendijk I, Temurhan M, Höllt T, van der Meulen-de Jong AE, Verspaget HW, Mearin ML, Mulder CJ, van Bergen J, et al. 2016. Mass cytometry of the human mucosal immune system identifies tissue- and disease-associated immune subsets. Immunity 44: 1227–1239. [DOI] [PubMed] [Google Scholar]
- Vu TN, Wills QF, Kalari KR, Niu N, Wang L, Rantalainen M, Pawitan Y. 2016. β-Poisson model for single-cell RNA-seq data analyses. Bioinforma Oxf Engl 32: 2128–2135. [DOI] [PubMed] [Google Scholar]
- Wang B, Zhu J, Pierson E, Ramazzotti D, Batzoglou S. 2017. Visualization and analysis of single-cell RNA-seq data by kernel-based similarity learning. Nat Methods 14: 414–416. [DOI] [PubMed] [Google Scholar]
- Zappia L, Phipson B, Oshlack A. 2017. Splatter: simulation of single-cell RNA sequencing data. Genome Biol 18: 174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeisel A, Muñoz-Manchado AB, Codeluppi S, Lönnerberg P, La Manno G, Juréus A, Marques S, Munguba H, He L, Betsholtz C, et al. 2015. Brain structure. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347: 1138–1142. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Chen K, Sloan SA, Bennett ML, Scholze AR, O'Keeffe S, Phatnani HP, Guarnieri P, Caneda C, Ruderisch N, et al. 2014. An RNA-sequencing transcriptome and splicing database of glia, neurons, and vascular cells of the cerebral cortex. J Neurosci 34: 11929–11947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng GXY, Terry JM, Belgrader P, Ryvkin P, Bent ZW, Wilson R, Ziraldo SB, Wheeler TD, McDermott GP, Zhu J, et al. 2017. Massively parallel digital transcriptional profiling of single cells. Nat Commun 8: 14049. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.