Detection and analysis of ancient segmental duplications in mammalian genomes

Abstract

Although segmental duplications (SDs) represent hotbeds for genomic rearrangements and emergence of new genes, there are still no easy-to-use tools for identifying SDs. Moreover, while most previous studies focused on recently emerged SDs, detection of ancient SDs remains an open problem. We developed an SDquest algorithm for SD finding and applied it to analyzing SDs in human, gorilla, and mouse genomes. Our results demonstrate that previous studies missed many SDs in these genomes and show that SDs account for at least 6.05% of the human genome (version hg19), a 17% increase as compared to the previous estimate. Moreover, SDquest classified 6.42% of the latest GRCh38 version of the human genome as SDs, a large increase as compared to previous studies. We thus propose to re-evaluate evolution of SDs based on their accurate representation across multiple genomes. Toward this goal, we analyzed the complex mosaic structure of SDs and decomposed mosaic SDs into elementary SDs, a prerequisite for follow-up evolutionary analysis. We also introduced the concept of the breakpoint graph of mosaic SDs that revealed SD hotspots and suggested that some SDs may have originated from circular extrachromosomal DNA (ecDNA), not unlike ecDNA that contributes to accelerated evolution in cancer.

Segmental duplications (SDs) are defined as long and similar sequences appearing in multiple locations in a genome (International Human Genome Sequencing Consortium 2001). Since SDs have contributed to the divergence between humans, apes, and Old World monkeys (Edelmann et al. 2001; Stankiewicz et al. 2001; Armengol et al. 2003; Bailey et al. 2004), studies of SDs are important for understanding primate evolution. SDs are hotbeds for genomic rearrangements followed by gene innovation and rapid adaptation (Zhang et al. 1998; Han et al. 2009; Marques-Bonet et al. 2009). Variations in SDs have been linked to various genetic diseases, including hemophilia A, Smith-Magenis syndrome, Angelman syndrome, and many others (Lupski 1998; Stankiewicz and Lupski 2002; Sharp et al. 2006).

SDs are often organized into complex mosaic structures (Jiang et al. 2007) that account for 5.15% of the human genome (SDs longer than 5 kb account for 3.50% of the human genome) (Bailey et al. 2002; Cheung et al. 2003). Although various studies revealed that the human genome has undergone tens of thousands of SDs during the last 35 million years (Hattori et al. 2000; International Human Genome Sequencing Consortium 2001; Bailey et al. 2002; Samonte and Eichler 2002; Cheung et al. 2003; Hillier et al. 2003), little is known about more ancient SDs and their contribution to evolution of the human genome. Also, while the existing estimates suggest that the human genome has the largest fraction of SDs among the sequenced primate genomes (Bailey et al. 2001; International Human Genome Sequencing Consortium 2001; She et al. 2008), it remains unclear whether it is simply a reflection of the fact that the draft human genome is more accurate than drafts of other mammalian genomes (existing assembly tools often collapse highly similar SDs).

The initial studies of SDs were focused on active SDs (Bailey et al. 2001) that can cause nonallelic homologous recombination (Antonacci et al. 2014). As a result, the originally introduced operational definition of SDs as long (≥1000 bp) and similar (at least 90% identity) sequences used somewhat strict parameters and had limitations with respect to answering the evolutionary question of finding all SDs in the human genome. For example, finding SDs with 70% identity would provide insights into the evolutionary process shaping the human genome beyond the current 35- million-year limit that previous methods analyzed. Although it is unlikely that the SDs started to populate the human genome just 35 million years ago, the extent of more ancient SDs in the human genome remains unknown. It is also unclear whether the previous methods identified all SDs under the current operational definition since no easy-to-use SD detection tools are available.

The 90% threshold for sequence identity in SDs was introduced because the existing algorithms for SD detection become rather time-consuming during the search for more diverged SDs (Bailey et al. 2002). We describe a new SDquest approach for finding SDs and use it to reveal previously unknown ancient SDs in the human genome, including many SDs that are only 70%–80% similar. SDquest decomposes mosaic SDs into elementary SDs that are more amenable to evolutionary analysis. It further constructs the breakpoint graph of mosaic SDs that reveal SD hotspots in the human genome.

Methods

Most studies of SDs were based on the BLAST-based whole-genome assembly comparison (Bailey et al. 2001; Bailey and Eichler 2006). An alternative whole-genome shotgun sequence detection approach (Bailey et al. 2002) uses raw reads instead of assembled genomes and identifies SDs based on their coverage by reads to identify SDs missing from the reference genome. SDquest uses a different approach based on analyzing repeated k-mers in a genome.

A k-mer is defined as a string of length k, and its position in a genome is defined as the position of its first character. The frequency of a k-mer in a genome is defined as the number of times it appears in the genome (considering both strands). A k-mer is repetitive if it appears multiple times in a genome, and nonrepetitive otherwise. SDquest uses the k-mer counting tool DSK (Rizk et al. 2013) to compute k-mer frequencies and find repetitive k-mers in a genome.

If duplicated regions in a genome were not subjected to mutations, all k-mers in these regions would be repetitive. In reality, mutations typically reduce the number of repetitive k-mers in duplicated regions and may even completely deplete these regions from repetitive k-mers. However, after masking common repeats in a genome, for a properly selected value of k (that reflects the level of divergence between SDs), repetitive k-mers are expected to appear more frequently in SDs than in non-SDs (regions outside SDs). SDquest uses the density of repetitive k-mers in a genomic segment as a proxy for deciding whether this segment is SD or non-SD (subject to a further verification step to compute the percent identity between such segments).

Below, we outline various steps of SDquest using the “hg19” assembly of the human genome from the UCSC Genome Browser (https://genome.ucsc.edu/; Kent et al. 2003). We used annotations of known SDs from the Segmental Duplications Database (http://humanparalogy.gs.washington.edu/) referred to as SD database below (She et al. 2004).

1. Removing common repeats from the genome. Similar to previous studies (Bailey et al. 2001), SDquest first uses RepeatMasker (Tarailo-Graovac and Chen 2009) to identify all common repeats and removes them from the genome. SDquest also removes all tandem repeats found by the Tandem repeats finder (Benson 1999), resulting in a compact genome. Removal of common repeats and tandem repeats makes it easier to reveal SDs and to distinguish them from spurious aggregates of common/tandem repeats. The size of the compact human genome is ∼1.4 Gb. Known SDs account for 5.44% of the compact human genome.

2. Identifying positions of all repetitive k-mers. SDquest uses DSK (Rizk et al. 2013) to identify all repetitive k-mers in the compact genome and further checks whether a k-mer at each position in the compact genome is repetitive. To ensure that the vast majority of k-mers in the compact genome are nonrepetitive, the parameter k is selected in such a way that the length of the compact genome is much smaller than the total number of k-mers equal to 4^k. SDquest sets k = 25 for analyzing the human genome and reveals 19,209,670 distinct repetitive 25-mers with total frequency 53,499,395. Even though known SDs only account for 5.44% of the compact human genome, they contain 90% of repetitive 25-mers. Supplemental Table S1 presents the distribution of frequencies of repetitive 25-mers in the compact human genome and known SDs and reveals 5,417,611 repetitive 25-mers in the compact human genome that are located outside of known SDs. Below, we show that many of these 25-mers reveal previously unknown SDs.

3. Identifying putative SDs. SDquest relies on the assumption that repetitive k-mers are more common in SDs than in non-SDs and assumes that there is at least one repetitive k-mer appearing in each d-nucleotide (nt) window within an SD (the default value d = 500 bp). Two repetitive k-mers are called d-paired if they appear within distance d from each other in the compact genome. A repetitive k-mer is called an orphan if there are no other repetitive k-mers within distance d from this k-mer. It turned out that 99% of repetitive 25-mers in the compact human genome are d-paired for the default value of d. Moreover, for the remaining 1% of orphan repetitive 25-mers, 99.9% of them (492,283 out of 492,721) are located outside of known SDs. Thus, the d-paired k-mers reveal the positions of SDs in the compact genome, and d = 500 offers a good trade-off for retaining repetitive k-mers in SDs and filtering orphan repetitive k-mers in non-SDs.

   SDquest identifies putative SDs in the genome as follows. It forms a graph on the set of all d-paired k-mers as vertices and connects two vertices by an edge if they are d-paired. Each connected component in the resulting graph corresponds to a putative SD with the span defined by the positions of its leftmost and rightmost d-paired k-mer. For d = 500, SDquest identifies 150,647 putative SDs in the compact human genome. These putative SDs contain 19,192,499 distinct repetitive k-mers with 53,443,537 occurrences in putative SDs.

4. Refining putative SDs. Putative SDs with the span below 500 bp are classified as short. While 86% of all putative SDs are short, they account for only 11% of the total length of putative SDs, and most of them are located outside of known SDs. To avoid false positives, SDquest refines the set of putative SDs based on the observation that the vast majority of putative SDs that fall outside known SDs are either short or have a lower density of repetitive 25-mers as compared to putative SDs that fall inside known SDs.

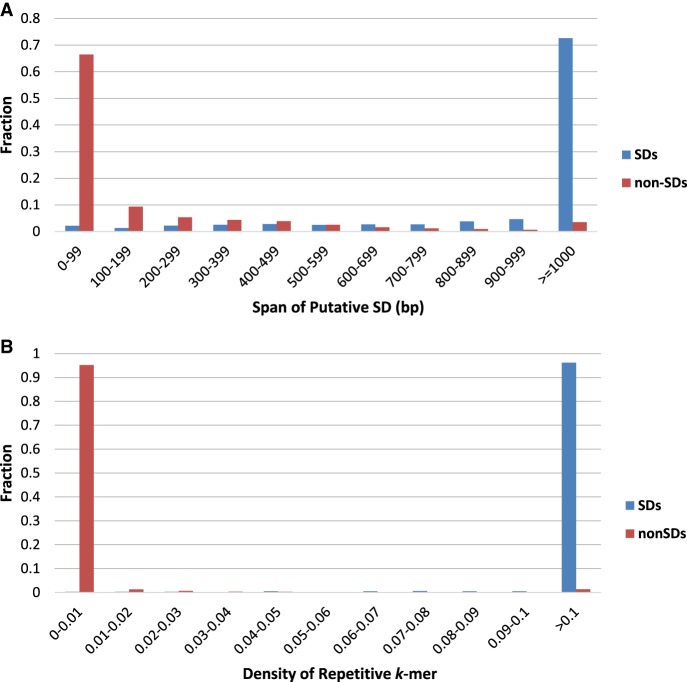
   Figure 1A presents the span distribution of putative SDs that are located in known SDs and non-SDs and illustrates that most putative SDs that fall outside known SDs are shorter than 100 bp, while most putative SDs that fall inside known SDs are longer than 1000 bp. By setting the length threshold on the span of putative SDs at 500 bp, SDquest filters out 129,096 putative SDs, resulting in only 150,647 − 129,096 = 21,551 putative SDs left for further consideration. Ninety-nine percent of filtered putative SDs (128,667 out of 129,096) are located outside of known SDs.

   We further compare the density distribution of repetitive k-mers in known SDs and non-SDs as follows. The density of repetitive k-mers in a segment of the compact human genome is defined as the ratio of the number of the repetitive k-mers to the length of the segment. In the compact human genome, we randomly sampled 1000 segments of length 500 bp from known SDs and non-SDs, respectively, and computed densities of repetitive k-mers in these 2000 segments. Figure 1B shows that the densities of repetitive 25-mers for most segments in non-SDs are below 0.01, while the densities of repetitive 25-mers for most segments in known SDs are larger than 0.1. SDquest thus sets the density threshold of putative SDs at 0.01 to maximize the sensitivity of searches for new SDs. At this step, SDquest filtered out 1542 putative SDs resulting in 21,551 − 1542 = 20,009 putative SDs left for further verification, which account for 6.85% (96.8 Mb) of the compact human genome.

   Each choice of the length and density thresholds (as well as parameters k and d) results in some false positive and false negative SDs. Although the false positive SDs are verified and filtered at the next step of SDquest, the extent of false negative SDs remains unknown, particularly since the length and density thresholds were selected based on analyzing the set of known SDs (rather than the set of true SDs). Thus, although SDquest revealed many previously unknown SDs, the set of true SDs in the human genome remains unknown.

5. Verifying putative SDs. Putative SDs are derived by checking whether they contain a sufficient number of d-paired k-mers but without checking what is the sequence identity and the exact endpoints of the corresponding alignments. To validate the putative SDs, SDquest performs an all-against-all comparison of putative SDs using the local alignment search tool LASTZ (Harris 2007). After this step, SDquest selected 130,405 pairwise alignments with at least 70% identity and at least 500-bp length. Although some of these pairwise alignments with high percent identity may be caused by misassemblies (Kelley and Salzberg 2010), recent finishing efforts minimized the number of misassemblies in the human genome sequence. Supplemental Figure S1 presents the distribution of the percent identity in the found pairwise alignments.

6. Refining SD boundaries. Similar to previous studies (Bailey et al. 2001), SDquest reinserts common repeats back into the pairwise alignments constructed in the previous step and refines the alignment boundaries. The boundaries of pairwise alignments constructed in the previous step may be inaccurate because (1) the SD spans defined by repetitive k-mers are typically smaller than the spans defined by the pairwise alignments, and (2) reinsertion of common repeats may artificially inflate spans when the LASTZ alignment slightly extends the span of a real SD. The approach for refining SD boundaries is described in the Supplemental Methods section, “Algorithm for refining SD boundaries.”

7. Revealing mosaic SDs. Each pairwise alignment found at the previous step reveals a pair of similar segments in the genome but does not reveal mosaic structure of SDs (Jiang et al. 2007). Pevzner et al. (2004) described how to transform a set of pairwise alignments into the A-Bruijn graph that reveals the mosaic structure of repeats within a genome. Below, we use a similar approach for revealing mosaic SDs (cf. Jiang et al. 2007).

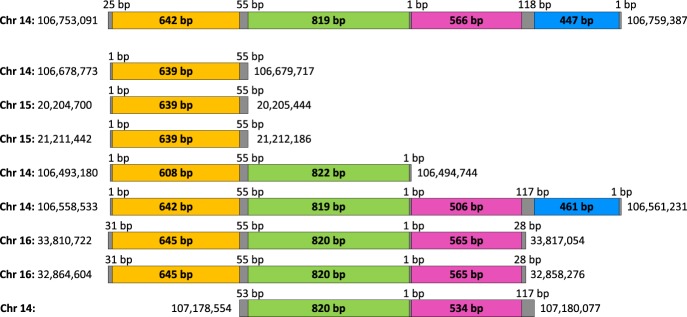
   To aggregate the found pairwise alignments into mosaic SDs, we consider intervals of all pairwise alignments in the genome (each alignment is represented by a pair of intervals) and iteratively aggregate these intervals into mosaic SDs (Fig. 2). Two intervals are combined into a single mosaic SD if they either overlap or if the distance between their endpoints does not exceed a parameter distance (the default value distance = 0). We found 16,231 (15,259) mosaic SDs covering 93.72 Mb (93.75 Mb) in the compact human genome and 187.39 Mb (187.44 Mb) in the human genome for distance = 0 (distance = 200 bp). Since each mosaic SD may be formed by multiple pairwise alignments, we define the percent identity of a mosaic SD as the maximum percent identity among all these alignments.

8. Revealing elementary SDs. We further break each mosaic SD into elementary SDs as described below. Although our concept of an elementary SD is similar to the concept of a duplication subunit defined in Jiang et al. (2007), SDquest improves on the algorithm in Jiang et al. (2007) by clustering the endpoints of pairwise alignments to derive elementary SDs.

   We consider all endpoints of pairwise alignments contributing to a mosaic SD and cluster them using the single linkage, clustering by iteratively combining closely located endpoints (within distance 100 bp from each other) into a single cluster. Every two consecutive clusters in a mosaic SD define an elementary SD between the midpoints of these clusters (Fig. 2 shows a mosaic SD formed by eight pairwise alignments and consisting of four elementary SDs). The multiplicity of an elementary SD (defined by two consecutive clusters) is defined as the number of pairwise alignments contributing to this SD, i.e., the number of alignments with span covering points from both clusters. In the human genome, 16,231 mosaic SDs are composed from 71,439 elementary SDs. Supplemental Table S2 shows the distribution of multiplicities and lengths of these elementary SDs.

   For each mosaic SD, we define its complexity as the number of its elementary SDs and its multiplicity as the average multiplicity of elementary SDs in this mosaic SD. Supplemental Table S3 shows the distribution of multiplicities and complexities of human mosaic SDs.

9. Revealing SD-blocks. We define two elementary SDs as equivalent if there exists a pairwise alignment between them. We further construct a graph on the set of all elementary SDs as vertices and edges corresponding to equivalent SDs. Connected components in the constructed graph define SD-blocks and reveal 14,344 SD-blocks in the human genome. The multiplicity (the length) of an SD-block is defined as the number (the average length) of elementary SDs in its connected component. The chromosomal multiplicity of an SD-block is defined as the number of chromosomes containing elementary SDs in this SD-block. For example, eight pairwise alignments shown in Figure 2 result in four SD-blocks (yellow, green, pink, and blue) with multiplicities 8, 6, 5, and 2, chromosomal multiplicities 3, 2, 2, and 1, and lengths 637, 820, 547, and 454 bp, respectively. Supplemental Table S4 shows the distribution of multiplicities and lengths of all SD-blocks in the human genome. Supplemental Figure S2 presents information about chromosomal multiplicities.

10. Constructing the breakpoint graph of SDs. Mosaic SDs are often built from many SD-blocks originating from multiple chromosomes (Supplemental Fig. S2). Since the question of what evolutionary forces contributed to the mosaic SDs remains poorly understood, we define the breakpoint graph of SDs to reveal which SD-blocks “interacted” with each other by contributing to the same mosaic SDs. We use the term “breakpoint graph” (rather than the term A-Bruijn graph as in Pevzner et al. 2004 and Jiang et al. 2007) since, as shown in Lin et al. (2014), these two concepts are equivalent.

    Each duplication creates two breakpoints (at its endpoints) that contribute to the mosaic structure of SDs. In studies of genome rearrangements, dependencies between various breakpoints are captured by the breakpoint graph (Compeau and Pevzner 2015) that represents a footprint of the evolutionary history of genomic architectures. However, while breakpoint graphs represent the workhorse of genome rearrangement studies, it remains unclear how to construct an analog of the breakpoint graph for SDs and further apply it for analyzing the evolutionary history of SDs.

    We represent each mosaic SD formed by n consecutive SD-blocks as a path on n edges (each edge is labeled by the corresponding SD-block). Similar to the construction of the breakpoint graph for analyzing genome rearrangements (Compeau and Pevzner 2015), we glue all identically labeled edges in all resulting paths to generate the breakpoint graph of SDs. Different connected components in the resulting graph are formed by SD-blocks that did not interact with each other, implying that each connected component reflects its own evolutionary history. For example, nine SDs shown in Figure 2 result in a simple “path” component in the breakpoint graph formed by four consecutive edges. Large connected components represent interacting duplications and thus allow one to analyze “bursts” of SDs during evolution.

    The breakpoint graph of SDs for the human genome consists of 4002 connected components, and 2836 of them represent trivial SDs formed by a single SD-block. However, most of the 14,344 SD-blocks in the human genome are organized into 4002 − 2836 = 1166 connected components, with the number of SD-blocks varying from 2 to 5838 (75 of them contain more than 10 SD-blocks).

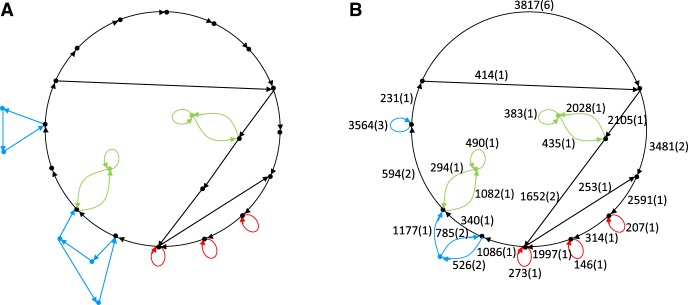
11. Constructing the contracted breakpoint graph of SDs. Figure 3A illustrates that the breakpoint graph has many nonbranching paths that resulted from fragmenting a single region of a genome by multiple SDs originating from this region. We thus contract each nonbranching path into a single edge called an SD-unit resulting in a contracted breakpoint graph (Fig. 3B). We define the length (complexity) of an SD-unit as the total length (number) of SD-blocks that contributed to this SD-unit. For example, four SD-blocks shown in Figure 2 result in a single SD-unit of length 2458 bp and complexity 4.

    There exist 8878 SD-units in the human genome (distributed over 4002 connected components), and 3599 of them form trivial connected components in the contracted breakpoint graph consisting of a single edge. The number of SD-units in the remaining 4002 − 3599 = 403 connected components varies from 2 to 3593 (24 connected components in the contracted breakpoint graph contain more than 10 SD-units). The largest connected component contains a vertex of degree 137, revealing a hotspot of SDs in the human genome. While the evolutionary forces that led to formation of this graph remain unknown, it is clear that the model of randomly occurring duplications cannot explain the complexity of SDs in the human genome. Supplemental Figure S3 presents an example of aggregation of SD-blocks into complex mosaic SDs resulting in a high degree vertex in the breakpoint graph.

    Supplemental Table S5 shows the distribution of multiplicities (maximal multiplicity among multiplicities of its SD-blocks) and lengths (total length of its SD-blocks) of all SD-units in the human genome. Two SD-units have very high multiplicities exceeding 200 (SD-unit of lengths 803 and 759 with multiplicities 262 and 232, respectively). It is not clear whether promiscuous SD-units (e.g., SD-units with multiplicities exceeding 200) should be reclassified as common repeats since their multiplicities are not significantly lower than the copy numbers of some repeat families in the human genome.

12. Analyzing cyclical components in the breakpoint graph of SDs.

Figure 1.

The distribution of the span (A) and density (B) of putative SDs in known SDs (blue) and non-SDs (red) in the hg19 assembly of the human genome.

Figure 2.

A mosaic SD on Chromosome 14 (spanning positions from 106,753,091 to 106,759,387) formed by eight pairwise alignments and containing four elementary SDs (“hg19” assembly of the human genome). The gray bars represent clusters formed by endpoints of pairwise alignments. Yellow, green, pink, and blue bars represent four elementary SDs in the mosaic SD shown on top. Eight segments below represent intervals aligned to the mosaic SD shown on top.

Figure 3.

Connected components of the breakpoint graph of SDs. (A) A connected component of the breakpoint graph of SDs in the hg19 assembly of the human genome formed by 38 SD-blocks. (B) The same connected component in the contracted breakpoint graph formed by 26 SD-units. Numbers on each edge show the length and complexity of the corresponding SD-unit. We colored edges of the graph to visualize the relationships between SD-blocks and SD-units.

Figure 3 presents a large connected component in the breakpoint graph of SDs and reveals a previously overlooked feature of SDs: Many connected components contain cycles. Out of 1166 nontrivial connected components, 169 contain cycles (70 of them contain cycles with more than two edges). To analyze each of such cyclical components, we remove all its edges that do not belong to cycles. As the result, a cyclical component may break into multiple connected components. We define the cyclic index of a component as the number of edges in the largest component after removal of all edges that do not belong to cycles; e.g., all the edges in the cyclical component in Figure 3A belong to cycles and thus no edges were removed; the cyclic index of Figure 3A is 38. Fifty-eight out of 169 cyclical components have a cycle index exceeding 3.

Since cycles in cyclical components are hard to explain by a series of independent duplications of linear chromosomal segments, we hypothesize that they are formed by one of the following scenarios:

• A cycle caused by a single mosaic SD with the same SD-block appearing multiple times is defined as a simple cycle. Ninety-one out of 169 cyclical components contain simple cycles (51 of them contain simple cycles with more than three edges). An example of a simple cycle is shown in Supplemental Figure S4.

• A cycle caused by an insertion of a segmental duplication inside another segmental duplication or by deleting consecutive SD-blocks from a segmental duplication. For example, mosaic SDs ABCD and AD (potentially caused by an insertion of BC inside AD or a deletion of BC from ABCD) consisting of four and two SD-blocks, respectively, result in a cycle BC in the breakpoint graph. We classify such a cycle as an indel cycle because, although there is an SD traversing this cycle from B to C, there is no SD traversing this cycle from C to B (see Supplemental Figure S5 for an example of an indel cycle). Seventy-four out of the remaining 169 − 91 = 78 cyclical components turned out to be indel components.

• A cycle caused by a series of duplications of circular extrachromosomal DNA (ecDNA), also known as amplisomes (Raphael and Pevzner 2004). Recent studies of cancer genomes (Turner et al. 2017) revealed that tumor cells often contain ecDNA that exchange genetic material with human chromosomes and contribute to accelerated evolution in cancer. Circular structure of the remaining 78 − 74 = 4 connected components in the breakpoint graph of human SDs suggests that a similar process may have contributed to accumulation of SDs in the human genome.

Results

We analyzed the SDs identified by SDquest in human, gorilla, and mouse genomes using the default parameters (k = 25, d = 500, length = 500, and density = 0.01). It turned out that SDquest is robust with respect to varying parameters.

Human SDs

SDquest identified 16,231 mosaic human SDs covering 6.05% (187.4 Mb) of the human genome, 50% of which represent common repeats (Supplemental Fig. S6 shows their length distribution). Table 1 shows the total length of SDs identified by SDquest with various sequence identity thresholds.

Table 1.

Total length of SDs in the human (version hg19) and mouse (version mm8) genomes identified by SDquest as compared to the total length of known SDs

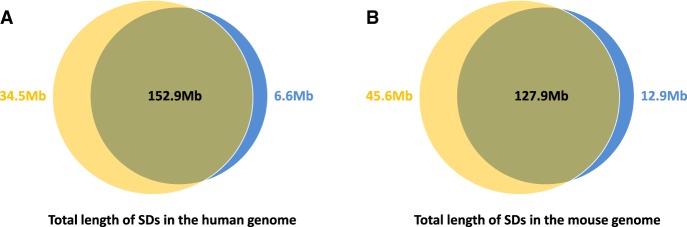
We compared SDs identified by SDquest with currently known SDs listed in the SD database. The known SDs cover 5.15% (159.5 Mb) of the human genome, of which SDquest identified 96% (152.9 Mb). Moreover, SDquest identified 34.5 Mb of novel SDs, among which 27.3 Mb are identified from 8628 previously unknown locations and the other 7.2 Mb are derived by extending known SDs. Figure 4A presents the comparison between the known SDs and SDs identified by SDquest. Many known SDs missed by SDquest (spanning only 159.5 − 152.9 = 6.6 Mb in the human genome) consist mainly of common repeats (e.g., Alu, LINE, etc.). Specifically, the fraction of common repeats in these SDs is 73% as compared to 51% in the remaining known SDs, suggesting that many known SDs may represent computational artifacts that we refer to as pseudo-SDs.

Figure 4.

The comparison between known SDs (shown in blue) and SDs identified by SDquest (shown in yellow) in the hg19 assembly of the human genome (A) and the mm8 assembly of the mouse genome (B).

We thus decided to analyze known SDs missed by SDquest in detail. This analysis revealed the following:

It turned out that 2982 pairs of known SDs have less than 500 bp of unique genomic sequence. As an example, Figure 5A presents a known SD on Chr 18 and Chr 4 that was missed by SDquest. However, since this SD contains only ∼300 bp of unique genomic sequence, it does not satisfy the length constraint that is usually imposed on SDs. It turned out that 1.4 Mb out of 6.6 Mb known SDs missed by SDquest are not supported by alignments with more than 500 bp of unique sequence and are classified as pseudo-SDs.

Figure 5.

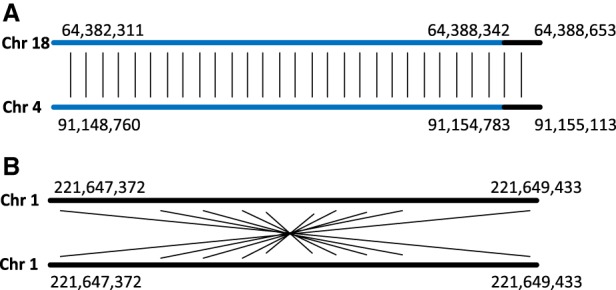
Known pseudo-SDs formed by common repeats and reverse palindromes in the hg19 assembly of the human genome. (A) A known SD starting at position 64,382,311 on Chromosome 18 (length 6343 bp) and at position 91,148,760 on Chromosome 4 (length 6353 bp) contains only ∼300 bp of unique genomic sequence (shown in black). This SD contains an L1PA3 repeat (shown in blue) from the L1 repeat family of length ∼6000 bp. (B) A known SD starting at position 221,647,372 on Chromosome 1 (length 2061 bp) represents a reverse palindrome.

Twenty-three pairs of known SDs are artifacts of self-alignments of reverse palindromes with some mutations. Figure 5B shows a known SD missed by SDquest, which is only supported by a self-alignment between its forward and backward strand. Besides, 717 pairs of known SDs represent self-overlapping alignments. In total, 1 Mb of known SDs missed by SDquest represent reverse palindromes or self-overlapping alignments that usually are not viewed as SDs. SDquest filters out reverse palindromes and self-overlapping alignments to avoid reporting pseudo-SDs as SDs.

A large fraction of the remaining 6.6 − 1.4 – 1 = 4.2 Mb of known SDs missed by SDquest reflect subtle differences in the definition of SD boundaries between SDquest and known SDs. Most of these pairwise SDs indicate large insertions or deletions of common repeats toward the end of the alignment, which are conservatively trimmed by SDquest but retained in known SDs. If we ignore the subtle differences in the definition of SD boundaries and remove pseudo-SDs from the set of known SDs, SDquest identifies 99.7% of known SDs.

Since there is no easy-to-use tool for SD identification, we treated the known mosaic SDs (7782 segments in the human genome from the SD database) as putative SDs obtained in Step (4) of SDquest and reanalyzed them using the remaining steps of the SDquest pipeline. The resulting “known SD statistics” in Table 1 illustrate that SDquest identifies many SDs absent in the SD database. Supplemental Figure S7A presents information about SDs identified by SDquest but missed in known SDs and known SDs missed by SDquest.

We also analyzed the latest GRCh38 version of the assembly of the human genome (Schneider et al. 2017) and the known SDs in this genome from the UCSC Genome Browser (https://genome.ucsc.edu/; Kent et al. 2003). We ignored alternative haplotypes in the GRCh38 assembly and only analyzed SDs on 22 autosomal chromosomes, the X Chromosome, and the Y Chromosome. The known SDs account for 5.38% (166.2 Mb) of the genome, among which 52.8% are common repeats. SDquest identified 95% (158.2 Mb) of the known SDs in the GRCh38 genome and 98% (76.6 Mb) of the known SDs in the compact genome. SDquest identified that 6.42% (198.3 Mb) of the GRCh38 genome represents SDs (51% of them are common repeats). These SDs are organized into 16,079 mosaic SDs, 73,259 elementary SDs, 14,467 SD-blocks, and 8837 SD-units.

Gorilla SDs

Currently, there is no publicly available SD database for the gorilla genome. We used SDquest to identify SDs in the “gorGor5” assembly of the gorilla genome (Gordon et al. 2016) from the UCSC Genome Browser (https://genome.ucsc. edu/; Kent et al. 2003).

Using the default parameters, SDquest identified 5.61% (173 Mb) of the gorilla genome as SDs, 50% (86.5 Mb) of which represent common repeats. These SDs are organized into 18,335 mosaic SDs in the gorilla genome (Supplemental Fig. S6 shows its length distribution), 69,703 elementary SDs, 15,395 SD-blocks, and 8921 SD-units. Supplemental Methods section, “Analysis of cyclic components in the breakpoint graph of SDs,” presents analysis of cyclic components in the breakpoint graph of gorilla SDs. Supplemental Table S6 presents the distribution of multiplicities and complexities of the mosaic SDs in the gorilla genome.

Each SD in the human-gorilla ancestor may either turn into a non-SD in either one or in both genomes (by retaining only one of its copies) or be present as an SD in both human and gorilla genomes. The latter case is interesting since it may represent evolutionary pressure on such SDs to retain copies over significant evolutionary time.

There exist 23,933,371 distinct 25-mers shared by the constructed human and gorilla SDs. These shared 25-mers point to ancestral SDs present in the human-gorilla ancestor but also contain many spurious 25-mers. We thus performed an all-against-all comparison between human SDs (the latest GRCh38 version) and gorilla SDs using LASTZ (Harris 2007) to find the ancestral SDs. It turned out that 68.6 Mb out of 198.3 Mb (35%) of SDs in the human genome do not have related SDs in the gorilla genome. These 68.6 Mb of SDs in the human genome represent SDs in the human genome that either emerged after the human-gorilla split ≈10 million years ago or the SDs in the human-gorilla ancestor that were lost in the gorilla genome but retained in the human genome.

The remaining 198.3 − 68.6 = 129.7 Mb SDs in human SDs with related SDs in the gorilla genome are composed from 65,851 elementary SDs in the human genome and 57,664 elementary SDs in the gorilla genome. These 65,851 + 57,664 = 123,515 elementary SDs are classified into 13,017 SD-blocks and 7703 SD-units. More information about SDs shared between human and gorilla SDs can be found in Supplemental Table S7. Ancestral human-mouse (gorilla-mouse) SDs are described in Supplemental Table S8 (Supplemental Table S9).

Mouse SDs

She et al. (2008) provided the coordinates of pairwise SDs and estimated that they account for 5.33% (140.8 Mb) of the “mm8” assembly of the mouse genome. We refer to these 140.8 Mb of SDs as “known mouse SDs” and compare them with mouse SDs identified by SDquest.

We analyzed the “mm8” assembly of the mouse genome from the UCSC Genome Browser (https://genome.ucsc.edu/; Kent et al. 2003). Using default parameters, SDquest identified 6.56% (173.5 Mb) of the genome as SDs, 53% of which represent common repeats. These mouse SDs are organized into 22,347 mosaic SDs (Supplemental Fig. S6 shows the length distribution), 86,308 elementary SDs, 15,108 SD-blocks, and 9340 SD-units. Supplemental Methods section, “Analysis of cyclic components in the breakpoint graph of SDs,” presents analysis of cyclic components in the breakpoint graph of mouse SDs. Supplemental Table S10 presents the distribution of multiplicities and complexities of mosaic SDs in the mouse genome. Table 1 shows the total length of SDs identified by SDquest in the mouse genome with various sequence identity thresholds.

Figure 4B presents a comparison between SDs identified by SDquest and known SDs in the mouse genome. SDquest identified 91% (127.9 Mb) of known SDs in the mouse genome and 96% (57.4 Mb) of known SDs in the compact mouse genome. Among the 140.8 − 127.9 = 12.9 Mb known SDs missed by SDquest, 83% represent aggregations of common repeats. However, in the remaining known SDs, only 55% are common repeats. Analysis of known SDs missed by SDquest shows similar results to the human genome and reveals a flaw in the previous analysis of pseudo-SDs formed by aggregation of common repeats. Supplemental Figure S7B presents information about SDs identified by SDquest but missed in known SDs and known SDs missed by SDquest.

We also analyzed the latest “mm10” assembly of the mouse genome and the known SDs in this genome from the UCSC Genome Browser (https://genome.ucsc.edu/; Kent et al. 2003). The known SDs account for 7.71% (210.2 Mb) of the mouse genome, among which 58.7% are common repeats. SDquest identified 97% (203.3 Mb) of the known SDs in the “mm10” assembly and 98% (85.2 Mb) of the known SDs in the compact genome. Additionally, SDquest identified many previously unknown SDs and estimated that 9.52% (259.5 Mb) of the mouse genome is formed by SDs, of which 56% are common repeats. This is a surprisingly large increase in the total SD length as compared to 6.56% (173.5 Mb) in the “mm8” assembly of the mouse genome.

We thus aligned all the SDs (259.5 Mb) identified in the “mm10” assembly of the mouse genome to the “mm8” assembly of the mouse genome using the LiftOver program from the UCSC Genome Browser (https://genome.ucsc.edu/; Kent et al. 2003); we found that 108.9 Mb of SDs failed to map to the “mm8” assembly of the mouse genome, suggesting that these SDs may represent newly assembled segments in the “mm10” assembly of the mouse genome that brought in BAC sequences that rescued additional SDs. There are 259.5 − 108.9 = 150.6 Mb left that align to the “mm8” assembly of the mouse genome. We also aligned the mouse SDs (173.5 Mb) identified in the “mm8” assembly of the mouse genome to the “mm10” assembly of the mouse genome and found that 5.6 Mb of them do not align to the “mm10” assembly. Those 5.6 Mb SDs may represent errors in the “mm8” assembly of the mouse genome that had been corrected in the “mm10” assembly of the mouse genome.

Discussion

We described a new algorithm for detecting SDs in large genomes and applied it to reveal many previously unknown ancient SDs in human, gorilla, and mouse genomes. Analysis of SDs found by SDquest revealed that previous attempts to characterize SDs in large genomes resulted in many false negatives (e.g., missing ancient SDs) and false positives (e.g., pseudo-SDs formed by aggregation of common repeats or diverged palindromes). We thus argue that it would be useful to run SDquest on all eukaryotic sequenced genomes to revise the list of known SDs and to re-evaluate evolution of SDs based on their more accurate representation across multiple genomes.

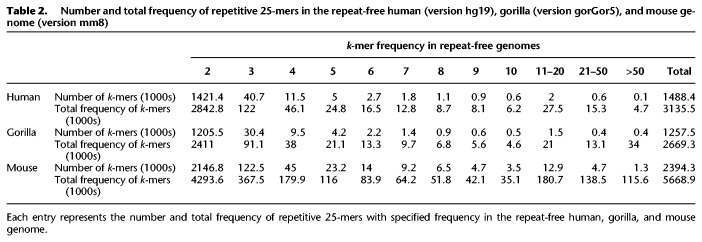
While SDquest significantly extended the set of known SDs in human and other genomes, there are undoubtedly many ancient SDs that still remain unknown. To estimate the extent of SDs that evaded SDquest, we formed repeat-free human, gorilla, and mouse genomes by removing all common repeats, tandem repeats, and SDs found by SDquest in these genomes. Table 2 demonstrates that there are many repetitive 25-mers in the resulting repeat-free genomes, suggesting that many ancient SDs (or common repeats) remain undetected.

Table 2.

Number and total frequency of repetitive 25-mers in the repeat-free human (version hg19), gorilla (version gorGor5), and mouse genome (version mm8)

SDquest revealed that SDs account for 6.05%, 5.61%, and 6.56% of human (build hg19 assembly), gorilla (build gorGor5 assembly), and mouse (build mm8 assembly) genomes, respectively. For the human genome, the fraction of common repeats in the entire genome (54%) is higher than the fraction of common repeats in SDs (50%). In contrast, for the mouse genome, the fraction of common repeats in the entire genome (44%) is lower than the fraction of common repeats in SDs (53%) (see Supplemental Table S11). The fraction of SDs significantly increased to 6.42% and 9.52% in the latest assemblies of the human (build GRCh38 assembly) and mouse (build mm10 assembly) genome, respectively. These results underscore the importance of improving the quality of the reference assemblies using a combination of short and long reads. Since SDs are implicated in most remaining gaps or misassemblies in the human genome (Chaisson et al. 2015), the recently released GRCh38 assembly of the human genome placed special emphasis on resolution of SDs (Schneider et al. 2017), thus leading to a more accurate view of SDs in the human genome. Supplemental Table S12 describes the running time and memory requirement of SDquest.

Software and data access

The SDquest software from this study is available on GitHub (https://github.com/SDquest/SDquest) and the source code of SDquest is also available as a zip file in Supplemental Materials. The coordinates of pairwise SDs and mosaic SDs for human (build GRCh38 and hg19 assembly), gorilla (build gorGor5 assembly), and mouse (build mm8 and mm10 assembly) genomes are also available in Supplemental Materials as well as on GitHub through the following links: pairwise SDs link, https://github.com/SDquest/SDquest/tree/master/Pairwise_SDs; and mosaic SDs link, https://github.com/SDquest/SDquest/tree/master/Mosaic_SDs.