Multidimensional Extension of Multiple Indicators Multiple Causes Models to Detect DIF

Abstract

A number of studies have found multiple indicators multiple causes (MIMIC) models to be an effective tool in detecting uniform differential item functioning (DIF) for individual items and item bundles. A recently developed MIMIC-interaction model is capable of detecting both uniform and nonuniform DIF in the unidimensional item response theory (IRT) framework. The goal of the current study is to extend the MIMIC-interaction model for detecting DIF in the context of multidimensional IRT modelling and examine the performance of the multidimensional MIMIC-interaction model under various simulation conditions with respect to Type I error and power rates. Simulation conditions include DIF pattern and magnitude, test length, correlation between latent traits, sample size, and latent mean differences between focal and reference groups. The results of this study indicate that power rates of the multidimensional MIMIC-interaction model under uniform DIF conditions were higher than those of nonuniform DIF conditions. When anchor item length and sample size increased, power for detecting DIF increased. Also, the equal latent mean condition tended to produce higher power rates than the different mean condition. Although the multidimensional MIMIC-interaction model was found to be a reasonably useful tool for identifying uniform DIF, the performance of the model in detecting nonuniform DIF appeared to be questionable.

Research on item bias and test fairness continues to advance in both applications and methodologies. Numerous methods have been developed for identifying differential item functioning (DIF) in test items. There is an increasing interest in the multiple indicators multiple causes model (MIMIC; Jöreskog & Goldberger, 1975) for assessing test fairness and measurement invariance properties of assessments, which has resulted in various applications of the MIMIC model to detecting DIF. The MIMIC model, which integrates causal indicators (i.e., covariates) with confirmatory factor analysis, can be easily transformed into a common item response theory (IRT) model (e.g., two-parameter IRT model) with regard to the model parameters (e.g., MacIntosh & Hashim, 2003; B. O. Muthén, Kao, & Burstein, 1991). The MIMIC model uses a single-group structural equation model with covariates; the unique feature of the MIMIC model is that it predicts a latent variable even when there is one observed variable, causal indicator (Woods, 2009; Woods & Grimm, 2011). B. O. Muthén (1988) also observed that the MIMIC model allows not only for detecting DIF but also for investigating a more comprehensive relationship between background variables and the latent trait.

There are two types of DIF that can arise in test items, depending on the direction of bias across the groups. In uniform DIF, the focal group consistently underperforms or outperforms the reference group, regardless of where individuals are located on the latent trait continuum. Previous studies on the MIMIC model have focused on significance tests for identifying uniform DIF because the parameterization of the MIMIC model was only suitable for detecting uniform DIF (e.g., Cheng, Shao, & Lathrop, 2016; Finch, 2005, 2012; Jin, Myers, Ahn, & Penfield, 2012; Shih & Wang, 2009; Wang & Shih, 2010; Wang, Shih, & Yang, 2009). The second type of DIF, known as nonuniform DIF, occurs when the direction of bias changes between the focal and reference groups along the latent trait continuum. Recently, Woods and Grimm (2011) established a parameterization of nonuniform DIF within the MIMIC model by including an interaction term between the latent trait and the categorical group variable. This model is referred to as the MIMIC-interaction model hereafter. Woods and Grimm evaluated the performance of the MIMIC-interaction model in detecting uniform and nonuniform DIF simultaneously within the same model. Based on their simulation results, the MIMIC-interaction model showed greater power than the typical MIMIC model without the interaction term in detecting nonuniform DIF. However, Type I error rates were inflated for the MIMIC-interaction model due to the violation of the assumption that the variables used for estimating the latent interaction are normally distributed.

To date, a number of studies have discussed the capabilities and benefits of the MIMIC model in detecting uniform and nonuniform DIF in the context of unidimensional test structures where there is a single latent trait that underlies either dichotomously or polytomously scored items (e.g., Finch, 2005, 2012; Jin et al., 2012; Kim, Yoon, & Lee, 2012; Wang et al., 2009; Wang & Shih, 2010; Wang & Yeh, 2003; Woods, 2009; Woods & Grimm, 2011). Recently, Cheng et al. (2016) proposed a multidimensional form of the MIMIC model by including external variables that may completely or partially mediate the DIF effect. However, this model also assumes a unidimensional test structure where items are designed to measure a single latent trait. A mediator, which can be either a manifest or latent variable, is incorporated into the model as an additional dimension to understand the relationship between a categorical covariate (e.g., gender) and the flagged DIF items.

This study aims to expand the MIMIC framework to testing DIF in several different aspects of the IRT framework. First, a multidimensional form of Woods and Grimm’s (2011) MIMIC-interaction model is introduced for testing both uniform and nonuniform DIF simultaneously in multidimensional test items for the first time. Second, because previous MIMIC studies have not considered multidimensional test structures, the performance of MIMIC in detecting DIF in nonsimple test structures is still unknown. In this study, the multidimensional MIMIC-interaction model is used to investigate DIF in both simple test structures in which each item measures a single latent trait and nonsimple test structures in which items can be associated with multiple latent traits. Finally, the performance of the multidimensional MIMIC-interaction model is examined under most practical conditions, such as various sample sizes of the focal and reference groups under both balanced and unbalanced designs and mean difference in the underlying latent trait conditions via a Monte Carlo simulation study. The following section provides the details of the multidimensional MIMIC-interaction model for detecting uniform and nonuniform DIF in multidimensional test structures.

MIMIC Models for Detecting DIF

Structural equation modeling (SEM) with latent variables provides a flexible way to test measurement invariance because it allows the use of continuous or discrete, and observed or latent covariates as a grouping variable (Barendse, Oort, Werner, Ligtvoet, & Schermelleh-Engel, 2012; Jak, Oort, & Dolan, 2010). Since Jöreskog and Goldberger (1975) introduced MIMIC models in the context of SEM, these models have been used in practice for identifying the presence of DIF for various types of items (e.g., Gallo, Anthony, & Muthén, 1994). For dichotomous items, testing for DIF using the MIMIC model is applied with a latent response variable formulation (B. O. Muthén & Asparouhov, 2002):

$$y_i=\left\{\begin{array}{c}\hfill 1,\mathrm{if}{y}_i^{*}\ge {\tau }_i\hfill \\ \multicolumn{1}{c}{0,\mathrm{if}{y}_i^{*}<{\tau }_i}\end{array}\right\},$$

where $y_i^{*}$ is the continuous latent response variable that underlies a dichotomous response variable ($y_i$), and the threshold parameter is denoted as ${\tau }_i.$ Based on the continuous latent response variable $y_i^{*},$ Equation 2 demonstrates Woods and Grimm’s (2011) MIMIC-interaction model that is capable of testing uniform and nonuniform DIF simultaneously in a dichotomous item:

$$y_i^{*}={\lambda }_i\theta +{\beta }_{i}z+{\omega }_i\theta z+{\epsilon }_i,$$

where ${\lambda }_i$ is the factor loading of item i on the latent variable $\mathrm{\theta },$${\mathrm{\beta }}_i$ indicates the uniform DIF effect or direct effect (when ${\beta }_i\ne 0$) showing the group difference in the threshold parameter after controlling for any mean ability difference on $\mathrm{\theta }$ between groups, $z$ is the categorical covariate (z = 0 for the reference group and z = 1 for the focal group), ${\omega }_i$ is the interaction term between the latent trait and the categorical covariate (i.e., group variable) that represents the nonuniform DIF effect (when ${\omega }_i\ne 0)$, and ${\epsilon }_i$ is the error term that is normally distributed and independent of θ and z. Note that the DIF detection in the MIMIC-interaction model is very similar to the DIF detection in the logistic regression approach by Swaminathan and Rogers (1990). Both approaches test the difference in the probability of answering a dichotomous item correctly due to group membership and the interaction between the group membership and the latent trait, after controlling for group differences in the latent trait.

Equation 3 demonstrates the multidimensional extension of the MIMIC-interaction model for a multidimensional test item that measures k latent traits:

$$y_i^{*}={\lambda }_{1i}{\theta }_1+\cdots +{\lambda }_{\mathrm{ki}}{\theta }_k+{\beta }_{i}z+{\omega }_{1i}{\theta }_{1}z+\cdots +{\omega }_{\mathrm{ki}}{\theta }_{k}z+{\epsilon }_i,$$

where ${\lambda }_{1i}$ through ${\lambda }_{\mathrm{ki}}$ are factor loadings linking item i to the latent traits ${\theta }_1$ through ${\theta }_k$, ${\omega }_{1i}$ through ${\omega }_{\mathrm{ki}}$ are the interaction terms that represent nonuniform DIF effects for item i, and the remaining terms are the same as those from Equation 2. Figure 1 displays a two-dimensional MIMIC-interaction model.

Figure 1.

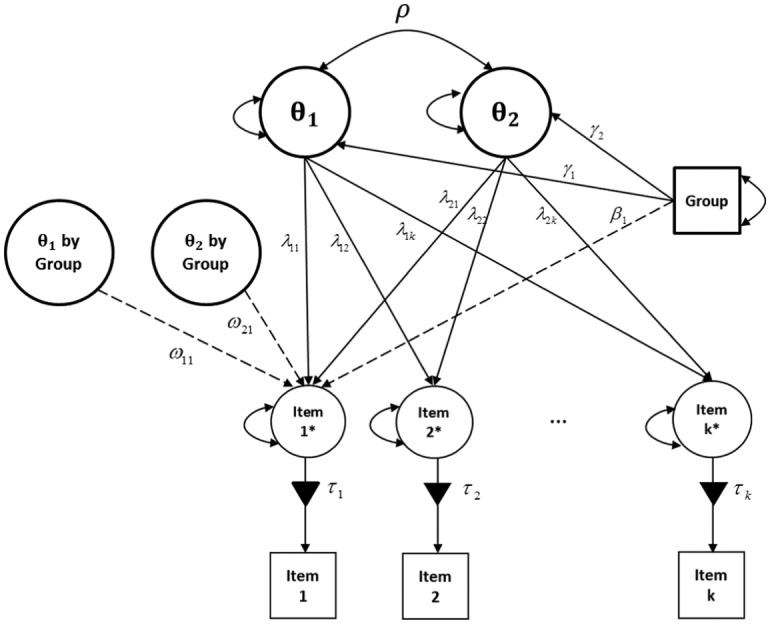
A MIMIC-interaction model for testing uniform and nonuniform DIF with the interaction between the group and the latent variables.

Note. Items $i=1,2,\dots ,k$; ρ = correlation between θ₁ and θ₂; γ_i = latent mean difference between the groups; λ_1i and λ_2i = factor loadings; τ_i = thresholds; β_i = uniform DIF effect; ω_1i and ω_2i = nonuniform DIF effects.

MIMIC models with one latent variable can be parameterized as unidimensional IRT models (for more details, see B. O. Muthén et al., 1991, and MacIntosh & Hashim, 2003). In the same vein, the multidimensional extension of the MIMIC-interaction model in Equation 3 can be presented as a multidimensional IRT (MIRT) model. For instance, the compensatory multidimensional extension of the 2PL (M-2PL; Reckase, 1985) model for k latent traits takes the following form in the conventional IRT notation:

$$P(U_{\mathrm{ij}}=1|{\mathbf{\theta }}_{\mathbf{j}},{\mathbf{a}}_i,d_i)=\frac{e^{{\mathit{a}}_{\mathit{i}}{\mathbf{\theta }}_{\mathit{j}}\mathbf{\prime }\mathbf{+}{\mathbf{d}}_{\mathbf{i}}}}{1+e^{a_i{\mathbf{\theta }}_{\mathbf{j}}\mathbf{\prime }\mathbf{+}{\mathbf{d}}_{\mathbf{i}}}},$$

where ${\mathbf{\theta }}_{\mathbf{j}}$ is a vector of abilities for person j on k latent traits (${\mathbf{\theta }}_{\mathbf{j}}={\theta }_{1j},\dots ,{\theta }_{\mathrm{kj}}$), ${\mathbf{a}}_{\mathbf{i}}$ is a vector of discrimination parameters for item i (${\mathbf{a}}_i=a_{1i},\dots ,a_{\mathrm{ki}}$), and d_i is the item intercept parameter related to the difficulty for item i. Discrimination parameters, $a_{1i}$ through $a_{\mathrm{ki}},$ in the MIRT model from Equation 4 can be calculated using the values of ${\lambda }_{1i}$ through ${\lambda }_{\mathrm{ki}}$ derived from the multidimensional MIMIC-interaction model in Equation 3 as

$$a_{1i}=\frac{{\lambda }_{1i}}{\sqrt{(1-{\lambda }_{1i}^2)\sqrt{{\sigma }_{{\theta }_1}}}}\mathrm{through}{a}_{\mathrm{ki}}=\frac{{\lambda }_{\mathrm{ki}}}{\sqrt{(1-{\lambda }_{\mathrm{ki}}^2)\sqrt{{\sigma }_{{\theta }_k}}}},$$

where ${\sigma }_{{\theta }_1}$ through ${\sigma }_{{\theta }_k}$ are the variances for the k latent variables. The item intercept parameter in the MIRT model (d_i) can be calculated using both λ and τ from the multidimensional MIMIC-interaction model in Equation 3:

$$d_i=\frac{[({\tau }_i-{\beta }_{i}z){\lambda }_{1i}^{-1}-{\mu }_{{\theta }_1}]+\cdots +[({\tau }_i-{\beta }_{i}z){\lambda }_{\mathrm{ki}}^{-1}-{\mu }_{{\theta }_k}]}{\frac{1}{\sqrt{{\sigma }_{{\theta }_1}}}+\cdots +\frac{1}{\sqrt{{\sigma }_{{\theta }_k}}}},$$

where ${\mu }_{{\theta }_1}$ through ${\mu }_{{\theta }_k}$ are the means of the latent variables ${\theta }_1$ through ${\theta }_k$. Equations 5 and 6 can be simplified when the latent variables are standardized (i.e., ${\mu }_{{\theta }_1}=\cdots ={\mu }_{{\theta }_k}=0$ and ${\sigma }_{{\theta }_1}=\cdots ={\sigma }_{{\theta }_k}=1$). In the simplified model, ${\beta }_i({\lambda }_{1i}^{-1}+\cdots +{\lambda }_{\mathrm{ki}}^{-1})$ becomes the effect size for uniform DIF.

According to Woods and Grimm (2011), computations in the MIMIC-interaction model are complicated because the latent variable cannot be simply multiplied by the group variable as is done with manifest variables. In the literature, there are various methods to compute nonlinear interactions of latent variables with categorical covariates, such as product indicator approaches and distribution-analytic approaches (Klein & Muthén, 2007; Moosbrugger, Schermelleh-Engel, Kelava, & Klein, 2009; Schermelleh-Engel, Werner, Klein, & Moosbrugger, 2010). However, the multivariate normality assumption is likely to be violated in the interaction between latent variables and categorical observed covariates, which may cause estimation problems for the maximum likelihood estimator (Barendse et al., 2012; Woods & Grimm, 2011). The present study applies a convenient estimation option for the MIMIC model using the “XWITH” command in Mplus (L. K. Muthén & Muthén, 1998-2015). The XWITH command estimates the interaction between continuous latent variables and categorical covariates using the latent moderated structural equations (LMS) method (Klein & Moosbrugger, 2000). The LMS method implements full-information maximum-likelihood estimation for analyzing nonnormally distributed interaction effects between a latent variable and an observed categorical variable (Klein & Moosbrugger, 2000). This method eliminates the nonnormality problem by conditioning on the latent variable and treating the distribution of the observed categorical variable as a mixture of multiple conditional distributions (Barendse et al., 2012).

The multidimensional MIMIC-interaction model described in this study has some constraints to ensure model identification. In case of a two-dimensional MIMIC-interaction model, both latent variables are constrained to have means of 0 and variances of 1, but the correlation between the two latent variables can be freely estimated. The other important assumptions of the MIMIC-interaction model are the local independence of items, independent observations, independent groups, and a logistic function to define the probability of obtaining a correct response. Similar constraints and assumptions were also used in Woods and Grimm’s (2011) MIMIC-interaction model.

Method

Simulation Design

The simulation design in this study included the following five conditions: (a) DIF type (non-DIF, uniform DIF, and nonuniform DIF), (b) test length (12 items with 2 DIF items, 14 items with 4 DIF items, and 24 items with 4 DIF items), (c) magnitude of DIF parameters (low and medium), (d) sample size differences for the reference group (R) and the focal group (F) (R500/F100, R1000/F200, R1500/F500, and R1000/F1000), (e) correlation between the two latent traits ($\rho =0,0.3,\mathrm{or}0.5$) for both groups, and (f) the latent trait means for the reference group and the focal group $({\mu }_{\mathrm{R}}={\mu }_{\mathrm{F}}=0$ or ${\mathrm{\mu }}_{\mathrm{R}}=0,{\mathrm{\mu }}_{\mathrm{F}}=-0.5)$. All simulation conditions were fully crossed except for the latent trait mean difference condition $({\mathrm{\mu }}_{\mathrm{R}}=0,{\mathrm{\mu }}_{\mathrm{F}}=-0.5)$, which was examined only using two sample sizes (R1500/F500 and R1000/F1000), two correlations $(\mathrm{\rho }=0\mathrm{and}0.5)$, and two test lengths (14-item and 24-item). For each simulation condition, 100 replications were generated in R (R Core Team, 2015). Details on the simulation conditions and data generation are provided in the following sections.

Data Generation

The current study was conducted with two-dimensional dichotomous data. The data were generated using the M-2PL model shown in Equation 4. Two latent traits, ${\theta }_{1j}$ and ${\theta }_{2j}$, were drawn from a bivariate normal distribution with means and variances of 0 and 1, respectively.

DIF Pattern and DIF Magnitude

Multidimensional dichotomous item response data were simulated for three item sets: 12 items, 14 items, and 24 items. For the 12-item test and the 14-item test, 10 anchor items were used, and for the 24-item test, 20 anchor items were used. Anchor item parameters for the three tests (see Table 1) were chosen to emulate the values used in a previous analysis (see Reckase, 2009, p. 204) and were used to generate anchor item responses for both reference and focal groups. Regarding the number of test items, two test lengths (12 and 24 items) were chosen to be similar to the part of Woods and Grimm’s study (2011), in which 6, 12, and 24 test items were used. Fourteen items with 4 DIF items were chosen to examine the effect of shorter anchor items on DIF detection compared to 24 items with 4 DIF items. A short test length such as 10 items appears often especially in psychological inventories (e.g., Ware & Sherbourne, 1992). A short test length of 10, 20, and 30 items can be also found in Wang and Shih’s (2010) simulation study.

Table 1.

Anchor Item Parameter Values Used in the Two-Dimensional M-2PL Model for Non-DIF items.

Item	a 1	a 2	d
12-Item and 14-item tests
1	1.04	0.00	−0.09
2	1.17	0.02	−0.23
3	0.98	0.02	−0.12
4	0.09	1.03	0.09
5	0.00	0.96	0.90
6	0.06	1.00	−0.88
7	0.80	0.76	0.01
8	0.73	0.68	−0.18
9	0.82	0.68	−0.16
10	0.64	0.72	0.04
Mean	0.61	0.61	−0.06
SD	0.43	0.42	0.43
24-Item test
1	1.04	0.00	−0.09
2	0.88	0.13	0.27
3	1.17	0.02	−0.23
4	0.97	0.19	−0.22
5	0.98	0.02	−0.12
6	0.92	0.08	−0.77
7	0.09	1.03	0.09
8	0.00	0.96	0.90
9	0.04	0.97	−0.58
10	0.06	1.00	−0.88
11	0.15	1.13	1.15
12	0.14	0.95	−0.38
13	0.74	0.75	0.29
14	0.70	0.73	−0.91
15	0.71	0.72	−0.47
16	0.80	0.76	0.01
17	0.69	0.69	0.10
18	0.73	0.68	−0.18
19	0.67	0.63	−0.33
20	0.64	0.72	0.04
Mean	0.61	0.61	−0.12
SD	0.38	0.38	0.52

A nonsimple (i.e., complex) test structure in which test items were associated with both of the latent traits was considered in this study because few studies have considered nonsimple test structures in the multidimensional DIF literature. The anchor items used in the present study were selected to form three clusters of loading patterns. For example, for the 10 anchor items, the first three items were dominantly loaded on the first latent trait, θ₁, the second three items were dominantly loaded on the second latent trait, θ₂, and the last four items were loaded almost equally on both latent traits, θ₁ and θ₂. For the 20 anchor items, the number of items for each cluster was doubled. Using the anchor items and DIF items, three types of data sets were generated: (a) non-DIF condition, (b) uniform DIF condition, and (c) nonuniform DIF condition. For the structural brevity, items that were tested for DIF were placed to the end of the test (Items 11 and 12 for the 12-item test, Items 11-14 for the 14-item test, and Items 21-24 for the 24-item test).

Table 2 shows item parameters used to generate the DIF items. The non-DIF conditions were generated by using the parameters of the reference group for both groups. For simulating the uniform and nonuniform DIF conditions, various DIF item patterns were selected for each test length condition. Two DIF items were simulated for the 12-item test and four DIF items were simulated for the 14-item and 24-item tests: (a) 2 (or 4) uniform DIF items (d-DIF only; hereafter, this condition is referred to as “U-A”), (b) 2 (or 4) nonuniform DIF items ($a_2$-DIF with and without d-DIF; hereafter, this condition is referred to as “N-B”), and (c) 2 (or 4) nonuniform (both a₁- and a₁-DIF with and without d-DIF; hereafter, this condition is referred to as “N-C”). For each of the three types of DIF, two levels of DIF magnitude were introduced: low and medium levels, yielding six DIF conditions in total.

Table 2.

Item Parameters Used in the Generating DIF Conditions for the Last Two or Four Items.

						Focal group
			Reference group			Low DIF			Medium DIF
Condition	Test length	Item	a 1	a 2	d	a 1	a 2	d	a 1	a 2	d
Uniform DIF (U-A)	12	11	1.0	0.1	0.0	1.0	0.1	0.25	1.0	0.1	0.5
		12	0.1	1.0	0.0	0.1	1.0	0.25	0.1	1.0	0.5
	14	11	1.0	0.1	0.0	1.0	0.1	0.25	1.0	0.1	0.5
		12	0.1	1.0	0.0	0.1	1.0	0.25	0.1	1.0	0.5
		13	0.7	0.7	0.0	0.7	0.7	0.25	0.7	0.7	0.5
		14	0.7	0.7	0.0	0.7	0.7	0.25	0.7	0.7	0.5
	24	21	1.0	0.1	0.0	1.0	0.1	0.25	1.0	0.1	0.5
		22	0.1	1.0	0.0	0.1	1.0	0.25	0.1	1.0	0.5
		23	0.7	0.7	0.0	0.7	0.7	0.25	0.7	0.7	0.5
		24	0.7	0.7	0.0	0.7	0.7	0.25	0.7	0.7	0.5
Nonuniform DIF (N-B)	12	11	1.0	0.1	0.0	1.0	0.4	0.25	1.0	0.7	0.5
		12	0.1	1.0	0.0	0.1	1.3	0.00	0.1	1.6	0.0
	14	11	1.0	0.1	0.0	1.0	0.4	0.25	1.0	0.7	0.5
		12	0.1	1.0	0.0	0.1	1.3	0.25	0.1	1.6	0.5
		13	0.7	0.7	0.0	0.7	1.0	0.25	0.7	1.3	0.5
		14	0.7	0.7	0.0	0.7	1.0	0.00	0.7	1.3	0.0
	24	21	1.0	0.1	0.0	1.0	0.4	0.25	1.0	0.7	0.5
		22	0.1	1.0	0.0	0.1	1.3	0.25	0.1	1.6	0.5
		23	0.7	0.7	0.0	0.7	1.0	0.25	0.7	1.3	0.5
		24	0.7	0.7	0.0	0.7	1.0	0.00	0.7	1.3	0.0
Nonuniform DIF (N-C)	12	11	1.0	0.1	0.0	1.3	0.4	0.25	1.6	0.7	0.5
		12	0.1	1.0	0.0	0.4	1.3	0.00	0.7	1.6	0.0
	14	11	1.0	0.1	0.0	1.3	0.4	0.25	1.6	0.7	0.5
		12	0.1	1.0	0.0	0.4	1.3	0.25	0.7	1.6	0.5
		13	0.7	0.7	0.0	1.0	1.0	0.25	1.3	1.3	0.5
		14	0.7	0.7	0.0	1.0	1.0	0.00	1.3	1.3	0.0
	24	21	1.0	0.1	0.0	1.3	0.4	0.25	1.6	0.7	0.5
		22	0.1	1.0	0.0	0.4	1.3	0.25	0.7	1.6	0.5
		23	0.7	0.7	0.0	1.0	1.0	0.25	1.3	1.3	0.5
		24	0.7	0.7	0.0	1.0	1.0	0.00	1.3	1.3	0.0

To generate responses for the DIF items in the reference group, the same item parameters from Table 2 were always used regardless of DIF conditions, whereas the item parameters for the focal group were manipulated to introduce different levels of DIF magnitude. As for the level of DIF magnitudes, the d parameters for the studied items in the focal group were 0.25 higher than those in the reference group, representing a low¹ level of uniform DIF magnitude. The difference of 0.5 in the d parameters was used as a medium level of uniform DIF magnitude. The 0.3 and 0.6 differences in a₁ and/or a₁ parameters were used to represent low and medium DIF magnitude, respectively. The differences in the a and d parameters between the focal and the reference groups were manipulated to reflect previous multidimensional IRT DIF studies (e.g., Oshima, Raju, & Flowers, 1997; Suh & Cho, 2014).

Sample Design

Three unbalanced sample size conditions and one balanced sample size condition between the reference and focal groups were implemented in the current study: small (R500/F100), medium (R1000/F200), large unbalanced (R1500/F500), and large balanced (R1000/F1000) sample sizes. The three different sizes of unbalanced sample design between the focal and reference groups were selected to reflect operational testing settings. Furthermore, one balanced sample size was included to compare the sample size effect between balanced and unbalanced sample designs. The manipulated sample size levels and ratios between groups were also found in previous simulation studies (e.g., Finch, 2005; Jin et al., 2012).

Evaluation Criteria

Tests for detecting uniform and nonuniform DIF simultaneously were conducted for every studied DIF item in Mplus (L. K. Muthén & Muthén, 1998-2015) using the Mplus Automation package (Hallquist & Wiley, 2014) in R (R Core Team, 2015). An example of Mplus codes for estimating the multidimensional MIMIC-interaction model is provided in the appendix. In operational testing settings, it is often unknown which items are free of DIF, and thus a scale purification stage may be necessary to define a set of DIF-free anchor items. However, in this study, it is assumed that anchor items have already been identified. Type I error rates and power rates of the MIMIC-interaction model for identifying uniform DIF and nonuniform DIF were examined as the evaluation criteria.

Type I error rate indicates the probability of detecting DIF when there is in fact no DIF in the studied item (i.e., false positive rates), while power represents the probability of detecting DIF when there is DIF in the studied item (i.e., true positive rates). Therefore, for each non-DIF condition, Type I error rates were computed as the proportion of significant MIMIC-interaction models at the nominal alpha level (at $\alpha =.05$) out of 100 replications. Based on a preliminary analysis, somewhat inflated Type I error rates were observed. Therefore, the Benjamini-Hochberg procedure (BH; Benjamini & Hochberg, 1995; Thissen, Steinberg, & Kuang, 2002) was used to control Type I error rates by sequentially comparing the observed p value for each studied DIF item against to critical BH values that were computed based on the number DIF tests used for the same data set (see Raykov, Marcoulides, Lee, & Chang, 2013, for details of the BH procedure in the context of latent variable modeling). For each DIF condition, power rates were calculated as the proportion of significant MIMIC-interaction models in the same manner. The simulation results are summarized separately for the BH adjusted Type I error rates and average power rates from the multidimensional MIMIC-interaction in the following section. In addition, the recovery of correlation between two latent traits for the M-2PL was reported.

Results

Effects of DIF Type and DIF Magnitude

Non-DIF

Table 3 shows the BH-adjusted Type I error rates for the MIMIC-interaction model under the non-DIF conditions. Type I error rates for the 14-item test were relatively larger compared to those from the 12-item test in the item level, although Type I error rates for the 12-item test ranged from .01 up to and .09, whereas those for the 14-item test ranged from 0 up to .08. In the 14-item test, Item 11 produced the highest Type I error rates on average, and Item 14 showed the lowest Type I error rates. Item-level Type I error rates for the 24-item test ranged from 0 and .11, showing somewhat inflated Type I error rates for a couple of items in certain conditions (e.g., Item 23 under R1000/F200, R1500/F500, and R1000/F1000 with $\rho =.3$, and Item 22 under R1000/F1000 with $\rho =.5$).

Table 3.

The BH-Adjusted Type I Error Rates of the MIMIC-Interaction Model in the Non-DIF Conditions.

Test length	ρ	DIF item	R500/F100	R1000/F200	R1500/F500	R1000/F1000	Average
12	0.0	11	.01	.04	.04	.08	.04
		12	.02	.02	.05	.04	.03
	Average		.02	.03	.05	.06
	0.3	11	.04	.04	.02	.06	.04
		12	.03	.02	.02	.01	.02
	Average		.04	.03	.02	.04
	0.5	11	.05	.05	.05	.09	.06
		12	.01	.01	.02	.02	.02
	Average		.03	.03	.04	.06
14	0.0	11	.08	.06	.07	.07	.07
		12	.04	.04	.05	.05	.05
		13	.04	.02	.05	.08	.05
		14	.02	.04	.03	.01	.03
	Average		.05	.04	.05	.05
	0.3	11	.08	.07	.07	.08	.08
		12	.08	.06	.04	.04	.06
		13	.06	.02	.08	.07	.06
		14	.02	.00	.02	.04	.02
	Average		.06	.04	.05	.06
	0.5	11	.05	.06	.06	.05	.06
		12	.02	.04	.05	.06	.04
		13	.03	.04	.09	.04	.05
		14	.00	.03	.05	.03	.03
	Average		.03	.04	.06	.05
24	0.0	21	.05	.06	.08	.08	.07
		22	.05	.03	.04	.08	.05
		23	.05	.07	.07	.07	.07
		24	.00	.02	.06	.01	.02
	Average		.04	.05	.06	.06
	0.3	21	.05	.05	.04	.03	.04
		22	.05	.02	.06	.09	.06
		23	.06	.09	.11	.11	.09
		24	.00	.01	.03	.03	.02
	Average		.04	.04	.06	.07
	0.5	21	.07	.10	.04	.05	.07
		22	.06	.03	.04	.10	.06
		23	.02	.07	.01	.03	.03
		24	.00	.01	.03	.01	.01
	Average		.04	.05	.03	.05

Average Type I error rates ranged from .02 to .06 for the 12-item test, from .02 to .08 for the 14-item test, and from .01 to .09 for the 24-item test. It appeared that Type I error was controlled better in shorter test length conditions. The two smaller sample sizes (R500/F100 and R1000/F200) tended to produce Type I error rates closer to the BH adjusted nominal levels than the two larger sample sizes (R1500/F500 and R1000/F1000), although this pattern was not consistent.

Uniform and Nonuniform DIF

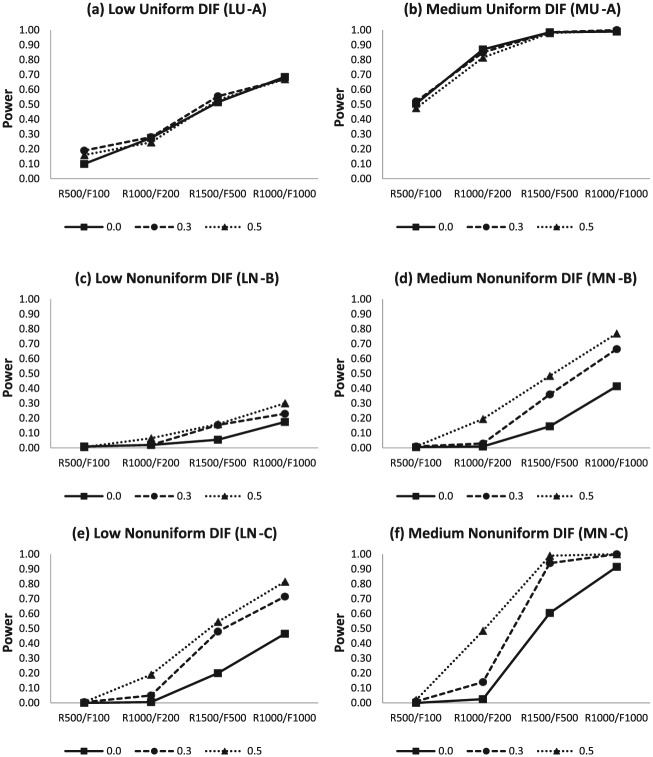
Figures 2 through 4 show the average power rates of the MIMIC-interaction model for detecting uniform and nonuniform DIF in the 12-item, 14-item, and 24-item tests at $\alpha =.05$. The multidimensional MIMIC-interaction model produced higher average power rates under the uniform DIF conditions (LU-A and MU-A) than the nonuniform DIF conditions (LN-B, LN-C, MN-B, and MN-C). For example, as shown in Figure 2, the average power rates of uniform DIF conditions (Figure 2a and b) were higher than those of nonuniform DIF (N-B and N-C) conditions (Figure 2c, d, and f), with an exception of the LN-C conditions (Figure 2e) which showed higher power than the uniform DIF conditions.

Figure 2.

Average power rates for the MIMIC-interaction model using the 12-item test with uniform and nonuniform DIF across sample sizes and correlations between latent traits.

Figure 4.

Average power rates for the MIMIC-interaction model using the 24-item test with uniform and nonuniform DIF across sample sizes and correlations between latent traits.

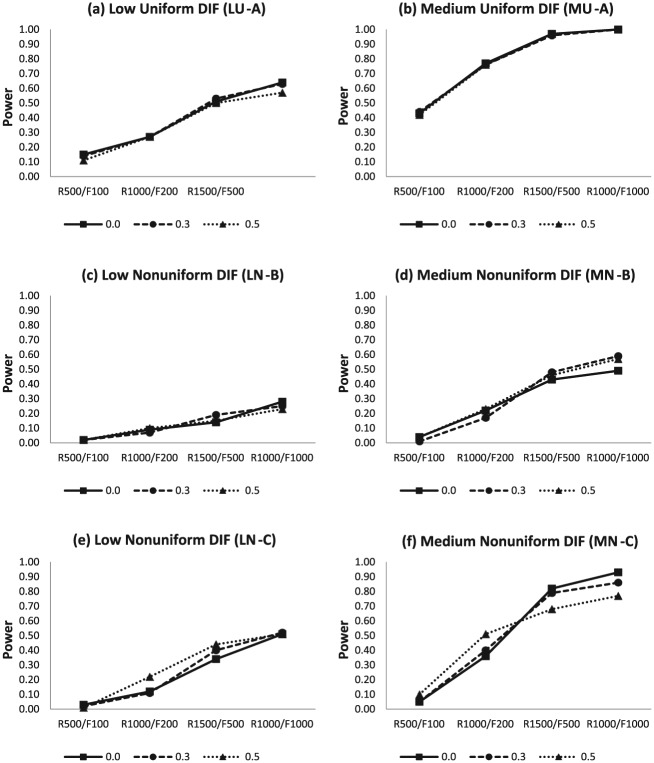
In general, the average power rates of the LN-C and MN-C conditions (e.g., Figure 2e and f) were higher than those of the LN-B and MN-B conditions (e.g., Figure 2c and d). This is primarily because DIF was introduced in more parameters for the LN-C and MN-C conditions than for the LN-B and MN-B conditions. Both nonuniform DIF conditions (i.e., N-B and N-C) showed smaller power rates than the uniform DIF conditions. Especially in the low DIF conditions, power rates of uniform DIF conditions were much higher than those of nonuniform DIF conditions. Figures 3 and 4 show the average power rates in the 14-item and 24-item tests, respectively. These two figures showed similar patterns to those from Figure 2 with no exception.

Figure 3.

Average power rates for the MIMIC-interaction model using the 14-item test with uniform and nonuniform DIF across sample sizes and correlations between latent traits.

Low DIF Versus Medium DIF

As shown in Figures 2 through 4, a clear pattern was found in terms of DIF magnitude. Regardless of all other simulation conditions, the average power rates of medium DIF magnitude (e.g., Figure 2b, d, and f) were substantially higher than the average power rates of low DIF magnitude (e.g., Figure 2a, c, and e) for the 12-item test. The 14-item test and 24-item test conditions in Figures 3 and 4 showed the same pattern with the 12-item test. This pattern seemed more evident under the uniform DIF conditions (U-A) and large sample conditions (i.e., R1500/F500 and R1000/F1000).

Sample Size Effect

Regarding small, medium, and large sample sizes within unbalanced sample design, the average power rates increased as the sample size increased, because the power of a test statistic is substantially affected by sample size. This general pattern was also observed in Woods and Grimm (2011); however, the average power rates in this study appeared to be lower than those reported in their study based on the unidimensional MIMIC-interaction model. For example, compared to their results of R1000/F200 with the 24-item test in which the average power rate was around .82 in nonuniform conditions, the average power rate of the same condition in this study was substantially low (.42) in the medium nonuniform DIF conditions with no correlation (e.g., Figure 4f). In addition, Figures 2, 3, and 4 also show a comparison of average power rates for the unbalanced sample design of R1500/F500 and the balanced sample design of R1000/F1000. The power rates of the balanced sample condition were higher than those of the unbalanced sample conditions across all DIF conditions regardless of DIF type and DIF magnitude.

Correlation Effect

Correlation effects on the average power rates for the multidimensional MIMIC-interaction model can also be seen in Figures 2 through 4. The average power rates for correlation conditions of 0, 0.3, and 0.5 were close to each other in the uniform DIF conditions (U-A) across three test lengths and in the first nonuniform DIF conditions (N-B) of the 12-item and 24-item tests. For other conditions, the average power rates increased as the correlation between latent traits increased. There were exceptions for this pattern; MN-C conditions in the 12-item (Figure 2f) and 24-item tests (Figure 4f). In these cases, the patterns across different correlations varied depending on sample size. Average power rates increased as the correlation increased for the two small sample size conditions (i.e., R500/F100 and R1000/F200), whereas the pattern was reversed for the two large sample size conditions (i.e., R1500/F500 and R1000/F1000). Additionally, the recovery of correlation for the M-2PL using the MIMIC-interaction model was examined.² Overall, correlation parameters were somewhat overestimated across all DIF conditions. For example, the average estimates for the 0, 0.3, and 0.5 correlation conditions were 0.168, 0.437, and 0.619 for the U-A conditions, 0.174, 0.425, and 0.622 for the N-B conditions, and 0.180, 0.447, and 0.626 for the N-C conditions in the 24-item test.

Test Length Effect

Regarding the test length effect, the 12-item test and 24-item test conditions were first compared, because the 14-item test condition had a different proportion of DIF items (40%) compared to the 12-item and 24-item test conditions (20%). The effect of test length seemed to vary depending on other simulation conditions. As test length increased from 12 items to 24 items, regardless of DIF magnitude, sample size, and the correlation between the latent traits, the power of uniform DIF conditions tended to decrease slightly. Unlike for the uniform DIF conditions, the effect of test length was more erratic for the nonuniform DIF conditions. In general, the 12-item test demonstrated better power rates than the 24-item test. Especially when the sample size was large and the correlation between the dimensions was moderate ($\rho =0.5$), average power rates from the 12-item test were much higher than those from the 24-item test. Both the 12-item test and the 24-item test performed better in detecting uniform and nonuniform DIF, when sample size became larger. Regarding the effect of having different proportions of anchor items in a test, the results in the 14-item test with 4 DIF items and 24-item test with 4 DIF items were compared. The average power rates in the 14-item test were always smaller than those in the 24-item test, implying that having a longer anchor item set may lead to produce higher power rates in detecting uniform and nonuniform DIF with the multidimensional MIMIC-interaction model.

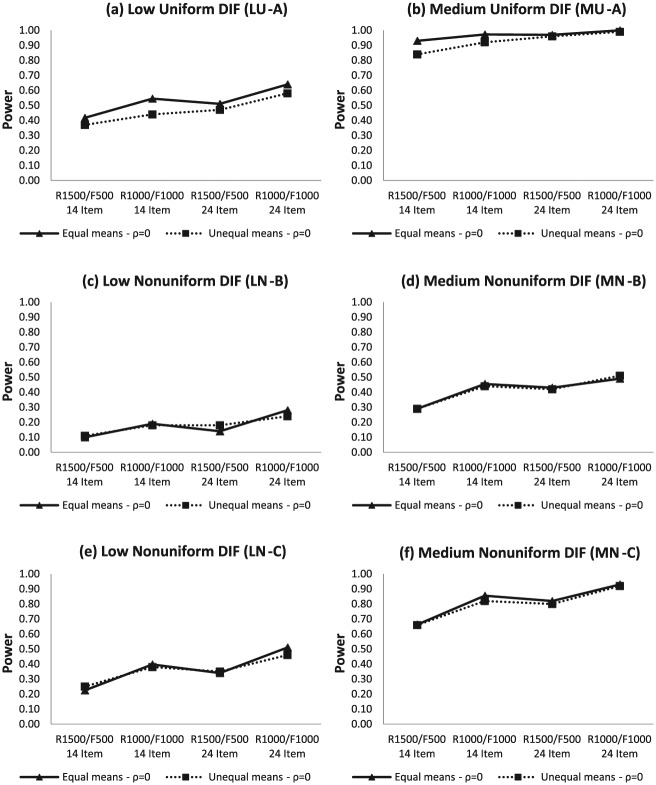
Latent Mean Difference Effect

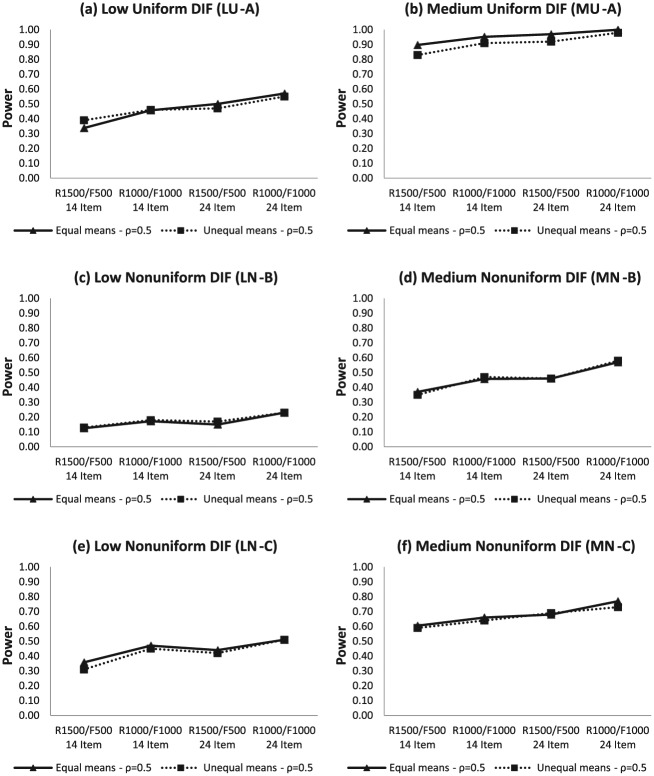
Figures 5 and 6 show the average power rates in detecting low and medium DIF when the means of latent traits are equal and unequal between the focal and reference groups. When the latent means were the same for the both groups, average power rates were either equal to or higher (the difference ranging from 0 to 0.11) than power rates when the latent means were different between the focal and reference groups. This pattern occurred across most correlation conditions ($\rho =0$ and $\rho =0.5)$, test length conditions (14-item and 24-item), and DIF magnitude (low and medium). However, some exceptions were found in the low uniform condition (see Figure 6a) and in the low nonuniform condition (see Figure 5c and Figure 6c). For the medium DIF conditions, the results in Figure 5 ($\rho =0)$ and Figure 6 ($\rho =0.5)$ were almost identical regardless of test length, sample size, and DIF type.

Figure 5.

Average power rates for the MIMIC-interaction model with and without latent mean differences between the groups.

Note. $\rho =0$ between the latent traits.

Figure 6.

Average power rates for the MIMIC-interaction model with and without latent mean differences between the groups.

Note. $\rho =0.5$ between the latent traits.

Discussion

The goal of this study was to demonstrate the utility of the multidimensional MIMIC-interaction model in detecting uniform and nonuniform DIF and to assess its performance under various testing conditions in terms of Type I error rates and power rates via a Monte Carlo study. This study evaluated the multidimensional MIMIC-interaction model implemented in Mplus like the previous study of Woods and Grimm (2011), in which the unidimensional MIMIC-interaction model was considered to study uniform and nonuniform DIF.

The results of this study provide an important contribution to the development of new multidimensional DIF methods, given a few DIF studies are available in the context of multidimensional IRT models (e.g., Oshima et al., 1997; Suh & Cho, 2014). In general, Type I error rates of the MIMIC-interaction model were close to or below the expected alpha value of .05 on average across all non-DIF conditions. Our results do not concur with Woods and Grimm (2011), who found unacceptably high Type I error rates with MIMIC-interaction models due to the violation of normality assumption in the interaction between continuous latent variables and the categorical covariate. Another potential reason for this difference is that Woods and Grimm’s (2011) study did not implement any adjustment (e.g., Bonferroni or the BH procedure) on p values, whereas this study used the BH procedure when testing DIF under the non-DIF conditions.

The average power rates from the large sample size conditions of R1500/F500 and R1000/F1000 were high (over .90) in the medium uniform DIF (MU-A) condition. The corresponding average power rates with the medium nonuniform DIF (MN-C) were relatively lower (over .60). In general, the two nonuniform conditions (N-B and N-C) showed significantly lower power rates than the uniform DIF conditions. The power rates of the N-C conditions were higher than those of the N-B conditions. The reason for the difference between the N-B condition and N-C condition is that DIF was introduced in a₂ parameter in the N-B condition, whereas DIF was introduced in both a₁ and a₂ parameters in the N-C condition. Therefore, a larger DIF effect was expected in the latter condition.

Regardless of the DIF type, average power rates increased as sample size and DIF magnitude increased, as expected. Also, power increased when the anchor item length increased and when the latent means were equal between the focal and reference groups. Test length and correlation effects were less apparent and varied depending on other simulation conditions. One interesting finding regarding test length was that when nonuniform DIF was present with small and medium sample sizes, power rates increased as test length increased. This implies that the performance of the MIMIC-interaction model in detecting nonuniform DIF can be improved by using longer tests as opposed to shorter tests, especially when sample sizes are small. In other words, the effects of test length and sample size may compensate for each other in terms of power rates in detecting nonuniform DIF. With respect to this observation, further investigation including more comprehensive simulation conditions is needed.

In the future, we would like to extend our study using the mediated MIMIC model that showed improvement in detecting the mediation effect that fully or partially explained DIF. The mediated MIMIC model allows revealing what causes of DIF (Cheng et al., 2016; Yao & Li, 2010). However, there are few clear distinctions between the mediated MIMIC model and our MIMIC-interaction model. First, our MIMIC-interaction model is the multidimensional generalization of the traditional MIMIC model and closer to the MIRT framework, whereas the mediated MIMIC model focuses on the mediation effect on an auxiliary (or nuisance) dimension. In other words, the mediated MIMIC model assumes the unidimensionality of the test, but there is also an auxiliary latent trait that should not be measured by the test but it exists and helps understand the relationship between the categorical covariate and the latent trait. In contrast, the multidimensional MIMIC-interaction model assumes that the test is multidimensional and multidimensionality is intentional. That is, there are two or more latent traits underlying the item response data because the test is designed in this way. However, a mediator can be still incorporated into the multidimensional MIMIC-interaction model to investigate potential reasons for DIF in a multidimensional test structure.

Future DIF research should also consider other traditional approaches, such as multidimensional simultaneous item bias test (MULTISIB; Stout, Li, Nandakumar, & Bolt, 1997) or likelihood ratio test using item response theory (IRT-LR). Especially, comparing the MIMIC and MIMIC-interaction models with the IRT-LR test can provide interesting findings, because both approaches have been commonly used in the latent variable modeling and IRT modeling approaches, respectively. Previous studies compared the performances of unidimensional MIMIC and IRT-LR approaches under various conditions. For example, Woods and Grimm (2011) found that the recovery of the discrimination and difficulty parameter of the IRT-LR-DIF (Thissen, Steinberg, &, Wainer, 1988) was better than that of the MIMIC-interaction models in nonuniform DIF conditions with ordinal responses. Furthermore, Woods (2009) showed that MIMIC models with small samples (N = 50) of focal group in uniform DIF conditions with dichotomous or ordinal responses produced more accurate parameter estimates than the IRT-LR-DIF. Future studies can investigate the performances of the multidimensional MIMIC and IRT-LR approaches under similar conditions.

Finally, this study did not consider any scale purification process to select DIF-free anchor items because the main focus of the study was to examine the performance of the multidimensional MIMIC model for the selected DIF items. However, especially in operational testing settings, assessments may contain several DIF items, and it may not be possible to determine DIF-free items without a scale purification process. Future studies can focus on scale purification methods for determining DIF-free anchor items in the context of the multidimensional MIMIC-interaction model.

Appendix

Mplus Code for the Multidimensional MIMIC-Interaction Model

TITLE: Detecting DIF with Multidimensional MIMIC-Interaction Model

DATA:

 FILE IS data.dat;

 FORMAT IS FREE;

 TYPE IS INDIVIDUAL;

 NGROUPS=1;

VARIABLE:

 !12 dichotomous items and one group variable

 NAMES ARE item1-item12 z;

 CATEGORICAL ARE item1-item12;

MODEL:

 !LATENT TRAIT 1;

 [theta1@0];

 [item1$1-item12$1];

 theta1 BY item11* item1-item3 item7-item10;

 theta1@1;

 theta1 on z;

 !UNIFORM DIF;

 item11 on z;

 !NONUNIFORM DIF;

 zxtheta1 | z XWITH theta1;

 item11 ON zxtheta1;

 !LATENT TRAIT 2;

 [theta2@0];

 theta2 BY item12* item4-item10;

 theta2@1;

 

 theta2 on z;

ANALYSIS:

 ESTIMATOR = MLR;

 TYPE = RANDOM;