Beyond total treatment effects in randomised controlled trials: Baseline measurement of intermediate outcomes needed to reduce confounding in mediation investigations

Abstract

Background:

Random allocation avoids confounding bias when estimating the average treatment effect. For continuous outcomes measured at post-treatment as well as prior to randomisation (baseline), analyses based on (A) post-treatment outcome alone, (B) change scores over the treatment phase or (C) conditioning on baseline values (analysis of covariance) provide unbiased estimators of the average treatment effect. The decision to include baseline values of the clinical outcome in the analysis is based on precision arguments, with analysis of covariance known to be most precise. Investigators increasingly carry out explanatory analyses to decompose total treatment effects into components that are mediated by an intermediate continuous outcome and a non-mediated part. Traditional mediation analysis might be performed based on (A) post-treatment values of the intermediate and clinical outcomes alone, (B) respective change scores or (C) conditioning on baseline measures of both intermediate and clinical outcomes.

Methods:

Using causal diagrams and Monte Carlo simulation, we investigated the performance of the three competing mediation approaches. We considered a data generating model that included three possible confounding processes involving baseline variables: The first two processes modelled baseline measures of the clinical variable or the intermediate variable as common causes of post-treatment measures of these two variables. The third process allowed the two baseline variables themselves to be correlated due to past common causes. We compared the analysis models implied by the competing mediation approaches with this data generating model to hypothesise likely biases in estimators, and tested these in a simulation study. We applied the methods to a randomised trial of pragmatic rehabilitation in patients with chronic fatigue syndrome, which examined the role of limiting activities as a mediator.

Results:

Estimates of causal mediation effects derived by approach (A) will be biased if one of the three processes involving baseline measures of intermediate or clinical outcomes is operating. Necessary assumptions for the change score approach (B) to provide unbiased estimates under either process include the independence of baseline measures and change scores of the intermediate variable. Finally, estimates provided by the analysis of covariance approach (C) were found to be unbiased under all the three processes considered here. When applied to the example, there was evidence of mediation under all methods but the estimate of the indirect effect depended on the approach used with the proportion mediated varying from 57% to 86%.

Conclusion:

Trialists planning mediation analyses should measure baseline values of putative mediators as well as of continuous clinical outcomes. An analysis of covariance approach is recommended to avoid potential biases due to confounding processes involving baseline measures of intermediate or clinical outcomes, and not simply for increased precision.

Introduction

There exists an extensive literature on how to handle baseline measures of a continuous clinical outcome variable in randomised controlled trials (RCTs). This literature relates to estimating the total treatment effect in terms of the clinical outcome.^1–4 Mediation investigations that partition total intervention effects into mediated and non-mediated components have become increasingly popular, in particular in trials of mental health interventions such as psychological therapies. The UK National Institute for Health Research and the Medical Research Council fund the Efficacy and Mechanism Evaluation programme, which has as one of its aims understanding treatment mechanisms – in our view, ideally evaluated using an appropriate and valid analysis of mediation. But little advice is available on how to deal with baseline measures when attempting such mediation analyses, or indeed whether baseline measurement of clinical and putative mediator outcomes is necessary. This article is focused on comparing approaches for dealing with baseline measures of outcomes when total treatment effect estimation is to be supplemented by mediation assessment in trials.

Intention-to-treat analyses aim to evaluate the effect of treatment offer (effectiveness) or treatment receipt (efficacy, assuming full compliance with treatment offer). There are three well-known approaches for estimating this total treatment effect when the clinical outcome has also been measured before randomisation (baseline):

• (A)  Post approach: compare post-treatment clinical outcomes between trial arms.

• (B)  Change score approach: construct change scores by subtracting baseline values from the post-treatment values and compare the change scores between trial arms.

• (C)  Analysis of covariance (ANCOVA) approach: estimate the trial arm difference from a regression model that contains baseline measures of the outcome as a covariate, and models a linear effect of the baseline measure on post-treatment outcome.

The three intention-to-treat estimators are from a wider class of unbiased baseline adjusted estimators. Under a linear model the best adjustment is achieved by ANCOVA and so approach (C) is the most precise estimator.^1–4

Trials of psychological therapies increasingly supplement total treatment effect estimation by a mediation analysis.^5–9 The development of a psychological therapy is typically based on a theory regarding modifiable target factors and it is of interest to assess empirically how much of the total intervention effect can be attributed to changes in such a target intermediate outcome (an indirect effect). On occasions, it can also be of interest to demonstrate that an effect does not only come about by changing an intermediate variable (e.g. by changing adherence with medication), that is, to show a direct effect.

The traditional Baron and Kenny¹⁰ steps for mediation assessment fit three regression models: (1) a regression model describing the treatment effect on the clinical outcome, (2) a regression model describing the treatment effect on the intermediate outcome and (3) a regression model describing the joint effects of the intermediate variable and the treatment on the clinical outcome. Traditionally, none of these models contain interactions between treatment and baseline variables nor do models (1) or (3) contain an interaction between treatment and the intermediate variable. Inferences regarding indirect and direct treatment effects can be obtained by fitting two of these regression models. We focus on fitting models (2) and (3) which is more prominent in the behavioural/social sciences. Trialists again have three choices for incorporating baseline measures:

• (A)  Post approach for mediation. Use the intermediate outcome as the dependent variable for model (2); use the clinical outcome as the dependent and the intermediate outcome as an explanatory variable for model (3); ignore the baseline measures.

• (B)  Change score approach for mediation. Use change in the intermediate variable as the dependent variable for model (2); use change in the clinical outcome as the dependent and change in the intermediate outcome as an explanatory variable for model (3).

• (C)  ANCOVA approach for mediation: Use the intermediate outcome as the dependent variable for model (2); use the clinical outcome as the dependent and the intermediate outcome as an explanatory variable for model (3); include baseline measures of both variables in both models.

To our knowledge, there exists little advice as to how to choose between these competing approaches and the practitioner might be forgiven for thinking that this is solely a matter of precision, as is the case for total effects. In this article, we demonstrate that despite randomisation such arguments are too simplistic for mediation investigations. Indeed, we conclude that measurement of baseline variables and subsequent incorporation into analysis models is necessary to avoid particular biases in estimators of causal mediation effects, and end up recommending approach (C) on the grounds of bias reduction.

Methods

Causal treatment effects

We consider trials that have observed a continuous putative mediator variable and a continuous clinical outcome at baseline $(t=0)$ and at a post-randomisation time point. We focus on the scenario where the assessment time point of the mediator $(t=1)$ precedes that of the clinical outcome $(t=2)$ as such time separation supports the theory of a temporal causal chain from treatment to mediator to clinical outcome.^11,12

We observe the following variables for trial participants $i\in \{1,\dots ,n\}$:

• $R_i$ is the treatment offered to participant $i$ with possible values $r=0$ for being allocated to the control arm and $r=1$ for the therapy arm.

• $M_{i,0}$ and $M_{i,1}$ are the values measured on the putative mediator variable for participant $i$ at $t=0$ and $t=1$, respectively.

• $Y_{i,0}$ and $Y_{i,2}$ are the values measured on the clinical outcome variable for participant $i$ at $t=0$ and $t=2$ respectively.

We consider potential outcomes¹³ for individuals from the trial’s target population:

• $M_{i,1}(R=r)=M_{i,1}(r)$ the intermediate outcome that would have been observed at $t=1$ if individual $i$ had been allocated to trial arm $r$.

• $Y_{i,2}(R=r)=Y_{i,2}(r)$ the clinical outcome that would have been observed at $t=2$ if individual $i$ had been allocated to trial arm $r$.

• $Y_{i,2}(R=r,M_1=m)=Y_{i,2}(r,m)$ the clinical outcome that would have been observed at $t=2$ if individual $i$ had been allocated to trial arm $r$ and the intermediate outcome had been set to value $m$.

This allows us to define a causal individual treatment (offer) effect in terms of the clinical outcome as the contrast

$${\Delta }_i:=Y_{i,2}\left(1\right)-Y_{i,2}\left(0\right)$$

and the causal average treatment (offer) effect in the trial’s target population as

$$\mathrm{AT}{\mathrm{E}}_Y:={\mathrm{E}}_{\mathrm{\Delta }}\left({\mathrm{\Delta }}_i\right)$$

$\mathrm{AT}{\mathrm{E}}_Y$ is an estimand quantifying the total treatment effect. Following the work of VanderWeele and his colleague,^14,15 we define an individual natural direct treatment (offer) effect as

$${\Phi }_i:=Y_{i,2}[1,M_{i,1}\left(0\right)]-Y_{i,2}[0,M_{i,1}\left(0\right)]$$

and the individual natural indirect treatment (offer) effect as

$${\Psi }_i:=Y_{i,2}[1,M_{i,1}\left(1\right)]-Y_{i,2}[1,M_{i,1}\left(0\right)]$$

This leads to definitions of a causal (average) natural direct treatment (offer) effect as

$$\mathrm{NDE}:={\mathrm{E}}_{\mathrm{H}}\left({\Phi }_i\right)$$

and a causal (average) natural indirect treatment (offer) effect as

$$\mathrm{NIE}:={\mathrm{E}}_{\Psi }\left({\Psi }_i\right)$$

so that $\mathrm{AT}{\mathrm{E}}_Y=\mathrm{NDE}+\mathrm{NIE}$ holds in the continuous case. Importantly, the natural direct effect (NDE) and the natural indirect effect (NIE) represent total treatment effect components that have causal interpretations.

These causal mediation estimands can be expressed as functions of parameters of structural models. Let denote $\alpha$ the effect of changing treatment offer in a linear structural model for $M_1(r)$. Then the average treatment effect with respect to the intermediate variable $\mathrm{AT}{\mathrm{E}}_M:=\mathrm{E}[M_{i,1}(1)-M_{i,1}(0)]$, which we term the target effect, is $\mathrm{AT}{E}_M=\alpha$. Furthermore, let $\gamma$ be the effect of changing treatment offer and $\beta$ the effect of increasing the value of the mediator variable by one unit in a linear structural model for $Y_2(r,m)$ that does not contain an interaction between treatment and mediator. Then it follows that $\mathrm{NDE}=\gamma$ and $\mathrm{NIE}=\alpha \beta$.¹⁶ Under sequential ignorability, linearity and no-interactions assumptions causal mediation analysis can be performed by targeting model parameters $\alpha ,\beta$ and $\gamma$ and using the product of coefficient method.¹⁷

Causal mediation analysis in trials

We turn our attention to understanding how baseline variables $M_0$ or $Y_0$ should be incorporated into regression models when the natural direct and indirect effects as well as the intention-to-treat effect are of interest. We start by considering what might be a realistic data generating model for trial outcomes. Then we describe the analysis models that would be assumed by the competing mediation analysis approaches and contrast them with the true data generating model to assess their potential for producing biased estimates. Finally, we confirm our bias predictions by means of a Monte Carlo simulation study.

We will employ linear structural equation modelling diagrams to describe models graphically. The resulting linear structural model equations are straightforward to read from these graphs. Briefly, observed variables are indicated by square boxes and unobserved variables by circles. A single-headed arrow represents a causal effect of one variable on another and the associated path coefficient has a causal interpretation. A double-headed arrow indicates an un-modelled correlation between two variables. Importantly, the absence of an unblocked path connecting two variables reflects an independence assumption; for more details including path tracing rules see study by Pearl¹⁸ or Spirtes et al.¹⁹

Data generating model for trial outcomes

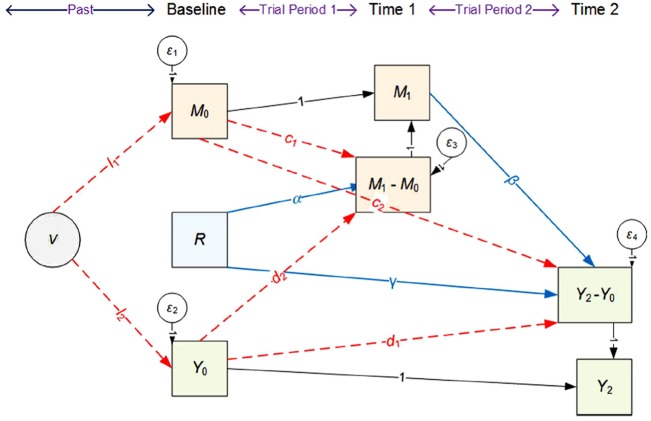
Figure 1 represents a realistic data generating model for RCTs. It is a simple change score model for longitudinal data: Baseline measures on the left-hand side are measured first ($R$, $M_0$ and $Y_0$), followed by the mediator at the first post-randomisation assessment time point, $M_1$, and the clinical outcome at the second time point, $Y_2$, at the right-hand side. The characteristic feature of the change score model is that variables measured at earlier time points affect variables at later time points by driving their change over the relevant time periods.²⁰ Thus, in our trials context baseline measures and treatment can cause change in the mediator or the clinical outcome ($M_1-M_0$ and $Y_2-Y_0$, respectively). In addition, the level of the post-randomisation mediator $M_1$ can cause change in the clinical outcome. Mediation occurs if treatment offer $(R)$ has a causal effect on the change score $M_1-M_0$ and so also on $M_1$ (target effect $\alpha$), and $M_1$ has a causal effect on $Y_2-Y_0$ and so also on $Y_2$ (path coefficient $\beta$). Under this change score model the NIE is given by the product $\alpha \beta$ and the non-mediated (natural direct) effect is the path coefficient $\gamma$. (Some path coefficients in Figure 1 have been fixed at the value ‘1’ to ensure that a participant’s score on a variable measured at a post-randomisation time point is the sum of the participant’s baseline and change scores.)

Figure 1.

Linear structural equation diagram describing a realistic data generating model for trials.

Importantly, Figure 1 includes three processes involving baseline measures of outcomes (indicated by dashed paths).

• $M_0$ observed common cause of intermediate and clinical outcome: Baseline measures of the putative mediator drive $M_1$ (directly by determining its level or indirectly by affecting changes over the follow-up period, path coefficient $c_1$) as well as $Y_2$ (by affecting changes over the longer follow-up period, path coefficient $c_2)$.

• $Y_0$ observed common cause of intermediate and clinical outcome: Baseline measures of the clinical outcome drive $Y_2$ (directly by determining its level or indirectly by affecting changes, path coefficient $d_1$) as well as $M_1$ (by affecting changes, path coefficient $d_2)$.

• V common cause of baseline levels: A past unobserved variable $V$ affects baseline levels of the mediator (path coefficient $l_1$) and the outcome (coefficient $l_2$). (It does not affect R due to random treatment offer allocation.) Since baseline measures form part of the respective post-treatment measures, $V$ is a latent common cause of $M_1$ as well as $Y_2$.

Each of these scenarios is plausible, in particular the existence of V. The measures taken at baseline do not represent the first occasion that the measures occur in the individual, but instead represent the first occasion that the investigators have observed the measures. Therefore, it is reasonable to assume that something has driven the values of M and Y at the first time they are measured. In practice, there will be multiple factors but we can represent these by a single unmeasured latent construct V.

Predicted biases of causal mediation effect estimators

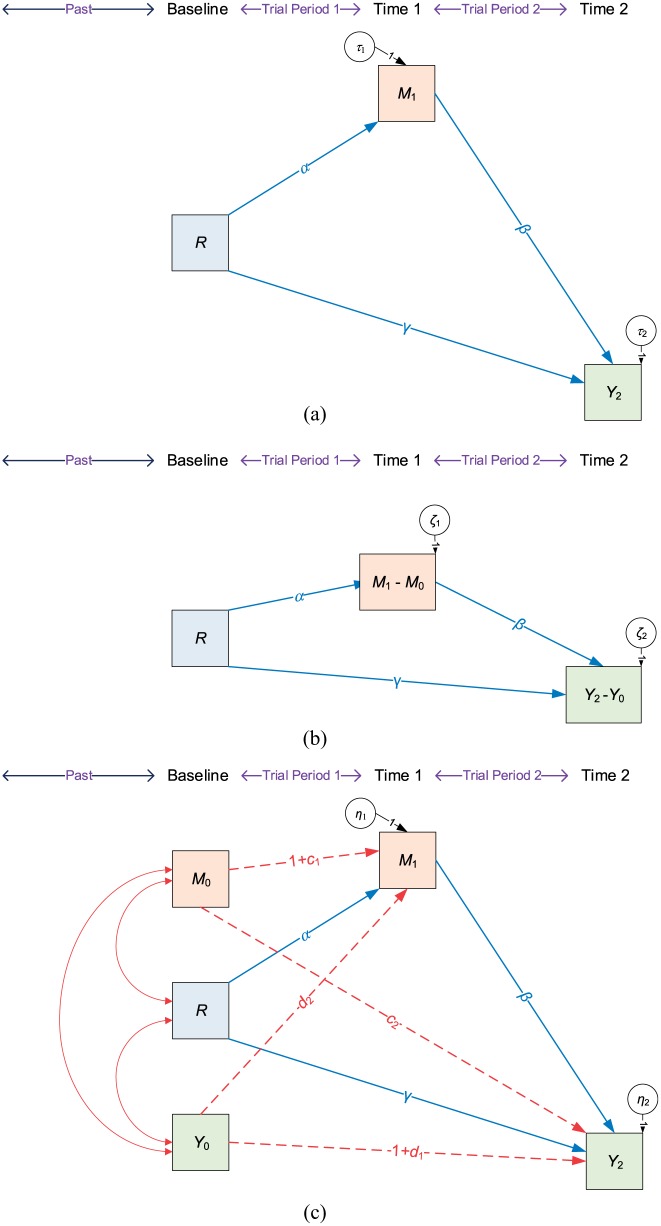
We proceed to contrast the (true) data generating model in Figure 1 with the analysis models assumed by the three competing mediation approaches. These analysis models are fully described by the structural equation diagrams shown in Figure 2. Importantly, the diagrams in Figure 2 provide a graphical representation of the assumptions made by the various approaches as absences of paths between variables indicate independence assumptions. We can therefore utilise these graphs to make predictions about scenarios under which confounding biases might arise in estimators of mediation effects.

Figure 2.

Linear structural equation diagrams describing the analysis models assumed by three approaches to mediation analysis: (a) post approach, (b) change score approach and (c) ANCOVA approach.

Under each mediation analysis approach, the target effect is estimated by the path coefficient labelled $\alpha$ in the structural equation diagrams in Figure 2. Similarly, the NDE is estimated by the path coefficient labelled $\gamma$ in Figure 2. Finally, the NIE is estimated by constructing the product of path coefficients labelled $\alpha$ and $\beta$, with inferences for this product estimator often constructed by bootstrapping as sampling distributions can be skewed.²¹

The analysis model in Figure 2(a) implies that there are no paths connecting R and $M_1$ other than the causal effect of treatment offer. This model assumption agrees with the data generating model in Figure 1 due to randomisation in a trial. As a result, we predicted that the target effect can be estimated without bias using the post approach (A). This analysis model also assumes that there are no paths connecting $M_1$ and $Y_2$ other than the causal effect of the mediator. This model assumption is not in agreement with the data generating model. Instead Figure 1 shows a number of possible paths connecting $M_1$ and $Y_2$. For example, if $c_2\ne 0$ then there exists a so-called backdoor path via $M_0$. As a result of these unaccounted backdoor paths, we predicted that parameters of the true structural model for $Y_2$ cannot be estimated without bias by approach A. Consequently, estimators of both the natural direct and indirect effects may suffer from confounding bias.

The analysis model in Figure 2(b) implies that there are no paths connecting R and $M_1-M_0$ other than the causal effect of treatment offer. This model assumption agrees with the data generating model in Figure 1 and we predicted that the target effect can be estimated without bias using the change score approach (B). This analysis model also implies that there are no backdoor paths connecting $M_1-M_0$ and $Y_2-Y_0$. This causal model assumption is not generally in agreement with the data generating model. Instead, Figure 1 shows a number of possible paths connecting $M_1-M_0$ and $Y_2-Y_0$. For example, if $c_1\ne 0$ then there exists a backdoor path via $M_0$. These paths only cease to exist if some baseline measures are not predictive of subsequent changes. As a result, we predicted that estimators of both natural direct and indirect effects may suffer from confounding bias under approach (B).

The analysis model in Figure 2(c) assumes that all of R, $M_0$ and $Y_0$ have causal effects on $M_1$ and might be correlated with each other. This analysis model includes all the true causes of $M_1$ and is more general than the data generating model in that it leaves all the correlations between the baseline variables to be freely estimated. As a result, we predicted that the target effect can be estimated without bias using the ANCOVA approach (C). This analysis model also assumes that all of $M_1$, R, $M_0$ and $Y_0$ affect $Y_2$. Again, all the true causes of $Y_2$ are included and we predicted that the natural direct and indirect effects can be estimated without bias by approach (C).

To validate our graphically derived bias predictions, we considered six pertinent data generating models for which we could make bias predictions. Table 1 summarises these data generating models together with our predictions. The models were chosen such that they reflected each of the three potential confounding processes (Models 1, 2 and 5 in Table 1). In addition, for each confounding process a second model was included that was subject to additional or altered parameter restrictions, since we predicted that the change score approach would perform favourably under these particular restrictions.

Table 1.

Bias predictions for three different estimators of causal mediation effects.^a

Process involving baseline measures	Parameter restrictionsin data generating model (Figure 1)	(A) Postapproach	(B) Changescore approach	(C) ANCOVAapproach
Model 1: Only $M_0$ observed common cause	$c_1\ne 0;c_2\ne 0$ $l_2=0;d_2=0$	Biased	Biased	Asymptotically unbiased
Model 2: Only $Y_0$ observed common cause	$d_1\ne 0;d_2\ne 0$ $l_2=0;c_1=0$	Biased	Biased	Asymptotically unbiased
Model 3: Only $M_0$ observed common cause and not predictive of $M_1-M_0$	$c_1=0;c_2\ne 0$ $l_2=0;d_2=0$	Biased	Asymptotically unbiased	Asymptotically unbiased
Model 4: Only $Y_0$ observed common cause and not predictive of $M_1-M_0$	$d_1\ne 0;d_2=0$ $l_2=0;c_1=0$	Biased	Asymptotically unbiased	Asymptotically unbiased
Model 5: Only V common cause of baseline levels, assuming $M_0$ not predictive of $M_1-M_0$ and $Y_0$ not predictive of $Y_2-Y_0$	$l_1\ne 0;l_2\ne 0$ $c_1=0;d_1=0$	Biased	Biased	Asymptotically unbiased
Model 6: Only V common cause of baseline levels, assuming $M_0$ not predictive of $M_1-M_0$ and $Y_0$ not predictive of $M_1-M_0$	$l_1\ne 0;l_2\ne 0$ $c_1=0;d_2=0$	Biased	Asymptotically unbiased	Asymptotically unbiased

ANCOVA: analysis of covariance

^aThe target effect can be estimated without bias by either approach. Biases refer to estimators of the natural direct and indirect effects.

Results

Simulation study

Details of our simulation study design are provided in the Supplementary Material. Briefly, we simulated outcomes from a parallel group trial with n = 500 participants (250 per arm) under each of the six models listed in Table 1. Monte Carlo simulation techniques (s = 10,000 simulations) were used to evaluate the statistical properties of the three competing estimation approaches.

Table 2 shows the bias results from the simulation study. The expected values of the competing estimators can be compared against the true estimand values to assess bias:

Table 2.

Bias results from simulation study: expected values of estimators based on s = 10,000 simulations.^a

Process involving baseline measures	Estimation approach	True estimand value
		$\mathrm{AT}{E}_M=0.5$	NIE = 0.125	NDE = 0.375	$\mathrm{AT}{E}_Y=0.5$
Model 1: Only $M_0$ observed common cause	(A)	0.500	0.104	0.395	0.500
	(B)	0.500	0.093	0.407	0.501
	(C)	0.500	0.125	0.375	0.500
Model 2: Only $Y_0$ observed common cause	(A)	0.501	0.115	0.387	0.502
	(B)	0.500	–0.062	0.563	0.500
	(C)	0.500	0.125	0.375	0.501
Model 3: Only $M_0$ observed common cause and not predictive of $M_1-M_0$	(A)	0.501	0.084	0.418	0.502
	(B)	0.500	0.125	0.375	0.500
	(C)	0.500	0.125	0.375	0.501
Model 4: Only $Y_0$ observed common cause and not predictive of $M_1-M_0$	(A)	0.501	0.084	0.418	0.502
	(B)	0.500	0.125	0.375	0.500
	(C)	0.500	0.125	0.375	0.501
Model 5: Only V common cause of baseline levels, assuming $M_0$ not predictive of $M_1-M_0$ and $Y_0$ not predictive of $Y_2-Y_0$	(A)	0.500	0.248	0.253	0.502
	(B)	0.500	0.148	0.352	0.500
	(C)	0.500	0.125	0.375	0.500
Model 6: Only V common cause of baseline levels, assuming $M_0$ not predictive of $M_1-M_0$ and $Y_0$ not predictive of $M_1-M_0$	(A)	0.500	0.136	0.366	0.502
	(B)	0.500	0.125	0.375	0.500
	(C)	0.500	0.126	0.375	0.501

ATE: average treatment effect; NIE: natural indirect effect; NDE: natural direct effect.

Biased estimators are shown in italics.

^aSimulations assumed that treatment effects or mediator effects did not vary between individuals (effect homogeneity).

• Target effect estimation: As expected all three estimation approaches can estimate the target effect without bias. The ANCOVA approach (C) was the most precise across all data generating models. In models where an effect of baseline measures on change in the intermediate variable was assumed absent ($c_1=0$ in Models 2–6) the precision of the change score estimator and the ANCOVA estimator was comparable. This is because under this assumption the true effect of the baseline variable on the post-treatment measure is unity (Figure 1).

• Causal mediation effects estimation: As expected, approach (A) suffered bias in estimates of natural direct and indirect effects under all models. Approach (B) was only able to provide unbiased estimates of mediation effects under Models 3, 4 and 6. As predicted, for approach (B) not to suffer from bias, a necessary assumption is the absence of some effects of baseline measures on change scores. In particular, these absences must be such that they remove any backdoor paths connecting the mediator change score and the clinical outcome change score. As predicted, approach (C) was able to provide unbiased estimates of mediation effects under all models.

• Intention-to-treat effect estimation (clinical outcome): All three estimation approaches were able to estimate the average treatment effect on the clinical outcome without bias. This suggests that respective biases in estimates of NIE and NDE cancel each other out. Out of the three estimators considered here the ANCOVA approach (C) was the most precise under all models.

Worked example in a randomised trial

The Fatigue Intervention by Nurses Evaluation (FINE) trial (IRCTN74156610) was an RCT comparing pragmatic rehabilitation with supportive listening, a non-directive counselling treatment and treatment as usual by the general practitioner for patients in primary care with chronic fatigue syndrome/myalgic encephalomyelitis or encephalitis. When the findings of the trial were reported, pragmatic rehabilitation and supportive listening were each compared with treatment as usual in an intention-to-treat analysis.²²

Wearden and Emsley⁶ examined the potential mediators of the effect of pragmatic rehabilitation on improvements in fatigue. The outcome was the Chalder fatigue scale score at 70 weeks. Reduction in limiting activities at 20 weeks was found to mediate the positive effect of pragmatic rehabilitation on fatigue at 70 weeks. The focus here is on a secondary data analysis of the trial data in order to illustrate the different methods (A)–(C) for dealing with baseline variables in the mediation analysis.

In the trial, 95 patients were randomised to pragmatic rehabilitation and 100 to treatment as usual. We analyse a complete-case dataset containing 146 patients (70 in pragmatic rehabilitation and 76 in treatment as usual), with observed data on seven variables: the outcome (Chalder fatigue score, scored 0–33, high score means more fatigue) at baseline and 70 weeks, the mediator (limiting activities, lower scores indicating more adaptive behaviours) at baseline and 20 weeks, randomisation indicator and the stratification variables (whether the patient was non-ambulatory (y/n) and London myalgic encephalomyelitis criteria).

The analysis was conducted in Stata version 14.2 using the paramed command.¹² Since we assume no interactions and have continuous mediators and outcomes, this produces the same estimates as a structural equation modelling approach would. Note that this differs slightly from the analysis presented by Wearden and Emsley,⁶ which also adjusted for other potential mediators at baseline.

Table 3 shows the results of fitting the three analysis models. For all the three methods, the intention-to-treat result is statistically significant indicating that pragmatic rehabilitation improves fatigue score relative to treatment as usual and estimates vary from −2.76 to −3.25 points. All three estimators are valid with approach (C) providing the most precise estimate. The post approach (A) decomposes this into an NIE of −1.59, with 57% of the total effect mediated. The change score approach (B) indicated that the indirect effect accounted for 68% of the total effect. The ANCOVA approach (C), which the simulations have shown to be the unbiased estimator, gives an indirect effect of −2.55 accounting for 86% of the total effect. While approach (C) appears to remove bias, for the NIE this comes at the price of standard error (SE) inflation. However, the bias correction outweighs this inflation. Consistent with the results of our supplementary simulation study for the NIE, the closed form of the SEs is close to the bootstrap SEs for methods (A) and (B), whereas for method (C) the closed form estimated SE of 0.71 is an underestimate of the bootstrap SE of 0.85.

Table 3.

Causal treatment effect estimates from the FINE trial ((standard errors in brackets).

Estimation approach	Intention-to-treat effect	Natural direct effect	Natural indirect effect	PM%
(A)	−2.76 (1.27), p = 0.03	−1.18 (1.28), p = 0.36	−1.59 (0.57), p = 0.01	57
(B)	−3.25 (1.30), p = 0.01	−1.04 (1.33), p = 0.43	−2.21 (0.68), p < 0.01	68
(C)	−2.98 (1.25), p = 0.02	−0.43 (1.28), p = 0.74	−2.55 (0.71), p < 0.01	86

PM% is percentage of total effect mediated by natural indirect effect.

For all the three approaches, the indirect effect is statistically significant while the direct effect is not significant. This indicates that there is mediation through limiting activities. Qualitatively, the methods all give this conclusion, but as the aim of mediation is to accurately decompose the total effect into an indirect effect and a direct effect, the methods give various estimates, and we conclude that method (C) provides the correct estimate.

Discussion

We recommend that trialists measure baseline values of putative mediator variables as well as the clinical outcome when planning to conduct mediation investigations. Of the three mediation approaches considered here, we recommend the ANCOVA approach which includes baseline measures of the intermediate and clinical variable as covariates in all regression models. It was the only approach that was able to provide valid estimates under all the scenarios that we considered. Importantly, in contrast to total treatment effect estimation, when partitioning effects into mediated and non-mediated components, the decision for ANCOVA is based on bias reduction rather than precision arguments.

Mediation investigations based purely on post-treatment measures of the putative mediator and clinical outcome were found to suffer from bias under all the processes involving baseline variables that we considered. Importantly, the change score approach, often favoured by practitioners, only removes biases under additional assumptions regarding independence of measures of baseline values and change over time. The minimum assumptions necessary are that neither baseline measures of the putative mediator nor of the clinical variable predict change in the mediator variable. Such predictive effects might be present due to baseline values predicting illness trajectories. In addition, negative predictive effects of baseline levels on change in the same variable might occur as a result of regression to the mean, especially in populations that have been selected as ‘severe’ on the basis of outcome variables that might be subject to measurement error.²³ Independence assumptions have been questioned before (e.g. Gollob and Reichardt²⁴ or Cole and Maxwell¹¹) and are unlikely to hold in mental health trials.

Our findings are consistent with the literature. The estimation of the causal effect of a treatment in an observational study suffers from the same confounding issue. Lepage et al.²⁵ found that when treatment assignment was driven by baseline variables only the ANCOVA approach was unbiased for the average treatment effect. A change score approach was again found to be suffering from bias when baseline measures predicted subsequent change. Finally in line with the study by Vandenberghe et al.,²⁶ we found that for continuous mediators and outcomes results were robust against misspecification of the mediator model.

For simplicity, we have here assumed no interactions between baseline variables and treatment allocation and no interaction between the mediator and the treatment in the model for the clinical outcome (moderated mediation). However, we anticipate that the bias results also hold under more complex data generating models. The ANCOVA approach to mediation analysis can be generalised to situations in which there is treatment moderation by including relevant interaction terms in the models.^27–29 In practice, any ‘no interaction assumption’ should be verified before proceeding to use the simpler ANCOVA approach.