Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Jun 8.
Published in final edited form as: Appl Geogr. 2016 Sep 28;76:173–183. doi: 10.1016/j.apgeog.2016.09.025

Mapping Resource Selection Functions in Wildlife Studies: Concerns and Recommendations

Lillian R Morris 1,2, Kelly M Proffitt 3, Jason K Blackburn 1,2,*
PMCID: PMC5992917  NIHMSID: NIHMS819993  PMID: 29887652

Abstract

Predicting the spatial distribution of animals is an important and widely used tool with applications in wildlife management, conservation, and population health. Wildlife telemetry technology coupled with the availability of spatial data and GIS software have facilitated advancements in species distribution modeling. There are also challenges related to these advancements including the accurate and appropriate implementation of species distribution modeling methodology. Resource Selection Function (RSF) modeling is a commonly used approach for understanding species distributions and habitat usage, and mapping the RSF results can enhance study findings and make them more accessible to researchers and wildlife managers. Currently, there is no consensus in the literature on the most appropriate method for mapping RSF results, methods are frequently not described, and mapping approaches are not always related to accuracy metrics. We conducted a systematic review of the RSF literature to summarize the methods used to map RSF outputs, discuss the relationship between mapping approaches and accuracy metrics, performed a case study on the implications of employing different mapping methods, and provide recommendations as to appropriate mapping techniques for RSF studies. We found extensive variability in methodology for mapping RSF results. Our case study revealed that the most commonly used approaches for mapping RSF results led to notable differences in the visual interpretation of RSF results, and there is a concerning disconnect between accuracy metrics and mapping methods. We make 5 recommendations for researchers mapping the results of RSF studies, which are focused on carefully selecting and describing the method used to map RSF studies, and relating mapping approaches to accuracy metrics.

Keywords: habitat model, species distribution model map, elk

1. Introduction

Understanding the spaced used by animals is an important component to wildlife management, conservation and population health. For example, predicting a species’ distribution has been used to inform endangered species management and habitat conservation efforts (Dzialak et al., 2013; Dzialak, Olson, Harju, Webb, & Winstead, 2012; Fortin, Courtois, Etcheverry, Dussault, & Gingras, 2008; Richardson, Stirling, & Hik, 2005; Roever, Van Aarde, & Leggett, 2013). As one example, such modeling has been employed to address concerns including the evaluation of conservation networks for African elephants (Loxodonta africana oxyotis;(Roever et al., 2013). Predicting species distributions has also been used to evaluate anthropogenic effects on wildlife distribution (Bleich, Davis, Marshal, Torres, & Gonzales, 2009; Mark Hebblewhite & Merrill, 2008; Jiang, Ma, Zhang, & Stott, 2009; Johnson et al., 2005; Merkle, Krausman, Decesare, & Jonkel, 2011; Seip, Johnson, & Watts, 2007). For example, Johnson et al. (2005) modeled the potential distribution for three arctic species and evaluated the effect of mineral exploration on habitat suitability in an effort to inform management. Species distribution modeling is also an important tool for evaluating the effect of environmental and climatic changes on habitat use (Alamgir, Mukul, & Turton, 2015; Ramirez-Villegas et al., 2014). Additionally, predicting the spatial distribution of a species has also played a role in understanding the distribution of important animal diseases (Brook & McLachlan, 2009; Dugal, Beest, Wal, & Brook, 2013; Morris, Proffitt, Asher, & Blackburn, 2015; Proffitt et al., 2011). For example, studies have modeled the interaction of disease reservoirs and susceptible hosts. Proffitt et al. (2011) identified regions where elk (Cervus elaphus) and livestock were at risk of commingling in a brucellosis endemic region, and Morris et al. (2015) predicted landscapes where elk distributions may overlap with an anthrax zone in the Greater Yellowstone Ecosystem.

Each of the examples above employed some form of species distribution modeling. Generally, these approaches aim to measure non-random relationships between locations that describe an animal’s position in space and environmental conditions. Recent advancements in the availability of spatial environmental data, wildlife telemetry technologies, and developments in modeling methods have transformed the realm of species distribution modeling (Elith & Leathwick, 2009). Digital elevation models of the earth surface, climate parameters, and remotely sensed imagery of land surface conditions are accessible for landscapes across the globe (in many cases at no cost), and software to integrate and analyze these data sets in a geographic information system (GIS) framework is widely available. Wildlife tracking has been transformed by the advent of satellite telemetry, which allows animals to be tracked 24 hours a day with global positioning system (GPS) locations recorded in rapid succession for extended periods of time. The implementation of GPS telemetry has led to extensive datasets and the accompanying development of quantitative methods for their analysis (Mark Hebblewhite & Haydon, 2010). The integration of detailed environmental information and fine spatial-temporal scale wildlife location data provides an exciting opportunity to address critical questions related to wildlife conservation and management through species distribution modeling. The notable increase in studies employing species distribution modeling in recent years reflects the importance of these models and their applicability to a wide range of ecological, management and conservation objectives. At the same time, the expansive data sets and complexities associated with modeling approaches raises important concerns about the accurate and appropriate implementation of modeling approaches (Cagnacci, Boitani, Powell, & Boyce, 2010; Mark Hebblewhite & Haydon, 2010).

There are several methods that are frequently used to model wildlife and livestock distributions across multiple scales from local to global. Ecological niche modeling (ENM) approaches include a suite of methods (Peterson, 2011) that identify the potential distribution of species or communities (Alvarado-Serrano & Knowles, 2014; Ferrier & Guisan, 2006). ENM approaches can evaluate presence only, presence absence, or presence pseudo-absence occurrence data. Commonly, presence only modeling approaches capitalize on idiosyncratic data from field surveys, natural history collections, published ranges, and public databases for occurrence data for ENM models (Alvarado-Serrano & Knowles, 2014). These approaches often result in range-wide estimates of a species’ distribution (Blackburn, 2010), though several studies have developed local scale niche-based geographic predictions.

Smaller scale, local studies often aim to model resources preferred or avoided by a population using resource selection function (RSF) modeling of wildlife telemetry data. One approach to RSF modeling is to compare the environmental or landscape attributes of used locations to the attributes of a set of available locations (Manly, McDonald, Thomas, McDonald, & Erickson, 2002). Used locations are frequently represented by telemetry fixes (e.g. GPS fixes or VHF relocations) or survey observations and available locations are defined by the researcher based on the spatial-temporal scale and scope of the research question. RSF model outputs are used to predict wildlife distributions; however, methods of mapping distributions from RSF model outputs are variable and often poorly described. The focus of this review is on the appropriate methods for mapping predicted species distributions from RSF outputs.

There has recently been an increased demand for mapped products in the fields of conservation and land management (Elith & Leathwick, 2009), which includes RSF studies. Mapping RSF outputs may make model results more accessible and relevant to managers (Johnson, Nielsen, Merrill, McDonald, & Boyce, 2006). For example, a map identifying the predicted resource selection of male elk during the anthrax season is likely more informative than reporting the sign and significance of model covariates for a manager implementing disease surveillance efforts (Morris et al., 2015). Maps illustrating predicted resource selection can provide an important tool to managers, highlighting the need for easily interpretable and accurate maps.

Presently, there is not a consensus in the literature on the most appropriate method for mapping RSF outputs. There are multiple challenges associated with RSF mapping and interpretation and the methods for mapping RSF results onto the landscape are variable and inconsistent across studies. For example, splitting RSF values into bins (e.g. (Morris et al., 2015), converting RSF values into a binary variable (Oehlers, Bowyer, Huettmann, Person, & Kessler, 2011), and employing a linear stretch on RSF values rescaled from 0 to 1 (Mark Hebblewhite & Merrill, 2008) have all been employed to map RSF outputs derived from the same modeling approach. There are also a large number of studies where methods for mapping RSF outputs are not reported (Proffitt et al., 2011), or map legends are nonexistent or uninformative. Even with appropriate map legends, interpreting RSF values is challenging, as these values are not equivalent to the true probability of selection (Keating & Cherry, 2004). Harzel et al. (2006) suggested that displaying RSF results as a continuous surface can be misleading and RSF values should be reclassified, or binned, for map creation to provide honest and relevant predications. However, there has been minimal discussion on the most appropriate binning methods, and displaying RSF values as a continuous surface remains common (Brook & McLachlan, 2009; Dellinger, Proctor, Steury, Kelly, & Vaughan, 2013; Dugal et al., 2013; Fortin et al., 2008; Horne et al., 2014; Teichman, Cristescu, & Nielsen, 2013).

In contrast to the sparse discussion of RSF mapping methods, approaches for testing the predictive accuracy of RSF models have been discussed at length in the literature (Boyce, Vernier, Nielsen, & Schmiegelow, 2002; Fortin & Fortin, 2009; Hirzel et al., 2006; Johnson et al., 2006; Keating & Cherry, 2004; Manly et al., 2002; Wiens, Dale, Boyce, & Kershaw, 2008). Wiens et al. (2008) advise that the failure to appropriately test the predictive accuracy of RSF models could lead to management errors resulting in grave consequences for the species of concern. Mapping approaches are not discussed as a component of accuracy metrics, which suggests that RSF maps might not be displaying accurate information. Our objectives were to 1) summarize the methods used to map RSF outputs, 2) discuss the relationship between mapping approaches and accuracy metrics, 3) conduct a case study on the implications of employing different mapping methods, and 4) provide recommendations as to appropriate mapping techniques for RSF studies.

2. Methods

2.1 Literature Review

We performed a literature review using the Google Scholar and Web of Science search engines to identify RSF studies with a mapping component. In Google Scholar, we searched for the exact phrase “resource selection function” and the word “map” found anywhere in the article. We inspected the articles resulting from this search for 1) peer-reviewed journal sources; 2) a logistic RSF modeling approach the employs a use-verses-availability design (Manly et al., 2002),3) The inclusion of a map representing RSF results. In Web of Science we searched for “resource selection function and map” found anywhere in the article. A filter to include only peer-reviewed journal articles, and fields of study related to wildlife were applied. We inspected Web of Science results for 1) a logistic RSF modeling approach and 2) the inclusion of a map representing RSF outputs. We did not include RSF’s with a Bayesian framework, or studies that solved a resource selection probability function (RSPF) where the true probability was estimated. For each article that met the above criteria, we classified the method used to map RSF outputs and the method to test model predictive accuracy. We were specifically interested in summarizing the relationship between the method for partitioning data and the method used to calculate accuracy metrics. We reported the percentages of papers included in the review that used each method. The following caveats apply to these methods: We assumed that Web of Science and Google Scholar were unbiased sources. We assumed relevant literature would include the phrase “resource selection function” and the word “map”. We also limited our search to peer-reviewed journal articles in English.

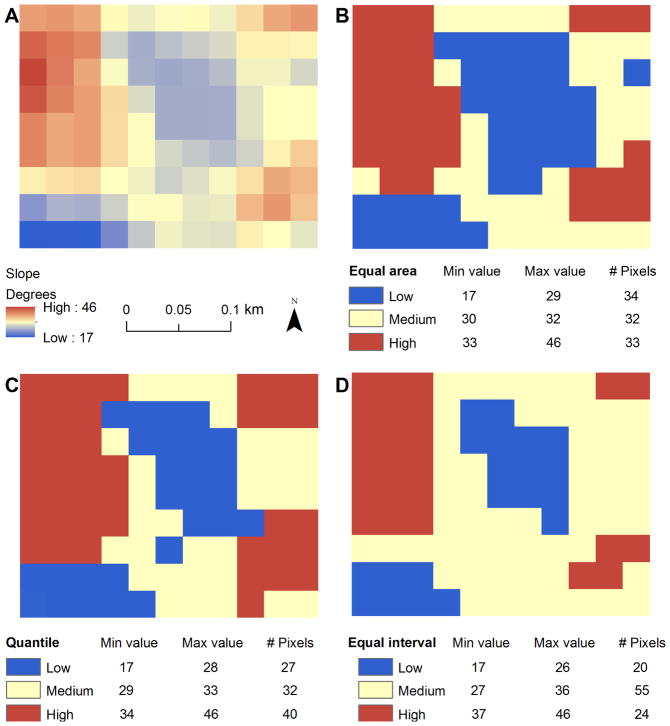
The primary classifications were a stretched display of RSF results compared to a binned approach, which requires splitting continuous values into bins. A continuous surface can re-scale values from 0 to 1, stretch from the minimum to maximum value, use standard deviations, or a histogram smoother. Commonly used binning approaches include quantiles, equal intervals, and equal area bins (Figure 1). A quantile classification splits values into groups that contain an equal number of values. An equal interval classification divides values into groups that contain an equal range of values. We also mapped our model following the most common method for mapping RSF values in predictive accuracy tests (10 equal area bins; Figure 1). An equal area classification divides values into groups that cover the same amount of area on the landscape.

Figure 1.

Figure 1

Open in a new tab

Using slope to exemplify the most commonly used display schemes and binning classifications in resource selection function studies: stretched display from low to high (panel A), equal area bins (panel B), quantile bins (panel C), and equal interval bins (panel D). The number of minimum and maximum slope value, and the number of pixels in each classification are reported for methods using binning.

2.2 Case Study

To illustrate differences in the most commonly used mapping approaches from our literature review, we projected an existing RSF model onto a geographic landscape for several of these methods. We used an existing landscape-level RSF model for male elk during summer months in southwest Montana developed with a use-availability framework (Morris et al., 2015). The model was developed using a generalized linear mixed effect model including fixed and random effects to estimate resource selection. Used points were derived from GPS telemetry fixes from 13 collared male elk tracked from June to August 2010–2012 and we generated five random points for each used point within a population-level minimum convex polygon (MCP) to represent availability. The dependent variable was a binary variable representing use verses availability.

We created an a priori model list composed of all subsets of environmentally meaningful variables extracted from the literature. We selected the most parsimonious model using Akaike’s Information Criterion (AIC). Environmental covariates considered in model development included two land cover types: forested and non-forested (2010 Montana Spatial Data Infrastructure land cover dataset; http://geoinfo.montanastatelibrary.org/data/msdi/landuse/), elevation (national elevation dataset; http://ned.usgs.gov/), slope, aspect categorized as southerly (134 – 224°) and not southerly (0 – 135°, 225 – 360°), distance to primary, secondary and tertiary roads following Montgomery et al. (2013), and wolf predation. We standardized all continuous variables to allow for a direct comparison between model coefficients. We fit a generalized linear fixed effect model to each model in the list using the lme4 package in R (Bates, Maechler, Bolker, & Walker, 2014). We projected the final model results onto the landscape by solving the logistic equation:

w(x)=exp(β0+β1X1+⋯+βiXi)

where w(x) is the relative probability of a pixel being selected, β0 is the intercept, and β1 is the estimated coefficient for variable X1. If β > 1 a preference for that resource is indicated, and a β < 1 indicates avoidance of that resource (Manly et al. 2002). The logistic equation for our final model was solved using unstandardized model coefficients in raster calculator in ArcGIS 10.1 (ESRI, Redlands, CA), which resulted in a raster-based continuous RSF surface across our study area. We used the three most commonly found methods for displaying RSF outputs, derived from our literature review, to create maps of our model (0 to 1 continuous surface, 5 quantiles, 4 equal intervals, and 10 equal area bins; Figure 1).

We validated the RSF model by dividing our dataset of used elk GPS fixes into 5 groups of 25% testing, and 75% training and employing a k-fold cross validation approach described by Boyce et al. (2002). The model was fit with each of the training datasets and projected onto the study area. The resulting RSF surface was split into bins following the three most common mapping methods that used binning as identified in the literature review (5 quantiles, 4 equal intervals) and the most common binning method employed for predictive accuracy metrics following Boyce et al. (2002) (10 equal area bins). The lowest bin rank (1) corresponded to the lowest probability of selection and the highest bin rank (10) corresponded to the highest probability of selection.

To quantify differences in map results we calculated the percentage of the study area landscape that was made up of the top 50% estimate for each map approach. We calculated the percentage of the study area with linear values ≥ 0.5, quantile bins 3 through 5, equal interval bins 3 and 4, and equal area bins 5 through 10. To test the relationship between predicted selection and use for each binning approach, testing data were overlaid on each model and the number of testing points falling in each bin was calculated. A spearman rank correlation coefficient between bin rank and number of points per bin was calculated. A strong, positive correlation coefficient is indicative of a strong relationship between used locations and predicted selection. The average correlation coefficient for all 5 folds was calculated for each mapping approach.

3. Results

3.1 Literature Review

Our Google Scholar search had 906 results, and our Web of Science search had 283 results. 101 peer-reviewed articles met our criteria and were included in the literature review. We identified two primary mapping approaches: stretched displays (34 studies, ~34% reviewed studies) and binned displays (68 studies, ~66% reviewed studies). We found 5 different stretched display approaches (Table 1). Stretching values from 0 to 1 (15 studies, ~44% stretched display studies) and stretching values from low to high (14 studies, ~41% stretched display studies) were the most common methods using a stretched display. Stretching values from the minimum to maximum values (3 studies, ~9% stretched display studies), using a histogram smoother (1 study, ~3% stretched display studies), and standard deviations (1 study, ~3% stretched display studies) were also used to generate stretched displays.

Table 1.

Summary of methods for mapping resource selection function model results that employ stretched displays based on a review of the literature. The number of studies employing each method, the percentage of studies using each method, and references are reported.

Method Number of studies % studies References
Histogram smoother 1 2.94% (M Hebblewhite, Merrill, & McDonald, 2005)
0 – 1 stretch 15 44.12% (Boyce & Waller, 2003; Brook & McLachlan, 2009; DeCesare et al., 2012; Dellinger et al., 2013; Dugal et al., 2013; Fortin et al., 2008; Mark Hebblewhite & Merrill, 2008; Horne et al., 2014; Hough & Dieter, 2009; Johnson, Seip, & Boyce, 2004; Mace et al., 1999; Mashintonio et al., 2014; Richardson et al., 2005; Squires et al., 2013; Teichman et al., 2013)
min – max stretch 3 8.82% (Allred, Fuhlendorf, Engle, & Elmore, 2011; Allred, Fuhlendorf, & Hamilton, 2011; Singh, Yoccoz, Bhatnagar, & Fox, 2009)
Low to high stretch 14 41.18% (Anderson et al., 2005; Barker & Derocher, 2010; Boyce & Waller, 2003; Durner et al., 2009; Fattebert, Robinson, Balme, Slotow, & Hunter, 2015; Irwin, Rock, & Rock, 2012; Joly, 2011; Krebs, Lofroth, & Parfitt, 2007; Loe, Bonenfant, Meisingset, & Mysterud, 2012; Merkle et al., 2011; Morehouse & Boyce, 2013; Niemuth, Estey, & Loesch, 2002; Recio, Mathieu, Virgós, & Seddon, 2014; Weckworth et al., 2013)
Standard deviations 1 2.94% (Newsome, Ballard, Dickman, Fleming, & Howden, 2013)
Total 34 100%
Open in a new tab

We found 9 primary RSF mapping methods using a binned approach (Table 2). Splitting RSF values into quantiles (28 studies, ~41% binned display studies) was the most common binned method. The number of quantile bins ranged from 2 to 20, and 5 (9 studies) bins was the most common approach. Approximately 19% of studies using a binned approach split RSF values into equal interval bins. The number of equal interval bins ranged from 3 to 10, and 4 bins was the most common approach (4 studies). Approximately 9% of studies using a binned approach split RSF values into categorical bins (e.g. high, medium, low), and did not report how bins were defined. Approximately 7% of studies using a binned approach used standard deviations to define bin breaks. Approximately 6% of studies using a binned approach split the study area into 5 or 10 equal areas based on RSF values. Approximately 6% of studies using a binned approach used observed data to define break points, and 4 different methods were found for this approach. Approximately 3% of studies using a binned approach rescaled RSF values from 0–1 and split values into bins with arbitrary cutoffs. Approximately 3% of studies using a binned approach used geometric means to define bin breaks. Approximately 2% of studies using a binned approach created a binary variable from RSF values by defining a threshold for high verse low probability.

Table 2.

Summary of methods for mapping resource selection function model results that employ binned displays based on a review of the literature. The number of studies, percentage of studies, are references to the specific studies are reported.

Bin Method # studies % studies using bins References
Quantiles 28 41.18%
2 bins 1 (Kunkel, Atwood, Ruth, Pletscher, & Hornocker, 2013)
3 bins 1 (Carroll, Noss, & Paquet, 2001)
4 bins 7 (Beckmann, Murray, Seidler, & Berger, 2012; Clark et al., 2014; Coe et al., 2011; Hodder, Johnson, Rea, & Zedrosser, 2014; Jiang et al., 2009; Johnson et al., 2005; Loring et al., 2014)
5 bins 9 (Costello, Cain, Nielson, Servheen, & Schwartz, 2013; Doherty, Naugle, & Walker, 2010; Dzialak et al., 2013, 2012; Harju, Olson, Dzialak, Mudd, & Winstead, 2013; Lewis et al., 2011; Smith, Kirol, Beck, & Blomquist, 2014; Webb et al., 2013; White et al., n.d.)
6 bins 1 (Johnson & Gillingham, 2005)
7 bins 1 (Pigeon, Nielsen, Stenhouse, & Côté, 2014)
10 bins 7 (Dickson et al., 2014; Dzialak et al., 2013; Dzialak, Olson, Webb, Harju, & Winstead, 2015; Florkiewicz, Maraj, Hegel, & Waterreus, 2007; Northrup, Stenhouse, & Boyce, 2012; J. Polfus, Hebblewhite, & Heinemeyer, 2011; Takahata, Nishino, Kido, & Izumiyama, 2013)
20 bins 1 (Proffitt et al., 2011)
Equal Interval 13 19.12%
3 bins 3 (Chimeddorj, Buuveibaatar, Onon, Munkhtogtokh, & Reading, 2013; Enari & Sakamaki–Enari, 2013; Singleton, Lehmkuhl, Gaines, & Graham, 2010)
4 bins 4 (Campos, Gatica, & Bellis, 2015; Dillard, Russell, & Ford, 2008; Miller, Jhala, Jena, & Schmitz, 2015; Pedersen, Jepsen, Yoccoz, & Fuglei, 2007)
5 bins 3 (Girard, Bork, Nielsen, & Alexander, 2013; Gottschalk, Ekschmitt, İsfendiyaroglu, Gem, & Wolters, 2007; Shanley, Pyare, & Smith, 2013)
8 bins 1 (Shanley, Kofinas, & Pyare, 2013)
10 bins 2 (Shanley & Pyare, 2011; Speed, Woodin, Tømmervik, Tamstorf, & van der Wal, 2009)
categorical bins w/undefined methods 6 8.82%
3 bins 2 (Ciarniello, Boyce, Heard, & Seip, 2007; Ciarniello, Boyce, Seip, & Heard, 2009)
4 bins 1 (Erickson, McDonald, & Skinner, 1998)
5 bins 2 (Elbroch, Lendrum, Newby, Quigley, & Craighead, 2013; Roever et al., 2013)
4 to 9 bins 1 (Chetkiewicz & Boyce, 2009)
Standard deviations 5 7.35%
4 bins 2 (Bleich et al., 2009; May et al., 2008)
5 bins 2 (Beerens, Gawlik, Herring, & Cook, 2011; Nielsen et al., 2004)
6 bins 1 (Montgomery, Roloff, Millspaugh, & Nylen-Nemetchek, 2014)
Equal Area 4 5.88%
5 bins 1 (Matthews & Spooner, 2014)
10 bins 3 (Mark Hebblewhite, Miquelle, Murzin, Aramilev, & Pikunov, 2011; J. L. Polfus, Heinemeyer, & Hebblewhite, 2014; Roever et al., 2013)
Breakpoint defined by observed data 4 5.88%
4 classes defined by true positive = true negative 1 (Kinley, Whittington, Dibb, & Newhouse, 2014)
Percentiles from observed data-10 1 (Seip et al., 2007)
binary based on minimum score for used home ranges 1 (Broman, Litvaitis, Ellingwood, Tate, & Reed, 2014)
4 bins based on predictive accuracy 1 (Jędrzejewski et al., 2008)
0 – 1 rescale with arbitrary bin breaks 2 2.94%
4 bins 1 (Sakuragi et al., 2003)
5 bins 1 (Tamstorf, Aastrup, & Cuyler, 2005)
Geometric Mean 3 4.41%
5 bins 1 (Masse, Tefft, & McWilliams, 2014)
8 bins 1 (Carpenter, Aldridge, & Boyce, 2010)
10 bins 1 (Aldridge, Saher, Childers, Stahlnecker, & Bowen, 2012)
binary cutoff 2 2.94%
threshold between .4 – .6 1 (Oehlers et al., 2011)
highest 10% values = high probability 1 (Bleich et al., 2008)
Total 68 100%
Open in a new tab

We identified 4 methods for testing the predictive accuracy of RSF models (Table 3), and ~18% of studies did not report a method for testing predictive accuracy. All of the reported methods required splitting RSF values into bins. Approximately 50% of studies employed k-fold cross validation using spearman rank correlation coefficient between bin number and number of testing points per bin. The number of bins ranged from 3 to 20 and binning methods included quantiles, equal area bins, and undefined methods. The most common binning approach was to split RSF values into 10 equal area bins. Approximately 15% of studies used receiver operating characteristics (ROC; (McNyset, 2005)) or area under the curve (AUC; (McNyset, 2005)) approaches. The AUC and ROC approaches both require defining an arbitrary cutoff to create a binary variable that defines presence and absence. Approximately 14% of studies used regression to compare bin rank and expected number of points per bin following (Johnson et al., 2006). The number of bins ranged from 5 to 20, and methods for binning included quantiles, equal area bins, and undefined methods. The most common bin method was 10 equal area bins. Approximately 3% of studies reported the spearman rank correlation coefficient of used verses random points within each strata following the methods of Fortin et al. (2009), which is an accuracy approach for discrete choice RSF’s. Both studies used equal area bins and the number of bins ranged from 10 to 21.

Table 3.

Summary of the most frequently used methods to test the predictive accuracy of Resource Selection Functions (RSF). The number of bins and bin classification method is described in addition to the number of percentage of studies (out of 101 studies reviewed) that used the method.

Method Description Number of Studies % studies reviewed
Number of bins Bin classification
Spearman rank correlation between bin rank and testing points in each bin following Boyce et al. (2002) 3 – 20 Undefined, equal area, quantiles 50 49.50%
No method for testing predictive accuracy reported N/A N/A 17 17.83%
Receiver Operating Characteristics (ROC) / Area Under Curve (AUC) 2 binary 15 14.85%
Regression between bin rank and expected number of points in each bin following Johnson et al. (2006) 5 – 20 Undefined, equal area, equal probability, quantile 14 13.86%
Frequency of testing data in RSF bins following Fortin et al. (2009) 5, 20 Equal area 2 2.97%
Alternative methods with a sample size of 1 11 10.89%
Open in a new tab
**

some studies used multiple accuracy metrics, and percentages do not sum to 100%.

We found 11 studies that used unique predictive accuracy metrics. Some of these approaches included visual comparison of an RSF map and used points (Mashintonio, Pimm, Harris, van Aarde, & Russell, 2014), generating a contingency table (Mace, Waller, Manley, Ake, & Wittinger, 1999), calculating a correlation between two RSF surfaces built with different data (Brook & McLachlan, 2009), and reporting the percentage of location data in 5 equal sized bins (Webb, Dzialak, Kosciuch, & Winstead, 2013). Multiple studies employed more than one approach to testing predictive accuracy, which is why the methods we describe do not sum to the total number of studies reviewed (101).

3.2 Case Study

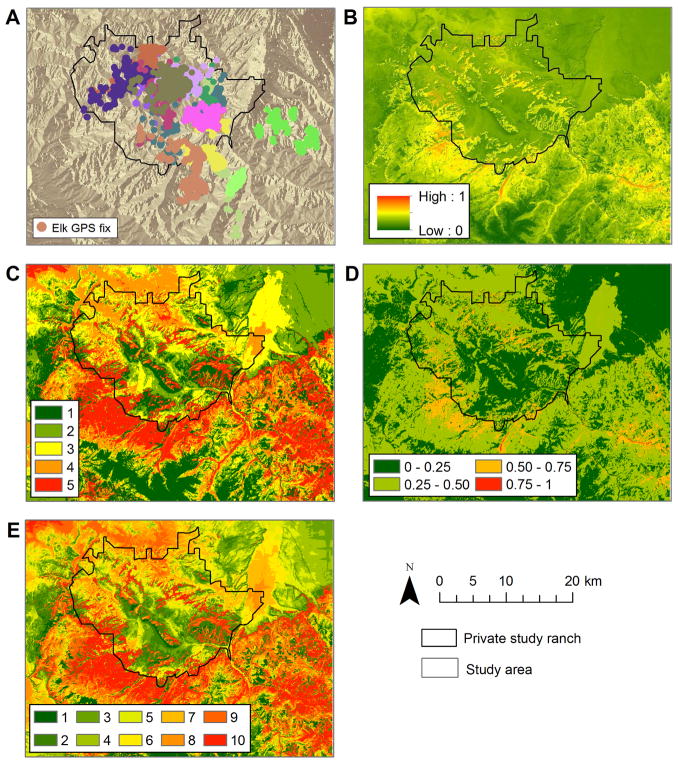
The most parsimonious RSF model for male elk during summer months indicated elk selection for areas in closer proximity to tertiary roads, further proximity to secondary roads, forested land cover (compared to shrubland and grasslands), gentler slopes, and lower elevations (see Table 4 (Morris et al., 2015)). There appeared to be drastic differences in the visual interpretation between the four mapping approaches employed to map our RSF output (0 to 1 linear stretch, 5 quantiles, and 4 equal intervals, 10 equal area bins; Figure 2). Linear stretch values > 0.5 covered ~6.4 % of the study area. Bins 3 through 5 for the quantile classification made up 59.78% of the study area. The top two bins using the linear stretch classification composed ~6.4% of the study area. The top 5 bins using the 10 equal area bin classification was ~63% of the study area.

Table 4.

Standardized coefficient estimates and 95% confidence intervals for covariates included in the final resource selection function model for male elk during the anthrax risk period (June to August) in southwest Montana, USA using elk location data from 2010 –2012.

95% Confidence Interval
Variable Estimate Lower Upper
(Intercept) −2.0724 *** −2.1255 −2.0200
Distance to Tertiary Roads −0.0352 * −0.0731 0.0024
Distance to Secondary Roads 0.1660 *** 0.1263 0.2058
Forest (as compared to grassland and shrubland) 0.8490 *** 0.7750 0.9233
Slope −0.1794 *** −0.2160 −0.1429
Elevation −0.2602 *** −0.3089 −0.2117
Open in a new tab
***

indicates significance with 99% confidence;

**

indicates significance with 95% confidence;

*

indicates significance with 90% confidence

Figure 2.

Figure 2

Open in a new tab

Male elk resource selection function in southwest Montana, USA using location data from June to August 2010 – 2012. Resource selection function results were mapped following the primary methods extracted from our literature review. Telemetry GPS points for bull elk used in model development are shown in panel A, and each individual elk is a unique color. RSF results were mapped using 4 methods: rescaled 0 to 1with a stretched display (panel A), 5 quantile bins (panel B), 4 equal interval bins (panel C), and 10 equal area bins (panel D).

The spearman rank correlation coefficient between bin number and number of points per bin for the 5 quantile map ranged from 0.7 to 0.9 with an average of 0.86, and 4 out of 5 folds were significant at 90% confidence. The spearman rank correlation coefficient between bin number and number of points per bin for the 4 equal interval map was −0.8 across all 5 folds, which suggests there were more testing points in lower ranked bins, but the relationship was not significant at 90%. The Spearman rank correlation coefficient between bin number, and number of points per bin for the 10 equal area bins ranged from 0.733 to 0.927 with an average of 0.847 across the five iterations. All correlations were significant with 90% confidence. The linear stretch map was difficult to validate, as all methods described in the literature for a use - availability approach required binning RSF values. A visual inspection of used points overlaid on the map surface suggested that the model was not successfully predicting used points as higher probability of selection (Figure 1).

4. Discussion

Currently, there is not a consensus in the literature on the most appropriate method for mapping RSF results, the mapping methods are not reported or are difficult to interpret, and maps do not reflect methods that were used to test predictive accuracy for many studies. These findings are concerning, as the spatial predictions resulting from RSF studies are an invaluable tool in animal conservation and wildlife management. Our results show that methods for mapping RSF outputs must be clearly defined and carefully selected.

We found a high degree of variability across studies in approaches for mapping RSF outputs, and 38 different approaches were found for the 101 studies reviewed. Displaying RSF values as a continuous surface (~34%), and splitting RSF values into bins (~66%) were the two primary approaches used for mapping. The display of a continuous RSF surface is a popular mapping approach despite recommendations from Hirzel et al. (2006) that a continuous RSF surface can be misleading. The majority of binning approaches grouped RSF values based on the number of values in each group, which included quantiles, equal area, and geometric mean classifications. These classification schemes successfully manage outliers and convert non-normal distributions into ranked bins where the relative probability of selection is clearly defined. The alternative binning approaches involve splitting the range of values without considering the number of data points in each break, which include equal interval, and standard deviation classifications. These approaches are more sensitive to outliers and non-normal distributions. Several studies, including many of the equal interval classifications, rescaled RSF values from 0 to 1. A RSF predicts the relative probability of selection, and is not equivalent to a true probability (Keating & Cherry, 2004); therefore, rescaling values is not necessary for RSF results (Boyce et al., 2002).

In addition to variability in mapping approaches, we identified a lack of detail in methods descriptions. The methods section of a publication is arguably the most important component, as it provides the necessary information for the reader to determine the validity of the results and associated conclusion (Azevedo et al., 2011). Reported methods should also provide enough detail for the reader to replicate the analysis (Azevedo et al., 2011). For many studies included in this review, the methods for mapping RSF outputs were not clearly described, or were not replicable for multiple studies in our review. For example, ~14% of studies displayed a continuous RSF surface labeled as low to high without describing how the surface was derived, which could be indicative of multiple methods including a histogram smoother, standard deviation display, and a low to high display. An additional ~6% of studies displayed categorical bins (e.g. low, medium, high), but did not describe the categorization procedure, which makes it impossible for the approach to be replicated. This lack of detail also makes the interpretation of maps difficult, as classifying bins using quantiles has a different interpretation than an equal interval classification. For example, the results of our case study reflect that the method selected for mapping RSF predictions has an impact on the resulting map. The stretched map and 4 equal interval classifications were similar to each other, but significantly different from the 5 quantile and 10 equal area binned maps. The number of bins also appeared to affect the amount of detail that could be derived from the map, and the 10 equal area bins appeared to be more informative than the 5 quantile bins. These results suggest that mapping methods are not interchangeable and should be carefully selected.

In addition to variability in RSF mapping methodologies, we found a concerning disconnect between methods used to test the predictive accuracy of RSF predictions and methods used to display predictions of resource selection. The usefulness of RSF models is dependent on their accuracy (Boyce et al., 2002) and the results of these studies are frequently summarized in maps. Therefore, for a map to provide useful information it is important to integrate accuracy metrics and mapping methods. However, we found that the binning method for map production did not align with the method used to test productive accuracy for the majority of studies reviewed. For example, the primary methods used for accuracy metrics, accounting for ~50% of reviewed studies, suggest splitting RSF values into 10 equal area bins (Boyce et al., 2002); however, ~34% of studies displayed maps as a continuous surface. Approximately 30% of studies split RSF values into 10 equal area bins to test predictive accuracy, and only ~3% of studies displayed a map with 10 equal area bins. These findings suggest that the majority of RSF papers are displaying maps with a classification scheme that has not been tested for accuracy.

The results of our case study reflect that there are clear differences between commonly used mapping approaches in terms of visual interpretation and accuracy metrics. For example, the equal interval classification did not successfully predict locations used by elk, and predicted more elk locations in RSF bins with a lower relative probability of selection. The same model divided into quantile or equal area bins successfully predicted more testing points in bins with a higher probability of selection. Using one of these classification schemes for accuracy metrics, and the other for map display is misleading. In our case study, the objective of developing our RSF map was to inform anthrax disease risk management in a high risk elk population (Morris et al., 2015), and selecting a mapping approach that had been tested for accuracy was important for accurately informing surveillance efforts. Boyce et al. (2002) define a good RSF model as one that reliably predicts the location of organisms, and we advise that the classification used to test the relationship between selection and use should also be used to map RSF outputs to ensure maps reflect accurate information on predicted resource selection.

5. Conclusion

We make the following recommendations for RSF studies with a mapping component:

  1. Methods employed to create RSF maps and binning classifications should be clearly and explicitly described. We suggest that vague language, such as “equal bins”, leads to challenges in interpretation, and advocate the use of detailed descriptions, such as “equal area” or “equal interval”.

  2. Map legends should be informative and enhance the interpretation of RSF results. Predictions shown as low to high, and categorical classifications without further description of methods do not provide a meaningful or accurate representation of RSF results.

  3. We recommend avoiding the display of continuous RSF surfaces, as there is not an established method in the RSF literature for testing the predictive accuracy of a continuous RSF surface.

  4. The classification for mapped RSF bins should be in line with the classification employed for accuracy metrics. For example, if 10 equal bins are used to test the predictive accuracy of an RSF model, 10 equal area bins should also be used to map the predicted resource selection.

  5. The bin classification technique should be selected based on the method with the highest predictive accuracy. Johnson et al. (2006) recommend trying a different binning technique if predictive accuracy is low, and we suggest that exploring the accuracy associated with multiple binning classifications is an important component to producing accurate maps. RSF binning classifications have been described in multiple studies (Boyce et al., 2002; Hirzel et al., 2006; Wiens et al., 2008).

  • Methods for mapping the results of resource selection functions in wildlife studies are not clearly defined in many studies, and there is a high degree of variability in methods across studies.

  • The method used for mapping frequently does not consider accuracy metrics.

  • The method employed for mapping resource selection results has a notable effect on the visual interpretation of results.

  • The method for mapping the results of resource selection studies should be explicitly stated, and selected based on accuracy metrics.

Acknowledgments

Extensive logistical support was provided by Turner Enterprises and the ranch personnel for elk data collection. We thank I.T. Kracalik, M. Traught, and M.C. Blackburn for field work support. We thank the Montana FWP Region 3 staff for animal capture and collar recovery support. Funding for this study was provided by the National Institutes of Health Grant 1R01GM117617-01 to JKB, the College of Liberals Arts and Sciences and the Emerging Pathogens Institute at the University of Florida.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Alamgir M, Mukul SA, Turton SM. Modelling spatial distribution of critically endangered Asian elephant and Hoolock gibbon in Bangladesh forest ecosystems under a changing climate. Applied Geography. 2015;60:10–19. [Google Scholar]
  2. Aldridge CL, Saher DJ, Childers TM, Stahlnecker KE, Bowen ZH. Crucial nesting habitat for gunnison sage-grouse: A spatially explicit hierarchical approach. The Journal of Wildlife Management. 2012;76(2):391–406. [Google Scholar]
  3. Allred BW, Fuhlendorf SD, Engle DM, Elmore RD. Ungulate preference for burned patches reveals strength of fire–grazing interaction. Ecology and Evolution. 2011;1(2):132–144. doi: 10.1002/ece3.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Allred BW, Fuhlendorf SD, Hamilton RG. The role of herbivores in Great Plains conservation: comparative ecology of bison and cattle. Ecosphere. 2011;2(3):art26. [Google Scholar]
  5. Alvarado-Serrano DF, Knowles LL. Ecological niche models in phylogeographic studies: applications, advances and precautions. Molecular Ecology Resources. 2014;14(2):233–248. doi: 10.1111/1755-0998.12184. [DOI] [PubMed] [Google Scholar]
  6. Anderson DP, Turner MG, Forester JD, Zhu J, Boyce MS, Beyer H, Stowell L. Scale-dependent summer resource selection by reintroduced elk in Wisconsin, USA. Journal of Wildlife Management. 2005;69(1):298–310. [Google Scholar]
  7. Azevedo L, Canário-Almeida F, Fonseca JA, Costa-Pereira A, Winck J, Hespanhol V. How to write a scientific paper—writing the methods section. Revista Portuguesa de Pneumologia. 2011;17(5):232–238. doi: 10.1016/j.rppneu.2011.06.014. [DOI] [PubMed] [Google Scholar]
  8. Barker OE, Derocher AE. Habitat selection by arctic ground squirrels (Spermophilus parryii) Journal of Mammalogy. 2010;91(5):1251–1260. [Google Scholar]
  9. Bates D, Maechler M, Bolker B, Walker S. lme4: Linear mixed-effects models using Eigen and S4. R package version 1.1–7. 2014 This Is Computer Program (R Package). The URL of the Package Is: http://CRAN.R-Project.Org/package=lme4.
  10. Beckmann JP, Murray K, Seidler RG, Berger J. Human-mediated shifts in animal habitat use: sequential changes in pronghorn use of a natural gas field in Greater Yellowstone. Biological Conservation. 2012;147(1):222–233. [Google Scholar]
  11. Beerens JM, Gawlik DE, Herring G, Cook MI. Dynamic habitat selection by two wading bird species with divergent foraging strategies in a seasonally fluctuating wetland. The Auk. 2011;128(4):651–662. [Google Scholar]
  12. Blackburn JK. Emerging and Endemic Pathogens. Springer; 2010. Integrating geographic information systems and ecological niche modeling into disease ecology: a case study of Bacillus anthracis in the United States and Mexico; pp. 59–88. [Google Scholar]
  13. Bleich VC, Davis JH, Marshal JP, Torres SG, Gonzales BJ. Mining activity and habitat use by mountain sheep (Ovis canadensis) European Journal of Wildlife Research. 2009;55(3):183–191. [Google Scholar]
  14. Bleich VC, Johnson HE, Holl SA, Konde L, Torres SG, Krausman PR. Fire history in a chaparral ecosystem: implications for conservation of a native ungulate. Rangeland Ecology & Management. 2008;61(6):571–579. [Google Scholar]
  15. Boyce MS, Vernier PR, Nielsen SE, Schmiegelow FK. Evaluating resource selection functions. Ecological Modelling. 2002;157(2):281–300. [Google Scholar]
  16. Boyce MS, Waller JS. Grizzly bears for the Bitterroot: predicting potential abundance and distribution. Wildlife Society Bulletin. 2003:670–683. [Google Scholar]
  17. Broman DJ, Litvaitis JA, Ellingwood M, Tate P, Reed GC. Modeling bobcat Lynx rufus habitat associations using telemetry locations and citizen-scientist observations: are the results comparable? Wildlife Biology. 2014;20:229–237. [Google Scholar]
  18. Brook RK, McLachlan SM. Transdisciplinary habitat models for elk and cattle as a proxy for bovine tuberculosis transmission risk. Preventive Veterinary Medicine. 2009;91(2):197–208. doi: 10.1016/j.prevetmed.2009.05.021. [DOI] [PubMed] [Google Scholar]
  19. Cagnacci F, Boitani L, Powell RA, Boyce MS. Animal ecology meets GPS-based radiotelemetry: a perfect storm of opportunities and challenges. Philosophical Transactions of the Royal Society B: Biological Sciences. 2010;365(1550):2157–2162. doi: 10.1098/rstb.2010.0107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Campos VE, Gatica G, Bellis LM. Remote sensing variables as predictors of habitat suitability of the viscacha rat (Octomys mimax), a rock-dwelling mammal living in a desert environment. Mammal Research. 2015;60(2):117–126. [Google Scholar]
  21. Carpenter J, Aldridge C, Boyce MS. Sage-grouse habitat selection during winter in Alberta. The Journal of Wildlife Management. 2010;74(8):1806–1814. [Google Scholar]
  22. Carroll C, Noss RF, Paquet PC. Carnivores as focal species for conservation planning in the Rocky Mountain region. Ecological Applications. 2001;11(4):961–980. [Google Scholar]
  23. Chetkiewicz CB, Boyce MS. Use of resource selection functions to identify conservation corridors. Journal of Applied Ecology. 2009;46(5):1036–1047. [Google Scholar]
  24. Chimeddorj B, Buuveibaatar B, Onon Y, Munkhtogtokh O, Reading RP. Identifying Potential Conservation Corridors Along the Mongolia-Russia Border Using Resource Selection Functions: A Case Study on Argali Sheep. Sciences. 2013;11:1–2. [Google Scholar]
  25. Ciarniello LM, Boyce MS, Heard DC, Seip DR. Components of grizzly bear habitat selection: density, habitats, roads, and mortality risk. The Journal of Wildlife Management. 2007;71(5):1446–1457. [Google Scholar]
  26. Ciarniello LM, Boyce MS, Seip DR, Heard DC. Comparison of grizzly bear Ursus arctos demographics in wilderness mountains versus a plateau with resource development. Wildlife Biology. 2009;15(3):247–265. [Google Scholar]
  27. Clark PE, Lee J, Ko K, Nielson RM, Johnson DE, Ganskopp DC, … Hardegree SP. Prescribed fire effects on resource selection by cattle in mesic sagebrush steppe. Part 1: spring grazing. Journal of Arid Environments. 2014;100:78–88. [Google Scholar]
  28. Coe PK, Johnson BK, Wisdom MJ, Cook JG, Vavra M, Nielson RM. Validation of elk resource selection models with spatially independent data. The Journal of Wildlife Management. 2011;75(1):159–170. [Google Scholar]
  29. Costello CM, Cain SI, Nielson RM, Servheen C, Schwartz CC. Response of American black bears to the non-motorized expansion of a road corridor in Grand Teton National Park. Ursus. 2013;24(1):54–69. [Google Scholar]
  30. DeCesare NJ, Hebblewhite M, Schmiegelow F, Hervieux D, McDermid GJ, Neufeld L, … Morgantini LE. Transcending scale dependence in identifying habitat with resource selection functions. Ecological Applications. 2012;22(4):1068–1083. doi: 10.1890/11-1610.1. [DOI] [PubMed] [Google Scholar]
  31. Dellinger JA, Proctor C, Steury TD, Kelly MJ, Vaughan MR. Habitat selection of a large carnivore, the red wolf, in a human-altered landscape. Biological Conservation. 2013;157:324–330. [Google Scholar]
  32. Dickson BG, Sisk TD, Sesnie SE, Reynolds RT, Rosenstock SS, Vojta CD, … Rundall JM. Integrating single-species management and landscape conservation using regional habitat occurrence models: the northern goshawk in the Southwest, USA. Landscape Ecology. 2014;29(5):803–815. [Google Scholar]
  33. Dillard LO, Russell KR, Ford MW. Macrohabitat models of occurrence for the threatened Cheat Mountain salamander, Plethodon nettingi. Applied Herpetology. 2008;5(3):201–224. [Google Scholar]
  34. Doherty KE, Naugle DE, Walker BL. Greater Sage-Grouse Nesting Habitat: The Importance of Managing at Multiple Scales. The Journal of Wildlife Management. 2010;74(7):1544–1553. [Google Scholar]
  35. Dugal CJ, Beest FM, Wal E, Brook RK. Targeting hunter distribution based on host resource selection and kill sites to manage disease risk. Ecology and Evolution. 2013;3(12):4265–4277. doi: 10.1002/ece3.788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Durner GM, Douglas DC, Nielson RM, Amstrup SC, McDonald TL, Stirling I, … DeWeaver E. Predicting 21st-century polar bear habitat distribution from global climate models. Ecological Monographs. 2009;79(1):25–58. [Google Scholar]
  37. Dzialak MR, Olson CV, Harju SM, Webb SL, Winstead JB. Temporal and hierarchical spatial components of animal occurrence: conserving seasonal habitat for greater sage-grouse. Ecosphere. 2012;3(4):art30. [Google Scholar]
  38. Dzialak MR, Olson CV, Webb SL, Harju SM, Winstead JB. Incorporating within-and between-patch resource selection in identification of critical habitat for brood-rearing greater sage-grouse. Ecological Processes. 2015;4(1):1–15. [Google Scholar]
  39. Dzialak MR, Webb SL, Harju SM, Olson CV, Winstead JB, Hayden-Wing LD. Greater sage-grouse and severe winter conditions: identifying habitat for conservation. Rangeland Ecology & Management. 2013;66(1):10–18. [Google Scholar]
  40. Elbroch LM, Lendrum PE, Newby J, Quigley H, Craighead D. Seasonal foraging ecology of non-migratory cougars in a system with migrating prey. PloS One. 2013;8(12):e83375. doi: 10.1371/journal.pone.0083375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Elith J, Leathwick JR. Species distribution models: ecological explanation and prediction across space and time. Annual Review of Ecology, Evolution, and Systematics. 2009;40(1):677. [Google Scholar]
  42. Enari H, Sakamaki–Enari H. Resource use of Japanese macaques in heavy snowfall areas: implications for habitat management. Primates. 2013;54(3):259–269. doi: 10.1007/s10329-013-0343-9. [DOI] [PubMed] [Google Scholar]
  43. Erickson WP, McDonald TL, Skinner R. Habitat selection using GIS data: a case study. Journal of Agricultural, Biological, and Environmental Statistics. 1998:296–310. [Google Scholar]
  44. Fattebert J, Robinson HS, Balme G, Slotow R, Hunter L. Structural habitat predicts functional dispersal habitat of a large carnivore: how leopards change spots. Ecological Applications. 2015 doi: 10.1890/14-1631.1. [DOI] [PubMed] [Google Scholar]
  45. Ferrier S, Guisan A. Spatial modelling of biodiversity at the community level. Journal of Applied Ecology. 2006;43(3):393–404. [Google Scholar]
  46. Florkiewicz R, Maraj R, Hegel T, Waterreus M. The effects of human land use on the winter habitat of the recovering Carcross woodland caribou herd in suburban Yukon Territory, Canada. Rangifer. 2007;27(4):181–197. [Google Scholar]
  47. Fortin D, Courtois R, Etcheverry P, Dussault C, Gingras A. Winter selection of landscapes by woodland caribou: behavioural response to geographical gradients in habitat attributes. Journal of Applied Ecology. 2008;45(5):1392–1400. [Google Scholar]
  48. Fortin D, Fortin ME. Group-size-dependent association between food profitability, predation risk and distribution of free-ranging bison. Animal Behaviour. 2009;78(4):887–892. [Google Scholar]
  49. Girard TL, Bork EW, Nielsen SE, Alexander MJ. Seasonal variation in habitat selection by free-ranging feral horses within Alberta’s forest reserve. Rangeland Ecology & Management. 2013;66(4):428–437. [Google Scholar]
  50. Gottschalk TK, Ekschmitt K, İsfendiyaroglu S, Gem E, Wolters V. Assessing the potential distribution of the Caucasian black grouse Tetrao mlokosiewiczi in Turkey through spatial modelling. Journal of Ornithology. 2007;148(4):427–434. [Google Scholar]
  51. Harju SM, Olson CV, Dzialak MR, Mudd JP, Winstead JB. A flexible approach for assessing functional landscape connectivity, with application to Greater Sage-Grouse (Centrocercus urophasianus) PloS One. 2013;8(12):e82271. doi: 10.1371/journal.pone.0082271. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Hebblewhite M, Haydon DT. Distinguishing technology from biology: a critical review of the use of GPS telemetry data in ecology. Philosophical Transactions of the Royal Society of London B: Biological Sciences. 2010;365(1550):2303–2312. doi: 10.1098/rstb.2010.0087. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Hebblewhite M, Merrill E. Modelling wildlife–human relationships for social species with mixed-effects resource selection models. Journal of Applied Ecology. 2008;45(3):834–844. http://doi.org/10.1111/j.1365-2664.2008.01466.x. [Google Scholar]
  54. Hebblewhite M, Merrill E, McDonald T. Spatial decomposition of predation risk using resource selection functions: an example in a wolf–elk predator–prey system. Oikos. 2005;111(1):101–111. [Google Scholar]
  55. Hebblewhite M, Miquelle DG, Murzin AA, Aramilev VV, Pikunov DG. Predicting potential habitat and population size for reintroduction of the Far Eastern leopards in the Russian Far East. Biological Conservation. 2011;144(10):2403–2413. [Google Scholar]
  56. Hirzel AH, Le Lay G, Helfer V, Randin C, Guisan A. Evaluating the ability of habitat suitability models to predict species presences. Ecological Modelling. 2006;199(2):142–152. [Google Scholar]
  57. Hodder DP, Johnson CJ, Rea RV, Zedrosser A. Application of a species distribution model to identify and manage bear den habitat in central British Columbia, Canada. Wildlife Biology. 2014;20:238–245. [Google Scholar]
  58. Horne JS, Craig T, Joly K, Stout GW, Cebrian MR, Garton EO. Population characteristics, space use and habitat selection of two non-migratory caribou herds in central Alaska, 1994–2009. Rangifer. 2014;34(1):1–20. [Google Scholar]
  59. Hough MJ, Dieter CD. Resource selection habitat model for northern flying squirrels in the Black Hills, South Dakota. The American Midland Naturalist. 2009;162(2):356–372. [Google Scholar]
  60. Irwin LL, Rock DF, Rock SC. Habitat selection by northern spotted owls in mixed-coniferous forests. The Journal of Wildlife Management. 2012;76(1):200–213. [Google Scholar]
  61. Jędrzejewski W, Jędrzejewska B, Zawadzka B, Borowik T, Nowak S, Mysłajek R. Habitat suitability model for Polish wolves based on long-term national census. Animal Conservation. 2008;11(5):377–390. [Google Scholar]
  62. Jiang G, Ma J, Zhang M, Stott P. Effects of human activities on the spatial distribution of eastern roe deerCapreolus pygargus bedfordi in the Lesser Khingan Mountains, northeastern China. Acta Theriologica. 2009;54(1):61–76. [Google Scholar]
  63. Johnson CJ, Boyce MS, Case RL, Cluff HD, Gau RJ, Gunn A, Mulders R. Cumulative effects of human developments on arctic wildlife. Wildlife Monographs. 2005:1–36. [Google Scholar]
  64. Johnson CJ, Gillingham MP. An evaluation of mapped species distribution models used for conservation planning. Environmental Conservation. 2005;32(2):117–128. [Google Scholar]
  65. Johnson CJ, Nielsen SE, Merrill EH, McDonald TL, Boyce MS. Resource selection functions based on use-availability data: theoretical motivation and evaluation methods. Journal of Wildlife Management. 2006;70(2):347–357. [Google Scholar]
  66. Johnson CJ, Seip DR, Boyce MS. A quantitative approach to conservation planning: using resource selection functions to map the distribution of mountain caribou at multiple spatial scales. Journal of Applied Ecology. 2004;41(2):238–251. [Google Scholar]
  67. Joly K. Modeling influences on winter distribution of caribou in northwestern Alaska through use of satellite telemetry. Rangifer. 2011;31(2):75–85. [Google Scholar]
  68. Keating KA, Cherry S. Use and interpretation of logistic regression in habitat-selection studies. Journal of Wildlife Management. 2004;68(4):774–789. [Google Scholar]
  69. Kinley TA, Whittington J, Dibb AD, Newhouse NJ. Badger Resource Selection in the Rocky Mountain Trench of British Columbia. Journal of Ecosystems and Management. 2014;14(3) [Google Scholar]
  70. Krebs J, Lofroth EC, Parfitt I. Multiscale habitat use by wolverines in British Columbia, Canada. The Journal of Wildlife Management. 2007;71(7):2180–2192. [Google Scholar]
  71. Kunkel KE, Atwood T, Ruth T, Pletscher DH, Hornocker M. Assessing wolves and cougars as conservation surrogates. Animal Conservation. 2013;16(1):32–40. [Google Scholar]
  72. Lewis JS, Rachlow JL, Horne JS, Garton EO, Wakkinen WL, Hayden J, Zager P. Identifying habitat characteristics to predict highway crossing areas for black bears within a human-modified landscape. Landscape and Urban Planning. 2011;101(2):99–107. [Google Scholar]
  73. Loe LE, Bonenfant C, Meisingset EL, Mysterud A. Effects of spatial scale and sample size in GPS-based species distribution models: are the best models trivial for red deer management? European Journal of Wildlife Research. 2012;58(1):195–203. [Google Scholar]
  74. Loring PH, Paton PW, Osenkowski JE, Gilliland SG, Savard JL, Mcwilliams SR. Habitat use and selection of black scoters in southern New England and siting of offshore wind energy facilities. The Journal of Wildlife Management. 2014;78(4):645–656. [Google Scholar]
  75. Mace RD, Waller JS, Manley TL, Ake K, Wittinger WT. Landscape evaluation of grizzly bear habitat in western Montana. Conservation Biology. 1999;13(2):367–377. [Google Scholar]
  76. Manly B, McDonald L, Thomas D, McDonald T, Erickson W. Resource selection by animals: statistical analysis and design for field studies. Nordrecht, The Netherlands: Kluwer; 2002. [Google Scholar]
  77. Mashintonio AF, Pimm SL, Harris GM, van Aarde RJ, Russell GJ. Data-driven discovery of the spatial scales of habitat choice by elephants. PeerJ. 2014;2:e504. doi: 10.7717/peerj.504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. Masse RJ, Tefft BC, McWilliams SR. Multiscale habitat selection by a forest-dwelling shorebird, the American woodcock: Implications for forest management in southern New England, USA. Forest Ecology and Management. 2014;325:37–48. [Google Scholar]
  79. Matthews A, Spooner PG. Using a resource selection approach to predict the suitability of alpine habitats for a common herbivore. Austral Ecology. 2014;39(2):170–180. [Google Scholar]
  80. May R, Van Dijk J, Wabakken P, Swenson JE, Linnell JD, Zimmermann B, … Landa A. Habitat differentiation within the large-carnivore community of Norway’s multiple-use landscapes. Journal of Applied Ecology. 2008;45(5):1382–1391. doi: 10.1111/j.1365-2664.2008.01527.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. McNyset K. Use of ecological niche modelling to predict distributions of freshwater fish species in Kansas. Ecology of Freshwater Fish. 2005;14(3):243–255. [Google Scholar]
  82. Merkle JA, Krausman PR, Decesare NJ, Jonkel JJ. Predicting spatial distribution of human–black bear interactions in urban areas. The Journal of Wildlife Management. 2011;75(5):1121–1127. [Google Scholar]
  83. Miller JR, Jhala YV, Jena J, Schmitz OJ. Landscape-scale accessibility of livestock to tigers: implications of spatial grain for modeling predation risk to mitigate human–carnivore conflict. Ecology and Evolution. 2015;5(6):1354–1367. doi: 10.1002/ece3.1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  84. Montgomery RA, Roloff GJ, Millspaugh JJ. Variation in elk response to roads by season, sex, and road type. The Journal of Wildlife Management. 2013;77(2):313–325. [Google Scholar]
  85. Montgomery RA, Roloff GJ, Millspaugh JJ, Nylen-Nemetchek M. Living amidst a sea of agriculture: predicting the occurrence of Canada lynx within an ecological island. Wildlife Biology. 2014;20(3):145–154. [Google Scholar]
  86. Morehouse AT, Boyce MS. Deviance from truth: Telemetry location errors erode both precision and accuracy of habitat-selection models. Wildlife Society Bulletin. 2013;37(3):596–602. [Google Scholar]
  87. Morris LR, Proffitt KM, Asher V, Blackburn JK. Elk resource selection and implications for anthrax management in Montana. The Journal of Wildlife Management. 2015;80(2):235–244. doi: 10.1002/jwmg.1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  88. Newsome TM, Ballard GA, Dickman CR, Fleming PJ, Howden C. Anthropogenic resource subsidies determine space use by Australian arid zone dingoes: an improved resource selection modelling approach. PloS One. 2013;8(5):e63931. doi: 10.1371/journal.pone.0063931. [DOI] [PMC free article] [PubMed] [Google Scholar]
  89. Nielsen SE, Herrero S, Boyce MS, Mace RD, Benn B, Gibeau ML, Jevons S. Modelling the spatial distribution of human-caused grizzly bear mortalities in the Central Rockies ecosystem of Canada. Biological Conservation. 2004;120(1):101–113. [Google Scholar]
  90. Niemuth ND, Estey ME, Loesch CR. Developing spatially explicit habitat models for grassland bird conservation planning in the Prairie Pothole Region of North Dakota. Presented at the Bird conservation implementation and integration in the Americas: proceedings of the Third International Partners in Flight Conference.2002. pp. 469–477. [Google Scholar]
  91. Northrup J, Stenhouse G, Boyce M. Agricultural lands as ecological traps for grizzly bears. Animal Conservation. 2012;15(4):369–377. [Google Scholar]
  92. Oehlers SA, Bowyer RT, Huettmann F, Person DK, Kessler WB. Sex and scale: implications for habitat selection by Alaskan moose Alces alces gigas. Wildlife Biology. 2011;17(1):67–84. [Google Scholar]
  93. Pedersen Å, Jepsen J, Yoccoz N, Fuglei E. Ecological correlates of the distribution of territorial Svalbard rock ptarmigan (Lagopus muta hyperborea) Canadian Journal of Zoology. 2007;85(1):122–132. [Google Scholar]
  94. Peterson AT. Ecological niches and geographic distributions (MPB-49) Princeton University Press; 2011. [Google Scholar]
  95. Pigeon KE, Nielsen SE, Stenhouse GB, Côté SD. Den selection by grizzly bears on a managed landscape. Journal of Mammalogy. 2014;95(3):559–571. [Google Scholar]
  96. Polfus J, Hebblewhite M, Heinemeyer K. Identifying indirect habitat loss and avoidance of human infrastructure by northern mountain woodland caribou. Biological Conservation. 2011;144(11):2637–2646. [Google Scholar]
  97. Polfus JL, Heinemeyer K, Hebblewhite M. Comparing traditional ecological knowledge and western science woodland caribou habitat models. The Journal of Wildlife Management. 2014;78(1):112–121. [Google Scholar]
  98. Proffitt KM, Gude JA, Hamlin KL, Garrott RA, Cunningham JA, Grigg JL. Elk distribution and spatial overlap with livestock during the brucellosis transmission risk period. Journal of Applied Ecology. 2011;48(2):471–478. [Google Scholar]
  99. Ramirez-Villegas J, Cuesta F, Devenish C, Peralvo M, Jarvis A, Arnillas CA. Using species distributions models for designing conservation strategies of Tropical Andean biodiversity under climate change. Journal for Nature Conservation. 2014;22(5):391–404. [Google Scholar]
  100. Recio MR, Mathieu R, Virgós E, Seddon PJ. Quantifying fine-scale resource selection by introduced feral cats to complement management decision-making in ecologically sensitive areas. Biological Invasions. 2014;16(9):1915–1927. [Google Scholar]
  101. Richardson E, Stirling I, Hik DS. Polar bear (Ursus maritimus) maternity denning habitat in western Hudson Bay: a bottom-up approach to resource selection functions. Canadian Journal of Zoology. 2005;83(6):860–870. [Google Scholar]
  102. Roever CL, Van Aarde RJ, Leggett K. Functional connectivity within conservation networks: delineating corridors for African elephants. Biological Conservation. 2013;157:128–135. [Google Scholar]
  103. Sakuragi M, Igota H, Uno H, Kaji K, Kaneko M, Akamatsu R, Maekawa K. Seasonal habitat selection of an expanding sika deer Cervus nippon population in eastern Hokkaido, Japan. Wildlife Biology. 2003;9(2):141–153. [Google Scholar]
  104. Seip DR, Johnson CJ, Watts GS. Displacement of mountain caribou from winter habitat by snowmobiles. The Journal of Wildlife Management. 2007;71(5):1539–1544. [Google Scholar]
  105. Shanley CS, Kofinas GP, Pyare S. Balancing the conservation of wildlife habitat with subsistence hunting access: A geospatial-scenario planning framework. Landscape and Urban Planning. 2013;115:10–17. [Google Scholar]
  106. Shanley CS, Pyare S. Evaluating the road-effect zone on wildlife distribution in a rural landscape. Ecosphere. 2011;2(2):art16. [Google Scholar]
  107. Shanley CS, Pyare S, Smith WP. Response of an ecological indicator to landscape composition and structure: Implications for functional units of temperate rainforest ecosystems. Ecological Indicators. 2013;24:68–74. [Google Scholar]
  108. Singh NJ, Yoccoz NG, Bhatnagar YV, Fox JL. Using habitat suitability models to sample rare species in high-altitude ecosystems: a case study with Tibetan argali. Biodiversity and Conservation. 2009;18(11):2893–2908. [Google Scholar]
  109. Singleton PH, Lehmkuhl JF, Gaines WL, Graham SA. Barred owl space use and habitat selection in the eastern Cascades, Washington. The Journal of Wildlife Management. 2010;74(2):285–294. [Google Scholar]
  110. Smith KT, Kirol CP, Beck JL, Blomquist FC. Prioritizing winter habitat quality for greater sage-grouse in a landscape influenced by energy development. Ecosphere. 2014;5(2):art15. [Google Scholar]
  111. Speed JD, Woodin SJ, Tømmervik H, Tamstorf MP, van der Wal R. Predicting habitat utilization and extent of ecosystem disturbance by an increasing herbivore population. Ecosystems. 2009;12(3):349–359. [Google Scholar]
  112. Squires JR, DeCesare NJ, Olson LE, Kolbe JA, Hebblewhite M, Parks SA. Combining resource selection and movement behavior to predict corridors for Canada lynx at their southern range periphery. Biological Conservation. 2013;157:187–195. [Google Scholar]
  113. Takahata C, Nishino S, Kido K, Izumiyama S. An evaluation of habitat selection of Asiatic black bears in a season of prevalent conflicts. Ursus. 2013;24(1):16–26. [Google Scholar]
  114. Tamstorf MP, Aastrup P, Cuyler LC. Modelling critical caribou summer ranges in West Greenland. Polar Biology. 2005;28(9):714–724. [Google Scholar]
  115. Teichman KJ, Cristescu B, Nielsen SE. Does Sex Matter? Temporal and Spatial Patterns of Cougar-Human Conflict in British Columbia. PloS One. 2013;8(9):e74663. doi: 10.1371/journal.pone.0074663. [DOI] [PMC free article] [PubMed] [Google Scholar]
  116. Webb SL, Dzialak MR, Kosciuch KL, Winstead JB. Winter Resource Selection by Mule Deer on the Wyoming-Colorado Border Prior to Wind Energy Development. Rangeland Ecology & Management. 2013;66(4):419–427. [Google Scholar]
  117. Weckworth BV, Musiani M, DeCesare NJ, McDevitt AD, Hebblewhite M, Mariani S. Preferred habitat and effective population size drive landscape genetic patterns in an endangered species. Proceedings of the Royal Society B: Biological Sciences. 2013;280(1769):20131756. doi: 10.1098/rspb.2013.1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  118. White KS, Gregovich DP, Pendleton GW, Barten NL, Crupi A, Scott R, Larsen DN. Modeling resource selection of mountain goats in southeastern Alaska: Applications for population management and highway development planning n.d [Google Scholar]
  119. Wiens TS, Dale BC, Boyce MS, Kershaw GP. Three way k-fold cross-validation of resource selection functions. Ecological Modelling. 2008;212(3):244–255. [Google Scholar]

RESOURCES