Influence of Demographic and Health Survey Point Displacements on Raster-Based Analyses

Abstract

With this paper we explore the sensitivity of study results to spatial displacements associated with Demographic and Health Survey (DHS) data in research that integrates ancillary raster data. Through simulation studies, we found that the impact of DHS point displacements on raster-based analyses can be moderated through the generation of covariates representing average values from neighborhood buffers. Additionally, raster surface characteristics (i.e., spatial smoothness) were found to affect the extent of bias introduced through point displacements. Although simple point extraction produced unbiased estimates in analyses involving smooth continuous surfaces, it is not recommended in analyses that involve categorical raster surfaces.

1 Background

Demographic and Health Survey (DHS) spatial data are widely used to evaluate the effects of environmental or contextual exposures on health outcomes (for example, see Balk et al. (2004); Simler (2006); Baschieri (2007); Feldacker et al. (2010); Jankowska et al. (2012); Messina et al. (2010, 2011); De Castro and Fisher (2012)). One of the most common uses of this data involves linking DHS clusters to environmental or contextual data in order to generate new covariates of interest. However, because the locations of DHS clusters are randomly displaced to protect the confidentiality of survey respondents, measurement error and covariate misspecification can be introduced by spatial uncertainty associated with the displacement procedure.

Statistical impacts of positional error have been noted in previous studies. For instance, the recently described Uncertain Geographical Context Problem (UGCoP), in which statistical bias is introduced when the method of delineating contextual areas/neighborhoods, affects the results of an analysis Kwan (2012). In the case of UGCoP, when buffers around clusters are used to generate an ecological variable (such as percentage of crop land or degree of exposure to traffic pollution), the buffer must be large enough to incorporate the true area associated with the cluster locations prior to displacement, which complicates the already difficult task of defining the proper contextual area/neighborhood associated with a cluster. Monte Carlo simulation can be used as one approach to handle spatial error associated with UGCoP. With this approach, positional error can be modeled through a simulated sampling of inputs whose errors behave according to a known probability distribution Hengl et al. (2010); Heuvelink et al. (1989). Heuvelink et al. (1989) note that Monte Carlo simulation techniques have essentially taken over the field of error propagation modeling.

Other efforts to characterize the bias introduced by positional error have used sensitivity analysis as a tool. This approach has been used in studies attempting to understand the effects of environmental exposure on a variety of health outcomes. Zandbergen and Green (2007ab), for example, compared methods of street geocoding with modeling of children's exposure to traffic pollution. Their results found bias and error in proximity analyses of distances less than 500 m, with consistent overestimation of exposed children Zandbergen (2007); Zandbergen and Green (2007). Whitsel et al. (2006) also found exposure misspecification in their study on the accuracy of commercial geocoding techniques Whitsel, Quibrera, Smith, Catellier, Liao, Henley, and Heiss (Whitsel et al.). A study conducted by Ward et al. (2005) of non-Hodgkins lymphoma compared two geocoding methods to characterize the positional error and test the sensitivity and specificity of each to crop occurrence within 500 m, 250 m, and 100 m of both sets of geocoded households Ward et al. (2005). They found that geocoding errors affected crop exposure classification at 100 m. Each of these studies shows that the spatial scale of the analysis is an important consideration, analogous to concerns related to the use of ancillary raster data with displaced DHS clusters.

A related concern involves studies that extract data from raster surfaces using map overlay techniques. Zandbergen et al. (2012) examined the effect of geocoding error on association with 30-m resolution land cover by generating an error matrix to determine the agreement between the results for reference locations and geocoded locations in six US counties. They found that areas with relatively homogenous land cover resulted in fewer errors in matching points with the correct land cover type, whereas areas with heterogeneous land cover types were associated with larger error. One solution they offer is, if possible, to reclassify areas with heterogeneous land cover types into fewer categories Zandbergen et al. (2012).

With this paper we explore the sensitivity of study results to spatial displacements associated with DHS data in studies involving integration of ancillary raster data, and provide guidelines on the use of DHS spatial data to reduce the impact of resulting covariate misspecification. We propose simulation studies to investigate how the random displacement of DHS cluster locations affect statistical inferences and conclusions drawn from analyses involving covariates generated from ancillary raster data. We address how covariates generated from continuous as well as categorical raster surfaces can be altered differentially by point displacement, and propose the use of buffer means to mitigate the potential bias associated with misspecification of covariates due to these random displacements. We evaluate the performance of these methods (i.e., buffer means) across raster surfaces with varying levels of spatial smoothness (i.e., spatial autocorrelation) and varying coverage of raster cell types (for categorical rasters). It is expected that raster characteristics such as these would likely influence the extent of bias brought about through point displacements. Therefore, the effectiveness of proposed neighborhood definitions (for obtaining buffer means) to reduce the bias associated with point displacement is evaluated across several simulated raster surfaces.

2 Methods

2.1 GPS Data Displacement

DHS data have geo-located survey locations dating to 1986. The collection of GPS locations for surveys has become fairly standard practice since the early 2000s. Currently, there are over 130 surveys with GPS or geo-located data. To protect the confidentiality of respondents the geo-located data is displaced. The displacement process moves the latitude and longitude to a new location under set parameters. Urban locations are displaced 0-2 km while rural locations are displaced 0-5 km with 1% (or every 100^th point) displaced 0-10 km. The displacement is a random direction/random distance process. The steps in the displacement are: (1) A random direction (angle) between 0 and 360 degrees is chosen; (2) A random distance according to the urban and rural parameters is chosen; (3) The new location is created combining steps 1 and 2 to create a new latitude and longitude for the cluster; and (4) The new location is checked to ensure it falls within designated administrative boundaries Burgert et al. (2013). In surveys after 2008 this is usually administrative 2 boundaries while surveys before 2008 were restricted to DHS regional boundaries or national boundaries.

For purposes of this analysis, we used the Uganda DHS 2011 data, including the GPS data for the 404 clusters covered in the survey. GPS points represented the approximate center of a cluster of households. The data were verified by DHS Program staff to be in the proper administrative areas; 7 points were gazetted to the nearest village. A total of 400 clusters were verified and 4 were listed as missing GPS data and removed from subsequent analyses. The verified cluster locations were displaced according to DHS protocol restricting the displacement to the first administrative level.

2.2 Generation of Raster Surfaces

When linking DHS data with ancillary raster data investigators should consider the potential effects of surface characteristics on covariate assignments. For instance, the spatial smoothness of an ancillary surface (i.e., how similar nearby cells are to each other) could impact the extent to which the cell value at a displaced location differs from that of the true location. Thus, if neighboring cell values are very similar, then displacement will likely have little effect on covariate assignment. A second consideration relates to the relevant scale of analysis for a given spatial process. In other words, investigators should consider whether interest lies in capturing data that represent point-level processes, or data that correspond to contextual effects occurring at some defined neighborhood scale. In subsequent simulation studies, we consider the effect of point displacements on both point-level and contextual spatial processes, as well as varying degrees of surface smoothness. Details regarding the simulation of corresponding raster surfaces are provided in the following sections.

2.2.1 Continuous Raster Surfaces

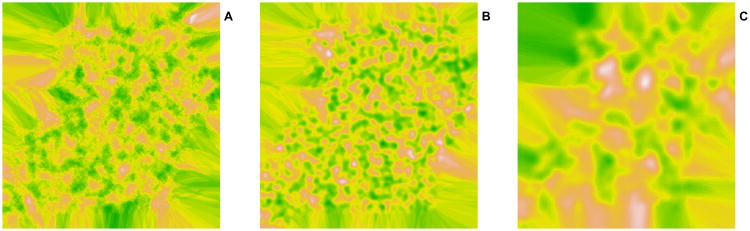
In both simulation studies (continuous and discrete raster), we require simulated raster surfaces in order to define the covariates of interest. Continuous raster surfaces were simulated to represent varying degrees of spatial smoothness (Figure 2). First, a regular grid of 65×65 points was generated to encompass the entire Uganda study area. For each point in the regular grid, neighboring points were identified within a 10 km radius of the point, and a row-standardized weights matrix (W) was generated from the resulting neighbors list. Each grid point (i, j) for row i and column j was then assigned a value Z_ij which was dependent on the mean values of its neighbors. Specifically, the spatial autoregressive random vector Z = (Z_1,1, …, Z_65,65)^T was generated by: (1) constructing the 65×65 inverse matrix V = (I – ρW)⁻¹ Bivand (2013), where ρ represents a predefined autoregressive parameter, and (2) defining the product Z = Vq, where q was a vector of independent standard normal random variables. The resulting vector Z represented a spatially correlated multivariate normal random vector with mean equal to the zero vector and covariance equal to VV^T = (I — ρW)⁻¹(I – ρW)^−T. Z was defined for three different values of ρ, i.e., 0.05, 0.50, and 0.95. Using different ρ values, the spatial autoregressive point process could take on varying levels of smoothness such that at ρ = 0.05 the point process would exhibit very low levels of spatial autocorrelation, whereas at ρ = 0.95 the point process would exhibit very high levels of spatial autocorrelation. The generated gridded points for each level of ρ were then used to interpolate a continuous surface by using the kriging tool in ArcMap 10 ESRI (2011) with an output cell size of 500 m.

Figure 2.

Continuous raster surfaces used in subsequent simulation studies. Each panel represents the surface generated assuming alternate definitions of ρ: (A) ρ = 0.05, (B) ρ = 0.50, and (C) ρ = 0.95.

2.2.2 Categorical Raster Surfaces

For categorical raster surfaces, smoothness may be better described according to degrees of “patch-iness” of certain cell types. Landscape ecologists have described “patchiness” of such surfaces using a variety of indices (see Mcgarigal et al. (2002); McGarigal et al. (2009) for examples), though the external validity of such metrics across categorical surfaces is questionable. As with analyses involving the assignment of covariate values from continuous raster surfaces, sensitivity of results to point displacements could be affected by the proportion of cell types within an ancillary categorical raster surface. For instance, the proportion of a given cell type within a given study area can influence the probability that neighboring cells are of the same type; however, prevalence alone cannot account for shape complexity resulting from patches of similar cell types. Moreover, grid cell sizes will also influence this patchiness and the resulting sensitivity of point displacements to raster-based covariate assignments. With a binary raster surface, covariate misclassification due to point displacement may contribute to bias in effect size estimates associated with point-level spatial processes. For instance, the more frequently observed cluster locations lie along boundaries of binary grid cell patches, the higher the probability of covariate misclassification will be for these locations. In this way, guidelines associated with the integration of data from ancillary discrete raster surfaces can be based on misclassification rates estimated from these surfaces. We provide an R function to estimate misclassification rates, i.e. proportion of locations with non-zero probability of misclassification, for displaced DHS cluster locations via simulation in Appendix C.

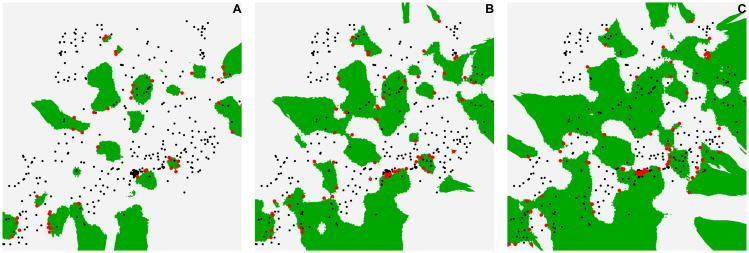
For the purposes of this study we generated multiple categorical raster surfaces with varying surface characteristics, namely cell type prevalence and patch aggregations, to evaluate sensitivity of results to point displacement. Specifically, continuous rasters described above were discretized into categorical rasters that represented rare, moderately prevalent, and prevalent cell types (approximated 15, 30, and 45% coverage, respectively). Continuous raster values were converted to binary values by setting all grid cells with values less than those pertaining to the 15^th, 30^th, and 45^th percentiles, respectively, to one, and all other values to zero for rare, moderately prevalent, and prevalent cell types. We considered more surfaces for this simulation study, compared to the continuous raster simulation study, in order to account for the effect of a wide range of surface misclassification rates on bias. This was done by discretizing continuous surfaces generated using using ρ= -0.95, -0.50, 0.05, 0.50, and 0.95, rather than just the latter three. The resulting surfaces, along with associated misclassification rates, are shown in Appendix D. Figure 3 presents a subset of three generated surfaces that differ with respect to misclassification rates.

Figure 3.

Subset of categorical raster surfaces used in subsequent simulation studies. Each surface represented in the first row varies with respect to average misclassification probabilities: (A) Misclassification rate ≤ 11%, (B) 11% < Misclassification rate < 20%, and (C) Misclassification rate ≥ 20%. The second row of plots demonstrates how the probability of misclassification for specific locations is affected by the number of and positioning of patch edges within a given categorical raster surface. Points highlighted in red correspond to locations in which probability of misclassification was greater than 0.

2.3 Generation of Analysis Datasets

2.3.1 Continuous Raster Simulation Study

For the simulation study, we generated datasets for analysis, and collected covariate data during each analysis to aid in answering proposed questions of interest. We defined the true covariate of interest as the average of the continuous values within a 2 km buffer of the true DHS cluster location for urban clusters and 5 km for rural clusters. The choice of 2 km and 5 km neighborhood scales for the truth was based on cell sizes comprising the simulated raster surfaces, 500 m in this case. Neighborhood sizes were therefore defined to capture data from multiple cells. Neighborhoods less than 2 km were expected to reflect results overly similar to point extraction, thus, this was set as the minimum distance at which neighborhood processes would differ from local point processes. Next, we considered the form of statistical model we planned to evaluate with respect to bias in parameter estimates. For these analyses we focused on Poisson regression, since count data from DHS clusters is commonly used to define outcome variables of interest. We chose regression coefficient values for the Poisson statistical regression model considered in the study such that β₀ = 1.00 and β₁ = −0.27. These values were obtained as random variates from a normal distribution with mean 0 and standard deviation 1.5. Using these fixed β = (β₀, β₁)^T parameters, we are able to generate a dataset of Poisson distributed data, one datapoint for each DHS cluster. The proposed model is given as

$$\begin{array}{cc}{Y}_i|{\lambda }_i\stackrel{\mathit{\text{ind}}}{~}\text{Poission}({\lambda }_i),& ln({\lambda }_i)={\beta }_0+{\beta }_1{\mathrm{x}}_i^{(t)}\end{array}$$ (1)

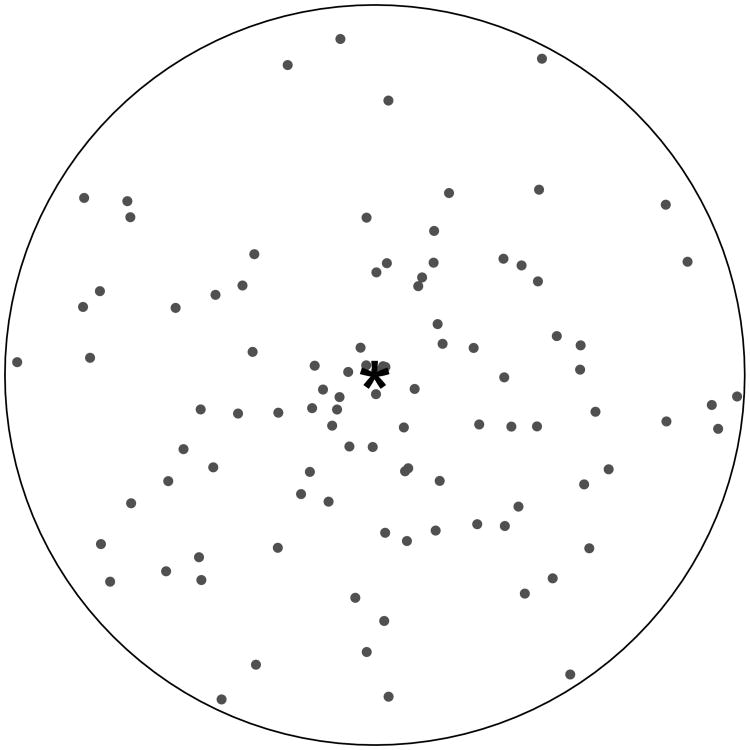
where ${\mathrm{x}}_i^{(t)}$ is the average of the continuous values within the specified buffer created around the true location of DHS cluster i. Recall that the covariate ${\mathrm{x}}_i^{(t)}$ is unknown to researchers in practice due to the random displacement. Multiple displaced datasets were created for the simulations. To facilitate this process a displacement function was created in R that mirrored the DHS displacement python script in ArcGIS. The codes are listed in the additional files (Appendix A). For each location (i.e., DHS cluster) we simulated 100 displaced point datasets, and these points were used in subsequent simulation case studies (Figure 1). We generated 100 independent datasets, each associated with a particular joint displacement of DHS clusters. By repeating the process under each spatial smoothness setting we simulated a total of 300 datasets.

Figure 1.

Schematic of 100 randomly generated displaced locations based on DHS displacement guidelines. The central point in red represents the true DHS cluster point, while the black dots that fill the circular buffer around the true point represent randomly displaced locations.

Noting that continuous raster surfaces will vary with regard to their respective scales of measurements for the data they represent, for this empirical study the covariate of interest was standardized to have a mean and variance of one in order to allow for the generation of more generalizable guidelines. Because the variability of a surface (i.e., how wide the spread of possible values spans), in addition to its smoothness, can influence the magnitude of the estimated effect sizes and corresponding standard errors, standardization of covariates extracted from such surfaces allows for the sole consideration of spatial smoothness without loss of generalizability when developing guidelines. Thus, since guidelines here are developed based on standardized data, investigators should center and scale their covariate data accordingly when applying proposed guidelines from this study.

2.3.2 Categorical Raster Simulation Study

In order to simulate a single dataset, we used the true (non-displaced) Uganda DHS cluster locations along with the created raster surfaces which have been reclassified to represent binary data. We then defined the true covariate of interest as the proportion of the considered cell type within a 2 km buffer of the true DHS cluster location for urban clusters and 5 km for rural clusters. As a separate analysis considering a difference spatial scale, we also defined the true covariate of interest as the precise cell values which overlaid the true DHS cluster locations. We made use of the same regression coefficient values used for the continuous raster simulation study, i.e. β₀ = 1.00 and β₁ = −0.27, and defined the outcome variable using the Poisson model from (1). In this setting, however ${\mathrm{x}}_i^{(t)}$ corresponds to the proportion of a considered cell type within the specified buffer created around the true location of DHS cluster i. Recall that this proportion covariate ${\mathrm{x}}_i^{(t)}$ is unknown to researchers in practice. Using the 100 sets of displaced locations, we generated 100 independent datasets and repeated the process under each simulated surface for a total of 1100 datasets.

2.4 Analysis

We propose 14 statistical models, each associated with a different method of covariate assignment, to analyze the generated datasets of interest; they include the following:

• Method 1 (True covariate assignment): Maximum likelihood estimation of the data using the true buffer average covariate (for neighborhood-level covariates) or true cell extraction value (for point-level covariates) based on the true DHS cluster location ( ${\mathrm{x}}_i^{(t)}$) (unknown to researcher),

• Method 2 (Simple point extraction): Maximum likelihood estimation of the data using the point extracted cell value based on the displaced DHS cluster location ( ${\mathrm{x}}_i^{(0)}$), and

• Methods (u, r) (Buffer means): Maximum likelihood estimation of the data using the estimated neighborhood mean covariate created using a combination of three urban (u=1 km, 2 km, 5 km) and four rural (r=1 km, 5 km, 10 km, and 20 km) buffer sizes created around the displaced DHS location ( ${\widehat{\mathrm{x}}}_i^{(t)}(u,r)$).

Method 1 represents the optimal analysis, based on the true covariate of interest. Use of Method 1 is not possible in practice because access to the true DHS locations needed to calculate true covariate values is not available. Method 2 represents the naive analysis which has been used in previous studies. This analysis fits the correct statistical model, similar to Method 1, with the incorrect covariate ${\mathrm{x}}_i^{(0)}$) based on cell extraction of the displaced DHS location. Methods (u, r) fits the same statistical model as methods 1 and 2, while using estimates of the true neighborhood-level covariate ${\widehat{\mathrm{x}}}_i^{(t)}(u,r)$. These estimates are obtained using a combination of urban/rural buffer sizes and calculating the buffer averages accordingly.

In addition to being able to provide urban and rural-specific guidelines, assessment of the different combinations of these two neighborhood definitions would also allow for the determination of optimal combinations of urban and rural buffer settings that minimize the bias associated with point displacements. Method (u, r) can be used by all researchers since it is based on the displaced DHS cluster locations and represents a compromise between methods 1 and 2.

2.4.1 Simulation Study

For each of the continuous and categorical raster surfaces generated we fit each of the fourteen methods defined above to a single generated dataset and collected information from each of the model fits. We collect the estimate of β₁, β̂₁^(j), for each method j = 1, …, 14. β₁ represents the main parameter of interest in the study because it describes the association between the average cell values surrounding a DHS cluster and the target outcome. Collection of β̂₁^(j) allowed us to estimate the bias of the estimator from each method, E[β̂₁^(j)] – β₁.

We used standard linear mixed models, which account for the fact that each method is applied to the same dataset through use of random effects. We then tested whether the bias of the estimator associated with each method was significantly different from zero and whether this bias changes across spatial smoothness and cell prevalence settings. These analyses are repeated separately for each of the raster surfaces considered. Determining what combinations of urban-rural buffer definitions and surface characteristics lead to unbiased effect size estimates will help develop guidelines pertaining to the use of DHS GPS data in studies linking data from ancillary raster surfaces. Specifically, results here will define appropriate scales of analysis needed to minimize bias associated with effect estimates and covariate misspecification.

2.4.2 Case Study: Anemia Risk and Parasite Prevalence

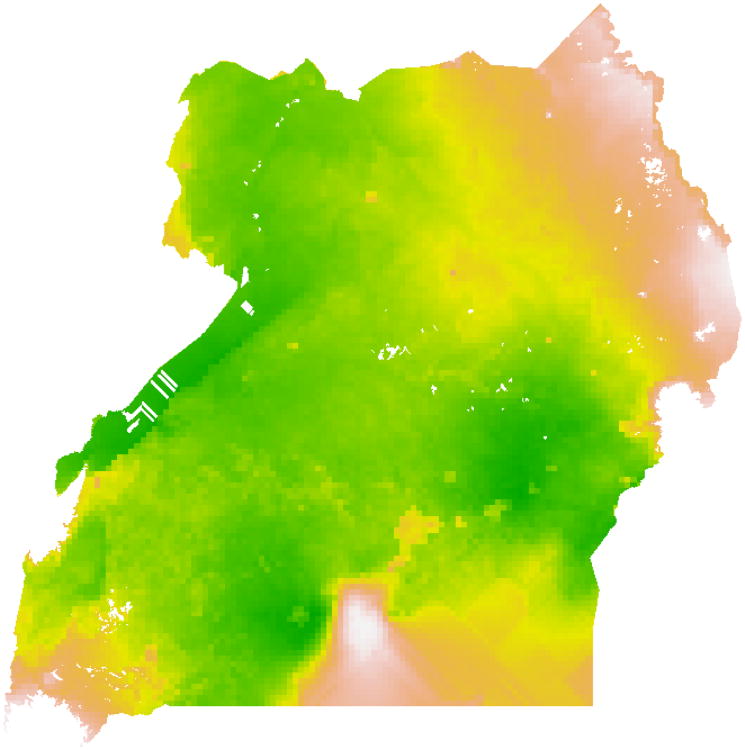
The goal of this case study was to determine whether the predicted prevalence of malarial parasite infections in a neighborhood is associated with the number of people who are anemic (among all respondents tested) in a DHS cluster. Raster data on Plasmodium falciparum prevalence was obtained from the Malaria Atlas Project (Gething et al. (2011); Figure 5). The outcome of interest, i.e., number of respondents who are anemic in DHS clusters, was obtained from the 2011 Uganda DHS.

Figure 5.

Malaria Atlas Project parasite prevalence data used in subsequent analyses. Data provided in this raster file pertained to parasite prevalence throughout the study area, with cell values corresponding to probabilities between zero and one. Prevalence ranged from 0 (white) to 0.60 (green), with the color scheme of orange to yellow representing prevalence values ranging approximately between 0.20 to 0.40.

To determine how smooth a raster surface is, in terms of proposed guidelines, investigators can convert a raster surface to a points shapefile, and fit a simultaneous autoregressive regression model on the points generated from the raster (Appendix B). Average parasite prevalence was calculated using urban and rural buffer sizes determined by simulation study results. Using both, true, non-displaced DHS cluster locations, along with the publicly available displaced locations, effect estimates associated with predictor variables generated for both true and displaced clusters were compared. Specifically, a Poisson regression model was fit to the data with anemia counts per cluster as the outcome variable, neighborhood parasite prevalence as the predictor variable, and an offset accounting for cluster-level population size. Slope parameters and standard errors were compared for the true and displaced datasets.

2.4.3 Case Study: Anemia Risk and Cropland Cover

The motivating research question for this case study was to determine whether the amount of cropland cover in a neighborhood is associated with the number of women who are anemic (i.e., anemia of any severity) within a DHS cluster. Raster data on land cover was acquired from LP DAAC (https://lpdaac.usgs.gov/; Figure 7). The outcome of interest, i.e., number of women who are anemic in DHS clusters, was obtained from the 2011 Uganda DHS.

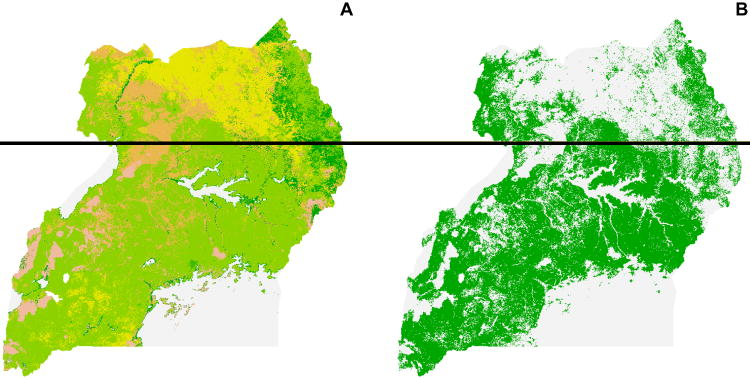
Figure 7.

LP DAAC Land Cover data used in subsequent analyses. (A) The original raster file was reclassified to include seven categories of land cover types ranging in values from 0 to 6: water, forest, woody savanna, savanna, cropland, urban, and other. (B) Cropland cover (green) accounted for roughly 50% of all land cover in Uganda with this dataset.

For this case study, the percentage of cropland cover for the displaced data was calculated using urban and rural buffer sizes determined by simulation study results. To determine misclassification rates, in terms of proposed guidelines, investigators can use the function provided in the additional files (Appendix C). True percentage of cropland cover for DHS cluster i was calculated as the proportion of cells within the corresponding circular radius of 2 or 5 km, for urban and rural locations respectively. Using both true, non-displaced DHS cluster locations along with the publicly available displaced locations, effect estimates associated with predictor variables generated for both true and displaced clusters were compared. Specifically, a Poisson regression model was fit to the data with anemia counts per cluster as the outcome variable and neighborhood percent cropland cover as the predictor variable; slope parameters and standard errors were compared for the true and displaced datasets. Additionally, for illustrative purposes, the analysis was repeated using the method of exact cell extraction.

3 Results and Discussion

3.1 Continuous Raster Simulation Study

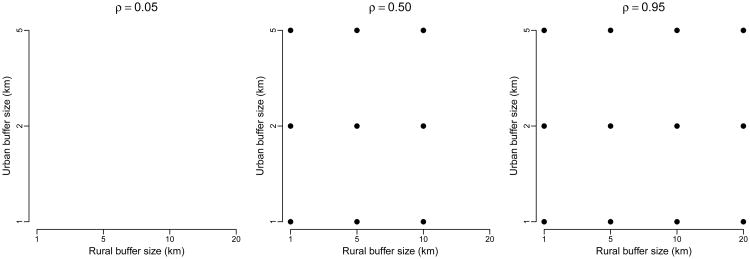
One-sample t-tests from linear mixed models that addressed whether the bias in regression parameter estimates associated with neighborhood definitions (i.e., buffers around displaced points) was significantly different than zero indicated that across surfaces with moderate to high levels of spatial autocorrelation, estimates were unbiased when coverage was calculated for neighborhoods composed of rural buffer sizes between 1 and 10 km and urban buffer sizes between 1 and 5 km (Fig. 4B and 4C). The bias of estimates was dependent on the smoothness of the ancillary surface, with sensitivity to point displacements being higher when using surfaces with very low autocorrelation (ρ = 0.05; Fig. 4A). In other words, for a very noisy, unsmooth surface, point displacements can drastically alter observed raster values, and buffer averaging fails to help reduce any resulting bias. For an extremely smooth surface, however, any urban-rural buffer definition is adequate (among those considered) because neighboring values will be similar up to very large distances away from the true DHS location. Interestingly, however, for a moderately smooth surface, if rural buffers are too large, the potential to capture data outside of a smooth region increases and neighborhood averages begin to deviate more significantly from values obtained at true DHS cluster locations.

Figure 4.

Circular buffer sizes associated with nonsignficant bias in effect estimates due to point displacement across multiple spatial smoothness levels of ancillary continuous raster data sets. Overall, use of urban buffer sizes between 1 - 5 km, and rural buffers between 1 - 10 km resulted in unbiased effect estimates across surfaces with moderate to high spatial autocorrelation (ρ ≥ 0.5). Under surfaces of low spatial autocorrelation, no neighborhood combinations yielded unbiased effect size estimates.

Low levels of bias were noted with one-sample t-tests from linear mixed models addressing whether the bias in regression parameter estimates associated with point extraction was significantly different than zero. Overall, point extraction provided unbiased results across most autocorrelation surfaces tested, and was thus shown to be relatively robust to point displacement (Table 1). Only point extractions from surfaces with very low spatial autocorrelation(ρ = 0.05) were found to be associated with significantly biased results.

Table 1.

Bias associated with point extraction from continuous rasters. Results of one-sample t-tests addressing the significance of bias associated with raster cell extraction. Point extraction is not recommended for non-smooth surfaces (ρ = 0.05) because it yielded significantly biased effect size estimates.

ρ	t-statistic	p-value	Mean bias	Lower 95% CI	Upper 95% CI
0.05	9.6234	0.0000	0.0289	0.0230	0.0348
0.50	0.6381	0.5239	0.0019	-0.0040	0.0078
0.95	1.3989	0.1629	0.0042	-0.0017	0.0101

3.1.1 Proposed Guidelines: Continuous Raster Data

According to results from this simulation study, in studies that integrate ancillary continuous raster data for analyses with DHS GPS data, the random displacements used to protect the privacy of DHS survey respondents could result in misspecified assignments of predictor variables at the DHS cluster-level depending on characteristics of the surface from which data is being linked. For relatively smooth surfaces, bias was low for both point extraction and most urban/rural neighborhood definitions. Thus, when working with ancillary continuous surfaces with high spatial autocorrelation either buffer means or point extraction will provide unbiased regression parameter estimates. Moreover, because highly non-smooth surfaces yielded biased estimates from both point extraction and neighborhood buffer approaches, we further recommend that if investigators plan on working with such rasters, they attempt to smooth the surface in some way to mitigate the effects of such potential bias.

Table 3 provides an overview of proposed guidelines. Note that these guidelines provide general rules to consider when linking continuous raster data to randomly displaced DHS point data. We have shown that the extent of bias in inferences drawn from linking ancillary continuous data to displaced DHS GPS data depends heavily on the smoothness of the ancillary raster surface.

Table 3.

Overview of general guidelines for neighborhood definitions for studies linking DHS GPS data to ancillary raster data.

Raster Type	Considerations		Recommendations
	Surface Characteristics	Covariate Spatial Scale
Continuous	ρ ≤ 0.05	Point-level	Not recommended
	ρ > 0.05		Unbiased
	ρ ≤ 0.05	Neighborhood-level:	Not recommended†
	ρ > 0.05	Urban: 2 km, Rural: 5 km	Urban: 1-5 km, Rural: 1-10 km
Categorical	Misclassification Rate ≥ 20%	Point-level	Not recommended
	Misclassification Rate < 20%		Not recommended
	Misclassification Rate ≥ 20%	Neighborhood-level:	Not recommended†
	Misclassification Rate < 20%	Urban: 2 km, Rural: 5 km	Urban: 1-5 km, Rural: 5-10 km

^†require smoother surface and/or change in scale

3.2 Categorical Raster Simulation Study

One-sample t-tests addressing whether the bias in regression parameter estimates associated with neighborhood definitions (i.e., buffers around displaced points) was significantly different than zero indicated that misclassification rates, which are a function of both surface smoothness and cell type prevalence, could affect bias in effect size estimates. In other words, depending on the overall rate of misclassification, different neighborhood definitions would yield unbiased effect size estimates. Thus, guidelines on the usage of DHS GPS data will depend on these factors.

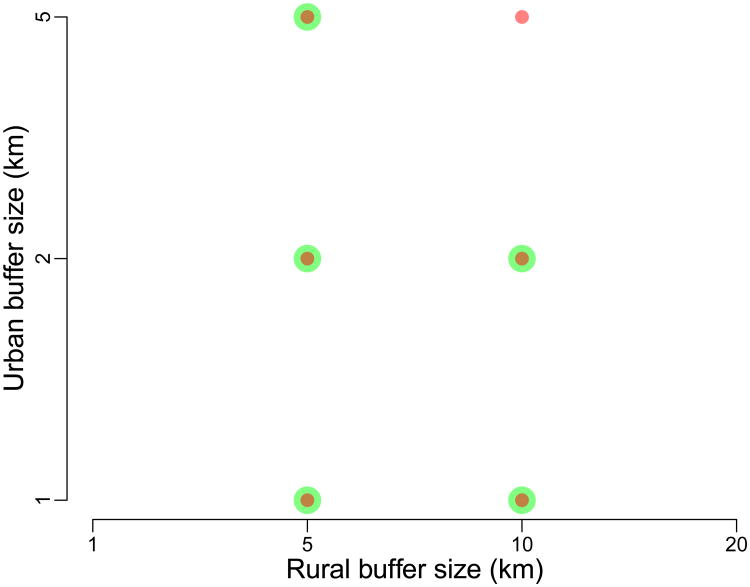
Across simulated categorical raster surfaces, average misclassification rates across all locations ranged between 0.11 and 0.78. Only two surfaces associated with average misclassification probabilities of less than 0.20 yielded covariates for which results were unbiased (Figure 3AB). These surfaces corresponded to discretized versions of continuous surfaces with high spatial autocorrelation (ρ = 0.95) and cell type prevalence less than 45% (Figure 2C). Overall, estimates corresponding to these surfaces were unbiased when coverage was calculated for neighborhoods composed of rural buffer sizes between 5 and 10 km and urban buffers between 1 and 5 km (Figure 6).

Figure 6.

Circular buffer sizes associated with nonsignficant bias in effect estimates due to point displacement across multiple misclassification levels for ancillary categorical raster data sets. When misclassification rates are less than 20%, use of urban buffer sizes between 1 and 5 km, and rural buffer sizes at or exceeding 5 km resulted in unbiased effect estimates; however when rate of misclassification is greater than 20%, investigators should either refrain from conducting analyses in which data from such surfaces is integrated with DHS data, or should consider more coarse spatial processes when defining covariates of interest.

One-sample t-tests of mean bias addressing whether the bias in regression parameter estimates associated with point extraction was significantly different than zero indicated strong bias. Overall, point extraction failed to provide unbiased results across all surfaces tested, and was thus shown to be highly sensitive to point displacement (Table 2).

Table 2.

Bias associated with point extraction from discrete rasters. Results of one-sample t-tests addressing the significance of bias associated with raster cell extraction. Point extraction is not recommended since it yielded significantly biased effect size estimates throughout most scenarios tested.

Misclassification rate	t-statistic	p-value	Mean bias	Lower 95% CI	Upper 95% CI
≤ 11%	4.69	< 0.0001	0.019	0.011	0.026
11%–20%	4.53	< 0.0001	0.018	0.010	0.026
≥ 20%	5.38	< 0.0001	0.018	0.012	0.025

3.2.1 Proposed Guidelines: Categorical Raster Data

According to results from this simulation, in studies that integrate ancillary categorical raster data for analyses with DHS GPS data, the random displacements used to protect the privacy of DHS survey respondents could result in misclassified assignment of predictor variables at the DHS cluster level, depending on how the ancillary data is linked to DHS data. The magnitude of this bias, however, could be made negligible by use of mean cell values across urban and rural neighborhoods of 1 and 5 km radii. Direct cell extraction is not recommended, because this sort of data and subsequent inferences from analyses are highly sensitive to random point displacements. Given that most displacements for DHS GPS data occur between 0 and 5 km, the proposed minimum buffer sizes of 1 and 5 km for urban and rural locations is reasonable. We found that surface misclassification rates, which are a function of both the smoothness of the ancillary raster surface and the prevalence of cell types of interest, could also influence proper specification of covariate data and bias in regression estimates. Surfaces associated with misclassification rates less than 20% resulted in lower bias than surfaces associated with higher misclassification rates. Thus, investigators who plan to link environmental surface data to DHS GPS data should also consider the nature of the raster surface in question; for example, the prevalence of boundaries or edges along which points may lie could contribute to high misclassification rates. Table 3 presents an overview of proposed guidelines. As before, these guidelines provide general rules to consider when linking categorical raster data to randomly displaced DHS point data. We have shown that the extent of bias in inferences drawn from linking ancillary categorical data to displaced DHS GPS data will depend on the scale of neighborhoods used to define the process of interest and characteristics of the ancillary surface that could result in higher rates of covariate misspecification. Single point extraction is highly discouraged, because our empirical results suggest that using a neighborhood average will best mitigate the potential bias associated with systematic geographic displacements.

3.3 Case Study: Anemia Risk and Parasite Prevalence

The raster surface associated with P. falciparum prevalence fit under the highly autocorrelated surface category explored in the simulation study (ρ = 0.998). Proposed guidelines suggest that to avoid bias in effect estimates when using continuous raster data from highly smooth surfaces investigators could either use point extraction or define neighborhoods around DHS clusters as having buffers of 5 km radius. Thus, average parasite prevalence was calculated using urban and rural buffer sizes of 5 km radii for each DHS cluster. For comparative purposes, simple point extraction was also used to assign covariate values to the DHS clusters. Using neighborhood definitions from the proposed guidelines, the estimated effect sizes for the true and displaced datasets did not differ significantly. The estimated slope parameter, using the true dataset, was 0.137 (95% CI: 0.054, 0.219); for the displaced data, it was 0.132 (95% CI: 0.049, 0.214). If direct cell extraction was used to generate covariates of interest, effect estimates obtained from the displaced and true DHS GPS data were also similar. The estimated slope parameter obtained using direct cell extraction with the true data was 0.978 (95% CI: 0.353, 1.604); for the displaced data, it was 0.995 (95% CI: 0.369, 1.620).

3.4 Case Study: Anemia Risk and Cropland Cover

Estimated misclassification rate for the cropland cover surface was 92%. Based on guidelines, the scale of underlying spatial processes should be re-evaluated. Rather than trying to capture a neighborhood process occurring within 2 or 5 km of DHS cluster locations, the resulting covariate should thus represent a more coarse spatial process, such as that within a 10 km radius. After rescaling the measurement of the cropland cover covariate, estimated effect sizes for the true and displaced datasets did not differ significantly. The estimated slope parameter for the analysis using the true data was 0.064 (95%CI: -0.017, 0.145); for the displaced dataset, the estimated slope parameter was 0.072 (95%CI: -0.009, 0.154).

If misclassification probabilities were ignored, and the targeted spatial scale of the process remained at 2 or 5 km, differences between true and observed parameter estimates were more pronounced. The estimated slope parameter for the analysis using the true data was 0.12 (95% CI: 0.041, 0.208); for the displaced dataset, the estimated slope parameter was 0.097 (95% CI:0.014, 0.179). Moreover, if proposed guidelines were further disregarded with respect to point extraction, effect estimates obtained from the true and displaced DHS GPS data also differed and yielded different conclusions based on p-values. The estimated slope parameter obtained using direct cell extraction with the true data was 0.202 (95% CI: 0.021, 0.383); for the displaced data, it was 0.161 (95% CI: -0.012, 0.334).

4 Conclusions

Guidelines on the usage of DHS GPS data in the context of integrating ancillary raster data should be based on minimizing bias in the effect estimates of interest. Based on the continuous raster simulation results, for studies aimed at addressing the influence of contextual environmental data on DHS cluster-level outcomes, use of urban buffer sizes between 1 and 5 km and rural buffer sizes between 1 and 20 km provided unbiased estimates under surfaces of moderate to high autocorrelation. Under surfaces of low spatial autocorrelation, all neighborhood definitions failed to provide unbiased parameter estimates. Moreover, point extraction led to unbiased parameter estimates for continuous surfaces with moderate to high spatial autocorrelation, but performed poorly for non-smooth surfaces. Based on the categorical raster simulation results, for studies aimed at addressing the influence of contextual environmental data on DHS cluster-level outcomes, it is appropriate to use a buffer between 1 and 5 km to define urban neighborhoods if misclassification rates for the ancillary raster surface is less than 20%. The definition of rural neighborhoods will depend on specific characteristics of the surface at hand; however, generally, rural buffers of 5 km will provide unbiased estimates for surfaces that are associated with misclassification rates less than 20%. These are general and conservative guidelines because we note that prevalence of cell types along with surface smoothness and cell size can influence the bias of an estimate (Appendix D).

This analysis of anemia risk and malaria parasite prevalence in Uganda was carried out for purposes of illustration; it is likely that the true effect of malaria prevalence on anemia incidence will be moderated by other unaccounted variables. The purpose of this case study was to demonstrate how well guidelines, which were established following empirical results of a simulation study, perform in a realistic application of DHS GPS data. Results showed that the proposed guidelines performed well in practice.

We note here that the impacts of point displacements on misspecification of covariates and interpretation of analytic results are affected by the smoothness of the raster surface to which DHS GPS data is linked. Overall, empirical results obtained using simulated surfaces indicated that the impact of this displacement could be moderated through the generation of average values using neighborhood buffers. Guidelines here were developed based on standardized data, thus investigators should center and scale their covariate data accordingly (i.e., convert values to z-scores) when applying proposed guidelines from this study. Point extraction is generally not recommended with categorical raster data because this most often leads to biased results; however, it may be an adequate approach with continuous raster data. Empirical results suggest taking averages across circular rural and urban buffers of around 5 km. We note, however, that other continuous and/or categorical raster surfaces may yield different results due to differences in misclassification rates associated with smoothness and/or grid cell size.

In addition to surface smoothness, the guidelines presented in this report are also dependent on the scale of true processes of interest. With the raster-based simulations we demonstrated how buffer means could be used to generate covariates of interest. There we assumed that the true process of interest was occurring at a particular neighborhood scale, i.e., 2 km in urban areas and 5 km in rural areas. If, however, interest lay in understanding mechanisms associated processes occurring at a larger spatial scale, say 10 km neighborhoods, then covariates generated at this scale or something slightly larger would likely be more appropriate than those generated using a 5 km buffer. In other words, based on the raster simulation results, neighborhood-level covariates should be defined with regard to the spatial scale of underlying processes under investigation. Moreover, when working with categorical raster surfaces that yield misclassification rates of greater than 20%, investigators may consider re-evaluating the scale of spatial processes if it is too fine.

Guidelines provided here also assume that ancillary data are of good quality and relevant to DHS GPS data with regard to temporal overlap. Failure to uphold these assumptions will likely lead to further problems in generating interpretable and relevant study results. For example, linking DHS data to an interpolated surface with high levels of prediction error will result in misspecification of covariates due to problems with the ancillary data file, rather than issues associated with random DHS point displacement. Likewise, if linking DHS data to temporally varying data such as census-based data or land cover data, special care should be given to ensuring that the time periods represented by the ancillary datasets correspond to the time periods associated with the DHS surveys to which data will be linked. Otherwise, any associations identified in subsequent analyses are likely to be confounded by temporally disjunct processes.

Supplementary Material

Appendix_A. Additional File 1 – Appendix A.

Appendix A corresponds to a.txt file containing the R code used to simulate the point displacement procedure.

Appendix_B. Additional File 2 – Appendix B.

In order to determine the level of smoothness, i.e. spatial autocorrelation coefficient, of an ancillary raster dataset, investigators can run the following R function, which calls the raster dataset as its sole argument.

Appendix_C. Additional File 3 – Appendix C.

Appendix C is an R function that returns a vector of misclassification probabilities for all locations, and an estimate of the resulting misclassification rate of a given categorical raster surface.

Appendix_D. Additional File 4 – Appendix D.

Appendix D contains figures of all categorical raster surfaces that were used in simulation studies, and the relationship between estimated bias and misclassification rate of simulated surfaces.