Parity-time–symmetric optoelectronic oscillator

A parity-time–symmetric optoelectronic oscillator was demonstrated without the use of a narrowband microwave or optical filter.

Abstract

An optoelectronic oscillator (OEO) is a hybrid microwave and photonic system incorporating an amplified positive feedback loop to enable microwave oscillation to generate a high-frequency and low–phase noise microwave signal. The low phase noise is ensured by the high Q factor of the feedback loop enabled by the use of a long and low-loss optical fiber. However, an OEO with a long fiber loop would have a small free spectral range, leading to a large number of closely spaced oscillation modes. To ensure single-mode oscillation, an ultranarrowband optical filter must be used, but such an optical filter is hard to implement and the stability is poor. Here, we use a novel concept to achieve single-mode oscillation without using an ultranarrowband optical filter. The single-mode operation is achieved based on parity-time (PT) symmetry by using two identical feedback loops, with one having a gain and the other having a loss of the same magnitude. The operation is analyzed theoretically and verified by an experiment. Stable single-mode oscillation at an ultralow phase noise is achieved without the use of an ultranarrowband optical filter. The use of PT symmetry in an OEO overcomes the long-existing mode-selection challenge that would greatly simplify the implementation of OEOs for ultralow–phase noise microwave generation.

INTRODUCTION

The generation of a microwave signal with a low phase noise at a high frequency is of great importance for applications such as modern radars and communications systems (1–3). A quartz resonator can have a high Q factor and can be incorporated in an electronic oscillator to generate a low–phase noise microwave signal. However, the frequency range of an electronic oscillator using a quartz resonator is limited to 10 to 100 MHz. For high-frequency microwave signal generation, frequency multiplication has to be used, which will deteriorate the phase noise performance. Microwave generation based on a cryogenic sapphire oscillator can produce a microwave signal at a higher frequency with a very low phase noise, but its practical applications are limited owing to the requirement of an ultralow-temperature cooling system (4–7).

Optical techniques have been proven to be effective in generating high-frequency and low–phase noise microwave signals. For example, a microwave signal with a central frequency of around 10 GHz and a phase noise down to −170 dBc/Hz at an offset frequency of 10 kHz can be generated by beating two comb lines from an optical comb (8, 9). Optical frequency division implemented by phase-locking an optical frequency comb to a cavity-stabilized laser source can generate a 10-GHz microwave signal with a phase noise of −150 dBc/Hz at an offset frequency of 10 kHz (10, 11).

On the other hand, a microwave signal with a low phase noise can be generated by an optoelectronic oscillator (OEO) (12–15). An OEO is a hybrid microwave and photonic system incorporating an amplified positive feedback loop to enable microwave oscillation to generate a high-frequency and low–phase noise microwave signal. The low phase noise is ensured because of the high Q factor of the feedback loop enabled by the use of a long and low-loss optical fiber. Since the advent of an OEO two decades ago (12), researchers have managed to generate a microwave signal at an ultralow phase noise. For example, a 10-GHz microwave signal with a phase noise as low as −163 dBc/Hz at an offset frequency of 6 kHz was demonstrated by using a 16-km-long optical fiber delay line in the feedback loop (13, 14).

The increase in the cavity length of an OEO is motivated by the low phase noise (15), which is feasible since the loss of a state-of-the-art optical fiber is as small as 0.2 dB/km in comparison to that of 360 dB/km of a typical microwave coaxial cable (1). The use of a 20-km fiber would only introduce a 4-dB insertion loss that can be easily compensated by an amplifier, but can result in a phase noise better than −150 dBc/Hz at an oscillation frequency of several gigahertz (15). Although the loss is not likely an issue, the greatest challenge in implementing an OEO with a long loop is the large number of closely spaced longitudinal modes because of its small free spectral range (FSR), which makes stable single-mode oscillation extremely difficult. One solution to achieve a single-mode OEO is to use a highly frequency-selective filter to select one longitudinal mode and suppress the other modes (13). For example, to achieve single-mode oscillation in an OEO with a cavity length in the order of 10 km, an optical filter with a Q factor in the order of 10⁹ is required. However, most high-Q resonators (16–20) demonstrated so far can only have a Q factor of less than 10⁸. An optical resonator with a Q factor of more than 10⁹ is extremely difficult to manufacture as it requires a lengthy and complicated polishing process and stringent requirements for high-quality packaging. To implement a single-mode OEO using a more practical optical resonator that has a lower Q factor, a multiloop configuration that uses the spectral Vernier effect has to be adopted (21). In a multiloop OEO, the Q factor of the entire OEO cavity is determined by the longest feedback loop, while the FSR is determined by the shortest feedback loop. Thus, the phase noise is maintained low. Since the FSR is increased, the Q factor of the optical resonator could be much smaller. For example, by using dual loops in an OEO (21), the Q factor of the optical resonator can be reduced by a factor of 10³. However, a multiloop OEO has a very complicated structure, which will severely affect the stability of the operation.

Recently, parity-time (PT) symmetry has been proven to be a simple and effective solution for mode selection in an oscillator, such as an integrated optical ring laser (22–24) and a pure electronic oscillator (25). By using two cross-coupled resonators with an identical geometry but opposite gains, that is, the gain in one resonator is equal to the loss of the other resonator, PT symmetry is achieved. By manipulating the gain, loss, and the coupling ratio between the two resonators, PT symmetry can be broken for a specific mode, which would enjoy a much higher gain compared with other modes, and thus a stable single-mode oscillation can be achieved. Although such a technique has been demonstrated for single-mode lasing of a dual-cavity laser source and single-frequency oscillation of a dual-loop electronic oscillator, it has never been used in an OEO—a hybrid microwave and photonic system that can generate a high-frequency microwave signal at an ultralow phase noise.

Here, we propose a new scheme to achieve single-mode oscillation of an OEO without the use of an ultranarrowband optical filter. The single-mode operation is enabled based on PT symmetry by using two feedback loops with one having a gain and the other having a loss of the same magnitude for the oscillating microwave signal. By manipulating the gain, loss, and the coupling ratio between the two feedback loops, PT symmetry can be broken for one mode, and a single-mode oscillation at this mode is achieved. In the proposed PT-symmetric OEO, the two feedback loops are formed by splitting an intensity-modulated optical signal into two channels and detecting the signals from the two channels at a balanced photodetector (BPD; consisting of two PDs, PD1 and PD2). Two microwave signals are generated, which are combined and fed back to the intensity modulator. Note that balanced detection will introduce a π phase difference between the two signals at the output of the BPD. A tunable delay line (TDL) is incorporated before PD1, which is controlled to have a delay length equal to half of the wavelength of the oscillating microwave signal and thus functions as a π phase shifter, to offset the π phase shift due to the balance detection. Thus, the two microwave signals at the output of the BPD are summed in phase. Because of the PT-symmetric configuration, despite the fact that the OEO has a long loop length with a large number of densely spaced longitudinal modes, the OEO can support single-mode oscillation without the need for a high-Q filter to perform mode selection, and thus the system is significantly simplified. In addition, an added advantage of the proposed configuration using balanced detection is that the noise from the laser source can be partially suppressed (26), which would further enhance the noise performance of the OEO. The proposed PT-symmetric OEO is experimentally demonstrated. A microwave signal at 9.867 GHz with a phase noise as low as −142.5 dBc/Hz at an offset frequency of 10 kHz is generated. The phase noise density corresponding to the side modes is measured to be −68.7 dBc/Hz, which confirms the effectiveness of using PT symmetry for side-mode suppression.

The block diagram of the proposed PT-symmetric OEO is shown in Fig. 1. As can be seen, an LD is used to generate a light wave, which is coupled into an MZM via a PC1. Note that PC1 is used to minimize the polarization-dependent loss. The modulated signal at the output of the MZM is then launched into a coil of SMF for a long time delay. To exploit the effect of PT symmetry, two identical and mutually coupled feedback loops, with one having a gain and the other having a loss of the same magnitude, are constructed. This is done by using a PBS jointly with a second PC (PC2) to split the modulated signal into two channels. Considering that the light wave from the LD is linearly polarized, the joint operation of PC2 and the PBS can achieve light splitting with a tunable splitting ratio by tuning PC2. Note that PC2, which consists of a half–wave plate sandwiched between two quarter–wave plates, can be used to alter the polarization direction of the incoming light relative to the PBS by rotating the half–wave plate (27). Arbitrary power splitting ratios can be obtained at the inputs of PD1 and PD2. The two optical signals are then sent to a BPD to perform balanced detection to generate two microwave signals that are out of phase. A TDL is incorporated before PD1, which is controlled to have a delay length equal to half of the wavelength of the oscillating microwave signal and thus functions as a π phase shifter, to offset the π phase shift due to balance detection. The microwave signals are then combined in phase. Since the cross-coupling between the two loops can be controlled by tuning PC2, the gain and loss can be adjusted to be equal in magnitude, to achieve PT symmetry. The signals at the output of the BPD are then amplified by an EA and fed back to the MZM via a microwave splitter to close the OEO loop. The microwave splitter is used to tap a fraction of the microwave signal for spectrum analysis using an ESA and phase noise analysis using a signal analyzer.

Fig. 1. Block diagram of the PT-symmetric OEO.

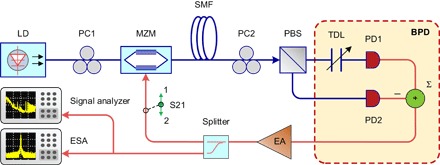
LD, laser diode; PC, polarization controller; MZM, Mach-Zehnder modulator, SMF, single-mode fiber; PBS, polarization beam splitter; Σ, microwave combiner; EA, electrical amplifier; ESA, electrical spectrum analyzer.

Under PT symmetry, the gain and loss of the two loops are equal in magnitude. The PT symmetry can be broken by tuning PC2 to allow a longitudinal mode with the highest gain to be selected to oscillate, while other modes will be suppressed. Single-mode oscillation is thus achieved. Compared with any other OEOs demonstrated so far, a distinct feature of the proposed OEO is that no high–Q factor optical or microwave filter is needed for single-mode oscillation. The oscillation occurs for an OEO mode that experiences the highest gain.

Because the gain and loss loops have identical lengths, the coupling between the two OEO loops breaks the degeneracy of the modes in each cavity, resulting in a frequency splitting of the original eigenmodes in each loop. The eigenfrequencies of the PT-symmetric system can be written as (23)

$${\mathrm{\omega }}_{\mathit{n}}^{(1,2)}={\mathrm{\omega }}_{\mathit{n}}+\mathit{i}\frac{{\mathrm{\gamma }}_{{\mathit{a}}_{\mathit{n}}}+{\mathrm{\gamma }}_{{\mathit{b}}_{\mathit{n}}}}{2}\pm \sqrt{{\mathrm{\kappa }}_{\mathit{n}}^2-{\left(\frac{{\mathrm{\gamma }}_{{\mathit{a}}_{\mathit{n}}}-{\mathrm{\gamma }}_{{\mathit{b}}_{\mathit{n}}}}{2}\right)}^2}$$ (1)

where a_n and b_n are the amplitude of the nth modes in the gain loop and the loss loop, respectively; ω_n is the nth eigenfrequency of the longitudinal modes of the two loops without PT symmetry coupling; κ_n is the coupling coefficient between the two loops for the nth modes; and ${\mathrm{\gamma }}_{{\mathit{a}}_{\mathit{n}}}$ and ${\mathrm{\gamma }}_{{\mathit{b}}_{\mathit{n}}}$ represent the gain and loss coefficients of the gain loop and the loss loop for the nth mode, respectively.

Assuming that the exact PT symmetry condition (identical gain and loss in magnitude) can be satisfied by tuning PC1 to achieve single-mode oscillation for a mode denoted by n = 0, that is, ${\mathrm{\gamma }}_{{\mathit{a}}_0}=-{\mathrm{\gamma }}_{{\mathit{b}}_0}={\mathrm{\gamma }}_0$, Eq. 1 can be written as

$${\mathrm{\omega }}_0^{(1,2)}={\mathrm{\omega }}_0\pm \sqrt{{\mathrm{\kappa }}_0^2-{\mathrm{\gamma }}_0^2}$$ (2)

It can be seen from Eq. 2 that, when the gain/loss coefficient is smaller than the coupling coefficient within each loop, the two loops exhibit broken degeneracy with an eigenfrequency splitting related to the coupling ratio. However, when the gain/loss coefficient exceeds the coupling coefficient, the eigenfrequency splitting becomes an imaginary number. The electrical field can be written as

$${\mathit{E}}_0^{(1,2)}= \text{exp}({\mathrm{\omega }}_0\mathit{t})\text{exp}(\pm \mathit{j}|{\mathit{g}}_0|\mathit{t})$$ (3)

where ${\mathit{g}}_0=\sqrt{{\mathrm{\kappa }}_0^2-{\mathrm{\gamma }}_0^2}$. As can be seen from Eq. 3, PT symmetry will be broken when the gain coefficient exceeds the coupling coefficient. A pair of amplifying and decaying modes will be generated in the PT-symmetric OEO with an identical frequency, which is the dominating mode that oscillates in the OEO.

It should be noted that, even in a conventional OEO, single-mode oscillation can be achieved as the net loop gain exceeds unity for a specific mode. This requirement is extremely stringent and impractical as the difference between the net gains of two adjacent OEO modes is too small to ensure a single and dominant mode due to the small FSR. PT symmetry can greatly enhance the gain difference between the dominant mode and a secondary mode. Note that a secondary mode is one that has a net gain smaller than that of the dominant oscillating mode. To analyze the gain difference enhancement, we denote the secondary mode with n = 1 and assume it in critical oscillation condition. In a single-loop OEO, the gain difference between the oscillating mode and the secondary mode in critical condition is given by

$$\mathrm{\Delta }\mathit{g}={\mathrm{\gamma }}_{{\mathit{a}}_0}-{\mathrm{\gamma }}_{{\mathit{a}}_1}$$ (4)

In comparison, the gain difference between the oscillating mode (n = 0) and a secondary mode (n = 1) in a PT-symmetric OEO can be deduced from Eq. 1, given by

$$\mathrm{\Delta }{\mathit{g}}_{\text{PT}}=\sqrt{{\mathrm{\gamma }}_0^2-{\left(\frac{{\mathrm{\gamma }}_{{\mathit{a}}_1}-{\mathrm{\gamma }}_{{\mathit{b}}_1}}{2}\right)}^2}$$ (5)

To visualize the effectiveness of using PT symmetry in enhancing single-mode oscillation, the gain difference between the oscillating mode and the secondary mode with and without PT symmetry is simulated based on Eqs. 4 and 5. In Fig. 2, as the gain/loss coefficient for the secondary mode decreases from 100 to 90% of that of the oscillating mode, the PT-symmetric loops have a significantly enhanced gain difference as compared with that of a single loop. The gain difference enhancement is especially strong when ${\mathrm{\gamma }}_{{\mathit{a}}_1}$ or $-{\mathrm{\gamma }}_{{\mathit{b}}_1}$ is close to γ₀, which is the case for our OEO. Owing to the strongly enhanced gain difference, the use of a PT-symmetric OEO to achieve stable single-mode oscillation is an effective solution.

Fig. 2. Gain difference enhancement with PT symmetry.

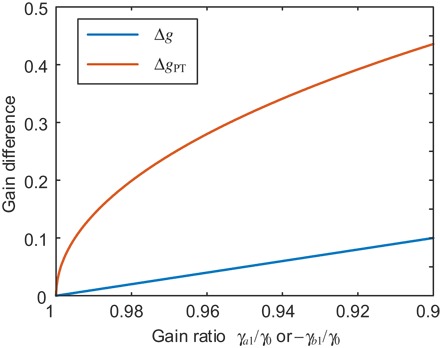
The gain difference between the oscillating mode and the secondary mode within a regular single-loop OEO (blue) and a PT-symmetric OEO (red) is illustrated for comparison.

In the proposed OEO, balanced detection is used to generate two out-of-phase microwave signals, corresponding to the two feedback loops with one having a gain and the other having a loss. One added advantage of using balanced detection is that the noise from the LD can be partially cancelled (26). Thus, the phase noise performance of the PT-symmetric OEO can be further improved.

RESULTS AND DISCUSSION

An experiment is performed to study the operation of the PT-symmetric OEO shown in Fig. 1. The optical carrier from the LD has a central wavelength of 1550 nm and an optical power of 16 dBm, which is sent to the input of the MZM via PC1. The MZM is biased at the quadrature point. We first measure the open-loop response of the OEO with only a single loop connected, which is carried out by tuning PC2 to direct all optical power to PD1. The long fiber in the loop is an SMF of 9.1 km. Since no microwave frequency-selective components are used, the OEO loop exhibits a relatively flat gain spectrum with a few gain peaks between 5 and 10 GHz, as shown in Fig. 3. The frequency range where the net loop gain exceeds unity is measured to be 12.1 GHz, which contains 5.33 × 10⁶ longitudinal modes. To select a single mode, an ultranarrowband optical filter or a microwave filter must be used in the OEO loop or a PT-symmetry scheme should be used.

Fig. 3. S21 magnitude response of the OEO with only one loop closed.

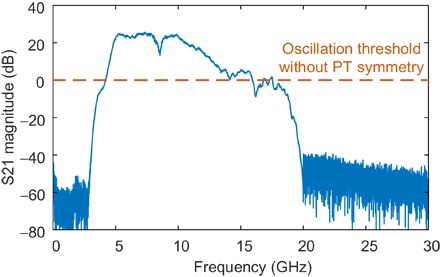
It is measured by a vector network analyzer (VNA) connected between the MZM and the EA with the measurement direction indicated in Fig. 1.

Then, we study the mode selection capability of the OEO when PT symmetry is used. To do so, we first close the two OEO loops by tuning PC2 to ensure that the first loop has a gain and the second loop has a loss of the same magnitude. The operations with three effective loop lengths of 20.31 m, 433.1 m, and 9.166 km corresponding to a mode spacing of 10.26 MHz, 481.0 kHz, and 22.73 kHz are evaluated. Stable single-mode oscillations are achieved for the PT-symmetric OEO with all the three different loop lengths. The generated microwave signal has a frequency of 9.867 GHz. In the experiment, the optical powers at the inputs of PD1 and PD2 are measured to be 6.25 and −1.5 dBm, respectively. In steady-state oscillation, the two loops provide a gain and a loss with the same magnitude to the oscillating microwave signal. A PT-symmetric OEO with single-mode oscillation can then be achieved.

Figure 4 shows the electrical spectra of the microwave signals generated by the OEO. Without PT symmetry, the OEO oscillates with multimode, as can be seen from Fig. 4A. By tuning PC2 to match the gain and loss in the two loops, single-mode oscillation is achieved with a long loop length of 9.166 km. The single-mode oscillation spectra are shown in Fig. 4 (B to D) with different frequency spans and RBWs. The spectrum with a 100-MHz span in Fig. 4B shows that the OEO only oscillates at one frequency, despite the fact that gain bandwidth of a single OEO loop can cover several gigahertz. The oscillation frequency selection is an effect of gain competition. Figure 4C shows the spectrum with a 1-MHz span. The oscillating longitudinal mode can be identified, and the mode spacing is measured to be 22.73 kHz. The oscillating mode is 26.4 dB higher over the highest side mode. No mode-hopping is observed in the experiment for a measurement time window of more than 10 min. Further reducing the frequency span to 1 kHz, the spectrum of the microwave signal is shown in Fig. 4D. It can be seen that the microwave signal has an extremely narrow bandwidth that is likely to be smaller than the RBW of the ESA. Moreover, the frequency drift of the microwave signal is less than 100 Hz in the 10-min measurement time window, which is among the most stable OEOs reported in literature.

Fig. 4. The electrical spectra of the microwave signals generated by the PT-symmetric OEO.

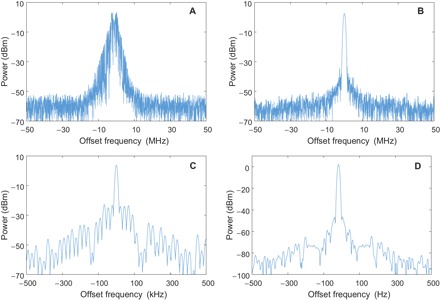
The spectra are measured at a central frequency at 9.867 GHz. (A) Multimode oscillation measured with a resolution bandwidth (RBW) of 3 MHz. (B) Single-mode oscillation measured with an RBW of 3 MHz. (C) Single-mode oscillation measured with an RBW of 9.1 kHz. (D) Single-mode oscillation measured with an RBW of 9 Hz.

The phase noise of the microwave signal is measured by a microwave signal analyzer, which is shown in Fig. 5. At an offset frequency of 10 kHz, the phase noise is −142.5 dBc/Hz. The phase noise peaks induced by the OEO side modes have a spacing of 22.73 kHz. The peaks are below −68.7 dBc/Hz, indicating that PT symmetry is a highly effective technique for mode selection. The peaks located at 890 Hz and their harmonics are introduced by a vibration interference existing in the laboratory environment. A similar phenomenon has been observed in other reported OEOs (28). Figure 5 also shows the phase noise measurements of a 9.876-GHz signal generated by a commercial electrical microwave signal generator (Agilent E8254A) and the PT-symmetric OEO with two shorter loop lengths of 20.31 and 433.1 m. The phase noise density induced by the side modes of the OEO with loop lengths of 20.31 m, 433.1 m, and 9.166 km are below −105, −76.1, and −68.7 dBc/Hz, respectively. A shorter loop enables a higher side-mode suppression. This is understandable because a shorter loop length has a larger mode spacing. The phase noise, on the other hand, would be higher for a shorter loop length. In the measurement, the phase noises are −92.94, −103.4, and −142.5 dBc/Hz for the OEO with loop lengths of 20.31 m, 433.1 m, and 9.166 km at an offset frequency of 10 kHz, respectively. In addition, the phase noise performance of the PT-symmetric OEO with a cavity length of 9.166 km surpasses the commercial microwave source by 26.6 dB.

Fig. 5. The phase noise measurements of the generated microwave signal.

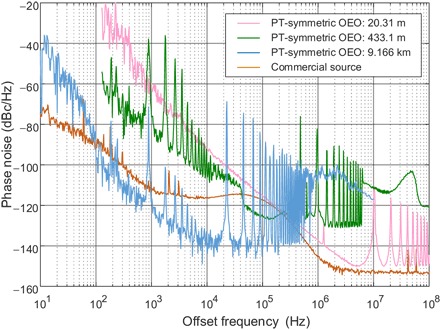
The PT-symmetric OEO is operating with three different loop lengths of 20.31 m, 433.1 m, and 9.166 km. The corresponding phase noise at an offset frequency of 10 kHz is −92.94, −103.4, and −142.5 dBc/Hz. For comparison, the phase noise of a microwave signal generated by a commercial microwave source is also presented, indicating a 26.6-dB phase noise improvement at an offset frequency of 10 kHz for the 9.166-km-long OEO.

It should be noted that the phase noise of the PT-symmetric OEO at an offset frequency below 100 Hz is not as good as a well-packaged commercial signal source because of environmental perturbations. Vibrations impose strong modulations on the phase and polarization state of the light wave propagating in the long optical loop. Because the PT-symmetric OEO incorporates polarization to implement tunable optical power splitting to the BPD, the system is polarization-sensitive. The 890-Hz interference only exists in the OEOs with a loop length of 433.1 m and 9.166 km. The OEO with a loop length of 20.31 m is free from such interference. To mitigate the environmental interference and reduce the phase noise at low-offset frequencies, a first solution is to use a polarization-insensitive optical power splitter, such as a dual-port MZM, to replace the PC and PBS. Another solution is to use an electrical feedback loop to detect the phase and polarization changes caused by environmental interference and carry out real-time compensations (29).

CONCLUSION

In summary, a PT-symmetric OEO was demonstrated to achieve stable single-mode oscillation without the need of a narrowband electrical filter or a high-Q optical filter. PT symmetry was realized by constructing two loops with one having a gain and the other having a loss of the same magnitude. The operation of the PT-symmetric OEO was evaluated experimentally for an OEO loop with three different loop lengths of 20.31 m, 433.1 m, and 9.166 km. Single-mode oscillation was achieved for the three loop lengths. For the longest loop length of 9.166 km, the phase noise was as low as −142.5 dBc/Hz at an offset frequency of 10 kHz, which is 26.6 dB lower than that of a commercial signal source. The phase noise density induced by the side modes of the OEO is suppressed below −68.7 dBc/Hz for the loop with the longest length of 9.166 km. The study demonstrated that PT symmetry is a supreme solution to achieve single-mode operation of an OEO with a long cavity length for low–phase noise microwave generation, compared with any other conventional techniques using a narrowband microwave filter or a high–Q factor optical resonator, with a single loop or multiple loops. The use of PT symmetry overcomes the long-existing mode-selection challenge, which would make OEOs the primary solution for simple, low-cost, and high-performance microwave generation for applications where an ultralow–phase noise microwave source is needed.

MATERIALS AND METHODS

The PT-symmetric OEO was implemented using commercial off-the-shelf optoelectronic components. The LD is an Agilent N7714A laser source, which provides a maximum output power of 16 dBm. The MZM is a Lucent intensity modulator (model, 2623CSA) with a bandwidth of 10 GHz. Two cascaded EAs [a MultiLink modulator driver (MTC5515-751) and a Litton microwave amplifier (DXA-5184-01)] were connected between the BPD and the MZM to provide a sufficient gain near the frequency of 10 GHz to enable single-mode oscillation at 9.876 GHz. The 9.1-km delay line is a spool of Lucent SMF (FSC-NZDSF-SPOOL-004C). The BPD consists of two identical cascaded PDs and a TDL connected to the input of one PD. The bandwidth of the BPD is 40 GHz, and the time delay tuning range of the delay line is ±300 ps (DSC740-39-FC/UPC-K-3).

The operation of the OEO was evaluated using several benchtop instruments including a VNA (Agilent E8364A) to measure the open-loop response, an ESA (Agilent E4448A) to measure the spectra of the generated microwave signals, and an signal analyzer (Agilent E5052B) to measure the phase noise. The signal analyzer works with a down-converter (Agilent E5053A) to extend the frequency measurement range from 7 to 26.5 GHz.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/6/eaar6782/DC1

section S1. Balanced photodetection

section S2. PT symmetry

section S3. Loop length–dependent phase noise

fig. S1. Block diagram of the BPD used in the experiment.

fig. S2. Optical to electrical conversion at the BPD.

fig. S3. Open-loop response of the OEO.

fig. S4. Phase noise enhancement with a long OEO loop.

movie S1. Phase noise of a 5.26 GHz signal from a PT-symmetric OEO.

movie S2. Electrical spectrum of the 5.26 GHz signal.

movie S3. A 10-GHz microwave signal generated by the OEO with PT symmetry.

movie S4. Output of the OEO without PT symmetry.