Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Apr 30;122(22):5870–5876. doi: 10.1021/acs.jpcb.8b03490

Observation of Ultrafast Vibrational Energy Transfer in Fibrinogen and Fibrin Fibers

Biplab Dutta †, Bart E Vos ‡, Yves L A Rezus §, Gijsje H Koenderink ‡, Huib J Bakker †,*
PMCID: PMC5995459  PMID: 29709181

Abstract

graphic file with name jp-2018-03490s_0006.jpg

We study the secondary structure of the blood protein fibrinogen using two-dimensional infrared spectroscopy. With this technique, we identify the amide I′ vibrational modes of the antiparallel β-sheets and turns of fibrinogen. We observe ultrafast energy flow among these amide I′ vibrational modes with a time constant of ∼7 ps. This energy transfer time constant does not change significantly upon fibrin fiber formation, indicating that the secondary structure of the fibrinogen monomers remains largely unchanged in the polymerization process.

1. Introduction

Blood clotting is an important biological process that occurs in response to an injury to a blood vessel.1 Blood clots are made up of an elastic network of flexible fibrin fibers formed from the giant protein fibrin (340 kDa). Fibrin networks exhibit remarkable elastomeric behavior in response to mechanical deformations, which is thought to originate from the secondary structure of the constituent proteins.2,3 The secondary structure of isolated fibrin proteins is known,4 but it is unclear if and how this changes upon incorporation in fibrils.

Fibrin networks have a remarkable ability to withstand the large shear forces present inside blood vessels.5 Fibrin also acts like a glue inside the blood clot, holding in place the platelets that provide reinforcement to the clot structure.6 Problems with blood clotting can lead to severe medical conditions, such as strokes and heart attacks.7,8 In addition to its central importance in hemostasis and vascular disease, fibrin is also relevant in regenerative medicine. Fibrin’s unique elasticity and extensibility make it a promising candidate for use as a cell scaffold to promote wound and tissue repair.9 Thus, a better understanding of the molecular structure of fibrin is important, as it could eventually lead to strategies for preventing thromboembolism and rationally designing fibrin-based biomaterials with fine-tuned properties.10,11

The macroscopic properties of blood clots and reconstituted fibrin gels have been extensively studied by shear, compression, and tensile measurements12−14 and linked to the underlying network and fiber structure that have been visualized by electron microscopy, atomic force microscopy, and optical microscopy.2 Molecular-scale structural information, showing the influence of assembly factors, such as thrombin and calcium ion concentration, and oxidation has been obtained by UV circular dichroism measurements.15 Recently, Fourier transform infrared (FTIR) spectroscopy16 and Raman17 spectroscopic experiments on bulk blood clots have revealed α-helix to β-sheet conversion upon stretching. However, these measurements are difficult to interpret because the spectral contributions of the different secondary structures strongly overlap.

Two-dimensional infrared (2D IR) spectroscopy is a relatively new technique that can provide unique structural and dynamical information on protein systems.18 Two-dimensional IR has been shown to be more sensitive than linear infrared absorption measurements.19 Up to now, 2D IR experiments have been extensively used to investigate peptides and proteins, mostly with sizes of at most a few kilodalton. It is often cumbersome to resolve the structure and dynamics of proteins consisting of a distribution of different secondary structures with 2D IR. A convenient method to achieve enhanced structural sensitivity in 2D IR experiments is to isotopically label certain amino acids to isolate their resonance from the congested amide I′ region.20,21 Another approach to attain structural sensitivity is to combine 2D IR experiments on the amide I′ and amide II′ regions.22 In this article, we study unlabeled fibrinogen and fibrin fibers with 2D IR spectroscopy. We show that the picosecond dynamics inferred from 2D IR spectra provides novel insights into the interaction between the amide vibrations of the turns and the β-sheets of the fibrinogen molecule, and that the energy flow among amide I′ vibrational modes does not appreciably change upon the incorporation of fibrin in fibers.

2. Experimental Section

2.1. Sample Preparation

Human fibrinogen was purchased from Enzyme Research laboratory (FIB3, Plasminogen, von Willebrand Factor and Fibronectin Depleted). It was dissolved at a concentration of 15 mg mL–1 in a deuterated saline solution (0.5 M NaCl) at 37 °C. Thereafter, the fibrinogen solution was dialyzed extensively against a deuterated Tris buffer composed of 0.5 M NaCl and 0.05 M Tris with a pD of 7.4 for 12 h in a cellulose membrane tubing (SpectralPor 4 dialysis membrane with a molecular weight cutoff of 12–14 kDa). To minimize exchange of D2O for H2O, the dialysis was performed inside a glovebox. After the dialysis, the final concentration of fibrinogen was determined by measuring the absorbance at 280 nm using a UV–vis spectrometer (NanoDrop, Thermo Fischer) and an extinction coefficient23 of 1.6 mg–1 mL cm–1. Fibrin gels were prepared by the addition of deuterated solutions of calcium chloride and human thrombin (Enzyme Research Laboratory) to bring the final concentrations to 2.5 mM calcium ions, 15 mg mL–1 fibrin, and 0.16 NIH per mL thrombin. The gels were polymerized in situ between two calcium fluoride windows at 37 °C for approximately 4 h. To perform confocal imaging experiments, we mixed fibrinogen with a 1:20 molar ratio of Alexa488-labeled fibrinogen monomers (Life Technologies, Bleiswijk, The Netherlands). The confocal imaging was performed using a Nikon Eclipse Ti inverted microscope with a 40× magnification air objective (numerical aperture 0.60) to confirm the presence of a network upon polymerization.

2.2. Two-Dimensional IR Spectroscopy

A detailed description of the custom-built 2D IR setup can be found elsewhere.24 In brief, the two-dimensional infrared (2D IR) experiment is done in a pump–probe geometry. A Mach–Zehnder interferometer is placed in the pump beam. The interferometer allows us to scan the coherence time and, thereby, enables us to resolve the pump–probe spectra along the frequency of the pump pulse. The polarization of the pump beam is s, whereas the polarization of the probe pulse is fixed to an angle of 45°. This polarization combination of pump and probe pulses allows us to probe simultaneously ⟨ZZZZ⟩ and ⟨ZZYY⟩ components of the 2D IR signal (see Supporting Information, SI). After the sample, a polarizing beam splitter separates ⟨ZZZZ⟩ and ⟨ZZYY⟩ components of the 2D IR signal into two beam paths. The signals are spectrally dispersed by a spectrograph and detected with a mercury–cadmium–telluride detection array. The bandwidth of the pump and the probe pulse are approximately 150 cm–1. In all our 2D IR measurements, the samples are held between two calcium fluoride windows separated by 50 μm thick teflon spacers. At the sample position, the energy of the pump and probe pulses are approximately 2 and 0.2 μJ, respectively. The samples scatter part of the pump light into the direction of the probe, leading to interference effects in the detected probe spectrum. This interference is suppressed by using a wobbler25 in the pump beam. As a result, we do not observe any spectral fringes in the diagonal cuts of our 2D IR traces (see SI).

3. Results

3.1. Polymerization of Fibrinogen

Fibrin fibers are produced by the polymerization of soluble fibrinogen precursor proteins through a cascade of events.26 Fibrinogen has two terminal D-regions, where the C-termini of the two sets of constituent polypeptide chains meet, connected to a central E-region, where the N-termini meet by three-stranded coiled coil regions4 (Figure 1). Human fibrinogen consists of almost 31% α-helix, 37% β-sheet, and 32% turns, loops, and random coils.4 Fibrin clot formation is initiated by enzymatic cleavage of two short, so-called, fibrinopeptides from the E-region of the molecule. This process produces the fibrin molecule, which can polymerize by lateral interactions of the central E-region with the distal D-region of an adjacent molecule and by longitudinal D:D interactions to form double-stranded protofibrils. Upon reaching a critical length, the protofibrils laterally associate via interactions of the disordered αC-regions that protrude from the surface of the molecule,27 resulting in the formation of a three-dimensional branched network of fibrin fibers (Figure 1c). In the presence of factor XIII, the fibers are covalently cross-linked to form an elastic network.28 Under the conditions of our experiments, the polymerization process takes approximately 2 h, as monitored by light scattering (see SI). To ensure complete polymerization, we waited for at least 4 h before performing the 2D IR measurements.

Figure 1.

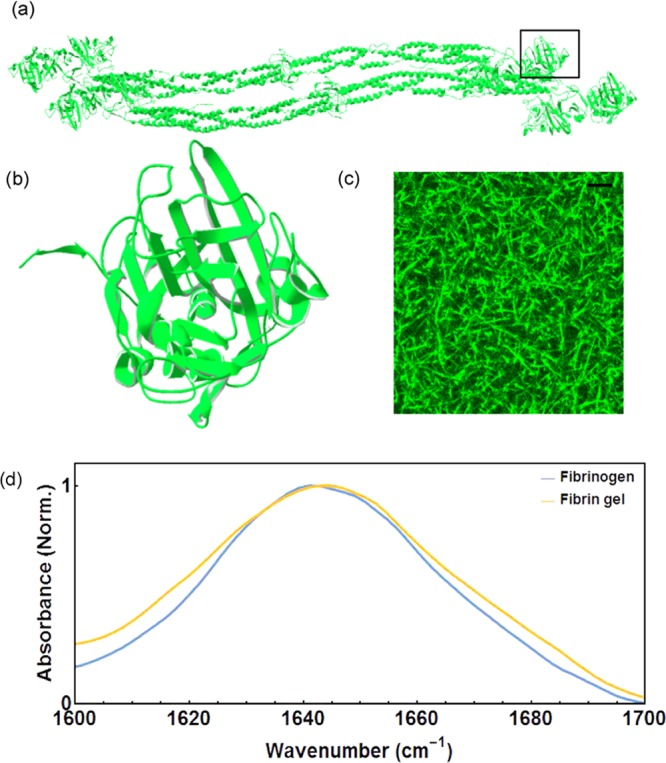
Figure 1

Open in a new tab

(a) Crystal structure of fibrinogen dimer4 (PDB code: 3ghg). (b) Zoomed-in section of the boxed area in (a) showing the β-sheets and turns (residues: Pro138–Gly395 in the L chain as designated in the PDB file). (c) Confocal fluorescence image of a fibrin gel (15 mg mL–1) shows the formation of a connected network of thick fibers. Scale bar: 12 μm. (d) FTIR spectra of fibrinogen and fibrin gel, both at a protein concentration of 15 mg mL–1. The amide I′ band of the fibrin gel is inhomogeneously broadened.

3.2. FTIR of Fibrinogen and Fibrin Gels

In Figure 1d, we present the linear FTIR spectrum of purified human plasma fibrinogen. The spectrum shows a single broad and almost featureless amide I′ peak. The large width of this band results from the overlapping contributions of different secondary structure motifs. The absorbance at 1600 cm–1 can be assigned to the response of the side chains of several amino acids (Asn, Arg, Gln). Typically, the amide I′ band of α-helical domains is observed near 1650 cm–1. This band has been assigned to the in-phase oscillation of the amide groups along the α-helical axis. The amide I′ response of β-sheets generally consists of two bands at 1610–1630 cm–1 (ν⊥ mode) and at 1670–1690 cm–1 (ν∥ mode). When fibrinogen is polymerized by the addition of thrombin in the presence of factor XIII (FXIII), thick bundles of protofibrils (radius above 100 nm) are formed (Figure 1c, also see SI). We find that upon polymerization, the amide I′ peak broadens by 5 cm–1, which could be the result of the loss of homogeneity upon gel formation.

Note that the total oligosaccharide content29 of fibrinogen is only 3%, and only 1.5% of the oligosaccharides (NeuAc and GlcNAc) will contribute to the amide I′ band. Hence, the contribution of oligosaccharides to the amide I′ band is negligible.

3.3. Two-Dimensional IR Spectra of Fibrinogen and Fibrin Gels

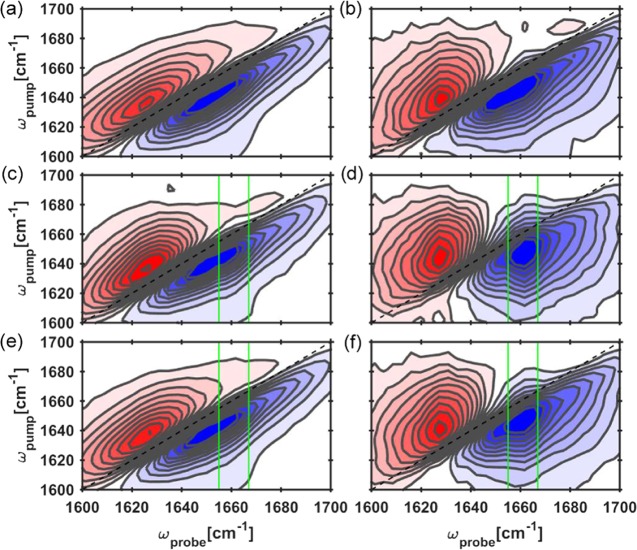
In Figure 2, we present the 2D IR spectra of fibrinogen at delay times of 0.3 and 3 ps. The red contours represent the bleaching signal of the |0⟩ to |1⟩ transition of the amide I′ mode, whereas the blue contours represent the excited state |1⟩ to |2⟩ absorption (esa) of this mode. The elongated shape of the contours in the 2D IR spectra shows that the amide I′ line shape is strongly inhomogeneously broadened.

Figure 2.

Figure 2

Open in a new tab

Two-dimensional IR spectra of fibrinogen in ⟨ZZZZ⟩ and ⟨ZZYY⟩ at 0.3 ps (a, b) delay and at 3 ps (c, d) delay exhibit a ridge along ωpump and at ωprobe = 1660 cm–1. The ridge is emphasized by the green vertical grid lines around ωprobe = 1660 cm–1. Blue and red contours represent bleach and esa, respectively. Isotropic 2D IR, (⟨ZZZZ⟩ + 2⟨ZZYY⟩)/3 spectra at pump–probe delay times of 0.3 ps (e) and 3 ps (f) clearly show changes in line shapes.

We observe that the 2D IR spectral line shape becomes more circular with increasing delay time, reflecting a spectral diffusion as a result of energy transfer and/or structural changes. For the fibrin gels, we observe similar 2D IR spectra (see SI). In addition to the so-called diagonal signals (ωpump = ωprobe), 2D IR spectra can also contain so-called cross-peak signals (ωpump ≠ ωprobe), reflecting the response of a vibration following the excitation of another vibration. The 2D IR spectra of fibrinogen in Figure 2 show a cross-peak signal in the form of an elongated bleaching signal along ωprobe = 1660 cm–1. This signal becomes more pronounced at large time delays Tw (Figure 2b,d,f). The cross-peak signal is stronger in the ⟨ZZYY⟩ compared to the ⟨ΖΖΖΖ⟩ configuration, as shown in Figure 2c,d. The cross-peak signals are clearly visible in Figure 3 as transient absorption dips near 1660 cm–1. We also examine the dynamics of fibrinogen by exciting the amide I′ modes and probing the amide II′ (1400–1500 cm–1) modes. We observe an instantaneous amide I′–amide II′ cross-peak. This cross-peak does not show an ingrowth with Tw (see the SI).

Figure 3.

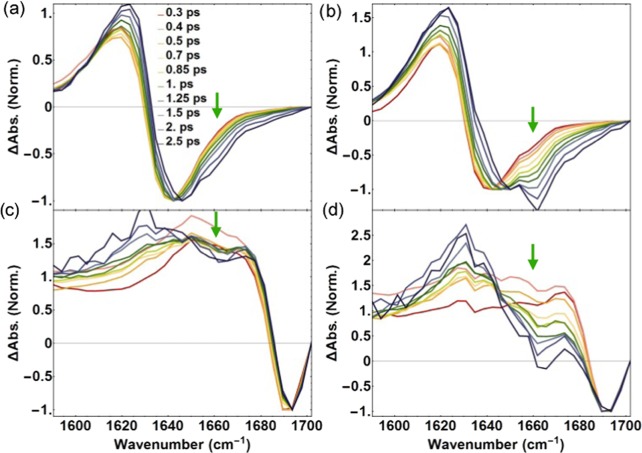
Figure 3

Open in a new tab

Slices taken through the 2D IR spectra of fibrinogen for ωpump = 1627 cm–1 (a, b) and ωpump = 1680 cm–1 (c, d). The ⟨ZZZZ⟩ (a,c) and ⟨ZZYY⟩ (b,d) 2D IR spectra at different time delays clearly represent the ingrowth around ωprobe = 1660 cm–1 as pointed out by the green arrows. Every slice is normalized with the corresponding bleach signal to illustrate the ingrowth. The time delays are displayed in the legends and the absorption change measured in 2D IR is denoted by ΔAbs.

To analyze the dynamics of the 2D IR signals, we record 2D IR spectra for different delay times between the excitation and the probe pulses. In Figure 3, we present transient absorption spectra at different delays for ωpump = 1627 cm–1 (Figure 3a,b) and ωpump = 1680 cm–1 (Figure 3c,d). These transient spectra represent slices of the 2D IR spectra taken at these excitation frequencies. Every spectral trace is normalized with respect to the minimum of the bleach (at ∼1640 cm–1 in Figure 3a,b, at ∼1680 cm–1 in Figure 3c,d), and the eventual heating signal has been subtracted. The normalized transient spectra at different delay times clearly show that the cross-peak signal at 1660 cm–1 shows a relative increase with increasing delay time. This ingrowth indicates the transfer of the excitation from vibrational modes that are excited at 1627 and 1680 cm–1 to a vibrational mode with its maximum response at 1660 cm–1. It should be noted that the reverse energy transfer from an excited mode at 1660 cm–1 to a probed mode at 1627 cm–1 cannot be observed, as this response overlaps with the strong excited state absorption band.

We assign the modes at 1627 and 1680 cm–1 to the ν⊥ and ν∥ modes of the antiparallel β-sheet structure.19,21,22 The mode at 1660 cm–1 represents an amide vibration that is either located in an α-helix or in a turn. The crystal structure4 of fibrinogen clearly shows the presence of β-sheets and a significant amount of turns at the C-termini (Figure 1). The observation of energy transfer between the β-sheet modes at 1627 and 1680 cm–1 to a mode at 1660 cm–1 implies that this latter mode must be in close proximity to the β-sheet. In view of the crystal structure of fibrinogen, in which the antiparallel β-sheets are close to the turns, we assign the 1660 cm–1 mode to amide vibrations located in the turns.30,31

From the subdivision of the transient spectra in spectral components associated with the two coupled vibrations, we can also determine the anisotropy by modeling the ⟨ZZZZ⟩ and the ⟨ZZYY⟩ 2D IR signals with these spectral components. We can thus extract a value of the anisotropy of the cross-peak of 0.29, which differs in both sign and magnitude from the cross-peak between the ν⊥ and ν∥ modes of a typical antiparallel β-sheet. For instance, the cross-peak of the β-sheet conformation of poly-l-lysine shows an anisotropy of −0.16 (see the SI). This difference corroborates our assignment of the 1660 cm–1 mode to the amide I′ vibration of turns.

3.4. Kinetic Modeling of the Vibrational Energy Transfer

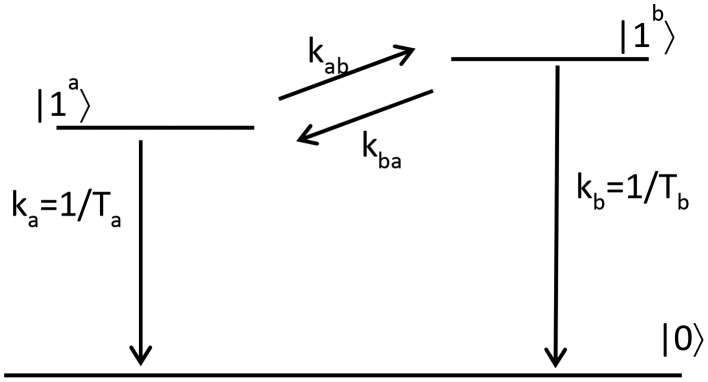
To extract the dynamics of the energy transfer between the amide I′ modes of the antiparallel β-sheets and the turns, we fit the transient spectra of Figure 3 with a kinetic model that is schematically depicted in Figure 4.

Figure 4.

Figure 4

Open in a new tab

Kinetic model: The two states |1a⟩ and |1b⟩ represent the first excited states of the vibrational modes at 1627 and 1660 cm–1, respectively. The ground state is represented by |0⟩. The vibrational relaxation time constants (or rate constants) are given by Ta (or ka) and Tb (or kb). The rate constants of the population exchange between the excited states are denoted by kab and kba. These rate constants are related by a Boltzmann factor.

We assume that the data sets can be decomposed into time-dependent populations Ni(τ) of the vibrational states and the corresponding spectral signatures represented by Δσi(ω). Thus, the transient spectrum, Δαiso(ω,τ), is given by the following expression: Δαiso(ω,τ) = Na(τ)·Δσa(ω) + Nb(τ)·Δσb(ω) + N0(τ)·Δσ0(ω), where the subscripts a, b, and 0 represent the first excited states of the respective vibrational modes at 1627 and 1660 cm–1, and the ground state. It should be noted that Δσi(ω) represents differential absorption spectra. The component Δσ0(ω) accounts for the heating effect on the ground state absorption spectrum that results from the vibrational relaxation of the excitation of the sample by the intense pump pulse. In all presented data sets, we have already subtracted this contribution. The time-dependent populations of the different states are governed by the following set of coupled equations

3.4.

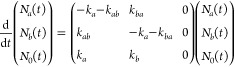Herein, we also assume that the uphill and the downhill rate constants kba and kab are related by the Boltzmann factor. The solutions of the rate equations, Ni(t) (where i = a, b, or 0), are calculated by determining the eigenvalues of the rate-constant matrix. The time-dependent populations are then used to extract the spectral signatures Δσa(ω) and Δσb(ω), and the rate constants from a global least square fit using the following expression

3.4.

In practice, initial guesses of the basis sets are helpful to reduce the complexity of the fitting routine. Thus, assuming no effective population transfer at early delay time, from the 2D IR horizontal slice at 0.3 ps, we determine an initial guess for Δσa(ini)(ω). Likewise, using the 2D IR horizontal slice at 2.5 ps and using Δσa(ω), we construct an initial guess for Δσb(ini)(ω). The resulting spectral signatures Δσa(ω) and Δσb(ω) of fibrinogen obtained from the global fitting routine are shown in Figure 5 (see also the SI).

Figure 5.

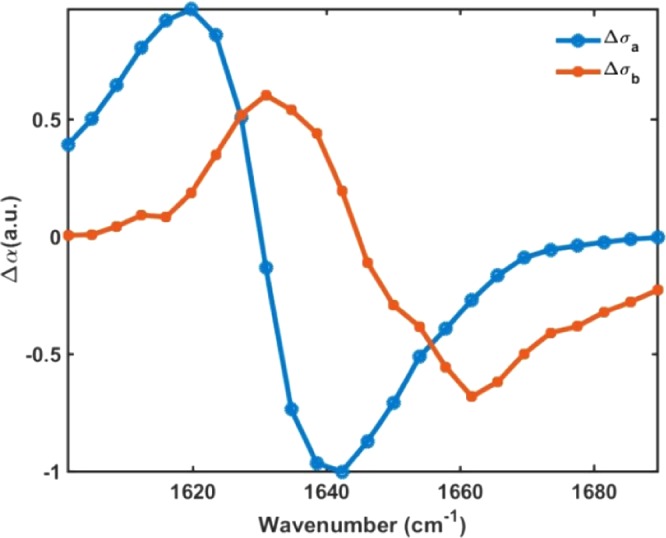
Figure 5

Open in a new tab

Transient spectra signatures Δσa(ω) and Δσb(ω) for fibrinogen obtained by fitting the isotropic 2D IR signals, (⟨ZZZZ⟩ + 2⟨ZZYY⟩)/3, with the fitting procedure described in the text.

The top panel of Figure 6 represents the measured spectra and the bottom panel the fitted spectra at the corresponding delay times. The kinetic model provides an excellent description of the ingrowth of the cross-peak signal at 1660 cm–1. From the fit we find the following rate constants for fibrinogen: ka = 1/(1.38 ± 0.03) ps–1, kb = 1/(2.67 ± 0.05) ps–1, kab = 1/(7.17 ± 0.49) ps–1. For the fibrin gel, we obtain ka = 1/(1.40 ± 0.04) ps–1, kb = 1/(2.71 ± 0.05) ps–1, and kab = 1/(6.68 ± 0.55) ps–1.

Figure 6.

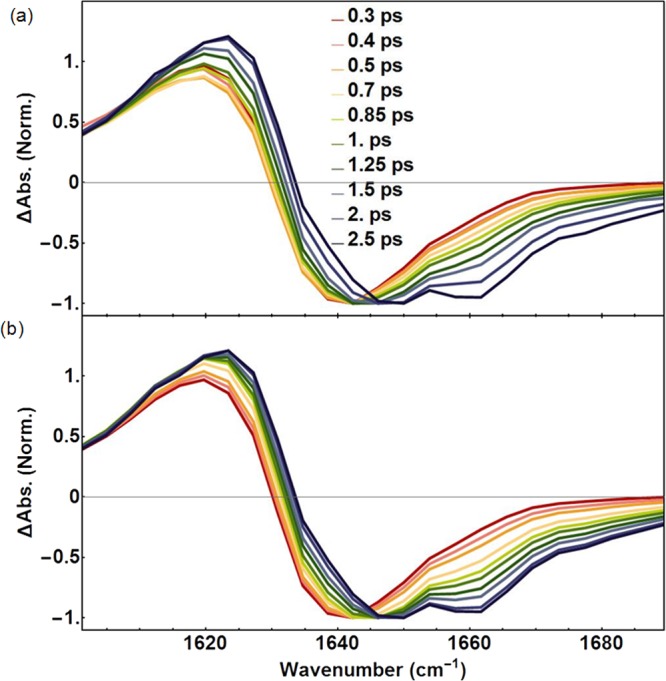
Figure 6

Open in a new tab

(a) Ten representative slices taken from isotropic 2D IR spectra at ωpump = 1627 cm–1 of fibrinogen. The corresponding fitted curves using the kinetic model depicted in Figure 4 are shown in (b).

4. Discussion

Our 2D IR results show that the broad and featureless linear infrared absorption spectrum of fibrinogen contains distinct amide I′ bands. The presence of these different modes becomes particularly clear, thanks to their quite different dynamics on the picosecond time scale. We observe energy transfer from the amide I′ vibrations of the antiparallel β-sheet structure to the amide I′ vibrations of the turns. For fibrin gels, we observe a similar ingrowing cross-peak signal (see the SI), thus allowing a similar distinction between the amide I′ vibrations of the antiparallel β-sheets and the turns.

We can estimate the average spatial distance between the excited and probed transition dipoles using the Förster-energy transfer rate equation.32 Using the rate constants obtained from the fit, εmax = 2.67 M–1 cm–1, assuming a homogeneous linewidth of 10 cm–1 for each of the modes, and an orientation factor ⟨κ2⟩ of 2/3, considering an isotropic distribution of the vibrational dipoles, we obtain an average distance of 14 Å between the interacting amide vibrations. This distance is consistent with the expected distance between an amide group within an antiparallel β-sheet and an amide group of a turn.

In a 2D IR study of tripzip2, very fast energy transfer was observed among the β-sheet amide I′ modes.33 Interestingly, for fibrin, we do not observe energy transfer between the β-sheet modes on a picosecond time scale, as is clear from the fact that excitation at 1627 cm–1 does not lead to a cross-peak signal at 1680 cm–1 and vice versa.

The rate of energy transfer between the amide I′ vibrations observed here is similar to the transfer rates observed for alanine tripeptide34 and antifreeze proteins.35 We find that neither the relaxation rates nor the energy-transfer rate change significantly upon fibrin fiber formation, indicating that the secondary structure of fibrin does not change upon polymerization.

5. Conclusions

We study the structure and dynamics of fibrinogen and fibrin gels using femtosecond two-dimensional infrared spectroscopy. The 2D IR spectra show distinct amide I′ bands that are not observed in the linear FTIR spectrum. Furthermore, we observe energy transfer between the amide I′ bands, indicating that these bands belong to amide groups of closely spaced antiparallel β-sheets and turns. The rate of energy transfer does not change significantly upon polymerization, indicating that the secondary structure of the fibrin monomers does not change upon fiber formation. We thus find that the dynamics of 2D IR spectra constitute a powerful approach to resolve secondary structures of large proteins. The presented approach can be used to investigate a wide range of natural fibril-forming proteins.36−38

Acknowledgments

This work was funded by the Netherlands Organisation for Scientific Research (NWO) in relation to the Topsectoren Innovation Contract 2016–2017. B.D. thanks Dr. Jan Helbing (University of Zurich, Switzerland) for helpful discussions. We also thank Dr. Jaap Koopman and Dr. Jos Grimbergen (Fibriant B.V.) for useful discussions and experimental advise. B.V. and G.H.K. acknowledge financial support from the Foundation for Fundamental Research on Matter (FOM Program grant no. 143).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.8b03490.

  • Polymerization of fibrinogen; 2D IR spectroscopy; kinetic modeling; anisotropy calculation (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp8b03490_si_001.pdf (1.2MB, pdf)

References

  1. Kattula S.; Byrnes J. R.; Wolberg A. S. Fibrinogen and Fibrin in Hemostasis and Thrombosis. Arterioscler., Thromb., Vasc. Biol. 2017, 37, e13–e21. 10.1161/ATVBAHA.117.308564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Brown A. E. X.; Litvinov R. I.; Discher D. E.; Purohit P. K.; Weisel J. W. Multiscale Mechanics of Fibrin Polymer: Gel Stretching with Protein Unfolding and Loss of Water. Science 2009, 325, 741–744. 10.1126/science.1172484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Piechocka I. K.; Jansen K. A.; Broedersz C. P.; Kurniawan N. A.; MacKintosh F. C.; Koenderink G. H. Multi-Scale Strain-Stiffening of Semiflexible Bundle Networks. Soft Matter 2016, 12, 2145–2156. 10.1039/C5SM01992C. [DOI] [PubMed] [Google Scholar]
  4. Kollman J. M.; Pandi L.; Sawaya M. R.; Riley M.; Doolittle R. F. Crystal Structure of Human Fibrinogen. Biochemistry 2009, 48, 3877–3886. 10.1021/bi802205g. [DOI] [PubMed] [Google Scholar]
  5. Brass L. F.; Diamond S. L. Transport Physics and Biorheology in the Setting of Hemostasis and Thrombosis. J. Thromb. Haemostasis 2016, 14, 906–917. 10.1111/jth.13280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Kim O. V.; Litvinov R. I.; Alber M. S.; Weisel J. W. Quantitative Structural Mechanobiology of Platelet-Driven Blood Clot Contraction. Nat. Commun. 2017, 8, 1274 10.1038/s41467-017-00885-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Canhão P.; Ferro J. M.; Lindgren A. G.; Bousser M. G.; Stam J.; Barinagarrementeria F. Causes and Predictors of Death in Cerebral Venous Thrombosis. Stroke 2005, 36, 1720–1725. 10.1161/01.STR.0000173152.84438.1c. [DOI] [PubMed] [Google Scholar]
  8. La Corte A. L. C.; Philippou H.; Ariëns R. A. S. Role of Fibrin Structure in Thrombosis and Vascular Disease. Adv. Protein Chem. Struct. Biol. 2011, 83, 75–127. 10.1016/B978-0-12-381262-9.00003-3. [DOI] [PubMed] [Google Scholar]
  9. Furie B.; Furie B. C. Mechanisms of Thrombus Formation. N. Engl. J. Med. 2008, 359, 938–949. 10.1056/NEJMra0801082. [DOI] [PubMed] [Google Scholar]
  10. Bridge K. I.; Philippou H.; Ariëns R. A. S. Clot Properties and Cardiovascular Disease. Thromb. Haemostasis 2014, 112, 901–908. 10.1160/th14-02-0184. [DOI] [PubMed] [Google Scholar]
  11. Brown A. C.; Baker S. R.; Douglas A. M.; Keating M.; Alvarez-Elizondo M. B.; Botvinick E. L.; Guthold M.; Barker T. H. Molecular Interference of Fibrin’s Divalent Polymerization Mechanism Enables Modulation of Multiscale Material Properties. Biomaterials 2015, 49, 27–36. 10.1016/j.biomaterials.2015.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ryan E. A.; Mockros L. F.; Weisel J. W.; Lorand L. Structural Origins of Fibrin Clot Rheology. Biophys. J. 1999, 77, 2813–2826. 10.1016/S0006-3495(99)77113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kim O. V.; Litvinov R. I.; Weisel J. W.; Alber M. S. Structural Basis for the Nonlinear Mechanics of Fibrin Networks under Compression. Biomaterials 2014, 35, 6739–6749. 10.1016/j.biomaterials.2014.04.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kang H.; Wen Q.; Janmey P. A.; Tang J. X.; Conti E.; MacKintosh F. C. Nonlinear Elasticity of Stiff Filament Networks: Strain Stiffening, Negative Normal Stress, and Filament Alignment in Fibrin Gels. J. Phys. Chem. B 2009, 113, 3799–3805. 10.1021/jp807749f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Upchurch G. R. Jr.; Ramdev N.; Walsh M. T.; Loscalzo J. Prothrombotic Consequences of the Oxidation of Fibrinogen and Their Inhibition by Aspirin. J. Thromb. Thrombolysis 1998, 5, 9–14. 10.1023/A:1008859729045. [DOI] [PubMed] [Google Scholar]
  16. Litvinov R. I.; Faizullin D. A.; Zuev Y. F.; Weisel J. W. The α-Helix to β-Sheet Transition in Stretched and Compressed Hydrated Fibrin Clots. Biophys. J. 2012, 103, 1020–1027. 10.1016/j.bpj.2012.07.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Fleissner F.; Bonn M.; Parekh S. H. Microscale Spatial Heterogeneity of Protein Structural Transitions in Fibrin Matrices. Sci. Adv. 2016, 2, e1501778 10.1126/sciadv.1501778. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hamm P.; Zanni M. T.. Concepts and Methods of 2D Infrared Spectroscopy; Cambridge University Press: Cambridge, U.K., 2011. [Google Scholar]
  19. Demirdöven N.; Cheatum C. M.; Chung H. S.; Khalil M.; Knoester J.; Tokmakoff A. Two-Dimensional Infrared Spectroscopy of Antiparallel Beta-Sheet Secondary Structure. J. Am. Chem. Soc. 2004, 126, 7981–7990. 10.1021/ja049811j. [DOI] [PubMed] [Google Scholar]
  20. Buchanan L. E.; Dunkelberger E. B.; Tran H. Q.; Cheng P.-N.; Chiu C.-C.; Cao P.; Raleigh D. P.; de Pablo J. J.; Nowick J. S.; Zanni M. T. Mechanism of IAPP Amyloid Fibril Formation Involves an Intermediate with a Transient β-Sheet. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 19285–19290. 10.1073/pnas.1314481110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kim Y. S.; Liu L.; Axelsen P. H.; Hochstrasser R. M. Two-Dimensional Infrared Spectra of Isotopically Diluted Amyloid Fibrils from Aβ40. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 7720–7725. 10.1073/pnas.0802993105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Deflores L. P.; Ganim Z.; Nicodemus R. A.; Tokmakoff A. Amide I′-II′ 2D IR Spectroscopy Provides Enhanced Protein Secondary Structural Sensitivity. J. Am. Chem. Soc. 2009, 131, 3385–3391. 10.1021/ja8094922. [DOI] [PubMed] [Google Scholar]
  23. Larsson U. Polymerization and Gelation of Fibrinogen in D2O. Eur. J. Biochem. 1988, 174, 139–144. 10.1111/j.1432-1033.1988.tb14073.x. [DOI] [PubMed] [Google Scholar]
  24. Selig O.; Siffels R.; Rezus Y. L. A. Ultrasensitive Ultrafast Vibrational Spectroscopy Employing the Near Field of Gold Nanoantennas. Phys. Rev. Lett. 2015, 114, 233004 10.1103/PhysRevLett.114.233004. [DOI] [PubMed] [Google Scholar]
  25. Bloem R.; Garrett-Roe S.; Strzalka H.; Hamm P.; Donaldson P. Enhancing Signal Detection and Completely Eliminating Scattering Using Quasi-Phase-Cycling in 2D IR Experiments. Opt. Express 2010, 18, 27067–27078. 10.1364/OE.18.027067. [DOI] [PubMed] [Google Scholar]
  26. Weisel J. W.; Litvinov R. I. Mechanisms of Fibrin Polymerization and Clinical Implications. Blood 2013, 121, 1712–1719. 10.1182/blood-2012-09-306639. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Protopopova A. D.; Litvinov R. I.; Galanakis D. K.; Nagaswami C.; Barinov N. A.; Mukhitov A. R.; Klinov D. V.; Weisel J. W. Morphometric Characterization of Fibrinogen’s αC Regions and Their Role in Fibrin Self-Assembly and Molecular Organization. Nanoscale 2017, 9, 13707–13716. 10.1039/C7NR04413E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Piechocka I. K.; Kurniawan N. A.; Grimbergen J.; Koopman J.; Koenderink G. H. Recombinant Fibrinogen Reveals the Differential Roles of α- and γ-Chain Cross-Linking and Molecular Heterogeneity in Fibrin Clot Strain-Stiffening. J. Thromb. Haemostasis 2017, 15, 938–949. 10.1111/jth.13650. [DOI] [PubMed] [Google Scholar]
  29. Townsend R. R.; Hilliker E.; Li Y. T.; Laine R. A.; Bell W. R.; Lee Y. C. Carbohydrate Structure of Human Fibrinogen. J. Biol. Chem. 1982, 257, 9704–9710. [PubMed] [Google Scholar]
  30. Krimm S.; Bandekar J. Vibrational Spectroscopy and Conformation of Peptides, Polypeptides, and Proteins. Adv. Protein Chem. 1986, 38, 181–364. 10.1016/S0065-3233(08)60528-8. [DOI] [PubMed] [Google Scholar]
  31. Barth A.; Zscherp C. What Vibrations Tell about Proteins. Q. Rev. Biophys. 2002, 35, 369–430. 10.1017/S0033583502003815. [DOI] [PubMed] [Google Scholar]
  32. Jang S.; Newton M. D.; Silbey R. J. Multichromophoric Förster Resonance Energy Transfer. Phys. Rev. Lett. 2004, 92, 218301 10.1103/PhysRevLett.92.218301. [DOI] [PubMed] [Google Scholar]
  33. Jansen T. L. C.; Knoester J. Two-Dimensional Infrared Population Transfer Spectroscopy for Enhancing Structural Markers of Proteins. Biophys. J. 2008, 94, 1818–1825. 10.1529/biophysj.107.118851. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Woutersen S.; Mu Y.; Stock G.; Hamm P. Subpicosecond Conformational Dynamics of Small Peptides Probed by Two-Dimensional Vibrational Spectroscopy. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 11254–11258. 10.1073/pnas.201169498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Lotze S.; Olijve L. L. C.; Voets I. K.; Bakker H. J. Observation of Vibrational Energy Exchange in a Type-III Antifreeze Protein. J. Phys. Chem. B 2014, 118, 8962–8971. 10.1021/jp503481e. [DOI] [PubMed] [Google Scholar]
  36. Gunning P. W.; Ghoshdastider U.; Whitaker S.; Popp D.; Robinson R. C. The Evolution of Compositionally and Functionally Distinct Actin Filaments. J. Cell Sci. 2015, 128, 2009–2019. 10.1242/jcs.165563. [DOI] [PubMed] [Google Scholar]
  37. Cheeseman I. M.; Desai A. Molecular Architecture of the Kinetochore-Microtubule Interface. Nat. Rev. Mol. Cell Biol. 2008, 9, 33–46. 10.1038/nrm2310. [DOI] [PubMed] [Google Scholar]
  38. Omary M. B.; Coulombe P. A.; Mclean W. H. I. Intermediate Filament Proteins and Their Associated Diseases. N. Engl. J. Med. 2004, 351, 2087–2100. 10.1056/NEJMra040319. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp8b03490_si_001.pdf (1.2MB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES