Flocking Transitions in Confluent Tissues

Abstract

Collective cell migration in dense tissues underlies important biological processes, such as embryonic development, wound healing and cancer invasion. While many aspects of single cell movements are now well established, the mechanisms leading to displacements of cohesive cell groups are still poorly understood. To elucidate the emergence of collective migration in mechanosensitive cells, we examine a self-propelled Voronoi (SPV) model of confluent tissues with an orientational feedback that aligns a cell’s polarization with its local migration velocity. While shape and motility are known to regulate a density-independent liquid-solid transition in tissues, we find that aligning interactions facilitate collective motion and promote solidification, with transitions that can be predicted by extending statistical physics tools such as effective temperature to this far-from-equilibrium system. In addition to accounting for recent experimental observations obtained with epithelial monolayers, our model predicts structural and dynamical signatures of flocking, which may serve as gateway to a more quantitative characterization of collective motility.

Graphical abstract

1 Introduction

The main cause of mortality in cancer patients is the spreading of primary cancer cells that generate metastatic foci through complex and still poorly understood processes. The invasiveness of metastatic cells is facilitated by their ability to adapt to the microenvironment and change their identity to invade healthy tissues and proliferate^1,2. Key to invasion is cell migration. Migratory phenotypes are intrinsically flexible and include both single and collective cell motility modes^3,4. For example, migrating cells can display both mesenchymal and epithelial phenotypes or frequently interconvert between these two states in a process commonly referred to as Epithelial-to-Mesenchymal Transition (EMT). Cells undergoing EMT detach from the surrounding cells and become hyper-motile. This allows them to reach distal sites, where they can seed metastatic foci by reverting their state back to epithelial⁵.

EMT is not, however, the only process that may favor metastatic dissemination. A complementary process that may help drive collective cell migration is cellular unjamming^6,7. Recent experiments suggest that cell motion in tissues may be understood in terms of physical laws and parameters typically employed to study the transition between amorphous solid and liquid states of inert materials. Within this framework, epithelial cell monolayers below confluence exhibit liquid-like dynamics. As the cell density is increased due to proliferation, cellular displacements are progressively inhibited, and cells become increasingly caged by their neighbors in a glassy or jammed state^8,9 that shares many similarities with molecular or colloidal glasses¹⁰.

Notably, the transition to a jammed, arrested state has been proposed to ensure the proper development of elasticity in mature epithelial tissues. Conversely, monolayer unjamming is needed whenever a tissue must adapt to changes or perturbations of its physiological homeostatic state. Decreasing density is not the only way to cause unjamming. Recent experiments showed that an increase of cell-cell adhesion due to mechanical compression⁷ or to perturbation of endocytic processes¹¹ also leads to unjamming. This gateway to collective motility can be termed Jamming-to-Unjamming transition (JUT)¹² and it may be exploited by tumors for interstitial dissemination¹¹. In contrast with EMT that requires a partial of full rewiring of genetic programs and cell identity, small changes in biomechanical parameters are predicted to promote JUT and collective migration.

Particle-based models of motile cells are widely used to describe the dynamics of dense cell collectives^13–16 and predict jamming as a function of cell density^17,18, but seem inadequate to describe confluent cell layers where packing fraction is essentially always unity. Recent theoretical work has combined the well-established Vertex Model, that describes a confluent epithelial cell sheet as a disordered polygonal tiling of the plane and has been used successfully to model the development of the fruit fly embryo¹⁹, with ideas from active matter physics to develop a Self-Propelled Voronoi (SPV) model of motile tissue. The SPV model exhibits a JUT tuned by cell motility and cellular shape, which in turn embodies the competition of contractility and cell-cell adhesion^7,20–24. None of these models, however, accounts for a striking set of experimental observations¹¹, in which the elevation of RAB5A, a master regulator of endocytosis, induces large-scale directed migratory patterns, which resemble the onset of flocking in other living systems²⁵. Additionally, experiments show that cells alter their polarization and direction of migration due to interactions with surrounding cells^26–28. This mechanical feedback was incorporated in Ref.¹¹ by extending the SPV model to include a local interaction that tends to direct cell polarization. While this simple modification yields flocking phases similar to those observed in the experiments¹¹, suggesting that the observed reawakening of motility requires a simultaneous increase of cell-cell adhesion and coordination of cell polarization, the properties of such flocking phases and the comparison with flocking transitions in particle-based models have not yet been explored.

Here we characterize the full phase diagram of the SPV model with alignment interactions and examine the structural and dynamical properties of the various phases.

We obtain a number of significant results. First, the flocking transition, known to be first order in particle models where the interaction range is defined through a metric criterion, where each agent interacts only with agents within a prescribed range²⁹, appears to be continuous here in both the liquid and the solid. This is consistent with results from Vicsek models which display a continuous transition when agents align with their topological neighbors defined as those belonging to the first shell of a Voronoi tessellation, instead of metric ones³⁰. Given interactions in the SPV are controlled by topology and not by metric distance, this finding suggests the possibility that a continuous transition may be a generic property of systems with metric-free interactions. Secondly, we examine the interplay of alignment and structural properties in both solid and liquid states and show that alignment promotes solidification by suppressing fluctuations transverse to the direction of mean motion. Flocking glassy and crystalline states have been reported before in particle models^31,32 and in continuum theories³³, but alignment was suggested to drive fluidification in particulate systems³². Extending tools from statistical physics to these far-from-equilibrium systems, we also develop a generalized expression for the effective temperature and caging timescale to self-propelled systems that helps us understand how alignment interactions drive solidification in confluent models. Finally, the flocking states are characterized by strongly anisotropic fluctuations. In the fluid such anisotropy is evident in both structural and dynamical properties that reveal a behavior similar to that of 2D smectics, as recently suggested for incompressible particulate flocking fluids³⁴. Collective rearrangements observed as the solid is approached from the fluid side are strongly anisotropic and take the form of correlated cell streaming. This morphology provides a distinct signature of of the collective dynamics of flocking liquids that could be probed in future experiments.

2 Model

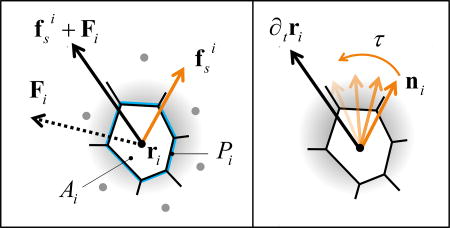
The SPV model describes a confluent monolayer as a network of polygons covering the plane^20–22. Each cell is characterized by its position r_i and cell shape as determined by the Voronoi tessellation of all cell positions (Fig. 2). As in the vertex model³⁵, cell-cell interactions are determined by an effective tissue energy^19,35–39,

$$E\equiv \sum _i[K_A{(A_i-A_0)}^2+K_P{(P_i-P_0)}^2],$$ (1)

with A_i and P_i the cross-sectional area and the perimeter of the i-th cell, and K_A and K_P area and perimeter stiffnesses. The first term, quadratic in the fluctuations of the cell area around the target value A₀, arises from the constraint of incompressibility in three dimensions and encodes bulk elasticity. The second term, quadratic in the deviation of cell perimeter from the target value P₀, represents the competition between active contractility in the actomyosin cortex and cell-cell adhesion, resulting in an effective boundary tension proportional to P₀. We consider N cells in a square box of area L² with periodic boundary conditions. In the following, we set both the average cell area Ā = L²/N and the target area A₀ equal to one, Ā = A₀ = 1, though changing Ā in a periodic system has no effect on the cell dynamics⁴⁰. The system is initialized with random initial positions for the N cells. The configurational energy in Eq. 1 has been extensively used in the past to model biological tissues, but only recently it has been shown that this simple model exhibits a rigidity transition that takes place at constant density and it is controlled by a single non-dimensional parameter, the target shape index $p_0\equiv P_0/\sqrt{A_0}$²¹. In our model, we assume that cell proliferation is negligible on the time scales of interest, as experimentally shown in ¹¹.

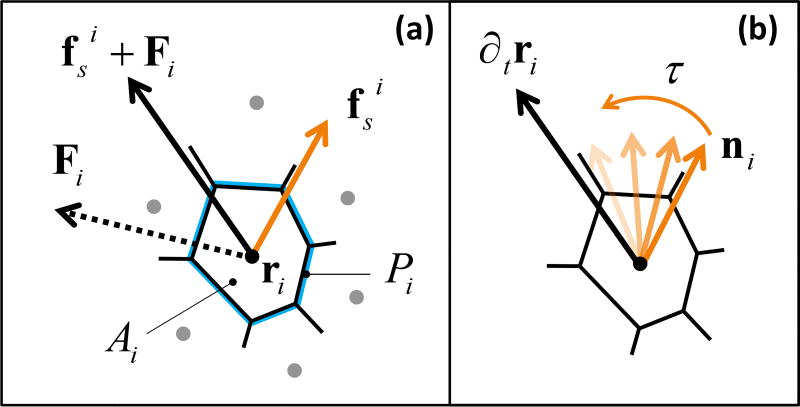
Fig. 2.

Schematic representation of the model. (a) Each cell is a polygon obtained by the Voronoi tessellation of initially random cell positions r_i, characterized by the area A_i and the perimeter P_i of the polygon. The cell experiences a force F_i = −∇E due to its neighbors and an internal propulsive force f_sⁱ along the direction n_i of its polarization (Eq. 2). (b) An active orientation mechanism reorients each cell’s propulsive force towards its migration velocity over a characteristic response time τ = J⁻¹ (Eq. 3).

Each cell is additionally endowed with motility described by a self-propulsive force f_sⁱ = f⁰n_i of fixed magnitude f₀ = v₀/μ, with v₀ the cell motility and μ a mobility, pointing along the direction n_i = (cos θ_i, sin θ_i) of cell polarization and θ_i is the polarization angle. Assuming overdamped dynamics, the equation of motion of cell i is

$${\partial }_t{\mathbf{r}}_i=\mu ({{\mathbf{f}}_{\mathbf{s}}}^i+{\mathbf{F}}_i),$$ (2)

with F_i = −∇_riE the force arising from the tissue energy. Many cell types are known to sense mechanical and biochemical stimuli from neighboring cells and actively respond by adjusting their polarization⁴¹. Following earlier work ^31,42, we model these interactions as an active feedback mechanism at the single cell level that tends to align each cell’s polarization with its migration velocity, which is in turn controlled by interactions with other cells. The polarization dynamics is then governed by the equation

$${\partial }_t{\theta }_i=-J\text{sin}({\theta }_i-{\varphi }_i)+{\eta }_i,$$ (3)

where ϕ_i is the direction of the cell velocity, ∂_tr_i = v_i = v_i (cos ϕ_i, sin ϕ_i), and η_i a white noise, i. e., 〈η_i(t)〉 = 0 and 〈η_i(t)η_j(s)〉 = 2D_rδ_ijδ(t − s). The angular dynamics is controlled by the interplay of rotational diffusion at rate D_r and alignment at rate J, whose inverse τ = J⁻¹ is the response time required by the cell reorient its polarization in the direction of the resultant force exerted by its neighbors.

In the following, we use $\sqrt{A_0}$ as the unit length and (μK_AA₀)⁻¹ as the unit time²². Additionally, we set K_P/(K_AA₀) = 1, $f_0/(K_A{A}_0^{\frac{3}{2}})=1$, D_r/(μK_AA₀) = 0.5. The free parameters are thus the (dimensionless) alignment rate J and the target shape index p₀. For J = 0 and v₀ = 0 our model is related to the vertex model in Ref.²¹, while for J = 0 and finite v₀ we obtain the SPV model of Ref.²².

To study the solid-liquid transition, we use the mean-square-displacement $\mathit{\text{MSD}}(t)=N^{-1}\langle {{\sum }_i[{\mathbf{r}}_i^{\prime }(t+t_0)-{\mathbf{r}}_i^{\prime }(t_0)]}^2\rangle$ evaluated in the reference frame of the center of mass r_CM = N⁻¹ Σ_i r_i, with ${\mathbf{r}}_i^{\prime }={\mathbf{r}}_i-{\mathbf{r}}_{\mathit{\text{CM}}}$. Here and in the following, the brackets 〈…〉 denote a time average (see ESI for further details). The normalized self-diffusivity $D_{\mathit{\text{self}}}\equiv {\text{lim}}_{t\to \infty }\frac{\mathit{\text{MSD}}(t)}{4t{D}_0}$ is a dynamical order parameter for the onset of rigidity, which can also be identified via a structural order parameter given by the cellular shape index²², $q=N^{-1}\langle {\sum }_i{P}_i/\sqrt{A_i}\rangle$. The transition line D_self ≤ 10⁻³ corresponds to q = 3.813. When v₀ = 0, the rigidity transition occurs for $p_0=p_0^{\ast }=3.81$²¹. This model also has an additional transition at p₀ ~ 4.2, which is very close to the shape index for a Voronoi-tesselated uniform point pattern (p₀ = 4.186), suggesting that above this value cells are effectively non-interacting and behave like a gas.

We quantify the emergence of flocking by using the Vicsek order parameter φ ≡ N⁻¹ 〈|(Σ_i v_i/|v_i|) |〉, where the angular brackets indicate the average over trajectories. This quantity vanishes when cells are moving in random directions and attains a value of 1 when all cells coordinate their motion. The susceptibility χ_φ = 〈(φ(t)−〈φ〉)²〉 exhibits a maximum at the flocking transition, which we use to separate flocking from non-flocking states. In the following, we study the phase diagram of a system composed by N = 400 cells. In estimating finite size effects on the flocking transition, we considered systems of N =100, 400, 1600, 3200 cells. Dynamical heterogeneities are investigated in larger systems of N = 4900 cells.

3 Results

3.1 Alignment promotes a continuous flocking transition in epithelial tissues

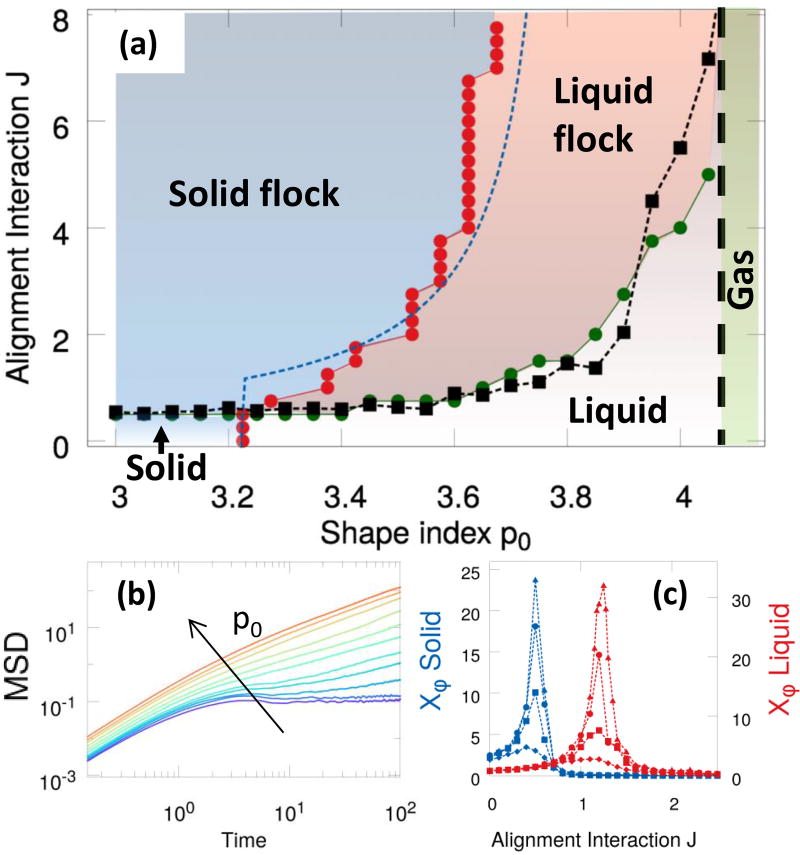
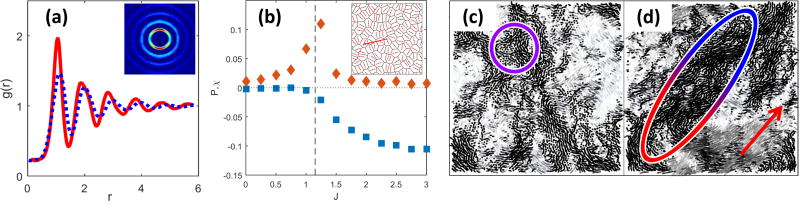
As shown in Fig. 1, we find four distinct phases by varying the alignment rate J and the target shape index p₀: (a) a stationary solid with vanishing D_self, corresponding to the absence of cellular rearrangements, and φ = 0; (b) a stationary liquid with finite D_self and vanishing mean motion (φ = 0); (c) a novel flocking liquid where cells flow collectively (D_eff and φ are both finite); and (d) a flocking solid where the tissue migrates as a unit (φ finite), while maintaining its rigidity. A phase diagram for the system is shown in Fig. 3-a. The solid/liquid transition (red circles) has been determined by examining the MSD that evolves from diffusive to saturated with increasing p₀ (Fig. 3(b)), resulting in the vanishing of the long time diffusivity D_self (see Fig. S3). The line separating the non-flocking from the flocking phases (green circles) corresponds to the peak in the susceptibility shown in panel (c). The dashed blue line and the black squares are theoretical estimates described below. In contrast with particulate Vicsek models with metric interactions⁴³, the onset of collective directed motion in our Voronoi model appears to be a continuous phase transition. Strong evidence for this is provided by a finite-size scaling analysis of both flocking transitions (see Fig. 3(c)) that reveals a power-law scaling of the susceptibility peak ${\chi }_{\phi }^{\mathit{\text{max}}}(L)~L^b$, with $L=\sqrt{N}$ the linear size of the system and b = 1.0±0.1 (see SI).

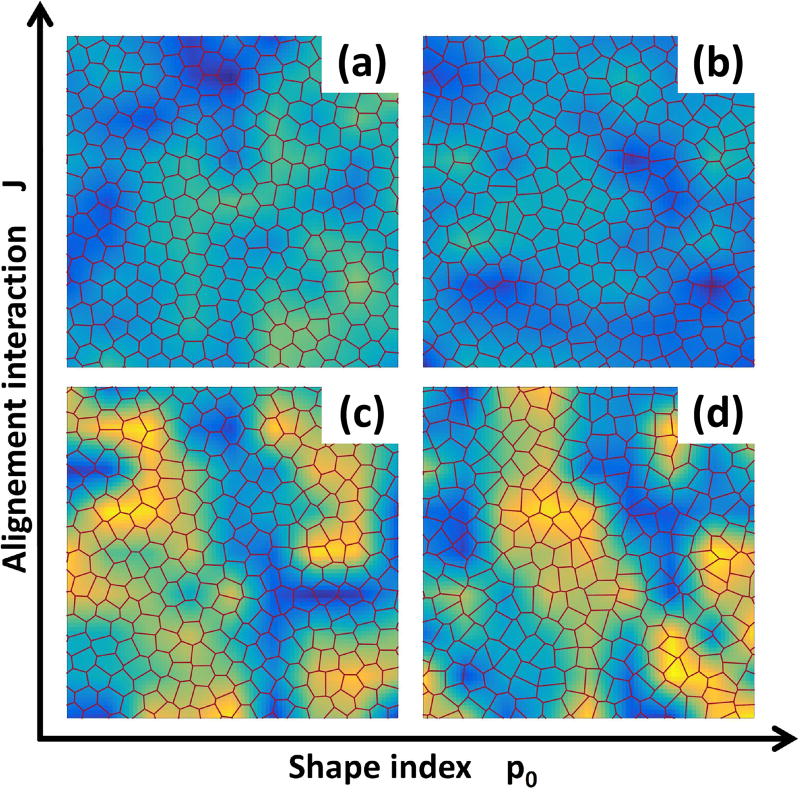
Fig. 1.

Four distinct dynamical phases. Strong alignment interaction yield solid-like (a) and liquid-like (b) flocking states. For weak polar coupling between cells the system is either in a stationary solid (c) or stationary liquid (d) phase. The heat map represents the cosine of the angle of the instantaneous velocity field with respect the horizontal axis: a uniform color indicates coherent migration in a given direction.

Fig. 3.

Phase diagram. (a) Different phases in the (p₀,J) plane. The solid/liquid transition line (red circles) is obtained from the vanishing of D_eff and the flocking transition line (green circles) corresponds to the peak in the susceptibility χ_φ. The dashed blue curve is the theoretical prediction J_c(v₀,p₀) given in (4). The black squares (the dashed line is a guide to the eye) are the estimate for J_flock(p₀) in terms of the numerically calculated cage lifetime τ_cage at J = 0. The vertical dashed black line marks the transition to a gas-like state, observed for p₀ ≳ 4.2, where flocking cannot occur. (b) The mean square displacement for J = 2.0 for a range of p₀ ∈ [3.4,4] across the liquid/solid transition (curves from red to violet). (c) The susceptibility χ_φ for p₀ = 3.1 (blue symbols, solid) and p₀ = 3.7 (red symbols, liquid) and sizes N = 100, 400, 1600, 3200, diamonds, squares, circles, and triangles, respectively.

3.2 Flocking promotes solidification

Inspection of the phase boundary separating in Fig. 3 the flocking liquid from the flocking solid reveals that alignment promotes solidification. This can be understood via a simple argument that also provides an estimate for the liquid-solid transition line in the flocking region, p_c(v₀,J). Briefly, as suggested in Ref.²², fluidification can be understood qualitatively in terms of an “effective temperature” that allows cells to rearrange by overcoming the energy barriers associated with T₁ transitions. When cell alignment is faster than rotational diffusion (i.e., J ≫ D_r) cells can move coherently without being disrupted by noise, which results in a lower effective temperature, and therefore promotes solidification.

To flesh out this argument we first recall that in Ref.²¹ it was shown that in a static vertex model described by the tissue energy of Eq. 1, with v₀ = 0, the transition from solid to liquid is associated with the vanishing of the mean energy barriers ΔE for T₁ transitions and that these barriers scale as $\mathrm{\Delta }E\propto p_0^{\ast }-p_0$ when the target shape index p₀ approaches its critical value $p_0^{\ast }=3.813$ from the solid side. Following²², we assume that in the SPV model the effect of cell motility can be accounted for through a single particle effective temperature T_eff controlled by the fluctuations in cells positions that allow each cell to locally explore its energy landscape. We stress that this effective temperature does not have a thermodynamic interpretation, but is simply a useful measure of the role of activity at the single particle level. In the absence of cell-cell alignment (J = 0) this argument was used in²² to obtain an excellent fit to the liquid-solid transition line at finite v₀ using $T_{\mathit{\text{eff}}}={\mathit{\text{cv}}}_0^2$, with c a dimensionful fitting parameter. Here we make the argument more precise and generalize it to finite J.

In the gas phase, where both interactions and alignment can be neglected, an exact calculation of the mean-square displacement of a single cell yields the identification $k_B{T}_{\mathit{\text{eff}}}^g=v_0^2/\mu D_r$⁴⁴. In the solid, the cells are caged by their neighbors. Considering first J = 0, caging can be modeled by assuming that each cell is tethered to a spring of force constant k. An exact calculation of the mean square displacement of a tethered motile cell in the presence of orientational noise (see SI) yields ${\text{lim}}_{t\to \infty }\mathit{\text{MSD}}(t)=v_0^2/[\mu k(\mu k+D_r)]$. Comparison with the corresponding result for a Brownian particle tethered to a spring, lim_t→∞〈[Δr(t)]²〉th=k_BT/k suggests the identification of an effective temperature $k_B{T}_{\mathit{\text{eff}}}^s=v_0^2/[\mu (\mu k+D_r)]$⁴⁵. By assuming that the transition is controlled by the balance of the energy barrier and this effective thermal energy, $\mathrm{\Delta }E~p_0^{\ast }-p_c(v_0,J=0)~T_{\mathit{\text{eff}}}^s$, we obtain a critical line for the solid-liquid transition $p_c(v_0,J=0)=p_0^{\ast }-v_0^2/[\mu (\mu k+D_r)]$, consistent with the result of²². As discussed in²² this argument works best at large D_r, where the effect of rotational noise resembles that of thermal fluctuations.

A similar argument accounts for the role of alignment. For J ≪ D_r = 0.5, the alignment interaction is ineffective and does affect the location of the solid-liquid transition. For large J, however, the system is in a solid flocking state, characterized by a finite mean velocity $\overrightarrow{v}=\overline{v}(\text{cos }\overline{\varphi },\text{sin }\overline{\varphi })$. We consider again a single cell tethered to a spring of force constant k to describe caging by neighbors, but also moving at mean velocity $\overrightarrow{v}$. Fluctuations about this ordered state are mainly transverse to the direction of mean motion. Treating such fluctuations as small, the mean square displacement of such a solid flocking cell is given by (see ESI for details) ${\text{lim}}_{t\to \infty }\mathit{\text{MSD}}(t)=v_0^2{D}_r/[\mu \mathit{\text{kJ}}(\mu k+J(1-v_0/\overline{v})]$. Assuming $\overline{v}~v_0$, the corresponding effective temperature is $T_{\mathit{\text{eff}}}^f=v_0^2{D}_r/({\mu }^2\mathit{\text{kJ}})$. Equating again this thermal energy to the energy barriers for T1 transition, we obtain an estimate for the transition line between solid and liquid flocks as $p_c(v_0,J\gg D_r)~p_0^{\ast }-v_0^2{D}_r/({\mu }^2\mathit{\text{kJ}})$. This yields the transition from flocking solid to flocking liquid as

$$J_c(v_0,p_0)~\frac{v_0^2{D}_r}{{\mu }^{2}k}\frac{1}{p_0^{\ast }-p_0},$$ (4)

which provides a good fit to the data with k = 0.85±0.03 (dashed blue line in Fig. 3).

3.3 Flocking requires slow structural rearrangements

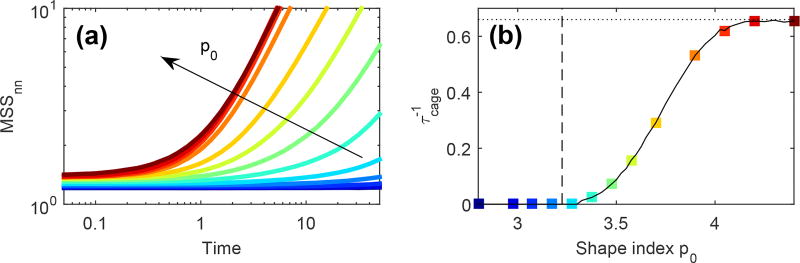
The line separating the stationary (non-flocking) liquid phase from the flocking liquid phase (represented in Fig. 3 as green connected dots) can be estimated by equating the time scale τ = J⁻¹, with which a cell aligns its polarization along the migration direction, with τ_cage, the lifetime of the local cages. Deep in the solid, τ_cage is infinite and structural rearrangements are controlled solely by the time scale τ_r for rotational diffusion. Cells will align with their neighbors provided that τ < τ_r, giving a critical value $J_{\mathit{\text{flock}}}(p_0\ll p_0^{\ast })=D_r$ for the onset of flocking in the solid, independent of p₀ and in agreement with Fig. 3. As the solid-liquid transition is approached, τ_cage becomes finite. When J = 0, τ_cage can be estimated as the time over which the mean-square separation of two cells i and j that are in contact at t = t₀, defined as MSS_nn(t) = 〈[r_i(t + t₀)−r_j(t + t₀)]²〉, remains constant (see ESI for details). The neighbors mean-square separation is shown in Fig. 4(a) for J = 0 and several values of p₀ spanning the liquid-solid transition. In the solid, MSS(t) is constant at all times. Upon melting, i.e., for $p_0>p_0^c(v_0,J)$, MSS_nn(t) shows an initial plateau and then starts to grow. The resulting inverse lifetime of the cage is shown in Fig. 4(b) as a function of p₀. The lifetime τ_cage reaches a constant value for p₀ ≳ 4.2, where q ≃ 4.19. As discussed earlier, this is the shape index for a random point pattern, and so the cells no longer interact. In this gas regime MSS_nn still shows an initial plateau at short time that corresponds to the time τ_free = a/v₀ taken by a cell of motility v₀ to travel freely a distance of the order of its size $a~\sqrt{A_0}$. We then define the true cage lifetime ${\tau }_{\mathit{\text{cage}}}^{\ast }$ by correcting the lifetime calculated from the MSS_nn as ${\tau }_{\mathit{\text{cage}}}^{\ast }={\tau }_{\mathit{\text{cage}}}-{\tau }_{\mathit{\text{free}}}$.

Fig. 4.

Identifying the caging timescale in the absence of alignment. (a) The neighbors mean-square separation MSS_nn(t) as a function of the the time increment t becomes constant as p₀ is decreased across the liquid-solid transition, showing the onset of caging. (b) The inverse cage lifetime ${\tau }_{\mathit{\text{cage}}}^{-1}$ at J = 0 as a function of p₀ calculated as described in the text. The vertical line denotes the critical value $p_0^{\ast }$ of the J = 0 rigidity transition, while the horizontal dotted line is the asymptotic value ${\tau }_{\mathit{\text{free}}}^{-1}$ attained by ${\tau }_{\mathit{\text{cage}}}^{-1}$ in the gas phase.

In the liquid, structural rearrangements can occur via both the relaxation of the local cage on time scale ${\tau }_{\mathit{\text{cage}}}^{\ast }$ and noisy reorientation on time scales τ_r. Neighbor exchanges are controlled by the faster of the two processes. Flocking will only occur if the alignment rate J is faster than the total rate $1/{\tau }_{\mathit{\text{cage}}}^{\ast }+1/{\tau }_r$ for neighbor exchanges, giving an estimate for the flocking transition in the liquid as $J_{\mathit{\text{flock}}}(p_0)=1/{\tau }_{\mathit{\text{cage}}}^{\ast }+D_r$. This prediction yields the black squares in Fig. 3 in good agreement with the phase boundary shown in green. Finally, we note that the existence of a gas phase also explains the observed vertical asymptote in J_flock(p₀): if cells are not interacting they cannot align their polarization vectors, no matter how rapidly the mutual alignment occurs.

3.4 Flocking impacts on structure and dynamics of the monolayer

When observed in a co-moving frame of reference, the flocking tissue reveals strong dynamical and structural anisotropies that provide distinct testable signatures of directed collective motion. In what follows we will focus on the properties of flocking liquid state, where these effects are particularly evident. However, the impact of self-propulsion and alignment on the elastic properties and the vibrational spectrum of the solid represents an intriguing open issue that deserves a more detailed investigation in future work.

3.4.1 Structure

The flocking liquid exhibits an anisotropic structure akin to that of two-dimensional smectics, with rows of cells marching along the direction of mean motion. This is evident in the radial distribution function g(r) calculated in a moving frame aligned with the instantaneous flocking direction (see ESI for details) that shows strong anisotropy with pronounced peaks along the flocking direction (Fig. 5a). Individual cell morphology and orientation are also significantly affected by alignment. In the flocking liquid individual cells are elongated in the direction perpendicular to that of mean motion. This squashing of flocking cells is quantified by measuring the nematic-like parameter $P=2\langle {\text{cos}}^2(\stackrel{\sim }{\theta })\rangle -1$, where $\stackrel{\sim }{\theta }$ is the angle between the instantaneous flocking direction and the cell’s major axis (see ESI for details). In the stationary liquid P fluctuates around zero, while in the flocking liquid it becomes negative, as shown in Fig. 5b. Such orientational order of cell shape is unique to the flocking state and was not observed in models without alignment²¹.

Fig. 5.

Structural and dynamical anisotropy of the flocking liquid. (a) Radial distribution function g(r_‖,r_⊥) for a flocking liquid (p₀ = 3.5, J = 2), evaluated along (g(0,r_⊥), red solid line) and perpendicular (g(r_‖,0), blue dotted line) the direction of flocking. The inset shows an intensity plot of the 2D g(r), with the horizontal axis chosen along the flocking direction. (b) Order parameter P (blue squares) as a function of J for p₀ = 3.7. In the non-flocking state P = 0, while at the flocking transition, identified by the peak in the susceptibility χ (orange triangles), P becomes negative, indicating a tendency of the cells to elongate in the direction normal to that of mean motion. Inset: representative snapshot of a flocking liquid (J = 2, p₀ = 3.7); the small arrows indicate the orientation of the principal axis of each cell and the large arrow is in the direction of flocking. (c,d) Maps of the displacements Δr_i averaged over a time τ_α = 10² for (b) J = 0 and (c) J = 2 in a system of 4900 cells. Ellipses are guides to the eye for highlighting the anisotropy of the collective rearrangements in the flocking state. The red arrow indicates the average migration direction. (e,f) Spatial correlations C(x_‖,0) (red triangles) and C(0,x_⊥) (blue circles) along axes longitudinal (x_‖) and perpendicular (x_⊥) to the direction of mean motion of a given sample for J = 0 (e) and J = 2 (f), averaged over 10² samples (see ESI for details).

3.4.2 Dynamics

The structural anisotropy of the flocking liquid is accompanied by anisotropy in the dynamics. This is evident in the difference between the MSD along (MSD_‖(t)) and perpendicular (MSD_⊥) to the flocking direction (SI, Figs. S4 and supplementary movies M1w, M2w, M3w and M4w). We find that at any given time MSD_⊥(t) is systematically larger MSD_‖(t). This difference can be used to quantify the transition to the flocking state, as shown in Fig. S5. Additionally, in the flocking liquid we observe transverse superdiffusive behavior, as observed previously in particle models⁴⁶. Finally, the anisotropic nature of the flocking state also affects the onset of jamming, as evident in the morphology of dynamical heterogeneities shown in Fig. 5 b. For J = 0 (Fig. 5c), the collective rearrangements observed when the jammed state is approached form the liquid side are isotropic swirls, while for J = 2 they become and anisotropic, taking the shape of local flocks (Fig. 5d). We stress that all the displacements are computed in the center of mass frame, hence the local flocks are not due to mean motion, but to heterogeneities in the local collective dynamics.

These effects can be quantified by studying the spatial correlation of cell displacements, which become significantly more long-ranged along the direction of mean motion compared to the perpendicular direction as J increases (SI Fig S2). We can also quantify the timescale associated with correlated motion by analyzing the angular trajectories, which exhibit signatures of dynamical heterogeneities with a characteristic timescale of about t ~ 10 (SI text and Fig S7). Since the time scale of angular relaxation is an order of magnitude smaller than that of structural relaxation, flocking excitations dominate the displacement statistics.

4 Conclusions

In this work, we describe a minimal model for collective migration in biological tissues. Our model treats a confluent cell monolayer as a Voronoi tessellation of the plane and encodes mechanical properties of the cells, such as intracellular adhesion, cortical tension, and motility. Motivated by experiments at both the tissue and cellular scales, we introduce a polar interaction mechanism similar to the one leading to flocking in other active matter systems^25,42,43 that captures the feedback between local dynamics and cell polarization. By tuning the strength of the polar interaction and the preferred perimeter of the cells, we find a rich phase diagram with four phases. At low polar interaction strengths, we find standard liquid and amorphous solid phases. Increasing polarization alignment leads to the emergence of an amorphous flocking solid, and a flocking liquid phase, both exhibiting collective directed motion or migration. We are able to understand and predict the location of these transitions by extending ideas from statistical physics, such as effective temperature and caging timescales, to self-propelled agents.

Remarkably, our phase diagram captures the JUT observed in recent experiments on epithelial monolayers, where overexpression of the endocytic protein RAB5A triggers the onset of directed collective motion in an otherwise quiescent monolayer and promotes local fluidization¹¹. Cell migration patterns in this state are compatible with the flocking liquid state predicted by our model in the regime where both the polar interaction strength and the target perimeter p₀ are large.

A more quantitative comparison between the experiments and our model is made difficult by the challenges posed by the quantification of cell polarization in multicellular sheets. As of today, there are no direct measures of how a cell’s polarization changes in response to changes in its local environment. An exciting direction for future work is the study of subcellular structures or intercellular markers for cell polarization in multicelluar monolayers to correlate those with cell shapes and interfacial tensions and test the hypothesis that cells polarize according to mechanical forces generated by neighboring cells. If so, it may even be possible to extract the time constant J⁻¹ associated with this alignment. Moreover, our model predicts that the onset of directed migration impacts on the structural organization of the monolayer, leading to anisotropic positional fluctuations and rearrangements and inducing the alignment of the elongated cells perpendicularly to the migration direction. These predictions could be more likely directly tested experimentally, which offers an exciting opportunity for future studies addressing the interplay between collective motion and structural properties in confluent tissues⁴⁷.