Origins of the mechanochemical coupling of peptide bond formation to protein synthesis

Abstract

Mechanical forces acting on the ribosome can alter the speed of protein synthesis, indicating that mechanochemistry can contribute to translation control of gene expression. The naturally occurring sources of these mechanical forces, the mechanism by which they are transmitted 10 nm to the ribosome’s catalytic core, and how they influence peptide bond formation rates are largely unknown. Here, we identify a new source of mechanical force acting on the ribosome by using in situ experimental measurements of changes in nascent-chain extension in the exit tunnel in conjunction with all-atom and coarse-grained computer simulations. We demonstrate that when the number of residues composing a nascent chain increases, its unstructured segments outside the ribosome exit tunnel generate piconewtons of force that are fully transmitted to the ribosome’s P-site. The route of force transmission is shown to be through the nascent polypetide’s backbone, not through the wall of the ribosome’s exit tunnel. Utilizing quantum mechanical calculations we find that a consequence of such a pulling force is to decrease the transition state free energy barrier to peptide bond formation, indicating that the elongation of a nascent chain can accelerate translation. Since nascent protein segments can start out as largely unfolded structural ensembles these results suggest a pulling force is present during protein synthesis that can modulate translation speed. The mechanism of force transmission we have identified and its consequences for peptide bond formation should be relevant regardless of the source of the pulling force.

Graphical abstract

Introduction

Two sources of mechanical forces acting on the ribosome have recently been shown to modulate its elongation speed during extreme pausing events. A co-translationally folding domain was found to generate twelve piconewtons of force¹ and relieve stalling caused by so-called translational-arrest peptides in the exit tunnel^1–4. Similarly, the SecA motor protein – which binds particular N-terminal signal sequences – co-translationally pulls on nascent proteins and speeds up protein synthesis during translocation through membranes^5,6. Such mechanochemical effects on the ribosome-nascent chain complex are biologically important because changes in translation-elongation kinetics influence translation control of gene expression^7,8 - affecting protein structure^9,10, function^11,12, chaperone binding¹³, translocation and targeting^14,15, and consequently many different downstream cellular processes such as chronobiology¹⁶.

There are a number of fundamental, unanswered questions concerning the origins of mechanical forces on the ribosome, the mechanism of force transmission, and the consequences for peptide bond formation. With up to eleven different co-translational processes acting on a nascent chain^8,17, it is unlikely that all of the naturally occurring sources of mechanical forces have been identified. It is unknown how much of the mechanical force pulling on the nascent chain outside of the exit tunnel will be transmitted back to the catalytic core of the ribosome, located 100 Å away. Interactions between the nascent chain and the tunnel wall, for example, have the potential to attenuate the force reaching the ribosome’s P-site. Furthermore, it has been speculated that there are two potential routes of force transmission to the catalytic core¹⁸ – one through the nascent chain, and the other through the ribosome exit tunnel wall, or a combination of the two. Indeed, allosteric signals through molecular components of the ribosome have been implicated in coordinating protein synthesis¹⁹, lending credence to the route of force transmission through tunnel components and/or peptide-tunnel interactions. Finally, how such mechanical forces accelerate translation elongation at the molecular level is unknown, although disruption of interactions between the nascent chain and exit tunnel wall appears important in the case of evolutionarily programmed stalling sequences²⁰.

One unidentified source of mechanical force may be the unfolded nascent protein itself. In the field of polymer physics it has long been established that unstructured polymers confined to spaces of varying volume can experience entropic pulling forces as they move to regions of larger volume^21–23. This phenomenon may also apply to the ribosome, which contains a narrow tunnel that bisects the large ribosomal subunit through which the elongating nascent protein progresses until it emerges into a more voluminous compartment. This tunnel is 100 Å in length, has a variable diameter of 10 to 20 Å, and connects the ribosome’s catalytic core to the cellular milieu²⁴.

Here, we use four different resolution levels of theory and simulation modeling to resolve these outstanding issues. We first test the hypothesis that, even in the absence of all other co-translational processes, largely unstructured segments of the nascent chain residing immediately outside the exit tunnel can generate pulling forces. To do this, we use a combination of experimental measurements and computer simulations to demonstrate that lengthening the nascent chain on arrested ribosomes generates piconewtons of force. We show that such a force, arising from outside the exit tunnel, is fully transmitted back to the ribosome’s P-site, and that its primary route of transmission is through the nascent peptide backbone. At the molecular level, we find that the transition state barrier to peptide bond formation is decreased by such forces, indicating they might accelerate the rate of peptide bond formation. These results suggest that translation speed has the potential to be continuously modulated by the mechanochemical consequences induced by nascent-chain elongation.

Results

Unstructured segments outside the exit tunnel stretch the nascent chain segment inside the tunnel

To measure the influence of any pulling force that might be generated by a largely unstructured nascent chain segment we applied a PEGylation accessibility assay to stalled ribosome-nascent-chain constructs (RNCs) to estimate changes in distance between nascent chain residues and the P-site²⁵. This assay measures the fraction of nascent chains in a sample that have their cysteine side-chains covalently modified with a PEG adduct (F_peg polyethyleneglycol maleimide). For RNCs that contain the ‘tape measure’ (TM; 95 residues) sequence shown in Table 1, pegylation monotonically increases with distance along the tunnel from peptide residue 27 to 33 from the P-site (Fig. 1). This TM sequence adopts an extended conformation in the exit tunnel²⁵, meaning that the projection of the C_α atoms, between neighboring residues, onto the long-tunnel axis gives C_α–C_α distances of 3.2 Å. Thus, the increase in pegylation indicates an increase in the accessibility of the cysteine as it enters the tunnel vestibule, a wider portion of the tunnel that includes the last 20 Å of the tunnel. Since the tunnel is 100 Å in length, TM residues emerge from it when they are more than 33 residues from the P-site²⁵. More importantly, as we illustrate below, this distance-dependent pegylation allows us to estimate the spatial distance between a reporter cysteine and the P-site residue, and consequently the extent to which the nascent chain segment in the exit tunnel stretches due to an increase in nascent chain length.

Table 1. The nascent chain sequences arrested on the ribosome.

Sequences are written from left to right with the C-terminal (P-site) residue first.

Nascent Chain Label	Sequence
Tape Measure	SRNRDFFYENRLPDFYRMRDGLLTEPFQSQT $\mathrm{C}$FRLGSINIVVREGSSDQEGAAPL … M
3Ala10	SRS $\text{AAAAAAAAAA}$PDFYRMRDGLLTEPFQSQT $\mathrm{C}$FRLGSINIVVREGSSDQEGAAPL … M
3Gly10	SRS $\text{GGGGGGGGGG}$PDFYRMRDGLLTEPFQSQT $\mathrm{C}$FRLGSINIVVREGSSDQEGAAPL … M
2Ala10	SR $\text{AAAAAAAAAA}$PDFYRMRDGLLTEPFQSQT $\mathrm{C}$FRLGSINIVVREGSSDQEGAAPL … M
2Gly10	SR $\text{GGGGGGGGGG}$PDFYRMRDGLLTEPFQSQT $\mathrm{C}$FRLGSINIVVREGSSDQEGAAPL … M

Figure 1. Fraction of PEGylated nascent chains for the different ribosome-nascent-chain constructs.

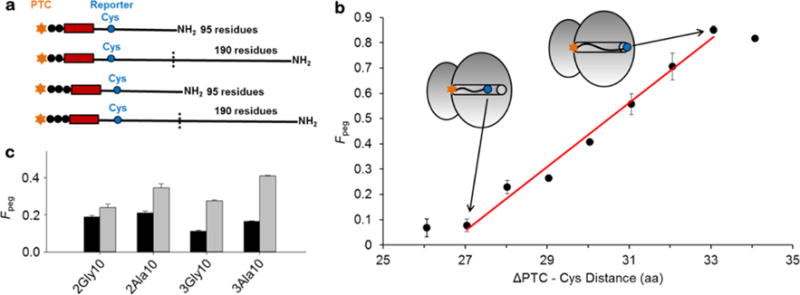
(a) Illustration of key features of the different nascent-chain constructs. The arrested nascent chains are either 95 or 190 residues in length, with a stretch of 10 Ala or Gly residues (red rectangle) that are either two or three residues (black circles) removed from the P-site. The reporter cysteine (blue circle) is at residue position 32 (top) or 33 (bottom) from the PTC. Thus, the nomenclature 3Gly10 indicates that the 10 glycine stretch starts 3 residues removed from the P-site. (b) The fraction of PEGylated nascent chains (F_peg for the extended TM sequence (Table 1) as a function of the number of residues the reporter cysteine is removed from the PTC. This is a cysteine scanning experiment – the identities of all other residues remain the same, but the Cys is substituted in at different positions along the TM sequence, as illustrated by the inset ribosomes. A high fraction of PEGylation corresponds to high accessibility of the reporter cysteine to the PEG molecule. (c) Fraction of PEGylated nascent chains for each nascent chain construct (Table 1) that are either 95 (black) or 190 (gray) residues in length

To determine the extension of a peptide in the exit tunnel as a function of the nascent chain length we engineered the TM sequence to contain two features. First, we mutated either ten consecutive alanines (Ala10) or ten consecutive glycines (Gly10) into the TM sequence, located two or three residues from the C-terminus (e.g., 2Ala10 or 3Ala10 in Table 1). The purpose of these alanine and glycine cassettes is to bias the corresponding portions of the TM sequence from an extended conformation towards a compact conformational ensemble. We showed previously that Ala10 forms a helix at specific tunnel locations²⁶, which shortens the distance between the reporter cysteine and the P-site residue, thereby retracting the reporter cysteine further back into the tunnel²⁵. The highly flexible glycines also lead to compaction. The cysteine in these sequences is either 32 or 33 residues from the C-terminus, depending on where the alanine and glycine cassettes were inserted. The second feature we engineered was an additional TM sequence covalently attached to the N-terminus of each of the four constructs (Fig. 1a), thereby doubling the length of the nascent protein from 95 to 190 residues.

For each construct, we find that F_peg increases when the nascent chain length is doubled (Fig. 1c), indicating that the cysteine becomes more accessible. Converting this fraction pegylated into an estimate of the spatial separation of the cysteine from the P-site residue (Table 2; see Methods), indicates the cysteine has moved 2 to 6 Å away from the P-site (e.g., from 86 Å to 92 Å for construct 3Ala10). Since the TM sequence is not capable of folding²⁵, we conclude that the increased nascent-chain length (from 95 to 190 residues) stretches the nascent-chain segment inside the exit tunnel, indicating a pulling force is generated by the additional unstructured segments outside the exit tunnel.

Table 2.

The experimentally determined spatial distance of the reporter cysteine from the P-site residue.

Nascent Chain Label	dPTC (Å)a 190-residue RNC	dPTC(Å) 95-residue RNC
3Ala10	92.0	85.8
2Ala10	90.4	87.0
3Gly10	88.6	84.5
2Gly10	87.7	86.4

^adPTC is the spatial distance between the C-terminal nascent chain residue and the reporter cysteine

A pulling force is transmitted to the P-site tRNA

To test if a pulling force is transmitted to the P-site tRNA, which sits at the center of the catalytic core of the ribosome, we constructed a cropped, all-atom model of the 3Ala10 RNC (Figure 2a) and ran two sets of simulations with the reporter cysteine restrained to the experimentally determined distances of 86 Å or 92 Å from the P-site. We ran 10 independent, 200-ns trajectories of this RNC for each restrained distance and calculated the force experienced by the C-terminal residue at the P-site for each trajectory. We find that the mean force (computed using Eq. 3) acting at the P-site is 25 pN (99% Confidence Interval (CI): 2.1–50.0 pN, 2-sample t-test, p=0.01) larger in the case when 3Ala10’s nascent chain length is doubled. Thus, as the nascent chain is lengthened from 95 residues to 190 residues, a statistically significant, non-zero pulling force is generated and transmitted to the ribosome’s P-site. However, the large error bars (i.e., 99% CI: 2.1–50.0 pN) mean that the average pulling force cannot be determined precisely from these simulations.

Figure 2. All-atom model and force experienced by the reporter cysteine and P-site residue.

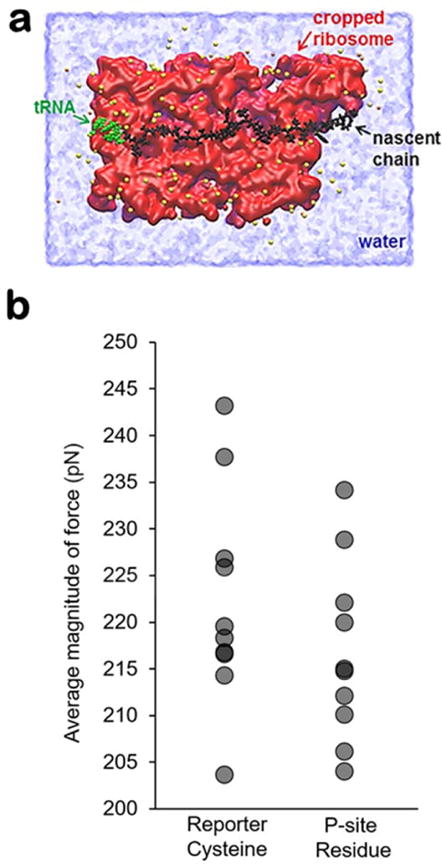
(a) A cross-section of the cropped, all-atom ribosome-nascent chain complex along the long-axis of the exit tunnel. The tRNA (green), ribosome (red), nascent chain (black), TIP3P water (blue), and ions (yellow) are shown. (b) The mean force at the C_α atom of the reporter cysteine and P-site residue calculated from each trajectory using Eq. 2 for the 190-residue 3Ala10 nascent chain construct. The distributions are statistically the same at these two sites along the nascent chain (p-value=0.3, Wilcoxon Rank Sum Test), indicating there is no force attenuation.

Such large error bars suggest that the all-atom simulations are not converged and are out of equilibrium. Quantities, such as the average pulling force, calculated from non-equilibrium simulations can be inaccurate, having the potential to change dramatically with longer simulations or different starting structures. We assessed whether the simulations were out of equilibrium by examining the time-dependent self-averaging of the force experienced at the P-site (i.e., $\langle \left|F_{\mathrm{k}}\right|\left(t\right)\rangle =\frac{1}{N_{\mathrm{S}}}{\displaystyle {\sum }_{j=1}^{N_{\mathrm{S}}}\left|F_{\mathrm{k}}\left(j\right)\right|}$, where N_S is the number of saved structures in a trajectory – see Methods), as well as the coefficient of variation of this force. If the trajectories are at equilibrium the self-average should converge quickly relative to the time-scale of the simulation and the coefficient of variation should be very small. We find, however, that the self-average of the pulling force does not converge during the 200-ns trajectories (Fig. 3a), and that the percent coefficient of variation of the mean force is around 8% (Table 3), which is two orders-of-magnitude larger than in the coarse-grained simulations of these systems (see below). Thus, the all-atom simulations are not at equilibrium, and the equilibrium, average pulling force (Eq. 3) could very likely vary widely from the 25 pN force calculated from these simulations. This result is consistent with experimentally measured equilibration time scales of microseconds to tens-of-microseconds for unstructured proteins^27–29, suggesting the simulation time of individual trajectories would need to be on the order of tens to hundreds of microseconds to calculate precise force averages from the all-atom model. Running such long simulations of the ribosome is not yet computationally feasible.

Figure 3. Self-averaging plots of the magnitude of the force experienced at the P-site residue versus time indicate that the all-atom simulations do not achieve equilibrium, while the coarse-grained simulations do.

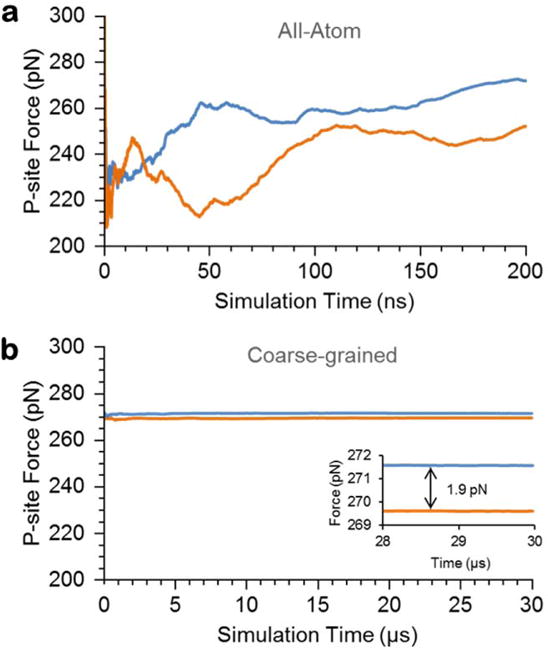
(a) Force experienced at the P-site residue for the 3Ala10 RNC with the reporter cysteine restrained to either 92 Å (blue curve; arising from the 190-residue-long nascent chain) or 86 Å (orange curve; arising from the 95-residue-long nascent chain) from the P-site residue. The force was computed from Eq. 2. (b) Same as (a) except for the coarse-grained simulation of the 3Ala10 RNC. Inset shows the force difference (Eq. 3) is 1.9 pN.

Table 3.

Percent coefficient of variation of the P-site mean force in the 3Ala10 RNC all-atom and coarse-grained simulations.

All-atom Simulations	Coefficient of Variation (×100%)
190-residue RNC	8.8
95-residue RNC	8.4
Coarse-grained Simulations
190-residue RNC	0.07
95-residue RNC	0.09

Piconewtons of force is transmitted to the P-site

To overcome the limited sampling of the all-atom simulations, which led to imprecise force estimates, we turned to coarse-grained simulations to determine a precise magnitude of the pulling force associated with increased nascent-chain length. We employed a coarse-grained model of RNCs that has been developed and extensively applied over the past several years^30–32. This coarse-grained model allows 10’s of microseconds to be simulated, and the smoothed energy landscape and low-friction Langevin Dynamics results in a million-fold acceleration of dynamics³¹. Thus, individual trajectories correspond to tens of seconds of experimental time. Full details of the model can be found in the Methods Section. Briefly, individual residues are represented by one interaction site centered at the backbone C_α location and nucleotides by three or four interaction sites (Fig. 4a). Transferable energy terms representing bond, bond-angle, dihedral angle, van der Waals interactions, and electrostatic interactions are included in the force field.

Figure 4. A force on the order of piconewtons is generated upon increasing the nascent chain length from 95 to 190 residues.

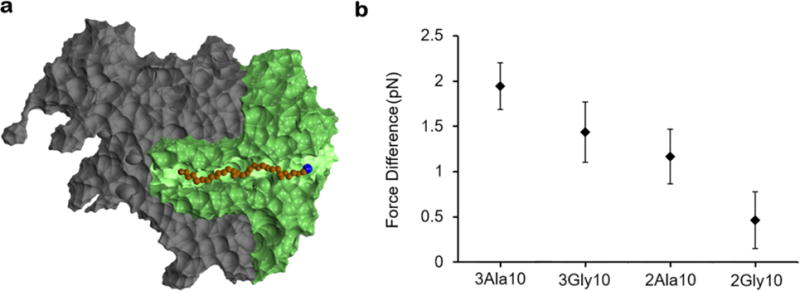
(a) A cross-section of the cropped coarse-grained ribosome used in these simulations (green) superimposed onto the large ribosomal subunit (gray). The nascent chain is shown in brown, the reporter cysteine in blue, and the P-site residue as glossy brown. (b) The difference in force (Eq. 3) experienced by the P-site residue upon lengthening the nascent chain from 95 to 190 residues is on the order of piconewtons for the different RNCs. Error bars represent the 99% confidence interval about the mean computed from bootstrapping.

We carried out 10 independent simulations for each of the four nascent-chain sequences (Table 1) with the reporter cysteine restrained at its experimentally determined distance (Table 2) from the P-site. Each trajectory is at equilibrium as indicated by the constant, self-averaged force at the C-terminus (Fig. 3b) and percent coefficient of variation of 0.09 or less (Table 3). The force transmitted to the P-site due to the lengthening of the nascent chain ranges from 0.5 to 1.9 pN (Fig. 4b, the distribution of forces is reported in Fig. S1). Thus, the additional unstructured nascent-chain segment generates piconewtons of force that is transmitted to the P-site of the ribosome.

All of the force is transmitted to the P-site

Many different types of inter-molecular interactions occur between the nascent chain and ribosome exit tunnel. These include van der Waals, ionic, hydrogen bonding, and hydrophobic interactions. Because of these interactions, it is possible that not all of the force that is experienced by the reporter cysteine is transmitted back to the P-site. For example, a strong electrostatic interaction between the tunnel wall and nascent chain might pin the nascent chain to the wall and thereby attenuate force transmission. To test if force attenuation occurs in the all-atom simulations, we calculated the distribution of forces experienced at the reporter cysteine’s C_α atom and at the C-terminal residue’s C_α atom in the all-atom simulations of the 3Ala10 construct (see Methods). We find that these distributions are indistinguishable in both the 95- and 190-residue RNC simulations (Fig. 2b, Wilcoxon Rank Sum Test, p=0.3), indicating that all of the force that is generated by the presence of the unstructured nascent-chain segments outside the exit tunnel is transmitted to the P-site.

Force attenuation is also possible in the coarse-grained model, as electrostatic interactions are present between the ribosomal phosphate groups and charged residues in the nascent chain. To determine whether all of the force generated by unstructured segments outside the exit tunnel was transmitted to the P-site, we calculated the pulling force at the P-site and reporter cysteine (see Methods). The average pulling force experienced by the reporter cysteine is statistically indistinguishable from the average pulling force acting on the C-terminal residue (Fig. 5). If force attenuation had occurred due to the nascent chain binding to the tunnel wall these pulling forces would be different. Thus, both the coarse-grained and all-atom models indicate that all of the pulling force is transmitted through the nascent protein to the P-site.

Figure 5. The force due to doubling the nascent chain length (∆〈|F_k|〉, Eq. 3) at the P-site is not statistically different from the force difference at the reporter cysteine (32 residues from the P-site).

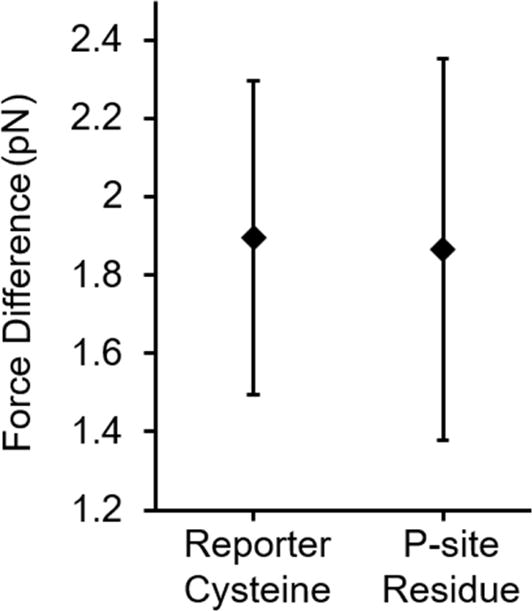
Results are from the coarse-grained simulations of the 3Ala10 RNC at 295 K. Error bars represent the 99% confidence interval about the mean.

Force is transmitted through the protein backbone, not the tunnel wall

In the simulations the ribosome interaction sites are harmonically restrained to remain in their crystallographically determined positions, and the pulling force can therefore only be transmitted through the polypeptide’s backbone. Beckmann and coworkers previously hypothesized that force transmission could potentially occur through the tunnel wall¹⁸. To test this hypothesis we ran all-atom simulations of the 3Ala10-RNC in which we did not harmonically restrain the ribosome components lining the exit tunnel but instead we harmonically restrained the fourth nascent-chain residue from the P-site, thereby blocking the possibility of force transmission through the backbone but allowing possible routes through the tunnel wall. We find there is no difference in force experienced by the C-terminal residue in the 95- and 190-residue RNC simulations (0.16 pN, 99% CI: −26.4 to 26.8 pN, 2-sample t-test, p=0.9). Thus, these simulations indicate there is no force transmission through the tunnel wall, and the primary route of force transmission is through the nascent chain backbone. The aforementioned limited sampling of such all-atom simulations should be kept in mind when interpreting these results, Nonetheless, these results suggest that force transmission through the wall, if it occurs at all, is likely to be a minor secondary mechanism.

Consistency with estimates based on polymer theory

As an independent estimate of the force generated due to doubling the nascent chain length, we utilized a polymer theory that estimates the force required to stretch a polymer that is confined within a uniform, inert cylinder³³. The relevant parameters for this calculation are the temperature, cylinder diameter, and the polymer’s contour length, persistence length, and end-to-end distance. Assuming a temperature of 295 K, a diameter of 15 Å for the exit tunnel, a polymer contour length equal to that of the 33 C-terminal residues of the nascent protein, and a persistence length (L_p) that can vary between 9 and 24 Å^[34,35], we computed the force required to stretch this polymer, starting from an end-to-end distance of 86 Å, to 92 Å. We find that the force ranges from 2.4 to 5.3 pN, with the spread arising from the various L_p values tested (Table 4 and Supplementary File 1). Similarly, a Worm-like Chain polymer model under a high-force regime in bulk solution can represent polymer behavior under cylindrical confinement³⁶. This model estimates forces as high as 1.5 pN occur (Supplementary File 1). These results are consistent with the estimates from the coarse-grained simulations and fall within the 99% Confidence Interval of the force estimated from the all-atom simulations, providing further evidence that unstructured nascent chain segments outside the exit tunnel generate piconewtons of force at the P-site.

Table 4. Polymer-theory-based estimate.

³³ of P-site force using a Generalized Bead-Rod polymer model at a range of different persistence lengths.

Nascent Chain Label	Force (pN)
	(Lp = 9 Å)	(Lp = 12 Å)	(Lp = 24 Å)
3Ala10	5.3	4.2	2.4
3Gly10	3.0	2.3	1.3
2Ala10	2.9	2.2	1.3
2Gly10	1.4	0.9	0.5

Increased force decreases the energy barrier to peptide bond formation

To a first approximation, the force acting on the P-site residue can influence the transition state barrier for peptide bond formation by an amount proportional to the work performed by the force during the reaction³⁷. This work is equal to the dot product of the force vector with the displacement vector of the system upon transitioning from reactants to products. This means that if the force is applied anti-parallel to the reaction coordinate the transition state barrier will increase, while a parallel force would decrease the barrier. To determine whether the transition state barrier to peptide bond formation increases or decreases due to such pulling forces we carried out Quantum Mechanics – Molecular Mechanics (QM/MM) simulations of peptide bond formation for the 95- to 190-residue RNC. Specifically, using several different starting conformations derived from the all-atom simulations of the 3Ala10 RNC, we inserted an alanine residue in the A-site (which was empty in the previous simulations), and then calculated the minimum free-energy path to peptide bond formation using a QM/MM methodology (Fig. 6). We find that the transition state barrier height decreases when the nascent chain is longer compared to when it is shorter (t-test, p=0.00052). Due to the non-equilibrium nature of the all-atom simulations, and the low level of theory utilized (AM1), the decrease in transition state barrier height is more likely to be accurate than the specific value of the difference in the transition state barriers. Thus, pulling forces from outside the exit tunnel can decrease the transition state barrier to peptide bond formation, suggesting such forces can accelerate the rate of peptide bond formation.

Figure 6. The influence of the unstructured nascent chain pulling force on the free energy of peptide bond formation.

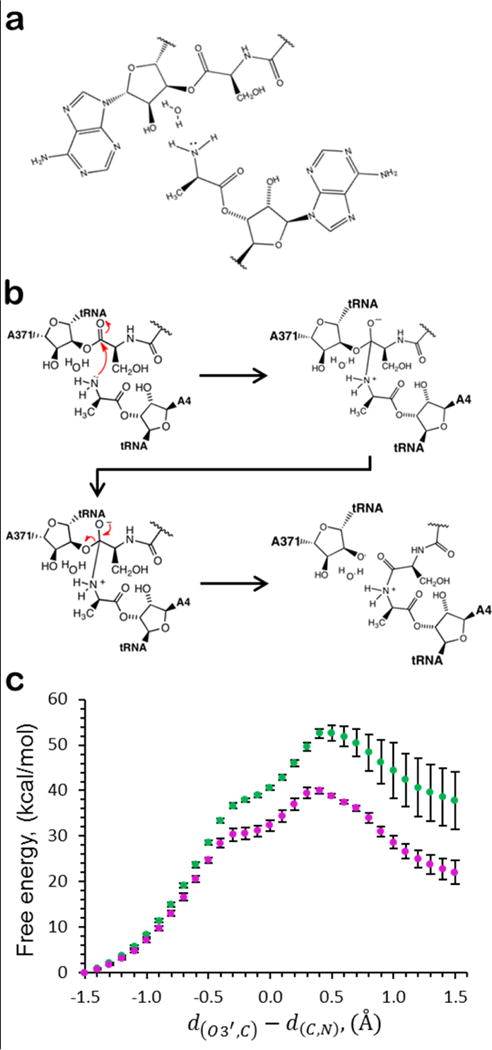
(A) The atoms shown were treated quantum mechanically in the QM/MM simulations. (B) A pictorial representation of the reaction that was simulated quantum mechanically. Red arrows denote the movement of electrons. Note well that the final structure depicted represents the rate limiting transition intermediate of the peptidyl transfer and not the final product. (C) The free energy as a function of the reaction coordinate for peptide bond formation for the 95-residue (green dots) and 190-residue (magenta dots) 3Ala10 RNC. Error bars represent the 95% confidence intervals. Because we modeled the reaction only up to the transition state (panel b), reaction coordinate values greater than 0.5 Å result in exploration of what is no longer the relevant free energy pathway and, consequently, larger error bars.

Discussion

Translation kinetics can modulate nascent protein structure and function, and thereby influence cellular processes^1,5,38–45. A number of factors are responsible for regulating the rate of protein synthesis, including the chemical identity of nascent-chain residues inside the ribosome exit tunnel^18,46. The molecular mechanism by which many of these factors alter translation speed at the ribosome’s catalytic core remains unclear¹, yet it is key to understanding the origins and consequences of the coupling of nascent protein behavior to translation dynamics. Given that a nascent protein is a polymer composed of amino acids whose behavior must obey fundamental principles of polymer physics, we hypothesized that unstructured nascent-chain segments outside the ribosome exit tunnel might generate a pulling force. And we explored how such pulling forces are transmitted to the ribosome’s catalytic core and influence peptide bond formation.

To test this unstructured-protein hypothesis, we utilized a PEGylation assay to measure the extent to which a nascent-chain segment inside the exit tunnel is stretched due to a pulling force generated upon increasing the nascent protein from 95 to 190 residues. These stretched distances, when incorporated into models involving classical and QM/MM simulations, yield three fundamental and novel conclusions. First, piconewtons of pulling force are generated due to the largely unstructured nascent protein segments outside the tunnel. Second, pulling forces are transmitted through the peptide backbone to the P-site residue. Third, pulling forces can decrease the transition state barrier height of peptide bond formation. These findings have important physiological consequences. Since protein segments typically start out unfolded, this suggests many proteins can experience piconewtons of force at some point during their synthesis. This pulling force might increase with increasing length of the unstructured chain and could thus continuously modulate translation speed when peptide bond formation is rate limiting.

Co-translational force is not a new concept². Twelve piconewtons of force is generated by the co-translational folding of the Top7 protein, and this force, determined using Laser Optical Tweezers (LOT), can relieve translational stalling of an arrested peptide.¹ Our study differs in several ways. First, we examined force generation due to largely unstructured segments rather than to the folding process. This explains why we measured a pulling force that is a factor of 5 to 10 times smaller; the additional free-energy from folding is not present in our RNCs. Second, our measurements were performed in situ by a relatively non-perturbing methodology that didn’t require an externally applied force (as in LOT experiments), which is in addition to any naturally occurring forces experienced by the ribosome. Finally, our RNC complex does not contain evolutionarily programmed arrest peptides to stall translation. Arrest peptides are vanishingly rare in nature, only 16 have been identified across 10 organisms.⁴⁷ Based on cryo-EM structures^18,46 and mutational studies⁴⁸, particular residues within such peptides appear to bind and interact^20,46 in a spatially precise manner to specific residues lining the exit tunnel. In some cases, such binding can cause tRNA, ribosomal side chains and nucleotides to shift by several angstroms²⁰. Non-arrest peptides have not been shown to exhibit this behavior. Therefore, the nascent chain sequences used in our study might better reflect the mechanical behavior of commonly occurring protein sequences.

Use of computer simulations allowed us to test two proposed hypotheses¹⁸ – one of which is that the transmission of pulling forces occurs through the exit tunnel wall, while the other posits it is transmitted through the nascent protein backbone. Our results demonstrate that force transmission to the P-site residue occurs through the nascent protein backbone rather than through ribosomal protein or RNA lining the exit tunnel wall. This suggests that the ribosome did not evolve specific force-transmission pathways through ribosomal components, at least not for the non-arresting peptides used in this study.

Our calculations allowed us to determine whether the pulling force was attenuated as it traversed along the nascent chain backbone to the P-site. We find that even in the presence of non-specific attractive interactions between the nascent chain and tunnel wall, all of the force is transmitted to the P-site. This result might be surprising considering the electrostatic and hydrophobic interactions that can occur in the all-atom simulations. However, having attractive intermolecular interactions is not sufficient to attenuate force; the distribution of these interactions along the tunnel is also important. To illustrate this, consider a water molecule in the liquid phase. In a given spatial configuration, a water molecule will make on average four hydrogen bonds, each worth around 2 kcal/mol of potential energy. Thus, a typical water molecule has an interaction energy of around 8 kcal/mol from hydrogen bonding, which is large compared to thermal energy (0.6 kcal/mol at room temperature). Based on these values, the water molecule might be expected to stay locked in its configuration. Yet, such a water molecule rapidly (on the order of ps) reorients and samples a wide range of configurations because a broken hydrogen bond can rapidly reform with another nearby water molecule. Likewise, if there are many interactions between the nascent chain and tunnel along the tunnel, then stretching the nascent chain will not be energetically difficult because any intermolecular interactions that are disrupted will be reformed as the chain slides along the tunnel wall. In contrast, when we introduced a single, strong attractive interaction site in the exit tunnel (see Methods), force transmission was attenuated. Thus, both the strength and distribution of intermolecular interactions along the tunnel will influence force attenuation. In the case of abundant, nonspecific interactions, the pulling force is less likely to be attenuated.

A biological consequence of such pulling forces is suggested by our QM/MM simulations, in which we calculated the transition state barrier height to peptide bond formation as a function of nascent chain length. We found that the longer nascent chain, and the correspondingly larger pulling force, leads to a decrease in the transition state barrier. This implies that such pulling forces can accelerate peptide bond formation, and hence can accelerate codon translation rates when this step of translation is rate limiting.

Other potential sources of co-translational pulling forces can arise from outside of the exit tunnel, such as the co-translational binding of chaperones, enzymes or translocons. Our findings are relevant to these cases as well. Specifically, the mechanism of force transmission through the nascent peptide backbone and the acceleration of peptide bond formation should be independent of the origin of the pulling force. Thus, these findings provide general insights into molecular mechanisms and consequences of other sources of co-translational forces.

A 2 pN pulling force can accelerate peptide bond formation by as much as 15% according to the Bell model³⁷ (assuming a 0.3 nm distance between the reactant and transition state²⁰). Speeding up translation elongation by 12 to 28% has been found to alter nascent protein structure⁴⁹, the specific activity of a protein by as much as 30%^50,51, and the folding rate of another protein by 51%⁵². 2 pN’s of force can also cause conformational changes in enzymes that can influence their turnover rate^53,54. Indeed, preceding the chemical step of peptide bond formation, the adenosine in the CCA arm of the tRNA in the P-site, and its covalently attached nascent-chain residue, can move several angstroms⁴⁶ towards the A-site when piconewtons of force are applied to the nascent chain⁵⁵. Thus, piconewtons of pulling force from unstructured nascent chain segments has the potential to modulate translation speed and the efficiency of various co-translational processes involving the nascent chain. More importantly, our results suggest that there may be a tendency for pulling forces to accelerate peptide bond formation regardless of the source from which they arise outside the tunnel. Thus, other sources of force that are greater in magnitude can have an even bigger effect. For example, the 12 pN force from the co-translational folding of the protein Top7¹ would accelerate peptide bond formation by 55% according to the Bell model.

A potential technical criticism of our force calculation (Eq. 3) is that we calculated the average force difference arising from the harmonic restraint, 〈|F_k|〉, as the difference in the average magnitudes of the force at the P-site residue, rather than as the difference in the magnitudes of the average force vector at the P-site residue. The latter approach is not appropriate as the average force vector is not representative of most instantaneous force vectors that arise due to thermal motion. Indeed, for this reason, Laser Optical Tweezer experimental analyses calculate force differences in the way we have done in this paper. By calculating the magnitude, we technically have not ruled out the possibility that the P-site is experiencing a compressive force instead of a pulling force. Therefore, for the sake of completeness, we computed the average force vector experienced at the P-site residue, and find values of [−26.3, 2.6, 8.2 pNs] and [−42.9, 2.4, 11.6 pNs], respectively, for the 95- and 190-residue 3Ala10 RNCs. Since the exit tunnel lies along the positive x-axis in the local coordinate system in our simulations, these results demonstrate that the P-site residue is experiencing a pulling force.

In summary, we have used a unique combination of experimental, computational and theoretical models to understand at multiple levels the coupling of mechanical forces generated by unstructured nascent chain segments outside the exit tunnel and their chemical consequences at the catalytic core of the ribosome. Since protein segments tend to start out unfolded, this pulling force could be a common phenomenon during translation, making mechanochemistry a common feature of protein synthesis.

Methods

Constructs and In Vitro Translation

Standard methods of bacterial transformation, plasmid DNA preparation, and restriction enzyme analysis were used. The nucleotide sequences of all mutants were confirmed by automated cycle sequencing performed on an ABI 3730XL Sequencer using Big dye terminator chemistry (ABI). All mutant DNAs were sequenced throughout the entire coding region. All tape measure (TM) constructs were derived initially from the T1 domain of cysteine-free Kv1.3 with a E64C mutation²⁵. Cys71 is a native cysteine and was replaced with serine. Two α-helices, α1 (from Leu67 to Leu70) and α2 (from Pro81 to Arg83) in the wild-type T1 domain, were deleted and a new BstEII restriction site was engineered at Arg101. NsiI site was introduced at the N–terminus of TM in order to engineer extended TMs using a ligation method. Constructs substituted with 10 consecutive alanines or glycines were made using the TM E64C mutant as a template. All deletions and substitutions were introduced into TM constructs using Stratagene’s QuikChange Site-Directed Mutagenesis Kit. Rapid DNA Ligation Kit and a standard protocol (Roche, NJ) were used to create extended TMs.

Capped cRNA was synthesized in vitro from linearized templates using Sp6 RNA polymerase (Promega, Madison, WI). Linearized templates for Kv1.3 translocation intermediates were generated using a restriction enzyme, BstEII, to produce DNA constructs lacking a stop codon. Proteins were translated in vitro with [35S]Methionine (2μl/25 μl translation mixture; ~10 μCi/μl Express, Dupont/NEN Research Products, Boston, MA) for 1 h at 22°C in a rabbit reticulocyte lysate (2 mM final [DTT]) according to the Promega Protocol and Application Guide.

Gel Electrophoresis and Fluorography

All samples were treated with RNase (20 μg/ml) before loading on the gel. Electrophoresis was performed using the NuPAGE system and precast Bis-Tris 10% or 12% gels and MOPS running buffer. Gels were soaked in Amplify (Amersham Corp., Arlington Heights, IL) to enhance³⁵S fluorography, dried and exposed to a phosphor screen cassette. Quantitation of gels was carried out directly using a Molecular Dynamics Typhoon FLA 9500 PhosphorImager (GE Healthcare Life Sciences, Marlborough, MA).

Accessibility Assay

Translation reaction (10–20 μl) was added to 500 μl Hepes buffered saline (100 mM, 4 mM MgCl₂, 20 mM Hepes, pH 7.3) also containing 2 mM DTT. The suspension was centrifuged at 70,000 rpm/20 min/4°C (TLA100.3 Beckman rotor) through a sucrose cushion (120 μl, containing 0.5M sucrose, 100 mM KCl, 50 mM Hepes, 5 mM MgCl₂, 2 mM DTT, pH 7.5). The pellet was resuspended in 100 μl Hepes buffered saline (see above) with 25 μM DTT and treated with 1 mM PEG-MAL (SunBio) at 4°C for 2–3 h. To quench the pegylation reaction each sample was treated with DTT to neutralize PEG-MAL (200:1 ratio), incubated at room temperature for 15 min and centrifuged at 70,000 rpm/20 min/4°C (TLA100.3 Beckman rotor).

Calculating the reporter cysteine distance from the P-site

The distance between the reporter cysteine and the P-site residue was calculated using the experimentally determined tape measure curve of the extended TM protein (Fig. 1b). This curve plots the fraction of nascent chains that contain a reporter cysteine that is PEGylated as a function of ΔPTC, the number of residues separating the reporter from the P-site tRNA. The fraction of nascent chains in which cysteine was PEGylated was then measured for each nascent chain construct (Table 1), and this value was converted into a spatial distance from the P-site as follows. First, the average residue length, projected onto the long exit-tunnel axis, was measured by simulating the extended 3Ala nascent chain with the backbone dihedral angles constrained to be in the β-strand region of the Ramachandran plot. The distance from the C_α atom of the most C-terminal residue to the C_α atom of the most N-terminal residue of 3Ala was calculated and divided by the number of virtual bonds between C_α atoms in the chain. For instance, there are 33 residues between the cysteine and P-site residue in the 3Ala nascent chain and thus 32 (=33–1) virtual bonds. This calculation revealed that in the extended configuration each residue is 3.2 Å in length, when projected onto the end-to-end distance vector. (Note well that 3.2 Å is not the contour length⁵⁶). Second, Eq. 1 was then used to convert the distance from the P-site to the cysteine in units of amino acids into units of angstroms.

$$d\text{PTC}(\stackrel{°}{\mathrm{A}})=3.2\frac{\stackrel{°}{\mathrm{A}}}{\text{aa}}\left(\mathrm{\Delta }\text{PTC}\left(\text{aa}\right)-1\right)$$ (1)

Here, we illustrate Eq. 1’s application to the 190-residue 3Ala10 RNC construct. The fraction of nascent chains that are pegylated for this RNC is 0.41 (Fig. 1c). The experimentally determined tape measure curve (red line, Fig. 1b) indicates that, for this pegylation value, 29.74 amino acids reside between the reporter cysteine and the P-site tRNA. According to Eq. 1, the reporter cysteine in this construct is 92.0 Å from the P-site.

All-atom model and initial structures

An all-atom model of the ribosome-nascent-chain complex was created to simulate the arrested ribosome-nascent chain complexes used in the experiments. The model was prepared and simulated using the CHARMM36 force field⁵⁷ in the c38 version of CHARMM. When this project was started only a low resolution (9.5 Å) structure of the rabbit (Oryctolagus cuniculus) ribosome was available, meaning backbone and sidechain positions were unresolved. Therefore, we utilized a high-resolution T. Thermophilus ribosome (PDB ID: 4LNT) that had fewest unresolved nucleotides and residues. The structure and many of the chemical features of the exit tunnel are conserved across organisms^58,59. For computational efficiency, the simulation model only includes the large subunit of this ribosome and P-site tRNA, and was further cropped to form a rectangular box around the long-axis of the ribosome exit tunnel with dimensions of ~100 Å × 60 Å × 60 Å (Fig. 2a). This resulted in a system composed of approximately 50,000 atoms, including the CCA tail of the P-site tRNA. Sodium and chloride ions (at 100 mM concentration) as well as magnesium ions (5 mM) were added to achieve the experimental concentration of ions in a periodic box size of 110 Å × 70 Å × 70 Å. To allow the ions to rapidly find their binding sites on the ribosome the system was then simulated in the NVT ensemble, in the gas phase, for 200 ps at 295 K, holding the ribosome interactions fixed in space. After this, a pre-equilibrated box of TIP3P water molecules⁶⁰ was used to solvate the system, maintaining a 5 Å water buffer around the edges of the cropped ribosome.

The full nascent chain sequence was not represented in this model, instead only the 32 or 33 C-terminal residues (i.e., up to, and including the reporter cysteine) were explicitly modeled. We simplified the model in this way because the influence of the remaining portion of the nascent chain on the reporter cysteine positioning in the tunnel has been measured by the change in its position in the tunnel (Table 2). Thus, by restraining the reporter cysteine to the experimentally measured distances we are implicitly accounting for the effect of those additional unstructured nascent chain segments outside the ribosome exit tunnel. The nascent chain configuration on the ribosome was created by first inserting the nascent chain into the tunnel with dihedral angles in the β-strand region of the Ramachandran plot. The C-terminal serine residue was then covalently attached to the P-site tRNA via a custom patch residue introduced into the CHARMM topology and parameter files (Supplementary File 2). The patch residue parameters were chosen by adopting the parameters from similar chemical groups already in the CHARMM c38 force field. The nascent chain was minimized and relaxed on the ribosome for 1 ns at 295 K.

All-atom model simulations

For each RNC, the reporter cysteine was harmonically restrained to the corresponding distance from the PTC reported in Table 2. The RNCs were equilibrated in the NPT ensemble for 1 ns at 1 atm and 350 K using NAMD/2.10⁶¹. NAMD was used because of its efficient scaling to a large number of computer cores. The RNCs were then equilibrated in the NVT ensemble at 350 K for 1 ns. For the production simulations, ten independent trajectories of each RNC were run for 200 ns of simulation time at 350 K with an integration time step of 0.002 ps. SHAKE⁶² was applied to covalent bonds involving hydrogen. System coordinates were saved every 5 ns. 5 ns was chosen through block averaging tests that indicated that this resulted in uncorrelated error estimates (data not shown). We use a temperature of 350 K because measures of convergence were extremely poor in initial test simulations at the experimental temperature of 295 K. In both the equilibration and production phases spherical harmonic restraints, with restoring force constants, k_C, of 2.5 kcal mol⁻¹ Å⁻², were applied to the C_α, P, and O atoms of the tRNA, ribosome, and the C-terminal serine residue of the nascent chain after it had been placed at its most probable position. In one set of simulations, a planar restraint (k_C =2.5 kcal mol⁻¹ Å⁻²) was applied to the C_α atom of the reporter cysteine of the nascent chain so that the exit tunnel could be sampled orthogonal to the long-tunnel axis, while in another set of simulations a spherical harmonic restraint was applied to that atom to test if the force was attenuated or not.

To test if the pulling force could be transmitted through the tunnel wall, simulations were prepared by removing the harmonic restraints on the ribosomal components lining the exit tunnel - to allow for the potential of force transmission through them - and adding a spherical harmonic restraint (k_C = 10 kcal mol⁻¹ Å⁻²) to the fourth nascent-chain residue from the P-site -thereby blocking force transmission through the nascent chain backbone. Spherical harmonic restraints (k_C = 2.5 kcal mol⁻¹ Å⁻²) were applied, to those ribosomal C_α, P, and O atoms that were within 5 Å of the edges of the cropped ribosome. As before, a planar restraint was applied to the C_α atom of the reporter cysteine and a system temperature of 350 K and an integration time step of 0.002 ps were used in the production simulations. For each RNC, ten independent trajectories were simulated for 200 ns of simulation time. XSEDE’s Stampede cluster was utilized to run all the production simulations in NAMD.⁶³

Coarse-grained model

The coarse-grained simulation model of the RNC, consisting of 14,250 interaction sites, was prepared as previously described³². In this model residues are represented by a single interaction site, while three and four interaction sites represent the pyrimidines and purines, respectively. Interaction sites representing positively charged residues were assigned a +1e charge, and interaction sites representing negatively charged nascent chain residues and nucleotide phosphate groups were assigned a −1e charge. The large ribosomal subunit was cropped by removing ribosomal beads that were more than approximately 30 Å away from the long-axis of the exit tunnel. Ribosomal interaction sites surrounding the tunnel opening were maintained (Fig. 4a). This cropped ribosome contains 3,875 interaction sites. Eight coarse-grained starting structures were prepared; one for each nascent chain of the 95- and 190-residue RNCs.

The coarse-grained force field consists of five energy terms representing bonded and non-bonded interaction terms. The total potential energy for a given system configuration is E_total = E_bond + E_angle + E_dihedral + E_{electrostatic} + E_{Lennard−Jones}, i.e., the sum of terms representing virtual bond, bond-angle, and dihedral fluctuations, and electrostatic and van der Waals interactions. The standard CHARMM functional forms⁵⁷ were used for each term. All five terms are fully transferable between different nascent protein sequences. As previously described³², we use a double-well bond-angle term that captures the different characteristic bond angles associated with α and β secondary structure, a dihedral potential that is sequence specific, electrostatic interactions modeled using Debye-Huckel theory with a Debye length of 10 Å and a dielectric constant of 78.5, the 12-10-6 Lennard-Jones potential⁶⁴ to describe solvent separated minima between chemical moieties, and Lennard-Jones parameters reported in Ref. 32 that are proportional to the experimentally measured partial molar volumes of individual amino acids. The force field does not include bonded terms for ribosomal interaction site, since the interaction sites representing the ribosome were fixed during the simulations (see below).

Langevin dynamics simulations

To maintain the reporter cysteine at the experimentally measured position in the tunnel (Table 2), two classes of coarse-grained simulations were run. The first included a harmonic restraint on the C-terminal bead of the nascent chain (k_C = 10 kcal mol⁻¹ Å⁻²) to keep it at the P-site and a planar, harmonic restraint (k_C = 2.5 kcal mol⁻¹ Å⁻²) on the reporter cysteine to keep it at the correct distance from the P-site. Additionally, the planar restraint on the reporter cysteine allowed the reporter cysteine to sample the ribosomal exit tunnel orthogonal to the long-axis of the tunnel. These simulations were used to calculate the pulling force experienced at the C-terminal bead of the nascent chain. The second class of coarse-grained simulations imposed spherical harmonic restraints (k_C = 10 kcal mol⁻¹ Å⁻²) on both the reporter cysteine and C-terminal bead of the nascent chain. This class of simulation was used to determine if all of the force due to an increase in nascent chain length is transmitted to the P-site of the ribosome.

Ten independent Langevin dynamics simulations were run for each of the arrested RNCs, each containing either the truncated 32- or 33-residue C-terminal portion of the nascent chain. SHAKE⁶² was applied to all virtual bonds. The Langevin equation of motion was integrated every 15 fs and the temperature was set to the experimental temperature of 295 K. The collision frequency of the system was set to 0.005 ps⁻¹ and each trajectory was run for 30 μs of simulation time.

Calculating the magnitude of the pulling force on the P-site residue and reporter cysteine

Post-simulation analysis of the average harmonic force, 〈|F_k|〉, acting on the C_α atom or coarse-grained bead of the P-site residue or reporter cysteine in the nascent chain was computed as

$$\langle \left|F_k\right|\rangle =\frac{1}{N_{\mathrm{T}}{N}_{\mathrm{S}}}{\displaystyle {\sum }_{i=1}^{N_{\mathrm{T}}}{\displaystyle {\sum }_{j=1}^{N_S}\left|F_k\left(i,j\right)\right|}},$$ (2)

where N_T and N_T are, respectively, the number of independent trajectories and saved structures from each trajectory, and |F_k(i, j)| is the magnitude of the force acting on site k in trajectory j of structure j. $\left|F_k\left(i,j\right)\right|=\sqrt{f_{\mathrm{x}}^2\left(k,i,j\right)+f_{\mathrm{y}}^2\left(k,i,j\right)+f_{\mathrm{z}}^2\left(k,i,j\right)}$, where f₁(k,i, j) is the l^th force component from the harmonic restraining potential acting on site k in the j^th structure of the i^th trajectory. The difference in the magnitude of the pulling force upon doubling the nascent-chain length was calculated as

$$\mathrm{\Delta }\langle \left|F_k\right|\rangle ={\langle \left|F_k\right|\rangle }_{190}-{\langle \left|F_k\right|\rangle }_{95}$$ (3)

where 〈|F_k|〉₁₉₀ and 〈|F_k|〉₉₅ are, respectively, the average harmonic force arising from the 190- and 95-residue RNCs. f_x, f_y, and f_z denote the x, y, and z components of the force due to the harmonic restraining potential. The trajectory facility in CHARMM was used to extract the time series of force components f_x, f_y, and f_z from the trajectories.

Control experiment on force attenuation in the coarse-grained model

To evaluate the ability of our coarse-grained model to capture the phenomenon of force attenuation, we carried out an in silico positive control. We introduced a strong attractive interaction (a Lennard-Jones well-depth of −80 kcal/mol) between a phenylalanine residue of the nascent chain (14 residues from the P-site) and a guanine nucleic acid (residue 443 in PDB ID: 4LNT) lining the ribosome tunnel wall, tightly binding the nascent chain to the wall. We predicted that in this test the pulling force experienced by reporter cysteine due to an increased chain length should not be transmitted to the P-site. For 10 independent simulations at 295 K, we find there is no difference in the force experienced by the C-terminal residue when the nascent chain is 95 or 190 residues in length (−0.18 pN, 99% CI: −0.84 pN to 0.47, 2-sample t-test, p = 0.49). Thus, this coarse-grained model can detect attenuation of force transmission when it occurs.

Classical Dynamics

To simulate peptide bond formation we inserted a tRNA-bound alanine into the A-site of our ribosome structure by first aligning the tRNA-bound alanine to the orthodox A-site region of the ribosome. Then, successive minimizations on the tRNA-bound alanine were performed and the system was equilibrated in the NPT and NVT ensembles. Starting with the final structures obtained from aforementioned all-atom simulations, classical NVT Langevin Dynamics was performed for two 3Ala10 RNC conformations defined by harmonically restraining PTC-reporter cysteine distances to values obtained experimentally (e.g., 85.8 Å and 92.0 Å, see Table 2). Periodic boundary conditions were applied with image updating on only the waters and ions, and a rectangular box of size 123.358 × 62.754 × 76.704 Å was used. van der Waals interactions between 8 Å and 10 Å were gradually switched off⁶⁵, and electrostatics were calculated with the Particle Mesh Ewald (PME)^66,67 approach using a fast Fourier transform grid of 150x100x100, k=0.33 Å⁻¹, and a real-space cutoff of 12 Å. Three 1.5 ns simulations, each beginning with a different random velocity seed, were carried out for both the 95- and and 190-residue 3Ala10 RNC conformations. Each simulation had a time step of 2 fs, a collision frequency of 0.05 ps⁻¹, and a temperature of 295 K. In addition to restraining the PTC-reporter cysteine distance, position restraints were applied to the heavy atoms of the ribosome (i.e., not the nascent chain). All restraints had a force constant of 2.5 kcal/mol*Ų and SHAKE⁶⁸ was applied to all hydrogens. Simulations were performed using the domain decomposition module available in CHARMM for the sake of expediency⁶⁹.

RESD Minimizations

QM/MM calculations were performed on the 3Ala10 RNC using AM1 in the MNDO97 module available in CHARMM^57,70,71. The QM region consisted of 82 atoms (Fig. 6A, with 3 link atoms placed between the carbonyl carbon and C_α of the Arg one residue removed from the P-site, the A-site sugar and phosphate group, and the P-site sugar and phosphate group. QM/MM electrostatics for link atoms were removed and all electrostatic calculations were performed using QM/MM PME in a manner identical to the classical setup previously mentioned using a k-vector setup of 40×20×25. Extended Lagrangian Born-Oppenheimer molecular dynamics with dissipation^72,73 using a 9^th-order expansion and five SCF steps was used to accelerate SCF convergence in QM/MM calculations. Similar to the classical system, all ribosome heavy atoms were restrained (excluding the QM region). In order to successfully model the eight-membered transition state⁷⁴ of the ribosome mechanism, harmonic restraints between the 8 atoms involved (excluding distances between atoms along the reaction coordinate - i.e. the alanine N, adenosine O3′, and serine carbonyl C) were placed to ensure interatomic distances of at least 2 Å. All hydrogens in the MM region were treated with SHAKE.

QM/MM minimizations

The endpoint structures of the 3Ala10 RNC, from the 1.5 ns classical simulation, were then classically minimized using adopted basis Newton Raphson minimization to within a gradient RMS tolerance of 0.02 kcal/mol. Once this RMS tolerance was achieved, an additional minimization using QM/MM was performed in a similar manner. Upon completion, the distance between the A-site Ala N and the P-Site Ser carbonyl C as well as the P-Site Ser carbonyl C and P-Site adenosine O3′ was calculated. The difference between the two distances (e.g., = d(C,03′) – d(N,C) serves as the reaction coordinate of interest. Using the values from the initial QM/MM minimization, a harmonic restraint was placed on the reaction coordinate with a force constant of 1000 kcal/mol*Ų and another QM/MM minimization was performed. After each minimization the reaction coordinate restraint was increased by 0.1 Å until a reaction coordinate of −1.5 Å was achieved. From this, the systems were driven forward and backwards between a reaction coordinate of −1.5 to 1.5 using minimizations until a smooth potential energy surface was obtained.

QM/MM Dynamics and Free Energies

The coordinates of each step along the last minimization were then used as a starting point for performing QM/MM dynamics of the 3Ala10 RNC (i.e., 3 sets of minimized coordinates for each restrained conformation). Each simulation had an equilibration of 200 ps, a time step of 1 fs, and a production period of 250 ps with a coordinate saving frequency of 25 fs (i.e., 30,000 coordinate snapshots). Each simulation was set up in a manner identical to the QM/MM minimizations, with the exception of the reaction coordinate distance restraint now having a force constant of 250 kcal/mol*Ų. Free energy profiles were generated using multistate Bennett’s acceptance ratio, and 95% confidence intervals were estimated through block averaging^75,76.