Optical Calorimetry in Microfluidic Droplets

Abstract

A novel microfluidic calorimeter that measures the enthalpy change of reactions occurring in 100 µm diameter aqueous droplets in fluoropolymer oil has been developed. The aqueous reactants flow into a microfluidic droplet generation chip in separate fluidic channels, limiting contact between the streams until immediately before they form the droplet. The diffusion-driven mixing of reactants is predominantly restricted to within the droplet. The temperature change in droplets due to the heat of reaction is measured optically by recording the reflectance spectra of encapsulated thermochromic liquid crystals (TLC) that are added to one of the reactant streams. As the droplets travel through the channel, the spectral characteristics of the TLC represent the internal temperature, allowing optical measurement with a precision of ≈6 mK. The microfluidic chip and all fluids are temperature controlled, and the reaction heat within droplets raises their temperature until thermal diffusion dissipates the heat into the surrounding oil and chip walls. Position resolved optical temperature measurement of the droplets allows calculation of the heat of reaction by analyzing the droplet temperature profile over time. Channel dimensions, droplet generation rate, droplet size, reactant stream flows and oil flow rate are carefully balanced to provide rapid diffusional mixing of reactants compared to thermal diffusion, while avoiding thermal “quenching“ due to contact between the droplets and the chip walls. Compared to conventional microcalorimetry, which has been used in this work to provide reference measurements, this new continuous flow droplet calorimeter has the potential to perform titrations ≈1000-fold faster while using ≈400-fold less reactants per titration.

Graphical abstract

A novel microfluidic optical calorimeter that can measure millidegree Celsius temperature changes in sub-nanoliter droplets has been developed.

Introduction

Screening efforts during drug development including high-throughput screening (HTS) have historically relied on binding assays using labelled (fluorescent, radioactive) reporter constructs or enzymatic assays using labelled substrates. Artefacts associated with labelling have led to the erroneous identification of compounds that act on the labelled substrate rather than the intended target¹. Modifications of the ligand or substrate can sometimes have adverse effects on binding/catalysis², leading to false positives / false negatives. For example, in the case of sirtiun 1 (SIRT1), a deacetylase and potential cancer therapeutic target, activators were identified that interact with the fluorophore on the substrate rather than with the enzyme^{1, 3–5}. In cases such as these, the availability of a label-free primary screening assay would prevent delays in identifying the desired compounds – potentially resulting in a significant reduction in overall drug development costs. A label-free, solution-based HTS method would facilitate identification of compounds acting specifically on the intended targets and eliminate the substantial assay development work associated with labelled ligands and substrates.

Isothermal titration calorimetry (ITC) is a powerful label-free solution based technique for characterizing biochemical interactions, including enzymatic reactions, ligand binding, and organelle and cellular activity. Calorimetry directly measures the heat evolved or absorbed during a reaction, and a calorimetric titration provides a complete thermodynamic characterization by revealing the enthalpy change (ΔH), binding constant (K_d=exp(ΔG₀/RT)), and entropy change (ΔS₀) of reaction^{6, 7}. ITC is used in drug discovery and basic sciences, where its minimal assay development time and label-free aspects are an acceptable compromise⁶ for large sample requirements (≈0.2 mL) and long measurement times (typically 30 min per sample).

With high-throughput calorimeters, as in quantitative HTS (qHTS)⁸, the potency and efficacy of an entire library of candidate molecules could be fully characterized during a screening campaign, in contrast to the limited number of high-value measurements obtainable by ITC. In addition, the binding stoichiometry and, for enzyme activity assays, full enzyme kinetic profile is measured in the presence of each library compound, enabling structure-activity relationships, non-stoichiometric binding, and determination of the mode of inhibition during the primary screen. This potential has led to the development of nanocalorimeters by a number of organizations and research groups as summarized by Torres et al⁹. Enthalpy arrays, for example, have been used to measure binding and enzymatic reactions and to screen for small molecule enzyme inhibitors^10–14. These thermistor-based arrays have a high throughput (100’s of compounds per day) and require low sample quantities (≈1/10th of ITC requirements). However, these arrays are not sufficient to meet the needs of high-throughput screening of libraries containing thousands of compounds due to limitations on sample consumption, sensitivity, and throughput. The work presented here is aimed at closing the gap between the demands on screening technologies in HTS applications and the technological capabilities of calorimeters.

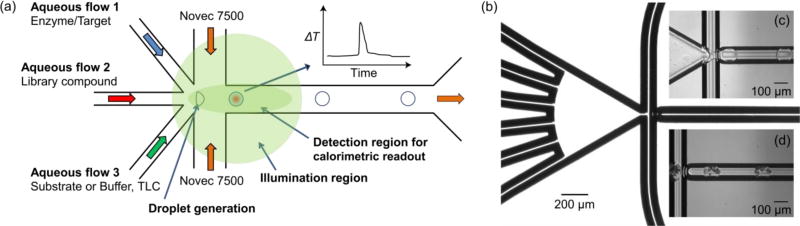
The novel optical calorimeter introduced here (Figure 1) uses microfluidics and an optical readout to achieve orders of magnitude higher sensitivity and throughput with lower sample consumption compared to state-of-the-art nanocalorimeters. This method comprises three key elements: a microfluidic platform to create a drop of mixed target and ligand, a thermochromic material to convert the temperature change to a shift in detection wavelength, and a sensitive wavelength shift detector. Figure 1(a) shows a schematic view of this concept. Inlet channels containing aqueous solutions of a target, a library compound, and a substrate (or buffer) converge at a junction. One or more of these solutions contains a thermochromic reporter compound. At the junction, additional flows of an immiscible fluoropolymer oil (Novec 7500) cause the aqueous phase to split off into discrete aqueous droplets (with a volume ≈500 pL) surrounded by an oil sheath flow in the outlet channel. In addition to facilitating the breakup of the aqueous phase into droplets, the fluoropolymer oil serves as a thermal insulator, maximizing retention of the heat generated by a reaction inside the droplet.

Figure 1.

Microfluidic optical calorimetry. (a) System schematic. Solutions (containing a thermochromic reporter compound) of the target, the library compound from a well plate, and substrate (or buffer) are introduced via aqueous flows 1, 2, and 3 respectively. The aqueous flows merge with a perpendicular flow of fluoropolymer oil (Novec 7500), yielding small volume droplets. The droplets flow through the detection region where the change in temperature due to a binding or enzymatic reaction is measured. In this schematic, only three aqueous streams are shown, but additional inlets were used as shown in (b). (b) Microphotograph of the microchannel network. The six inlets for aqueous streams are on the left and the two inlets for fluorocarbon oil are in the center of the image. Image was acquired using a 4× lens. (c) Bright field microphotograph of droplet generation. The aqueous streams were CaCl₂ on the outer two aqueous inlets, buffer in the middle aqueous inlets, and fluo-4 in the center two aqueous inlets. (d) Bright field microphotograph of droplet generation with thermochromic liquid crystal (TLC) particles encapsulated within the aqueous droplets. The TLC microparticles were included in the buffer stream.

When a binding or enzymatic reaction with a non-zero enthalpy change occurs in a droplet, the droplet temperature changes, causing the thermochromic reporter to change color. This color change is recorded as a function of time using a sensitive wavelength shift detector as the droplet flows through the detection region of the outlet channel. In this semi-adiabatic calorimeter¹⁵, each droplet is a calorimetric vessel. The temperature of the droplet rises (or falls) as the exothermic (or endothermic) reaction occurs, and heat exchange with the surroundings causes the droplet to return to the original temperature at the conclusion of the reaction (Figure 1(a), inset). Using automated sample handling and data analysis routines – required of any HTS system – this approach allows for on-chip titration of compounds delivered with an auto sampler¹⁶ from a compound library. Low sample consumption and the omission of sample containers result in reduced waste and cost while the potential throughput could be as high as 18,000 compounds per day with ≈1,500 relevant concentration data points and appropriate line cleaning cycles.

Experimental setup and sample preparation

Three microfluidic experiments are reported here. First, droplets containing thermochromic liquid crystal (TLC) reporter particles were generated and imaged in order to verify the integrity of the two-phase flow with TLC-containing droplets. Second, the mixing efficiency of small molecules in droplets was assessed using a fluorescent (non-thermal) proxy. Finally, temperature measurements of droplets undergoing a calibrated chemical reaction were carried out. The temperature was measured using an optical readout based on the reflectivity spectra of the TLC.

Thermochromic liquid crystal slurries

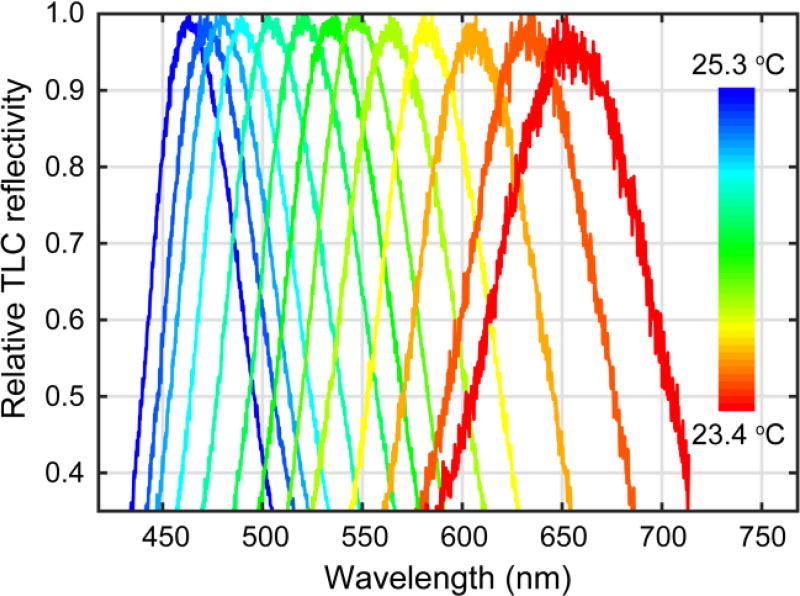
Thermochromic liquid crystals change color in response to a change in temperature. Commonly available as a micro-encapsulated mixture of organic chemicals, these ≈10 µm diameter particles are referred to as “TLCs” throughout this work. Over a range of temperatures referred to as the color play range, the reflectivity peak of a TLC shifts over the visible spectrum (400–700 nm) in response to a change in temperature. As experimentally demonstrated below (Figure 5), this shift can be 200 nm/K or more. Thus a wavelength shift of 0.01 nm, measurable using a commercial spectrometer, corresponds to a temperature resolution of 50 µK. In this study TLCs function as a noncovalent, extrinsic reporter of temperature within a droplet. In contrast to noncovalent extrinsic fluorescent dyes used in protein characterization¹⁷, TLCs, due to their 7–10 µm diameter, do not intercalate with the reactants, limiting any potential interaction between reactants and the surface of the microparticle. To prevent non-specific interaction of reactants with the TLC microparticles, we included the non-ionic detergent Triton X-100 at a concentration (0.015%; w/v) which has been shown to prevent aggregate-based non-specific interactions of compounds with proteins. This non-specific interaction occurs via adsorption of proteins on the surface of aggregates and is reversed by Triton X-100¹⁸. Other label free methods of temperature sensing, for example the use of thermal cameras, are currently limited in their sensitivity to approximately 20 mK (e.g. Flir T1k/T1020), which is not sensitive enough to measure the sub-mK temperature changes associated with a binding or enzymatic reaction. Temperature transducers such as fluorescent ratiometric thermometers, fluorescent proteins, quantum dots, or nanodiamonds, also lack sufficient resolution^19–21. In summary, to the best of our knowledge, TLCs are the only temperature transducer to satisfy the requirements of (1) a contact free read-out, (2) resolution below 1 mK, and (3) an appropriate size, all of which are required to measure small temperature changes within sub-nanoliter aqueous droplets.

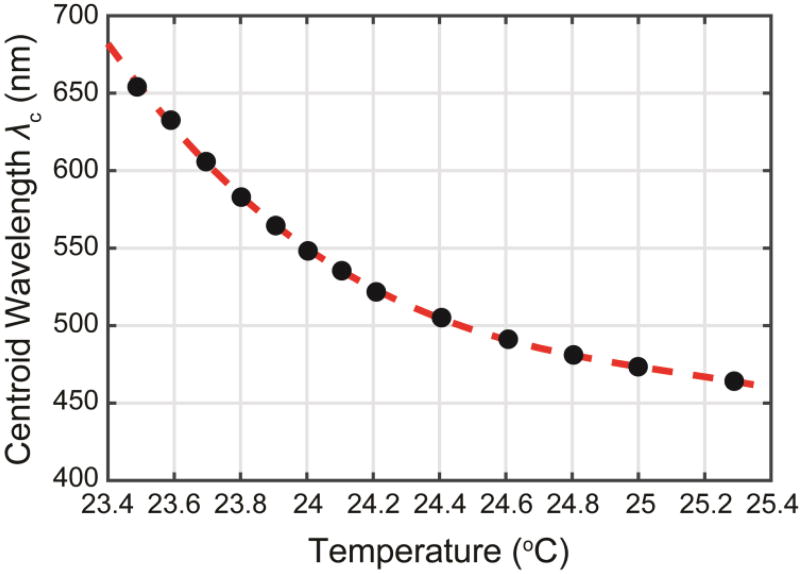
Figure 5.

Measured centroid wavelength λ_c of the TLC reflectivity (black filled circles) vs chip temperature and polynomial fit from Eq. 6 (red dashed line).

Microencapsulated chiral nematic TLCs were purchased from LCR Hallcrest (Glenview, IL) as a 40% (w/w) slurry. For the specific formulation used here (R24C1W; lot number 160712-6), Hallcrest specified the following color play range: Red start = 23.9°C; green start = 24.2°C; and blue start = 24.5°C.

Aqueous slurries of TLCs (10% (w/w)) were prepared in Milli-Q water containing 0.015% (w/v) Triton X-100 and filtered through a 20 µm nylon net filter (Millipore Sigma). For use in droplets, this slurry was diluted to 4% (w/w) in the appropriate buffer containing 0.015% (w/v) Triton X-100 and filtered again through 20 µm nylon net filter. The average TLC particle size after filtration was 7 µm.

The TLCs were not expected to have a significant effect on the thermal mass of the droplets. Both the density (approximately 1.02 g cm⁻³)²² and heat capacity (3.1 kJ kg⁻¹ K⁻¹)²³ of the microencapsulated TLC were similar to water. At the concentration used in this work, they represented ≤2% of the mass of the droplet, so we did not anticipate large perturbations of the thermal mass of the droplets due to presence of the TLCs.

Microfluidic droplet generation

The microfluidic devices were custom fabricated by Dolomite Microfluidics. The chips (22.5mm long × 15mm wide × 4mm thick) were fabricated in glass and treated with a fluorophilic coating.

To form monodisperse aqueous droplets in a fluorocarbon oil (Novec 7500), a flow-focusing geometry²⁴ consisting of six aqueous inlets and two oil inlets was used (Figure 1(b)). Up to three different aqueous streams were flowed into the chip and into the droplet-forming junction: one containing CaCl₂, the second, optional, stream containing buffer, and the third containing EDTA and TLC. The flow rates were varied to produce droplets 100 µm in diameter at a rate of 200–1,000 Hz (Figure 1(b)). This was achieved by flowing the combined aqueous streams at 6–22.5 µL min⁻¹ and the oil stream at 37.3 µL min⁻¹ through the outlet of the droplet-forming junction.

Flow through the channels was driven by three separate pressure pumps (Mitos P Pump; Dolomite Microfluidics) using closed-loop flow control. One pump drove the flow of the continuous phase (Novec 7500), the second drove the flow of two aqueous streams (reactant 1 and buffer, if present), and the third drove the flow of the aqueous dispersion of TLC microparticles (with or without EDTA). All pump commands and status queries were controlled using Flow Control Centre software (Dolomite Microfluidics).

Experiments to characterize droplet formation were performed on an inverted microscope (Nikon TE2000) using a 4× or 10× objective, and images were captured using a high sensitivity CCD camera with an exposure time of 10 µs exposure (Retiga EXi; QImaging) (Figure 1).

Mixing in droplets

The mixing rate was assessed via the non-thermal measurement of the binding of Ca²⁺ ions to the calcium sensitive dye fluo-4²⁵. The fluorescence of fluo-4 increases more than 100-fold upon the rapid (≈10⁹ M⁻¹ s⁻¹)^{25, 26} binding of Ca²⁺. An aqueous stream containing 5 mM CaCl₂ was combined with an aqueous stream containing buffer and an aqueous stream containing 54 µM fluo-4, and the increase in fluorescence in the resulting droplets was recorded as a function of time. All reagents were prepared with MilliQ water and dissolved in 20 mM MOPS pH 7.2, and both the buffer-only and fluo-4 samples contained 1 mM EDTA. The buffer stream containing 1 mM EDTA was included to minimize fluorescence generation due to binding of fluo-4 to any trace divalent metal ions present in the buffer. Experiments were performed on an inverted microscope (Nikon TE2000) using a 4× objective and images (2 s exposure) were captured using a high sensitivity CCD camera.

The relative normalized intensity of fluorescence as a function of distance travelled by the droplets was obtained from images such as the one shown in Figure 6 using ImageJ software for image processing. The mixing time was calculated based on the time required to travel a given distance based on linear velocity in the exit channel at a given flow rate. Flat-field correction (https://imagej.net/Image_Intensity_Processing) was used to correct for uneven illumination. An image (2 s exposure) of a slide with fluo-4 premixed with CaCl₂ covering the entire field of view was used as the “flat-field” reference image.

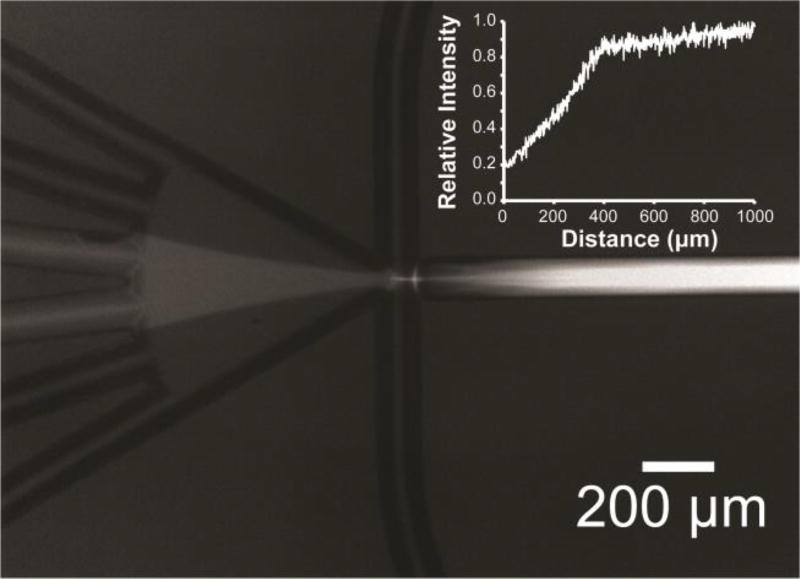
Figure 6.

Microphotograph (2 s exposure, individual droplets are invisible) showing time-averaged fluorescence arising from mixing inside droplets formed by combining equal volumes of CaCl₂ (5 mM), EDTA (1 mM), and Fluo-4 (54 µM), in MOPS (20 mm, pH 7.2). Aqueous streams were in the same configuration as described in Figure 1. Inset: Relative normalized intensity (I) of fluorescence obtained from images as a function of distance travelled by the droplets.

Detection of reflectance spectra

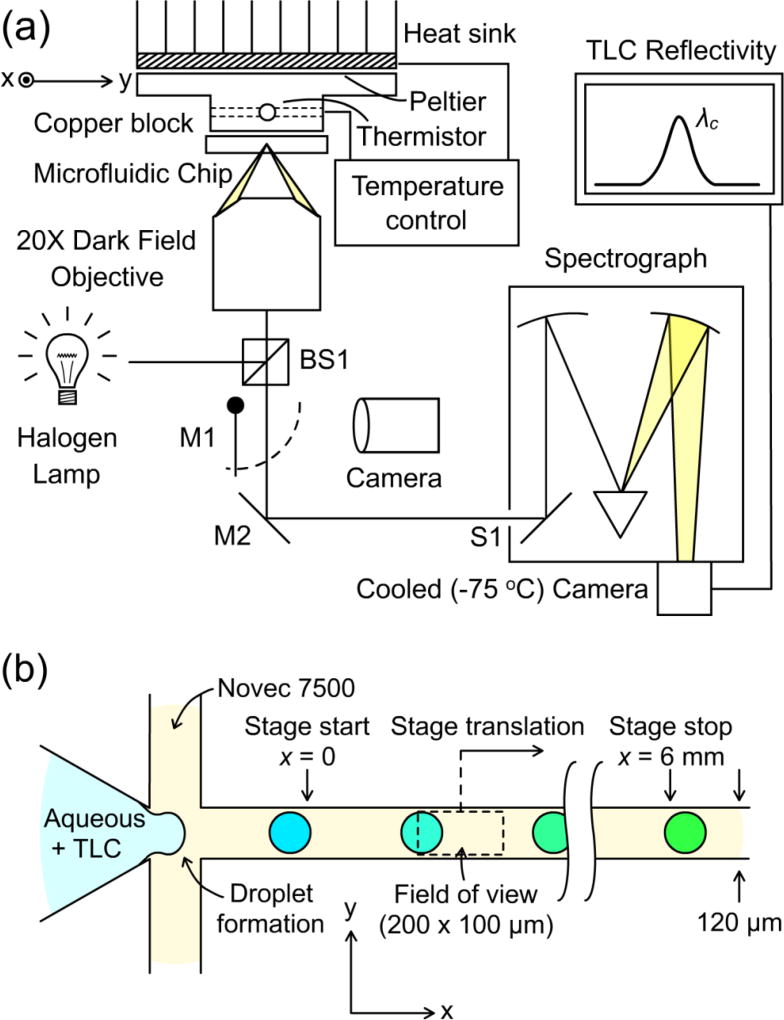
Reflectance spectra of TLC-containing droplets were measured using an inverted microscope (Leica DMI 3000M) along with a grating spectrograph (Princeton Instruments Acton SP2300, Figure 2). The chip was illuminated in dark field using a 100 W halogen lamp, and the optical power at the sample plane was measured to be approximately 500 µW. Light reflected from the chip was collected by a 20× objective (NA = 0.4) and was directed to the input slit, S1, of the spectrograph. Alternatively, a flip mirror, M1, directed the chip image to the microscope eyepiece to ensure that the outlet channel was in focus and centered in the sample plane. The chip was oriented such that the long axis of the outlet channel aligned with the long axis of input slit S1 on the spectrograph. This slit was adjusted to restrict the field of view to a 200 × 100 um region (Figure 2b), ensuring that no more than one droplet was imaged at a given time. A blazed grating with 300 lines/mm was used in the spectrograph. The grating resolution and blaze wavelength (500 nm) were chosen in order to capture the full range of TLC colors (400–750 nm) on the spectrograph’s detector, a Pixis 100 camera cooled to −75°C. All control commands and image capture commands were performed using Lightfield software (Princeton Instruments). The total power incident on the spectrograph camera was approximately 180 pW, and spectra were acquired using an exposure time of 100 ms.

Figure 2.

Experiment to track the temperature shift of picoliter droplets undergoing a chemical reaction by measuring shifts in the spectral reflectivity of TLC reporter particles. (a) Light from a halogen lamp is directed to a microfluidic chip using beamsplitter BS1 and focused onto the outlet channel using a 20× dark-field objective. Scattered light from the sample returns through BS1 and is directed either to the input slit S1 of a spectrograph using mirror M2 or to a camera using flip mirror M1. (b) Detailed schematic top view of the chip’s outlet channel. Aqueous droplets pinch off in a fluoropolymer oil sheath flow and move down the outlet channel at a rate of 70–80 mm/s. Scattered light is collected from a field of view of 200 × 100 µm. By translating the chip along the × direction and detecting the TLC color as in (a), snapshots of the temperature throughout the ongoing reaction are acquired. The color shift is exaggerated for clarity.

Temperature stabilization

The baseline temperature of the experiment was controlled by placing the fluidic chip in contact with a thermal block (Figure 2) made of copper. The interface between the thermal block and the fluidic chip was coated in a carbon black (optically absorbing) conductive thermal paste to reduce background reflections from the copper surface. The temperature of the block was adjusted using a Peltier plate on the top side of the block. A heat sink on the top side of the Peltier provided excess heat rejection to the environment. A 10 kΩ thermistor inserted into a pre-drilled hole in the block provided a readout of the block temperature. Using the thermistor in combination with the Peltier element, the block temperature was regulated using a Thorlabs TED 200C benchtop temperature controller. With the controller feedback engaged, the observed stability of the thermistor resistance (< 1 Ω) implied a temperature stability of the thermal block to within 2 mK of the set point.

The thermal block was used to equilibrate all fluid components to a common, adjustable temperature set point. The stability of this scheme was experimentally verified by perturbing the temperature of the input oil lines by placing them in contact with an ice block or by heating them with a heat gun. No change in the optically measured temperature was observed under such conditions. This stability was theoretically justified based on a comparison between the thermal diffusion time for each fluid and the residence time of the fluids in the chip before droplet formation. The 1/e thermal diffusion time t_eq,i of fluid i with the chip was estimated based on simple diffusion: t_eq,i ≈ r²/D_i, where r = 60 µm was the channel radius and D_i was the thermal diffusivity of fluid i. Diffusivity D_i was calculated using D_i = K_i/ρ_ic_pi, where K is the thermal conductivity, ρ is the density, and c_p is the heat capacity at constant pressure, using the thermal properties in Table 1. The thermal properties of the dilute aqueous solutions were approximated as those of pure water. From this calculation the thermal diffusion times for the aqueous reagents and Novec 7500 were found to be 25 ms and 100 ms, respectively, compared to a residence time of 1400 ms and 380 ms in the chip before the droplet forming region. Thus for both fluids the residence time was more than 3 diffusion times. This theoretical analysis, along with the experiments described above, led us to conclude that both fluids were well equilibrated with the chip at a temperature close to the set point of the copper block.

Table 1.

Relevant thermal properties of the aqueous and oil fluid components flowing through the microfluidic chip

Property	Value	Units	Description
Tref	25	[°C]	Reference temperature
KNovec	0.06477	[W/m*K]	Thermal conductivity of Novec 7500 at Tref
Kw	0.607	[W/m*K]	Thermal conductivity of water at Tref
CpNovec	1128.455	[J/kg*K]	Specific heat capacity of Novec 7500 at Tref
Cpw	4138	[J/kg*K]	Specific heat capacity of water at Tref
ρNovec	1613.6875	[kg/m3]	Density of Novec 7500 at Tref
ρw	997	[kg/m3]	Density of water at Tref
Vdroplet	520	[pL]	Droplet volume

The total energy generated in a droplet by the chemical reactions discussed below was around 1 µJ. In comparison, the illumination energy absorbed by a droplet passing through the field of view was less than 10⁻⁴ µJ, or 0.01% of the reaction energy. The remaining energy from the illumination was absorbed in the carbon black thermal paste and rapidly conducted into the copper block. Thus we expect that the effect of lamp heating was insignificant at the illumination power used in this experiment.

Calculating TLC reflectivity

The reflectivity of a TLC-containing droplet in the microfluidic chip had two additive contributions: a temperature-dependent reflectivity r_TLC(λ) from the TLC and a background component r_bg(λ) from specular and diffuse reflections at the channel walls and other chip interfaces. The measured reflection spectrum S_TLC was the product of the summed reflectivity and the lamp spectrum s(λ):

$${\mathit{S}}_{\mathit{\text{TLC}}}(\mathit{\lambda })=({\mathit{r}}_{\mathit{\text{TLC}}}(\mathit{\lambda })+{\mathit{r}}_{\mathit{\text{bg}}}(\mathit{\lambda }))\mathit{s}(\mathit{\lambda })$$ Eq. 1

Two reference measurements were carried out in order to calculate the TLC reflectivity alone. First, a spectrum S_bg(λ) was measured with the TLC flow shut off, such that only the background reflectivity was acquired (Eq 2).

$${\mathit{S}}_{\mathit{\text{bg}}}(\mathit{\lambda })={\mathit{r}}_{\mathit{\text{bg}}}(\mathit{\lambda })\mathit{s}(\mathit{\lambda })$$ Eq. 2

Second, the sample was replaced by a Teflon block with the property that r_tef(λ) ≈ r_tef, i.e., the reflectivity was independent of wavelength. The spectrum S_tef(λ) measured under these conditions was thus a scaled version of s(λ), given by:

$${\mathit{S}}_{\mathit{\text{tef}}}(\mathit{\lambda })={\mathit{r}}_{\mathit{\text{tef}}}\mathit{s}(\mathit{\lambda })$$ Eq. 3

From Eq. (1–3) it can be shown that:

$${\mathit{r}}_{\mathit{\text{TLC}}}(\mathit{\lambda })={\mathit{r}}_{\mathit{\text{tef}}}\frac{{\mathit{S}}_{\mathit{\text{TLC}}}(\mathit{\lambda })-{\mathit{S}}_{\mathit{\text{bg}}}(\mathit{\lambda })}{{\mathit{S}}_{\mathit{\text{tef}}}(\mathit{\lambda })}$$ Eq. 4

Figure 4 shows examples of r_TLC(λ) measured at various temperatures. In general, r_TLC(λ) is peaked around the centroid wavelength λ_c of the reflectivity distribution. The centroid wavelength λ_c is given by:

$${\mathit{\lambda }}_{\mathit{c}}=\frac{{\int }_{{\mathit{\lambda }}_{\mathit{i}}}^{{\mathit{\lambda }}_{\mathit{f}}}\mathit{\lambda }{\mathit{r}}_{\mathit{\text{TLC}}}(\mathit{\lambda })}{{\int }_{{\mathit{\lambda }}_{\mathit{i}}}^{{\mathit{\lambda }}_{\mathit{f}}}{\mathit{r}}_{\mathit{\text{TLC}}}(\mathit{\lambda })}$$ Eq. 5

Figure 4.

Relative TLC reflectivity measured for chip temperatures between 23.4–25.3 °C.

where λ_i and λ_f define the wavelength range measured by the spectrometer, around 410-720 nm. The temperature dependence of the TLC reflectivity was summarized by the dependence λ_c(T) of the centroid of the reflectivity distribution on temperature T (Figure 5). This calibration enabled calculation of the time and concentration dependent temperature development of a droplet, based on the measured reflectance spectrum.

Tracking reaction progress

To measure the dynamic temperature evolution in droplets, the TLC temperature was sampled along the length of the outlet channel. This sampling was achieved by scanning the field of view along the direction of the outlet channel (Figure 2(b), × direction). Starting from a reference position x = 0 just after the region of droplet formation, the microscope stage was moved by a total displacement of 6 mm along the outlet channel. Scanning was accomplished by fitting the stage with a stepper motor (Nema 17) which moved the stage continuously at a rate of 330 µm/s. At 200 points along the channel a reflectance spectra was measured, and a reflectivity centroid wavelength λ_c was calculated as described above. From λ_c, the TLC temperature was calculated using the measured T to λ_c calibration in Figure 5. During the exposure time of 100 ms, 17–20 droplets passed through the field of view, and the measured reflectivity at each point was the sum total of the reflectivity of this small group of droplets. The next exposure captured the spectrum of a different group of droplets at a location further along the channel due to the motion of the stage. In this manner, the average droplet temperature as a function of × was built up as a series of snapshots along the outlet channel. The total time to scan the outlet channel was about 20 seconds. From the droplet position × (0–6 mm) along the channel and the known droplet velocity v (70–80 mm/s), the local droplet time t was determined as t = x/v. The time for a given droplet to go from x = 0 to x = 6 mm was 80–90 ms. In summary, the temperature of droplets as a function of time was measured by scanning the field of view along the outlet channel while acquiring the droplets’ spectra and using measured calibration data to infer the droplet temperature and local time.

Isothermal titration calorimetry (ITC)

Microcalorimetric measurements were performed using a commercial isothermal titration calorimeter (MicroCal iTC200; Malvern Instruments Ltd). Binding of CaCl₂ to EDTA was measured at 25°C in 100 mM Tris-HCl (pH 7.5), 0.015% (w/v) Triton X-100. The sample cell (200 µL) contained EDTA (500 µM), and the injection syringe contained 5 mM CaCl₂.

Following an initial injection (0.4 µl), titrations were performed by making 24 injections (1.2 µl each) of CaCl₂ into EDTA to produce an approximate final 2:1 ratio of CaCl₂ to EDTA. Titration data were analyzed with Origin ITC software version 7.0 (Microcal Software Inc.), and curves were fit to a single binding site model⁷. Results reported represent an average of two experiments. The measured thermodynamic parameters were used for the modelling and simulation described below.

Microfluidic optical calorimetry

Optical calorimetry measurements were performed at 23.8°C in 100 mM Tris-HCl (pH 7.5), 0.015% Triton X-100.

In one set of experiments, hereafter referred to as “with spacer”, three different aqueous streams were flowed into the chip: one stream containing 1 M calcium chloride, the second stream containing buffer, and the third containing 4% (w/w) TLC and either 50 mM, 25 mM or 0 mM EDTA, to the drop-forming junction. The flow rates were set to produce 100 µm droplets at a rate of 550 Hz. This was achieved by flowing the combined aqueous streams at 17.5 µL min⁻¹ and the oil stream at 37.3 µL min⁻¹ through the outlet of the droplet-forming junction.

In another set of experiments, hereafter referred to as “no spacer”, two different aqueous streams were flowed into the chip: one stream containing 1 M calcium chloride, and the second containing 4% (w/w) TLC and either 50 mM, 25 mM or 0 mM EDTA, to the drop-making junction. The flow rates were set to produce 100 µm droplets at a rate of 400 Hz. This was achieved by flowing the combined aqueous streams at 12.5 µL min⁻¹ and the oil stream at 37.3 µL min⁻¹ through the outlet of the droplet-forming junction.

Thermal Modelling and Simulation

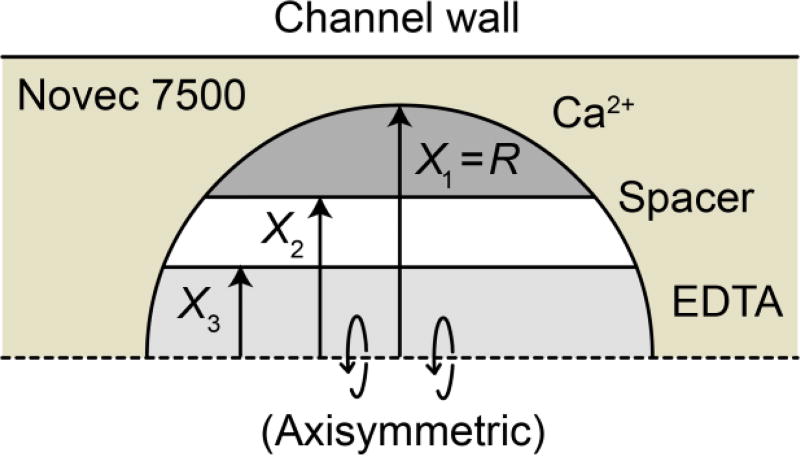
The thermal characteristics of an aqueous droplet surrounded by a carrier oil were modelled in COMSOL. This simulation combined reactant diffusion, heat generation due to the reaction, and heat transfer in a multiphysics model. A single droplet was modelled using a 2-D axisymmetric geometry (Fig. 3). The channel diameter was 120 µm and the droplet diameter was 100 µm, corresponding to the dimensions of the fluidic chip used in experiments

Figure 3.

2D axisymmetric geometry used to model reactant diffusion, kinetics, and heat transfer effects. The axis of rotational symmetry is the dashed horizontal line at X = 0.

The initial condition of the droplet was defined by three layers of aqueous solutions: Ca²⁺, spacer, and EDTA. The droplet was surrounded by Novec 7500 carrier oil. A selection of the thermal properties used in the simulation are listed in Table 1. The radii (X₁, X₂, X₃) defining the thickness of the layers for a given simulation run (Fig. 3) were chosen to match the volume flow rate fraction of reactants used in a given experiment (Table 2). Likewise, the concentration of reactants was chosen to match that used in experiments. A complete list of the parameters used for the multiphysics model is available in the ESI.

Table 2.

Widths of various reactant zones within the drop at t = 0 (formation) used in the COMSOL model.

Flow condition	X1	X2	X3
‘no spacer’	50 µm	33.8 µm	33.8 µm
‘with spacer’	50 µm	37.6 µm	27.9 µm

Outputs of the model included the droplet temperature and reactant concentrations as functions of space and time. The computed droplet temperatures were used for comparison with experimental temperature measurements for the same flow rates & reactant concentrations.

Results and discussion

Droplet size and thermodynamics

The droplet size and generation method were chosen based on a complex trade-off of resolution, throughput, and sample consumption. For a calorimetric measurement to be feasible, it was critical to design the layout of the droplet chip such that the mixing time (τ_mix) for reactants was comparable to or less than the thermal dissipation time constant (τ_dis) of the droplets in the carrier fluid. Otherwise, heat generated by a reaction would rapidly propagate out of the droplet instead of contributing to a temperature increase. Where true adiabatic operation would be described by τ_mix << τ_dis, the condition of τ_mix ≤ τ_dis characterized the droplets as semi-adiabatic reaction vessels.

The droplet size has a significant influence on both τ_mix and τ_dis. While small droplets have smaller diffusion length scales and correspondingly faster mixing times (e.g. t_mix≈2.9ms for a 2 pL droplet), this benefit is outweighed by a significantly shorter τ_dis (≈0.7ms), leading to a violation of the semi-adiabatic condition and corresponding attenuation (>75%) of the temperature signal in binding reactions along with a small steady-state ΔT (0.16 µK) in enzymatic reactions. Conversely, larger droplets such as the 500 nl droplets used in nanocalorimetry use significantly more sample per reaction than standard HTS assays, and these droplets present mixing challenges requiring micro stir bars²⁷. Ultimately, a diameter of 100 µm (volume ≈524 picoliters) was chosen because droplets of that dimension satisfy the following: (1) τ_mix ≈ τ_dis, (τ_dis = 33 ms in 3M Novec 7500, K_Novec =0.065 W/mK; Table 1, t_mix≈45 ms for D=10⁻⁹ m²s⁻¹ and a diffusion length of 10 µm), (2) the calculated temperature shift ΔT for enzymatic reactions was sufficiently large (5 µK, assuming k_cat=10 s⁻¹, ΔH=−5 kcal mol⁻¹, [E]=10 µM), and (3) the sample consumption per titration was less than 10 pmoles. Additionally, this droplet size ensured that both τ_mix and τ_dis were long compared to the thermal response time of TLCs (<5 ms)²⁸. In summary, these and other thermodynamic considerations of heat flow in droplets informed a careful design of the microfluidic layout, enabling an optical temperature measurement with a satisfactory resolution, throughput, and sample consumption.

Mixing in droplets

Fluo-4, which is weakly fluorescent in the absence of calcium, shows a large increase in fluorescence when complexed with Ca²⁺. Because the rate of binding of Ca²⁺ to fluo-4 is rapid, this increase in fluorescence can be used as a quantitative measure of the mixing of Ca²⁺ in droplets²⁵. We obtained a complete time-resolved reaction profile at various flow rates by acquiring a single spatially resolved long-exposure image of the fluorescence²⁵.

Each image was integrated over two seconds to give the average fluorescence intensity of hundreds of droplets (≈ 500 pL in volume) and non-fluorescent Novec 7500 (Figure 6 and ESI). For the flow rate shown here (aqueous 22.5 µL min⁻¹; oil 37.3 µL min⁻¹), a substantial amount (>80%) of fluo-4 was bound to Ca²⁺ within 400 µm, and nearly complete binding (>90%) of fluo-4 to Ca²⁺ in the droplets was achieved within ≈750 µm (Figure 6, inset), which corresponded to a sufficient amount of CaCl₂ mixing with fluo-4 in about 9 ms. At lower aqueous flow rates, some mixing was observed prior to droplet formation (see ESI).

A binding time of 9 ms is far less than would be expected based on the time for Ca²⁺ to diffuse uniformly throughout the droplet (>600 ms). There are two reasons for this difference: first, because the Ca²⁺ was present at a ≈20-fold excess, only a small fraction of the available Ca²⁺ needed to diffuse through the droplet to bind all of the fluo-4. Second, droplets propagating through a straight channel are known to undergo advective mixing^{25, 29}, decreasing the effective length for diffusion and thereby decreasing the mixing time.

As will be shown in the simulation and optical calorimetry sections below, the lack of complete rapid mixing limits the range of reactions that can be measured currently.

Thermal response of the TLC in droplets

As described above, in this optical calorimeter the temperature of a droplet was determined from the color of the TLC in that droplet. More precisely, the measured reflectivity r_TLC(λ) of the TLC was concentrated around the centroid λ_c of the reflectivity distribution (Figure 2), that depended on the temperature^{22, 30}. The temperature of a droplet was inferred from a calibration of λ_c to a set of known temperatures.

To obtain this calibration, droplets containing only TLC and buffer were generated, and the TLC reflectivity was measured as described above for different values of the thermal block temperature (Figure 4). The spectra were each measured 180 s after changing the temperature set point to allow for thermal equilibration of the chip with the thermal block. As the temperature was increased, the centroid of the reflectivity spectrum shifted from red (650 nm) to blue (450 nm) (Figure 4). The centroid wavelength λ_c as a function of temperature is shown in Figure 5. A polynomial fit³¹ to this data provided an approximate relation for λ_c (T):

$${\lambda }_c(\mathit{T})=-\mathbf{29.8}{\mathit{T}}^{\mathbf{3}}+\mathbf{2250}{\mathit{T}}^{\mathbf{2}}-\mathbf{56600}\mathit{T}+\mathbf{475000}$$ Eq. 6

Equation 5 implicitly defines a relation T(λ_c) for the TLC temperature, measured in °C, as a function of the observed centroid wavelength, measured in nm. Thus, it provides the desired calibration of centroid wavelength to droplet temperature.

ITC results

To characterize the thermodynamics of the Ca²⁺-EDTA interaction under the buffer conditions used for the optical calorimetry, measurements were performed using conventional ITC (see ESI for titration data). The binding of Ca²⁺ to EDTA at 25°C yields a K_d of 26 nM, ΔH_obs of −12.1 kcal mol⁻¹, and a stoichiometry of 0.92. The non-ionic detergent appeared to have no significant effect on the thermodynamics of this interaction, as these results are consistent with values reported in the literature for binding of Ca²⁺ to EDTA in Tris (pH 8) in the absence of Triton X-100³².

Simulation and optical calorimetry

Plots of the concentration of EDTA and CaCl₂ versus distance from the center of the droplet at selected times during the simulation are shown in Figure 7a (no spacer) and Figure 7c (with spacer). The initial concentration of EDTA was 50 mM.

Figure 7.

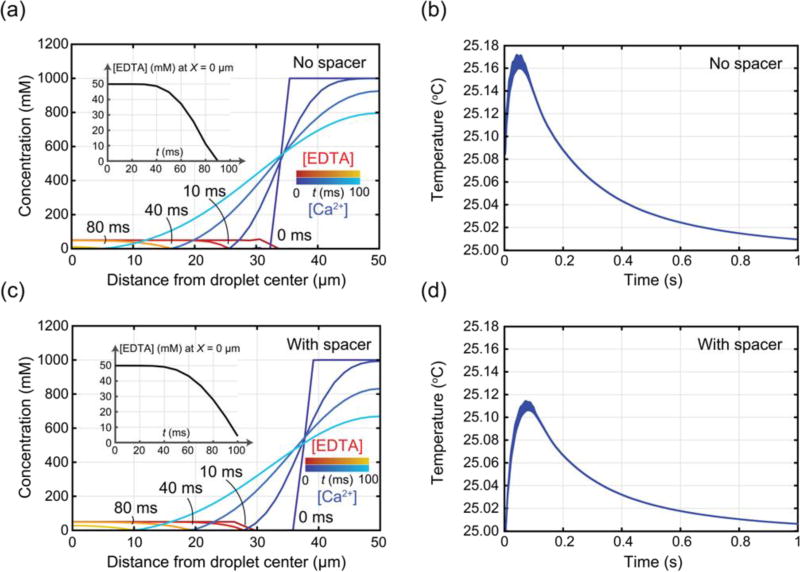
simulation (a) Concentration profiles of EDTA (red-yellow; initial 50 mM) and CaCl₂ (blue-cyan; initial 1 M) over time for the ‘no spacer’ condition (at t = 0, 10, 40, and 80 ms). Inset shows unbound EDTA concentration at the center of the droplet. (b) Temperature evolution inside the droplet over 1 s, with temperature variation along the radius from r = 0 to the surface represented as line thickness, for the ‘no spacer’ condition (initial 50 mM EDTA and 1 M CaCl₂). (c) Concentration profiles of EDTA (initial 50 mM) and CaCl₂ (initial 1 M) over time for the ‘with spacer’ condition (at t = 0, 10, 40, and 80 ms). Inset shows unbound EDTA concentration at the center of the droplet. (d) Temperature evolution inside the droplet over 1 s, with temperature variation along the radius from r = 0 to the surface represented as line thickness, for the ‘with spacer’ condition (initial 50 mM EDTA and 1 M CaCl₂).

In Figure 7a it is clear that the Ca²⁺ is initially present at a large excess around the outside edge of the droplet. As time progresses, Ca²⁺ diffuses, binding the available EDTA along a front that moves from the outside towards the center of the droplet. The inset in Figure 7a shows the concentration of EDTA at the center of the droplet over time, indicating that all of the EDTA is bound by around 90 ms after the start of the simulation. Figure 7c shows the same quantities for the case of a spacer layer between the EDTA and Ca²⁺. The presence of a spacer delays the mixing of Ca²⁺, such that it takes more than 100 ms for all of the EDTA to be bound. In either case – spacer or no spacer – all of the available EDTA is bound long before the reagents have fully mixed across the droplet, which occurs around 600 ms after the start of the simulation. These results confirm through simulation that the use of an excess of Ca²⁺ accelerates the binding of EDTA compared to diffusive mixing alone. The resulting total reaction times of 90–100 ms are compatible with the droplet observation times (90 ms) attainable in the experiment of Figure 2.

Figures 7b and 7d show the simulation results for the droplet temperature as a function of time (blue line) under the same conditions as Figures 7a and 7c, respectively. In both curves, the exothermic binding of Ca²⁺ to EDTA causes a rapid, positive temperature shift above the baseline temperature of 25°C within the first 100 ms. As the droplet is a semi-adiabatic calorimetric vessel, once the reaction is in progress, the droplet begins losing heat to the surrounding carrier fluid and ultimately to the channel walls. The variability in temperature over distance from the droplet center is represented by the line thickness in Figures 7b and 7d, showing that temperature variability within the droplet is below 10% of the overall shift due to the reaction. In the absence of a spacer (Figure 7b), the temperature increases rapidly with the ongoing reaction, achieving a maximum shift of 160 mK at around 47 ms. With the spacer present (Figure 7d) the temperature increases more slowly to a maximum shift of 130 mK, occurring at around 76 ms. The lower magnitude, delayed temperature shift with the spacer is consistent with slower mixing of the reactants in the presence of a spacer. This simulation data demonstrates a positive correlation between the speed of mixing and the resulting temperature change.

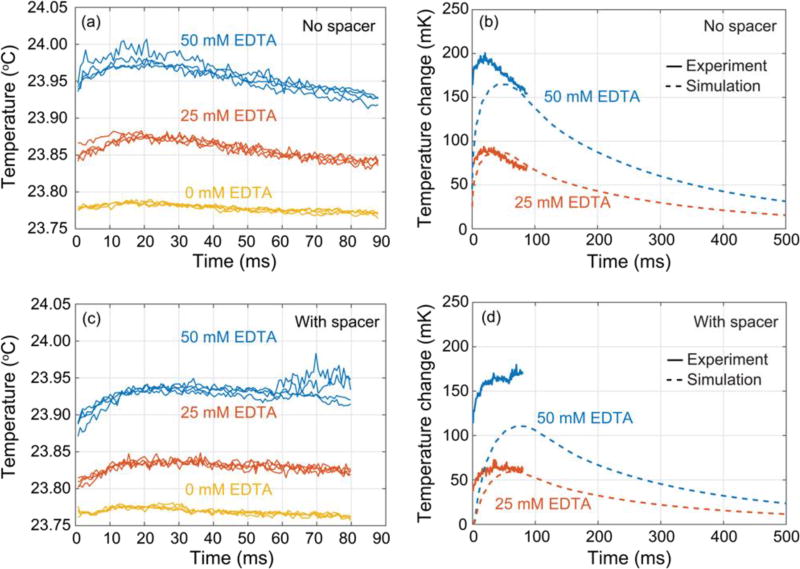
Binding of Ca²⁺ to EDTA was measured using the optical calorimetry technique (Figure 8). The CaCl₂ concentration (1 M) was kept constant. The measured time-dependent temperature data with no spacer flow is shown in Figure 8a for three concentrations of EDTA: 0 mM (yellow), 25 mM (red), and 50 mM (blue). The 0 mM EDTA concentration was included to establish a temperature baseline, as it captured both temperature effects from the dilution of CaCl₂ and also any systematic offsets in the measurement system. The data were highly reproducible across the four replicates measured at each condition.

Figure 8.

(a) Time-dependent temperature measurements for Ca²⁺-EDTA reactions performed under the “no spacer” flow conditions. Each drop contained 200 pmol CaCl₂ and either 0, 7.5, or 15 pmol EDTA (for 0 mM, 25 mM, or 50 mM EDTA respectively). (b) Comparison of optical calorimetry measurements and simulations of expected temperature changes for binding of Ca²⁺ to EDTA at two concentrations for the “NO spacer” flow configuration. The experimental data (solid lines) is shown following subtraction of 0 mM EDTA baseline data. The data shown represents the average of four replicates. (c) Time-dependent temperature measurements for Ca²⁺-EDTA reactions performed under the “with spacer” flow conditions. Each drop contained 140 pmol CaCl₂ and either 0, 5.4, or 10.7 pmol EDTA (for 0 mM, 25 mM, or 50 mM EDTA respectively). (d) Comparison of optical calorimetry measurements and simulations of expected temperature changes for binding of Ca²⁺ to EDTA at two concentrations for the “with spacer” flow configuration. The experimental data (solid lines) is shown following subtraction of 0 mM EDTA baseline data. The data shown represents the average of four replicates.

Several key points are evident from this data: first, the droplet temperature increased above the baseline in the presence of EDTA. Second, the peak temperature increase observed at 50 mM EDTA was about twice that observed at 25 mM EDTA in either the “with spacer” or “no spacer” conditions (Table 3). Together, these features are consistent with a quantitative calorimetric measurement of the exothermic binding of Ca²⁺ to EDTA.

Table 3.

Heat transfer characteristics of droplets, including estimates of the effective thermal conductance and the efficiency of reaction energy contributing to a temperature change of the droplet.

Initial EDTA concentration	Flow configuration	Peak ΔT [K], Experimental	Heat Loss Rate [µW], Model	Effective Thermal Conductance [µW/K]	ΔQloss [nJ], Model	ΔQtot [nJ], Model	Efficiency ηth
25 mM	With spacer	0.058	0.926	15.97	83.34	283.73	71%
25 mM	No spacer	0.075	1.198	15.97	107.82	397.23	73%
50 mM	With spacer	0.16	2.556	15.98	230.04	567.47	59%
50 mM	No spacer	0.18	2.875	15.97	258.75	794.45	67%

Figure 8c shows the temperature measured with a spacer flow. The presence of the spacer reduced the temperature change by 25 mK and delayed the position of the temperature maximum by 5 ms. Figures 8b and 8d show the temperature measurements from Figures 8a and 8c, averaged over the 4 replicates and plotted relative to the 0 mM EDTA baseline along with simulation results for the same conditions. These figures show quantitative agreement between the measured temperature shift and the simulation. This agreement is remarkable in that only the known physical properties of the system were used as inputs – no fitting parameters were employed.

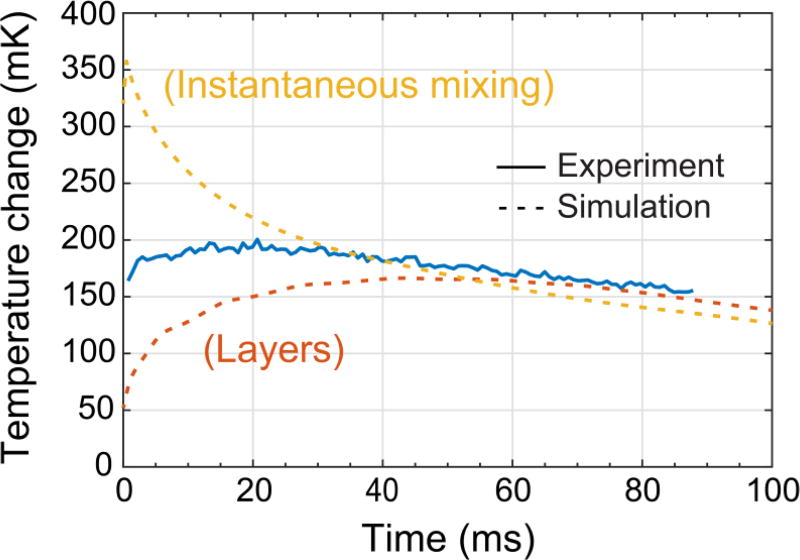
The optical calorimetry measurements consistently show a higher temperature change than the simulations, which suggests that mixing is faster in the droplets compared to the pure diffusion model used in the simulations. This discrepancy is especially pronounced in the case of a spacer flow where for [EDTA] = 50 mM the measured temperature shift significantly exceeds the simulation by 50 mK. A way to resolve this discrepancy is to recognize that the diffusive mixing assumed in the simulation represents a lower bound on the mixing rate. Advective flows induced in microfluidic droplets propagating through a channel are known to mix the droplet contents more rapidly than diffusion alone³³. In this experiment, such mixing would lead to an increase in the measured temperature shift. These flows are difficult to simulate in detail, so one way to understand the influence of convective mixing was to simulate the best case droplet with “instantaneous” mixing where the EDTA and CaCl₂ were evenly distributed across the drop at their final fully mixed concentrations at t= 0 (30 mM EDTA, 400 mM CaCl₂ in the “no spacer” case). Figure 9 shows a comparison of three curves: (1) the experimental temperature measurement (50 mM EDTA, “no spacer”), (2) the simulated temperature for mixing within the droplet occurring via diffusion between layers of reactants, and (3) the simulated temperature for instantaneous mixing. The experimental temperature data lies between the pure diffusion and the instantaneous mixing simulations. This suggests that the actual effectiveness of mixing in the droplet falls somewhere between these two extremes and also suggests that the temperature shift could be increased by improving the mixing.

Figure 9.

Comparison of optical calorimetry measurement (“no spacer”; 15 pmol EDTA) with simulations for mixing within the droplet occurring between layers of reactants or instantaneous "perfect" mixing.

Estimating the thermal conductance and efficiency

A stand-alone thermal model was implemented in COMSOL to study the heat transfer characteristics of the carrier fluid under the experimentally observed temperature differentials. The heat loss rates required to explain the observed temperature differences are summarized in Table 3. In all experimental configurations, the effective thermal conductance was found to be about 16 µW K⁻¹. Given the surface area of a 100 µm diameter droplet is 3.14×10⁻⁸ m², the overall heat transfer coefficient at the drop surface was 509 W m⁻² K⁻¹, which is in good agreement with the expected value of the heat transfer coefficient between water and fluoropolymer oil in this geometry^{34, 35}.

To estimate the efficiency η_th with which reaction enthalpy contributed to droplet heating, the reaction heat ΔQ_loss lost to the carrier fluid during the 90 ms measurement time was estimated based on the heat loss rates in Table 3. Next, the overall reaction enthalpy change ΔQ_tot in a droplet was calculated based on the starting quantity of EDTA and the known reaction enthalpy. Finally, the efficiency was calculated as η_th = 1− ΔQ_loss/ΔQ_tot. From this calculation it was estimated that about 60% – 70% of the energy released in a binding reaction was retained in a droplet during the 90 ms observation timeframe (Table 3). This relatively high value of η_th is favorable for calorimetric measurements in droplets: most of the reaction enthalpy goes to heating the droplet.

Estimating the calorimeter resolution

The calorimeter resolution was 6 mK, defined as the interval containing 95% of the temperature noise in the 0 mM EDTA baseline measurement (Figure 8 a, c). Referring to the procedure described in “Tracking reaction progress”, this minimum detectable temperature shift (MDTS) was the smallest measurable difference between the average temperature of subsequent groups of 17–20 droplets passing through the detection region during the 100 ms exposure time. From the thermal properties in Table 1, the heat ΔQ required to adiabatically increase the temperature of a droplet by 6 mK was ΔQ = C_pw ρ_w V_droplet (6 mK) = 13 nJ. From the ≈70% efficiency calculated above, the minimum measurable average heat difference between groups of droplets was thus around 20 nJ in a 100 ms integration time. This energy resolution and integration time are the first benchmarks of throughput and sensitivity of a TLC-based droplet microfluidic calorimeter. Notably, this resolution is on the same order as commercial ITC systems and ≈10-fold better than most nanocalorimeters³⁶ while using a reaction volume 1–4 orders of magnitude smaller.

Two primary improvements are necessary for this scheme to function as a practical HTS tool: the MDTS must be reduced, and the droplet measurement time must be increased. The MDTS must be reduced by a factor of at least 30, from 6 mK to 200 µK, in order to detect the temperature changes from binding reactions of biomolecules at relevant concentrations (10–20 µM). Improvements to the MDTS can be achieved through at least three means, which may be used in combination. First, it has been shown that the color play range of TLC’s is compressed by a factor of 10 or more when the illumination and collection paths are oriented at 90° when compared to normal incidence²². Thus the TLC temperature sensitivity dλ_c/dT can be enhanced by this same factor by orienting the illumination/collection optics at 90°. Second, the received power in this work was low (180 pW), because the system was assembled using a general purpose microscope that prioritized image formation over light collection efficiency. A specialized optical system could deliver more light to the sample plane while also collecting a greater fraction of the light scattered from TLCs. For example, in the detector noise limited case, an increase in the received power to 1 nW would improve the MDT by up to a factor of 5×. Finally, a component of the observed temperature noise may have been due to droplet-to-droplet variability in the mixing efficiency, leading to a different temperature in every droplet. Accelerated mixing by e.g. winding microfluidic channels²⁹ would both increase the temperature change for a given reaction enthalpy and also decrease variation in the temperature between droplets, both of which lead to a lower MDT and a correspondingly improved calorimeter resolution. Regarding measurement time, a study of binding reactions requires a droplet measurement time that meets or exceeds 500 ms, while in this work the total measurement time of a reaction was limited to around 90 ms by the clear aperture of the fluidic chip. To realize this 6× increase in measurement time, a longer outlet channel could be used, potentially in combination with a design that decelerates the droplets after they form by widening the fluidic channel. A spatially multiplexed optical readout could provide simultaneous measurements of droplets at multiple points along the outlet channel. In summary, a variety of straightforward modifications to the optical readout and microfluidic chip layout would enable this platform to function as a HTS tool.

Conclusions

The measurements presented here document a novel microfluidic calorimetry technique with the potential to be used for high-throughput screening (HTS) campaigns in drug discovery. In this method, thermochromic liquid crystal (TLC) reporter particles act as the temperature transducers, which, combined with an optical readout, provide a label-free method of measuring the droplet temperature. These temperature changes are interpreted to derive meaningful enthalpy estimations for chemical reactions occurring in the droplets. Experimental measurements of the temperature of 500 pL droplets were carried out using TLCs as the temperature indicator. Temperature measurements on droplets undergoing a binding reaction between Ca²⁺ and EDTA showed good quantitative agreement with thermal simulations. The experimentally demonstrated calorimeter resolution was 20 nJ in 100 ms, which is comparable to state of the art isothermal titration calorimeters (ITCs) while using a reactant volume at least 10× smaller. Several straightforward modifications to this platform are necessary to make it suitable for HTS applications, namely increasing the droplet measurement time, improving the mixing efficiency, and implementing a multiplexed optical readout. With these improvements in place, optical calorimetry of microfluidic droplets using TLCs could become a practical HTS tool for drug discovery and other applications.