A Finite Element Model to Assess Transtibial Prosthetic Sockets with Elastomeric Liners

Abstract

People with trans-tibial amputation often experience skin breakdown due to the pressures and shear stresses that occur at the limb-socket interface. The purpose of this research was to create a transtibial finite element model (FEM) of a contemporary prosthesis that included complete socket geometry, two frictional interactions (limb-liner and liner-socket), and an elastomeric liner. Magnetic resonance imaging scans from three people with characteristic transtibial limb shapes (i.e., short-conical, long-conical, and cylindrical) were acquired and used to develop the models. Each model was evaluated with two loading profiles to identify locations of focused stresses during stance phase. The models identified five locations on the participants’ residual limbs where peak stresses matched locations of mechanically induced skin issues they experienced in the nine months prior to being scanned. The peak contact pressure across all simulations was 98 kPa and the maximum resultant shear stress was 50 kPa, showing reasonable agreement with interface stress measurements reported in the literature. Future research could take advantage of the developed FEM to assess the influence of changes in limb volume or liner material properties on interface stress distributions.

Graphical Abstract

INTRODUCTION

Many people with transtibial amputation would like to meet or even exceed activity levels they achieved prior to amputation[58]. Attaining this goal is often a challenge because soft tissues of the residual limb are poorly suited to sustaining the ambulatory loads transmitted by a prosthesis (i.e., artificial limb). Inappropriate transmission of stresses between the rigid socket and delicate limb tissues often leads to mechanically induced skin breakdown[30, 31].

Clinical research to identify how prosthesis design features affect interface pressures and shear stresses that lead to tissue injury is challenging because of variables outside of the researcher’s control. For example, minute-by-minute changes in residual limb fluid volume may occur[51] and affect interface stress distributions[48]. Finite element models (FEMs) are ideal for challenging applications such as these. However, nearly all limb-socket FEMs reported in the literature to-date are based on an older socket design (i.e., a patellar tendon bearing design [PTB]) and include a foam (Pelite^™) liner or no liner at the limb-socket interface [38, 12, 27, 65, 67, 24, 28, 13, 21]. Recent data suggests that only 18% of sockets in clinical practice are PTB designs[64]. Instead, the majority of contemporary sockets are of a total surface bearing (TSB) or hydrostatic design. Contemporary sockets are intended to decrease peak pressures by distributing loads over the limb-socket interface, rather than focusing pressures in load-tolerant areas of the residual limb. This design philosophy has been made possible through use of elastomeric (i.e., gel) liners, which are now a part of as many as 85% of clinical prostheses[64]. The most notable feature of elastomeric liners are their incompressible, non-linear material response, and tendency to expand or ‘flow’ under compressive stresses[5]. This response is thought to contribute to contemporary sockets’ ability to distribute pressures over the limb-socket interface.

Changes in contemporary socket designs have also brought a subtle, but fundamental shift in the role of the prosthetic liner at the limb-socket interface. Elastomeric liners are in intimate contact with the residual limb while Pelite liners are in intimate contact with the socket wall. This difference is evidenced through patients’ use of prosthetic socks, which are applied to accommodate shape differences between the limb and socket[18, 7]. Prosthetic socks are worn between the limb and liner when using a Pelite liner, and between the liner and socket when using an elastomeric liner. For contemporary prostheses, this difference reflects a shift in the primary slipping interface from the limb-liner interface to the liner-socket interface. As a result, attributes of previous FEMs (e.g., application of a fixed boundary condition at the outer nodes of the Pelite liner as a proxy for the prosthetic socket) are not valid for prostheses used most often in practice today.

The goal of this research was therefore to develop and test a method for creating FEMs that captured the complete geometry of a transtibial limb-socket interaction, and provided the means to investigate a contemporary socket design (e.g. TSB). FEMs were created from limb-socket geometries for three people with transtibial amputation. Each FEM was tested with two load profiles reflective of clinical loading conditions. Locations of peak stresses obtained from the FEMs were compared to locations of skin issues experienced by participants over the previous nine months to assess the clinical accuracy of the FEM.

METHODS

A FEM that simulated the coupling between a residual limb and a contemporary prosthetic socket was designed and optimized to determine the interface stresses between the skin and prosthetic liner. To make the model broadly applicable, three transtibial prosthesis users with distinct limb shapes (i.e., short-conical, cylindrical, and long-conical) were recruited for the study. New prosthetic sockets were fabricated for each participant to standardize the liner interface to a 6 mm uniform profile, and to make the sockets compatible with magnetic resonance imaging (MRI).

Socket Design

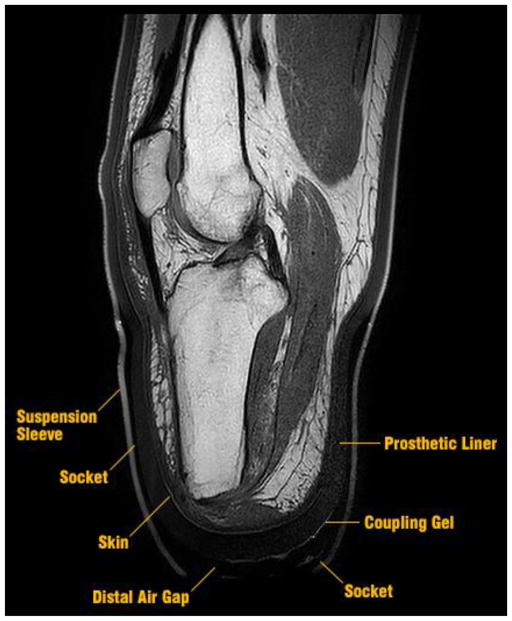
MRI was selected to determine geometries because of its capability to obtain accurate measurements of load bearing soft tissues (e.g., the patellar tendon). To eliminate major imaging artifacts, all metallic components in the participants’ prescribed sockets were replaced with MRI-compatible alternatives in the study sockets. New prosthetic sockets were made using an epoxy-acrylic resin (EAR1, Paceline, Matthews, North Carolina) and weave made from a polymeric fiber (Synthex^™, Fabtech Systems, Everett, Washington). The polymer composite socket was not visible in MRI images, so was identified as the void space between the prosthetic liner and suspension sleeve[Figure 1]. To identify the distal gap between the liner and socket, the bottom of the socket was coated in a thin layer of ultrasound coupling gel (Aquasonic 100, Parker Labs Inc, Fairfield, New Jersey) that produced a strong MRI signature. A polymer socket base was designed and fabricated (Objet RGD840, Stratasys, Eden Prairie, Minnesota) that bore participants’ weight on a fitting stool.

FIGURE 1.

Example MRI used to create finite element model geometry. The materials selected provided visible contours for the liner and suspension sleeve. These contours enabled boundary profiles to be established for the socket and distal air gap.

All study sockets were designed to fit a 6 mm uniform profile liner. Prosthetic liners are typically made from one of three base polymers: silicone, urethane, or thermoplastic elastomer (TPE) [6]. In preliminary testing all but polyurethane liners produced a visible MRI signature. The Össur Dermo liner (Reykjavik, Iceland) was selected for all participants because it is commonly used by people with transtibial amputation[15], and has material properties comparable with other liner products frequently used by transtibial prosthesis users[5].

Participant Recruitment and Limb-Socket Imaging

People with transtibial amputation and characteristic limb shapes (i.e., short-conical, cylindrical, and long-conical) were recruited to undergo limb-socket imaging. Informed consent was obtained from all individuals included in the study. Participants were eligible for the study if they (a) had no metallic implants below the waist (e.g., orthopedic bolts or plates), (b) had no MRI-incompatible implants above the waist, (c) normally wore an elastomeric liner with a uniform thickness profile (e.g., 3 mm or 6 mm), (d) needed less than 1.8 mm (~5 ply) of prosthetic socks[52] to achieve a comfortable fit in their prescribed prosthesis, and (e) were at least 24 months post amputation.

Three sessions were required to capture participants’ limb-socket geometries. To minimize the effects of daily limb volume fluctuations[50, 51], all sessions were conducted at an early and consistent time of day. The first session was used to characterize participants’ as-prescribed prostheses. First, the research prosthetist examined the participant’s prescribed prosthesis and documented the liner product, liner size, and sock thickness required to achieve a proper fit[4]. Next, the research prosthetist measured circumferences at the mid patellar tendon (MPT) and distal tibia (DT) to estimate the donned thickness (including stretch) of participants’ prescribed prosthetic liner. Circumferences were measured with and without the liner donned. Participants’ prescribed socket geometries were then measured using a coordinate measuring machine (Platinum Arm, Faro Technologies, Lake Mary, Florida) [53]. Lastly, participants were administered two surveys, the Prosthesis Evaluation Questionnaire Utility Subscale (PEQ-Utility) [26] and the Socket Comfort Score (SCS) [17] to establish a subjective point of comparison between the prescribed and study sockets. The PEQ-Utility subscale was selected from among the other PEQ subscales, as it included questions specific to the fit and comfort of the prosthesis [26].

After the first session, participants’ prescribed socket geometries were modified to create the study sockets. The geometry for the study sockets was defined as a surface-normal, uniform offset to the participants’ prescribed prosthesis[54] that accounted for the removal of prosthetic socks, the thinning of the prosthetic liner as it was stretched during the donning process, and any change in thickness between the prescribed and study liners. Two sockets of different uniform offsets were fabricated and tested for fit in the second session. The offset of the first socket was determined numerically as the mean difference between the change in effective radii of the MPT and DT. The offset of the second socket was determined subjectively by the research prosthetist.

During the second session, the study liner and sockets were fit by the research prosthetist. The research prosthetist was blinded to the individual sockets and evaluated with the same methods used to assess quality of socket fit in clinical practice (e,g., assess the number of sock needed to achieve no gaps between the limb and socket, discuss fit and comfort with the user). A socket was considered appropriately fit if no socks were needed to achieve an optimum fit and if the participant answered “yes” when queried if they would feel comfortable wearing the socket for an entire day. If one of the sockets met these criteria, it was selected as the final study socket and the participant proceeded to the third session for imaging. If neither socket could be appropriately fit without the use of socks, up to two additional sockets were fabricated and re-assessed on a different day.

At the third session, participants were imaged with their final study socket. Immediately before scanning, each participant donned the socket without socks and stood on a fitting stool, with equal weight on both limbs. Fit was verified by asking the participant if he or she would feel comfortable wearing the socket for an entire day. Upon confirmation, the participant was administered the PEQ-Utility and SCS questionnaires to rate the fit of the final study sockets. To confirm that the final study socket was a plausible representation of the prescribed socket, the socket fit questions from the PEQ-Utility subscale were modified to allow for an immediate assessment (“rate the fit of your prosthesis” and “rate your comfort while standing when using your prosthesis” ).

The participant’s residual limb, prosthetic liner, and socket were then imaged with a 3.0 tesla MRI scanner (Ingenia CX, Phillips Healthcare, Andover, Maine). The scanning profile was a T1 weighted fatscan sequenced by a fast spin echo with 1.0 mm slice spacing. A partially donned state was used since preliminary testing showed that a FEM created from a socket doffed image series would provide too stiff a soft tissue response as the limb deformed to fit the socket, and a FEM created from a fully donned image series would omit meaningful stresses from regions where the liner was compressed locally [Supplemental Figure 1]. A partially donned state was achieved by the participant bearing approximately half of his or her weight on the fitting stool and by answering “no” when asked if he or she felt their socket was fully donned. The suspension sleeve was rolled on in a manner that best preserved the current socket state. Participants were then moved to a supine position on the scanning bed. No external load was applied to the distal end of the socket, but sockets were braced to achieve a knee angle of 10–15°, similar to the weight acceptance portion of stance phase (i.e., 9–12°) reported for transtibial prosthesis users[41].

FEM Creation

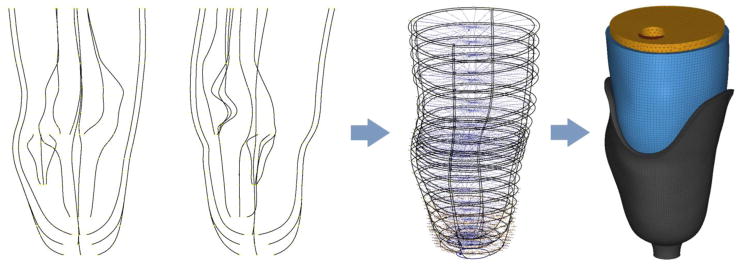
Building the FEMs was a four-step process. Slice images were first imported into a parametric modeling program (Inventor 2016, Autodesk, San Rafael, California), and fit with bounding splines [Figure 2]. Spline profiles were then imported into a 3D scan data processor (Geomagic Design X, 3D Systems, Rock Hill, South Carolina) to be lofted and smoothed. Limb-socket assemblies were meshed in a pre-processor (Hyperworks 14, Altair Engineering, Troy, Michigan) [Figure 2] and then imported into the FEM simulation software (Abaqus 6.16, Dassault Systèmes, Vèlizy-Villacoublay, France).

FIGURE 2.

Splined limb-socket geometry. A parametric modeling package was used to create proximal-distal guide splines (left), followed by transverse bounding splines (center). The splined geometry was then lofted and meshed (right).

The design focus for the FEM was the ability to assess the skin-liner interface in a variety of loading scenarios. A novel feature of the present model was the presence of two major frictional contact interactions, the skin-liner interface (i.e., skin-elastomer) and the socket-liner (i.e., laminate-fabric) interface. Simulating both interactions as frictional was required to model a contemporary socket design. The skin-liner interface was of greatest interest in this study, but reported coefficient of friction (CoF) values [63] indicated that slipping would be biased towards the socket-liner interface. To optimize the FEM for soft tissue contact interfaces[60], reduced-integration, 8-node hexahedral elements were used to mesh the socket (type C3D8R) and liner (type C3D8RH, a hybrid element that better emulated incompressibility). The pressure-overclosure response between surfaces was modeled with the penalty method. Both the socket and liner were meshed with four elements through their respective thickness to overcome issues with reduced shear stress distribution and artificial increases in bending stiffness associated with 8-node hexahedral elements. Two groups of soft tissues (i.e., the patellar tendon and the accumulated [remaining] soft tissues) were modeled. A preliminary model showed that it was not possible to further segregate the soft tissues without introducing significant convergence problems. For the same reason, solid bone models were omitted and implemented as a fixed boundary condition. All soft tissues were modeled with modified, 10-node tetrahedral elements (type C3D10M). Nodal spacing at the contact surfaces was approximately 2.5 mm (i.e., the length of an element with mid-side nodes was 5.0 mm); this was found to be the best compromise between element shape quality and geometric accuracy.

The General Contact algorithm, with only the skin-liner and liner-socket pairs designated as active contacts, was used as it produced a stable model with reasonable solution time while exhibiting no adverse effect on simulation results.

FEM Parameter Optimization

The cylindrical limb-socket model was chosen from among the three participant models to evaluate key parameters associated with convergence stability. The cylindrical limb-socket model was selected because the parallel loading surfaces on the anterior and posterior aspects of this model were expected to be least conducive to distributed load profiles and therefore the most challenging to simulate. Simulation parameters for all three models were subsequently defined from these initial evaluations.

Coefficients of friction

The socket-liner interface was set at 0.5, a median value reported in the prosthetic literature[19, 56]. CoFs greater than 3.0 at the skin-liner interface have been reported in amputee skin studies[63] and benchtop measurements of prosthetic liners[5]. However, the FEM would only converge up to a CoF of 2.0. Preliminary simulations evaluating the effect of varying COF (0.5, 1.0, 1.5, 2.0, and bonded-contact) on the softest and stiffest liners [5] showed that a CoF of 2.0 approximated a bonded contact, with converging stress, strain, and slipping [Supplemental Figure 2]. This result indicated a simulated CoF of 2.0 was a suitable representation of any liner with CoF greater than 2.0.

Liner

A hyperelastic material model was used for the prosthetic liner, with material response taken from a previous study[5] and model coefficients determined by a standalone application (Hyperfit, Brno University, Brno, Czech Republic). Preliminary simulations showed that Mooney-Rivlin and Yeoh constitutive models demonstrated the best combination of stability and accuracy. For the study liner (i.e., Össur Dermo), the root mean square error of the model fit was 0.4 kPa for Mooney-Rivlin and 0.2 kPa for Yeoh in compression, and 2.1 kPa for Mooney-Rivlin and 2.1 kPa for Yeoh in tension. The study liner was modeled with the Yeoh constitutive model for all simulations, with material coefficients of: C10 = 2.014E+04, C20 = −1.541E+03, and C30 = 4.094E+02. When performing a simulation of an incompressible material, FEM solvers typically recommend a maximum Poisson‘s ratio of 0.495. Prior limb-socket models have used values of 0.45[57] to 0.49[43]. For a hyperelastic material model, the Poisson‘s ratio is not set directly, instead the coefficient D1 is used, which is inversely related to the material‘s bulk modulus. To simulate material incompressibility of the prosthetic liner, D1 was set to 3.0e-06, which approximated a Poisson‘s ratio of 0.48. The selected value provided the best convergence stability with the closest possible representation of an incompressible material.

Soft tissues

It was not possible to simulate residual limb soft tissues with a hyperelastic material model because of convergence instability. Instead, a linear material model was used. Data from dermis studies were used[10, 9] to select an appropriate compressive modulus for the soft tissue model. Prior compression testing studies showed tissue stiffness over the anteromedial aspect of the tibia was between 150 and 220 kPa for an applied pressure of 50 kPa. This range in stiffness was of particular interest, because stiffness is dependent on applied load and 50 kPa is a common magnitude of stress exerted on residual limbs[48, 2]. A more recent study reported stiffnesses of 300–350 kPa over the anterior tibia, with applied pressures as high as 600 kPa[28]. Model stability was therefore evaluated at four stiffness values (i.e., 150, 220, 300, and 350 kPa), and 300 kPa and 350 kPa were found to be significantly more stable than 150 or 220 kPa. Therefore, the accumulated soft tissues were simulated with a modulus of 300 kPa and a Poisson‘s ratio of 0.45 across all simulations.

Patellar tendon

The patellar tendon stiffness has been reported to be as low as 260 kPa[66] and as high as 2.0 GPa[59]. Differences in reported values are likely due to differences in testing methods and orthotropic material composition of the tendon. In-vivo, out-of-plane compression testing of a relaxed tendon[66] would be expected to produce a significantly lower modulus than an ex-vivo, in-plane tensile measurement[59]. Since the quadriceps are active and the patellar tendon is under tension during stance phase, a stiffness of 150 MPa was selected as a compromise between the reported values.

Socket

Carbon fiber was modeled as a linearly elastic material with a stiffness of 19 GPa and a Poisson‘s ratio of 0.1. These values are consistent with manufacturer-reported values for the ±45° woven carbon fiber fabric used in prosthetic sockets[1].

FEM Validation

All three limb-socket models were evaluated with two distinct loading profiles to determine if observed trends were reasonable and consistent with data presented in the literature. The first profile (uniaxial) had only a vertical component, and was similar to the static load applied to the study sockets as they were being assessed by the participants and prosthetist. The second loading profile (compound) was a simulation of heel-strike to the first peak of the gait cycle, and contained components that included: vertical load, horizontal load, and sagittal moment. Loading was applied distally with no constraints placed on the sockets’ resultant displacements or rotations.

Locations of focused stress predicted by the models were compared to skin issues experienced by participants prior to imaging. Significant skin issues (i.e., incidences of skin breakdown) were assessed and documented in participants’ files (via photos and descriptions) by the study research prosthetist when participants came to the laboratory prior to the start of this study. Files from the nine months prior to imaging were reviewed to identify incidences of skin breakdown that were common for each participant. Documentation of each instance was subsequently reviewed with the study prosthetist to verify the skin issue was mechanically induced. Validity of the FEM was assessed by comparing locations of skin-breakdown to locations of high pressure and shear stresses indicated by the models.

RESULTS

Three prosthesis users with transtibial amputation were included in the study [Table 1]. Scores from the SCS and PEQ-Utility subscale questions demonstrated that on average the final study sockets were a comparable fit to participants’ as-prescribed prosthetic sockets. Study sockets scored 1.7 points (18%) higher on the SCS and 3.8 points (5%) higher on the PEQ-Utility questions [Table 2]. A difference of 1.7 points on the SCS is within the 2.7-point minimum detectable change (MDC, 90% confidence interval) of this instrument[16]. MDC for the PEQ-Utility subscale is only available for a 7-point version of the instrument, but results from that study suggest that a 17% change of the full scale range is needed to indicate a significant change in score[40]. Thus, the ~5% differences observed in PEQ responses are likely within the error of the instrument and do not reflect a measureable difference in quality of socket fit.

TABLE 1.

Participant data

	Participant
	1	2	3
Limb Shape	short- conical	cylindrical	long-conical
Height	185 cm	178 cm	180 cm
Weight	91.4 kg	87.3 kg	83.7 kg
Gender	male	male	male
K-Level	3	3	3
Time since amputation	42 years	9.5 years	38 years
Limb Length	13.2 cm	15.1 cm	19.0 cm
MPT Circumerence	34.4 cm	31.1 cm	30.5 cm
DT Circumference	26.0 cm	26.0 cm	19.3 cm
As-Presribed Liner	WillowWood Silicone	Össur Synergy	WillowWood Hybrid Select
Number of sessions over previous 9 months	11	18	9
Incidences of skin issues	2	2	1
SCS (as-prescribed socket)	9	8	6
PEQ-Utility (as- prescribed socket)	96	97	69

TABLE 2.

SCS and PEQ Scores. The participants’ perceived differences between the as-prescribed and study sockets were below the minimum detectable change of the survey, indicating a comparable fit

Socket Evaluation Metric	Participant
	1	2	3
SCS (as-prescribed)	9	8	6
SCS (study)	10	10	8
PEQ-U* (as-prescribed)	97	92	65
PEQ-U* (study)	95	100	71

^*Only two scores from the PEQ-U were applicable to both the as-prescribed and study sockets

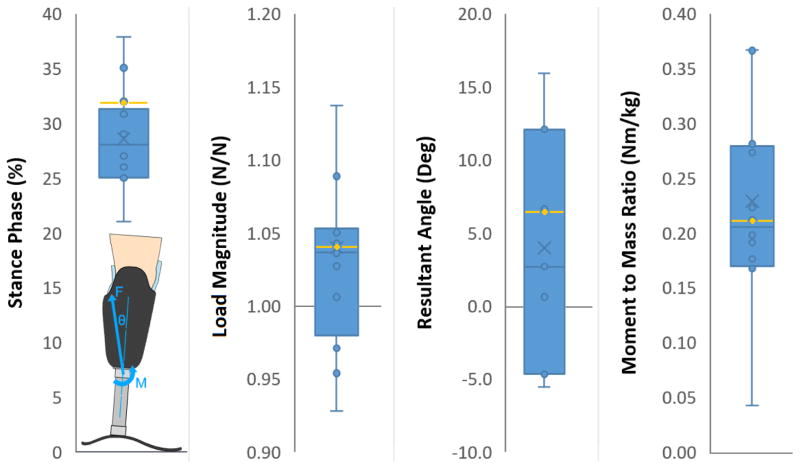
Sixteen data sets from pylon-mounted load cells were compared from the scientific literature [35, 34, 23, 42], and the median was chosen to be the compound load profile[35] [Figure 3]. Similarly, the magnitude of the uniaxial profile was selected to be 110% of participants’ body weight, because that scalar corresponded to peak ground reaction forces reported for eleven prosthetic limb users during normal ambulation[62]. A key difference between the uniform and compound load profiles was that the compound profile had greater total energy input to the simulation. This difference was evident in the results predominantly through an increase in stresses over the anterior aspect of the limbs [Supplemental Figure 3]. The medial, lateral, and posterior aspects of the limbs showed a trend of decreased contact stresses in the compound load profile compared to the uniform profile [Supplemental Figure 3]. However, the measured differences were small (2.8 kPa mean, 6.4 kPa max) compared to those on the anterior aspect (7.2 kPa mean, 24.2 kPa max). The mean limb-socket displacement for all simulations was 8.0 ± 0.8 mm; no limb geometry or load profile resulted in contact stresses applied to the distal end of the limb.

FIGURE 3.

Validation of selected shank loading conditions. The selected profile (yellow line) was compared against 16 datasets from the literature to ensure it was a reasonable representation of loads experienced by people with transtibial amputation. Dots represent individual data sets while X represents the mean.

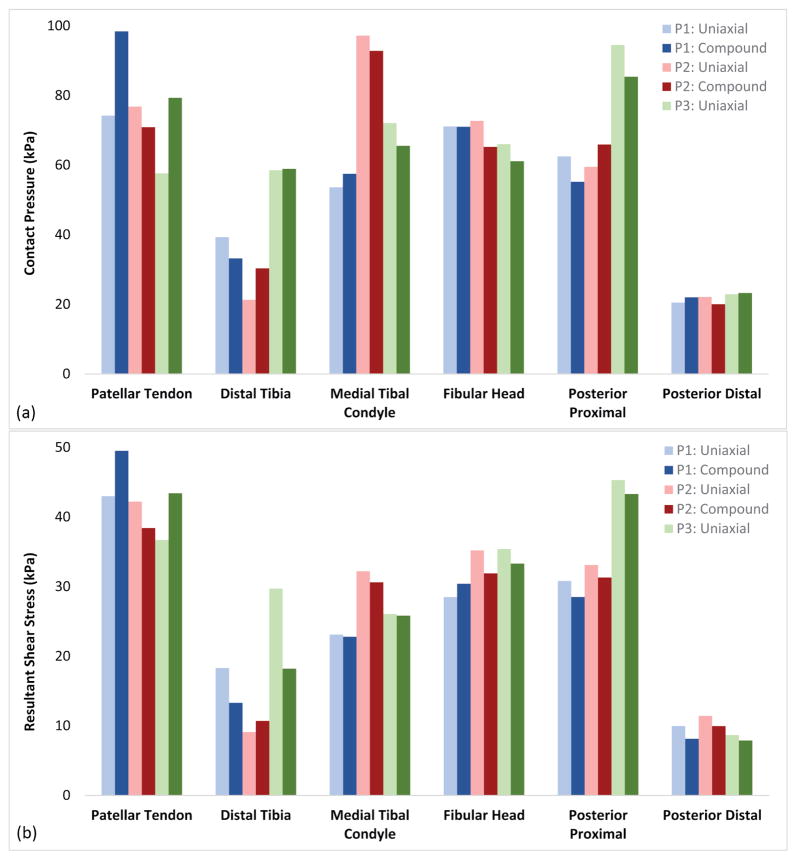
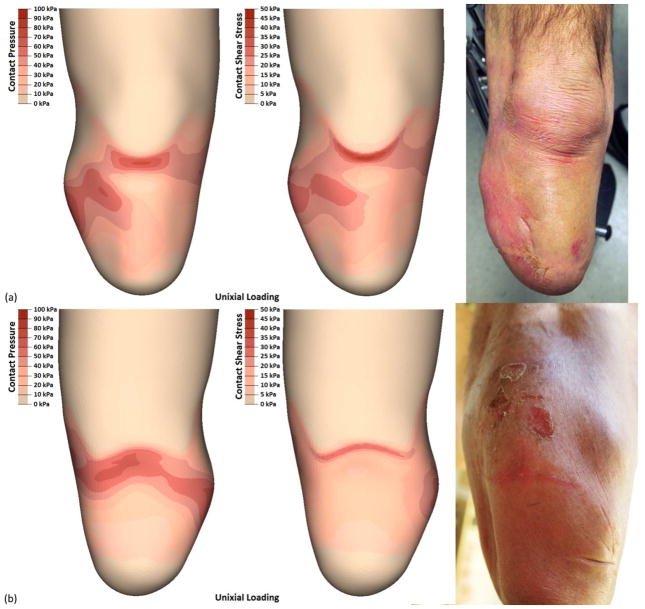
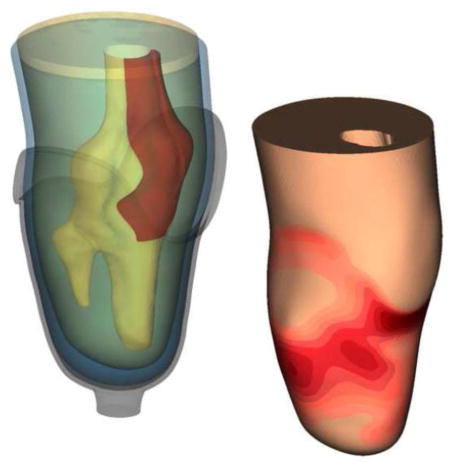
Participant 1 (i.e., short-conical limb) had the highest rated prescribed socket based on SCS and PEQ-Utility scores; this perceived quality of fit was generally reflected in the FEM. The output of both load profiles showed a relatively even pressure distribution that most closely resembled a TSB socket [Figure 4a]. However, areas of increased stress concentrations were observed. Participant 1 also showed focused stresses between the patellar tendon and fibular head, with the compound load profile exhibiting the highest stresses observed across all simulations. Contact pressures increased over the entire anterior-proximal region of the socket (98 kPa max) as loads were applied. Similarly, resultant shear stresses became more focused over the brim of the socket (50 kPa max). Posterior pressures were distributed over the proximal region of the socket (62 kPa max), with focused resultant shear stresses along the brim (31 kPa max) [Figure 4b].

FIGURE 4.

FEM results by location. Each limb-socket simulation produced a distinct point of peak pressure, but the location of the peak was participant specific. Stresses were typically highest over bony prominences and regions that are commonly considered clinically desirable for loading (e.g. patellar tendon and posterior brim). The additional energy input from the compound load profile was typically propagated through the anterior surfaces as increased contact pressures and resultant shear stresses.

Over a nine-month period prior to imaging, participant 1 had two observed instances of skin breakdown. The first instance was mechanically-induced, and presented over the patellar tendon and lateral aspect of the limb [Figure 5a]. This issue persisted for over a month, with wounds over the fibula being the last to heal. The second incidence of skin breakdown was a fungal infection on the posterior aspect, and was not likely a result of contact stresses. However, the distributed stresses seen in the posterior proximal region of the FEM suggested possible skin damage [Figure 5b]. Results of both load profiles showed good correlation with the observed instances of skin breakdown. However, the compound load profile better matched the first instance while the uniaxial simulation better matched the second instance.

FIGURE 5.

Participant 1 experienced breakdown on the anterior and posterior aspects of his limb that generally correlated with the results of the FEM. Most notable was that the breakdown over the patellar tendon included tearing of the skin, and this correlated to the highest FEM reported shear stresses across all limbs and locations.

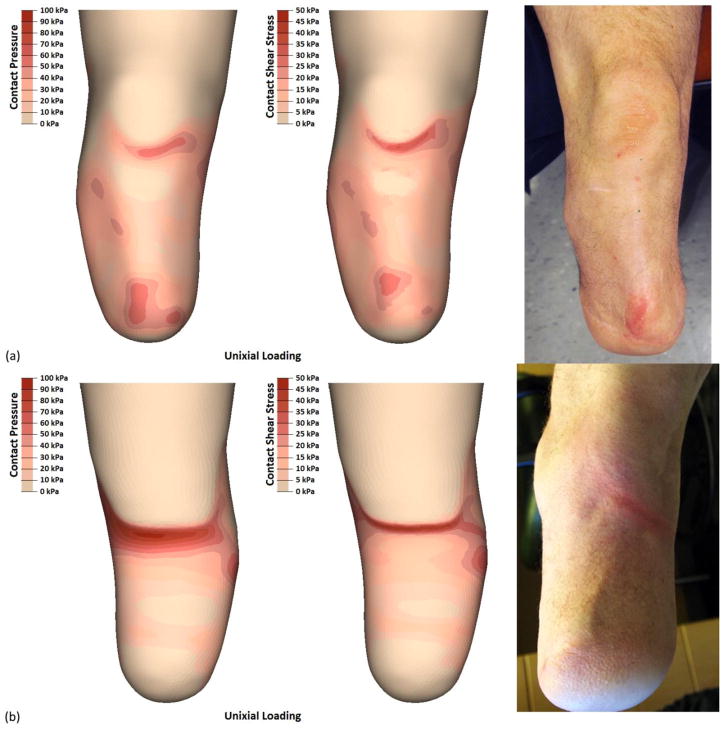
Participant 2 (i.e., cylindrical limb) had the second highest rated prescribed socket by SCS and PEQ-Utility scores. However, within two months of completing the study, the participant requested his prosthetist fabricate him a new socket. Interestingly, the FEM demonstrated discontinuous contact over desirable loading regions on the anterior aspect of the limb (e.g., flat face of the tibia) and focused stresses occurring over proximal and distal socket contours [Figure 6a]. Stresses on participant 2‘s distal tibia were the highest of the three limb-socket geometries (59 kPa) and were present below the tibial bevel, a region that is clinically poor at sustaining focused ambulatory loads. The posterior aspect exhibited the highest stresses [Figure 6b] with contact pressures (95 kPa) and resultant shear stresses (45 kPa) greater or equal to those seen over the patellar tendon. These elevated pressures likely contributed to participant 2‘s desire to have his as-prescribed socket replaced.

FIGURE 6.

Participant 2 experienced two instances of skin breakdown – in the distal tibia and posterior proximal regions. Results from the FEM identified three regions with higher than average contract pressures and resultant shear stresses. While only two of these locations sustained breakdown, the third (patellar tendon) exhibited callousing, a sign of increased skin stresses. The patellar tendon is a load tolerant region while the distal tibia is not, and this may have contributed to observed differences in skin breakdown and FEM reported stresses.

Participant 2 also had two mechanically-induced limb health issues observed over the nine-month period prior to imaging. The first was an instance of skin breakdown over the distal tibia that persisted for over a month [Figure 6a]. The location of both the initial and persistent wound were best represented by the uniaxial load profile. The second observed instance was a persistent sore spot along the posterior brim that never developed into a wound [Figure 6b], but tore the participant‘s prosthetic liner. Unlike participant 1, the posterior issue experienced by participant 2 was better described as edge loading. This issue was observed in the FEM output through higher peak stresses over a smaller area along the posterior socket brim. Both load profiles demonstrated the same type of stress distribution, and the peak stresses in the posterior region were distinct compared to the other two limb geometry models.

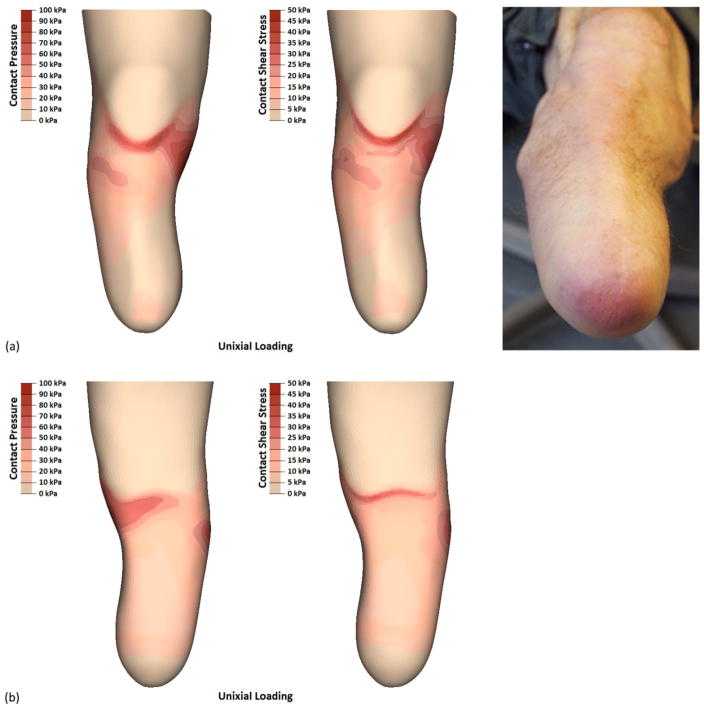
Participant 3 (i.e., long-conical limb) had the lowest rated prescribed socket. His SCS score of 6 was representative of a socket that likely needed adjustment[17]. Correspondingly, the FEM results showed a proximally-biased load distribution with limited contact stresses over the entire distal aspect of the limb [Figure 7a]. Two regions showed distinct contact stresses compared the other limb geometries; participant 3 had the lowest contact pressures over the distal tibia (30 kPa), and the highest contact pressures over the medial tibial condyle (98 kPa). This peak load distribution presented around the limb, where radiant stresses constituted the highest posterior contact pressures (66 kPa) and resultant shear stresses (33 kPa) [Figure 7b]. Throughout the rest of the socket, peak contact stresses were intermediate compared to the two other limb geometries.

FIGURE 7.

Participant 3 did not have any instances of skin breakdown. However, his distal limb tissues showed early signs of verrucous hyperplasia. FEM results show a proximally-biased load distribution with limited contact stresses over the entire distal aspect, consistent with conditions conducive to verrucous hyperplasia.

Participant 3 had one mechanically-induced limb health issue observed repeatedly over the nine-months prior to imaging, but no instance of skin break-down was reported. After doffing his socket, the distal end of participant‘s 3 limb was often red and purple in color [Figure 7a], returning to normal after approximately ten minutes. The research prosthetist identified this issue as a lack of distal end bearing, with the purple (oxygen depleted) tissue being a precursor to verrucous hyperplasia. While no skin issues were observed over the medial tibial condyle, it is worth noting that only the contact pressures were high; the resultant shear stresses were comparable to other locations inside the socket. This may have contributed to the socket‘s discomfort, while skin breakdown was belayed without a sufficient magnitude of compound stresses to induce soft tissue damage.

DISCUSSION

The models developed in this study reflect recent advancements in trans-tibial prosthetics. The models simulated limbs with elastomeric liners in TSB sockets, unlike most prior FEMs that simulated limbs with Pelite liners in PTB sockets [33, 39, 38, 25, 12, 13, 21, 24, 28, 20, 65, 67]. The majority of contemporary sockets are now TSB design, and as many as 85% of clinical prostheses use elastomeric liners [64]. The validation method focused on clinical outcomes – model results were compared to instances of skin breakdown rather than to interface stress measurements [37]. This validation procedure was selected because commercially-available interface stress measurement systems are unable to accurately measure normal and shear stresses at the limb-liner interface[8, 22, 55]. As a goal of this project was to develop a model with clinical utility, a clinical ground truth (i.e., accurate prediction of instances of skin breakdown at points of peak contact stresses) was deemed to be more relevant than validation against suspect in-socket measurements.

The strong match between model results and locations of clinical breakdown suggests that simulation of elastomeric liners using two frictional interfaces (skin-liner, liner-socket) is an appropriate modeling strategy. Elastomeric liners are sticky on the side next to the skin and less sticky on the outside (which is typically a fabric material) next to the socket. They generate a higher coefficient of friction against the skin than against the socket, thus favor liner-socket displacements over skin-liner displacements. Simulation of these interfaces correctly allowed our models to capture the functionality of elastomeric liners: low friction on the skin (meaning minimal slip and thus low abrasion) but moderate to high shear stress. Animal studies have demonstrated that skin is more tolerant to shear stress than to friction [14], and friction studies conducted on forearms of human participants showed that the lower the frictional force, the greater the amount of work the skin can withstand before rupture [32]. These results suggest that in terms of skin injuries most commonly experienced by prosthesis users (epidermal injury, blisters, corns/calluses) [29], shear stress is better tolerated than friction. FEM results in this study support the expectation that the TSB socket design, combined with a sticky elastomeric liner, accentuated load support by shear stress while reducing interface pressures. The FEM showed a mean shear stress of 27 kPa, higher than the mean of 11–16 kPa reported in the literature for participants wearing PTB sockets with Pelite liners [44–48]. Interface pressures in the present study indicated peak pressures of 90–95 kPa, lower than those measured on participants wearing PTB sockets with Pelite liners, 200–300 kPa [44–46, 49]. Further, FEM mean socket pressures were 58 kPa, and reported pressures for PTB sockets were 94–99 kPa [44, 46–48]. Measurements reported in literature collected from prosthesis users wearing TSB/elastomeric liner sockets do not support or refute the expectation that peak interface pressures are lower than with PTB/Pelite sockets [2, 3]. However, this result may reflect measurement errors from thin film pressure sensors positioned between the limb and liner in some of the studies [55].

Finally, the current FEM simulated the complete limb-socket interface, including the liner thickness change from the proximal to distal end (from 6 to 14 mm) as well as the distal gap between the liner and socket. It was anticipated that the FEMs would thus produce greater and more reasonable estimates of displacement than the 1 mm displacements reported in previous FEM studies[65, 38]. In clinical testing, Tucker et al. and Darter et al. measured 12–18 mm of limb-socket displacement depending on the method of suspension[61, 11]. Darter found that approximately 60% of this displacement occurred during initial weight acceptance (0–20% body weight), likely reflecting recovery from proximal displacements from the immediately prior swing phase [11]. The remaining 40% (5–7 mm) occurred during the final 80% of load bearing. This 5–7 mm distance range was comparable to results of the FEMs in the present study (7–9 mm) where only stance phase, without presence of the prior swing phase, was modeled. Thus the techniques used here to simulate the distal region of the socket may have been responsible for producing better matches to experimental measurements than previous FEM simulations.

CLINICAL RELEVANCE

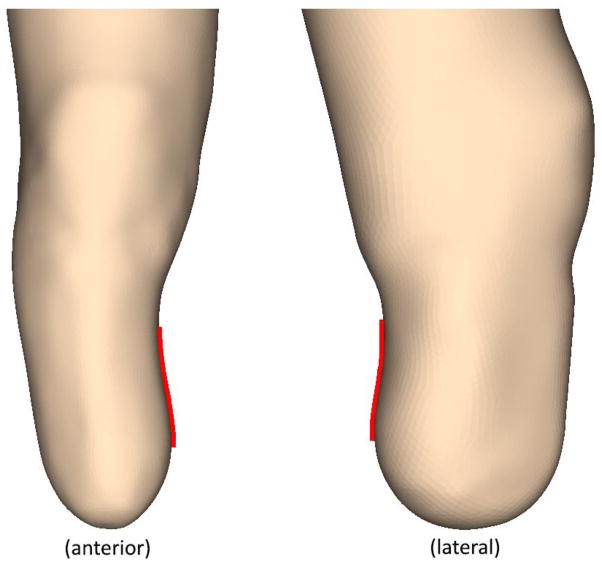
This study offers insight into several techniques used in clinical practice related to the theory of contemporary socket design. For example, the “total surface bearing” design reflects an idealized outcome of an equal load distribution across the entire surface of the residual limb. However, in this study only participant 1 had a limb shape that enabled total surface bearing in the most basic interpretation (i.e., all surfaces bearing at least some ambulatory load). Participants 2 and 3 both had limb geometries that decreased the load bearing capacity over specific areas of the limb [Figure 8]. In spite of this difference, the peak stresses were about the same across all limb geometries. Each limb and loading condition exhibited a peak pressure that was 2.1 ± 0.2 times the socket mean. This further contrasts with the traditional view of using pairs of desirable loading points on opposite sides of the socket that combine to provide vertical loading and horizontal stability. For example, a limb supported on the patellar tendon is generally thought to need opposing support on the posterior-proximal (popliteal) region of the limb. However, results from all three simulated limb geometries showed there was no location of similar stress magnitude to counter balance any of the primary loading points. This result may be a consequence of peak stresses occurring in regions close in proximity to bony prominences, where there is not sufficient thickness of the soft tissue or elastomeric liner to distribute evenly these applied loads.

FIGURE 8.

Inverted contact surfaces that inhibit equal load transfer. Participant 3 (left) had an inverted surface on the medial aspect of his limb, while participant 2 (right) had an inverted surface on the posterior aspect. These surfaces may reduce the capacity to transfer vertical directed ground reaction forces, and inhibit the function intended with the TSB socket design.

This study used incidences of skin breakdown to assess the clinical validity of the finite element model. Interestingly, comparison between the FEM and skin issues indicated that these models may have the potential to predict soft tissue damage. The soft tissue breakdown explored in this model was limited to acceptable sockets with superficial wounds, which were most likely to be related to skin stresses and abrasion. Deep tissue injuries could be explored in future studies, though the study design and FEM formulation might need to be adjusted to account for poorly fitting sockets. Additionally, research has shown that deep tissue injury is related to cellular strains rather than interface contact pressures[36, 37]. Given the highly non-linear mechanical response of soft tissues and the limits of numerical material models, damage may be better predicted in a FEM through strain-energy[37].

CONCLUSION

This research produced a novel method for creating a transtibial FEM that simulated modern prosthesis design, an elastomeric liner and a contemporary TSB socket. Novel features of this approach included complete liner-socket geometry and frictional interfaces between both the limb and liner and between the liner and socket. Additionally, an empirically-derived hyperelastic material was used for the elastomeric liner. Good matches between FEM results and participant tissue responses is encouraging. Future research should make use of these unique FEM features to evaluate clinically relevant issues such as the effects of different liner material properties and changes in residual limb volume on limb tissue response.

Supplementary Material

11517_2017_1758_Fig10_ESM. FIGURE S1.

FEM source scans of two participant states, socket partially donned and socket fully donned. The partially donned state was selected for the source geometry, because when the socket was fully donned the liner compressed locally inside the socket in a manner that could not be correct in the FEM.

11517_2017_1758_Fig11_ESM. FIGURE S2.

Effects of coefficient of friction between the limb and liner. Pressure and skin-liner slip distance are plotted for participant 1 along a sagittal slice aligned with the mid-patellar tendon. The peak in pressure and shear stress at 125 mm corresponds to the brim of the socket contacting the patellar tendon. As the CoF reached 2.0, the simulation outputs closely agreed with a bonded limb-liner contact. This implied that CoFs greater than 2.0 would result in minimal changes to the simulation output.

11517_2017_1758_Fig9_ESM. FIGURE S3.

The outputs of the uniaxial and compound load profiles were compared to ensure consistent locations of peak pressure and resultant shear stress. The compound load profile had a greater energy input into the simulation, and this resulted in greater magnitude of the anterior stresses compared to the uniaxial profile. However, no meaningful changes were observed in the locations of the primary loading points.

Biographies

John C Cagle, PhD

John Cagle is a research mechanical engineer in the Department of Bioengineering at the University of Washington. He received his B.S. in Mechanical Engineering from the University of Denver and Ph.D. from the University of Washington. His research interests include interface mechanics, sensors, and composite design.

Per G Reinhall, PhD

Per Reinhall is chair and professor of the Mechanical Engineering Department at the University of Washington and the CTO of VICIS and Marine Construction Technologies. He is also the Director of the Boeing Advanced Research Center at UW and a UW Presidential Entrepreneurial Faculty Fellow. He obtained his B.S. degree in Mechanical Engineering from University of Washington and his M.S. and Ph.D. in Applied Mechanics from Caltech. His main research interests include dynamical systems, mechanics, acoustics, and biomechanics with a focus on the development of biomedical devices, noise, shock and vibration control, and automated assembly.

Kate J Allyn, CPO

Kate Allyn, CPO/L, FAAOP, has practiced Prosthetics and Orthotics since 1992. She obtained her Orthotic and Prosthetic education at Northwestern University, and completed her residency in Orthotics at the Cleveland Clinic Foundation, Ohio. Kate works in the Department of Bioengineering at University of Washington, focusing on understanding and managing residual limb volume changes and improving prosthetic socket design. She is a member of the Research Council and an Executive Board Member of the American Academy of Orthotists & Prosthetists.

Jake McLean

Jake McLean is a research mechanical engineer in the Department of Bioengineering at the University of Washington, specializing in mechanical design and 3D surface modeling. He received his Bachelor of Science degree in Mechanical Engineering from the University of Idaho.

Paul Hinrichs

Paul Hinrichs is a research electrical engineer in the Department of Bioengineering at the University of Washington. He received his MSc in experimental physics from the University of Wisconsin–Madison and BSc degrees in physics and mathematics from the University of Minnesota. His expertise is in portable high-precision instrumentation design.

Brian J Hafner, PhD

Brian Hafner is an Associate Professor in Rehabilitation Medicine and Adjunct Associate Professor in Bioengineering at the University of Washington. His research is focused on measurement of performance, function, and quality-of-life in persons with limb loss. Dr. Hafner received his Bachelor of Science degree in Mechanical Engineering from Oklahoma State University, and his PhD in Bioengineering from the University of Washington.

Joan E Sanders, PhD

Joan Sanders is a Professor of Bioengineering at the University of Washington. She received a Bachelor of Science degree in Mechanical Engineering from Stanford University, a Master of Science degree in Mechanical Engineering from Northwestern University, and a PhD in Bioengineering from the University of Washington. Dr. Sanders’ research interests are in the development of new measurement techniques and interface mechanics and materials as applied to external prosthetics.