Dissipative structures in biological systems: bistability, oscillations, spatial patterns and waves

Abstract

The goal of this review article is to assess how relevant is the concept of dissipative structure for understanding the dynamical bases of non-equilibrium self-organization in biological systems, and to see where it has been applied in the five decades since it was initially proposed by Ilya Prigogine. Dissipative structures can be classified into four types, which will be considered, in turn, and illustrated by biological examples: (i) multistability, in the form of bistability and tristability, which involve the coexistence of two or three stable steady states, or in the form of birhythmicity, which involves the coexistence between two stable rhythms; (ii) temporal dissipative structures in the form of sustained oscillations, illustrated by biological rhythms; (iii) spatial dissipative structures, known as Turing patterns; and (iv) spatio-temporal structures in the form of propagating waves. Rhythms occur with widely different periods at all levels of biological organization, from neural, cardiac and metabolic oscillations to circadian clocks and the cell cycle; they play key roles in physiology and in many disorders. New rhythms are being uncovered while artificial ones are produced by synthetic biology. Rhythms provide the richest source of examples of dissipative structures in biological systems. Bistability has been observed experimentally, but has primarily been investigated in theoretical models in an increasingly wide range of biological contexts, from the genetic to the cell and animal population levels, both in physiological conditions and in disease. Bistable transitions have been implicated in the progression between the different phases of the cell cycle and, more generally, in the process of cell fate specification in the developing embryo. Turing patterns are exemplified by the formation of some periodic structures in the course of development and by skin stripe patterns in animals. Spatio-temporal patterns in the form of propagating waves are observed within cells as well as in intercellular communication. This review illustrates how dissipative structures of all sorts abound in biological systems.

This article is part of the theme issue ‘Dissipative structures in matter out of equilibrium: from chemistry, photonics and biology (part 1)’.

1. Dissipative structures: from spatio-temporal to functional organization

From the very beginning of his scientific work, Ilya Prigogine devoted his attention to non-equilibrium self-organization in chemical, physical and biological systems [1–3]. Although trained primarily in chemistry and physics, Prigogine was always attracted by the self-organizing properties of living organisms [4]. It is thus not surprising that when Prigogine started his investigations on the origin of order in chemical systems, he chose a biological example to study the conditions in which sustained oscillations occur in time. Prigogine & Balescu [5] thus used a chemical analogue of the model proposed by Volterra for predator--prey interactions to show that periodic behaviour can occur at a sufficient distance from thermodynamic equilibrium, provided the system is governed by nonlinear kinetic laws. Already one decade earlier, Prigogine, then aged 29, had written with Jean-Marie Wiame, a microbiologist also working at the Université Libre de Bruxelles, a brief note in French entitled ‘Biologie et thermodynamique des phénomènes irréversibles’ [6], where they applied the non-equilibrium thermodynamic approach to the evolution of biological systems.

Building on the pioneering work of Turing published in 1952 [7], in the 1960s Prigogine extended his analysis to self-organization in space [8,9]. To stress the fact that non-equilibrium self-organization in open systems requires the dissipation of energy, Prigogine coined the term ‘dissipative structures’, so as to distinguish them from equilibrium structures [3,10]. The conditions for dissipative structures are readily encountered in living systems, which are (i) open, (ii) governed by nonlinear evolution equations, and (iii) operate far from thermodynamic equilibrium. A major source of nonlinearity is provided by a variety of feedback processes, which evolved at the cellular and supracellular levels to optimize the operation and survival capability of biological systems. The special interest of Prigogine for self-organization in biological systems is again reflected by the title ‘Structure, dissipation and life’ that he gave in 1967 to the contribution, published in 1969, where he first introduced the concept of dissipative structures [10].

Dissipative structures occur far from equilibrium when a steady state becomes unstable at a critical bifurcation point [11,12]. Sustained oscillations in time represent temporal dissipative structures, while spatial dissipative structures, often referred to as Turing patterns, represent a stationary inhomogeneous distribution of chemical species in space [7,8,11]. Spatio-temporal structures in the form of propagating waves mix self-organization in time and space. Finally, the nonlinearity of the evolution equations allows for the coexistence of multiple attractors [11,13]. The latter situation corresponds to the appearance of a form of functional order. While bistability is associated with the coexistence of two stable steady states, each of which can be reached from different sets of initial conditions that represent their basins of attraction, the number of coexisting states may be larger. Thus, tristability refers to the situation where three stable steady states coexist. Other modes of coexistence may involve one stable steady state and one periodic attractor (hard excitation), two or three periodic attractors (birhythmicity or trirhythmicity), or the coexistence between periodic and aperiodic oscillations. The latter correspond to chaotic behaviour and to the evolution toward a strange attractor.

Many biological examples of self-organization do not represent dissipative structures, because their origin does not involve the passage by an instability or their maintenance does not require energy dissipation; this is the case, for example, for self-assembled structures such as biological membranes. Moreover, many, if not most biochemical reactions, even if they operate far from equilibrium, do not produce instabilities and simply evolve to a stable steady state. Examples of dissipative structures nevertheless abound in biological systems in which they play essential roles.

Given the rich repertoire of dissipative structures and the ubiquitousness of nonlinearity at the cellular and supracellular levels, it seems befitting to examine in this article how relevant is the concept of dissipative structure for understanding the dynamical bases of self-organization in biological systems, and to see where it has been applied to illuminate the dynamics of life processes in the five decades since it was initially proposed by Ilya Prigogine. Because innumerable articles were devoted to topics related to these issues in the last decades, the aim of this paper will be to give an overview of dissipative structures of various kinds in biological systems, without attempting to provide an exhaustive list of relevant publications, because such endeavour would exceed the scope of a brief review. I will examine, in turn, biological examples of multiple steady states, temporal structures in the form of oscillations, and, finally, spatial and spatio-temporal structures. As will become clear in the following, biological rhythms provide a particularly rich source of examples of dissipative structures in biology [14–16]; these were recently the topic of more detailed reviews [17,18].

2. Multiple steady states: bistability

While multiple steady states have been observed experimentally in biological systems, their occurrence has primarily been found in theoretical models. One reason is that observing experimentally multiple attractors is not as straightforward as observing oscillations. To demonstrate the coexistence between two stable steady states one needs to show either an all-or-none transition from one stable steady state to another upon suprathreshold perturbation, or the occurrence of hysteresis. In the latter phenomenon, the system follows one branch of steady states when increasing a control parameter until a critical limit point is reached at which the system jumps to another branch of stable steady states; upon decreasing the control parameter, the system then follows the second branch until it jumps back to the original branch when another limit point corresponding to a lower critical value of the control parameter is reached. By contrast, observing a regime of oscillations is less cumbersome and more straightforward as it does not require the use of suprathreshold perturbations nor any demonstration of hysteresis.

The mention of bistability in a biological context dates back at least to 1949, when Delbrück mentioned the possibility of a coexistence of multiple stable steady states in a genetic regulatory network [19]. A few years later bistability was considered theoretically in a model for a structured enzyme system [20]. With the surge of interest triggered in the 1960s by the development of thermodynamic studies initiated by Prigogine and the discovery of chemical oscillations in the Belousov–Zhabothinsky reaction, a number of theoretical studies focused in the early 1970s on the phenomenon of bistability. Such studies of bistability included models for an excitable membrane [21], an autocatalytic enzyme reaction [22] and autocatalytic synthesis of small oligomers in the context of chemical evolution [23], to cite but a few early examples.

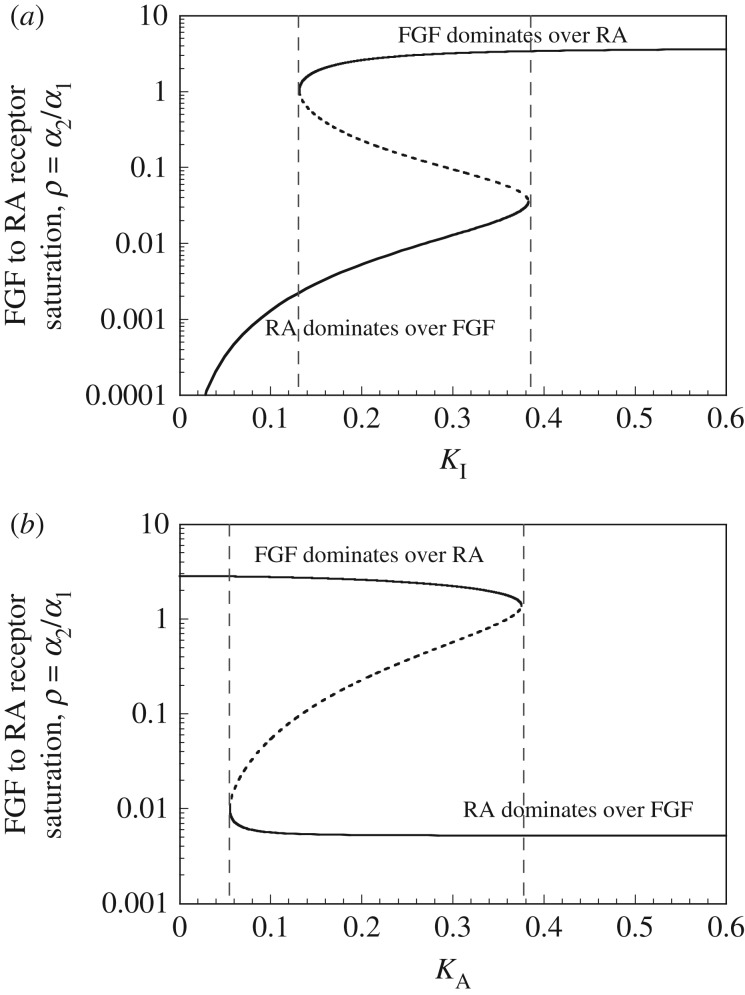
Observing bistability in theoretical models is relatively easier than in experiments, because bifurcation diagrams readily show how the steady state of a system changes as a function of a control parameter. In the case of bistability, the bifurcation diagram showing the steady state of a particular variable as a function of a control parameter takes the form of an S- or Z-shaped curve. Then, in a range bounded by two critical values of the control parameter, the system admits three steady states, two of which are stable whereas the intermediate steady state is unstable. To illustrate bistable behaviour we show in figure 1 the multiple steady states obtained in a model for a regulatory network involved in the control of somitogenesis [24]. This model is based on the mutual inhibition of the fibroblast growth factor (FGF) and retinoic acid (RA). The curves show the coexistence between two stable steady states (solid lines) and an unstable steady state (dashed line) as a function of two distinct control parameters of the model, an inhibition constant (figure 1a) and an activation constant (figure 1b).

Figure 1.

Bistability in a model for the regulatory network underlying the formation of somites, the precursors of vertebrae, in the course of development. The model is based on the mutual inhibition of fibroblast growth factor (FGF) and retinoic acid (RA). Two stable steady states (solid lines) separated by an unstable steady state (dashed line) coexist in a parameter range bounded by two critical values. The steady states are plotted as a function of two distinct parameters: (a) an inhibition constant and (b) an activation constant. See Goldbeter et al. [24] for details.

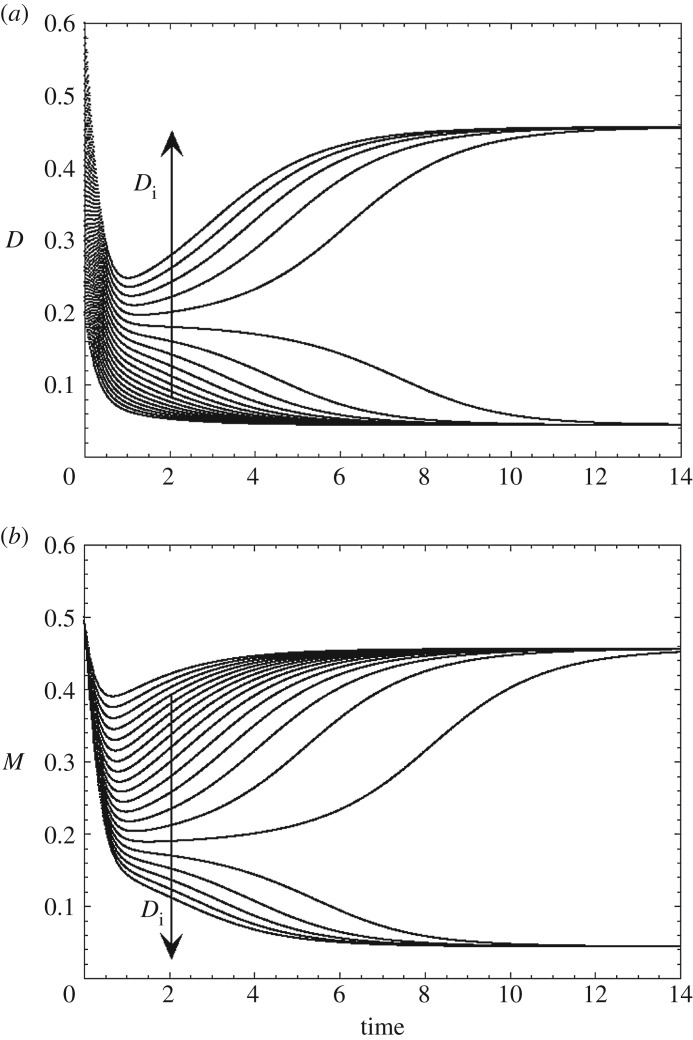
To demonstrate the coexistence of multiple stable attractors, as in the experiments, one can demonstrate the existence of hysteresis, by successively increasing and decreasing the value of some control parameters. In a range bounded by two critical values of this parameter, the system is capable of evolving to either one of two stable steady states, depending on initial conditions. The transition from one stable steady state to another can also be triggered by means of a suprathreshold perturbation, e.g. by increasing or decreasing the level of one of the variables of the system. This is illustrated in figure 2 in a model for bipolar disorders [25,26] based on the mutual inhibition of two neural circuits promoting, respectively, depression (D) or mania (M); the curves show the time evolution of variables D and M for 20 increasing initial values of D, denoted D_i. Above a critical value of D_i, M switches abruptly from a high to a low steady state, while D concomitantly switches from a low to a high steady state. Both stable steady states coexist for the same set of parameter values. Because the experimental demonstration of bistability is not as straightforward as observing oscillations, the examples of bistable transitions documented experimentally may represent only the tip of the iceberg of the phenomenon of multistability, which could be much more frequent, as suggested by the theoretical predictions of a variety of models.

Figure 2.

Transitions between two stable steady states in a model for bipolar disorders [25,26] based on the putative mutual inhibition of two neural circuits promoting depression (D) or mania (M), respectively. The curves show the time evolution of variables D and M for 20 increasing initial values of D, denoted D_i. Above a threshold value of D_i, D switches abruptly from a low to a high steady state (a), while M concomitantly switches from a high to a low steady state (b).

Theoretical studies of bistability have accumulated at an accelerating pace in the last decade. The phenomenon has been invoked in a wide variety of biological contexts. To illustrate how widespread is the range of these contexts let us mention 10 examples of the prediction of bistability in theoretical models—the list is by no means exhaustive, and a few additional examples will be mentioned below: (i) the calcium/calmodulin-dependent protein kinase II (CaMKII) switch implicated in long-term memory in the nervous system [27,28], (ii) an experimental and theoretical study of the enzyme isocitrate dehydrogenase [29], (iii) mechanisms for cellular signal transduction [30,31]; (iv) NF-κB signalling [32], (v) the dynamics of the lac operon in Escherichia coli [33–35], which provided one of the first experimental examples of all-or-none transition associated with the bistable phenomenon [36]; (vi) the dynamics of the immune response [37,38] (see [39] for a recent example); (vii) cell signalling involved in the control of the cytoskeleton [40,41]; (viii) programmed cell death, i.e. apoptosis, involving activation of the caspase cascade [42,43]; (ix) sex determination in Drosophila [44] and vertebrates [45]; and (x) transitions in cortical dynamics [46].

Bistable transitions have also been invoked in the pathophysiology of a number of diseases including type II diabetes [47,48], prion diseases [49], Alzheimer's disease [50] and autoimmune diseases [51]. In many of these models displaying bistability, the two branches of stable steady states correspond to the healthy and diseased states, respectively. By contrast, in a model for bipolar disorders [25,26], the two stable steady states correspond to the two poles of the disease, i.e. mania and depression (figure 2).

In spite of the huge range of topics for which bistability has been invoked in biological systems at the cellular and supracellular levels, cell differentiation remains the field in which the occurrence of multiple attractors has repeatedly been implicated [52–59] as a mechanism underlying cell fate specification. As conjectured by René Thomas [53,54], multistationarity requires the presence of positive circuits in the underlying regulatory network. Such positive circuits commonly originate in genetic regulatory networks from direct positive feedback or mutual inhibition [30,53]. Cell fate specification often involves a succession of binary choices between two stable steady states, due to mutual inhibition of two transcription factors, as discussed in detail by Zhou & Huang [59]. Theoretical models suggest that cell fate specification may sometimes involve more than two stable steady states [60–64].

Platelet aggregation, which has been studied for a long time [65,66], plays key physiological roles. In haemostasis, the aggregation of platelet cells underlies the formation of the haemostatic plug that leads to cessation of bleeding from small vascular injuries, while in pathological conditions platelet aggregation may result in thrombosis. Activated platelets secrete ADP in response to ADP stimulation—this self-amplification represents a form of direct positive feedback. As shown by Born [65,66], upon adding incremental amounts of ADP to a platelet suspension the cells irreversibly aggregate above a critical level of ADP stimulation. A preliminary theoretical study suggests [67] that this phenomenon may be viewed as a bistable transition. Platelet aggregation deserves to be studied theoretically in detail in view of its significance in physiological and pathological conditions.

Besides direct positive feedback, mutual inhibition as a source of bistability is a recurrent regulatory motif in biological systems [30,53]. This illustrates well how the same regulatory structure produces similar dynamical phenomena at different levels of biological organization. Two mutually inhibiting repressors were shown to produce bistability in a synthetic genetic network referred to as toggle switch [68]. As discussed above, in many instances cell fate specification appears to be based on mutual inhibition of two transcription factors [59]; a similar mechanism was proposed for the formation of a sharp determination front in the course of somitogenesis [24] (figure 1). Mutual inhibition resulting in bistability is also encountered in ecology, where competition of two animal populations for the same resource can lead either to their coexistence or to elimination of one or the other population; in the case of bistability, which population vanishes depends on initial conditions. Such a situation represents, since the work of Volterra on competing animal populations, a classical problem in theoretical ecology [69]. Mutual inhibition has been invoked as a source of bistability at other levels of biological organization. Two putative, mutually inhibiting neural circuits producing bistability have been implicated theoretically in the mechanism underlying REM-non-REM transitions during sleep [70,71] as well as transitions between mania and depression in bipolar disorders [25,26] (figure 2).

Bistable transitions originating from positive feedback abound in the cell cycle, which provides one of the richest sources for bistability at the cellular level. A network of enzymes known as cyclin-dependent kinases (Cdks) governs progression along the successive phases of the cell cycle [72]. Positive feedback in Cdk regulation was shown theoretically and experimentally to lead to bistable transitions [73,74]. The Cdk network presents many instances of positive feedback and therefore contains multiple sources of bistability, which contribute to render the transition from one to the next phase of the cycle irreversible [75,76]. As discussed in the following section, the dynamics of the Cdk network also provides an important example of oscillatory behaviour at the cellular level [77]. Theoretical studies of models of the Cdk network suggest that the multiplicity of positive feedback loops enhances the robustness of Cdk oscillations with respect to molecular noise, by increasing the range of bistability in the various Cdk modules prior to their coupling and, hence, the resistance of sustained oscillations to fluctuations [78,79].

Multiple attractors are not limited to the coexistence between two stable steady states, i.e. bistability. A stable steady state may thus coexist with a stable oscillatory regime; this situation of hard excitation has been observed experimentally in neuronal dynamics [80,81]. The coexistence may also involve two stable oscillatory regimes, either periodic or chaotic [82]. Such birhythmicity has been reported in a chemical system [83]. In a biological context, birhythmicity has been observed in the R15 neuron in Aplysia, which, upon perturbation, is capable of switching reversibly between tonic oscillations of the membrane potential and complex oscillations of the bursting type [84]. The control of transitions between multiple stable steady states or multiple stable rhythms has been investigated both in physical and biological systems [13,85].

Biological examples of bistability are not limited to the genetic, biochemical and cellular levels, or to the physiology of an organism. At a higher level, besides the dynamics of animal populations, the phenomenon has also been discussed in regard to the dynamics of microbial populations within the gut microbiome [86], and in ecology as a mechanism underlying the switch between different patterns of vegetation [87].

A particular situation arises when bistable transitions become irreversible [88,89]. This happens when one of the limit points at which the system switches from one branch of stable steady states to the other branch becomes physically inaccessible. Then the system can only pass from one of the two branches of steady states to the other upon changing the control parameter, and cannot undergo the reverse transition when the parameter changes in the other direction. Bistability in such a case is not associated with hysteresis. Because of their irreversible nature, such transitions could play important roles in physiological and pathological conditions. A recent experimental and theoretical study shows that irreversible bistability may occur in the life cycle of the parasite Trypanosoma brucei responsible for sleeping sickness [90].

3. Biological rhythms as temporal dissipative structures

Oscillations in chemical systems were initially observed in electrochemistry. Lotka in 1920 proposed a model for undamped chemical oscillations [91]. A few sparse examples of other chemical oscillations had occasionally been reported over the years, until the publication of the thermodynamic analysis of oscillatory behaviour by Prigogine & Balescu [5]. Interest in periodic chemical reactions began to surge at the end of the 1960s [92,93] for a number of concomitant reasons. While the Belousov–Zhabotinsky reaction provided a prototypic example of periodic chemical reaction whose mechanism was soon to be elucidated [94], the discovery of glycolytic oscillations in yeast cells and extracts around 1965 [95–98] provided another example of oscillatory behaviour, this time in a biochemical system. The thermodynamic and nonlinear kinetic framework developed at the same time by Prigogine and co-workers significantly contributed to putting chemical and biochemical oscillations into focus, and to transform them into a thriving, new topic of research. In subsequent years the field of chemical oscillations developed rapidly, and new families of oscillatory chemical reactions continue to be identified [99]. Over the years, it nevertheless became increasingly clear that biological systems provide the richest source of examples of periodic behaviour. This view was long supported by observations of periodic variations of the electric activity of nerve cells [100].

Rhythmic phenomena occur at all levels of biological organization, with periods that cover more than 10 orders of magnitude (see detailed list in Table 1 in a recent review [18]). Most of these rhythms occur at the cellular level (for more detailed accounts and additional references see [14–18,98,101]). New examples of biological rhythms continue to be uncovered, while artificial oscillatory networks based on gene regulation are being synthesized. The reason why rhythmic behaviour is so tightly associated with life is due to the many feedback processes that control the dynamics of biological systems at the biochemical, cellular and supracellular levels. Because oscillations are a systemic property associated with regulatory interactions between the constitutive elements of biological systems, from metabolic and genetic networks to cell and animal populations, rhythmic phenomena represent a prototypic field of research in Systems Biology. Starting with the work of Volterra [102] on the oscillatory dynamics of predator-prey systems in ecology, biological rhythms have been studied by means of both experimental and modelling approaches [14,98,103,104]. The mechanisms and roles of biological rhythms in physiology and disease were recently reviewed [18].

While bistability is often predicted by the analysis of a model before being observed experimentally, the opposite generally holds for oscillations: indeed, the experimental evidence for a particular example of oscillatory behaviour generally precedes its mathematical modelling. The experimental demonstration of oscillations is more straightforward. Moreover, the existence of many physiological rhythms is part of our everyday experience, as exemplified by the cardiac and respiratory rhythms, or the sleep--wake cycle.

Biological rhythms can be classified according to their period. The fastest rhythms occur in electrically excitable cells such as neurons, or cardiac and other muscle cells, with periods of a fraction of a second. Flight muscles involved in the beating of insect wings can oscillate as fast as 1000 beats per second [105]. The mechanism of spontaneous oscillations of the membrane potential has long been studied experimentally and theoretically in nerve and cardiac cells. The mechanism involves the interplay between several voltage-dependent membrane conductances dedicated to a few ionic species such as Na⁺, K⁺ and Ca⁺⁺, as modelled by Hodgkin & Huxley [106]. Whereas periodic behaviour generally takes the form of trains of action potentials, oscillations of the bursting type occur when additional ion conductances are implicated in the oscillations. Bursting consists of a periodic alternation of phases of high-frequency spiking and rest, as exemplified by the R15 neuron in Aplysia [107,108]. So many rhythms of different frequencies are observed in the brain that one may consider it as a truly rhythmic organ [109]. The electrocardiogram and the electroencephalogram are commonly used to probe the periodic activity of the heart and brain, respectively.

The cardiac rhythm is initiated in specialized tissues of the heart, called nodes, which contain a few thousands of cells. Thus, the periodic signal originates in the sinoatrial node, located in the right atrium of the heart. The atrioventricular node provides another potential source of cardiac oscillations. Models for the periodic variation of the membrane potential in these cells have been developed over time [110]. These models allow the role of each ion conductance in the origin of various types of cardiac arrhythmia to be tested. Moreover, such models are currently included in global models of the heart, with the aim of developing a virtual organ by means of a computational approach [111].

Besides electrical oscillations in neurons and cardiac cells, many types of oscillations have been observed in non-excitable cells. Examples include intracellular Ca⁺⁺ oscillations, oscillatory enzyme reactions, periodic signals controlling the aggregation of social amoebas after starvation, pulsatile hormone secretion and circadian rhythms.

Discovered some three decades ago, oscillations in intracellular Ca⁺⁺ occur in a wide variety of cells stimulated by a hormone or a neurotransmitter. The oscillations occur in a window of stimulation intensity; when stimulation is too weak or too strong, cells evolve to a low or high stable steady-state level of intracellular Ca⁺⁺, respectively [112]. The mechanism of oscillations involves both positive and negative feedback on Ca⁺⁺ release from intracellular stores. Models based on these regulations account for experimental observations [113–115]. A further interest of the phenomenon is that Ca⁺⁺ oscillations are encoded in terms of their frequency [113]. ‘Encoded’ means that the cellular response is controlled not by the amplitude of Ca⁺⁺ spikes (which are often all-or-none) but by their frequency. The mechanism for frequency decoding involves the enzyme calmodulin kinase II (CaMKII) [116–118]. Among the many roles played by Ca⁺⁺ oscillations, one is particularly significant in view of its key role in development. Egg fertilization by sperm induces a train of Ca⁺⁺ oscillations, which are required for the exit from meiosis and resumption of cell divisions leading to the subsequent development of the embryo into an adult organism [119]. The protein factor injected by sperm into the egg is an isoform of the enzyme phospholipase C [120] which triggers the onset of Ca⁺⁺ oscillations by raising the level of inositol 1,4,5-triphosphate, an intracellular messenger that elicits the release of Ca⁺⁺ from intracellular stores.

Glycolytic oscillations, discovered in yeast some five decades ago, still represent the prototype of oscillatory behaviour in a metabolic pathway [95–98,121]. This periodic phenomenon also provided an early example of biochemical clock isolated in vitro, around the time when the Belousov–Zhabotinsky reaction provided a prototypic example of chemical clock. Sustained oscillations occur in glycolysis with a period of several minutes as a result of the regulation of phosphofructokinase, a key allosteric enzyme in the pathway. Models taking into account the allosteric properties of the enzyme and its activation by a reaction product account for the in vitro observation that the oscillations occur in a range bounded by two critical values of the constant rate of substrate input [122,123]. Glycolytic oscillations can be entrained in vitro by a periodic input of substrate [124]. Coupling allows the synchronization of the oscillations in yeast cell populations [125,126]. Research on oscillating glycolysis continues to this day, with emphasis on periodic behaviour in individual yeast cells [127].

Another well-known biochemical oscillator controls the wavelike aggregation of Dictyostelium discoideum amoebas after starvation [128]. The cells respond chemotactically to signals of cyclic AMP (cAMP) emitted by aggregation centres with a periodicity of several minutes [129]. The mechanism responsible for cAMP oscillations involves both positive and negative feedback through the cAMP receptor present at the surface of the cell membrane: cAMP released by the cells binds to the receptor and triggers cAMP synthesis by adenylate cyclase inside the cells, while at the same time extracellular cAMP induces receptor desensitization [130]. This mechanism also underlies the frequency encoding of cAMP oscillations in these cells [131]. Intracellular regulation of phosphodiesterase, the enzyme degrading cAMP, may also play a role in the mechanism of oscillations [132]. The cAMP signalling system in D. discoideum represents a prototype for spatio-temporal organization and for pulsatile intercellular communication [133].

Frequency encoding based on receptor desensitization provides a link between cAMP oscillations in D. discoideum and pulsatile patterns of hormone secretion [98,134]. Most hormones are secreted in pulses rather than continuously [135]. The frequency ranges from one pulse every 10 min for insulin, to one pulse per hour for the hormone GnRH and one pulse of growth hormone (GH) every 3–5 h. As for Ca⁺⁺ and cAMP oscillations, pulsatile signals of GnRH and GH are encoded in terms of their frequency [136,137].

One of the most remarkable examples of spatio-temporal organization is provided by the segmentation clock, which controls the periodic formation of somites, the precursors of vertebrae, in the course of embryonic development. This clock has a period that ranges from 30 min in zebrafish to 90 min and 2 h in chicken and rat, respectively [138–141]. The molecular mechanism of oscillations is not fully clarified yet but is known to implicate the Notch, Wnt and Fgf signalling pathways [142]. Modelling the dynamics of the three pathways showed that they can all oscillate due to negative feedback, and synchronize, when taking into account their coupling through regulatory interactions [143]. Extending the model to take into account signal propagation in space allowed to address explicitly the periodic formation of somites along the developing embryo [144]. The existence of the segmentation clock was predicted theoretically [145] before it was demonstrated experimentally two decades later [146].

Circadian clocks remain the prototype of biological rhythms [147,148]. At the very core of chronobiology, these rhythms occur in all eukaryotes and some bacterial species with an autonomous period close to 24 h. Their role is to allow adaptation of living organisms to the periodic alternation of day and night, which characterizes the environment on earth. Innumerable articles—only a few will be mentioned here— have been devoted to the mechanism and function of circadian rhythms, since the seminal work of Konopka & Benzer, who showed [149] in 1971 that circadian rhythms of locomotion occur in Drosophila and involve a gene called Per (for ‘period’). In work which earned them the Nobel Prize in Physiology or Medicine in 2017, Rosbash, Hall and Young subsequently showed that the PER protein forms a complex with another protein, TIM, and that the mechanism of circadian oscillations in Drosophila involves negative autoregulation of gene expression by the PER--TIM complex; moreover, light controls the Drosophila circadian clock by modulating the rate of TIM degradation [150–152].

These studies were later extended to other organisms, including Neurospora and mammals, in which similar molecular mechanisms based on transcriptional regulation and protein modification were uncovered [153–155]. If the circadian mechanism in these cells still relies on negative autoregulation of gene expression, the nature of the dozen clock genes involved may differ, as well as the effect of light. Thus, in mammals, light acts by inducing gene expression, in contrast with the situation observed in Drosophila. The physiological importance of the circadian clock is reflected by the fact that it controls key functions such as the sleep--wake cycle [156] as well as the periodic expression of a majority of genes in mammals [157,158].

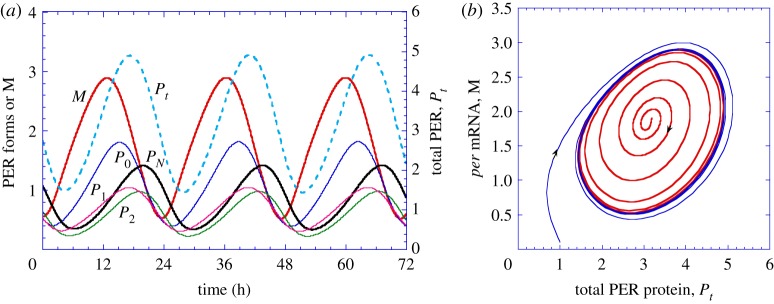
From a theoretical point of view, models for the circadian clock in Drosophila, Neurospora and mammals show that negative autoregulation of transcription can give rise to circadian oscillations of the limit cycle type in a domain in parameter space bounded by critical values of control parameters [159–162], as illustrated in figure 3. Circadian clocks thus represent temporal dissipative structures, which originate at the cellular level from regulatory feedback loops that destabilize a non-equilibrium steady state. In mammals, circadian rhythms synchronize among cells of the suprachiasmatic nucleus, which is the circadian pacemaker located in the hypothalamus [163]. In agreement with this observation, models show that coupled circadian oscillators do spontaneously synchronize [164,165].

Figure 3.

Sustained oscillations in a model for circadian oscillations of the PER protein in Drosophila. The oscillations (a) correspond to the evolution to a limit cycle (b), which is reached regardless of initial conditions. Two different initial conditions lead to the same closed trajectory (from Goldbeter [159]). (Online version in colour.)

In cyanobacteria, circadian rhythm may also originate from a non-transcriptional regulatory mechanism. Thus, in Synechococcus, in vitro studies show [166] that the mechanism of circadian oscillations relies on a cascade of phosphorylations of the KaiC protein. This oscillator appears to be coupled to a mechanism based on transcriptional regulation [167].

The cellular rhythm that controls cell division is referred to as mitotic oscillator. Experimental progress on the mechanism driving the cell division cycle was first made on early cell cycles in amphibian embryos, which occur with a period of 30 min. These early cycles are driven by the periodic activation of a mitosis promoting factor, MPF, which is a complex between a cyclin protein and a cyclin-dependent kinase, Cdc2 (aka Cdk1) [168]. The periodicity in Cdc2 activity again relies on a negative feedback loop. Early models for the embryonic cell cycles showed that sustained oscillations indeed occur as a result of such negative autoregulation [98,169]. Models incorporating positive feedback loops were proposed by Novák & Tyson [170] for the embryonic cell cycle. As recalled in the previous section, experimental studies based on theoretical models demonstrated in frog egg extracts the occurrence of bistability and of the associated phenomenon of hysteresis in which Cdc2 periodically undergoes abrupt transitions between a low and a high state of activity, driven by variations in the level of cyclin due to alternating phases of accumulation and Cdc2-induced degradation [73,74].

In mammals, a network of cyclin-dependent kinases controls the transitions between the successive phases G1, S (DNA replication), G2 and M (mitosis) of the cell cycle. The Cdks are controlled through phosphorylation--dephosphorylation, through cyclin synthesis and degradation, and also through association with protein inhibitors such as p21 [72]. A detailed model for the Cdk network shows that in the presence of sufficient amounts of growth factor the Cdk network is capable of temporal self-organization in the form of sustained oscillations of the limit cycle type [77,171]. The transition from cell quiescence to cell proliferation can be viewed as the switch from a stable to an unstable steady state of the Cdk network beyond a bifurcation point. Beyond this critical point of instability, instead of reaching a stable steady level in the course of time, the various cyclin/Cdk complexes undergo sustained oscillations, which correspond to the ordered, sequential activation of the various cyclin/Cdk complexes that control the successive phases of the cell cycle. The passage through the bifurcation point is also controlled by external factors such as the stiffness of the extracellular matrix and high cell density, which leads to cell cycle arrest [172]. Tyson & Novak [173] propose, alternatively, that the cell cycle behaves as a sequential machine rather than as an autonomous clock. The two views [174] are not necessarily incompatible when the oscillations are of a relaxation nature [175].

The cell cycle illustrates well how different cellular rhythms may interact within the same cell. Thus the circadian clock controls the expression of several genes of the cell cycle network [176]. Such coupling of the cell cycle to the circadian clock results in the synchronization of these two major cellular rhythms [177,178]. Pancreatic β cells, which secrete insulin, provide another example for the interaction of multiple cellular rhythms—in this case, membrane potential bursting and oscillations in both glycolysis and Ca²⁺ signalling [179]. The presence of multiple sources of instability in complex cellular regulatory networks, such as the Cdk network driving the mammalian cell cycle, raises the possibility that the interaction between such multiple oscillatory mechanisms might give rise to complex oscillatory behaviour, including chaos [180].

Since the year 2000 additional examples of cellular rhythms have been uncovered. These include the oscillatory synthesis of the tumour suppressor p53 [181,182] and of the transcription factor NF-κB [183] with a periodicity of a few hours, and oscillations with a period of several minutes in the nucleocytoplasmic shuttling of transcription factors such as Msn2 [184,185] and Crz1 [186] in yeast cells subjected to stress. Based on identified regulatory mechanisms, models for each of these oscillatory processes show that periodic behaviour occurs in precise conditions, beyond a critical point of instability of a non-equilibrium steady state [187–190].

The year 2000 signalled a new transition in the study of cellular rhythms, with the construction of a first example of synthetic oscillator. The latter, expressed in E. coli, was called Repressilator as it consists of a set of three repressors coupled cyclically [191]. This example was followed by the development of a variety of synthetic oscillatory networks expressed in bacteria or mammalian cells, mostly based on genetic regulation. These synthetic networks display oscillations with tunable frequencies covering a wide range, from tens of minutes up to 24 h [192,193].

All biological rhythms mentioned so far originate at the cellular level or in networks of interconnected cells [194], as is the case for neural networks that operate as central pattern generators which control movement [195]. Rhythms do also occur at the supracellular level, with longer periods. Examples include the ovarian cycle that controls ovulation, predator--prey oscillations in ecological systems—which were likely among the first biological rhythms to be described mathematically [102]—and seasonal rhythms which allow many insect, plant and animal species to adapt to the other, annual periodicity of the environment. Longer-period rhythms are known, such as those which characterize the emergence of some species of cicadas every 13 or 17 years. Some annual rhythms are driven by internal clocks entrained by changes in the photoperiod, which measures the duration of the light phase with respect to the duration of night; the photoperiod increases in spring and summer (long days) and decreases in fall and winter (short days). Cyclical processes such as the ovarian cycle and the life cycle of periodic cicadas involve the passage through a discontinuity—degeneration of the corpus luteum in the case of the ovulatory cycle, or death of an organism marking the end of a life cycle. These processes are cyclical but do nor represent self-sustained oscillations, in contrast with most cellular rhythms, which belong to the class of continuous or quasi-discontinuous (relaxation) oscillations of the limit cycle type.

4. Spatial and spatio-temporal dissipative structures

While the interest of Ilya Prigogine in non-equilibrium self-organization initially pertained to oscillations, it soon extended to patterns of self-organization in space, which were predicted mathematically by Turing [7]. Several examples of spatial dissipative structures at the supracellular level were proposed in the early 1970s. Thus the aggregation of social amoebae in response to a chemotactic signal emitted by the cells was viewed as an instability of the homogeneous steady-state distribution of cells, leading to the formation of a spatial structure in the form of distinct multicellular aggregates [196,197]. A prototypic example of periodic spatial pattern in developing embryos is provided by the emergence of body segments in Drosophila. The formation of the segments is associated with the appearance of bands of gene expression. This band pattern was seen, for a time, as a spatial dissipative structure. However, extensive genetic and modelling studies showed that the mechanism for the formation of the spatial pattern is based on gradients in maternal proteins acting on a cascade of gap, pair-rule and segment-polarity genes [198,199]. Mutations in some of these genes can suppress certain bands in the pattern, in contrast with what would be expected if the latter would form spontaneously as a spatial dissipative structure characterized by a unique wavelength.

Spatial dissipative structures involving instability with respect to diffusion, i.e. Turing patterns, were invoked in the formation of pigmented stripe or dot patterns in fish skin [200–202] (see [203] for a recent discussion of the genetic aspects of this patterning process), or scale patterns in lizards [204]. Another example of a Turing pattern studied experimentally and theoretically pertains to the formation of skeleton [205] and fingers [206,207] in the course of development. Patterns of spatial self-organization have also been observed and analysed at a more macroscopic level. One example is given by the vegetation patterns known as ‘tiger bush’, which have been analysed in terms of spatial dissipative structures [208,209].

Biological pattern formation viewed as spatial self-organization has further been discussed in the books of Meinhardt [210], Murray [211] and Camazine et al. [212]. The examples cover a wide range of scales, from spatial patterning in embryos to the construction of nests in insect societies. The case of social insects shows how regulatory feedback loops can take multiple forms, depending on the scale of observation. Thus, in ant colonies, because of trail reinforcement by recruited individuals, the deposition of pheromones by foraging ants gives an example of self-amplification, or positive feedback [213], which corresponds to autocatalysis in chemical and biochemical reactions.

Probably more common than purely spatial dissipative structures are spatio-temporal structures that combine non-equilibrium self-organization in time and space. Spatio-temporal patterns are observed in a variety of biological phenomena ranging from the axonal propagation of nerve impulses to the propagation of electrical excitation in the heart, both in physiological conditions and in cardiac fibrillation. Other examples include the propagation of intracellular and intercellular Ca⁺⁺ waves [114,214–216], and the spiral and concentric patterns of chemotactic movements associated with oscillations and waves of cAMP which govern aggregation in D. discoideum cells [128,217] (figure 4). Travelling waves were also observed and modelled in Myxococcus bacteria [218]. The phenomenon involves a biochemical oscillator, modelled as the Frizzilator (because it involves the Frz protein), which governs the spontaneous reversal of direction in cell swarming with a period of minutes [219].

Figure 4.

Wavelike aggregation of Dictyostelium discoideum amoebae after starvation. The amoebae aggregate in bands forming concentric or spiral patterns in response to pulses of cyclic AMP (cAMP) emitted with a period of 5–10 min by cells behaving as aggregation centres (reproduced from Alcantara & Monk [128]).

Spatial patterns may also originate from the combination of a clock and a moving wavefront involving the transition between two stables steady states [145]. One of the best examples of such spatial pattern originating from a combination of oscillations, diffusion and bistability is provided by the periodic formation of somites in vertebrate embryos [24,138,141,144,145]. Wave propagation has been demonstrated experimentally in this system both within the embryo [138,141] and in cell preparations removed from the embryo [220]. Wavelike propagation in embryos also occurs for cell division, as shown by recent experiments in Xenopus and Drosophila embryos, which provide yet further examples of spatio-temporal organization [221–223].

As discussed in §3, experiments in synthetic biology have allowed the construction of new, artificial oscillators, often with tunable periods. Coupling such oscillatory networks expressed in bacteria to a mechanism of quorum sensing capable of synchronizing cells gives rise to propagating waves in bacterial populations [224]. Another example of spatio-temporal organization in prokaryotes pertains to the wavelike growth of bacterial biofilms, associated with metabolic oscillations based on time-delayed negative feedback [225,226]. At a macroscopic level and on much longer time scales, waves are also observed in the spatial propagation of epidemies with a period of one up to a few years [227].

5. Concluding remarks

Some five decades since the introduction of the concept of dissipative structures by Ilya Prigogine [2,3,10] this issue of Philosophical Transactions A provides a good opportunity to assess how his pioneering work has resonated with developments in the field of self-organization, more specifically in the life sciences. As outlined in the Introduction, it is useful to subdivide the field of non-equilibrium self-organization into three main classes, which often overlap: multiple attractors, oscillatory behaviour and patterns of spatio-temporal organization. Each of these modes of self-organization has been found in chemistry and also in physics, notably in hydrodynamics and nonlinear optics; these fields are particularly rich in non-equilibrium instabilities [11–13]. This review makes it clear, however, that biological sciences represent a privileged domain for the occurrence of dissipative structures of all sorts.

Literally thousands of papers—only a minute fraction of which could be cited here—have been devoted to experimental and/or theoretical studies of bistability, oscillations, Turing patterns and propagating waves in biological systems. Among these various modes of non-equilibrium self-organization, oscillations and bistability appear to be the most common, followed by spatio-temporal and purely spatial non-equilibrium structures. The number of periodic processes in biology is truly staggering: as recalled in §3, and recently reviewed in further detail elsewhere [17,18], rhythms are observed at all levels of biological organization, with periods ranging from a fraction of a second to years. Rhythms underlie key physiological functions—the heartbeat, respiration, functioning of the brain, control of movements, ovulation, plant flowering, animal migrations, while a ubiquitous cellular rhythm, the circadian clock, controls the periodic expression of most genes as well as the sleep--wake cycle in mammals. Biological rhythms also play important roles in the aetiology of many physiological disorders [228]. Some examples of physiological disorders due to alterations of biological rhythms or to the spurious onset of oscillatory behaviour are listed in table 2 in ref. [18]).

Multiple attractors represent a form of functional organization, because the phenomenon endows a system with the capability of operating in either one of two stable states, in the same experimental conditions, or for the same set of parameter values in a theoretical model. As outlined in §2, the most common form of multiple attractors involves the coexistence of two stable steady states, i.e. bistability. The phenomenon of bistability has been observed experimentally in a number of biological systems, but much more frequently in theoretical models, for reasons explained above. In contrast with oscillatory behaviour, which occurs or not in a given set of experimental conditions, the observation of bistability requires suprathreshold perturbations to demonstrate that the system can switch from one stable state to another, or the demonstration of hysteresis. This is also easier to achieve in theoretical models than in experiments. Moreover, one begins to look experimentally for bistability once a model has suggested the possibility of its occurrence. What is striking, however, is the variety of biological contexts in which bistability has been invoked, mostly in theoretical models. In §2 we have mentioned more than a dozen examples; the list is far from being exhaustive, and in fact is rapidly growing. However, the field in which bistability appears to play major roles is definitely cell fate specification, which process is of key importance for successful embryonic development. A recent example studied theoretically and experimentally pertains to the preadipocyte-to-adipocyte conversion in fat cell differentiation [229,230]. Tristability, i.e. the coexistence between three stable steady states, can also be involved in cell differentiation into distinct cell fates. The development of an organism can thus be viewed as a succession of transitions between distinct cell fates produced by ever-changing genetic regulatory networks admitting multiple steady states [52,53,59,231].

Besides bistability, multiple attractors may also involve the coexistence between a stable steady state and a stable oscillatory regime (hard excitation), or between two or three stable periodic regimes (bi- or trirhythmicity). Hard excitation and birhythmicity, as recalled in §2, have been observed experimentally in neurobiology. They nevertheless remain more rare than bistability.

Spatial patterns of self-organization, known as Turing patterns, were discussed in §4. Several examples of such structures have been described and modelled, particularly in the context of morphogenesis. Examples of Turing patterns in biological systems are, so far, less numerous than those illustrating temporal oscillatory behaviour and, to a lesser extent, bistability. Spatial dissipative structures are encountered in embryogenesis, even if all types of morphogenetic processes do not necessarily represent Turing patterns. Besides purely spatial non-equilibrium structures, propagating waves are frequently observed at the cellular and supracellular levels, where they appear to be closely associated with cellular rhythms. Such patterns of spatio-temporal self-organization play roles in intracellular as well as intercellular communication.

Most non-equilibrium structures discussed in this review possess a chemical origin in the numerous feedback regulations that control the dynamics of cellular processes. Instabilities leading to bistability or oscillations are known to occur in physical systems, particularly in mechanics, hydrodynamics and nonlinear optics [11–13]. In biology, an additional source of instabilities is provided by mechanochemical coupling [232,233], which merges chemical or biochemical reactions with force-generating physical processes. Non-equilibrium instabilities of this nature play important roles in the mechanical movements of hair cells [234], in the contractile dynamics of the actomyosin cortex at the cellular level [40,41,235], in tissue shape changes during multicellular morphogenetic movements such as endocytosis or gastrulation [236,237], and in the morphology of cortical folding in the brain [238,239].

Why are dissipative structures so common in biological systems? If life is such a rich source for multiple attractors, oscillations and spatio-temporal organization, it is because life is inherently nonlinear. This nonlinearity is prone to give rise to instabilities, and originates from the cooperativity of allosteric proteins such as enzymes, ion channels or receptors, and from the multiple feedback loops which control the operation of biological systems at all levels, from cells to tissues, organs and animal populations. Life depends on feedback regulation. Positive feedback is required for bistability, while negative feedback is associated with oscillatory behaviour. Both types of feedback are often intertwined. The examples of the cell cycle and the circadian clock illustrate well how positive and negative feedback loops cooperate to confer on a complex regulatory network the capability of temporal self-organization in the form of sustained oscillations. The occurrence of nonlinear interactions capable of giving rise to bistability or oscillations might in fact be more widespread than envisaged on the basis of identified feedback loops. Thus, while a single cycle of protein phosphorylation–dephosphorylation can give rise to ultrasensitivity characterized by a steep threshold [240], multiple protein phosphorylation, which is commonly encountered in cell regulation, could by itself give rise to bistability under appropriate conditions [241–243]. Other types of protein-protein interactions provide further potential sources for bistable or oscillatory behaviour [244,245].

Some 50 years after Prigogine introduced dissipative structures in nonlinear science, it appears that this unifying concept has proved remarkably fruitful for apprehending the dynamic of life in its multiple aspects. It has also given a crucial impetus for the development of the field of nonlinear science, in which numerous problems remain open and new questions continually arise. Studies of non-equilibrium self-organization in biological systems, at the biochemical, cellular as well as supracellular levels, both in physiological and pathological conditions, are thriving more than ever.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

This work was supported by the F.R.S.-FNRS (CDR grant no. 26027580, ‘Auto-organisation in cell signalling’).