Topography of epithelial–mesenchymal plasticity

Significance

Cells can change their phenotype from epithelial to mesenchymal during development and in cancer progression, where this transition is often associated with metastasis and poor disease prognosis. Here we show this process involves the transit through a multitude of metastable hybrid phenotypes in a way that is similar to the driven dynamics of disordered materials. Our method shows that highly aggressive hybrid epithelial/mesenchymal cell phenotypes are located in metastable regions that can easily switch under external and internal perturbations. We propose a general mapping strategy that can be used for other pathways, providing a useful tool to visualize the ever increasing number of gene expression data obtained from single cells and tissues.

Abstract

The transition between epithelial and mesenchymal states has fundamental importance for embryonic development, stem cell reprogramming, and cancer progression. Here, we construct a topographic map underlying epithelial–mesenchymal transitions using a combination of numerical simulations of a Boolean network model and the analysis of bulk and single-cell gene expression data. The map reveals a multitude of metastable hybrid phenotypic states, separating stable epithelial and mesenchymal states, and is reminiscent of the free energy measured in glassy materials and disordered solids. Our work not only elucidates the nature of hybrid mesenchymal/epithelial states but also provides a general strategy to construct a topographic representation of phenotypic plasticity from gene expression data using statistical physics methods.

Epithelial (E) cells can transdifferentiate into mesenchymal (M) cells and vice versa under a cohort of transcription factors, including the Snail and Zeb families (1). The E to M transition (EMT), associated with the loss of cell–cell adhesion and the gain of invasive traits, is considered to be a hallmark of plasticity within a stem cell population and is particularly relevant for tumors. For this reason, a great effort has been devoted in the past to identify the critical biological functions regulating the EMT and its reverse, the M to E transition (MET). Almost 80% of human malignancies originate from E tissues, and a transition toward an M phenotype is usually associated with more aggressive potential (2–5). Emerging evidence shows that the EMT is a multiple-step process where cells express a mix of markers, both characteristic of E and M cells (6–8). These recent results are blurring the rigid distinction between E and M phenotypes, indicating that cancer cells can acquire hybrid E/M phenotypes, combining invasive capabilities with intracellular adhesion (9, 10), becoming extremely aggressive and associated with poor patient outcome (11, 12).

According to an old and influential metaphor from Waddington (13), the cell phenotype is analogous to a marble rolling over an epigenetic landscape, and phenotypic plasticity corresponds to the marble crossing a hill separating different valleys. This landscape should correspond to the attractors of the kinetics of gene regulatory networks (14–21) and be encoded in gene expression data (22, 23). Here, we combine numerical simulations of a large Boolean model for the EMT–MET network with the analysis of a wide set of bulk and single-cell gene expression data to reconstruct the topography underlying E/M plasticity. Genetic circuits regulating the EMT have been widely investigated theoretically, with models ranging from simple switches composed of a few genes (24) to large complex networks requiring extensive numerical simulations, in both discrete (25, 26) and continuous time (27). Some of these models have provided insights into particular EMTs, generating hypotheses that have later been experimentally tested (26). We show how these models can be used to rationalize and classify genetic drivers of the EMT and clarify the nature of hybrid E/M states guided by the Waddington picture (13).

Our results reveal that EMT/MET occurs across an extremely complex landscape characterized by a startling number of valleys and mountains organized according to a scale-free hierarchical statistical pattern. We observe a multitude of stable E/M states separated by a series of progressively less stable and more hybrid states that are increasingly prone to phenotypic changes in response to external perturbations. Hence, EMTs and METs can take place in widely different locations and across multiple paths, in close analogy with nonequilibrium phase transitions in disordered solids (28, 29).

Model

To reconstruct the topographic landscape of E/M plasticity, we chose to build on the large Boolean network model previously used to investigate EMT in hepatocellular carcinoma (25, 26). Since the model as it stands is hardwired toward EMT and MET is completely suppressed, we added to the model a missing contribution from the LIF/KLF4 pathway, whose role for MET has been widely reported (30, 31) ( see SI Appendix, Fig. S1, Dataset S1, and SI Appendix for details). In this way, we obtained a network of $N=72$ nodes, whose state is defined by a string of binary variables $\left\{s_i\right\}$, determining if each gene/factor $i$ is expressed/present ($s_i=1$) or not ($s_i=-1$). Regulatory relations between two nodes $i$ and $j$ were encoded into a (nonsymmetric) matrix $J_{ij}$ taking the value $J_{ij}=1$ if $j$ promotes $i$ and $J_{ij}=-1$ when $j$ inhibits $i$ (see Dataset S2). The network nodes evolve asynchronously according to a simple majority rule, so that the node is set to $s_i=1$ if the sum of its promoting interactions is larger than the sum of its inhibitory ones (see Fig. 1A) (32). In case of ties, the node was not updated, keeping its present state (15). This evolution rule is the binary version of the half-functional rule recently proposed in ref. 27 to construct continuum kinetic reaction models from pathways and can be formally expressed as

$$s_i\left(t+1\right)=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\sum _j{J}_{ij}{s}_j\left(t\right)\right),$$ [1]

which is the same equation used to simulate the zero-temperature dynamics in random ferromagnets (28) and spin glasses (29). (Modifications of the model that include local random fields and their relation to network reconstruction errors are discussed in SI Appendix. See also SI Appendix, Fig. S8.) Guided by the analogy with magnetic systems, we defined a pseudo-Hamiltonian $H=-{\sum }_{i,j}\hspace{0.17em}{J}_{ij}\hspace{0.17em}{s}_i{s}_j$. When interactions are strictly symmetric ($J_{ij}=J_{ji}$), the fixed points of Eq. 1 are local minima of $H$. This is not guaranteed in our case since the interaction matrix is not symmetric (33, 34). We can, however, still show that $H$ is lowered under repeated application of the evolution rule in Eq. 1 (see SI Appendix for full derivations and SI Appendix, Fig. S9). Hence, $H$ provides a measure of the stability of a network state, with low-$H$ states being more stable than high-$H$ states.

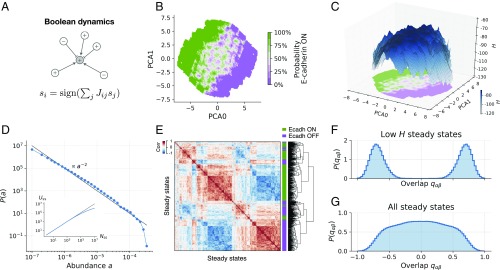
Fig. 1.

The topography of E/M states displays a hierarchical complex structure. (A) Illustration of the Boolean update rule. The state of a node $s_i$ depends on the state of its promoters ($J_{ij}=+1$, $\to$) and inhibitors ($J_{ij}=-1$, ). (B) PCA projection of $10^6$ steady states. Color corresponds to the ratio of steady states that express E-cadherin. The panel shows intricate patterns of transition between areas of high/low Ecadherin expression probability, colored in green/violet shades. (C) A 3D reconstruction of topography of EMT. The $xy$ projection reproduces the data in B. The $z$ axis corresponds to the value of $H$, showing that high-$H$ states (colored in darker blue shades) coincide with the central transition area in B. (D) Distribution of steady-state abundances, computed from $10^7$ steady states of the EMT model (blue symbols). The relative abundance $a$ of a steady state is the fraction of times it is found, starting from random initial conditions. The black line of slope −2 is shown only as a guide to the eye. The Inset shows the number of distinct steady states $U_{ss}$ as a function of the total number of steady states $N_{ss}$ found in the simulations. (E) Clustering of steady states, computed using 500 steady states of the model. The heat map shows the correlation between steady states. Colors adjacent to the dendogram mark the expression of E-cadherin (green) or lack of expression (violet). States expressing E-cadherin cluster together but display additional hierarchical organization. (F) Overlap distribution over the 20% of steady states with lowest $H$. A two-peak distribution marks the presence of two symmetric sets as in disordered magnets. (G) The broad overlap distribution over all steady states resembles the one observed in spin glasses.

Results

Simulated E/M Topography Displays Fractal Features.

A phenotypic landscape associated with our EMT/MET network can be reconstructed by performing a large number ($M_0=10^7$) of simulations, starting from random initial conditions until the network reaches a steady state where $s_i$ does not change. (No limit cycles are found; see SI Appendix for details.) In this way, we find a large number of distinct steady states that can be projected into a two-dimensional map using principal component analysis (PCA). We classify these steady states according to the expression of E-cadherin (CDH1), which we use as a reporter of the E/M phenotype (see Fig. 1B). The E/M map reconstructed from the model shows a clear separation between E and M states, with a boundary layer where E and M states coexist in very close proximity. A topographic representation of the stability of the states can be obtained by projecting $H$ on the same two-dimensional map (Fig. 1C) showing that the boundary layer is more elevated with respect to pure E/M states, suggesting that those states are less stable. Furthermore, the map displays a very rough topography, with two main valleys separated by a large barrier populated by smaller and smaller valleys.

Given the sheer amount of distinct steady states (see Fig. 1D, Inset), we resorted to a statistical analysis and computed the probability distribution $P\left(a\right)$ of the relative abundances of the states, where $a$ is the fraction of times we find a given state. Fig. 1D shows that $P\left(a\right)$ is a power law distribution, indicating that most of the states are very rarely found [when $a$ is small, $P\left(a\right)$ is large], but few states are found multiple times [when $a$ is large, $P\left(a\right)$ is small]. Alternative functional forms for $P\left(a\right)$ are discussed in SI Appendix and shown in SI Appendix, Fig. S10. The presence of a power law is a signature of a scale-free fractal organization of the map, as is also apparent by the correlation matrix of the states. Fig 1E shows the presence of large correlated clusters subdivided into smaller and smaller clusters. In the physics of disordered systems, a hierarchical organization of the states is traditionally revealed by a broad distribution $P\left(q_{\alpha \beta }\right)$ of states’ overlap $q_{\alpha \beta }={\sum }_i\left(s_i^{\alpha }{s}_i^{\beta }\right)/N$, measuring the similarity between two states $\left\{s_i^{\alpha }\right\}$ and $\left\{s_i^{\beta }\right\}$ (35). Hierarchical ground state structures have been observed in short-range Ising spin glasses (see refs. 36 and 37). When we restrict the sampling to low-$H$ states, $P\left(q_{\alpha \beta }\right)$ displays a two-peak structure, indicating the presence of two classes of distinct and separate states (Fig. 1F), but when we consider all steady states, the overlap distribution becomes very broad, resembling the one observed in spin glasses, as noticed a long time ago for random Boolean networks (38–40).

Simulated Phenotypic Transitions Reveal Scale-Free Stochastic Fluctuations.

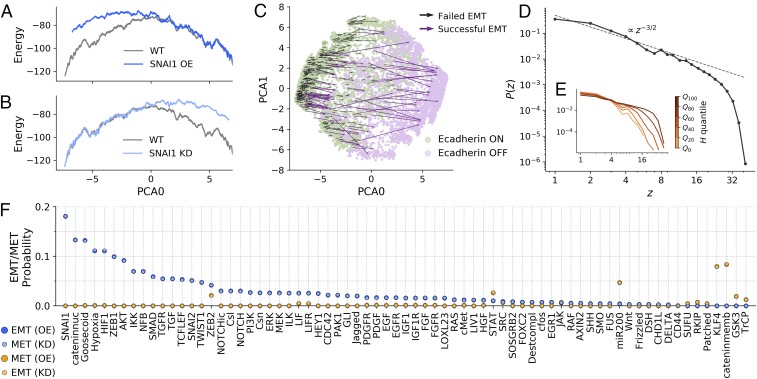
Once the topography associated with the E/M landscape has been established, we investigate how the landscape changes when each one of the nodes is held fixed to $s_i=\pm 1$, which simulates overexpression (OE) or knockdown (KD) of the corresponding gene (see SI Appendix for details). As an example, Fig. 2 A and B reports the one-dimensional projection of the topography under OE or KD of the SNAIL1 gene, a well-known inducer of the EMT. SNAIL1 OE leads to a rightward tilt of the landscape, favoring the M phenotype, while under SNAIL1 KD, the landscape tilts to the left, favoring the E state. This behavior is reminiscent of the effect of a magnetic field in a disordered magnet, where the free-energy landscape tilts in the direction of the field. If the network is initially in an E state, SNAIL1 OE can induce EMT, but the success rate and the trajectory crucially depend on the initial state (see Fig. 2C), with high-$H$ states much more likely to undergo EMT than low-$H$ states (see SI Appendix, Fig. S2). The variability in the outcome resulting from the OE/KD of a single gene can also be quantified by measuring the distribution of the number of nodes $z$ affected by the process (see Fig. 2D). The distribution decays as power law $P\left(z\right)\sim z^{-\tau }$, up to a cutoff value that increases with the $H$ value of the initial state (see Fig. 2E), a further indication that high-$H$ states are more susceptible to fluctuations (see also SI Appendix, Fig. S2). The avalanche exponent of the power law distribution is $\tau \simeq 3/2$, a value expected for mean-field avalanches in driven disordered systems (28).

Fig. 2.

EMT/MET occurs with different probabilities through multiple paths. The model shows many forms of EMT/MET, and these occur with different probabilities. (A and B) One-dimensional PCA projection of the $H$ landscape where (A) OE or (B) KD of SNAI1 tilts the landscape toward the M or E regions, respectively. (C) Transition map under SNAI1 OE. The model displays different forms of SNAI1-induced EMT. (D) The distribution of gene expression avalanches after individual KD/OE is a power law with exponent $\tau \simeq 1.5$. (E) The cutoff of the distribution depends on $H$, quantified here by quartiles, with high-$H$ states producing larger avalanches. (F) EMT/MET probabilities under KD/OE conditions. The model lays out a nondeterministic picture of EMT/MET, where well-known factors such as SNAI1 (EMT) or KLF4 (MET) induce phenotypic transitions with higher probability (see Materials and Methods and SI Appendix, Fig. S2 for further details).

Using the model, it is possible to perform OE/KD on all of the nodes and estimate the probability of each node to induce EMT or MET (see Fig. 2F). Ranking the nodes as a function of their relevance for EMT, we recover well-known EMT inducers such as SNAIL1, ZEB1, or TGF-$\beta$ and MET suppressors such as KLF4 and mir-200. The general pattern is that an inducer of EMT by OE also induces MET by KD and similarly for MET. We also simulate a transient version of OE/KD where a node is switched ($s_i\to -s_i$), but it is then allowed to eventually relax back to its previous state. The results summarized in SI Appendix, Fig. S2 are similar to those obtained under stable OE/KD, for which the node variable is held fixed throughout the simulation, but the probability of EMT/MET is always smaller.

E/M Topography Inferred from Gene Expression Data Agrees with Simulations.

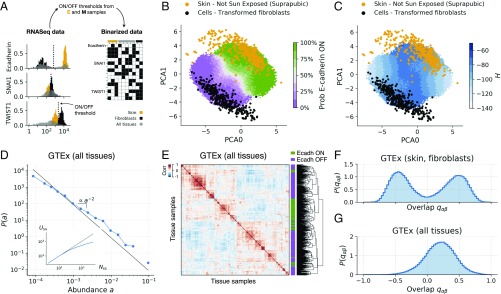
To confirm that the topographic representation of the E/M landscape obtained through the model provides an accurate representation of cellular phenotype, we examined the large cohort of gene expression data from human tissues provided by the GTEx project (41). To directly compare experimental data to the model, we designed a simple binarization strategy to decide whether a gene is expressed or not in a particular sample or cell. To calibrate the binarization scale, we used skin cells and fibroblasts as reference E and M states, respectively, and set a threshold based on the expression distribution of each gene in these two datasets (see Fig. 3A and SI Appendix). Genes whose expression was above the threshold were assigned to $s_i=1$ and otherwise to $s_i=-1$. The same threshold could then be used to binarize all of the 11,688 transcriptomes from different tissues present in the GTEx database.

Fig. 3.

Multitissue gene expression data display statistical features in agreement with simulations. (A) Illustration of the binarization process (see Materials and Methods for details). Gene-level expression data are casted into node-level binary data using binarization thresholds, computed using two reference samples (orange and black coloring). (B) Skin (orange) and fibroblast (black) samples from the GTEx project projected in PCA space. The E-cadherin expression probability in the model is shown with green (100%) to violet (0%) shades. Fibroblast samples tend to be in areas of very low E-cadherin expression probability. (C) Same as B but coloring the model steady states by average $H$. (D) Distribution of abundances, computed using all GTEx binarized samples and the 14 most relevant nodes (see SI Appendix and SI Appendix, Fig. S3 for details). (E) Clustering of 500 GTEx samples (all tissues), displaying a hierarchical structure qualitatively similar to that of the model (compare with Fig. 1E). (F) Overlap distribution over skin and fibroblast samples from the GTEx project (compare with Fig. 1F). (G) Overlap distribution over all GTEx samples (compare with Fig. 1G).

Using the topographic map of the E/M landscape constructed from simulations, we could then localize individual samples projecting their gene expression data on the map as shown in Fig. 3B. We then used the model to infer the stability of each phenotype by computing $H$ associated to each state (Fig. 3C). When we plotted skin cells and fibroblasts on a two-dimensional map, we saw that they correctly fell into E or M regions, respectively (see Fig. 3B), but not all samples had the same value of $H$ (see Fig. 3C). We used the same strategy to localize on the same topographic map the entire set of tissues present in the GTEx database (see SI Appendix, Figs. S4 and S5) and showed that they cover all of the available phase space. Assuming that the GTEx database contains an unbiased random sampling of all of the available states—which is a reasonable assumption given that the GTEx project provides multitissue gene expression data from healthy individuals only (41)—we analyzed the statistical properties of these states. As shown in Fig. 3D, the abundance distribution derived from GTEx data decays as a power law with an exponent that is very close to the one found numerically (compare with Fig. 1D and see SI Appendix and SI Appendix, Fig. S4 for technical details). Furthermore, clustering of the states showed a correlation matrix with hierarchical features that are in reasonable agreement with the prediction of the model (compare Fig. 3E with Fig. 1E). Finally, the overlap distribution displayed a two-peak structure when the statistics were restricted to fibroblasts and skin cells (Fig. 3F), while a single-peaked distribution was found when using all of the GTEx samples (Fig. 3G). This is in close agreement with the simulation results reported in Fig. 1 and confirms that experimental gene expression data give rise to a topographic landscape quantitatively similar to the one predicted by the model.

Tracing Bulk and Single-Cell RNA-Sequencing Trajectories Reveals the Nature of Hybrid E/M States.

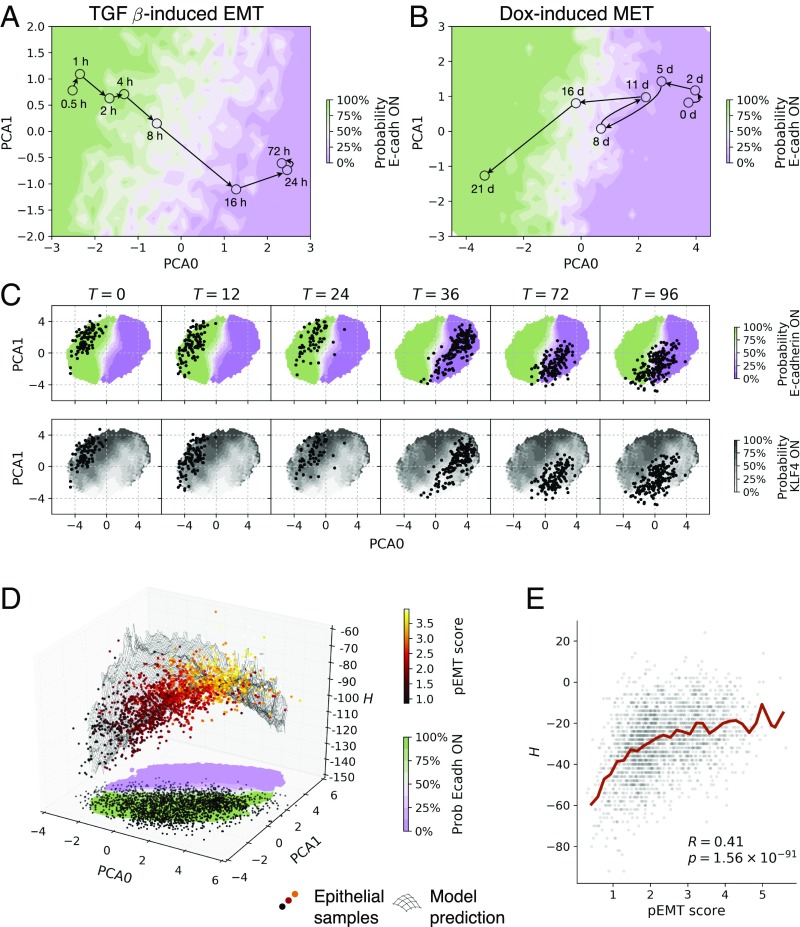
The topographic representation of E/M states derived above can be used to visualize and interpret RNA-sequencing (RNA-seq) data obtained while the cells are undergoing phenotypic transformations. We first consider the classical example of TGF-$\beta$–induced EMT in a human lung adenocarcinoma cell line (42). Fig. 4A reports the trajectory of the states obtained from the bulk RNA-seq data recorded at different time points after TGF-$\beta$ induction. As expected, the trajectory starts from the E region and crosses over to the M region of the map, as revealed by coloring the map according to the predicted expression of CDH1. Conversely, the trajectory obtained from RNA-seq data for DOX-induced MET during somatic cell reprogramming starts from the M valley and moves into the E valley of the landscape (30).

Fig. 4.

Single cells and bulk transcriptomic data yield trajectories through the E/M map with putative hybrid states lying on high-$H$ regions. (A) Data from TGF-$\beta$–treated lung adenocarcinoma cell lines [GSE17708 (42)] yield a trajectory moving from the E to the M region. (B) Data from Dox-induced somatic cell reprogramming [GSE21757 (30)] display a reverse trajectory from M to E. Experimental data are shown as colored symbols with time course marked with arrows. The colored background depends on the ratio of steady states of the model that express E-cadherin at a given location in PCA coordinates, ranging from 100% (green) to 0% (violet). (C) Experimental data from single-cell embryonic-to-endoderm differentiation [GSE75748 (43)] move across the map as cells undergo EMT. The background color indicates the ratio of steady states that express E-cadherin or KLF4 (see SI Appendix, Fig. S7 for more markers). (D) Localization of single-cell gene expression data from tumor cells obtained from head and neck squamous cell carcinoma patients (45). All tumor cells correctly lie in the E region of the map, with high pEMT-scored cells located toward high-$H$ areas. (E) The pEMT score correlates with $H$. Each gray dot represents a single cell. $R$ and $p$ denote the Pearson correlation coefficient and its associated P value (Student’s $t$ test, two-tailed). The red line shows the average $H$.

Our methodology is even more revealing when applied to single-cell RNA-seq (scRNA-seq) data, as shown in Fig. 4C, which reports the time course of the states obtained from scRNA-seq data undergoing EMT during embryonic to endoderm differentiation (43) [see also SI Appendix, Fig. S6 illustrating MET during fibroblast to cardiomyocyte reprogramming in single-cell and bulk samples (44)]. As time goes on, cells originally in the E region transition to the M region between 24 and 36 h. After this time, even though EMT is apparently completed, the kinetic evolution of the cell population does not stop, and the region occupied by single-cell states shrinks. If we color the map by the predicted expression of other markers, we observe that the evolution moves cells in a low-KLF4 region (Fig. 4C; see also SI Appendix, Fig. S7 for similar maps for other markers). Hence, when applied to scRNA-seq data, our method can reveal subtle features associated with phenotypic transformations.

This last point is best illustrated by analyzing recent data (6,000 single cells) obtained from 18 head and neck squamous cell carcinoma patients (45). The original analysis revealed the presence of an aggressive cancer cell population, associated with metastasis and poor prognosis, described as partial-EMT (pEMT) (45). Classification of cells as pEMT was based on a pEMT score computed from the expression values of a set of 100 genes (45), none of which directly maps into nodes of our model. It is thus particularly remarkable to see that the projection of the scRNA-seq data on our map reveals that tumor cells are correctly located in the E region of the map and cells with high pEMT score are typically located on higher ground with respect to low pEMT cells (see Fig. 4D). This is corroborated by the strong correlation between H and the pEMT score, as reported in Fig. 4E.

Discussion

Our work builds on the premise that cell phenotypic plasticity should emerge from the activity of a complex gene regulatory network. The general assumption is that network activity and the ensuing phenotypes are primarily determined by the topology on the network rather than the specific values of the rate constants of individual reactions (27). This allows us to rely on relatively simple Boolean networks, where individual nodes are only characterized by the presence or absence of activity (14). Application of this program to the EMT/MET networks unveils the topography of the epigenetic landscape (13) associated with this kind of phenotypic plasticity. The map reconstructed from the model and confirmed analyzing RNA-seq data shows a rugged landscape with scale-free fractal-like features that are reminiscent of disordered solids and glassy materials (35).

A direct consequence of the landscape we uncover is that individual cells can be found in an extremely large variety of E or M states with intermediate or mixed states hierarchically organized between two sets of more stable and phenotypically well-defined states. Intermediate E/M states are particularly prone to external perturbations, which can lead to scale-free distributed avalanches with the potential to trigger extensive phenotypic changes. This extreme phenotypic plasticity is associated with highly aggressive behavior of tumor cells, as we show by analyzing recent scRNA-seq data from head and neck carcinoma patients. Our topographic representation provides a quantitative representation of the cell phenotypic plastic potential, encoded here in the value of the pseudo-Hamiltonian $H$, which correlates extremely well with other independent measures of pEMT. Furthermore, a topographic representation of the E/M phenotypes allows for a graphical representation of EMTs and METs in a variety of different contexts, from cancer to development and stem cell differentiation. Our general methodological strategy is not restricted to EMT but could be readily applied to other gene regulatory networks relevant to understanding a variety of physiological functions and pathological conditions. The method appears to be a promising tool to build convenient and accessible maps to orient ourselves to the exploding amount of single-cell sequencing data.

Materials and Methods

Conversion of Gene-Level Expression Values to Node-Level Binary States.

We computed node-level expression values as follows: All nodes except Hypoxia and miR200 were mapped to one or more genes (see Dataset S1). If expression data for more than one gene of a given node were available, we took the average of these for noncomplexes and the minimum for complexes. We then binarized the node-level expression data using thresholds computed via a weighted average of the log2 expression of two reference samples (see Datasets for details). We used a weighted average to avoid subsampling when the reference samples were of unequal size. The statistical significance of the binarization procedure was assessed with the Fisher’s exact test. The EMT–MET model takes into account the localization of $\beta$-catenin by considering two separate nodes: one for $\beta$-catenin located in the nucleus, and one for $\beta$-catenin in the membrane. In gene-expression datasets, it is not possible to infer the localization of $\beta$-catenin looking only at the expression level of CTNNB1. To circumvent this issue, we considered $\beta$-catenin to be in the nucleus if its targets TCF/LEF were expressed, and in the membrane otherwise. If CTNNB1 was not expressed, the state of both nodes was set to −1 independently of the value of TCF/LEF.

Datasets.

Data in Fig. 3 came from the GTEx project (41) and were downloaded from the GTEx portal (https://gtexportal.org/home/datasets) on October 12, 2017. We used samples labeled as “Cells–Transformed Fibroblasts” and “Skin–Not Sun Exposed (Suprapubic)” as reference samples for binarization. The PCA basis presented in Fig. 3 B and C was computed using all GTEx samples. All nodes were included in this analysis. The TGB-$\beta$–induced EMT data presented in Fig. 4A were downloaded from the Gene Expression Omnibus (accession no. GSE17708) (42) on September 25, 2017. We used $T=0.5,1$ h and $T=\mathrm{24,72}$ h as reference samples for binarization. A total of 29 nodes with a binarization P value below 0.05 were included in the analysis. We used $10^7$ steady states from the model, restricted to such nodes, to compute the PCA basis in Fig. 4A. Dox-induced MET data in Fig. 4B were downloaded from the Gene Expression Omnibus (accession no. GSE21757) (30), on October 2, 2017. We used $T=0$ d and $T=21$ d as reference samples for binarization. With one single sample per time point, binarization P values could not be computed as explained above. As an alternative, we restricted the analysis to 47 nodes with a fold-change greater than or equal to 0.5. We used $10^7$ steady states from the model, restricted to such nodes, to compute the PCA basis in Fig. 4B. Single-cell data of embryonic-to-endoderm differentiation presented in Fig. 4C were downloaded from the Gene Expression Omnibus (accession no. GSE75748) (43), on September 25, 2017. We used $T=0$ h and $T=96$ h as reference samples. Given the large number of samples, the PCA basis presented in Fig. 4C was computed using the experimental data. All nodes were included in the analysis. Head and neck cancer single-cell data presented in Fig. 4 D and E were obtained from the Gene Expression Omnibus (accession no. GSE103322). We used E and fibroblast samples as reference samples for binarization. The PCA basis was fitted to the single-cell data using all nodes. The pEMT score was computed as the average expression of the 100 genes that constitute the pEMT program in ref. 45. Fibroblast-to-cardiomyocyte differentiation data in SI Appendix, Fig. S6 were downloaded from the Gene Expression Omnibus [accession nos. GSE98570 (bulk data) and GSE98567 (single-cell data)] (44), on November 22, 2017. We used samples labeled as “control” and “reprogramming cells” as reference samples for single-cell data binarization and samples labeled as “D0” and “D14” for bulk data binarization. Single-cell data were used to fit the PCA basis presented in SI Appendix, Fig. S7.