Specificity and robustness of long-distance connections in weighted, interareal connectomes

Significance

Interareal communication occurs along physical pathways. The prevailing hypothesis is that long-distance connections reduce the processing length between brain areas, facilitating efficient communication. We show, in five weighted interareal network datasets, that the correlation of connection weight with distance implies that long-distance connections play only a minor role in reducing path length. Instead, long-distance connections add diversity to brain area inputs and outputs, leading to increasingly complex brain dynamics. These findings help to clarify our understanding of how brain structure contributes to interareal communication.

Abstract

Brain areas’ functional repertoires are shaped by their incoming and outgoing structural connections. In empirically measured networks, most connections are short, reflecting spatial and energetic constraints. Nonetheless, a small number of connections span long distances, consistent with the notion that the functionality of these connections must outweigh their cost. While the precise function of long-distance connections is unknown, the leading hypothesis is that they act to reduce the topological distance between brain areas and increase the efficiency of interareal communication. However, this hypothesis implies a nonspecificity of long-distance connections that we contend is unlikely. Instead, we propose that long-distance connections serve to diversify brain areas’ inputs and outputs, thereby promoting complex dynamics. Through analysis of five weighted interareal network datasets, we show that long-distance connections play only minor roles in reducing average interareal topological distance. In contrast, areas’ long-distance and short-range neighbors exhibit marked differences in their connectivity profiles, suggesting that long-distance connections enhance dissimilarity between areal inputs and outputs. Next, we show that—in isolation—areas’ long-distance connectivity profiles exhibit nonrandom levels of similarity, suggesting that the communication pathways formed by long connections exhibit redundancies that may serve to promote robustness. Finally, we use a linearization of Wilson–Cowan dynamics to simulate the covariance structure of neural activity and show that in the absence of long-distance connections a common measure of functional diversity decreases. Collectively, our findings suggest that long-distance connections are necessary for supporting diverse and complex brain dynamics.

The functional repertoire available to any given brain area is shaped by its structural connections (1–5). The complete set of all areas and all connections comprises a connectome (6), which can be represented as a network and analyzed using tools from network science (7). The network-based approach for studying neural systems is central to the growing field of network neuroscience (8), which seeks to uncover the architectural principles by which the brain is organized and to both generate and test hypotheses of how the brain’s structure supports its function.

Among the most salient organizational features of brain networks is their cost-efficient spatial embedding. Across scales and species, neural elements are arranged such that the brain’s wiring cost—the total length of its connections—is small (9–14). Low wiring cost helps curtail the material and metabolic expense of forming, using, and maintaining connections and is thought to offer evolutionary advantages across species (15, 16). Despite favoring short-range, low-cost connections, brain networks also exhibit a small proportion of long, costly connections, potentially conferring additional functionality. The opposing drives to reduce wiring cost and promote functionally adaptive structural topology may allow nervous systems to maintain function with a low energy budget (17–19).

The precise function of long-distance connections is a matter of debate. According to the most widely accepted account, long-distance connections act as bridges to reduce the topological distance between brain areas, thereby facilitating rapid and efficient interareal communication (20–22). Though widespread, this account is unsatisfactory for two reasons. First, with advances in imaging and reconstruction techniques, it has become clear that connection weights tend to decay monotonically with interareal Euclidean distance (23–26). As a result, the most efficacious communication pathways—networks’ shortest weighted paths—involve predominantly strong, short-range connections (27, 28). Second, reductions in topological distance can occur in a nonspecific manner: Any long-distance connection that reduces topological distance is as good as any other, irrespective of its origin or termination. However, recent empirical evidence indicates that the brain’s long-distance architecture is conserved across and replicable within individuals, suggesting a high level of connectional specificity (29–32).

If long-distance connections are not simply random topological shortcuts, what are they? Here, we address this question through analysis of five weighted interareal network datasets representing mouse, Drosophila, macaque, and human (high- and low-resolution) connectomes. First, we characterize the spatiostructural architecture of brain networks, demonstrating remarkable consistency across species. Drawing upon decades of research in theoretical neuroanatomy, we demonstrate that clustering brain areas based on their connections’ spatial statistics recapitulates aspects of the brain’s intrinsic functional network organization, suggesting a spatiostructural basis for brain function. Next, we show that the brain’s most efficacious communication pathways—its shortest weighted paths—are dominated by short-range connections, undermining the hypothesis that it is the brain’s long-distance connections that reduce its average topological distance. Instead, we hypothesize that long-distance connections introduce diverse inputs and outputs to specific brain areas, in the process promoting dynamical complexity. In support of this hypothesis, we demonstrate the dissimilarity of the connectivity profiles of brain areas’ long-distance and short-range neighbors and that long-distance connectivity profiles form clusters, suggesting that the brain’s long-distance architecture is both specific and also robust. Finally, using dynamical simulations, we show a reduction in the diversity of functional profiles when long-distance connections are removed, whereas the opposite is true when we remove short-range connections. These findings help to clarify the functional role of the brain’s long-distance network architecture and inform future studies investigating network structure and function.

Results

Past studies of unweighted brain networks have reported that long-distance connections act to reduce the topological distance between brain areas, supporting efficient communication over long distances (12, 20). We argue, however, that with new empirical estimates of connections’ weights, this functional interpretation must be revisited. In its place, we propose an alternative set of functional roles for long-distance connections, building on the intuition that brain areas inherit functionality from their patterns of incoming and outgoing connections (1, 5, 33). We claim that the primary function of long-distance connections is to deliver unique inputs to brain areas and to serve as novel targets for brain areas’ outputs, thereby enhancing those areas’ functional diversity. We further hypothesize that long-distance connections are not “one-offs” but instead are insulated and reinforced by other long-distance connections. This architecture naturally leads to increased robustness. In support of these hypotheses, we performed a number of computational experiments involving five interareal connectivity datasets representing four different organisms: mouse, Drosophila, macaque, and human (low-resolution and high-resolution) (Fig. 1). In each network, nodes represent brain areas and connections represent physical pathways (e.g., fiber bundles or axonal projections). Nonetheless, each dataset was distinct in terms of imaging modality, reconstruction technique, and connection weighting scheme. This variability in processing strategy was unintentional, though we exploit this feature to demonstrate the universality of our findings and their robustness to acquisition and processing schemes. Details of network reconstruction and all network measures are provided in SI Appendix, Supplementary Materials, Network Datasets and SI Appendix, Supplementary Materials, Network Analysis. We describe the results of these experiments in the following sections.

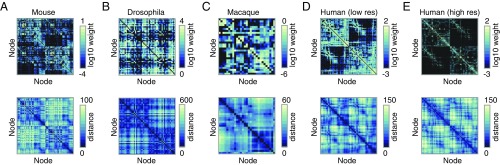
Fig. 1.

Connectivity (Top) and Euclidean distance (Bottom) matrices for (A) mouse, (B) Drosophila, (C) macaque, (D) human (low-resolution), and (E) human (high-resolution) connectome data.

Distance Shapes Weighted Network Architecture.

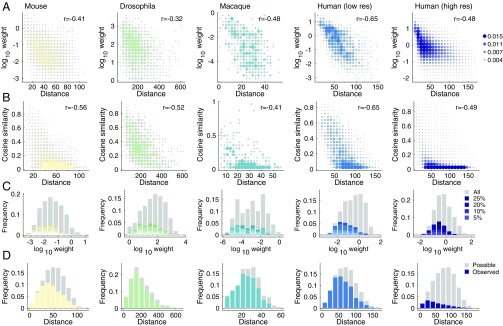
We sought to demonstrate that many network-level properties of weighted interareal networks depend upon distance. We focused on four properties in particular: (i) connection weight, (ii) cosine similarity of connectivity profiles, (iii) frequency of long-distance connections among connections of different lengths, and (iv) connection probability as a function of distance.

First, we computed the Pearson correlation of the logarithm of connections’ weights with Euclidean distances (Fig. 2A). We observed strong negative correlations across all species and scales (maximum $p<10^{-15}$; FDR-corrected). Second, we computed the pairwise cosine similarity among all areas’ connectivity profiles and computed its correlation with Euclidean distance (Fig. 2B). As before, we found that cosine similarity was negatively correlated with Euclidean distance (maximum $p<10^{-15}$; FDR-corrected). Third, we estimated the distributions of the logarithm of the connections’ weights and separately labeled the top 5%, 10%, 20%, and 25% of all connections by length. We then identified within each histogram bin the contributions made by long-distance connections relative to the contributions made by connections of any length (Fig. 2C). We observed that the weakest connections were most often associated with the longest connections, while the strongest connections almost always excluded long-distance connections. Finally, we computed the distribution of all possible interareal Euclidean distances—that is, the elements of the Euclidean distance matrix. Within each histogram bin, we identified which of those possible connections existed and compared with those that did not (Fig. 2D). We found that when possible, short-range connections were almost always observed, whereas many of the possible long-distance connections were not observed.

Fig. 2.

Network distance dependence. (A) Edge weight versus distance. (B) Cosine similarity versus distance. (C) Frequency of edge weights across all connections (gray) and long-distance connections (color; top 25% longest connections). (D) Frequency of connection lengths (gray) and lengths of existing connections (color).

Collectively, these results highlight the powerful role that interareal Euclidean distance plays in shaping the structural organization of weighted interareal brain networks. The consistency of these relationships across five datasets is remarkable considering the range of acquisition and reconstruction techniques and the gross differences in binary network density (the fraction of existing connections irrespective of weight out of all possible connections).

Similarity of Connection Length Distributions Shapes Areal Function.

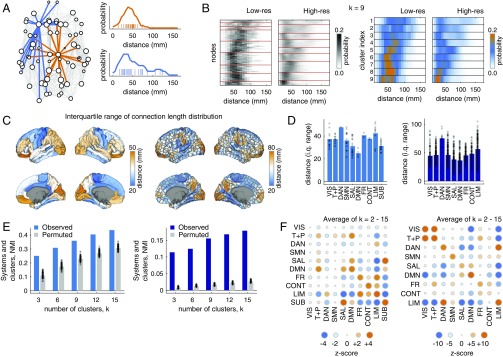
The functionality of brain areas depends on the configuration and weights of their incoming and outgoing connections (1, 5). However, these network properties are correlated with and shaped by distance. It follows, then, that the spatial embedding of a brain area and the lengths of its connections indirectly shape its function. Here, we tested this hypothesis directly by comparing areas’ connection length distributions with their assignments to putative functional systems (see SI Appendix, Supplementary Materials, Network Analysis for definitions of systems).

First, we computed each area’s connection length distribution (Fig. 3 A and B). Distributions showed rich topography and varied widely across the cortex. Some were focused and sharply peaked, while others were broad and included connections of different lengths. To quantify an area’s diversity of connection lengths, we computed the interquartile range of its connection length distribution (Fig. 3C). Broadly, we found that interquartile range varied across functional systems, with dorsal attention and limbic systems exhibiting the greatest levels of diversity in both low- and high-resolution network datasets (Fig. 3D).

Fig. 3.

Regional connection length profiles relate to functional specificity in the human network dataset. (A) Schematic illustrating connection length profiles for two example nodes. The orange node makes mostly short- and midrange connections, while the blue node exhibits some long-distance ($>$100 mm) connections. (B) Connection length distributions for a low- and a high-resolution human network dataset. Nodes are ordered according to the cluster to which they were assigned using a $k$-means algorithm. (C) Interquartile range of brain areas’ connection length distributions. (D) Interquartile range plotted for each functional system: visual (VIS), temporal + precuneus (T+P), dorsal attention (DAN), somatomotor (SMN), salience (SAL), default mode (DMN), frontal (FR), control (CONT), limbic (LIM), and subcortex (SUB; applies only to the low-resolution dataset). (E) Similarity of $k$-means partitions with functional system labels. (F) Standardized ($z$ score) overlap of clusters with functional systems. Circle size indicates the absolute value of the $z$ score, and color indicates the sign of the $z$ score. Large orange circles indicate that areas within pairs of systems were more likely to be coclustered based on their connection length distributions than expected by chance (permutation model).

Next, we clustered areas using a $k$-means algorithm by treating their connection length distributions as features. We implemented the algorithm with 100 random restarts, and we varied the number of clusters from $k=2$ to $k=15$. We compared areas’ cluster and functional system assignments using a normalized mutual information (NMI), where larger NMI values indicate greater overall similarity of clusters. In comparing the observed NMI values with those obtained by randomly permuting areas’ cluster assignments, we observed that NMI was consistently greater than expected by chance (1,000 permutations; $p<10^{-3}$, FDR-corrected) (Fig. 3E). Finally, to determine which functional systems were responsible for driving this similarity, we computed the co-cluster density between every pair of systems. This density represents the fraction of times that pairs of brain areas within those systems were coassigned to the same cluster by the $k$-means algorithm (Fig. 3F). In general, we find that pairs of areas within systems are more likely to be co-clustered than expected by chance. With the exception of the visual system in the low-resolution dataset, all $z$ score mean co-cluster densities were greater than zero, and with the exceptions of the low-resolution visual, dorsal attention, somatomotor, and salience systems, all $z$ scores were statistically significant ($p<0.05$, FDR-corrected).

Collectively, these results demonstrate that functional specialization of a brain area can be associated with the diversity of its connections and their lengths. This observation suggests that areas with dissimilar connection length distributions tend to have different functional roles within the network, allowing us to ascribe functional significance to connections and their lengths.

Long Connections Contribute Little to Shortest, Weighted Paths.

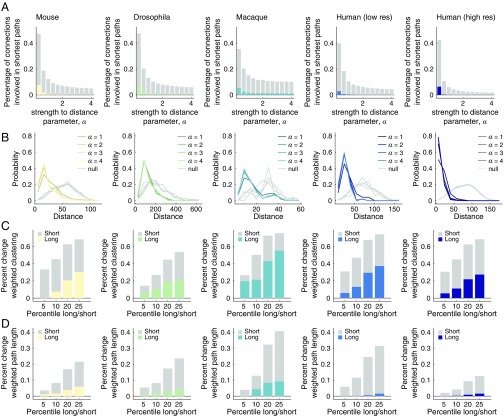
According to current literature, long-distance connections play important roles in networks’ shortest path structure and reduce the number of processing steps between brain areas (20). This observation, however, was made using binary networks where edges carry no weight (34). It is less clear what role long-distance connections play when connections are weighted and when those weights span multiple orders of magnitude. We hypothesized that, due to the disparity between the strongest and weakest connection weights and their dependence on distance, the network’s shortest weighted paths would be dominated by short-range connections.

To test this hypothesis, we computed a parameterized version of edge betweenness centrality, ${\mathcal{B}}_{ij}\left(\alpha \right)$. The $\alpha$ parameter, which we varied in increments of $1/3$ over the range $\left[\mathrm{0,4}\right]$, controlled the decay rate of the necessary mapping of connection weights to length. For each network and for each value of $\alpha$, we obtained an estimate of ${\mathcal{B}}_{ij}\left(\alpha \right)$, the fraction of shortest paths that contained the connection $\left\{i,j\right\}$. Then, we calculated the fraction of long-distance connections (top 25% by length) involved in at least one shortest path. We observed that long-distance connections played a minor role when $\alpha$ was small but an increasingly small role as $\alpha \to 4$ (Fig. 4A). We investigated this behavior further by computing the distribution of connection distances for all pairs of brain areas that participated in at least one shortest path (Fig. 4B). We found that across all datasets, the observed distributions were skewed toward short-range connections, while a null model in which connection topology was preserved but brain area locations were randomly permuted exhibited a broader distribution that involved many more long-distance connections ($p<10^{-5}$; FDR-corrected). These results demonstrate that long-distance connections play relatively minor roles in the shortest path structure of weighted interareal brain networks. Because a network’s shortest paths are interpreted as routes along which brain areas communicate with one another (see, however, refs. 28, 35 for alternative perspectives), these findings suggest that routing information along high-weight pathways composed of short-range connections is more efficient than using weak, long paths for interareal communication.

Fig. 4.

Shortest path use in weighted interareal networks. (A) The fraction of total connections used in shortest paths. The total fraction is shown in gray; the long-distance fraction (top 25% length) is shown in color. The x axis represents the edge strength-to-distance parameter, $\alpha$. Larger values of $\alpha$ increase the relative strength of already-strong connections compared with weak connections. (B) Edge length distributions of connections participating in shortest paths. Gray curves show the mean distribution under a permutation-based null model; colored curves show $\alpha =\mathrm{1,2,3,4}$. (C) Percent change in weighted clustering coefficient as a result of removing different fractions of long and short connections. (D) Percent change in weighted characteristic path length as a result of removing different fractions of long and short connections. Note: bar plots in D are shown with $\alpha =\frac{1}{3}$. At larger values of $\alpha$, long-distance connections play no role in shortest path structure and removing them leads to no change in the weighted characteristic path length.

Next, and for completeness, we demonstrated that removing short-range connections has a much greater impact on statistics related to small worldness than removing the same fraction of long connections. Specifically, we calculated the percent change in mean weighted path length and mean weighted clustering coefficient (Fig. 4 C and D). (Note: The percent change in weighted clustering coefficient and path length are shown as absolute values.) We systematically varied our definition of short-range versus long-distance connections, focusing on the shortest versus longest 5%, 10%, 20%, and 25% of connections according to the Euclidean distances. For all datasets, we observed that the effect of removing strong, short connections was consistently greater than that of removing long connections. These results paint a picture in which nervous system function and communication is dominated by strong, low-cost structural connections. These findings are inconsistent with the view of nervous system function in which most communication pathways are funnelled through a small proportion of long-distance connections.

Long and Short Connections Deliver Dissimilar Inputs and Outputs.

If long-distance connections play little or no role in the shortest weighted path structure of brain networks, what do they contribute? To understand the functional roles of long-distance connections, we compared them against short-range connections in terms of the character of connectivity profiles. An area’s connectivity profile specifies the other areas it can influence and be influenced by, thereby shaping its functional properties.

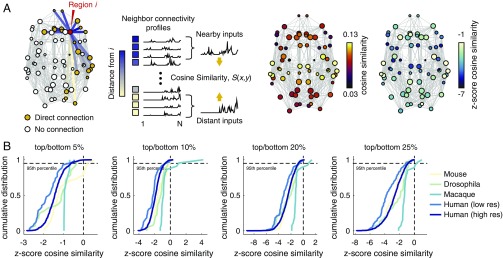
We considered the neighbors of brain area $i$ and examined the average connectivity profile of those nearest and those most distant. We hypothesized that, compared with short-range connections, long-distance connections would deliver unique inputs to and novel targets for an area, $i$, and as a result their respective connectivity profiles should be dissimilar. We quantified this dissimilarity with cosine similarity and compared the value observed in the empirical data to a null distribution generated by keeping the network topology fixed but permuting areas’ spatial locations (Fig. 5A). We computed the similarity of each area’s long-distance and short-range neighbors’ connectivity profiles, while varying the definition of long versus short connections (top/bottom 5%, 10%, 20%, and 25%). We observed that the distribution of standardized similarity scores was consistently negative, indicating that long-distance and short-range connections are more dissimilar from one another than expected by chance (Fig. 5B). More quantitatively, we observed that the cumulative distribution of standardized similarity scores reached 95% before a positive value was encountered (with the exception of the macaque and in one case the mouse dataset). These results confirm that the patterns of incoming and outgoing connections to brain areas are dissimilar compared with one another on the basis of their lengths. This observation suggests that a wealth of long-distance connections may enhance an area’s functional repertoire, by providing unique inputs as well as novel targets for output.

Fig. 5.

Similarity of long- and short-range connectivity profiles. (A) Schematic of processing pipeline for assessing the similarity of long- and short-range inputs. The network depicted is the human, low-resolution network, thresholded to a binary density of $\rho =0.25$ and with subcortical areas removed for visualization purposes only. For the empirical analysis, we performed no thresholding and retained all areas in all computations. All connections incident upon area $i$ are identified and their lengths are tabulated. Node $i$’s neighbors are then classified as either nearby or distant. Note: The same distance threshold was applied uniformly to all brain areas. Separately, the connectivity profiles of nearby versus distant neighbors are summed. The summed profiles, which represent possible inputs to node $i$ from its neighbors, are compared with one another using the cosine similarity measure. This process results in a single similarity score for each area (node). We compare these scores against a null distribution obtained by randomly reclassifying neighbors as nearby versus distant. (B) Cumulative distributions of area-level $z$ scores for each network. The different panels represent variation of the threshold for classifying neighbors as nearby versus distant. From Left to Right, nearby (distant) neighbors were those connected by the top (bottom) 5%, 10%, 20%, and 25% of connection lengths.

Long-Distance Connections Exhibit Degeneracies.

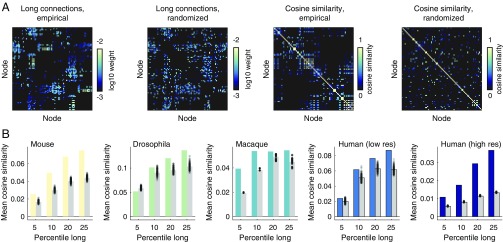
Short-range and long-distance connections lead to neighbors with dissimilar connectivity profiles. However, there are many scenarios in which this could occur. For instance, long-distance connections could be dissimilar not only from short-range connections but also from other long-distance connections. That is, each long-distance connection could link area $i$ to another area whose connectivity profile is not similar to the connectivity profile of any of area $i$’s other long-distance neighbors. In this scenario, each long-distance connection provides a truly unique set of inputs and output targets with respect to one another. This uniqueness, however, could belie a weakness; damage to a single connection would result in the absence of inputs or outputs to or from area $i$. Another possibility is that long-distance connections are reinforced in some way with built-in degeneracy. That is, from area $i$’s perspective, its long-distance connections lead to areas with similar connectivity profiles, so that if one or a small number of connections were damaged, then area $i$ would still receive similar inputs and deliver similar outputs.

To determine the relative evidence supporting either of these possibilities, we imposed distance thresholds on connectivity matrices so that connections below a certain length were excluded (Fig. 6A). We computed the pairwise similarity of each area’s long-distance connectivity profile, and we then computed the mean similarity over all pairs. Larger mean similarity scores are indicators of increased levels of degeneracy. In parallel, we compared these empirical scores against those obtained from a randomized null model in which a network’s degree sequence and edge weight distribution were exactly preserved and in which a network’s connection length distribution and length–weight relationship were preserved approximately (code available at https://www.richardfbetzel.com/code/). We repeated this process as we varied the definition of “long distance” (the top 5%, 10%, 20%, and 25% according to connection lengths). We observed that the mean similarity of long-distance connectivity profiles consistently exceeded that of the null model (nonparametric test, $p<0.01$; FDR-corrected). The lone exception was observed in the Drosophila dataset when using the most exclusive definition of long distance (top 5%). Otherwise, this result was observed across all network datasets.

Fig. 6.

Redundancy of long-range connectivity. (A) Example empirical and randomized networks thresholded to retain the 25% longest connections (Leftmost). We then compute the pairwise cosine similarity between areas’ long-range connectivity profiles (Rightmost). (B) Pairwise similarity measures are averaged for the empirical and randomized networks. We repeat this process using four different definitions of “long range”: 5%, 10%, 20%, and 25% longest connections as defined by Euclidean distance between regional center of mass.

These findings indicate that the long-distance architecture of brain networks exhibits nonrandom correlations. This observation is inconsistent with recently proposed stochastic models of brain network formation in which connections of all lengths are generated by the same wiring rules (23, 36). Instead, areas’ long-distance connections are organized in such a way that many brain areas exhibit highly similar patterns of incoming and outgoing connections.

Long-Distance Connections Lead to Diverse Patterns of Functional Coupling.

The results presented in the previous sections described the structural architecture of brain networks. Though we interpreted these results in terms of brain function and information transmission, the link between structure and function is complicated, and recent findings have cast doubt on the role of shortest paths in network communication (27, 35). In this section, we ground these intuitions in a dynamical model of neural activity and demonstrate that long-distance connections support the functional diversity of brain areas.

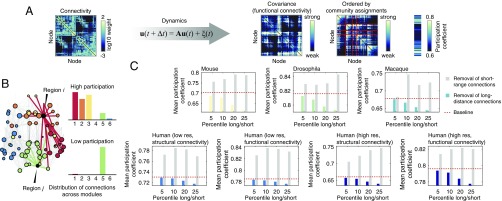
Specifically, we used a linearization of the Wilson–Cowan population model (37) and computed from this model the covariance matrix of brain areas’ temporal activity. The rows of this matrix represent brain areas’ functional fingerprints—their pattern of functional coupling to the $N-1$ other brain areas (Fig. 7A). We define an area’s functional diversity to be equal to its participation coefficient ($\mathcal{P}$) computed given its corresponding covariance matrix and given modules estimated from the structural connectivity network using modularity maximization (Fig. 7B). The functional diversity of the whole brain is defined as the average participation coefficient over all brain areas. We then repeated this procedure, removing the same number of short-range and long-distance connections, and computed the resultant change in average participation coefficient. Across all network datasets, we found that removing long-distance connections always resulted in decreased average participation coefficient, while removing short-range connections resulted in increased average participation coefficient. This finding suggests that reductions in the number of long-distance connections in the network will tend to decrease the overall functional diversity of the brain, resulting in a more specialized and less integrated network as a whole.

Fig. 7.

Linearized dynamics and participation coefficient. (A) Schematic illustrating analysis pipeline. The structural connectivity matrix is used to constrain a linearization of Wilson–Cowan dynamics, which results in an estimated covariance (FC) matrix. We compute network modules ahead of time, and based on those modules and on the simulated covariance structure, we compute brain areas’ functional participation coefficients. (B) Schematic illustrating the concept of the participation coefficient ($\mathcal{P}$). An area with high participation coefficient (red connections) forms connections to many different modules, while the connections of an area with low participation coefficient (green connections) are largely restricted to a single module. An area’s participation coefficient can be interpreted as a measure of its connectional diversity. When computed using a covariance matrix, an area’s participation coefficient measures its functional diversity. (C) Change in mean participation coefficient after removing different percentages of a network’s longest and shortest connections. The mean participation coefficient of the intact network is depicted as a red dashed line. Note that removing long-distance connections consistently reduces the mean participation coefficient (colored bars), indicating a decrease in functional diversity. Removing short-range connections (gray bars) has the opposite effect. Note that for the low- and high-resolution human datasets, we computed the participation coefficient with respect to structural and functional modules.

Discussion

Brain areas’ functional repertoires are shaped by their incoming and outgoing structural connections. Most connections are short-range and incur minimal cost to the network in terms of material and energy. Nonetheless, a small proportion of connections span long distances, leading to the hypothesis that the functionality conferred by these connections must outweigh their cost. Their precise function, however, is a matter of debate. The current hypothesis is that long-distance connections reduce the average topological distance between brain areas, facilitating interareal communication.

Here, we challenge this hypothesis on the grounds that it is not necessarily true for weighted brain networks and that it implies a nonspecificity of long-distance connections. We propose, instead, that long-distance connections serve to diversify brain areas’ inputs and outputs and to promote complex network dynamics. To test this hypothesis, we analyze five weighted interareal brain network datasets. As expected, we find that brain areas’ long-distance and short-range neighbors exhibit marked differences in terms of their connectivity profiles, suggesting that long-distance connections contribute to the specificity of areas’ connectivity profiles and serve as sources of dissimilar inputs and outputs for brain areas. Next, we show that in isolation, areas’ long-distance connectivity profiles exhibit nonrandom levels of similarity, suggesting that the communication pathways formed by long connections exhibit redundancies, which may help promote robustness. Finally, we simulate the covariance structure of neural activity using a linearization of Wilson–Cowan dynamics. We show that in the absence of long-distance connections, one measure of functional diversity—the mean participation coefficient—decreases, indicating that from a functional perspective, long-distance connections are necessary for supporting diverse and complex brain dynamics.

Interpreting the Functional Roles of Long-Distance Connections.

One of the open challenges of theoretical neuroanatomy is understanding how brain function is shaped by structure (38). Long-distance connections, because they are prevalent despite high material and metabolic cost, are believed to play critical functional roles. The earliest network analyses argued that long-distance connections acted as integrative structures that reduced topological distance between brain areas, which contributed to efficient interareal communication (20). This perspective was largely based on analogy between brain networks and other sociotechnical networks whose functions are better understood (39).

In the decade and a half since these early analyses, however, this narrative has largely remained unrefined (though there have been some recent advances; see, for example, ref. 22). In general, long-distance connections are almost universally regarded as key integrative structures. Recently, however, the functional role of long-distance connections has been revisited. In ref. 40, the authors demonstrated that in the macaque brain, the similarity of areas’ connectivity profiles decreased with distance, suggesting that long-distance connections contributed to an area’s specificity. More recently and using a different macaque network dataset, ref. 41 suggested that long-distance connections, those unanticipated by a model that penalized the formation of costly connections, form a dense cluster and may also perform some segregative functions.

Our work builds on these and other recent papers investigating the functional consequences of the brain’s spatial embedding and the roles of costly, long-distance connections (13, 19, 23, 26, 36, 42–44). Our findings show that, across species and scales, interareal communication along shortest paths is dominated by strong short-range connections, with long-distance connections contributing minimally. Instead, we find that brain areas’ neighbors via long-distance connections have markedly different connectivity profiles than their short-range neighbors. This finding is a clear demonstration that, from a structural perspective, long-distance connections allow brain areas to interact through novel configurations of inputs and outputs. The consistency of this observation across species is also suggestive of an evolutionarily conserved mechanism of interareal communication.

The Specificity of Long-Distance Connections.

In our work, we also showed that brain areas’ profiles of long-distance connections were similar to one another, a feature not accounted for by degree sequence, distance and weight distributions, and weight–distance relationships. This observation suggests that the organization of long-distance connections (and possibly connectomes as a whole) is shaped by an underlying latent structure that is a function of brain areas’ spatial locations but also some set of unknown factors, including cytoarchitectonic and transcription profile similarity (45–47), higher order topological organization (44, 48), or temporal staging in which connections are formed during developmental windows when brain areas are proximal to one another (49). The similarity of areas’ long-distance connectivity profiles also suggests a sense of connectional specificity that may not be explained by recent papers that proposed stochastic and globally enforced wiring principles (13, 23, 36). While these and other models can provide insight into brain-wide organizational principles (44, 48, 50, 51), they oftentimes lack the ability to accurately predict area-level statistics (41).

Communication Dynamics.

The aim of our study was to gain insight into how long-distance connections shape interregional communication patterns in brain networks. We focused on shortest path communication, in line with most studies in network neuroscience, where long-distance connections are thought to act as shortcuts to reduce the number of steps between nodes (52). Elsewhere, other communication strategies have been considered, including some that take into account suboptimal paths of various lengths (53) or that use decentralized navigation strategies to pass information from source to target nodes (54). These and other mechanisms contribute to our knowledge of the functional roles played by long-distance connections in facilitating efficient communication and information transfer in social, technological, and biological networks (55). Our study builds upon and extends this past work, finding the counterintuitive result that the longest physical connections in weighted brain networks contribute little to the efficiency of communication by weighted shortest paths. Instead, we find that these connections represent unique sources and targets for brain regions’ inputs and outputs and are arranged redundantly, rendering these pathways robust to perturbations. Our study motivates more detailed examinations of communication mechanisms in brain networks (27, 52, 56).

In dismissing the role of long-distance connections as topological shortcuts, we are not suggesting that they have no bearing on interareal communication (52). Rather, we propose that they serve as communication pathways in a nongeneric sense. Rather than simply increasing or decreasing global measures of efficiency and path length, long-distance connections help confer functional specificity to brain areas, enabling access to and transmission of novel inputs and outputs. Additionally, long-distance connections are clustered, forming robust and reinforced bridges between spatially specific neighborhoods and brain areas, ensuring reliable communication along specific pathways.

Interpreting Connection Weights.

The process of enumerating a network’s shortest paths does not incorporate information about spatial relationships. The observation that shortest paths are dominated by short-range connections is a direct result of the inverse relationship between connection weight and distance as well as the assumption that connections’ weights represent the communication efficacy between connected brain areas. This interpretation, however, exposes a shortcoming common in most empirical analyses of connectome data—namely, that the weights of connections are estimated from structural data alone and, while we ascribe functional significance to their values, may have no true bearing on brain function or communication (e.g., the number or fraction of reconstructed streamlines or projections does not imply that they are consistently used for signaling). Are we justified, then, in our functional interpretation of connection weights?

At the scale of brain areas, communication is determined in part by axonal diameter and myelination status, which place limits on nerve conduction velocity (57, 58). Interestingly, a number of studies have reported roughly lognormal-distributed fiber diameters (59), which is in broad agreement with the connection weight distributions reported here. Moreover, due to volumetric (11) and cost constraints (18), the probability of axonal projections spanning long distances is small (17, 60). So while the distributions of connection weights are both consistent across datasets and agree with previously reported results in which other variables relevant to communication were also measured, it still remains unclear whether the weights can be directly interpreted in terms of interareal communication. Ultimately, addressing this question remains an empirical challenge but would be of tremendous practical value as it would inform network modeling efforts, both of brain structural networks (51) but also of their function (61–63).

Limitations.

This study has a number of methodological limitations. First, we assume that we can make meaningful claims about the functional properties of nervous systems and brain areas by studying their structural networks alone. The validity of this assumption is built upon decades of empirical observations and recent simulation studies demonstrating that the covariance structure of temporally evolving neural activity can be predicted from properties of the structural matrix (35, 64–66). Our claims, however, are more nuanced than simply stating that function and structure are related to one another. We claim, specifically, that the shortest path structure of brain networks is of functional importance, a view that has been challenged of late (28, 35). While the precise role of shortest paths is, indeed, unclear, disruptions to shortest paths have been associated with disease, suggesting an important—if poorly understood—functional role (67, 68).

Second, the networks studied here were composites built from many single-subject observations. It remains unclear to what extent these networks are representative of the average individual. Moreover, it is important to note that in the absence of connection weights, long-distance and short-range connections are effectively weighted the same. In this extreme case, it is likely that networks’ shortest paths will, in fact, include many long-distance connections. We can begin to see this when we tune the parameter $\alpha$ closer to zero. In any case, the “correct” edge-weighting scheme is unknown. Lastly, diffusion imaging and tractography exhibit known biases that make it challenging to detect long-distance cortico–cortical tracts (69, 70). While future methodological advances may prove helpful (71), our results are bolstered by the inclusion of a high-resolution multiband diffusion imaging scan marking 257 diffusion directions.

Lastly, in line with previous studies (23–26), we treat a connection’s length as a proxy for its cost. While length plays a central role in determining cost (18), other factors also contribute, including connection diameter, axon packing density, and material composition (72, 73). However, experimentally quantifying these factors is often difficult and, due to technological limitations, is in some cases impossible for more than a small brain volume. In addition, the contribution of a connection’s weight to its cost remains unclear (73). Future work should be directed to establish more physically grounded estimates of connection cost at the level of the whole brain.

Conclusion

In conclusion, we present evidence that long-distance connections are not merely topological shortcuts. Instead, they introduce diversity among brain areas’ neighbors, which we show in human data can be related to brain function. We also confirm using simulations of brain dynamics that in the absence of long-distance connections, brain networks exhibit a decrease in their functional diversity. Lastly, long-distance connections exhibit degeneracies, so that many different areas have similar patterns of long-distance connectivity. We speculate that this degeneracy confers robustness to the system. Our findings contribute to a growing body of literature aimed at refining our understanding of how brain structure shapes its function.

Materials and Methods

We analyzed mouse, Drosophila, macaque, and human weighted, interareal network datasets. Each dataset was distinct in terms of imaging modality, reconstruction technique, and connection weighting scheme. In the case of the human data, all experimental procedures were approved by the Institutional Review Board of the University of Pennsylvania, and all participants gave informed consent. In the case of the mouse connectome data, and as per Oh et al. (72), “all experimental procedures related to the use of mice were approved by the Institutional Animal Care and Use Committee of the Allen Institute for Brain Science, in accordance with NIH guidelines.” In the case of the macaque connectome data, and as per Markov et al. (32), “surgical and histology procedures were in accordance with European requirements 86/609/EEC and approved by the ethics committe of the region Rhône-Alpes.” See SI Appendix, Supplementary Materials, Network Datasets for information on the origins and processing details of these datasets. See SI Appendix, Supplementary Materials, Network Analysis for derivations of network statistics and definitions of structural and functional modules.