Sieve Analysis Using the Number of Infecting Pathogens

Summary

Assessment of vaccine efficacy as a function of the similarity of the infecting pathogen to the vaccine is an important scientific goal. Characterization of pathogen strains for which vaccine efficacy is low can increase understanding of the vaccine's mechanism of action and offer targets for vaccine improvement. Traditional sieve analysis estimates differential vaccine efficacy using a single identifiable pathogen for each subject. The similarity between this single entity and the vaccine immunogen is quantified, for example, by exact match or number of mismatched amino acids. With new technology, we can now obtain the actual count of genetically distinct pathogens that infect an individual. Let F be the number of distinct features of a species of pathogen. We assume a log-linear model for the expected number of infecting pathogens with feature “f,” f = 1, …, F. The model can be used directly in studies with passive surveillance of infections where the count of each type of pathogen is recorded at the end of some interval, or active surveillance where the time of infection is known. For active surveillance, we additionally assume that a proportional intensity model applies to the time of potentially infectious exposures and derive product and weighted estimating equation (WEE) estimators for the regression parameters in the log-linear model. The WEE estimator explicitly allows for waning vaccine efficacy and time-varying distributions of pathogens. We give conditions where sieve parameters have a per-exposure interpretation under passive surveillance. We evaluate the methods by simulation and analyze a phase III trial of a malaria vaccine.

1. Introduction

Randomized clinical trials of vaccine candidates can provide a rich source of clues about vaccine mechanism in addition to a rigorous evaluation of overall efficacy. One important analysis for clues focuses on whether the vaccine has differential efficacy across different types of infecting pathogens (e.g., strains of Hepatitis C). The idea is that pathogens that are genetically or functionally similar to the vaccine immunogen may be more effectively blocked by the vaccine compared to pathogens that are different. Such analyses are known as sieve analyses as they reveal if the vaccine differentially blocks certain strains from infecting.

A broad and sophisticated literature for sieve analysis has developed; see for example, Gilbert et al. (1998, 2001), Gilbert (2000, 2001), Juraska and Gilbert (2013), Sun et al. (2013), and Juraska and Gilbert (2016). A traditional feature of these methods is that infection was categorized by a single strain of pathogen and thus infection by multiple strains was not considered. Recently, technology has improved so that counts of multiple infecting pathogen strains can be characterized. Intuitively, this additional information should yield more efficient analyses than when only infection yes/no by a single type of pathogen is recorded for each subject.

Follmann and Huang (2015) developed methods for analyzing vaccine trials where, at the time that infection was detected, the count of infecting pathogens was also determined. They assumed an underlying proportional intensity model for the risk of a potentially infectious exposure along with a log-linear model for the number of infecting pathogens. Vaccine efficacy was defined as the reduction in the mean number of infecting pathogens. Different parametric and semi-parametric methods for estimation of the overall vaccine efficacy were developed and evaluated. However, they did not consider the case where the infecting pathogens could be classified into multiple strains and did not consider sieving methods.

This article develops methods that blend the sieve approaches of Gilbert et al. cited above with the founder pathogen approaches developed by Follmann and Huang (2015). Both active and passive surveillance vaccine trials are considered. For passive surveillance trials, a log-linear model for the mean number of infecting pathogens with a given feature f over a fixed interval of follow-up is specified where f = 1, …, F characterize the features of interest. For active surveillance, we allow for a proportional intensity model on the incidence of exposures that can result in terminal infection, that is, infections that terminate follow-up. Following exposure, a vector of pathogen counts X₁, …, X_F is drawn. Infection occurs if any X_f > 0 and for example, X_f = 2 means two distinct pathogens with feature f infected the person. With parsimonious specification of the mean function, these approaches can be applied even if F is large.

This article is organized as follows: We describe the technology of how infecting pathogens can be characterized by long amino-acid strings and specify a log-linear model for the pathogen counts following exposure. We discuss how data are obtained under passive and active surveillance and provide conditions under which vaccine and sieve effects from such data estimate per-exposure effects. We conduct a small simulation to illustrate GEE estimation and compare it to old technology and to the within cluster resampling (WCR) method (Hoffman et al., 2001; Follmann et al., 2003). We next consider active surveillance methods and generalize the methods of Follmann and Huang (2015) to the sieve setting. A simple product estimator is developed, and then weighted estimating equations (WEE) are derived for a general model that allows for time-varying vaccine efficacy and pathogen distributions that vary with time. The asymptotic distribution of the WEE estimator is established. We conclude with an analysis of a malaria vaccine trial and explore the difference between the proposed and WCR approaches to active surveillance.

2. Pathogen Quantification and Sampling

Sieve analysis involves quantifying the similarity between the vaccine immunogen and the infecting pathogens. Vaccine efficacy is compared between those infected with vaccine-similar strains versus those with vaccine-dissimilar strains. In this article, we allow “infection” to mean either disease (e.g., clinical malaria) or evidence of replication (e.g., virus positive as in HIV or Zika infection). Historically, similarity was defined by simple methods where an infecting pathogen might be placed into one of several “races,” serotypes, or strains, depending on the era and technology. A single infecting pathogen would be identified for each infected individual.

While many infections are caused by a single infecting pathogen (or multiple identical clones), other pathogens can cause serial infections each by single or multiple unique infecting pathogens. If the infecting pathogens are genetically distinct it is possible to count them. To fix ideas, consider malaria which is caused by the parasite plasmodium falciparum. The infectious cycle starts by a mosquito bite of a human where the sporozoite form of the parasite is transferred from the mosquito to human. The sporozoite has an outer membrane of circumsporozoite (CS) protein which can induce an immune response. The RTS,S malaria vaccine uses part of this outer membrane as an immunogen and part of the amino acid (AA) sequence of the RTS,S immunogen is detailed in the first row of Table 1 (see Doud et al., 2012).

Table 1.

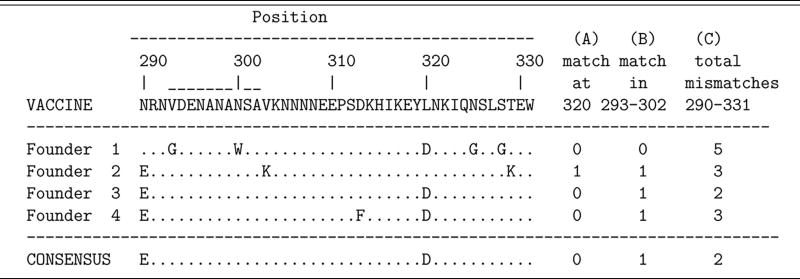
Partial amino acid sequence of the RTS,S vaccine immunogen along with an illustration of 4 infecting or founder parasites (aka haplotypes in malaria) that could have been recovered from an infected volunteer in a vaccine trial. A dot indicates agreement with the amino acid of the vaccine immunogen. The consensus sequence is given in the bottom row.

For ease of discussion, suppose that all subjects are followed for the same fixed interval of time. To identify infecting parasites, blood is drawn at the end of the study and a number of parasites sampled. The part of the parasite's DNA that codes for the CS region of Table 1 is amplified so that the DNA for each parasite is determined. This DNA sequence identifies the actual protein that coats the outside of the parasite. The middle four rows of Table 1 illustrate four different parasites. For malaria, the sampled parasites are genetically identical progeny of the infecting pathogens. Other diseases are different. For example, HIV undergoes replication and mutation within the infected host which adds further complexity to the identification of infecting pathogens (see e.g., Keele et al., 2008). Nonetheless, with detailed knowledge of the pathogen life cycle, assay technology, and amplification method, one can identify the genotypes and count the clonally distinct infecting pathogens.

The potential number of ways that the infecting pathogens can differ is large and simple metrics are often used to characterize the difference or “distance” between the vaccine and an infecting parasite. The final 3 columns of Table 1 give three examples of dissimilarity; (A) whether a vaccine/pathogen match occurs at amino acid location # 320, (B) whether a match occurs for all amino acids from location 293 through 302 (the DV10 region of the CS protein), or (C) the total number of mismatches from position 290 to 331.

To develop some notation, suppose that X_f is the number of infecting pathogens with feature f for a given subject following exposure and define the vector of counts as X = (X₁, …, X_F). For example, if we define feature by a match at location 320, with f = 1 denoting a match and f = 2 a mismatch, then F = 2 and from Table 1, we have (X₁, X₂) = (1, 3). If we define feature as the total number of mismatches (i.e., Hamming distance) over the 42 locations 290-331 then F = 43 and X_f is the number of pathogens with f–1 mismatches; for Table 1, X = (0, 0, 1, 2, 0, 1, 0, 0, …, 0). For malaria, multiple founders often follow from multiple infections so X₁ + X₂ > 1 from a single bite would be somewhat unusual.

A convenient regression model for count data is to assume that the log of the mean count is a linear function of covariates. Usually one has a single outcome X along with covariates W and one assumes that E(X|W) = exp(W′α). With sieve models we have a vector of outcomes X, a vaccine indicator Z and each element f has its associated covariate vector V_f. For the Hamming distance metric described above, we have V_f = (f – 1) and the mean model is

$$E(X_f|{\mathit{W}}_f)=exp({W\prime }_f\mathit{\alpha })=exp\{{\alpha }_1+{\alpha }_2(f-1)+{\alpha }_{3}Z+{\alpha }_{4}Z(f-1)\}.$$ (1)

The other metrics described above can be represented in a similar fashion.

Vaccine efficacy is typically defined as a percent reduction in an outcome on a vaccine relative to a placebo (see Halloran et al., 2010). A traditional metric is to use infection by a single pathogen as an outcome and thus vaccine efficacy against infection by a pathogen with feature f is

$$V{E}_{If}=1-\frac{P(X_f>0|Z=1)}{P(X_f>0|Z=0)}.$$

With the number of infecting pathogens with feature f, we can define vaccine efficacy in terms of the reduction in the mean number of infecting pathogens.

$$V{E}_{Mf}=1-\frac{E(X_f|Z=1)}{E(X_f|Z=0)}=1-{\mathrm{\Delta }}_f.$$

Follmann and Huang (2015) introduced the metric VE_M. While VE_If is typically more clinically relevant than VE_Mf, the latter may be more efficient at uncovering mechanistic clues.

While in vaccine challenge studies, X can be recorded after each controlled exposure in field trials, humans are exposed and infected during the course of follow-up, but when infection is detected depends on the study sampling framework. We postulate a process for exposure and infection where, at each exposure, a vector of counts of clonally unique infecting pathogens, X, is drawn from a distribution F(). For active follow-up, surveillance continues until an infection or censoring occurs. Whenever an infection occurs, we sample the infecting pathogens, determine X^A, and stop follow-up. We sometimes call this a “terminal” infection as follow-up stops. What constitutes a terminal infection varies. For HIV any infection is terminal, while for malaria multiple subclinical infections are possible before the first terminal infection (e.g., parasitemia plus symptoms). For passive surveillance, we follow until the end of the study and genotype any infecting pathogens which reveals X^P.

Figure 1 illustrates the intricacies of exposure, infection, and terminal infection under passive and active surveillance. The top trajectory is for an individual who has 4 exposures but remains uninfected until the end of follow-up. Under passive surveillance, we measure X^P = 0 while for active surveillance, we write X^A as 0. The second trajectory is where all infections are terminal such as HIV. Follow-up stops for active surveillance when infection is detected but continues for passive surveillance. Here, X^P = X^A though the sample is obtained at different times. Finally, the bottom trajectories are where subclinical infections can occur and possibly dissipate over time such as subclinical malaria. In this case, X^P and X^A may be weighted random sums of per exposure X's with bigger weights closer to the time of sampling. The difference is that the last infection in the sum comprising X^A must be terminal. Passive surveillance has no such requirement.

Figure 1.

Trajectories of the exposure, infection (possibly subclinical), and terminal infection processes for four individuals Exposure=e at which time X is drawn from F_Z(). X^A and X^P are the vector of counts obtained under active (solid line) and passive (dashed line) surveillance. Xs which result in subclinical infections do not terminate follow-up. Trajectory 2 corresponds to a disease where all infections are terminal (e.g., HIV) while trajectories 3 and 4 correspond to a disease with subclinical infections (e.g., malaria). Note that, we allow that old sub-clinical infections may be cleared (x1 from trajectory 3 under active surveillance).

In general, the distributions of X^A, X^P, and X are different and thus VE_Mf and sieve effects based on X^A, X^P, and X may be different. However for trajectories of type 1 and 2, X^A = X^P. We later provide conditions where the per-exposure VE_Mf can be recovered from X^A. This is not possible for passive surveillance but we can provide conditions under which the mean per-exposure sieve effect θ_f,_g = Δ_f/Δ_g is recoverable from X^P. If these conditions are not met, sieve effects can still be tested, but the estimates may not have the per-exposure interpretation. For simplicity, we have no covariates other than, Z, the vaccine indicator. We allow different patients to have different lengths of follow-up L.

Assumption 1. The per exposure counts of infecting pathogens X are independent and identically distributed draws from F_Z() both within and across subjects within randomization group Z. Thus, the distribution of circulating strains of pathogens at each exposure is constant over time. Note this forbids an all-or-none vaccine effect where placebos and some vaccinees repeatedly draw X from an F() while other vaccinees repeatedly draw from point mass at 0.

Assumption 2. Our setting is for the second trajectory of Figure 1, where any infection is terminal and stops active surveillance. Multiple infections are not allowed. The count vector X that obtain from a terminal infection is recorded without error.

Under these assumptions, for both active and passive surveillance the distribution of X^P = X^A follows $F_Z^P(\mathit{X})=F_Z(\mathit{X}|X_{+}>0)p_Z+{\delta }_0(\mathit{X})(1-p_Z)$, where Z = 0, 1 is the vaccine indicator, p_Z is the probability of a (terminal) infection during follow-up in group Z, $X_{+}={\sum }_{f=1}^F{X}_f$, and δ₀() is point mass at 0. Note that p_Z implicitly depends on the distribution of follow-up lengths, L, in group Z.

With passive surveillance, we can recover the per-exposure ratio of means:

$${\theta }_{f,g}^P=\frac{E(X_f^P|Z=1)/E(X_f^P|Z=0)}{E(X_g^P|Z=1)/E(X_g^P|Z=0)}=\frac{p_{1}E(X_f|X_{+}>0,Z=1)/\{p_{0}E(X_f|X_{+}>0,Z=0)\}}{p_{1}E(X_g|X_{+}>0,Z=1)/\{p_{0}E(X_g|X_{+}>0,Z=0)\}}=\frac{E(X_f|X_{+}>0,Z=1)/\{E(X_f|X_{+}>0,Z=0)\}}{E(X_g|X_{+}>0,Z=1)/\{E(X_g|X_{+}>0,Z=0)\}}=\frac{{\pi }_{1}E(X_f|X_{+}>0,Z=1)/\{{\pi }_{0}E(X_f|X_{+}>0,Z=0)\}}{{\pi }_{1}E(X_g|X_{+}>0,Z=1)/\{{\pi }_{0}E(X_g|X_{+}>0,Z=0)\}}=\frac{E(X_f|Z=1)/\{E(X_f|Z=0)\}}{E(X_g|Z=1)/\{E(X_g|Z=0)\}}={\theta }_{f,g},$$

where π_z is the per-exposure probability of infection P(X₊ > 0|Z). This result is analogous to that of Gilbert et al. (1998) who used the infection indicator I(X_f > 0) as outcome and only allowed for a single infecting strain.

3. Passive Surveillance

In trials with passive surveillance, volunteers are followed for a length of time. At the end of follow-up, infection status is determined and for infected volunteers, a sample of infecting pathogens genotyped. Let L_i be the length of followup for person i. Let Z_i be the vaccine indicator, ${\mathit{X}}_i^P=X_{1i}^P,\dots ,X_{Fi}^P$ the vector of counts of infecting pathogens, and W_fi a covariate vector, which depends implicitly on Z and which we sometimes write as W_fi(Z_i). Similar to (1), we specify

$$E(X_f^P|{\mathit{W}}_f)=exp({\mathit{W}\prime }_f\mathit{\alpha }).$$ (2)

We allow that W_f can include terms involving L to reflect different lengths of follow-up.

As in Gilbert et al. (1998), who parameterized sieve effects for the infection indicator $I(X_{fi}^P>0)$, we specify W_fi to allow for an arbitrary mean for feature f in the placebo group, with possibly structured vaccine effects. For example, one may postulate

$$E(X_f^P|{\mathit{W}}_f)=exp({\beta }_{0f}+{\gamma }_{1}L+Z{\mathit{V}\prime }_f\mathit{\psi }).$$ (3)

Unstructured vaccine effects occur with V_f = I_f identifying the fth feature, for example, 0, …, 1, …, 0. Ordinal effects occur with V_f as above but with ψ₁ ≤ ψ₂ · · · ≤ ψ_f. Another possibility is to specify a linear effect for the Hamming distance, for example, V_f = 1, f – 1 where f – 1 is the number of mismatches. These models can be fit using generalized estimating equations (GEE) with each individual a cluster (Zeger and Liang, 1986).

A small simulation was performed to evaluate the GEE estimation. We categorized pathogens as either matched (f = 1) or mismatched (f = 2) to the vaccine and generated counts ( $X_1^P$, $X_2^P$) using a bivariate negative binomial model with mean given by

$$E(X_{fi}^P|{\mathit{W}}_{fi},b_i)=exp\{b_i+{\alpha }_1+{\alpha }_{2}I(f=1)+{\alpha }_3{Z}_i+{\alpha }_4{Z}_{i}I(f=1)\}=exp\{b_i+{\mathit{W}\prime }_{fi}\mathit{\alpha }\},$$ (4)

where exp(b_i) follows a gamma distribution with μ = E{exp(b_i)} =.5 or 1 and ${\sigma }_{exp(b)}^2=\text{ver}\{exp(b_i)\}=0$, 1, or 2. We specify α = (0.96, 0, −0.32, −1.28) so that VE_M1 = .80 and VE_M2 = .27. In this model, α₄ quantifies the sieve effect.

For estimation, we use GEE with a working independence correlation matrix. To mimic the old technology where only a single infecting pathogen is characterized, we selected a pathogen at random from each infected subject and recorded whether it was a match or not. We then fit a logistic regression model with probability exp(α₂ + Z_iα₄)/{1 + exp(α₂ + Z_iα₄)} to the match indicator. As an alternate estimation procedure, one could repeat the above random selection many times and average the associated estimates of α₄. This averaging corresponds to a within cluster resampling (WCR) or multiple outputation approach to dealing with the multiple outcomes from each individual (Hoffman et al., 2001; Follmann et al., 2003). The WCR approach was introduced for use in sieve analysis in Neafsey et al. (2015). Here, we average over all possibilities and call this exhaustive WCR or EWCR. This approach may offer some robustness as an aberrant subject with large X₊ and a peculiar suite of infecting pathogens will have substantial weight under the GEE approach with working independence but not under WCR.

Table 2 summarizes the simulation results. The two left columns give the true mean and variance of exp(b_i) while the X̄ column summarizes the average count averaged over f = 1, 2, and Z. We define the squared Wald statistic as 𝒵² = θ̂̄² /S² (θ̂) or the squared sample average of an estimate divided by its sample variance. The far right columns give the ratio of 𝒵² for different estimators. This can be viewed as the relative efficiency of different estimators. For unbiased estimates, the ratio reduces to the ratio of variances, while for estimators that estimate different parameters, it approximates the ratio of sample sizes required to achieve a given power. So if ${\mathcal{Z}}_A^2/{\mathcal{Z}}_B^2$ is 2, then method B requires twice the sample size as method A to achieve the same power.

Table 2.

Simulated performance of different methods of estimation of a sieve effect using the match/mismatch metric for the mean number of infecting pathogens in a trial with passive surveillance. Pairs of rows report the average and variance of the estimated α₄ over 1000 simulated datasets. Data generated under a bivariate negative binomial model. X̄ is the mean X averaged over groups and f and then averaged over the simulations. Relative Efficiency is the ratio of squared Wald statistics or ${\mathcal{Z}}_A^2/{\mathcal{Z}}_B^2$, where 𝒵 is the sample average divided by the sample standard deviation.

						Relative efficiency
E{exp(bi)}	var{exp(bi)}	X̄	GEE	Single pathogen	EWCR	GEE/Single	GEE/ EWCR
Bivariate negative binomial
0.5	0.0	0.9	−1.302	−1.304	−1.304	2.68	1.18
			0.073	0.151	0.087
0.5	1.0	0.9	−1.314	−1.336	−1.325	2.51	1.51
			0.067	0.173	0.103
0.5	2.0	0.9	−1.289	−1.322	−1.292	3.49	1.82
			0.060	0.222	0.110
1.0	0.0	1.9	−1.283	−1.299	−1.283	3.33	1.31
			0.032	0.109	0.042
1.0	1.0	1.9	−1.295	−1.322	−1.299	4.89	1.96
			0.030	0.152	0.059
1.0	2.0	1.9	−1.279	−1.283	−1.278	5.00	2.19
			0.033	0.168	0.073
All-or-none
0.5	0.0	6.0	−0.997	−1.241	−1.237	1.21	0.78
			0.076	0.143	0.091
0.5	1.0	4.8	−0.863	−1.148	−1.137	1.02	0.72
			0.092	0.166	0.114
0.5	2.0	4.0	−0.799	−1.108	−1.075	2.75	0.68
			0.102	0.540	0.126
1.0	0.0	8.1	−0.742	−1.082	−1.065	1.34	0.62
			0.035	0.101	0.045
1.0	1.0	6.4	−0.660	−0.971	−0.965	1.24	0.65
			0.045	0.121	0.063
1.0	2.0	5.3	−0.610	−0.907	−0.899	1.20	0.63
			0.054	0.142	0.073

For the top half of Table 2, data are generated under (4) and all estimators are unbiased. The new technology where we characterize multiple infecting pathogens is more efficient than the old technology where only a single pathogen is identified; the variance ratio ranges from 2.68 to 3.49 when μ = 0.5 and from 3.33 to 5.00 when μ = 1. The final columns shows that GEE is more efficient than WCR with gains ranging from 18% to 119%.

The top half of Table 2 was generated using a conditional Poisson model for the mean count which is consistent with the models used for analysis. Another possibility is a kind of all-or-none vaccine effect where the vaccine reduces the probability of infection, but has no effect on the count of infecting pathogens once infection has occurred. We formalize this idea by perturbing (4) by replacing any X_f|X_f > 0 with a discrete uniform(1,21), irrespective of group. Results are given in the bottom half of Table 2. Simulations show that for this setting, the EWCR and GEE methods estimate different parameters. The GEE method is more powerful than the old technology, but the GEE approach is less powerful than EWCR with relative efficiencies between 0.62 and 0.78.

4. Field Trial Time to Event Analysis

In a field trial with active surveillance, the time to event (e.g., infection for HIV or first clinical disease for malaria) is recorded along with the counts of each type of infecting pathogen. In this section, we parallel the approach of Follmann and Huang (2015) and develop estimators of the V:P ratio of means. Our methods are best conceptualized with trajectory 2 of Figure 1 where any infection is terminal, that is, stops follow-up and we recover the per-exposure mean ratio. Our methods also apply to settings 3 and 4 though here X^A for the terminal infection may include some previous subclinical infections and the mean ratio may not have a crisp per-exposure interpretation.

4.1. Product Estimators of VE_Mf

Let ω(t) be the instantaneous risk of exposure by any pathogen. This risk should be free of Z in a blinded trial. Following exposure, X is generated from F_Z(). If ${\sum }_{f=1}^F{X}_f=X_{+}>0$ the person is infected and we see X^A while if X₊ = 0 they remain at risk of future infection. If no infection occurs during follow-up, we write X_A = 0. Under the assumption that the time of exposure and X are conditionally independent given Z, the instantaneous risk of (terminal) infection can be written as

$$\begin{array}{c}h(t|Z)=\omega (t)P(X_{+}>0|Z)=h_0(t)exp[log\{\frac{P(X_{+}>0|Z=1)}{P(X_{+}>0|Z=0)}\left\}Z\right]\\ =h_0(t)exp(Z\beta ).\end{array}$$ (5)

Thus, exp(β) is the V:P ratio of per exposure infection probabilities. Estimation of β can be achieved using standard software for Cox regression and the asymptotic distribution of β̂ is well known. Additionally, covariates that impact the risk of exposure can be easily incorporated in equation (5) if desired.

Given infection, we can drill down to get at feature specific vaccine efficacy and from that sieve effects. Similar to before, we assume that the expectation of $X_f^A|X_{+}^A>0$ is given by

$$E(X_f^A|{\mathit{W}}_f,X_{+}^A>0)=exp({\mathit{W}\prime }_f\alpha ).$$ (6)

Note that if all infections are terminal then ${\mathit{X}}^A\stackrel{d}{=}\mathit{X}$. The vector W_f can be parameterized as described previously and α can be estimated using the GEE method with data from infected individuals. Using arguments in Follmann and Huang (2015), we can blend the Cox estimator of β with an estimate of α to obtain a consistent estimate of VE_Mf. Specifically, as the sample size goes to infinity

$$\begin{array}{c}exp(\widehat{\beta })\frac{exp\{{\mathit{W}}_f{(1)}^{\prime }\widehat{\mathit{\alpha }}\}}{exp\{{\mathit{W}}_f{(0)}^{\prime }\widehat{\mathit{\alpha }}\}}\to \frac{P(X_{+}>0|Z=1)}{P(X_{+}>0|Z=1)}\frac{E(X_f|Z=1,X_{+}>0)}{E(X_f|Z=0,X_{+}>0)}\\ \begin{array}{c}=\frac{E(X_f|Z=1)}{E(X_f|Z=0)}\\ =1-V{E}_{Mf},\end{array}\end{array}$$

in probability. Here, W_f(Z) are the covariates for a person in group Z. Remarkably, even though, we only see $X_f^A|X_{+}^A>0$, we are able to obtain a consistent estimate of the ratio of unselected means. Asymptotics for the product estimator easily follow from the delta method as both β̂ and α̂ are asymptotically normal and independent given standard conditions including that the X_is are independent draws from X_i|W_1i, …, W_fi.

A sieving effect occurs if the VE_Mf are not constant over f which happens if

$$\frac{E\{X_f^A|{\mathit{W}}_f(1)\}}{E\{X_f^A|{\mathit{W}}_f(0)\}}=exp[\{{\mathit{W}\prime }_f(1)-{\mathit{W}\prime }_f(0)\}\mathit{\alpha }]$$

is nonconstant over f. Exactly what this means in terms of α depends on W_f. For example, with the Hamming distance metric parameterized as in equation (1), a sieve effect occurs if α₄ ≠ 0. For the mis-match metric sieving occurs if α₄ ≠ 0 with (f – 1) replaced by I(f = 1) in (1).

For certain diseases, such as malaria, subclinical infections can occur as suggested by trajectories 3 and 4 of Figure 1 and thus an X^A associated with a terminal infection (which has $X_{+}^A>0$) may include infecting pathogens from prior subclinical infection(s). Such an X^A can be represented as the sum of the count vector from the terminal infection plus a random number of other count vectors from recent subclinical infections. We might write ${\mathit{X}}^A={\sum }_{c=1}^C{\mathit{X}}_c^{\ast }$. The $X_1^{\ast }$, …, $X_C^{\ast }$ could have a complex distribution with, for example, C–1 iid subclinical infections drawn from $F_W^{\ast sc}$ followed by a terminal infection drawn from $F_Z^{\ast t}$. In this case, the product method recovers a ratio of means, but it does not have a crisp per-exposure interpretation.

Interestingly, we can repeat the above development by the indicator of infection yes/no I(X_f > 0) instead of X_f. This may be a more sensitive measure of vaccine efficacy if the vaccine has an impact on I(X_f > 0) but no impact on the count X_f|X_f > 0. We assume the same model for the risk of infection by any pathogen (5). But now our outcome is the indicator of an infection of type “f” given infection has occurred. For this, we assume that

$$E\{I(X_f^A>0)|{\mathit{W}}_f{X}_{+}^A>0\}=exp\{{\mathit{W}\prime }_f\mathit{\alpha }\}$$ (7)

Arguing as before it follows that as the sample size goes to infinity

$$exp(\widehat{\beta })\frac{exp({\mathit{W}}_f{(1)}^{\prime }\widehat{\mathit{\alpha }})}{exp({\mathit{W}}_f{(0)}^{\prime }\widehat{\mathit{\alpha }})}\to 1-V{E}_{If},$$

in probability with asymptotic normality following from the delta method.

4.2. Weighted Estimating Equations

While the product estimators of VE_If and VE_Mf for active surveillance are simple to obtain, they do not naturally allow for complex covariates that can model nonconstant vaccine efficacy nor allow for changing distributions of pathogens. In this section, we extend the WEE approach in Follmann and Huang (2015) to allow for these effects.

Let T_i be the time to infection and C_i the time to censoring for individual i. We assume that the censoring time C_i is independent of T_i conditioning on the covariates. Moreover, define Y_i = min(T_i, C_i), δ_i = I(T_i ≤ C_i) and N_i(t) = δ_iI(Y_i ≤ t). Motivated by Follmann and Huang (2015), we propose to construct unbiased estimating equations based on the observed stochastic processes $X_{fi}^{A}d{N}_i(t)$, f = 1, …, F and i = 1, …, n.

Define by W^E covariates that impact the exposure to pathogens and by ${\mathit{W}}_f^X$ covariates that impact the count of X_f given exposure to pathogens. Define $\mathit{W}=({\mathit{W}}^E,{\mathit{W}}_1^X,\dots ,{\mathit{W}}_F^X)$. We assume that the intensity of exposure to any pathogen is given by

$$\omega (t|\mathit{W})=\omega (t)exp(\mathit{\theta }\prime {\mathit{W}}^E),$$ (8)

while the mean of X given exposure at time t satisfies the proportional mean model

$$E(X_f|{\mathit{W}}_f)=E(X_f|{\mathit{W}}_f^X)=exp\{{\beta }_f(t)+\mathit{\varphi }\prime {\mathit{W}}^I+\mathit{\psi }\prime \mathit{Z}{\mathit{V}}_f\}.$$ (9)

With β_f(t) varying with t, we allow the mean response in the placebo group to change arbitrarily with time. We include W^I to allow for pan-feature effects such as innate immunity or actual/counterfactual immune response to the vaccine while V_f specifies the vaccine effect for feature f. In the appendix, we show these assumptions and only terminal infections imply that

$$E\{X_{fi}^{A}d{N}_i(t)|{\mathit{W}}_i\}={\lambda }_f(t)exp(\mathit{\alpha }\prime {\mathit{W}}_{fi}^u)P(Y_i\ge t|{\mathit{W}}_i)\mathit{\text{dt}}$$ (10)

where λ_f(t) = ω(t) exp{β_f(t)} is a nuisance function and ${\mathit{W}}_{fi}^u$ are the unique covariates in (W^E, W^I, ZV_f). Note that for a covariate included in both ${\mathit{W}}_i^E$ and ${\mathit{W}}_i^I$, the corresponding α is the sum of the corresponding θ and ϕ. When there are no such common covariates, we have ${\mathit{W}}_{fi}^u=({\mathit{W}}_i^E,{\mathit{W}}_i^I,Z_i{\mathit{V}}_{fi})$. A simple example is ${\mathit{W}}_{fi}^u=\{Z_i,Z_i(f-1)\}$.

Based on the zero-mean property of the observed stochastic processes, $X_{fi}^{A}d{N}_i(t)-E\{X_{fi}^{A}d{N}_i(t)\}$, we derive p = dim(α) unbiased estimating equations after profiling out the nuisance functions λ_f(t), f = 1, …, F,

$$U(\mathit{\alpha })=\sum _{i=1}^n{\int }_0^{\tau }\sum _{f=1}^F{X}_{fi}^A\{{\mathit{W}}_{fi}^u-\frac{{\sum }_{j=1}^n{\mathit{W}}_{fj}^{u}exp(\mathit{\alpha }\prime {\mathit{W}}_{fj}^u)I(Y_j\ge u)}{{\sum }_{k=1}^{n}exp(\mathit{\alpha }\prime {\mathit{W}}_{fk}^u)I(Y_k\ge u)}\}\times d{N}_i(u)=0.$$ (11)

Define the solution as α̂, which we call the weighted estimating equation (WEE) estimator. In Web Appendix A, we show that √n(α̂ – α₀) converges to a multivariate normal distribution with mean zero and variance-covariance matrix Γ⁻¹ΩΓ⁻¹ where Γ = −n⁻¹E{∂U(α)/∂α |_α=α0} and Ω = var{U_i(α₀)}.

Remarks

1. Stratification can be incorporated in the proposed WEE method in the usual way. Within each stratum, for example, sites in a field trial, we construct estimating equation (11) and then sum the equations over strata to estimate the regression coefficients.

2. Analogous to the product estimator, for trajectories of type 3 and 4 where X^A may include pathogens from prior nonterminal infections, the WEE estimator recovers a ratio of means, but they do not have a per-exposure interpretation.

3. The equations (11) for failure type f correspond to estimating equation from standard Cox regression based on a weighted partial likelihood where the ith failure of type f gets weight $X_{fi}^A$. The equations are summed over all f which have at least 1 failure which results in equation (11). Cox regression software which allows this sort of weighting can be re-purposed to solve these equations. Note that weighted Cox regression typically replicates a person $X_{fi}^A$ times including in the “risk set” or denominator of (11). The weight in equation (11) is different with an unchanged risk set but the contribution at T_i reproduced $X_{fi}^A$ times.

4. If such weighting is not allowed, the equations can still be solved with standard Cox regression software. Let 𝒦 be the set of subjects with an event. For subject k ∈ 𝒦 with an event at time T_k, we concatenate ${\sum }_{f=1}^F{X}_{kf}^A$ data sets. If an infection with feature f is observed for this subject k, a total of $X_{kf}^A>0$ identical datasets of failure type f are created from the risk set ℛ(T_k) of subjects under study at time T_k. Each data set has #ℛ(T_k) – 1 nonevents with covariate vectors W_ft from those ℓ in the risk set ℛ(T_k) (but excluding subject k) and a single infection with feature f with covariate vector W_fk for subject k. This results in ${\sum }_{k\in \mathcal{K}}{\sum }_{f=1}^F{X}_{fk}^A$ concatenated datasets. If each dataset defines its own stratum and stratified Cox regression is run then the a solution to (11) can be obtained. The bootstrap can be used to approximate standard errors for the regression coefficients.

5. The same arguments apply if we replace $X_{fi}^A$ with $I(X_{fi}^A>0)$ when our goal is to estimate VE_If. In this case, the estimating equations can be solved using stratified Cox regression software. For feature f, we create a Cox regression data set using time to infection with feature f as the failure time and the censoring indicator in the usual fashion along with W_fi as the covariate for person i in the fth dataset. We can then concatenate the datasets into a large dataset and apply stratified Cox software. Note that we only need concatenate U ≤ F datasets where U is the number of unique infection features observed in the data. Each feature that has an event defines a stratum so there are U strata. Again, the bootstrap can be used to obtain standard errors for the regression coefficients. This formulation extends Method B of Lunn and McNeil (1995) to multiple noncompeting events.

6. The assumption of a constant VE_Mf throughout follow-up can be weakened. For example, the mean at time t for feature f might be proportional to

   $$E(X_{fi}^A|{\mathit{W}}_f^u)=exp\{{\beta }_f(t)+Z({\alpha }_{f1}+{\alpha }_{f2}t)\},$$

   Thus, VE_Mf = 1 – exp(α_f1 + α_f2t) can wane smoothly over time. If we further require α_f2 = α_f for all f, then the ensemble VE_M1, …, VE_Mf can wane similarly over time. Another formulation would have

   $$E(X_{fi}^A|{\mathit{W}}_f^u)=exp[{\beta }_f(t)+Z\{I(t\le \tau ){\alpha }_{f1}+I(t>\tau ){\alpha }_{f2}\}],$$

   so that VE_Mf can differ before and after τ, for example, the median follow-up.

In Web Appendix B, we evaluate the performance of the WEE and product approaches via simulation. We consider pathogen distributions, that is, placebo draws from F_Z, that are constant, increase, or decrease over time, and allow for no and substantial subject level heterogeneity. The WEE method allows for changing pathogen distributions while the product methods does not. Both methods assume no subject-level heterogeneity. Interestingly, the simulations show that both methods are unbiased for the sieve effect θ_f,g for all scenarios. For feature specific vaccine efficacy, VE_Mf the performance differs. The WEE is unbiased for all null scenarios and only modestly biased at about 10% and then only when there is both substantial heterogeneity and the mean of F_Z() increases over time. WEE is unbiased for moderate heterogeneity. For both non and non-null scenarios, the product estimate shows bias with nonconstant F_Z and is substantially biased under heterogeneity for all F_Z.

5. Example

Malaria is an ancient parasitic disease that causes substantial illness and disease, primarily in the developing world. While vaccine development has been long and difficult, the RTS,S vaccine has demonstrated promising efficacy; see Agnandji et al. (2015); RTS et al. (2012). Investigation of potential sieve effects of the vaccine is of keen interest. Towards this end, next-generation PCR amplification of the CS region in AA positions 293–389 was undertaken and the infecting parasites characterized as illustrated in Table 1. Neafsey et al. (2015) conducted an extensive sieve analysis of the RTS,S vaccine using the mismatch metric for individual AA locations and subregions of the region defined by amino acid positions 293–389. Sophisticated methods that had been developed for single infecting pathogens were leveraged using the Monte Carlo WCR approach.

To illustrate our methods, we use children 5–17 months old from all trial sites of the RTS,S trial (Neafsey et al., 2015). There were 6912 children from 11 trial sites with a total of 2089 terminal infections, that is, first or only episodes of clinical malaria within the 1st year post vaccination. For illustration, we focus on the mismatch metric applied to the DV10 region of AA positions 293–302. We define $X_1^A$, $X_2^A$ as the counts of matched and mismatched pathogens at terminal infection. Of the 2089 infections for this AA region, 1722 had all infecting pathogens mismatched, 68 had all infecting pathogens matched and 299 had both matched and mismatched infecting pathogens. The top panel of Figure 2 displays a random sample of 165 children, 56 of them had an episode of first or only clinical malaria (parasitemia plus symptoms) and are denoted by a number providing the jittered total count of infecting pathogens at the time of terminal infection. The bottom panel is a jittered scatterplot of the count of mismatched and matched infecting pathogens; the correlation between the two is about 0.28.

Figure 2.

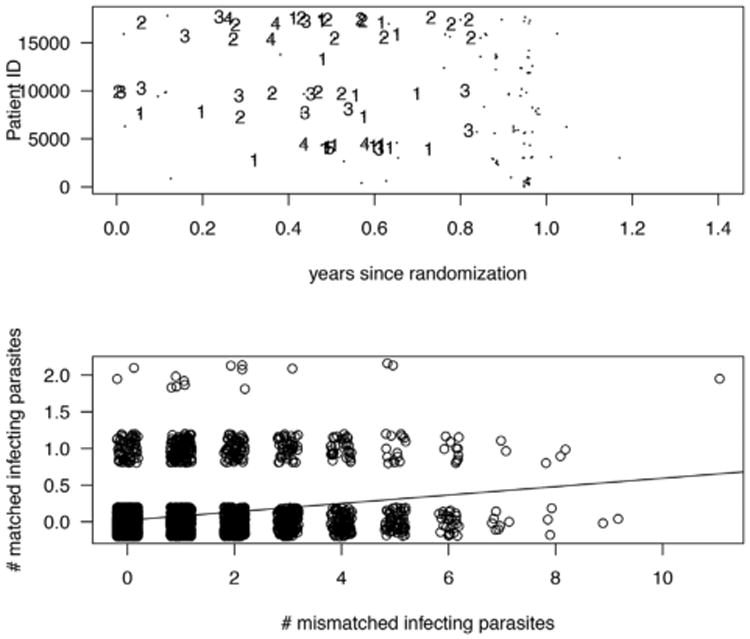
Top panel: Years to censoring or first/only episode of clinical malaria for 165 randomly selected children. Small dots denote censoring, numbers provide the number of infecting pathogens at the time of the detection of infection. Bottom panel: a scatterplot of the count of infecting pathogens by mismatch/match to the DV10 region.

We begin our analysis by evaluating three different estimators of VE_If: WCR, an analysis that approximates old technology where a single pathogen is identified, and the product estimator. For WCR we generated 10,000 datasets by selecting one infecting strain at random for each infected child. For each generated dataset, the Cox proportional hazards model was applied separately to matched (f = 1) and mismatched (f = 2) infections using the parametrization

$${\lambda }_f(t)={\lambda }_{0f}(t)exp[Z\{{\alpha }_{1I}+I(f=2){\alpha }_{2I}\}],$$

see Method B of (Lunn and McNeil, 1995). Here, α_1I, α_1I + α_2I correspond to matched and mismatched vaccine effects, and α_2I ≠ 0 indicates differential vaccine efficacy. An estimate of its variance is obtained as described in Hoffman et al. (2001) and Follmann et al. (2003). To mimic the old technology where a single infecting pathogen was identified, we selected the median α̂_2I and corresponding standard error. We view this an approximation to the estimate that would likely be obtained under the old technology. For the product method with I(X_f > 0) as outcome, we use (7) with W′_fα = α₁ + α_1IZ + α₂I(f = 2) + α_2IZI(f = 2). The estimator reduces to

$${\widehat{\text{VE}}}_{\mathit{\text{If}}}=1=exp(\widehat{\beta })\frac{\overline{I(X_{f1}^A>0)}}{\overline{I(X_{f0}^A>0)}}.$$ (12)

where $\overline{I(X_{fz}>0)}$ is the proportion infected with feature f among the infected in group z and β̂ is estimated from Cox regression. One can show that the estimate of the sieving effect simplifies to ${\widehat{\alpha }}_{2I}=log\{\overline{I(X_{11}^A>0)}/\overline{I(X_{10}^A>0)}\}-log\{\overline{I(X_{01}^A>0)}/\overline{I(X_{00}^A>0)}\}$.

For the product method with X_f as outcome, the development is similar. The estimates of VE_Mf, α_2M are analogous to VE_If, α_2I with $\overline{I(X_{fz}^A>0)}$ replaced by $\overline{X_{fz}^A}$. The nonparametric bootstrap was used to estimate the variance of the estimates based on the product method.

Table 3 reports the results. The first three columns all estimate VE_If. We see that the approximation of the old technology, where only one parasite was used for each infection, has a smaller Wald statistic than that from Monte Carlo WCR, which shows significant evidence of sieving. The use of the product method with the infection indicator as outcome, I(X_f > 0), gives a substantially larger Wald statistic than Monte Carlo WCR. The difference between the WCR and product estimators of VE_If was interesting and explored in detail analytically and via simulations in the Web Appendix C for the simple setting of constant pathogen distributions and exponential times to infection. We show that these two approaches actually estimate different parameters; the WCR approach estimates VE_If for a randomly selected pathogen while the product approach estimates a marginal VE_If. Limited simulations show that the relative efficiency ${\mathcal{Z}}_{\mathit{\text{PROD}}}^2/{\mathcal{Z}}_{\mathit{\text{WCR}}}^2$ was about 3.5 for these scenarios, suggesting the product method may be substantially more efficient. However, these simulations do not evaluate an all-or-none type vaccine effect.

Table 3.

Different methods of estimating differential vaccine efficacy applied to the DV10 region of the circumsporozoite protein. Data from a phase 3 trial of the RTS,S/AS01 malaria vaccine in African infants. The differential VE parameter α_2U = log{(1-VE_U1)/(1-VE_U2)}, where U = I for infection indicator or M for mean. 95% confidences in parentheses.

	VEIf on infection			VEMf on count
Parameter	One parasite	10,000 Monte Carlo WCR	Product method on I(Xf > 0)	Product method on Xf
Matched: VE1	0.55 (0.39,0.66)	0.56 (0.44,0.65)	0.60 (0.51,0.67)	0.61 (0.52,0.68)
Mismatched:VE2	0.43 (0.38,0.48)	0.43 (0.38,0.48)	0.44 (0.39,0.49)	0.52 (0.46,0.56)
Sieving effect
α̂2	−0.219	−0.245	−0.324	−0.211
Vâr(α̂2)	0.0244	0.0150	0.0097	0.0100
${\widehat{\alpha }}_2/\sqrt{\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}({\widehat{\alpha }}_2)}$	−1.40	−2.01	−3.29	−2.10

The final column estimates VE_Mf which are larger than the corresponding $\widehat{{\mathit{\text{VE}}}_{if}}s$ indicating a greater estimated effect of the vaccine on the mean than infection. However, the increase is more substantial for mismatched infections compared to matched infections. As a consequence, the Wald test of differential vaccine efficacy is less substantial (−2.01) than for the product estimator using I(X_f > 0) (−3.29).

6. Discussion

This article has developed methods to assess differential vaccine efficacy when multiple infecting strains can be quantified. While many pathogens typically have only a single clone infect a person, others, including HIV, malaria, and hepatitis C, can have multiple clones infect during the interval(s) between infection assessment. Such characterization offers the potential for increased efficiency in identifying clues about the mechanism of action of the vaccine. Methods for both passive and active surveillance were developed, the former is an obvious generalization of existing methods developed by Gilbert et al., while the latter is an extension of the methods of Follmann and Huang (2015). Because this article covered a lot of different approaches with different assumptions, in Table 4, we provide a summary of key assumptions required for the estimands of θ_f,g and 1-VE_Mf to achieve a per-exposure interpretation.

Table 4.

Key assumptions required to recover per-exposure estimands. All methods require that any infection be terminal (e.g., a trajectory of type 2 of Figure 1). If non-terminal (e.g., subclinical) infections are allowed, θ_f,g recovers a sieve effect and 1-VE_Mf a ratio of means, but neither has a clear per-exposure interpretation. In practice the assumptions below can be weakened further via stratification for any method or by allow use of time-varying covariates for the WEE and product methods.

Est. Met.	Data	Estimand	Assumptions
GEE	XP Wf L	Per-exposure ratio of means θf,g	$E(X_f^P|{\mathit{W}}_f)=exp({\mathit{\alpha }}^{\prime }{\mathit{W}}_f)$ per-exposure X iid FW () any infection is terminal
Prod	XA W δ, T	$V{E}_{Mf}=1-\frac{E\{X_f|{\mathit{W}}_{(1)}\}}{E\{X_f|{\mathit{W}}_{(0)}\}}$	Same V,P exposure: ω(t) exp(θ′WE) X independent draws from a dbn. with · $\frac{P(X_{+}>0|Z=1)}{P(X_{+}>0|Z=0)}=exp(\beta )$ · E(Xf|W, X+ > 0) = exp(W′fα) · $E(X_f|\mathit{W},X_{+}>0)=E(X_f^A|\mathit{W},X_{+}^A>0)$ any infection is terminal
WEE	XA W δ, T	$\mathrm{V}{\mathrm{E}}_{Mf}=1-\frac{E\{X_f|{\mathit{W}}_{(1)}\}}{E\{X_f|{\mathit{W}}_{(0)}\}}$	Same V,P exposure: ω(t) exp(θ′WE) X at time t an independent draw from a dbn. with · E(Xf|W) = exp{βf(t) + ϕ′W′ + ψ′ZVf} · $E(X_f|\mathit{W},X_{+}>0)=E(X_f^A|\mathit{W},X_{+}^A>0)$ any infection is terminal

Notes: X is the per exposure count vector; X^P is observed at end of follow-up L; X^A is observed at terminal infection at time T, 0 otherwise; T is the time to infection or censoring; δ is the infection indicator; f = 1, … F are the features of interest of the pathogen; ${\mathit{W}}_f^E$ are covariates that impact exposure; W_f are covariates that impact X_f; W¹ are covariates that impact X_f for vaccine and placebo; V_f are covariates that describe the vaccine efficacy for feature f; Z is the vaccine indicator; W = W^E, W₁, …, W_F; W(Z) denotes covariates in group Z = 1 vaccine or Z = 0 placebo.

For the RTS,S malaria vaccine trial, there were large Wald statistics for the new method compared to cataloging a single pathogen when yes/no infection was used as the readout. Additionally, in this dataset use of VE_If rather than VE_Mf had a more significant result. Whether VE_If would generally be more powerful than VE_Mf for malaria or other diseases will be answered in the analysis of additional trials. The example also showed that use of the marginal VE_If from active surveillance provided more evidence of sieving than the WCR estimator of VE_If for a randomly selected pathogen. This behavior was investigated analytically and reproduced in limited simulations. The two estimators do estimate different parameters and thus provide complementary information; as above, it will be interesting to see which approach is more powerful for different diseases.

Our weighted estimating equations were obtained by summing unbiased estimating equations over the different pathogen features. This is akin to the use of working independence correlation matrix in the GEE method and greater efficiency may be achievable if the equations were weighted based on the covariance cov(X|X₊ > 0). The method of generalized methods of moments approach could be used in future work to derive a more efficient estimator of α based on the “F × p” estimating equations.