Navigation of brain networks

Significance

We show that the combination of topology and geometry in mammalian cortical networks allows for near-optimal decentralized communication under navigation routing. Following a simple propagation rule based on local knowledge of the distance between cortical regions, we demonstrate that brain networks can be successfully navigated with efficiency that is comparable to shortest paths routing. This finding helps to conciliate the major progress achieved over more than a decade of connectomics research, under the assumption of communication via shortest paths, with recent questions raised by the biologically unrealistic requirements involved in the computation of optimal routes. Our results reiterate the importance of the brain’s spatial embedding, suggesting a three-way relationship between connectome geometry, topology, and communication.

Abstract

Understanding the mechanisms of neural communication in large-scale brain networks remains a major goal in neuroscience. We investigated whether navigation is a parsimonious routing model for connectomics. Navigating a network involves progressing to the next node that is closest in distance to a desired destination. We developed a measure to quantify navigation efficiency and found that connectomes in a range of mammalian species (human, mouse, and macaque) can be successfully navigated with near-optimal efficiency (>80% of optimal efficiency for typical connection densities). Rewiring network topology or repositioning network nodes resulted in 45–60% reductions in navigation performance. We found that the human connectome cannot be progressively randomized or clusterized to result in topologies with substantially improved navigation performance (>5%), suggesting a topological balance between regularity and randomness that is conducive to efficient navigation. Navigation was also found to (i) promote a resource-efficient distribution of the information traffic load, potentially relieving communication bottlenecks, and (ii) explain significant variation in functional connectivity. Unlike commonly studied communication strategies in connectomics, navigation does not mandate assumptions about global knowledge of network topology. We conclude that the topology and geometry of brain networks are conducive to efficient decentralized communication.

Nervous systems are networks and one of the key functions of a network is to facilitate communication. Complex topological properties such as small worldness (1, 2), modularity (3), and a core of highly interconnected hubs (4) are universally found across the brain networks of advanced and simple species, including mouse (5, 6), macaque (7, 8), and human connectomes (9). Support for efficient communication between neuronal populations is conjectured to be one of the main adaptive advantages behind the emergence of these complex organizational properties (10, 11).

Understanding how neural information is routed and communicated through complex networks of white matter pathways remains an open challenge for systems neuroscience (12, 13). To date, connectomics has largely focused on network communication based on optimal routing (14, 15), which proposes that information traverses the shortest path between two nodes. However, identifying shortest paths requires individual elements of nervous systems to possess global knowledge of network topology. This requirement for centralized knowledge has been challenged on the basis that nervous systems are decentralized, motivating alternative models of large-scale neural communication, such as spreading dynamics (11), path ensembles (16), communicability (17, 18), and diffusion models (19–21). These studies indicate that brain networks may support efficient communication without the need for centralized knowledge. For instance, random walkers can be biased to travel via efficient routes (22) and shortest paths help facilitate fast spreading of local stimuli (11).

Navigation is a network communication strategy that routes information based on the distance between network nodes (23). Navigating a network is as simple as progressing to the next node that is closest in distance to a desired target. Navigation is not guaranteed to successfully reach a target destination. Moreover, targets might be reached using long, inefficient paths. However, several real-world networks are known to be efficiently navigable, including biological, social, transportation, and technological systems (24–26). Successful navigation depends on certain topological properties such as small worldness (23) and a combination of high clustering and heterogeneous degree distribution (24), all of which are found in the brain networks of several species (9).

Here, we comprehensively investigate the feasibility of navigation routing as a model for large-scale neural communication. We develop a measure of navigation efficiency and apply it to publicly available connectomics data acquired from the macaque, mouse, and human brain. We find that brain networks are highly navigable, with connectome topology well poised between regularity and randomness to facilitate efficient navigation. In addition, we characterize the centrality of nodes and connections under navigability and investigate the relation between navigation path lengths and functional connectivity (FC) inferred from resting-state functional magnetic resonance imaging (MRI). Compared with shortest path routing, we find that navigation uses the brain’s resources more uniformly and yields stronger correlations with FC.

Results

Navigation Performance Measures.

We consider neural communication from the graph-theoretic standpoint of delineating paths (routes) in the connectome between pairs of nodes (gray matter regions). A routing strategy defines a set of rules for identifying a path from a source node to a target node. Path length refers to the number of connections that compose a path (hops) or the sum across the lengths of these connections. To minimize conduction latency, noise introduced by synaptic retransmission, and metabolic costs, neural communication should take place along paths with short path lengths (12, 13).

Navigation is a decentralized communication strategy that is particularly suited to spatially embedded networks (24, 25). Navigating a network involves following a simple rule: Progress to the next directly connected node that is closest in distance to the target node and stop if the target is reached (Fig. 1). To implement navigation, we defined the distance between pairs of nodes as the Euclidean distance between node centroids (27, 28). Importantly, navigation can fail to identify a path. This occurs when a navigation path becomes trapped between nodes without neighbors closer to the destination than themselves (Fig. 1B). The success ratio ($S_R$) measures the proportion of node pairs in a network that can be successfully reached via navigation.

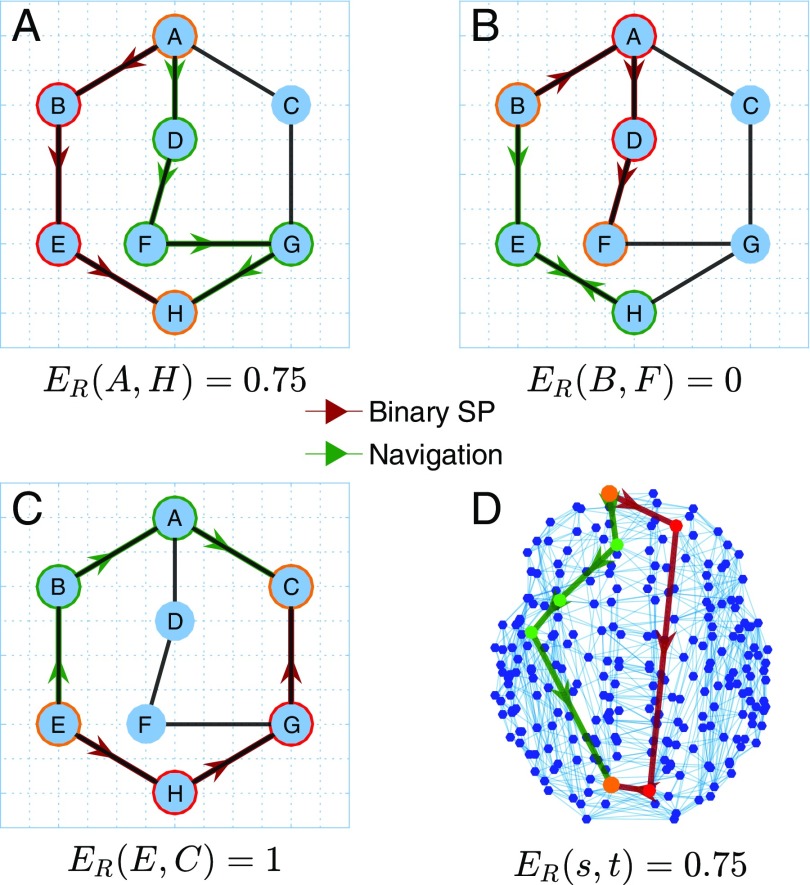
Fig. 1.

Illustrative examples of navigation (green) and shortest (red) paths from a source to the target node (circled in orange) in a binary network. Grid indicates spatial embedding of the networks. Efficiency ratios ($E_R\left(i,j\right)$) are the ratio of the number of hops in the navigation path to the number of hops in the shortest path. (A) The shortest path between A and H has three hops (A-B-E-H) while navigation leads to a four-hop path (A-D-F-G-H). Navigation routes information from A to H at 75% of optimal efficiency. (B) Navigation fails to find a path from B to F, becoming trapped between E and H. (C) Both strategies lead to three-hop paths, and navigation routes information from G to B at 100% of optimal efficiency. (D) Example of a successful navigation path in the human connectome that achieves 75% efficiency.

Let $L\hspace{0.17em}{\in \mathbb{R}}^{N\times N}$ denote a matrix of connection lengths for a network comprising $N$ nodes, where $L_{ij}$ measures the length of the connection from node $i$ to $j$, and let $\mathrm{\Lambda }$ denote the matrix of navigation path lengths. If node $i$ cannot navigate to node $j$, ${\mathrm{\Lambda }}_{ij}=\infty$. Otherwise, ${\mathrm{\Lambda }}_{ij}=L_{iu}+...+L_{vj}$, where $\left\{u,...,v\right\}$ is the sequence of nodes visited during navigation. We define navigation efficiency as $E=1/\left(N^2-N\right){\sum }_{i\hspace{0.17em}\ne \hspace{0.17em}j}1/{\mathrm{\Lambda }}_{ij}$. Analogous to global efficiency (29) [$E^{*}=1/\left(N^2-N\right){\sum }_{i\hspace{0.17em}\ne \hspace{0.17em}j}1/{\mathrm{\Lambda }}_{ij}^{*}$, where ${\mathrm{\Lambda }}_{ij}^{*}$ is the shortest path length from node $i$ to $j$], both measures characterize the efficiency of information exchange in a parallel system in which all nodes are capable of concurrently exchanging information. In the same way that global efficiency can incorporate network disconnectedness, navigation efficiency incorporates unsuccessful navigation paths ($E_{ij}=0$ if $i$ cannot reach $j$ under navigation). Therefore, $E$ quantifies both the number of failed paths and the efficiency of successful paths. We defined the efficiency ratio

$$E_R=\frac{1}{N^2-N}\sum _{i\hspace{0.17em}\ne \hspace{0.17em}j}\frac{{\mathrm{\Lambda }}_{ij}^{*}}{{\mathrm{\Lambda }}_{ij}}$$ [1]

to compare navigation with shortest path routing. For any network, $E^{*}\ge E$ and thus $0\le E_R\le 1$. The closer $E_R$ is to 1, the better navigation is at finding paths that are as efficient as shortest paths (Fig. 1).

We focus on binary ($E_R^{bin}$) and weighted ($E_R^{wei}$) navigation efficiency ratios, quantifying how efficient navigation paths are compared with shortest paths computed on binarized and weighted connectomes, respectively. In addition, we compute $E_R^{dis}$ to determine how close navigation paths are to routes that minimize the sum of physical (Euclidean) connection distances traversed between nodes.

Navigability of the Human Connectome.

High-resolution diffusion MRI data from 75 healthy participants of the Human Connectome Project (HCP) (30) were used to map structural brain networks at several spatial resolutions (N = 256, 360, 512, 1,024). Whole-brain tractography was performed for each individual and the number of streamlines interconnecting each pair of nodes was enumerated to provide a measure of structural connectivity (SI Appendix, Connectivity Data). A group-level connectome was computed as the average of all individual connectivity matrices (22). Connection weights were remapped into binary, weighted, and distance-based connection lengths to allow for the computation of communication path lengths (SI Appendix, Network Analysis).

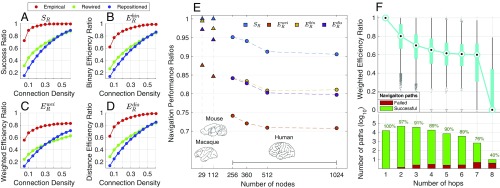
Consistent with previous reports (24, 25), we found that navigation can successfully identify paths for the majority of nodes pairs composing the human connectome ($S_R=$ 89%, 94%, and 96% for 10%, 15%, and 20% connection density, respectively, $N=360$; Fig. 2A). Remarkably, navigation was only marginally less efficient than shortest paths (e.g., $E_R^{wei}=$ 72%, $E_R^{bin}=$ 83%, and $E_R^{dis}=$ 83%, for $N=360$ at 15% connection density; Fig. 2 B–D), with navigation performance improving as connection density increased. Note that navigation does not use connection weights, and thus $E_R^{wei}$ quantifies the extent to which navigation can blindly identify weighted shortest paths. Navigation remained efficient and successfully identified paths for the majority of node pairs across various parcellation resolutions (SI Appendix, Fig. S1), with moderate decreases in success and efficiency ratios as the number of nodes increased ($S_R=$ 95%, 91%, and 90% and $E_R^{bin}=$ 84%, 80%, and 81% for N = 256, 512, and 1,024, respectively, at 15% connection density; Fig. 2E). When stratified by hop count, navigation performance remained high for long, multihop paths (61% median $E_R^{wei}$ and 79% median $E_R^{dis}$ benchmarked against five-hop shortest paths; Fig. 2F and SI Appendix, Fig. S2), suggesting that navigation efficiency is not due to directly connected node pairs or node pairs that can be navigated in only a few hops.

Fig. 2.

Navigability of mammalian connectomes. (A–D) Success ratio ($S_R$), binary efficiency ratio ($E_R^{bin}$), weighted efficiency ratio ($E_R^{wei}$), and distance efficiency ratio ($E_R^{dis}$) for human connectomes ($N=360$) at several connection density thresholds. Empirical measures (red) for group-averaged connectomes were compared with 1,000 rewired (green) and spatially repositioned (blue) null networks. Shading indicates 95% confidence intervals. (E) The same performance metrics shown across different parcellation resolutions of mammalian structural networks ($S_R$ shown in blue, $E_R^{wei}$ in orange, $E_R^{bin}$ in yellow, and $E_R^{dis}$ in purple). Triangles denote nonhuman species while circles denote human data. Dashed lines denote the same connection density (15%) across all human networks. (F) Navigability stratified by hop count ($N=360$ at 15% connection density). Blue box plots indicate the quartiles of $E_R^{wei}$ navigation paths benchmarked against shortest paths with matching hop count. Bar plots show the number of shortest paths for a given hop count, with colors indicating the proportion of successful (green) and failed (red) navigation paths. Brain diagrams reproduced from ref. 9, with permission from Elsevier.

Having established that the human connectome can be successfully and efficiently navigated, we next sought to determine whether efficient navigation is facilitated by the connectome’s topology or its spatial embedding. Navigation performance was benchmarked against ensembles of random null networks in which (i) the spatial position of nodes was shuffled; (ii) connectome topology was randomized (31); or (iii) connectome topology was randomized while preserving total network cost, defined as the sum of Euclidean distances between structurally connected nodes (10, 28) (SI Appendix, Network Analysis). Navigability of both the spatial and topological null networks was markedly reduced in comparison with the empirical networks (46% and 60% decrease in $E_R^{bin}$ and 48% and 60% decrease in $E_R^{wei}$, for topological and spatial randomization, respectively, at 15% connection density; Fig. 2 A–D, blue and green curves). In contrast, cost-preserving topological randomization resulted in null networks that, although significantly less navigable than the human connectome ($P<10^{-4}$; 13% and 11% decrease in $E_R^{bin}$ and $E_R^{wei}$, respectively, at 15% connection density; SI Appendix, Fig. S3), showed greater navigation performance than the less constrained null models. Taken together, these results suggest that navigation is jointly facilitated by both the connectome’s topology and its geometry. Randomization of either of these attributes markedly impeded navigation, while restricting topological randomization to realistic spatial embeddings accounted for a large extent of empirical navigation performance.

These findings were robust to variations in node distance measures and streamline count normalizations (SI Appendix, Supplementary Analyses and Figs. S4 and S5). Navigation performance of individual connectomes was comparable to the performance determined for the group-averaged connectome (SI Appendix, Fig. S6). Furthermore, navigation performance significantly deteriorated with age (SI Appendix, Fig. S7 and Table S1), but did not differ between males and females (SI Appendix, Fig. S8).

Navigability of Nonhuman Mammalian Connectomes.

Invasive tract-tracing studies provide high-quality connectomes for a number of nonhuman species (9). We aimed to determine whether a 112-region mouse connectome (52% connection density) (5, 6) and a 29-region macaque connectome (66% connection density) (8) were navigable. Navigation performed with $S_R=$ 100% and near-optimal communication efficiency for both species ($E_R^{bin}=$ 99%, 97%; $E_R^{dis}=$ 97%, 94%; and $E_R^{wei}=$ 87%, 84%, for the macaque and mouse, respectively; Fig. 2E). As with the human connectome, navigation performance was significantly increased compared with the topologically rewired and spatial null networks (all $P<10^{-4}$, with the exception of $P=0.012$ and $P=0.002$ for the macaque $S_R$ of topological and spatial null networks, respectively). However, the null hypothesis of equality in navigation performance between the connectomes of both species and the cost-preserving null networks could not be rejected (SI Appendix, Fig. S9).

The efficient navigation of connectomes across a variety of species, scales, and mapping modalities suggests that the topology and spatial embedding of nervous systems is conducive to efficient decentralized communication.

Connectome Topology and Navigation Performance.

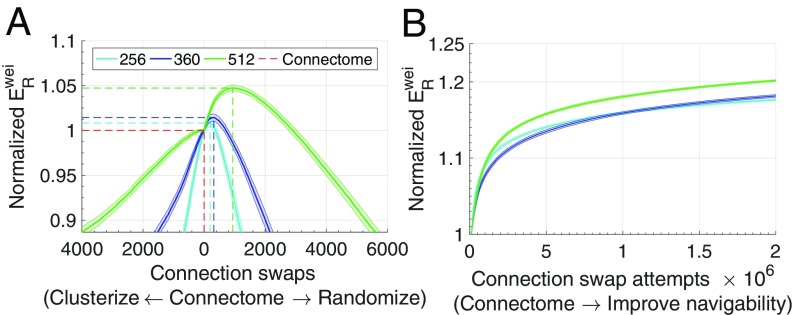
We sought to explore the impact of progressive topological alterations on the navigability of the human connectome. First, we tested whether navigation efficiency can be improved by progressively altering the topology of the human connectome to either increase its regularity (clusterize) or increase its randomness and wiring cost. Randomization was performed by progressively swapping connections between randomly chosen node pairs, while preserving connection density and degree distribution (31). With sufficient iterations, this yielded the topologically randomized null networks shown in Fig. 2 A–D (green curves). To clusterize topology, the same procedure was used with the additional constraint that each connection swap must lead to an increase in the overall clustering coefficient. Applying these procedures generated two sets of networks that progressively tended toward different ends of an order spectrum, ranging from orderly and regular networks with a high clustering coefficient to disordered and costly random networks (SI Appendix, Network Analysis). Clusterization was found to progressively decrease navigation efficiency, whereas slight randomization of connectome topology yielded networks with marginal increases in navigation performance (Fig. 3A). Specifically, peak $E_R^{wei}$ was, on average, 0.8%, 1.4%, and 4.7% more efficient than the connectome after 4.0%, 3.3%, and 4.8% of connections were randomly swapped, for N = 256, 360, 512, respectively. Further randomization beyond these peaks resulted in deterioration of navigation efficiency. Similar results were found for $E_R^{bin}$ (SI Appendix, Fig. S10).

Fig. 3.

Navigation performance ($E_R^{wei}$) of progressively rewired connectome topologies (at 15% connection density). The $E_R^{wei}$ of rewired topologies was normalized by the empirical value found for the human connectome. Curves indicate the mean values (inner line) and 95% confidence intervals (outer shadow) obtained from several runs of the rewiring routines. (A) Normalized $E_R^{wei}$ of clusterized and randomized networks for 100 runs of the randomization–clusterizing procedure and different parcellation resolutions. Dashed lines show performance peaks (vertical axis) and number of connection swaps (horizontal axis), with red indicating the values obtained for the empirical brain. (B) Normalized $E_R^{wei}$ obtained from direct optimization of the connectome’s empirical $E_R^{wei}$, as a function of connection swap attempts, for 50 ($N=256$), 50 ($N=360$), and 30 ($N=512$) independent rewiring runs.

Next, we investigated the effects of connectome rewiring aimed to explicitly increase navigability. To this end, we progressively performed connection swaps between randomly chosen node pairs that (i) preserved connection density and degree distribution, (ii) led to an increase of a measure of navigation performance, and (iii) preserved total network cost. We performed a total of $2\times 10^6$ connection swap attempts, with rejection of swaps that did not simultaneously meet all three conditions. Direct optimization of network navigability led to an 18–20% increase in $E_R^{wei}$, with 16–18% of the improvement taking place in the first $10^6$ swap attempts. Therefore, increasing connectome navigability rapidly became more difficult as a function of swap attempts, suggesting that the observed improvements converge to an asymptote. Comparable improvements between 5% and 22% were found for other measures of navigation performance (SI Appendix, Fig. S11). Collectively, these results indicate that the human connectome is well poised between randomness and regularity to facilitate efficient navigation, while explicit optimization by connectome rewiring converges to 5–22% improvements in navigability.

Navigation Centrality.

The number of shortest paths that traverse a node defines its betweenness centrality (BC), a measure that finds utility in identifying connectome hub nodes (12) and nodes mediating the bulk of neural communication (7). We defined a new path-based centrality measure called navigation centrality (NC), which quantifies the number of successful navigation paths that traverse each node (SI Appendix, Network Analysis).

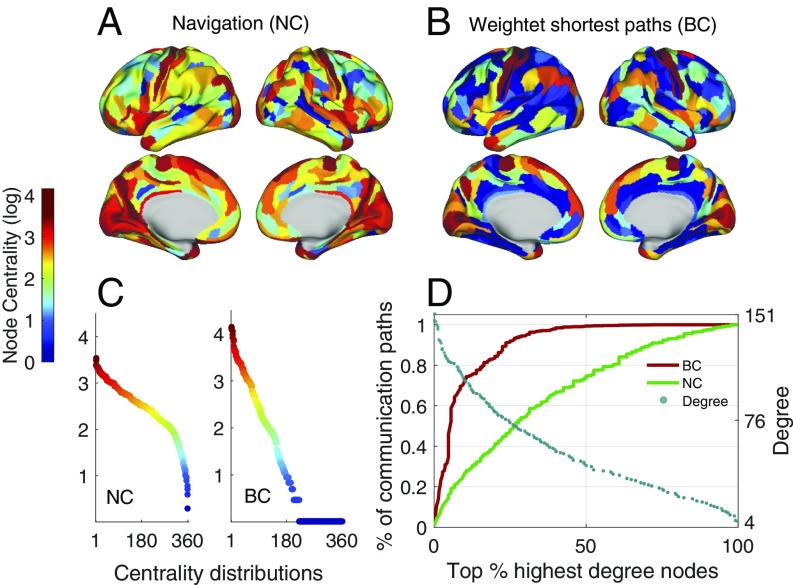
We computed NC and BC for the human connectome (group average, $N=360$, at 15% connection density), with BC based on weighted shortest paths. We found that both NC and BC spanned four orders of magnitude and were positively correlated (Pearson correlation coefficient $r=0.54$). Several regions were central to both shortest paths (BC) and navigation (NC), including portions of the left and right superior frontal gyrus, insula, central gyri, and precuneus (Fig. 4 A and B). However, NC was more uniformly distributed across nodes compared with BC, suggesting that navigation uses network resources more homogeneously (Fig. 4C). High values of BC were found only in a small group of high-degree nodes ($r=0.86$ between logarithm of BC and degree), which mediated most of the network’s communication routes. For instance, 99.3% of all shortest paths traveled exclusively through the top 50% most connected nodes (Fig. 4D). In contrast, although high-degree nodes showed high NC ($r=0.61$ between logarithm of NC and degree), medium- and low-degree regions were responsible for mediating a share of navigation paths, with the 50% least-connected nodes responsible for 26% of navigation paths. Greater diversity in paths may lead to fewer communication bottlenecks and less signal congestion (32), as well as stronger resilience against failure of network elements (16, 33). Similar results were obtained for BC computed in binarized connectomes (SI Appendix, Fig. S12) and for edge-centric definitions of BCs and NCs (SI Appendix, Fig. S13). All correlation coefficients ($r$) were significant ($P<10^{-8}$).

Fig. 4.

Comparison between navigation (NC) and weighted betweenness (BC) node centralities for $N=360$ at 15% connection density. Centrality values are logarithmically scaled. (A and B) NC (A) and BC (B) projected onto the cortical surface. (C) NC (Left) and BC (Right) sorted from highest to lowest values. (D) Relationship between the cumulative sum of centrality measures and degree. The horizontal axis is a percentage ranking of nodes from highest to lowest degree (e.g., for $N=360$, the 10% most connected nodes are the 36 nodes with highest degree). Solid curves (left-hand vertical axis) represent the cumulative sum of BC (red) and NC (green) over all nodes ordered from most to least connected, divided by the total number of communication paths in the network, indicating the fraction of communication paths mediated by nodes. Blue dots (right-hand vertical axis) show the original degree associated with each percentage of most-connected nodes.

Navigation and Functional Connectivity.

Finally, we tested whether navigation path lengths can explain variation in functional connectivity across nodes pairs of the human connectome. The strength of functional connectivity between node pairs that are not directly connected can be attributed to signal propagation along multisynaptic (multihop) paths (22, 34). Therefore, if multihop neural communication is indeed facilitated by navigation, we hypothesized that navigation path lengths should be inversely correlated with functional connectivity strength. Resting-state functional MRI data from the same 75 participants of the HCP were used to map functional brain networks. A group-averaged functional network was obtained by averaging FC across all participants (SI Appendix, Connectivity Data).

Given the geometric nature of navigation, an intuitive definition of navigation path length is the total distance traveled from one node to another along the navigation path (SI Appendix, Network Analysis). Navigation path lengths and FC were significantly associated across node pairs (SI Appendix, Fig. S14), with Pearson correlation coefficient $r=-0.32$ and $r=-0.43$, for the whole brain and right hemisphere, respectively, for $N=360$ at 15% connection density. This relationship was consistent across density thresholds, with navigation path lengths yielding stronger correlations with FC than shortest path lengths ($r=-0.35$, right hemisphere) and the direct Euclidean distance between node pairs ($r=-0.40$, right hemisphere). Correlations with navigation path lengths remained significant when stratified by structurally connected ($r=-0.51$, right hemisphere) and unconnected ($r=-0.28$, right hemisphere) node pairs. All correlations remained significant when interregional Euclidean distances were regressed from navigation path lengths and the resulting residuals correlated with FC ($P<10^{-5}$).

Discussion

This study investigated navigation as a model for large-scale neural communication. Using a measure of navigation efficiency, we evaluated the navigability of a range of mammalian connectomes. We found multiple lines of evidence suggesting that the topology (wiring) and spatial embedding (geometry) of nervous systems is conducive to efficient navigation. Our measure of navigation centrality indicated that navigation uses network resources more uniformly compared with shortest paths. We conclude that navigation is a viable neural communication strategy that does not mandate the centralized knowledge assumptions inherent to shortest paths, nevertheless achieving near-optimal routing efficiency.

Navigation performance was assessed for binary, weighted, and distance-based connectomes, each emphasizing a distinct attribute of network communication. While binary and weighted brain networks are commonly used in connectomics (12), distance-based connectomes were introduced to provide a geometric benchmark for navigation efficiency. Interestingly, navigation paths were simultaneously efficient in all three regimes, suggesting that neural signaling may favor communication routes that combine few synaptic crossings (binary), high axonal strength and reliability (weighted), and short propagation distances (distance based).

The topology of the human connectome was found to be well poised between regularity and randomness to promote efficient decentralized communication. While our focus on this order spectrum was motivated by canonical work on brain and real-world networks (1, 10), other dimensions of connectome topology such as degree diversity or hierarchical structure could be investigated (35). In fact, progressive rewiring explicitly seeking to optimize navigation indicates that connectome topology has a 5–22% margin for improvement in navigability. These findings support the notion that communication efficiency was likely only one of several evolutionary pressures that shaped connectome architecture (10, 13) (SI Appendix, Supplementary Analyses).

The significant association between navigation and FC is further evidence that neural communication is not necessarily constrained to optimal routes (22). This association could not be entirely attributed to navigation path lengths approximating interregional distances. Therefore, our findings build on previous work on the relationship between Euclidean distance and FC (27, 36), indicating that the combination of topological and geometric distances may contribute to the relationship between brain structure and function. Alternative formulations of interregional distances taking into account fiber-tract length or tract myelination could improve the biological relevancy of node distances, potentially improving the association between navigation path lengths and FC.

Connectome Geometry, Topology, and Communication.

Several recent studies have drawn attention to the link between geometry and topology in neural and other real-world networks (24, 27, 28). Our findings indicate that the interplay between connectome geometry and topology may be relevant for neural communication: The association between network geometry and topology (28, 37) contributes to the appearance of topological attributes conducive to navigation (24, 26), while the spatial positioning of nodes guides navigation of the topology, facilitating efficient decentralized communication. This notion is supported by our analyses of the navigation performance of different null models. Randomization of either connectome topology or geometry was sufficient to render connectomes less navigable, while topological randomizations that preserved characteristics of connectome geometry led to marked improvements in the navigability of null networks (see SI Appendix, Supplementary Analyses for further discussion).

Successful navigation has been linked to small-world topologies that combine spatially separated hubs and high-clustering coefficients (23, 24). Hub-to-hub long-range connections facilitate rapid information transfer across distant regions of the brain (although see ref. 38 for a counterpoint), while high clustering enables navigation to home in on specific destinations (4, 24) (SI Appendix, Fig. S15). This mechanism for information transfer is consistent with observations suggesting that nervous systems are small-world networks, balancing integration supported by long-range connections and segregation due to locally clustered modules (10).

Biological Plausibility and Communication Efficiency.

To date, the study of brain network organization has been anchored to the assumption of communication under shortest path routing (12, 15). Two examples are the characterization of the brain as a small-world network (1, 2) and the use of global efficiency as a measure of network integration (10, 14). These topological properties are derived from the shortest paths between all pairs of nodes. Building on previous work suggesting that efficient neural communication may take place in a decentralized manner (11, 22), we found that navigation can approximate the overall efficiency of shortest paths without requiring centralized knowledge of global network topology. Thus, we provide reassurance that previous findings obtained under the shortest paths assumption remain pertinent, despite the biologically implausible requirements for the computation of optimal routes, and reaffirm the importance of the brain’s small-world architecture in the light of decentralized routing schemes.

Navigation depends on network nodes possessing information about the relative spatial positioning between their direct neighbors and a target node. While the biological mechanisms that might endow nodes with this spatial information remain unclear, it is important to remark that navigation demands less information about network topology than shortest path routing and thus requires fewer assumptions to support its biological plausibility. Hence, in terms of biological plausibility, navigation occupies a middle ground between shortest paths and other decentralized models such as communicability (17, 18) and diffusion processes (19–21), which mandate fewer assumptions. However, navigation is near-optimally efficient and metabolically parsimonious (information is routed through a single path), thus overcoming important shortcomings of diffusion (39) and communicability (13) models, respectively.

Future research on large-scale neural communication models is necessary to explore alternative decentralized, efficient, and parsimonious network communication strategies. Exploring alternative spatial embeddings of brain networks (e.g., in hyperbolic space) may provide further insight into the navigability of nervous systems across species (40). In parallel, brain stimulation techniques could be used to evaluate evidence for competing communication strategies by means of electrophysiological tracking of local perturbations (41, 42).

Materials and Methods

Details on the acquisition and preprocessing of network datasets are described in SI Appendix, Connectivity Data. SI Appendix, Network Analysis provides details on network modeling. Supporting and replication analyses are presented in SI Appendix, Supplementary Analyses.

Navigation Implementation.

For a network with $N$ nodes, navigation routing from node $i$ to $j$ was implemented as follows. Determine which of $i$’s neighbors is closest (shortest Euclidean distance) to $j$ and progress to it. Repeat this process for each new node until $j$ is reached—constituting a successful navigation path—or a node is revisited—constituting a failed navigation path.

Navigation paths are identified based on network topology and the spatial positioning of nodes and thus independent from how connection lengths are defined. Navigation path lengths, however, are the sum of connection lengths composed in navigation paths and will vary depending on the definition of $L$. The matrix of navigation path lengths $\mathrm{\Lambda }$ was computed by navigating every node pair. Note that $\mathrm{\Lambda }$ is asymmetric, requiring $N^2-N$ navigation path computations. Using different connection length measures ($L^{bin},L^{wei},L^{dis}$), we computed binary (${\mathrm{\Lambda }}^{bin}$), weighted (${\mathrm{\Lambda }}^{wei}$), and distance-based (${\mathrm{\Lambda }}^{dis}$) navigation path lengths. Navigation efficiency ratios ($E_R^{bin}$, $E_R^{wei}$, $E_R^{dis}$) were computed by comparing navigation path lengths to shortest path lengths (${\mathrm{\Lambda }}^{bi{n}^{*}}$, ${\mathrm{\Lambda }}^{we{i}^{*}}$, ${\mathrm{\Lambda }}^{di{s}^{*}}$) using Eq. 1.

Data Sharing.

Human, macaque, and mouse datasets are publicly available. Our implementation of navigation routing is available at https://github.com/caioseguin/connectomics/.