Dynamic regimes of electrified liquid filaments

Significance

A viscous liquid filament subjected to an axial electric field exhibits different behaviors including jetting, coiling, and whipping, which result from the delicate interplay of viscous, electrostatic, and surface tension stresses. Control over these dynamic behaviors of electrified liquid filaments is crucial for applications such as the fabrication of nanosized architectures and analytical instrumentation. However, due to the narrow window of system parameters, the three dynamic regimes are never reported in a single system, which has prevented the investigation of transitions among these regimes. Using a low-interfacial-tension liquid−liquid system, we systematically characterize the transitions among all three dynamic regimes and elucidate underlying mechanisms, thus providing an important missing piece of the puzzle to the physics of electrified liquid filaments.

Abstract

We investigate the dynamics of an electrified liquid filament in a nozzle-to-substrate configuration with a close separation. The interplay between compressive viscous and electrostatic stresses dictates previously undocumented transitions between dynamic regimes of “jetting,” “coiling,” and “whipping.” In particular, the onsets of both coiling and whipping instabilities are significantly influenced by the minimum radius along the liquid filament. Using a low-interfacial-tension system, we unravel the physics behind the transitions between jetting, coiling, and whipping of an electrified filament for a range of liquid properties and geometric parameters. Our results enrich the overall physical picture of the electrically forced jets, and provide insights for the emerging high-resolution instability-assisted printing of materials such as folded assemblies and scaffolds.

Electrified liquid jets are ubiquitous in fundamental studies of electrohydrodynamics and industrial applications, such as electrosprays and electrospinning for manufacturing nanoparticles and nanofibers, respectively (1–4). Emerging applications, including flexible electronics and bioprinting, demand the printing of 3D architectures from multiple materials with control over both structure and functions (5–8). For instance, a variety of functional nanomaterials, such as metal nanowires, graphene nanosheets, carbon nanotubes, and protein nanofibrils, are incorporated into liquid precursors for printing (9–11). Electrically assisted printing techniques have enormous potential to achieve ultrafast and high-resolution printing with enhanced ordering of functional nanoobjects, where the liquid inks often form jets during printing (5, 10, 12–22). To engineer the printed structures at different length scales, understanding the dynamic behaviors of a liquid ink filament under an electrical field is crucial.

In electrically assisted printing, the electric stress provides a high shear that improves the alignment of the nanoobjects, while introducing new flow instabilities that influence the macroscopic structures (10, 12–16, 20, 23). Under an applied electric field, a liquid with a finite conductivity can adopt a conical shape, at the apex of which a thin jet is emitted. Subsequently, the jet either breaks into droplets rapidly, due to a symmetric instability, or it elongates until a lateral whipping instability develops (1, 24–34).

For electrified jets that connect the nozzle and substrate at small separation distances, such as on a printing platform, new dynamic behaviors of viscous liquid filaments occur. For example, recent studies show that a viscous filament can be triggered to coil steadily by applied electric stresses (18, 20, 26, 35–38). However, to the best of our knowledge, the electrically induced coiling and electrospinning have not been observed in a single system for at least two reasons. In the systems where electrically induced coiling is observed, as the electric field is increased further to trigger the whipping instability, the ambient air shows dielectric breakdown, which prevents the transition to whipping (39). Unlike a coiling jet, a whipping jet, which is often exploited in electrospinning applications, tends to be distant from the substrate and thus lacks the compression necessary to initiate the coiling instability; this feature again hides the possible transition between electrically induced coiling and whipping.

In this work, we demonstrate that, as the imposed electric field increases, the dynamics of a sufficiently short electrified filament passes through three regimes sequentially: “stable jetting,” “steady coiling,” and “chaotic whipping.” The minimum radius of the electrified liquid filament connecting the nozzle and substrate, which is controlled by the applied voltage, liquid properties, and geometric parameters, significantly influences the onsets of both the coiling and whipping instabilities. By varying the neck radius via the applied voltages, we demonstrate that the whipping instability competes with the coiling instability, and which of these occurs first determines the fate of the electrified liquid filament. Our work elucidates the underlying physics of the electrified liquid filament, and brings important insights to engineer the dynamic routes of liquid filaments for high-resolution electrically assisted printing applications.

Results

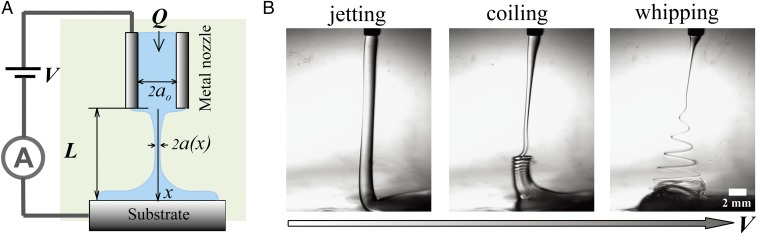
We use a setup to generate a liquid filament connecting the nozzle and substrate at a distance of L, as illustrated in Fig. 1A. We pump the working liquid with a volumetric flow rate, Q, through a metallic nozzle with a radius $a_0$ into a bath of immiscible dielectric oil or ambient air (see Materials and Methods). The working liquids for the jets have finite electrical conductivity and are characterized by both a dielectric response and a conductivity, thus referred to as leaky dielectrics (30). The leaky dielectric liquids can support both normal and tangential electrostatic stresses in the presence of an electric field (30). The applied electric field is tuned by changing the potential difference V between the metallic nozzle and the substrate, which is in contact with the working liquid. The dynamic behavior of the electrified filament is monitored using high-speed imaging coupled with a commercial lens (see Materials and Methods).

Fig. 1.

(A) The schematic of the experimental setup. (B) A series of high-speed images showing the dynamic behaviors jetting, coiling, and whipping, respectively, of an electrified liquid filament; the corresponding applied voltages are 0, 0.75, and 1.5 kV, respectively. A liquid filament of a solution of lecithin with a viscosity of μ = 7.5 Pa⋅s is extruded from a nozzle with a radius of $a_0$ = 0.92 mm at a fixed flow rate Q = 10 mL/h into a bath of silicone oil with a viscosity of μ = 10 mPa⋅s. The interfacial tension $\gamma$ between silicone oil and lecithin solution is 2 mN/m.

In the absence of the applied voltage, we observed jetting at a sufficiently large imposed flow rate $Q$, where the liquid filament connects the nozzle and substrate without breaking into droplets (Fig. 1B, jetting) (SI Appendix, section I) (40). At low voltages, the liquid filament becomes slightly thinner and remains stable against breakup. The tangential electric stress $\sigma E_t$ exerted on the liquid interface contributes to the stability of the thin filament, where $\sigma \hspace{0.17em}\text{and}\hspace{0.17em}{E}_t$ are the surface charge density of the liquid and the tangential component of the electric field, respectively (30, 31, 33). At intermediate voltages, the liquid filament starts to oscillate periodically at constant frequency and amplitude (Fig. 1B, coiling, and see Movie S1). The resultant regular helical coils stack together, resembling a pile of rope. The coiling of the liquid filament is steady in surrounding oils or air. At higher voltages, a sharp transition from coiling to whipping is observed. The whipping structure in air is usually chaotic (SI Appendix, Fig. S1), while, in silicone oil, it manifests a wavelike structure with an amplitude increasing along the axial direction (Fig. 1B, whipping) (24).

We performed experiments using leaky dielectric liquids with different finite conductivities, viscosities, and interfacial tensions with the surrounding perfect dielectric fluids. All experiments exhibit consistent behaviors that demonstrate the robustness of the phenomena. The largest electric field we applied, ∼0.2 kV/mm, is far below the dielectric breakdown of the surrounding dielectric oils, ∼15.4 kV/mm (41); thus the influence of any ionization due to the breakdown of the dielectrics in our systems is ruled out (39).

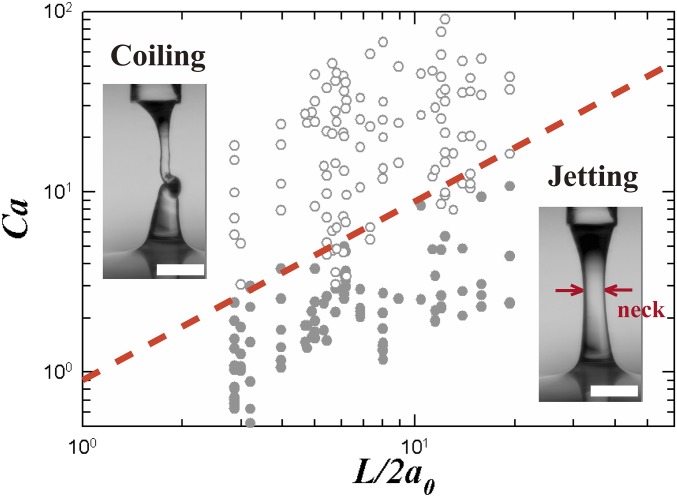
The coiling of a liquid jet usually occurs as a sufficiently large compressive stress bends the filament. Here the applied electric stress acting on the filament is analogous to a mechanical compression (36), as if the two ends of the liquid filament are pushed inward by a tangential electric stress (Fig. 2, Insets). The larger the applied electric stress the higher the fluid velocity generated, leading to a larger compression. The viscous compressive stress is characterized by $\mu U_{max}/L$, where $U_{max}\approx Q/\pi a_{min}^2$ is the local velocity at the minimum radius of the filament, $a_{min}$, and L is the separation between the nozzle and substrate. The surface tension $\gamma$ has a stabilizing effect, since it favors an axisymmetric filament of smaller surface area than a coiled filament. The consequent stretching stress drives the liquid toward the ends of filament, and can be expressed by $\gamma /a_0$, where $a_0$ is the nozzle radius. The surface tension can be neglected if $\gamma /a_0$ is smaller than the compressive stress $\mu U_{max}/L$, which is equivalent to a capillary number $Ca=\mu U_{max}/\gamma \ge L/a_0$ (Fig. 2) (36). This equation predicts that the critical capillary number Ca indicating the transition from jetting to coiling should scale linearly with the length to diameter ratio, $L/2a_0.$ Indeed, the experimental observations show that a coiling filament occurs at sufficiently high $Ca$, as demonstrated in the state diagram in Fig. 2, which highlights the regimes of jetting and coiling as functions of $L/2a_0$ and Ca. The observations indicate that the trigger for coiling of a given liquid thread is controlled by the minimum radius $a_{min}$ along the filament, which decreases with increasing $E.$ If the neck of the electrified filament gets thin enough to reach $Ca\ge L/a_0$, the filament loses stability and coils. However, how $a_{min}$ varies with the applied E is affected by factors such as the geometric parameters, liquid properties, and flow rates, in a complicated and unknown way.

Fig. 2.

A log−log state diagram showing the jetting and coiling of electrified liquid filaments, based on the capillary number $Ca=\mu U_{max}/\gamma$ at the neck and the relative separation between the nozzle and the substrate, $L/2a_0.$ The state diagram contains more than 150 individual measurements and is highly reproducible. The diagram is divided into two regimes: (i) jetting, closed circles; and (ii) coiling, open circles (Left and Right Insets are microscope images showing coiling and straight jets, respectively). (Scale bar: 2 mm.) The dashed line represents a linear relationship $Ca=\mu U_{max}/\gamma \approx L/2a_0$. Here $L/2a_0$ is in the range of 4 to 20, fulfilling the assumption of a slender jet (36).

Moreover, the thinning of the electrified filament also influences the onset of the whipping instability. An electrified liquid filament whips when the repulsion between surface charges with surface charge density $\sigma \approx {\epsilon }_o{E}_n$ dominates the surface tension, where ${\epsilon }_o$ $\text{and}\hspace{0.17em}{E}_n$ are the permittivity of the outer dielectric liquid and the normal component of the electric field outside the filament, respectively (25, 42) (SI Appendix, section II). Thus, the onset of whipping occurs when the electrocapillary number that describes the ratio of the electric stress to surface tension, ${\mathrm{ℰ}}_c=({\epsilon }_i-{\epsilon }_o)E^2{a}_0/\gamma \approx {\epsilon }_i{E}^2{a}_0/\gamma$, exceeds O(1), where ${\epsilon }_i$ $\text{is}$ the permittivity of the liquid filament (33, 43, 44) (SI Appendix, section II). For a liquid filament that connects two electrodes, the jet radius a must be sufficiently small that the surface electrical current, $I_{conv}=2\sigma Q/a$, dominates the bulk electrical conduction, $I_{cond}=\pi EK{a}^2$, where $K$ is the electrical conductivity of the liquid jet (24, 25, 27, 45, 46). Only then are the charges mainly convected along the interfaces, enabling a significant repulsion between surface charges. Thus, the shape of the thinning filament under an applied electric field is important for both coiling and whipping behaviors.

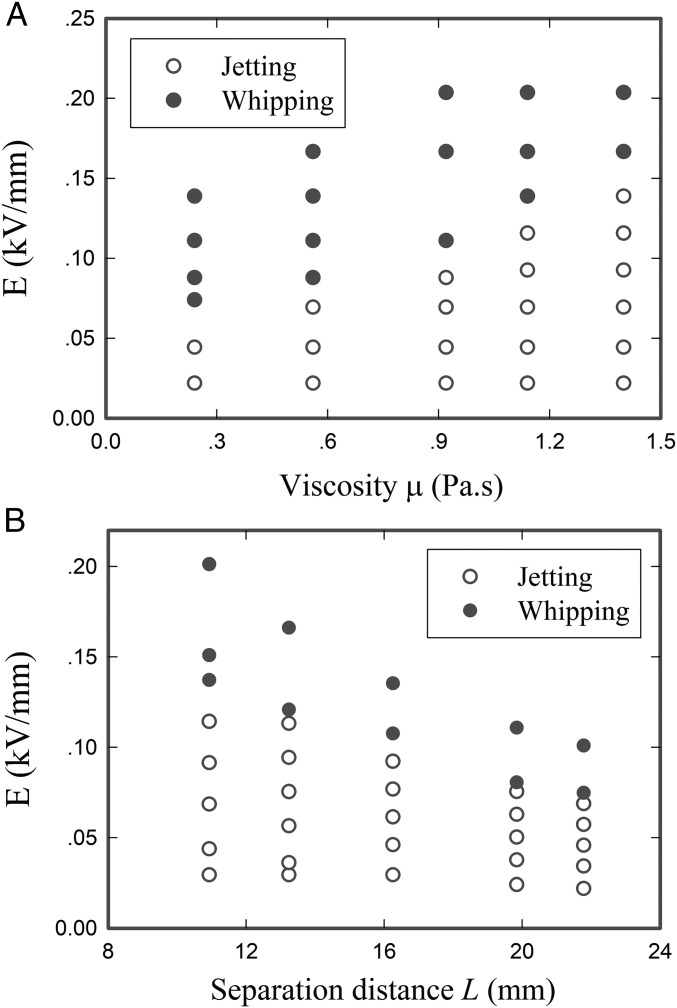
The shape of an electrified liquid filament connected by the nozzle and substrate is significantly influenced by the nozzle-to-substrate distance L. The distance L affects the relative importance of the viscous and inertial effects, which is described by the Reynolds number. We introduce a critical length $L_c=\mu A/\rho Q$, where $\rho \hspace{0.17em}\text{and}\hspace{0.17em}A$ are the density of the liquid and the cross-sectional area of the nozzle, respectively. For instance, with $L>L_c$ and thus Re >1, it has been reported that changing μ leaves the jet profile unchanged (27, 47, 48) (SI Appendix, Fig. S2A), while, for $L<L_c$, $\mu$ affects the shape of electrified filament (SI Appendix, Fig. S2B), and hence the onset of whipping instability (Fig. 3A). Owing to the lower interfacial tension in liquid−liquid systems than that in liquid−air systems, we are able to investigate the onset of whipping using an electric field that is far smaller than the dielectric breakdown strength of the surrounding oils (39). Moreover, the surprising stability against whipping is more pronounced with smaller L and larger viscosity $\mu$, as shown in Fig. 3. Thus, the shape of an electrified viscously dominated liquid filament with $L<L_c$ needs to be investigated to understand its stability against whipping.

Fig. 3.

State diagram in the (A) $E-\mu$ (Q = 20 mL/h, L = 16.4 mm) and (B) $E-L$ (Q = 5 mL/h, $\mu$ = 0.56 Pa⋅s) planes, representing where the jetting and whipping are observed. The open and closed circles denote the jetting and whipping, respectively. The viscosity and separation distance are varied for A and B while keeping other parameters constant. The surrounding dielectric liquids used are 1% Span 80 in hexadecane and paraffin for A and B, respectively.

We develop a model to account for the detailed profile of an electrified viscously dominated filament as the applied E increases (27, 45). The basic assumption of the fluid dynamical description is that the radial component of the jet velocity field is negligible, and the axial velocity is uniform across the cross-section of the jet (SI Appendix, section III). Applying Newton’s second law of motion to an element of the liquid filament for a steady one-dimensional motion (45, 49–52), we obtain

$$\frac{3\mu }{a^2}{\left(a^{2}v\prime \right)}^{\prime }-{\left(\frac{\gamma }{a}\right)}^{\prime }+\rho g+\frac{\sigma E_t}{a}=\rho vv\prime ,$$ [1]

where the first term on the left-hand side describes the viscous effects, ${\left(\right)}^{\prime }$ denotes “$d\left(\right)/dx$”, and $a\left(x\right)$ and $v\left(x\right)$ denote the local thread radius and jet velocity, respectively. The three remaining terms on the left-hand side of Eq. 1 denote the surface tension, gravitational, and tangential electric field effects, where $g$ is the gravitational acceleration$.$ The inertial term is on the right-hand side of Eq. 1. Because the Bond number that describes the relative importance of the gravitational to surface tension effects in our experiments is ${\rm O}$(10⁻²), the gravitational term can be neglected. The inertial term is negligible since the Reynolds number, which measures the ratio of inertial to viscous effects, is ${\rm O}$(10⁻²). The surface tension contribution is also neglected for $Ca=\text{O}\left(10\right)$, since the electrified liquids we describe below have large viscosities and low interfacial tension in immiscible oils.

The governing equation can thus be simplified to a balance between the viscous and electric stress terms. The corresponding boundary conditions are a = a₀ at x = 0 and $a\to \infty \hspace{0.17em}\text{at}\hspace{0.17em}x=L$, i.e., the radius becomes much larger than a₀ near the substrate. We find an analytical solution (SI Appendix, section III),

$$a\left(x\right)=\frac{K_1^2{c}_1}{2}\left({\left(\tan \left(\frac{\sqrt{c_1}}{2}x+d_1\right)\right)}^2+1\right),$$ [2a]

$$\text{where}\hspace{0.17em}\frac{L}{a_0}>\sqrt{2}{K}_1,\hspace{0.17em}{K}_1^2=\frac{6\mu Q}{\pi \sigma E{a}_0^3}\approx \frac{6\mu QL}{\pi {\epsilon }_o{E}^2{a}_0^4},\hspace{0.17em}{E}_t\cong E,\hspace{0.17em}{E}_n\approx \frac{a_0}{L}{E}_t,$$

with the additional parameters

$$\cos d_1=K_1\sqrt{\frac{c_1}{2}};\hspace{0.17em}(\cos d_1)\beta +d_1=\frac{\pi }{2};\hspace{0.17em}\beta =\frac{L}{\sqrt{2}{K}_1{a}_0}.$$ [2b]

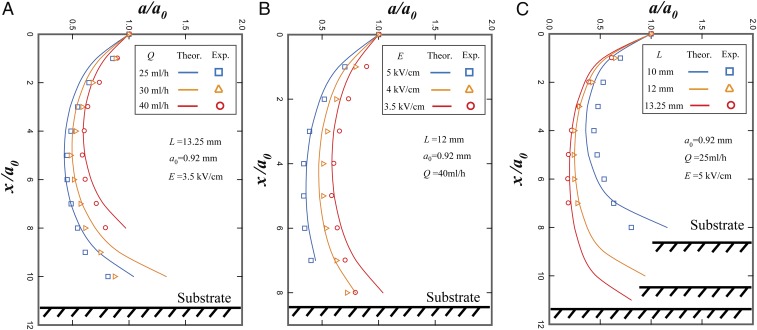
We compare this analytical solution with experimental results for the shape $a\left(x\right)$ by varying the flow rate, Q, applied electric field strength, E, and the separation, L, respectively, as shown in Fig. 4. Indeed, the normalized jet radius $a/a_0$ as a function of the normalized axial distance $x/a_0$ agrees well with the values predicted by Eq. 2 with no fitting parameters. The overall jet radius is larger for higher Q, lower E, and smaller L, as shown in Fig. 4. The model captures the main characteristics of the profile for the electrified viscous filament in an axial electric field. The consistency between the theoretical and experimental results confirms a good approximation of the bridge shape within a limited range of L. The separation L should not be too large to render Re > 1, nor too small, and hence become comparable with the nozzle size to make a one-dimensional analysis unreasonable.

Fig. 4.

The profile of the electrified liquid filament (A) at a constant separation L, nozzle radius $a_0$, and applied electric field strength E, but different volumetric flow rates of 25 mL/h (blue squares), 30 mL/h (yellow triangles), and 40 mL/h (red circles), respectively; (B) at a constant separation L, nozzle radius $a_0$, and volumetric flow rate Q, but different applied electric field strengths of 3.5 kV/cm (blue squares), 4 kV/cm (yellow triangles), and 5 kV/cm (red circles), respectively; and (C) at a constant applied electric field strength E, nozzle radius $a_0$, and volumetric flow rate Q, but different separations of 10 mm (blue squares), 12 mm (yellow triangles), and 13.25 mm (red circles), respectively. The solid lines represent the theoretical solutions (2), while the open symbols represent the measured radius of the electrified filament. The experimental results agree well with theoretical predictions with no fitting parameters. Exp, experimental; Theor, theoretical.

Next, we deduce a scaling law for the minimum radius along the electrified filament, as shown in Fig. 4. This local minimum radius corresponds to $a\prime =0$, and is deduced as $a_{min}={\cos }^2{d}_1$, where $d_1$ is a constant defined in Eq. 2b. Numerically, we find that ${\cos }^2{d}_1\approx {\beta }^{-2}$ by a power-law fitting (SI Appendix, section IV and Fig. S3), thus leading to

$$a_{min}\approx \frac{K_1^2{a}_0^3}{L^2}\approx \frac{\mu v_0{a}_0}{{\epsilon }_o{E}^{2}L}\hspace{0.17em}\left(\text{for}\hspace{0.17em}\beta >1\right),$$ [3]

where $v_0\approx Q/a_0^2$ is the typical velocity at the nozzle. Rearranging Eq. 3, we have $\mu v_0/a_{min}L\approx {\epsilon }_o{E}^2/a_0$, which is a representation of the viscous effects resisting bending caused by electrostatic stresses. This equation describes the thinning of a viscously dominated filament acted on by the electric field, and the minimum radius $a_{min}$ is dependent on both $\mu$ and L.

The scaling law of $a_{min}$ enables us to elucidate the dynamic behaviors for the electrified filament with different liquid properties and separation distances, as E increases. With Eq. 3, we obtain the coiling criterion of the maximum capillary number along the filament as

$$Ca\approx \frac{\mu Q}{\gamma a_{min}^2}\approx \frac{{\epsilon }_o^2{E}^4{L}^2{a}_0^2}{\mu Q\gamma }\hspace{0.17em}\hspace{0.17em}\left(\text{for}\hspace{0.17em}\beta >1\right).$$ [4]

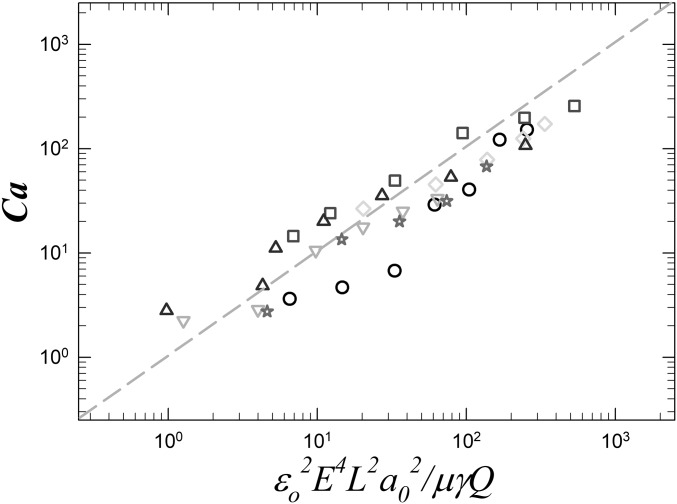
By changing E, L, a₀, γ, and Q, we verify that all of the data in the coiling regime falls near the dashed line represented by a power law fit of $Ca\approx {\epsilon }_o^2{E}^4{L}^2{a}_0^2/\mu \gamma Q$, confirming our theoretical prediction, Eq. 4, as shown in the log−log plot of Fig. 5. Substituting Eq. 4 into the coiling criterion, we have the onset E of the coiling for a viscously dominated filament as $E_{\mathrm{coiling}}\approx {\left(\mu \gamma v_0\right)}^{1/4}{L}^{-1/4}{a}_0^{-3/2}{\epsilon }_o^{-1/2}$ $\left(\text{for}\hspace{0.17em}\beta >1\right)$.

Fig. 5.

A log−log plot of the capillary number $Ca\approx \mu Q/\gamma a_{min}^2$ versus ${\epsilon }_o^2{E}^4{L}^2{a}_0^2/\mu \gamma Q$ for the transition to coiling. The grayscale symbols correspond to different experimental parameters: circles (○) (L = 11.4 mm, Q = 30 mL/h, $a_0$ = 0.92 mm, $\gamma$ = 32 mN/m); triangles-down (▿) (L = 12.7 mm, Q = 40 mL/h, $a_0$ = 0.92 mm, $\gamma$ = 32 mN/m); squares (□) (L = 8.2 mm, Q = 1 mL/h, $a_0$ = 0.92 mm, $\gamma$ = 2 mN/m); diamonds (◇) (L = 9.6 mm, Q = 0.5 mL/h, $a_0$ = 0.92 mm, $\gamma$ = 2 mN/m); triangles-up (▵) (L = 12.8 mm, Q = 10 mL/h, $a_0$ = 0.92 mm, $\gamma$ = 32 mN/m); and stars (☆) (L = 7.4 mm, Q = 8 mL/h, $a_0$ = 0.46 mm, $\gamma$ = 32 mN/m).The data points from the same symbols correspond to different applied electric field strengths. All symbols collapse onto a dashed line representing a linear relationship, confirming our scaling relationship ${\epsilon }_o^2{E}^4{L}^2{a}_0^2/\mu \gamma Q\cong Ca,$ as stated in Eq. 4.

Additionally, we can understand why small L and large $\mu$ enhance the stability of a filament against whipping (39). Both factors favor a larger $a_{min}$ of the electrified filament. A larger $a_{min}$ decreases the surface convection current (SI Appendix, section V), leading to a decrease of the surface charges and thus suppressing the effect of charge repulsion (24, 25, 27, 45). To trigger the whipping of a more viscous and shorter filament connecting the nozzle and substrate, a larger E has to be applied (SI Appendix, section VI and Fig. S4).

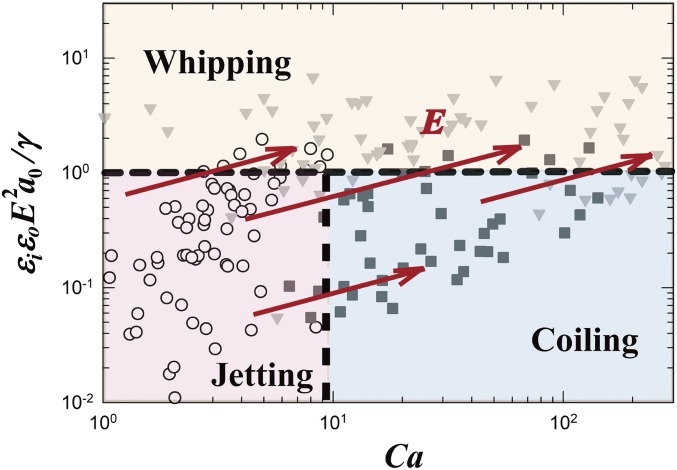
In summary, we identify and predict quantitatively the dynamical routes of an electrified filament for different liquid properties and configurations. A sufficiently large applied E could induce both the coiling and whipping instabilities for an electrified filament. As the local $Ca$ at the neck of the filament, or ${\mathrm{ℰ}}_c={\epsilon }_i{E}^2{a}_0/\gamma$, reach the critical value, the coiling and whipping of the filament, respectively, occur. Also, $Ca$ increases with increasing E, and the jet starts to coil upon reaching a critical $C{a}_c\approx L/2a_0$, while the whipping occurs approximately as ${\mathrm{ℰ}}_c$ approaches ${\rm O}\left(1\right)$. Therefore, depending on which dimensionless parameter reaches its critical value first, the charged filament has several possible dynamical paths. For instance, with viscous liquids, the local Ca at the filament neck increases rapidly; thus the jet coils first and whips in sequential order, as shown in Fig. 1B. For less viscous liquids, the local Ca at the neck increases slowly, and, before it reaches the critical value, the whipping criterion is already fulfilled, and the coiling is not observed. As an illustration, under a constant $L/2a_0\approx 10$, we characterize the three dynamical regimes “stable jetting,” “steady coiling,” and “chaotic whipping” as well as the four possible transitions of the electrified viscous liquid filament, as summarized in Fig. 6.

Fig. 6.

A state diagram for the dynamic behaviors of an electrified liquid filament based on $Ca\approx \mu U_{max}/\gamma$ and ${\mathrm{ℰ}}_c\approx {\epsilon }_i{E}^2{a}_0/\gamma$, with a fixed geometric separation $L/2a_0\approx 10$. The diagram is divided into three regimes: (i) jetting, closed circles; (ii) coiling, closed squares; and (iii) whipping, closed triangles-down. An electrified jet has several possible routes in the state diagram as the applied E increases: (i) jetting → coiling → whipping: The critical $Ca$ is reached before ${\mathrm{ℰ}}_c$; (ii) jetting → whipping: The critical ${\mathrm{ℰ}}_c$ is reached first; (iii) jetting → coiling: The critical $Ca$ is reached, and the dielectric breakdown of the surrounding liquids occurs before the critical ${\mathrm{ℰ}}_c$; and (iv) coiling → whipping: The viscous filament coils even for E = 0, and whips when the critical ${\mathrm{ℰ}}_c$ is fulfilled by increasing E. The arrows in Fig. 6 indicate that, as E increases, $Ca$ and ${\mathrm{ℰ}}_c$ scale with $E^4$ and $E^2$, respectively.

Conclusions

We show that the dynamics of electrified liquid filaments could pass through all three regimes—stable jetting, steady coiling, and chaotic whipping—using a low-interfacial-tension immiscible liquid system. We have uncovered the minimum radius of the bridge-shaped viscous filament as the control parameter for the onsets of both coiling and whipping instabilities. A model is developed for predicting the detailed shape profile of a viscously dominated electrified liquid filament, with good agreement with the experimental results. Based on this model, we identify the scaling relationship of the neck radius as a function of liquid properties and geometric parameters, as well as the dynamic paths of the electrified viscous filament as the charging voltage increases. Thus, we have confirmed that electrically induced coiling and whipping are not exclusive for different liquids or separation distance, but can be observed in the same system if the dynamical criteria are satisfied sequentially. The mechanism behind the transitions of these dynamical regimes provide a thorough understanding for the dynamic of electrified liquid filaments, and thus enrich the physical picture of the electrically forced jets. These results also have important implications for emerging applications of electrically assisted dispensing and printing that combines topology design and manufacturing.

Materials and Methods

We use a nozzle−substrate setup to generate a liquid filament as illustrated in Fig. 1A. The working liquids for jets include mixtures of glycerin and deionized water that varied from 0 wt% to 5 wt%, and lecithin from soybean oil (Wing Hing Chemicals). These liquids with finite electrical conductivity, possibly due to the presence of ions, are referred to as leaky dielectrics, which can support both normal and tangential electrostatic stresses in the presence of an electric field. The surrounding fluids were perfect dielectric fluids such as silicone oil, liquid paraffin, hexadecane, or air. The interfacial tension ranged from 10⁻² mN/m to 32 mN/m. The low oil−water interfacial tensions were adjusted by adding Tween 20 in aqueous mixtures and Span 80 in the dielectric oils. They were measured by either a spinning drop tensiometer (Krüss 100) or the pendant drop method. The dielectric constants were measured by a dielectric constant meter (Brookhaven Instruments). The permittivity of the inner jet, ${\epsilon }_i$, varied from 1.68 $\times$ 10⁻¹⁰ F/m to 3.71 $\times$ 10⁻¹⁰ F/m, while the permittivity of the surrounding outer liquid, ${\epsilon }_o$, was 8.85 $\times$ 10⁻¹² F/m and 1.77 $\times$ 10⁻¹¹ F/m for ambient air and silicone oil, respectively. The viscosity of the liquids used in our experiments were measured using a rheometer (R/S series; Brookfield) and are listed and summarized in SI Appendix, Table S1. All of the viscous liquids we used in this manuscript are Newtonian. The electrical conductivities of the aqueous solutions were carefully tuned by doping potassium chloride, and measured by a conductivity meter (CyberScan CONT 610; Eutech Instruments). The measured conductivities of the working liquids ranged from 10⁻⁸ S/m to 10⁻⁴ S/m, which were at least four orders of magnitude higher than the corresponding values, 10⁻¹² S/m and 10⁻¹⁵ S/m, for the surrounding dielectric liquids and air, respectively (53).

We pumped the working liquid through a metallic nozzle with a radius $a_0=$ 0.46 mm or 0.92 mm, which was surrounded by a bath of immiscible dielectric oils or ambient air. A metallic substrate was placed underneath the nozzle at a distance L. To apply the external electric field, we established a potential difference V between the metallic nozzle and substrate, which was in contact with the working liquid. The resultant electric field strength E was estimated as E = V/L. We adjusted the volumetric flow rate, Q, of the working liquid by a syringe pump (Longer Pump) to form a liquid filament connecting the nozzle and substrate. We then varied the potential difference V to obtain different dynamic behaviors of the electrified filament, which was monitored using a high-speed camera (Photon) coupled with a commercial lens (Nikon).