Metastable quasicrystal-induced nucleation in a bulk glass-forming liquid

Significance

A model alloy, Mg₆₉Zn₂₇Yb₄, concurrently forms bulk metallic glass, metastable quasicrystals (QCs), and crystalline approximant phases from the melt. We demonstrate that a transient QC phase nucleates first from the melt and subsequently transforms into an equilibrium approximant phase. This nucleation path is likely to be a general mechanism in metastable QC-forming systems. We observed a metastable-to-stable phase transformation when we deployed fast differential scanning calorimetry using the experimental strategy of interrupted cooling after the onset of crystallization followed by heating at ultrafast rates to “up-quench” the previously frozen structure. This strategy can yield the discovery of hidden transient phases that are key to understanding the crystallization behavior in metallic systems, polymers, biological solutions, and pharmaceutical substances.

Abstract

This study presents a unique Mg-based alloy composition in the Mg–Zn–Yb system which exhibits bulk metallic glass, metastable icosahedral quasicrystals (iQCs), and crystalline approximant phases in the as-cast condition. Microscopy revealed a smooth gradual transition from glass to QC. We also report the complete melting of a metastable eutectic phase mixture (including a QC phase), generated via suppression of the metastable-to-stable phase transition at high heating rates using fast differential scanning calorimetry (FDSC). The melting temperature and enthalpy of fusion of this phase mixture could be measured directly, which unambiguously proves its metastability in any temperature range. The kinetic pathway from liquid state to stable solid state (an approximant phase) minimizes the free-energy barrier for nucleation through an intermediate state (metastable QC phase) because of its low solid–liquid interfacial energy. At high undercooling of the liquid, where diffusion is limited, another approximant phase with near-liquid composition forms just above the glass-transition temperature. These experimental results shed light on the competition between metastable and stable crystals, and on glass formation via system frustration associated with the presence of several free-energy minima.

When a liquid is cooled below its melting point, it is expected to solidify due to a driving force resulting from the Gibbs free-energy difference between solid and liquid. However, the formation of a solid particle requires additional energy to create an interface between the liquid and solid; therefore, the liquid needs to be undercooled to overcome this barrier and crystallize by nucleation and growth (1, 2). Turnbull (3) demonstrated that metallic liquids have the ability to deeply undercool, and Frank (4) explained these observations by the occurrence of energetically favorable icosahedral short-range order in the liquid—which is incompatible with translational periodicity and, therefore, acts as a barrier to crystal nucleation (with an exception for quasicrystals). This conjecture was confirmed by molecular dynamics simulations (5, 6) and scattering experiments (7, 8) in various metallic liquids. The frequency of icosahedral-order formation in liquids increases with increased undercooling (9). Accordingly, metallic glasses inherit the structure of the undercooled liquid at the stage immediately before its glass transition, and therefore they also exhibit dominant icosahedral order (10–13).

While the prevalence of icosahedral order in the liquid increases the barrier to crystal nucleation and facilitates glass formation, it can also act as a template for the nucleation of icosahedral quasicrystals (iQCs)—which in turn hinders glass formation (14). QC–liquid interfacial energy is about one order of magnitude smaller than the crystal–liquid interfacial energy, signifying a low barrier to QC nucleation (15). Therefore, metastable iQCs are the most likely candidates to form initially from the melt (14). The molecular dynamics simulations of An et al. (16) support this conjecture. They observed a two-step crystallization process in a NiAl alloy: first from a liquid to a metastable phase attaining polyhedra of fivefold symmetry, and then subsequently from a metastable to an equilibrium phase, generating polyhedra of four- and sixfold symmetries. As to polymeric systems, Gillard et al. (17) observed the formation of dodecagonal QCs by rapid cooling of a sphere-forming diblock copolymer liquid and their subsequent transformation into a Frank–Kasper phase. Taffs and Royall (18) also recently demonstrated that the degree of fivefold symmetry determines the prevalence between a cubic crystal, an icosahedra-rich phase, and a glass upon cooling from the metallic melt. Russo and Tanaka (19) demonstrated that relatively ordered liquid structures driven by bond-order fluctuations can act as seeds of nucleation or frustrate crystallization by favoring the formation of fivefold structures.

Although it is generally accepted that QCs and some metallic glasses originate from icosahedral clusters (20, 21), to our knowledge no as-cast alloy composition concomitantly reveals both bulk metallic glass (BMG) and QC in its microstructure. Typically, glasses with high glass-forming ability (GFA) produce QCs upon devitrification (22, 23). The degree of icosahedral order in a metallic melt is sensitive to the atomic-size ratio and the electronic interactions between the constituting elements of the alloy (24). While Mg–Zn–RE (rare earth, RE = Y, Gd, Tb, Dy, Ho, and Er) alloys form highly ordered stable iQCs (25), Mg–Zn–Ca alloys can form BMGs (26, 27). Ca has a much larger atomic radius than the RE elements and generates well-reported icosahedral short- and medium-range order in the undercooled liquid (28). Interestingly, another RE element, Yb, has chemophysical properties similar to those of Ca; for example, they have similar atomic sizes in divalent form and are miscible with each other (29). Hence, Yb can act as a model electronic and topological substitute for Ca, for observing its effect on GFA in various alloy systems (30). Yu et al. (31) synthesized 20-µm-thick glassy ribbons in the Mg–Zn–Yb system, and verified their good ductility and extended in vitro biocompatibility. However, no QCs were reported in their study either.

We have discovered a unique composition in the Mg–Zn–Yb system which forms a BMG with a critical casting diameter of 1 mm, and metastable iQCs and approximant phases as a function of cooling rate. We can demonstrate that crystallization of the approximant phase from the liquid occurs via a two-step mechanism, involving direct formation of metastable QCs in the melt due to their low solid–liquid interfacial energy and their subsequent transformation to an approximant phase. The structural rearrangements from a metastable state to a stable one occur on a rather short time scale, which makes experimental observation of such rearrangements difficult. Using chip-based fast differential scanning calorimetry (FDSC) with a very high time resolution and scan rate (32, 33), we investigated the pathway of phase transitions by freezing the phases at various cooling rates and performing FDSC investigations at a high heating rate. This enabled us to “up-quench” the previously frozen phase and thus to even melt it without any structural change. Our experimental strategy makes possible the observation and determination of distinct melting temperatures and enthalpies of metastable and stable states. A metastable eutectic including a QC phase could thus be fully melted without experiencing a solid-state transition.

Results

We discovered QC-forming compositions in the Mg–Zn–Yb alloy system via casting of the melt into a wedge-shaped copper mold. Fig. 1A shows a 2–3 μm dendritic primary phase with fivefold symmetry. Electron backscatter diffraction (EBSD) analysis of the primary phase produced a Kikuchi pattern with icosahedral symmetry, where the intersections of the Kikuchi lines reveal two-, three-, and fivefold zone axes of an iQC (as indicated in Fig. 1B). The microstructure and QC symmetry were further investigated by transmission electron microscopy (TEM), together with selected-area electron diffraction (SAED) analysis. Fig. 1C shows the microstructure of an as-cast Mg₆₉Zn₂₇Yb₄ alloy obtained by TEM. The TEM lamella was extracted from a particle and its surrounding, as shown in the SEM image in Fig. 1D. With increased Mg and decreased Yb content, the morphology of the primary phase becomes globular instead of dendritic and the surrounding Mg-rich phase forms dendrites. SAED patterns of the primary phase shown in Fig. 1 E–G reveal typical two-, three-, and fivefold symmetries, demonstrating that the primary phase is indeed an iQC. According to spots along the fivefold symmetry axis in the twofold pattern (indicated by an arrow in Fig. 1E) scaling with τ³ (where τ denotes the golden ratio), the iQC is recognized as having a primitive lattice in six-dimensional space. Distorted diffraction spots in the SAED patterns (Fig. 1 E–G) corroborate the presence of atomic-size defects, which may be correlated to the metastable behavior of these QCs (34). After nucleation and growth of the iQCs with a composition of about Mg₃₈Zn₅₄Yb₈, the liquid is enriched in Mg around the particle, generating α-Mg to nucleate and form dendrites. Finally, coupled growth of iQCs and hexagonal α-Mg phases produces a eutectic microstructure with compositions of Mg₃₇Zn₅₆Yb₇ and Mg_96.4Zn₃Yb_0.6, respectively. SAED investigations show that the iQC phase in the eutectic mixture grows from a primary QC phase with the same orientation.

Fig. 1.

(A) Backscattered SEM image showing iQC particles in as-cast Mg₆₄Zn₂₇Yb₉ and (B) EBSD Kikuchi pattern of icosahedral symmetry for iQC phase with fivefold morphology; indicated are: two-, three-, and fivefold symmetry axes. (C) TEM image of iQC particle and eutectic microstructure in as-solidified Mg₆₉Zn₂₇Yb₄, also seen via SEM in D. Also presented are electron diffraction patterns of the iQC phase along the (E) twofold, (F) threefold, and (G) fivefold symmetry axes. An enlarged pattern in G shows the distorted diffraction spots clearly.

Besides iQC and Mg, a few other phases form in Mg₆₄Zn₂₇Yb₉ as a function of cooling rate. Fig. 2 shows the phase competition obtained from casting the alloy into a wedge-shaped mold via a cross-section perpendicular to the mold height. Close to the mold surface, nucleation of a crystalline phase is avoided by the high cooling rate, and a 100–200 μm thick metallic glass layer forms (left side in Fig. 2A). As the cooling rate decreases toward the inner part of the sample (from left to right in Fig. 2A), a gradual transition from a fully amorphous structure to an approximant Mg₅₁Zn₂₀-type phase (SI Appendix, Fig. S1) and a QC phase occurs over a range of a few micrometers without exhibiting a distinct boundary (Fig. 2). Initially, the size of the approximant particles increases from a few nanometers to a few micrometers; subsequently, with a decrease in cooling rate, primary QC phase formation proceeds with a eutectic growth of QC and Mg.

Fig. 2.

Metallic glass–approximant–QC transition. (A) Metallic glass to QC transition in an as-cast Mg₆₄Zn₂₇Yb₉ alloy shown from a cross-section perpendicular to the mold wall. (B) A magnified backscattered electron SEM image of the region indicated by a rectangle in A. (C) Scanning TEM image of the microstructure of a lamella extracted from the region indicated by the rectangle in B (electron diffraction patterns of particles, in SI Appendix, Fig. S1, demonstrate the formation of an approximant phase, i.e., Mg₅₁Zn₂₀ type). The cooling rate decreases from left to right for all micrographs.

After the observation of a metallic glass layer in Mg₆₄Zn₂₇Yb₉, we continued to search for good glass-forming compositions in the Mg–Zn–Yb system. We used a predictive topological model which selects compositions related to efficiently packed atomic clusters, with structural conditions such that efficient local packing occurs around all three atom species simultaneously (35). Binary eutectic compositions may introduce icosahedral clusters (36), which are recognized as prevalent atomic motifs of metallic glasses (12). In this context, the approximant crystal Zn₁₇Yb₃ (37) is isomorphic to the Cd₆Yb crystal, which lies next to the stable binary Cd_5.7Yb QC (38). Such approximant phases appear useful in searching for clusters with icosahedral order. By constructing cluster lines that refer to a straight composition line binding (i) Zn₁₇Yb₃ to Mg and (ii) eutectic Mg_71.1Zn_28.9 to Yb (SI Appendix, Fig. S2), it is seen that the Mg₆₉Zn₂₇Yb₄ alloy composition is located near the intersection of these two lines. Via suction casting of Mg₆₉Zn₂₇Yb₄ into cylindrical molds, we discovered that this alloy forms a BMG with a critical diameter of 1 mm (SI Appendix, Fig. S3).

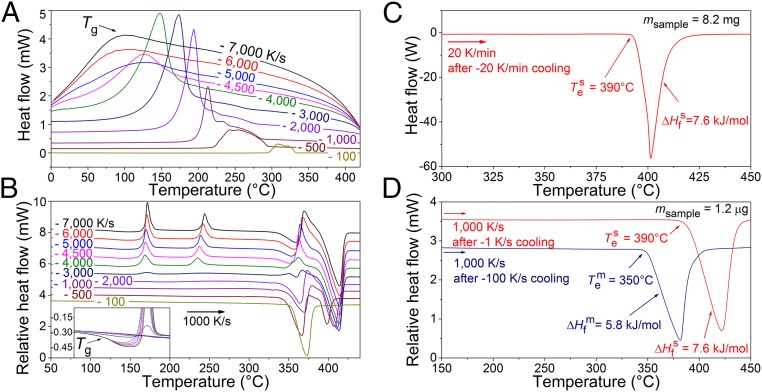
As illustrated in Fig. 3, with the help of FDSC we can determine the various phases that form in the Mg₆₉Zn₂₇Yb₄ alloy by making use of our experimental strategy, i.e., we cool the liquid at various rates between 100 and 7,000 K/s (Fig. 3A) and up-quench the frozen structure at a rate of 1,000 K/s. Fig. 3A shows FDSC curves at the various cooling rates. The nucleation temperature upon cooling of the liquid, which corresponds to the onset of the exothermic crystallization peak, decreases with increasing cooling rate, and vanishes when it shifts to a temperature below the glass transition. The latter happens at a critical cooling rate of ≥5,000 K/s, where a metallic glass forms. Fig. 3B shows the subsequent FDSC heating curves at a rate of 1,000 K/s, after cooling at rates of 100–7,000 K/s. Fig. 3B (Inset) illustrates a close-up of the glass transition for cooling rates between 3,000 and 7,000 K/s. After the glass transition at around 110 °C during heating, crystallization of the undercooled liquid and solid–solid phase transitions occur at higher temperatures. Above 300 °C the alloy experiences a series of endothermic and exothermic phase transitions (as also seen in ref. 39 for a Au-based glass) and finally transforms into the liquid state. This behavior is not valid for the alloy solidified at a rate of 100 K/s, which becomes, surprisingly, fully liquid at a temperature about 40 °C lower than those of alloys solidified at higher rates. This characterizes the formation of a metastable liquid in which the stable solid phase does not nucleate—in contrast to the other FDSC scans.

Fig. 3.

Phase transitions at different rates and melting of the metastable state. FDSC curves of Mg₆₉Zn₂₇Yb₄ during (A) cooling at different rates between 100 and 7,000 K/s and (B) subsequent heating at a rate of 1,000 K/s. The prior cooling rates for each heating scan are indicated on each curve. (Inset) Illustration of the glass transition during heating after sample solidification at cooling rates higher than 2,000 K/s. (C) DSC curve of Mg₆₉Zn₂₇Yb₄ at a rate of 20 K/min heating after cooling at a rate of 20 K/min, showing melting of the stable equilibrium solid. (D) FDSC curves during heating at a rate of 1,000 K/s after solidification at cooling rates of 1 and 100 K/s, clearly demonstrating melting of stable and metastable solid states, respectively.

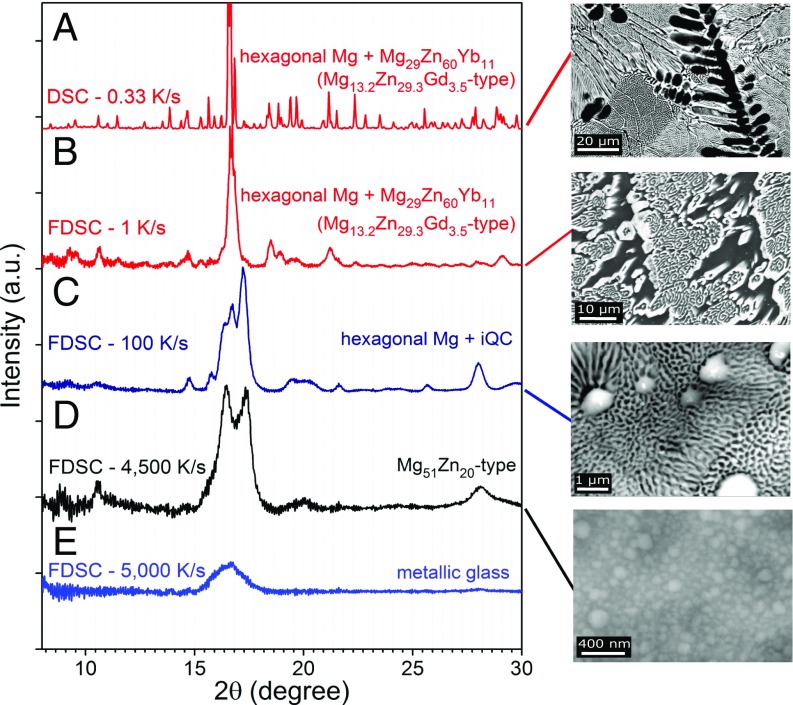
Fig. 3C shows a conventional DSC curve of Mg₆₉Zn₂₇Yb₄ during heating at a rate of 20 K/min after cooling at a rate of 20 K/min (= 0.33 K/s). The solidified microstructure at a rate of 20 K/min (Fig. 4A) reveals that primary Mg dendrites form first and solidification proceeds with equilibrium eutectic formation of Mg and Mg₂₉Zn₆₀Yb₁₁ intermetallic phase. The equilibrium eutectic temperature determined by the onset of melting is 390 ± 2 °C and the enthalpy of fusion is 7.6 ± 0.3 kJ/mol. Fig. 3D shows two FDSC heating scans at a rate of 1,000 K/s of the same specimen solidified at 1 and 100 K/s cooling rates. Stable equilibrium phases (Mg and Mg₂₉Zn₆₀Yb₁₁) also form at 1 K/s cooling rate, as confirmed by FDSC, X-ray diffraction (XRD), and SEM analyses (Figs. 3D and 4B and SI Appendix, Fig. S4). Because of the formation of the same phases in DSC at 20 K/min and FDSC at 1 K/s, the mass of the FDSC specimen can be deduced using the mass of the DSC specimen and the enthalpies of fusion measured by DSC and FDSC (40). With 100 K/s cooling rate, metastable primary QCs and Mg–QC eutectic phases form, as demonstrated by XRD and SEM (Fig. 4C and SI Appendix, Fig. S5 and Table S1). Heating of these metastable phases at a rate of 1,000 K/s prevents the transformation of metastable QC phase into the equilibrium one and succeeds in melting the metastable phase completely (Fig. 3D). The measured metastable eutectic temperature is 350 ± 2 °C and its enthalpy of fusion is assessed as 5.8 ± 0.2 kJ/mol.

Fig. 4.

XRD patterns and SEM microstructures of Mg₆₉Zn₂₇Yb₄ solidified at different cooling rates using DSC and FDSC. Indicated are the cooling rates and formation of different phases, and their microstructures are shown next to each XRD pattern. (Indexed XRD patterns in SI Appendix, Figs. S4 and S5 clearly demonstrate the formation of approximant Mg₂₉Zn₆₀Yb₁₁ and iQCs at different cooling rates.)

A metastable approximant phase, Mg₅₁Zn₂₀ type (41) (Fig. 4D), forms at cooling rates of between 1,000 and 4,500 K/s, which is also reported as the first crystal that nucleates from a Mg–Zn–Ca metallic glass (42). Nucleation is fully inhibited and metallic glass forms when the cooling rate is above 5,000 K/s, as indicated by the XRD trace in Fig. 4E.

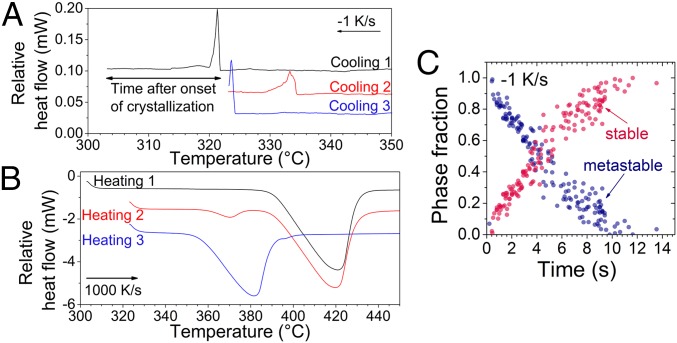
To understand the pathway of crystal formation, we interrupted the FDSC experiments performed at a low cooling rate of 1 K/s (Fig. 5A) and up-quenched the so-obtained microstructure at a rate of 1,000 K/s (Fig. 5B). During the cooling experiments at a rate of 1 K/s, at which solidification microstructures at room temperature (Fig. 4B) and subsequent up-quenching (upper scan in Fig. 3D) reveal equilibrium-phase formation, we observe that the nucleation temperatures (onset temperatures of crystallization peak) are always below the metastable eutectic temperature of 350 °C (lower scan in Fig. 3D). This means that the liquid is undercooled 55–80 °C below the equilibrium eutectic melting temperature (Fig. 5A). When cooling is interrupted at about 20 °C below the nucleation temperature, as can be seen for “cooling 1,” the subsequent “heating 1” (Fig. 5B) indicates equilibrium melting. However, if cooling is interrupted only 1 °C below the nucleation temperature of the solid phase, as in the case of “cooling 3,” then “heating 3” reveals metastable melting behavior with an onset temperature of 350 °C and a very small equilibrium melting peak at 390 °C. At an intermediate waiting time of 11 s after the first solid nucleation on “cooling 2,” melting of both metastable and stable phases is visible on “heating 2.” Fig. 5C shows the phase fractions of metastable and stable states after the interruption of cooling and subsequent heating depending on the time after the onset of crystallization (as indicated in Fig. 5A on “cooling 1”). These were calculated according to the distinct enthalpies of fusion for the metastable and stable states (Fig. 3D). These experiments demonstrate unambiguously that even at a very low cooling rate, a metastable QC phase nucleates first from the melt and acts as an intermediate state for the formation of the equilibrium stable state.

Fig. 5.

Transient QC formation. FDSC curves during (A) cooling at a rate of 1 K/s and (B) subsequent heating (up-quenching) at a rate of 1,000 K/s exhibit initial metastable QC formation from the melt, even at the low cooling rate applied, and subsequent solid–solid phase transformation. Shown in C are the stable and metastable phase fractions versus time after the onset of crystallization as indicated in A. The time spent during heating at 1,000 K/s before melting was neglected. The formation of the metastable phase and subsequent solid-state transition occur between 300 and 335 °C during cooling; therefore, the phase fraction values for a certain time scatter significantly.

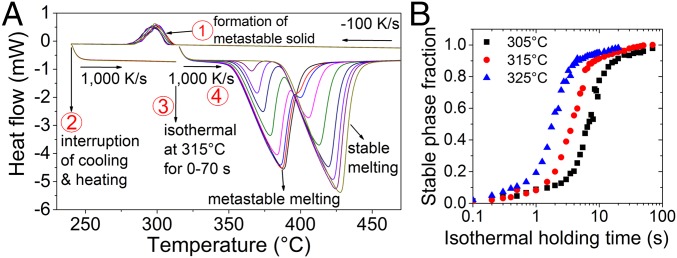
To study the effect of temperature on the metastable-to-stable solid-state transition we initially formed the metastable state during cooling at a rate of 100 K/s (point 1 in Fig. 6). Then cooling was interrupted at 240 °C (point 2) and the temperature of the metastable solid was increased to isothermal treatment temperatures (305, 315, 325 °C) at a rate of 1,000 K/s. The metastable solid was held (point 3; case of 315 °C shown in Fig. 6A) at these temperatures for different time intervals (0–70 s), and the FDSC experiments were then continued with the same rate of 1,000 K/s (point 4). The degree of the metastable-to-stable phase transition depends on the isothermal treatment and thus generates different degrees of metastable and stable melting, as can be seen in Fig. 6A. (For details on the temperature–time profiles, see also SI Appendix, Fig. S6.) The stable phase fractions were then measured by the enthalpies of fusion and plotted in Fig. 6B. The phase fractions of the QC phase in the metastable solid mixture (Mg + QC) and the approximant phase in the stable solid mixture (Mg + approximant) calculated by the lever rule are 0.47 and 0.42, respectively. Therefore, the solid-state transformation that occurs from the metastable QC to stable Mg plus approximant phases was analyzed by the Johnson–Mehl–Avrami model at different isothermal temperatures (43, 44). Although the transformation is not polymorphic, an Avrami plot (Fig. 6B) yields a straight line between 0.15 and 0.85 of stable phase fraction with relatively low slopes—similar to those observed in Al₈₆Mn₁₄ (45). The slope decreases systematically from 1.87 to 1.61 with increasing temperature from 305 to 325 °C.

Fig. 6.

Isothermal metastable-to-stable phase transition. (A) FDSC curves showing the effect of isothermal holding time on the metastable-to-stable phase transition at 315 °C. FDSC experiments were designed in four consecutive steps: (i) The Mg₆₉Zn₂₇Yb₄ melt is solidified at a cooling rate of 100 K/s, which results in the formation of metastable QC and Mg phases. (ii) Cooling is interrupted at 240 °C and the temperature of the metastable solid is increased to isothermal treatment temperatures (305, 315, and 325 °C) at a rate of 1,000 K/s. (iii) The metastable solid is then held at these temperatures for various time intervals (0–70 s), which results in a metastable-to-stable phase transition. (iv) The alloy is melted at a rate of 1,000 K/s. (B) Stable phase fractions as a function of isothermal holding time at different temperatures. The phase fractions are calculated using melting enthalpies of the metastable and stable states.

Discussion

Let us start the discussion with the surprising result that metallic glass and iQC coexist in the Mg₆₉Zn₂₇Yb₄ alloy. Here we should mention that the relation between the atomic radii of the elements and the valence electron concentration plays an important role in the formation of stable QCs. In Mg–Zn–RE alloys that form stable iQCs (25), RE elements have atomic radii of between 1.76 and 1.80 Å in trivalent form (46). In contrast, Ca has a large atomic radius (1.97 Å) in divalent form (46), and forms BMG compositions in the Mg–Zn–Ca system (26, 27) without (any known) formation of QC phase. Yb and Eu are the only two elements in the lanthanide group that show both divalent and trivalent electronic character due to the stability of their 4f orbitals (Yb has completely filled and Eu has half-filled 4f orbitals), and lack of electrons in the 5d shell. The atomic size of divalent Yb (1.94 Å) is larger than that of trivalent Yb (1.74 Å) (46). The element Yb is known to exist in divalent form from magnetic measurements on metastable Zn₇₆Mg₁₀Yb₁₄ QCs (47), but nevertheless it can have an intermediate valence state with an intermediate effective radius in QCs and approximant compounds (48). Lee et al. (49) recently argued that different atoms in a metal can exchange spin-dependent charges during a phase transition. In this context, they conjectured that atoms can adjust their effective size in different complex, low-symmetry crystal structures with variations in coordination and magnetic moments, so that even metals such as Mn (50) or Pu (51) may be considered intermetallic alloys. The fluctuations in electron valence state and atomic radius of Yb thus provide a reasonable explanation for the concurrent formation of BMG, two approximant (metastable Mg₅₁Zn₂₀-type and stable Mg_13.2Zn_29.3Gd_3.5-type) phases and iQCs in dependence on the cooling rate of the Mg–Zn–Yb melt.

As discussed in more detail in the following, FDSC analysis at various cooling rates and subsequent up-quenching (Fig. 3) provides a great opportunity to study the phase competition between stable and metastable states. Although the nucleation and growth kinetics of the different phases influence the exothermic crystallization peak shapes, and/or the glass transition induces slope changes during cooling (Fig. 3A), the formation of different phases can be clearly understood by comparing their subsequent heating scans at a fixed rate (Fig. 3B). Above 2,000 K/s cooling rate, the liquid can be sufficiently undercooled to form a glassy phase, and therefore we observe a glass transition at about 110 °C and crystallization peaks during heating at a rate of 1,000 K/s. Because the eutectic melting temperature of the stable state was measured as 390 °C (Fig. 3C), the endothermic peak at around 350 °C corresponds to the formation of a metastable liquid due to the high heating rate, which prevents the metastable-to-stable phase transition. This occurrence of metastable melting has also recently been observed for a Au-based BMG (39) and may be observed for any metastable crystalline phase if a sufficiently high heating rate can be provided. At a cooling rate of 100 K/s (Fig. 3D), a eutectic Mg–QC mixture forms, which via up-quenching melts completely below the eutectic melting temperature of the stable state. The fact that the Mg–QC phase mixture has both a lower melting onset and lower melting enthalpy than the Mg–approximant stable equilibrium-phase mixture clearly verifies the metastability of the QC phase in any temperature range.

A limited number of stable QCs, such as high- and low-temperature QCs in Al–Pd–Mn (52, 53) and Ti–Zr–Ni (14), have been discovered in the past and placed in equilibrium phase diagrams. This has, however, not yet been possible for metastable QCs (15) due to the experimental difficulties of measuring their thermodynamic quantities, such as melting temperature and enthalpy of fusion. With our method of up-quenching such metastable phases (Fig. 3D), we can place metastable QCs in a Gibbs free-energy diagram, which is the key to understanding the pathway of equilibrium crystal formation. In Mg₆₉Zn₂₇Yb₄ the following phases were observed at room temperature at increasing cooling rate (Fig. 4): firstly, stable Mg and approximant Mg₂₉Zn₆₀Yb₁₁ phase mixture; secondly, metastable Mg and iQC phase mixture; thirdly, approximant Mg₅₁Zn₂₀-type metastable particles; and finally, a glassy phase. However, we noticed that the Mg₂₉Zn₆₀Yb₁₁ phase never forms directly from the melt in FDSC experiments; instead, metastable QC phase first nucleates in the liquid and then transforms into a stable approximant phase (Fig. 5). Such a transition path (undercooled liquid → metastable QCs → stable equilibrium phase) has significant effects on control over solidification microstructures via grain refinement. For example, (i) the appearance of twinned dendrites in direct-chill casting of Al alloys, and (ii) the grain-refining effect of Cr in Al–Zn alloys were recently explained by a mechanism which indicates that Cr addition promotes the icosahedral short-range order in the liquid (54). There, metastable QCs transform into the stable fcc phase with a heteroepitaxial relationship (55, 56). This may also explain the underlying mechanism of grain refinement in gold alloys by Ir addition (57). However, in these examples metastable QCs could not be observed directly, because the phase fraction of metastable QCs is low and/or the metastable-to-stable transition rate is much higher than the liquid-to-metastable rate (58).

According to classical nucleation theory, nucleation of a metastable state occurs if its nucleation barrier is lower than that of the stable state (19). Therefore, if the solute diffusion rates in the liquid are much faster than the interfacial attachment kinetics, then the inequality

$${\gamma }_{\text{ml}}^{3}f\left({\theta }^{\text{m}}\right)/{(\mathrm{\Delta }{S}_{\text{f}}^{\text{m}}\hspace{0.17em}\mathrm{\Delta }{T}^{\text{m}})}^2<{\gamma }_{\text{sl}}^{3}f\left({\theta }^{\text{s}}\right)/{(\mathrm{\Delta }{S}_{\text{f}}^{\text{s}}\hspace{0.17em}\mathrm{\Delta }{T}^{\text{s}})}^2$$ [1]

must be satisfied at the nucleation temperature, where $\gamma$ is the interfacial energy, $f\left(\theta \right)$ is the shape factor with a wetting angle of $\theta$ for heterogeneous nucleation, $\mathrm{\Delta }{S}_{\text{f}}$ is the volumetric entropy of fusion, $\mathrm{\Delta }T$ is the nucleation undercooling ($\mathrm{\Delta }T=T_{\text{f}}-T_{\text{n}}$, where $T_{\text{f}}$ is the melting/liquidus temperature and $T_{\text{n}}$ is the nucleation temperature), and the scripts m, s, and l refer to metastable, stable, and liquid phases, respectively. Since the stable state has the greater driving free energy at a nucleation temperature less than the metastable eutectic temperature, i.e., $T_{\text{n}}<350°\text{C}$ in the current case, the preferential nucleation of the iQC phase demonstrates that its solid–liquid interfacial energy is less than that of the stable phase for a similar wetting angle of metastable and stable states. However, if the nucleation barrier difference for nucleating solids was attributed to a change in $f\left(\theta \right)$, very low values of $f\left(\theta \right)$ had to be assumed for the metastable phase because the nucleation barrier depends on the interfacial energy with the third power, but is only a linear function of $f\left(\theta \right)$. Because such low values of $f\left(\theta \right)$ are not physical, a low solid–liquid interfacial energy has to be assumed for the QC phase. This indicates that the metastable QC is structurally similar to the liquid that acts as a template for its nucleation. However, the short-range order of the liquid can either facilitate or prevent crystal nucleation, depending on the similarity between the structure of the liquid and that of the competing solid phases.

While the solid–liquid interfacial energy of the Mg phase was calculated as 89.9 mJ/m² (59), a very low interfacial energy for a MgZn₂ Frank–Kasper polytetrahedral phase (0.8–2 mJ/m²) was reported in the Ga–Mg–Zn system, which forms stable QCs and crystalline approximants (60). The structure of the crystalline approximant phase in this study, Mg_13.2Zn_29.3Gd_3.5-type Mg₂₉Zn₆₀Yb₁₁ phase, is closely related to that of the MgZn₂ phase (61). Therefore, it should also have a low solid–liquid interfacial energy. Our FDSC experiments show that the transition path, liquid → metastable QC → stable approximant, is kinetically more favorable than the transition path, liquid → approximant, which clearly demonstrates a lower interfacial energy for the QC phase than for the approximant. At high cooling rates (1,000–4,500 K/s; Fig. 3A), another approximant Mg₅₁Zn₂₀-type phase forms below 225 °C, at which atomic rearrangements with slow diffusion are not sufficient to form Mg, Mg₃₈Zn₅₄Yb₈ QC, and Mg₂₉Zn₆₀Yb₁₁ phases, which have very different compositions than that of the liquid (Figs. 2 and 4D and SI Appendix, Fig. S1).

In conclusion, we have shown that the model alloy Mg₆₉Zn₂₇Yb₄ allows us to obtain unique insights into the link between QC, approximant phase, and metallic glass formation. We have demonstrated that QC-induced nucleation may be a general mechanism for metastable QC-forming alloys, because the formation of such QCs establishes a low nucleation barrier path due to their low solid–liquid interfacial energy. FDSC studies of other alloy systems may also yield new, hidden transient phases that induce stable phase formation using the experimental strategy of interrupted cooling after the onset of crystallization and subsequent up-quenching at ultrafast rates—which was not formerly possible using conventional calorimetry. This also paves the way for experimental determination of thermodynamic parameters of metastable phases, such as melting point and enthalpy of fusion, which may be of great importance for including metastable phases in thermodynamic databases. Finally, our bulk GFA composition, Mg₆₉Zn₂₇Yb_4, may also be useful in biomedical applications.

Materials and Methods

Alloy Preparation.

Mg (99.99 wt %), Zn (99.99 wt %), and Yb (99.99 wt %) were alloyed in graphite crucibles using an induction furnace purged with argon (99.997 wt %). The alloys were tilt cast into a wedge-shaped (10:1 taper) copper mold at temperatures ∼100 to 150 °C above their liquidus temperatures to determine the critical casting thickness of the amorphous phase.

Thermal Analysis.

FDSC analysis was performed using a Mettler-Toledo Flash-DSC 1. The sample mass for FDSC, $m^{\text{FDSC}}$ (0.1–3 µg), was determined using the melting enthalpy of equilibrium phases measured by FDSC at 1 K/s cooling rate, $\mathrm{\Delta }{H}_{\text{f}}^{\text{s},\text{FDSC}}$; conventional DSC (Mettler-Toledo DSC1/700) at 20 K/min cooling rate, $\mathrm{\Delta }{H}_{\text{f}}^{\text{s},\text{DSC}}$; and its mass, $m^{\text{DSC}}$, with the relation

$$m^{\text{FDSC}}=m^{\text{DSC}}\left(\mathrm{\Delta }{H}_{\text{f}}^{\text{s},\text{FDSC}}/\mathrm{\Delta }{H}_{\text{f}}^{\text{s},\text{DSC}}\right).$$ [2]

Equilibrium phases formed using various techniques were verified as being the same via XRD analysis of FDSC and DSC specimens (Fig. 4 A and B). The temperature of the FDSC curves was calibrated by comparing the melting onsets of the stable state in FDSC and DSC.

Structural Characterization.

Microstructural investigation of the samples was performed using a Hitachi SU-70 SEM and an FEI Tecnai F30 TEM, operated at 300 kV accelerating voltage. The microstructure of the FDSC samples was observed on the as-cast surface and also confirmed by investigations performed on the surface cleaned by focused ion beam (FIB). TEM lamellae were extracted from the as-cast alloy and FDSC samples using the same FIB system (FEI Helios 600i). Phase compositions were determined using energy dispersive X-ray spectroscopy elemental analyses via both SEM and TEM. XRD characterization of the FDSC samples (with a volume of about 30 × 100 × 100 µm³) was performed using the spinning mode of an Xcalibur Oxford Diffraction X-ray diffractometer with a Mo Kα radiation source. XRD analyses of large samples (conventional DSC and as-cast, and to verify the glassy as-cast structure) were performed using a Phillips MRD instrument fitted with a 0.5-mm microcapillary tube and a Cu Kα radiation source.