Ankle and foot power in gait analysis: Implications for science, technology and clinical assessment

Abstract

In human gait analysis studies, the entire foot is typically modeled as a single rigid-body segment; however, this neglects power generated/absorbed within the foot. Here we show how treating the entire foot as a rigid body can lead to misunderstandings related to (biological and prosthetic) foot function, and distort our understanding of ankle and muscle-tendon dynamics. We overview various (unconventional) inverse dynamics methods for estimating foot power, partitioning ankle vs. foot contributions, and computing combined anklefoot power. We present two case study examples. The first exemplifies how modeling the foot as a single rigid-body segment causes us to overestimate (and overvalue) muscle-tendon power generated about the biological ankle (in this study by up to 77%), and to misestimate (and misinform on) foot contributions; corroborating findings from previous multi-segment foot modeling studies. The second case study involved an individual with transtibial amputation walking on 8 different prosthetic feet. The results exemplify how assuming a rigid foot can skew comparisons between biological and prosthetic limbs, and lead to incorrect conclusions when comparing different prostheses/interventions. Based on analytical derivations, empirical findings and prior literature we recommend against computing conventional ankle power (between shank-foot). Instead, we recommend for foot power to be computed, either in addition to an alternative estimate of power generated about the ankle joint complex (between shank-calcaneus), or within a combined anklefoot power calculation. We conclude that treating the entire foot as a rigid-body segment is often inappropriate and ill-advised. Including foot power in biomechanical gait analysis is necessary to enhance scientific conclusions, clinical evaluations and technology development.

Introduction

Muscles and tendons about the ankle, knee and hip are typically considered the main mechanical power producers during human gait. Using inverse dynamics to estimate net power generated about these joints has become ubiquitous in human gait analysis studies (Robertson et al., 2013; Winter, 2009, 1991). Substantial effort has gone into characterizing how ankle, knee and hip kinetics are adapted during different locomotor tasks and varying task intensities (e.g., Farris and Sawicki, 2012a; Winter, 1984, 1983; Zelik and Kuo, 2010), and understanding how power about each of these three joints contributes functionally to movement biomechanics (e.g., Roger A. Mann and John Hagy, 1980; Inman et al., 1981; Perry, 1992; Levine et al., 2012; Zelik and Adamczyk, 2016). However, in gait analysis studies, far less attention has been given to power contributions from the foot.

Foot power, the rate of mechanical work performed collectively by active and passive structures of the foot (sometimes including the shoe), is not typically estimated in gait analysis studies (Zelik et al., 2015). The standard convention in the gait analysis field is to model the entire foot as a single rigid-body segment, which neither absorbs nor generates mechanical power. This convention is found throughout biomechanics textbooks (Baker, 2013; Inman et al., 1981; Ranchos Los Amigos National Rehabilitation Center, 2001; Robertson et al., 2013; Whittle, 2014; Winter, 2009), and is reflected in commonly-used motion capture marker sets. However, there is compelling evidence that foot power contributes meaningfully to walking (Bruening et al., 2012a; MacWilliams et al., 2003; Siegel et al., 1996; Takahashi et al., 2012; Takahashi and Stanhope, 2013; Zelik et al., 2015) and running (Kelly et al., 2015; McDonald et al., 2016; Riddick and Kuo, 2016; Stearne et al., 2016; Stefanyshyn and Nigg, 1997), due to a complex biomechanical interplay between muscles and passive structures (Kelly et al., 2014; Ker et al., 1987; Venkadesan et al., 2017; Zelik et al., 2014).

Currently there remains a lack of clarity in the scientific literature regarding if, when and how foot power should be calculated in the study of gait biomechanics. A critical question looms: is modeling the entire foot as one rigid-body segment, which neither absorbs nor generates mechanical power, adequate for addressing the types of the scientific questions that are commonly investigated in gait analysis studies, or adequate for obtaining biomechanical estimates that properly inform the design, prescription and evaluation of clinical interventions (e.g., foot prostheses)? Here we present experimental evidence and analytical arguments suggesting that, in many cases, neglecting foot power is inadequate for scientific studies and may be inappropriate (misleading) for clinical gait analysis or informing technology development.

The purpose of this article is two-fold: (i) to use case study examples in conjunction with analytical arguments and prior literature to highlight why foot power should be estimated within the context of whole-body or lower-limb gait analysis studies, and then (ii) to discuss how to experimentally estimate (and interpret) foot and ankle power. This article is principally intended for individuals who employ conventional gait analysis methods (e.g., 3 degree-of-freedom (3DOF) rigid-body inverse dynamics) to understand bio- or neuro-mechanical aspects of human locomotion, to inform device design, or to evaluate clinical interventions. Some of the observations contained within this article may be banal or obvious to foot experts and enthusiasts. But if so, this is all the more reason to resolve the discontinuity between scientists, engineers and clinicians focused specifically on the foot, and those who use gait analysis methods such as inverse dynamics to more broadly investigate how constituents of the body (e.g., individual joints, segments, muscles or tendons) contribute to whole-body movement.

Methods

We performed two gait analysis case studies that exemplify how and why to compute foot power, and implications on ankle power. The first case study was on a healthy individual during treadmill walking at fixed speed. We used an extended marker set to compute and contrast various estimates of ankle power, foot power, and combined ankle plus foot (termed anklefoot) power. The second case study involved a person with unilateral transtibial amputation walking sequentially on eight different prosthetic feet. We computed anklefoot power for each of the prostheses, and also for the biological limb. We contrasted estimates of anklefoot power against one of the most commonly-used ankle estimates (3DOF rotational Ankle power, which neglects foot power contributions). Power calculations are summarized below, followed by a discussion of key terminology, then experimental protocol details.

Power Calculations

Figure 1 summarizes the various power estimates computed in this study: two estimates of ankle power and four estimates of anklefoot power. See Supplementary Material (Appendices A-C) for comprehensive details on calculations. All estimates are based on inverse dynamics analysis, but each estimate uses a slightly different model and/or different underlying assumptions. To maximize generalizability of our conclusions, we focused on a subset of analyses that can be estimated from ground reaction forces and motion capture measurements, which are common in many gait analysis studies. Estimation methods that require additional measurement modalities (e.g., pressure, MacWilliams et al., 2003) or specialized data collection protocols (e.g., Bruening et al., 2012a; Scott and Winter, 1993; Takahashi et al., 2017) were not included in our present study, nor were in vitro approaches.

Figure 1. Methods to compute ankle and anklefoot power.

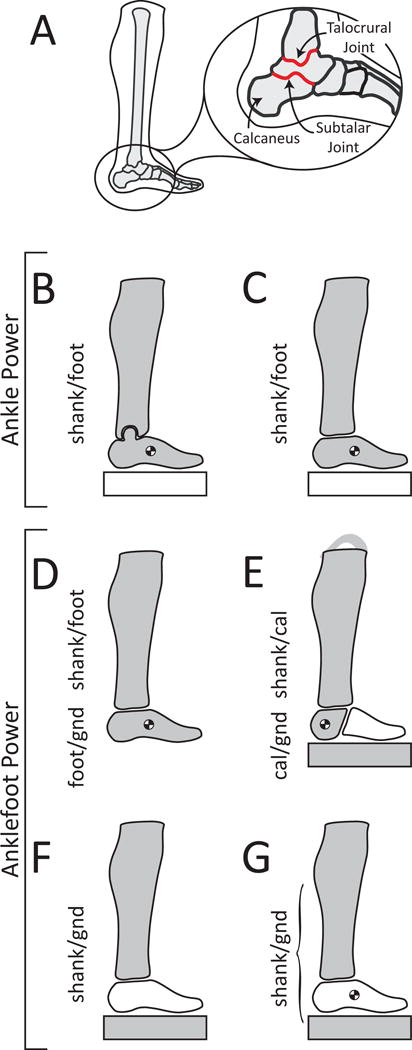
(A) Biological ankle joint complex (AJC), comprised of the talocrural and subtalar anatomical joints. (B) 3DOF Ankle: rotational power between the shank and foot. All other power estimates are 6DOF (capturing rotational and translational power). (C) Ankle: rotational and translational power between the shank and foot. Methods (B) and (C) only estimate ankle dynamics, assuming a single rigid-body foot segment, but do not estimate power due to the motion of the foot relative to the ground (gnd). (D) Ankle + Distal Foot: anklefoot power computed by summing power of shank relative to foot plus power of foot relative to the ground. This method also assumes a single rigid-body foot segment. (E) AJC + Distal Calcaneus: anklefoot power computed by summing power of the shank relative to the calcaneus (cal) plus power of the calcaneus relative to the ground. This method does not treat the entire foot as a single rigid-body segment; rather it only assumes a portion of the foot, the calcaneus, is rigid. (F) Distal Shank: anklefoot power due to motion of the shank relative to the ground. This estimate assumes negligible foot mass and inertia. (G) Intersegmental: power flow in/out of a given landmark; in this case, the distal end of the shank. This estimate can be formulated to include (or not include) effects due to foot mass and inertia. Gray signifies segments (and the ground in anklefoot cases) used to compute power. Brackets indicate power calculated between two grey segments. White indicates that power was not explicitly computed relative to a given segment or the ground. The center-of-mass symbol on a segment signifies that the mass and moment of inertia of this segment were used in the calculation of power. See Supplementary Material (Appendix A) for detailed explanations and equations for each method.

Terminology

Here we define and clarify key terminology. First, we distinguish an anatomical joint vs. the model of an anatomical joint. Anatomical joint is used to specify the physical interface between two adjacent anatomical structures in the body. The term anatomical ankle joint refers specifically to the talocrural joint (Wu et al., 2002), located between the talus bone in the foot and the bones of the shank (tibia and fibula, see Fig. 1A). The term anatomical ankle joint complex (AJC) describes, collectively, the subtalar joint (talus-calcaneus anatomical joint, Fig. 1A) and the anatomical ankle joint. In effect, the AJC describes the interaction between the shank and the calcaneus (Wu et al., 2002). In contrast, the term joint is used in this manuscript to signify the modeled biomechanical interaction between two body segments (or between one body segment and the ground). Note that two segments need not be adjacent to each other to model a joint between them. For instance, the AJC is comprised of two anatomical joints, but the net relative motion between the shank and calcaneus can nonetheless be modeled/quantified as a single equivalent 6 degree-of-freedom (6DOF) joint. Also note that a joint can be modeled in various other ways, such as assuming a 1DOF rotational hinge, or a 3DOF ball-in-socket joint (Fig. 1B). 1DOF and 3DOF joints are the most prevalent models used in the gait analysis literature, while 6DOF joints provide the most comprehensive estimates (Buczek et al., 1994; Duncan et al., 1997; Zelik et al., 2015). Unless otherwise specified, joints (and thus joint powers) modeled in this study are 6DOF (3 rotational, 3 translational).

The lower-case term ankle power is used, colloquially and in a general manner, to signify the net power due to all structures – muscle-tendon units and other passive tissues – acting about the anatomical ankle joint. This is necessary because there is no consistent usage of the term ankle power in literature. Lower-case terms foot power and anklefoot power are used in an analogous colloquial manner.

Capitalized power terms refer to specific experimental estimates, as detailed hereafter. The capitalized term Ankle power refers to estimates that model the interaction between a rigid-body shank and rigid-body foot (Fig. 1 B,C). Typically, skin-mounted markers are distributed over the shank, and also over the foot (e.g., from the calcaneus to the metatarsal heads). The foot is tracked in space as if it were a single rigid-body segment. These data are then used to compute either 3DOF (rotational) Ankle power, or 6DOF (rotational and translational) Ankle power. AJC power refers to estimates that model the interaction between a rigid-body shank and rigid-body calcaneus segment. In other words, the calcaneus is treated as its own rigid-body, separate from the rest of the foot. The calcaneus bone is sufficiently large and superficial that it can typically be tracked reasonably well with skin-mounted markers (MacWilliams et al., 2003; Reinschmidt et al., 1997; Stebbins et al., 2006). AJC power (or a similar hindfoot power) is often estimated in multi-segment foot modeling studies (Bruening et al., 2012a, 2012b; Dixon et al., 2012; Leardini et al., 2007; Stebbins et al., 2006; Westblad et al., 2002); however, AJC power is otherwise uncommon in gait analysis studies. As detailed in the Discussion and Appendix A, AJC power likely provides a better estimate of plantarflexor muscle-tendon contributions (than Ankle power), given that the soleus and gastrocnemius muscles insert onto the calcaneus, and that the mid-foot is known to undergo substantial motion during locomotion (Bruening et al., 2012a; Kelly et al., 2015; MacWilliams et al., 2003).

Distal Segment power refers to the power due to 6DOF motion of a rigid-body segment relative to the ground, thereby estimating the combined contributions from all structures and anatomical joints distal to a given segment. In other words, Distal Segment power describes 6DOF joint power between a given segment and the ground (see Appendix B for detailed derivation). For instance, Distal Foot power signifies net power due to the 6DOF motion of the rigid-body foot segment relative to the ground. Similarly, Distal Calcaneus power signifies the power due to 6DOF motion of the calcaneus relative to the ground. Distal Foot power and Distal Calcaneus power are sometimes referred to as deformable-body estimates because they are often interpreted to reflect power due to deformation of structures within the foot segment (Takahashi et al., 2012). However, it is important to note that methodologically these Distal Segment estimates do not directly measure or model soft tissue deformations (e.g., using finite element analysis). Rather, each method is simply a type of rigid-body inverse dynamics analysis that estimates mechanical power due to the relative motion of two bodies which are each assumed to be rigid (analogus to prior work on human-exosuit interface dynamics, Yandell et al., 2017). Distal Segment power estimates can then, in certain situations, be used to infer the kinetics of deformable structures located between the two rigid bodies (Fig. 1, see Appendix B for further details), circumventing the need to apply more complex finite element methods from continuum mechanics.

The term anklefoot power encompasses a variety of different estimates of power due to relative motion between the shank and ground (Fig. 1). The names of specific anklefoot power estimates are capitalized: Ankle + Distal Foot (Fig. 1D), AJC + Distal Calcaneus (Fig. 1E), Distal Shank (Fig. 1F) and Intersegmental (Fig. 1G, Prince et al., 1994). See Appendix A for further explanation of each anklefoot estimate.

Finally, note that our preferred terminology throughout the article is principally in relation to the assumed rigidity of the entire foot: we discuss the consequences of modeling the entire foot as a single rigid body (Fig. 1B–D) vs. not assuming the entire foot is a single rigid body (Fig. 1E–G). An alternative way of phrasing this same distinction is in terms of foot segmentation: in essence, here we are discussing the consequences of estimating power when modeling the foot as a single segment (Fig. 1B–D) vs. assuming multiple segments of the foot (Fig. 1E), and vs. being segmentally-agnostic (in which we make no assumptions about how the foot is modeled/segmented, Fig. 1F–G).

Case Study 1

The purpose of this case study was to present an example of each of the ankle and anklefoot power estimates during normal walking, with a focus on biological limb function. A healthy female participant (23 years, 1.73 m tall, 61 kg) walked on a level, instrumented treadmill at 1.25 m/s (a typical walking speed) barefoot and then at the same speed with shoes (New Balance Fresh Foam 1080, a common running shoe). Twenty-two steps were analyzed from each walking condition. Prior to the study, the subject gave informed consent to the protocol which was approved by the Vanderbilt University Institutional Review Board. The subject had 24 passive reflective markers attached to her lower limbs (Fig. 2A). Markers were placed on the pelvis (4), and unilaterally on the thigh (4), knee (2), shank (4), ankle (2), calcaneus (5), and forefoot (3). We collected ground reaction forces (Bertec) and motion capture data (Vicon) at 1000 and 200 Hz, respectively. Force data were low-pass filtered at 10 Hz, and motion data at 6 Hz, using a 3rd order, zero-lag Butterworth filter. We then computed each ankle and anklefoot power estimate (Fig. 1, Appendix A). We compared 6DOF Ankle power and each of the 4 anklefoot power estimates vs. a commonly-used gait analysis estimate, 3DOF Ankle power. This comparison highlights the importance of including foot power in gait analysis. We also compared the two methods that partition ankle vs. foot power (i.e., Ankle + Distal Foot power vs. AJC + Distal Calcaneus power, Fig. 1). This comparison exemplifies how the choice of inverse dynamics method can affect scientific interpretations of foot and ankle function.

Figure 2. Motion capture marker sets.

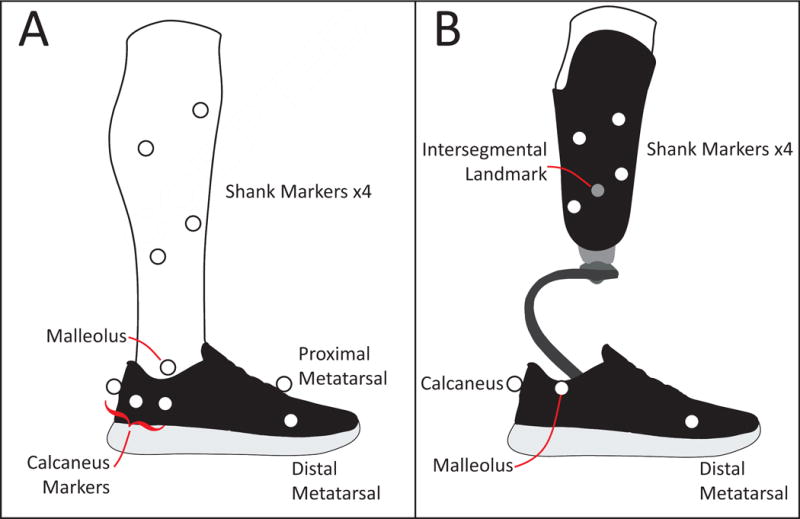
Lateral view shown for case study 1 (A) and case study 2 (B). (A) This marker set was used to track the shank, calcaneus and foot. Shown here is the shod case. The marker set for the barefoot case was identical. Shank motion was determined from the four shank markers. Ankle joint center was approximately midway between the medial malleolus (not shown, behind foot) and lateral malleolus markers. The calcaneus motion was determined from five markers: one on the posterior of the shoe/foot, one on the sustsentaculum tali (ST, on medial side of the foot), one on the peroneal trochlea (PT, the most anterior of the calcaneus markers shown), one between the posterior calcaneus and the ST (on medial side of the foot), and one between the posterior calcaneus and the PT. Foot segment motion was determined by four markers: one posterior on the calcaneus, two on the distal heads of 1^st and 5^th metatarsals (one shown) and one on the proximal head of the 1^st metatarsal. (B) Prosthesis side marker set used to track the shank and the foot. Four markers on the socket were used to track the motion of the shank. The Intersegmental landmark (virtual marker, gray) was defined to be midway between the two most distal shank markers. The ankle joint center was defined as midway between the medial and lateral malleolus markers (lateral one shown). On the intact limb these markers were placed on the malleoli and on the affected limb, these markers were placed on the shoe. Foot motion was estimated by the motion of three markers: one posterior on the calcaneus and two on the approximate location of distal heads of 1^st and 5^th metatarsals (one shown). The intact foot mirrored this marker placement.

Case Study 2

The purpose of this case study was to apply ankle and anklefoot power estimates to a variety of prostheses, then to show how methodological choices can affect comparisons between (and interpretations of) different feet. This case study exemplifies the importance of including foot power (i.e., computing anklefoot power rather than just ankle power) when comparing clinical interventions like prosthetic feet, and when assessing the degree to which they restore biological limb function. A individual with unilateral, transtibial amputation (37 years, 1.78 m tall, 81 kg, male) walked sequentially on 8 different prosthetic feet (Table 1) at 1.25 m/s. Eight walking trials (one per prosthesis) were performed on a split-belt, force-instrumented treadmill (Bertec). For each trial, 14-19 strides were analyzed (after removing unusable data due to cross-over steps). The subject provided written, informed consent prior to participation. Each prosthetic foot was aligned by a certified prosthetist, and worn inside the same shoe.

Table 1.

Prosthetic feet in case study 2. Reported weight is the prosthesis inside the foot shell and shoe.

Prosthesis	Weight (kg)
Rush	1.12
All-Pro	0.81
Vari-Flex XC	1.06
Soleus	1.07
Panthera	0.92
Kinterra	1.07
Game Changer	1.09
Raize	1.58

The same prosthetic socket was used for all conditions, and no adjustments to the socket were made after beginning the study. The subject was given a few minutes to acclimate to each foot; most of which he was already accustomed to wearing since he had worn them at home prior to participating in this experiment. Ground reaction forces and lower-body kinematics were simultaneously recorded during walking trials, at 2000 Hz and 100 Hz, respectively. 34 retroreflective motion capture markers were placed on the subject (Fig. 2B): pelvis (4), right/left thigh (8), right/left knee (4), right shank (4), left socket (4), right ankle (2), right foot (3), left prosthesis/shoe (5). Force data were low-pass filtered at 10 Hz, and motion data at 6 Hz, using a 3rd order, zero-lag Butterworth filter. We then computed each ankle and anklefoot power estimate, except AJC + Distal Calcaneus power (since many prostheses either do not have, or differ considerably from, the calcaneus morphology of the human foot). Although the past decade has seen an increase in the use of anklefoot power analysis for prosthetic studies (Adamczyk et al., 2017; Collins and Kuo, 2010; De Asha et al., 2013; Ebrahimi et al., 2017; Morgenroth et al., 2011; Segal et al., 2012; Takahashi et al., 2014; Wezenberg et al., 2014; Zelik et al., 2011), the use of conventional 3DOF Ankle power is still the de facto standard (e.g., Crimin et al., 2014; Sawers and Hahn, 2011). Therefore, we compared conventional 3DOF Ankle power estimates vs. 6DOF Ankle power, and vs. each anklefoot power estimate (besides AJC + Distal Calcaneus power). For the Intersegmental power calculation, we did not include the inertial terms because we did not measure the moment of inertia for each individual prosthesis.

Statistical comparisons were not performed on the case study results. Case studies were intended to serve as clear, tangible examples of how methodological choices can affect estimates of ankle and foot biomechanics. All generalized conclusions and recommendations are based on analytical arguments and/or corroborated by previously published, multi-subject gait analysis studies.

Results

Case Study 1

Ankle power estimates were similar with both 3DOF and 6DOF methods in terms of peak power and positive work (Fig. 3). These findings are consistent with prior studies, each on 10 subjects (Buczek et al., 1994; Zelik et al., 2015). Anklefoot power estimates were also similar to each other (Fig. 3). This result is consistent with Takahashi et al. (2012), who previously demonstrated strong similarity between Distal Shank power and Ankle + Distal Foot power. However, Ankle power and positive work were substantially greater than anklefoot power and work, for all anklefoot estimation methods. This result is consistent with Zelik et al. (2015, N=10) and Takahashi and Stanhope (2013, N=11).

Figure 3. Ankle and anklefoot power and work for barefoot walking of able-bodied individual at 1.25 m/s.

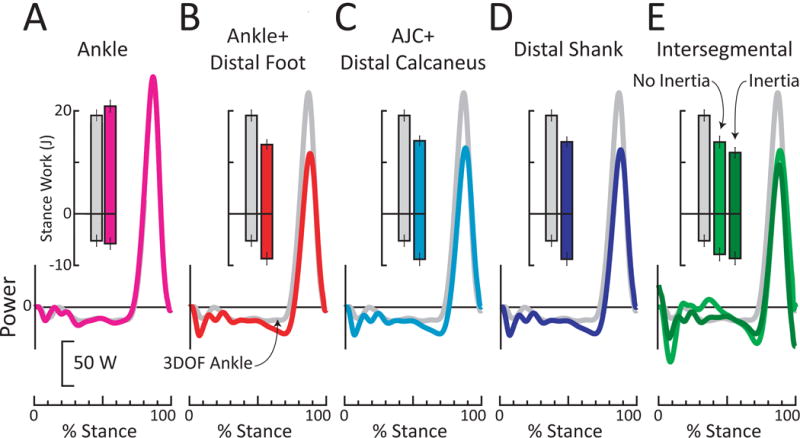
Each Ankle or anklefoot power is plotted over the stance phase of gait, relative to conventional 3DOF Ankle power (gray curve, representing power due to rotation of the shank relative to the foot). Inset bars represent positive and negative work over stance phase of gait. Standard deviation bars represent inter-step variability. (A) 6DOF (rotational + translational) Ankle power (pink) was similar to 3DOF (rotational) Ankle positive power (grey). (B-E) Peak 3DOF Ankle power was ~40% (~70 W) higher than peak anklefoot power estimates, and positive 3DOF Ankle work was ~40% (~6 J) higher than anklefoot positive work estimates. (B) Ankle + Distal Foot power (red). (C) AJC + Distal Calcaneus power (cyan). (D) Distal Shank power (blue). (E) Intersegmental power (green), assuming zero foot mass and inertia. When foot mass and inertia were included into the calculation of Intersegmental power (dark green), then peak power was decreased by 16 W and positive work decreased by 2 J over stance phase, relative to Intersegmental power calculation that neglected foot mass and inertia.

Ankle + Distal Foot power was nearly identical to AJC + Distal Calcaneus power (Fig. 4); however, there were substantial differences between Ankle vs. AJC power, and Distal Foot vs. Distal Calcaneus power (Fig. 4).

Figure 4. Power calculations relative to foot vs. relative to calcaneus, for able-bodied individual during shod (top row) and barefoot (bottom row) walking at 1.25 m/s.

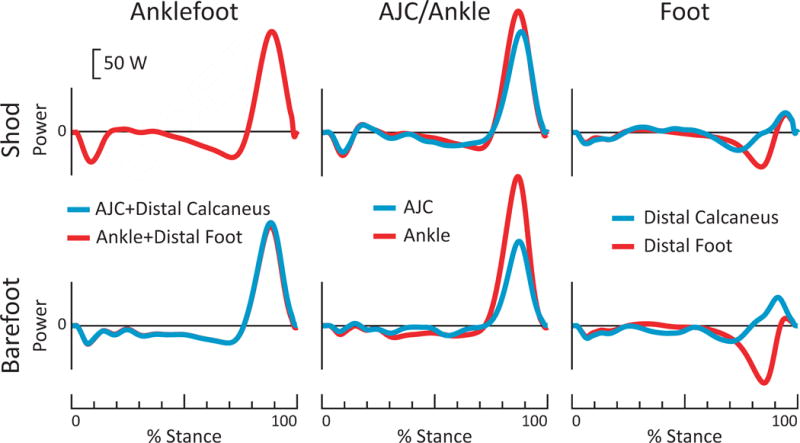
Both methods yielded very similar anklefoot power. However, large differences were observed in the partitioning Ankle/AJC vs. foot power sources. Peak Ankle (shank-foot) power was 20% (35 W) higher than peak AJC (shank-calcaneus) power during shod walking, and 77% higher (112 W) during barefoot walking. Positive Ankle work was 21% (3 J) and 79% (9 J) higher than positive AJC work during shod and barefoot walking, respectively. The magnitude of Distal Foot negative work was 53% (3 J) and 77% (5 J) more than the magnitude of Distal Calcaneus work during shod and barefoot walking, respectively. The magnitude of Distal Foot positive work was 45% (1 J) and 81% (3 J) less than the magnitude of Distal Calcaneus work during shod and barefoot walking, respectively.

Case Study 2

Anklefoot power estimates generally yielded similar results to each other when applied to prosthetic feet. An example is depicted in Fig. 5. For most prostheses, anklefoot power estimates differed substantially from 3DOF Ankle power, in terms of positive and/or negative power. However, the sign and magnitude of this difference was prosthesis-specific. For instance, three of eight prostheses showed fairly similar positive work (energy return) when comparing Distal Shank power estimates to 3DOF Ankle power, one prosthesis showed considerably more positive work, and four prostheses showed substantially less positive work for the Distal Shank estimate (Fig. 6). Prosthesis-specific variability was also observed for negative work (energy absorption, Fig. 6).

Figure 5. Ankle and anklefoot power for an example prosthesis (All Pro) during walking at 1.25 m/s.

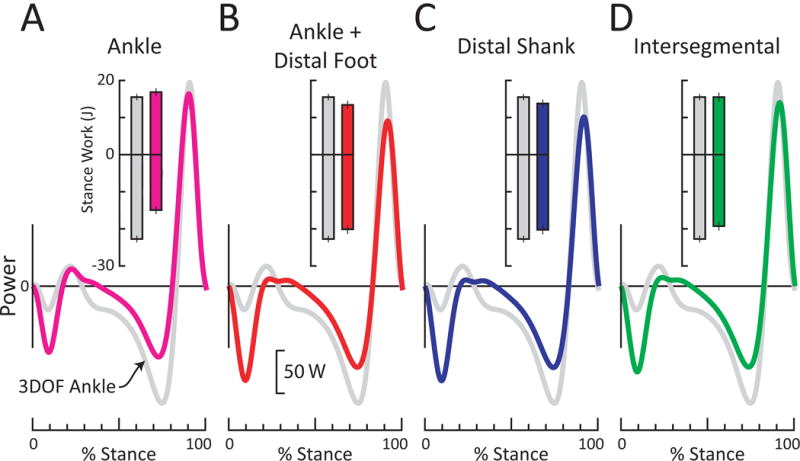
Each ankle or anklefoot power is plotted over the stance phase of gait, relative to conventional 3DOF Ankle power (gray curve, representing power due to rotation of the shank relative to the foot). Inset bars represent positive and negative work over stance phase of gait. Standard deviation bars represent inter-step variability. (A) 6DOF Ankle power (pink). When comparing 6DOF vs. 3DOF Ankle estimates, this particular prosthesis exhibited less negative work, slightly more positive work and similar peak power. (B) Ankle + Distal Foot power (red). (C) Distal Shank power (blue). (D) Intersegmental power (green), assuming zero foot mass and inertia. These different anklefoot estimates yielded power curves similar to each other. However, compared to 3DOF Ankle power, the anklefoot powers exhibited more negative power after foot contact (0-20% of stance), less negative power in mid-stance (40-85% stance), and slightly less positive power at the end of stance.

Figure 6. Anklefoot (Distal Shank) power vs. 3DOF Ankle power for all 8 prostheses during walking at 1.25 m/s.

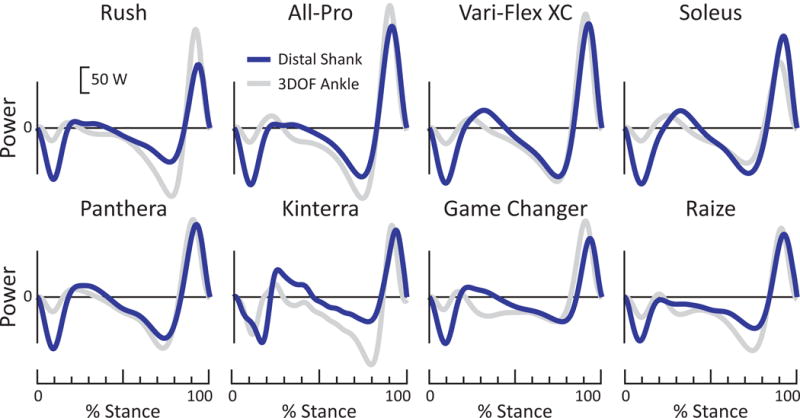
For all prostheses, the anklefoot power exhibited more negative power after foot contact (0-20% stance), relative to 3DOF Ankle power. For most prostheses, anklefoot power exhibited less negative power in mid-stance (~40-85% stance). Peak anklefoot power was notably less than 3DOF Ankle power for 4 of 8 prostheses (Rush, All Pro, Vari-Flex XC and Game Changer), roughly equivalent for 3 of 8 prostheses (Panthera, Kinterra and Raize), and greater for one prosthesis (Soleus).

Intact vs. prosthetic limb power differences were generally larger when using conventional 3DOF Ankle power analysis, than when estimating anklefoot power. A striking example was with the Soleus foot (Fig. 7). Based on 3DOF Ankle power analysis, the peak prosthetic Ankle power and positive Ankle work were 193 W and 12 J lower than the intact limb. However, when Distal Shank power was computed, these differences decreased by ~60-70% to 78 W and 4 J, indicating much more symmetry between intact and prosthetic limbs. On average (across all 8 feet), intact limb 3DOF peak Ankle power was 147 W higher than the prosthetic limb; however, peak Distal Shank power was only 100 W higher. Similarly, intact limb 3DOF positive Ankle work was 13 J higher than the prosthetic limb, whereas this difference was only 8 J when computing Distal Shank power.

Figure 7. Ankle and anklefoot power for intact (dashed) vs. prosthetic (solid) limb, while an individual walked on 8 different prostheses at 1.25 m/s.

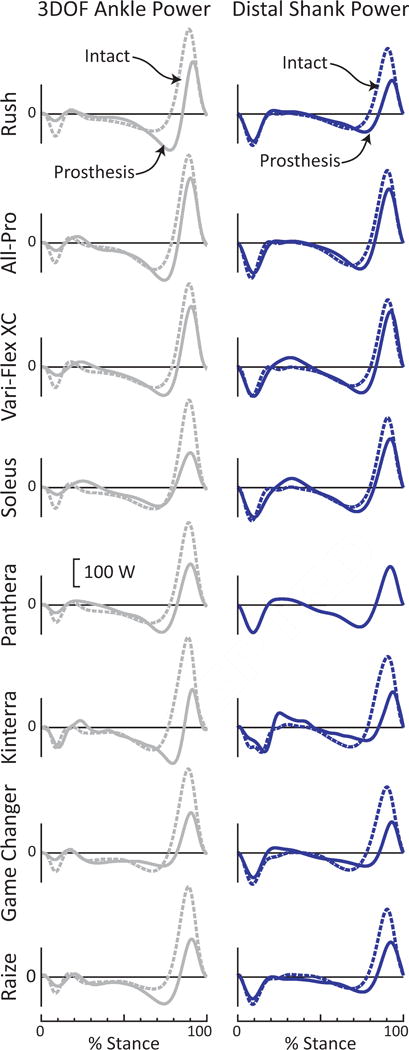
3DOF Ankle power estimates (left column) showed greater asymmetry between intact vs. prosthetic limb power generation, as compared to anklefoot power (Distal Shank, right column).

Discussion

These case studies exemplify problems that can arise when the entire foot is treated as a single rigid-body segment. Below we discuss scientific, clinical and technological implications, which highlight why it is important to include foot power in gait analysis studies; either explicitly by computing it, or implicitly by taking the (non-rigid) anatomy of the foot into account when estimating power about the ankle. Based on these empirical examples, analytical arguments and corroborating evidence from prior literature, we then recommend how to estimate biological and prosthetic power. In short, we recommend against computing conventional Ankle (shank-foot) power, and instead suggest AJC (shank-calcaneus) power as a more physiologically-relevant alternative. We also recommend estimating foot power, either using Distal Calcaneus (calcaneus-ground) power in addition to AJC (shank-calcaneus) power, or within a combined anklefoot power calculation (Fig. 1). Relaxing the assumption that the entire foot is a rigid body and including foot power in gait analysis is expected to enhance the quality and completeness of biomechanical estimates, help ensure proper evaluation of clinical interventions, and better inform the design of biomimetic devices.

Scientific Implications

Here we highlight two specific scientific implications, one related to the foot, and one to the ankle. First, treating the entire foot as a rigid body can skew our understanding of biological foot function. In the extreme, yet common case when only Ankle power is computed, the foot is implicitly assumed to contribute negligible power; however, there is substantial evidence to the contrary (Bruening et al., 2012a; Dixon et al., 2012; Ker et al., 1987; MacWilliams et al., 2003; Takahashi et al., 2017; Zelik et al., 2015). The more critical point to bring to bear is that even if Distal Foot power is computed, scientific interpretations of biological foot function may still be skewed because the entire foot is assumed to be a single rigid body. This is evident when comparing Distal Foot vs. Distal Calcaneus power (Fig. 4). Distal Foot power indicates a large amount of energy absorption, particularly during the Push-off (end-of-stance) phase of gait (Takahashi et al., 2012; Zelik et al., 2015). Interpreting Distal Foot power to signify net power due to structures within the foot is (and has been) perplexing because: (i) such foot energy absorption would undermine the beneficial Push-off power generated about the ankle (Kuo, 2002; Kuo and Donelan, 2010; Zelik and Adamczyk, 2016), and (ii) this dissipative behavior of the foot is inconsistent with the more spring-like behavior of the foot arch and plantar fascia observed in prior in vivo and in vitro studies (Ker et al., 1987; Stearne et al., 2016). However, both these issues are resolved by computing Distal Calcaneus power instead, which does not model (or track) the entire foot as a single rigid-body segment (Fig. 1E, see Appendix A). Functionally, the foot appears to be returning substantial energy in late Push-off (see Distal Calcaneus positive power in Fig. 4) and not dissipating large amounts of energy (per Distal Foot negative power in Fig. 4). Takahashi et al. (2017, N=14) provides more extensive corroborating evidence. We interpret these results to signify that Distal Foot power overestimates net energy dissipation by structures in the foot during the Push-off phase of gait. Thus it is not recommended to assume the entire foot is a single rigid-body segment in gait analysis; particularly when the goal is to understand net power contributions from the foot.

Second, treating the entire foot as a rigid body can distort our understanding of the ankle plantarflexors. Our results suggest that Ankle power (both 3DOF and 6DOF) overestimates Push-off power generated by calf muscle-tendon units (MTUs). Figure 4 shows that Ankle power (which assumes a rigid foot) was 77% higher than AJC power (which only assumes the calcaneus is rigid) during barefoot walking, and 20% higher during shod walking. These findings are corroborated by multi-subject studies using multi-segment foot models. Various studies have found that Ankle (shank-foot) Push-off power was substantially overestimated – by an average of 66% (MacWilliams et al., 2003), 74% (Dixon et al., 2012), 35% (Bruening et al., 2012a) and 27% (Segal et al., 2018) – as compared to an estimate of AJC (shank-calcaneus) power that is based on a multi-segment modeling approach. Ankle power tends to overestimate power generated by the ankle plantarflexor MTUs for the following reason: When the foot is modeled as a single rigid body, then motion within the foot (e.g., articulation at the mid-foot joint) bleeds over into the experimental ankle kinematics estimate, appearing as extra rotation of the foot segment relative to the shank. Thus, there appears to be more ankle joint rotation (and angular velocity), than is really occurring physiologically (Leardini et al., 2007). When this overestimate of Ankle angular velocity is multiplied by the estimated Ankle moment, then it yields an overestimate of Ankle power, relative to power generated by biological structures that cross the ankle. There are likely no physiological structure(s) crossing the ankle that actually generate the magnitude of peak power estimated via 3DOF or 6DOF Ankle analysis. Likewise, there may not be any physiological structure(s) in the foot that actually generate the peak (negative) powers estimated by Distal Foot calculations. Rather these high peak powers are due in large part to methodological choices (i.e., assuming the entire foot is one rigid body). In contrast, AJC power provides a more physiologically-relevant estimate of power generated by the ankle plantarflexors, since the Achilles tendon inserts on the calcaneus and the AJC model mitigates errors due to mid-foot or forefoot articulation (see Appendix A for extended explanation).

Compounding the overestimation problems described above is the fact that experimentally-estimated Ankle kinetics (e.g., power) are often used to infer the functional role of individual muscles and tendons. For instance, inverse dynamics Ankle power has been paired with B-mode ultrasound to infer Achilles tendon function (e.g., Farris and Sawicki, 2012b; Lichtwark and Wilson, 2006). Overestimating Ankle power may cause elastic energy return from tendons to be overestimated as well (Zelik and Franz, 2017), though this warrants further investigation. Also, musculoskeletal simulations often use optimization procedures that seek to match experimental kinematics such as ankle angle or kinetics such as ankle power (Bogey et al., 2005; Hof et al., 1993; Honert and Zelik, 2016; Neptune et al., 2001). Therefore, errors in experimental Ankle estimates could lead to quantitative, and potentially even qualitative errors, in simulation-based predictions of muscle and tendon dynamics. Finally, overestimating Ankle power may cause us to overvalue contributions from the plantarflexors, relative to muscles about other joints (e.g., knee, hip, or within the foot). This can distort our understanding of how power is distributed amongst various sources in the body.

Clinical Implications

Figures 6–8 highlight how treating the entire foot as a rigid body (and thereby neglecting foot power) can impair our ability to reliably compare different interventions (e.g., prosthetic feet) to each other, or to a biological norm. Ankle power estimates impose a rigid-shank/rigid-foot model onto prosthetic feet which, in large part, do not contain an explicit ankle joint and do not mechanically resemble this rigid-body model (Geil et al., 2000; Prince et al., 1994; Sawers and Hahn, 2011). In contrast, anklefoot power estimates can capture power (the rate of prosthetic energy storage and return) that occurs along the entire prosthesis. Figures 6–7 highlight the discrepancy between a conventional 3DOF Ankle power estimate vs. a more complete anklefoot estimate. For some prosthetic feet (e.g., Rush), 3DOF Ankle power overestimated the prosthetic anklefoot Push-off power (e.g., via Distal Shank estimate, Fig. 6). For other prosthetic feet (e.g., Soleus) 3DOF Ankle power underestimated prosthetic anklefoot Push-off power. And for yet other feet (e.g., Panthera), 3DOF Ankle power was similar to anklefoot Push-off power. As such, for a given prosthesis we may be unable to predict a priori how 3DOF Ankle power is related to anklefoot power. If we were to compare Push-off power generated by the Rush vs. Soleus based on 3DOF Ankle power, then we would conclude that the Rush provided ~30% higher peak Push-off power (162 W vs. 120 W peak, Figs. 7–8). However, if we were to compare these same two feet using a more complete anklefoot estimate (Distal Shank power), then it becomes apparent that the conclusion based on Ankle power was incorrect. Distal Shank power indicates exactly the opposite: Soleus exhibited ~50% greater peak Push-off than the Rush (170 W vs. 114 W, Figs. 7–8). This example highlights the danger of relying on Ankle power estimates alone. Moreover, if we were to compute the mechanical efficiency of these passive prosthetic feet (i.e., energy returned relative to energy absorbed), we see that the choice of estimation method can have a tremendous effect. For instance, for the Kinterra, mechanical efficiency was estimated to be 29% vs. 89% when using 3DOF Ankle vs. Distal Shank power. Computing anklefoot power is also important when comparing between intact vs. prosthetic limb biomechanics, for example, to assess gait symmetry. The Soleus provides a compelling example. Based on 3DOF Ankle power, the intact vs. prosthetic limb contributions appeared to be highly asymmetric (Fig. 7); however, Distal Shank power revealed a much higher level of symmetry – the Soleus actually generated ~85% of the positive work performed by the intact anklefoot.

Figure 8. Example of how choice of method can mislead conclusions when comparing two prosthetic feet.

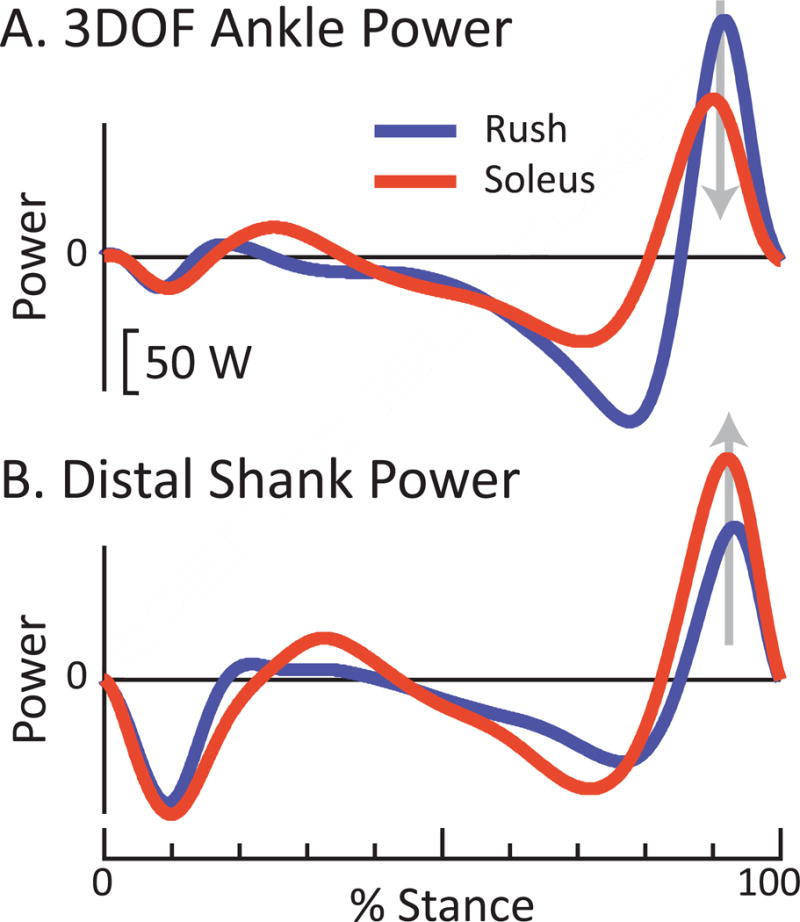
(A) Conventional 3DOF Ankle power indicates that peak Push-off power from the Soleus foot (red) was decreased relative to the Rush foot (blue); however, (B) the more complete Anklefoot power estimate indicates the opposite, that peak Push-off power with the Soleus was increased relative to the Rush foot. Power curves are for walking at 1.25 m/s, for one individual with transtibial amputation.

Using Ankle power is also expected to skew comparisons of other clinical interventions such as footwear and orthoses. Figure 4 shows how interventions affecting the rigidity of the foot (e.g., shoe, in-shoe orthosis, foot plate, exoskeleton) will also affect the quality of the Ankle power estimate, relative to anklefoot or AJC power estimates. Imagine a person generated exactly the same amount of Push-off power with their plantarflexor muscle-tendon units during both shod and barefoot walking. Figure 4 suggests that experimental Ankle power estimates would nonetheless appear higher for barefoot walking simply because the foot is less rigid without shoes, and thus more motion within the foot bleeds over into the Ankle estimate. To visualize this effect, look at the peak power magnitude difference between Ankle vs. AJC power for barefoot walking, and then look at this same comparison for shod walking. During barefoot walking, Ankle power grossly overestimated AJC power (by 77%). When shoes (or other interventions) are worn, which increase rigidity of the foot segment, then the magnitude of overestimation is reduced. Note that Distal Foot vs. Distal Calcaneus power estimates are similarly skewed when comparing barefoot vs. shod (Fig. 4). A variety of supporting evidence is found in prior literature. For example, Arch and Fylstra (2016) found that peak Ankle power was higher while walking barefoot than with a rigid footplate, even though combined anklefoot power was similar. Likewise, Bregman et al. (2012) found that peak Ankle power (and work) was higher when walking shod than with an ankle-foot orthosis (with a carbon-composite foot plate). Finally, Desloovere et al. (2006) found peak 3DOF Ankle power was highest barefoot (least rigid foot condition), next highest while shod, and the lowest while wearing an ankle-foot orthosis (most rigid foot condition) during gait. In all these cases, the critical danger is that one might interpret changes in Ankle power (with vs. without an intervention) as a reflection of how the intervention is benefitting or degrading biomechanical performance. In actuality, some of the estimated changes simply reflect methodological errors inherent in conventional Ankle power estimates. Thus, observed differences may have little to do with biomechanical adaptations by the user. This highlights why Ankle power should not be used to compare interventions that affect the rigidity of the foot.

One final example: imagine we had sought in this study to test the hypothesis that our subject generated more Push-off power with her calf musculature when walking barefoot, relative to shod. Based on 3DOF Ankle power (Fig. 9) we would have concluded that plantarflexor Push-off power increased by 20% when barefoot (supporting our hypothesis). However, AJC power contradicts this conclusion, suggesting that plantarflexor Push-off power actually decreased by 17% while barefoot (Fig. 9). This again exemplifies how Ankle power can potentially lead to the wrong conclusion when evaluating different conditions/interventions, and not simply inaccuracies in numerical estimates.

Figure 9. Example of how choice of method can mislead conclusions when comparing shod vs. barefoot walking.

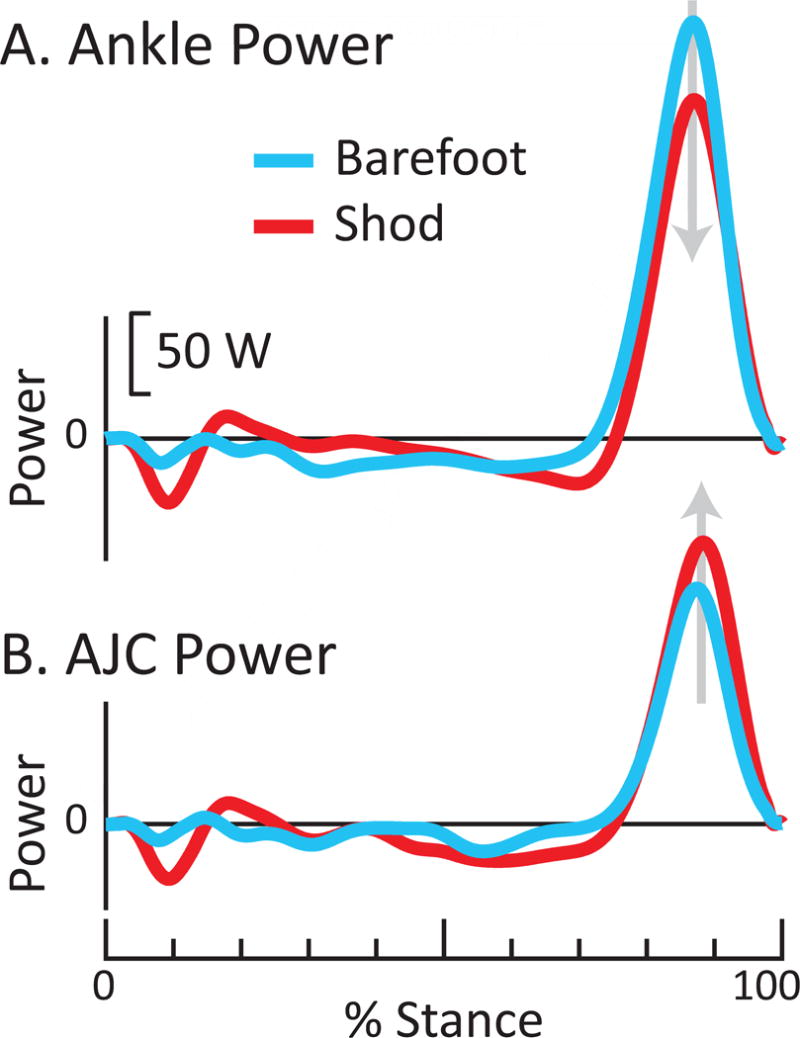
(A) Ankle power indicates that Push-off decreased while shod (red) relative to barefoot (blue); however, (B) AJC power indicates the opposite, that Push-off increased while shod. Power curves are for walking at 1.25 m/s, for one able-bodied person.

The comparison of 8 prosthetic feet (Figs. 6–7) highlights why it is problematic to assume that the foot is a single rigid-body, or to rely solely on Ankle power for interpretation. The subsequent discussion then shows how similar problems can occur with studies involving different footwear and orthoses. In short, conventional Ankle power – absolute power magnitudes and also relative power differences between conditions – can potentially mislead conclusions as a result of assuming the entire foot is a single rigid body. Based on these findings, it is recommended to compute anklefoot power when comparing lower-limb clinical interventions, and to avoid Ankle power.

Technological Implications

Treating the entire foot as a rigid segment can also result in inaccurate engineering design specifications for devices that aim to mimic or restore natural limb function. For instance, if we sought to design a new prosthetic foot, then relying on conventional 3DOF Ankle power would result in a substantial overestimate of the mechanical power generation requirements for our device. This is because prosthetic feet replace the entire anklefoot, not simply Ankle power. Overestimating power requirements could affect selection of motors, gears, batteries and control parameters, and ultimately impact device weight, cost and complexity. This overestimation problem is evident in Figure 3, which shows that peak biological Ankle power (and work) tends to be much larger than anklefoot power (and work); consistent with prior multi-subject studies (Takahashi et al., 2017; Takahashi and Stanhope, 2013; Zelik et al., 2015). This same issue is also evident in Figure 7, where 3DOF Ankle power provides a skewed perspective on the degree to which existing prosthetic feet mimic intact anklefoot power. Another potential problem is that we may perceive functional deficiencies that do not actually exist, then use them as motivation to design new technology. From the perspective of 3DOF Ankle power, all 8 prosthetic feet tested were highly deficient in terms of positive Push-off power (Fig. 7), resulting in large asymmetry between limbs. This may suggest the need for a dramatically different foot design to restore natural anklefoot function. However, once the more complete anklefoot power estimate is computed then it becomes evident that some of the prostheses tested actually came quite close to replicating intact anklefoot power for this individual at this speed. These observations highlight why it is inadvisable to assume the entire foot is a rigid body if the goal is to use biomechanical estimates of the biological limb to identify design requirements for biomimetic devices.

Selecting an Appropriate Method

It is important to select an appropriate method to capture both ankle and foot power contributions in gait analysis. However, method selection is nuanced, and depends on the precise objective of a given gait analysis study. In some cases it is beneficial to estimate ankle and foot power separately, though as shown in Fig. 4, the assumed model (shank-foot vs. shank-calcaneus) can substantially affect interpretation. In other cases it is more appropriate to estimate combined anklefoot power via Distal Shank power or Intersegmental calculations (e.g., when analyzing prostheses that do not contain an articulating ankle joint). Below we briefly summarize general recommendations. Conventional 3DOF Ankle power (shank-foot) is not recommended because it consistently overestimates net power produced by plantarflexing muscle-tendon units during walking (Zelik et al., 2015) and ignores foot power contributions (Fig. 4). 6DOF Ankle power also neglects important foot power contributions; however, it can be summed with Distal Foot power to provide a complete estimate of anklefoot power. The critical caveat here is that interpretation of biological ankle vs. foot power via this method may be misleading (Fig. 4). Summing AJC (shank-calcaneus) and Distal Calcaneus power is preferred because it provides: (i) a more physiologically-relevant partitioning of ankle vs. foot power in the biological limb, and (ii) sums to provide an estimate of anklefoot power that is nearly identical to Ankle + Distal Foot (Fig. 4). Power sources within the foot can be further decomposed using previously-published multi-segment foot modeling approaches (Bruening et al., 2012a; Dixon et al., 2012; MacWilliams et al., 2003; Takahashi et al., 2017). AJC + Distal Calcaneus power estimates provide some of the same benefits as multi-segment foot models, except with fewer foot markers required, and without the need to track/model mid- or fore-foot segments, or to partition ground reaction forces amongst various foot segments. Finally, combined anklefoot power estimates are also recommended using either Distal Shank or Intersegmental power calculations; though these do not allow for partitioning of power between ankle and foot. These two methods yield similar results to each other, and also to Ankle + Distal Foot power, and to AJC + Distal Calcaneus power (Figs. 3 & 5).

Limitations

There are well-understood limitations to case studies; however, there are also benefits. The purpose of this article was to provide concrete examples as to why it is important to compute foot power. Case studies here were intended to provide clear and unambiguous evidence of what can happen when the foot is treated as a single rigid-body segment. There is no uncertainty related to inter-subject variability or confounding factors. We also cited corroborating evidence from previously-published multi-subject studies, which further substantiate our main findings and conclusions. We focus on walking, but prior studies suggest that foot power is also meaningful in other locomotor tasks such as running (Kelly et al., 2015; Wager and Challis, 2016). Methods detailed here may help elucidate the puzzlingly large energy absorption estimated within the foot during running (10-25 J, McDonald et al., 2016; Stefanyshyn and Nigg, 1997) and sprinting (25-70 J, Stefanyshyn and Nigg, 1997). Calcaneus motion is generally well approximated by skin-mounted markers; however, may still slightly overestimate AJC rotation based on bone pins (Reinschmidt et al., 1997). Further research is warranted to understand confounds due to placing markers on the shoe vs. skin. Relatively low cut-off frequencies were used to process force and motion data (10 Hz and 6 Hz, respectively) based on the typical frequency content of human walking (Antonsson and Mann, 1985). When higher cut-off frequencies were applied to our data (e.g., 25 Hz and 10 Hz, respectively) we found that this had no effect on any key trends, conclusions or interpretations. We acknowledge that there are limitations to all experimental estimates, include anklefoot estimates presented. Each estimate is an imperfect approximation based on a simplified biomechanical model. For instance, none of the estimates presented explicitly model or account for multiarticular muscles crossing the ankle and metatarsophalangeal joints (Honert and Zelik, 2016). And many of the estimates depend on foot mass and inertia being relatively small. Nevertheless, the critical point is that some models (i.e., used to estimate anklefoot power) are more complete and more physiologically-relevant than other models (e.g., that only estimate Ankle power, assuming a single rigid-body foot segment). These more complete models highlight why certain body dynamics, most notably foot power due to having a non-rigid foot, should not be neglected when performing gait analysis or interpreting results.

Conclusion

Treating the entire foot as a single rigid-body segment can result in obscuring (or even completely missing) important dynamics, re-affirming conclusions from prior multi-segment foot modeling studies. Here we overview why this is important to the gait analysis community, and how to better estimate anklefoot dynamics experimentally.

Specifically, we highlight how neglecting foot power can hinder our scientific understanding of movement, confound our ability to make robust clinical comparisons (e.g., between prosthetic feet), and mislead the design of assistive devices aimed at mimicking or restoring biological limb function. To mitigate these problems, it is recommended to compute foot power in gait analysis using one or more of the methods outlined, and not to rely on conventional estimates of Ankle power.