Skip to main content
PMC home page
NASA Author Manuscripts logoLink to NASA Author Manuscripts
. Author manuscript; available in PMC: 2018 Jun 19.
Published in final edited form as: J Hydrometeorol. 2017 Mar 9;18(3):837–843. doi: 10.1175/JHM-D-16-0285.1

A Data-Driven Approach for Daily Real-Time Estimates and Forecasts of Near-Surface Soil Moisture

Randal D Koster 1, Rolf H Reichle 1, Sarith P P Mahanama 1,2
PMCID: PMC6006515  NIHMSID: NIHMS945983  PMID: 29930485

Abstract

NASA’s Soil Moisture Active Passive (SMAP) mission provides global surface soil moisture retrievals with a revisit time of 2–3 days and a latency of 24 hours. Here, to enhance the utility of the SMAP data, we present an approach for improving real-time soil moisture estimates (“nowcasts”) and for forecasting soil moisture several days into the future. The approach, which involves using an estimate of loss processes (evaporation and drainage) and precipitation to evolve the most recent SMAP retrieval forward in time, is evaluated against subsequent SMAP retrievals themselves. The nowcast accuracy over the continental United States (CONUS) is shown to be markedly higher than that achieved with the simple yet common persistence approach. The accuracy of soil moisture forecasts, which rely on precipitation forecasts rather than on precipitation measurements, is reduced relative to nowcast accuracy but is still significantly higher than that obtained through persistence.

1. Introduction

The SMAP (Soil Moisture Active Passive, Entekhabi et al. 2010) mission provides estimates, across the globe, of moisture in the top several centimeters of soil at a spatial resolution of about 40 km and with a revisit time of 3 days or less. To promote the use of the data in the community, the data are produced with a mean latency of 24 hours, close to real time for many applications. We posit, as motivation for the present paper, that some users of these data may find utility in products of even lower latency (soil moisture “nowcasts”, i.e., with a latency of 0 hours) as well as in soil moisture forecasts, out several days. Such information could benefit, for example, those who use soil moisture to evaluate current and near-future ground trafficability or the potential for certain hazards such as flash floods and landslides.

The objective of this paper is to describe an approach for deriving improved real-time and forecasted surface soil moisture estimates from the SMAP data. Given a soil moisture retrieval, WN, on Day N, our approach considers the forward evolution of soil moisture from this value using precipitation estimates (either measured or forecasted) in combination with a loss function, the latter being derived from a history of SMAP retrievals and precipitation observations. The resulting real-time and forecasted soil moisture estimates are thus data-driven (independent of land model formulation) and are statistically consistent with the original retrieval product, greatly facilitating their use in applications that already utilize near-real time SMAP data, at least in areas with adequate precipitation data. (The approach will not provide reliable soil moisture estimates where precipitation is poorly measured.)

The datasets used here and the estimation approach are described in section 2. The accuracy of the estimates so produced is illustrated in section 3 through quantitative comparisons with subsequent SMAP retrievals. For context, this accuracy is compared to that obtained with an approach already applied, knowingly or not, by many data users: assuming simple persistence, i.e., assuming that the best estimate of the current soil moisture state is the most recently measured value for that state, even if that measurement is a day to several days old.

2. Data and Approach

a. Datasets Used

We use SMAP Version 3 Level 2 soil moisture retrievals (O’Neill et al. 2016; Jackson et al. 2016), which are based on L-band radiometer measurements. These data represent volumetric soil moisture in roughly the top 5 cm of soil and are provided on a 36 km equal-area Earth-fixed grid (Brodzik et al. 2012). As in Koster et al. (2016), we ignore the retrieval flag associated with “recommended quality” to allow greater spatial and temporal coverage.

The precipitation data used to derive the soil moisture loss functions are from the Climate Prediction Center Unified Gauge-Based Analysis of Global Daily Precipitation (CPCU; ftp://ftp.cpc.ncep.noaa.gov/precip/CPC_UNI_PRCP/GAUGE_GLB/). As in Koster et al. (2016), this 0.5°× 0.5° dataset was converted to the SMAP grid using a conservative regridding (areal weighting) approach. In CONUS, a precipitation amount listed for a given day corresponds to water falling over the 24 hours up to 12Z on that day; 12Z corresponds to 6AM in the middle of the country, the approximate local solar time of the SMAP retrievals.

The 2016 precipitation forecasts (also regridded to the SMAP grid) are from the Goddard Earth Observing System, Version 5.13.1 (GEOS-5) model (https://gmao.gsfc.nasa.gov/GMAO_products). For each day considered in the evaluation phase of the study (May-September of 2016; see below), precipitation forecasts from GEOS-5 are available for the following 5 days beginning at 12Z.

b. Estimation Approach

In the following, we assume that a SMAP soil moisture retrieval (in volumetric units, m3/m3) for Day N, WN, is available on Day N+1 (given the 24-hour latency) and that we require estimates of WN+1 through WN+5. (For example, if the current day is N+1, we require a “nowcast” of soil moisture on that day as well as soil moisture forecasts for the next four days based on the previous day’s measurement WN.) Our approach involves updating W through those five days by integrating equations that address how soil moisture increases with precipitation and decreases with evapotranspiration and drainage. Given a SMAP retrieval on Day N, we update soil moisture over the next five days (hour by hour) with:

W(t+Δt)=W(t)−L(W(t))⋅Δt+Wadd, (1)

where t is the hour of integration, the time step Δt is set to 3600 s, and L(W(t)) is the assumed rate of soil moisture loss via evapotranspiration and drainage (volumetric units per second). The term Wadd is the soil moisture increase associated with I (mm/s), the assigned infiltration rate:

Wadd=IΔt/D, (2)

where the depth D is set to 50 mm and Wadd is thus in volumetric units. The infiltration rate I is in turn set equal to the measured or forecasted precipitation rate P (mm/s) unless that rate, if it were to be applied over a full day, would exceed the current soil water deficit:

I=min{P,D(Wmax−W(t))/nd}, (3)

where nd is the number of seconds in a day and Wmax is the assumed maximum allowable value for W. If I is set to the second term (associated with the soil water deficit) in (3), the excess precipitation water is assumed to run off the surface. The somewhat arbitrary use of a daily total to determine the excess reflects in part our lack of knowledge of the sub-diurnal character of the daily precipitation.

The precipitation rate P is taken from observations (to the extent possible, up to the present time) or from a weather forecast model. Test runs were performed to verify that an hourly time step for the integration of the equations is indeed adequate; the results presented in section 3 below are essentially reproduced when the time step is decreased, for example, to 6 minutes.

c. Loss Function Estimation

Using (1)–(3) to update soil moisture requires a description of the loss function L and an estimate for Wmax. For this we jointly analyze SMAP soil moisture retrievals and CPCU precipitation measurements during May–September 2015. At each grid cell, we determine the lowest and highest soil moisture retrieval values, Wlow and Whigh, attained at that cell during that period. The low end of the assumed soil moisture range, Wmin, is set to Wlow, and the high end of the range, Wmax, is arbitrarily set to Whigh + 0.1*(Whigh-Wmin). We set the value of the loss function at the low end, L(Wmin), to 0. At Wmax, we set it to an arbitrarily high value: L(Wmax)=Wmax volumetric units per day. Note that such a high loss rate cannot be maintained for long – in our simulations with L, unrealistic soil moistures at the high end quickly adjust themselves to produce loss rates of reasonable magnitude. We tested different high values for L(Wmax) and different definitions for Wmax, with little impact on our results.

We next identify the three intermediate soil moisture values (WA, WB, and WC) that divide the range between Wmin and Wmax into four equal segments. Estimating the loss function amounts to determining L at these intermediate moistures; once these values are determined, the value of L at any other soil moisture can be estimated through linear interpolation. We establish the optimal values of L(WA), L(WB), and L(WC) through brute force. To test a set of L values at a given grid cell, we initialize an integration with the first SMAP retrieval at the cell in May 2015 and use (1)–(3) along with the 2015 gauge-based precipitation data to produce a time series of soil moisture spanning May–September of that year, and we then compute the root mean square error (RMSE) between the simulated soil moistures and the SMAP retrievals in the cell as they occur. (Note that we could have chosen in these integrations to reset W(t) to the SMAP retrieval values as they occurred, after noting the error; tests indicate, however, that this modification has very little impact on our results.) We test a comprehensive suite of L(WA), L(WB), and L(WC) values in this way, limiting the search space by assuming that L never decreases with increasing soil moisture, and find the one set that best reproduces the SMAP retrieval time series.

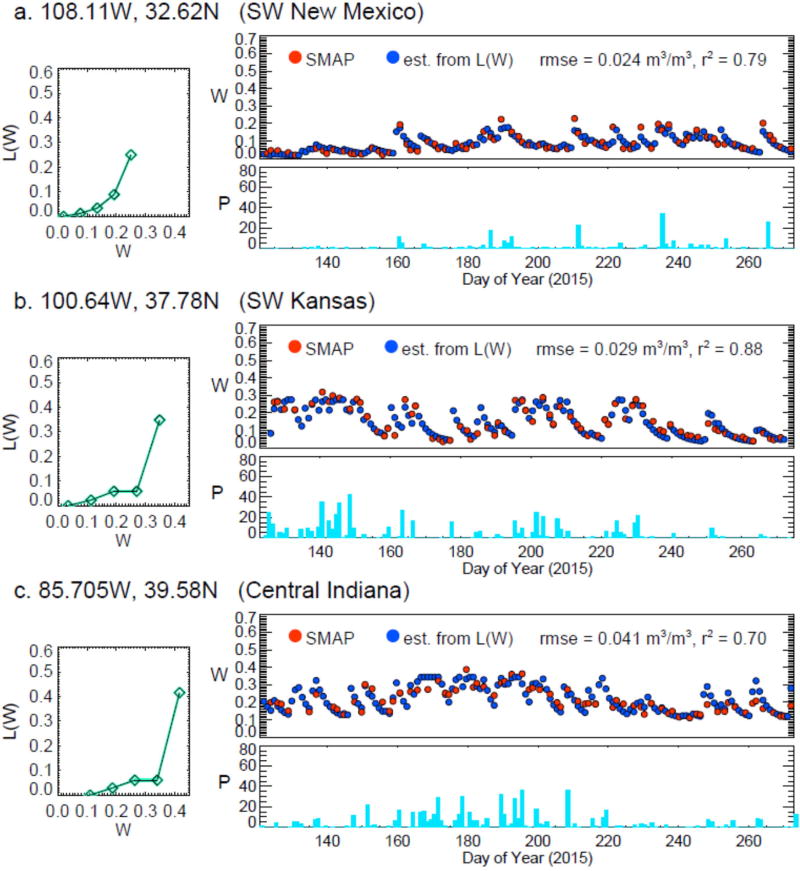
Figure 1 displays the loss functions derived at three representative interior sites. For each site, the leftmost panel shows the optimized loss function itself, and the top right panel shows the time series (covering May–September 2015) of the SMAP Level 2 retrievals there (as red dots) as well as the soil moisture estimates (blue dots) derived with (1)–(3) using the loss function in conjunction with CPCU rainfall data. For reference, the rainfall data are shown in the bottom right panel.

Figure 1.

Figure 1

Open in a new tab

Representative results from loss function estimation. a. Left panel: derived (optimized) loss function for a grid cell in southwestern New Mexico, showing, as a function of volumetric soil moisture, how much of that soil moisture (shown here in m3 m−3 day−1) is expected to be removed from the near surface through evaporation and drainage. Top right panel: SMAP Level 2 soil moisture retrievals (m3 m−3) at the grid cell (red dots) and corresponding simulated values obtained using the loss function in conjunction with the observed CPCU precipitation data over the time period (blue dots; see text). Bottom right panel: CPCU precipitation (mm day−1). The x-axis on the rightmost plots begins on May 1, 2015. b. Same, but for a grid cell in southwestern Kansas. c. Same, but for a grid cell in central Indiana.

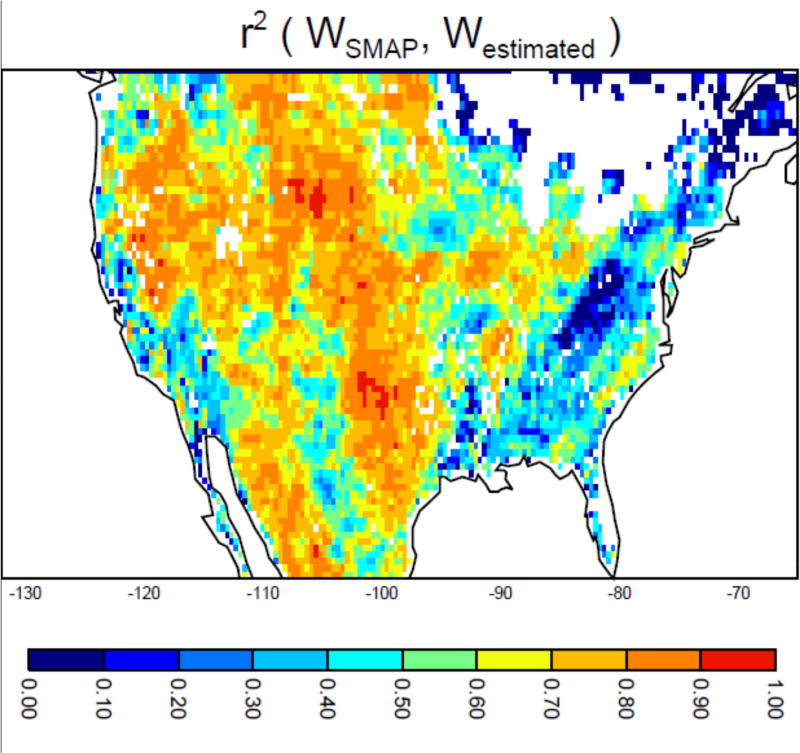
Although they have the same basic form, the loss functions at the three sites differ, with larger soil moisture losses occurring, for example, at low soil moistures for the New Mexico site relative to the Arkansas site. The comparisons of the retrievals with the estimated soil moistures generally show strong agreement in terms of RMSE and the square of the correlation coefficient (r2), indicating that the loss functions do indeed capture the hydrological behavior of the near-surface soil. Again, these are representative results for the interior of CONUS; as shown in Figure 2, however, the r2 values are a bit lower, and thus the optimization of L is more questionable, in the wet and highly vegetated areas of the East (perhaps due to the quality of the SMAP retrievals under thick vegetation) and in the very dry areas of the Southwest (perhaps due to irrigation impacts or to the low variability of soil moisture there during summer).

Figure 2.

Figure 2

Open in a new tab

Spatial distribution of the square of the correlation coefficient between the 2015 SMAP Level 2 soil moisture retrievals and the soil moisture estimates produced using the loss functions fitted to that year’s data. To generate the estimates, soil moisture at each grid cell was initialized on 1 May 2015 and then updated through September using the locally optimized loss function and the time series of local precipitation.

The concept of loss functions has an extensive history (e.g., Manabe, 1969). Direct estimates of loss functions from observations are rare, but where they exist, it is encouraging to note that they have the same basic form as those shown in Figure 1, with an increase in L with soil moisture at the very dry end, a plateauing out of the relationship in the midrange (as in Figure 1b and 1c), and a high sensitivity of L to soil moisture at the wet end (see, e.g., Salvucci et al. 2001, their Figure 3; Sun et al. 2011, their Figure 2). Such functions in the literature are sometimes normalized by net radiation or potential evaporation to account for seasonal variations in the drivers of surface evaporation; we reduce the need for this here (and also mitigate snow cover issues) by focusing on the May-September period over CONUS.

Figure 3.

Figure 3

Open in a new tab

(a) Skill of 1-day lead soil moisture estimates (computed as the RMSE of estimated soil moisture versus SMAP retrieval value, if it exists, one day after a given retrieval) for the loss function approach using gauge-measured precipitation (left panel, relevant to soil moisture nowcasts), the loss function approach using forecasted precipitation (middle panel, relevant to soil moisture nowcasts and forecasts), and the persistence approach (right panel). Results are shown for 2016, a period independent of that used to optimize the loss functions. (b) Same, but for 2-day lead estimates. (c) Same, but for 3-day lead estimates. (d) Same, but for 5-day lead estimates.

d. Simulations Performed and Accuracy Metric

We evaluate soil moisture nowcast and forecast skill obtained with our approach during May–September of 2016, a period independent of that used (May–September of 2015) to estimate the loss function L at each site. For each SMAP retrieval at each location, we integrate (1)–(3) forward in time 5 days (starting with the retrieval value) using two sets of precipitation estimates: (i) precipitation forecasts from the GEOS-5 modeling system, and (ii) CPCU rainfall measurements, the type of data that might be available for producing soil moisture nowcasts. We then compare the resulting soil moisture updates to any later SMAP retrievals appearing during the 5-day window. For example, a grid cell with a SMAP retrieval on both Day N and Day N+3 effectively produces a data pair ([Westimated(N+3), Wretrieved(N+3)]) that can be included in a 3-day-lead RMSE calculation. We compute the RMSE over all such 3-day-lead data pairs during May–September of 2016. We similarly compute the RMSE for the other leads; at a given grid cell, each RMSE will be based on a unique collection of dates. Naturally, our interpretation of accuracy here is tempered by the knowledge that SMAP soil moisture retrievals have their own errors; we are, in effect, quantifying the skill in predicting a SMAP retrieval before it is available.

Our analyses focus on CONUS (including neighboring parts of Canada and Mexico), a large-scale area with two important features: (i) precipitation measurements of suitable spatial and temporal coverage, and (ii) climatic regimes that range from very dry (in the west) to wet and humid (in the east).

3. Results

For a lead of one day, the leftmost and middle panels of Figure 3a show the accuracy of near-surface soil moisture estimates produced with (1)–(3) using, for P, gauge-based rainfall data and precipitation forecasts, respectively. For context, the rightmost panel shows the results obtained by assuming soil moisture persistence, i.e., by assigning the value of the soil moisture retrieval on day N to each of the subsequent five days. The next three rows show the corresponding results for leads of 2, 3, and 5 days. Results for a 4-day lead are not shown; the number of retrievals separated by exactly 4 days is severely limited over the US due to the orbital characteristics of the SMAP observatory.

As expected, soil moisture estimates are more accurate when CPCU data rather than precipitation forecasts are used in (1)–(3). Of course, the accuracy levels in the first column are only relevant to nowcasts, and only in areas where real-time rainfall measurements are in fact available. CPCU data are generally available to users with a latency of 1–2 days, which is relatively high. We expect, however, that users in many areas will have more immediate access to local rainfall measurements for local nowcast calculations, and some satellite-based precipitation datasets have low latencies and may prove useful for the nowcasts – some components of the IMERG product (Huffman et al., 2014), for example, feature a latency of several hours. If precipitation measurements of any kind are not available, soil moisture nowcasts will need to rely on precipitation forecasts (or analyzed precipitation products), and all soil moisture forecasts must rely on precipitation forecasts; for these, the second column in Figure 3 is more relevant. Note that for some estimations, measured precipitation may be available during the first part of the simulation, in which case the relevant accuracies would lie in between the first and second columns.

At all leads, RMSE values obtained with the loss function approach tend to lie below 0.04 m3/m3 in the western part of the continent and in areas along the eastern coast, using either rainfall dataset. The higher RMSEs obtained with the loss function approach when using forecasted rainfall still lie below 0.06 m3/m3 over most of the continent, particularly for leads of 3 days or less. To provide some perspective, the SMAP mission imposes an accuracy requirement of 0.04 m3/m3, though this is for evaluations against in situ data, something not attempted here.

Using either rainfall dataset, the RMSE values of our soil moisture estimates are lower almost everywhere, for all leads, than those obtained with the persistence approach. Again, the persistence approach is effectively employed by anyone who uses the most recent SMAP retrieval in their particular application. Figure 3 suggests that using the loss function approach instead for the application could prove beneficial.

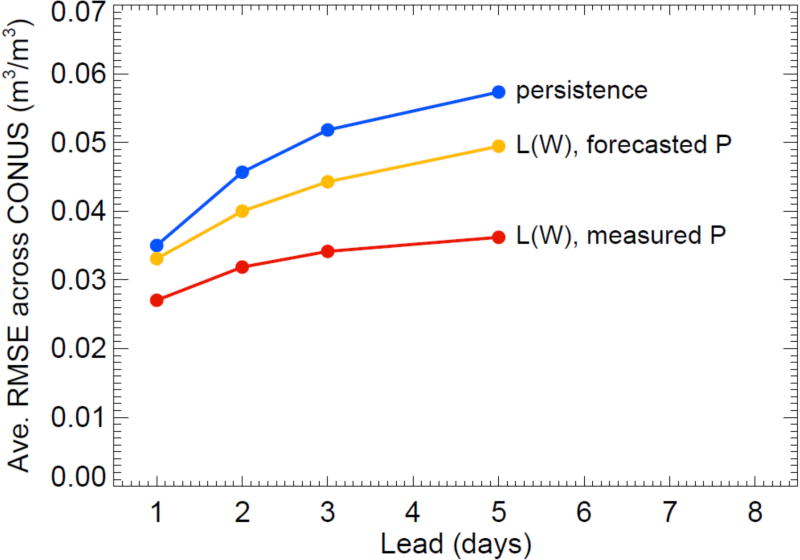
The results are summarized in Figure 4, which shows the average RMSE computed across the area at each lead for the different approaches. Again, using gauge-based precipitation in (1)–(3) produces more accurate estimates than using precipitation forecasts, and both sets of estimates outperform persistence. While persistence performs about as well as the loss function approach with forecasted precipitation at a lead of one day (soil moistures do take some time to diverge from initial values), the accuracy decreases relatively quickly with lead.

Figure 4.

Figure 4

Open in a new tab

Areal averages of the RMSE values in Figure 3 as a function of lead for the persistence approach (blue), the loss function approach using forecasted precipitation (yellow), and the loss function approach using gauge-measured precipitation (red), of relevance to potential nowcast calculations.

4. Summary and Discussion

The nowcasts and forecasts described in section 3 are fair, not being based on information from the period following the retrieval. As seen in Figures 3 and 4, integrating (1)–(3) forward in time produces nowcasts or forecasts that are more accurate – at least in terms of being able to predict the next SMAP retrieval – than those obtained by assuming persistence.

Damped persistence, in which a soil moisture anomaly evolves with an assigned time scale toward a climatological value during the forecast period, is another estimation approach, one that can be tested once the SMAP data record is large enough to provide a reliable climatology. Alternatively, real-time or forecasted soil moistures could be extracted directly from weather forecast products. The approach described here, however, has some notable advantages. Unlike damped persistence, the loss function approach, which implicitly uses locally-optimized damping time scales, also makes use of measured or forecasted precipitation information. Unlike weather forecast model soil moisture products, which are subject to inaccuracies in model formulation and are characterized, in any case, by model-dependent statistical moments (Koster et al. 2009), our approach makes direct use of the most recent SMAP retrieval and produces data that are, by construction, statistically consistent with SMAP retrievals and are thus immediately relevant to applications already using SMAP data. Note, however, that raw precipitation forecasts generated with numerical weather prediction models can have statistics in conflict with those of the true precipitation at a site (e.g., due to differences in spatial scale), and such deficiencies could affect the statistics of the loss function-based soil moisture forecasts discussed herein. As a remedy, the forecast precipitation rates could be suitably adjusted with established procedures (e.g., Clark et al. 2004, Charba and Samplatsky 2011).

Another important caveat is the fact that the soil moisture estimation approach described herein is limited to regions with adequate precipitation estimates, necessary for the construction of accurate loss functions. Note that as the size of the SMAP data record increases, the accuracy of the derived loss functions in these regions should increase. Also worth noting is that the precipitation forecasts used herein were produced by GEOS-5, an experimental forecast system; soil moisture forecasts might improve if bias-corrected precipitation forecasts from an operational weather center were used instead.

We fully expect that many applications would benefit from more up-to-date (and forecasted) soil moisture information than allowed by operational SMAP product latency. Not discussed here, but also relevant, is the potential for using the approach to back-fill temporal gaps in the SMAP data record – gaps caused by the unavoidable 2–3 day return time of the SMAP sensor and potentially exacerbated by, for example, intermittent radio frequency interference or by active rainfall during the time of overpass. Given adequate precipitation data and a suitable time period over which to fit the functions, the data-driven loss function approach indeed has the potential to transform the SMAP data record into a daily record of soil moisture with no missing data, all the way up to real time or even a few days into the future.

Acknowledgments

This work was supported by NASA through its funding of the SMAP Science Team (announcement NNH12ZDA001N-SMAP). We thank Qing Liu, Austin Conaty, and Jana Kolassa for help with the datasets.

References

  1. Brodzik MJ, Billingsley B, Haran T, Raun B, Savoie MH. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS International Journal of Geo-Information. 2012;1(1):32–45. [Google Scholar]
  2. Charba JP, Samplatsky FG. High-resolution GFS-based MOS quantitative precipitation forecasts on a 4-km grid. Monthly Weath. Rev. 2011;139:39–68. [Google Scholar]
  3. Clark M, Gangopadhyay S, Hay L, Rajagopalan B, Wilby R. The Schaake Shuffle, A method for reconstructing space-time variability in forecasted precipitation and temperature fields. J. Hydromet. 2004;5:243–262. [Google Scholar]
  4. Entekhabi D. The Soil Moisture Active Passive (SMAP) mission. Proc. IEEE. 2010;98:704–716. and Co-authors. [Google Scholar]
  5. Huffman GJ, Bolvin DT, Braithwaite D, Hsu K, Joyce R, Xie PP. Algorithm Theoretical Basis Document, Version 4.4. National Aeronautics and Space Administration; 2014. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG) Available at https://pps.gsfc.nasa.gov/Documents/IMERG_ATBD_V4.pdf. [Google Scholar]
  6. Jackson T. Soil Moisture Active Passive (SMAP) Project Calibration and Validation for the L2/3_SM_P Version 3 Data Products. Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California: JPL Publication, JPL D-93720; 2016. and Co-authors. [Google Scholar]
  7. Koster RD, Guo Z, Yang R, Dirmeyer PA, Mitchell K, Puma MJ. On the nature of soil moisture in land surface models. J. Climate. 2009;22:4322–4335. [Google Scholar]
  8. Koster RD, Brocca L, Crow WT, Burgin MS, De Lannoy GJM. Precipitation estimation using L-band and C-band soil moisture retrievals. Water Resources Research. 2016;52:7213–7225. doi: 10.1002/2016WR019024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Manabe S. Climate and the ocean circulation, I, The atmospheric circulation and the hydrology of the Earth's surface. Mon. Wea. Rev. 1969;97:739–774. [Google Scholar]
  10. O'Neill PE, Chan S, Njoku EG, Jackson T, Bindlish R. SMAP L2 Radiometer Half-Orbit 36 km EASE-Grid Soil Moisture, Version 3. Boulder, Colorado USA: NASA National Snow and Ice Data Center Distributed Active Archive Center; 2016. [Accessed June, August, and October 2016]. [DOI] [Google Scholar]
  11. Salvucci GD. Estimating the moisture dependence of root zone water toss using conditionally averaged precipitation. Water Resour. Res. 2001;37:1357–1365. doi:0.1029/2000WR900336. [Google Scholar]
  12. Sun J, Salvucci GD, Entekhabi D, Farhadi L. Parameter estimation of coupled water and energy balance models based on stationary constraints of surface states. Water Resour. Res. 2011;47:W02512. doi: 10.1029/2010WR009293. [DOI] [Google Scholar]

RESOURCES