Influence of Na⁺ and Mg²⁺ ions on RNA structures studied with molecular dynamics simulations

Abstract

The structure of ribonucleic acid (RNA) polymers is strongly dependent on the presence of, in particular Mg²⁺ cations to stabilize structural features. Only in high-resolution X-ray crystallography structures can ions be identified reliably. Here, we perform molecular dynamics simulations of 24 RNA structures with varying ion concentrations. Twelve of the structures were helical and the others complex folded. The aim of the study is to predict ion positions but also to evaluate the impact of different types of ions (Na⁺ or Mg²⁺) and the ionic strength on structural stability and variations of RNA. As a general conclusion Mg²⁺ is found to conserve the experimental structure better than Na⁺ and, where experimental ion positions are available, they can be reproduced with reasonable accuracy. If a large surplus of ions is present the added electrostatic screening makes prediction of binding-sites less reproducible. Distinct differences in ion-binding between helical and complex folded structures are found. The strength of binding (ΔG^‡ for breaking RNA atom-ion interactions) is found to differ between roughly 10 and 26 kJ/mol for the different RNA atoms. Differences in stability between helical and complex folded structures and of the influence of metal ions on either are discussed.

INTRODUCTION

Positively charged ions play an essential role for the structural stability of RNA molecules. Especially, Mg²⁺ ions facilitate high structural complexity and folding arrangements that allow RNA molecules to perform various cellular functions (1). Apart from canonical functions assigned to RNA molecules such as being involved in protein synthesis, like messenger (m) or transfer (t) RNA, it is nowadays well established that RNAs act in many other biological processes. RNA molecules are for instance involved in gene regulation (e.g., small nuclear (sn), micro (mi) and small interfering (si) RNAs) and in enzymatic activity (e.g. ribozymes and ribonucleoprotein). In eukarya they also play a role in resistance to pathogenic and parasitic invaders (2,3). Some of these functions depend on the presence of metal ions. Mg²⁺ ions do not only stabilize specific RNA structures (4), but do also help to recognize binding partners and mediate catalytic processes (5–7). Hammerhead ribozymes are one well-known example that require metal ions to be present both for obtaining the correct three-dimensional fold and performing the ribozymes’ function (8–12).

The need for positively charged ions in close proximity to RNA molecules is not surprising given their negatively charged backbone. Each RNA nucleotide contains one phosphate group that carries one negative charge. Positive ions shield negative charges on the RNA backbone by reducing repulsive forces, thereby allowing intramolecular interactions and compact RNA-biopolymers. RNA molecules are stabilized internally by hydrogen bonds between nucleotides in the same plane and by base stacking.

Positively charged ions can be divided into two main groups: (a) ions that bind to structurally well-defined sites in direct contact with or close to the RNA and (b) ions that form a cloud surrounding the RNA molecule (13). The classification of Mg²⁺ binding has been further refined (1,14,15): inner-sphere ions that form direct bonds with RNA atoms, outer-sphere ions that bind via a single hydration shell to the RNA, diffuse Mg²⁺ ions that bind via multiple hydration shells, and free ions where the RNA’s charge has no direct effect on the ions. Monovalent ions can also be part of the first group and can bind sequence- specific to electronegative pockets formed by RNA structures (16–18); they should not just be considered to be part of a diffuse ionic cloud as described by Manning (19). Folding studies have shown that tRNA thermodynamic stability increases when adding monovalent (in particular Na⁺ and K⁺) and divalent (Mg²⁺) ions (20–23). Mg²⁺ ions are however the most effective for stabilizing the native structure of RNA molecules (22,24).

For compensating negative RNA backbone charges, fewer divalent ions are required compared to the number of monovalent ions. In addition, divalent ions bind stronger and are able to bind several phosphate oxygen atoms at once. Finally, Mg²⁺ is small compared to other divalent ions and can bind to narrow well-defined pockets within RNA structures (13,25–30).

Despite the growing number of experimentally solved RNA structures, the number of structures with well-resolved ion binding sites is still limited (31,32). A non-redundant data set of RNA structures (May 2017) contains in total 1155 structures with a resolution better than 4 Å. Just 37% of the RNA structures, solved by X-ray crystallography include Mg²⁺ and 10% Na⁺ ion positions. Less than one percent of the structures solved by NMR contain Mg²⁺ or Na⁺ ions. An important reason for this is that Mg²⁺ ions, Na⁺ ions, and water molecules have the same number of electrons. Thus, it is difficult to distinguish them from one another in electron density maps alone. They can only be assigned unambiguously in very high-resolution X-ray crystal structures (13,33–35). During the last years special NMR protocols have been developed to be able to study metal ion binding to RNA. However, a special sample preparation is needed to be able to detect Mg²⁺ and Na⁺ ions (36).

Recent studies describe monovalent- and divalent ion binding and the influence of different ions on RNA structures. Molecular dynamics (MD) simulations of have been reported suggesting that many Mg²⁺ ions are strongly associated with RNA, but not directly bound (15). A review by Lipfert et al. (37) describes in detail the difference between direct binding of ions and longer range (‘ion atmosphere’) association to nucleic acids and how this influences structure and stability of RNA and DNA.

In this paper, we apply explicit solvent molecular dynamics simulations on a dataset of twenty-four RNA structures. Therefore, we can compare the implications of applying Na⁺ or Mg²⁺ ions on helical and complex folded structures, solved by either X-ray crystallography or NMR techniques. By combining results from different structures and running simulations in triplicate we can statistically distinguish true effects of ions from stochastic fluctuations inherent to MD simulations. Obviously the findings are still dependent on force field quality and force fields for RNA have not been scrutinized (38) to the same extent as those for proteins (39).

MATERIALS AND METHODS

Dataset of RNA structures

A dataset of 24 RNA structures was selected consisting of twelve helical and twelve complex folded ones, (Table 1) from the Protein Data Bank (PDB, http://www.rcsb.org/pdb/) (40) (Supplementary Figure S1). In both groups six of the twelve structures were obtained by X-ray crystallography and six by NMR experiments. When present in experimental structures, we removed water molecules, ions, or other small molecules to ensure identical starting conditions for all structures in the dataset. In the case of 1D4R (41) we also deleted one separate single RNA strand (chain C) and in 1QC0 (42) the smaller RNA double helix (chain A and B).

Table 1. Dataset of 24 RNA structures, twelve X-ray (six helical and six complex folded) and twelve NMR (six helical and six complex folded) structures, taken from the Protein Data Bank (PDB, http://www.rcsb.org/pdb/) (40). The fraction of single nucleotides (Nuc.) is calculated for each structure. Helical structures that have only base pairs have a fraction of 0.

Method/PDB id	Classification/system	Fraction unpaired	Nuc.	A	C	G	U	Mg2+	K+
X-ray	Helical
1D4R (41)	Single recognition particle RNA	0.04	54	8	18	22	6	4
1QC0 (42)	Plasmid copy control related RNA	0.00	38	6	13	13	6
2QEK (49)	HIV-1 dimerization initiation site	0.04	46	14	12	12	8	1	3
4K31 (43)	rRNA A-site	0.05	44	8	12	14	10
413D (44)	A-form RNA double helix	0.04	26	2	8	8	8
420D (50)	RNA with A(anti)-G(syn) mispairs	0.00	32	10	6	8	8
X-ray	Complex folded
4B5R (51)	SAM-I riboswitch	0.30	94	28	22	32	12
4FEJ (52)	Guanine riboswitch aptamer	0.31	67	16	17	17	17
4FRG (53)	Cobalamin riboswitch aptamer	0.34	84	27	19	22	16	7
4JF2 (54)	Class II preQ1 riboswitch	0.37	76	19	19	18	20	4
4KQY (55)	S-box (SAM-I) riboswitch	0.34	119	40	27	33	19	2
4P5J (56)	tRNA-like structure	0.36	83	17	28	22	16	2
NMR	Helical
1A4D (45)	Loop D/Loop E arm of 5S rRNA	0.07	41	6	10	17	8
2D18 (57)	HIV-1 dimerization initiation site	0.00	34	8	10	12	4
2KYD (58)	A-form RNA double helix	0.00	32	10	6	6	10
2L2J (48)	R/G stem loop RNA	0.10	42	7	13	13	9
2LPS (46)	ai5(gamma) group II intron	0.12	34	8	8	11	7
2LV0 (47)	Stem–loop from 23S rRNA	0.17	24	8	4	6	6
NMR	Complex folded
1YMO (59)	Telomerase RNA pseudoknot	0.36	47	13	13	9	12
2ADT (60)	Tetraloop–receptor complex	0.31	86	22	16	26	22
2LKR (61)	U2/U6 snRNA	0.37	111	29	22	25	35
2MHI (62)	CR4/5 domain of telomerase RNA	0.25	53	7	15	17	14
2MTK (63)	Ribozyme’s III-IV-V junction	0.36	47	7	13	16	11	6
2M8K (64)	Telomerase RNA pseudoknot	0.30	48	12	9	6	21
Total	Average		56	13	14	16	13

We define helical structures as those that form one double helix composed of either one or two nucleotide strands. In these structures, there are only very few unpaired nucleotides present, i.e. single nucleotides at the strand’s ends (1D4R (41), 4K31 (43) and 413D (44)). In the case of one nucleotide strand forming a double helix there are unpaired nucleotides in the loop region (1A4D (45), 2LPS (46), 2LV0 (47) and 2L2J (48)). In two structures, one single nucleotide is sticking out of the helical main structure (2LPS (46) and 2QEK (49)). In contrast to helical RNAs, complex folded RNA structures typically have a more globular shape, are often multi-helical RNAs, and may be categorized as, e.g., ribozymes or pseudoknots.

Ion selection and parameters

MD simulations that intend to mimic cellular conditions should use K⁺ as monovalent ion, since it is the monovalent ion primarily found inside cells. However, we observed formation of salt crystals of K⁺ and Cl^- ions in test simulations (data not shown). The same issue was previously described by other groups (65) when using K⁺ instead of Na⁺ ions. For this reason, we chose Na⁺ as representative for monovalent ions in most of the simulations. Furthermore, we used for Mg²⁺ force field parameters refined by Allner et al. (66), that reproduce Mg²⁺ hydration free energies and exchange rates well.

Although it is known that the identity of the counter-ion matters to the composition of the ion cloud around nucleic acids (67) we have only used Cl^- ions in this work. Furthermore, we note that other cation force field parameters have been proposed for use in conjunction with nucleic acids (68), however rather than comparing many different ion parameter sets we here focus on comparing different RNA structures.

Molecular dynamics simulations

RNA topologies were built using the parm99 (69) force field with the GROMACS simulation package (version 4.6.7) (70). First, an in vacuo minimization was carried out. Then, each structure is placed in a rhombic dodecahedron box filled with TIP3P water molecules to reach a ratio of 550 water molecules/nucleotide. During this step four different systems are created (Supplementary Table S1), either with just counterions (CI) or at physiological salt (PS) concentration:

• Na⁺_CI, just Na⁺ counterions,

• Na⁺_PS, Na⁺ counterions plus 0.15 M/l NaCl,

• Mg²⁺_CI, just Mg²⁺ counterions,

• Mg²⁺_PS, Mg²⁺ counterions plus 0.15 M/l NaCl.

All ions were placed randomly in the simulation box. We monitored that Mg²⁺ ions maintain a specific initial distance (>2 Å to any RNA atom) to the RNA and that direct interactions did not occur during the minimization and first four ns of the equilibration phase.

All systems were minimized once more to eliminate any possible clashes and bad contacts. Subsequently, seven equilibration steps are carried out to provide a careful equilibration protocol. First, an NVT ensemble was conducted for 2 ns using position restraints with a force constant of 1000 kJ/(mol×nm²)) to all heavy atoms. During this step the system was heated up to 300 K. Then, six NPT ensembles are conducted at 1 bar and 300 K for 26 ns in total. The number of restrained RNA atoms and the restraining force constant were gradually reduced while ions were given time to occupy preferred binding sites.

Finally, production runs were carried out for 50 ns at 300 K and 1 bar, with no restraints. An integration step of 2 fs was applied and all bonds were constrained using the LINCS (71,72) algorithm. A cutoff of 10 Å was used for Lennard–Jones and short-range Coulomb interactions and the particle mesh Ewald (PME) method (73) for long-range electrostatic interactions. Velocity rescaling (74) was used for temperature coupling with a time constant of 0.1 ps in order to ensure correct temperature fluctuations. For simulations at constant pressure we used the Parrinello-Rahman pressure coupling algorithm (75) with a time constant of 2 ps.

Each of the four systems was simulated three times in order to ensure statistical significance of our analyses. This resulted in 288 simulations and an overall simulation time of 14.4 μs for all production phases.

Force field evaluations

Since most of our simulations were done using a somewhat old force field, an updated set of force field parameters for nucleic acids was tested, namely parmbsc0 (82) in conjunction with parmOL (83,84) for a subset of four RNA structures. For this subset, we also evaluated the difference between K⁺ and Na⁺ counterions.

RMSD and εRMSD

The root mean square deviation (RMSD) was computed using GROMACS between the in vacuo minimized structure and the snapshots taken every 10 ps during the 50 ns production run (Supplementary Figures S4 and S5). The same was done to obtain the εRMSD values with a method developed by Bottaro et al. (76) (Supplementary Figures S6 and S7). Since each RNA structure was simulated three times in four different ionic conditions the mean and standard deviation of the RMSD values for each replica was determined. The mean RMSD values were subtracted from the individual values for all four systems for each structure. The 18 standardised RMSD/εRMSD values in each system Na⁺_PS and Mg²⁺_PS in all four structure groups were used to determine the p-values using a t-test between system Na⁺_PS and system Mg²⁺_PS. Finally, we calculated mean RMSD values over the three replicas and the error for each structure in each of the four ionic conditions.

Radial distribution functions

The radial distribution functions (RDFs) were determined using GROMACS and trajectories with structures taken every 10 ps of the 50 ns production run. For each of the four systems the RDFs are calculated between each of the RNA base (A-N1, A-N3, A-N6, A-N7, A-N9, G-O6, G-N1, G-N2, G-N3, G-N7, G-N9, C-O2, C-N1, C-N3, C-N4, U-O2, U-O4, U-N1 and U-N3), the two phosphate oxygen (O1P, O2P), or sugar oxygen (O2′, O3′, O4′ and O5′) atoms and positively charged ions (Na⁺ or/and Mg²⁺) present in the system. In all structures, O1P is the atom that points towards the solvent and O2P (particularly in helical structures) towards the minor groove. The average RDFs are calculated for each RNA atom over the 12 helical and 12 complex folded structures.

Free energy of activation

The same RNA atoms and positively charged ions as described in the RDF analysis were used to determine the free energy of activation ΔG^‡ for contact breaking. To specify the contact distance that is required as input parameter between an ion and a certain RNA atom we used the minimum between the first and second maxima from the corresponding RDF values for each structural replica. Similarly, the minimum between the second and third maxima determines the contact distance for second shell contacts. When no peak could be detected within a certain cutoff distance (3.5 or 6.0 Å) the contact distance for this RNA atom was calculated as the average over all minima of all other RNA atoms in this structure.

Ion binding sites in RNA structures

The occupancies of Na⁺ and Mg²⁺ ions in close proximity of RNA structure were computed using the program MobyWat (80,81). Of the seven RNA structures with experimentally determined ion positions, structures were taken every 500 ps from the equilibration phase and every 250 ps from the production phase trajectory. These structures were superimposed to the experimental RNA structure while only considering atoms with <4 Å root mean square fluctuation (RMSF) values. RMSF values are obtained to the RNA structure closest to the average structure of the second half of the production run. The input parameters for MobyWat that differ to the default parameters are the following: the maximum and minimum distance limits were set to 6.0 and 1.0 Å and the clustering tolerance to 1.5 Å. The results are based on the MER clustering algorithm that yield the best results comparing experimental- and predicted ion binding sites. The top 50 predicted ion binding sites were used and RMSD values with respect to the experimental ones calculated for each of them. The predicted ion binding site with the smallest RMSD to an experimental ion binding site was considered as a potential binding site.

RESULTS

Structural changes

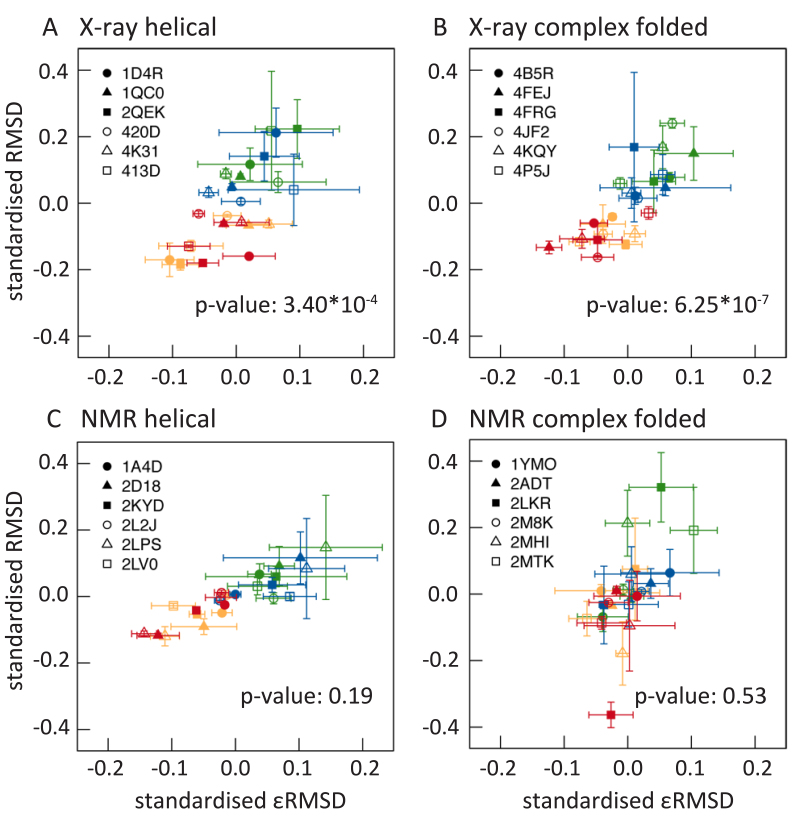
Figure 1 illustrates how the surrounding environment, especially the presence or absence of Mg²⁺ ions, influences RNA structural changes during MD simulations. In agreement with other studies, root mean square deviation (RMSD) values are lower for RNA structures simulated with Mg²⁺ ions than without.

Figure 1.

Standardized mean RMSD (nm) values are plotted against standardized mean εRMSD values for each RNA structure. RMSD and εRMSD values for helical X-ray and NMR as well as for complex folded X-ray and NMR structures are obtained during the production run for each replica and each system. First, an average value is determined over the production run RMSD values for all simulations. Second, a mean value over the three average replica values for each structure and system is calculated resulting in 4 x 24 data points with corresponding standard errors. In a last step, these data points are standardized by the mean over the four data points of each structure for each structure separately. This results in 4 x 24 data points with standard errors for RMSD and εRMSD values, which are plotted against each other. Each RNA structure is represented with a different symbol and the four systems are represented with: Na⁺_CI (green), Na⁺_PS (blue), Mg²⁺_CI (orange), Mg²⁺_PS (red). The p-values are calculated with a t-test between system Na⁺_PS and system Mg²⁺_PS.

In addition to RMSD values, we calculated εRMSD values (76). This metric discriminates effectively between structurally and kinetically different RNA conformations. It directly describes variations in base-base interactions and therefore captures whether or not important structural characteristics, like base pairs, are preserved during the simulation. Bottaro et al. (76) showed that multiple different secondary RNA structures can be found within 4 Å RMSD of each other. Such two RNA structures with low RMSD values to a reference structure do not necessarily have the same secondary structures. Indeed, the base-base interactions could be completely lost in one structure and not in the other. This kind of structural differences is described by εRMSD values that takes structural information about base-pairing into account. An εRMSD of <0.8 indicates all base-base contacts are close to the native experimental structure and an εRMSD of >1 suggests non-native base-base contacts occur in the structure (76). There are more structures with an average (over three replicas) εRMSD >1 for systems simulated without Mg²⁺ than systems simulated with Mg²⁺ ions (Supplementary Table S2). The six complex folded NMR structures have almost always εRMSD values >1 regardless of the surrounding ionic environment, except for one structure (PDB id: 2ADT) and another structure (PDB id: 2MTK), when simulated with Mg²⁺ and NaCl. None of the structures obtained by X-ray crystallography have average εRMSD values >1 when Mg²⁺ ions were present during the simulation. In general, structures simulated with Mg²⁺ ions have lower RMSD and εRMSD values compared to structures simulated without Mg²⁺ ions.

We performed a statistical (kernel density) comparison test that compares the distributions of two-dimensional data points. It returns a p-value that is higher for better fits between the two distributions. Our null hypothesis is that the distributions are independent of whether Mg²⁺ ions are present in the simulations. When thus comparing simulations with a 0.15 M/l NaCl salt concentration with and without Mg²⁺ ions, the P-values for X-ray structures are both less than 0.001 (Figure 1 for individual P-values). This indicates that Mg²⁺ is significantly responsible for maintaining native base-base contacts during the simulations, at least for X-ray RNA structures. The P-values for NMR structures are higher and therefore statistically not significant.

Ion binding

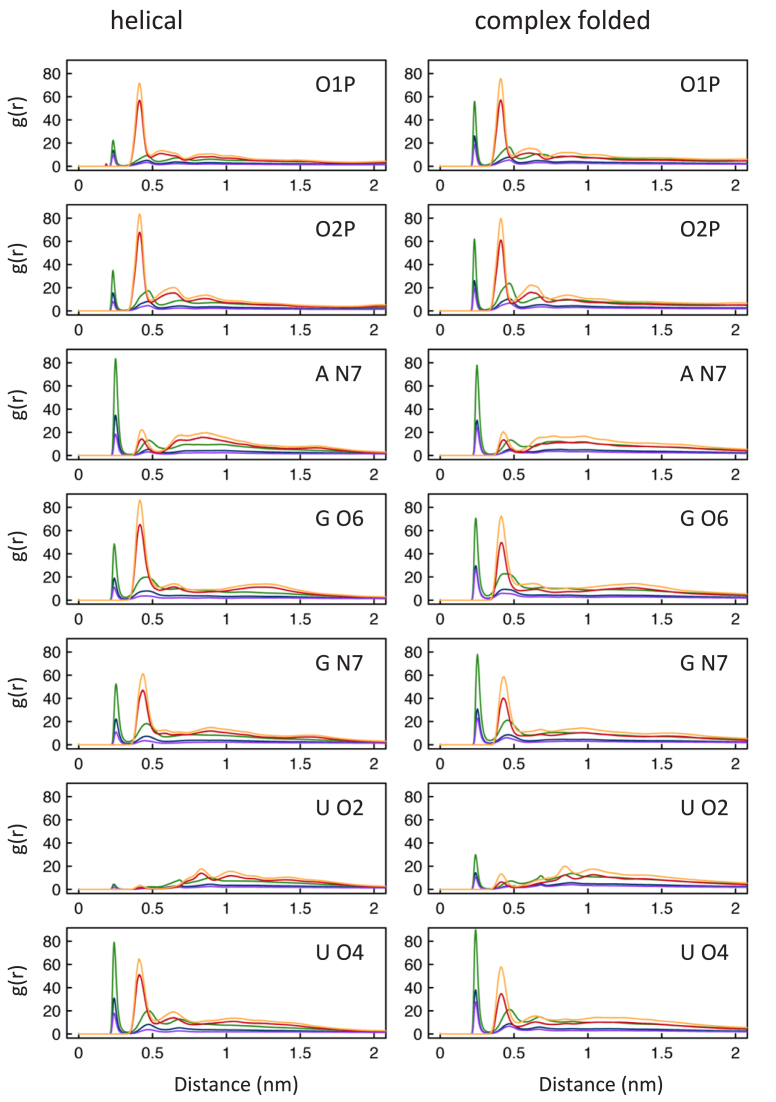
In order to analyze where ions are located during the simulations, radial distribution functions (RDFs) were derived for positively charged ions present during the simulation and all RNA atoms. Direct contacts are identified between Na⁺ and 16 RNA atoms (O1P, O2P, sugar oxygen atoms, A-N1, A-N3, A-N7, G-O6, G-N7, C-O2, C-N3, U-O2 and U-O4). Mg²⁺ ions form direct contacts in the simulations only twice with one of the RNA atoms. In one case Mg²⁺ binds directly to an O1P atom and in another structure to a cytosine oxygen (C-O2). All other Mg²⁺ interactions with RNA occur indirectly via water molecules. Clearly recognisable first and second shell contacts between positively charged ions and RNA atoms can be determined for seven RNA atoms in RDFs (Figure 2).

Figure 2.

Average radial distribution functions (RDFs) for Na⁺ and Mg²⁺ present in the simulations and seven RNA atoms (O1P, O2P, A N7, G O6, G N7, U O2, U O4). The average RDFs for 12 helical and 12 complex folded structures are colored according for each system: Na⁺_CI (green), Na⁺_PS (blue), Mg²⁺_CI (orange) and in system Mg²⁺_PS there are Mg²⁺ (red) and Na⁺ (purple).

The RDF peaks are higher for Na⁺ ions in system Na⁺_CI compared to Na⁺ ions in system Na⁺_PS and Mg²⁺_PS and for Mg²⁺ ions in system Mg²⁺_CI compared to Mg²⁺ ions in system Mg²⁺_PS. In both systems (Na⁺_CI and Mg²⁺_CI) fewer positively charged ions are therefore present in the bulk water surrounding the RNA molecule. We use the same arbitrary definition of bulk water/ions (distance >20 Å to any RNA atom) as described by Hayes et al. (15). In system Mg²⁺_PS when both Na⁺ and Mg²⁺ ions are present more Mg²⁺ ions are found in the bulk solvent than in system Mg²⁺_CI. Nevertheless, fewer Na⁺ ions are found close to the RNA in system Mg²⁺_PS compared to system Na⁺_PS and also system Na⁺_CI. When comparing helical versus complex folded RDFs, fewer Na⁺ ions are in direct contact with helical phosphate oxygen atoms compared to complex folded ones. In both structure groups there is a preference for O2P over O1P for Na⁺ as well as Mg²⁺ ions. For the nitrogen atom in adenine (A-N7) we observe only differences of the RDFs of Na⁺ ions in the second and forth system between helical and complex folded structures. For A-N7 there seems to be a preference for Na⁺ first shell binding compared to Mg²⁺ second shell binding interactions. When comparing Na⁺ direct binding between helical and complex folded structures for both favoured guanine atoms (G-O6 and G-N7), there are more occurrences in complex folded structures with a slight preference for G N7. This is in contrast to second shell Mg²⁺ interactions, where G-O6 is the preferred atom. The peak for helical G-O6 atoms and Mg²⁺ ions in system Mg²⁺_PS is the highest determined for all RDFs. For U-O2 atoms very few ion contacts were found, and most of them are found in complex folded structures. Since helical structures mostly form Watson-Crick base pairs U-O2 atoms lie in the minor groove and it is likely therefore they not easily accessible to ions (Figure2). The other uracil oxygen atom (U-O4) is slightly preferred by Na⁺ ions in first shell interactions in complex folded structures and by Mg²⁺ ions in second shell binding for helical structures.

Ion binding energetics

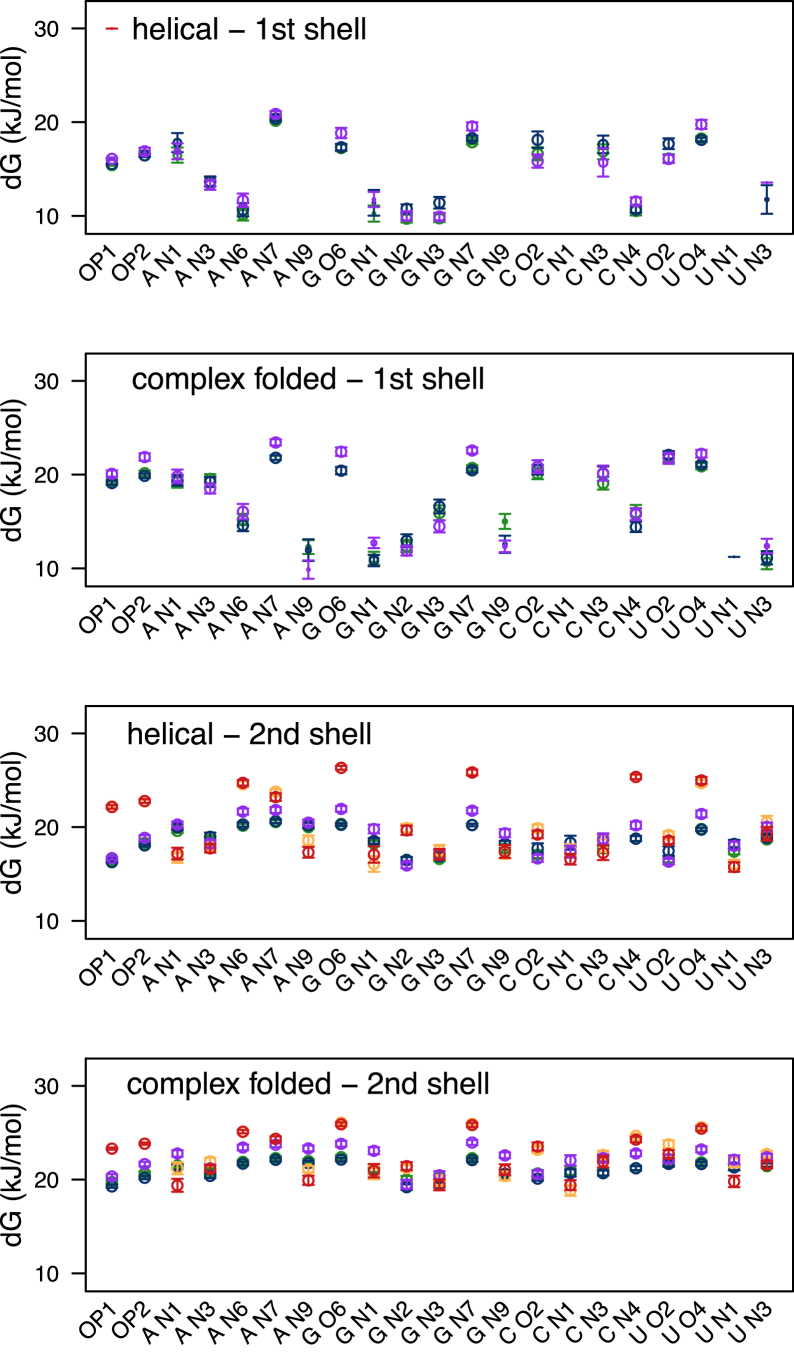
An analysis method that was developed to study kinetics of hydrogen bond breaking and forming (77) and thermodynamics of hydrogen bond breaking in different environments (78) was used here for studying ion-binding energetics. This method yields the Gibbs energy of activation ΔG^‡ for contact breaking and was previously applied on RNA-ion contacts in a study of viral RNA (79). The highest energy for breaking first shell contacts was found between one phosphate oxygen atom (O1P) and a Mg²⁺ ion (Figure 3). This is the result of one of the two direct interactions between a Mg²⁺ ion and an RNA atom that occurred in the simulations, as also observed in the RDF analysis. The energy of first shell contacts between Na⁺ ions and RNA phosphate oxygen atoms (O1P and O2P) is not as high compared to other RNA atoms (A-N7, G-O6, G-N7, C-O2, C-N3, U-O2 and U-O4). These results differ from the RDF results insofar that the RDF peaks for C-O2, C-N3, and U-O2 atoms are very low especially compared to the peaks of phosphate oxygen atoms. The main difference between helical and complex folded first shell contacts is for atoms that are only available for interactions in complex folded structures (A-N3, A-N9, G-N9, U-N1). A-N3 lies in the minor groove in helical structures and the other atoms are the base atoms that are closest to the sugar ring. Therefore, they are not easily accessible to ions in helical RNA structures.

Figure 3.

Gibbs energy of activation for contact breaking between RNA atoms and ions. The average energy values for 12 helical (A, C) and 12 complex folded (B, D) structures are determined for first shell interactions (direct bonds, A, B) and second shell interactions (C, D). Second shell energies are the sum of first and second shell interactions. The colors represent the corresponding ion in each of the four systems: Na⁺_CI (green), Na⁺_PS (blue), Mg²⁺_CI (orange) and in system Mg²⁺_PS Mg²⁺ (red) and Na⁺ (purple).

Ion binding positions

To investigate whether Mg²⁺ ions find experimentally identified binding sites, when initially placed randomly in the solvent (with a distance >2 Å to any RNA atom), we determined the occupancy of Na⁺ and Mg²⁺ ions during the simulation using the software MobyWat (80,81).

Figure 4 shows the top 10 predicted binding sites for Mg²⁺ and Na⁺ ions for one of the three replicas of each system during the equilibration phase superimposed on the X-ray structure of 2QEK (49). We chose 2QEK as example structure, because both monovalent (K⁺) and divalent (Mg²⁺) ions are present in this structure. When only Na⁺ ions are present in the simulation both K⁺ and Mg²⁺ binding sites are occupied (Figure 4A and B). This can also be observed for other structures (Table 2). In some cases it seems as if the binding site can be occupied by both Na⁺ and Mg²⁺ ions. Mg²⁺ binding sites are more difficult to predict with MD simulations since the hydration layer around Mg²⁺ ions is almost never dismantled. When only Mg²⁺ are present in the simulation, ions are closer to RNA atoms compared to when both Mg²⁺ and Na⁺ are present. The closest distance between experimentally predicted Mg²⁺ binding sites and those observed in our simulation is 1-2 Å. Overall, Mg²⁺ binding sites are predicted better than K⁺ binding sites. This indicates a preference of Mg²⁺ ions to experimentally predicted Mg²⁺ ion binding sites. When both, Na⁺ and Mg²⁺ ions are present in the simulations the distances to experimentally predicted binding sites are higher compared to other systems. This is surprising since it does not correlate with lower RMSD or εRMSD values for those structures. It indicates that although specific ion positions are not found during MD simulations the overall structure maintains a native-like fold, potentially due to there being a ‘sufficient’ amount of screening of electrostatic interactions. In general we observe Mg²⁺ ions present along the minor groove of the RNA and in some specific binding sites.

Figure 4.

Experimental and predicted ion binding sites. The helical structure (PDB id: 2QEK) has one Mg²⁺ (solid green) and three K⁺ (solid purple) binding sites. During the equilibration phase we observe Mg²⁺ and Na⁺ in close proximity to the experimentally predicted binding sites. The RMSD between experimental and predicted binding sites are given in Å. The 10 top ranked ion binding sites predicted with MobyWat for one replica for each of the four systems is shown: (A) Na⁺_CI (green), (B) Na⁺_PS (blue), (C) Mg²⁺_CI (orange), (D) in Mg²⁺_PS there are Mg²⁺ (red) and Na⁺ (purple).

Table 2. Average RMSD values between experimental and predicted binding sites during the production phase. The position of ions are predicted with MobyWat (80,81). The resulting top 50 ion positions are considered for each replica.

System	Na+CI	Na+PS	Mg2+CI	Mg2+PS
Ion	Na+	Na+	Mg2+	Na+	Mg2+
1D4R
MG-90	2.8±1.7	2.4±1.0	1.0±0.5	4.2±1.2	1.1±0.5
MG-91	6.0±1.0	6.9±2.1	5.0±0.7	5.6±1.5	4.4±0.7
2MTK
MG-48*	7.5±0.9	7.7±0.8	7.4±3.2	8.1±4.0	5.8±1.9
MG-49	5.2±1.2	4.3±1.2	3.9±0.9	5.6±3.0	2.9±1.6
MG-50	4.2±1.0	4.6±1.7	6.7±3.0	4.7±1.4	5.7±2.3
MG-51	2.6±0.7	1.7±1.0	3.2±0.8	3.9±1.3	3.5±0.4
MG-52	5.9±0.4	4.1±1.3	3.6±0.5	3.9±2.5	3.8±2.4
MG-53	3.3±1.2	3.1±1.5	2.1±0.4	3.2±0.5	2.3±1.1
2QEK
K-47	3.3±1.2	2.7±0.3	2.1±0.6	2.8±2.4	1.8±0.5
K-48	3.3±0.7	3.4±0.5	3.4±0.1	3.7±2.4	5.2±2.4
MG-49	3.6±0.6	2.4±1.1	2.5±0.2	2.9±0.8	2.5±1.3
K-50	1.6±0.7	2.1±0.6	2.0±0.7	4.4±3.7	2.5±0.4
4FRG
MG-179	2.2±0.8	2.2±0.3	2.4±0.7	1.6±0.2	4.4±0.8
MG-180	1.5±0.5	1.4±0.2	2.4±0.8	1.7±0.2	5.3±0.4
MG-181	2.5±1.0	4.2±2.8	2.8±0.5	8.5±0.8	1.4±0.5
MG-182*	8.0±0.6	9.1±2.3	7.6±0.5	11.5±3.6	7.0±0.6
MG-183	5.7±1.2	4.7±1.2	3.7±1.5	3.5±1.7	4.7±2.9
MG-184	1.5±0.6	1.6±0.6	1.1±0.3	3.5±1.4	2.0±1.5
MG-185	3.2±1.3	3.4±0.7	3.7±1.3	2.1±0.3	5.9±1.4
4JF2
MG-94	1.4±0.7	1.5±0.4	2.2±1.1	2.5±1.7	2.7±1.0
MG-95*	7.0±0.7	6.5±1.8	3.2±0.6	4.7±1.8	4.6±0.7
MG-96	1.8±0.1	1.6±0.8	2.5±0.8	2.6±0.3	2.9±0.9
MG-97*	26.6±7.7	31.1±6.3	18.3±2.7	24.9±6.1	20.6±0.8
4KQY
MG-121	1.8±0.5	1.6±0.7	1.8±0.4	0.8±0.6	3.4±0.9
MG-122*	3.4±1.9	5.0±0.4	1.8±0.5	8.4±2.3	4.2±2.0
4P5J
MG-85	2.3±0.4	2.9±0.6	1.1±0.7	3.1±1.4	1.8±0.2
MG-86	2.2±0.4	2.5±0.2	2.5±0.5	5.3±3.2	3.5±2.1

The predicted binding sites are in good agreement with experimentally identified ion locations in close proximity to the RNA (Table 2). There are some cases for which the experimental binding site was not detected, however, in particular for ions directly bound to RNA. This is expected, due to the high barrier for desolvation of Mg^{2 +} ions (66). Most of these sites are located at the surface of the RNA and only one RNA atom can be identified as potential contact site in experimentally predicted structures. For this reason RMSD values to the experimental binding sites are marked with an asterisk in Table 2 for these ions.

DISCUSSION

The structural analyses indicate (at least in X-ray structures and most NMR structures) that Mg²⁺ ions have a stronger stabilizing effect for helical structures than for complex folded structures (Figure 1). Although εRMSD values of complex folded structures, when simulated with and without Mg²⁺ ions are comparable, they are in general high (above 1), indicating that these structures do not maintain their native fold (76). This might be due to the fact that the quality of complex folded NMR structures is not as good as that of X-ray structures (Supplementary Table S1), for instance because structures that are inherently more flexible and difficult to solve by X-ray crystallography instead are solved by NMR techniques. Especially, the RNA backbone seems not to be as well defined for NMR structures based on the validation results of X-ray and NMR structures (Supplementary Table S1).

It has been reported (38) that helical RNA structures undergo irreversible structural changes in longer MD simulations (over 50 ns) when using parm99 and parmbsc0 (82). They change into a ladder–like structure, similar to what we observe in the majority of helical RNA structures with high RMSD values. The reason for this is that the glycoside torsion angle χ is shifted from the anti to the high-anti region. A specific force field parameter set, called parmOL (83,84), has been developed to eliminate this artifact. Since we did not use these parameters for most of the simulation, the correct backbone angle of some helical RNA structures was not maintained in this work. We did, however, use the combination of parmOL (83,84) and parmbcs0 (82) parameters specifically developed for RNA, for a subset of our structures. These structures undergo less structural changes and have lower RMSD and εRMSD values compared to structures that were simulated with the same ion conditions (Supplementary Figure S2). However, our observation that Mg²⁺ results in more stable simulations still holds. The comparison between Na⁺ and K⁺ as a counterion (Supplementary Figures S2 versus S3 and Supplementary Figures S8–S11) suggest potassium stabilizes the structures somewhat more than does sodium.

Both Na⁺ and Mg²⁺ ions bind sequence specific and also to specific binding sites (Figure 4). In both helical and complex folded structures certain RNA atoms are preferred. In complex folded structures atoms are available for binding that are not sterically accessible for ions in helical RNA structures. For example, one of the oxygen atom in uracil (U-O2) is hidden in the minor groove of a helical RNA with classical Watson-Crick base pair interactions. In complex folded structures we find this atom to be more accessible to ions (Figure 2), consistent with findings reported by Kirmizialtin et al. (18). We think it is appropriate to distinguish between adenine and guanine N7 atoms unlike what was done in previous studies (15,18). Doing so reveals that more ions are close to the guanine N7 atom than can be explained based just on accessibility and indeed the distributions are quantitatively different for both atoms (Figure 2).

At low ion concentrations a larger fraction of the Na⁺ and Mg²⁺ ions are in direct contacts with the RNA in our simulations than at higher concentrations (2). When, however, both Na⁺ and Mg²⁺ ions are present, more Mg²⁺ ions are closer to the RNA (distance less than 10 Å) than Na⁺. This is in agreement with the ‘ion atmosphere’ as described by Lipfert et al. (37). It seems therefore that the overall salt concentration should be factored in when considering the properties of the ‘ion atmosphere’.

Zheng et al. (13) investigated Mg²⁺ ion binding sites experimentally, in particular the difference between first and second shell binding frequencies. Since we only observe two direct contacts for Mg²⁺ ions in our simulations we cannot compare our simulations with the first shell contact frequencies derived in that work (13). The main reason for this is that it is very difficult to replace the hydration shell around Mg²⁺ by direct contacts during explicit MD simulations (66). Although refined Mg²⁺ ion parameters (64) were used, the activation energy remains slightly higher and the ion–water exchange rate faster than experimental values (66,85).

When we compare our Gibbs activation energies for second shell dissociation/binding of Mg²⁺ ions (Figure 3) to the experimental frequencies reported in (13) we see a preference for the same RNA atoms. The calculations fit the results by Zheng et al. (13) remarkably well. The RNA atoms with the highest experimental frequencies are (starting from the highest): G-O6, G-N7, O2P, U-O4, A-N7, O1P and A-N6 (13). For helical structures the RNA atoms with highest ΔG‡ are for system Mg²⁺_PS (starting from the highest): G-O6, G-N7, C-N4, U-O4, A-N6, A-N7, O2P, and O1P. For complex folded structures for system Mg²⁺_PS (starting from the highest): G-O6, G-N7, U-O4, A-N6, A-N7, C-N4, O2P, U-O2 and O1P. For helical structures the RNA atoms with highest free energies of activation ΔG‡ are for system Mg²⁺_CI (starting from the highest): G-O6, G-N7, C-N4, U-O4, A-N6, A-N7, O2P and O1P. For complex folded structures for system Mg²⁺_CI (starting from the highest): G-O6, G-N7, U-O4, A-N6, A-N7, C-N4, O2P, C-O2 and O1P. Although the activation energy is higher for O2P than O1P it seems to be underestimated in all simulations compared to the energies calculated for other RNA atoms. The main difference between helical and complex folded structures is that in helical ones the activation energy is higher for C-N4. When we compare the activation energy of the Mg²⁺ ion directly in contact with O1P (30.0 kJ/mol) to experimentally predicted activation energies ΔG‡ between Mg²⁺ ions and DNA (53.1–55.7 kJ/mol) (85) it is quantitatively underestimated.

After the equilibration phase we could reproduce all experimentally predicted ion binding sites with good accuracy (Table 2, Figure 4). Especially when Na⁺ or Mg²⁺ ions are present (system Na⁺_PS and Mg²⁺_PS) without any additional salt concentration the binding sites are reproduced well using the MobyWat (80,81) analysis (Supplementary Table S3). The reason for this is likely that in simulations at low ionic strength the ions are found in close proximity to the RNA. We find, however, that the occupancy of the experimental ion binding sites calculated from the simulation is not reproduced with the same accuracy as the positions. A similar study focused on ion-binding to helical DNA was able to reproduce experimental ion-counts quantitatively (86), possibly because of improved cation force field parameters (67).

An interesting study by Lemkul et al. (87) applied grand-canonical Monte Carlo-MD (GCMC-MD) in order to predict ion-binding for four different RNA molecules. Although this approach most likely is more suited to find first shell binding locations than the MD approach we used, the use of pure MD allows to deduce time-dependent properties such as ΔG‡ for contact breaking (Figure3). A combination of the two techniques, prediction using GCMC-MD followed by regular MD would therefore yield a more complete picture of binding thermodynamics and kinetics. Nevertheless it seems the quality of binding site predictions is similar in both methods. Ion binding site prediction is inherently difficult for these systems with long exchange times. It is likely as well that ion binding sites are missed by any structural analysis since ion-binding and conformational flexibility are interdependent. In fact, it is remarkable that Mg²⁺ ions are predicted so close to experimental binding sites in normal simulation, while they maintain their hydration shell.

In comparison to previous studies our dataset contains a large number (24) of structures yielding rigorous results. Binding site positions and kinetics can be studied, and the relative influence of different ions studied. Based on our results (e.g. Figure 1) there is no justification for using Na⁺ ions rather than Mg²⁺ ions in RNA simulations, unless, as in this work, the purpose of the study is to investigate the difference in RNA properties due to the ‘ion atomosphere’ (37). Further improvement of force fields for RNA, water and ions remain needed to describe the complex energy landscape formed by these flexible biomolecules.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.

FUNDING

Swedish research council [2013-5947 to D.S.]; eSSENCE e-Science collaboration [to N.M.F]; Coordination for the Improvement of Higher Education Personnel (CAPES) [to M.D.P.]; Swedish National Infrastructure for Computing (SNIC) at PDC Centre for High Performance Computing (PDC-HPC) [SNIC2016/34-44]. Funding for open access charge: Vetenskapsrådet, [2013-5947]; faculty funding.

Conflict of interest statement. None declared.