Promoting Vibrations and the Function of Enzymes. Emerging Theoretical and Experimental Convergence

Abstract

A complete understanding of enzyme catalysis requires knowledge of both transition state features and the detailed motions of atoms that cause reactant molecules to form and traverse the transition state. The seeming intractability of the problem arises from the femtosecond lifetime of chemical transition states, preventing most experimental access. Computational chemistry is admirably suited to short time scale analysis but can be misled by inappropriate starting points or by biased assumptions. Kinetic isotope effects provide an experimental approach to transition state structure and a method for obtaining transition state analogues but, alone, do not inform how that transition state is reached. Enzyme structures with transition state analogues provide computational starting points near the transition state geometry. These well-conditioned starting points, combined with the unbiased computational method of transition path sampling, provide realistic atomistic motions involved in transition state formation and passage. In many, but not all, enzymatic systems, femtosecond local protein motions near the catalytic site are linked to transition state formation. These motions are not inherently revealed by most approaches of transition state theory, because transition state theory replaces dynamics with the statistics of the transition state. Experimental and theoretical convergence of the link between local catalytic site vibrational modes and catalysis comes from heavy atom (“Born–Oppenheimer”) enzymes. Fully labeled and catalytic site local heavy atom labels perturb the probability of finding enzymatic transition states in ways that can be analyzed and predicted by transition path sampling. Recent applications of these experimental and computational approaches reveal how subpicosecond local catalytic site protein modes play important roles in creating the transition state.

Graphical abstract

An area of continued debate within biochemistry is how protein dynamics is involved in enzyme function distinct from the obvious need for movement to allow binding of substrates and release of products. This dialogue is central to biochemistry because it adds mechanistic understanding to the standard view that transition state stabilization is the motive force of enzymatic catalysis. Catalytic mechanism in turn informs artificial enzyme creation, because if the standard view is correct, creating an active site architecture complementary to a transition state should suffice. The field of catalytic antibodies was built on this hypothesis, and the lack of efficient catalysts from this field can at least partially be attributed to the inability of these complementary molecules to recapitulate the dynamic features that have evolved in enzymes.^1,2

We have developed new approaches to study and describe the mechanistic contribution of fast (femtosecond to picosecond) dynamics to passage over the chemical barrier. The purpose of this work is to combine unbiased, rigorous computation [within the approximation of approximate quantum mechanics and quantum mechanics/molecular mechanics (QM/MM) approaches] and rigorous experimental study. This review summarizes aspects of our work and places it within the context of different views of the same question: “How do enzymes work?” The scientific debate surrounding this question makes it a question of intellectual interest. The details of enzymatic mechanism also have currency if we are to accelerate progress on the vexing problem of artificial biocatalyst design. A demonstration that dynamics is a central design feature of enzymatic catalysis requires that design methodologies incorporate dynamic contributions to catalytic efficiency as an “engineering principle”. This review will focus mainly on our own contributions to this area, but we also put our work in the context of some of the other views of this same question. We hope this survey will be insightful, rather than providing a complete review of the field.

This review begins with recent work and follows with the background origins. As “no one reads anymore”, a modern reader may first survey recent evidence for the involvement of rapid protein dynamics in enzyme catalysis. We provide examples where theory and experiment are interdigitated to provide both clarity and validation of the other. This section will be followed by foundational work where our coupled experimental and theoretical methods were developed. We show the origins for concepts that led to the proposal of promoting vibrations in enzymes. And we explicitly develop the connections to solution phase chemistry. This will involve a description of the development of Transition Path Sampling and Reaction Coordinate identification along with the development of the “heavy enzyme” or Born–Oppenheimer enzyme technology. Finally, while not a review of the broader field we conclude with discussion of how these concepts fit with other views of enzymatic catalysis.

PROMOTING VIBRATIONS IN ENZYMES: RECENT THEORETICAL AND EXPERIMENTAL EVIDENCE

The deceptively simple question of how enzymes work still elicits controversy at the atomistic level. In particular, the question of whether there is a connection between fast enzyme dynamics and enzyme catalysis remains contentious. It has been suggested that this disagreement is due to semantics,³ but these questions deserve new experimental evidence and thoughtful inquiry. The question of what is catalytic and what is not^4,5 is also a question of philosophical significance, but not scientific significance if there are effects that can be readily identified as central to enzyme function. The central question of significance is a temporal, atomistic description of how enzymes promote chemistry; in other words, what are the atomic level mechanisms that cause the extraordinary lowering of free energy barriers in biochemical reactions? We emphasize that statements such as “enzymes work by lowering free energy barriers” and matching barrier heights are inadequate to provide atomistic, temporal mechanistic insight. Energetic analysis reiterates the obvious that enzymes work by making the rate of chemical reactions increase. This is a practical question. If we understand how naturally occurring enzymes manage to accelerate reactions by as much as 15 orders of magnitude in relative rate, we gain mechanistic knowledge that can be extrapolated to protein engineering principles in the design or artificial enzymes. Although major effort has been expended on artificial enzyme design, rate enhancement has proven to be modest except in a few rare cases.^5,6

The chemical step defines catalytic mechanism, and our focus is on the rapid protein dynamics involved in transition state barrier crossing. We have termed such motions promoting vibrations.⁷ These are motions within the protein body of an enzyme that are part of the reaction coordinate, both necessary and sufficient for reaction to occur. While there is no specific definition based on time scale, the definition is based on necessary inclusion of such motions in a reaction coordinate using methods to be described below. In many of the cases we have investigated, such motions occur on the 100–200 cm⁻¹ time scale, which corresponds to approximately 100–300 fs vibrational periods. These motions are slower than a single bond vibration, but far faster than large conformational changes or the turnover rate of an enzyme. Most enzymes exhibit catalytic turnover times on the millisecond time scale. Other investigators^8–12 have discussed networks of coupled or promoting motions related to statistically identified motions on the millisecond time scale. Our definition is distinct and is in the range of hundreds of femtoseconds.

The combination of transition path sampling and experimental enzyme dynamics is focused on identifying motions directly coupled to the chemical step(s) of transition state barrier passage. Another way to describe this is identification the “reaction coordinate” of the enzymatic system. This is the set of all atomic motions that is necessary and sufficient for reaction to occur. From the theoretical standpoint, this has involved the application of a method known as transition path sampling or TPS.^13–18 This approach is part of the theory of enhanced sampling techniques, first developed in David Chandler’s group. It has since been modified and used in investigations of enzymatic reactions (e.g., refs ^19–23). Details of the method are provided below. The basic idea is that barrier passage in an enzymatic reaction is fast, on the time scale of single bond vibrations, while turnover of an enzyme is many orders of magnitude slower. Thus, the chemical step at the transition state is en face a rare event on the time scale of enzyme turnover. An important question to answer is how motions so many orders of magnitude faster than the statistical rate of turnover can possibly influence the reaction. Focus on the transition state places the enzyme in the context of how are related to biological function and regulation.

PROMOTING VIBRATIONS IN PURINE NUCLEOSIDASE PHOSPHORYLASE (PNP)

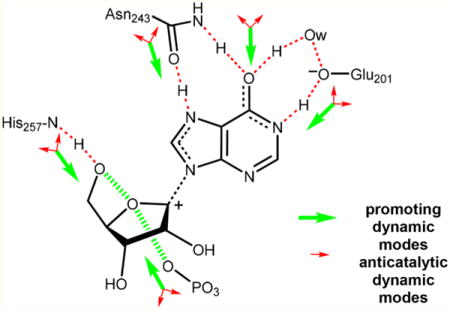
The reaction catalyzed by purine nucleoside phosphorylase provides a biochemical example for exploring promoting vibrations. The chemical reaction causes inversion of stereochemistry, formally a nucleophilic attack by the phosphate moiety concerted with glycosidic bond scission (Figure 1). Experiments and computation agree that the glycosidic bond cleavage occurs before formation of the bond to the phosphate group.^24,25 Compression of the ribosyl O4′ and O5′ atoms of the substrate by His257 at the active site weakens the scissile N- ribosyl bond. Interactions with Asn243 and Glu201 neutralize the purine leaving group leading to transition state formation. The compression of reactive site oxygen atoms by the active site residues is an integral part of the reaction coordinate. The reaction coordinate is simply the set of all atomic motions that are both necessary and sufficient for chemistry to occur. This mechanistic picture extends the reaction coordinate beyond the atoms directly involved in bond formation and breaking. A focus on only the bond breaking and forming atoms is likely to give an incomplete picture if, for example, only these are used in umbrella sampling free energy calculations.^17–22 Numerous reports of umbrella sampling calculations yield free energies remarkably close to the experimentally measured values for the overall rates of catalysis for specific enzymes. This is surprising, given that a majority of experimental free energy values are not for the chemical step, but for slower steps, including product release rates. The ability of such calculations to reproduce experiment may reflect biased parameter selections to coordinate the energies.

Figure 1.

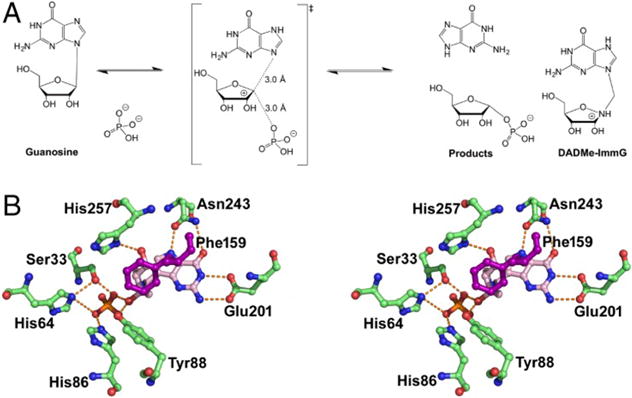
Phosphorolysis of guanosine by purine nucleoside phosphorylase (PNP) (A), its transition state analogue (DADMe-ImmG), and the catalytic site environment stereoview for DADMe-ImmG and phosphate in human PNP (B). In the PNP homotrimer, all amino acid contacts except Phe159 are from the parental subunit. Phe159 is from the adjacent subunit. Reprinted with permission from ref ³³. Copyright 2017 National Academy of Sciences.

COORDINATION OF UNBIASED TRANSITION PATH SAMPLING AND HEAVY ENZYME EXPERIMENTS WITH HUMAN PNP

Transition path sampling (detailed below) provides an unbiased approach to understanding the ensemble motions associated with the chemical step.^13–18 The approach comes with the caveat that quantum mechanical models (in our case semiempirical) and all QM/MM models are inherently approximate; we do not solve the Schrodinger equation exactly for thousands of atoms. However, these improved mechanistic predictions for barrier crossing provide a guide for developing experimental tools to allow interrogation of the promoting vibration. The original idea of the Born–Oppenheimer or heavy enzyme is to affect the frequency of fast atomic motions in the enzymatic system without affecting the potential energy surface that controls chemistry.^26,27 Changing the mass of heavy atoms and all exchangeable hydrogens alters the vibrational frequencies without altering the potentials within the limits of the Born–Oppenheimer assumption.

In critical investigations with human PNP, it was demonstrated that the altered nuclear mass had no effect on slow protein motions that would affect steady state system parameters, including K_m and k_cat. A full analysis of transition state structure by substrate kinetic isotope effect analysis (KIEs) also indicated that the transition state structure was unchanged.²⁶ The conclusion was that changes in molecular mass have no effects on properties that would inform on slow protein rearrangements such as reactant binding and product dissociation, nor do they alter the ability of the protein atoms to form the same transition state that is found in the parent enzyme.

Effects of the mass change in the protein are seen onlywhen the chemical step is isolated from steady state parameters by pre-steady state and substrate trapping (forward commitment) experiments. In the PNP case, the heavy enzyme was found to decrease the rate of the chemical step on the enzyme by 30%. Suggestions that the non-Born–Oppenheimer properties of deuterium in CD versus CH bonds could explain the slowed chemical step³ were experimentally disproven in subsequent work in which the effects of ²H were separated from those of ¹³C and ¹⁵N and found to be mass-proportional.²⁸ A transition path sampling analysis of these heavy enzyme effects revealed that the only change in dynamics in the transition path ensemble was a mistiming of the critical compressions between the enzyme and reactants.²⁹ The mistiming of multidimensional, mass-dependent interactions to form the transition state results in a decreased probability of locating the transition state by mass-altered promoting vibrations. This picture is similar to a classic picture of reduced transition state stabilization. However, rather than a static picture, the stabilization is created by the coincident motions within the protein, perturbed by altered mass.

MUTATIONAL EXPLORATION OF HEAVY ENZYME COUPLING IN HUMAN PNP

The predictive power of the TPS methodology and reaction coordinate analysis was tested by exploring second-sphere mutations surrounding the catalytic site of PNP. The hypothesis to be tested was that the naturally evolved protein structure of PNP, including promoting vibrational interactions between protein and the catalytic site, could be uncoupled by a small increase in the size of the catalytic site pocket caused by second-sphere mutations. Two methylene groups were deleted in the second sphere of amino acids surrounding the catalytic site by Glu258Asp and Leu261Ala mutations. The size of the catalytic site increased without altering the primary contacts between the enzyme and reactants as indicated by crystallographic analysis (Figure 2). TPS indicated that the coupling of promoting vibrations between the protein and the reactants at the catalytic site of PNP would be altered by this mutation. Heavy atom PNP of the same construct was used to test if the promoting vibrations were uncoupled in the mutant PNP.

Figure 2.

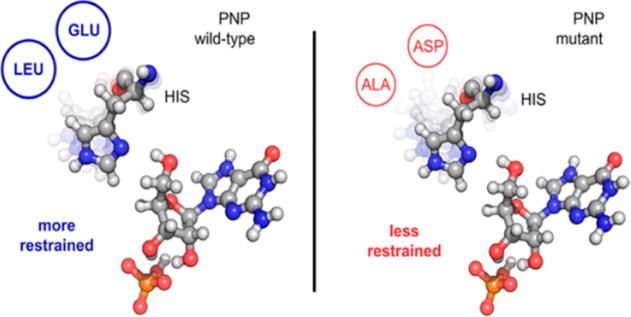
Expanding the catalytic site of PNP by Glu258Asp and Leu261Ala second-sphere mutations. Adapted ref ³⁰. Copyright 2016 American Chemical Society.

Introduction of the two mutations caused a 2-fold reduction in the steady state k_cat, for both the heavy and light mutated PNPs. The rate-limiting step in human PNPs is product release; thus, the protein architecture involved in product release is reduced slightly. In contrast, the chemical step (k_chem) for the mutant proteins was reduced by 100-fold. The k_chem values for heavy and light enzymes were the same. This means that enlargement of the catalytic site by two methylene groups uncouples the heavy enzyme (promoting vibration) effect.³⁰

Coupling of fast protein motions to the transition state is not a universal requirement for catalysis. Thus, in Escherichia coli dihydrofolate reductase (DHFR), both computational analysis by TPS and experimental probing by heavy enzyme analysis agree that finding the transition state is not coupled to fast, mass-sensitive protein motions.^31,32 In human PNP, the expansion of the catalytic site volume converts a promoting vibration mechanism into a protein mass-insensitive mechanism.

CREATING A FAST HEAVY PNP, AN INVERSE HEAVY ENZYME KIE

Can we predict mutations in human PNP to create a heavy enzyme with dynamic properties more favorable for locating the transition state than the same enzyme at natural isotope abundance? This would create a rare inverse heavy enzyme isotope effect with the chemical step being faster in the heavy enzyme. Systematic computational analysis by TPS searched for mutations that “improve” dynamic interactions along a reaction coordinate as a result of heavy isotope substitution in the enzyme. In native PNP, the heavy atom substitution desynchronizes the motion of specific residues involved in transition state formation. Here, the search was for substitutions to improve motions favoring barrier crossing. Testing this hypothesis further explores the promoting vibration proposal and the predictive power of TPS.

Transition path sampling was used to explore individual second-sphere mutations near the catalytic site of human PNP. Two parameters for linking promoting vibrations to the frequency of transition state formation were considered, His257, the residue creating the promoting vibrations between O4′ and O5′ of the ribosyl group, and Asn243, a leaving group interaction by virtue of its hydrogen bond interaction with the guanine leaving group. We screened mutations near the catalytic site and monitored the O4′–O5′ and Asn243 distances and conformational probabilities over a 500 fs dynamic window that includes the transition state. Analysis of the bond breaking minus bond forming distance (BB – BF) provided a guide to the effects of heavy atom substitution and of the selected catalytic site mutation, viz., Phe159Tyr (F159Y) (Figure 3). Dynamic distribution maps indicated the most likely paths of reaction according to the O4′–O5′ dynamic parameter (Figure 4).³³

Figure 3.

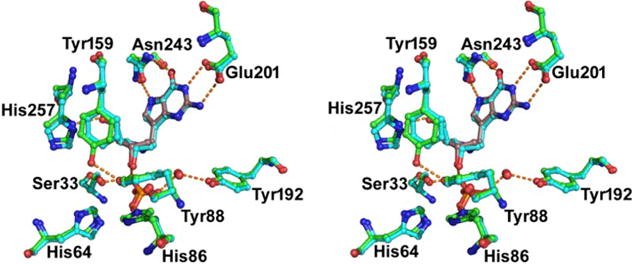
Transition path sampling calculations predicted an inverse heavy enzyme isotope effect via conversion of human PNP to Phe159Tyr PNP. The crystal structure contacts with bound DADMe-ImmG and phosphate are shown in stereoview. Adapted from ref ³³. Copyright 2017 National Academy of Sciences.

Figure 4.

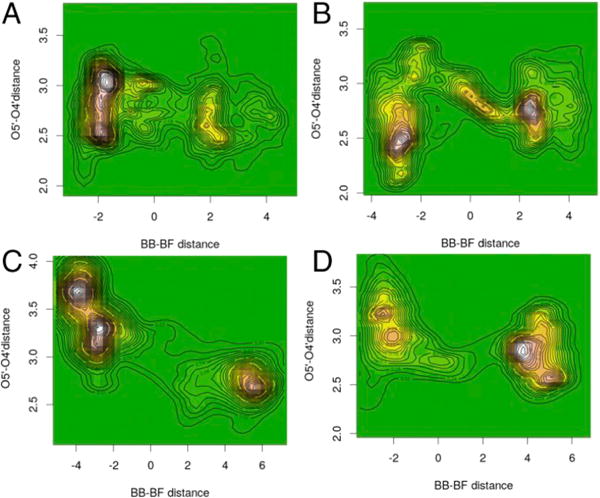
Structures in the reaction coordinate (500 fs) for native light (A), native heavy (B), F159Y light (C), and F159Y heavy (D) PNPs from the perspective of the O5′–O4′ distance. Negative values of BB – BF are reactant states, and positive values of BB – BF are product states. Transition states are near zero on the abscissa scale. Contour lines join points with equal population densities. Adapted from ref ³³. Copyright 2017 National Academy of Sciences.

Isotope labeling (²H, ¹³C, ¹⁵N) of native PNP alters the population and distribution of the reactant states and decreases the probability of reaching the transition state (Figure 4A,B). A shorter O4′–O5′ distance at the transition state correlates with faster chemistry as the formation of the ribocationic transition state is more favored. For the light and heavy native PNPs, the distances are 2.56 and 2.94 Å, respectively, making the heavy enzyme slower. By contrast, light and heavy F159Y PNPs show these distances to be 3.02 and 2.60 Å, respectively, at the transition states, favoring transition state formation for the heavy F159Y. Similar analyses of the interaction of Asn243 with the guanine leaving group at the transition state indicated a more favorable interaction in heavy F159Y PNP (2.82 Å) than in light F159Y PNP (3.8 Å).³³ These analyses led to the production and experimental kinetic analysis of the light and heavy F159Y PNPs.

Analysis of the heavy and light F159Y PNPs gave results consistent with the TPS analysis. The normal heavy enzyme isotope effect for native PNP was 1.31 (k_{chem light}/k_{chem heavy}), while the same analysis for the F159Y enzyme gave a value of 0.75 (k_{chem light}/k_{chem heavy}).³³ In a recent summary review of 29 reported heavy enzyme isotope effects on the rate constant of the chemical step, only three inverse effects were observed (0.89–0.92), smaller than that observed for the F159Y PNP.³⁴ Although heavy enzyme isotope effects are still a developing technology, it appears that inverse isotope effects are rare but can be expected in some cases and can be engineered in certain enzymes.

Altering F159Y to generate the inverse enzyme isotope effects in PNP had no effect on the steady state k_cat values. Pre- steady state measurements comparing native and F159Y PNPs indicated a decrease in the chemical step by a factor of 32 in F159Y PNP.³³ Analyses of heavy enzyme isotope effects in enzymatic catalysis that use steady state analysis are at risk of reporting only on the slow conformational changes associated with substrate binding, conformational changes, or product release, rather than providing an understanding of the chemical interactions involved in transition state formation.

These recent publications demonstrate that promoting vibrations can be confirmed experimentally and that these ideas form a logical basis for enzyme design. We suggest that at least one of the reasons that artificial enzyme design has yielded less than robust rate enhancement is the lack of considering fast protein dynamics as a design feature. Given the low proficiency of artificial enzymes, it would seem these concepts have the potential to make a significant contribution to enzyme design.

THEORETICAL AND EXPERIMENTAL METHOD DEVELOPMENT AND EARLY APPLICATIONS

The recent results support the concept of catalytic site promoting vibrations and indicate the possibility of designing experiments that interrogate such complex motions. These theories and experiments have been built on a decade and a half of theory and experiment. We describe the genesis of these ideas to different types of chemical and enzyme systems.

CHEMICAL MODELS FOR UNDERSTANDING THE ATOMIC BASIS OF PROMOTING VIBRATIONS

Initial work deciphering the importance of promoting vibrations came from a model chemical system, the proton transfer reactions between phenol and amine in aprotic solvents.^35,36 This reaction was studied with a theoretical approach we called the quantum Kramers approach.³⁷ Details of this method are beyond the scope of this review but provided an insightful formalism for proton transfers in benzoic acid crystals. The initial theoretical approach was refined to demonstrate that transfers are due to the symmetric motion of carboxyl groups in these dimers (Figure 5).³⁰ These studies led to a realization that similar motions can be important in atomic substrate motions in enzymatic reactions.³⁹ In 2001, we extended the proposal to include fast coupled enzyme motion as a contributor to enzyme activity.⁴⁰ New methods were developed to identify these motions using spectral density analysis, with the first application to alcohol dehydrogenase, including mutational analysis.^7,41,42 Isozymes of lactate dehydrogenase were analyzed for modulation of the donor– acceptor distance,⁴³ and most pertinent here, studies of promoting vibrations in purine nucleoside phosphorylase recognized the dynamic contributions of His257 to ribocation formation.²⁵

Figure 5.

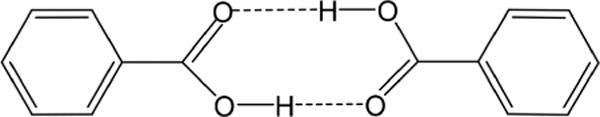
Benzoic acid dimer shown with a symmetrically coupled vibration, the prototype for a rate-promoting vibration.³⁸

APPLICATION OF TRANSITION PATH SAMPLING TO ENZYMATIC MECHANISMS

Catalytic mechanism at its most fundamental requires knowledge of how all atoms in the reaction coordinate contribute to formation of the transition state and generation of products. What was needed was a direct way to study the reaction in the enzyme matrix and to identify the exact motion of the protein and its link to the motions of the substrate, including the chemical conversion to the transition state. This missing link was found by modifying the method of TPS developed by David Chandler’s group.^13–18 TPS is a statistical mechanical method that belongs to the group of approaches known as enhanced sampling or rare event methods. The basic idea of rare event methods is to develop ways to identify events that happen individually rapidly, but only very rarely on the actual time scale. An example is a barrier crossing event. The method is a Monte Carlo simulation in trajectory space rather than a more commonly applied configuration space. In an enzyme, the crossing of an individual chemical barrier (the single-molecule event) is complete in femtoseconds, while the overall chemical rate is many orders of magnitude slower. The enzyme steady state turnover rate occurs on an even slower time scale related to slow protein conformational changes associated with reactant binding or product release. Our methods of transition path sampling and related techniques have been reviewed.⁴⁴ The enzymatic reaction with human lactate dehydrogenase was the first enzymatic reaction to which TPS was applied.⁴⁵ In all reactive trajectories, a compression of the donor and acceptor for hydride transfer occurred (Figure 6). While the occurrence of this compression in all reactive trajectories was suggestive, additional rigor was needed. This motion could be concomitant with reaction rather than causative. We applied the method of committor distribution analysis to test if these motions were part of the reaction coordinate, the atomic motions being both necessary and sufficient for reaction to occur.⁴⁶ We applied the same methods to PNP.^20,47–49 The joint experimental and theoretical analysis of this overall body of results was summarized in 2009.⁵⁰

Figure 6.

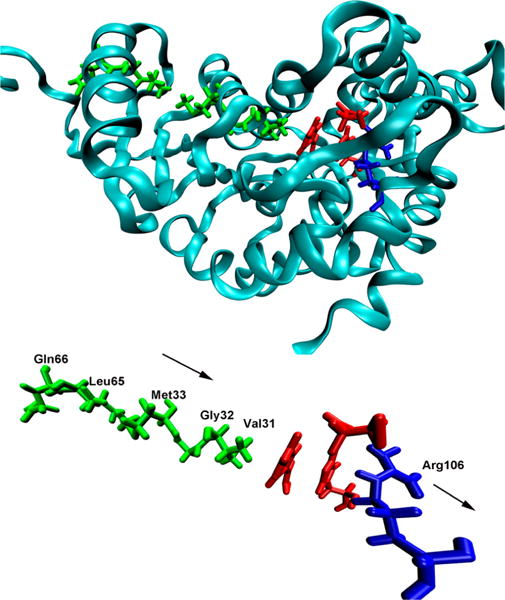
Monomer of LDH with the promoting vibration highlighted. The nicotinamide ring and substrate are colored red, and the residues involved in the promoting vibration are colored green and blue. Adapted from ref ⁴⁶. Copyright 2007 National Academy of Sciences.

These developments required computational definition of the transition state parameters.^51,52 Slower protein motions that lead to catalytically productive complexes were also characterized (in a range of promoting vibrations).^53,54 Further refinements of this work using Markov state models have strengthened this approach.^55,56 Other important developments support the promoting vibration concept. First, we showed that in lactate dehydrogenase, the promoting vibration is a preferred thermal channel; i.e., the enzyme takes thermal energy and transmits it along this channel.⁵⁷ Second, we showed that in the highly studied DHFR enzyme from E. coli, there is not a promoting vibration.³¹

Other investigators had used the lack of promoting vibration in E. coli as a reason to question the concept.⁵⁸ In DHFR, the enzyme brings the hydride donor and acceptor into promoting vibration distance, and transfer occurs from reactant, rather than protein promoring vibrations.

EXPERIMENTAL CHALLENGES IN HEAVY ENZYME STUDIES

Expression, purification, and analysis of distinct heavy and light proteins present experimental challenges because of unequal purity, catalytic integrity, and protein concentrations. Methods for analyzing isotopically labeled proteins must minimize potential inaccuracies. Stopped-flow, pre-steady state analysis with excess enzyme isolates a single enzymatic turnover that can be analyzed by pseudo-first-order reaction kinetics, a chemical rate that is independent of enzyme concentration.^26,27 Substrate trapping experiments, pioneered by Rose, also provide information about the relative chemical rates of reactants in the Michaelis complex.⁵⁹ In this approach, an isotopically labeled substrate bound to the enzyme is followed for conversion through the transition state to the product relative to the release into the free reactant pool. When the steady state K_m values are equivalent for light and heavy enzymes, the forward commitment factor provides an analysis of barrier crossing probability. Substrate trapping experiments are also independent of the concentration of enzyme protein and provide a second, independent measure of transition state formation in heavy and light enzymes.

RELATION TO VIEWS OF ENZYMATIC CATALYSIS OF OTHER INVESTIGATORS

The importance of dynamics in enzymatic catalysis is a contentious area of biochemistry. While this Perspective is principally concerned with our own work, we wish to make connection to some other views in the field: some closely related, some rather different. There are other investigators in biochemistry who have found similar dynamics contributions to the mechanism to enzymes.^60–68 There are also a variety of differing views. These other views have now been segregated into three main categories.

SOLUTION VERSUS PROTEIN DYNAMICS

The most contrarian view of the dynamic contribution to catalysis is summarized as proteins move, but their motions are not catalytic. Warshel and his colleagues have stated that dynamics are not involved in catalysis.^69–73 Justification for this view is most commonly explained as while all proteins move, and this motion changes the potential energy surface on which reaction occurs, this motion is not catalytic because similar motions occur in solution. Decades of theory on solution phase chemistry support this position.^74–77 For example, in solution phase proton transfer reactions, reaction happens when the donor and acceptor are contained in a solution “cage” and transfer is facilitated when the cage decreases the donor– acceptor distance. A protein promoting vibration does the same. However, enzymatic promoting vibrations are created in a protein backbone that allows it to be successful 10¹⁵ times more frequently than the solution phase reaction. In alcohol dehydrogenase, the promoting vibration reduces the effective free energy barrier to hydride transfer from almost 30 to 1 kcal/ mol, in other words lower than the thermal energy (k_BT). Even though promoting vibrations occur in solution and enzymatic reactions, the protein provides an efficiency difference, distinguishing it from promoting vibrations from the solvent cage.

However, it is misleading to conclude that enzyme promoting vibrations are not catalytic because the same physics is involved. The analysis is akin to comparing truck versus Corvette acceleration. Both use the same fuel (gasoline) and the same mechanism (piston strokes), but one accelerates more rapidy. Enzymes are Corvettes, promoting vibrations are the common fuel, and the physical process is 10¹⁵ times more efficient in the enzyme. Neither the Corvette nor the truck will move without fuel. The enzyme will not function efficiently without the promoting vibration. Solvent-based promoting vibrations are not efficient.

TRANSITION STATE THEORY

Another argument against dynamics in enzymatic reactions is based on the use of transition state theory (TST) to model enzymatic rates.^78–83 Practitioners have achieved remarkable agreement with experiment and argue that TST is sufficient to explain catalysis. TST depends on a small value for the recrossing term k, essential in transition state theory to obtain a rate: K = kK_TST. Some investigators have equated recrossing to “dynamics”, and if k is equal to 1.0, the statement is made that dynamics is unimportant. The fallacy of this statement is apparent in the basics of TST. The basic concept is that if one appropriately chooses a dividing hypersurface in free energy space, known collectively as the transition state (this would correspond to the transition state ensemble we compute from the stochastic separatrix⁵¹), then an exact dynamics theory for the rate may be replaced by a statistical theory that measures the population of states on the dividing surface. If classical mechanics holds, TST provides an upper bound to the true rate. Errors come from the inexactness of this statistical assumption and are manifest by “recrossing” of the transition state hypersurface. Thus, k is a number less than or equal to 1 and is said to represent dynamics in the sense that it corrects for errors in the statistical approximation dependent on the choice of the dividing surface. Thus, k has nothing to do with motions that promote the chemical reaction. Recrossing simply decreases the apparent rate.

Another rigorous reason why k is unrelated to promoting dynamics comes from the approach to implement a transition state theory calculation. One identifies the transition state hypersurface and finds the height of the free energy barrier. The recrossing term is obtained by initiating short trajectories from the transition state in the manner of a Bennett–Chandler calculation.^84,85 If a suitable transition state is selected, there is minimal recrossing. For example, in dehydrogenase enzymes, the donor and acceptor are within transfer distance. Motion in the enzyme that causes this distance to decrease from the crystal structure distance is exactly the promoting vibration. It has been built into the TST computation. Stating that TST disproves the importance of the promoting vibration is inconsistent with TST. In fact, the difference between the crystal structure and the transition state supports the importance of the protein motion that causes this to happen.

GATED MOTIONS

The work of Klinman et al. has connections to the views presented in this Perspective.^86–88 Their proposal of “gating motions”⁸⁸ is similar to our dynamic work and studies of proton transfer in benzoic acid crystals.^38,39 Klinman recognized that Marcus theory^89,90 had been expanded to apply to hydrogen transfer by Levich and Dogonadze,^91–93 Kuznetsov and Ulstrup,⁹⁴ and Jortner.⁹⁵ The critical addition of those formulations was required by the more rapid decay of a hydrogen wavefunction when compared to the electron wavefunction of the original Marcus theory. This decay meant that energy equalization via bath reorganization was not the only operative physical effect in determining a measured rate, but transfer distance was also critical. Transfer distance is modulated by motion of the substrate, described in the benzoic acid case, and is also possibly under the control of protein motion in an enzyme, a promoting vibration. Klinman and her group used these formulations to fit their experimental results to find gating motions with frequencies similar to those we found using our original spectral density studies and our rigorous TPS coupled with reaction coordinate identification. The difference (aside from the obvious difference provided by a methodology for interpreting experimental results vs first- principles theoretical study) is in interpretation. Klinman et al. described the catalytic motion as a statistical fluctuation. Transition path sampling examines an atomistic view of specific catalytic sites from an ensemble of trajectories. Putative reaction coordinates are statistically evaluated to find dynamic motions that are both necessary and sufficient for the enzymatic reaction. We also identify residues in the protein involved in the creation of the motion. This link among dynamics, structure, and reaction coordinates provides a guide to enzyme design. In some ways, we are using a different language to describe the same phenomenon.

This review details work demonstrating the importance of rapid protein motion in the function of enzymes. Our goal has been to rigorously state what we have shown and to compare other theoretical approaches for rate calculations. We have also sought to present our experimental data clearly and without excessive interpretation. Our goal is to use this body of knowledge to further both the analysis of naturally occurring enzymes and the future design of new functionality.