Flexible sensorimotor computations through rapid reconfiguration of cortical dynamics

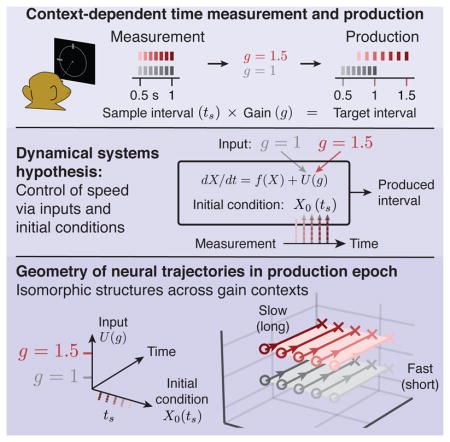
Summary

Neural mechanisms that support flexible sensorimotor computations are not well understood. In a dynamical system whose state is determined by interactions among neurons, computations can be rapidly reconfigured by controlling the system’s inputs and initial conditions. To investigate whether the brain employs such control mechanisms, we recorded from the dorsomedial frontal cortex of monkeys trained to measure and produce time intervals in two sensorimotor contexts. The geometry of neural trajectories during the production epoch was consistent with a mechanism wherein the measured interval and sensorimotor context exerted control over the cortical dynamics by adjusting the system’s initial condition and input, respectively. These adjustments, in turn, set the speed at which activity evolved in the production epoch allowing the animal to flexibly produce different time intervals. These results provide evidence that the language of dynamical systems can be used to parsimoniously link brain activity to sensorimotor computations.

eTOC

Remington et al. employ a dynamical systems perspective to understand how the brain flexibly controls timed movements. Results suggest that neurons in frontal cortex form a recurrent network whose behavior is flexibly controlled by inputs and initial conditions.

Introduction

Humans and nonhuman primates are capable of generating a vast array of behaviors, a feat dependent on the brain’s ability to produce a vast repertoire of neural activity patterns. However, identifying the mechanisms by which the brain flexibly selects neural activity patterns across a multitude of contexts remains a fundamental and outstanding problem in systems neuroscience.

Here, we aimed to answer this question using a dynamical systems approach. Work in multiple modalities has provided support for a hypothesis that neural activity can be understood at the level of neural populations and viewed as neural trajectories of a dynamical system (Fetz, 1992; Buonomano and Maass, 2009; Rabinovich et al., 2008; Shenoy et al., 2013). For example, recent studies have provided compelling evidence that low dimensional activity in motor cortex can be largely explained by inherent dynamical interactions (Churchland et al., 2010, 2012; Michaels et al., 2016; Seely et al., 2016). A dynamical systems view has also been used to provide explanations for neural trajectories in premotor and prefrontal cortical areas in various cognitive tasks (Rigotti et al., 2010; Mante et al., 2013; Hennequin et al., 2014; Carnevale et al., 2015; Rajan et al., 2016; Wang et al., 2018). This line of investigation has been complemented by efforts in developing, training, and analyzing recurrent neural network models that can emulate a range of motor and cognitive behaviors, leading to novel insights into the underlying latent dynamics (Rigotti et al., 2010; Laje and Buonomano, 2013; Mante et al., 2013; Hennequin et al., 2014; Sussillo et al., 2015; Chaisangmongkon et al., 2017; Wang et al., 2018). These early successes hold promise for the development of a more ambitious “computation-through-dynamics” as a general framework for understanding how activity patterns in the brain support flexible behaviorally-relevant computations.

The behavior of a dynamical system can be described in terms of three factors: (1) the interaction between state variables, (2) the system’s initial state, and (3) the external inputs to the system. Accordingly, the hope for using the mathematics of dynamical systems to understand flexible generation of neural activity patterns and behavior depends on our ability to understand the co-evolution of behavioral and neural states in terms of these three components. Assuming that synaptic couplings between neurons and other biophysical properties are approximately constant on short timescales (i.e. trial to trial), we asked whether behavioral flexibility can be understood in terms of adjustments to initial states and low-dimensional external inputs with minimal dynamics.

There is evidence that certain aspects of behavioral flexibility can be understood in terms of these factors. For example, it has been proposed that preparatory activity prior to movement initializes the system such that ensuing movement-related activity follows the appropriate trajectory (Churchland et al., 2010). Similarly, the presence of a static context input can enable a recurrent neural network to perform flexible rule- (Mante et al., 2013; Song et al., 2016; Wang et al., 2018) and category-based decisions (Chaisangmongkon et al., 2017). However, whether these initial insights would apply more broadly when both inputs and initial conditions change is an important outstanding question.

For many behaviors, distinguishing the effects of synaptic coupling, inputs and initial conditions in neural activity patterns is challenging. For example, neural activity during a reaching movement is likely governed by both local recurrent interactions and distal inputs from time-varying and condition-dependent reafferent signals (Todorov and Jordan, 2002; Scott, 2004; Pruszynski et al., 2011). Similarly, in many perceptual decision making tasks, it is not straightforward to disambiguate the sensory drive from recurrent activity representing the formation of a decision and the subsequent motor plan (Mante et al., 2013; Meister et al., 2013; Thura and Cisek, 2014). This makes it difficult to tease apart the contribution of recurrent dynamics governed by initial conditions from the contribution of dynamic inputs (Sussillo et al., 2016). To address this challenge, we designed a sensorimotor task for nonhuman primates in which animals had to measure and produce time intervals using internally-generated patterns of neural activity in the absence of potentially confounding time varying sensory and reafferent inputs. Using a novel analysis of the geometry and dynamics of in-vivo activity in the dorsal medial frontal cortex (DMFC) and in-silico activity in recurrent neural network (RNN) models trained to perform the same task, we found evidence that behavioral flexibility is mediated by the complementary action of inputs and initial conditions controlling the structural organization of neural trajectories.

Results

Ready, Set, Go (RSG) task

Our aim was to ask whether flexible control of internally-generated dynamics could be understood in terms of systematic adjustments made to initial conditions and external inputs of a dynamical system. We designed a “Ready, Set, Go” (RSG) timing task to directly investigate the role of these two factors. The basic sensory and motor events in the task were as follows: after fixating a central spot, monkeys viewed two peripheral visual flashes (“Ready” followed by “Set”) separated by a sample interval, t_s, and produced an interval, t_p, after Set by making a saccade to a visual target that was presented throughout the trial. In order to obtain juice reward, animals had to generate t_p as close as possible to a target interval, t_t (Figure 1B), which was equal to t_s times a “gain factor”, g (t_t = gt_s). The demand for flexibility was imposed in two ways (Figure 1C). First, t_s varied between 0.5 and 1 sec on a trial-by-trial basis (drawn from a discrete uniform “prior” distribution). Second, g switched between 1 (g =1 context) and 1.5 (g = 1.5 context) across blocks of trials (Figure 1D, mean block length = 101, std = 49 trials).

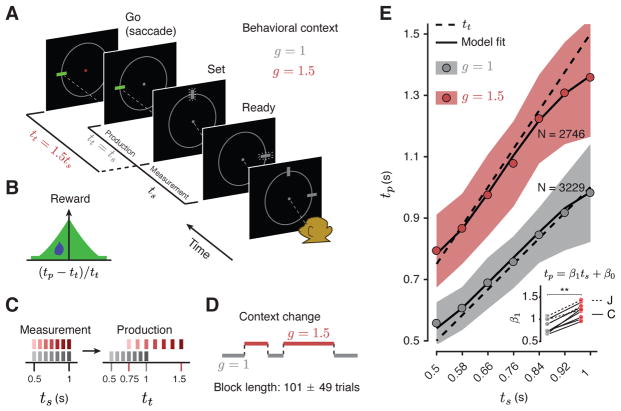
Figure 1. The RSG task and behavior.

(A) RSG task. On each trial, three rectangular stimuli associated with “Ready,” “Set,” and “Go” events were shown on the screen arranged in a semi-circle. Following fixation, Ready and Set cues were extinguished. After a random delay, first Ready and then Set stimuli were flashed (small lines around the rectangles signify flashed stimuli). The time interval between Ready and Set demarcated a sample interval, t_s. The monkey’s task was to generate a saccade (“Go”) to a visual target such that the interval between Set and Go (produced interval, t_p) was equal to a target interval, t_t, equal to t_s multiplied by a gain factor, g (t_t = gt_s). The animal had to perform the task in two behavioral contexts, one in which t_t was equal to t_s (g = 1 context), and one in which t_t was 50% longer than t_s (g = 1.5 context). The context was cued throughout the trial by the color of fixation and the position of a context stimulus (small white square below the fixation). (B) Reward. Animals received juice reward when the error between t_p and t_t was small, and the reward magnitude decreased with the size of error (see Methods for details). On rewarded trials, the saccadic target turned green (panel A). (C) Sample and target intervals. For both contexts, t_s was drawn from a discrete uniform distribution with seven values equally spaced from 0.5 to 1 sec (left). The values of t_s were chosen such that the corresponding values of t_t across the two contexts were different but partially overlapping (right). (D) Context blocks. The context changed across blocks of trials. The number of trials in a block was varied pseudorandomly (mean and std shown). (E) Behavior. t_p as a function of t_s for each context across both monkeys and all recording sessions (behavior of each animal is shown separately in Figure S1). Circles indicate mean t_p across all sessions, shaded regions indicate +/− one standard deviation from the mean, dashed lines indicate t_t, and solid lines are the fits of a Bayesian observer model to behavior. Inset: Slope of the regression line (β₁) relating t_p to t_s in the two contexts. Regression slopes were larger in the g = 1.5 context, with a significant interaction between t_s and g (p < 0.0001) for all sessions (see text; ** indicates p < 0.002 for signed-rank test). Regression intercepts (β₀) were also larger for the g = 1.5 context (0.14 vs. 0.18 sec, p = 0.04). In all panels, different shades of gray and red are associated with g =1 and g = 1.5, respectively. See Figure S1 for individual animals.

To verify that animals learned the task (Figure 1E, S1), we used regression analyses to assess the dependence of t_p on t_s and g. First, we verified that animals learned to measure t_s by analyzing the relationship between t_s and t_p within each context (t_p = β_o +β₁t_s). Results indicated that t_p increased monotonically with t_s (β₁ > 0, p ≪ 0.001 for all sessions). Next, we verified that animals learned the gain by comparing regression slopes relating t_p to t_s across the two contexts. The slopes (β₁) were significantly higher in the g = 1.5 context compared to g = 1 context (mean β₁ = 1.2 vs. 0.84; signed-rank test p = 0.002, n = 10 sessions; Figure 1E, inset). As a complementary analysis to show that animals displayed sensitivity to gain in individual sessions, we fit a regression model to behavior across both contexts that included additional regressors for gain and its interaction with t_s (t_p = β₀ + β₁t_s + β₂g+β₃gt_s). Results indicated a significant positive interaction between t_s and g (mean β ₃ = 0.73; β₃ > 0, p < 0.0001 in each session). Finally, we asked whether animals switched between contexts rapidly by fitting a regression model relating t_p z-scored for each t_s (z_p), to the number of trials n following a context switch (z_p = β₀ +β₁n, 1 ≤ n ≤ 25 trials after switches). There was no evidence that z_p changed as a function of number of trials after switch (one-tailed test for β₁, p > 0.25), suggesting that the switching was rapid. Together, these results confirmed that animals used an estimate of t_s to compute t_p and were able to flexibly and rapidly adjust their responses according to the gain information.

For both gains, responses were variable, and average responses exhibited a regression to the mean (mean β₁ <1, p = 0.005 for g = 1, and mean β₁ < 1.5, p = 0.0001 for g = 1.5, one-sided signed-rank test). As with previous work (Acerbi et al., 2012; Jazayeri and Shadlen, 2010, 2015; Miyazaki et al., 2005), these behavioral characteristics were accurately captured by a Bayesian model (Figure 1E, Methods) indicating that animals integrated their knowledge about the prior distribution, the sample interval and the gain to optimize their behavior.

Neural activity in the RSG task

To assess the neural computations in RSG, we focused on the dorsal region of the medial frontal cortex (DMFC) comprising supplementary eye field, dorsal supplementary motor area (i.e., excluding the medial bank) and presupplementary motor area. DMFC is a natural candidate for our task because it plays a crucial role in timing as shown by numerous studies in humans (Coull et al., 2004; Cui et al., 2009; Halsband et al., 1993; Macar et al., 2006; Pfeuty et al., 2005; Rao et al., 2001), monkeys (Isoda and Tanji, 2003; Kunimatsu and Tanaka, 2012; Kurata and Wise, 1988; Merchant et al., 2011, 2013; Mita et al., 2009; Ohmae et al., 2008; Okano and Tanji, 1987; Romo and Schultz, 1992), and rodents (Kim et al., 2009, 2013; Matell et al., 2003; Murakami et al., 2014; Smith et al., 2010; Xu et al., 2014), and because it is involved in context-specific control of actions (Brass and von Cramon, 2002; Isoda and Hikosaka, 2007; Matsuzaka and Tanji, 1996; Ray and Heinen, 2015; Shima et al., 1996; Yang and Heinen, 2014).

We recorded from 324 units (129 from monkey C and 195 from monkey J) in DMFC (Figure S2, S11). Between 11 and 82 units were recorded simultaneously in a given session, however in this study, we combined data across all units irrespective of whether they were recorded simultaneously. Firing patterns were heterogeneous and varied across units, task epochs, and experimental contexts. In the Ready-Set epoch, responses were modulated by both gain and elapsed time (e.g. units #1, 3, and 5, Figure 2A). For many units, firing rate modulations underwent a salient change at the earliest expected time of Set (0.5 sec). For example, responses of some units increased monotonically in the first 0.5 sec but decreased afterwards (Figure 2A, units #1, 3).

Figure 2. Neural responses in dorsomedial frontal cortex during the RSG task.

(A) Example neurons. Firing rates of 5 example units during the various phases of the task aligned to Ready (left column), Set (middle) and Go (right). Responses aligned to Ready and Set were sorted by t_s. Responses aligned to Go were sorted into 5 bins, each with the same number of trials, ordered by t_p. Gray and red lines correspond to activity during the g =1 and g = 1.5 contexts, respectively, with darker lines corresponding to longer intervals. (B) Population activity during Ready-Set. Visualization of population activity in the Ready-Set epoch sorted by t_s. The “gain axis” corresponds to the axis along which responses were maximally separated with respect to context at the time of Set. The other two dimensions (“PC1 and PC2”) correspond to the first two principal components of the data after removing the context dimension. Inset: fraction of variance explained by first 25 principal components. Dashed line indicates 100%. (C) Population activity during Set-Go. Visualization of population activity in the Set-Go epoch sorted into 5 bins, each with the same number of trials, ordered by t_p. Top: Activity plotted in 2 dimensions spanned by PC1 and the dimension of maximum variance with respect to t_p within each context (“Interval axis”). Bottom: Same as Top rotated 90 degree (circular arrow) to visualize activity in the plane spanned by the context axis (“Gain axis”) and PC1. For plotting purposes, PCs were orthogonalized with respect to the interval and gain axes. Squares, circles, and crosses in the state space plots represent Ready, Set, and Go, respectively. Percentage variance explained by interval and gain are shown numerically near the corresponding axes. See methods for the calculation of percent variance explained by interval and gain. See Figure S2 for individual animals and Figure S11 for different recording sites.

Following Set, firing rates were characterized by a mixture of 1) transient changes after Set (unit #1 and 3), 2) sustained modulations during the Set-Go epoch (units #1 and 5), and 3) monotonic changes in anticipation of the saccade (units #1, 2 and 4). These characteristics were not purely sensory or motor and varied systematically with t_s and gain. For example, the amplitude of the early transient response (unit #1) depended on both t_s and gain, indicating that it was not a visually-triggered response to Set. The same was true for the sustained modulations after Set and activity modulations prior to saccade initiation.

We also examined the representation of t_s and gain across the population by projecting the data on dimensions along which activity was strongly modulated by context and interval in state-space (i.e. the space spanned by the firing rates of all 326 units; see Methods). Similar to individual units, population activity was modulated by both elapsed time and gain during both the Ready-Set (Figure 2B) and Set-Go (Figure 2C) epochs. We used this rich dataset to investigate whether the flexible adjustment of intrinsic dynamics across the population with respect to t_s and gain could be understood using the language of dynamical systems.

Flexible neural computations: a dynamical systems perspective

We pursued the idea that neural computations responsible for flexible control of saccade initiation time can be understood in terms of the behavior of a dynamical system established by interactions among neurons. To formulate a rigorous hypothesis for how a dynamical system could confer such flexibility, we considered the goal of the task and worked backwards logically. The goal of the animal was to flexibly control the saccade initiation time to a fixed target. Previous motor timing studies proposed that saccade initiation is triggered when the activity of a subpopulation of neurons with monotonically increasing firing rates (i.e., “ramping”) reaches a threshold (Romo and Schultz, 1987; Hanes and Schall, 1996; Roitman and Shadlen, 2002; Tanaka, 2005; Mita et al., 2009; Kunimatsu and Tanaka, 2012). For these neurons, flexibility requires that the slope of the ramping activity be adjusted (Jazayeri and Shadlen, 2015). More recently, it was found that actions are initiated when the collective activity of neurons with both ramping and more complex activity patterns reach an action-triggering state (Churchland et al., 2006; Wang et al., 2018), and that flexible control of initiation time can be understood in terms of the speed with which neural activity evolves toward that terminal state (Shinomoto et al., 2011; Wang et al., 2018).

In a dynamical system, the speed with which activity evolves over time is determined by the derivative of the state. If we denote the state of the system by X, the derivative is usually specified by two factors, a function of the current state, f (X), and an external input, U, that may be constant or context- and/or time-dependent:

$$\frac{dX}{dt}=f(X)+U$$

When analyzing the collective activity of a specific population of neurons, this formulation has a straightforward interpretation. The state represents the collective firing rate of neurons under investigation, f (X) accounts for the interactions among those neurons, and U corresponds to external inputs coming from other populations of neurons, possibly driven by external stimuli. The only additional information needed to determine the behavior of this system is its initial condition, X₀, which specifies the initial neural state prior to generating a desired dynamic pattern of activity.

To assess the utility of the dynamical systems perspective for understanding behavioral flexibility, we assumed that f(X) (i.e., synaptic coupling in DMFC) is fixed across trials. Furthermore, we only considered external inputs U of low dimensionality and low temporal complexity (i.e. tonic and transient inputs), as a complex input could trivially account for the observed dynamics without providing any meaningful insight regarding the observed neural activity. This leaves initial conditions and low-dimensional inputs as the only “dials” for achieving flexibility with respect to t_s and gain (Figure 3).

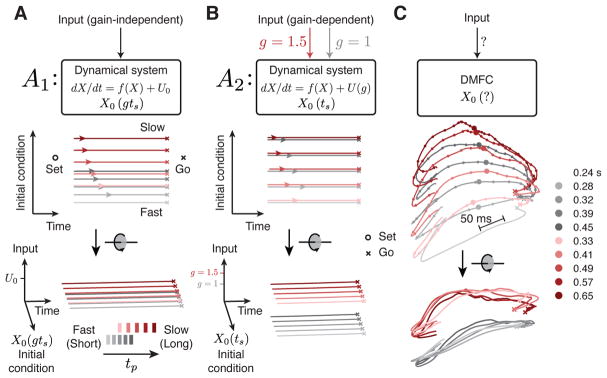
Figure 3. Dynamical systems predictions for the RSG task.

(A,B) Schematic illustrations of two hypothetical dynamical systems solutions to RSG across contexts through manipulation of initial conditions or external inputs. (A) The first solution (A₁). Top: In A₁, the initial condition (X₀) depends on the target interval t_t = gt_s (g, gain, t_s, sample interval), and the system is driven by a gain-independent input (U₀). Middle: state trajectory between Set and Go in the plane spanned by initial condition and time axes. After Set (open circles), activity evolves towards an action-triggering state (crosses) with a speed (colored arrows) fully determined by position along the initial condition axis (ordinate). Activity across contexts is organized according to t_t = gt_s. Bottom: same trajectories, rotated to show an oblique view. Trajectories are separated only along the initial condition axis across both contexts such that trajectory structure reflects t_t explicitly. There is no separation along the Input axis. (B) The second solution (A₂). Top: In A₂, X₀ depends on t_s within contexts, but the system is driven by a tonic gain-dependent input (U (g) ; red and gray arrow for the two gains). Middle: state trajectory between Set and Go in the plane spanned by initial condition and time axes. Because initial condition encodes t_s and not t_t, in this plane, trajectories associated with the same t_s but different gains appear overlapping. Bottom: oblique view. A context-dependent external input creates two sets of neural trajectories in the state space for the two contexts in the Set-Go epoch. This input controls speed in conjunction with initial conditions, generating a structure which reflects t_s and g explicitly, but not t_t. In both A₁ and A₂, responses would be initiated when activity projected onto the time axis reaches a threshold. (C) DMFC data. Top: unknown mechanism of RSG control in DMFC. Middle, bottom: 3-dimensional projection of DMFC activity in the Set-Go epoch (from Figure 2C). Middle: qualitative assessment indicated that neural trajectories within each context for different t_p bins were associated with different initial conditions and remained separate and ordered through the response. Bottom: Across the two contexts, neural trajectories formed two separated sets of neural trajectories without altering their relative organization as a function of t_p. Both of these features were consistent with A₂. Filled circles depict states along each trajectory at a constant fraction of the trajectory length, illustrating speed differences across trajectories (circles are closer for the longer intervals associated with slower speed).

First, we focused on behavioral flexibility with respect to t_s for each gain context. How can a dynamical system adjust the speed at which activity during Set-Go evolves in a t_s-dependent manner? In RSG, within each context, there are no sensory inputs (exafferent or reafferent) that could serve as a t_s-dependent input drive. Therefore, we hypothesized that the t_s-dependent adjustment of speed in the Set-Go epoch results from a parametric control of initial conditions at the time of Set. Because the speed of the dynamics at any given point in time is governed by the current state of the system, if the initial conditions at Set determine the path that neural activity takes through the state space, then it follows that initial conditions control speed. The corollary to this hypothesis is that the time-varying activity during the Ready-Set epoch is responsible for adjusting this initial condition based on the desired speed during the ensuing Set-Go epoch.

Second, we asked how speed might be controlled across the two gain contexts. One possibility is that the system uses initial conditions to encode t_t = gt_s, which has implicit information about both gain and t_s (i.e., X₀(gt_s)). This would predict that neural trajectories form a single organized structure with respect to the target time (t_t = gt_s). In the extreme case, neural trajectories associated with the same value of gt_s across the two contexts (e.g, 1.5×0.5 and 1.0×0.75) should terminate in the same state at the time of Set and should evolve along identical trajectories during the Set-Go epoch. We refer to this solution as A₁ (Figure 3A).

Alternatively, a tonic gain-dependent input could be responsible for rapid reconfiguration of dynamics across contexts (Figure 3B). As exemplified by previous work, a tonic input inevitably pushes activity in recurrent neural network models to a different region of the state space (Mante et al., 2013; Hennequin et al., 2014; Song et al., 2016; Sussillo et al., 2015; Chaisangmongkon et al., 2017; Wang et al., 2018). This solution, which we refer to as A₂, makes the following predictions. First, it predicts that the two gains should lead to two sets of neural trajectories in two different regions of the state space. Second, it predicts that neural trajectories should be organized with respect to t_s and t_p (i.e., within each context) but not necessarily with respect to t_t (i.e., across contexts). Because the context information in RSG was provided as an external visual input (fixation cue), and was available throughout the trial, we predict that this solution offers the more plausible prediction for how the brain might solve the task.

We thus set out to characterize the geometry of the observed neural trajectories quantitatively to determine the most likely explanation for their structure. The dynamical systems perspective in RSG leads us to the following specific hypotheses: 1) the evolution of activity in the Ready-Set epoch parametrizes the initial conditions needed to control the speed of dynamics in the production epoch within each context, and 2) the context cue acts as a tonic external input leading the system to establish structurally similar yet distinct sets of neural trajectories associated with the two gains, consistent with A₂.

Visualization of neural trajectories from Set to Go in state space (Figure 3C, same as in Figure 2C) provided qualitative support for these hypotheses. First, within each context, neural trajectories for different t_p bins were clearly associated with different initial conditions and remained separate and ordered throughout the Set-Go epoch. Second, context information seemed to displace the entire group of neural trajectories to a different region of neural state space without altering their relative organization as a function of t_p. Third, indexing time along nearby trajectories suggested that the speed with which responses evolved along each trajectory was systematically related to the desired t_t; i.e, slower for longer t_t. To validate these observations quantitatively, we developed an analysis technique which we termed “kinematic analysis of neural trajectories” (KiNeT) that helped us measure the relative speed and position of multiple, possibly curved (Figure S3), neural trajectories.

Control of neural trajectories by initial condition within contexts

We first employed KiNeT to validate that animals’ behavior was predicted by the speed with which neural trajectories evolved over time. We reasoned that neural states evolving faster will reach the same destination on the trajectory in a shorter amount of time. Therefore, we estimated relative speed across the trajectories by performing a time alignment to identify the times when neural activity reached nearby points on each trajectory (Figure 4A). We then used this approach to analyze the geometrical structure of trajectories through the Set-Go epoch.

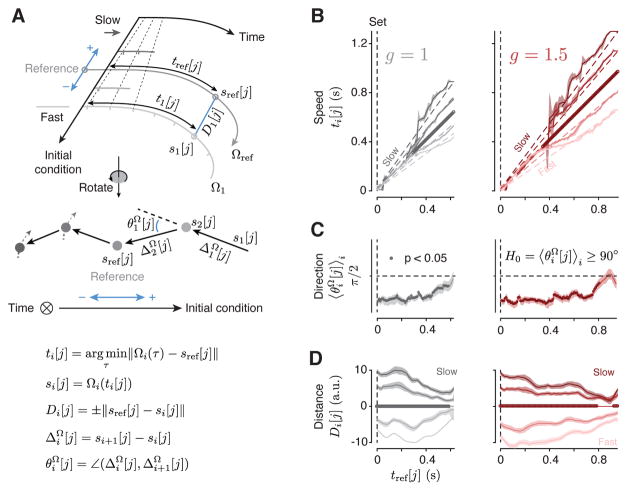
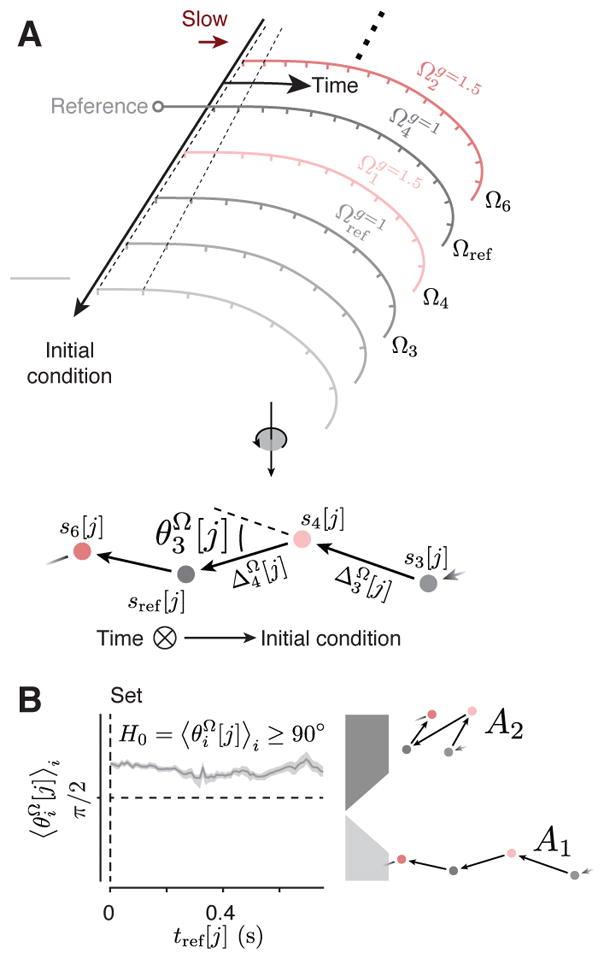
Figure 4. Kinematic analysis of neural trajectories (KiNeT).

(A) Illustration of KiNeT. Top: a collection of trajectories originate from Set, organized by initial condition, and terminate at Go. Tick marks on the trajectories indicate unit time. Darker trajectories evolve at a lower speed as demonstrated by the distance between tick marks and the dashed line connecting tick marks. KiNeT quantifies the position of trajectories and the speed with which states evolve along them relative to a reference trajectory (middle trajectory, Ω_ref). To do so, it finds a collection of states {s_i[j]}_j on each Ω_i that are closest to Ω_ref through time. Trajectories which evolve at a slower speed require more time to reach those states leading to larger values of t_i[j]. KiNet quantifies relative position by a distance measure, D_i[j] (distance between Ω_i and Ω_ref at t_i[j]) that is signed (blue arrows) and is considered positive when Ω_i corresponds to larger values of t_p (slower trajectories). Middle: trajectories rotated such that the time axis is normal to the plane of illustration, denoted by a circle with an inscribed cross. Filled circles represent the states {s_i[j]}_j aligned to s_ref[j] for a particular j. Vectors ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ connect states on trajectories of shorter to longer t_p. Angles ${\theta }_i^{\mathrm{\Omega }}[j]$ between successive ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ provide a measure of t_p-related structure. Bottom: equations defining the relevant variables. (B) Speed of neural trajectories compared to Ω_ref computed for each context separately. Shortly after Set, all trajectories evolved with similar speed (unity slope). Afterwards, Ω_i associated with shorter t_s evolved faster than Ω_ref as indicated by a slope of less than unity (i.e., {t_i [j]}_j smaller than {t_ref [j]}_j), and Ω_i associated with longer t_s evolved slower than Ω_ref. Filled circles on the unity line indicate j values for which {t_i [j]}_j was significantly correlated with i (bootstrap test, r > 0, p < 0.05, n = 100). (C) Relative position of adjacent neural trajectories computed for each context separately. ${\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i$ (angle brackets signify average across trajectories) were significantly smaller than 90 degrees (filled circle) for the majority of the Set-Go epoch (bootstrap test, ${\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i<90$, p < 0.05, n = 100) indicating that ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ were similar across Ω_i. (D) Distance of neural trajectories to Ω_ref computed for each context separately. Distance measures (D_i[j]) indicated that {Ω_i}_i had the same ordering as the corresponding t_p values. The magnitude of D_i[j] decreased with time indicating that trajectories coalesce as they get closer to the time of Go. When trajectories coalesce, small deviations in their relative position due to variability in firing rate estimates may cause trajectories to appear disorganized. This is consistent with the observation that ${\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i$ were closer to 90 degrees near the time of Go (panel C). Significance was tested using bootstrap samples for each j (p < 0.05, n = 100). See Figure S5 for individual animals and Figure S11 for different recording sites.

To perform KiNeT, we binned trials from each gain and recording session into five groups according to t_p. Neural responses from these trials were averaged, then PCA was applied to generate five neural trajectories within the state space spanned by the first 10 PCs that explained 89% of variance. We denote each trajectory after the time of Set by Ω_i (see Table S1 for an abridged list of notations and symbols) where the subscript i indexes the trajectory. We use curly brackets to refer to a collection of trajectories ({Ω_i}_i). We estimated speed and position along each Ω_i relative to the trajectory associated with the middle (third) bin, which we refer to as the reference trajectory, Ω_ref. We denoted neural states on the reference trajectory by s_ref[j], where j indexes states through time along Ω_ref. We also use curly brackets to refer to a collection indexes over times. For example, {s_ref [j]}_j refers to all states on Ω_ref, and {t_ref[j]}_j corresponds to time points on Ω_ref associated with those states.

For each s_ref [j], we found the nearest point on all non-reference trajectories (i ≠ ref) as measured by Euclidean distance. We denoted the collection of the nearest states on Ω_i to Ω_ref by {s_i[j]}_j, and the corresponding time points by {t_i[j]}_j. The corresponding time points along different trajectories provided the means for comparing speed: if {t_i [j]}_j were systematically greater than {t_ref[j]}_j, we could conclude that Ω_i evolves at a slower speed compared to Ω_ref (Figure 4A). This relationship can be readily inferred from the slope of the line that relates {t_i[j]}_j to {t_ref[j]}_j. While a unity slope indicates that the speeds are the same, higher and lower values would indicate slower and faster speeds of Ω_i compared to Ω_ref, respectively.

Applying KiNeT to neural trajectories in the Set-Go epoch indicated that Ω_i evolved at similar speeds immediately following the Set cue (unity slope). Later, speed profiles diverged such that neural trajectories associated with longer intervals slowed down and and trajectories associated with shorter intervals sped up for both gain contexts (Figure 4B). This is consistent with previous work that the key variable predicting t_p is the speed with which neural trajectories evolve (Wang et al., 2018). One common concern in this type of analysis is that averaging firing rates across trials of slightly different duration could lead to a biased estimate of neural trajectory. To ensure that our estimates of average speed were robust, we applied KiNeT to neural trajectories while aligning trials to Go instead of Set. Results remained unchanged and confirmed that the speed of neural trajectories predicted t_p across trials (Figure S4).

Having validated speed as the key variable for predicting t_p, we focused on our first hypothesis that the evolution of activity in the Ready-Set epoch parametrizes the initial conditions to control the speed of dynamics in the production epoch for each context. Because speed is a scalar variable and has an orderly relationship to t_p, this hypothesis predicts that the neural trajectories (and their initial conditions) should also have an orderly organizational structure with respect to t_p. In other words, there should be a systematic relationship between the vectors connecting nearest points across neural trajectories and the t_p to which they correspond. We tested this prediction in two complementary ways. First, we performed an analysis of direction testing whether the vectors connecting nearby trajectories were more aligned than expected by chance. Second, we performed an analysis of distance asking whether the distance between the reference trajectory and the other trajectories respected the distance between the corresponding speeds.

Analysis of direction

We used KiNeT to measure the angle between vectors connecting nearest points (Euclidean distance) across consecutive trajectories ordered by t_p. We used ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ to denote the vector connecting nearest points across trajectories (superscript Ω) between s_i[j] and s_i+1[j]. According to our hypothesis, the direction of ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ should be similar to ${\mathrm{\Delta }}_{i+1}^{\mathrm{\Omega }}[j]$ connecting s_i+1[j] to s_i+2[j]. To test this, we measured the angle between these two vectors, denoted by ${\theta }_i^{\mathrm{\Omega }}[j]$. The null hypothesis of unordered trajectories predicts that ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ and ${\mathrm{\Delta }}_{i+1}^{\mathrm{\Omega }}[j]$ should be unaligned on average ${\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i=90\text{degrees}$; angle brackets with the subscript i signify average over index i). Results indicated that ${\theta }_i^{\mathrm{\Omega }}[j]$ was substantially smaller than 90 degrees for both contexts (Figure 4C, S5). This provides the first line of quantitative evidence for an orderly organization of neural trajectories with respect to t_p.

Analysis of distance

We used KiNeT to measure the length of the vectors connecting nearest points on Ω_i and Ω_ref, denoted by D_i[j], at different time points. This analysis revealed that trajectories evolving faster than Ω_ref and those evolving slower than Ω_ref were located on the opposite sides of Ω_ref, and that the magnitude of D_i[j] increased progressively for larger speed differences (Figure 4D, S5). This analysis provided evidence that, for each context, the relative position of neural trajectories and their initial conditions in the state space were orderly and predictive of t_p.

Control of neural trajectories across contexts by external input

To identify the mechanism by which speed might be controlled across contexts, we first tested whether t_t = gt_s was encoded by initial conditions (A₁). According to this alternative, neural trajectories should follow the organization of t_p across both contexts (Figure 3A), in addition to within each context (Figure 4C). To test A₁, we sorted neural trajectories across the two contexts according to t_p (Figure 5A, top), and asked whether the angle between vectors connecting nearest points ( ${\theta }_i^{\mathrm{\Omega }}[j]$) was significantly less than 90 degrees (Figure 5A, bottom). Unlike the within-context results (Figure 4C), when neural trajectories from both contexts were combined, the angle between nearby neural trajectories was not less than 90 degrees (Figure 5B, S6). This indicates that trajectories across contexts do not have a orderly relationship to t_t (A₁: less than 90 deg).

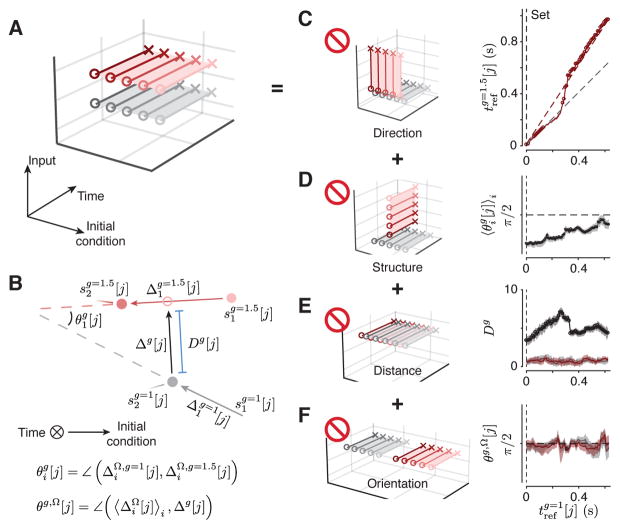
Figure 5. Neural trajectories across contexts do not form a single structure reflecting.

t_p.

(A) A schematic illustrating neural trajectories across the two contexts after Set. Top: The expected geometrical structure under A₁. Neural trajectories for the gain of 1 (gray) and 1.5 (red) are organized along a single initial condition axis and ordered with respect to t_p. Tick marks indicate unit time. Bottom: A rotation of the top showing neural trajectories with the time axis normal to the plane of illustration. If the neural trajectories were organized as such, then the angle between vectors connecting nearby points (e.g., ${\theta }_3^{\mathrm{\Omega }}[j]$) would be less than 90 (A₁, Figure 3A). (B) Left: orientation of vectors connecting adjacent neural trajectories combined across the two contexts. Right: possible geometrical structures A₁ (bottom), and A₂ (top). ${\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i$ was larger than 90 degrees for all j in the Set-Go interval, consistent with A₂. Shaded regions represent 90% bootstrap confidence intervals. See Figure S6 for individual animals and Figure S11 for different recording sites.

Next, we investigated the hypothesis that the context cue acts as a tonic external input (A₂; Figure 3B), leading the system to establish structurally similar but distinct collections of neural trajectories across contexts (Figure 6A,B). This hypothesis imposes a set of specific geometrical constraints on neural trajectories in the Set-Go epoch. We determined whether the data met these constraints by testing whether the converse of each could be rejected, as illustrated in Figure 6C–F. If we denote the collection of neural trajectories in the two contexts by ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$, these constraints and tests can be formalized as follows:

Figure 6. Neural trajectories comprise distinct but similar structures across gains.

(A) A schematic showing the organization of neural trajectories in a subspace spanned by Input, Initial condition and Time if context were controlled by tonic external input. If DMFC were to receive a gain-dependent input, we would expect neural trajectories from Set to Go to be separated along an input subspace, generating two similar but separated t_p-related structures for each context (A₂, Figure 3B). We verified this geometrical structure by excluding alternative structures (interdictory circles indicate rejected alternatives). (B) An illustration of neural trajectories for g =1 (gray filled circle) and g = 1.5 (red filled circle) with the time axis normal to the plane of illustration. Gray and red arrows show vectors connecting nearby points in each context independently (Δ^Ω,g=1.5 and Δ^Ω,g=1). When the neural trajectories associated with the two gains are structured similarly, these vectors are aligned and the angle between them (θ^g) is less than 90 deg. We used KiNeT to test this possibility (see Methods). (C) Left: Schematic illustrating a condition in which the time axis for trajectories in the two contexts (gray and red) are not aligned. Right: ${\left\{t_{\text{ref}}^{g=1}[j]\right\}}_j$ increased monotonically with ${\left\{t_{\text{ref}}^{g=1.5}[j]\right\}}_j$ indicating that the time axes across contexts were aligned. Values of ${\left\{t_{\text{ref}}^{g=1.5}[j]\right\}}_j$ above the unity line indicate that activity evolved at a slower speed in the g = 1.5 context. The dashed gray line represents unity and the dashed red line represent expected values for ${\left\{t_{\text{ref}}^{g=1.5}[j]\right\}}_j$ if speeds were scaled perfectly by a factor of 1.5. (D) Left: Schematic illustrating an example configuration in which ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ establish dissimilar t_p-related structures. Right: ${\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i$ was significantly less than 90 degrees for all j indicating that the t_p-structure was similar across the two contexts. (E). Left: Schematic illustrating a condition in which ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ are overlapping. Right: The minimum distance D^g across contexts (black line) was substantially larger than that found between subsets of trajectories within contexts (red and gray lines, see Methods) indicating the two sets of trajectories were not overlapping. (F) Left: Schematic illustrating a condition in which ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ are separated along the same direction that neural trajectories within each context were separated. Right: The vector associated with the minimum distance between the two manifolds (Δ^g[j]) was orthogonal to the vector connecting nearby states for both $g=1(\text{gray},{\langle {\mathrm{\Delta }}_i^{\mathrm{\Omega },g=1}[j]\rangle }_i)$ and $g=1.5(\text{red},{\langle {\mathrm{\Delta }}_i^{\mathrm{\Omega },g=1.5}[j]\rangle }_i)$. In (C–E), shaded regions represent 90% bootstrap confidence intervals, and circles represent statistical significance (p < 0.05, bootstrap test, n = 100). See Figure S7 for individual animals and Figure S11 for different recording sites.

1. ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ should evolve in the same direction as a function of time with different average speeds (i.e. slower for ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$). If the converse were true (i.e., trajectories evolving in different directions, Figure 6C, left), we would expect no systematic relationship between time points across the two contexts. Results from KiNeT across contexts (see Methods) revealed a monotonically increasing relationship between ${\left\{t_{\text{ref}}^{g=1}[j]\right\}}_j$ and ${\left\{t_{\text{ref}}^{g=1.5}[j]\right\}}_j$, confirming that Set-Go trajectories across contexts evolved in the same direction (Figure 6C right, S7A,E). Moreover, ${\left\{t_{\text{ref}}^{g=1.5}[j]\right\}}_j$ had a higher rate of change than ${\left\{t_{\text{ref}}^{g=1}[j]\right\}}_j$ indicating that average speeds were slower in the g = 1.5 condition. This suggests that speed control played a consistent role across contexts (Figure 6A). Consistent with the within-gain analyses (Figure 4B), KiNeT indicated that Ω_i evolved at similar speeds across context immediately following the Set cue (unity slope).

2. ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ should be organized similarly with respect to t_p. In other words, the vector that connects nearby points in ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ should be aligned to its counterpart that connect nearby points in ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$. To evaluate this constraint, we used the angle between pairs of vectors that connect nearby points within each context. We use an example to illustrate the procedure (Figure 6B). Consider one vector connecting nearby points in two successive neural trajectories in the gain of 1 (e.g. ${\mathrm{\Omega }}_1^{g=1}$ and ${\mathrm{\Omega }}_2^{g=1}$), and another vector connecting the corresponding points in the gain of 1.5 (e.g., ${\mathrm{\Omega }}_1^{g=1.5}$ and ${\mathrm{\Omega }}_2^{g=1.5}$). A similar orientation between the two groups of trajectories (Figure 6A) would cause the angle between these vectors ( ${\theta }_1^g$) to be significantly smaller than 90 degrees. If instead, ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ were oriented differently (Figure 6D left) or had no consistent relationship, these vectors would be on average orthogonal. Using KiNeT, we found that this angle ( ${\theta }_i^g[j]$) was consistently smaller than 90 degrees throughout the Set-Go epoch (Figure 6D right, S7B,F), providing quantitative evidence that the collection of neural trajectories associated with the two gains were structurally similar (Figure 6A).

3. if context information is provided as a tonic input, ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ should be separated in state space along a context axis throughout the Set-Go epoch. To verify this constraint, we assumed that neural trajectories for each context were embedded in distinct manifolds and compared the minimum distance between the two manifolds (D^g) to an analogous distance metric within each manifold (Figure 6B; see Methods). These distance measures should be the same if the groups of trajectories associated with the two contexts overlap in state space (Figure 6E, left). However, we found distances to be substantially larger across contexts compared to within contexts (Figure 6E right, S7C,G). This confirms that the groups of trajectories associated with the two contexts were separated in state space (Figure 6A).

4. The results so far reject a number of alternative hypotheses (Figure 6C,D,E) and leave two possibilities: either ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ are separated along the same dimension that separates trajectories within each context (Figure 6F, left), or they are separated along a distinct input axis in accordance with A₂ (Figure 6A). To distinguish between these two, we asked whether the vector associated with the minimum distance D^g[j] (Δ^g[j]) between the two manifolds was aligned to vectors connecting nearby states within each context ( ${\left\{{\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]\right\}}_i$). Analysis of the angle between these vectors (θ^{g, Ω}[j]) indicated that the two were orthogonal for almost all j (Figure 6F right, S7D,H). This ruled out the remaining possibility that trajectories across contexts were separated along the same dimension as within-context (Figure 6F, left).

Having validated these constraints quantitatively, we concluded that population activity across gains formed two groups of isomorphic speed-dependent neural trajectories (Figure 6A). These results support our primary hypothesis that flexible control of speed based on gain context was established by a context-dependent tonic external input (Figure 3B).

Variability in neural trajectories systematically predicted behavioral variability

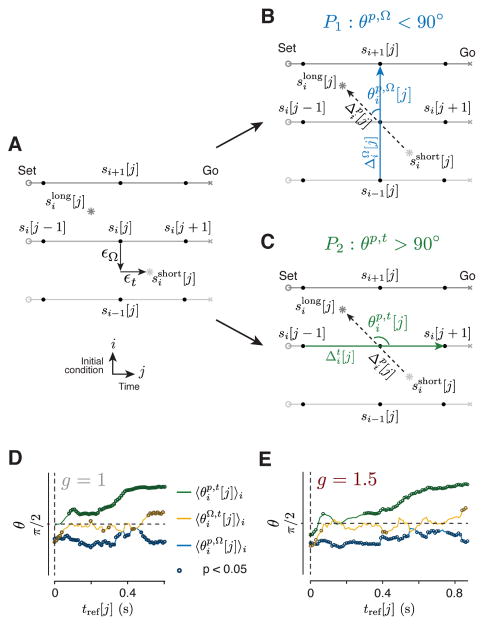
To further substantiate the link between the geometry of neural trajectories and behavior, we asked whether variability in t_p for each t_s and gain could be explained in terms of systematic fluctuations of speed and location of neural trajectories in the space. Considering the orderly structure of nearby neural trajectories, we reasoned that two types of deviations along neural trajectories should lead to systematic biases in t_p. First, on trials in which the trajectory deviates toward the trajectory associated with a shorter (or longer) t_s, the trial should result in a shorter (or longer) t_p. Second, when a trajectory evolves too slowly (closer to its positions at Set) or too fast (closer to its positions at Go), the trial should result in a longer (or shorter) t_p. We tested this by using KiNeT to examine the relative geometrical organization of neural trajectories associated with larger and smaller values of t_p for the same t_s and gain. If we denote deviations across trajectories by ò^Ω and deviations along trajectories by ò^t (Figure 7A), these predictions can be formalized as follows:

Figure 7.

Relating neural variability to behavioral variability. (A). Schematic showing states (filled circles) along three neural trajectories (gray lines) between Set (circle) and Go (cross) associated with three different t_s values. The light and dark stars depict two neural states that are deviated from the average neural trajectory (the middle trajectory). The light star corresponds to trials in which t_p was shorter than median $t_p(s_i^{\text{short}}[j])$), and the dark star, to trials in which t_p was longer than median ( $s_i^{\text{long}}[j]$). $s_i^{\text{short}}[j]$ is deviated from the average trajectory in the direction of shorter t_s (toward s_{i − 1}[j] by vector ò^Ω) and in the direction of the Go state (toward s_i[j+1] by vector ò^t). The opposite is true for $s_i^{\text{long}}[j]$. (B) Prediction 1 (P₁): deviations ò^Ω off of one trajectory toward a trajectory associated with longer t_s should lead to longer t_p, and vice versa. The dashed arrow represents ${\mathrm{\Delta }}_i^p[j]$, the vector pointing from $s_i^{\text{short}}[j]$ to $s_i^{\text{long}}[j]$, and the blue arrow represents ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$, the vector pointing from s_{i − 1}[j] to s_{i +1}[j]. P₁ is satisfied if the angle between these vectors, denoted by ${\theta }_i^{p,\mathrm{\Omega }}[j]$, is acute. (C) Prediction 2 (P₂): deviations ò^t along trajectories should influence the time it takes for activity to reach the Go state and should therefore influence t_p. The green arrow represents ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$, the vector that connects s_i [j − 1] to s_i [j + 1]. If P₂ is correct, the angle ${\theta }_i^{p,t}[j]$ between ${\mathrm{\Delta }}_i^p[j]$ and ${\mathrm{\Delta }}_i^t[j]$ should be obtuse. (D,E) Testing P₁ and P₂ for the g = 1 (D) and g = 1.5 (E) contexts. Consistent with P₁, average ${\theta }_i^{p,\mathrm{\Omega }}[j]({\langle {\theta }_i^{p,\mathrm{\Omega }}[j]\rangle }_i,\text{blue})$ was less than 90 deg from Set to Go indicating that t_p was longer (shorter) when neural states deviated toward a trajectory associated with a longer (shorter) t_s. Consistent with P₂, ${\langle {\theta }_i^{p,t}[j]\rangle }_i$ (green) was greater than 90 deg, indicating that t_p was longer (shorter) when speed along the neural trajectory was slower (faster). The average angle between ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ and ${\mathrm{\Delta }}_i^t[j]{\langle {\theta }_i^{\mathrm{\Omega },t}[j]\rangle }_i$ (yellow) was not significantly different than expected by chance (90 deg) for most time points. We determined when (at what j) an angle was significantly different from 90 deg (p < 0.05) by comparing angles to the corresponding null distribution derived from 100 random shuffles with respect to t_p. Angles that were significantly different from 90 deg are shown by darker circles. See Figure S8 for individual animals and Figure S11 for different recording sites.

P₁. Deviations ò^Ω off of one trajectory toward a trajectory associated with longer t_s should lead to longer t_p, and vice versa (Figure 7B). To test P₁, we divided trials for each t_s into two bins. One bin contained all trials in which t_p was shorter than median t_p and the other, all trials in which t_p was longer than median t_p. We computed neural trajectories for the short and long t_p bins, and denoted the corresponding states by $s_i^{\text{short}}[j]$ and $s_i^{\text{long}}[j]$, respectively. If P₁ is correct, then the geometric relationship between $s_i^{\text{short}}[j]$ and $s_i^{\text{long}}[j]$ should be similar to that between s_i−1[j] (shorter t_s) and s_{i +1}[j] (longer t_s). Therefore the vector pointing from $s_i^{\text{short}}[j]$ to $s_i^{\text{long}}[j]({\mathrm{\Delta }}_i^p[j])$ and the vector pointing from s_{i − 1}[j] to s_i+1[j] ( ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$) should be aligned, and the angle between them, denoted by ${\theta }_i^{p,\mathrm{\Omega }}[j]$, should be acute. See Methods description for calculation of ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ for t_s.

Consistent with P₁, we found that average ${\theta }_i^{p,\mathrm{\Omega }}[j]({\langle {\theta }_i^{p,\mathrm{\Omega }}[j]\rangle }_i)$, was less than 90 deg throughout the Set-Go epoch (Figure 7D,E, S8A,C blue trace). This result indicates that neural trajectories that correspond to larger values of t_p were shifted in state space toward larger values of t_s. Notably, the systematic relationship between t_p and neural activity was already present at the time of the Set, indicating that t_p was influenced by variability during the Ready-Set measurement epoch and thus the initial condition in the production epoch.

P₂. Deviations ò^t along trajectories should influence the time it takes for activity to reach the Go state and should therefore influence t_p (Afshar et al., 2011; Michaels et al., 2015). If P₂ is correct, then $s_i^{\text{short}}[j]$ should be ahead of $s_i^{\text{long}}[j]$. Therefore, ${\mathrm{\Delta }}_i^p[j]$ should point backwards in time, and the angle between ${\mathrm{\Delta }}_i^p[j]$ and ${\mathrm{\Delta }}_i^t[j]$ that connects s_i[j − 1] to s_i[j + 1], denoted by ${\theta }_i^{p,t}[j]$ should be obtuse. See methods description for calculation of ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$.

Consistent with P₂, we found that ${\langle {\theta }_i^{p,t}[j]\rangle }_i$ was greater than 90 deg. This result indicates that t_p was larger (smaller) when speed along the neural trajectory was slower (faster) (Figure 7D,E, S8B,D, green trace). The angle ${\langle {\theta }_i^{p,t}[j]\rangle }_i$ was initially close to 90 deg consistent with the observation that trajectories evolved at similar speeds early in the Set-Go epoch (Figure 4B). We also measured the angle between ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ and ${\mathrm{\Delta }}_i^t[j]$, denoted by ${\theta }_i^{\mathrm{\Omega },t}[j]$. ${\langle {\theta }_i^{\mathrm{\Omega },t}[j]\rangle }_i$ was not significantly different than expected by chance (90 deg) for most time points.

We also considered whether deviations of neural trajectories along the gain axis that presumably reflect variability in the context-dependent input might be related to systematic changes in t_p. We did not find evidence that this was the case. While there was statistically significant alignment between ${\mathrm{\Delta }}_i^p[j]$ and vectors connecting trajectories of identical t_s across gains ( ${\mathrm{\Delta }}_i^g[j]$), this alignment was explained by the component of ${\mathrm{\Delta }}_i^g[j]$ along the direction of ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ (Figure S9).

This analysis extends the correspondence between behavior and the organization of neural trajectories to include animals’ within-condition variability. Together, these results provide evidence for our hypothesis that activity during Ready-Set epoch parametrically adjusts the system’s initial condition (i.e., neural state at the time of Set) within contexts, which in turn controls the speed of neural trajectory in the Set-Go epoch and the consequent t_p.

RNN models recapitulate the predictions of inputs and initial conditions

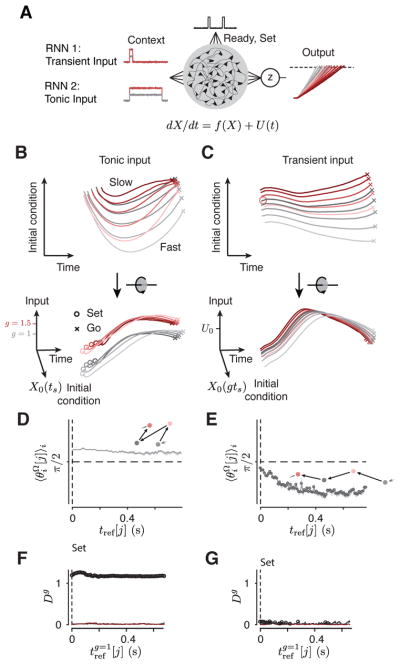
The geometry and dynamics of DMFC responses were consistent with the hypothesis that behavioral flexibility in the RSG task relies on systematic adjustments of initial conditions and external inputs of a dynamical system. Motivated by recent advances in the use of recurrent neural networks (RNNs) as a tool for testing hypotheses about cortical dynamics (Chaisangmongkon et al., 2017; Hennequin et al., 2014; Mante et al., 2013; Sussillo et al., 2015; Wang et al., 2018), we investigated whether RNNs trained to perform the RSG task would establish similar geometrical structures and dynamics.

We created RNNs with two different architectures, one in which the gain information was provided by the magnitude of a tonic input, and another in which the gain information was provided by the magnitude of a transient pulse before the Ready cue. We refer to these networks as tonic-input RNNs and transient-input RNNs, respectively (Figure 8A). We used the tonic-input RNN as a direct test of whether a context-dependent tonic input could emulate the geometrical structure of responses in DMFC. The transient-input RNN, on the other hand, tested whether this structure would naturally emerge in a network without such an input.

Figure 8. RNNs with tonic but not transient input captured the structure of activity in DMFC.

(A) Schematic illustration of the RNNs. The networks receive brief Ready and Set pulses separated in time by t_s. Additionally, each network is provided with a context-dependent “input” which either terminates prior to Ready (“Transient input,” top), or persists throughout the trial (“Tonic input,” bottom). All networks were trained so that the output (z) would generate a ramp after Set that would reach a threshold (dashed line) at the context-dependent t_t. (B) Top: state-space projections of tonic-input RNN activity in the Set-Go epoch. The axes for 3D projections were identified using the same method as in Figure 2C. (C) Same as panel B for the transient-input RNN. (D) Analysis of direction in the tonic-input RNN with the same format as Figure 5B. ${\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i$ was larger than 90 deg for the entire the Set-Go epoch. This indicates that the tonic network forms two separate context-specific sets of isomorphic neural trajectories (inset). (E) Same as panel D for the transient-input network. ${\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i$ was consistently less than 90 deg consistent with a geometry in which neural trajectories are organized with respect to t_p regardless of the gain context (inset). (F,G) Trajectory separation (D^g) across contexts for the tonic-input (F) and transient-input (G) networks with the same format as Figure 6E. D^g was substantially larger through the Set-Go epoch in the tonic-input network (F). In (D–G), shaded regions represent 90% bootstrap confidence intervals, and circles represent statistical significance (p < 0.05, bootstrap test, n = 100). See Figure S10 for a more detailed analysis of RNN results.

All networks comprised synaptically coupled nonlinear units that received nonspecific background activity, and were provided an input encoding Ready and Set as two brief pulses separated by t_s. We trained these RNNs to generate a linear output function after Set that reached a threshold (Go) at the desired production interval, t_t = gt_s on average. Within-context analysis of successfully trained RNNs revealed that they controlled t_p by adjusting the speed of neural trajectories within a low-dimensional geometrical structure parameterized by initial conditions (Figure 8B,C, Figure S10). These results are qualitatively similar to what we found in DMFC (Figure 2C, Figure 4). See Figure S10 for a more detailed treatment of the networks’ response properties.

Using PCA and KiNeT to analyze activity across contexts, we found that neural trajectories in the tonic- and transient-input networks were structured differently. In the tonic-input RNN, trajectories formed two isomorphic structures separated along the dimension associated with the gain-dependent tonic input (Figure 8B). In contrast, trajectories generated by the transient-input RNN were better described as coalescing towards a single structure parameterized by initial condition (Figure 8C). To verify these observations quantitatively, we evaluated the geometry of neural trajectories in the two RNN variants using the same analyses we performed on DMFC activity. In particular, we sorted trajectories with respect to t_p across the two gain contexts (g =1 and g = 1.5) and quantified the angle between vectors connecting nearest points ( ${\theta }_i^{\mathrm{\Omega }}[j]$). As noted in the analysis of DMFC, this angle is expected to be acute if trajectories form a single structure ( $A_{\mathit{1}}:{\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i<90deg$), and obtuse if trajectories form two gain-dependent structures ( $A_{\mathit{2}}:{\langle {\theta }_i^{\mathrm{\Omega }}[j]\rangle }_i\ge 90deg$). As predicted, the tonic-input solved the task by forming two isomorphic structures (A₂) indicating that when a tonic gain-dependent input is present, RNNs rely on a solution with separate gain-dependent geometrical structures (Figure 8E). In contrast, in the transient-input RNNs, angles between consecutive trajectories were acute (A₁). This result underscores the importance of a tonic gain-dependent input in establishing separate isomorphic structures (Figure 8D).

We also compared the two RNNs in terms of the distance between trajectories across the two contexts using the same metric (D^g) we used previously used for the analysis of DMFC (Figure 6E). The minimum distance between ${\left\{{\mathrm{\Omega }}_i^{g=1}\right\}}_i$ and ${\left\{{\mathrm{\Omega }}_i^{g=1.5}\right\}}_i$ at the time of Set was consistently smaller in the transient-input RNNs compared to tonic-input RNNs (Figure 8F,G). To quantify this feature, we compared values of D^g in each RNN normalized by the distance between the trajectories that correspond to the shortest and longest t_p bin for the g =1 context in the same RNN. In the tonic networks, the minimum normalized distance ranged between 0.4 and 1.6, which was at least 10 times larger than the that observed in the transient networks (0.003 to 0.04). Furthermore, trajectories in all transient networks gradually established a t_t-related structure consistent with A₁. In contrast, trajectories in the tonic networks, like the DMFC data, were characterized by two separate t_p-related structures, one for each gain context. These results provide an important theoretical corroboration of our intuition that when gain information is provided as tonic input, a natural solution is for the system to establish distinct and isomorphic gain-dependent sets of neural trajectories.

Discussion

Our results indicate that flexible control of behavior could be parsed in terms of systematic adjustments to initial conditions and simple external inputs of a dynamical system. Activity structure within each gain context was consistent with the hypothesis that the system’s initial conditions controlled t_p by parameterizing the speed of neural trajectories (Shinomoto et al., 2011; Jazayeri and Shadlen, 2015; Wang et al., 2018). The displacement of neural trajectories in DMFC state space (Shinomoto et al., 2011; Wang et al., 2018) as a function of gain, and the lack of structural representation of t_p across both gains suggested that neurons received the gain information as a context-dependent tonic input. Following recent advances in using RNNs to generate and test hypotheses about dynamical systems (Rigotti et al., 2010; Mante et al., 2013; Hennequin et al., 2014; Sussillo et al., 2015; Rajan et al., 2016; Chaisangmongkon et al., 2017; Wang et al., 2018), we corroborated this interpretation by analyzing the behavior of different RNN models trained to perform the RSG task with either tonic or transient context-dependent inputs. Although both types of networks used initial conditions to set the speed of neural trajectories, only the tonic-input RNNs reliably established and maintained separate structures of neural trajectories across gains, similar to what we found in DMFC.

Although we do not know the constraints that led the brain to establish separate geometrical structures, we speculate about potential computational advantages associated with this particular solution. First and foremost, this may be a particularly robust solution; as the gain information was provided by a persistent visual cue, the brain could use this input as a reliable signal to modulate neural dynamics in RSG. This solution may also reflects animals’ learning strategy. We trained monkeys to perform the RSG tasks with two gain contexts. At one extreme, animals could have treated these as completely different tasks leading to completely unrelated response structures for the two gains. At the other extreme, animals could have established a single parametric solution that would enable the animal to perform the two contexts as part of a single continuum (e.g., represent t_t). DMFC responses, however, did not match either extreme. Instead, the system established what might be viewed as a modular solution comprised of two separate isomorphic structures. We take this as evidence that the brain sought similar solutions for the two contexts, but it did so while keeping the solutions separated in the state space. This strategy preserves a separable, unambiguous representation of gain and t_s at the population level (Machens et al., 2010; Mante et al., 2013; Kobak et al., 2016;) and provides the additional flexibility of parametric adjustments to the two parameters independently. Future extensions of our experimental paradigm to cases where context information is not present throughout the trial (e.g., internally inferred rules) might provide a more direct test of these possibilities.

Regardless of the learning strategies and constraints that shaped DMFC responses, our results highlight an important computational role for inputs that deviate from traditional views. We found that changing the level of a static input can be used to generalize an arbitrary stimulus response mapping in the RSG task to multiple contexts while preserving the computational mechanisms within contexts. Similar inferences can be made from other recent studies that have evaluated the computational utility of inputs that encode task rules and behavioral contexts (Mante et al., 2013; Song et al., 2016; Chaisangmongkon et al., 2017; Wang et al., 2018). Extending this idea, it may be possible for the system to use multiple orthogonal input vectors to flexibly and rapidly switch between sensorimotor mappings along different dimensions. Together, these findings suggest that a key function of cortical inputs may be to flexibly reconfigure the intrinsic dynamics of cortical circuits by driving the system to different regions of the state space. This allows the same group of neurons to access a reservoir of latent dynamics needed to perform different task-relevant computations.

Our results raise a number of additional important questions. First, future work should directly confirm and identify the neurobiological substrate of the putative context-dependent input to DMFC in the RSG task, which may be among various cortical and subcortical areas (Bates and Goldman-Rakic, 1993; Lu et al., 1994; Wallis et al., 2001; Wang et al., 2005; Akkal et al., 2007). The mechanism by which such putative input modulates cortical activity is also unknown. In our RNN models, context information was provided by an external drive and the model was agnostic with respect to the exact mechanism. In cortex, the control of speed of dynamics may be mediated by either an input that drives cortical neurons toward their saturating nonlinearity (Wang et al., 2018) or modulates the synaptic properties or activation functions of a subset of cortical neurons (Harris and Thiele, 2011; Nadim and Bucher, 2014; Dipoppa et al., 2018). Second, while the signals recorded in this study were consistent with a prominent role for DMFC in RSG, other brain areas such as the thalamus (Guo et al., 2017; Schmitt et al., 2017) and prefrontal cortex (Miller and Cohen, 2001) are also likely to help maintain the observed dynamics. In particular, while we argue that the initial conditions in DMFC appear sufficient to set the speed of the dynamics within contexts, other areas may provide interval-dependent input during the Set-Go epoch (Wang et al., 2018). Recording from these areas would test this possibility. Third, although we assumed that recurrent interactions were fixed during our experiment, it is almost certain that synaptic plasticity plays a key role as the network learns to incorporate context-dependent inputs (Pascual-Leone et al., 1995; Kleim et al., 1998; Xu et al., 2009; Yang et al., 2014). Finally, it is possible that factors not measured by extracellular recording (e.g., short-term synaptic plasticity) contribute to both interval (Buonomano and Merzenich, 1995; Karmarkar and Buonomano, 2007; Murray and Escola, 2017) and contextual control (Stokes et al., 2013) in RSG. These open questions aside, our results provide a novel “computation through dynamics” framework to link neural activity to behavior.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Mehrdad Jazayeri (mjaz@mit.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experimental procedures conformed to the guidelines of the National Institutes of Health and were approved by the Committee of Animal Care at the Massachusetts Institute of Technology. Two adult monkeys (Macaca mulatta), one female (C) and one male (J), were trained to perform the Ready, Set, Go (RSG) behavioral task. Both subjects were pair housed and had not participated in previous studies. Monkeys were seated comfortably in a dark and quiet room. Stimuli and behavioral contingencies were controlled using MWorks (https://mworks.github.io/) on a 2012 Mac Pro computer. Visual stimuli were presented on a frontoparallel 23-inch Acer H236HL monitor at a resolution of 1920×1080 at a refresh rate of 60 Hz, and auditory stimuli were played from the computer’s internal speaker. Eye positions were tracked with an infrared camera (Eyelink 1000; SR Research Ltd, Ontario, Canada) and sampled at 1 kHz.

METHOD DETAILS

RSG Task

Task contingencies

Monkeys had to measure a sample interval, t_s, and subsequently produce a target interval t_t whose relationship to t_s was specified by a context-dependent gain parameter (t_t = gain × t_s) which was set to either 1 (g = 1 context) or 1.5 (g = 1.5 context). On each trial, t_s was drawn from a discrete uniform prior distribution (7 values, minimum = 500 ms, maximum = 1000 ms), and gain (g) was switched across blocks of trials (101 +/− 49 trials (mean +/− std)).

Trial structure

Each trial began with the presentation of a central fixation point (FP, circular, 0.5 deg diameter), a secondary context cue (CC, square, 0.5 deg width, 3–5 deg below FP), an open circle centered at FP (OC, radius 8–10 deg, line width 0.05 deg, gray) and three rectangular stimuli (2.0×0.5 deg, gray) placed 90 deg apart over the perimeter of OC with their long side oriented radially. FP was red for the g =1 context and purple for the g = 1.5 context. CC was placed directly below FP in the g =1 context, and was shifted 0.5 deg rightward in the g = 1.5 context. Two of the rectangular stimuli were presented only briefly and served as placeholders for the subsequent ‘Ready’ and ‘Set’ flashes. The third rectangle served as the saccadic target (‘Go’), which together with FP, CC, and OC remained visible throughout the trial. Ready was always positioned to the right or left of FP (3 o’clock or 9 o’clock position). Set was positioned 90 deg clockwise with respect to Ready and the saccadic target was placed opposite to Ready (Figure 1A).

Monkeys had to maintain their gaze within an electronic window around FP (2.5 and 5.5 deg window for C and J, respectively) or the trial was aborted. After a random delay (uniform hazard), first the Ready and then the Set cues were flashed (83 ms, white). The two flashes were accompanied by a short auditory cue (the “pop” system sound), and were separated by t_s. The produced interval t_p was defined as the interval between the onset of the Set cue and the time the eye position entered a 5-deg electronic window around the saccadic target. Following saccade, the response was deemed a “hit” if the error ò = | t_p − t_t| was smaller than a t_t-dependent threshold ò_thresh = αt_t +β where α was between 0.2 and 0.25, and β was 25 ms. The exact choice of these parameters were not critical for performing the task or for the observed behavior; instead, they were chosen to maintain the animals motivated and willing to work for more trials per session. On hit trials, the target, animals received juice reward and FP turned green. The reward amount, as a fraction of maximum possible reward, decreased with increasing error according to ((ò_thresh −ò /ò_thresh)^1.5, with a minimum fraction 0.1 (Figure 1B). Trials in which t_p was more than 3.5 times the median absolute deviation (MAD) away from the mean were considered outliers and were excluded from further analyses.

As an initial analysis of whether monkeys learned the RSG task across gains, we fit linear regression models to the behavior separately for each gain:

$$t_p={\beta }_o+{\beta }_1{t}_s$$

To quantify the difference in slopes between the two contexts. We also fit models with an interaction term across both contexts:

$$t_p={\beta }_0+{\beta }_1{t}_s+{\beta }_{2}g+{\beta }_{3}g{t}_s$$

If the animals successfully learned to apply the gain, β₃ should be positive.

We further applied a Bayesian observer model (Miyazaki et al., 2005; Jazayeri and Shadlen, 2010, 2015; Acerbi et al., 2012), which captured the behavior in both contexts (Figure 1E). Full details of the model can be found in previous work (Jazayeri and Shadlen, 2010, 2015). Briefly, we assumed that both measurement and production of time intervals are noisy. Measurement and production noise were modeled as zero-mean Gaussian with standard deviation proportional to the base interval (Rakitin et al., 1998), with constant of proportionality of of w_m and w_p, respectively. A Bayesian model observer produced t_p after deriving an optimal estimate of t_t from the mean of the posterior. To account for the possibility that the mental operation of mapping t_s to t_t according to the gain factor might be noisier in the g = 1.5 context than in the g = 1 context (Remington and Jazayeri, 2017), we allowed w_m and w_p to vary across contexts.

Recording

We recorded neural activity in dorsomedial frontal cortex (DMFC) with 24-channel linear probes (Plexon, inc.). Recording locations were selected according to stereotaxic coordinates with reference to previous studies recording from the supplementary eye field (SEF; Schlag and Schlag-Rey, 1987; Huerta and Kaas, 1990; Shook et al., 1991; Fujii et al., 2002) and presupplementary motor area (Pre-SMA; Matsuzaka et al., 1992; Fujii et al., 2002), and the existence of task-relevant modulation of neural activity. We sampled DMFC starting from the center of the stereotaxically identified region and moved outward a quasi-systematic fashion looking for regions with strong modulation during either epoch of the RSG task. In monkey C, recordings were made using single probes in seven sessions between 3 mm to 7 mm lateral of the midline and 0.5 mm posterior to 5.5 mm anterior of the genu of the arcuate sulcus. In monkey J, we recorded using paired probes (48 total channels, 1.5 mm separation between probes) in three sessions from between 3 mm to 4.5 mm lateral of the midline and 0.75 mm to 5 mm anterior of the genu of the arcuate sulcus. We conservatively refer to the recorded regions as dorsomedial frontal cortex (DMFC), potentially comprising SEF, Pre-SMA and dorsal SMA (no recordings were made in the medial bank). Recording sites are shown in Figure S2 and S11. Data were recorded and stored using a Cerebus Neural Signal Processor (NSP; Blackrock Microsystems). Preliminary spike sorting was performed online using the Blackrock NSP, followed by offline sorting using the Phy spike sorting software package using the spikedetekt, klusta, and kilosort algorithms (Pachitariu et al., 2016; Rossant et al., 2016). Sorted spikes were then analyzed using custom code in MATLAB (The MathWorks Inc.).

Analysis of DMFC data

Average firing rates of individual neurons were estimated using a 150 ms smoothing filter applied to spike counts in 1 ms time bins. We used PCA to visualize and analyze recorded activity patterns. For both animals, neural trajectories (Figure S2) and the KiNeT results (Figures S5–S8) were qualitatively similar. We thus performed the main analyses on the combined population of neurons across animals. Combined analysis would not be warranted if results were substantially different across animals. PCA was applied after a soft normalization: spike counts measured in 10 ms bins were divided by the square root of the maximum spike count across all bins and conditions. The normalization was implemented to minimize the possibility high firing rate neurons dominating the analysis.

When binning data according to increasing values of t_p, we ensured that all bins had equal number of trials, independently for each session. To average firing rates across trials within a group, we truncated trials to the median t_p, and averaged firing rates with attrition. Analyses of neural data were applied to all 10 sessions across both monkeys. For most analyses, we included neurons for which at least 15 trials were recorded in each condition and which had a minimum unsmoothed modulation depth of 15 spikes per second. Because the comparison of t_s - vs. t_p-related structure (Figure 8) required grouping trials into substantially more bins than the other analyses (14 vs. 7 or 5), we reduced the minimum number of trials required to 10 for this analysis (273 units; 95 from monkey C and 178 from monkey J). We did not find that the results of any of the analyses were dependent on the specific threshold chosen, and results were similar in individual subjects. We did not separately analyze trials immediately following context switches due to the low number of context switches per session (mean = 6.8 switches).

For visualization of neural trajectories in state space, we projected population firing rates onto axes along which responses were maximally separated with respect to context (“gain axis,” Figure 2B,C and “input,” Figure 3C) and additionally with respect to interval within context (“interval axis,” Figure 2B,C, and “initial condition,” Figure 3C) for the Set-Go epoch. For the Ready-Set epoch (Figure 2B), the gain axis was defined as the vector connecting population firing rates averaged over t_s across contexts at the time of Set. For the Set-Go epoch, the interval axis was defined as the vector between neural activity for the shortest and longest t_p averaged over time and context. This component of the activity was then subtracted away from the full activity, and the gain axis was defined as the vector between neural activity for the two contexts averaged over time and t_p. For the Ready-Set epoch, we additionally plotted PCs 1 and 2 with the context component removed (Figure 2B). For the Set-Go epoch, we additionally plotted PC 1 with the context and t_p components removed (Figures 2C and 3C). Axes used to plot the RNN activity were calculated using the same method (Figure 8B,C).

Kinematic analysis of neural trajectories (KiNeT)

We developed KiNeT to compare the geometry, relative speed and relative position along a group of neural trajectories that have an orderly organization and change smoothly with time. To describe KiNeT rigorously, we developed the following symbolic notations. Square and curly brackets refer to individual items and groups of items, respectively.

The algorithm for applying KiNeT can be broken down into the following steps: 1) Choose a Euclidean coordinate system to analyze the neural trajectories. We chose the first 10 PCs in the Set-Go epoch, which captured 89% of the variance in the data. 2) Designate one trajectory as reference, Ω_ref. We used the trajectory associated with the middle t_p bin as reference. 3) On each of the non-reference trajectories Ω_i (i ≠ ref), find {s_i[j]}_j with minimum Euclidean distance to {s_ref [j]}_j and their associated times {t_i[j]}_j according to the following equations:

$$\begin{gathered} t_i[j]=\underset{\tau }{argmin}\Vert {\mathrm{\Omega }}_i(\tau )-s_{\text{ref}}[j]\Vert \\ {s}_i[j]={\mathrm{\Omega }}_i(t_i[j]) \end{gathered}$$

Organization of trajectories in state space

The distances {D_i[j]}_j were used to characterize positions in neural state space of each Ω_i relative to Ω_ref. The magnitude of D_i[j] was defined as the norm of the vector connecting s_i[j] to s_ref [j], which we refer to as ${\mathrm{\Delta }}_i^{\text{ref}}[j]$. The sign of D_i[j] was defined as follows: for the trajectory Ω₁ associated with the shortest t_p, and Ω₅ associated with the longest, D_i[j] was defined to be negative and positive, respectively. For all other trajectories, D_i[j] was positive if the angle between ${\mathrm{\Delta }}_i^{\text{ref}}[j]$ and ${\mathrm{\Delta }}_5^{\text{ref}}[j]$ was smaller than the angle between ${\mathrm{\Delta }}_i^{\text{ref}}[j]$ and ${\mathrm{\Delta }}_1^{\text{ref}}[j]$, and negative otherwise.

Analysis of neural trajectories across contexts

We analyzed the geometry across gains in three ways. First, we analyzed the relationships between the two sets of trajectories. This required aligning the activity between the two contexts in time. To do this, we started with the aligned times found within each context, and using successive groups of neural states in the g = 1 context indexed by ${\left\{t_{\text{ref}}^{g=1}[j]\right\}}_j$, found the reference time ${\left\{t_{\text{ref}}^{g=1.5}[j]\right\}}_j$ in the g = 1.5 context for which the mean distances between neural states in paired trajectories (i.e. the first t_p bins of both gains, second t_p bins, etc.) were smallest. This resulted in an array of times from ${\left\{t_{\text{ref}}^{g=1.5}[j]\right\}}_j$, indexed by ${\left\{t_{\text{ref}}^{g=1}[j]\right\}}_j$, such that the trajectories across gains were aligned in time for subsequent analyses (Figure 6C). The second way that we analyzed geometry across gains was to collect trajectories across both gains, order according to trajectory duration, and run the standard KiNeT procedure. Finally, we measured the distance D^g between the structures using the across-context time alignment. For successive j, we measured the minimum distance between line segments connecting consecutive trajectories within each context. For five t_p bins, this meant four line segments for each context, and 4²=16 distances. We chose the minimum of these distance values as the value of D^g between the two structures. As a point of comparison, we generated set of “null” distances by splitting trajectories from each context into odd- and even- numbered trajectories and calculating the minimum distance between the sets of connecting line segments (Figure 6E).

Using KiNeT to calculate variance explained by interval and gain

To quantify the fraction of variance explained by task parameters, we used a marginalization procedure described previously (Kobak et al., 2016). Briefly, this is done by successively subtracting away neural activity averaged over each task parameter to create centered signals, then measuring the variance of these centered signals. This marginalization procedure, however, cannot be directly applied to neural activity when trajectories are of different duration. In the Ready-Set epoch, we tackled this problem by concatenating trajectories across t_s to create one trajectory for each gain.

For the Set-Go epoch, we first used KiNeT to transform all trajectories to sequences of states ({s_i[j]}_j) of equal length, and applied the marginalization on the resulting same-length sequences. With this procedure, we were able to compute variance associated with different factors. Interval (i.e. the five t_p bins) accounted for 21% of the variance in the full dataset, and 18% of the variance in PCs 1-10 used for KiNeT-related analyses. Gain accounted for 8% of the variance in the full dataset, and 7% of the variance in PCs 1-10. The interaction between Interval and Gain accounted for 6% and 1.5%, respectively, while condition-independent (i.e. time-related) variability accounted for 65% and 73% of the variance. This is consistent with previous studies which have found time varying, condition-independent signals to account for a large percentage of variance of neural responses in frontal cortex (Kaufman et al., 2016; Kobak et al., 2016).

Calculation of ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ for comparing variability within and across neural trajectories

For the analyses in Figure 7, we binned trials according to t_s, rather than t_p, and redefined ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ such that there was one vector for each ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ trajectory Ω_i, instead of one fewer (Figure 4A). For most values of i, this vector was calculated as:

$${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]=s_{i+1}[j]-s_{i-1}[j]$$

Because there was a finite number of t_s values, we could not compute ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ for i = 1 and i = 7 (s_{i − 1}[j] was not defined for i = 1 and s_{i +1}[j] was not defined for i = 7). Therefore, for the shortest t_s, we defined ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$ as s₂ [j] − s₁[j] (instead of s₂[j] − s₀[j]), and for the longest t_s, as s₇[j] − s₆[j] (instead of s₈[j] − s₆[j]).

Calculation of ${\mathrm{\Delta }}_i^t[j]$ for comparing variability within and across neural trajectories

For the analyses in Figure 7, ${\mathrm{\Delta }}_i^t[j]$ was calculated similarly to ${\mathrm{\Delta }}_i^{\mathrm{\Omega }}[j]$, with:

$${\mathrm{\Delta }}_i^t[j]=s_i[j+1]-s_i[j-1]$$

Because there was a finite number of time points, we could not compute ${\mathrm{\Delta }}_i^t[j]$ for j = 1 and j = N (where N is the number of states in Ω^ref; s_i[j−1] was not defined for j = 1 and s_i[j + 1] was not defined for j = N). Therefore, for the first time point, we defined ${\mathrm{\Delta }}_i^t[j]$ as s_i[2] − s_i[1] (instead of s_i[2] − s_i[0]), and for the last time point, to s_i[N] − s_i[N − 1] (instead of s_i[N+1] − s_i[N − 1]).

Recurrent neural network

We constructed a firing rate recurrent neural network (RNN) model with N = 200 nonlinear units. The network dynamics were governed by the following differential equation:

$$\begin{gathered} \tau \stackrel{.}{\mathbf{x}}(t)=-\mathbf{x}(t)+\mathbf{Jr}(t)+\mathbf{Bu}+{\mathbf{c}}_{\mathbf{x}}+{\mathbf{\rho }}_{\mathbf{x}}(t) \\ \mathbf{r}(t)=tanh[\mathbf{x}(t)] \end{gathered}$$

x(t) is a vector containing the activity of all units. and r(t) represents the firing rates of those units by transforming x through a tanh nonlinearity. Time t was sampled every millisecond for a duration of T = 3300 ms. The time constant of decay for each unit was set to τ = 10ms. The unit activations also contain an offset c_x and white noise ρ_x(t) at each time step with standard deviation in the range [0.01–0.015]. The matrix J represents recurrent connections in the network. The network received multi-dimensional input u through synaptic weights B = [b_c, b_s]. The input u was comprised of a gain-dependent context cue u_c(t) and an input u_s (t) that provided Ready and Set pulses. In u_s(t) Ready and Set were encoded as 20 ms pulses with a magnitude of 0.4 that were separated by time t_s.

Two classes of networks were trained to perform the RSG task with multiple gains. In the tonic-input RNNs, the gain-dependent input u_c(t) was set to a fixed offset for the entire duration of the trial. In contrast, in the transient-input RNNs, u_c(t) was active transiently for 440 ms and was terminated 50–130 ms before the onset of the Ready pulse. The amplitude of u_c(t) was set to 0.3 for g = 1 and 0.4 for g = 1.5. The transient network received an additional gain-independent tonic input of magnitude 0.4, similar to the tonic networks. Both types of networks produced a one-dimensional output z(t) through summation of units with weights w_o and a bias term.

$$z(t)={{\mathbf{w}}_{\mathbf{o}}}^T\mathbf{r}(t)+c_z$$

Network Training

Prior to training, model parameters (θ), which comprised J, B, w_o, c_x and c_z were initialized. Initial values of matrix J were drawn from a normal distribution with zero mean and variance 1/N, following previous work (Rajan and Abbott, 2006). Synaptic weights B = [b_c, b_s] and the initial state vector x₀ and unit biases c_x were initialized to random values drawn from a uniform distribution with range [−1,1]. The output weights, w_o and bias c_z, were initialized to zero. During training, model parameters were optimized by truncated Newton methods using backpropagation-through-time (Werbos, 1990) by minimizing a squared loss function between the network output z_i(t) and a target function f_i(t), as defined by:

$$H(\mathbf{\theta })=\frac{1}{\mid TI\mid }\sum _i\sum _t{(z_i(t)-f_i(t))}^2$$

Here i indexes different trials in a training set (I = different gains (g) x intervals (t_s) x repetitions (r)). The target function f_i(t) was only defined in the Set-Go epoch (the output of the network was not constrained during the Ready-Set epoch). The value of f_i(t) was zero during the Set pulse. After Set, the target function was governed by two parameters that could be adjusted to make f_i(t) nonlinear, scaling, non-scaling or approximately-linear:

$$f_i(t)=A(e^{\frac{t}{\alpha t_t}}-1)$$

For the networks reported, f_i(t) was an approximately-linear ramp function parametrized by A = 3 and α = 2.8. Variable t_t represents the transformed interval for a given t_s and gain g. Solutions were robust with respect to the parametric variations of the target function (e.g., nonlinear and non-scaling target functions). In trained networks, the production time, t_p was defined as the time between the Set pulse and when the output ramped to a fixed threshold (z_i = 1).

During training, we employed two strategies to obtain robust solutions. First, we trained the networks to flexibly switch between three gain contexts, the two original values (g =1 and g = 1.5) and an additional intermediate value of g = 1.25 for which the amplitude of u_c(t) was set to 0.35. However, the behavior of networks trained with the two original gains were qualitatively similar. Second, we set ρ(t) to zero, and instead, the context-dependent input, u_c(t) received white noise with standard deviation of 0.005, per unit time (Δt = 0 ).

QUANTIFICATION AND STATISTICAL ANALYSIS

Confidence intervals for KiNeT performed on trajectories binned according to t_p were computed by a bootstrapping procedure, randomly selecting trials with replacement 100 times. To test for statistical significance of metrics generated through the KiNeT procedure, we used bootstrap tests, where p was the fraction of bootstrap iterations for which the metric was consistent with the null hypothesis. For analyses relating neural variability to behavioral variability, we performed permutation tests in which null distributions were derived from 100 random shuffles with respect to t_p. Unless otherwise stated, significance of a measure for individual time points was set to p < 0.05. The results of KiNeT were similar for different methods of data smoothing.

KEY RESOURCES TABLE

REAGENT or RESOURCE	Source	Identifier
Experimental Models: Organisms/Strains
Rhesus macaque (Macaca mulatta)	Alpha Genesis	N/A
Software and Algorithms
MATLAB	Mathworks	https://www.mathworks.com/products/matlab.html
KiloSort	(Pachitariu et al., 2016)	https://github.com/cortex-lab/KiloSort
Other
Cerebus system	Blackrock Microsystems	http://blackrockmicro.com/neuroscience-research-products/neural-data-acquisition-systems/cerebus-daq-system/
Plexon V-Probes	Plexon	https://plexon.com/products/plexon-v-probe/
Eyelink 1000 eye tracker	SR Research	https://www.sr-research.com/products/

Highlights.

• Monkeys performed a timing task demanding flexible cognitive control

• The organization of neural trajectories in frontal cortex reflected task demands

• Flexible control was best explained in terms of inputs and initial conditions

• Recurrent neural network models validated the inferred control principles