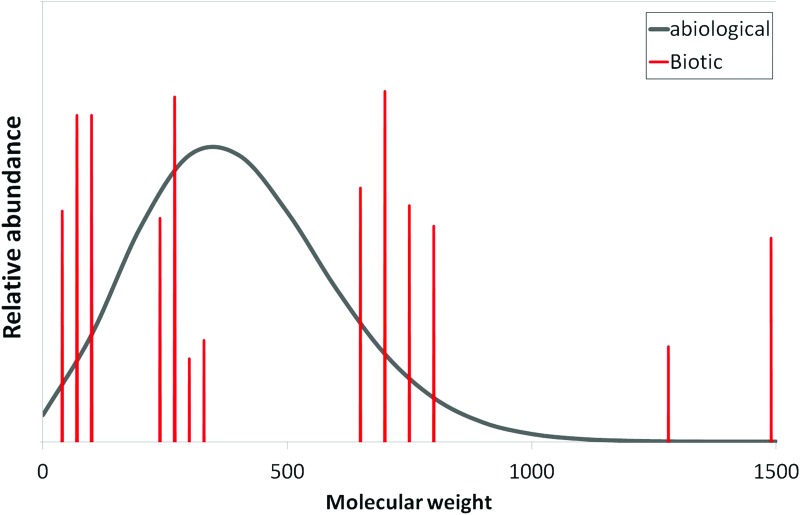
Abstract
We introduce a Bayesian method for guiding future directions for detection of life on exoplanets. We describe empirical and theoretical work necessary to place constraints on the relevant likelihoods, including those emerging from better understanding stellar environment, planetary climate and geophysics, geochemical cycling, the universalities of physics and chemistry, the contingencies of evolutionary history, the properties of life as an emergent complex system, and the mechanisms driving the emergence of life. We provide examples for how the Bayesian formalism could guide future search strategies, including determining observations to prioritize or deciding between targeted searches or larger lower resolution surveys to generate ensemble statistics and address how a Bayesian methodology could constrain the prior probability of life with or without a positive detection. Key Words: Exoplanets—Biosignatures—Life detection—Bayesian analysis. Astrobiology 18, 779–824.
Table of Contents
3. Detecting Unknown Biology on Unknown Worlds: A Bayesian Framework
3.1. Habitability in the Bayesian framework for biosignatures
5.3.1. Life as a coevolution with its planet: Earth as an example
5.3.2. Calculating conditional probabilities in biological evolution from past biogeochemical states
6.1. P(emerge): constraining the probability of the origins of life
6.2. Biological innovations and the conditional probabilities for living processes
7. A Bayesian Framework Example: Detecting Atmospheric Oxygen
References
Abbreviations Used
1. Introduction
Over the past two decades, thousands of exoplanets have been discovered orbiting other stars, inspiring a quest to understand the diversity of planetary environments that could potentially host life. Soon we will be positioned to search for signs of life on these worlds. Upcoming missions are targeted at obtaining atmospheric spectra of planets that may, like Earth, sustain liquid water oceans on their surfaces. To date, efforts to identify biosignatures on alien worlds have focused on the dominant chemical products and surface features of examples of life known from Earth, as well as some theoretically modeled cases (reviewed by Schwieterman et al., 2018, this issue).
If we are lucky, we may be able to identify “Earth-like” life on “Earth-like” worlds. If we are unlucky, and true Earths with Earth-like life are rare, our current approaches could entirely fail to discover alien life or to place constraints on the processes of life or their frequency. Expanded efforts are necessary to develop quantitative approaches to remote biosignature detection, applicable both in cases where the stellar or planetary context, or biochemistry is like Earth, and in cases where these diverge significantly from what is known from Earth.
With the exception of modern Earth, there are currently no known planets that can provide an unambiguous, easily detectable, true-positive biosignature of life—a so-called smoking gun. Even Earth throughout most of its history may not have had remotely detectable biosignatures, despite the presence of life (Reinhard et al., 2017). A major challenge is that the diversity of exoplanets greatly exceeds the variety of planetary environments found within our own solar system, such that the majority of exoplanets have no analogues in our solar system. Examples include water worlds, massive rocky planets, and small ice giants. The majority of discovered exoplanets orbit low-mass stars and are subjected to very different radiation and space plasma environments than planets in our own solar system (Coughlin et al., 2016; Twicken et al., 2016).
A metabolic product such as O2 might be a smoking gun signal of life on one world and not a biosignature at all on another, leading to the possibility of false positives (see Meadows et al., 2018, this issue, for an in-depth treatment of O2). Given the limited data we can collect on exoplanets (see review of observation capabilities in Fujii et al., 2018, this issue), and the stochasticity of planetary evolution (Lenardic and Crowley, 2012), we may only be able to predict the properties of exoplanets statistically (Iyer et al., 2016; Wolfgang et al., 2016). Our uncertainty in exoplanet properties such as bulk composition, geochemistry, and climate—due both to lack of knowledge and technical limitations on what we can directly infer from observational data—is a major hurdle to be overcome in our search for life outside our own solar system.
Another major hurdle is that we face significant uncertainty in our understanding of what life is (Cleland and Chyba, 2002; Walker and Davies, 2013). Our views of life and its defining features have expanded in recent years with discoveries of novel metabolisms (Hughes et al., 2001; Rappé and Giovannoni, 2003; Sogin et al., 2006; Li and Chen, 2015), and advances in synthetic biology and systems chemistry, which challenge our assumptions about what chemistries can participate in terrestrial life and in prebiotic chemistry (Chaput et al., 2012; Malyshev et al., 2014; Sadownik et al., 2016). From a first principles perspective, life is more readily understood in terms of dynamic processes than chemical products. Yet, in biosignature research for exoplanets, we so far have focused primarily on the chemical products of Earth's life.
The focus on chemical products has primarily been driven by practical limitations of current detection methods: current or planned exoplanet missions will be geared to detect the presence or absence of materials, leading to a focus on what materials could be biologically derived. In particular, this led to a focus on the idea of the smoking gun biosignature. O2 is the most notable example. However, even beyond the challenges associated with false positives, this particular smoking gun was not abundant in Earth's atmosphere for several billion years of its history (Lyons et al., 2014), rendering Earth's life undetectable by current methods for the first few billion years of Earth's history. Thus, even though the process of photosynthesis was present, our current product-based strategy would miss detecting it on inhabited worlds like early Earth. Ultimately, in our search to discover life, we are interested in answers to questions like: How frequently does photosynthesis (or other life processes) evolve in a given planetary context?
Beyond the biosignature community, life is not typically characterized in terms of its products, but instead in terms of its processes. Hallmark features of life, such as information processing, metabolism, reproduction, homeostasis, and evolution are all processes, which may generate different products in different evolutionary and environmental contexts. To advance our capabilities for life detection, next-generation biosignature research must bridge our product-based detection strategy with an understanding of the underling living processes, to identify signatures of life in diverse planetary contexts.
A process-based understanding will allow extrapolation to contexts different from Earth, where presumably the same universal processes of life (e.g., evolution, information processing, and metabolism) should operate, but may lead to very different outcomes—that is, to different remotely detectable products of life. The multitude of exoplanets discovered provides unprecedented opportunity to address fundamental questions regarding the nature and distribution of life with large statistical data sets, but we must first better understand the processes governing both planets and life. Bridging processes with detectable products necessitates new cross-disciplinary collaborations. To make progress, we must address the following questions:
What fundamental life processes could underlie the chemistry we can detect on exoplanets?
How do we infer the presence (or absence) of these processes?
How can understanding the processes of life inform new ways to identify and interpret the chemical signatures of life?
In what follows, we introduce a Bayesian framework appropriate and timely for the long-term goal of searching exoplanets for signs of life. A Bayesian method provides a language to define quantitatively the conditional probabilities and confidence levels of future life detection and, importantly, may constrain the prior probability of life with or without positive detection. To understand what is needed to quantify these probabilities, we review emerging and future developments of the study of life processes, their origins, their planetary contexts, the integrated tools necessary to model them, and the methodological tools necessary to detect their consequences. These inevitably require continued expansion of a cross-disciplinary community to develop the conceptual frameworks required to interpret the increasing (yet sparse) data upon which claims for the presence of life beyond our solar system will eventually be made.
Because we are focused on future directions, we note that the views presented herein do not represent community consensus. The myriad challenges that come with adopting a probabilistic framework for life detection drive the organization of this article, as resolving these challenges should be a priority for the exoplanet research community over the coming decade.
2. Setting the Stage: What Is Life? What Is a Biosignature?
Des Marais et al. (2002) defined a biosignature as an “object, substance, and/or pattern whose origin specifically requires a biological agent” (Des Marais and Walter, 1999; Des Marais et al., 2008). In this article, we follow this convention and refer to a substance or pattern that is known to be an indicator of biological activity (in a given planetary context) as a biosignature, for example, a “biosignature molecule” or “biosignature pattern.” More specifically, we quantify a biosignature as a molecule, pattern, or other signal that has a nonzero probability of occurring, conditioned on the presence of a living process (see Section 3 wherein we define the probability of occurrence, and its conditionality on the presence of life, formally P(data|life), and provide a quantitative definition for a biosignature within a Bayesian framework). Importantly, a biosignature does not imply life, it only implies a signal consistent with life. To qualify as evidence for life, a biosignature should be much more likely to be produced by living processes than by abiotic processes (see Sections 7 and 8 for an in-depth discussion, and Catling et al., 2018, this issue, for additional perspective). That is, a molecule, pattern, or signal must be able to be produced by life to be a biosignature, but it does not qualify as evidence for life unless life is the best explanation for its production in a given environmental context.
A challenge for developing a quantitative framework for assessing biosignature candidates is that life—the very thing we hope to measure—is notoriously difficult to define. For example, the definition of Des Marais et al. (2002) specifically refers to biological agency, yet we are far from a quantitative framework that precisely captures what we mean by “agent” (Barandiaran et al., 2009). The state of the field is such that >100 definitions for life exist, alongside many attempts to analyze them (Chyba and McDonald, 1995; Kolb, 2007; Benner, 2010; Trifonov, 2011; Bains, 2014; Mix, 2015). Some of the most common words used in defining life are given in Table 1, demonstrating just how far from consensus we truly are. Some have argued that it does not make sense to define life until we have a theory for life (Cleland, 2012; Walker, 2017). Cleland and Chyba (2002) compared the need of motivating theory for precisely defining life with how water became precisely defined as H2O only after the advent of molecular theory. A thorough review on the literature of attempts to define life is outside of the scope of this article. However, it is important to acknowledge the critical challenge we face in biosignature research due to ambiguities in our ability to precisely quantify what “life” is.
Table 1.
Common Words Used in Definitions for Life
| System | Organic | Genetic | Biological |
| Matter | Evolution | Internal | Capacity |
| Systems | Materials | Replication | Different |
| Environment | Reproduction | Change | Force |
| Energy | Growth | External | Form |
| Chemical | Information | Means | Functional |
| Process | Open | Molecules | Mutation |
| Metabolism | Processes | Order | Network |
| Organisms | Reproduce | Organisms | Objects |
| Organization | Complex | State | Organized |
| Complexity | Evolve | Time | Reactions |
| Self-reproduction |
Adopted from Trifonov (2011), with modifications to remove common filler words closely related to life (e.g., alive and living).
Owing to our lack of quantitative understanding of life, standards for the search for life have historically been qualitative in nature (true for both exoplanets and within the solar system). As an example, consider an approach to the search for life that follows the adage “I'll know it when I see it.” For different disciplines “it” means different things: biochemists might cite the molecular species that constitute “life-as-we-know-it,” such as DNA, RNA, and amino acids, whereas a physicist might discuss the emergence of collective behavior and so on. We outline some of these differences between disciplines, based on our own experiences as researchers in diverse areas given in Table 2. The table is not intended to be exhaustive (which would be a research program in its own right), nor representative of a majority opinion, but merely to highlight how diverse, and controversial, approaches to the question “what is life?” can be, just within the thinking of the authors of this article.
Table 2.
Disciplinary Perspectives on Signatures of Living Processes
| Scientific discipline | Typical measures of life and objects of study | Biosignature relevance |
|---|---|---|
| Mathematics | Theorems, proofs, calculus, algebra, number theory, geometry, probability and statistics, computational science (Chaitin, 2012). | The language of science. Quantitative frameworks of relationships in nature. |
| Physics | Motion of mass and electromagnetic energy, quantum behavior, organization, dissipative structures, collective behavior, emergence, information, networks, molecular machines (Schrodinger, 1943; Goldenfeld and Woese, 2011; Walker, 2017) | Conservation laws to constrain abiotic context. Systems interactions of biological processes |
| Chemistry, biophysics | Redox potential, Gibbs free energy (Hoehler, 2007; Smith and Morowitz, 2016) | Metabolic processes that alter the redox state of the environment |
| Microbiology, molecular biology, biochemistry | Cells, genes, genomes, RNA, proteins, metabolism (Woese, 1998) | Constraints on evolutionary path requirements for a type of life to emerge. Metabolic products that can be strictly biogenic. |
| Geologists, geophysics | Isotope fractionation, morphology, fossils (Knoll, 2015) | Planet formation factors that determine prebiotic elements. Plate tectonics to allow a carbon cycle. |
| Philosophy | Emergence, meaning, goal-directedness (many reviewed in Mix, 2015) | Definitions of intelligence, optimality. |
| Ecology | Ecosystem, community dynamics, scaling laws, keystone species (May et al., 1974; Pikuta et al., 2007; Amaral-Zettler et al., 2011) | System interactions that lead to dominance or community mixes of particular kinds of life, determining what biosignatures will be detectable. |
| Biochemistry, geochemistry | Elemental cycling (Schlesinger, 2013), serpentinization | Budgeting of the fluxes and stocks of particular molecules, wherein the net accumulated stock or phasing of fluxes may be detectable biosignatures. |
| Astronomy | Planetary-scale spectral signatures, molecular line lists, remote observation (Meadows, 2005; Seager, 2014; Seager and Bains, 2015; Seager et al., 2016) | Stellar context for life determines the radiative balance and elemental composition of a planet. Detection of biosignatures in planetary spectra from transits or direct imaging. |
To evolve into a scientific discipline with testable hypotheses, biosignature science needs to make quantitative predictions based on the hypothesis that life is or is not present in a given environment. Gradually, we are developing a language and the quantitative frameworks required for this, but further progress will require even greater convergence of the disciplinary perspectives given in Table 2 and more. No one discipline is “right” with respect to its perspectives on life, and each adds just one part of an emerging mosaic of what could be the most universal and fundamental properties of life. Here, we leverage this diversity of perspectives to develop a unified framework for how to assess the likelihood of life on a planet (or ensemble of planets) with a Bayesian method.
Our goal is to liberate our search strategies as much as possible from being entrained to specific definitions for life or its signatures, and instead to frame the problem in terms of what is observable and importantly what we can infer from those observables based on what is known about nonliving and living processes. As this article illustrates, we have much work ahead as a community to realize the promising future directions that could finally enable us to detect life on another world (and be confident in our assertion of success).
3. Detecting Unknown Biology on Unknown Worlds: A Bayesian Framework
To qualify as evidence for life in a given environment, a biosignature should be much more likely to be produced by living processes than by abiotic processes. For example, with some caveats (Meadows et al., 2018, this issue), current understanding provides confidence that geochemistry on a planet bearing liquid water will not generate an atmosphere containing >1% O2, so O2 is a priori a good biosignature. However, O2 as a biosignature may be rare: the likelihood of oxygenic photosynthesis on other worlds is unknown. In addition, the existence of oxygenic photosynthesis does not guarantee the presence of detectable atmospheric O2. Oxygenic photosynthesis on Earth predates the great oxidation event (GOE) at 2.33 Ga (Luo et al., 2016) by at least hundreds of millions of years (Buick, 2008), and O2 concentrations may not have been detectable to a remote observer until the past ∼500 million years of Earth history (Reinhard et al., 2017). By contrast, we might expect that if life exists on a world with hydrothermal systems and sulfate in its oceans, life will evolve to produce H2S; however, we are also confident that hydrothermal systems on such a world will make H2S abiotically, too. So, H2S on such a world would be an ambiguous indicator of life.
These examples illustrate how, to claim detection of life, measurements must be qualified by our expectations. Here, we introduce a Bayesian framework for quantifying our expectations in life detection and how new data change them, which permits the possibility of generalizing our search strategy beyond biosignatures of known life. We incorporate process-based approaches to constrain the probabilities of both living and nonliving processes to generate a particular observational signal, as required for Bayesian inference. Catling et al. (2018, this issue) suggest evaluation of four sets of criteria in order: (1) the stellar properties of the exoplanetary system (e.g., if the planet can support surface liquid water), (2) characterization of the exoplanet surface and atmosphere, (3) identification of biosignatures in the available data, and (4) exclusion of false positives. Their proposed scheme is based on current knowledge of biosignatures to increase confidence levels and is based on production of biosignatures similar to those of known life. Here, we focus on unifying diverse research areas within a common quantitative framework to better constrain likelihoods of living and nonliving processes, providing a means to organize current and future data in the assessment of upcoming observational data.
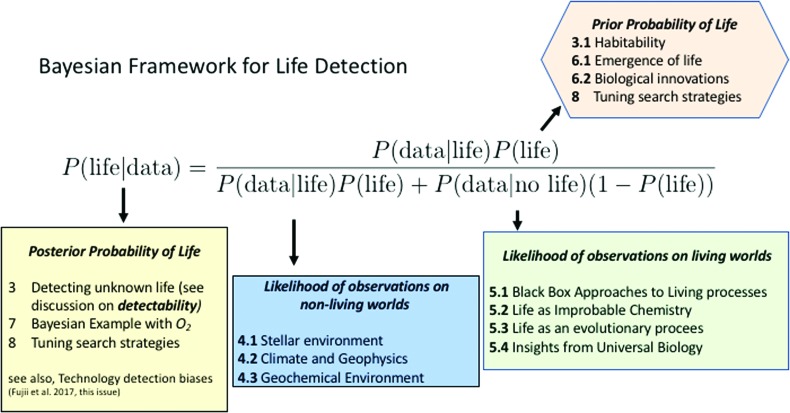
Bayesian inference permits evaluating the probability of a hypothesis (e.g., the presence of life) given a set of observed data. The posterior probability quantifies the probability of a hypothesis once the evidence has been taken into account. It is calculated based on prior probability, quantifying the probability a hypothesis is true, and a likelihood function, which quantifies the compatibility of the evidence with the hypothesis, that is, the probability of observing the data given the hypothesis. Specifically, a Bayesian claim of detection of life requires quantifying the following:
The likelihood of the signal arising due to living processes.
The likelihood of the signal arising due to abiotic processes.
The prior probability of the living process.
These likelihoods are cast in terms of conditional probabilities, where a conditional probability is the likelihood of observing an event, given another event has already occurred. For example, the conditional probabilities P(H2S|anaerobic respiration) and P(H2S|hydrothermal systems) quantify the likelihood of abundant atmospheric H2S arising due to living processes or to abiotic processes, respectively (here and throughout the “|” operator means “given” or “conditioned on” and indicates a conditional probability). H2S is not a good biosignature in the example provided earlier precisely because biotic production and abiotic production are both potentially important, such that we would estimate that P(H2S|anaerobic respiration) ∼ P(H2S|hydrothermal systems) without additional contextual information. Likewise, on modern Earth O2 is a good biosignature because the likelihood of it arising due to life, P(O2| oxygenic photosynthesis), is much higher than by the abiotic processes of photodissociation or volcanic outgassing, quantified as P(O2|abiotic), for example, we expect P(O2| oxygenic photosynthesis) >> P(O2|abiotic).
In modeling biosignatures, we have so far focused on the likelihood of generating a particular set of observational signatures, given the presence of life. However, soon we will have observational data to actually search for life. In analyzing these data, we are interested in the inverse problem: what is the likelihood of life, given a set of observational data?
A Bayesian framework permits determining the posterior probability of life (e.g., the likelihood of life, given an observation), for a given set of observational data, based on Bayes theorem:
 |
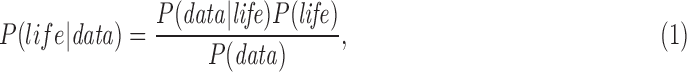where data is intended to indicate any observable indicative of life. This can refer to different kinds of observations: the statistics from planet surveys, the context of a particular planetary system, or the observation of the planet itself. Here, we will not be asking about the probability of the observation of a planet relative to instrument capabilities and distributions in the galaxy, as we leave this for the review by Fujii et al. (2018, this issue) and we are in any case interested in quantifying the likelihood of life on already identified targets. Instead, we focus on “data” with regard to direct observations of a planetary system and a planet that could host life. More often, a suite of these kinds of data will be utilized. Planetary statistics as well as insights from life on Earth can then provide theoretical support to interpret the direct observation of a planet by contributing to the relevant conditional probabilities.
For example, detection of a gas in an atmosphere requires a process-based model of that atmosphere to determine the contexts in which a certain mixture may be geochemically plausible and thus whether it is a signal of abiotic or biological processes (or both). The measured variables could be the near-infrared (NIR) absorbance features (NIR), the planet's mass (M), density (ρ), orbital parameters (o) (for transiting planets), and the expected planetary elemental composition (c), which may be based on the star's composition. Some contextual parameters will depend on the presence of life and some will not [e.g., in general (excluding significantly advanced technological civilizations), we do not expect biology to significantly contribute to a planet's mass], leading to differences in their treatment in a Bayesian framework (see also Catling et al., 2018, this issue). Of those listed here, only NIR absorbance features (NIR) are in general expected to depend on the presence of life. As such,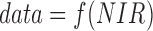 
. The remaining observables should, therefore, be considered as the context of the observation, and the likelihoods and priors must be conditioned on these. Thus, for example, P(data|life) = f(M, ρ, o, c) and P(data|abiotic) = g(M, ρ, o, c) are both functions of the planetary observables (these functions could also include stellar observables as well, or other atmospheric constituents that are not themselves biosignatures but provide context for interpreting them, see Section 7 and Meadows et al., 2018, this issue). In addition, these will in general depend on a number of variables that are not directly observable, which must be inferred. Obviously, it is a long way to go from the values of a planet's mass, density, etc. to predicting the observational signatures of life on its surface: hence the need for new cross-disciplinary collaboration.
The denominator of Eq. 1 is the total likelihood of observing a given data set, and can be expanded further:
 |
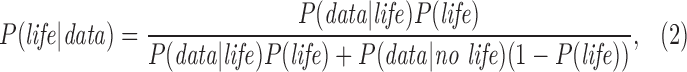where P(data| no life) is the probability of the data in the absence of life, and we have used the law of total probability to substitute P(no life) = 1 − P(life) for the prior probability there is no life.
P(life|data) is what we would like to know: the posterior probability of life, given a set of observational data. To determine the likelihood of life in a given data set, we must tightly constrain P(data|life) the probability of the observational data given life is present, and P(data| no life) the probability of the observations arising if life is not present. The latter term includes contributions from abiotic sources (life is absent) or experimental noise:
 |
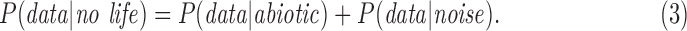In addition, knowledge of P(life), the prior probability of living processes, is required to assess the likelihood of life.
In Section 7, we explicitly treat Eq. 2 including contextual information by expanding terms as joint probabilities, for example, P(data|life) is expanded to P(data|life, Ci), where Ci includes relevant contextual information for the observation, such as the presence or absence of liquid water (see Section 7, Eq. 14 and also Catling et al., 2017). The measurement probability P(data|no life, Ci) can then be interpreted as the probability of the observable in the presence of life and relevant context. To simplify discussion of each term in the Bayesian framework presented in Eq. 2, in most of what follows (up to Section 7), we include context as implicit in the probabilities for living or nonliving processes as these must in any case be conditioned on what is known about the context for the observation.
The utility of the Bayesian approach is that it permits separating the calculation of the prior probability of life, P(life), from the likelihood of observational data if life is present P(data|life) or if life is not present P(data|abiotic). That is, it permits quantifying the detectability of life from a specific type of data, and thereby provides a tool for identifying promising targets in our search for life without necessarily knowing the prior probability of life itself, which is currently unconstrained (discussed more in Section 7). In the Bayesian framework, detectability can be quantified as
 |
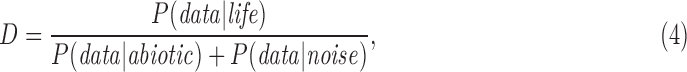where the denominator is again the probability that the signal was not generated by living processes. In the limit of no experimental noise
 |
Equation (5) provides an operational definition of detectability, providing a guide for our search for the best targets for observing life, in terms of both what to look for and where to look. As one example, the best places to look may or may not coincide with the places life is most likely, see, for example, the work of Desch et al. (2018). In other words, detectability provides a quantitative means to answer the question: given if we detect a candidate biosignature, can we be confident life produced it?
The detectability criterion is distinct from habitability: a world might be habitable, but could host life that is not detectable. The example of H2S previously mentioned provides one such example, as do cryptic or marginal biospheres, or phosphate-dependent life on water worlds (Desch et al., unpublished data). D > 1 is a quantitative threshold for the definition of a detectable biosignature. More detectable biosignatures have higher values of D. It should be clear that a given observational signal may be a detectable biosignature in one environment and not another, depending on the value of P(data|abiotic) and how the expected measurements for life and no life depend on context (see Sections 7 and 8 for worked examples). This is related to the point made earlier that a given signal may be a biosignature, but not be evidence for life if D ≤ 1.
To bridge observations to biosignatures, the surface chemistry, atmospheric mass, temperature profile, outgassing rate, and photochemistry of a planet must all be modeled, along with any putative biological processes that could be occurring on its surface. The modeled atmospheres can then be compared with observed spectral features, and the plausibility evaluated of the biogenicity of the observations. If no plausible abiotic model can reproduce the atmospheric context for the gas at the same level of detection, but a model including life processes can, then we could conclude that the gas is biogenic. In such cases, we should expect D >> 1. In such cases, confirmation of life becomes less sensitive to the unknown prior of the a priori probability of life (see, e.g., Sections 7 and 8).
A Bayesian approach requires good models for exoplanet properties in the absence of life to tightly constrain P(data|abiotic). In many ways, this seems like it should be easier than building models of inhabited planets: removing the biosphere could significantly simplify models. But, we do not know what Earth would be like without life. To model Earth without life requires extrapolation from uninhabited environments on Earth, from worlds considered uninhabited or from the identification and separation of biosphere processes from geological processes. Most of the input parameters to such models are not known.
One effort to make a distinction at the planetary scale between inhabited and uninhabited worlds was conducted by Krissansen-Totton et al. (2016) to compare global properties of the Earth's atmospheric chemical disequilibrium with that of other (presumably uninhabited) worlds in our solar system, including Venus, Mars, Titan, Jupiter, Uranus, and Earth. They quantified thermodynamic disequilibria in terms of the Gibbs free energy of the observed atmosphere minus that of atmospheric gases reacted to equilibrium. This approach was able to distinguish Earth's biogenic disequilibrium as a significant departure from that of a dead planet. The exhaustive chemical composition will not be known, of course, for exoplanets, so understanding of critical informative species through models and Bayesian inference will be important to applying similar methodology outside the solar system.
Features unobservable with current technology or at wavelengths accessible to a specific mission may become observable given more sensitive measurements or through instruments capable of measuring different wavelengths (e.g., for the case of GJ1214b; see Charnay et al., 2015). For example, volatile molecule chemistry outside the major constituents of Earth's atmosphere in Earth's atmosphere is not even known. The unpierceable “flatness” of the visible-NIR (0.6–2.5 μm) transmission spectrum of GJ1412b (Kreidberg et al., 2014) illustrates that not seeing a spectral feature does not necessarily mean that a gas is not there. Some currently unobservable properties could in the future become observable as technology advances. If no plausible abiotic model can reproduce observed spectral features at a given detection level, but no models including life processes can reproduce observed spectral features either, we cannot confirm the presence of life. The advantage of the Bayesian framework is that even these null cases will provide valuable constraints on estimates of priors (see Section 9), which can be updated as additional observations become possible.
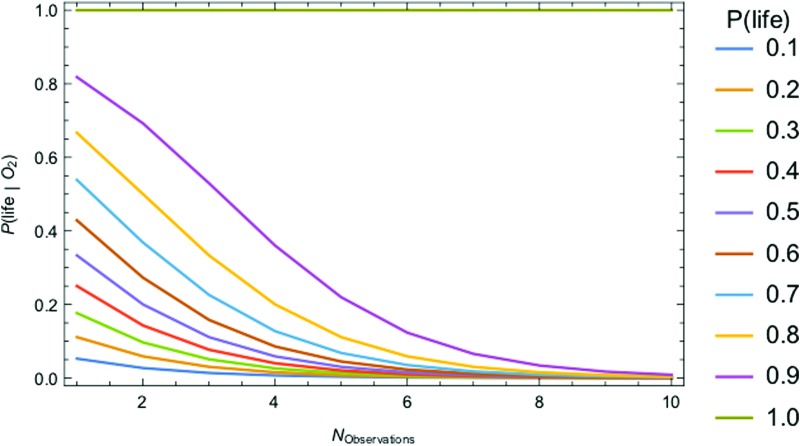
The most challenging parameter to constrain is P(life) itself, the very thing we aim to determine by detecting life. In the absence of a theory for life's origins, we do not have a means to calculate this probability ab initio. There may be biospheres that are undetectable because the signal-to-noise is too low or because they do not produce a measureable signal. This is a problem of detectability (e.g., D ≤ 1), which is distinct from the problem of estimating the probability of the prior occurrence of life on those worlds. Attempts have been made to estimate P(life) within a Bayesian framework by Carter and McCrea (1983) and more recently by Spiegel and Turner (2012). Both concluded that P(life) could be close to 1 or 0 based on our current state of knowledge (we know of only one inhabited planet, on which we have evidence of only one origin for life) and that evidence for a second sample of life is necessary to distinguish the likelihood that life is common from the likelihood it is rare. This is of course the goal of the exoplanet life-detection community. The question is, how can we develop the most effective strategies for searching for life, faced with the challenge that we have only trivial bounds on its prior occurrence?
One strategy is to focus on detectability, as already noted, since we can at least identify targets where we are most likely to detect life should it exist on a planetary surface. Another is to leverage the statistical data sets promised by future exoplanet science to constrain the value of this prior (see Section 9 for discussion).
P(life) will, in practice, be decomposed into probabilities for different living processes. We will not detect life as an abstract concept but as a specific chemical process or organization, and different processes or organizations have different probabilities. For example, the probabilities for life using oxygenic photosynthesis versus sulfate reduction will, in general, be different. We do not know the frequency of planets with oxygen-containing atmospheres, although we can model this for abiotically produced O2, and in the next 20–30 years, we will start to have measured frequencies. There are many stages of evolution in the history of life on Earth (Maynard Smith and Szathmáry, 1995; Bains and Schulze-Makuch, 2016), some depend strongly on history and others have occurred independently within the branching history of life—for example, multicellularity has evolved independently at least seven times (Knoll, 2011; Niklas and Newman, 2013)—although as far as we know all life on Earth shares common origins, so statements of evolutionary “independence” must always be made with caution due to an ultimate common evolutionary root for known life.
Assumptions about what biological processes are happening within a given planetary context must be made with care. These should be informed by knowledge of potential evolutionary pathways in a particular planetary environment, as well as how many distinct environments a planet could potentially have on its surface. Even on Earth, there is debate about the stages of evolution in the history of life, which may potentially confound our analysis when extrapolating to other worlds. This necessitates deeper connection between the exoplanet and evolutionary biology communities.
| Exoplanet Biosignature Terminology Quantified in a Bayesian Framework |
|---|
| Biosignature: an object, substance, and/or pattern of biological origin, such that observational data of the object, substance, or pattern yield P(data|life) > 0 |
| Detectability (D): confidence in biological origins for an observed biosignature signal, in the Bayesian framework D = P(data|life)/P(data|abiotic) (in the absence of noise). A biosignature is indicative of life if D > 1. (see Section 7, e.g., of why having D > 1 is important). |
| Habitable: conditions suitable for life, where the expectation of the prior probability of life is nonzero, P(life) > 0. It is commonly implied P(life) > 0 for “Earth-like” life (P(life)Earth-like) on planets with surface liquid water (as this delineates traditional boundaries of the “habitable zone”). |
| False positive: abiotic observations that mimic biologically produced observables, occurring when P(data|abiotic) is large, such that D ≤ 1. |
| False negative: biosignatures that are not detectable, occurring when P(data|life) is small, such that D ≤ 1, even in cases where life may be present. |
| Antibiosignature: an object, substance, and/or pattern that diminishes the likelihood the signal is generated by life, such that P(data|life) is less than in its absence (e.g., a given piece of contextual information C is an antibiosignature if P(data|life, C) < P(data|life), see Section 7) |
In what follows, we treat each relevant term in the Bayesian framework in turn. P(data|abiotic), P(data|life), and P(life) (Fig. 1). P(data|abiotic) and P(data|life) are more readily constrained, we, therefore, first assess what is known and future directions for calculating these likelihoods, before moving to the harder problem of constraining P(life). Toward the end, we provide an illustrative example of the Bayesian framework and potential directions for informing search strategies.
FIG. 1.
Conceptual diagram of the Bayesian framework for detection of exoplanet biosignatures, with section guides to this article. Color images available at www.liebertonline.com/ast
3.1. Habitability in the Bayesian framework for biosignatures
One of the most important metrics for guiding the search for life discussed within the exoplanet biosignature community is the concept of habitability, where a habitable world is one where we expect surface environmental conditions to be compatible with Earth life. It is outside of the scope of this article to provide a detailed discussion of habitability (see Catling et al., 2018; Meadows et al., 2018; Schwieterman et al., 2018, this issue), or any ambiguities associated with definitions of habitability in relation to either life-as-we-know-it or life-as-we-don't-know-it. However, it is important to acknowledge the relationship between standard definitions of “habitability” and its relationship with terms in the Bayesian framework.
The most commonly referenced definition of the “habitable zone” is the radiative habitable zone, defined to be that region around a star in which an Earth-like planet with an N2-CO2-H2O-dominated atmosphere can have a surface temperature that could support liquid water (Kasting et al., 1993; Kopparapu et al., 2014). The concept of habitability implicitly makes assumptions about both P(life) and P(data|life), such that P(life)Earth-like and P(data| life)Earth-like > 0 within the “habitable zone,” where P(life)Earth-like and P(data|life)Earth-like > 0 are the prior probability for Earth-like life (by whatever definition) and the likelihood of observing the data given Earth-like life, respectively. The former is concerned with assumptions about the origins of life and its evolutionary innovations (discussed in Sections 6.1 and 7.2, respectively), the latter is concerned with life's ability to evolve and thrive in habitable environments (discussed in Section 5.3).
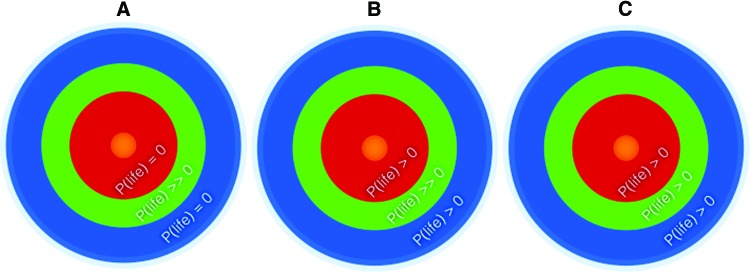
Depending on the expectation of how habitability maps to the habitable zone, different priors can be constructed for P(life) as a function of radius from a star (and likewise for P(data|life)). If one assumes inhabited worlds to be limited to a habitable zone, then the assumption is P(life) = 0 outside of the habitable zone (Fig. 2A). If one assumes that inhabited worlds are possible outside of the habitable zone, but much more likely inside the habitable zone, then P(life) > 0 but small, outside the habitable zone, and P(life) >> 0 inside the habitable zone (Fig. 2B) (and could be such that P(life)Earth-like > 0 in the habitable zone and 0 outside). If one assumes that the habitable zone is unrelated to the distribution of inhabited worlds, and life is equally likely at any radius from the host star, then P(life) = constant everywhere (Fig. 2C). These are only a fraction of all possible prior scenarios (there are as many as there are hypotheses about the prior probability of life), and are given with the intent to help clarify how assumptions about habitability could translate to the quantitative formulation of biosignature assessment within a Bayesian framework. For example, assuming an inner radius around a host star where conditions are too hot or radiating to allow habitable planets implies P(life) = 0 within that boundary.
FIG. 2.
Examples of the relationship between the canonical definitions of the habitable zone and our assumptions about P(life), based on different priors. (A) A prior where a nonzero prior probability for life is limited to the canonical habitable zone. (B) A prior where a nonzero prior probability for life is not limited to the habitable zone, but where P(life)inside_HZ >> P(life)outside_HZ. (C) A flat prior where the prior probability for life is equally likely at any distance from the host star (not dependent on the habitable zone). By definition, the concept of a habitable zone implies that we expect P(life) > 0 (but of unknown value) for worlds within the habitable zone. See Section 6.3 for further discussion on P(life) and the habitable zone. This article focuses on detectability as opposed to habitability. Many other distributions could be considered. These examples are given to clarify how habitability might integrate into the Bayesian framework we already outline, but we do not go into further detail on this topic in this article. Color images available at www.liebertonline.com/ast
Currently, the value of P(life) in the habitable zone, or outside it, is not well understood. P(data|life) is much better constrained, especially for oxygenic photosynthetic life (see Catling et al., 2018; Meadows et al., 2018; Schwieterman et al., 2018, this issue for discussion of biosignature observables in the habitable zone). We discuss how to advance our understanding of P(data|life) to other scenarios for alien biospheres in Section 5, and P(life) in Section 6.
In this article, we focus on the detectability of life, quantified in terms of likelihoods for biotic and abiotic signals, rather than habitability since the latter is discussed so extensively elsewhere (see Catling et al., 2018; Meadows et al., 2018; Schwieterman et al., 2018, this issue). Importantly, we do not necessarily need to know what makes a planet habitable to identify planets where biosignatures can be measured by our instruments (although habitability can of course provide guidelines for detectability). Detectability is distinct from habitability: a world might be habitable, but could host life that is not detectable. Alternatively, a world may be “uninhabitable” (based on our limited understanding of planetary habitability, or the definition of habitable used, e.g., lacking presence of liquid water on its surface), yet could host life that is detectable (e.g., utilizing a different solvent than liquid water). This distinction between detectability and habitability allows us to, in this article, expand the concepts of P(life) and P(data|life) implicitly underlying discussions of habitability and make them explicit and quantitative. By focusing on detectability, we hope the framework laid out in this article will be useful for guiding the future directions of biosignature science, and will readily accommodate changes to the community's understanding of planetary habitability.
4. P(data|abiotic)
To reliably distinguish worlds with life from those without it, we must improve our understanding of worlds without life and their observational signatures. That is, we must constrain P(data|abiotic). This is being pursued through modeling (Domagal-Goldman et al., 2014; Harman et al., 2015; Luger and Barnes, 2015; Krissansen-Totten et al., 2016; Schwieterman et al., 2016), but is a much more difficult problem observationally. To guarantee the absence of life, it would not be sufficient, for example, to make observations of planets outside of the habitable zone alone: those worlds may well be inhabited (see discussion in Section 3.1), and in any case may not be representative of planets inside the habitable zone (as illustrated by the differences between modern Earth and Venus).
Our assumptions regarding what worlds are likely to be uninhabited are most certainly incomplete—different forms of life may thrive in environments not compatible with our current concepts of habitability, for example, subsurface life may somehow have an unexpected connection to the atmosphere. Furthermore, planets within the habitable zone that have no obvious “smoking gun” biosignature may nevertheless be inhabited, as exemplified by the early Earth that possessed a photosynthetically active biosphere, where net production and consumption fluxes balanced rendering atmospheric biosignatures challenging to detect (Reinhard et al., 2017).
These examples make clear that more work must be done to improve models to identify observational signatures of planets without life if we are to understand planets with life. This can be done through a combination of detailed understanding of abiotic processes, as developed from theoretical models, and observational surveys that select with care likely uninhabited worlds for observation to constrain P(data|abiotic). By better constraining the observables of strictly abiotic planets, it will become easier to disentangle true-positive biosignatures from false-positive biosignatures and to understand cases where life might be present, but not detectable. Here, we focus on what is known and what needs to be known to determine P(data|abiotic), including constraining external planetary system parameters and internal planet characteristics in the absence of life. Each context considered—stellar environment, climate, and geochemistry—also impacts P(data|life) and P(life) as the likelihood and prior probability of life cannot be disentangled from its planetary context; we, therefore, also discuss these terms where appropriate.
4.1. Stellar environment
Stars both influence planetary processes and affect our ability to detect planetary properties, including any potential biosignatures. Catling et al. (2018, this issue) thoroughly summarize basic features of a parent star that influence or serve as indicators of a planet's atmosphere and potential development of life, including stellar age, effective temperature, composition (metallicity), spectral irradiance to the planet including flaring and particle flux, and whether it is part of a multiple-star and multiple-planet system. If we are to study the statistical probabilities for the emergence and likelihoods of life on different worlds, assessing the probability distributions of each of these stellar quantities throughout our galaxy is a key component, as each will affect the planet, influencing P(data|abiotic) and P(data|life), and its potential to be inhabited, influencing P(life).
Stellar surveys to characterize properties of stars of different masses, and hence temperatures, continue to add to our understanding of the potential impacts of stellar temperature on the search for life. The host star's temperature defines the radiative habitable zone, where we expect P(life) > 0 (at least for life like Earth's, see Section 3.1). Astronomers are able to measure a star's temperature typically to better than 2–5% providing an accurate measure of the stellar irradiation, at least for wavelengths dominated by the star's Planck (black body) function. A star's temperature is closely tied to its mass, and we have strong constraints on the mass distribution in the stars in our galaxy (Reid et al., 2002; Bochanski et al., 2010; Bovy, 2017). The relative abundance of spectral types is much greater for cooler long-lived stars, for which the habitable zone is closer to the star (0.1–0.4 AU). This makes for a higher probability of observing transiting planets in the habitable zone of cooler stars. The spectral energy distribution of a star's radiation will have different impacts on a planet's climate, due to the spectral properties of its atmospheric gas photochemistry and surface albedo, affecting potentially all three terms of the Bayesian framework: P(data|abiotic), P(data|life), and P(life).
The lifetime exposure of planets to damaging stellar ultraviolet (UV) radiation is a key environmental factor for calculating the likelihoods and priors in the Bayesian framework. Increased stellar activity, through UV emission and associated particle flux, can have dramatic effects on a planet's atmosphere (Segura et al., 2010; Luger and Barnes, 2015). Studies have examined effects on the destruction and generation of secondary products of biogenic gases (Segura et al., 2003, 2005; Domagal-Goldman et al., 2011; Hu et al., 2012, 2013; Hu and Seager, 2014). Although predicting atmospheric chemistry and biosignature gases through coupled radiative-convective/photochemical models is a mature method for Earth, atmospheric evolution of planets and the subsequent time dependence around perpetually UV-active stars are not understood.
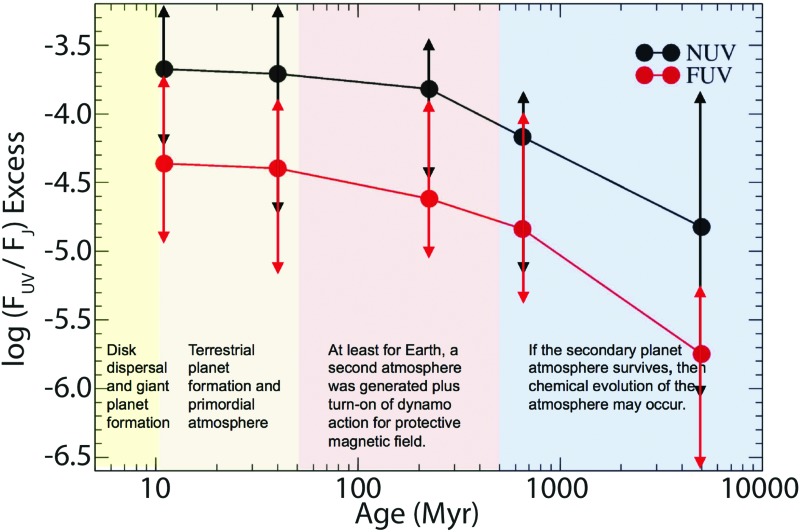
Unlike G-type stars like the Sun, M dwarfs are known to be active, with high emission levels and frequent flares when they are young, and this activity reduces as they age (see Fig. 3; Shkolnik and Barman, 2014). The large variability in M star UV outputs compared with Sun-like stars throughout their lives is just now being quantified and shows an increased level of activity toward cooler stars (Miles and Shkolnik, 2017). The effects of sustained high levels of stellar activity on planetary atmospheres have not yet been studied, in part, due to our lack of knowledge of UV flare rates and energies across stellar ages. However, efforts to resolve this are underway.
FIG. 3.
Median X-ray, FUV, and NUV excess fractional fluxes, including upper limits, as a function of stellar age for early M stars. The radiation environment changes in time and is more intense for young stars, potentially impacting the probability of life emerging P(life). Adopted from Shkolnik and Barman (2014). FUV, far-UV; NUV, near-UV. Color images available at www.liebertonline.com/ast
Explorations of the parent star role in planetary processes are recently expanding from one-dimensional (1D) models to three-dimensional (3D) general circulation model (GCM)-based techniques. Rigorously quantifying atmospheric and water vapor loss can be informed through 1D models, but is dependent on magnetospheric shielding, which requires improved constraints through measurements and additional modeling. Interactive chemistry in GCMs for exoplanet studies is still in its early stages; few GCMs have the radiation capability to study atmospheric compositions that differ substantially from modern Earth. In general, climatological GCMs can perform time slice equilibrium climate simulations given atmospheric composition (which may be provided by 1D models) or with photochemistry within Earth-like ranges. Conditions such as reducing atmospheres, absence of oxygen, condensation of greenhouse gases, and change in atmospheric mass at the edges of the habitable zone require further long-term model development. Thus P(data|abiotic) is currently relatively unconstrained with respect to how stellar activity impacts atmospheric observables.
This is, therefore, an important area for future research: M dwarfs have far-UV to near-UV flux ratios ∼1000 times greater than the Sun (France et al., 2016; Miles and Shkolnik, 2017), and represent 75% of stars. Small planets in the habitable zones of M dwarfs are common, and could have abiotic O2 and O3 levels two to three orders of magnitude greater than for a planet around a Sun-like star, due to hydrogen escape from stellar activity or photolysis of CO2 (Domagal-Goldman et al., 2014; Harman et al., 2015; Luger and Barnes, 2015). This is an example of a false positive biosignature of oxygenic photosynthesis (Domagal-Goldman et al., 2014; Tian et al., 2014; Harman et al., 2015; see also Meadows et al., 2018, this issue). False positives suggest the presence of life, but occur where P(data|abiotic) is comparable with (or larger than) P(data|life) confounding interpretation of biogenicity.
Conversely, M stars may also become quiescent as they age such that they emit very little UV. The lack of UV to generate ·OH radicals can increase the detectability of biologically generated gases that would otherwise be removed by OH (Segura et al., 2005), increasing P(data|life). It is, therefore, critical to determine the lifetime exposure of such planets to stellar UV radiation, from quiescent and flare emission levels, and explore the limitations on our ability to predict the resultant atmospheric properties.
In terms of detectability, we should expect that for most observables, we might associate as biosignatures, D > 1 in some environments, but not others. For example, O2 can accumulate to high levels on lifeless planets due to runaway water loss around premain sequence M stars (Luger and Barnes, 2015), as already discussed. The observation of collisionally induced absorption of O4 (e.g., Misra et al., 2014) would allow one to calibrate P(data|abiotic) for this process. In this case, P(O2|abiotic) would be large, where the presence of atmospheric O2 is the data due to knowledge of these abiotic processes, and we should expect D < 1. In contrast, a planet in the habitable zone of a G-type star with properties similar to modern-day Earth (liquid water, ∼1 bar of total atmospheric pressure, percentage levels of O2, and relatively low levels of CO2 and CO) strongly suggests a photosynthetic origin for atmospheric oxygen (Meadows, 2018, this issue)—in this case it is P(O2|life) is large permitting the possibility D > 1. Again, evaluating P(data|abiotic) for the presence of O2 requires contextual information about stellar environment, background atmospheric characteristics, and co-occurring atmospheric species, but this case would yield P(data|life) >> P(data|abiotic) (see Section 7 for a worked toy example).
As we increase our knowledge of how planetary systems are influenced by stellar properties, through modeling and observations, there is a rich set of relevant phenomena to explore. Photochemistry interacting with radiation from different stellar types can inform our understanding of atmospheric chemical disequilibrium and detectable primary and secondary biogenic species, and research on the effect of the parent star's UV flares on prebiotic chemistry for the origins of life will be useful for constraining P(life) (Airapetian et al., 2016).
4.2. Climate and geophysics
The distribution of climate types and their variation in time result from star–planet orbital dynamics, and interaction between landmass and ocean configuration with circulation patterns. To address these nuances, in recent years 3D GCM of rocky planet climates has emerged as a viable means to characterize circulation patterns on a planet and its potential to host detectable life (Leconte et al., 2013; Way et al., 2016). Although 1D models remain extremely useful (Schwieterman et al., 2018, this issue), GCMs offer a tool to explore the variation in climate over a planet. Their strengths are that they offer self-consistent, spatially, and temporally varying treatment of moist convection, clouds, atmospheric/ocean transports, and surface ice. They can be used to investigate the effects of obliquity (Williams and Holloway, 1982; Abe et al., 2005), eccentricity (Williams and Pollard, 2002), and rotation rate, including tidal locking (Del Genio et al., 1993; Del Genio and Zhou, 1996; Joshi et al., 1997; Joshi, 2003; Merlis and Schneider, 2010; Edson et al., 2011; Heng et al., 2011; Pierrehumbert, 2011; Wordsworth et al., 2011; Yang et al., 2014), providing a direct way to model the impact of exoplanet observables on climate, necessary to constrain the values of P(data|abiotic) (and also P(data|life)). Where 1D models are subject to extreme responses, the circulation patterns in GCMs generally have moderating effects (Shields et al., 2013), broadening the expected range where P(life)Earth-like > 0 compared with that predicted by average conditions alone (assuming P(life)Earth-like = 0 outside of the canonical habitable zone).
GCMs can be used to broaden concepts of superhabitability, where a world is superhabitable if it can support a larger habitable surface area than Earth (Heller and Armstrong, 2014). Examples discussed by Heller and Armstrong (2014) include planets with more surface area for liquid water than the Earth has, or more islands with a higher ratio of contact between land and sea than the Earth. Given that we do not understand the conditions from which life arose, defining superhabitability is a challenge. For superhabitable worlds, P(data|life) is expected to be larger than it is for Earth-like worlds, as great habitable area lends to higher signal strength. GCMs can also be used to study habitability of less Earth-like planets (expanding the potential for life to worlds where P(life) would otherwise be assumed to be close to 0).
The role of ocean/continental configuration in influencing the distribution of planetary surface conditions has yet to be explored, with existing studies limited largely to either Earth's continents or all land or aqua planet configurations. Some studies have experimented with having a planet with one hemisphere covered by land and the other by ocean (Joshi, 2003), continents at high or low latitudes at different obliquities (Williams and Pollard, 2003), an equatorial supercontinent, an aqua planet, and planets with configurations similar to modern Earth continents (Charnay et al., 2013). Life feeds back to a planet's climate by altering the composition of greenhouse gases in the atmosphere and changing surface albedo and water vapor conductance, which may reinforce or enhance the detectability of life. The potential of GCMs to characterize the extent and temporal variability of surface conditions remains to be explored. Future directions should add more realistic physics for alternative planetary contexts than Earth and focus on generating large statistics for the likelihoods of a given set of observations for both living and nonliving worlds.
GCMs also offer a means to distinguish clouds from hazes (a potential biosignature) and to map climate zones over the planet's surface to surmise potential productivity, providing models to predict P(data|life). For example, differential insolation on rocky planets can drive up-down circulations that cause large spatial differences in cloud cover and altitude, showing what windows through the atmosphere may be available to observe biosignatures for different stellar types and planetary rotation rates. Other questions to explore include whether a haze is universally a feature of homogeneous planets, or, in cases where atmospheric water vapor is detected, whether surface liquid water could be inferred through modeling, informing P(data|abiotic).
Given the large parameter space, a perturbed parameter ensemble approach is often used with Earth climate modeling and could be used to establish a library of a large number of GCM simulations covering a wide range of conditions. From this data set, the probability that observed properties arise from specific features such as clouds or hazes can be inferred, generating the large statistics necessary for getting tight bounds on both P(data|abiotic) and P(data|life). In addition, conditions conducive to observing biosignatures could be identified for target selection on future missions, or the large statistics may reveal patterns to classify planetary climates (Forget and Leconte, 2014).
Surface albedo plays a principal role in the surface energy balance of a planet, but exoplanet-observing missions in the near future will not be able to measure this directly. GCM studies typically prescribe the land surface albedo of a hypothetical planet to 0.1–0.3 (Abe et al., 2005, 2011; Wordsworth et al., 2011; Yang et al., 2014). However, mineral shortwave albedos can range from black volcanic rocks to white salts. A small change in albedo can significantly change climate. For example, for an instellation S (W/m2) and albedo a, the stellar energy intercepted per surface area of a planet is E = S(1-a)/4. Therefore, a change in a of, say, da = 0.01 with S = 1361 W/m2 (the estimated solar constant; Kopp and Lean, 2011) gives an energy balance change of 3.4 W/m2. There is currently lack of a theory for planetary evolution that would allow prediction of a planet's surface albedo or distribution of albedos, which is a necessary parameter for P(data|abiotic). A community effort is needed to develop such a theory, which would depend on element abundances, processed by mantle melting, crystallization, the presence of water, and other system factors.
Other parameters difficult to constrain from observational data as well as theory include atmospheric pressure, atmospheric mass, land/ocean ratio, land topography, and ocean depth. With near-term missions, it may be possible to measure obliquity, eccentricity, and rotation rate through photometric temporal variability (see Fujii et al., 2018, this issue). Theory may also constrain rotation and obliquity in some cases: planets sufficiently far from their star will have had little tidal evolution, and rotation and obliquity will be hard to constrain from physics alone (Rodríguez et al., 2012).
4.2.1. Coupled tectonic–climate models
In addition to surface properties, determining the composition and internal structure of exoplanets from orbital and transit data is moving toward statistical approaches (Rogers and Seager, 2010; Dorn et al., 2015). Composition sets the stage for quantifying life potential in terms of available biological building blocks and their likelihoods. How those building blocks are cycled over the geological evolution of a planet to allow for conditions conducive to the development and evolution of life brings a temporal element, expanding the necessity of applying statistical approaches. GCMs are being used to investigate potential climatic states that may or may not be favorable for life. As GCMs perform time slice equilibrium simulations, they are effectively instantaneous models when it comes to planetary evolution—they do not track variable greenhouse forcing due to volcanic–tectonic activity on geological timescales.
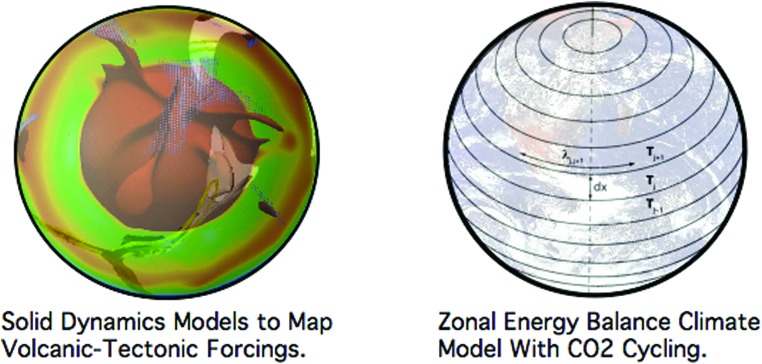
Climate variability, on an Myr timescale or greater, is influenced by a greenhouse forcing that is modulated by a balance between the rates at which CO2 is expelled from volcanoes and drawn down from the atmosphere through chemical weathering processes (Walker et al., 1981; Staudigel et al., 1989; Dessert et al., 2001; Coogan and Dosso, 2015). The global rate of CO2 outgassing is governed by the character and pace of a planet's volcanic activity. Chemical weathering is mechanically paced by the rates at which new surfaces are created (Sleep and Zahnle, 2001; Whipple and Meade, 2004; Roe et al., 2008; Lee et al., 2013, 2015). The protracted clement climate of the Earth is, in part, a consequence of this long-term carbon cycle not having gone so far out of balance as to initiate a transition to a runaway greenhouse or a protracted hard snowball state. The degree to which this may be possible for planets beyond Earth, over a significant portion of their evolution, remains unanswered. Addressing that question has moved the community toward coupled tectonic–climate models, as shown in Figure 4.
FIG. 4.
Modeling methodology used to explore the effects of variable volcanic–tectonic activity on planetary climate. Solid planet dynamic models of coupled mantle convection and surface tectonics (Lenardic et al., 2016) are used to map out variations in volcanic and tectonic activity over time for a range of planetary parameter values (left image). Results from the solid dynamics models are then used to generate volcanic–tectonic forcing functions for zonal energy balance climate models (Pierrehumbert, 2010) that include volcanic degassing, topography generation, and CO2 drawdown from the atmosphere due to surface weathering (right image). Color images available at www.liebertonline.com/ast
Using coupled tectonic–climate models to address life potential will demand a statistical treatment given the number of parameters associated with coupled models and given the potential of planetary scale transitions over time. The capacity of the global climate of a planet to transition between multiple stable states has long been acknowledged (Budyko, 1969). Such climate transitions were initially investigated in terms of how orbital forcings could trigger them. However, volcanic–tectonic forcings can also trigger transitions in the climate state of a planet (Lenardic et al., 2016), and it has been argued that the volcanic–tectonic state of a planet can itself also transition between multiple states (Sleep, 2000). The potential of bistable tectonic behavior (multiple tectonic states existing under similar parameter conditions) has now been demonstrated by several studies (Crowley and O'Connell, 2012; Weller et al., 2015; Bercovici and Ricard, 2016).
Tectonic and climate transitions, over timescales of planetary evolution, bring historical thinking into the mix in a direct way for models that explore planetary conditions over time, permitting the possibility of constraining P(data|abiotic) and P(data|life) for different stages of planetary history and for different histories. This introduces the potential of variable paths for planetary evolution springing from initial conditions that can be very similar: acknowledging this in a modeling framework moves us away from a classical deterministic approach aimed at prediction. Instead, the objective is to map planetary potentialities in terms of their likelihoods, constrained within the bounds of physical and chemical laws. For example, a goal is to determine the likelihood a planet of a given size and composition (with uncertainties) orbiting a particular star in a particular orbital path, conditioned on a specified geological time window, variable initial formation conditions, and time variable climate forcings (orbital and/or volcanic–tectonic). Constraints on these planetary potentialities would yield a significant improvement in our ability to produce relative values of P(data|abiotic) and P(data|life)—these will be crucial to maximizing detectability of biosignatures.
4.2.2. Community GCM projects for generating ensemble statistics for P(data|abiotic) and P(data|life)
Many of the planetary parameters to configure a GCM will not be measurable, or will be difficult to obtain given available observation technology, and require large computational resources. Furthermore, efficient sampling of the parameter space is necessary for climate sensitivity studies and generating statistical models. Constraining the parameter space theoretically is much needed and provides avenues for cross-disciplinary research. This may seem like a daunting task, but the initial steps are well within reach. GCM models, for example, can address long-term temporal evolution through ensemble simulations that capture time slice equilibrium climates along some evolutionary path. For example, Way et al. (2016) performed model experiments run under different solar forcings associated with different points along the Sun's luminosity evolution. At the same time, models of volcanic–tectonic evolution have been progressively mapping potential volcanic–tectonic forcings that can be linked to simplified climate models (Lenardic et al., 2016).
As the use of GCMs becomes more common to explore climates of exoplanets as well as of solar system planets, model intercomparison studies will be necessary to gain confidence in their predictions. These complex models are subject to their own biases as a result of particular choices in numerical resolution and representation of physics. The Earth climate modeling community has coordinated projects for model intercomparisons that the exoplanet community may consider emulating. The Palaeoclimate Modelling Intercomparison Project (Joussaume et al., 1999; Pinot et al., 1999; Saito et al., 2013) began in the 1990s to compare studies of the Holocene. These studies also contribute to the Climate Model Intercomparison Project, established in 1995 under the World Climate Research Program (Meehl et al., 2000), which coordinates studies covering preindustrial, current, and future climate scenarios. These experiments serve as important material for the Intergovernmental Panel on Climate Change. The modelling intercomparison project serve to define common climate scenarios, compile data sets for model inputs and evaluation, and agree on common model diagnostics to aid intercomparison (Eyring et al., 2015). Modeling groups contribute ensembles of simulations that are archived for community analysis, providing insights into model biases and strengths and weaknesses in scientific understanding of specific aspects of climate. The exoplanet community could utilize similar methods.
4.3. Geochemical environment
As discussed previously, the simplest approach for identifying a promising biosignature would be to search for a “smoking gun” (which we discussed is unlikely to exist), something that on its own provides strong evidence for a biosphere (e.g., for which P(data|life) >> P(data|abiotic)). However, this type of signal is intrinsically vulnerable to “false positives” as discussed in Section 4.1 (see also Meadows et al., 2018, this issue and the example Bayesian treatment in Section 7): contextual information about the geochemical environment is critical for accurately evaluating P(data|abiotic). Another challenging problem is that of false negatives (Reinhard et al., 2017), or scenarios in which biological activity at the surface is overprinted by internal recycling and thus remains cryptic to characterization through atmospheric chemistry. Oxygen again provides an instructive example (see Meadows et al., 2018, this issue)—it may have taken hundreds of millions of years or more (Lyons et al., 2014) subsequent to the emergence of oxygenic photosynthesis on Earth before O2 (or O3) could be remotely detectable in Earth's atmosphere.
The mechanisms underpinning the timing of this biogeochemical disconnect are still not entirely understood, but doubtless involve large-scale planetary processes unfolding on protracted timescales, such as hydrogen escape from the upper atmosphere (Catling et al., 2001), differentiation of Earth's upper crust (Lee et al., 2016), and potentially a range of other factors. An important challenge moving forward will be to distinguish between the P(data|life) values of false negatives and the P(data|abiotic) of truly lifeless worlds for a range of potential biosignatures. This provides strong impetus for the development of robust models for the range of geochemical environments produced by sterile planets.
A complementary approach toward evaluating individual biosignature species is to search for chemical disequilibrium within a planetary atmosphere, or between an atmosphere and a planet's surface (Hitchcock and Lovelock, 1967). For example, it has become common wisdom that atmospheric chemical disequilibrium on a planet can be a strong indication of life (Lovelock, 1965). However, free energy from stellar irradiance as well as from volcanic outgassing, tidal energy, and internal heat all lead to disequilibrium even on a dead planet. Rigorous efforts to quantify disequilibria specifically associated with life are an active area of research. Different metrics that have been proposed, including fluxes required for maintaining disequilibrium (Seager et al., 2013a; Simoncini et al., 2013; Gebauer et al., 2017), and topological measures of the directionality of chemical reaction networks in an atmosphere (Estrada, 2012) (see Section 6.4.1 for more discussion of network theory applied to planetary atmospheres).
Krissansen-Totton et al. (2016) use a metric of thermodynamic disequilibrium for solar system planets, quantified as the difference between the Gibbs energy of observed atmospheric and (in the case of Earth) surface oceanic constituents and the Gibbs free energy of the same atmosphere and ocean if all its constituents were reacted to equilibrium, under prevailing surface conditions of temperature and pressure (for those planets with surfaces). This measure is able to show that Earth's atmospheric chemical disequilibrium is orders of magnitude greater than that of the other solar system planets, and is characterized less by the simultaneous presence of O2 and CH4 than by the disequilibrium between N2, O2, and a liquid H2O ocean. It is important to note that the diagnostic potential of this thermodynamic biosignature on Earth relies to some extent on being able to delineate both the presence and basic characteristics (e.g., ionic strength) of a surface ocean (Krissansen-Totton et al., 2016), which provides another example of the type of broader contextual information required for evaluating both P(data|abiotic) and P(data|life).
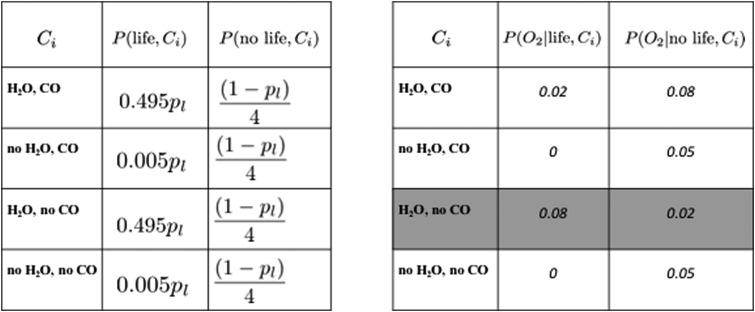
Interpreting atmospheric chemical disequilibrium as a biosignature depends very much on the geochemical and planetary system context. The disequilibrium may be tipped in different directions if the extant life primarily derives its energy from the available chemical disequilibrium or from an endergonic utilization of stellar energy for photosynthesis. An observed disequilibrium maintained by the star or photochemistry may also be interpreted as an antibiosignature, indicative of available energy that is not being exploited by life. In the presence of an antibiosignature, the likelihood P(data|life) is decreased relative to its value in the absence of the antibiosignature (CO in the presence of H2O shown in Figure 15 is an antibiosignature in this respect).
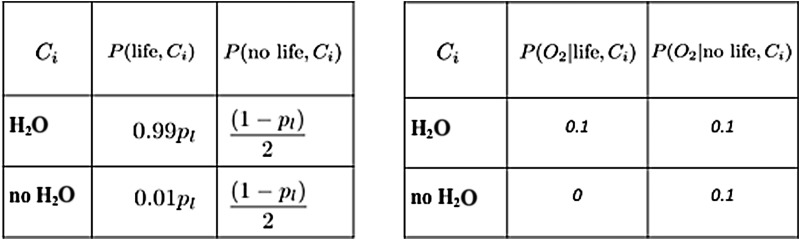
FIG. 15.
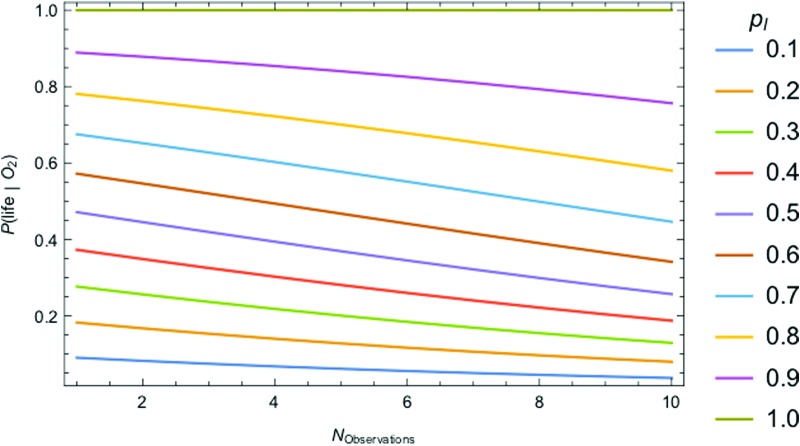
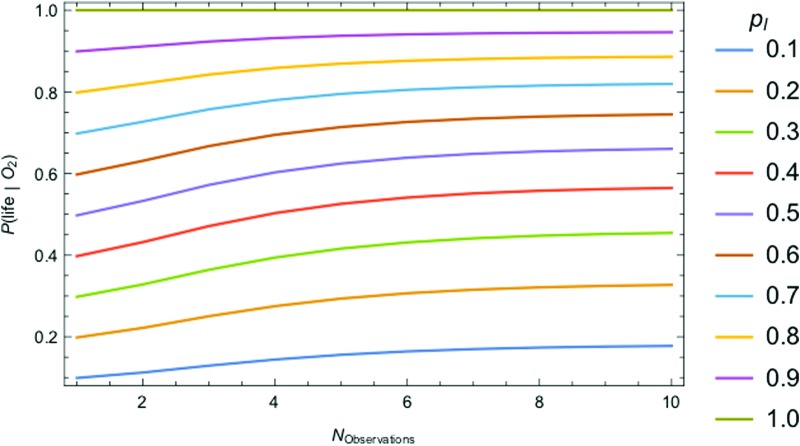
Parameters for the toy model case of detecting O2 with additional contextual information of the joint probability of O2, H2O, and CO for living and nonliving worlds. The prior probability is again distributed between our two hypotheses, either life produced the signal (with total probability pl) or it did not (with probability 1-pl): we assume life is much more likely in the presence of H2O than not, and uniformly distributed over worlds with CO. The likelihoods of observing O2 are set to illustrative values of 10% for life and 20% for no life, where nonliving processes are most likely to support atmospheric O2 when H2O and CO are also present, and living processes are most likely to support atmospheric O2 when H2O is present but CO is not. Highlighted in blue is the case where D > 1, i.e., P(O2|life) > P(O2|no life).
The counterargument to suggesting a given disequilibrium is an antibiosignature is of course the evolutionary one that life on that world has not evolved mechanisms to exploit the relevant energy source; alternatively, the kinetics of consumption through microbial metabolism may be outpaced by abiotic production fluxes because biological consumption is limited by some other factor. Future exploration of disequilibrium metrics are needed to investigate other atmospheric compositions, unusual gases, surface (liquid bodies and rock) reactions, orbital temporal effects, planetary evolution pathways that affect outgassing and internal heat, alternative coupled ecosystem–planet interactions, kinetic metrics to deduce surface fluxes of biogenic and abiotic gases, and the uncertainties in determining species abundances, temperature, and pressure in future remote observations. Generating statistical data sets quantifying how different planetary parameters and living processes affect atmospheric disequilibria will place new constraints on P(data|abiotic) and P(data|life).
4.3.1. Anticipating the unexpected: statistical approaches to characterizing atmospheres of non-Earth-like worlds
One approach that sidesteps the need to either define the biosignatures produced by life or the processes that produce them is to search for any signal that is unexpected from an abiological model of a planet. Recalling Eq. 5, we can maximize detectability by either maximizing the numerator, P(data|life), or minimizing the denominator, P(data|abiotic). Even if there is an extremely small probability that a signal is consistent with life, we can still identify it as a biosignature if we can demonstrate there is yet a smaller (perhaps 0) probability for the signal to be consistent with an abiotic origin. As highlighted previously (and in Catling et al., 2018, this issue), there are many challenges associated with modeling abiotic production of biosignatures on Earth-like worlds. The next frontier challenge to address is that most work so far has assumed that we know what gases we are modeling, with a bias toward gases that are potential biosignatures for life on Earth. We must develop strategies to avoid this Earth-centric approach if we are to determine P(data|abiotic) and P(data|life) for the many worlds that do not fit the narrow box of Earth-like parameters.
Expanding beyond Earth-like worlds was the impetus behind Seager et al.'s (2016) “All Small Molecules” project. This project, explicitly aimed at volatiles that could be atmospheric signatures, seeks to determine all gases that could stably accumulate in any atmosphere. There are a very large number of such molecules, and so filters are necessary to reduce this to a manageable number. In their initial study, Seager et al. (2016) limited the data set to molecules with no more than six nonhydrogen atoms that were likely to be stable in the presence of liquid water. The size limit was imposed because the number of possible molecules goes up more than exponentially with the number of nonhydrogen atoms, and so this made the problem computationally tractable: seven- and eight-atom molecules could be added in future iterations. Water stability was required as any molecule made by life that diffuses to the atmosphere has to be stable to passage through the water in that life, and must be stable in the presence of oceans, rain, etc. This is a constraint that could be relaxed if nonaqueous solvents were considered a realistic option for future searches for life.
The goal of the project is not the ∼14,000 molecules in the initial database in itself; this is a starting point. The goal is twofold: to provide a database for future work on biosignatures and to provide a database of potential molecules to probe biochemical “laws” proposed to govern life on other words. We discuss the first here, and the second in Section 5.4 on universal approaches to biosignatures.
To provide a database for future work on biosignatures, work currently planned includes estimating from thermodynamic and kinetic parameters those molecules that might be formed geologically, and hence would be weak as evidence for life, for example, because P(data|abiotic) is nonzero and detectability is potentially low. For those molecules that are highly unlikely to be geologically formed on a planet, NIR signatures could be calculated to see whether they are detectable. This requires thermodynamic and kinetic modeling of each molecule in a planetary context, calculation of NIR signatures, and integration of that with the atmospheric composition of the target planet. This is a substantial task in its own right, and is representative of the interdisciplinary work essential to the future of exoplanet life detection. Rapid methods for estimating kinetic parameters, NIR spectral features, etc. are a research goal for this program. Chemical calculations of this sort are the domain of expertise of computational chemists usually involved in materials or pharmaceuticals discovery or in research into catalysis, not astrobiology. A major gap in atmospheric modeling pointed out particularly by the Seager et al. (2016) work is lack of measured kinetic data for reaction rates of the vast array of possible biosignature molecules with plausible atmospheric or surface components. Even thermodynamic data for nearly all the molecules in Seager et al.'s list (2016) have neither been measured nor accurately estimated. Moreover, solubilities in water are unknown, and atmospheric reaction chemistry and kinetics are unknown. As a consequence, modeling the atmospheric chemistry of these molecules will be an exercise in expert-informed inference.
A major issue is not only that these measurements have not been done, but also that there is little community interest in carrying them out. Measuring the kinetics of gas reactions at different temperatures and pressures is exacting work, but is not rewarded by high-profile publications; at best, the data become one set of points in a large database and it is the database curators who get the citation. A topic for future research is, therefore, to find new technologies for making kinetic and thermodynamic measurements on gases, gas mixtures, and solutions substantially faster and easier, so the collection of meaningful data sets becomes a single experiment in its own right rather than a decade-long program for an entire laboratory (an analogy is DNA sequencing, which can only be used to compile the databases mentioned previously for evolutionary studies because sequencing a bacterial genome is now a high school project, and not, as it was 20 years ago, a feat worthy of a major publication).
5. P(data|life)
Moving from a product-based to processed-based search strategy will better bridge biosignature research with other active areas of research regarding universal features of life. Product-based biosignatures are practical: due to the limitations of current detection methods, it is ultimately the chemical products of life that we will directly observe. To interpret data on chemical products and assess biogenicity, the likelihood of a given signature to be the product of life must be determined. A process-based approach is necessary to quantify these likelihoods. Therefore, to constrain P(data|life), we must understand the living processes generating a given observational signal. By better constraining observables based on the kinds of living processes present, it will be possible not only to detect life but also begin to infer its properties to achieve the longer term goal of characterizing it on other worlds.
5.1. Black-box approaches to living processes
In the absence of knowledge about the processes of life on exoplanets, models typically assume biological sources based on production rates for biology on Earth. These are what we term Input/Output models of biosignatures. The steady-state concentration of any atmospheric gas is a function of its source and sink fluxes. For life detection, we are interested in inferring the existence of biological sources. Sinks can be studied using chemical models of atmospheric or surface chemistry and photochemistry. Nothing need be assumed about the internal workings of life on a planet—it is a black box that consumes some gases and emits other gases.
To enable expanding our search beyond looking for Earth-like life on Earth-like worlds, new approaches are necessary. One proposed framework from Seager et al. (2013a) advocates classifying biosignatures based on the processes that produced them, with the idea to use this as a guide to whether those processes could be predicted to be different in a different environment. Their classification scheme still regards life processes each as a “black box” of unknown mechanism. It is taken as a given that life requires free energy to operate, and mass to grow and replicate. Their classification, therefore, considers the potential inputs and outputs of the system that could provide energy and mass to that system. Potential biosignature waste products are considered as the output from processes that (1) capture chemical energy, (2) capture biomass, or (3) other processes. They conclude that the first two can be constrained (if not predicted) by the chemistry of the planet, whereas the third cannot. Here, we briefly summarize their classification scheme. Although this scheme does not have consensus in the community, it serves as a useful jumping off point for further exploring process-based biosignature classification schemes.
5.1.1. Type classification
The type classification of Seager et al. (2013a) provide four classification types for biosignatures.
5.1.1.1. Energy capture (type I)
Energy capture can be achieved through life's exploitation of chemical gradients in the environment, as well as through harvesting of light energy. Biogenic molecules signaling such energy capture include gases as waste products, as well as pigments that provide the mechanism for light energy harvesting (in some cases these could be classified as type IV, due to their role in photoprotection). Examples of biogenic gases on Earth are CH4 from methanogenesis, H2S from sulfate reduction, and CO2 from respiration.
In principle, the type I gas products can be predicted from knowledge of the chemical environment of life, thus providing a methodology for building statistical databases of expected products as a function of environment, needed for calculating P(data|abiotic). For example, Seager et al. (2013a,b) predicted that ammonia could be a detectable atmospheric biosignature on a terrestrial planet with a hydrogen-dominated atmosphere on the basis of the thermodynamics of the atmospheric and crustal chemistries (Bains and Seager, 2012; Hu et al., 2013; Seager et al., 2013a), combined with a hypothetical energy-yielding metabolism in that environment, with N2 + 2H2 → 2NH3.
One challenge for this approach is the diverse range of chemical environments on Earth, as illustrated by the production of a reduced waste product (CH4) by life on Earth, which has a generally oxidized surface. On an “averaged Earth,” methane cannot be a type I biosignature gas, but in reduced environments it can be produced as a by-product of energy capture from methanogenesis or from biomass fermentation. Earth has many reducing niches today because it has biology producing oxygen. Electrons are conserved, and oxidation does not exist without reduction. Organic matter produced by oxygenic photosynthesis serves as the substrate for methane production during decay processes. Buried organic matter then creates anoxic subsurface environments conducive to the production of methane.
Future work should take the diversity of coupled environmental sources and sinks into account. It is unknown whether a diversity of chemical environments comparable with those of Earth is necessary for life (or whether this diversity is itself a biosignature). The values of both P(data|life) and P(data|abiotic) may not only be a function of the bulk composition of a planet, but also the number and variety of distinct environments on its surface (see also Scharf and Cronin, 2016, for a discussion of the role of diverse environments in potentially increasing P(life)).
Seager et al. (2013a) demonstrated that it is possible to extend the type I concept to estimate not only whether a gas could be the result of exploitation of a redox disequilibrium on a planet, but also whether that source is a plausible source of a detectable biosignature gas. The pilot study of Seager et al. suggests that further research on life's need for energy would help to focus which type I products are plausible as detectable biosignatures.
5.1.1.2. Biomass capture (type II)
The carbon on planet-sized bodies with thin (Earth-, Venus-, or Titan-like) atmospheres is likely to be mostly oxidized (CO2) or mostly reduced (CH4), as these are thermodynamic minima for carbon in an oxidized or reduced environment, respectively. Life needs to convert this into carbon in intermediate redox states to build complex molecules; this is a chemical universal, deriving from the nature of chemical bonds to carbon (Bains and Seager, 2012). This requires the oxidation or reduction of an environmental material, respectively. The input is an environmental chemical and environmental carbon, the output is biomass and a material out of thermodynamic equilibrium with the abiotic environment. The possible inputs and hence outputs are, again, predictable in principle allowing the possibility of constructing probabilities for the products of biomass capture, informing P(data|life).
The case of photosynthesis illustrates both the power and the limitation of considering a whole organism as a black box, which considers only looking at the net reaction rather than the individual components being reacted (e.g., in a biochemical pathway). Considered as a whole, the net mass balance for an oxygenic photosynthetic organism can be expressed as input of CO2, H2O, and light and output biomass and O2 as an oxidized waste product of the reductant H2O:
 |
Here, CH2O is a simplified representation for a carbohydrate or sugar. In this context, oxygen is the principal output gas, and is Earth's most notable type II biosignature (indeed, Earth's most notable biosignature of any sort). Similarly, other oxidized (nongaseous) waste materials are generated by anoxygenic photosynthesis (see Kiang et al., 2007a; Schwieterman et al., 2018, this issue). The same logic can be applied to any life in any environment—indeed in principle the same logic could be applied to noncarbon-based life. Using just the overall stoichiometry and thermodynamics of the net process of taking in environmental carbon and energy and outputting biomass, other oxidized (Haas, 2010) or reduced (Bains et al., 2014) products have been suggested for other worlds. Thus this “organism-level black box” approach has power in providing a framework for suggesting overall inputs and outputs before understanding of internal mechanism is available for any biomass capture process.
5.1.1.3. Other uses (type III)
Life on Earth produces a wide range of volatiles for signaling, defense, and other functions. Here, a “black-box” approach is relatively powerless as an explanatory tool as these processes are highly contingent. There is no known way to predict what signaling or defense chemicals an organism will make, starting only from the overall physics and chemistry of its environment. The production of type III gases is a result of the ecological or physiological demands on the organism, themselves the result of evolutionary contingencies and of relationships with other organisms: data that are not accessible for exoplanets. As a result, in principle we might consider any chemical to be a type III biosignature, which was the motivation behind Seager et al.'s (2016) compilation of all possible small molecule volatile biosignatures.
5.1.1.4. Products of modification of gases (type IV)
Gases produced by life can be modified by the environment, providing a source of secondary signatures of life. Examples include ozone (the photolytic product of oxygen) and dimethyl sulfoxide (the oxidation product of dimethyl sulfide—DMS). These could in principle be predicted if the environment and products of life are known, for example, for types I and II biosignature gases, but will not be predictable for type III biosignature gases.
5.1.2. Alternatives for type classification
Seager et al.'s original classification (2013a) was introduced as a pragmatic approach to the specific task of extending our understanding of the input/output model of biosignature generation, permitting moving beyond basing models solely on terrestrial production rates. Suggestions at refinement do not necessarily converge on agreed classification systems, suggesting that there may be no exhaustive categorization method. The goal of devising such process-based classification schemes is to probe why life might evolve to produce a given chemical signature, as the Seager et al. (2013a) classification was explicitly devised to do. A process-based classification particularly is needed for systems modeling to simulate the production of biosignatures as well as to explore possible novel biosignatures resulting from complex interactions along the entire pathway from metabolism through biosynthesis to postprocessing in a given planetary biogeophysicochemical system. This approach is also useful for formalizing conditional probabilities in a Bayesian framework as it can inform the likelihoods of producing a particular gas conditioned on a given environmental context.
Other disciplinary perspectives pose alternatives to the Seager et al. approach, expanding our ability to calculate P(data|abiotic) and P(data|life) based on black-box methods. For example, although the Seager et al. type classes focus on gaseous biogenic products and their secondary products in the environment, the classification could be further generalized to include surface biosignatures that also result from these type processes, or properties of the chemical networks that generate them (see Section 5.4.1). Possible surface biosignatures include pigments, or even morphological features. Suggestions for generalizing and making the type classifications more precise include the following:
5.1.2.1. Type I, energy capture
Light harvesting pigments can be included as type I biosignature molecules; although they are not the products of energy capture, they are the means to energy capture. These include pigments of oxygenic photosynthetic organisms, microbial rhodopsins of archaea, and other light absorbing molecules, as summarized by Schwieterman et al. (2018, this issue). Fluorescence as a result of excess energy release or waste product from light harvesting could also be considered a type I biosignature. Moving from the level of individual molecules to the networks of their interactions, certain chemical networks may be better at energy capture than others, suggesting yet another metric for assessing the potential for life (see Section 5.4.1).
5.1.2.2. Type II, biomass capture
Biomass capture could be elaborated further. The biomass itself can be a biosignature and produce waste products that can also be biosignatures. Biomass capture can be through autotrophy (reducing inorganic carbon, CO2) but also through heterotrophy (incorporation of already reduced carbon). Reduction of CO2 into biomass does not necessarily produce waste products immediately, but only after that biomass itself is involved in other activities. Incorporation of inorganic carbon into biomass can be highly complex, and the “black-box” approach to metabolism can be insufficient for identifying biosignatures. If, for example, it was found that the use of reducing equivalents generated by photon capture to reduce CO2 necessarily produced by-products or required other detectable properties of an organism, then these would be candidate type II biosignatures (see Section 5.1.3 for more details on the subtleties of type classification). Bains and Seager (2012) made an initial attempt at such a theory when they claimed that any biomass capture must of necessity produce an oxidized by-product on an oxidized world or a reduced by-product on a reduced world. However, this statement, although being a class of explanation for why terrestrial life produces oxygen as a by-product, does not explain why oxygen and not, for example, hydrogen peroxide is made. Advances in this type of analysis require an understanding of what aspects of photosynthesis are requirements of the steps in the chemical processes, and which are evolutionarily contingent, posing challenges for constraining P(data|life) (see Section 6.2).
Another candidate type II biosignature is seasonal oscillations of atmospheric CO2 content due to shifting balances of autotrophic carbon fixation versus respiration. This is exemplified by the observed ∼2% seasonal amplitude in CO2 concentration in the northern hemisphere caused primarily by the growth and decay or senescence of land vegetation (Keeling, 1960; Keeling et al., 1976; Keeling et al., 1996; see Figure 12). However, care must be taken to distinguish biotic from abiotic causes of seasonal fluctuations; the composition of the atmosphere of Mars changes substantially with the seasons, including gases of biological interest such as CO and CO2 (Mahaffy et al., 2013). Although the orbital and climate reasons for these changes are obvious to us, they may be less obvious to an observer at interstellar distances.
FIG. 12.
Posterior probability of life as a function of repeated independent observations of O2 (Nobservations is discrete, continuous curves are shown here to better illustrate trends). Model parameters are from Figure 10 (with ɛ = 0), using Eq. 13 for the measurement distribution as described in the text. Shown are cases for varying assumptions about the prior probability of life P(life). Color images available at www.liebertonline.com/ast
5.1.2.3. Type III, “other uses”
The type III classification is a catch-all to describe compounds whose production is not predictable on the basis of planetary chemistry, and as such includes biosignatures with diverse functions other than metabolic energy or biomass capture. These can include ecophysiological functions such as nutrient capture and heat tolerance (e.g., isoprene), ecological functions such as antibacterial and antimicrobial compounds (e.g., methyl bromide), and intra- and interorganismal signaling (e.g., ethane). Schwieterman et al. (2015) summarized a variety of ecophysiological and ecological functions of numerous types of biochemicals, which include phototrophy, antioxidants, photoprotection (screening), thermal tolerance, nutrient acquisition, growth regulation, and ecological functions such as antibiotics and signaling. Even nonchemical properties of organisms, such as bioluminescence (Miller et al., 2005), used for signaling, can be classed as “type III” (see Schwieterman et al., 2018, this issue). The type III classification is, therefore, one that provides a “catch-all” for cases where the biosphere (considered as a black box) modeled only in terms of metabolic processes cannot be predicted to produce that signature. This is important in estimating the probabilities P(data|life): for type III biosignatures our uncertainties in biological origins mean that the signal-to-noise will not be sufficient for unambiguous detection and more context will be necessary to confirm biogenicity.
Type III could be extended in two ways. It could be subdivided into biosignatures likely to be produced for specific purposes. Examples are retinal pigments that are unlikely to be used as visual signaling molecules in an exclusively microbial biosphere, although they may function in related activities such as phototaxis or ion transport. It could also be divided into functional classes in cases where modeling of a biosphere was sufficiently sophisticated to infer functional roles for particular class of signatures.
5.1.2.4. Type IV
Products of modification of gases were originally considered to be the products of environmental modification of gases, which, in turn, produce other gases. This could be generalized to products of environmental modification and degradation of biogenic molecules, including gases, liquid, and solid molecules to produce other gases, liquids, or solids. For example, the terrestrial “Black Earth” Chernozem soils are the result of substantial modification of local geology by biology, and would not be found on an uninhabited world.
Some biosignatures may be of more than one type. For example, marine algae produce DMS as a by-product of the breakdown of a complex biochemical dimethylsulfoniopropionate (DMSP). DMS can be classified as a type IV product. However, DMSP is also probably the principal energy source for the predatory zooplankton that feed on DMSP-containing algae, and so for them DMS is a type I biosignature (see Schwieterman et al., 2018, this issue, for more details). There is some debate what type O2 should be classified as, depending around what process(es) one draws one's black box. For example, Seager et al. (2013a) classified O2 as a type II biosignature involved in carbon or biomass capture, for reasons outlined previously: considering the organism as a single system, photosynthesis involves input of CO2 and light, production of biomass, and output of O2. However, oxygen is produced as a result of oxygenic photosynthesis, which is achieved through several steps in series. In the “light reactions,” photon energy is used to acquire electrons from water, whereas biomass capture through fixation of carbon from CO2 occurs in a separate subsequent step in the Calvin–Benson–Bassham cycle, which is the same process used by anoxygenic phototrophs.
These steps are detailed in Schwieterman et al. (2018, this issue). Photon energies in series drive successively more oxidized states of the oxygen evolving complex (OEC), a highly oxidizing metallocluster that, upon reaching a critical state, catalyzes oxidation of water, thus generating oxygen. Part of that photon energy is further used to excite the electron to a lower redox potential, the energy of which can then be used in redox reactions for storage of that energy. Photosynthesis self-generates its own chemical gradients, both to acquire electrons from water and to support redox reactions for energy storage. In this more detailed analysis, oxygen is a by-product of the step of energy capture and excitation of electrons; it is in effect the by-product of capture of energy from an internally generated redox gradient, and so is a type I product.
5.1.3. When is it appropriate to deconstruct a black box?
The black-box method can be used as a first approach to understanding biosignature production when the underlying biological mechanism(s) are unknown. However, the final example in the previous section highlights the potential ambiguities involved in such a classification scheme. Further challenges arise when the black box fails to work entirely, and more detailed resolution of the mechanisms “hidden” in the black box may be necessary.
For example, Eq. 6 is a net mass balance equation for an oxygenic photosynthetic organism, in which similar terms on both sides of the equation have been canceled. It does not express the stoichiometry when other oxidized (nongaseous) waste materials are generated by anoxygenic photosynthesis. Applying a black box to the inputs and outputs for anoxygenic photosynthetic organisms reveals that some terms cannot be canceled, which can then motivate further investigation to explain these extra terms. As just one example, drawing black boxes around many similar organisms and finding that some things about them are common while others fail to fit the same net reaction model would motivate dissection of the mechanism(s) of photosynthesis (dividing the black box into smaller black boxes, defined by our understanding of mechanisms). This is necessary, for example, to generalize for both oxygenic photosynthesis and the several types of anoxygenic photosynthesis.
It turns out that photosynthesis involves processes that separate the activities of energy capture and biomass capture in sequence, so a more generalized black box is expressed in the equation:
 |
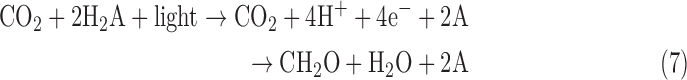The intermediate reaction reveals that the reductant H2A must first be split to donate electrons, and the CO2 is reduced subsequently. When the reductant is H2O, then the equation yields:
 |
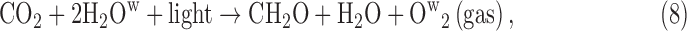where the superscript “w” denotes that the molecules in the produced oxygen gas come from the water molecules and not from the CO2. In the simpler black-box equation, the H2O on the right-hand side canceled with that on the left, but in fact it is not the same, since the source of the oxygen atom is different. If the reductant is instead, for example, H2S, in anoxygenic photosynthesis, then the net reaction is:
 |
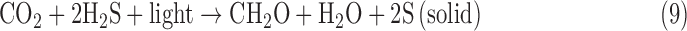This shows that specific waste products can be viewed as obeying a common set of processes. Both the O2 and S are the results of oxidation of an input reductant from input for light energy to obtain electrons. In this context, they can be seen as the type I product of energy extraction from an internal redox gradient. Even our last generalized equation is still a simplistic black box, depending on one's question. For example, as discussed in the work of Schwieterman et al. (2017), this equation does not reveal how the light energy is partitioned, and in fact only a fraction of it is used in oxidizing the reductant. If addressing what wavelengths of light can be used in different types of photosynthesis, the black boxes must be dissected further. The reader is directed to Schwieterman et al. (2017), which provides more details and literature. Understanding more of the process by which photosynthesis occurs changes our perception of how oxygen is produced. (“Why” it is produced, the final cause in an Aristotelian sense, then depends on how one asks the question.)
The example of photosynthesis exemplifies the value of an interdisciplinary discussion to address biosignatures, wherein the approaches of physicists, chemists, and biologists are together leveraged to identify the useful level of parsimony versus complexity. The power of the black box type of input/output model of life is that it can be implemented on the basis of environmental parameters alone. This is also its limitation, in that it says nothing about process or mechanism—it assumes that these are unknowable at interstellar distances. It remains an open question to what extent this last point is indeed true, and to which either universal “laws of life” or more detailed understanding of the necessary chemistry of specific processes could unpack the black box (both discussed more extensively hereunder).
5.2. Life as improbable chemistry
A different kind of “black-box” approach focuses on the complexity of chemical products of life, rather than classification of how they are produced. One major observable that discriminates living things from inanimate matter is their ability to generate similar, complex, or nonrandom architectures in large abundance, or to affect the background. Abiotic distributions of organics tend to be smooth, and dominated by low-molecular weight species, whereas in life, natural selection yields distributions that are more “spikey” as a result of selection of functional sets of molecules (Lovelock, 1965; McKay, 2011, see Fig. 5). Life also reliably produces high molecular weight polymers with discrete structures and molecular weights. Although abiotic processes can produce polymers (such as kerogens, and a wide range of 3D mineral polymers such as diamond), they have a wide distribution of sizes and informationally simple structures. Relating to the Bayesian framework, the idea of searching for low probability chemistry is the same as guiding our search for life by high detectability D: we should look for life where we expect no abiotic system could produce such a signal.
FIG. 5.
Schematic illustrating the difference between abiotic (smooth curve) and biological (spikes) distributions of organic molecules. Nonliving systems tend to produce smooth thermodynamic distributions, whereas in living processes, only a subset of molecule species are selected (through natural selection) to form a functional set. Adopted from McKay (2011). Color images available at www.liebertonline.com/ast
One potential biosignature could be the entropy of a distribution of molecules, distributions that are very unlikely to occur abiotically (e.g., those that require natural selection) are less probable. In this case, the biosignature is itself the probability of a molecule or a distribution of molecules occurring abiotically: if the probability is very low (low entropy), we can be confident the signal arises due to life. Caution must be taken in assigning biological origins to nonrandom processes, however. An example is the periodic distributions of masses of peptides displayed in living organisms, which have a mathematical rather than biological explanation: rather than being a product of natural selection, this pattern can be shown to arise purely as a result of the properties of finite ordered sums combining 20 natural numbers (corresponding to the 20 or so biological amino acids) (Hubler and Craciun, 2012).
Based on the probabilistic framework, complex artifacts are themselves biosignatures, since they can potentially be discriminated from an abiotic background. For example, technetium (Tc) is a rare element, not produced naturally, and has been proposed as a possible indicator of a technological civilization, since creating it requires knowledge of nuclear physics (Paprotny, 1977; Whitmire and Wright, 1980). Complex information processing systems such as computers and brains are also biosignatures for the same reasoning; it is unlikely that a laptop would form spontaneously without the long sequence of evolutionary steps necessary to evolve intelligence capable of constructing such technology. Although highly improbable structures are most often discussed as biosignatures in the search for extraterrestrial intelligence (SETI) research (Drake, 1965; Sagan and Shklovskii, 1966), the concept of improbability is equally applicable to molecular signatures of life. The challenge is that we must threshold a minimum complexity above which we can be confident P(data|life) > P(data|abiotic) for the molecule of interest.
It is not obvious how it might be possible to generalize an approach that aims to evaluate complex objects as possible biosignatures, particularly with respect to chemical signatures of life. In the context of exoplanet searches for life, achieving this on a planetary scale requires the probabilistic search for anomalies that themselves have in-built structure. Marshall et al. (2017), Murray et al. (2018) developed one possible complexity measure, they call Pathway Assembly, which quantifies the complexity of any given object as the shortest pathway for its assembly. The measure identifies the shortest pathway to assemble a given object by allowing the object to be dissected into a set of basic building units, and rebuilding the object using those units. Pathway assembly bounds the likelihood of natural occurrence by modeling a naive synthesis of the observation from populations of its basic parts, where at any time, pairs of existing objects can join in a single step. An object of sufficient complexity causing an observable feature, if formed in the absence of life, would have its formation competing against a combinatorial explosion of all other possible features that are equally probable.
Pathway assembly can be seen as a way to rank the relative complexity of objects made up of the same building units on the basis of the pathway, exploiting their combinatorial nature. The motivation for the formulation of pathway assembly is to place a lower bound on the likelihood that a population of identical objects or observations could have formed or occurred abiotically, that is, without the influence of any biological system or biologically derived agent. Thus, it is assumed that objects with high pathway assembly will only be observed if produced by life. Conceptually, the measure is similar to Bennett's logical depth, a measure of complexity based on the number of computational steps necessary to recreate a piece of information (Bennett, 1988). The key difference is that pathway assembly looks at the intrinsic routes for connecting objects based upon the resources within the system. Locally, pathway assembly could be used to rank molecules in order of complexity, identifying a threshold above which the molecule must have been produced by a biological system. Chemical methods based on retrosynthesitic analysis (taking a molecule and “splitting” it in stages to reverse engineer transformations chemists would use in the laboratory to synthesize the molecule) could be used to estimate the likelihood of different pathways for the abiotic synthesis of chemical structures (Corey, 1967; Ravitz, 2013).
For exoplanets, we are unlikely to remotely detect large macromolecules, and the pathway assembly for remotely detectable small molecules is in general low. In principle, exceptions to low pathway assembly could include molecules such as DMS and dimethyl disulfide (DMDS). These volatile gases are produced as indirect metabolic and decay products of both eukaryotic and prokaryotic organisms, require several independent enzymatically mediated steps to produce, and have no known abiotic sources (see overview in Schwieterman et al., 2017, their Section 4.2.5). In its current formulation, pathway assembly cannot account for biogenicity of small molecules such as DMS and DMDS, as it is necessarily a combinatorial measure to be computable from only knowledge of the object. Since DMS and DMDS are less than the threshold complexity set for origins from living processes (above which we can be confident life produced it), they would have low pathway assembly despite their complex biological synthesis pathways. In addition, these specific example gases are unlikely to build up to detectable levels in planets orbiting stars other than inactive M dwarfs, although they might be indirectly indicated by a C2H6 over abundance relative to that expected for the photochemical processing of CH4 (Domagal-Goldman et al., 2011).
Despite current limitations, the concepts driving pathway assembly are promising for exoplanet research, and there are potential ways forward for characterization of small molecules. Expanded versions of pathway assembly can account for the occurrence of many small molecular species occurring simultaneously, by analyzing the number of possible network pathways. This might provide fruitful new directions for assessing biological origins, or at least bound P(data|life). More broadly, pathway assembly should be able to be used to connect spectroscopic signatures looking for patterns of improbable “complex” behavior. An example could be exoplanets that have complex spectroscopic signatures made of many narrow discrete lines (such as are emitted by “white” light LEDs) that occur in abundance yet cannot be explained without technology. The key to expanding this will be using the pathway assembly to develop thresholds that are accessible by current technology or inspire the development of new technologies, experiments, and approaches.
5.3. Life as an evolutionary process
The “black-box” approaches of the previous sections are not concerned with the specific mechanisms mapping the planetary input to biological output, which is both their strength and primary limitation. The internal mechanisms of biological processes inside the “black box” are the result of evolution, necessitating a better understanding of the universals of evolution to determine the universals in an input/output framework. In applying Earth life as the standard of reference, we have only one past and one present to guide inferences of how integration over microscopic effects produces specific macroscopic biosignatures. One challenge is disentangling contingent events (which take the form of temporal conditional probabilities) in the evolution of life on Earth from universal constraints that we might expect to apply to life anywhere. Using Earth's history of evolution, we are effectively substituting timing, frequency, and diversity for likelihoods applicable to the study of exoplanets.
The universality of the genetic code and central dogma indicate all known life on planet Earth originated from a last universal common ancestor (LUCA) (Koonin and Novozhilov, 2009). However, components of LUCA, such as archaeal and bacterial cell membrane components and metabolic capabilities, may have arisen independently multiple times. Our understanding of early evolution is complicated by the common occurrence of horizontal gene transfer (Woese, 2004; Mushegian, 2008; Lombard et al., 2012). For example, respiratory chain components needed for aerobic respiration may have been laterally transferred between bacteria and archaea, and the origins of these genes are unclear (Kennedy et al., 2001; Boucher et al., 2003). As a result, it is conceivable that the last common ancestor of each extant gene may or may not have been present within the LUCA population.
With respect to the origins of life on Earth, the existence of an LUCA implies our sample size is N = 1, which does not provide enough data for statistical inference about the processes or likelihood of abiogenesis (see Section 6.1). However, the evolutionary process on Earth has driven innovations over many temporal and spatial scales, permitting the possibility of understanding more universal features of evolutionary processes by studying many events (Fig. 6). Generalities could then be extrapolated to other chemistries. Thus, when taken in light of the diverse biogeochemical contexts for life on Earth, we might consider that we have N = many examples for calculating P(data|life) for evolutionary processes, rather than being restricted to N = 1, as is the case for the origins of life (see discussion on P(life) for cautions in assuming independence of evolutionary innovations for constructing likelihoods).
FIG. 6.
Life on Earth radiated from a LUCA with a single standard genetic code. With respect to core biochemical components of life, this common ancestry leaves a sample size N = 1. However, the subsequent evolution of diverse metabolic capabilities and evolutionary lineages has resulted in diverse trajectories, allowing the possibility of mapping N = 1 to N = many, considering the varying coupled environmental and biological states over geological timescales and the number of independent convergent evolutionary innovations and transitions (only a few of which are shown for illustrative example). It is unknown how frequently these evolutionary events, including the origin of life, should be expected to occur on other worlds. Adopted from Schulze-Makuch and Bains (2017). LUCA, last universal common ancestor. Color images available at www.liebertonline.com/ast
Extinction has been a hallmark feature of life on Earth. Therefore, in calculating P(data|life) we must not only consider the probability of an evolutionary innovation emerging but also its persistence in time. It would be worth knowing whether a planet being observed has extant life or, if not, is otherwise suitable for the emergence of future life, or whether observables indicate that life was once present in the past. Better understanding of evolutionary processes and how they couple to planetary scale signatures is necessary to make progress on these unknowns.
5.3.1. Life as a coevolution with its planet: Earth as an example
In the years since the work of Des Marais et al. (2002), the community has increasingly recognized the fundamental importance of understanding biosignatures as resulting from the coupled evolution of a planet with the life upon it. Life is a phenomenon that manifests and maintains itself at molecular and microscopic scales, and, through evolutionary processes tightly coupled to geochemical cycles, has led to macroscale changes in the Earth system. Again, using atmospheric O2 as the standard example, oxidation of water by photosynthesis occurs at the molecular scale, and the evolution of oxygen and the growth of organisms may be observed in the laboratory and field in situ, but the expression of O2 as an exoplanet biosignature requires planetary-scale accumulation over geological timescales. Owing to the coevolution of the biosphere, lithosphere, hydrosphere, and atmosphere of Earth, life itself may be considered as a planetary process (Smith and Morowitz, 2016).
Planets are not static, but evolve in response to stellar context and planetary feedbacks: for living worlds, these feedbacks include those between a biosphere and geosphere. As evidenced by Earth's transitions, it is possible for precursors to biotic processes to emerge on an abiotic planet, mediating the transition to a living world, and for a living world to transition through different phases. Because Earth life has been exclusively microbial for the majority of Earth's history, it is possible that primitive unicellular life-forms are the most common and longest lasting stage of life on a planet (Whitman et al., 1998). Microorganisms are thought to have evolved on Earth after catalytic and genetic macromolecules were compartmentalized into membrane envelopes (Lombard et al., 2012). The degree to which these early life-forms may have metabolic activities like modern microbes, such as lithotrophic or photosynthetic processes, is currently unknown. It is still not well understood how feedback between the biosphere and the geosphere shaped the gases that would have been detectable in our own atmosphere during the period after life first emerged on Earth (>3.8 Ga), but before the rise of oxygen in the Earth's atmosphere made O2 a remotely detectable biosignature (Reinhard et al., 2017).
What we do know is that biological innovations on Earth have driven major changes in the redox state of our planet, leading to distinct observable states and planetary biosignatures (Kaltenegger et al., 2007). The prime example is the dramatic global scale transition to an oxidizing atmosphere resulting from oxygenic photosynthesis carried out by ancient cyanobacteria, detectable in the fossil rock record in the GOE at 2.3–2.4 Ga (Luo et al., 2016). Innovations like this are dependent on the environmental conditions that allow them to arise and, in turn, drive the environment, leading to successional innovations and planetary geochemical states that coevolve in a history-dependent manner. These states may be stable locally or globally at different temporal scales. Because life and the planet's redox state coevolve, a complication for building probability distributions for P(data|life) is that the probabilities are time dependent in a manner that depends on the states (e.g., the dynamics are state dependent, regarded as a hallmark feature of life (Goldenfeld and Woese, 2011; Walker and Davies, 2013)), that is the probabilities we must construct are necessarily conditional.
On Earth, the changes in oxygen content of the Earth's atmosphere through geological time corresponded with biological innovations of oxygenesis, nitrogen fixation, eukaryotic cells, multicellularity, and the arrival of plants on land (Berner et al., 2003; Ward et al., 2016; Gebauer et al., 2017). Each may have been made possible by the changing geochemistry of the planet, sometimes fostered by earlier life, and there are a number of hypotheses to support this idea. For example, the input of H2O2 to the oceans from the thawing of a Snowball Earth state has been proposed to serve as a transitional electron donor in the emergence of oxygenic photosynthesis (Liang et al., 2006).
Another hypothesis is that the scarcity of ammonium as a nutrient in the face of oxidation at the GOE may have necessitated the development of nitrogen fixation (Blank and Sanchez-Baracaldo, 2010). The availability of oxygen allowed by aerobic respiration drives increases in organism size and productivity (Catling et al., 2005). In addition, the formation of the ozone layer from atmospheric oxygen altered the spectral quality of surface irradiance, protecting it from UV radiation and allowing the emergence of advanced life on land, as well as altering the color balance of light for photosynthesis and phototrophy (DasSarma, 2006; Kiang et al., 2007a). Many of the evolutionary developments that brought about these transformations remain enigmatic. Some of these innovations have arisen independently multiple times, whereas others appear unique, some with evidence of an evolutionary pathway, but others without a clear origin. The probability of these innovations is a separate term in our Bayesian framework, P(life), to be treated in more detail in Section 6.2.
For other planets, surmising evolutionary path and geological epochs for life that are not Earth-like offers a rich challenge for interdisciplinary science. One question is what false positives (high values of P(data|abiotic)) and negatives (low values of P(data|life)) arise over time. Oxygen and water on a young planet orbiting a flaring M star could be a false positive, or ambiguous where the age of the star and timescale for life's evolution are unknown (Luger and Barnes, 2015). False negatives may result when biosignatures are not detectable until long after initial development of the producing organisms. This could occur when time is required to build up a biogenic product in an atmosphere, and for the planet's climate and geochemistry to shift to a different equilibrium, as exemplified by the possible 2 billion years between the first emergence of oxygenic photosynthesis and its detection in the GOE (Lyons et al., 2014; Cole et al., 2016).
Astrobiologists must accept that they are unlikely to detect marginal biospheres that have little detectable impact on a planet (e.g., where P(data|life) << P(data|abiotic), even if we expect P(life) >0). In many cases, we may be unable to detect biosignatures from earlier organisms that are subsequently suppressed by later organisms and evolving chemical and climate conditions, those that may exist only in obscure niches such as deep hydrothermal vents, or are relicts in refugia toward the end of a planet's residence in the habitable zone (O'Malley-James et al., 2013). Yet, these marginal biospheres might explain extant life, being its precursor, or relict planetary chemistry. They are also important in estimating the prior probability of life P(life), and in obtaining reasonable estimates of the distribution of life on other worlds.
5.3.2. Calculating conditional probabilities in biological evolution from past biogeochemical states
From the foregoing discussion, it is clear that our planet has gone through many different states as Earth and its living systems have coevolved with one another over geological timescales. Extending our understanding of life through its history, our N = 1 sample permits the study of many distinct biophysicochemical modes that differ from the current configuration of the coupled biosphere, geosphere, and atmosphere. Within the exoplanet biosignature community, it is often noted that terrestrial life represents at least two end-member examples of an inhabited planet: the early Earth (low or absent oxygen) and the modern Earth (high oxygen) (e.g., Lyons et al., 2014; see also Meadows et al., 2018, this issue). Expanding this idea, each time life has radiated into a new geochemical niche could be considered as an additional data point: each example provides new insights into how selective processes can yield new biochemical mechanisms for energy acquisition and generation of biomass.
To understand potential biosignatures and their likelihoods requires linking the history of different modes of biological innovation and environmental states on Earth to their potential planetary-scale signatures. By extension, it is only by piecing together the histories of key molecular components that couple metabolic activity to planetary reservoirs that we may begin to estimate the temporal frequency and distribution of comparable biosignatures on other planets (Claire et al., 2006; Lyons et al., 2014). Two data sets, the geological record and the genetic content of extant organisms, provide complementary insights into this history of how key molecular components have shaped or driven global environmental and macroevolutionary trends (Fischer et al., 2016; Caron and Fournier, 2017; Kacar et al., 2017b, 2017c). Changes in global physiochemical modes over time are thought to be a constant rather than ephemeral feature, as life has continuously evolved protein functions for the >3.8 billion years of life's history on Earth. Organismal survival depends on how well critical genetic and metabolic components can adapt to their environments, necessitating an ability to adapt to changing conditions. These adaptations can produce viable biosignatures where biological rates exceed abiotic rates, for example, where P(data|life) > P(data|abiotic).
The geological record provides a number of biologically dependent indicators of macroscale atmospheric and oceanic composition, but provides little information by way of the exact behavior of the molecular components that altered the compositions of these reservoirs. One proposed way to infer the activity of ancestral molecular components is to reconstruct protein sequences that might have been present in ancient organisms, downselecting to a subset of possible sequences that may have been adapted to these ancient environmental conditions. It should be noted that such sequences are inferred based on the most parsimonious ancient sequence(s), given the diversity of modern sequences, and are subject to historical ambiguity (Benner et al., 2007; Kacar and Gaucher, 2012). With that caveat, reconstructing ancestral phenotypes that can lead to large-scale planetary biosignatures can be accomplished by identifying primitive biomolecular protein sequences that have impacted the cycling of C, N, S, O, or P through global reservoirs (Kacar et al., 2017c).
Studying the interface of past molecular behavior and environmental conditions may provide new insights into the interpretation of deep time biosignatures on Earth. For example, organismal and community fitness can be studied in the laboratory, as well as rates of production of biosignature gases. Data reconstructed through these studies may then be compared and contrasted with independent data obtained from primitive organic material for which there is a suspected or known biological imprint. Such findings may be critical for establishing biosignature baselines that are persistent and thus considered more broadly “universal,” or to identify cases where protein activity was not uniform in Earth's past. However, experiments incorporating these methods also require careful design to rule out signals from other potential artifacts impacting biosignature assessment, such as sequence reconstructive biases or organismal responses to nonadapted substituted components. Properly accounting for these ambiguities, the data generated from these approaches can inform how likely a given biosignature signal is within the space of understood catalytic proteins, contributing to our understanding of P(data|life).
There is an analogous approach searching for ancestral metabolic pathways by comparing modern pathways and, in turn, reconstructing putative ancient ancestors. This has been an established approach to studying the evolution of metabolic capabilities for >70 years (see, e.g., Waley, 1969). Smith and Morowitz (2016) argue that this approach can probe the pregenetic epoch of biogenesis, and be used to understand the chemistry from which life arose. Although our ability to reconstruct the exact history of life-on-Earth is debated, these approaches illustrate that a combination of genetic, structural, and chemical analyses of the product of 3.5 billion years of evolution can provide insights into intermediate states in that evolution.
Understanding the function of ancestral components can also provide a novel means of gaining access to configurations of life that deviate from extant norms. For example, it is possible that life could have started with, evolved from, or subsisted by uptake of a different set of monomers than those utilized by current life on Earth (Forterre and Gribaldo, 2007; Braakman and Smith, 2012). By engineering modern organisms with the behavioral properties of these ancient components, we may explore variations of so-called weird life, which can yield yet more significant insights into the essential requirements for life as a universal phenomenon. This is a common approach in the field of synthetic biology, and indeed components of organismal genetic machinery have been successfully replaced with synthetic parts in functioning organisms. Examples include expanded genetic alphabets (Malyshev et al., 2014), synthetic minimal bacterial genomes (Hutchison et al., 2016), ancient genes inside modern bacterial genomes (Kacar et al., 2017a, 2017c), and alternative nucleic acids (Taylor et al., 2015).
5.4. Insights from universal biology
All of the candidate biosignatures discussed thus far in this review have focused on chemical signatures of life. Searching for “life as we know it” implies searching for “biochemistry as we know it,” for example, DNA, proteins, and metabolisms like Earth's, such as oxygenic photosynthesis. Therefore, moving beyond “life as we know it” to “life as we don't know it” with unknown biochemistry will require developing new frameworks that address universal aspects of living processes. The idea of “universal biology” has been proposed with the intent of transcending the chemistry of life as we know it to uncover universal organizational properties of living systems (Goldenfeld and Woese, 2011; Davies and Walker, 2016)—perhaps associated with patterns in information flow or energy transfer—that should apply to any kind of life, even if it is based on a radically different biochemistry.
Of the candidates for universal biology, chemical disequilibria have been the most widely discussed as a potential biosignature (Krissansen-Tottan et al., 2018). But, it is unclear whether disequilibria associated with life quantitatively differ from other planetary disequilibria, as already discussed. In addition, some have argued that life exists to facilitate a more rapid approach to equilibrium than would be possible with geochemical processes alone (Shock and Boyd, 2015), such that living planets should be closer to equilibrium rather than farther as compared with nonliving planets. Other candidates include universal scaling laws (West et al., 2002; Okie, 2012), collective behavior (Goldenfeld and Woese, 2011), network structure (Jeong et al., 2000), or informational structure (Davies and Walker, 2016). Although we are only in the early stages of developing a universal biology, insights into common organization properties of biological systems gained over the past decade hold promise for providing novel approaches to biosignatures in near-term searches for life and for longer term mission planning, providing new frameworks for constraining P(data|life) (Krissansen-Totton et al, 2018).
5.4.1. Network biosignatures
Networks are used to quantify the properties of living systems across all scales of organization, from the chemistry within cells (Jeong et al., 2000) and the structure of food webs (Dunne et al., 2002) to the organization of cities (Bettencourt, 2013). A network is most simply described as the pattern of connections among a system of interacting entities. Mathematically, networks are studied using the tools of graph theory, where entities are represented by nodes and their interactions by edges. Familiar examples include social networks, such as Facebook, where individuals are represented by nodes and their friendships by edges (e.g., an edge is present if two individuals “like” each other). Likewise, chemical species reacting with one another in a planetary atmosphere can be represented graphically with a network, where one node type represents molecular species and a second node type represents the reactions that occur among these species (left panel, Fig. 7). Other graphical representations are possible, such as those involving only molecular species (and no reaction nodes), which are connected if they participate in the same reaction (right panel, Fig. 7).
FIG. 7.
Two different graph-theoretic representations of the same chemical network, consisting of the reactions: H + HCl → H2 + Cl, HCl + O → Cl + OH, and HCl + OH → Cl + H2O. Network examples adopted from Solé and Munteanu (2004). (A) Bipartite representation where both reactions and substrates are treated as nodes. (B) Unipartite representation where only substrates are treated as nodes.
Network representations have been used to study biochemical networks associated with metabolism. Jeong et al. (2000) demonstrated that the metabolic networks of 43 organisms, representing all three domains of life, are scale-free networks, meaning their degree distributions follow a power law P(k) ∼ k-α, where P(k) is the probability that a given molecular species participates in k reactions (in network parlance k is the degree of the node, corresponding to the number of edges connected to that node). Earth's metabolic networks are, therefore, highly heterogeneous in that there exist a few highly connected nodes (hubs) that link numerous less connected nodes together. This property has been explained in terms of enhanced robustness: heterogeneous networks are known to be more robust to the loss of random nodes than random networks. It is, therefore, a candidate signature of evolutionary processes at work, providing new ways to potentially constrain the value of P(data|life).
The universality of metabolic network organization suggests that life on other worlds might evolve to exhibit network topology similar to that of Earth's metabolic networks (Kim et al., 2018) and, therefore, that network topology is itself a biosignature. One hypothesis is that life could additionally leave a topological imprint on atmospheric chemistry. To test this hypothesis, several studies have examined the network topology of Earth's atmosphere (Fig. 8) and compared it with that of other worlds in our solar system (Gleiss et al., 2001; Solé and Munteanu, 2004; Holme et al., 2011; Estrada, 2012). The results of these comparative analyses indicate that the Earth's atmospheric reaction network structure differs from other planetary atmospheres, and specifically that it is more like biochemical metabolism in its topological structure than it is like other atmospheres. In particular, Solé and Munteanu (2004) showed that Earth's atmospheric chemical reaction network exhibits scale-free topology, much like biochemical networks, whereas other planetary atmospheres, including Mars, Venus, Titan, the Jovian planets, are structured more like random networks. These results resonate with the view that life is indeed a planetary process and is deeply embedded in the Earth system, to the point that even the network arising from the chemical dynamics of the atmosphere is driven by life (and not just its molecular constituents such as O2).
FIG. 8.
A network representation of Earth's stratospheric chemical reaction network. High degree nodes are highlighted in warm tones and lower degree nodes in blue. Data are from DeMore et al. (1997). Color images available at www.liebertonline.com/ast
There are observational biases that must be accounted for in network analyses, as we know Earth's chemical constituents and its reaction network to a much greater level of detail than we do other planetary atmospheres. However, even the major constituents contained in Earth's atmosphere may require a more complex network to fully explain them. The fundamental reason for this is the same as the foundations of traditional thinking on “nonequilibrium” or nonsteady-state biosignatures that have been in the minds of the exoplanet community for decades (Lovelock, 1965; see also Section 4.3).
The introduction of nonsteady-state gases by biology leads to additional atmospheric reactions that would otherwise not take place. Conversely, the presence of these same gases in a steady-state condition that does not require biological fluxes to maintain them implies that the chemistry of the atmosphere is such that their destruction rates are slow, a result of the atmospheric chemistry being less complex. We can consider the classic example of O2 to illuminate this. The known mechanisms for accumulating detectable amounts of O2 in a planetary atmosphere are all associated with atmospheres that are deficient in H. The results of this are atmospheres with chemical networks dramatically less complex due to the lack of H-bearing species and their reactions. Similarly, a planet without biological O2 fluxes would not have the additional reactions that are caused by its presence in the atmosphere. The network complexity would instead be greatest when O2 is present in an atmosphere that would otherwise destroy it rapidly. Similar trends are hinted at in studies of alternative biosignatures as well, such as the additional chemistry resulting from biogenic sulfur gases that causes C2H6 to be detectable in exoplanet environments (Domagal-Goldman et al., 2011).
To validate this proposal, and utilize network-theoretic biosignatures for remote detection, several lines of research must come together. The properties that are unique to inhabited worlds need to be fully explicated. Recent work has shown that scale-free topology is not as common as previously claimed (Clauset et al., 2009), and requires rigorous statistical tools to confirm. In particular, relatively few molecular species are confirmed to be present in many planetary atmospheres, meaning atmospheric networks are small, making it difficult to obtain statistically rigorous fits for the degree distribution. For exoplanets we will have even less data. Other topological properties must, therefore, be studied to determine in what ways Earth's atmosphere differs from other worlds. Topological properties should be analyzed across a range of kinetic and dynamic models, varying temperature, pressure, and composition to determine how physical effects influence atmospheric reaction network topology to isolate possible biological origin, and constrain P(data|life) for network topology. A systematic analysis of the topology of different models for planetary atmospheres could be used to determine the likelihood of specific features, given planetary and stellar context. In addition, deeper analysis should be done for Earth to determine how biology is driving the distinctive topological properties observed. Finally, if validated as a biosignature, it remains to be demonstrated how we can extract large-scale statistical properties of an atmosphere's network from the limited data we will obtain through remote observation. One possibility is to use Bayesian retrieval methods, used for extracting cloud properties from atmospheric data (Line et al., 2012).
This concept is relatively new—to the exoplanet field at least—and thus warrants further investigation. Studies of the kinetic properties of various terrestrial worlds can test the overarching hypothesis that Earth's network is more complex, and that the increased complexity is due to biology. The application of this approach to multiple inhabited planets—including that of Early Earth—should also be conducted. This will allow us to understand how well this hypothesis holds, how useful it is to constraining P(data|life), and in, turn, how useful it will be to future exoplanet astrobiology missions.
This illustrates one example of how considering the general chemistry-independent properties of life may lead to specific research proposals in life detection strategies. Deeper research questions should also examine whether there are other equally fundamental properties of life that can potentially lead to remotely detectable consequences.
5.4.2. Universal scaling laws applicable to other worlds?
Another candidate for universal biology is the scaling laws associated with trends across different biological organisms. Familiar examples from physics include critical phenomena near phase transitions, where physical properties such as heat capacity, correlation length, and susceptibility all follow power law behavior. Scaling relationships take the form:
 |
where λ is an arbitrary scaling parameter with scaling coefficient β, N is typically a measure of the size of the system, and Y measures a property characteristic of the system. Thus, the scaling relation provides a direct mapping from the value of the parameter of interest, Y, for a system of size N, to the value of the same parameter measured on a system of size λN. The scaling Y(λN)/Y(N) is then parameterized by a single dimensionless number, the scaling exponent β. A simple solution is the power law relationship associated with scale-free network topology as discussed in the previous section. In addition to power laws in networks, scaling relations have been studied in biology in phenomena as varied as patterns in species diversity (Locey and Lennon, 2016), the organization of cities (Bettencourt, 2013), and the structure of neural systems (Zhang and Sejnowski, 2000). A scaling relationship of interest for identifying universal patterns in biology, applicable to other worlds, is the allometric scaling relations, which relate features such as metabolic rate to body to size (West et al., 2002; Okie, 2012). These scaling relations change through the major transitions in biological architecture (e.g., from prokaryotes to protists to metazoans, see Fig. 9) and appear to be universally held across life on Earth (Delong et al., 2010).
FIG. 9.
Empirically observed scaling laws for metabolic rate as a function of body mass exhibits three major regimes, associated with prokaryotes, protists, and metazoans (Delong et al., 2010). If these trends are universal and can be derived from an underlying common theory, it may be possible to apply the universal scaling relations to inform P(data|life) on other worlds. Adopted from Okie (2012). Color images available at www.liebertonline.com/ast
One pertinent question for exoplanet biosignature research is whether these scaling relations hold at the level of the biosphere as a whole (as it is ultimately an entire biosphere we will detect remotely). It seems in many cases they do. A recent example is work by Kim et al. (2018) demonstrating the topology of biochemical network scales as a function of network size across individuals and ecosystems up to and inclusive of the biosphere-level chemical reaction network. Biosphere and ecosystem level chemical reaction networks are shown to have topological organization similar to that of individual organisms. It is perhaps the fact that global biochemistry displays these topological properties that the atmosphere has been driven toward the particular organization in chemical network structure (discussed in the previous section); however, this is a connection that remains to be worked out and is a subject of future work. Other examples of scaling relations applicable to ecosystems that can be scaled to biosphere-level properties include patterns in global species biodiversity (Locey and Lennon, 2016) and in the mass allocated to predators and prey (Hatton et al., 2015).
Scaling relations, due to their ability to predict values of system parameters based on other measured quantities, represent one of the closest approaches so far to a predictive theoretical biology, akin to theoretical physics. Using the observation that cells and organisms are constrained in their growth by resource distribution networks, predictive models can be generated that accurately provide values for the scaling exponents observed in a number of diverse biological systems (West et al., 1999). However, there is as yet no unified theory that explains the observed allometric scaling relations across different levels of organization, nor when transitions in scaling regimes should occur. Nonetheless, the existence of these scaling relations suggests integrative frameworks for constraining P(data|life). For example, modeling flux rates of biosignature gases on exoplanets could be informed by fundamental bounds on flux rates for given biomass estimates provided by universal scaling (given minimal assumptions of a particular biological architecture), allowing us to extrapolate to metabolisms that might exist in non-Earth-like environments. It should be noted that the universal properties associated with scaling laws and network structure are both statistical constraints on P(data|life), providing fundamental chemistry-independent bounds on our expectations for life to generate a given observable.
6. P(life)
So far, we have focused discussion on calculation of P(data|abiotic) and P(data|life). The final term necessary for calculating the posterior likelihood of life (apart from knowledge of experimental noise) is the prior probability for life to exist in the first place, P(life). This is the least constrained and most challenging term to quantify. As we pointed out previously, it is not sufficient to simply assign a probability that life-as-we-know-it exists on another world (which is unknown), but instead P(life) should be considered as decomposable into a family of conditional probabilities for the existence of different living processes on other worlds, which may be similar or dissimilar to those on Earth.
Life is a path-dependent process, so each new biological innovation is dependent on those that preceded it, thus P(life) takes the form of conditional probabilities for each evolutionary step (which itself may be difficult to define; what are the relevant steps?). As an example, in assessing the probability for multicellularity to evolve, we might decompose it into the following series of conditional probabilities:
 |
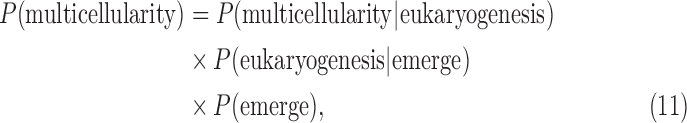where we have here considered only two of the most significant “major” steps. There are many more unspecified steps that will be necessary to articulate to map the limited observables of exoplanets to a reasonable estimate of the prior probabilities of living processes. The prior probability of any living process will ultimately depend on P(emerge), the probability for life to originate. Thus, how well we can constrain P(life) depends on how well we can constrain the probabilities for the candidate living processes that may have generated the signal, its evolutionary history, and ultimately the origins of life within that planetary context.
6.1. P(emerge): constraining the probability of the origins of life
As noted in Section 3, attempts have been made to constrain P(emerge) within a Bayesian framework by Carter and McCrea (1983) and more formally by Spiegel and Turner (2012), with the conclusion that P(emerge) could be arbitrarily close to 1 or 0. In other words, P(emerge) is currently unconstrained (apart from the trivial statement that it is not identically 0). In Spiegel and Turner (2012), it was estimated that the likelihood for the emergence of life follows a Poisson distribution with time, such that life was most likely to arise early in a planet's evolution. However, for M dwarf stars, the early stellar environment may not be conducive to life (see Section 4.1 on stellar context) and in general it is unknown whether life must arise early in a planet's evolution, or whether it could occur at any time. Ideally, we would be able to calculate P(emerge) from theory, but there currently are no theoretical bounds—we do not have a quantitative definition for life nor a theory of the emergence of life from which to do such ab initio calculations (Walker, 2017). We must better understand the mechanisms underlying the origins of life to make a case for P(emerge).
If the emergence and evolution of life requires time, then knowing the age of the star is valuable to assessing the potential for life, and thus avoiding systems wherein P(life) might be too low to confidently detect life. Measuring the ages of stars is more accurately done for the youngest ages when the youth diagnostics (spectroscopy, photometry, kinematics, chemistry, etc.) are more clearly measureable. For stars much older than 1 billion years, we must rely on less precise techniques. However, from statistical studies of many stars in various regions of our galaxy, we are able to better refine the ages of old stars by their location in the galaxy (i.e., disk or halo), by the composition of the stars (high or low metallicity) and by their level of stellar activity as most stars tend to be less active (i.e., less flaring and slower rotation) as they age.
In Scharf and Cronin (2016), a formalism akin to the Drake equation was proposed for estimating P(emerge) at a planetary scale. The mean expected number of abiogenesis events on a planet in a given time interval was suggested to depend on four parameters: the number of potential building blocks, the mean number of building blocks per organism (acknowledging ambiguities in the definition of “organism”), the size of the subset of building blocks available to life during a fixed time interval, and the probability of assembly of those building blocks. The latter term, based on the probability of assembly, was intended as a “catch-all” that does not require detailed knowledge of mechanism and could, for example, include the probability per unit time of vesicle self-assembly, or a sequential series of steps leading to an evolvable system. In this formulation, this probability is the least constrained parameter, necessitating input to constrain it from in vitro and in silico research.
One potentially fruitful path for estimating these probabilities is “messy chemistry,” wherein the goal is to study the statistical properties of chemical systems and their interactions with other compounds, formation structures, etc. in cases where precise composition and mechanism are not known (Guttenberg et al., 2017). Here, “messy” refers to high diversity of products, intermediates, and reaction pathways that cannot all be precisely identified. Analysis of the bulk properties of geochemical organic samples provides one example, wherein the petroleum industry has developed methods for classifying crude oils quickly by measuring a small subset of its properties. Applied to chemistries relevant to the origins of life, the emergence of “life-like” features could be studied statistically to estimate the likelihood of functional polymers emerging from random mixtures, as just one example. This could, in turn, be tied to different environmental contexts through explorations of a diversity of environmental parameters. One such parameter is the rate of hydration–dehydration cycling, where wet–dry cycles have recently become a prominent mechanism in origins of life research for driving the abiotic synthesis of far-from-equilibrium biopolymers (Hud and Anet, 2000; Walker et al., 2012; Mamajanov et al., 2013). For polypeptide synthesis, the duration of the dry phase has been shown to affect product yield, along with other environmental parameters such as temperature, number of cycles, initial monomer concentrations, and pH (Rodriguez-Garcia et al., 2015). For cycling driven by tides, or day–night cycling, this type of data could place bounds on P(emerge) for exoplanets based on their rotation rate. These and other environmental parameters should be explored in large-scale parallel chemical experiments to generate the necessary statistics.
In Scharf and Cronin (2016), it was also suggested that multiple planet systems would have a higher value of P(emerge), because impact ejecta exchanged between neighboring planets with parallel chemistry and parallel chemical evolution could enhance rates for development of molecular complexity. Future modeling will need to determine whether rates for the origins of life (or its persistence and evolution) are enhanced for worlds that are closely neighboring other habitable worlds.
6.2. Biological innovations and the conditional probabilities for living processes
Since the emergence of life on Earth, life has undergone a number of different stages of evolution (Szathmáry and Smith, 1995; Braakman and Smith, 2012; Bains and Schulze-Makuch, 2016). Tracing the history of biological innovations allows the possibility of leveraging the diverse history of life on Earth, where N = many (see Section 5.3), to infer the likelihood of evolutionary events based on their frequency of independent origins. However, care must be taken to determine what is meant by “independent.” For example, the probability of evolving multicellularity is dependent on the prior probability of eukaryogenesis (at least for Earth life), since all obligately multicellular organisms are eukaryotes (as in the previous example). It is also dependent on the prior probability of photosynthesis, since complex life evolved in the presence of O2, and because O2 is widely believed to be a precondition for large multicellular animal life.
There are many more such conditional probabilities we could assess. Thus, although the transition to multicellularity is itself a common occurrence in the history of life on Earth (having evolved independently at least seven times; Knoll, 2011; Niklas and Newman, 2013), multicellularity may not be universally common on inhabited planets if either the probability of eukaryogenesis or oxygenic photosynthesis, or any other steps in the pathway to multicellular life are rare. We also must consider that all life on Earth shares a common ancestry, so when considerations of evolutionary “independence” get blurrier the further we trace conditional probabilities for evolutionary events into deep history. Until we discover another example of life with independent origins (or have a guiding universal theory), it will be difficult to say with certainty what the likelihood of similar evolutionary events would be from a different starting point (e.g., a different biogenesis, with different chemistry).
Rare events in evolution are often associated with major transitions or innovations. Maynard Smith and Szathmáry (1995) identified eight major transitions, with respect to changes in units of selection, in the history of life on Earth, each associated with transitions in the nature of information transfer between and within individuals. These include the transitions of replicating molecules to populations of molecules in compartments, unlinked replicators to chromosomes, the RNA to DNA-protein world (genetic code), prokaryotes to eukaryotes, asexual clones to sexual populations, multicellularity, eusociality, and linguistic societies. Missing from Maynard and Smith's scheme are metabolic innovations that did not necessarily change what constitutes a selectable individual, but nonetheless had a significant impact on the biogeochemical evolution of the Earth system, such as the origins of photosynthesis and nitrogen fixation. An important question for understanding the evolution of life on Earth is whether or not we should expect the same innovations to occur again if we “rewound the tape of life” (Gould, 1990). A more critical question for exoplanet biosignature research is, how frequently should we expect these same or different biological innovations to happen on other inhabited worlds?
In Bains and Schulze-Makuch (2016), three possible hypotheses were proposed for the conditional probabilities of evolutionary innovations to occur: the critical path hypothesis, the random walk hypothesis, and the many paths hypothesis. In the critical path scheme, innovations require preconditions that take time to develop (determined by the nature of the event and the geological and environmental conditions of the planet), but once the preconditions exist, the event happens on a well-defined timescale. In the random walk hypothesis, the innovation is unlikely to occur (being based on one or more highly improbable events), thus significant time must elapse (on average) before the event occurs (a complication arises in interpreting this hypothesis in the event of postselection, wherein the event already occurred, in which case a rare event could have happened rapidly, see Carter, 2008 for discussion).
In the many paths hypothesis, the innovation requires many random events to create a complex new function, but many combinations can generate the same functional output, so the chance of the innovation is high. The key steps in the evolution of life, development of prebiotic chemistry, synthesis of cellularity, and the invention of metabolism and what pathway they took are not entirely clear. Although modern geological, chemical, and genomic methodological approaches are extremely powerful, there nevertheless remain considerable challenges to precise understanding of the events, leading to the expansion of life on our planet. Considerable effort may be required to understand the detailed history of evolution from methods as varied as radiocarbon dating, paleobiology, and molecular evolution.
We summarize here some critical gaps in our knowledge of early events in the evolution of life on Earth. The formation of a cell envelope serving as a permeability barrier and preventing the free diffusion of chemicals into and out of cells and ability to produce and store cellular energy were probably an essential prerequisite of the emergence of life on Earth. It is unclear whether life is necessarily “cellular,” although it is difficult to envision possible alternatives. Our current knowledge of how chemiosmotic coupling and cellular energy metabolism evolved from cellularity and set the stage for evolution of the LUCA, most likely with an universal genetic code already established, which subsequently evolved into all life on Earth, is sketchy at best (Weiss et al., 2016).
The very early appearance of the electron transport chain, membrane complexes responsible for fundamental respiratory processes in all prokaryotic cells, also remains an enigma. Although they are found in both bacteria and archaea on Earth and may be used for redox reactions of nitrogen, sulfur, and oxygen gases, the precise evolutionary steps taken in their development still confound modern molecular phylogenomic analysis (Castresana and Saraste, 1995). Similarities between a variety of chromophores—for example, porphyrins with different metal ion centers within membrane proteins of the electron transport chain and photosynthesis—remain tantalizing (see review in Schwieterman et al., 2018, this issue). Generation of an electrochemical gradient used to drive adenosine triphosphate synthesis through chemiosmotic coupling is a common nearly universal theme (Racker and Stoeckenius, 1974), the basis of which deserves further attention.
The emergence of oxygenic photosynthesis involved conservation of photosystem structures that evolved in earlier organisms but also added a unique molecule, the OEC, which is responsible for oxidation of water but whose origin remains elusive. A number of hypotheses have been forth, though none yet has reached consensus. These hypotheses span approaches from the biophysics of transitional electron donors, generally in the context of geochemical environment (Blankenship and Hartman, 1998; Dismukes et al., 2001; Sauer and Yachandra, 2002; reviewed at the time by Blankenship et al., 2007; Fischer et al., 2016); phylogenetics to constrain lineage and timing (Xiong and Bauer, 2002; Soo et al., 2017); and reconstruction of evolutionary relationships among the reaction center proteins and their biosynthesis pathway (Cardona et al., 2015; Cardona, 2016). This work to date advances knowledge of the origins of oxygenic photosynthesis on Earth. However, the likelihood of the OEC capability arising given a conducive geochemical setting, that is, the likelihood of another planet developing oxygenic photosynthesis by the same method, is difficult to constrain.
The light-harvesting apparatus for photosynthetic organisms, both oxygenic and anoxygenic, has arisen in multiple forms, utilizing a variety of pigments, all of which, however, obey the same principles, reviewed in Schwieterman et al. (2018, this issue). This variety of colors, of interest to astrobiologists as potential biosignatures such as the vegetation red edge (again see Schwieterman et al., 2018, in this issue for a review), arises from adaptation as well as acclimation to optimize for the organisms' spectral light environment. Only a very few theoretical modeling efforts have attempted to predict the optimal absorbance spectrum for light harvesting based on various efficiency constraints, with notably different approaches by Milo (2009), Marosvölgyi and Gorkom (2010), and Punnoose et al. (2012). Long-held assumptions about the primacy of chlorophyll a (Mauzerall, 1973; Björn et al., 2009) have now been challenged by the recent discoveries of far-red chlorophylls in oxygenic phototrophs (Li and Chen, 2015; Allakhverdiev et al., 2016; Ho et al., 2017). The details of these optimality models are beyond the scope of this article, but their diverse approaches and the existence of far-red chlorophylls indicate unknowns about the innovations that lead to diversity in the same type of life process.
Biological innovations may be classified through disciplinary perspectives in addition to that of biologists, raising the question of where to draw the black box for biosignatures. For example, light-capturing chemistry is not unique to photosynthesis, but a range of other structurally and evolutionarily unrelated pigments are used for the capture of light energy (DasSarma, 2006). The key pigment in terrestrial photosynthesis—the family of chlorophyll molecules—is structurally related to a number of other porphyrin derivatives such as heme used in energy transfer and oxygen handling (see summary in Schwieterman et al., 2018, this issue). However, other light-capturing pigments include a range of isoprene pathway derivatives such as carotenoids and retinal, although not all of these are used for obtaining electrons for carbon reduction on Earth. These both suggest that the evolution of light-capturing chemistry is not a unique event and opens questions about what features are universal (as opposed to evolutionarily contingent) that we might search for signs on other worlds. At the same time, whether some types of pigments had to evolve first or were completely independent, including their evolution, relative abundance, and by-products is of significant interest for detection of biosignatures.
7. A Bayesian Framework Example: Detecting Atmospheric Oxygen
So far, we have introduced the Bayesian framework as a quantitative formalism for life detection and discussed each of the terms necessary to implement it with high confidence to the problem of detecting life on an exoplanet. To demonstrate how our proposed framework might work in practice, we work through a toy model of detection of O2. We focus on O2 as it is one of the best characterized biosignature candidates: biological production of O2, as well as the possibilities for false positives, is better understood than other potential exoplanet biosignatures (see, e.g., Meadows et al., 2018, this issue). As should be clear by now, we do not know the relevant probabilities to properly assess likelihoods or priors yet—this is a major subject for future exoplanet research as we have emphasized throughout this article. In the examples we provide here, we, therefore, assume an example and number for illustrative purposes only. In the absence of known likelihoods and priors, our examples are meant to be conceptual, rather than rigorously quantitative: we aim to illustrate how the possibility of false positives can inform design of optimal search strategies.
From Eq. 2, assuming detection of O2 is the relevant observable, the posterior probability of life given a set of observational data may be formulated as
 |
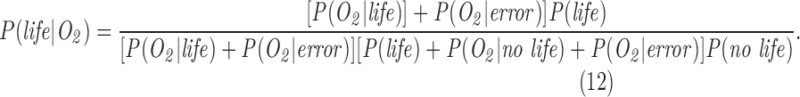Here, the likelihoods correspond to possible measurement outcomes: P(O2|error) is the likelihood of failure in our detection apparatus and captures the possibility of falsely detecting a positive signal of O2 when there is no O2 present (or conversely formulated differently could correspond to failure to detect O2 when it is present); P(O2|life) and P(O2|no life) are the two mutually exclusive hypotheses for explaining a positive measurement of the presence of O2 (viz. biotic or abiotic production, respectively). The goal is to determine P(life|O2)—that is the probability of the detection of O2 in a planetary atmosphere is actually indicative of life. For illustrative purposes, we assume P(O2|life) = 0.1, such that 10% of worlds with life will produce detectable signatures of atmospheric O2: this estimate is approximately the fraction of time Earth has had detectable levels of biologically produced O2 in its atmosphere (whether or not it is a reasonable estimate is another story, see Section 6.2). P(O2| no life) will eventually be constrained by observations of planets without life and by better planetary models (discussed in Section 5). Here, we somewhat arbitrarily assume P(O2| no life) = 0.2, that is, 20% of planets without life have detectable O2 in their atmosphere (for reasons that will become clear hereunder). Typically we expect (or want) the measurement error to be small P(O2|error) = ɛ (where ɛ is much smaller than the likelihoods for true detection). The relevant likelihoods are summarized in Figure 10 for the two hypotheses: life and no life.
FIG. 10.
Parameters for the toy model case of detecting O2 without additional knowledge of false positives. The prior probability is distributed between our two hypotheses: either life produced the signal (with probability pl) or it did not (with probability 1-pl). The likelihoods of observing O2 are set to illustrative values of 10% for life and 20% for no life (such that nonliving worlds produce detectable atmospheric O2 more frequently than worlds with life).
In the examples that follow, we assume the prior probability for life is unconstrained (see Section 7 for discussion), that is, it is uniformly distributed with a value given by P(life) = pl, and to simplify calculations we assume ɛ = 0. Although determining ɛ will be critical for weighing options for optimal mission designs, we can simplify calculations for the conceptual example presented here by treating it as a negligible term. The posterior probability of life using these values is plotted in Figure 11, which yields the trivial result our confidence in detection of life scales with our prior belief in the presence of life as the correct hypothesis (see also Fig. 19).
FIG. 11.
In the absence of additional contextual information, the posterior probability of life after detection of O2 scales with our assumptions about its prior probability (which is currently unconstrained, see Section 7), see also Figure 19.
FIG. 19.
The posterior probability of life after detection of O2 will depend on the likelihood the observed signal can be produced abiotically. If life is not common (e.g., P(life) <0.1, vertical gridline), even in cases where uninhabited worlds rarely produce O2 atmospheres (red curve, P(O2|abiotic) = 0.001), detection of O2 on a single exoplanet leaves the posterior probability of life is much less than certain (e.g., P(life|O2) < 0.9), meaning we cannot conclude the world is “very likely inhabited.” Color images available at www.liebertonline.com/ast
The power of Bayesian analysis is it permits updating confidence in a hypothesis based on accumulation of evidence and additional knowledge constraining likelihoods and priors. Repeated measurements can enable posterior probabilities to deviate significantly from the priors due to filtering through likelihoods, allowing confidence in statistical inference even in cases where the priors are unknown (as is the case for the unknown prior P(life)). For our toy model example, we can imagine a scenario where independent observations of exoplanets each yield a positive result for detection of O2 (or conversely we might consider narrowing our focus on a single target and taking repeated independent measurements each transit, see end of this section). Naively, we might get out the champagne to celebrate the discovery of life, but running the proper Bayesian analysis could lead to a different conclusion depending on the relative likelihoods for our observation.
Assuming for simplicity our measurements are Bernoulli distributed (“yes” or “no”—we detect O2 or we don't), the number of positive results will follow a Binomial distribution, with probability mass function:
 |
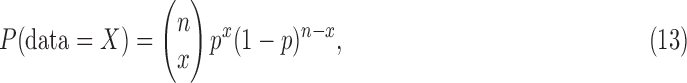where x is our measurement (in this example, the number of planets with confirmed O2), n is the number of planets we have taken measurements (the same as x in this example since we assume every observation yields a positive result for simplicity), and p is the probability of positive measurement (taken from the likelihoods in Fig. 11).
If our prior probability of life is anything less than certain (pl = 1), using Eq. 13 as our measurement distribution and assuming we have positive detection of O2 for every planet in our sample, our posterior likelihood of life actually decreases as we gain more evidence for atmospheric O2, as shown in Figure 12. In this case, increasing our number of independent measurements decreases our confidence in detection of life. Why? This is due to the existence of false positives, and more specifically that false positives have a higher likelihood of generating the observational signal. In our example, the false positive is more likely to yield the measurement than a true positive: we said 20% of lifeless worlds have atmospheric O2, whereas only 10% of worlds with life have O2 atmospheres. Even if life is the more likely prior hypothesis, our confidence in biogenicity can be significantly diminished if nonliving processes are more likely to produce the same signal. This example illustrates why it is important to tightly constrain the likelihood of the data both in the presence of life and in its absence: if a biosignature is more likely to be produced abiotically than biotically, we will not be able to use it to confidently detect life without additional context.
The importance of context is already well established for the case of interpreting biogenicity of O2, as reviewed in Meadows et al. The Bayesian framework allows us to quantify when and how context can permit distinguishing between the hypotheses of biogenic or abiotic sources. Context can be included within the Bayesian framework by expanding Eq. 12 with respect to context for the observation:
 |
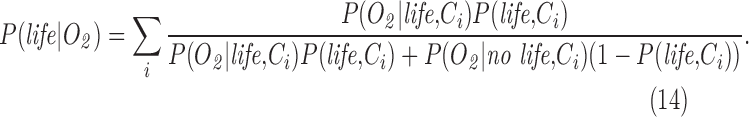Here, i sums over all contributing context, where each Ci represents contextual information necessary for interpreting the biogenicity of the given biosignature(s) (O2 in this example). In Meadows et al. (2018, this issue), several different examples of relevant contextual information were presented, which could enable identifying false positive cases of O2. These include the concomitant presence of CO2 and/or CO in the atmosphere, or the absence of H2O (see Fig. 2, Meadows et al., 2018).
To illustrate a case where context is included, we next consider an example wherein the relationship between biological and abiotic O2 production and the presence or absence of H2O are taken into account, and assign probabilities following the tables in Figure 13 (ignoring measurement error). In this example, we assign a uniform prior for the probability there is no life and a highly heterogeneous prior for life: 99% of life occurs in aqueous environments and just 1% with no water (again we are pulling numbers out of hats for illustrative purposes, for this example it does not matter much except that the probability of life in the presence of water should be higher than in its absence). We assume life cannot produce atmospheric O2 without water (hence P(O2|life, no H2O) = 0), and we assume half of our 20% of abiotic worlds producing O2-rich atmospheres do not have appreciable H2O. Substituting these probabilities into Eq. 14, we see in Figure 14 our confidence in our detection of life is significantly improved relative to the example shown in Figure 12 after many observations, but nonetheless declines with increasing observations as the measurements become more and more consistent with the abiotic explanation.
FIG. 13.
Parameters for the toy model case of detecting O2 with additional contextual knowledge of the joint probability of O2 and H2O for living and nonliving worlds. The prior probability is again distributed between our two hypotheses: either life produced the signal (with total probability pl) or it did not (with total probability 1-pl). We assume life is much more likely in the presence of H2O than not. The likelihoods of observing O2 are set to illustrative values of 10% for life and 20% for no life, where nonliving processes are just as likely to yield atmospheric O2 whether H2O is also present or not and it is assumed life does not produce O2 in the absence of H2O.
FIG. 14.
Posterior probability of life as shown in Figure 12, where now additional contextual information about the co-occurrence of O2 with H2O is taken into account (as shown in Fig. 12, Nobservations is discrete, continuous curves are shown here to better illustrate trends, and observations can be interpreted as independent measurements). Model parameters are from Figure 13, using Eq. 14. Shown are cases for varying assumptions about the prior probability of life P(life). Color images available at www.liebertonline.com/ast
We next consider a second piece of context from the O2 false positives literature: the presence or absence of atmospheric CO, with probabilities assigned now as shown in Figure 15 (again, numbers are purely illustrative). Adding this piece of contextual information does finally yield an increased confidence in our detection of life with repeated confirmation of atmospheric O2 on repeated independent observations, as shown in Figure 16 (where our confidence is now more heavily constrained by our prior because the likelihoods are less distinctive with respect to the two hypotheses). The reason is we have finally isolated a case where P(O2|life) > P(O2|no life) in the left table of Figure 15 (row 3, highlighted in blue). Note, this condition is precisely that we described as Detectability in Section 4, Eq. 5. Here, we see an explicit example of why detectability is important: it is only in cases where a biosignature is detectable that we even have a chance of increasing confidence levels in detection of life above our prior assumptions.
FIG. 16.
Posterior probability of life as shown in Figures 12 and 14, where now additional contextual information about the co-occurrence of O2 with H2O and CO is taken into account (as shown in Fig. 12, Nobservations is discrete, continuous curves are shown here to better illustrate trends, and observations can be interpreted as independent measurements). Model parameters are from Figure 15, using Eq. 14. Shown are cases for varying assumptions about the prior probability of life P(life). Color images available at www.liebertonline.com/ast
The examples provided here are highly contrived and serve to illustrate a few key points. The only observational data we included in any of the examples were detection of atmospheric O2. The posterior probability of life changed through each of the examples presented not because of additional observational data on the frequency of planets with atmospheric O2, but because of additional contextual information provided by other data (which could be due to constraints from models or observational data), which permitted placing the likelihood of the observed signal within a larger set of possibilities. Our posterior probability for life only increased once we isolated at least one scenario with high detectability, that is, where P(data|life) > P(data|no life). This highlights the importance of constraining both P(data|life) and P(data|abiotic).
Identifying cases where P(data|life) > P(data|abiotic) will be critically important to discovering life with high probability (especially in the face of unknown priors) and provides a guide for what contextual information must be better constrained to increase our confidence in discovery of life. In particular, we did not consider cases where context is an observable (e.g., where presence of H2O or CO is detected in addition to O2). Detection of contextual observables that discriminate between true and false positives will further constrain the posterior probability of life. Cases where a given piece of contextual information significantly increases detectability should inform prioritized measurements for future missions. In addition, any constraints on P(life) coming from origins of life research or evolutionary biology (Section 7) or from statistical analysis of exoplanet data sets (Section 9) are important for narrowing the space of possibilities—in this regard, information about what environments life cannot emerge or be sustained is just as valuable as information about where it can be.
One point of note from the mentioned example was the use of multiple independent measurements taken on different exoplanets to confirm biological origin for atmospheric O2. Currently, our search strategies are designed to get high resolution spectra by repeated measurements of a single target, for example, by accumulating independent observations over multiple transit events to accumulate enough information to resolve spectral features, since single transits may miss important signals. An example is the analysis of the thermal emission spectrum of the hot Jupiter HD 209458b by Line et al. (2016), where five transits where analyzed with the fourth producing no detectable signal (see Line et al., 2016). In this example, the detection error ɛ would be quite high (ɛ = 0.2).
We did not consider detection error explicitly in the examples presented here, but it could significantly impact our ability to determine whether or not a signal is due to the presence of life. For example, one could do an analysis similar to that presented here, but instead of using observations over multiple planets, consider multiple transits for the same exoplanet. In this case, measurement error coupled with the possibility of false positives (see, e.g., Gunn et al., 2016) could make it such that even in cases we might a priori expect a positive signal to be indicative of life, high confidence in detection of life might not be possible even with many transits worth of data. It is unclear at present whether a search strategy focused on getting high-resolution spectra for a single target or lower resolution data on multiple target will ultimately be the best strategy for high-confidence detection of life (the trade-offs are discussed in more detail in the next section). Bayesian analysis, properly weighing the impact of measurement error, and accounting for the likelihoods of abiotic and biotic signals could help inform future mission design by determining search strategies that maximize confidence in true detection of life.
8. Tuning Search Strategies Based on the Bayesian Framework
From the forgoing examples, it should be clear that our best strategy for life detection is to identify those cases where P(data|life) >> P(data|abiotic), that is, those scenarios where a given biosignature is overwhelmingly more likely to be produced by life than not (see, e.g., “life as improbable chemistry” in Section 6.2). This is true whether we aim to target individual worlds and obtain high-resolution data over many transits, or whether we target many worlds to generate ensemble statistics on exoplanet properties. Even in cases where detectability is high, the posterior for life may be difficult to constrain if the discriminating context is not directly observable and/or P(life) is low. We also face the challenge P(life) is currently poorly constrained. Based on the statistical framework provided by the Bayesian approach, there are two strategies that can be employed in the development of future missions to search for life: the first is to maximize our confidence in P(data|life) and the second is to maximize our confidence in P(data|abiotic). These are not necessarily mutually exclusive, and we next provide examples to demonstrate how our confidence in these terms, coupled with constraints on P(life), can inform mission design.
As noted previously, current search methods for detecting life focus on observing a single target over long periods of time to increase the resolution of our data. If we have properly accounted for context, we might expect that over time observations of an inhabited planet should lead to an increase in the likelihood a given observed signal is produced by life, P(data|life). Conversely, subsequent observations of an uninhabited world should lead to a decrease in P(data|life).
As an illustrative example, we can consider the case of an inhabited planet, observed with a UV-visible-infrared mission such as HabEx or LUVOIR (see Fujii et al., 2018, this issue). Over time, either of these missions would provide continued accumulation of knowledge of the exoplanet system. In terms of biosignatures, such a mission might first detect O3, then O2, then CH4. This would be followed by tighter constraints on the compositions of each of these gases, and detection and measurement of the surface distribution of oceans, continents, and potentially a red edge-like effect from pigments. Eventually, we may see seasonal variations in gases (Fig. 17), which we could hypothesize reflected their production or consumption by biology. And with subsequent missions operating at different wavelength ranges, the surface climate could be determined, isotopic measurements made, and trace gases identified. In each of these steps, our confidence in the presence of life, P(data|life), would increase as we expect for many of these observables P(data|life) >> P(data|abiotic) (the more such observables the better).
FIG. 17.
Seasonal variation in pCO2 as an example where we might expect P(data|life) >> P(data|abiotic), leading into an enhanced posterior probability for life. Volume mixing ratio measurements CO2 are sourced from the NOAA at Mauna Loa, Hawaii, for the 1995–2000 time interval (Thoning et al., 2015). The seasonal change in CO2 in the northern hemisphere is mostly reflective of the seasonal growth and decay/senescence of land-based vegetation (Keeling et al., 1996). These data were obtained from the NOAA's Earth System Research Laboratory (https://www..esrl.noaa.gov/). NOAA, National Oceanic and Atmospheric Association. Color images available at www.liebertonline.com/ast
As mentioned at the end of Section 7, one of the advantages of a well-developed Bayesian framework is that it can quantitatively inform observational strategies. For example, in the mentioned scenario, detectability provides a metric to determine the more valuable observations (those where P(data|life) >> P(data|abiotic), which is true whether targeting individual exoplanets or ensembles), for placing tighter constraints on the concentrations of biogenic gases or observations of the temporal variability of those gases over seasonal time periods.
Another scenario is that the observational spectra do not match our models, which could occur either for P(data|life) or for P(data|abiotic). Although there are challenges with constraining both P(data|abiotic) and P(data|life), arguably the latter term is the one that will provide the greater statistical uncertainty. One question is then how can we best constrain P(data|abiotic) based on our planetary models to maximize our confidence that deviations from the expected observations arise due to life?
The best way to constrain P(data|abiotic) will be to conduct large statistical surveys of uninhabited worlds, as discussed in Section 4. So far, data sets of this nature are scarce for exoplanets and nonexistent for Earth-like worlds. One notable example for hot Jupiter exoplanets is the 19 transiting examples with published transmission spectra obtained with the Hubble/WFC3 G141 NIR grism. A majority of these (10 of 19) report a detection of H2O in their atmosphere (see Iyer et al., 2016). Recently, it was shown that the individual spectra of these planets coherently average to produce a predictable characteristic spectrum (Iyer et al., 2016), which is reproducible with simple forward models, providing confidence that there exists a representative spectrum for at least a significant fraction of hot Jupiter exoplanets (Fig. 12). In this case, individual spectra do not fit our models well (P(data|abiotic) is small), due to stochasticity in planetary evolution and in our measurements. However, the characteristic averaged spectrum can be reproduced by models (high P(data|abiotic)). It is an open question whether representative spectra will also accurately describe ensemble spectra of Earth-like worlds. Given the limited data we can collect on exoplanets (see review of observation capabilities in Fujii et al., 2018, this issue), and the stochasticity of planetary evolution (Lenardic and Crowley, 2012), it may be that we are only able to assign with high confidence a likelihood P(data|abiotic) for exoplanet spectra by fitting our models probabilistically (Fig. 18).
FIG. 18.
Top: Normalized HST/WFC3 IR transmission spectra of 10 exoplanets with reported H2O detections combined with a weighted mean to create a representative spectrum of H2O-bearing exoplanets. Bottom: Comparison of representative spectrum (black) to single planet models (see Iyer et al., 2016 for details). Adopted from Iyer et al. (2016). If this turns out to be the case, the community may need to shift focus to thinking about also detecting life deterministically, by analyzing coherently averaged spectra of many candidate worlds. HST, Hubble Space Telescope; IR, infrared. Color images available at www.liebertonline.com/ast
An advantage of a statistical approach to life detection is that it allows for the combination of a range of observations, including integrating over time and sampling large statistical data sets. The combination can place bounds on the three terms of the Bayesian framework. For example, we can sum observations across planets and ask how our confidence that life exists on an exoplanet is changed by a new observation. If P(life) = 0.25 (e.g., life is not rare, with a 1 in 4 chance of an exoplanet being inhabited) for an ensemble of 11 exoplanets, then a simplistic calculation suggests that we have a 95% chance that life exists on at least one of them. Here, a null result is almost as significant as a positive result. If we survey a sample of planets that are candidates for supporting a particular life process, and we find no evidence of that process on those worlds, we gain important information for constraining P(life), for example, P(life) << 1.
This kind of analysis can also provide a guide to direct how many planets we must survey to detect life, depending on how frequently we expect life to occur. Building on the examples of the previous section, we provide another toy model to illustrate how, within a Bayesian framework, large statistical surveys can increase our confidence level in detection of life. One challenge for the community is to decide credible levels for detection of life. In Catling et al. (2018, this issue), confidence levels were proposed in terms of the value of the posterior probability, for example, >90% was proposed as “very likely inhabited.” In the examples of the previous section, we mostly focused on cases where life is fairly common, with a 10% or greater probability for a given planet to be inhabited. Even in the final example, where our confidence level increases with successive measurements, we are still sensitive to our prior, and would not be confident in our measurement if life if it were not extremely common (observing additional context could help).
What happens if life is rare? Or if we do not get lucky and draw 10 worlds each with detectable atmospheric O2? We showed in Figure 11 an example of how P(life|O2) can vary with P(life) for a hypothetical case where P(O2|life) < P(O2|no life). As we illustrated, this scenario is not favorable for detectability. However, even if P(O2|life) ∼ P(O2|no life) or P(O2|life) >> P(O2|no life), such that the scenario does favor detection, we might still not have high confidence in our detection of O2 as evidence for life if our prior probability for life is small. Figure 19 shows how our posterior probability of life changes (assuming one transit measurement) for different values of P(no life|O2). Even in cases where the signal is unlikely to be produced abiotically (red curve, P(O2|abiotic) = 0.001, corresponding to a 0.1% probabilty for an uninhabited world to have detectable levels of atmospheric O2), if life is not common (e.g., P(life) < 0.1, vertical gridline) our posterior probability for life will not be “very likely inhabited” (e.g., it is <90%). In this case, data on more worlds are necessary to determine whether life is a viable hypothesis.
Our current approach to biosignature assessment on exoplanet assumes we will be lucky enough to identify a target with detectable atmospheric O2 to begin with. In cases where life is rare, or the biosignature of interest (atmospheric O2) is rare, an ensemble approach to detection provides an alternative strategy for discovering life to that of repeating measurements on a single target. To illustrate this, we assume the number of inhabited worlds is Poisson distributed (see, e.g., Spiegel and Turner, 2012), rather than uniformly distributed as in the previous examples. That is, for a sample of exoplanets of size N, the probability of life arising k times is assumed to take the form
 |
where λ is the probability per planet of life developing. The probability to have no life in a sample of N worlds is then
 |
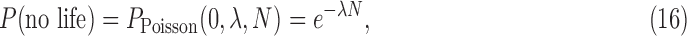with
 |
For illustrative purposes, we assume life is detectable when O2 is observed, but also that life is rare. We assume P(O2|life) > P(O2|no life), with P(O2|life) = 0.1 (10% of inhabited worlds produce detectable O2 in their atmospheres) and P(O2|no life)) = 0.01 (only 1% of uninhabited worlds produce detectable atmospheric O2, in contrast to the 20% of the last section). We consider two cases: life occurs on 1 in 100 worlds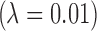 
and life occurs on 1 in 1000 worlds 
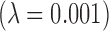and assess the posterior probability of life assuming the fraction f(O2) of the total number of exoplanets observed (Nexoplanets) have detectable O2 (a positive signal in Eq. 13). The trends for P(life| O2) are shown in Figure 20, for measurement distributions with 1%, 2%, 3%, 4%, and 5% of worlds having detectable atmospheric O2. When the percentage of observed planets with O2 is low ∼1%, consistent with the expected abiotic likelihood of P(O2|no life)) = 0.01 (1% of uninhabited worlds have detectable O2), our posterior probability for life approaches zero as additional data are accumulated. However, if the percentage of observed planets with O2 is much higher than our expectation for an ensemble of exoplanets with no life, then our confidence in the hypothesis of life as the correct explanation for the data increases with our number of samples at a rate determined by the rarity of our prior (here whether we have a 1 in 100 or 1 in 1000 chance of a world being inhabited).
FIG. 20.
The posterior probability of life assuming a fraction f(O2) of the Nexoplanets observed have detectable levels of atmospheric O2. Shown are cases where the prior probability of life is 0.01 (A) and 0.001 (B). Color images available at www.liebertonline.com/ast
It is worth noting that a small sample size with a large fraction of O2 is not sufficient to generate a posterior for life that is “very likely,” since it is also possible for a random sample of worlds without life to produce such a distribution. As the sample size increases, it becomes increasing unlikely that the abiotic distribution of uninhabited worlds with O2 atmospheres will deviate significantly from the expected value of 1%. In large samples of observations, deviations from the expected abiotic value, therefore, lend support to the hypothesis that life is generating O2 on a fraction of the worlds (here, we consider a case where P(O2|life) > P(O2|no life), but this works equally well if the inverse is true, so long as the expected fraction of planets with atmospheric O2 differs far significantly for inhabited and uninhabited worlds).
The mentioned example highlights how the actual (as yet) unknown value of P(life) can be critical to determining the most effective search strategy. If life is common (P(life) >> 0), it may make sense to target individual worlds and obtain high-resolution spectra, as is the proposed search strategy for James Webb Space Telescope. However, if life is uncommon, we may be highly unlikely to be so lucky as to stumble on the right target. In this scenario, a more optimized search might, for example, take lower resolution spectra of more worlds to generate better statistics. This was the strategy for Kepler, as at the time P(planets) was unknown. Kepler observed a huge field of stars, rather than obtaining more data on a smaller number of stars, as the likelihood of stars hosting planets at the time was unknown. A similar strategy may be necessary to determine the likelihood of planets hosting life.
In other more established fields, such as particle physics, confidence intervals are set at standard values for claiming discovery. For example, discovery of the Higgs particle was announced only after the five-sigma detection level was met (even though there were hints previously), meaning there is a chance of only 1 in 3.5 million the signal was generated by a random process. Astrobiologists could adopt a similar standard, using a statistical approach to place bounds on the credible interval (the Bayesian's answer to the confidence interval) for the prior probability of life (e.g., a credible interval for λ in the previous example, which for a given sample size, expected distributions of P(data|abiotic) and P(data|life) could be statistically constrained). Such an approach would increase confidence in the value of the prior probability of life, in turn increasing our ability to infer its presence on individual exoplanets. Future community efforts should focus on establishing community standards for credible intervals for detection of life.
9. Conclusions
The continued rapid increase in discovered exoplanets in the coming years will make it necessary—as well as possible—to calculate the likelihood of a given observation being produced by an inhabited planet. This, in turn, requires a concerted effort to build comprehensive systems models of planets that include the myriad interactions of the biosphere with other planetary systems as we have reviewed here. Such models must also be flexible to be applicable to planets with a variety of compositions, sizes, orbital properties, orbiting stars with a variety of properties, etc. In this article, we have presented a discussion of the necessary tools, disciplines, and methods necessary to build, assess, and improve such models and improve our estimates of P(data|life), P(data|abiotic), and P(life). We summarize many of these in Table 3.
Table 3.
Summary of Observational, Theoretical, and Empirical Research Necessary to Constrain Variables in a Bayesian Framework for Life Detection
| P(data|abiotic) | P(data|life) | P(life) | |
|---|---|---|---|
| Stellar context | |||
| Stellar observations Statistical constraints on age, Teff, composition, irradiance, etc. |
✓ | ✓ | ✓ |
| Stellar impact on atmospheres Models of stellar activity on atmospheric observables, e.g., lifetime exposure to UV |
✓ | ✓ | |
| Planetary context | |||
| Planets without life Observational data of planets without life to constrain abiotic models |
✓ | ||
| Atmosphere observations Statistical data on frequency of biosignature gases in exoplanet atmospheres |
✓ | ✓ | |
| Global climate models of exoplanets Identify favorable/unfavorable conditions for life and generate statistical data sets of likelihood of observations |
✓ | ✓ | |
| Geochemical modeling Model physical contexts more relevant for exoplanets than that of Earth |
✓ | ✓ | |
| Catalog small molecules Expand available data on kinetic and thermodynamic properties of small molecules that may be present in exoplanet atmospheres |
✓ | ✓ | |
| Living processes | |||
| Coevolution of life and Earth Statistical data and models for past biogeochemical states in the history of Earth |
✓ | ✓ | |
| Frequency of major transitions Constraints on the likelihood of major evolutionary innovation |
✓ | ||
| Origins of life Theory and experiments to constrain probability for life to emerge |
✓ | ||
| Thresholds in chemical complexity Identify cases where observable much more likely to be produced by life than not |
✓ | ||
| Universal biology Identify network and other properties of life on Earth likely to be universal |
✓ | ✓ | |
UV, ultraviolet.
We highlighted a set of possible future directions for research on exoplanet biosignatures, suggesting promising directions that are not yet mainstream methods, but hold potential to revolutionize our search strategies in years to come. A major hurdle to be overcome in the coming decades is our lack of constraints on P(life), and in particular P(emerge), the likelihood for the origins of life. This is one area where exoplanet science will need to interface with new communities, including those studying evolutionary biology, the coevolution of Earth and life, and the origins of life. Exoplanet scientists will gain knowledge of constraints on the relevant terms in the Bayesian framework, informed by Earth's life and attempts to attract universal principles. In turn, our expanding observational searches for life should take advantage of the ensemble statistics we will be able to generate in the coming decades to inform our understanding of the distribution of life, placing additional observational constraints on P(data|abiotic), P(data|life), and possibly even P(life), for example, by identifying planetary environments where no life is found (P(data|abiotic) matches well with observations) and those environments where life may be generating the observed spectra (eight P(data|abiotic) are not explanatory, but P(data|life) could be).
By combining the efforts of these diverse communities, amalgamating deep knowledge of Earth, its life, and their coevolution with constraints afforded by the plurality of exoplanets, we have the first opportunity in history to put quantitative bounds on the distribution of life in the Universe. As emphasized in this article, this will require a concerted multidisciplinary and international effort, as should be expected from the enormity of the task of discovering life beyond Earth.
Abbreviations Used
- DMDS
dimethyl disulfide
- DMS
dimethyl sulfide
- DMSP
dimethylsulfoniopropionate
- FUV
far-UV
- GCM
general circulation model
- GOE
great oxidation event
- HST
Hubble Space Telescope
- IR
infrared
- LUCA
last universal common ancestor
- NIR
near-infrared
- NOAA
National Oceanic and Atmospheric Association
- NUV
near-UV
- OEC
oxygen evolving complex
- UV
ultraviolet
Acknowledgments
E.W.S. is grateful for support from the NASA Postdoctoral Program, administered by the Universities Space Research Association. S.D. was supported by NASA Exobiology grant NNX15AM07G. S.I.W. and H.B.S were supported by NASA Exobiology grant NNX15AL24G. This work benefitted from collaborations and/or information exchange within NASA's Nexus for Exoplanet System Science (NExSS) research coordination network sponsored by NASA's Science Mission Directorate.
Author Disclosure Statement
No competing financial interests exist.
References
- Abe Y., Abe-Ouchi A., Sleep N.H., and Zahnle K.J. (2011) Habitable zone limits for dry planets. Astrobiology 11:443–460 [DOI] [PubMed] [Google Scholar]
- Abe Y., Numaguti A., Komatsu G., and Kobayashi Y. (2005) Four climate regimes on a land planet with wet surface: effects of obliquity change and implications for ancient Mars. Icarus 178:27–39 [Google Scholar]
- Airapetian V.S., Glocer A., Gronoff G., Hebrard E., and Danchi W. (2016) Prebiotic chemistry and atmospheric warming of early Earth by an active young Sun. Nat Geosci 9:452–455 [Google Scholar]
- Allakhverdiev S.I., Kreslavski V.D., Zharmukhamedov S.K., Voloshin R.A., Korol'kova D.V., Tomo T., and Shen J.R. (2016) Chlorophylls d and f and their role in primary photosynthetic processes of cyanobacteria. Biochemistry (Mosc) 81:201–212 [DOI] [PubMed] [Google Scholar]
- Amaral-Zettler L.A., Zettler E.R., Theroux S.M., Palacios C., Aguilera A., and Amils R. (2011) Microbial community structure across the tree of life in the extreme Rio Tinto. ISME J 5:42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bains W. (2014) What do we think life is? A simple illustration and its consequences. Int J Astrobiol 13:101–111 [Google Scholar]
- Bains W. and Schulze-Makuch D. (2016) The cosmic zoo: the (near) inevitability of the evolution of complex, macroscopic life. Life 6:25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bains W. and Seager S. (2012) A combinatorial approach to biochemical space: description and application to the redox distribution of metabolism. Astrobiology 12:271–281 [DOI] [PubMed] [Google Scholar]
- Bains W., Seager S., and Zsom A. (2014) Photosynthesis in hydrogen-dominated atmospheres. Life 4:716–744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barandiaran X.E., Di Paolo E., and Rohde M. (2009) Defining agency: individuality, normativity, asymmetry, and spatio-temporality in action. Adapt Behav 17:367–386 [Google Scholar]
- Benner S.A. (2010) Defining life. Astrobiology 10:1021–1030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benner S.A., Sassi S.O., and Gaucher E.A. (2007) Molecular paleoscience: systems biology from the past. Adv Enzymol Relat Areas Mol Biol 75:1–132 [DOI] [PubMed] [Google Scholar]
- Bennett C. (1988) Logical depth and physical complexity. In The Universal Turing Machine: A Half-Century Survey, edited by Herken R., Oxford University Press, Oxford, UK, pp 227–257 [Google Scholar]
- Bercovici D. and Ricard Y. (2016) Grain-damage hysteresis and plate-tectonic states. Phys Earth Planet Int 253:31–47 [Google Scholar]
- Berner R.A., Beerling D.J., Dudley R., Robinson J.M., and Wildman R.A., Jr (2003) Phanerozoic atmospheric oxygen. Annu Rev Earth Planet Sci 31:105–134 [Google Scholar]
- Bettencourt L.M. (2013) The origins of scaling in cities. Science 340:1438–1441 [DOI] [PubMed] [Google Scholar]
- Björn L.O., Papageorgiou G.C., Blankenship R.E., and Govindjee. (2009) A viewpoint: why chlorophyll a? Photosynth Res 99:85–98 [DOI] [PubMed] [Google Scholar]
- Blank C.E. and Sanchez-Baracaldo P. (2010) Timing of morphological and ecological innovations in the cyanobacteria—a key to understanding the rise in atmospheric oxygen. Geobiology 8:1–23 [DOI] [PubMed] [Google Scholar]
- Blankenship R.E. and Hartman H. (1998) The origin and evolution of oxygenic photosynthesis. Trans Biol Sci 23:94–97 [DOI] [PubMed] [Google Scholar]
- Blankenship R.E., Sadekar S., and Raymond J. (2007) Chapter 3: The evolutionary transition from anoxygenic to oxygenic photosynthesis A2—Falkowski, Paul G. In Evolution of Primary Producers in the Sea, edited by Knolls A.H., Academic Press, Burlington, MA, pp 21–35 [Google Scholar]
- Bochanski J.J., Hawley S.L., Covey K.R., West A.A., Reid I.N., Golimowski D.A., and Ivezić Ž. (2010) The luminosity and mass functions of low-mass stars in the galactic disk. II. The fiel. Astron J 139:2679–2699 [Google Scholar]
- Boucher Y., Douady C.J., Papke R.T., Walsh D.A., Boudreau M.E., Nesbø C.L., Case R.J., and Doolittle W.F. (2003) Lateral gene transfer and the origins of prokaryotic groups. Annu Rev Genet 37:283–328 [DOI] [PubMed] [Google Scholar]
- Bovy J. (2017) Stellar inventory of the solar neighborhood using Gaia DR1. Mon Not R Astron Soc 470:1360–1387 [Google Scholar]
- Braakman R. and Smith E. (2012) The compositional and evolutionary logic of metabolism. Phys Biol 10:011001. [DOI] [PubMed] [Google Scholar]
- Budyko M.I. (1969) The effect of solar radiation variations on the climate of the Earth. Tellus 21:611–619 [Google Scholar]
- Buick R. (2008) When did oxygenic photosynthesis evolve? Philos Trans R Soc Lond B Biol Sci 363:2731–2743 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardona T. (2016) Reconstructing the origin of oxygenic photosynthesis: do assembly and photoactivation recapitulate evolution? Front Plant Sci 7:257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardona T., Murray J.W., and Rutherford A.W. (2015) Origin and evolution of water oxidation before the last common ancestor of the cyanobacteria. Mol Biol Evol 32:1310–1328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caron A.M. and Fournier G.P. (2017) Phylogenetic proxies for the rise of atmospheric oxygen. In Astrobiology Science Conference 2017 (LPI Contrib. No. 1965) [Google Scholar]
- Carter B. (2008) Five-or six-step scenario for evolution? Int J Astrobiol 7:177–182 [Google Scholar]
- Carter B. and McCrea W.H. (1983) The anthropic principle and its implications for biological evolution and discussion. Phil Trans Roy Soc A 310:347–636 [Google Scholar]
- Castresana J. and Saraste M. (1995) Evolution of energetic metabolism: the respiration-early hypothesis. Trends Biochem Sci 20:443–448 [DOI] [PubMed] [Google Scholar]
- Catling D.C., Krissansen-Totton J., Kiang N.Y., Crisp D., Robinson T.D., DasSarma S., Rushby A.J., Del Genio A., Bains W., and Domagal-Goldman S. (2018) Exoplanet biosignatures: A framework for their assessment. Astrobiology 18:709–738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catling D.C., Glein C.R., Zahnle K.J., and McKay C.P. (2005) Why O2 is required by complex life on habitable planets and the concept of planetary “oxygenation time.” Astrobiology 5:415–438 [DOI] [PubMed] [Google Scholar]
- Catling D.C., Zahnle K.J., and McKay C.P. (2001) Biogenic methane, hydrogen escape, and the irreversible oxidation of early Earth. Science 293:839–843 [DOI] [PubMed] [Google Scholar]
- Chaitin G. (2012) Proving Darwin: Making Biology Mathematical, Vintage. Pantheon Books, New York, 2012 [Google Scholar]
- Chaput J.C., Yu H., and Zhang S. (2012) The emerging world of synthetic genetics. Chem Biol 19:1360–1371 [DOI] [PubMed] [Google Scholar]
- Charnay B., Forget F., Wordsworth R., Leconte J., Millour E., Codron F., and Spiga A. (2013) Exploring the faint young Sun problem and the possible climates of the Archean Earth with a 3-D GCM. J Geophys Res Atmos 118:10414–10431 [Google Scholar]
- Charnay B., Meadows V., Misra A., Leconte J., and Arney G. (2015) 3D modeling of GJ1214b's atmosphere: formation of inhomogeneous high clouds and observational implications. Astrophys J 813:L1 [Google Scholar]
- Chyba C.F. and McDonald G.D. (1995) The origin of life in the solar system: current issues. Annu Rev Earth Planet Sci 23:215–249 [DOI] [PubMed] [Google Scholar]
- Claire M.W., Catling D.C., and Zahnle K.J. (2006) Biogeochemical modelling of the rise in atmospheric oxygen. Geobiology 4:239–269 [Google Scholar]
- Clauset A., Shalizi C.R., and Newman M.E. (2009) Power-law distributions in empirical data. SIAM Rev 51:661–703 [Google Scholar]
- Cleland C.E. (2012) Life without definitions. Synthese 185:125–144 [Google Scholar]
- Cleland C.E. and Chyba C. (2002) Defining “life.” Orig Life Evol Biosph 32:387–393 [DOI] [PubMed] [Google Scholar]
- Cole D.B., Reinhard C.T., Wang X.L., Gueguen B., Halverson G.P., Gibson T., Hodgskiss M.S.W., McKenzie N.R., Lyons T.W., and Planavsky N.J. (2016) A shale-hosted Cr isotope record of low atmospheric oxygen during the Proterozoic. Geology 44:555–558 [Google Scholar]
- Coogan L.A. and Dosso S.E. (2015) Alteration of ocean crust provides a strong temperature dependent feedback on the geological carbon cycle and is a primary driver of the Sr-isotopic composition of seawater. Earth Planet Sci Lett 415:38–46 [Google Scholar]
- Corey E.J. General methods for the construction of complex molecules. Pure Appl Chem 14:19–38 [Google Scholar]
- Coughlin J.L., Mullally F., Thompson S.E., Rowe J.F., Burke C.J., Latham D.W., Batalha N.M., Ofir A., Quarles B.L., Henze C.E., and Wolfgang A. (2016) Planetary candidates observed by Kepler. VII. The first fully uniform catalog based on the entire 48-month data set (Q1–Q17 DR24). Astrophys J Suppl Ser 224:12 [Google Scholar]
- Crowley J.W. and O'Connell R.J. (2012) An analytic model of convection in a system with layered viscosity and plates. Geophys J Int 188:61–78 [Google Scholar]
- DasSarma S. (2006) Extreme halophiles are models for astrobiology. Microbe 1:120–126 [Google Scholar]
- Davies P.C.W. and Walker S.I. (2016) The hidden simplicity of biology. Rep Prog Phys 79:102601. [DOI] [PubMed] [Google Scholar]
- Del Genio A.D. and Zhou W. (1996) Simulations of superrotation on slowly rotating planets: sensitivity to rotation and initial condition. Icarus 120:332–343 [Google Scholar]
- Del Genio A.D., Zhou W., and Eichler T.P. (1993) Equatorial superrotation in a slowly rotating GCM: implications for Titan and Venus. Icarus 101:1–17 [Google Scholar]
- DeLong J.P., Okie J.G., Moses M.E., Sibly R.M., and Brown J.H. (2010) Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc Natl Acad Sci U S A 107:12941–12945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeMore W.B., Sander S.P., Golden D.M., Hampson R.F., Kurylo M.J., Howard C.J., Ravishankara A.R., Kolb C.E., and Molina M.J. (1997) Chemical Kinetics and Photochemical Data for Use in Stratospheric Modeling, Evaluation No. 12, JPL Publication 97-4, NASA, Pasadena, CA [Google Scholar]
- Desch S., Hartnett H., Glaser S., Neuer S., Zolotov M., Kane S., Fisher T., Anbar A., Walker S.I., and Unterborn C. (2018) Detectability of life, on aqua planets and water worlds. In review [Google Scholar]
- Des Marais D.J., Harwit M.O., Jucks K.W., Kasting J.F., Lin D.N.C., Lunine J.I., Schneider J., Seager S., Traub W.A., and Woolf N.J. (2002) Remote sensing of planetary properties and biosignatures on extrasolar terrestrial planets. Astrobiology 2:153–181 [DOI] [PubMed] [Google Scholar]
- Des Marais D.J., Nuth J., Allamandola L.J., Boss A.P., Farmer J.D., Hoehler T.M., Jakosky B.M., Meadows V.S., Pohorille A., Runnegar B., and Spormann A.M. (2008) The NASA Astrobiology Roadmap. Astrobiology 8:715–730 [DOI] [PubMed] [Google Scholar]
- Des Marais D.J. and Walter M.R. (1999) Astrobiology: exploring the origins, evolution, and distribution of life in the Universe. Annu Rev Ecol Syst 30:397–420 [DOI] [PubMed] [Google Scholar]
- Dessert C., Dupre B., Francois L.M., Schott J., Gaillardet J., Chakrapani G.J., and Bajpai S. (2001) Erosion of Deccan Traps determined by river geochemistry: impact on the global climate and the 87Sr/86Sr ratio of seawater. Earth Planet Sci Lett 188:459–474 [Google Scholar]
- Dismukes G.C., Klimov V.V., Baranov S.V., Kozlov Y.N., DasGupta J., and Tyryshkin A. (2001) The origin of atmospheric oxygen on Earth: the innovation of oxygenic photosynthesis. Proc Natl Acad Sci U S A 98:2170–2175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domagal-Goldman S.D., Meadows V.S., Claire M.W., and Kasting J.F. (2011) Using biogenic sulfur gases as remotely detectable biosignatures on anoxic planets. Astrobiology 11:419–441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domagal-Goldman S.D., Segura A., Claire M.W., Robinson T.D., and Meadows V.S. (2014) Abiotic ozone and oxygen in atmospheres similar to prebiotic Earth. Astrophys J 792:90 [Google Scholar]
- Dorn C., Khan A., Heng K., Connolly J.A.D., Alibert Y., Benz,W., and Tackley P. (2015) Can we constrain the interior structure of rocky exoplanets from mass and radius measurements? Astron Astrophys 577:A83 [Google Scholar]
- Drake F. (1965) The radio search for intelligent extraterrestrial life. In Current Aspects of Exobiology, edited by Mamikunian G., Pergamon Press, Jet Propulsion Laboratory, pp 323–345 [Google Scholar]
- Dunne J.A., Williams R.J., and Martinez N.D. (2002) Food-web structure and network theory: the role of connectance and size. Proc Natl Acad Sci U S A 99:12917–12922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edson A., Lee S., Bannon P., Kasting J.F., and Pollard D. (2011) Atmospheric circulations of terrestrial planets orbiting low-mass stars. Icarus 212:1–13 [Google Scholar]
- Estrada E. (2012) Returnability as a criterion of disequilibrium in atmospheric reactions networks. J Math Chem 50:1363–1372 [Google Scholar]
- Eyring V., Bony S., Meehl G.A., Senior C., Stevens B., Stouffer R.J., and Taylor K.E. (2015) Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci Model Dev Discuss 8:10539–10583 [Google Scholar]
- Fischer W.W., Hemp J., and Johnson J.E. (2016) Evolution of oxygenic photosynthesis. Annu Rev Earth Planet Sci 44:647–683 [Google Scholar]
- Forget F. and Leconte J. (2014) Possible climates on terrestrial exoplanets. Philos Trans R Soc Lond A 372:20130084. [DOI] [PubMed] [Google Scholar]
- Forterre P. and Gribaldo S. (2007) The origin of modern terrestrial life. HFSP J 1:156–168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- France K., Loyd R.P., Youngblood A., Brown A., Schneider P.C., Hawley S.L., Froning C.S., Linsky J.L., Roberge A., Buccino A.P., and Davenport J.R. (2016) The MUSCLES Treasury Survey. I. Motivation and overview. Astrophys J 820:89 [Google Scholar]
- Fujii Y., Angerhausen D., Deitrick R., Domagal-Goldman S., Grenfell J.L., Hori Y., Kane S.R., Palle E., Rauer H., Siegler N., Stapelfeldt K., and Stevenson K.B. (2018) Exoplanet biosignatures: observational prospects. Astrobiology 18:739–778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebauer S., Grenfell J.L., Stock J.W., Lehmann R., Godolt M., Paris P.V., and Rauer H. (2017) Evolution of Earth-like extrasolar planetary atmospheres: assessing the atmospheres and biospheres of early Earth analog planets with a coupled atmosphere biogeochemical model. Astrobiology 17:27–54 [DOI] [PubMed] [Google Scholar]
- Gleiss P.M., Stadler P.F., Wagner A., and Fell D.A. (2001) Relevant cycles in chemical reaction networks. Adv Complex Syst 4:207–226 [Google Scholar]
- Goldenfeld N. and Woese C. (2011) Life is physics: evolution as a collective phenomenon far from equilibrium. Annu Rev Condens Matter Phys 2:375–399 [Google Scholar]
- Gould S.J. (1990) Wonderful Life: The Burgess Shale and the Nature of History. W.W. Norton & Company, New York [Google Scholar]
- Gunn L.J., Chapeau-Blondeau F., McDonnell M.D., Davis B.R., Allison A., and Abbott D. (2016) Too good to be true: when overwhelming evidence fails to convince. Proc R Soc A 472:20150748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guttenberg N., Virgo N., Chandru K., Scharf C., and Mamajanov I. (2017) Bulk measurements of messy chemistries are needed for a theory of the origins of life. Phil Trans R Soc A 375:20160347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas J.R. (2010) The potential feasibility of chlorinic photosynthesis on exoplanets. Astrobiology 10:953–963 [DOI] [PubMed] [Google Scholar]
- Harman C.E., Schwieterman E.W., Schottelkotte J.C., and Kasting J.F. (2015) Abiotic O2 levels on planets around F, G, K, and M stars: possible false positives for life? Astrophys J 812:137 [Google Scholar]
- Hatton I.A., McCann K.S., Fryxell J.M., Davies T.J., Smerlak M., Sinclair A.R., and Loreau M. (2015) The predator-prey power law: biomass scaling across terrestrial and aquatic biomes. Science 349:aac6284. [DOI] [PubMed] [Google Scholar]
- Heller R. and Armstrong J. (2014) Superhabitable worlds. Astrobiology 14:50–66 [DOI] [PubMed] [Google Scholar]
- Heng K., Menou K., and Phillipps P.J. (2011) Atmospheric circulation of tidally locked exoplanets: a suite of benchmark tests for dynamical solvers. Mon Not R Astron Soc 413:2380–2402 [Google Scholar]
- Hitchcock D.R. and Lovelock J.E. (1967) Life detection by atmospheric analysis. Icarus 7:149–159 [Google Scholar]
- Ho M.-Y., Gan F., Shen G., Zhao C., and Bryant D.A. (2017) Far-red light photoacclimation (FaRLiP) in Synechococcus sp. PCC 7335: I. Regulation of FaRLiP gene expression. Photosynth Res 131:173–186 [DOI] [PubMed] [Google Scholar]
- Hoehler T.M. (2007) An energy balance concept for habitability. Astrobiology 7:824–838 [DOI] [PubMed] [Google Scholar]
- Holme P., Huss M., and Lee S.-H. (2011) Atmospheric reaction systems as null-models to identify structural traces of evolution in metabolism. PLoS One 6:e19759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu R. and Seager S. (2014) Photochemistry in terrestrial exoplanet atmospheres. III. Photochemistry and thermochemistry in thick atmospheres on super Earths and mini Neptunes. Astrophys J 784:63 [Google Scholar]
- Hu R., Seager S., and Bains W. (2012) Photochemistry in terrestrial exoplanet atmospheres. I. Photochemistry model and benchmark cases. Astrophys J 761:166 [Google Scholar]
- Hu R., Seager S., and Bains W. (2013) Photochemistry in terrestrial exoplanet atmospheres. II. H2S and SO2 photochemistry in anoxic atmospheres. Astrophys J 769:6 [Google Scholar]
- Hubler S.L. and Craciun G. (2012) Periodic patterns in distributions of peptide masses. BioSystems 109:179–185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hud N.V. and Anet F.A. (2000) Intercalation-mediated synthesis and replication: a new approach to the origin of life. J Theor Biol 205:543–562 [DOI] [PubMed] [Google Scholar]
- Hughes J.B., Hellmann J.J., Ricketts T.H., and Bohannan B.J.M. (2001) Counting the uncountable: statistical approaches to estimating microbial diversity. Appl Environ Microbiol 67:4399–4406 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison C. I.II, Chuang R.Y., Noskov V.N., Assad-Garcia N., Deerinck T.J., Ellisman M.H., Gill J., Kannan K., Karas B.J., Ma L., Pelletier J.F., Qi Z.Q., Richter R.A., Strychalski E.A., Sun L., Suzuki Y., Tsvetanova B., Wise K.S., Smith H.O., Glass J.I., Merryman C., Gibson D.G., and Venter J.C. (2016) Design and synthesis of a minimal bacterial genome. Science 351:aad6253. [DOI] [PubMed] [Google Scholar]
- Iyer A.R., Swain M.R., Zellem R.T., Line M.R., Roudier G., Rocha G., and Livingston J.H. (2016) A characteristic transmission spectrum dominated by H2O applies to the majority of HST/WFC3 exoplanet observations. Astrophys J 823:109 [Google Scholar]
- Jeong H., Tombor B., Albert R., Oltvai Z.N., and Barabási A.L. (2000) The large-scale organization of metabolic networks. Nature 407:651. [DOI] [PubMed] [Google Scholar]
- Joshi M.M. (2003) Climate model studies of synchronously rotating planets. Astrobiology 3:415–427 [DOI] [PubMed] [Google Scholar]
- Joshi M.M., Haberle R.M., and Reynolds R.T. (1997) Simulations of the atmospheres of synchronously rotating terrestrial planets orbiting M dwarfs: conditions for atmospheric collapse and the implications for habitability. Icarus 129:450–465 [Google Scholar]
- Joussaume S., Taylor K.E., Braconnot P.J.F.B., Mitchell J.F.B., Kutzbach J.E., Harrison S.P., Prentice I.C., Broccoli A.J., Abe‐Ouchi A., Bartlein P.J., and Bonfils C. (1999) Monsoon changes for 6000 years ago: results of 18 simulations from the Paleoclimate Modeling Intercomparison Project (PMIP). Geophys Res Lett 26:859–862 [Google Scholar]
- Kacar B. and Gaucher E.A. (2012) Towards the recapitulation of ancient history in the laboratory: combining synthetic biology with experimental evolution. Artif Life 13:11–18 [Google Scholar]
- Kacar B., Ge X., Sanyal S., and Gaucher E.A. (2017a) Experimental evolution of Escherichia coli harboring an ancient translation protein. J Mol Evol 84:69–84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kacar B., Guy L., Smith E., and Baross J. (2017c) Resurrecting ancestral genes in bacteria to interpret ancient biosignatures. Phil Trans A Math Phys Eng Sci 375:20160352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kacar B., Hanson-Smith V., Adam Z.R., and Boekelheide N. (2017b) Constraining the timing of the Great Oxidation Event within the Rubisco phylogenetic tree. Geobiology 15:628–640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaltenegger L., Traub W.A., and Jucks K.W. (2007) Spectral evolution of an Earth-like planet. Astrophys J 658:598–616 [Google Scholar]
- Kasting J.F., Whitmire D.P., and Reynolds R.T. (1993) Habitable zones around main sequence stars. Icarus 101:108–128 [DOI] [PubMed] [Google Scholar]
- Keeling C.D. (1960) The concentration and isotopic abundances of carbon dioxide in the atmosphere. Tellus 12:200–203 [Google Scholar]
- Keeling C.D., Bacastow R.B., Bainbridge A.E., Ekdahl C.A., Jr., Guenther P.R., Waterman L.S., and Chin J.F.S. (1976) Atmospheric carbon dioxide variations at Mauna Loa Observatory, Hawaii. Tellus A 28:538–551 [Google Scholar]
- Keeling C.D., Chin J.F.S., and Whorf T.P. (1996) Increased activity of northern vegetation inferred from atmospheric CO2 measurements. Nature 382:146–149 [Google Scholar]
- Kennedy S.P., Ng W.V., Salzberg S.L., Hood L., and DasSarma S. (2001) Understanding the adaptation of Halobacterium species NRC-1 to its extreme environment through computational analysis of its genome sequence. Genome Res 11:1641–1650 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiang N.Y., Segura A., Tinetti G., Govindjee, Blankenship R.E., Cohen M., Siefert J., Crisp D., and Meadows V.S. (2007a) Spectral signatures of photosynthesis II: Coevolution with other stars and the atmosphere on extrasolar worlds. Astrobiology 7:252–274 [DOI] [PubMed] [Google Scholar]
- Kiang N.Y., Siefert J., Govindjee, and Blankenship R.E. (2007b) Spectral signatures of photosynthesis. I: Review of Earth organisms. Astrobiology 7:222–251 [DOI] [PubMed] [Google Scholar]
- Kim H., Smith H., Mathis C., Raymond J., and Walker S.I. (2018) Universal Scaling Across Biochemical Networks on Earth. bioRxiv 212118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knoll A.H. (2011) The multiple origins of complex multicellularity. Annu Rev Earth Planet Sci 39:217–239 [Google Scholar]
- Knoll A.H. (2015) Life on a Young Planet: The First Three Billion Years of Evolution on Earth. Princeton University Press, Princeton, NJ [Google Scholar]
- Kolb V.M. (2007) On the applicability of the Aristotelian principles to the definition of life. Int J Astrobiol 6:51–57 [Google Scholar]
- Kopp G. and Lean J.L. (2011) A new, lower value of total solar irradiance: evidence and climate significance. Geophys Res Lett 38:L01706 [Google Scholar]
- Kopparapu R.K., Ramirez R.M., SchottelKotte J., Kasting J.F., Domagal-Goldman S., and Eymet V. (2014) Habitable zones around main-sequence stars: dependence on planetary mass. arXiv:1404.5292v1 [astro-ph.EP]
- Kreidberg L., Bean J.L., Désert J.-M., Benneke B., Deming D., Stevenson K.B., Seager S., Berta-Thompson Z., Seifahrt A., and Homeier D. (2014) Clouds in the atmosphere of the super-Earth exoplanet GJ1214b. Nature 505:69–72 [DOI] [PubMed] [Google Scholar]
- Krissansen-Totton J., Bergsman D.S., and Catling D.C. (2016) On detecting biospheres from chemical thermodynamic disequilibrium in planetary atmospheres. Astrobiology 16:39–67 [DOI] [PubMed] [Google Scholar]
- Krissansen-Totton J., Stephanie O., and David C.C. “Disequilibrium biosignatures over Earth history and implications for detecting exoplanet life.” Science advances 4, no. 1 (2018): eaao5747 [DOI] [PMC free article] [PubMed]
- Koonin E.V., and Novozhilov A.S. (2009) Origin and evolution of the genetic code: the universal enigma. IUBMB Life 61:99–111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leconte J., Forget1 F., Charnay B., Wordsworth R., Selsis F., Millour E., and Spiga A. (2013) 3D climate modeling of close-in land planets: circulation patterns, climate moist bistability, and habitability. Astron Astrophys 554:A69 [Google Scholar]
- Lee C.T., Shen B., Slotnick B.S., Liao K., Dickens G.R., Yokoyama Y., Lenardic A., Dasgupta R., Jellinek M., Lackey J.S., Schneider T., and Tice M.M. (2013) Continental arc–island arc fluctuations, growth of crustal carbonates, and long-term climate change. Geosphere 9:21–36 [Google Scholar]
- Lee C.T., Thurner S., Paterson S., and Cao W. (2015) The rise and fall of continental arcs: interplays between magmatism, uplift, weathering, and climate. Earth Planet Sci Lett 425:105–119 [Google Scholar]
- Lee C.A., Yeung L.Y., McKenzie N.R., Yokoyama Y., Ozaki K., and Lenardic A. (2016) Two-step rise of atmospheric oxygen linked to the growth of continents. Nat Geosci 9:417–424 [Google Scholar]
- Lenardic A. and Crowley J.W. (2012) On the notion of well-defined tectonic regimes for terrestrial planets in this solar system and others. Astrophys J 755:132 [Google Scholar]
- Lenardic A, Jellinek A.M., Foley B., O'Neill C., and Moore W.B. (2016) Tectonic-climate coupling: variations in the mean, variations about the mean, and variations in mode. J Geophys Res Planets 121:1831–1864 [Google Scholar]
- Li Y.Q. and Chen M. (2015) Novel chlorophylls and new directions in photosynthesis research. Funct Plant Biol 42:493–501 [DOI] [PubMed] [Google Scholar]
- Liang M.C., Hartman H., Kopp R.E., Kirschvink J.L., and Yung Y.L. (2006) Production of hydrogen peroxide in the atmosphere of a Snowball Earth and the origin of oxygenic photosynthesis. Proc Natl Acad Sci U S A 103:18896–18899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Line M.R., Stevenson K.B., Bean J., Desert J.M., Fortney J.J., Kreidberg L., Madhusudhan N., Showman A.P., and Diamond-Lowe H. (2016) No thermal inversion and a solar water abundance for the hot Jupiter HD209458b from HST/WFC3 spectroscopy. Astron J 152:203 [Google Scholar]
- Line M.R., Zhang X., Vasisht G., Natraj V., Chen P., and Yung Y.L. (2012) Information content of exoplanetary transit spectra: an initial look. Astrophys J 749:93 [Google Scholar]
- Locey K.J. and Lennon J.T. (2016) Scaling laws predict global microbial diversity. Proc Natl Acad Sci U S A 113:5970–5975 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lombard J., Lopez-Garcia P., and Moriera D. (2012) The early evolution of lipid membranes and the three domains of life. Nat Rev Microbiol 10:507–515 [DOI] [PubMed] [Google Scholar]
- Lovelock J.E. (1965) A physical basis for life detection experiments. Nature 207:568–570 [DOI] [PubMed] [Google Scholar]
- Luger R. and Barnes R. (2015) Extreme water loss and abiotic O2 buildup on planets throughout the habitable zones of M dwarfs. Astrobiology 15:119–143 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo G., Ono S., Beukes N.J., Wang D.T., Xie S., and Summons R.E. (2016) Rapid oxygenation of Earth's atmosphere 2.33 billion years ago. Sci Adv 2:e1600134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons T.W., Reinhard C.T., and Planavsky N.J. (2014) The rise of oxygen in Earth's early ocean and atmosphere. Nature 506:307–315 [DOI] [PubMed] [Google Scholar]
- Mahaffy P.R., Webster C.R., Atreya S.K., Franz H., Wong M., Conrad P.G., Harpold D., Jones J.J., Leshin L.A., Manning H., Owen T., Pepin R.O., Squyres S., Trainer, M.; MSL Science Team. (2013) Abundance and isotopic composition of gases in the Martian atmosphere from the Curiosity rover. Science 341:263–266 [DOI] [PubMed] [Google Scholar]
- Malyshev D.A., Dhami K., Lavergne T., Chen T., Dai N., Foster J.M., Corrêa I.R., Jr., and Romesberg F.E. (2014) A semi-synthetic organism with an expanded genetic alphabet. Nature 509:385–388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mamajanov I., Lannan F.M., and Hud N.V. (2013) 49 Nucleic acids in anhydrous media: G-quadruplex folding governed by Kramers rate theory. J Biomol Struct Dyn 31(Suppl 1):29–30 [Google Scholar]
- Marosvölgyi M.A. and van Gorkom H.J. (2010) Cost and color of photosynthesis. Photosynth Res 103:105–109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall S.M., Murray A.R.G., and Cronin L. (2017) A probabilistic framework for identifying biosignatures using Pathway Complexity. Phil Trans R Soc A 375.2109:20160342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauzerall D. (1973) Why chlorophyll? Ann N Y Acad Sci 206:483–494 [DOI] [PubMed] [Google Scholar]
- May R.M., Conway G.R., Hassell M.P., and Southwood T.R.E. (1974) Time delays, density-dependence and single-species oscillations. J Anim Ecol 43:747–770 [Google Scholar]
- Maynard Smith J. and Szathmáry E. (1995) The Major Transitions in Evolution. Freeman, Oxford University Press, New York, NY [Google Scholar]
- McKay C. (2011) The search for life in our Solar System and the implications for science and society. Phil Trans R Soc A 369:594–606 [DOI] [PubMed] [Google Scholar]
- Meadows V.S. (2005) Modelling the diversity of extrasolar terrestrial planets. Proc Int Astron Union 1:25–34 [Google Scholar]
- Meadows V.S. (2017) Reflections on O2 as a biosignature in exoplanetary atmosphere. Astrobiology 17:1022–1052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meadows V.S., Reinhard C.T., Arney G.N., Parenteau M.N., Schwieterman E.W., Domagal-Goldman S.D., Lincowski A.P., Stapelfeldt K.R., Rauer H., DasSarma S., Hegde S., Narita N., Deitrick R., Lustig-Yaeger J., Lyons T.W., Siegler N., and Grenfell J.L. (2018) Exoplanet biosignatures: understanding oxygen as a biosignature in the context of its environment. Astrobiology 18:630–662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meehl G.A., Boer G.J., Covey C., Latif M., and Stouffer R.J. (2000) The coupled model intercomparison project (CMIP). Bull Am Meteorol Soc 81:313–318 [Google Scholar]
- Merlis T.M. and Schneider T. (2010) Atmospheric dynamics of Earth-like tidally locked aquaplanets. J Adv Model Earth Syst 2:17 [Google Scholar]
- Miles B. and Shkolnik E. (2017) HAZMAT II. Ultraviolet variability of low-mass stars in the Galex archive. XI. Astron J 154:67 [Google Scholar]
- Miller S.D., Haddock S.H., Elvidge C.D., and Lee T.F. (2005) Detection of a bioluminescent milky sea from space. Proc Natl Acad Sci U S A 102:14181–14184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milo R. (2009) What governs the reaction center excitation wavelength of photosystems I and II? Photosynth Res 101:59–67 [DOI] [PubMed] [Google Scholar]
- Misra A., Meadows V., Claire M., and Crisp D. (2014) Using dimers to measure biosignatures and atmospheric pressure for terrestrial exoplanets. Astrobiology 14:67–86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mix L.J. (2015) Defending definitions of life. Astrobiology 15:15–19 [DOI] [PubMed] [Google Scholar]
- Murray A., Stuart M., and Leroy C. “Defining Pathway Assembly and Exploring its Applications.” arXiv preprint arXiv:1804.06972 (2018)
- Mushegian A. (2008) Gene content of LUCA, the last universal common ancestor. Frontiers 13:4657–4666 [DOI] [PubMed] [Google Scholar]
- Niklas K.J. and Newman S.A. (2013) The origins of multicellular organisms. Evol Dev 15:41–52 [DOI] [PubMed] [Google Scholar]
- Okie J.G. (2012) Microorganisms. In Metabolic Ecology: A Scaling Approach, edited by Sibly R.M., Brown J.H., and Kodric‐Brown A., John Wiley & Sons Ltd., Oxford, pp 133–153 [Google Scholar]
- O'Malley-James J.T., Greaves J.S., Raven J.A., and Cockell C.S. (2013) Swansong biospheres: refuges for life and novel microbial biospheres on terrestrial planets near the end of their habitable lifetimes. Int J Astrobiol 12:99–112 [Google Scholar]
- Paprotny Z. (1977) Nonradio methods of SETI. Postepy Astronautyki 10:39–67 [Google Scholar]
- Pierrehumbert R.T. (2010) Principles of Planetary Climate. Cambridge University Press, New York, p 652 [Google Scholar]
- Pierrehumbert R.T. (2011) A palette of climates for Gliese 581g. Astrophys J Lett 726:5 [Google Scholar]
- Pikuta E.V., Hoover R.B., and Tang J. (2007) Microbial extremophiles at the limits of life. Crit Rev Microbiol 33:183–209 [DOI] [PubMed] [Google Scholar]
- Pinot S., Ramstein G., Harrison S.P., Prentice I.C., Guiot J., Stute M., and Joussaume S. (1999) Tropical paleoclimates at the Last Glacial Maximum: comparison of Paleoclimate Modeling Intercomparison Project (PMIP) simulations and paleodata. Clim Dyn 15:857–874 [Google Scholar]
- Punnoose A., McConnell L., Liu W., Mutter A.C., and Koder R. (2012) Fundamental limits on wavelength, efficiency and yield of the charge separation triad. PLoS One 7:e36065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Racker E. and Stoeckenius W. (1974) Reconstitution of purple membrane vesicles catalyzing light-driven proton uptake and adenosine triphosphate formation. J Biol Chem 249:662–663 [PubMed] [Google Scholar]
- Ravitz O. (2013) Data-driven computer aided synthesis design. Drug Discov Today Technol 10:e443–e449 [DOI] [PubMed] [Google Scholar]
- Reinhard C.T., Olson S.L., Schwieterman E.W., and Lyons T.W. (2017) False negatives for remote life detection on ocean-bearing planets: lessons from the early Earth. Astrobiology 17:287–297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rappé M.S. and Giovannoni S.J. (2003) The uncultured microbial majority. Annu Rev Microbiol 57:369–394 [DOI] [PubMed] [Google Scholar]
- Reid I.N., Gizis J.E., and Hawley S.L. (2002) The Palomar/MSU nearby star spectroscopic survey. IV. The luminosity function in the solar neighborhood and M dwarf kinematics. Astron J 124:2721 [Google Scholar]
- Rodríguez A., Callegari N. J.r., Michtchenko T.A., and Hussmann H. (2012) Spin-orbit coupling for tidally evolving super-Earths. Mon Not R Astron Soc 427:2239–2250 [Google Scholar]
- Rodriguez-Garcia M., Surman A.J., Cooper G.J., Suárez-Marina I., Hosni Z., Lee M.P., and Cronin L. (2015) Formation of oligopeptides in high yield under simple programmable conditions. Nat Commun 6:8385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roe G.H., Whipple K.X., and Fletcher J.K. (2008) Feedbacks between climate, erosion, and tectonics in a critical wedge orogen. Am J Sci 308:815–842 [Google Scholar]
- Rogers L.A. and Seager S. (2010) A framework for quantifying the degeneracies of exoplanet interior compositions. Astrophys J 712:974 [Google Scholar]
- Sadownik J.W., Mattia E., Nowak P., and Otto S. (2016) Diversification of self-replicating molecules. Nat Chem 8:264–269 [DOI] [PubMed] [Google Scholar]
- Sagan C. and Shklovskii I.S. (1966) Intelligent Life in the Universe. Holden-Day, Inc., San Francisco, CA, p 406 [Google Scholar]
- Saito K., Sueyoshi T., Marchenko S., Romanovsky V., Otto-Bliesner B., Walsh J., Bigelow N., Hendricks A., and Yoshikawa K. (2013) LGM permafrost distribution: how well can the latest PMIP multi-model ensembles perform reconstruction? Clim Past 9:1697 [Google Scholar]
- Sauer K. and Yachandra V.K. (2002) A possible evolutionary origin for the Mn4 cluster of the photosynthetic water oxidation complex from natural MnO2 precipitates in the early ocean. Proc Natl Acad Sci U S A 99:8631–8636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharf C. and Cronin L. (2016) Quantifying the origins of life on a planetary scale. Proc Natl Acad Sci U S A 113:8127–8132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlesinger W.H. (2013) Biogeochemistry: An Analysis of Global Change. Academic Press, San Diego [Google Scholar]
- Schrodinger E. (1943) What Is Life? University Press, Cambridge [Google Scholar]
- Schulze-Makuch D. and Bains W. (2017) The Cosmic Zoo: Complex Life on Many Worlds. Springer, Berlin [Google Scholar]
- Schwieterman E.W., Cockell C.S., and Meadows V.S. (2015) Non-photosynthetic pigments as potential biosignatures. Astrobiology 15:341–361 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwieterman E.W., Kiang N.Y., Parenteau M.N., Harman C.E., DasSarma S., Fisher T.M., Arney G.N., Hartnett H.E., Reinhard C.T., Olson S.L., Meadows V.S., Cockell C.S., Walker S.I., Grenfell J.L., Hegde S., Rugheimer S., Hu R., and Lyons T.W. (2018) Exoplanet biosignatures: a review of remotely detectable signs of life. Astrobiology. 18:663–708 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwieterman E.W., Meadows V.S., Domagal-Goldman S.D., Deming D., Arney G.N., Luger R., Harman C.E., Misra A., and Barnes R. (2016) Identifying planetary biosignature impostors: spectral features of CO and O4 resulting from abiotic O2/O3 production. Astrophys J 819:L13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seager S. (2014) The future of spectroscopic life detection on exoplanets. Proc Natl Acad Sci U S A 111:12634–12640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seager S. and Bains W. (2015) The search for signs of life on exoplanets at the interface of chemistry and planetary science. Science advances 1(2), p.e1500047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seager S., Bains W., and Hu R. (2013a) A biomass-based model to estimate the plausibility of exoplanet biosignature gases. Astrophys J 775:104 [Google Scholar]
- Seager S., Bains W., and Hu R. (2013b) Biosignature gases in H2-dominated atmospheres on rocky exoplanets. Astrophys J 777:95 [Google Scholar]
- Seager S., Bains W.W., and Petkowski J.J. (2016) Toward a list of molecules as potential biosignature gases for the search for life on exoplanets and applications to terrestrial biochemistry. Astrobiology 16:465–485 [DOI] [PubMed] [Google Scholar]
- Segura A., Kasting J.F., Meadows V., Cohen M., Scalo J., Crisp D., Butler R.A.H., and Tinetti G. (2005) Biosignatures from Earth-like planets around M dwarfs. Astrobiology 5:706–725 [DOI] [PubMed] [Google Scholar]
- Segura A., Krelove K., Kasting J.F., Sommerlatt D., Meadows V., Crisp D., Cohen M., and Mlawer E. (2003) Ozone concentrations and ultraviolet fluxes on Earth-like planets around other stars. Astrobiology 3:689–708 [DOI] [PubMed] [Google Scholar]
- Segura A., Walkowicz L.M., Meadows V., Kasting J., and Hawley S. (2010) The effect of a strong stellar flare on the atmospheric chemistry of an Earth-like planet orbiting an M dwarf. Astrobiology 10:751–771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shields A.L., Meadows V.S., Bitz C.M., Pierrehumbert R.T., Joshi M.M., and Robinson T.D. (2013) The effect of host star spectral energy distribution and ice-albedo feedback on the climate of extrasolar planets. Astrobiology 13:715–789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shkolnik E.L. and Barman T.S. (2014) HAZMAT. I. The evolution of far-UV and near-UV emission from early M stars. Astron J 148:64 [Google Scholar]
- Shock E.L. and Boyd E.S. (2015) Principles of geobiochemistry. Elements 11:395–401 [Google Scholar]
- Sleep N.H. (2000) Evolution of the mode of convection within terrestrial planets. J Geophys Res 105:17563–17578 [Google Scholar]
- Sleep N.H. and Zahnle K. (2001) Carbon dioxide cycling and implications for climate on ancient Earth. J Geophys Res 106:1373–1400 [Google Scholar]
- Simoncini E., Virgo N., and Kleidon A. (2013) Quantifying drivers of chemical disequilibrium: theory and application to methane in the Earth's atmosphere. Earth Syst Dynam 4:317–331 [Google Scholar]
- Smith D.E. and Morowitz H. (2016) The Origin and Nature of Life on Earth: The Emergence of the Fourth Geosphere. Cambridge University Press, Cambridge, p 691 [Google Scholar]
- Sogin M.L., Morrison H.G., Huber J.A., Welch D.M., Huse S.M., Neal P.R., Arrieta J.M., and Herndl G.J. (2006) Microbial diversity in the deep sea and the underexplored “rare biosphere.” Proc Natl Acad Sci U S A 103:12115–12120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solé R.E. and Munteanu A. (2004) The large-scale organization of chemical reaction networks in astrophysics. EPL Europhys Lett 68:170 [Google Scholar]
- Soo R.M., Hemp J., Parks D.H., Fischer W.W., and Hugenholtz P. (2017) On the origins of oxygenic photosynthesis and aerobic respiration in Cyanobacteria. Science 355:1436–1440 [DOI] [PubMed] [Google Scholar]
- Spiegel D.S. and Turner E.L. (2012) Bayesian analysis of the astrobiological implications of life's early emergence on Earth. Proc Natl Acad Sci U S A 109:395–400 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staudigel H., Hart S.R., Schmincke H.-U., and Smith B.M. (1989) Cretaceous ocean crust at DSDP Sites 417 and 418: carbon uptake from weathering versus loss by magmatic outgassing. Geochim Cosmochim Acta 53:3091–3094 [Google Scholar]
- Szathmáry E. and Smith J.M. (1995) The major evolutionary transitions. Nature 374:227–232 [DOI] [PubMed] [Google Scholar]
- Taylor A.I., Pinheiro V., Smola M.J., Morgunov A.S., Peak-Chew S., Cozens C., Weeks K., Herdewijn P., and Holliger P. (2015) Catalysts from synthetic genetic polymers. Nature 518:427–430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoning K.W., Kitzis D.R., and Crotwell A. (2015) Atmospheric Carbon Dioxide Dry Air Mole Fractions from Quasi-Continuous Measurements at Mauna Loa, Hawaii. National Oceanic and Atmospheric Administration (NOAA), Earth System Research Laboratory (ESRL), Global Monitoring Division (GMD), Boulder, Colorado. Version 2016-8 [Google Scholar]
- Tian F., France K., Linsky J.L., Mauas P.J., and Vieytes M.C. (2014) High stellar FUV/NUV ratio and oxygen contents in the atmospheres of potentially habitable planets. Earth Planet Sci Lett 385:22–27 [Google Scholar]
- Trifonov E.N. (2011) Vocabulary of definitions of life suggests a definition. J Biomol Struct Dyn 29:259–266 [DOI] [PubMed] [Google Scholar]
- Twicken J.D., Jenkins J.M., Seader S.E., Tenenbaum P., Smith J.C., Brownston L.S., Burke C.J., Catanzarite J.H., Clarke B.D., Cote M.T., and Girouard F.R. (2016) Detection of potential transit signals in 17 quarters of Kepler data: results of the final Kepler mission transiting planet search (DR25). Astron J 152:158 [Google Scholar]
- Waley S.G. (1969) Some aspects of the evolution of metabolic pathways. Comp Biochem Physiol 30:1–11 [DOI] [PubMed] [Google Scholar]
- Walker J.C.G., Hays P.B., and Kasting J.F. (1981) A negative feedback mechanism for the long-term stabilization of Earth's surface temperature. J Geophys Res 86:9776–9782 [Google Scholar]
- Walker S.I. (2017) The origins of life: a problem for physics, a key issues review. Rep Prog Phys 80:092601. [DOI] [PubMed] [Google Scholar]
- Walker S.I. and Davies P.C.W. (2013) The algorithmic origins of life. J R Soc Interface 10:20120869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker S.I., Grover M.A., and Hud N.V. (2012) Universal sequence replication, reversible polymerization and early functional biopolymers: a model for the initiation of prebiotic sequence evolution. PLoS One 7:e34166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward L.M., Kirschvink J.L., and Fischer W.W. (2016) Timescales of oxygenation following the evolution of oxygenic photosynthesis. Orig Life Evol Biosph 46:51–65 [DOI] [PubMed] [Google Scholar]
- Way M.J., Del Genio A.D., Kiang N.Y., Sohl L.E., Grinspoon D.H., Aleinov I., Kelley M., and Clune T. (2016) Was Venus the first habitable world of our solar system? Geophys Res Lett 43:8376–8383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss M.C., Sousa F.L., Mrnjavac N., Neukirchen S., Roettger M., Nelson-Sathi S., and Martin W.F. (2016) The physiology and habitat of the last universal common ancestor. Nat Microbiol 25:16116. [DOI] [PubMed] [Google Scholar]
- Weller M., Lenardic A., and O'Neill C. (2015) The effects of internal heating and large scale climate variations on tectonic bi-stability in terrestrial planets. Earth Planet Sci Lett 420:85–94 [Google Scholar]
- West G.B., Brown J.H., and Enquist B.J. (1999) The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science 284:1677–1679 [DOI] [PubMed] [Google Scholar]
- West G.B., Woodruff W.H., and Brown J.H. (2002) Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc Natl Acad Sci U S A 99:2473–2478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitman W.B., Coleman D.C., and Weibe W.J. (1998) Prokaryotes: the unseen majority. Proc Natl Acad Sci U S A 95:6578–6583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitmire D.P. and Wright D.P. (1980) Nuclear waste spectrum as evidence of technological extraterrestrial civilizations. Icarus 42:149–156 [Google Scholar]
- Whipple K.X. and Meade B.J. (2004) Controls on the strength of coupling among climate, erosion, and deformation in two-sided, frictional orogenic wedges at steady state. J Geophys Res 109:F01011 [Google Scholar]
- Williams D.M. and Pollard D. (2002) Earth-like worlds on eccentric orbits: excursions beyond the habitable zone. Int J Astrobiol 1:61–69 [Google Scholar]
- Williams D.M. and Pollard D. (2003) Extraordinary climates of Earth-like planets: three-dimensional climate simulations at extreme obliquity. Int J Astrobiol 2:1–19 [Google Scholar]
- Williams G.P. and Holloway J.L. (1982) The range and unity of planetary circulations. Nature 297:295–299 [Google Scholar]
- Woese C. (1998) The universal ancestor. Proc Natl Acad Sci U S A 95:6854–6859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woese C.R. (2004) A new biology for a new century. Microbiol Mol Biol Rev 68:173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfgang A., Rogers L.A., and Ford E.B. (2016) Probabilistic mass–radius relationship for sub-Neptune-sized planets. Astrophys J 825:19 [Google Scholar]
- Wordsworth R.D., Forget F., Selsis F., Millour E., Charnay B., and Madeleine J.B. (2011) Gliese 581d is the first discovered terrestrial-mass exoplanet in the habitable zone. Astrophys J Lett 733:5 [Google Scholar]
- Xiong J. and Bauer C.E. (2002) Complex evolution of photosynthesis. Annu Rev Plant Biol 53:503–521 [DOI] [PubMed] [Google Scholar]
- Yang J., Liu Y.G., Hu Y.Y., and Abbot D.S. (2014) Water trapping on tidally locked terrestrial planets requires special conditions. Astrophys J Lett 796:L22 [Google Scholar]
- Zhang K. and Sejnowski T.J. (2000) A universal scaling law between gray matter and white matter of cerebral cortex. Proc Natl Acad Sci U S A 97:5621–5626 [DOI] [PMC free article] [PubMed] [Google Scholar]