Skip to main content
PMC home page
Chemical Science logoLink to Chemical Science
. 2016 Apr 1;7(8):5139–5147. doi: 10.1039/c5sc04786b

Machine learning exciton dynamics†

Florian Häse a,b, Stéphanie Valleau a, Edward Pyzer-Knapp a, Alán Aspuru-Guzik a,✉
PMCID: PMC6020119  PMID: 30155164

graphic file with name c5sc04786b-ga.jpgMachine learning ground state QM/MM for accelerated computation of exciton dynamics.

Abstract

Obtaining the exciton dynamics of large photosynthetic complexes by using mixed quantum mechanics/molecular mechanics (QM/MM) is computationally demanding. We propose a machine learning technique, multi-layer perceptrons, as a tool to reduce the time required to compute excited state energies. With this approach we predict time-dependent density functional theory (TDDFT) excited state energies of bacteriochlorophylls in the Fenna–Matthews–Olson (FMO) complex. Additionally we compute spectral densities and exciton populations from the predictions. Different methods to determine multi-layer perceptron training sets are introduced, leading to several initial data selections. In addition, we compute spectral densities and exciton populations. Once multi-layer perceptrons are trained, predicting excited state energies was found to be significantly faster than the corresponding QM/MM calculations. We showed that multi-layer perceptrons can successfully reproduce the energies of QM/MM calculations to a high degree of accuracy with prediction errors contained within 0.01 eV (0.5%). Spectral densities and exciton dynamics are also in agreement with the TDDFT results. The acceleration and accurate prediction of dynamics strongly encourage the combination of machine learning techniques with ab initio methods.

1. Introduction

Studying the exciton dynamics of large photosynthetic complexes, such as the Fenna–Matthews–Olson (FMO) and light-harvesting II (LHII) complexes, has been a topic of much theoretical and experimental interest in recent years.1–14 The theoretical community has focused on employing and developing reduced models to understand and describe the dynamics of these complexes.2–7,13–30 These models rely on the knowledge of a system Hamiltonian for the interacting chromophores as well as spectral densities to describe the coupling of chromophores to their environments (protein, solvent).31 Computing a system Hamiltonian or spectral density is an arduous computational task due to the large number of degrees of freedom in these complexes. The most detailed approaches used to obtain these quantities have been mixed quantum mechanics/molecular mechanics (QM/MM) or semi-classical simulations.32,33 In particular, one QM/MM approach which has become popular in recent years consists in propagating the nuclei in the electronic ground state of the photosynthetic complex.9,10,34,35 This approximation ignores the change in electronic structure due to excitation of the chromophores. Subsequently, for a subset of time frames, excited state energies for the chromophores are computed using a quantum method such as time-dependent density functional theory (TDDFT).10 The energy trajectories are then employed to extract system-bath correlation functions and finally spectral densities to use in exciton dynamics.

The downside of this approach is the large computational cost. Long molecular dynamics (MD) equilibration times of several tens of nanoseconds are required.36,37 The typical computational scaling of MD codes with the system size N is 𝒪(N log N).38 In contrast, TDDFT calculations scale as 𝒪(N2).39 Very often calculations need to be repeated for identical chromophores in similar environments to account for the effect of small variations. For instance in the case of a single-point mutation typically one would need to rerun the entire set of simulations.

In this work we propose an alternative route: using multi-layer perceptrons, a special class of neural networks, to predict the excited state along a MD trajectory. Such approaches typically scale as 𝒪(N) and were found to perform significantly faster than TDDFT approaches. As a test system we consider the Fenna–Matthews–Olson (FMO) complex of P. aestuarii. Neural networks have previously been used to predict potential-energy surfaces.40 We use multi-layer perceptrons as fully connected neural networks to predict the values of the first singlet excited state for the chromophores. We train the neural networks on the excited state energies obtained from QM/MM calculations. Several sampling methods are used to select the training data for the neural networks. In particular we tested a sampling method based on correlations of nuclear positions to improve on the spectral density predictions. Once trained, the neural networks are employed to make excited state energy predictions. Then one can build a Hamiltonian from the predictions and compute the exciton dynamics.

With optimal neural network training and 12 trained neural networks per BChl we predicted excited state energies with errors contained to 0.01 eV (0.5%) from the neural network ensemble average. Further, with neural networks trained on data based on correlation sampling we correctly predict the shape of the spectral density and observe an error which is squared with respect to the excited state prediction error. This demonstrates the power of machine learning in chemistry, as has also been found in recent work where machine learning was employed to extract other chemical properties.41–44

2. Methods and computational details

2.1. Ground state QM/MM simulations

A semi-classical description of the FMO complex was obtained by combining ground state MD simulations with TDDFT calculations of the first singlet excited state, known as the Qy state,45 at given molecular conformations along the time-dependent trajectories. The MD runs were carried out using the NAMD software package46 with the AMBER99 force field (ff99SB).47 The BChl-a parameters employed are reported in ref. 48. The X-ray crystal structure of the FMO trimer in P. aestuarii (PDB ; 3EOJ,49 see Fig. 1) was chosen as initial configuration. The trimer was solvated using a TIP3P water box.50 The minimum distance between the crystal structure and edges of the solvent box was taken to be 15 Å.37,51 The charge was neutralized by adding sodium ions. The total number of atoms in the system was 141624. The simulation was equilibrated for 4 ns and the production run was 40 ps long with a 2 fs time-step. Electrostatic interactions were calculated with the particle-mesh Ewald method. Shake constraints were used for all bonds containing hydrogen. Simulations were carried out at 300 K and 1 atm using a Langevin thermostat and a Langevin piston as implemented in NAMD.

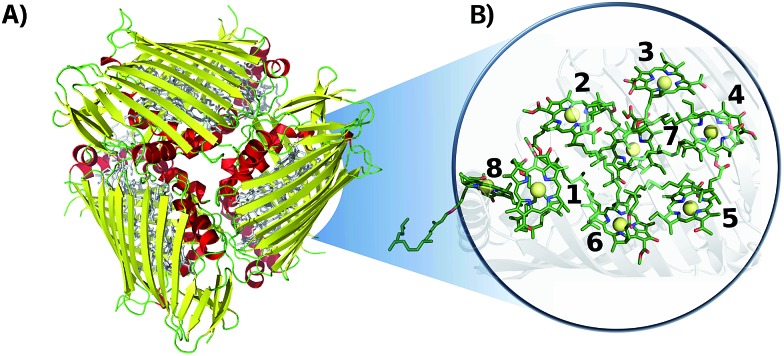
Fig. 1. Crystal structure of the FMO complex in P. aestuarii (PDB ; 3EOJ).49 (A) ; 3EOJ trimer crystal structure. (B) BChls' geometric arrangement in monomer A (residues 360 to 367, corresponding to sites 1 to 8). Hydrogens are not shown in this representation.

Fig. 1

Open in a new tab

The time-dependent Qy excited ground state gaps of the BChl-a molecules were obtained using TDDFT with the PBE0 functional,52 within the Tamm–Dancoff Approximation (TDA),53 using Q-Chem.54 We employed the 3-21G basis set due to the high computational cost of these simulations. The Qy excited state was taken to be the one with the largest oscillator strength and the orientation of the transition dipole was verified using the same methodology as in ref. 37 and 55. Excited state energy distributions are shown in the ESI (see Section S.1.4†) and trajectories can be downloaded from ref. 56. Excited state energies were computed at every 4 fs of the production run. The number of TDDFT calculations performed initially is based on the time scale and time step required to reproduce the dynamics accurately. Some values were excluded based on the oscillator strength/angle criterion/failed convergence. The excluded values were at most 2.15% of the full trajectory.

2.2. Machine learning: neural networks training

2.2.1. Input data representation

Multi-layer perceptrons (neural networks) were used to predict quantum mechanical excited state energies of BChls in the FMO complex from the MD classical coordinate trajectory. Neural networks were trained in a supervised training scheme using the back propagation algorithm.57 Excited state energies from the TDDFT calculations described previously were provided to the neural network as targets. BChl conformations were represented by Coulomb matrices,43 which were successfully used to predict excited state energies of various molecules with one neural network.58 Both, input and target feature distributions, were rescaled to a zero mean and a unitary standard deviation prior to neural network training.59

By using Coulomb matrices as input features, neural networks can be trained on a representation of BChls which is translation and rotation invariant. Coulomb matrices are particularly suitable to describe BChls in the FMO complex as these molecules do not undergo large conformational changes within time scales of several tens of picoseconds.36,37,60 Coulomb matrices were adapted to account for external charges within and around the represented BChl. The electrostatic influence of particles in the environment N was described by adding additional Coulomb potential terms to the corresponding Coulomb matrix entries (see eqn (1)):

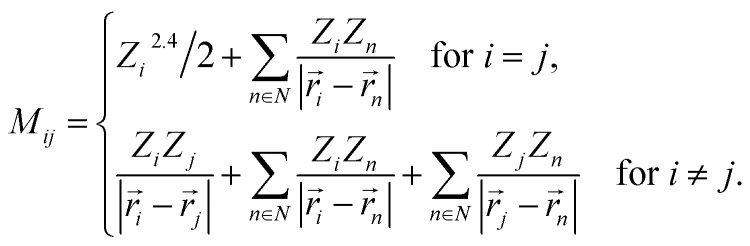2.2.1. 1

Partial charges Zi of atoms in the system were taken from the system topology (Amber 99SB force field,47 and ref. 48). Studies have shown that the tails of the BChls have little influence on the Qy excited state energies.37,61 Thus, instead of representing the entire BChl in a Coulomb matrix, the phytyl tail was neglected and only the 90 atoms closest to the magnesium in the BChls were represented in Coulomb matrices to reduce their dimensionality. We included all external partial charges present in the system to generate Coulomb matrices.

2.2.2. Neural network architecture, choice of BChl molecule and over-fitting

We chose to use multi-layer perceptrons (neural networks) with logistic activation functions and two hidden layers. This set-up has been shown to perform particularly well for supervised regression problems.62 Optimal neural network hyperparameters were identified from a grid search. Both the learning rate and the number of neurons in the first and second hidden layer were varied to find the lowest deviations between predictions and target data.

Instead of performing the grid search on each BChl in the FMO complex individually, only the most representative BChl was used to determine optimal neural network hyperparameters to reduce the computational cost. We identified this BChl in terms of shared Coulomb matrix space. Coulomb matrices of all eight BChls were clustered and compared. We found that site 3 shares the most Coulomb matrix space with all other sites (see ESI Section S.1.1†).

From the grid search, we found that a learning rate of 10–4 with 204 neurons in the first hidden layer and 192 neurons in the second hidden layer results in the smallest average absolute deviation of predicted and target excited state energies.

Target feature over-fitting was avoided by using early stopping.63 For all training sessions a total of 4000 trajectory frames was assigned to the training set as a balance between information and computational cost. Neural networks were trained on Intel(R) Xeon(R) CPUs (X5650 @ 2.67 GHz). Training one neural network on four cores took about (23.9 ± 5.0) h. Training times for other investigated training set sizes ranging from 500 to 5000 frames are reported in the ESI (see Section S.1.2†).

2.2.3. Reducing training set redundancies through clustering: taxicab, Frobenius and “correlation” clustering

We employed different methods to select Coulomb matrices and corresponding excited state energies for neural network training. In a first approach training set Coulomb matrices were drawn randomly from the entire trajectory.63 This led to excited state energy predictions with an average accuracy of 13 meV.

However, as BChl conformations in the data set are not uniformly distributed a training set consisting of randomly drawn Coulomb matrices likely contains redundant information. MD simulations were carried out in the NPT ensemble with constant temperature and pressure. Thus, the BChl conformations are sampled from a Boltzmann distribution.64 To avoid selecting many similar conformations and thus similar Coulomb matrices we performed a cluster analysis on all Coulomb matrices of the entire trajectory to determine the most distinct Coulomb matrices. We implemented a Coulomb matrix cluster algorithm following the principles of the gromos method.65

Distances between Coulomb matrices were measured using p-norms. Two different metrics were applied: p = 1 (taxicab norm) and p = 2 (Frobenius norm). Both clustering approaches resulted in more accurate predictions of excited state energies with accuracies of 9 meV but the prediction of exciton dynamics remained quite inaccurate (see Section 3.2).

To improve the prediction of exciton dynamics, we developed a clustering method based on coordinate correlations in the classical MD trajectory. We will refer to this approach as the “correlation” clustering method. The Qy state in BChls is mostly distributed along one of the diagonals which connects opposite nitrogen atoms.37 Training set frames were thus selected based on high correlations in the nitrogen root-mean square deviation (RMSD). In particular, for the n-th BChl we sampled from

|CRMSDn(t)|2 = | = |〈Dnitrogenn(t)Dnitrogenn(0)(0)〉||2. 2

until 4000 frames with the largest RMSD correlation were selected. Here, 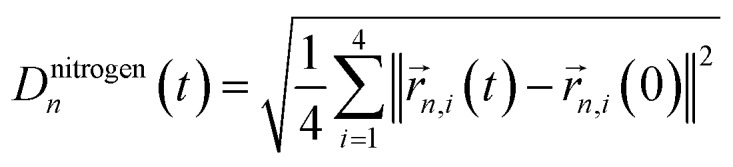Inline graphic refers to the root-mean square difference in position of the four nitrogen atoms in the n-th BChl at a given time t with respect to their position in the energy minimized crystal structure at time t = 0. This sampling led to a more accurate prediction of the spectral density (see Section 3.2).

2.3. Exciton dynamics and spectral densities

To further compare the predicted excited state energy trajectories with the TDDFT trajectories we computed the exciton dynamics in the FMO complex using two different methods. The first is a stochastic integration of the Schrödinger equation as used in previous work.10 The second method is the Markov Redfield master equation.66 Both of the methods are Markovian but the first relies only on the excited state energy trajectories while the latter also depends on the spectral density. Here we focus on the sensitivity of these methods to the changes related to using neural networks rather than to more subtle questions on dynamics such as those addressed by the comparison of Markovian with non Markovian methods (e.g. the hierarchy equation of motion approach).2

Finally the spectral density j(ω), as used in the Redfield equations of motion (see eqn (3)), is obtained by normalizing the Fourier transform of the two-time correlation function as we discussed in previous work.31

2.3. 3

The superscript “harm” refers to the harmonic prefactor which is needed to connect the QM/MM results to the open quantum system approach. Following the notation of previous work,31Ccl(t) denotes the classical correlation function.

3. Results and discussion

3.1. Excited state energy prediction using neural networks

3.1.1. Acceleration of excited state energy computations with neural networks

Intel(R) Xeon(R) CPUs (X5650 @ 2.67 GHz) were used to train neural networks and predict excited state energies. A total of 12 neural networks was trained for each of the eight BChls in monomer A of the FMO complex. Predictions of each of the 12 neural networks per BChl were averaged in a neural network ensemble averaging approach to obtain a more accurate prediction for the excited state energy trajectory. The spread of predictions of individual neural networks is given in the ESI (see Section S.1.3†).

Training sets were generated with all four training set selection methods (see Section 2.2.3). Predicting Qy excited state energies for the entire trajectory (104 frames) for one BChl with one neural network took on average (3.9 ± 0.8) s on one core. In contrast, the quantum chemistry calculations using the TDDFT (PBE0/3-21G) model chemistry required approximately 60 000 h for the entire trajectory on one core. Target feature generation is only necessary if trained neural networks are not available and independent of the number of frames to be predicted, thus reducing the reported costs if longer trajectories are predicted. Required calculation times to compute excited state energy trajectories for each of the eight BChls in the FMO complex are reported in Table 1. While two cores of an Intel(R) Xeon(R) CPU (X5650 @ 2.67 GHz) were used for TDDFT calculations and neural networks were trained on four cores the recorded calculation times were multiplied by the number of used cores for comparison reasons.

Table 1. Time required to compute excited state energies (10000 frames) for all bacteriochlorophylls (BChls) for TDDFT (PBE0/3-21G) and neural network (NN) predictions from correlation clustered Coulomb matrices. Reported times include neural network training (ttrain) on 4000 frames with input (tinputCoul) and target feature (ttargetE) generation, excited state calculations/predictions (tCalc) and the total time (ttot). If trained neural networks are available, only Coulomb matrices need to be calculated for neural network predictions, reducing the required time to 48 h. Reported times correspond to training a total of 12 neural networks independently to obtain ensemble averaged excited state energies. All reported times refer to calculations on a single core of an Intel(R) Xeon(R) CPU (X5650 @ 2.67 GHz).
Method Training [h]
 Calculation [h] Total [h]
t input Coul t target E t train t Calc t tot
PBE0/3-21G — — — 480000 480000
NNCorr 48 192000 9178 <0.1 201226
Open in a new tab

If trained neural networks are available, excited state energies of given BChl conformations can be predicted directly from Coulomb matrices representing the BChl conformations. Thus, to obtain the excited state energies of an entire trajectory consisting of 10 000 frames, Coulomb matrices need to be calculated first. With a calculation time of 2.19 s per Coulomb matrix on one Intel(R) Xeon(R) CPU (X5650 @ 2.67 GHz) core, about 6 h are needed to compute all 10 000 Coulomb matrices. With excited state energy predictions requiring less than a minute, excited state energy trajectories can be obtained from neural networks about four orders of magnitude faster compared to TDDFT calculations.

3.1.2. Accuracy of neural network predictions

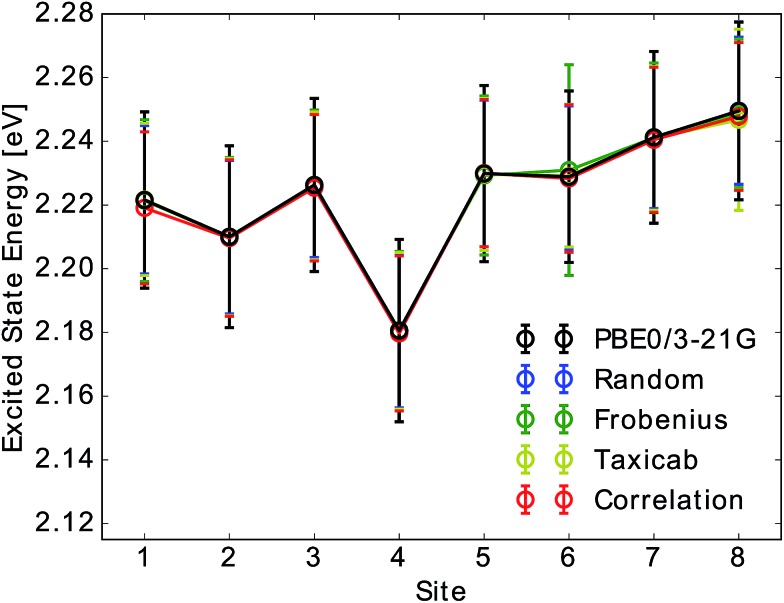
As can be seen in Fig. 2 neural network predictions agree well with the TDDFT data. Predictions from the average over 12 networks deviate from TDDFT values by ∼0.3 meV regardless of the site and the input selection method. Ensemble averaging was found to improve the prediction accuracy for all sites (see Table S.2†). When considering excited state energies predicted from a single network, we observed a deviation of σsingles,random < 14 meV for all sites s when the neural network was trained on randomly drawn Coulomb matrices. This prediction error can be decreased to σsingles,taxicab < 9 meV by selecting the training set based on the Coulomb matrix space clustering taxicab method (see Section 2.2.3). The uncertainty of neural network predictions therefore corresponds to roughly 14% of the typical FWHM (64 meV) of the sites. Frobenius clustering showed similar deviations. In contrast, predictions from neural networks trained on correlation clustered Coulomb matrices show a slightly higher deviation of σsingles,correlation < 15 meV on average. The obtained prediction errors are about one order of magnitude smaller than those in ref. 58. This difference is due to the fact that we predict excited state energies of the same molecule in different time-dependent geometries while in ref. 58 the neural network was trained to predict the excited state energies of many different molecules.

Fig. 2. Mean and standard deviation of Qy excited state energy distributions for all eight sites obtained from TDDFT calculations (PBE0/3-21G) and compared to neural network predictions. Presented distributions were obtained from single neural network predictions. Neural networks were trained on Coulomb matrices selected from the classical MD trajectory by the indicated selection method. Error bars indicate the width of the excited state energy distribution.

Fig. 2

Open in a new tab

3.1.3. Cross-predictions: predicting excited state energies for other bacteriochlorophylls

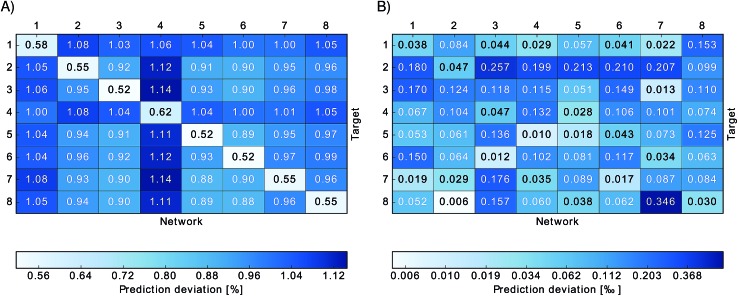
Since all BChl-a molecules in the FMO complex consist of the same atoms and show similar geometrical conformations, we also used neural networks trained on one BChl to predict excited state energies of other BChls in the same monomer. This enabled us to understand how well the trained network can adapt to changes in the environment from changes in the Coulomb matrices. We observed that for any clustering method, the prediction error is about two times larger when performing this type of cross-prediction, see Fig. 3. Nonetheless, as we see in panel A, the largest observed average absolute deviation is still below 1.14% (corresponding to 25 meV).

Fig. 3. Relative absolute deviations of predicted excited state energies from TDDFT excited state energies. Neural networks trained on one particular site (indicated by “Network”) were used to predict excited state energies of another site (indicated by “Target”). Panel (A) shows the relative absolute deviation σ̄relBChl of predicted excited state energies from TDDFT excited state energies for each BChl, 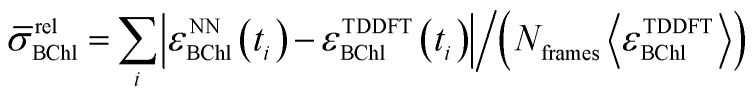Inline graphic, in percent. Panel (B) shows the deviation σmeanBChl of the mean of the predicted excited state energies from the mean of the TDDFT calculated excited state energies, σBChlmean = | = |〈εNNBChl〉 − 〈 – 〉 − 〈εTDDFTBChl〉|/〈|/〉|/〈εTDDFTBChl〉 in per-thousand. in per-thousand.

Fig. 3

Open in a new tab

3.1.4. Predicting excited state energies of bacteriochlorophylls in other monomers

All neural networks were trained on BChl-a molecules in monomer A. These neural networks were then used to predict excited state energies of BChls in the other two FMO monomers. Each neural network predicted the excited state energies of the BChl corresponding to the one on which it was trained (i.e. a neural network trained on site 1 in monomer A predicted site 1 in monomer B and C).

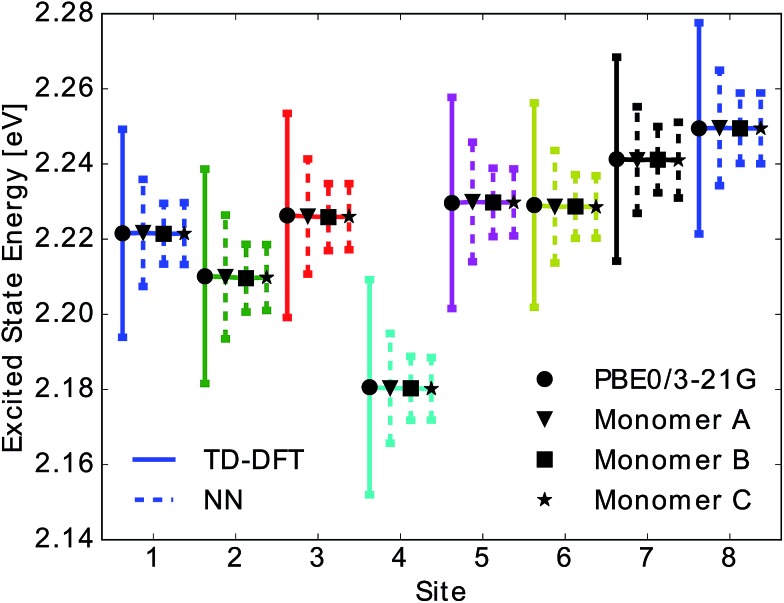
Due to the fact that the FMO complex is a homo-trimer, similar BChl conformations should be sampled during the MD simulation in each monomer. Thus, excited state energy averages are expected to be identical for corresponding BChls of different monomers, provided that the same phase space regions were covered in the simulation time. The results are presented in Fig. 4. In that figure, we show the time-averaged excited state energy predicted from 12 independently trained neural networks for each monomer as well as the time-averaged Qy energies obtained from TDDFT for monomer A. The bars represent the spread of the distribution and not an error. The predicted distributions are narrower than the TDDFT distributions. This is probably due to the fact that frames corresponding to energies at the tails of the distribution are less sampled. Regarding the error on the other hand, the largest deviation encountered between mean values of excited state energy distributions is 3 meV.

Fig. 4. Mean and standard deviation of excited state energy distributions for all eight sites obtained using TDDFT PBE0/3-21G (solid line with circle), for monomer A, and using neural network prediction with training on 40% of all Coulomb matrices of monomer A for all three monomers (dashed lines and triangle, square and star symbol for monomers A, B, C). Presented distributions were obtained from the ensemble averaged predictions of 12 neural networks. Error bars indicate the standard deviation of the obtained excited state energy distributions.

Fig. 4

Open in a new tab

We have found that trained neural networks can accurately predict TDDFT excited state energies. This allows for a large reduction of computational time. It is possible to train on a single BChl and predict excited state energies of other BChls in the same monomer or in different monomers.

3.2. Spectral densities and exciton dynamics with neural networks

We then used the calculated excited state energy trajectories of all BChls to obtain information about interactions of the BChls with their environment by computing spectral densities. In addition, we built a Hamiltonian to extract the exciton dynamics in the system.

The spectral density Jharm(ω) (see eqn (3)) was computed for all eight sites in the FMO complex from the TDDFT excited state energies and neural network predicted excited state energies.31 Spectral densities for each site were averaged over all BChls to obtain an averaged spectral density Jave(ω). To minimize spurious effects in the Fourier transform, we multiplied the correlation function by a Gaussian of σ2 = 0.09tmax2 with tmax = 1600 fs.31 The Gaussian is normalized to have unitary area in frequency domain so that in frequency domain this corresponds to a convolution with a Gaussian with a FWHM of 26 cm–1.

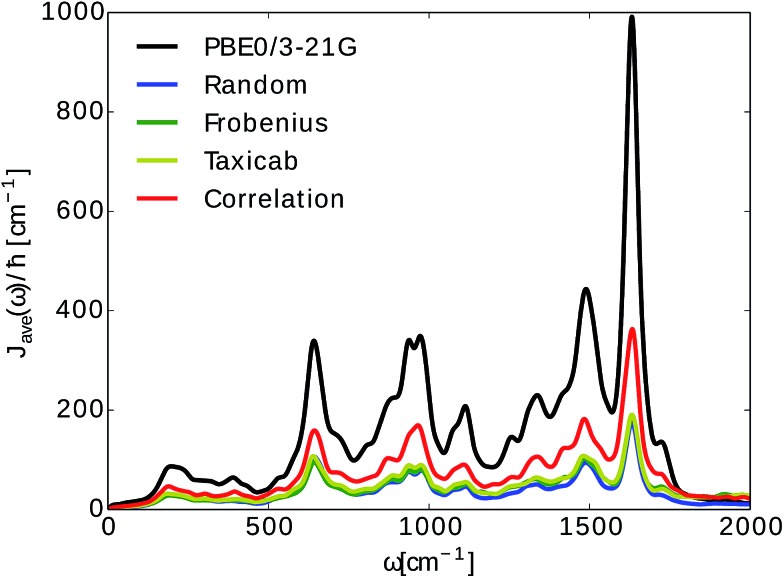
In Fig. 5 we show the comparison to our neural network prediction with training and prediction on the same site and the various Coulomb matrix selection methods. We found that predicted spectral densities all have a shape which resembles the overall shape of the TDDFT spectral density. However, the height and accurate position of the peaks in the spectral density is most accurately predicted using correlation clustering.

Fig. 5. Spectral density averages 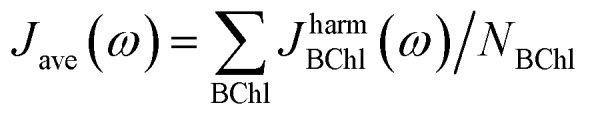Inline graphic. The spectral densities were computed from excited state energy trajectories obtained from TDDFT calculations (PBE0/3-21G) and compared to spectral densities from neural network predicted excited state energy trajectories. Neural networks were trained on the bacteriochlorophyll they predicted with the indicated Coulomb matrix selection method. The correlation method (see Section 2.2.3) gives the best prediction.

Fig. 5

Open in a new tab

Spectral densities for each BChl, calculated from TDDFT excited state energies and excited state energies predicted from neural networks trained on all input selection methods are plotted in the ESI (see Fig. S.11 in Section S.1.5†).

Average spectral densities were used to calculate the reorganization energy 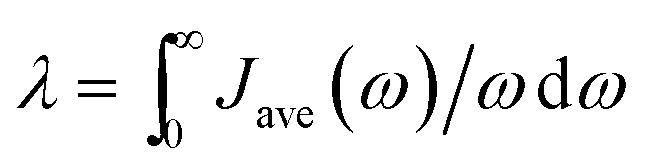Inline graphic. Comparisons of reorganization energies are reported in Table 2. We observe that the smallest deviation between neural network predicted results and TDDFT results occurs for neural networks trained on correlation clustered Coulomb matrices.

Table 2. We report the percentage deviation of neural network predicted reorganization energies λNN,β from TDDFT (PBE0/3-21G) calculated reorganization energies λTDDFT as σλ = |λTDDFT – λNN,β|/λTDDFT, where β indicates the method used for Coulomb matrix selections. Results are given in percent (%).

Method (β) Random Frobenius Taxicab Correlation
σ λ [%] 70.0 54.9 53.4 46.6
Open in a new tab

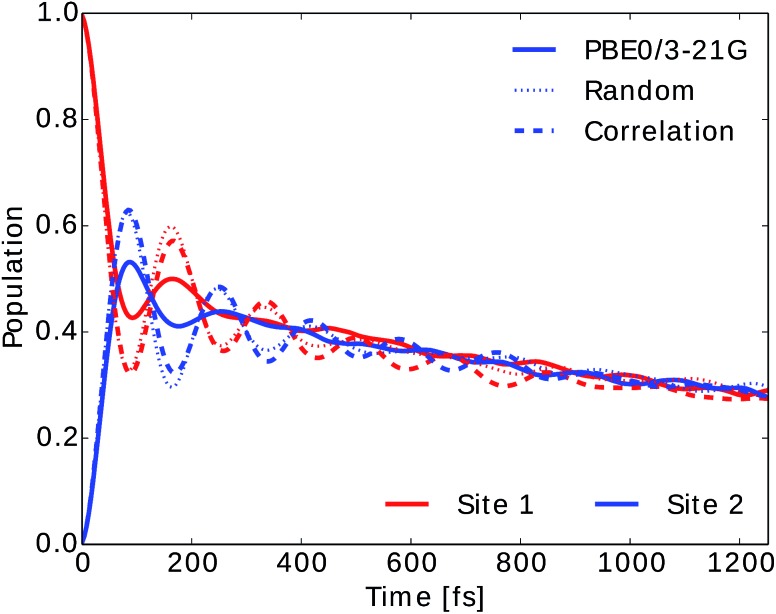
We also computed the population dynamics in the FMO complex monomer with a stochastic integration method.10 We averaged 4000 stochastic trajectories to obtain converged population dynamics. The initial excited site was chosen to be site 1 and the dynamics was propagated for all eight coupled sites at 300 K. The couplings of the Hamiltonian were taken from ref. 55 and 67. Results are shown in Fig. 6. We see that neural network predictions from neural networks trained on randomly drawn and correlation clustered Coulomb matrices predict the exciton dynamics in agreement with TDDFT calculations.

Fig. 6. Population dynamics of the FMO complex calculated at 300 K with initial state in site 1. Here only two site populations are shown but dynamics was carried out for the 8 BChls. Excited state energy trajectories were obtained from TDDFT calculations (PBE0/3-21G) as well as neural networks trained on randomly drawn and correlation clustered Coulomb matrices.

Fig. 6

Open in a new tab

We also employed the Markovian Redfield method to compute the exciton dynamics in the FMO complex (see Section 2.3).66 In this case there is an explicit dependence of the exciton dynamics on the spectral density. The energies in the Hamiltonian were taken to be the averages from the TDDFT or neural network predicted excited state energy trajectories. The same couplings as for the stochastic integration method were used.

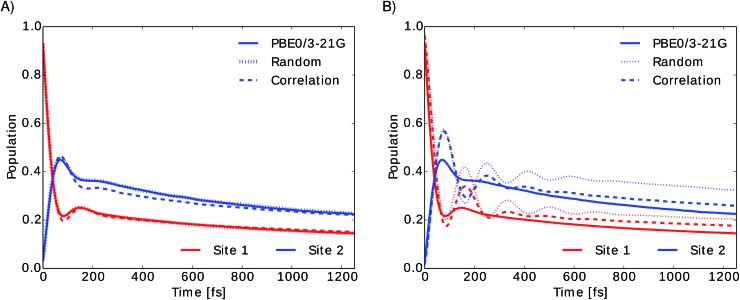
To investigate the importance of excited state energies and spectral densities on the Redfield exciton dynamics we calculated the exciton dynamics in two different ways. First, we computed the exciton dynamics with neural network predicted excited state energies and the average spectral density obtained from TDDFT calculations and then we used the neural network predicted energies as well as the neural network predicted spectral densities. Results are presented in Fig. 7 panel A, for predicted excited state energies and TDDFT spectral densities and panel B, for excited state energies and spectral densities predicted by neural networks. We initialized the dynamics with the excitation in BChl 1 and propagated the dynamics for all eight coupled sites at 300 K.

Fig. 7. Time evolution of the exciton population for BChl 1 (red) and BChl 2 (blue) in the FMO complex calculated from excited state energy trajectories and average spectral densities using the Redfield method. The initial state is site 1 excited. Panel (A) shows the exciton dynamics for neural network predicted excited state energies using the same TDDFT calculated average spectral density in all cases. Panel (B) shows the exciton dynamics with both, excited state energy trajectories and harmonic average spectral densities predicted by neural networks trained with the indicated selection method.

Fig. 7

Open in a new tab

In panel A we see that given a constant spectral density the error on energies is small and does not strongly influence the exciton dynamics. The main role is played by the spectral density as can be seen in panel B. Here we see much larger differences depending on the neural network sampling method and we notice that the prediction of neural networks trained on correlation clustered Coulomb matrices agrees better with the TDDFT exciton dynamics. Deviations of neural network predicted exciton dynamics from TDDFT calculated exciton dynamics are listed in detail in the ESI (see Section S.1.5†). Further methods should be investigated to improve the prediction of the spectral density, the error on the energy should be reduced further by an order of magnitude to predict spectral densities with the optimal reorganization energy.

4. Conclusion

The computational study presented in this article showed that multi-layer perceptrons (neural networks) can be used to successfully predict excited state energies of BChls in the FMO complex. Using different methods to select a training data set for neural network training from features in the classical MD trajectory alone we were able to generate neural networks which can predict TDDFT excited state energies with high accuracy (0.01 eV).

Furthermore, the neural networks can predict properties such as QM/MM derived spectral densities or exciton population dynamics. The prediction of excited state energies using the neural networks is about seven orders of magnitude faster than TDDFT. If we include training feature generations we still observe a speed-up of about four orders of magnitude. Even if neural networks need to be trained first, excited state energies are obtained in less than half the time needed for TDDFT. Based on the observations we made on the FMO complex we recommend the following procedure to apply machine learning to predict excited state properties of other systems:

(1) Represent all molecules of interest and their chemical environment with Coulomb matrices.

(2) Obtain optimal neural network architectures from hyperparameter grid searches. In particular, it is important identify the most representative molecule in terms of the space which contains the features used for neural network predictions.

(3) Determine an optimal training set. Training sets for neural networks with optimal network architecture can be generated by selecting Coulomb matrices based on properties which are related to the desired quantum mechanical properties. We observed that selecting Coulomb matrices which represent Coulomb matrix space clusters improves excited state energy predictions. However, these do not necessarily work well for dynamics. Investigate on the role of higher sampling of the tails of the energy distribution when selecting the training set.

(4) Make predictions. To predict spectral densities and exciton dynamics with high accuracy, Coulomb matrices should be selected for the training set if they reveal high excited state energy correlations. We found that nitrogen RMSD correlations in the BChls are a good indicator for excited state energy correlations. Thus, we selected Coulomb matrices based on high nitrogen RMSD correlations. Of course this might be complicated for some molecules with very delocalized excited states.

In conclusion, this approach provides a gigantic speedup to ground state QM/MM. From a neural network trained on a single BChl molecule, we can predict the excited states of 23 other molecules in the system at very low additional computational costs. This will be particularly useful to speed up or simply to enable the simulation of larger, more complex and challenging light-harvesting systems. Further, it will be helpful to study, for instance, the role of small changes in the environment on the exciton dynamics. Future questions we would like to address include the possibility of extending the prediction to other temperatures using for example multi-target machine learning.

Supplementary Material

Click here for additional data file. (1.1MB, pdf)

Acknowledgments

S. V. and A. A.-G. acknowledge support from the Center for Excitonics and Energy Frontier Research Center funded by the U.S. Department of Energy under award DE-SC0001088. Computations were run on the Harvard University's Odyssey cluster, supported by the Research Computing Group of the FAS Division of Science.

Footnotes

†Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sc04786b

References

  1. Adolphs J., Renger T. Biophys. J. 2006;91:2778–2797. doi: 10.1529/biophysj.105.079483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ishizaki A., Fleming G. R. Proc. Natl. Acad. Sci. U. S. A. 2009;106:17255–17260. doi: 10.1073/pnas.0908989106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Kreisbeck C., Kramer T., Rodriguez M., Hein B. J. Chem. Theory Comput. 2011;7:2166–2174. doi: 10.1021/ct200126d. [DOI] [PubMed] [Google Scholar]
  4. Sarovar M., Fleming G. R., Wahley K. B. Nat. Phys. 2010;6:462–467. [Google Scholar]
  5. Moix J., Wu J., Huo P., Coker D., Cao J. J. Phys. Chem. Lett. 2011;2:3045–3052. [Google Scholar]
  6. Mohseni M., Rebentrost P., Lloyd S., Aspuru-Guzik A. J. Chem. Phys. 2008;129:174106. doi: 10.1063/1.3002335. [DOI] [PubMed] [Google Scholar]
  7. Plenio M. B., Huelga S. F. New J. Phys. 2008;10:113019. [Google Scholar]
  8. Krueger B. P., Scholes G. D., Fleming G. R. J. Phys. Chem. B. 1998;102:5378–5386. [Google Scholar]
  9. Olbrich C., Kleinekathöfer U. J. Phys. Chem. B. 2010;114:12427–12437. doi: 10.1021/jp106542v. [DOI] [PubMed] [Google Scholar]
  10. Shim S., Rebentrost P., Valleau S., Aspuru-Guzik A. Biophys. J. 2012;102:649–660. doi: 10.1016/j.bpj.2011.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Scholes G. D., Curutchet C., Mennucci B., Cammi R., Tomasi J. J. Phys. Chem. B. 2007;111:6978–6982. doi: 10.1021/jp072540p. [DOI] [PubMed] [Google Scholar]
  12. Huo P., Coker D. F. J. Chem. Phys. 2010;133:184108. doi: 10.1063/1.3498901. [DOI] [PubMed] [Google Scholar]
  13. Cao J., Silbey R. J. J. Phys. Chem. A. 2009;113:13825–13838. doi: 10.1021/jp9032589. [DOI] [PubMed] [Google Scholar]
  14. Wu J., Liu F., Shen Y., Cao J., Silbey R. J. New J. Phys. 2010;12:105012. [Google Scholar]
  15. Jang S., Newton M. D., Silbey R. J. J. Phys. Chem. B. 2007;111:6807–6814. doi: 10.1021/jp070111l. [DOI] [PubMed] [Google Scholar]
  16. Rebentrost P., Mohseni M., Kassal I., Lloyd S., Aspuru-Guzik A. New J. Phys. 2009;11:033003. [Google Scholar]
  17. Ishizaki A., Fleming G. R. J. Phys. Chem. B. 2011;115:6227–6233. doi: 10.1021/jp112406h. [DOI] [PubMed] [Google Scholar]
  18. Abramavicius D., Mukamel S. J. Chem. Phys. 2010;133:064510. doi: 10.1063/1.3458824. [DOI] [PubMed] [Google Scholar]
  19. Skochdopole N., Mazziotti D. A. J. Phys. Chem. Lett. 2011;2:2989–2993. [Google Scholar]
  20. Ritschel G., Roden J., Strunz W. T., Aspuru-Guzik A., Eisfeld A. J. Phys. Chem. Lett. 2011;2:2912–2917. [Google Scholar]
  21. Rebentrost P., Aspuru-Guzik A. J. Chem. Phys. 2011;134:101103. doi: 10.1063/1.3563617. [DOI] [PubMed] [Google Scholar]
  22. Singh N., Brumer P. Faraday Discuss. 2011;153:41–50. doi: 10.1039/c1fd00038a. [DOI] [PubMed] [Google Scholar]
  23. Singh N. and Brumer P., arXiv:1106.5911v1, 2011.
  24. Pachón L. A., Brumer P. Phys. Chem. Chem. Phys. 2012;14:10094–10108. doi: 10.1039/c2cp40815e. [DOI] [PubMed] [Google Scholar]
  25. Vlaming S. M., Silbey R. J. J. Chem. Phys. 2012;136:055102. doi: 10.1063/1.3682988. [DOI] [PubMed] [Google Scholar]
  26. Caruso F., Saikin S. K., Solano E., Huelga S., Aspuru-Guzik A., Plenio M. B. Phys. Rev. B: Condens. Matter Mater. Phys. 2012;85:125424. [Google Scholar]
  27. Mohseni M., Shabani A., Lloyd S. and Rabitz H., arXiv:1104.4812v1, 2011.
  28. Zhu J., Kais S., Rebentrost P., Aspuru-Guzik A. J. Phys. Chem. B. 2011;115:1531–1537. doi: 10.1021/jp109559p. [DOI] [PubMed] [Google Scholar]
  29. de Vega I. J. Phys. B: At., Mol. Opt. Phys. 2011;44:245501. [Google Scholar]
  30. Roden J., Eisfeld A., Wolff W., Strunz W. T. Phys. Rev. Lett. 2009;103:058301. doi: 10.1103/PhysRevLett.103.058301. [DOI] [PubMed] [Google Scholar]
  31. Valleau S., Eisfeld A., Aspuru-Guzik A. J. Chem. Phys. 2012;137:224103. doi: 10.1063/1.4769079. [DOI] [PubMed] [Google Scholar]
  32. Mercer I. P., Gould I. R., Klug D. R. J. Phys. Chem. B. 1999;103:7720–7727. [Google Scholar]
  33. Tao G., Miller W. H. J. Phys. Chem. Lett. 2010;1:891–894. [Google Scholar]
  34. Olbrich C., Jansen T. L. C., Liebers J., Aghtar M., Strümpfer J., Schulten K., Knoester J., Kleinekathöfer U. J. Phys. Chem. B. 2011;115:8609–8621. doi: 10.1021/jp202619a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Damjanović A., Kosztin I., Kleinekathöfer U., Schulten K. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2002;65:031919. doi: 10.1103/PhysRevE.65.031919. [DOI] [PubMed] [Google Scholar]
  36. Olbrich C., Strümpfer J., Schulten K., Kleinekathöfer U. J. Phys. Chem. Lett. 2011;2:1771–1776. doi: 10.1021/jz2007676. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Jurinovich S., Curutchet C., Mennucci B. ChemPhysChem. 2014;15:3194–3204. doi: 10.1002/cphc.201402244. [DOI] [PubMed] [Google Scholar]
  38. Shan Y., Klepeis J. L., Eastwood M. P., Dror R. O., Shaw D. E. J. Phys. Chem. 2005;122:054101. doi: 10.1063/1.1839571. [DOI] [PubMed] [Google Scholar]
  39. Rappoport D. and Hutter J., Excited-State Properties and Dynamics, in Fundamentals of Time-Dependent Density Functional Theory, Lecture Notes in Physics 837, Springer Berlin/Heidelberg, 2012, pp. 317–336. [Google Scholar]
  40. Behler J., Parrinello M. Phys. Rev. Lett. 2007;98:146401. doi: 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]
  41. Ramakrishnan R., Hartmann M., Tapavicza E., von Lilienfeld O. A. J. Chem. Phys. 2015;143:084111. doi: 10.1063/1.4928757. [DOI] [PubMed] [Google Scholar]
  42. Hansen K., Biegler F., Ramakrishnan R., Pronobis W., von Lilienfeld O. A., Müller K.-R., Tkatchenko A. J. Phys. Chem. Lett. 2015;6:2326–2331. doi: 10.1021/acs.jpclett.5b00831. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Rupp M., Tkatchenko A., Müller K.-R., von Lilienfeld O. A. Phys. Rev. Lett. 2012;108:058301. doi: 10.1103/PhysRevLett.108.058301. [DOI] [PubMed] [Google Scholar]
  44. Pyzer-Knapp E. O., Li K., Aspuru-Guzik A. Adv. Funct. Mater. 2015;25:6495–6502. [Google Scholar]
  45. Olivucci M., Density Functional Methods for Excited States: Equilibrium Structure and Electronic Spectra, in Computational Photochemistry, Elsevier, 2005, pp. 93–128. [Google Scholar]
  46. Phillips J. C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R. D., Kale L., Schulten K. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Cornell W. D., Cieplak P., Bayly C. I., Gould I. R., Merz K. M., Ferguson D. M., Spellmeyer D. C., Fox T., Caldwell J. W., Kollman P. A. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
  48. Ceccarelli M., Procacci P., Marchi M. J. Comput. Chem. 2003;24:129–142. doi: 10.1002/jcc.10198. [DOI] [PubMed] [Google Scholar]
  49. Tronrud D., Wen J., Gay L., Blankenship R. Photosynth. Res. 2009;100:79–87. doi: 10.1007/s11120-009-9430-6. [DOI] [PubMed] [Google Scholar]
  50. Jorgensen W. L., Madura J. D. J. Am. Chem. Soc. 1983:1407–1413. [Google Scholar]
  51. Olbrich C., Strümpfer J., Schulten K., Kleinekathöfer U. J. Phys. Chem. B. 2011;115:758–764. doi: 10.1021/jp1099514. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Perdew J. P., Ernzerhof M., Burke K. J. Chem. Phys. 1996;105:9982–9985. [Google Scholar]
  53. Taylor J. C. Phys. Rev. 1954;95:1313–1317. [Google Scholar]
  54. Shao Y., Gan Z., Epifanovsky E., Gilbert A. T. B., Wormit M., Kussmann J., Lange A. W., Behn A., Deng J., Feng X., Ghosh D., Goldey M., Horn P. R., Jacobson L. D., Kaliman I., Khaliullin R. Z., Kús T., Landau A., Liu J., Proynov E. I., Rhee Y. M., Richard R. M., Rohrdanz M. A., Steele R. P., Sundstrom E. J., Woodcock III H. L., Zimmerman P. M., Zuev D., Albrecht B., Alguire E., Austin B., Beran G. J. O., Bernard Y. A., Berquist E., Brandhorst K., Bravaya K. B., Brown S. T., Casanova D., Chang C.-M., Chen Y., Chien S. H., Closser K. D., Crittenden D. L., Diedenhofen M., DiStasio Jr R. A., Dop H., Dutoi A. D., Edgar R. G., Fatehi S., Fusti-Molnar L., Ghysels A., Golubeva-Zadorozhnaya A., Gomes J., Hanson-Heine M. W. D., Harbach P. H. P., Hauser A. W., Hohenstein E. G., Holden Z. C., Jagau T.-C., Ji H., Kaduk B., Khistyaev K., Kim J., Kim J., King R. A., Klunzinger P., Kosenkov D., Kowalczyk T., Krauter C. M., Lao K. U., Laurent A., Lawler K. V., Levchenko S. V., Lin C. Y., Liu F., Livshits E., Lochan R. C., Luenser A., Manohar P., Manzer S. F., Mao S.-P., Mardirossian N., Marenich A. V., Maurer S. A., Mayhall N. J., Oana C. M., Olivares-Amaya R., O'Neill D. P., Parkhill J. A., Perrine T. M., Peverati R., Pieniazek P. A., Prociuk A., Rehn D. R., Rosta E., Russ N. J., Sergueev N., Sharada S. M., Sharmaa S., Small D. W., Sodt A., Stein T., Stück D., Su Y.-C., Thom A. J. W., Tsuchimochi T., Vogt L., Vydrov O., Wang T., Watson M. A., Wenzel J., White A., Williams C. F., Vanovschi V., Yeganeh S., Yost S. R., You Z.-Q., Zhang I. Y., Zhang X., Zhou Y., Brooks B. R., Chan G. K. L., Chipman D. M., Cramer C. J., Goddard III W. A., Gordon M. S., Hehre W. J., Klamt A., Schaefer III H. F., Schmidt M. W., Sherrill C. D., Truhlar D. G., Warshel A., Xua X., Aspuru-Guzik A., Baer R., Bell A. T., Besley N.N. A.A., Chai J.-D., Dreuw A., Dunietz B. D., Furlani T. R., Gwaltney S. R., Hsu C.-P., Jung Y., Kong J., Lambrecht D. S., Liang W., Ochsenfeld C., Rassolov V. A., Slipchenko L. V., Subotnik J. E., Van Voorhis T., Herbert J. M., Krylov A. I., Gill P. M. W., Head-Gordon M. Mol. Phys. 2015;113:184–215. [Google Scholar]
  55. Chandrasekaran S., Aghtar M., Valleau S., Aspuru-Guzik A., Kleinekathöfer U. J. Phys. Chem. B. 2015;119:9995–10004. doi: 10.1021/acs.jpcb.5b03654. [DOI] [PubMed] [Google Scholar]
  56. Häse F., Valleau S., Pyzer-Knapp E. and Aspuru-Guzik A., Machine learning for exciton dynamics: Qy trajectories, figshare, 2015. [DOI] [PMC free article] [PubMed]
  57. Rumelhart D. E., Hinton G. E. and Williams R. J., Learning Internal Representations by Error Propagation, Parallel Distributed Processing: Explorations in the Microstructure of Cognition, MIT Press, Cambridge, MA, USA, 1986, pp. 318–362. [Google Scholar]
  58. Montavon G., Rupp M., Gobre V., Vazquez-Mayagoitia A., Hansen K., Tkatchenko A., Müller K.-R., von Lilienfeld A. New J. Phys. 2013;15:095003. [Google Scholar]
  59. Heaton J. J. Mach. Learn. Res. 2015;16:1243–1247. [Google Scholar]
  60. von Lilienfeld O. A., Ramakrishnan R., Rupp M., Knoll A. Int. J. Quantum Chem. 2015;115:1084–1093. [Google Scholar]
  61. List N. H., Curutchet C., Knecht S., Mennucci B., Kongsted J. J. Chem. Theory Comput. 2013;9:4928–4938. doi: 10.1021/ct400560m. [DOI] [PubMed] [Google Scholar]
  62. Riedmiller M. Comput. Stand. Interfac. 1994;16:265–278. [Google Scholar]
  63. Prechelt L. Neural Network. 1998;11:761–767. doi: 10.1016/s0893-6080(98)00010-0. [DOI] [PubMed] [Google Scholar]
  64. Frenkel D. and Smit B., Free Energies and Phase Equilibria, in Understanding Molecular Simulation, Academic Press, 2002, pp. 165–199. [Google Scholar]
  65. Daura X., Gademann K., Jaun B., Seebach D., van Gunsteren W. F., Mark A. E. Angew. Chem., Int. Ed. 1999;111:249–253. [Google Scholar]
  66. Breuer H.-P. and Petruccione F., The Theory of Open Quantum Systems, Oxford University Press, New York, 2002. [Google Scholar]
  67. Aghtar M., Strümpfer J., Olbrich C., Schulten K., Kleinekathöfer U. J. Phys. Chem. B. 2013;117:7157–7163. doi: 10.1021/jp311380k. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (1.1MB, pdf)

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES